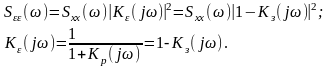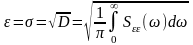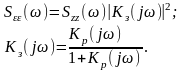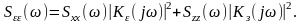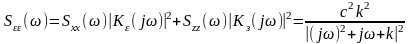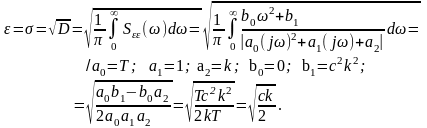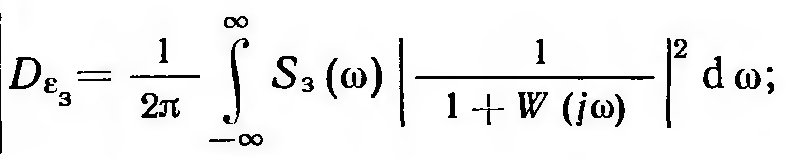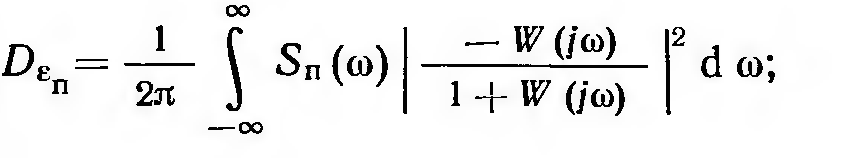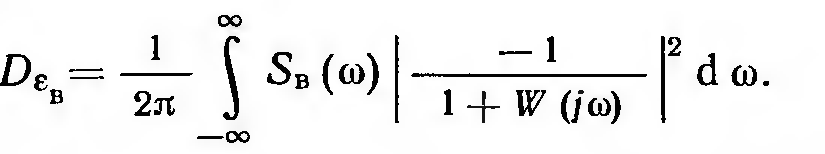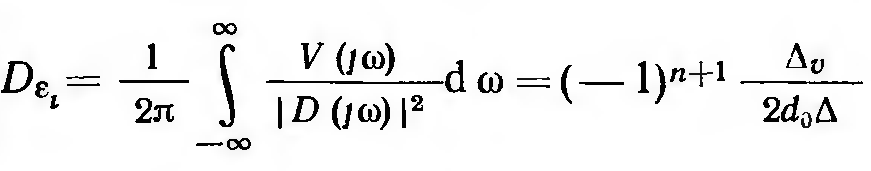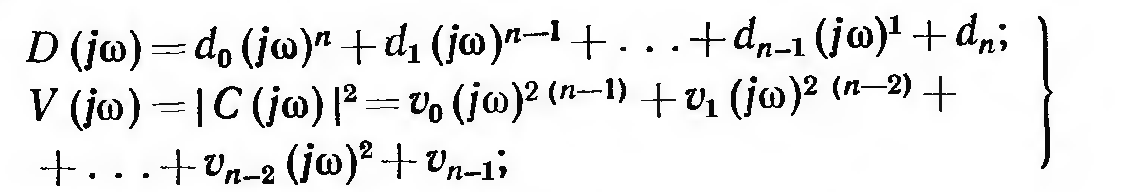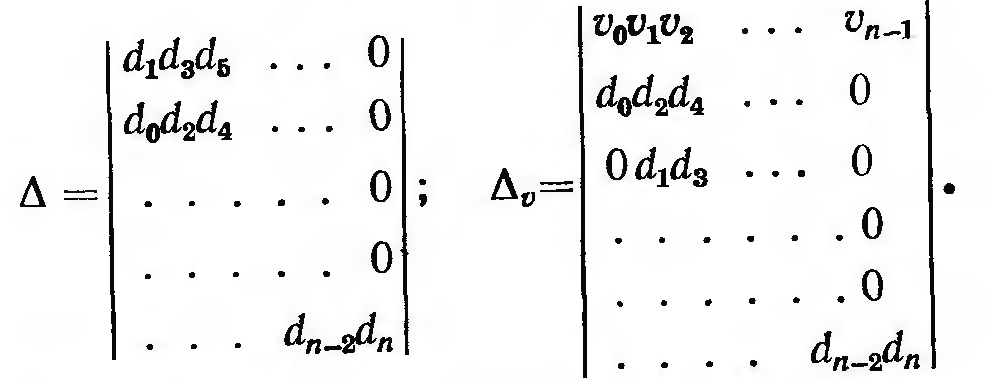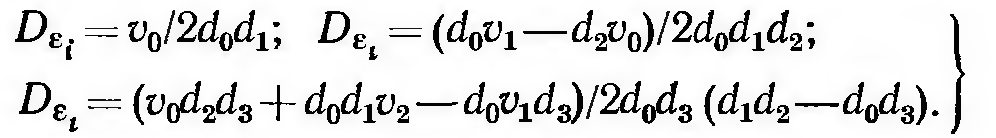Расчет ошибок с сау при случайных воздействиях
Рассмотрим
порядок расчета ошибок в системах
управления при случайных воздействиях.
Пусть задана система, приведенная на
рис.11.3.3
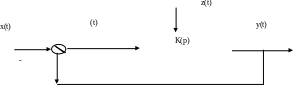
Рис.11.3.3
Необходимо
определить величину средней квадратичной
ошибки -
если заданы Sxx()
и Szz().
Рассмотрим
несколько случаев.
Пусть
действует только полезный сигнал x(t) а
помеха z(t) отсутствует.
Спектральная
плотность ошибки определяется
соотношением:
(11.3.8)
Величина
средней квадратичной ошибки -
определяется по формуле:
.
(11.3.9)
Значения
интеграла от спектральной плотности
табулированы и могут быть вычислены
через коэффициенты полиномов выражения
для спектральной плотности.
Пусть
действует только помеха z(t) а полезный
сигнал x(t) отсутствует.
Действие
помехи рассматривается на выходе
системы.
Спектральная
плотность ошибки при этом определяется
соотношением:
(11.3.10)
3.
Пусть действует и полезный сигнал x(t)
и помеха z(t) и они не коррелированны.
Суммарная
спектральная плотность ошибки при этом
определяется соотношением:
(11.3.11)
Пример
11.3.2. Для приведенной ниже системы
(рис.11.3.4), определить величину средней
квадратичной ошибки -,
если заданы Sxx()
= c2 и Szz()
= 0.
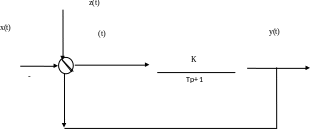
Рис.
11.3.4
Если
сигнал и помеха некоррелированны, то
суммарная спектральная плотность
ошибки при этом определяется
соотношением:
.
Значения
интеграла от спектральной плотности
вычислим через коэффициенты полиномов
выражения для спектральной плотности.
Величина
средней квадратичной ошибки -
определяется по формуле:
.
Пример
11.3.3. Для системы приведенной на рис.3
определить спектральную плотность
ошибки, вызванную действием помехи
-z(t) со спектральной плотностью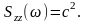

Р
y
ис. 11.3.5
Решение:
Спектральная плотность ошибки
определяется из соотношений: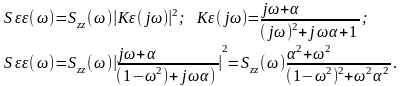
Вычисление и минимизация дисперсии сигнала ошибки замкнутой системы
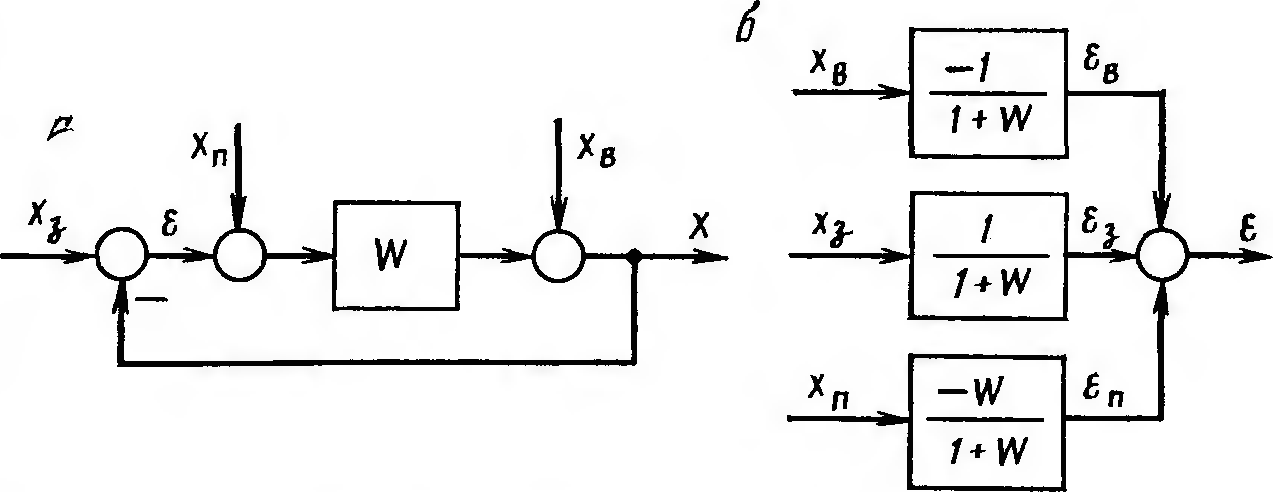
Обобщенная
алгоритмическая схема которой показана
на рис. 11.3.5,
а.
Будем
считать, что передаточная функция W
(р), равная произведению передаточных
функций объекта и управляющего
устройства, известна. Не заданы могут
быть лишь некоторые параметры управляющего
устройства.
На
систему действуют случайные возмущения
хп
и
хв
с известными спектральными плотностями
и
.
Задающее воздействие
также является случайным сигналом со
спектральной плотностью
.Пусть
все три воздействия — центрированные
сигналы. Тогда и сигнал ошибки
будет центрированным.
Если
указанные внешние воздействия не
коррелированы между собой, то сигнал
ошибки
,
возникающий в системе, может рассматриваться
как сумма трех независимых составляющих
(рис. 11.3.5,
б):
(11.3.12)
Составляющая
обусловлена неточным воспроизведением
задающего воздействия, а составляющие
и
— неполным подавлением возмущений хп
и хв.
Соответственно
и дисперсия сигнала ошибки может быть
представлена в виде суммы трех дисперсий:
(11.3.13)
Каждая
из этих дисперсий может быть вычислена
по формуле (11.2.17)
независимо друг от друга:
Рис.
11.3.5
(11.3.14)
(11.3.15)
(11.3.16)
Если
внешние воздействия коррелированы
между собой, то и составляющие (11.3.12)
сигнала ошибки будут коррелированы,
поэтому полную дисперсию
можно вычислить только путем интегрирования
общей спектральной плотности
,
найденной с учетом свойства (11.1.30).
При
подстановке в формулы (11.2.28) — (11.2.30)
конкретных функций
и
получаются
довольно сложные выражения, интегрирование
которых обычными методами затруднительно.
Поэтому используют методику для
вычисления квадратичных интегральных
оценок. В соответствии с этой методикой
каждую из трех дисперсий определяют
по формуле:
(11.3.17)
где
полиномы
,
и определители
и
составляются по формулам
и
.
В
простейших случаях, когда наибольшая
степень полинома
,
формула (11.3.17)
будет иметь вид:
(11.3.18)
В
полином
в виде сомножителя входит характеристическая
функция
замкнутой
системы. Поэтому при приближении системы
к границе устойчивости [при
]
интеграл (11.3.17)
резко возрастает.
Для
систем с запаздыванием подынтегральное
выражение нельзя привести к виду
(11.3.17)
и дисперсию можно вычислить только
приближенно, заменяя запаздывание
дробно-рациональной
функцией.
С
помощью формул (11.3.13)
— (11.3.18)
можно получить аналитическое выражение,
связывающее полную дисперсию сигнала
ошибки
с параметрами внешних воздействий и с
параметрами системы (например,
):
.
(11.3.19)
Минимизируя
функцию (11.3.19)
по параметрам
и
можно
определить их оптимальные значения.
Покажем,
что минимум функции (11.3.19),
как правило, существует. Пусть на систему
действуют задающее воздействие
и помеха хп.
Как правило, спектр задающего воздействия
находится в области низких частот (рис.
11.3.6,
а),
а спектр помехи равномерен
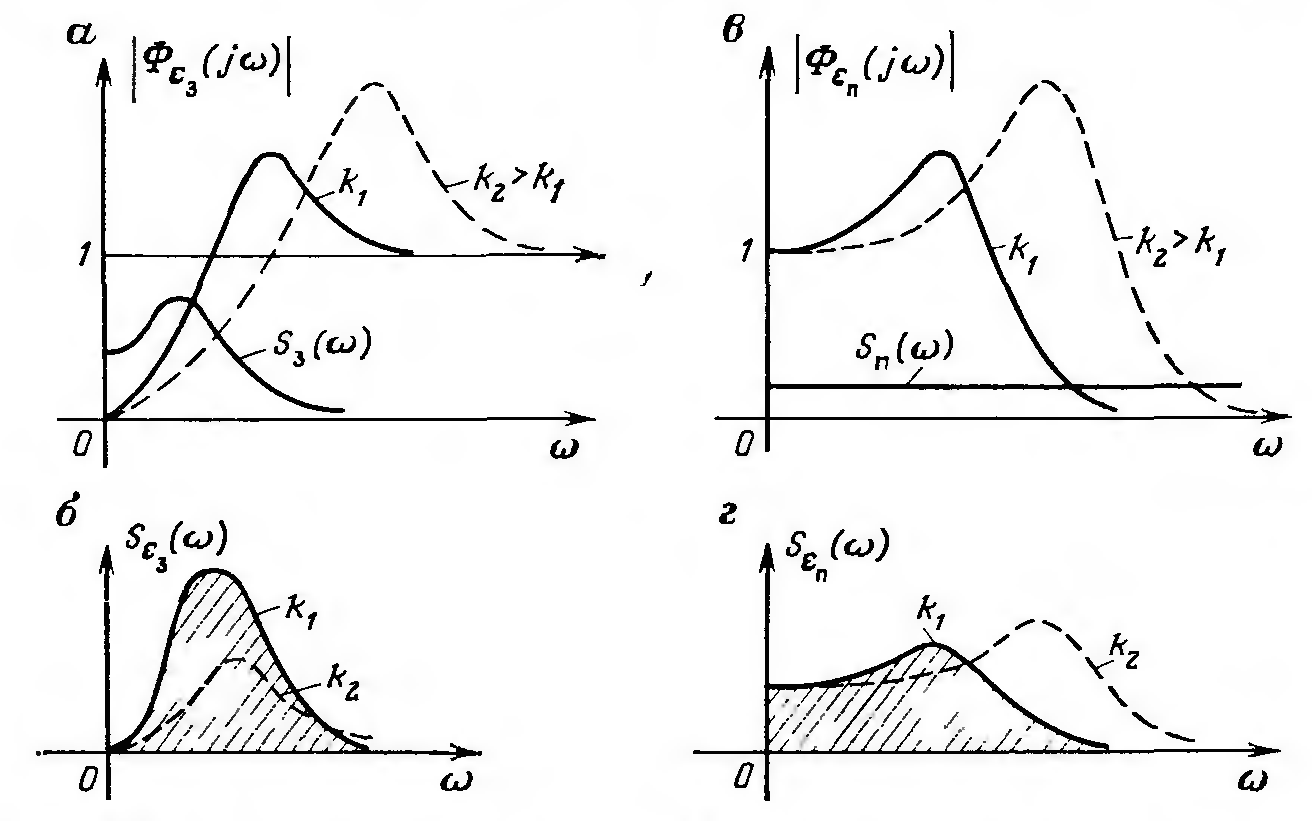
Рис
11.3.6
Влияние
передаточного коэффициента разомкнутого
контура на спектральную плотность
сигнала ошибки
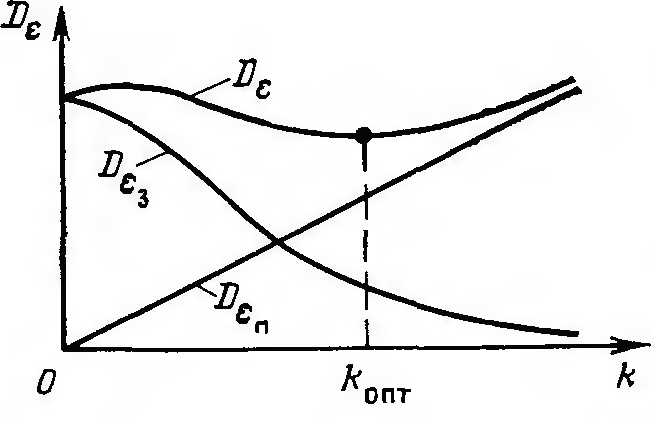
Рис.
11.3.7.
График зависимости дисперсии сигнала
ошибки от передаточного коэффициента
разомкнутого контура
в
широкой полосе частот (рис. 11.3.6,
в).
С увеличением передаточного коэффициента
k
разомкнутого контура а. ч. х.
и
по
каналам
и
смещаются
в область более высоких частот, а
резонансный пик становится выше (см.
рис. 11.3.6,
а, в,
пунктирные кривые).
Так
как спектральные плотности равны
произведениям
и
на соответствующие а. ч. х. замкнутой
системы, то при увеличении k
ординаты функции
уменьшаются (рис. 11.3.6,
б), а ординаты функции
увеличиваются (рис. 11.3.6,
г).
Соответственно меняются и составляющие
полной дисперсии:
уменьшается при увеличении k,
a
—
увеличивается (рис. 11.3.7).
Очевидно, что суммарная дисперсия
при
некотором значении
k = koпm
будет иметь минимум.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Макеты страниц
на него возмущающим воздействием (флюктуациями, вызываемыми непрерывным изменением коэффициента и центра отражения цели). Для решения поставленной задачи составим уравнение системы

где 

Из выражения (7.16) видно, что значение управляемой величины получается в результате сложения реакций системы 



Подставив значение 

откуда уравнение системы для ошибки

или

где 


В случае, когда 

Подставив полученное значение 

или

где

дисперсия составляющей ошибки, вызываемой задающим воздействием 

дисперсия составляющей ошибки, вызываемой помехой 

Рис. 7.6. Структурная схема системы, в которой задающее а 

Если 


где 

Случай 2. Задающее и возмущающее воздействия приложены в различных точках системы (рис. 7.6). Уравнения элементов системы:

Найдя из первого уравнения 

или

где 
Перепишем последнее выражение в виде

где 

В соответствии с формулой (7.7) спектральная плотность ошибки для случая некоррелированных 

Подставив значения 

где 


Рис. 7.7. К примеру определения среднеквадратической ошибки: а — спектральная плотность помехи; б — амплитудно-частотная характеристика системы по помехе.


Среднеквадратическое значение ошибки системы

Пример 1. Определить СКО системы, вызванной помехой. Помеха представляет собой «белый шум», спектральная плотность которого постоянна и равна 

Спектральная плотность помехи на выходе системы, или спектральная плотность ошибки, вызванной помехой:

Среднее значение квадрата ошибки

Среднеквадратическое значение ошибки


В приведенном примере рассмотрена система с весьма простой передаточной функцией и найдена ошибка только от помехи. Вычисление среднеквадратической ошибки реальных систем является более сложной задачей.
Предмет:
«Теория автоматического управления статических систем»
Тема:
«Анализ качества САУ при случайных воздействиях и их оптимизация»
Анализ качества САУ при случайных воздействиях
Так как устойчивость линейных систем является свойством системы и не зависит от характера воздействия, то устойчивость при случайных воздействиях определяется также, как и для детерминированных.
Качество систем при детерминированных воздействиях оценивается с помощью показателей качества, таких как tp, , T и т.д. При случайных воздействиях они теряют смысл, так как входные и выходные величины являются случайными функциями времени и при исследовании рассматривают не сами процессы, а их статистические свойства, т.е. определяют не мгновенные значения процессов, а их средние значения.
При случайных воздействиях ошибка системы (t) = x(t)-y(t) также является случайной величиной, при этом используют ее усредненное значение – среднюю квадратичную ошибку
(1)
Эта ошибка используется для оценки точности или качества систем при случайных воздействиях.
Недостатки средней квадратичной ошибки:
1.Она обеспечивает минимум не мгновенного, а среднего значения, при этом мгновенное значение может быть недопустимо большим.
2. Она недооценивает малые ошибки и придает чрезмерное значение большим ошибкам, так как ее значение возводится в квадрат.
Расчет ошибок с САУ при случайных воздействиях
Рассмотрим порядок расчета ошибок в системах управления при случайных воздействиях. Пусть задана система, приведенная на рис.1.
Рис.1
Необходимо определить величину средней квадратичной ошибки — если заданы Sxx() и Szz().
Рассмотрим несколько случаев.
Пусть действует только полезный сигнал x(t) а помеха z(t) отсутствует.
Спектральная плотность ошибки определяется соотношением:
(2)
Величина средней квадратичной ошибки — определяется по формуле:
. (3)
Значения интеграла от спектральной плотности табулированы и могут быть вычислены через коэффициенты полиномов выражения для спектральной плотности.
Пусть действует только помеха z(t) а полезный сигнал x(t) отсутствует.
Действие помехи рассматривается на выходе системы.
Спектральная плотность ошибки при этом определяется соотношением:
(4)
3. Пусть действует и полезный сигнал x(t) и помеха z(t) и они не коррелированны.
Суммарная спектральная плотность ошибки при этом определяется соотношением:
(5)
П
ример 1. Для приведенной ниже системы (рис.2), определить величину средней квадратичной ошибки -, если заданы Sxx() = c2 и Szz() = 0.
Рис. 2
Если сигнал и помеха некоррелированны, то суммарная спектральная плотность ошибки при этом определяется соотношением:
.
Значения интеграла от спектральной плотности вычислим через коэффициенты полиномов выражения для спектральной плотности.
Величина средней квадратичной ошибки — определяется по формуле:
.
П
ример 2. Для системы приведенной на рис.3 определить спектральную плотность ошибки, вызванную действием помехи -z(t) со спектральной плотностью
y
Рис. 3
Решение: Спектральная плотность ошибки определяется из соотношений:
Статистическая оптимизация систем управления
При статистических исследованиях систем решаются задачи оптимизации, т.е. определение систем наилучших в определенном смысле (по точности, быстродействию, надежности и т.д.).
Оптимальной системой называют систему, обеспечивающую экстремум некоторого функционала, называемого критерием оптимальности.
При статистической оптимизации систем решаются следующие задачи:
Задача анализа.
Задача синтеза.
Задача анализа
Формулировка задачи
Дано: система с заданной структурой; статистические характеристики полезного сигнала x(t) и помехи z(t).
О
пределить: параметры системы, обеспечивающие минимальную величину средней квадратичной ошибки.
Рис.4
Схему исследуемой системы можно представить в виде, показанном на рис.1. При этом Ки(р) – передаточная функция идеальной системы, которая определяет закон преобразования полезного сигнала.
В системах, находящихся под действием случайного (или регулярного) входного сигнала и помехи возникает задача отделения сигнала от помехи и подавления (фильтрации) помехи. Кроме фильтрации в зависимости от оператора Ки(р) задача фильтрации сочетается с задачами:
1. Ки(р) = const – это задача воспроизведения, т.е. отделения полезного сигнала от помехи. Эта задача чаще всего используется для следящих систем.
2. Ки(р) = L(p) –задача преобразования и фильтрации. При этом L(p)- оператор преобразования.
Алгоритм решения задачи
. (6)
Величина средней квадратичной ошибки определяется по формуле:
(7)
С
хему исследуемой системы можно представить в виде, показанном на рис.2.
Рис. 5
Изображение ошибки равно:
(7)
Спектральная плотность ошибки равна:
Если сигналы не коррелированны то
Для определения дисперсии выходного сигнала необходимо вычислить интеграл вида
(8)
где
Табулированные значения этих интегралов, вычисленные через коэффициенты полиномов A(j) и B(), приведены в литературе по системам управления.
В таблице 1 приведены табулированные значения интегралов для n 3.
Таблица 1
D1 2 3
|
|
|
b0 2a0 a1 |
|
|
a0b1 –b0a2 2a0a1a2 |
|
|
a0a3b1 – a2a3b0 –a0a1b2 2a0a3 (a0a3 –a1a2) |
Используя таблицу, получим зависимость
. (9)
Оптимальные значения параметров получим с помощью частных производных.
(10)
Решив систему уравнений, получим оптимальные значения параметров k0, T10, …, Tn0.
Если путем изменения варьируемых параметров системы не удается добиться требуемого качества, то необходимо решать задачу синтеза, т.е. менять структуру системы.
Литература
-
Егупов Н.Д., Пупков К.А., Баркин А.И. Методы классической и современной теории автоматического управления: В 5 тт: Т. 4: Теория оптимизации систем автоматического управления Изд-во: МГТУ им. Н.Э. Баумана, 2004.
-
Зотов М.Г. Многокритериальное конструирование систем автоматического управления Издательство: БИНОМ. Лаборатория знаний, 2004. – 375с.
-
Меркин Д.Р. Введение в теорию устойчивости движения, 198
-
Светлицкий В.А., Стасенко И.В. Сборник задач по теории колебаний, 1973
-
Теория автоматического управления. Учеб. для вузов по спец. «Автоматика и телемеханика». В 2-х ч./ Н.А. Бабаков, А.А. Воронов и др.: Под ред. А.А. Воронова. — 2-е изд., перераб. и доп. — М.: Высш. шк., 198 — 367с., ил.