Показатели,
характеризующие форму распределения.
Понятие
нормального распределения
Что
такое статистическое распределение
данных.
Статистическим
распределением данных
называют
перечень вариантов и соответствующих
им частот или относительных частот.
Основная
задача анализа вариационных рядов –
это выявление подлинной закономерности
распределения.
Первое
представление о характере распределения
данных в изучаемой совокупности можно
получить при построении гистограммы
или полигона частот.
Если
увеличить объем совокупности и уменьшить
интервал группировки, изобразить эти
данные графически, по полигон (гистограмма)
распределения все более будут приближаться
к некоторой плавной линии, носящей
название кривой распределения (красная
линия на рисунке).
Различают
следующие разновидности кривых
распределения:
-
одновершинные
кривые:-
симметричные,
-
умеренно
асимметричные -
крайне
асимметричные;
-
-
многовершинные
кривые.
Для
однородных совокупностей, как правило,
характерны одновершинные распределения.
Многовершинность свидетельствует о
неоднородности изучаемой совокупности.
Появление двух и более вершин делает
необходимой перегруппировку данных с
целью выделения более однородных групп.
Если
Ваше распределение получится похожим
на симметричный холм, то оно называется
нормальным распределением. Нормальным
такое распределение называется потому,
что оно очень часто встречалось в
естественнонаучных исследованиях и
казалось «нормой» всякого массового
случайного проявления признаков.
Нормальное распределение часто
встречается в природе и в общественных
явлениях. Доказано, что нормальное
распределение получается в результате
воздействия многих независящих друг
от друга факторов. Несмотря на это не
все распределения, которые встречаются
в жизни, являются нормальными.
Свойства
нормального распределения
Как
уже неоднократно отмечалось, часто
пользуются типом распределения, которое
называется нормальным. Нормальное
распределение можно построить по
формуле.
Особенности
кривой нормального распределения:
-
кривая
симметрична и имеет максимум в точке,
соответствующей значению
(среднее значение признака) = Ме (медиана)
= Мо (мода); -
кривая
асимптотически приближается к оси
абсцисс, продолжаясь в обе стороны до
бесконечности (чем больше отдельные
значения X отклоняются от X , тем реже
они встречаются); -
коэффициенты
асимметрии и эксцесса для кривой
нормального распределения равны нулю; -
ПРАВИЛО
ТРЕХ СИГМ
-
68%
всех наблюдений лежат в диапазоне ±1
стандартное отклонение ()
от среднего значения (),
-
диапазон
±2 стандартных отклонения ()
от среднего значения ()
содержит 95% значений, -
а
диапазон ±3 стандартных отклонения
()
от среднего значения ()
содержит 99,7% значений.
Многие
методы исследования, которые будут
рассмотрены в дальнейшем, требуют
нормального распределения анализируемых
переменных.
Показатели,
характеризующие форму распределения
Форму
распределения хорошо видно на рисунке,
но для анализа нужны конкретные значения.
Кроме того, очень редко встречаются
абсолютно нормальные распределения,
преобладающее большинство распределений,
встречающихся при анализе природных и
общественных процессов, являются
чуть-чуть не нормальными. Поэтому для
выяснения
общего характера распределения необходимо
оценить его однородность
и вычислить показатели формы распределения
(показатель асимметрии и эксцесс).
Определение
симметричности распределения
(коэффициент
ассиметрии)
Для
симметричных распределений среднее
значение признака, мода и медиана равны
(на
рисунке А – симметричное распределение,
Б – ассиметричное распределение).
Кроме
симметричных распределений, различают
распределения с левосторонней и с
правосторонней ассиметрией.
А)
Симметричное распределение
(
= Ме = Мо);
Б)
Распределение с правосторонней
ассиметрией (
Ме > Мо);
в)
Распределение с левосторонней
ассиметрией (
Ме < Мо);
Для
оценки симметричности распределения
используют коэффициенты ассиметрии:
-
Моментный
коэффициент ассиметрии
С
помощью этого показателя измеряют не
только направление ассиметрии, но и
степень скошенности или ассиметричности
распределения.
– моментный
коэффициент ассиметрии
– центральный
момент третьего порядка
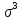
среднеквадратическое отклонение в кубе
(для
вариационного ряда)
(для
несгруппированных данных)
В
симметричных распределениях
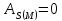
Если 
то асимметрия правосторонняя
и относительно максимальной ординаты
вытянута в сторону правая ветвь; если ,
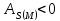
то асимметрия левосторонняя (на
графике это соответствует вытянутости
в сторону левой ветви).
Степень
существенности асимметрии можно оценить
с помощью средней квадратической ошибки
коэффициента асимметрии, которая зависит
от объема изучаемой совокупности и
рассчитывается по формуле:
где
n — число единиц совокупности.
Если
отношение
>3,
асимметрия считается существенной
и распределение нельзя считать нормальным;
если
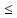
то асимметрия признается несущественной,
вызванной влиянием случайных обстоятельств,
а распределение
признается умеренно симметричным и
приближенным к нормальному распределению
Основной
недостаток моментного коэффициента
асимметрии заключается в том, что его
величина зависит от наличия в совокупности
резко выделяющихся единиц. Для таких
совокупностей этот коэффициент
малопригоден,
-
структурный
коэффициент ассиметрии Пирсона
или
Значение
коэффициентов Пирсона может быть
положительным или отрицательным.
Если
As>0,
то распределение с правосторонней
асимметрией,
Если
As<0
— с левосторонней ассиметрией.
Если
< 0.25, то ассиметрия считается
незначительной.
Если
0.25
< 0.5, то ассиметрия считается умеренной.
Если
0.5, то ассиметрия считается существенной.
Структурные
коэффициенты асимметрии характеризуют
ассиметричность только в центральной
части распределения, т. е. для основной
массы единиц, и в отличие от моментного
коэффициента не зависят от крайних
значений признака.
Эксцесс
(показатель, характеризующий «крутизну»
распределения)
Другим
свойством рядов распределения является
эксцесс (Ex).
Под
эксцессом понимают островершинность
или плосковершинность распределения
по сравнению с нормальным распределением
при той же силе вариации.
Другими
словами, эксцесс — это отклонение вершины
эмпирического распределения вверх или
вниз от вершины кривой нормального
распределения.
При
этом эксцесс определяется только для
симметричных и умеренно асимметричных
распределений.
Наиболее
точно эксцесс (Ex)
определяется по формуле с использованием
центрального момента четвертого
порядка:
(для
вариационного ряда)
(для
несгруппированных данных)
Для
нормальных распределений Ex=0.
Распределения более островершинные,
чем нормальные, обладают положительным
эксцессом (Ех > 0), более плосковершинные
— отрицательным (Ех < 0).
Положительный
эксцесс свидетельствует о том, что в
совокупности есть слабоварьирующее по
данному признаку «ядро», а в плосковершинных
распределениях такого «ядра» нет и
единицы рассеяны по всем значениям
признака более равномерно.
Чтобы
оценить существенность эксцесса
распределения, рассчитывают
среднеквадратическую ошибку эксцесса.
Среднеквадратическая
ошибка эксцесса (σEх)
рассчитывается по формуле:
где п –
число наблюдений
Если
отношение
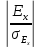
то отклонение от нормального можно
считать существенным и распределение
нельзя считать нормальным; если
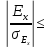
то отклонение признается несущественным,
а распределение
признается приближенным к нормальному
распределению.
Хотя
показатели асимметрии и эксцесса
характеризуют непосредственно лишь
форму распределения признака в пределах
изучаемой совокупности, но их определение
имеет не только описательное значение.
Часто асимметрия и эксцесс дают
определенные указания для дальнейшего
исследования социально-экономических
явлений. Так появление значительного
отрицательного эксцесса может указывать
на качественную неоднородность
исследуемой совокупности. Кроме того,
эти показатели позволяют сделать вывод
о возможности применения данного
эмпирического распределения к типу
кривых нормального распределения.
4
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
Федеральное
агентство по образованию
Государственное
образовательное учреждение
высшего
профессионально образования
«
Сибирский федеральный университет»
Статистика
Методические
указания
к
выполнению лабораторных работ
для
студентов направления 080100.62 Экономика
профиль
080100.62.08.09 Экономика предприятий и организаций
(металлургия)
профиль
080100.62.06.09 Экономика предприятий и организаций
(горная
промышленность)
Красноярск
2014
УДК 311 (07)
ББК 60.6я73
Статистика:
методические указания к выполнению лабораторных работ для студентов направления
080100.62 Экономика профиль 080100.62.08.09 Экономика предприятий и
организаций(металлургия), профиль 080100.62.06.09 Экономика предприятий и
организаций (горная промышленность)
Изложены порядок выполнения, структура, содержание и
требования к оформлению лабораторных работ по дисциплине «Статистика».
Для студентов направления 080100.62 Экономика профиль
080100.62.08.09 Экономика предприятий и организаций (металлургия), профиль
080100.62.06.09 Экономика предприятий и организаций (горная промышленность)
Институт
управления бизнес процессами
и экономики,2014
Учебно-методическое
издание
СТАТИСТИКА
Методические
указания
к
выполнению лабораторных работ
для
студентов направления 080100.62 Экономика
профиль
080100.62.08.09 Экономика предприятий и организаций
(металлургия)
профиль
080100.62.06.09 Экономика предприятий и организаций
(горная
промышленность)
Составители: Сатарова Вероника
Павловна, Майлова Татьяна Петровна, Евстигнеева Ольга Александровна
ОГЛАВЛЕНИЕ
Введение4
1Лабораторная работа №1
Сводка
и группировка статистической информации5
2Лабораторная работа №2
Средние величины.
Показатели вариации12
3Лабораторная работа №3
Анализ вариационных рядов18
4Лабораторная
работа №4
Виды дисперсий23
5 Лабораторная работа №5
Выборочное наблюдение29
6 Лабораторная работа №6
Анализ рядов динамики33
7 Лабораторная работа №7
Индексы количественных и
качественных показателей41
Библиографический список43
ВВЕДЕНИЕ
Лабораторный
практикум по дисциплине «Статистика» выполняется в соответствии с учебными
планами и является одной из профилирующих дисциплин в системе подготовки
студентов направления 080100.62 Экономика, профиль 080100.62.08.09 Экономика
предприятий и организаций
(металлургия),
профиль 080100.62.06.09 Экономика предприятий и организаций(горная
промышленность).
Статистика является одной из профилирующих дисциплин
в системе подготовки студентов вышеназванных специальностей.
Целью лабораторного практикума является приобретение
знаний и закрепление навыков построения статистических показателей, применения
основных методов статистического анализа социально-экономических явлений,
использования компьютерных программ при проведении статистических расчетов.
Выполнение лабораторной работы включает следующие
этапы:
• ознакомление
с теорией;
• выполнение
работы;
• формулировка
выводов;
• оформление
отчета по лабораторной работе в соответствии с требованиями стандарта;
• сдача
отчета и защита лабораторной работы преподавателю.
Лабораторная
работа 1
СВОДКА
И ГРУППИРОВКА СТАТИСТИЧЕСКОЙ ИНФОРМАЦИИ
Цель работы. Изучить
основные принципы проведения сводки и группировки статистических данных и
освоить их практическое применение с использованием стандартных функций MicrosoftExcel.
Краткие
теоретические сведения
Важнейшим этапом исследования социально-экономических
явлений
и
процессов является систематизация первичных данных и получение на этой основе
сводной характеристики объекта в целом при по мощи обобщающих показателей, что
достигается путем сводки и группировки первичного статистического материала.
Сводка — это комплекс
последовательных операций по обобщению конкретных единичных факторов,
образующих совокупность, для выявления типичных черт и закономерностей,
присущих изучаемому явлению в целом.
Группировкой называется
разбиение совокупности на группы, однородные по какому-либо признаку.
Группировка является важнейшим статистическим методом
обобщения статистических данных, основой для правильного исчисления статистических
показателей.
С помощью метода группировок решаются следующие
задачи:
·
выделение социально-экономических типов
явлений;
·
изучение структуры явления и структурных
сдвигов, происходящих в нем;
·
выявление связи и зависимости между
явлениями.
Все группировки могут быть построены по какому-то
одному (простая группировка) или нескольким существенным признакам (сложная
группировка). При построении сложной группировки сначала группы формируются по
одному признаку, затем эти группы делятся на подгруппы по другому признаку,
которые, в свою очередь, делятся на группы по третьему признаку и т.д. Сложные
группировки дают возможность изучить единицы совокупности одновременно по
нескольким признакам.
Построение группировки начинается с определения
состава группировочных признаков.
Группировочным признаком
называется признак, по которому проводится разбиение единиц совокупности на
отдельные группы. От правильного выбора группировочного признака зависят
выводы статистического исследования.
В основание группировки могут быть положены как количест—
венные, так и атрибутивные признаки. Первые имеют числовое выражение
(объем производства продукции, возраст человека, прибыль предприятия и т.д.),
а вторые отражают состояние единицы совокупности (пол человека, семейное
положение, отраслевую принадлежность предприятия, его форму собственности и
т.д.).
После того как определено основание группировки, следует решить
вопрос о количестве групп, на которые надо разбить исследуемую совокупность.
Число групп зависит от задач исследования и вида показателя, положенного
в основание группировки, численности совокупности, степени вариации признака.
Если группировка строится по атрибутивному признаку, то групп, как
правило, будет столько, сколько имеется градаций, видов состояний у этого
признака (например, группировка работников по образованию).
Если группировка проводится по количественному признаку, то
необходимо обратить особое внимание на число единиц исследуемого объекта и
степень колеблемости группировочного признака.
При небольшом объеме совокупности не следует образовывать большое
количество групп, так как группы будут включать недостаточное число единиц
объекта. Поэтому показатели, рассчитанные для таких групп, не будут
представительными и не позволят получить адекватную характеристику исследуемого
явления.
Часто группировка по количественному признаку имеет задачу
отразить распределение единиц совокупности по этому признаку. В этом случае
количество групп зависит в первую очередь от степени колеблемости
группировочного признака: чем она больше, тем больше групп следует образовать.
Чем больше групп, тем точнее будет воспроизведен характер исследуемого объекта.
Однако слишком большое число групп затрудняет выявление закономерностей при
исследовании социально- экономических явлений и процессов. Поэтому в каждом
конкретном случае при определении числа групп следует исходить не только из степени
колеблемости признака, но и из особенностей объекта и цели исследования.
Определение числа
групп с можно осуществить математическим путем, используя формулу
Стерджесса:
n = 1 + 3,322 • lgN,
(1)
где п — число
групп; N — число единиц
совокупности.
Недостаток формулы Стерджесса состоит в том, что ее применение
дает хорошие результаты, если совокупность состоит из большого числа единиц,
распределение единиц по признаку, положенному в основание группировки, близко
к нормальному и при этом в группах применяются равные интервалы.
Чтобы получить группы, адекватные действительности, необходимо
руководствоваться сущностью изучаемого явления.
Когда определенно
число групп, следует определить интервалы группировки.
Интервал — это значения
варьирующего признака, лежащие в определенных границах. Каждый интервал имеет
свою величину, верхнюю и нижнюю границы или хотя бы одну из них. Нижней
границей интервала называется наименьшее значение признака в интервале, а верхней
границей является наибольшее значение признака в нем. Величина интервала
представляет собой разность между верхней и нижней границами интервала.
Интервалы группировки в
зависимости от их величины бывают равные и неравные.
Если вариация признака
проявляется в сравнительно узких границах и распределение носит равномерный
характер, то строят группировку с равными интервалами.
Величина равного
интервала вычисляется по формуле
i =(Хmax— Xmin) /n, (2)
где хmах и xmin — максимальное и
минимальное значения признака в совокупности.
Прежде чем определять
максимальное и минимальное значения, из совокупности рекомендуется исключить
аномальные наблюдения.
Если максимальное и
минимальное значения сильно отличаются от смежных с ними значений вариантов в
упорядоченном ряду значений группировочного признака, то для определения
величины интервала следует использовать не максимальное и минимальное значения,
а значения, несколько превышающие минимум и несколько меньше, чем максимум.
Полученное значение
величины интервала необходимо округлить, как правило, в большую сторону.
Если размах вариации
признака совокупности велик и значения признака варьируются неравномерно, то
следует использовать группировку с неравными интервалами. Использование
неравных интервалов характерно для большинства социально-экономических явлений,
особенно при анализе макроэкономических показателей. |
Неравные интервалы могут
быть прогрессивно возрастающими или прогрессивно убывающими в арифметической
или геометрической прогрессии, а также произвольными и специализированными.
Использование прогрессивно-возрастающихи
прогрессивно-убывающих интервалов объясняется тем, что количественные
изменения размера признака имеют неодинаковые значения в низших и высших по
размеру признака группах.
Специализированные
интервалы используются для выделения из совокупности одних и тех же типов
по одному и тому же признаку для явлений, находящихся в различных условиях.
При
изучении социально-экономических явлений на макроуровне часто применяют
группировки, интервалы которых не будут ни прогрессивно-возрастающими, ни
прогрессивно-убывающими. Такие интервалы называются произвольными и, как
правило, используются при группировке предприятий, например, по уровню
рентабельности.
Интервалы
группировок могут быть закрытыми и открытыми. Закрытыми называются
интервалы, у которых имеются верхняя и нижняя границы. У открытых
интервалов указана только одна граница: верхняя — у первого, нижняя — у
последнего.
При
группировке единиц совокупности по количественному признаку границы интервалов
могут быть обозначены по-разному, в зависимости от того, непрерывный это
признак или прерывный.
Если
основанием группировки служит непрерывный признак, то одно и то же значение
признака выступает и верхней, и нижней границами двух смежных интервалов.
Таким образом, нижняя граница (i + 1)-го интервала
равна верхней границе i—ro интервала.
Если
в основании группировки лежит прерывный признак, то нижняя граница (i
+ 1)-го интервала равна верхней границе i—ro
интервала, увеличенной на 1.
После определения границ групп строится
ряд распределения.
Статистический
ряд распределения — это упорядоченное распределение единиц
совокупности на группы по определенному варьирующему признаку.
В
зависимости от признака, взятого за основу группировки, различают атрибутивные
и вариационные ряды распределения.
Атрибутивные
ряды распределения построены по качественным признакам
(распределение по полу, национальности, профессии и т.д.).
Вариационные
ряды распределения построены по количественному признаку.
Ряд распределения принято оформлять в виде
таблиц.
Любой
вариационный ряд состоит из двух элементов: вариантов и частот.
Вариантами
считаются отдельные значения признака, которые он принимает в вариационном
ряду, т.е. конкретное значение варьирующего значения признака.
Частоты
— это численности отдельных вариантов или каждой группы вариационного ряда,
т.е. это числа, показывающие как часто встречаются те или иные варианты в ряду
распределения. Сумма всех частот определяет численность всей совокупности, ее
объем.
Порядок выполнения работы*
1. Выбор группировочного признака.
2. Определение количества групп.
3. Расчет величины интервала группировки.
4.Установление границ групп.
5.Построение ряда распределения.
6.Выбор показателей для характеристики групп.
7.Расчет величины показателей по каждой группе.
8.Сведение данных группировки в таблицу.
Пример выполнения работы
Задание.
Произвести группировку предприятий региона по стоимости основных средств и
определить средний объем выпуска продукции в каждой группе. Исходные данные
для расчета приведены в табл. 1.
Таблица 1
Характеристика предприятий региона по стоимости
основных средств и объему выпуска продукции
|
Номер предприятия |
Стоимость |
Объем |
Номер предприятия |
Стоимость |
Объем млн |
|
1 |
5999 |
5349 |
16 |
6413 |
7079 |
|
2 |
6925 |
6882 |
17 |
9387 |
6339 |
|
3 |
6925 |
7046 |
18 |
3949 |
1544 |
|
4 |
10097 |
7248 |
19 |
10826 |
11431 |
|
5 |
8097 |
5256 |
20 |
6695 |
4105 |
|
6 |
11116 |
14090 |
21 |
6633 |
13366 |
|
7 |
5880 |
3525 |
22 |
6472 |
6340 |
|
8 |
7355 |
5431 |
23 |
6183 |
3624 |
|
9 |
9566 |
7680 |
24 |
8107 |
4917 |
|
10 |
7884 |
8226 |
25 |
9369 |
9040 |
|
11 |
7038 |
4081 |
26 |
11817 |
5359 |
|
12 |
4950 |
10473 |
27 |
4894 |
6266 |
|
13 |
4550 |
6097 |
28 |
8488 |
17093 |
|
14 |
3427 |
5307 |
29 |
7560 |
11641 |
|
15 |
6062 |
7400 |
30 |
6429 |
12328 |
В
соответствии с заданием группировочным признаком является стоимость основных
средств предприятия.
Количество групп n = 1 + 3,322 * Ig(30) = 6.
Следовательно, совокупность необходимо разбить на 6 групп.
Теперь определяется минимальное и максимальное
значения признака в совокупности, для этого используются стандартные функции MSExcel МАКС, МИН
(категория «Статистические»). Минимальное значение составляет 3427 млн руб.,
максимальное -118/7 млн руб.
Рассчитывается величина равного интервала группировки:
i = (11817 — 3427) / 6 = 1400 млн
руб.
Таким образом, величина интервала составляет 1400 млн
руб.
Определяются границы групп (табл. 2).
Таблица 2
Расчет границ групп и частот
|
Номер |
Нижняя |
Верхняя |
Количество |
|
1 |
3427 |
3427+1400=4827 |
3 |
|
2 |
4827 |
4827+1400=6227 |
6 |
|
3 |
6227 |
6227+1400=7627 |
10 |
|
4 |
7627 |
7627+1400=9027 |
4 |
|
5 |
9027 |
9027+1400=10427 |
4 |
|
6 |
10427 |
10427+1400=11827 |
3 |
Рассчитывается
количество предприятий (частота), вошедших в каждую группу с использованием
стандартной функции MicrosoftExcelЧАСТОТА
(категория «Статистические»).
Функция
ЧАСТОТА должна задаваться в качестве формулы массива. Для этого необходимо сделать
следующее:
1.Выделить диапазон ячеек, равный количеству
интервалов, начиная с ячейки, содержащей формулу.
2.Нажать клавишу F2.
3.Нажать одновременно клавиши CTRL
+ SHIFT
+ ENTER
Если формула не будет введена как формула массива, единственное
значение будет равно 1.
Результаты расчетов сводятся в табл. 3. В таблице
представлен вариационный ряд распределения промышленных предприятий региона по
стоимости основных средств.
Таблица 3
Группировка предприятий региона
по стоимости основных средств
|
Группы |
Количество |
Средняя |
Средний |
|
3427-4827 |
3 |
4127 |
4316 |
|
4827-6227 |
6 |
5527 |
6106 |
|
6227-7627 |
10 |
6927 |
7830 |
|
7627-9027 |
4 |
8327 |
8873 |
|
9027-10427 |
4 |
9727 |
7577 |
|
10427-11827 |
3 |
11127 |
10293 |
|
Итого |
30 |
7347 |
7485 |
Вариантами ряда распределения являются отдельные
значения стоимости основных средств промышленных предприятий региона, частотами
— количество предприятий, вошедших в каждую группу.
По каждой группе предприятий определяется средняя
стоимость основных средств предприятия и средний объем выпуска продукции.
Выводы:
В
ходе проведения сводки и группировки статистической информации разбили
совокупность, состоящую из 30 промышленных предприятий, на 6 групп.
В
качестве группировочного признака взяли показатель стоимости основных средств
предприятий. Данный признак является количественным. Получилась простая
группировка.
По
каждой группе предприятий рассчитали показатели — среднюю стоимость основных
средств предприятия и средний объем выпуска продукции.
Лабораторная
работа 2
СРЕДНИЕ ВЕЛИЧИНЫ.
ПОКАЗАТЕЛИ ВАРИАЦИИ
Цель работы. Изучить
основные принципы расчета средних величин и показателей вариации и по
несгруппированным и сгруппированным данным и освоить их практическое
применение с использованием стандартных функций Microsoft Excel.
Краткие теоретические сведения
Изучая зарегистрированные в процессе статистического
наблюдения величины того или иного признака у отдельных единиц совокупности,
можно обнаружить различия между ними. Поэтому, чтобы определить значение
признака, характерное для всей изучаемой совокупности единиц, используют
средние величины.
Средняя величина
представляет собой обобщенную количественную характеристику признака в
статистической совокупности в конкретных условиях места и времени. Показатель
в форме средней величины выражает типичные черты и дает обобщенную
характеристику однотипных явлений по одному из варьирующих признаков.
Средняя величина является наиболее распространенной
формой статистических показателей.
Средние величины делятся на два больших класса:
степенные средние и структурные средние.
Степенные средние в зависимости от представления исходных
данных могут быть простыми и взвешенными.
Простая
средняя рассчитывается по не сгруппированным
данным и имеет следующий общий вид:

где — величина осредняемого
признака у каждой единицы совокупности; n
— объем совокупности; z — показатель
степени средней.
Взвешенная
средняя вычисляется по сгруппированным данным и
имеет общий вид

где
fi—
частота или повторяемость индивидуальных значений признака
в совокупности.
Выбор вида средней определяется экономическим содержанием
показателя и исходных данных. В каждом конкретном случае применяется одна из
степенных средних.
Наиболее распространенным видом средних величин является
средняя арифметическая. Она применяется в тех случаях, когда объем варьирующего
признака для всей совокупности выражается суммой значений признаков отдельных
ее единиц.
Средняя арифметическая простая рассчитывается по формуле
,(5)
Средняя
арифметическая взвешенная -по формуле
.(6)
Кроме степенных средних в статистической практике
применяются структурные (или распределительные) средние. Они используются для
изучения внутреннего строения и структуры рядов распределения признака. К ним
относятся мода и медиана.
Модой называется наиболее
часто встречающийся вариант или то значение признака, которое соответствует
максимальной точке теоретической кривой распределения. В дискретном ряду мода
— это вариант с наибольшей частотой.
В интервальном вариационном ряду модой приближенно
считают центральный вариант так называемого модального интервала.
Модальный интервал
— это интервал, который имеет наибольшую частоту.
Конкретное значение моды для интервального ряда
распределения с равными интервалами определяется формулой
Мо=Хмо+imo(7)
где где xмо
— нижняя граница модального интервала; iMO–
величина модаль-ного интервала; fmo—
частота, соответствующая модальному интервалу;
fmo-1
— частота интервала, предшествующая модальному
интервалу; fM0+i
— частота интервала, следующего за модальным.
Медиана – это величина, которая
делит численность упорядоченного вариационного ряда на две равные части: одна
часть имеет значение варьирующего признака меньше, чем средний вариант, другая
— больше, чем средний вариант.
В дискретном ряду с четным числом индивидуальных величин медианой
будет средняя арифметическая из двух смежных вариант, а с нечетным числом
медианой будет варианта, расположенная в центре ряда.
Для интервального ряда медиана определяется по
формуле
Мме=Хме+iме
где хме
— нижняя граница медианного интервала; iмe
— величина медианного интервала; sMe-1
— сумма частот, накопленная до медианного интервала; fмe
— частота, соответствующая медианному интервалу.
Медианный
интервал — это первый интервал, в котором накопленная частота составляет
половину или больше половины общей суммы частот.
Различие
индивидуальных значения признака внутри изучаемой совокупности в статистике
называется вариацией признака. Она возникает в результате того, что его
индивидуальные значения признака складываются под совокупным влиянием
разнообразных факторов, которые по-разному сочетаются в каждом отдельном
случае.
Колеблемость
отдельных значений характеризуют показатели вариации. Статистические
показатели, определяющие вариацию, делятся на две группы: абсолютные и
относительные. К абсолютным относятся размах вариации, среднее линейное
отклонение, дисперсия и среднее квадратическое отклонение. Вторая группа
показателей вычисляется как отношение абсолютных показателей вариации к средней
арифметической. Относительными показателями вариации являются коэффициенты
осцилляции, вариации, относительное линейное отклонение.
Самым
простым абсолютным показателем является размах вариации. Размах вариации
показывает, насколько велико различие между единицами совокупности, имеющими
наименьшее и наибольшее значение признака:
R=xmax—xmin
, (9)
где хmах
и хmin — соответственно, наибольшее и наименьшее
значения признака в совокупности.
Среднее линейное отклонение вычисляется
как средняя арифметическая (простая или взвешенная в зависимости от исходных
данных) из абсолютных значений отклонений вариант и среднего значения признака
в совокупности по следующим формулам:
=
, (10)
=
,
(11)
Среднее линейное отклонение
дает обобщенную характеристику степени
колеблемости признака в совокупности.
Общепринятыми мерами вариации являются дисперсия и среднее
квадратическое отклонение. Данные показатели нашли широкое применение в
статистических исследованиях, а также в других отраслях знаний.
Дисперсия представляет собой средний квадрат отклонений индивидуальных
значений признака от их средней величины и в зависимости от исходных данных
вычисляется по формулам простой и взвешенно
(12)
(13)
Среднее квадратическое
отклонение равно корню квадратному из дисперсии:
(14)
Среднее квадратическое отклонение — это обобщающая характеристика
размеров вариации признака в совокупности. Оно выражается в тех же единица
измерения, что и признак (в метрах, тоннах, рублях, процентах и т.д.)
Для целей сравнения колеблемости различных признаков в одного и
того же признака в нескольких совокупностях представляют интерес показатели
вариации, приведенные в относительных величинах. Относительные показатели
вариации выражаются в процентах и определяют не только сравнительную оценку
вариации, но и дают характеристику однородности совокупности.
Коэффициент осцилляции вычисляется как отношение размаха вариации к средней
арифметической:
Ко=
(15)
Относительное
линейное отклонение вычисляется как
отношение среднего линейного отношения к средней арифметической:

(16)
Наиболее
часто в практических расчетах применяется показатель относительной вариации —
коэффициент вариации.
Коэффициент
вариации вычисляется как отношение
среднего квадратического отклонения к средней арифметической:

(17)
Для
распределений, близких к нормальному, совокупность считается однородной, если
коэффициент вариации не превышает 33 %
Средняя
величина только тогда отражает типичный уровень признака, когда она рассчитана
по качественно однородной совокупности.
При расчете
средних величин и показателей вариации по не сгруппированным данным используют
стандартные функции MicrosoftExcel (табл. 4).
Таблица 4
Стандартные функции Microsoft Excel‘ используемые
при расчете показателей по не сгруппированным данным
|
Показатель |
Используемая функция |
|
Средняя арифметическая простая Мода дискретного ряда Медиана дискретного ряда Минимальное значение Максимальное значение Среднее линейное отклонение Дисперсия Среднее квадратическое отклонение |
СРЗНАЧ МОДА МЕДИАНА МИН МАКС СРОТКЛ ДИСПР СТАНДОТКЛОН |
Порядок выполнения работы
1.Определение средних величин и
показателей вариации по не сгруппированным данным.
2. Определение средних величин и показателей вариации по сгруппированным
данным.
3.
Формулировка выводов об
однородности исследуемой совокупности по изучаемому признаку.
4.
Формулировка выводов о
типичности среднего значения признака.
Пример выполнения работы
Задание. Рассчитать среднее значение, структурные средние, показатели
вариации, используя данные о стоимости основных средств предприятий региона
(табл. 1). Определить однородность совокупности предприятий региона по стоимости
основных средств. Оценить типичность рассчитанного среднего значения.
При расчете показателей по сгруппированным
данным необходимо использовать формулы для вычисления взвешенных величин. Для
удобства расчета используется табл. 5.
Таблица 5
Вспомогательная таблица для расчета средних показателей и
показателей вариации
|
Группы предприятий по стоимости основных средств хi, млн руб. |
Количество предприятий fi |
Середина интервалаxi‘, млн руб. |
x‘i·fi |
|хi‘-xср|*fi |
(х‘i— |
Накопленные частоты |
|
3427-4827 |
3 |
4127 |
12381 |
31105200 |
3 |
|
|
4827-6227 |
6 |
5527 |
33162 |
10920 |
19874400 |
9 |
|
6227-7627 |
10 |
6927 |
69270 |
4200 |
1764000 |
19 |
|
7627-9027 |
4 |
8327 |
33308 |
3920 |
3841600 |
23 |
|
9027-10427 |
4 |
9727 |
38908 |
9520 |
22657600 |
27 |
|
10427-11827 |
3 |
11127 |
33381 |
11340 |
42865200 |
30 |
|
Итого |
30 |
— |
220410 |
49560 |
122108000 |
— |
Среднее значение признака =
220410/30=7347 млн руб.
Модальным интервалом является интервал
(6227-7627), имеющий максимальную частоту (10ед.)
Мода Мо = 6227+(7627-6227) млн руб.
Медианным интервалом является интервал
6227-7627, в котором накопленная частота S=19, что больше половины общей суммы частот.
Медиана Ме= 6227+(7627-6227)·=7067 млн.
руб.
Размах вариации R=11827-3427=8400 млн. руб.
Среднее линейное отклонение =49560/30=1652
млн. руб.
Дисперсияϭ2 =122108000/30=4070267
Среднеквадратическое отклонениеϭ==2017 млн.
руб.
Коэффициент осцилляции Ко =8400·100/7347=114%.
Относительное линейное отклонение =1652·100/7347=22%.
Коэффициент вариации v=1652·100/7347=27%.
Результаты расчета по не сгруппированным
данным с использованием стандартных функций Microsoft Excel составляют: среднее значение — 7302 млн. руб., мода — 6925 млн.
руб., медиана — 6914 млн. руб.,
размах вариации — 8390 млн. руб., среднее линейное отклонение —
1649 млн. руб., дисперсия — 4382880, среднее квадратическое отклонение —
2094 млн. руб., коэффициент осцилляции — 115%, линейный коэффициент вариации —
23 %, коэффициент вариации — 29 %.
Выводы
Приведенные расчеты показали, что
коэффициент вариации не превышает 33 %, следовательно, совокупность можно
считать однородной. Типичность среднего значения в данной совокупности —
удовлетворительная.
Лабораторная работа 3
АНАЛИЗ ВАРИАЦИООНЫХ РЯДОВ
Цель работы. Изучить основные принципы определения общего характера
распределения и освоить их практическое применение.
Краткие теоретические сведения
Выяснение общего характера распределения предполагает оценку
степени его однородности, а также вычисление показателей асимметрии и эксцесса.
Статистический ряд
распределения — это упорядоченное распределение
единиц совокупности на группы по определенному варьирующему признаку.
В зависимости от признака, взятого за
основу группировки, различают атрибутивные и вариационные ряды распределения.
Атрибутивные ряды
распределения построены по качественным признакам (распределение по полу,
национальности, профессии и т.д.).
Вариационные ряды
распределения построены по количественному признаку.
В зависимости от характера вариации
признака различают дискретные и интервальные вариационные ряды.
Дискретный вариационный ряд
характеризует распределение единиц совокупности по дискретному признаку.
Интервальный вариационный ряд
используется в случае непрерывной вариации признака, а также если дискретная
вариация проявляется в широких пределах (т.е. число вариантов дискретного
признака достаточно велико).
В вариационных рядах существует
определенная связь между изменением частот и изменением величины варьирующего
признака: с увеличением варьирующего признака величина частот вначале возрастает
до определенной величины, а затем уменьшается. Такого рода изменения
называются закономерностями распределения.
Одна из важных целей статистического
изучения вариационных рядов состоит в том, чтобы выявить закономерность
распределения и определить ее характер.
Под кривой
распределения понимается графическое изображение в виде непрерывной линии
изменения частот в вариационном ряду, функционально связанного с изменением
вариант.
Положение кривой распределения на оси
абсцисс и ее рассеивание являются двумя наиболее существенными свойствами
кривой. Наряду с ними существует ряд других важных свойств кривой распределения:
степень ее асимметрии, высоко- или низковершинность, которые в совокупности
характеризуют форму или тип кривой распределения.
В практике статистических исследований
приходится встречаться с самыми различными распределениями. Различают следующие
разновидности кривых распределения: одновершинные кривые (симметричные,
умеренно асимметричные и крайне асимметричные) и многовершинные кривые. Для
однородных совокупностей, как правило, характерны одновершинные распределения.
Определение формы кривой является важной
задачей, так как статистический материал в обычных для него условиях дает по
определенному признаку характерную, типичную для него кривую распределения.
Всякое искажение формы кривой означает
нарушение или изменение нормальных условий возникновения материала: появление
двухвершинной или асимметричной кривой говорит о разнотипном составе совокупности
и о необходимости перегруппировки данных в целях выделения более однородных
групп.
Выяснение общего характера распределения
предполагает оценку степени его однородности, а также вычисления показателей
асимметрии и эксцесса.
При сравнительном изучении асимметрии
нескольких распределений с разными единицами измерения вычисляется
относительный показатель асимметрии.
Наиболее точным и распространенным
является показатель асимметрии, основанный на определении центрального момента
третьего порядка:
(18)
где μ3 – центральный момент третьего порядка.
Центральный момент третьего порядка
рассчитывается по формуле
(19)
При симметричном распределении коэффициент асимметрии
равен нулю. При Аs< 0
асимметрия левосторонняя. При Аs>0 асимметрия правосторонняя.
Оценка степени существования показателя ассиметрии
дается с помощью среднеквадратической ошибки:
(20)
где
n—
объем наблюдений.
Если
,то асимметрия существенная и распределение
признака в совокупности не симметрично. Если, то асимметрия
несущественна и ее наличие может быть объяснено влиянием различных случайных
факторов.
Кроме того, в симметричных распределениях
рассчитывается показатель эксцесса (островершинности), использующий
центральный момент четвертого порядка:
,
(21)
где μ4 –
центральный момент четвертого порядка.
Центральный момент четвертого порядка вычисляется по
формуле
 |
(22)
Эксцесс представляет собой выпад вершины эмпирического
распределения вверх или вниз от вершины кривой нормального распределения, где
μ4
/ ϭ4 =3
Если Ех=0, то распределение является нормальным. Если Ех<0
(отрицательный эксцесс), то распределение является плосковершинным
(низковершинным).
Низковершинностъ
означает отрицательный эксцесс и характеризует большую разбросанность членов
ряда.
Если Ех >0 (положительный эксцесс), то
распределение является островершинным (высоковершинным).
Высоковершинность
означает положительный эксцесс и характеризует скопление частот (т.е. членов
вариационного ряда) в середине.
Оценка степени существенности этого показателя дается
с помощью среднеквадратической ошибки эксцесса:

(23)
 |
|||
Если
, то эксцесс существенный. Если , то эксцесс
несущественный.
Оценка существенности показателей асимметрии и эксцесса позволяет
сделать вывод о том, можно ли отнести данное эмпирическое распределение к типу
кривых нормального распределения.
Для того чтобы эмпирическое распределение можно было отнести к
нормальному типу, необходимо, чтобы и асимметрия и эксцесс были признаны
несущественными.
Порядок выполнения работы
1.
Построение графического
изображения эмпирического распре-
деления.
2.
Анализ вариационного ряда
распределения.
3.
Формулирование вывода о
возможности отнесения данного эм лирического распределения к типу кривых
нормального распределения.
Пример
выполнения работы
Задание. На
основании анализа вариационного ряда распределения (табл.3) сделайте вывод о возможности
отнесения данного эмпирического распределения к типу кривых нормального
распределения.
Для удобства вычисления показателей асимметрии и
эксцесса используется табл.6.
Таблица 6
Вспомогательная таблица для расчета
показателей асимметрии и эксцесса
|
Группы |
Количество fi |
Середина |
(хi‘-xср)3*fi |
(хi‘-xср)4*fi |
|
3427-4827 |
3 |
4127 |
-100158744000 |
1000121643731520 |
|
4827-6227 |
6 |
5527 |
-36171408000 |
408783873291846 |
|
6227-7627 |
10 |
6927 |
-740880000 |
47077239334410 |
|
7627-9027 |
4 |
8327 |
3764768000 |
113592964 |
|
9027-10427 |
4 |
9727 |
53925088000 |
12403483772164 |
|
10427-11827 |
3 |
11127 |
162030456000 |
165905890703523 |
|
Итого |
30 |
— |
82649280000 |
1634292244426430 |
Среднее значение признака составляет 7347 млн. руб.,
мода- 6787 млн. руб., медиана – 7067 млн. руб., среднеквадратическое отклонение
– 2017 млн. руб.
Центральный момент третьего порядка
μ3
=82649280000 / 30 = 2754976000.
Показатель асимметрии: As
= 2754976000/ 20173 = 0,3.
Положительный показатель асимметрии (Аs>0)
свидетельствует о наличии правосторонней асимметрии.
Среднеквадратическая ошибка асимметрии составляет
Ϭas
= = 1,6
Отношение ,
следовательно, асимметрия несущественна и ее
наличие
может быть объяснено влиянием различных случайных обстоятельств.
В симметричных распределениях рассчитывается
показатель эксцесса (островершинности).
Центральный момент четвертого порядка
μ4
= 1634292244426430 / 30 = 54476408147548.
Показатель эксцесса( островершинности) Ех
=54476408147548 / 20174 —3=0,3.
Положительный эксцесс (Ех>0) говорит об
островершинности распределения. Островершинность означает положительный эксцесс
и характеризует скопление членов вариационного ряда в середине.
Среднеквадратическая ошибка эксцесса составляет
ϬEx=
= 0,56
Отношение , следовательно, эксцесс
несущественный.
Так как и асимметрия и эксцесс несущественны, то
данное эмпирическое распределение можно отнести к типу кривых нормального
распределения.
Выводы
Вариационный ряд имеет правостороннюю асимметрию,
которая признана несущественной и ее наличие может быть объяснено влиянием
различных случайных обстоятельств.
Положительный эксцесс указывает на качественную
однородность исследуемой совокупности.
Оценка существенности показателей асимметрии и
эксцесса позволяет сделать вывод о том, что данное эмпирическое распределение
можно отнести к типу кривых нормального распределения.
Положительный эксцесс указывает на качественную
однородность исследуемой совокупности.
Оценка существенности показателей асимметрии и
эксцесса позволяет сделать вывод о том, что данное эмпирическое распределение
можно отнести к типу кривых нормального распределения.
Лабораторная
работа 4
ВИДЫ
ДИСПЕРСИЙ
Цель работы. Изучить
основные принципы расчета различных видов дисперсий и освоить их практическое
применение для анализа взаимосвязей.
Краткие
теоретические сведения
Если статистическая совокупность разбита на группы по
какому-либо признаку, то для оценки влияния различных факторов, определяющих
колеблемость индивидуальных значений признака, можно воспользоваться
разложением дисперсии на составляющие: на межгрупповую и внутригрупповую
дисперсии.
Общая дисперсия
измеряет вариацию признака по всей совокупности под влиянием всех факторов,
обусловивших эту вариацию.
Она определяется по формулам как простая или
взвешенная дисперсия:
=
, (24)
=
,
(25)
где
— общая средняя для всей
изучаемой совокупности.
Межгрупповая дисперсия
характеризует систематическую вариацию, т.е. вариацию изучаемого признака под
воздействием факторного признака, положенного в основу группировки.
Она характеризует колеблемость групповых средних около
общей средней:
=
,(26)
=
,(27)
где
– численность отдельных
групп; – средняя в группах.
Внутригрупповая (частная) дисперсия характеризует
случайную вариацию в каждой отдельной группе, т.е. часть вариации, возникающую
под влиянием других, неучтенных факторов, и не зависящую от фактора,
положенного в основу группировки.
Внутригрупповые
дисперсии рассчитываются по каждой группе:
=
,
(28)
=
.
(29)
Средняяизвнутригрупповыхдисперсийопределяетсянаоснованиивнутригрупповыхдисперсийпокаждойгруппе:
=
.
(30)
Общая дисперсия равна сумме величин межгрупповой дисперсии и средней из
внутригрупповой дисперсии:
=
+
.
(31)
Это
правило имеет большую практическую значимость, так как позволяет выявить
зависимость результатов от определяющих факторов.
Очевидно, что чем больше доля межгрупповой дисперсии в общей дисперсии, тем
сильнее влияние группировочного признака на изучаемый признак.
Поэтому в статистическом анализе широко используется такой показатель, как эмпирический
коэффициент детерминации:
η2
= .
(32)
Выраженный в процентах, он показывает, какая доля всей вариации результативного
признака обусловлена факторным признаком, положенным в основу группировки.
Эмпирический коэффициент детерминации изменяется в
пределах
0 ≤ ≤ 1.
Эмпирическое корреляционное отношение
показывает тесноту связи между группировочным и результативным признаками:
η = .
(33)
Эмпирическое корреляционное отношение также изменяется
в пределах 0 ≤ ≤ 1.
Для качественной оценки тесноты связи на основе
показателя эмпирического корреляционного отношения можно воспользоваться
соотношениями Чэддока (табл.7).
Таблица
7
Соотношения
Чэддока
|
|η| |
0 |
0,1-0,3 |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
0,9-0,99 |
1 |
|
Сила |
Отсутствует |
Слабая |
Умеренная |
Заметная |
Тесная |
Весьма |
Функциональная |
Порядок
выполнения работы
1. Определение
средних значений выработки по каждой группе и в целом по совокупности.
2. Определение
групповых дисперсий по каждой группе и средней из групповых дисперсий.
3. Определение
межгрупповой дисперсии.
4. Определение
общей дисперсии.
5. Проверка
правильности расчетов с использованием закона сложения дисперсий.
6. Определение
эмпирического коэффициента детерминации.
7. Определение
эмпирического корреляционного отношения.
8. Формулировка
вывода о наличии связи между группировочным (факторным) и результативным
признаком.
Пример
выполнения работы
Задание.
Используя данные табл. 8, 9, сделайте
вывод о наличии связи между прохождением рабочими повышения квалификации и
выработкой.
Средняя выработка рабочих, не прошедших повышение
квалификации, составляет 45,48 шт./см.
Средняя выработка рабочих, прошедших повышение
квалификации, составляет 53,13 шт./см.
Средняя выработка рабочих цеха составляет 50,07
шт./см.
Определим дисперсии с помощью стандартных функций Microsoft Excel.
Общая дисперсия выработки всех рабочих равна 33,03.
Дисперсия выработки рабочих, не прошедших повышение
квалификации, составляет 10,00.
Дисперсия выработки рабочих, прошедших повышение
квалификации, составляет 24,92.
Средняя из внутригрупповых дисперсий
=
= 18,95 .
Межгрупповая дисперсия
=
= 14,08 .
Используя закон сложения дисперсий, проверим
правильность расчетов:
= 14,08 + 18,95 = 33,03.
Эмпирический коэффициент детерминации
= 14,08 / 33,03 = 0,43.
Рассчитаем эмпирическое корреляционное отношение:
η = = 0,65.
Выводы
Средняя выработка рабочих, не
прошедших повышение квалификации, составляет 45,48 шт./см, прошедших повышение
квалификации – 53,13 шт./см. Средняя выработка рабочих цеха равна 50,07 шт./см.
Доля вариации выработки рабочего, которая обусловлена
прохождением рабочими повышения квалификации, равна 43 %.
Эмпирическое корреляционное отношение равно 0,65.
Следовательно, связь между выработкой и прохождением рабочими повышения
квалификации заметная.
Лабораторная
работа 5
ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
Цель
работы. Изучить основные принципы проведения
выборочного исследования и освоить практическое применение результатов
выборочного наблюдения для оценки величины параметров генеральной совокупности.
Краткие
теоретические сведения
Под выборочным наблюдением понимается
такое несплошное наблюдение, при котором статистическому обследованию
(наблюдению) подвергаются единицы изучаемой совокупности, отобранные случайным
способом.
Выборочное наблюдение ставит перед
собой задачу по обследуемой части дать характеристику всей совокупности единиц
при условии соблюдения всех правил и принципов проведения статистического
наблюдения и научно-организованной работы по отбору единиц.
Совокупность, из которой
производится отбор, называется генеральной и все ее обобщающие
показатели – генеральными.
Совокупность отобранных для
обследования единиц в статистике принято называть выборочной и все ее
обобщающие показатели – выборочными.
При
собственно-случайной выборке отбор из генеральной совокупности осуществляется
случайным образом, наугад, без каких-либо элементов системности.
Собственно-случайный
отбор может быть повторный и бесповторный.
Разность
между величиной параметра в генеральной совокупности и его величиной,
вычисленной по результатам выборочного наблюдения, называется ошибкой
выборочного наблюдения.
Величина ошибки выборки зависит от способа отбора
единиц совокупности в выборку, от объема выборки и от вариации изучаемого
признака в генеральной совокупности.
Для определения возможных границ генеральных
характеристик рассчитываются средняя и предельная ошибки выборки.
Средняя ошибка выборочной средней при повторном отборе вычисляется
по формуле:
=
, (34)
где – дисперсия изучаемого показателя в генеральной совокупности (при
большом числе наблюдений выборочная дисперсия равна генеральной);
n–
численность выборки,
Средняя ошибка выборочной средней при бесповторном отборе равна
=
,
(35)
где N –
численность генеральной совокупности.
Средняя ошибка выборочной доли
(альтернативного признака) при повторном отборе и бесповторном отборе
рассчитывается по формулам
=
,
(36)
=
.
(37)
где w –
выборочная доля единиц, обладающих изучаемым признаком;
w(l — w) – дисперсия доли
(альтернативного признака).
Выборочная
доля единиц, обладающих изучаемым признаком, определяется по формуле
w
= m
/ n,
(38)
где m
– число единиц, обладающих изучаемым (альтернативным) признаком.
Предельная ошибка выборки дает
возможность выяснить, в каких пределах находится величина генеральной средней.
Предельная ошибка выборки рассчитывается по формуле
∆ = tμ, (39)
где t — коэффициент
доверия, показатель, определяющий размер ошибки в зависимости от того, с какой
вероятностью Ф(t) она находится.
Наиболее часто употребляемые
уровни доверительной вероятности и соответствующие значения t для выборок достаточно большого объема (n≥ 30)приведены в табл. 10.
Таблица 10
Наиболее
часто употребляемые уровни доверительной вероятности и соответствующие значения
t
|
t |
1,00 |
1,50 |
1,96 |
2,00 |
2,50 |
2,58 |
3,00 |
3,50 |
|
Ф(t) |
0,683 |
0,866 |
0,95 |
0,954 |
0,988 |
0,990 |
0,997 |
0,999 |
Предельная ошибка выборки позволяет определить предельные значения
характеристик генеральной совокупности и их доверительные интервалы:
–
≤
≤
+
, (40)
w– ≤ p ≤ w +
.
(41)
Это означает, что с заданной вероятностью
можно утверждать, что значение генеральной средней (доли) следует ожидать в
указанных пределах.
При подготовке выборочного наблюдения с
заранее заданным значением допустимой ошибки выборки очень важно правильно
определить численность выборочной совокупности, которая с определенной
вероятностью обеспечит заданную точность результатов наблюдения.
Объем
выборки при определении среднего размера признака при повторном и бесповторном
отборе вычисляется следующим образом:
n
= ,
(42)
n
= .(43)
Объем выборки при определении доли альтернативного
признака при повторном и бесповторном отборе вычисляется следующим образом:
n
= ,
(44)
n
= .(45)
Механический
отбор единиц из генеральной совокупности осуществляется в установленной
пропорции через равные интервалы.
При расчете
средней ошибки механической выборки используется формула средней ошибки при
собственно-случайном бесповторном отборе.
Для определения средней ошибки механической выборки используется
формула средней ошибки при собственно-случайном бесповторном отборе.
Порядок
выполнения работы
1. Проведение
отбора единиц в выборку с помощью процедуры MicrosoftExcel СЕРВИС
/ АНАЛИЗ ДАННЫХ / ВЫБОРКА.
2. Определение
основных выборочных характеристик (выборочной средней и выборочной доли
изучаемого признака). Расчет количества единиц, обладающих альтернативным
признаком, производится с помощью процедуры MicrosoftExcelСЧЕТЕСЛИ.
3. Определение
средней ошибки выборки.
4. Определение
предельной ошибки выборки с заданной вероятностью.
5. Определение
пределов, в которых с заданной вероятностью будут находиться генеральные
характеристики.
6. Определение
необходимой численности выборки, при которой средняя ошибка выборки снизится вХ
раз.
Пример
выполнения работы
Задание.
В табл. 11 приведены примеры случайного повторного 10%-го отбора изделий из
партии готовой продукции в выборку. Оцените средний вес изделия и долю
стандартных изделий во всей партии с вероятностью 0,866. Определите оптимальный
объем выборки при условии, что предельная ошибка выборки сократится в 2 раза.
Таблица
11
Вес
изделия, г, по результатам случайного повторного 10 %-го отбора изделий в
выборку
|
48,0 |
47,0 |
48,0 |
51,0 |
50,0 |
51,0 |
47,0 |
51,0 |
47,0 |
47,0 |
|
50,0 |
51,0 |
51,0 |
50,0 |
48,0 |
49,0 |
48,0 |
49,0 |
51,0 |
48,0 |
|
51,0 |
48,0 |
47,0 |
49,0 |
48,0 |
51,0 |
50,0 |
47,0 |
47,0 |
49,0 |
|
48,0 |
48,0 |
51,0 |
51,0 |
51,0 |
51,0 |
51,0 |
50,0 |
47,0 |
48,0 |
Средний
вес изделий в выборке составил 49,13 г.
Средняя
ошибка выборки =
= 0,25 г.
Предельная
ошибка выборки с вероятностью 0,866 составляет
= 1,5 ∙ 0,25
= 0,375 г.
Таким
образом, с вероятностью 0,866 можно утверждать, что вес изделия во всей партии
находится в границах
49,13 – 0,375 ≤ ≤ 49,13 + 0,375 ,
48,755 ≤ ≤ 49,505 .
Для того чтобы сократить предельную ошибку выборки в 2
раза, необходимо, чтобы численность выборки составила
n = = 158 изделий.
В выборке лишь 5 изделий имеют стандартный вес, равный
50 г.
Доля изделий, соответствующих требованию стандарта,
составляет
w=5/
40=0,125.
Дисперсия
доли изделий, соответствующих требованию стандарта, составляет w (1– w) = 0,125
(1–0,125) = 0,109.
Средняя
ошибка доли =
= 0,052.
Предельная
ошибка доли равна = 1,5 ∙ 0,052 = 0,078 .
Таким образом, с вероятностью 0,866 можно утверждать,
что доля стандартных изделий во всей партии находится в границах
0,125 – 0,078 ≤ p ≤ 0,125 +
0,078,
0,047 ≤ p ≤ 0,203.
Для того чтобы сократить предельную ошибкувыборки в 2
раза, необходимо, чтобы численность выборки составила
n = = 162 изделия.
Выводы
В результате 10 %-го выборочного обследования партии
изделий (используя случайную схему повторного отбора) в выборку отобрано 40
изделий. Средний вес изделия в выборке составил 49,13 г.
С вероятностью 0,866 можно утверждать, что вес одного
изделия во всей партии составляет от 48,755 до 49,505
Для того чтобы сократить среднюю ошибку выборки в 2
раза, необходимо, чтобы численность выборки составила 158 изделий.
В выборке лишь 5 изделий имеют стандартный вес, равный
50 г.
Доля
изделий, соответствующих требованию стандарта, составляет 12,5 %.
С вероятностью 0,866 можно утверждать, что доля
стандартных изделий во всей партии составляет 4,7–20,3 %.
Для того чтобы сократить среднюю ошибку в выборки в 2
раза, необходимо, чтобы численность выборки составила 162 изделия.
Лабораторная
работа 6
АНАЛИЗ
РЯДОВ ДИНАМИКИ
Цель работы. Изучить
основные принципы расчета показателей динамики и освоить их практическое
применение для анализа рядов динамики и выявления тенденций развития явлений и
процессов.
Краткие
теоретические сведения
Процесс развития, движения социально-экономических
явлений во времени в статике принято называть динамикой.
Рядами динамики называются
последовательно расположенные в хронологическом порядке статистические данные,
отражающие развитие изучаемого явления во времени.
В каждом ряду динамики имеются два основных элемента:
показатель времени tи соответствующие
им уровни развития изучаемого явления y.
Существуют различные виды рядов динамики.
В зависимости от способа выражения уровней ряды
динамики подразделяются на ряды абсолютных, относительных и средних величин.
В зависимости от того, как выражают уровни ряда
состояние явления на определенные моменты времени или его величину за
определенные интервалы времени, различают, соответственно, моментные и
интервальные ряды динамики.
Моментные ряды динамики
отражают состояние изучаемых явлений на определенный момент времени (дату). Интервальные
ряды динамики отображают итоги развития изучаемых явлений за отдельные
периоды (интервалы).
В зависимости от расстояния между уровнями ряды
динамики подразделяются на ряды с равноотстоящими и неравноотстоящими уровнями
во времени.
В основе расчета показателей рядов динамики лежит сравнение его уровней.
Абсолютный
прирост является важнейшим из показателей
динамики. Он характеризует увеличение (уменьшение) уровня ряда за определенный
промежуток времени.
Абсолютный
прирост базисный выражается формулой
∆ =
–
,
(46)
где
– уровень сравниваемого
периода; – уровень, базисного
периода.
Абсолютный прирост цепной выражается формулой
∆ =
–
, (47)
где
— уровень предшествующего
периода.
Между базисными и цепными абсолютными приростами
имеется связь: сумма цепных абсолютных приростов равна базисному абсолютному
приросту последнего периода ряда динамики:
=
=
–
(48)
Темп роста характеризует интенсивность
изменения уровня ряда. Он может выражаться
в виде коэффициента или процента:
=
,
(49)
=
,
(50)
Тр = Кр ∙
100. (51)
Между базисными и цепными коэффициентами роста имеется
взаимосвязь: произведение последовательных цепных коэффициентов роста равно
базисному коэффициенту роста последнего периода ряда динамики:
∙
∙
=
=
/
.
(52)
Частное
от деления последующего базисного коэффициента роста на предыдущий равно
соответствующему цепному коэффициенту роста:
/
=
.
(53)
Темп
прироста показывает, на сколько процентов
сравниваемый уровень больше (меньше) уровня, принятого за базу сравнения:
=
100 /
,
(54)
=
100 /
,
(55)
Между темпами роста и прироста имеется взаимосвязь:
(%) =
(%) –
100, (56)
=
–
1. (57)
Абсолютное значение одного процента прироста определяется
как частное абсолютного прироста к темпу прироста:
=
/
= (
–
) /
=
/ 100 = 0,01
. (58)
Темп наращивания говорит о затухании или усилении
темпов роста:
=
=
=
–
=
—
. (59)
Для получения обобщающих показателей динамики рассчитываются средние
показатели.
Средний
уровень ряда динамики характеризует типическую
величину абсолютных уровней.
В зависимости от вида ряда динамики средний уровень определяется по-разному.
В интервальных рядах динамики с равностоящими уровнями его рассчитывают по
формуле
=
=
,
(60)
где n
– число уровней ряда;
в
интервальных рядах динамики с неравностоящими уровнями – по формуле:
=
=
, (61)
где
– уровни ряда динамики,
сохранившиеся без изменения в течение промежутка времени ;
– интервал времени между
снежными уровнями.
В моментных рядах динамики с равноотстоящими уровнями его вычисляют по формуле
=
,
(62)
где
n
– число уровней ряда; – уровни ряда динамики;
в моментных рядах динамики с неравностоящими уровнями – по формуле:
=
=
=
. (63)
Средний абсолютный прирост является
обобщающим показателем скорости изменения явления во времени. Этот показатель
дает возможность установить, насколько в среднем за единицу времени должен
увеличиться уровень ряда (в абсолютном выражении), чтобы, отправляясь от
начального уровня за данное число периодов (например, лет), достигнуть
конечного уровня:
=
=
.
(64)
Сводной
обобщающей характеристикой интенсивности изменения уровней ряда динамики служит
средний темп роста, показывающий, во сколько раз в среднем за единицу времени
изменился уровень динамического ряда. Необходимость исчисления среднего темпа
роста возникает вследствие того, что темпы роста из года в год колеблются.
Кроме того, средний темп роста часто следует определить в тех случаях, когда
имеются данные об уровне в начале какого-либо периода и в конце его, а
промежуточные данные отсутствуют.
Средний
коэффициент роста вычисляется по формуле
=
=
=
=

Средний темп прироста можно определить на
основе взаимосвязи между коэффициентами (темпами) роста и прироста:
=
– 1
, (66)
=
– 100
. (67)
Одна из задач анализа рядов динамики – установить закономерность изменения
уровней изучаемого показателя во времени, т.е. определить основную тенденцию
развития явления (тренд).
Основная
тенденция развития (тренд) это достаточно плавное и
устойчивое изменение уровня явления во времени, более или менее свободное от
случайных колебаний.
Для определения тренда используют специальные методы выравнивания (сглаживания)
рядов динамики. При выравнивании отклонения, обусловленные случайными причинами,
взаимопогашаются (сглаживаются), в результате четко обнаруживается действие
основных факторов изменения уровней (общая тенденция).
Основную тенденцию можно представить либо графически, либо аналитически – в
виде уравнения (модели) тренда.
Методы выравнивания рядов динамики таковы:
1. Метод
укрупнения интервалов;
2. Метод
усреднения по левой и правой половине;
3. Метод
простой скользящей средней;
4. Аналитическое
выравнивание.
Наиболее эффективным способом выявления тренда является аналитическое выравнивание,
при этом уровни ряда динамики выражаются в виде функции: = f
(t).
Аналитическое выравнивание проводится на основе адекватной математической
формулы – полиномов разной степени, экспонент и других функций. Выбор функции
производится на основе анализа характера закономерности динамики данного
явления.
Для оценки надежности линии тренда применяется величина :
= 1–

где y
– исходный уровень ряда динамики.
Наиболее
надежной является та функция, для которой значение равно или близко к 1.
Порядок
выполнения работы
1.
Определение показателей ряда динамики.
2.
Определение средних показателей ряда
динамики.
3.
Проведение аналитического выравнивания
ряда динамики с использованием процедуры MicrosoftExсelМАСТЕР
ДИАГРАММ / ДОБАВЛЕНИЕ ЛИНИИ ТРЕНДА.
4.
Проверка надежности моделей тренда и выбор
наиболее адекватной модели основной тенденции развития исследуемого явления.
5.
Прогнозирование развития изучаемого
явления в будущем.
6.
Формулировка вывода о наличии основной
тенденции развития исследуемого явления.
Пример выполнения работы
Задание.
Используя данные табл. 12, рассчитайте
показатели динамики. Определите наличие основной тенденции развития ряда
динамики. Сделайте прогноз на 3 периода вперед.
Исследуемый
ряд динамики является интервальным рядом с равноотстоящими уровнями.
Рассчитанные
показатели динамики сведены в табл. 12.
Таблица 12
Расчет показателей динамики
|
Период |
Выпуск продукции, тыс. т |
Абсолютный прирост, тыс. т |
Темп роста, % |
Темп |
Абсолютное значение 1 % прироста, тыс. т |
Темп наращивания, % |
|||
|
базисный |
цепной |
базисный |
цепной |
базисный |
цеп- ной |
||||
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
21 22 24 25 27 28 31 33 33 36 38 39 41 43 45 |
– 1 3 4 6 7 10 12 12 15 17 18 20 22 24 |
– 1 2 1 2 1 3 2 0 3 2 1 2 2 2 |
– 105 114 119 129 133 148 157 157 171 181 186 195 205 214 |
– 105 109 104 108 104 111 106 100 109 106 103 105 105 105 |
– 5 14 19 29 33 48 57 57 71 81 86 95 105 114 |
– 5 9 4 8 4 11 6 0 9 6 3 5 5 5 |
– 0,21 0,22 0.24 0.25 0,27 0,28 0,31 0.33 0,33 0,36 0,38 0,39 0,41 0.43 |
– 0,048 0,095 0.048 0,095 0,048 0,143 0,095 0,0000,143 0,095 0,048 0,095 0,095 0,095 |
Средний выпуск продукции, рассчитанный с помощью
стандартной функции Microsoft Excel, составляет
32,4 тыс. т., средний абсолютный прирост равен
y =
= 1,7 тыс. т.
Средний темп роста выпуска продукции =
, средний темп прироста
= 105 – 100 = 5 % .
Используя процедуру Microsoft ExcelМАСТЕР
ДИАГРАММ/ ДОБАВЛЕНИЕ ЛИНИИ ТРЕНДА, построим линии тренда нескольких моделей
(рис. 2–6).
Наиболее надежной моделью основной тенденции развития
исследуемого ряда динамики является полиноминальный (2-ой степени) тренд: y
= 0,0136x2 +
1,5185x + 19,13, так как значение параметра = 0,9961 является
максимально приближенным к 1.
Прогнозное значение объема выпуска продукции в 16-м
периоде составит 0,0136 + 1,5185 · 16 + 19,13 = 46,9
тыс. т.
Рис. 2. Динамика выпуска продукции и
линейный тренд, полученный методом аналитического выравнивания
Рис. 3. Динамика выпуска продукции и логарифмический
тренд, полученный методом аналитического выравнивания
Рис. 4. Динамика выпуска продукции и
степенной тренд, полученный методом аналитического выравнивания
Прогнозное значение объема выпуска продукции в 17-м
периоде составит 0,0136 · 172 + 1,5185 ·
17 + 19,13 = 48,9 тыс. т.
Прогнозное значение объема выпуска продукции в 18-м
периоде составит 0,0136 · 182 + 1,5185 ·
18 + 19,13 = 50,9 тыс. т.
Рис. 5. Динамика выпуска продукции и
экспоненциальный тренд, полученный методом аналитического выравнивания
Рис. 6. Динамика выпуска продукции и
полиномиальный тренд, полученный методом аналитического выравнивания
Выводы
Средний выпуск продукции в исследуемом периоде
составил 32,4 тыс. т., средний абсолютный прирост – 1,7 тыс. т., средний темп
роста – 105 %. Наблюдается постоянный рост объемов производства продукции. В
процессе анализа ряда динамики выявлена основная тенденция развития выпуска по
полиному 2-й степени (y
= 0,0136x2 +
1,5185x + 19,13).
Прогнозное значение объема выпуска продукции в 16-м
периоде составит 46,9 тыс. т, в 17-м 48,9 тыс. т, в 18-м периоде – 50,9 тыс. т.
Лабораторная
работа 7
ИНДЕКСЫ
КОЛИЧЕСТВЕННЫХ И КАЧЕСТВЕННЫХ ПОКАЗАТЕЛЕЙ
Цель работы. Изучить
теоретические основы индексов и освоить их практическое применение с
использованием стандартных функций MicrosoftExcel.
Краткие
теоретические сведения
Индексами называют
сравнительные относительные величины, которые характеризуют изменение сложных
социально-экономических показателей (показатели, состоящие из несуммируемых
элементов) во времени, в пространстве, по сравнению с планом.
Индексные
показатели позволяют осуществить анализ результатов деятельности предприятий и
организаций, выпускающих самую разнообразную продукцию или занимающихся
различными видами деятельности. С помощью индексов можно проследить роль
отдельных факторов при формировании важнейших экономических показателей,
выявить основные резервы производства. Индексы широко используются в
сопоставлении международных экономических показателей при определении уровня
жизни, деловой активности, ценовой политики и т.д.
Существует
два подхода в интерпретации возможностей индексных показателей: обобщающий
(синтетический) и аналитический, которые в свою очередь определяются
разными задачами.
Суть
обобщающего подхода — в трактовке индекса как показателя среднего изменения
уровня исследуемого явления. В этом случае основной задачей, решаемой с помощью
индексных показателей, будет характеристика общего изменения многофакторного
экономического показателя.
Аналитический
подход рассматривает индекс как показатель изменения уровня результативной
величины, на которую оказывает влияние величина, изучаемая с помощью индекса.
Отсюда и иная задача, которая решается с помощью индексных показателей:
выделить влияние одного из факторов в изменении многофакторного показателя.
От
содержания изучаемых показателей, методологии расчета первичных показателей,
целей и задач исследования зависят и способы построения индексов.
По
степени охвата элементов явления индексы делят на индивидуальные и
общие (сводные).
Индивидуальные индексы (i) — это
индексы, которые характеризуют изменение только одного элемента совокупности.
Общий (сводный) индекс (I) характеризует
изменение по всей совокупности элементов сложного явления. Если индексы
охватывают только часть явления, то их называют групповыми.
В
зависимости от способа изучения общие индексы могут быть построены или
как агрегатные (от лат. аggrega — присоединяю) индексы, или как средние
взвешенные индексы (средние из индивидуальных).
Способ
построения агрегатных индексов заключается в том, что при
помощи так называемых соизмерителей можно выразить итоговые величины сложной
совокупности в отчетном и базисном периодах, а затем первую сопоставить со
второй.
В
статистике имеют большое значение индексы переменного и фиксированного
состава, которые используются при анализе динамики средних показателей.
Индексом переменного состава называют отношение
двух средних уровней.
Индекс фиксированного состава есть средний из
индивидуальных индексов. Он рассчитывается как отношение двух стандартизованных
средних, где влияние изменения структурного фактора устранено, поэтому данный
индекс называют еще индексом постоянного состава.
В
зависимости от характера и содержания индексируемых величин различают
индексы количественных (объемных) показателей и индексы
качественных показателей.
К
индексам количественных (объемных) показателей
относятся такие индексы, как индексы физического объема производства продукции,
затрат на выпуск продукции, стоимости продукции, а также индексы показателей,
размеры которых определяются абсолютными величинами. Используются различные
виды индексов количественных показателей.
Индекс физического
объема продукции (ФОП) отражает изменение выпуска продукции. Индивидуальный
индекс ФОП отражает изменение выпуска продукции одного вида и определяется по
формуле

где
q1 и q0 — количество продукции данного вида в натуральном выражении в текущем и
базисном периодах.
Агрегатный
индекс ФОП (предложен Э. Ласпейресом) отражает изменение
выпуска всей совокупности продукции, где индексируемой величиной является
количество продукции q, а соизмерителем — цена р:

где
q1 и q0 — количество выработанных единиц отдельных видов продукции
соответственно в отчетном и базисном периодах; p0 — цена единицы продукции
(отдельного вида) в базисном периоде.
При
вычислении индекса ФОП в качестве соизмерителей может выступать также
себестоимость продукции или трудоемкость.
Средние
взвешенные индексы ФОП используются в том случае, если известны индивидуальные
индексы объема по отдельным видам продукции и стоимость отдельных видов
продукции (или затраты) в базисном или отчетном периоде.
Средний
взвешенный арифметический индекс ФОП определяется по формуле

где
iq — индивидуальный индекс по каждому виду продукции; q0 p0 — стоимость
продукции каждого вида в базисном периоде.
Средний
взвешенный гармонический индекс ФОП

где
q1 p1 — стоимость продукции каждого вида в текущем периоде.
Аналогично
рассчитывается индекс затрат на выпуск продукции (ЗВП),
который отражает изменение затрат на производство и может быть как
индивидуальным, так и агрегатным.
Индивидуальный
индекс ЗВП отражает изменение затрат на производство одного вида и определяется
по формуле

где
z1 и z0 — себестоимость единицы продукции искомого вида в текущем и базисном
периодах; q1 z1 и q0 z0 — суммы затрат на выпуск продукции искомого вида в
текущем и базисном периодах.
Агрегатный
индекс ЗВП характеризует изменение общей суммы затрат на выпуск продукции за
счет изменения количества выработанной продукции и ее себестоимости и
определяется по формуле

где
q1 z1 и q0 z0 — затраты на выпуск продукции каждого вида соответственно в
отчетном и базисном периодах.
Рассмотрим
построение индекса стоимости продукции (СП), который может
определяться и как индивидуальный, и как агрегатный.
Индивидуальный
индекс СП характеризует изменение стоимости продукции данного вида и имеет вид:

где
p1 и p0 — цена единицы продукции данного вида в текущем и базисном периодах; q1
p1 и q0 p0 — стоимость продукции данного вида в текущем и базисном периодах.
Агрегатный
индекс СП (товарооборота) характеризует изменение общей стоимости продукции за
счет изменения количества продукции и цен и определяется по формуле

Качественные
показатели определяют уровень исследуемого итогового показателя и определяются
путем соотношения итогового показателя и определенного количественного
показателя (например, средняя заработная плата определяется путем соотношения
фонда заработной платы и количества работников). К индексам качественных
показателей относятся индексы цен, себестоимости, средней заработной платы,
производительности труда.
Самым
распространенным индексом в этой группе является индекс цен.
Индивидуальный индекс цен характеризует
изменение цен по одному виду продукции и определяется по формуле

где
p1 и p0 — цена за единицу продукции в текущем и базисном периодах.
Соответственно
определяются индексы себестоимости и затрат рабочего времени по каждому виду
продукции.
Агрегатный
индекс цен
определяет среднее изменение цены р по совокупности определенных видов
продукции q.
Для
характеристики среднего изменения цен на потребительские товары используют индекс
цен, предложенный Э. Ласпейресом:

где
q0 — потребительская корзина (базовый период); p0 и p1 — соответственно цены
базисного и отчетного периодов.
Если
количество набора продуктов принимается на уровне отчетного периода (q1 ), то в
этом случае индекс цен именуется индексом Пааше:

Если
известны индивидуальные индексы цен по отдельным видам продукции и стоимость
отдельных видов продукции, то применяются средние взвешенные индексы цен
(средний взвешенный арифметический и средний взвешенный гармонический индексы
цен).
Формула
среднего взвешенного арифметического индекса цен

где
i — индивидуальный индекс по каждому виду продукции; p0 q0 — стоимость
продукции каждого вида в базисном периоде.
Формула
среднего взвешенного гармонического индекса цен

где
p1 q1 — стоимость продукции каждого вида в текущем периоде.
В
статистической практике очень широко используется агрегатный территориальный
индекс цен, который может быть рассчитан по следующей формуле:

где
pA pB — цена за единицу продукции каждого вида соответственно на территории А и
В; qA — количество выработанной или реализованной продукции каждого вида по
территории А (в натуральном выражении).
Из
формулы видно, что в данном индексе в качестве фиксированного показателя (веса)
принят объем продукции территории А. При расчете данного индекса в качестве
веса можно принять также объем продукции территории В или суммарный объем
продукции двух территорий.
Возможны
два способа расчета индексов: цепной и базисный.
Цепные индексы получают путем
сопоставления текущих уровней с предшествующим, при этом база сравнения
постоянно меняется.
Базисные индексы получают путем
сопоставления с тем уровнем периода, который был принят за базу сравнения.
В
качестве примера можно привести цепные и базисные индексы цен.
Цепные
индивидуальные индексы цен имеют следующий ряд расчета:
… . (83)
Базисные
индивидуальные индексы цен:
… . (84)
Следует
помнить, что произведение цепных индивидуальных индексов цен равно последнему
базисному индексу:
(85)
Цепные
агрегатные индексы цен:

Базисные
агрегатные индексы цен:

Между
индексами существует также взаимосвязь и взаимозависимость, как и между самими
экономическими явлениями, что позволяет проводить факторный анализ. Благодаря
индексному методу можно рассматривать все факторы независимо друг от друга, что
дает возможность определить размер абсолютного изменения сложного явления за
счет каждого фактора в отдельности.
Предположим,
что результативный признак зависит от трех факторов и более. В этом случае
результативный индекс примет вид
(88)
Изменение
результативного индекса за счет каждого фактора может быть выражено следующим
образом:
(89)
Для
выявления роли каждого фактора в отдельности индекс сложного показателя
разлагают на частные (факторные) индексы, которые характеризуют роль каждого
фактора. При этом используют два метода:
метод
обособленного изучения факторов;
последовательно-цепной
метод.
При
первом методе сложный показатель берется с учетом изменения лишь того фактора,
который взят в качестве исследуемого, все остальные остаются неизменными на
уровне базисного периода.
Последовательно-цепной
метод предполагает использование системы взаимосвязанных индексов, которая
требует определенного расположения факторов. Как правило, на первом месте в
цепи располагают качественный фактор. При определении влияния первого фактора
все остальные сохраняются в числителе и знаменателе на уровне базисного
периода, при определении второго факторного индекса первый фактор сохраняется
на уровне базисного периода, а третий и все последующие — на уровне отчетного
периода, при определении третьего факторного индекса первый и второй факторы
сохраняются на уровне базисного периода, четвертый и все остальные — на уровне
отчетного периода и т.д.
Пример выполнения работы
Задание. Динамика
средних цен и объема продажи в крупных супермаркетах города характеризуется следующими
данными, представленными в таблице 13 ниже.
Таблица 13
Данные для расчета
|
Продукция |
Продано |
Средняя |
||
|
Базисный |
Отчетный |
Базисный |
Отчетный |
|
|
Супермаркет |
||||
|
помидоры |
4.0 |
4.2 |
6.4 |
7.6 |
|
огурцы |
2.5 |
2.4 |
7.2 |
8.4 |
|
Супермаркет |
||||
|
помидоры |
10.0 |
12.0 |
7.6 |
7.0 |
Вычислите:
1. Для
супермаркета №1 (по двум видам продукции вместе):
1.1.
Общий индекс товарооборота
1.2.
Общий индекс цен
1.3.
Общий индекс физического объема
товарооборота
Определите в
отчетном периоде абсолютный прирост товарооборота и разложите по факторам (за
счет изменения цен и объемов продаж овощей) .
2. Для
супермаркетов вместе по помидорам:
2.1.
Индекс цен переменного состава
2.2.
Индекс цен постоянного (фиксированного)
состава
2.3.
Индекс влияния изменения структуры объема
продаж помидор на динамику средней цены
Сформулируйте
выводы.
Решение:
1.1.
Общий индекс товарооборота можно
рассчитать по формуле:
где p-цена,q-количество
проданной продукции
1.2 Общий индекс цен вычисляем по
формуле:
1.3 Общий индекс цен физического
товарооборота можно рассчитать по формуле:
Эти индексы связаны между
собой формулой:
Таким образом,
товарооборот увеличился на 19,4%,в том числе за счет увеличения физического
объема товарооборота на 1,3 %.
Абсолютный прирост
товарооборота:
В том числе за счет
изменения цены:
В том числе за счет
изменения продажи товаров:
Абсолютные приросты
связаны между собой формулами:
Таким
образом, товарооборот увеличился на 8,48 млн.руб. , в том числе за счет
увеличения цен на 7,92 млн.р. за счет увеличения физического объема
товарооборота на 0,56 млн.р.
2.1.Вычислим для 2-х супермаркетов
по помидорам индекс цен переменного состава
Вычислим индекс цен
постоянного состава:
2.2 Вычислим индекс
влияния структуры объема продаж помидор на динамику средней цены:
Разница
между индексами переменного и постоянного состава заключаются в том ,что индекс
переменного состава равен соотношению средних уровней цены, а постоянного
характеризует изменение средней цены за счет изменения только цен на каждом
рынке.
Таким
образом, средняя цена в супермаркетах уменьшилась на 1,4%.Если бы в обоих магазинах
структура рынка была одна и та же, средняя цена уменьшилась на 1,9 %.Увеличение
доли более дорогого супермаркета в структуре продаж увеличило среднюю цену на
0,4%
2.3 Определим общее абсолютное
изменение цены помидор:
Общее абсолютное
изменение цены из-за непосредственного изменения уровней цен на помидоры:
Общее абсолютное изменение цены за счет изменения
структуры продажи помидор:
Таким образом, средняя цена на помидоры снизилась на
0,11 тыс.р., в том числе за счет непосредственного изменения уровней цен на
0,14 тыс.р. Увеличение доли рынка с более дорогими помидорами увеличило
результативный показатель на 0,03 тыс.р.
БИБЛИОГРАФИЧЕСКИЙ
СПИСОК
1.Курс социально-экономической статистики : учебник для студентов вузов по
специальности «Статистика» . -8-е изд., стер.
Москва: Омега-Л, 2010 — 1013с.
2.Статистика [Электронный ресурс] : электронный
учебник : рекомендовано УМО / под ред. Михаил Георгиевич Назаров . — Москва :
Кнорус, 2009 .
3.Практикум по статистике финансов [Текст] : учебное пособие
для высших учебных заведений по специальности 080601 «Статистика» и
другим экономическим специальностям : рекомендовано Учебно-методическим
объединением по образованию в области статистики и антикризисного управления,
математических методов в экономике / Академия бюджета и казначейства ; под ред.
М. Г. Назаров. — Москва : Кнорус, 2009. — 295 с.
4.Социально-экономическая статистика [Текст] :
учебник по специальности 080507 (061100) «Менеджмент организации» /
Государственный университет управления ; под ред. М. Р. Ефимова. — М. : Высшее
образование : Юрайт-Издат, 2009. — 590 с.
5.Статистика:
теория и практика в EXCEL [Текст] : учебное пособие для студентов вузов по
специальности 080601 «Статистика» и другим экономическим
специальностям : рекомендовано Учебно-методическим объединением по образованию
в области статистики и антикризисного управления, математических методов в
экономике / В. С. Лялин, И. Г. Зверева, Н. Г. Никифорова. — МоскваМосква :
Финансы и статистика : ИНФРА-М, 2010. — 447 с.
6.Статистика [Электронный ресурс] : электронный учебник :
рекомендовано УМО / под ред. М. Г. Назаров. — Москва : Кнорус, 2009.
7.Статистика [Текст] : учебник для бакалавров по экономическим
специальностям : рекомендовано Министерством образования РФ /
Санкт-Петербургский университет экономики и финансов [ФИНЭК] ; под ред. И. И.
Елисеева. — Москва : Юрайт, 2011. — 565 с.
8.Общая теория статистики [Текст] : учебное пособие
для студентов вузов по специальности «Статистика» и другим
экономическим специальностям / С. Н. Лысенко, И. А. Дмитриева. — Москва :
Вузовский учебник, 2011. — 218 с.
9.Выборочный
метод в социально-экономической статистике [Текст] : учебное пособие для
студентов вузов по специальности «Статистика» и другим экономическим
специальностям / Э. К. Васильева, М. М. Юзбашев. — МоскваМосква : Финансы и
статистика : ИНФРА-М, 2010. — 255 с.
10.Теория
статистики [Текст] : учебное пособие / С. А. Бардасов, В. И. Лукина ; Тюменский
университет [ТюмГУ]. Институт дистанционного образования, Тюменский университет
[ТюмГУ]. Международный институт финансов, управления и бизнеса. — Изд. 3-е. —
Тюмень : Тюменский университет, 2010. — 267 с.
11.Практикум
по статистике населения и демографии [Текст] : учебное пособие
для студентов вузов по специальности «Статистика» и другим
экономическим специальностям : допущено Учебно-методическим объединением по
образованию в области статистики / О. Д. Воробьева, А. В. Багат [и др.] ; под
общ. ред. О. Д. Воробьева. — Москва : Финансы и статистика, 2011. — 271 с.
12.Развитие
социально-экономической статистики [Текст] : избранные труды / Н. Н. Ряузов ;
редкол.: А. Н. Романов, В. М. Симчера, Д. Е. Сорокин ; Российская академия наук
[РАН]. Научный совет Программы фундаментальных исследований Президиума РАН
«Издание трудов выдающихся ученых», Российская академия наук [РАН].
Институт экономики. — Москва : Наука, 2009. — 259 с.
13.Финансовая
статистика: денежная и банковская [Текст] : учебник по специальностям
«Финансы и кредит», «Статистика» : рекомендовано
Учебно-методическим центром «Классический учебник» / С. Р. Моисеев,
М. В. Ключников, Е. А. Пищулин. — 2-е изд., перераб. и доп. — Москва : Кнорус,
2010. — 200 с.

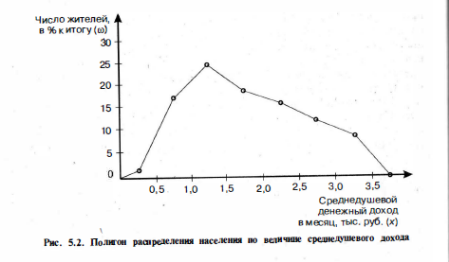

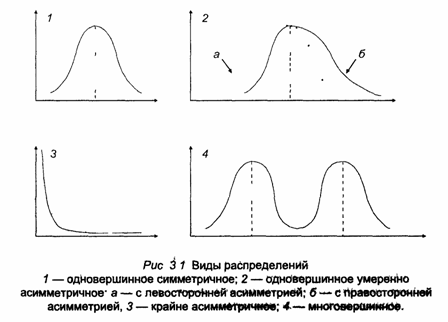



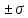 )
)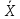 ),
),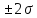 )
) )
)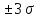 )
)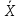 )
)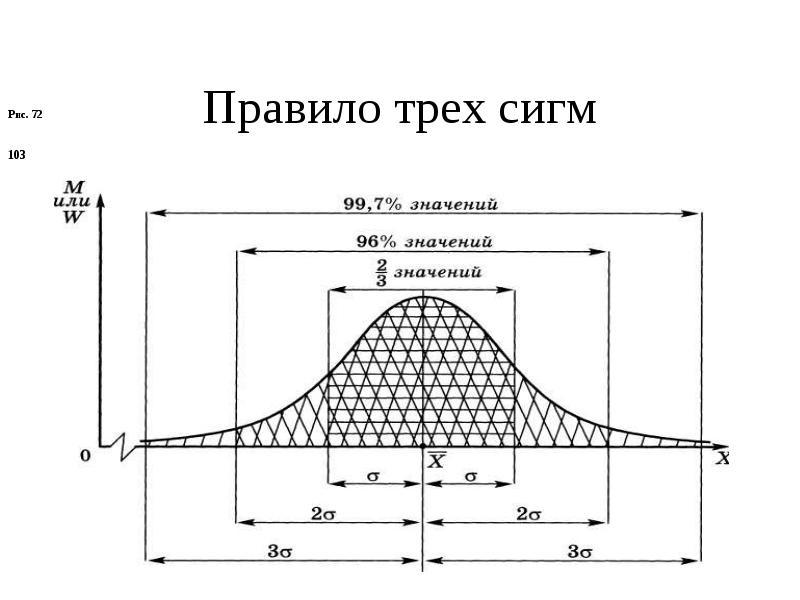
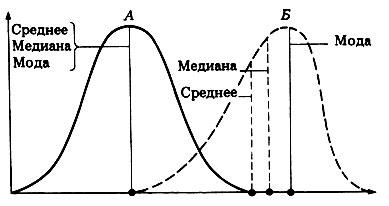
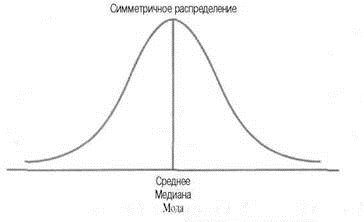

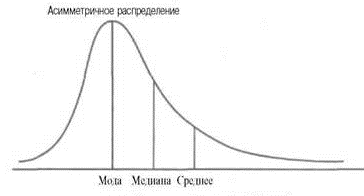

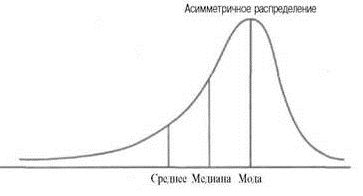
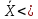
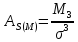
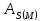
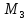
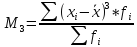
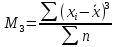
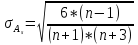
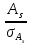
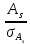

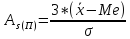


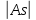
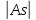

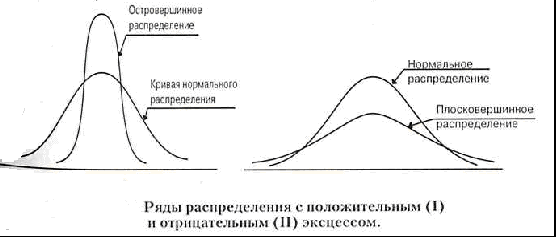

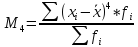
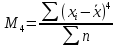
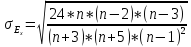
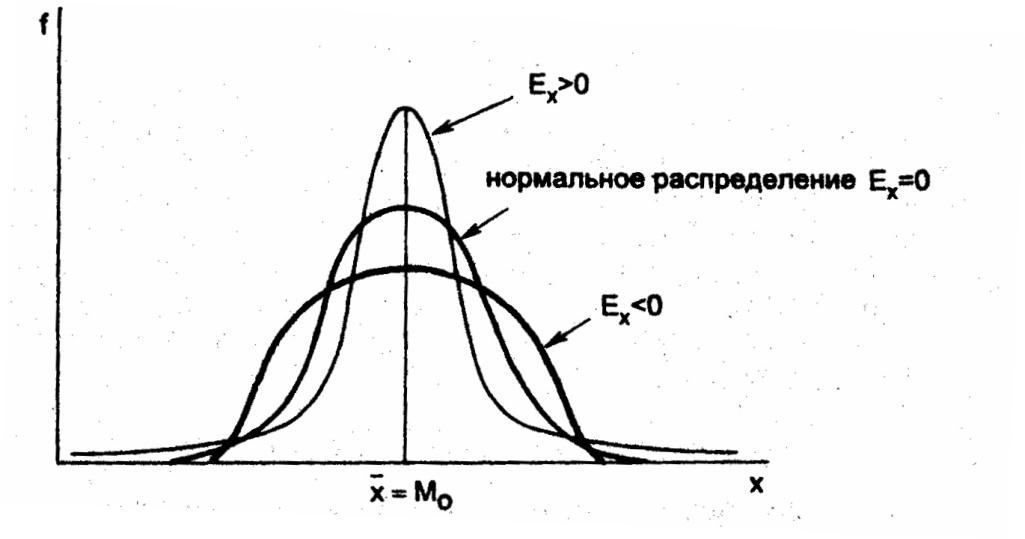



![{displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0e1b3bac58f9ba2d2f4ff8b85b2e35a8f4bf78)

![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}\&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ac524a751828f971013e1297a33ca1cc4c38cd6)
![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]\&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}\&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864646cf4426e2b62a3caf9460382eec1a77fe4e)

![{displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4647a2cc4c8f9a4c90b628faad2dcf80c4aae84)



![{displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]\&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}\&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}\&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf22322412b8454c706d78671e5d94208675a6e0)















