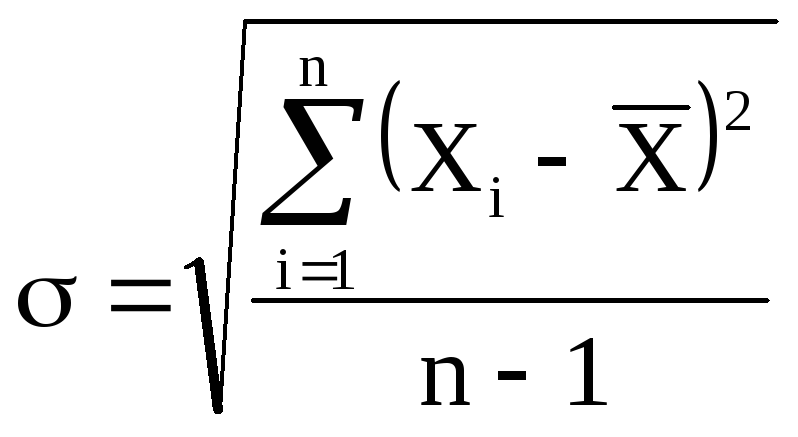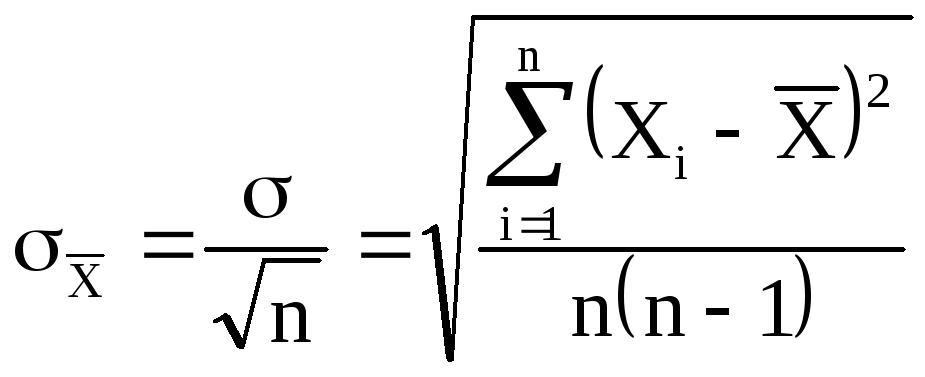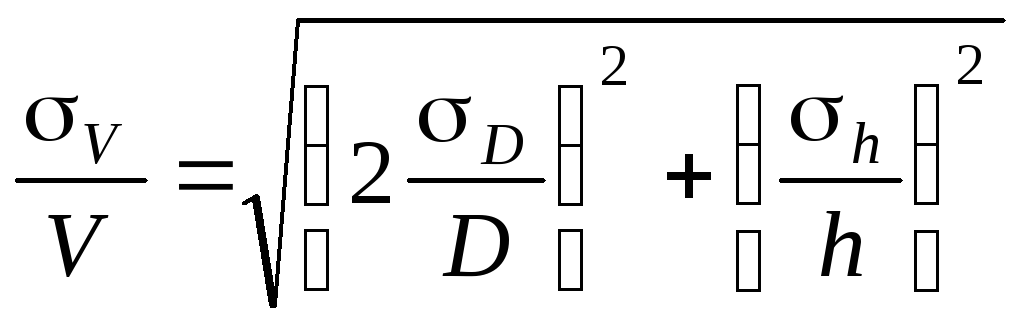From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):
Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:
Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:
Рассчитаем квадрат разницы между Y и Ỹ:
Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott
Средняя квадратичная ошибка.
При ответственных
измерениях, когда необходимо знать
надежность полученных результатов,
используется средняя квадратичная
ошибка (или
стандартное отклонение), которая
определяется формулой
(5)
Величина
характеризует отклонение отдельного
единичного измерения от истинного
значения.
Если мы вычислили
по n
измерениям среднее значение
по формуле (2), то это значение будет
более точным, то есть будет меньше
отличаться от истинного, чем каждое
отдельное измерение. Средняя квадратичная
ошибка среднего значения
равна
(6)
где — среднеквадратичная
ошибка каждого отдельного измерения,
n
– число измерений.
Таким образом,
увеличивая число опытов, можно уменьшить
случайную ошибку в величине среднего
значения.
В настоящее время
результаты научных и технических
измерений принято представлять в виде
(7)
Как показывает
теория, при такой записи мы знаем
надежность полученного результата, а
именно, что истинная величина Х с
вероятностью 68% отличается от
не более, чем на
.
При использовании
же средней арифметической (абсолютной)
ошибки (формула 2) о надежности результата
ничего сказать нельзя. Некоторое
представление о точности проведенных
измерений в этом случае дает относительная
ошибка (формула 4).
При выполнении
лабораторных работ студенты могут
использовать как среднюю абсолютную
ошибку, так и среднюю квадратичную.
Какую из них применять указывается
непосредственно в каждой конкретной
работе (или указывается преподавателем).
Обычно если число
измерений не превышает 3 – 5, то
можно использовать среднюю абсолютную
ошибку. Если число измерений порядка
10 и более, то следует использовать более
корректную оценку с помощью средней
квадратичной ошибки среднего (формулы
5 и 6).
Учет систематических ошибок.
Увеличением числа
измерений можно уменьшить только
случайные ошибки опыта, но не
систематические.
Максимальное
значение систематической ошибки обычно
указывается на приборе или в его паспорте.
Для измерений с помощью обычной
металлической линейки систематическая
ошибка составляет не менее 0,5 мм; для
измерений штангенциркулем –
0,1 – 0,05 мм;
микрометром – 0,01 мм.
Часто в качестве
систематической ошибки берется половина
цены деления прибора.
На шкалах
электроизмерительных приборов указывается
класс точности. Зная класс точности К,
можно вычислить систематическую ошибку
прибора ∆Х по формуле
где К – класс
точности прибора, Хпр – предельное
значение величины, которое может быть
измерено по шкале прибора.
Так, амперметр
класса 0,5 со шкалой до 5А измеряет ток с
ошибкой не более
Погрешность
цифрового прибора равна единице
наименьшего индицируемого разряда.
Среднее значение
полной погрешности складывается из
случайной и систематической
погрешностей.
Ответ с учетом
систематических и случайных ошибок
записывается в виде
Погрешности косвенных измерений
В физических
экспериментах чаще бывает так, что
искомая физическая величина сама на
опыте измерена быть не может, а является
функцией других величин, измеряемых
непосредственно. Например, чтобы
определить объём цилиндра, надо измерить
диаметр D и высоту h, а затем вычислить
объем по формуле
Величины D и h будут измерены с
некоторой ошибкой. Следовательно,
вычисленная величина V
получится также с некоторой ошибкой.
Надо уметь выражать погрешность
вычисленной величины через погрешности
измеренных величин.
Как и при прямых
измерениях можно вычислять среднюю
абсолютную (среднюю арифметическую)
ошибку или среднюю квадратичную ошибку.
Общие правила
вычисления ошибок для обоих случаев
выводятся с помощью дифференциального
исчисления.
Пусть искомая
величина φ является функцией нескольких
переменных Х,
У, Z…
φ(Х,
У, Z…).
Путем прямых
измерений мы можем найти величины
,
а также оценить их средние абсолютные
ошибки
…
или средние квадратичные ошибки Х,
У,
Z…
Тогда средняя
арифметическая погрешность
вычисляется по формуле
где
— частные
производные от φ по
Х, У, Z. Они
вычисляются для средних значений
…
Средняя квадратичная
погрешность вычисляется по формуле
Пример.
Выведем формулы погрешности для
вычисления объёма цилиндра.
а) Средняя
арифметическая погрешность.
Величины
D и h
измеряются соответственно с ошибкой
D
и h.
Погрешность
величины объёма будет равна
б) Средняя
квадратичная погрешность.
Величины
D и h
измеряются соответственно с ошибкой
D,
h.
Погрешность
величины объёма будет равна
Если формула
представляет выражение удобное для
логарифмирования (то есть произведение,
дробь, степень), то удобнее вначале
вычислять относительную погрешность.
Для этого (в случае средней арифметической
погрешности) надо проделать следующее.
1. Прологарифмировать
выражение.
2. Продифференцировать
его.
3. Объединить
все члены с одинаковым дифференциалом
и вынести его за скобки.
4. Взять выражение
перед различными дифференциалами по
модулю.
5. Заменить
значки дифференциалов d
на значки абсолютной погрешности .
В итоге получится
формула для относительной погрешности
Затем,
зная ,
можно вычислить абсолютную погрешность
=
Пример.
Аналогично можно
записать относительную среднюю
квадратичную погрешность
Правила
представления результатов измерения
следующие:
-
погрешность должна
округляться до одной значащей цифры:
правильно = 0,04,
неправильно —
= 0,0382;
-
последняя значащая
цифра результата должна быть того же
порядка величины, что и погрешность:
правильно
= 9,830,03,
неправильно —
= 9,8260,03;
-
если результат
имеет очень большую или очень малую
величину, необходимо использовать
показательную форму записи — одну и ту
же для результата и его погрешности,
причем запятая десятичной дроби должна
следовать за первой значащей цифрой
результата:
правильно —
= (5,270,03)10-5,
неправильно —
= 0,00005270,0000003,
= 5,2710-50,0000003,
=
= 0,0000527310-7,
= (5273)10-7,
= (0,5270,003)
10-4.
-
Если результат
имеет размерность, ее необходимо
указать:
правильно – g=(9,820,02)
м/c2,
неправильно – g=(9,820,02).
Соседние файлы в папке Методички физика
- #
02.04.2015275.46 Кб40оформление заготовки и отчета.ppt
- #
Добро пожаловать на щелчок «Алгоритм и программирование красоты» ↑ Следуйте за нами!
Эта статья начинается с WeChat Public Number: «Алгоритм и программирование красоты», добро пожаловать внимание, своевременно понимаю большую часть этой серии статей.
Значение и формула средней ошибки
Среднеквадратическая ошибка представляет собой более удобный способ измерения «средней ошибки», а степень изменения в данных могут быть оценены. Из категории к прогнозирующей оценке и предиктивной комбинации; от буквальной точки зрения, «все» относятся к среднему, то есть, среднее значение, «дисперсия» используются для измерения случайной величины и его оценки в вероятности метрика. степень отклонения между средним значением, «Mrror» может быть понята как ошибка между измеренным значением и реальным значением.
Формула средней квадратичной ошибки:
MSE =
Деринг двоичных ошибок
Среднеквадратичная ошибка может быть получена с помощью средней ошибки:
Площадь ошибка: указывает на отклонение между экспериментальной ошибки размера. При тех же условиях, каждое измеренное значение XI отказывается подводить для отклонения от истинного значения х, а именно:
Средний квадрат ошибка среднего число расстояния между отклоняются данные от реальной стоимости, поэтому расчетное значение ошибки вычитают реальное значение, а среднее число получается, а именно:
Оцененное значение представляет собой формулу по quascing формулы на величине X и значение Y из предыдущих условий, через формулу, недавно полученное значение Х экстрагируют в оцененном значение Y, в то же время, будет истинное значение Y. В формуле оценок Y и в реальных значениях средней квадратичной ошибки, значение средней квадратичной ошибки получается. Если значение среднеквадратичной ошибки, конструкция подгонки экспериментального данные сильна, но не может сделать это равно 0. Если он равен 0, эта модель показывает , что эта модель полностью оборудована с условиями мы перечисляем, но могут быть некоторые части мы не рассмотрели в реальности.
Это может привести к большим колебаниям модели, поэтому, когда среднее значение квадрата ошибки 0, эта модель не применима, и мы лучше не использовать эту модель.
Разница между тремя среднеквадратической ошибкой и среднеквадратичной ошибкой и средней абсолютной погрешностью
Для того , чтобы лучше понять среднеквадратической ошибки, мы должны понимать знания , подобный среднеквадратичной ошибки, то мы будем понимать среднеквадратической ошибки (MSE) и ошибка корня (СКО) и средняя абсолютная ошибка (МАЕ) Что это :
(1) среднеквадратичная ошибка: среднеквадратическая ошибка является показателем, который отражает степень разницы между расчетной суммой и предполагаемой суммой. Т представляет собой средний квадрат ошибки оцененного кванта Т устанавливаются как сумма оценки общего параметра θ, определяемого в соответствии с образцом. Она равна σ2 + b2, где σ2 и Ь Т, соответственно, дисперсия и смещение Т. Среднеквадратичная ошибка относится к ожидаемому значению разности между значением оценки параметров и истинным значением параметра, он может оценить степень изменения в данных Когда значении СКО, предсказанные данные описания модели эксперимента имеет. более высокая точность.
(2) среднеквадратичная Ошибка: Корень среднеквадратичная ошибка также известна как стандартная ошибка, которая определяется как, i = 1, 2, 3, … п. В ограниченном числе конечных измерений, корень среднего квадрата ошибка часто представляется: √ [σdi2 / п] = RE, режим: п число измерений; Di представляет собой набор измерений и истинных значений. В ограниченном числе конечных измерений, корень среднего квадрата ошибка часто представляется: √ [σdi2 / п] = RE, режим: п число измерений; Di представляет собой набор измерений и истинных значений. Если статистическое распределение ошибок является нормальным распределением, то вероятность случайной ошибки составляет 68% в ± σ. Корень среднего квадрата ошибка является арифметическим квадратным корнем из среднего квадрата ошибки.
(3) средние абсолютная Ошибка: Также называется средняя абсолютная дисперсия, среднее из абсолютных значений все одно значения наблюдения и среднего арифметического. Средняя абсолютная ошибка может избежать проблем ошибки взаимной отмены, так что он может точно отражать размер фактической прогнозной ошибки. Средняя абсолютная погрешность составляет в среднем абсолютных ошибок, а средняя абсолютная ошибка может лучше отражать реальную ситуацию ошибки предсказанного значения.
Резюме
Благодаря этому исследование среднеквадратической ошибки, мы узнали, что средняя ошибка, и вывод среднеквадратичной ошибки достигаются, а также разница между средней квадратической ошибкой, среднеквадратической ошибкой и средней абсолютной погрешностью, мы знаю , как использовать средние меры квадрата ошибки , может ли модель соответствует экспериментальным данным. в практике в будущем, мы стремимся использовать среднюю квадратическую ошибку измерения , может ли модель , которую мы конструкт реализовать ожидаемый эффект , который мы хотим достичь.
Если есть ошибка, надеюсь, что Бог верен!
Более захватывающие статьи:
Советы:Нажмите на правый угол страницы«Напишите сообщение»Опубликовать комментарий, с нетерпением ждем вашего участия! Ждем вашей экспедиции!
17 авг. 2022 г.
читать 3 мин
В статистике регрессионный анализ — это метод, который мы используем для понимания взаимосвязи между переменной-предиктором x и переменной отклика y.
Когда мы проводим регрессионный анализ, мы получаем модель, которая сообщает нам прогнозируемое значение для переменной ответа на основе значения переменной-предиктора.
Один из способов оценить, насколько «хорошо» наша модель соответствует заданному набору данных, — это вычислить среднеквадратичную ошибку , которая представляет собой показатель, который говорит нам, насколько в среднем наши прогнозируемые значения отличаются от наших наблюдаемых значений.
Формула для нахождения среднеквадратичной ошибки, чаще называемая RMSE , выглядит следующим образом:
СКО = √[ Σ(P i – O i ) 2 / n ]
куда:
- Σ — причудливый символ, означающий «сумма».
- P i — прогнозируемое значение для i -го наблюдения в наборе данных.
- O i — наблюдаемое значение для i -го наблюдения в наборе данных.
- n — размер выборки
Технические примечания:
- Среднеквадратичную ошибку можно рассчитать для любого типа модели, которая дает прогнозные значения, которые затем можно сравнить с наблюдаемыми значениями набора данных.
- Среднеквадратичную ошибку также иногда называют среднеквадратичным отклонением, которое часто обозначается аббревиатурой RMSD.
Далее рассмотрим пример расчета среднеквадратичной ошибки в Excel.
Как рассчитать среднеквадратичную ошибку в Excel
В Excel нет встроенной функции для расчета RMSE, но мы можем довольно легко вычислить его с помощью одной формулы. Мы покажем, как рассчитать RMSE для двух разных сценариев.
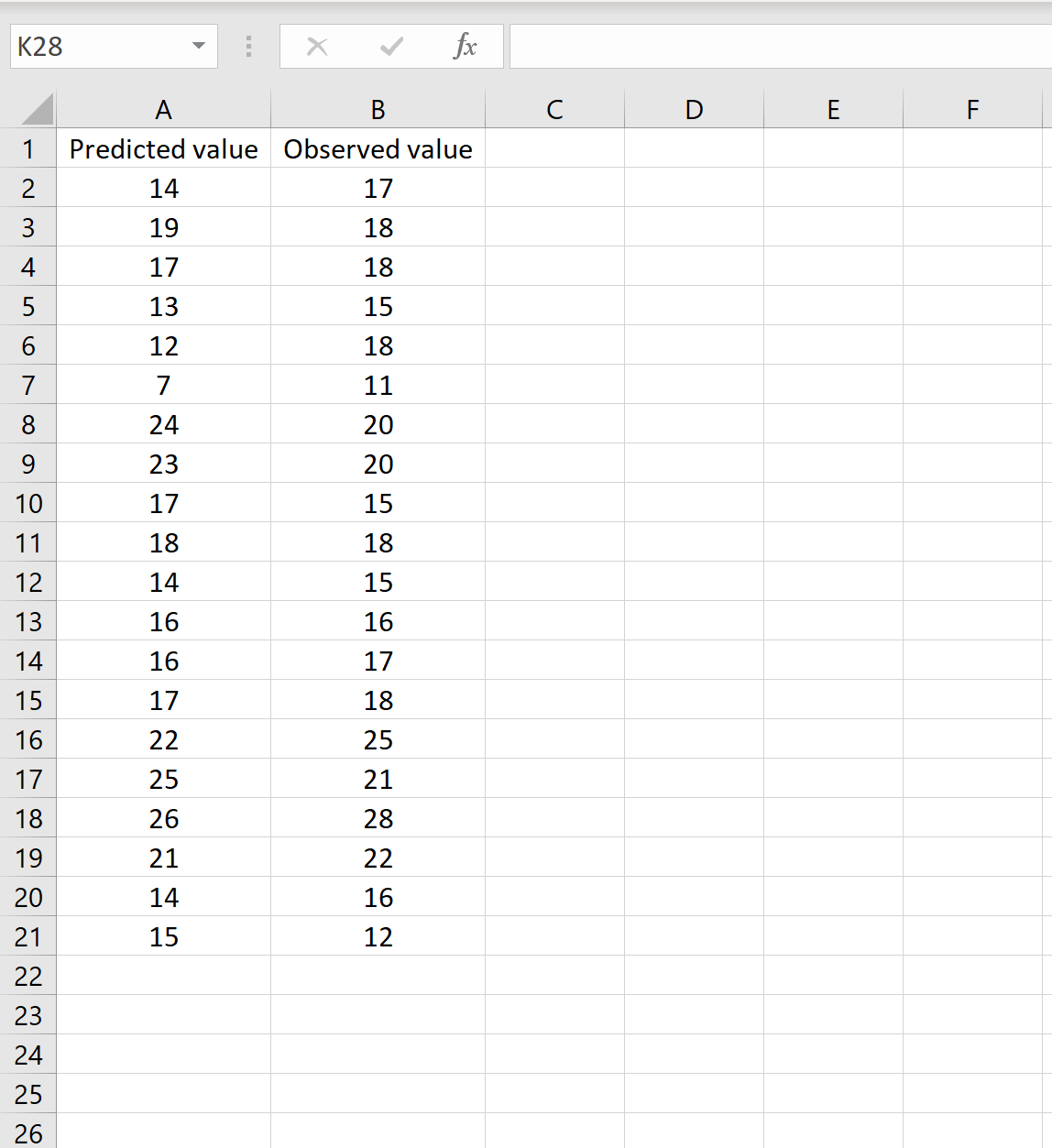
Сценарий 1
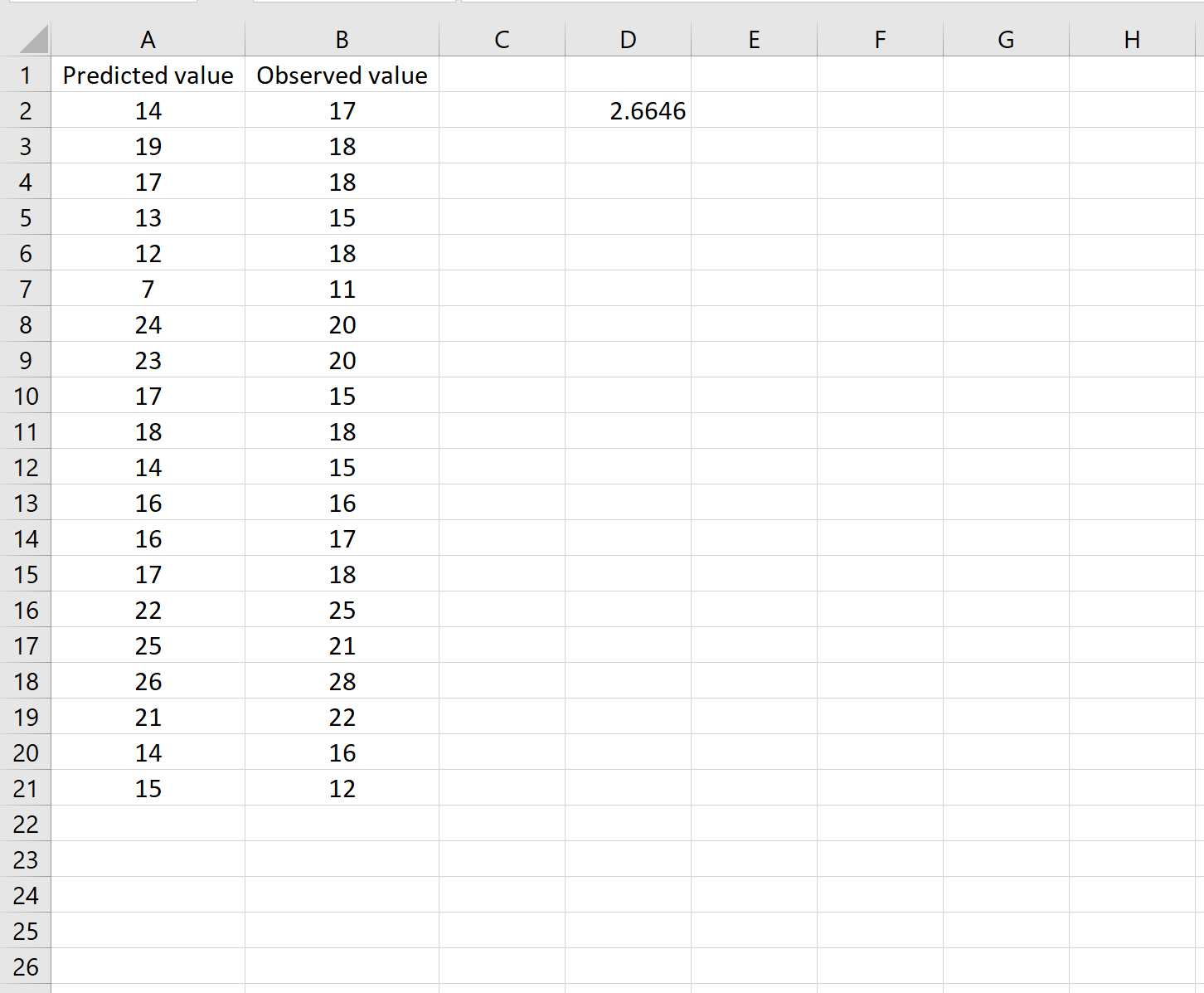
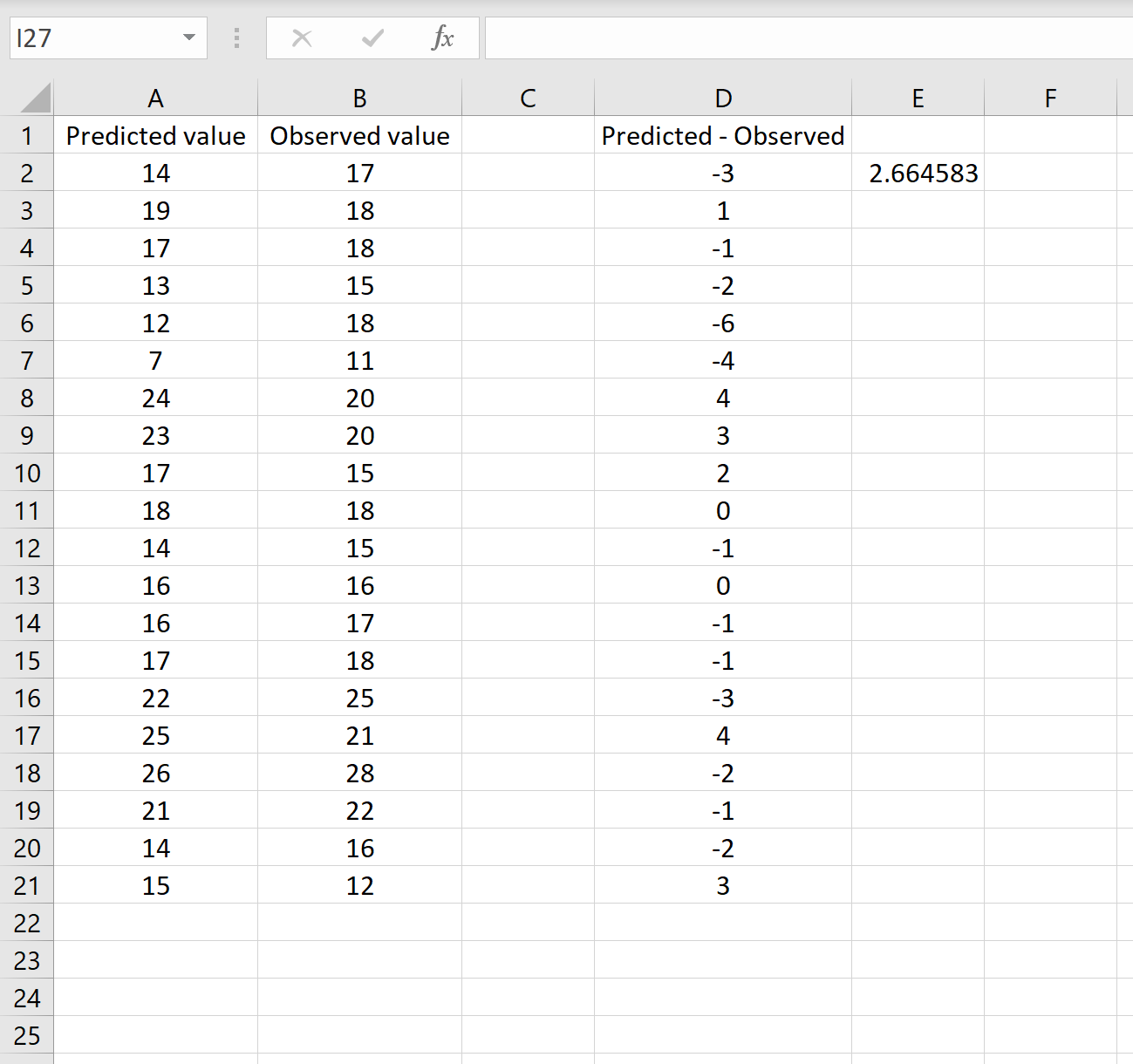
В одном сценарии у вас может быть один столбец, содержащий предсказанные значения вашей модели, и другой столбец, содержащий наблюдаемые значения. На изображении ниже показан пример такого сценария:
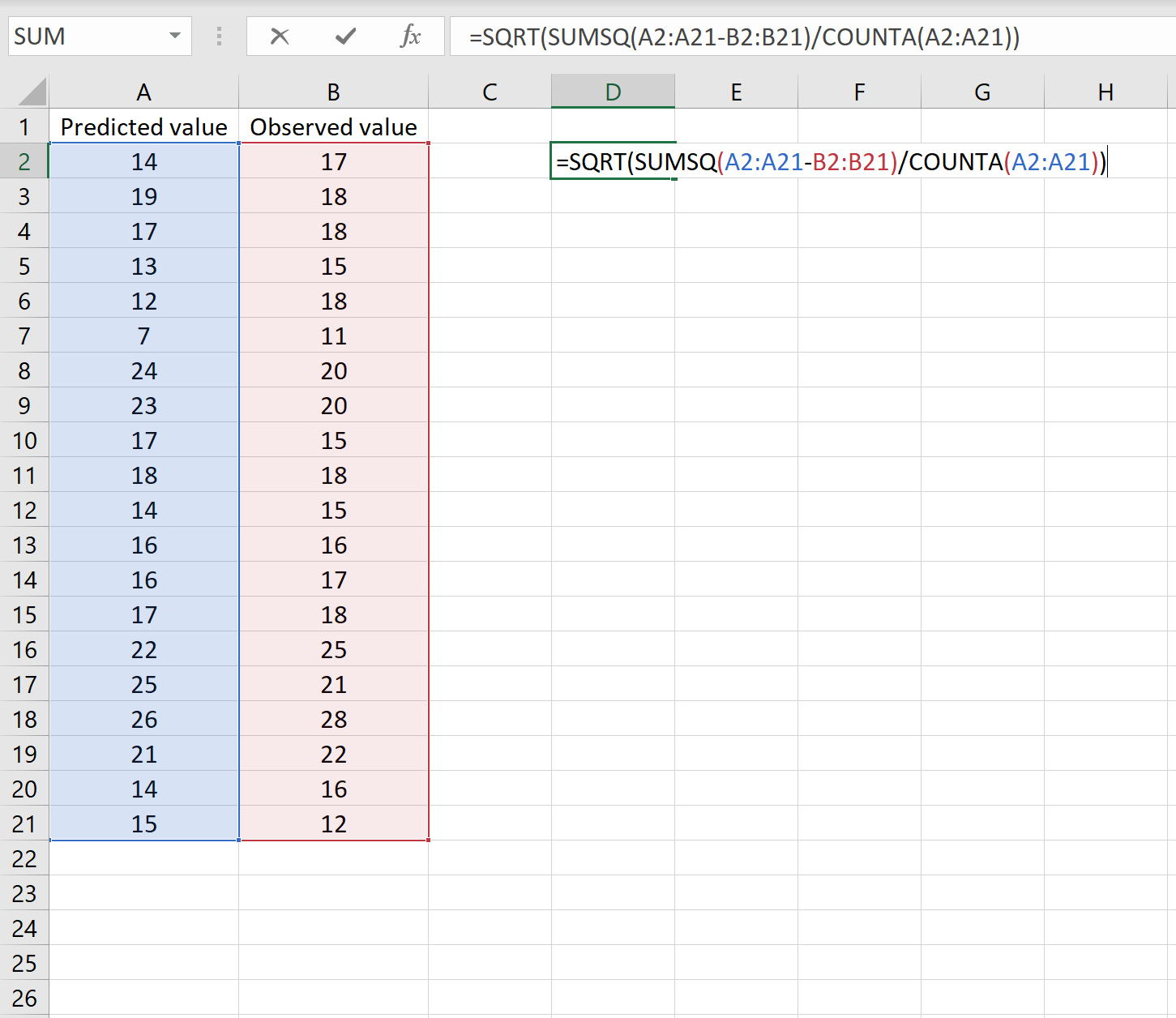
Если это так, то вы можете рассчитать RMSE, введя следующую формулу в любую ячейку, а затем нажав CTRL+SHIFT+ENTER:
=КОРЕНЬ(СУММСК(A2:A21-B2:B21) / СЧЕТЧ(A2:A21))
Это говорит нам о том, что среднеквадратическая ошибка равна 2,6646 .
Формула может показаться немного сложной, но она имеет смысл, если ее разобрать:
= КОРЕНЬ( СУММСК(A2:A21-B2:B21) / СЧЕТЧ(A2:A21) )
- Во-первых, мы вычисляем сумму квадратов разностей между прогнозируемыми и наблюдаемыми значениями, используя функцию СУММСК() .
- Затем мы делим на размер выборки набора данных, используя COUNTA() , который подсчитывает количество непустых ячеек в диапазоне.
- Наконец, мы извлекаем квадратный корень из всего вычисления, используя функцию SQRT() .
Сценарий 2
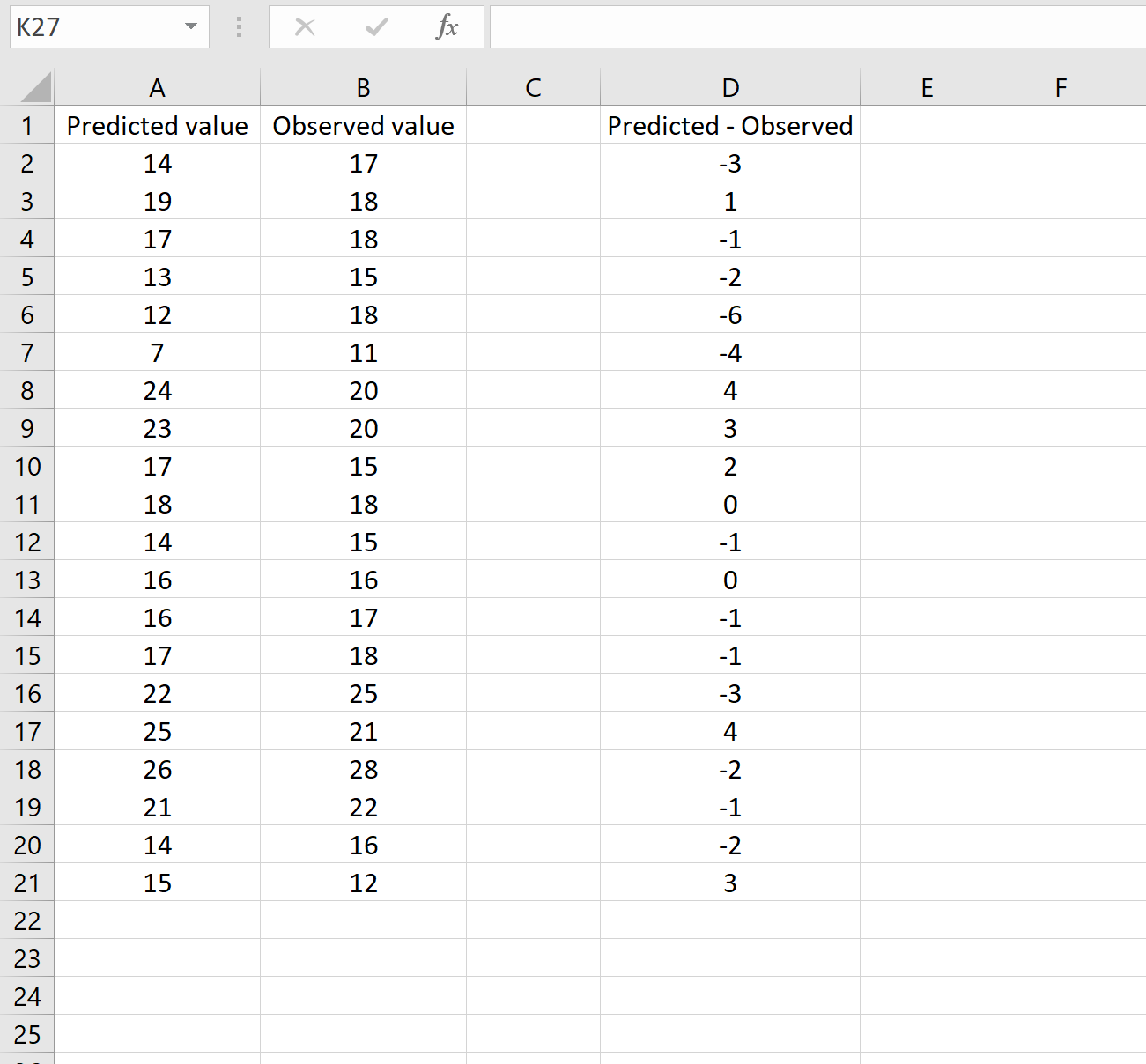
В другом сценарии вы, возможно, уже вычислили разницу между прогнозируемыми и наблюдаемыми значениями. В этом случае у вас будет только один столбец, отображающий различия.
На изображении ниже показан пример этого сценария. Прогнозируемые значения отображаются в столбце A, наблюдаемые значения — в столбце B, а разница между прогнозируемыми и наблюдаемыми значениями — в столбце D:
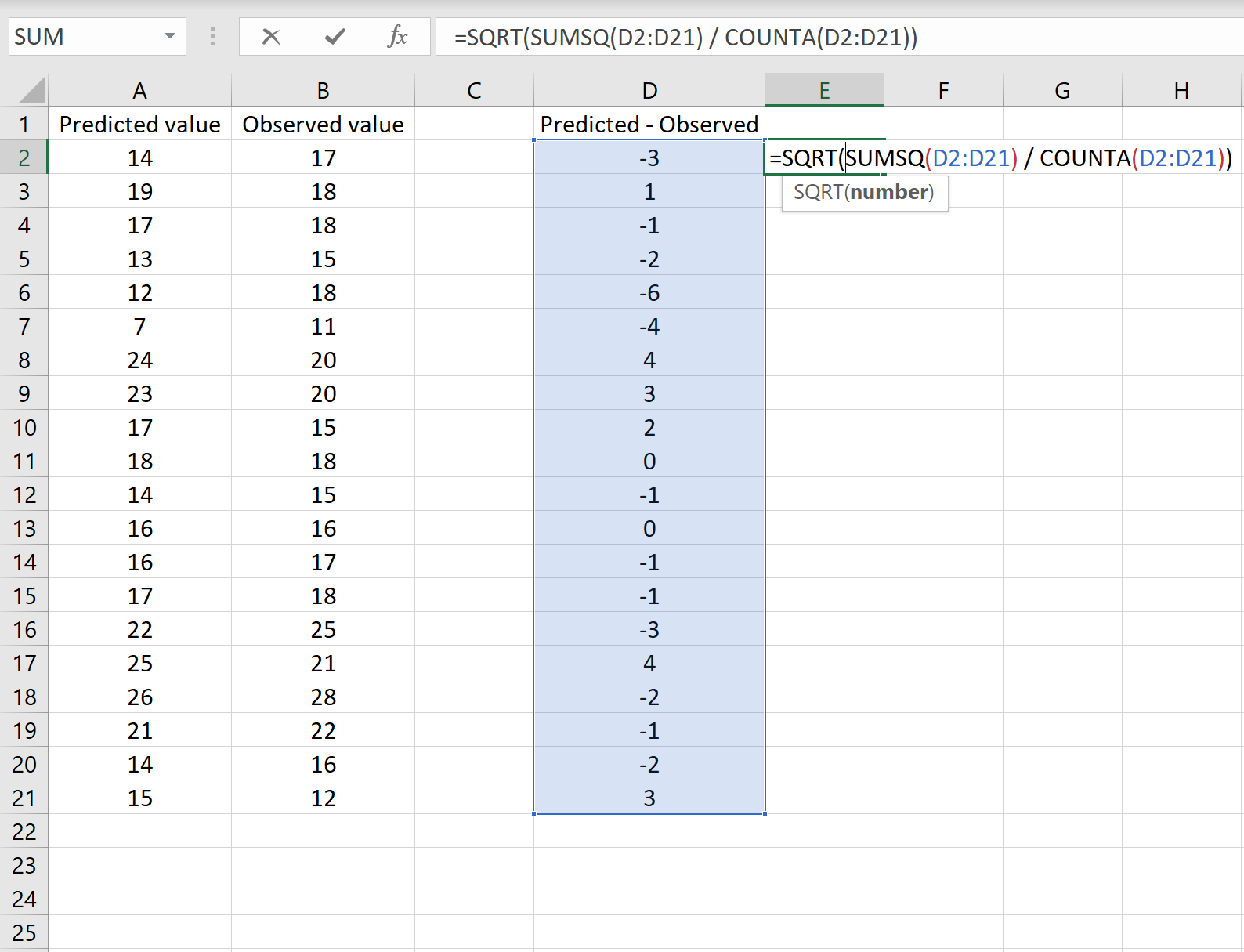
Если это так, то вы можете рассчитать RMSE, введя следующую формулу в любую ячейку, а затем нажав CTRL+SHIFT+ENTER:
=КОРЕНЬ(СУММСК(D2:D21) / СЧЕТЧ(D2:D21))
Это говорит нам о том, что среднеквадратическая ошибка равна 2,6646 , что соответствует результату, полученному в первом сценарии. Это подтверждает, что эти два подхода к расчету RMSE эквивалентны.
Формула, которую мы использовали в этом сценарии, лишь немного отличается от той, что мы использовали в предыдущем сценарии:
= КОРЕНЬ (СУММСК(D2 :D21) / СЧЕТЧ(D2:D21) )
- Поскольку мы уже рассчитали разницу между предсказанными и наблюдаемыми значениями в столбце D, мы можем вычислить сумму квадратов разностей с помощью функции СУММСК().только со значениями в столбце D.
- Затем мы делим на размер выборки набора данных, используя COUNTA() , который подсчитывает количество непустых ячеек в диапазоне.
- Наконец, мы извлекаем квадратный корень из всего вычисления, используя функцию SQRT() .
Как интерпретировать среднеквадратичную ошибку
Как упоминалось ранее, RMSE — это полезный способ увидеть, насколько хорошо регрессионная модель (или любая модель, которая выдает прогнозируемые значения) способна «соответствовать» набору данных.
Чем больше RMSE, тем больше разница между прогнозируемыми и наблюдаемыми значениями, а это означает, что модель регрессии хуже соответствует данным. И наоборот, чем меньше RMSE, тем лучше модель соответствует данным.
Может быть особенно полезно сравнить RMSE двух разных моделей друг с другом, чтобы увидеть, какая модель лучше соответствует данным.
Для получения дополнительных руководств по Excel обязательно ознакомьтесь с нашей страницей руководств по Excel , на которой перечислены все учебные пособия Excel по статистике.
Перевод
Ссылка на автора
Показатели эффективности прогнозирования по временным рядам дают сводку об умениях и возможностях модели прогноза, которая сделала прогнозы.
Есть много разных показателей производительности на выбор. Может быть непонятно, какую меру использовать и как интерпретировать результаты.
В этом руководстве вы узнаете показатели производительности для оценки прогнозов временных рядов с помощью Python.
Временные ряды, как правило, фокусируются на прогнозировании реальных значений, называемых проблемами регрессии. Поэтому показатели эффективности в этом руководстве будут сосредоточены на методах оценки реальных прогнозов.
После завершения этого урока вы узнаете:
- Основные показатели выполнения прогноза, включая остаточную ошибку прогноза и смещение прогноза.
- Вычисления ошибок прогноза временного ряда, которые имеют те же единицы, что и ожидаемые результаты, такие как средняя абсолютная ошибка.
- Широко используются вычисления ошибок, которые наказывают большие ошибки, такие как среднеквадратическая ошибка и среднеквадратичная ошибка.
Давайте начнем.
Ошибка прогноза (или остаточная ошибка прогноза)
ошибка прогноза рассчитывается как ожидаемое значение минус прогнозируемое значение.
Это называется остаточной ошибкой прогноза.
forecast_error = expected_value - predicted_valueОшибка прогноза может быть рассчитана для каждого прогноза, предоставляя временной ряд ошибок прогноза.
В приведенном ниже примере показано, как можно рассчитать ошибку прогноза для серии из 5 прогнозов по сравнению с 5 ожидаемыми значениями. Пример был придуман для демонстрационных целей.
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
forecast_errors = [expected[i]-predictions[i] for i in range(len(expected))]
print('Forecast Errors: %s' % forecast_errors)При выполнении примера вычисляется ошибка прогноза для каждого из 5 прогнозов. Список ошибок прогноза затем печатается.
Forecast Errors: [-0.2, 0.09999999999999998, -0.1, -0.09999999999999998, -0.2]Единицы ошибки прогноза совпадают с единицами прогноза. Ошибка прогноза, равная нулю, означает отсутствие ошибки или совершенный навык для этого прогноза.
Средняя ошибка прогноза (или ошибка прогноза)
Средняя ошибка прогноза рассчитывается как среднее значение ошибки прогноза.
mean_forecast_error = mean(forecast_error)Ошибки прогноза могут быть положительными и отрицательными. Это означает, что при вычислении среднего из этих значений идеальная средняя ошибка прогноза будет равна нулю.
Среднее значение ошибки прогноза, отличное от нуля, указывает на склонность модели к превышению прогноза (положительная ошибка) или занижению прогноза (отрицательная ошибка). Таким образом, средняя ошибка прогноза также называется прогноз смещения,
Ошибка прогноза может быть рассчитана непосредственно как среднее значение прогноза. В приведенном ниже примере показано, как среднее значение ошибок прогноза может быть рассчитано вручную.
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
forecast_errors = [expected[i]-predictions[i] for i in range(len(expected))]
bias = sum(forecast_errors) * 1.0/len(expected)
print('Bias: %f' % bias)При выполнении примера выводится средняя ошибка прогноза, также известная как смещение прогноза.
Bias: -0.100000Единицы смещения прогноза совпадают с единицами прогнозов. Прогнозируемое смещение нуля или очень маленькое число около нуля показывает несмещенную модель.
Средняя абсолютная ошибка
средняя абсолютная ошибка или MAE, рассчитывается как среднее значение ошибок прогноза, где все значения прогноза вынуждены быть положительными.
Заставить ценности быть положительными называется сделать их абсолютными. Это обозначено абсолютной функциейабс ()или математически показано как два символа канала вокруг значения:| Значение |,
mean_absolute_error = mean( abs(forecast_error) )кудаабс ()делает ценности позитивными,forecast_errorодна или последовательность ошибок прогноза, иимею в виду()рассчитывает среднее значение.
Мы можем использовать mean_absolute_error () функция из библиотеки scikit-learn для вычисления средней абсолютной ошибки для списка прогнозов. Пример ниже демонстрирует эту функцию.
from sklearn.metrics import mean_absolute_error
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
mae = mean_absolute_error(expected, predictions)
print('MAE: %f' % mae)При выполнении примера вычисляется и выводится средняя абсолютная ошибка для списка из 5 ожидаемых и прогнозируемых значений.
MAE: 0.140000Эти значения ошибок приведены в исходных единицах прогнозируемых значений. Средняя абсолютная ошибка, равная нулю, означает отсутствие ошибки.
Средняя квадратическая ошибка
средняя квадратическая ошибка или MSE, рассчитывается как среднее значение квадратов ошибок прогноза. Возведение в квадрат значений ошибки прогноза заставляет их быть положительными; это также приводит к большему количеству ошибок.
Квадратные ошибки прогноза с очень большими или выбросами возводятся в квадрат, что, в свою очередь, приводит к вытягиванию среднего значения квадратов ошибок прогноза, что приводит к увеличению среднего квадрата ошибки. По сути, оценка дает худшую производительность тем моделям, которые делают большие неверные прогнозы.
mean_squared_error = mean(forecast_error^2)Мы можем использовать mean_squared_error () функция из scikit-learn для вычисления среднеквадратичной ошибки для списка прогнозов. Пример ниже демонстрирует эту функцию.
from sklearn.metrics import mean_squared_error
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
mse = mean_squared_error(expected, predictions)
print('MSE: %f' % mse)При выполнении примера вычисляется и выводится среднеквадратическая ошибка для списка ожидаемых и прогнозируемых значений.
MSE: 0.022000Значения ошибок приведены в квадратах от предсказанных значений. Среднеквадратичная ошибка, равная нулю, указывает на совершенное умение или на отсутствие ошибки.
Среднеквадратическая ошибка
Средняя квадратичная ошибка, описанная выше, выражается в квадратах единиц прогнозов.
Его можно преобразовать обратно в исходные единицы прогнозов, взяв квадратный корень из среднего квадрата ошибки Это называется среднеквадратичная ошибка или RMSE.
rmse = sqrt(mean_squared_error)Это можно рассчитать с помощьюSQRT ()математическая функция среднего квадрата ошибки, рассчитанная с использованиемmean_squared_error ()функция scikit-learn.
from sklearn.metrics import mean_squared_error
from math import sqrt
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
mse = mean_squared_error(expected, predictions)
rmse = sqrt(mse)
print('RMSE: %f' % rmse)При выполнении примера вычисляется среднеквадратичная ошибка.
RMSE: 0.148324Значения ошибок RMES приведены в тех же единицах, что и прогнозы. Как и в случае среднеквадратичной ошибки, среднеквадратическое отклонение, равное нулю, означает отсутствие ошибки.
Дальнейшее чтение
Ниже приведены некоторые ссылки для дальнейшего изучения показателей ошибки прогноза временных рядов.
- Раздел 3.3 Измерение прогнозирующей точности, Практическое прогнозирование временных рядов с помощью R: практическое руководство,
- Раздел 2.5 Оценка точности прогноза, Прогнозирование: принципы и практика
- scikit-Learn Metrics API
- Раздел 3.3.4. Метрики регрессии, scikit-learn API Guide
Резюме
В этом руководстве вы обнаружили набор из 5 стандартных показателей производительности временных рядов в Python.
В частности, вы узнали:
- Как рассчитать остаточную ошибку прогноза и как оценить смещение в списке прогнозов.
- Как рассчитать среднюю абсолютную ошибку прогноза, чтобы описать ошибку в тех же единицах, что и прогнозы.
- Как рассчитать широко используемые среднеквадратические ошибки и среднеквадратичные ошибки для прогнозов.
Есть ли у вас какие-либо вопросы о показателях эффективности прогнозирования временных рядов или об этом руководстве?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
In the previous post, we saw the various metrics which are used to assess a machine learning model’s performance. Among those, the confusion matrix is used to evaluate a classification problem’s accuracy. On the other hand, mean squared error (MSE), and mean absolute error (MAE) are used to evaluate the regression problem’s accuracy.
F1 score is useful when the size of the positive class is relatively small.
ROC Area Under Curve is useful when we are not concerned about whether the small dataset/class of dataset is positive or not, in contrast to F1 score where the class being positive is important.
In today’s post, we will understand what MAE is and explore more about what it means to vary these metrics. In addition to this, we will discuss a few more metrics that will help us decide if the machine learning model would be useful in real-life scenarios or not.
1. Mean Absolute Error or MAE
We know that an error basically is the absolute difference between the actual or true values and the values that are predicted. Absolute difference means that if the result has a negative sign, it is ignored.
Hence, MAE = True values – Predicted values
MAE takes the average of this error from every sample in a dataset and gives the output.
This can be implemented using sklearn’s mean_absolute_error method:
from sklearn.metrics import mean_absolute_error
# predicting home prices in some area
predicted_home_prices = mycity_model.predict(X)
mean_absolute_error(y, predicted_home_prices)But this value might not be the relevant aspect that can be considered while dealing with a real-life situation because the data we use to build the model as well as evaluate it is the same, which means the model has no exposure to real, never-seen-before data. So, it may perform extremely well on seen data but might fail miserably when it encounters real, unseen data.
The concepts of underfitting and overfitting can be pondered over, from here:
Underfitting: The scenario when a machine learning model almost exactly matches the training data but performs very poorly when it encounters new data or validation set.
Overfitting: The scenario when a machine learning model is unable to capture the important patterns and insights from the data, which results in the model performing poorly on training data itself.
P.S. In the upcoming posts, we will understand how to fit the model in the right way using many methods like feature normalization, feature generation and much more.
2. Mean Squared Error or MSE
MSE is calculated by taking the average of the square of the difference between the original and predicted values of the data.
Hence, MSE =
Here N is the total number of observations/rows in the dataset. The sigma symbol denotes that the difference between actual and predicted values taken on every i value ranging from 1 to n.
This can be implemented using sklearn‘s mean_squared_error method:
from sklearn.metrics import mean_squared_error
actual_values = [3, -0.5, 2, 7]
predicted_values = [2.5, 0.0, 2, 8]
mean_squared_error(actual_values, predicted_values)In most of the regression problems, mean squared error is used to determine the model’s performance.
3. Root Mean Squared Error or RMSE
RMSE is the standard deviation of the errors which occur when a prediction is made on a dataset. This is the same as MSE (Mean Squared Error) but the root of the value is considered while determining the accuracy of the model.
from sklearn.metrics import mean_squared_error
from math import sqrt
actual_values = [3, -0.5, 2, 7]
predicted_values = [2.5, 0.0, 2, 8]
mean_squared_error(actual_values, predicted_values)
# taking root of mean squared error
root_mean_squared_error = sqrt(mean_squared_error)4. R Squared
It is also known as the coefficient of determination. This metric gives an indication of how good a model fits a given dataset. It indicates how close the regression line (i.e the predicted values plotted) is to the actual data values. The R squared value lies between 0 and 1 where 0 indicates that this model doesn’t fit the given data and 1 indicates that the model fits perfectly to the dataset provided.
import numpy as np
X = np.random.randn(100)
y = np.random.randn(60) # y has nothing to do with X whatsoever
from sklearn.linear_model import LinearRegression
from sklearn.cross_validation import cross_val_score
scores = cross_val_score(LinearRegression(), X, y,scoring='r2')Where to use which Metric to determine the Performance of a Machine Learning Model?
MAE: It is not very sensitive to outliers in comparison to MSE since it doesn’t punish huge errors. It is usually used when the performance is measured on continuous variable data. It gives a linear value, which averages the weighted individual differences equally. The lower the value, better is the model’s performance.
MSE: It is one of the most commonly used metrics, but least useful when a single bad prediction would ruin the entire model’s predicting abilities, i.e when the dataset contains a lot of noise. It is most useful when the dataset contains outliers, or unexpected values (too high or too low values).
RMSE: In RMSE, the errors are squared before they are averaged. This basically implies that RMSE assigns a higher weight to larger errors. This indicates that RMSE is much more useful when large errors are present and they drastically affect the model’s performance. It avoids taking the absolute value of the error and this trait is useful in many mathematical calculations. In this metric also, the lower the value, better is the performance of the model.
You may also like:
- How Good is my Machine Learning Model? How do I improve its Performance?
- Machine Learning — How to deal with missing data using Python?
- Machine Learning and Data Visualization using Orange
- Designing a Learning System | The first step to Machine Learning
In the previous post, we saw the various metrics which are used to assess a machine learning model’s performance. Among those, the confusion matrix is used to evaluate a classification problem’s accuracy. On the other hand, mean squared error (MSE), and mean absolute error (MAE) are used to evaluate the regression problem’s accuracy.
F1 score is useful when the size of the positive class is relatively small.
ROC Area Under Curve is useful when we are not concerned about whether the small dataset/class of dataset is positive or not, in contrast to F1 score where the class being positive is important.
In today’s post, we will understand what MAE is and explore more about what it means to vary these metrics. In addition to this, we will discuss a few more metrics that will help us decide if the machine learning model would be useful in real-life scenarios or not.
1. Mean Absolute Error or MAE
We know that an error basically is the absolute difference between the actual or true values and the values that are predicted. Absolute difference means that if the result has a negative sign, it is ignored.
Hence, MAE = True values – Predicted values
MAE takes the average of this error from every sample in a dataset and gives the output.
This can be implemented using sklearn’s mean_absolute_error method:
from sklearn.metrics import mean_absolute_error
# predicting home prices in some area
predicted_home_prices = mycity_model.predict(X)
mean_absolute_error(y, predicted_home_prices)But this value might not be the relevant aspect that can be considered while dealing with a real-life situation because the data we use to build the model as well as evaluate it is the same, which means the model has no exposure to real, never-seen-before data. So, it may perform extremely well on seen data but might fail miserably when it encounters real, unseen data.
The concepts of underfitting and overfitting can be pondered over, from here:
Underfitting: The scenario when a machine learning model almost exactly matches the training data but performs very poorly when it encounters new data or validation set.
Overfitting: The scenario when a machine learning model is unable to capture the important patterns and insights from the data, which results in the model performing poorly on training data itself.
P.S. In the upcoming posts, we will understand how to fit the model in the right way using many methods like feature normalization, feature generation and much more.
2. Mean Squared Error or MSE
MSE is calculated by taking the average of the square of the difference between the original and predicted values of the data.
Hence, MSE =
Here N is the total number of observations/rows in the dataset. The sigma symbol denotes that the difference between actual and predicted values taken on every i value ranging from 1 to n.
This can be implemented using sklearn‘s mean_squared_error method:
from sklearn.metrics import mean_squared_error
actual_values = [3, -0.5, 2, 7]
predicted_values = [2.5, 0.0, 2, 8]
mean_squared_error(actual_values, predicted_values)In most of the regression problems, mean squared error is used to determine the model’s performance.
3. Root Mean Squared Error or RMSE
RMSE is the standard deviation of the errors which occur when a prediction is made on a dataset. This is the same as MSE (Mean Squared Error) but the root of the value is considered while determining the accuracy of the model.
from sklearn.metrics import mean_squared_error
from math import sqrt
actual_values = [3, -0.5, 2, 7]
predicted_values = [2.5, 0.0, 2, 8]
mean_squared_error(actual_values, predicted_values)
# taking root of mean squared error
root_mean_squared_error = sqrt(mean_squared_error)4. R Squared
It is also known as the coefficient of determination. This metric gives an indication of how good a model fits a given dataset. It indicates how close the regression line (i.e the predicted values plotted) is to the actual data values. The R squared value lies between 0 and 1 where 0 indicates that this model doesn’t fit the given data and 1 indicates that the model fits perfectly to the dataset provided.
import numpy as np
X = np.random.randn(100)
y = np.random.randn(60) # y has nothing to do with X whatsoever
from sklearn.linear_model import LinearRegression
from sklearn.cross_validation import cross_val_score
scores = cross_val_score(LinearRegression(), X, y,scoring='r2')Where to use which Metric to determine the Performance of a Machine Learning Model?
MAE: It is not very sensitive to outliers in comparison to MSE since it doesn’t punish huge errors. It is usually used when the performance is measured on continuous variable data. It gives a linear value, which averages the weighted individual differences equally. The lower the value, better is the model’s performance.
MSE: It is one of the most commonly used metrics, but least useful when a single bad prediction would ruin the entire model’s predicting abilities, i.e when the dataset contains a lot of noise. It is most useful when the dataset contains outliers, or unexpected values (too high or too low values).
RMSE: In RMSE, the errors are squared before they are averaged. This basically implies that RMSE assigns a higher weight to larger errors. This indicates that RMSE is much more useful when large errors are present and they drastically affect the model’s performance. It avoids taking the absolute value of the error and this trait is useful in many mathematical calculations. In this metric also, the lower the value, better is the performance of the model.
You may also like:
- How Good is my Machine Learning Model? How do I improve its Performance?
- Machine Learning — How to deal with missing data using Python?
- Machine Learning and Data Visualization using Orange
- Designing a Learning System | The first step to Machine Learning




![{displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0e1b3bac58f9ba2d2f4ff8b85b2e35a8f4bf78)

![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}\&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ac524a751828f971013e1297a33ca1cc4c38cd6)
![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]\&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}\&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864646cf4426e2b62a3caf9460382eec1a77fe4e)

![{displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4647a2cc4c8f9a4c90b628faad2dcf80c4aae84)



![{displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]\&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}\&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}\&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf22322412b8454c706d78671e5d94208675a6e0)