Среднеквадратичная ошибка нейронной сети - Исправление ошибок и поиск оптимальных решений проблем

Заранее хочу отметить, что тот кто знает как обучается персептрон — в этой статье вряд ли найдет что-то новое. Вы можете смело пропускать ее. Почему я решил это написать — я хотел бы написать цикл статей, связанных с нейронными сетями и применением TensorFlow.js, ввиду этого я не мог опустить общие теоретические выдержки. Поэтому прошу отнестись с большим терпением и пониманием к конечной задумке.

При классическом программировании разработчик описывает на конкретном языке программирования определённый жестко заданный набор правил, который был определен на основании его знаний в конкретной предметной области и который в первом приближении описывает процессы, происходящие в человеческом мозге при решении аналогичной задачи.

Например, может быть запрограммирована стратегия игры в крестики-нолики, шахмат и другое (рисунок 1).

Рисунок 1 – Классический подход решения задач

В то время как алгоритмы машинного обучения могут определять набор правил для решения задач без участия разработчика, а только на базе наличия тренировочного набора данных.
Тренировочный набор — это какой-то набор входных данных ассоциированный с набором ожидаемых результатов (ответами, выходными данными). На каждом шаге обучения, модель за счет изменения внутреннего состояния, будет оптимизировать и уменьшать ошибку между фактическим выходным результатом модели и ожидаемым результатом (рисунок 2).

Рисунок 2 – Машинное обучение

Нейронные сети

Долгое время учёные, вдохновляясь процессами происходящими в нашем мозге, пытались сделать реверс-инжиниринг центральной нервной системы и попробовать сымитировать работу человеческого мозга. Благодаря этому родилось целое направление в машинном обучении — нейронные сети.

На рисунке 3 вы можете увидеть сходство между устройством биологического нейрона и математическим представлением нейрона, используемого в машинном обучении.

Рисунок 3 – Математическое представление нейрона

В биологическом нейроне, нейрон получает электрические сигналы от дендритов, модулирующих электрические сигналы с разной силой, которые могут возбуждать нейрон при достижении некоторого порогового значения, что в свою очередь приведёт к передаче электрического сигнала другим нейронам через синапсы.

Персептрон

Математическая модель нейронной сети, состоящего из одного нейрона, который выполняет две последовательные операции (рисунок 4):

вычисляет сумму входных сигналов с учетом их весов (проводимости или сопротивления) связи
${sum= vec{X}}^Tvec{W}+vec{B}=sum_{i=1}^{n}{x_iw_i}+b$
применяет активационную функцию к общей сумме воздействия входных сигналов.

Рисунок 4 – Математическая модель персептрона

В качестве активационной функции может использоваться любая дифференцируемая функция, наиболее часто используемые приведены в таблице 1. Выбор активационной функции ложиться на плечи инженера, и обычно этот выбор основан или на уже имеющемся опыте решения похожих задач, ну или просто методом подбора.

Заметка

Однако есть рекомендация – что если нужна нелинейность в нейронной сети, то в качестве активационной функции лучше всего подходит ReLU функция, которая имеет лучшие показатели сходимости модели во время процесса обучения.

Таблица 1 — Распространенные активационные функции

Процесс обучения персептрона

Процесс обучения состоит из несколько шагов. Для большей наглядности, рассмотрим некую вымышленную задачу, которую мы будем решать нейронной сетью, состоящей из одного нейрона с линейной активационной функции (это по сути персептрон без активационной функции вовсе), также для упрощения задачи – исключим в нейроне узел смещения b (рисунок 5).

Рисунок 5 – Обучающий набор данных и состояние нейронной сети на предыдущем шаге обучения

На данном этапе мы имеем нейронную сеть в некотором состоянии с определенными весами соединений, которые были вычислены на предыдущем этапе обучения модели или если это первая итерация обучения – то значения весов соединений выбраны в произвольном порядке.

Итак, представим, что мы имеем некоторый набор тренировочных данных, значения каждого элемента из набора представлены вектором входных данных (input data), содержащих 2 параметра (feature) . Под в модели в зависимости от рассматриваемой предметной области может подразумеваться все что угодно: количество комнат в доме, расстояние дома от моря, ну или мы просто пытаемся обучить нейронную сеть логической операции И, или ИЛИ.

Каждый вектор входных данных в тренировочном наборе сопоставлен с вектором ожидаемого результата (expected output). В данном случае вектор выходных данных содержит только один параметр, которые опять же в зависимости от выбранной предметной области может означать все что угодно – цена дома, результат выполнения логической операции И или ИЛИ.

ШАГ 1 — Прямое распространение ошибки (feedforward process)
На данном шаге мы вычисляем сумму входных сигналов с учетом веса каждой связи и применяем активационную функцию (в нашем случае активационной функции нет). Сделаем вычисления для первого элемента в обучающем наборе:

$y_{predicted}=sum_{i=1}^{n}{x_iw_i}=1cdot0.1+0.5cdot0.2=0.2$

Рисунок 6 – Прямое распространение ошибки

Обратите внимание, что написанная формула выше – это упрощенное математическое уравнение для частного случая операций над тензорами.

Тензор – это по сути контейнер данных, который может иметь N осей и произвольное число элементов вдоль каждой из осей. Большинство с тензорами знакомы с математики – векторы (тензор с одной осью), матрицы (тензор с двумя осями – строки, колонки).
Формулу можно написать в следующем виде, где вы увидите знакомые матрицы (тензоры) и их перемножение, а также поймете о каком упрощении шла речь выше:

${vec{Y}}_{predicted}= {vec{X}}^Tvec{W}=left[begin{matrix}x_1\x_2\end{matrix}right]^Tcdot left [ begin{matrix} w_1\ w_2 end{matrix} right ]=left [ begin{matrix} x_1 & x_2 end{matrix} right ] cdot left [ begin{matrix} w_1\ w_2 end{matrix} right ] =left [ x_1w_1+x_2w_2 right ]$

ШАГ 2 — Расчет функции ошибки
Функция ошибка – это метрика, отражающая расхождение между ожидаемыми и полученными выходными данными. Обычно используют следующие функции ошибки:
— среднеквадратичная ошибка (Mean Squared Error, MSE) – данная функция ошибки особенно чувствительна к выбросам в тренировочном наборе, так как используется квадрат от разности фактического и ожидаемого значений (выброс — значение, которое сильно удалено от других значений в наборе данных, которые могут иногда появляться в следствии ошибок данных, таких как смешивание данных с разными единицами измерения или плохие показания датчиков):

$L=frac{1}{N}sum_{i=1}^{N}left(y_{predicted(i)}-y_{expected(i)}right)^2$

— среднеквадратичное отклонение (Root MSE) – по сути это тоже самое что, среднеквадратичная ошибка в контексте нейронных сетей, но может отражать реальную физическую единицу измерения, например, если в нейронной сети выходным параметров нейронной сети является цена дома выраженной в долларах, то единица измерения среднеквадратичной ошибки будет доллар квадратный ( $$^2$ ), а для среднеквадратичного отклонения это доллар ($), что естественно немного упрощает задачу анализа человеком:

$L=sqrt{frac{1}{N}sum_{i=1}^{N}left(y_{predicted(i)}-y_{expected(i)}right)^2}$

— среднее отклонение (Mean Absolute Error, MAE) -в отличии от двух выше указанных значений, является не столь чувствительной к выбросам:

$L=frac{1}{N}sum_{i=1}^{N}left|y_{predicted(i)}-y_{expected(i)}right|$

— перекрестная энтропия (Cross entropy) – использует для задач классификации:

$L=-sum_{i=1}^{N}sum_{j=1}^{M}{y_{expected(ij)}log(y_{predicted(ij)})}$

где
$N$ – число экземпляров в тренировочном наборе
$M$ – число классов при решении задач классификации
$y_{expected}$ — ожидаемое выходное значение
$y_{predicted}$ – фактическое выходное значение обучаемой модели

Для нашего конкретного случая воспользуемся MSE:

$L=frac{1}{N}sum_{i=1}^{N}left(y_{predicted(i)}-y_{expected(i)}right)^2={(0.2-1)}^2=0.64$

ШАГ 3 — Обратное распространение ошибки (backpropagation)
Цель обучения нейронной сети проста – это минимизация функции ошибки:

Одним способом найти минимум функции – это на каждом очередном шаге обучения модифицировать веса соединений в направлении противоположным вектору-градиенту – метод градиентного спуска, и это математически выглядит так:

${vec{w}}^{(k+1)}={vec{w}}^k-munabla L({vec{w}}^k)$

где $k$ – k -ая итерация обучения нейронной сети;
$mu$ – шаг обучения (learning rate) и задается инженером, обычно это может быть 0.1; 0.01 (о том как шаг обучения влияет на процесс сходимости обучения отметить чуть позже)
– градиент функции-ошибки
Для нахождения градиента, используем частные производные по настраиваемым аргументам :

$nabla Lleft(vec{w}right)=left[begin{matrix}frac{partial L}{partial w_1}\vdots\frac{partial L}{partial w_N}\end{matrix}right]$

В нашем конкретном случае с учетом всех упрощений, функция ошибки принимает вид:

$Lleft(w_1,w_2right)={(y_{predicted}-y_{expected})}^2={(x_1w_1+x_2w_2-y_{expected})}^2=$

$={(1cdot w_1+0.5cdot w_2-1)}^2$

Памятка формул производных

Напомним некоторые формулы производных, которые пригодятся для вычисления частных производных

Найдем следующие частные производные:

$frac{partial}{partial w_1}{(w_1+0.5w_2-1)}^2=2cdotleft(w_1+0.5w_2-1right)frac{partial}{partial w_1}left(w_1+0.5w_2-1right)=$

$frac{partial}{partial w_2}{(w_1+0.5w_2-1)}^2=2cdotleft(w_1+0.5w_2-1right)frac{partial}{partial w_2}left(w_1+0.5w_2-1right)=$

Тогда процесс обратного распространения ошибки – движение по модели от выхода по направлению к входу с модификацией весов модели в направлении обратном вектору градиента. Задавая обучающий шаг 0.1 (learning rate) имеем (рисунок 7):

$w_1^{(k+1)}=w_1^{(k)}-mufrac{partial Lleft(w_1,w_2right)}{partial w_1}=0.1-0.1cdotleft(-1.6right)=0.26$

$w_2^{(k+1)}=w_2^{(k)}-mufrac{partial Lleft(w_1,w_2right)}{partial w_2}=0.2-0.1cdotleft(-0.8right)=0.28$

Рисунок 7 – Обратное распространение ошибки
Таким образом мы завершили k+1 шаг обучения, чтобы убедиться, что ошибка снизилась, а выход от модели с новыми весами стал ближе к ожидаемому выполним процесс прямого распространения ошибки по модели с новыми весами (см. ШАГ 1):

$y_{predicted}=x_1w_1+x_2w_2=1cdot0.26+0.5cdot0.28=0.4$

Как видим, выходное значение увеличилось на 0.2 единица в верном направлении к ожидаемому результату – единице (1). Ошибка тогда составит:

$L={(0.4-1)}^2=0.36$

Как видим, на предыдущем шаге обучения ошибка составила 0.64, а с новыми весами – 0.36, следовательно мы настроили модель в верном направлении.

Следующая часть статьи:
Машинное обучение. Нейронные сети (часть 2): Моделирование OR; XOR с помощью TensorFlow.js
Машинное обучение. Нейронные сети (часть 3) — Convolutional Network под микроскопом. Изучение АПИ Tensorflow.js

Источник

Содержание

Нейронные сети: 4. Обучение
Введение
Нейрон
Однослойная сеть
Усреднение градиента
Контроль уверенности нейрона
Двухслойная сеть
Обратное распространение ошибки
Нейронные сети: 1. Основы
Введение
Объекты и их признаки
Обучение с учителем
Нейрон
Сеть нейронов
Нейрон как гиперплоскость
Уверенность нейрона
Полезность нейрона
Несколько выходов
Когда нужен скрытый слой
Нейроны как логические элементы
Четыре варианта xor
Аппроксимация функции y=f(x)
Аппроксимация функции на Phyton
Нечёткая логика

Нейронные сети: 4. Обучение

Введение

Этот документ продолжает тему нейронных сетей. Мы обсудим различные методы их обучения и трудности, возникающие при этом.

Нейрон

SBigr(sum^n_ omega_i x_i Bigr),

S(d) = frac<1><1+e^<-d>> $$ Производную сигмоидной функции можно выразить через значение выхода нейрона: beginlabel S'(d) = frac><(1+e^<-d>)^2>=S(d),bigr(1-S(d)bigr) = y,(1-y). end Если $ysim 0$ или $ysim 1$ производная $S'(d)$ очень мала (горизонтальные участки сигмоиды). Максимальное значение $1/4$ производной (наибольшая чувствительность нейрона) достигается при при $y=1/2$ или $d=0$.

Однослойная сеть

Пусть на вход нейрона подаётся вектор $mathbf$, в результате чего на выходе получется значение $y$. И пусть на самом деле значению $mathbf$ должен соответствовать выход $Y$. Определим ошибку «работы нейрона», как среднеквадратичное отклонение желаемого выхода от фактического: $$ E^2 = bigr(Y-y(omega,,mathbf)bigr)^2. $$ Задача обучения нейрона состоит в минимизации этой ошибки. Вычислим градиент ошибки. Он направлен в сторону её максимального роста (в обратном направлении ошибка убывает): $$ frac <partial E^2>

-2,(Y-y)cdot y,(1-y)cdot x_i, $$ где учтена производная сигмоидной функции (ref). Таким образом, вектор нормали $boldsymbol<omega>$ и смещение необходимо сдвинуть против градиента на величины: begin Deltaboldsymbol <omega>= 2,gamma,(Y-y),y,(1-y),mathbf,

Deltaomega_0 = 2,gamma,(Y-y),y,(1-y), end где абсолютную величину сдвига (шаг) задаёт параметр $gamma$.

Геометрический смысл этих формул прост. Пусть $Y=1$, а нейрон выдаёт $y ll 1$. Тогда вектор нормали (и плоскость) повернётся в сторону примера $mathbf$, а $omega_0$ увеличится, т.е. плоскость сдвинется в противоположную от входа сторону. Когда $Y=0$, а $y sim 1$, множитель $Y-y$ становится отрицательным и всё произойдёт с точностью до наоборот.

На самом деле, множители $ycdot(1-y)$ вредят обучению. Например, пусть $ysim 0$, а необходимо иметь $Y=1$. В этом случае сдвиг $omega_i$ должен быть существенным, а этого не происходит. Без изменения направления градиента, можно использовать другие формулы: $$ Deltaboldsymbol <omega>= gamma,f(Y-y),mathbf,

Deltaomega_0 = gamma,f(Y-y), $$ где $f(z)$ — гладкая, нечётная функция, имеющая малые значения при $zsim 0$ (когда $Yapprox y$) и большие по модулю при $zneq 0$. Вместо линейной зависимости, можно, например, выбрать $(Y-y)^3$.

Усреднение градиента

Минимизируемая поверхность с кучей вмятинок будет приводить к «дёрганью» градиента. Чтобы уменьшить такой эффект, прежде чем изменять параметры нейрона $omega_i=<omega_0,boldsymbol<omega>>$, приращения $Deltaomega_i$ усредняются по нескольким примерам. Такую «пачку» объектов называют bunch. В банче могут быть, как примеры различных классов, так и одного. В последнем случае скорость передвижения вдоль градиента необходимо существенно уменьшить.

Ещё один способ сглаживания градиента — это скользящее среднее. Получив очередное значение $Deltaomega_i(t)$, вычисляется $$ overline<Deltaomega_i>(t) = betacdotoverline<Deltaomega_i>(t-1)+(1-beta)cdotDeltaomega_i(t). $$ Если параметр $beta=0$, то усреднения нет. При $betato 1$ происходит сильное усреднение. Параметры нейрона меняются по формулам: $$ omega_i(t+1) = omega_i(t) — gammacdotoverline<Deltaomega_i>(t). $$

Контроль уверенности нейрона

frac<partial E^2> <partial N>= -lambda. $$ Соответственно, в процессе обучения происходит подправка всех параметров по формулам: $$ begin omega_i(t+1)&=&omega_i(t) — gamma_1cdot(-2,(Y-y),y,(1-y),x_i + 2lambda,omega_i),\[2mm] lambda(t+1) &=& lambda(t) — gamma_2cdot(omega^2_1+. +omega^2_n-N),\[2mm] N(t+1) &=& N(t) + gamma_3cdotlambda(t). end $$ Естественно, для каждого нейрона множитель Лагранжа $lambda$ и целевая норма $n$ должны быть свои (но одни и те же для всех весов нейрона $omega_i$)

Двухслойная сеть

Пусть сеть имеет один скрытый слой и один выход. На самом деле, любую сеть с $K$ выходами можно заменить на $K$ сетей с одним выходом. Такие сети распознают (отличают) свой класс от любых других, т.е. строит отделяющую поверхность только для примеров своего класса. Понятно, что такая система имеет больше возможностей для подстройки параметров.

Выход сети имеет вид: $$ y = SBigr(sum^n_ omega^<(2)>_cdot SBigr(sum^_omega^<(1)>_,x_jBigr),Bigr) = SBigr( omega^<(2)>_ <0>+ omega^<(2)>_<1>, SBigr(sum^_omega^<(1)>_<1j>,x_jBigr)+. +omega^<(2)>_, SBigr(sum^_omega^<(1)>_,x_jBigr),Bigr), $$ где $n$ — число нейронов в скрытом слое, а $n_I$ — число входов сети. Вычислим производную ошибки $E^2=(Y-y)^2$ по весам выходного нейрона: $$ frac<partial E^2><partial omega^<(2)>_i > = -2,(Y-y)

Сумка симпотная	Дорогая	Красного цвета	Такая есть у подруги	Моя машина красная	У меня депрессия	Покупаю эту сумку!
x₁	x₂	x₃	x₄	x₅	x₆	y
1.0	0.0	1.0	1.0	0.0	0.0	0.0
1.0	1.0	1.0	0.0	1.0	0.0	1.0
0.5	0.5	0.5	0.5	0.5	1.0	1.0

y^<(1)>_i, $$ где $y^<(1)>_i$ — текущий выход $i$-того нейрона скрытого слоя и $y^<(1)>_0=1$. Аналогично для производной по весам скрытого слоя: $$ frac<partial E^2><partial omega^<(1)>_ >

Обратное распространение ошибки

Пусть $omega^alpha_$ — вес входа $i$-того нейрона в слое $alpha$, который получает сигнал от $j$-того нейрона предыдущего слоя $alpha-1$. От весов $omega^alpha_$ непосредственно зависит выход нейрона $y^<alpha>_i$. Поэтому производная ошибки по весам (как сложная функция) имеет вид: $$ frac<partial E^2><partial omega^alpha_>

y^<alpha-1>_j. $$ При этом $i=1. ,n_alpha$ и $j=0. ,n_<alpha-1>$. Вычислим производную ошибки $E$ по $y^alpha_i$. От выхода $y^alpha_i$ непосредственно зависят выходы всех нейронов следующего слоя $y^<alpha+1>_i$. Поэтому при взятии производной необходимо поставить сумму: $$ frac<partial E^2><partial y^<alpha>_i>

sum^>_ Bigr[frac<partial E^2><partial y^<alpha+1>_j> S'(d^<alpha+1>_j)Bigr],omega^<alpha+1>_. $$ Умножим левую и правую части на $S'(d^alpha_i)=y^<alpha>_i,(1-y^<alpha>_i)$. Это даёт рекуррентную формулу для определения коэффициентов $chi^alpha_i$: beginlabel chi^alpha_i =y^<alpha>_i,(1-y^<alpha>_i),sum^>_ chi^<alpha+1>_j,omega^<alpha+1>_. end Таким образом, алгоритм ообратного распространения ошибки имеет вид:

Источник

Нейронные сети: 1. Основы

Введение

Этим документом начинается серия материалов, посвящённых нейронным сетям. Иногда к ним относятся по принципу: человеческая нейронная сеть может решать любые задачи, поэтому и достаточно большая искусственная нейронная сеть на это способна. Чаще всего архитектура сети и параметры её обучения являются предметом многочисленных экспериментов. Сеть при этом оказывается чёрным ящиком, происходящее в котором загадочно даже для её учителя.

Мы постараемся совмещать эмпирические советы и математическое понимания природы нейронов как разделяющих гиперплоскостей и функций нечёткой логики. Сначала будут рассмотрены различные модельные примеры двумерных пространств признаков. Наша цель — выработать интуитивное понимание выбора архитектуры сети. В дальнейшем мы перейдём к многомерным задачам, распознанию графических образов, свёрточным и рекуррентным сетям. Приведенные ниже примеры можно запустить, потренировавшись в подборе параметров обучения.

Объекты и их признаки

Пусть есть однотипные объекты (бутылки с вином, посетители в больнице, позиции на шахматной доске):

Каждый объект характеризуется набором (вектором) признаковx =1,x₂. x_n>. Признаки могут быть:

вещественными (вес, рост)

бинарными (женщина/мужчина)

нечисловыми (красный,синий. )

Далее будем считать признаки вещественными числами из диапазона [0. 1]. Этого всегда можно достичь при помощи нормировки, например: x -> (x-x_min)/(x_max-x_min). Бинарные признаки, соответственно, принимают значение 0 или 1. Нечисловые признаки, увеличив размерность вектора x, можно сделать бинарными (красный/не красный, синий/не синий). Кроме этого, пока будем считать, что объекты между собой причинно не связаны и их порядок не существенен.

Пусть объекты данного типа разбиваются на классы (человек: <здоровый, больной>, вино: <итальянское, французское, грузинское>). С каждым объектом можно также связать некоторое число y (степень преимущества белых в шахматной позиции; качество вина по усреднённому мнению экспертов и т.д.). Часто решаются следующие две, тесно связанные задачи:

Классификация: к какому из K классов принадлежит объект.

Регрессия: какое число y соответствует объекту.

Для успешного решения задач классификации или регрессии, признаки, характеризующие объект, должны быть значимыми, а вектор признаков — полным (достаточным для классификации объектов или определение регрессионной величины y ).

Однажды Джед и Нед захотели различать своих лошадей. Джед сделал на ухе лошади царапину. Но лошадь Неда поцарапала о колючку тоже самое ухо. Тогда Нед прицепил голубой бант на хвост своей лошади, но лошадь Джеда его сожрала. Фермеры долго размышляли и выбрали признак, который не так легко изменить. Они тщательно измерил высоту лошадей, и оказалось, что черная кобыла Джеда на один сантиметр выше белого жеребца Неда.

Обучение с учителем

Пусть есть множество объектов, каждый из которых принадлежит одному из k пронумерованных (0,1,2. k-1) классов. На этом обучающем множестве, предоставленнным «учителем» (обычно человеком), система обучается. Затем, для неизвестных системе объектов (тестовом множестве), она проводит их классификацию, т.е. сообщает к какому классу принадлежит данный объект. В такой постановке — это задача распознавания образов после обучения с учителем.

Число признаков n называется размерностью пространства признаков. Пусть признаки лежат в диапазоне [0. 1]. Тогда любой объект представим точкой внутри единичного n-мерного куба в пространстве признаков.

Распознающую систему представим в виде чёрного ящика. У этого ящика есть n входов, на которые подаются значения признаков x =1,x₂. x_n> и k выходов y =1. y_k> (по числу классов). Значение выходов также будем считать вещественным числами из диапазона [0. 1]. Система считается правильно обученной, если при подаче на входы признаков, соответствующих i-тому классу, значение i-того выхода равно 1, а всех остальных 0. На практике, такого результата добиться трудно и все выходы оказываются отличными от нуля. Тогда считается что номер выхода с максимальным значением и есть номер класса, а близость этого значения к единице говорит о «степени уверенности» системы.

Когда есть только два класса, ящик может иметь один выход. Если он равен 0, то это один класс, а если 1 — то другой. При нечётком распознавании вводятся пороги уверенности. Например, если значение выхода лежит в диапазоне y=[0 . 0.3] — это первый класс, если y=[0.7 . 1] — второй, а при y=(0.3 . 0.7) система «отказывается принимать решение».

Ящик с одним выходом может также аппроксимировать функцию y=f(x₁. x_n), значения y которой непрерывны и обычно также нормируются на единицу, т.е. y=[0 . 1]. В этом случае решается задача регрессии.

Нейрон

Нейронная сеть — одно из возможных наполнений чёрного ящика. Узел сети — это нейрон, имеющий n входов x =1,x₂. x_n> и один выход y. С каждым входом связан вещественный параметр синаптического веса ω =1,w₂. w_n>. Кроме этого, нейрон имеет также «параметр смещения» w. Таким образом, любой нейрон с n входами полностью определяется n+1 параметром.

Выход нейрона вычисляется следующим образом. Значение каждого входа x_i умножают на соответствующий ему синаптический вес w_i и эти произведения складывают. К сумме добавляют параметр смещения w. Результат d приводят к диапазону [0 . 1] при помощи нелинейной сигмоидной функции y=S(d):

Сигмоидная функция стремится к 1 при больших положительных d и к 0 при больших отрицательных d. Когда d=0, она равна S(0)=0.5. Таким образом, нейрон это нелинейная функция n переменных порогового вида:

Сеть нейронов

Сеть является множеством соединённых между собой нейронов. Возможны различные способы соединения и, следовательно, различные архитектуры сети. Пусть нейроны располагаются слоями и значения выходов нейронов i-того слоя подаётся на входы всех нейронов следующего i+1 слоя. Такую сеть называют полносвязной сетью прямого распространения. Входы сети мы будем обозначать квадратиками и называть входными нейронами. В отличии от «обычных» нейронов — это просто линейная функция y=x. Выходы нейронов последнего слоя сети являются выходами чёрного ящика и обозначаются треугольниками.

Ниже на первом рисунке сеть состоит из трёх входов (нулевой слой) и двух выходных нейронов. Такую архитектуру будем кодировать следующим образом: [3,2], где цифры — это число нейронов в слое. Первая цифра — всегда количество входов, а последняя — количество выходов. На следующем рисунке представлена сеть [2,3,1]. Она содержит один скрытый слой с тремя нейронами. Он скрыт в том смысле, что находится внутри чёрного ящика (пунктир) между входным и выходным слоем (нейроны выходного слоя, впрочем, также частично скрыты и наружу «торчат» только их выходы). На третьем рисунке представлена сеть [2,3,3,2] с двумя скрытыми слоями.

Эти сети названы сетями прямого распространения потому, что данные (признаки объекта) подаются на вход и последовательно, без петель, передаются (распространяются) к выходам. К такому же типу сетей относятся т.н. свёрточные сети, в которых соединены между собой не все нейроны двух соседних слоёв (ниже первый рисунок). Часто при этом веса у всех нейронов свёрточного слоя одинаковые. Подробнее о таких сетях будет говориться при распознавании изображений. На втором рисунке ниже представлен вариант сети в которой понятие слоя отсутствует, однако это по-прежнему сеть прямого распространения.

Последний рисунок — это уже сеть не прямого распространения, а т.н. рекуррентная сеть. В ней сигналы с одного или нескольких выходных нейронов подаются обратно на вход. Обычно такая рекурсия, проводится в несколько циклов, пока на выходах сети не установятся стационарные значения. Рекуррентные сети обладают памятью и последовательность подачи объектов для них важна. Такое поведение полезно, если объекты упорядочены во времени (например при предсказании временных рядов).

Обучение любой сети состоит в подборе параметров w,w₁. w_n каждого нейрона, таким образом, чтобы для данного объекта (подаём на входы сети x₁. x_n), выходы сети имели значения, соответствующие классу объекта.

Отметим, что, хотя нейрон всегда имеет только один выход, он может «подаваться» на входы различных нейронов. Аналогично, в живых нейронах аксон расщепляется на отдельные отростки, каждый их которых воздействует на синапсы («точки соединения») дендридов других нейронов. Если нейрон возбудился, то это возбуждение передаётся по аксону к дендридам его соседей.

Нейрон как гиперплоскость

Чтобы чёрный ящик распознающей системы сделать прозрачнее, рассмотрим геометрическую интерпретацию нейрона. В n-мерном пространстве каждая точка задаётся n координатами (вещественными числами x = 1. x_n>). Плоскость (как и в обычном 3-мерном пространстве) задаётся вектором нормали ω =1. w_n> (перпендикуляр к плоскости) и произвольной точкой x =01. x_0n>, лежащей в этой плоскости. Когда n > 3 плоскость принято называть гиперплоскостью.

Расстояние d от гиперплоскости до некоторой точки x =1. x_n> вычисляется по формуле

При этом d > 0, если точка x лежит с той стороны плоскости, куда указывает вектор ω и d d = 0 — точка x лежит в плоскости. Это ключевое для дальнейшего изложения утверждение, которое стоит запомнить.

Изменение параметра w сдвигает плоскость параллельным образом в пространстве. Если w уменьшается, то плоскость смещается в направлении вектора ω (расстояние меньше), а если w увеличивается — плоскость смещается против вектора ω. Это непосредственно следует из приведенной выше формулы.

Если длина w=|ω| вектора ω нормали к плоскости отлична от единицы, то d в w раз больше ( w>1) или меньше ( w n-мерном пространстве. Когда векторы x — x и ω направлены в противоположные стороны: d n измерений, то гиперплоскость это (n-1)-мерный объект.
Она делит всё пространство на две части. Для наглядности рассмотрим 2-мерное пространство. Гиперплоскостью в нём будет прямая линия (одномерный объект). Справа на рисунке кружок изображает одну точку пространства, а крестик — другую. Они расположены по разные стороны от линии (гиперплоскости). Если длина вектора ω много больше единицы, то и расстояния d от точек к плоскости по модулю будут существенно большими единицы.

Вернёмся к нейрону. Несложно видеть, что он вычисляет расстояние d от точки с координатами x =(x₁. x_n) (вектор входов) до гиперплоскости ( w, ω). Параметры нейрона ω =(w₁. w_n) определяют направление нормали гиперплоскости, а w связан со смещение плоскости вдоль вектора ω. На выход нейрона подаётся нормированное на диапазон [0. 1] расстояние S(d). При больших w_i объект, нарисованный выше кружком, приведёт к выходу нейрона близкому к единице, а крестик — к нулю. Отношение w0/|ω| равно расстоянию от плоскости до начала координат (0. 0). По модулю оно не должно превышать n ½

1. Нейрон является гиперплоскостью. Значение его выхода равно нормированному расстоянию от вектора входов до гиперплоскости. В процессе обучения, плоскость каждого нейрона меняет свою ориентацию и сдвигается в пространстве признаков.

Уверенность нейрона

При обучении сети необходим критерий, в соответствии с которым подбираются параметры нейронов. Обычно для этого служит квадрат отклонения выходов сети от их целевых значений. Так, для двух классов и одного выхода, ошибкой Error сети считаем

где y — фактический выход, а y_c — его правильное значение, равное 0 для одного класса и 1 — для второго. Сумма ведётся по N обучающим примерам. Эту среднеквадратичную ошибку по всем обучающим объектам стараются сделать минимальной. Методы минимизации ошибки (подбор параметров нейронов) мы обсудим позднее.

Рассмотрим 2-мерное пространство признаков x₁,x₂ и два класса 0 и 1. На рисунке ниже объекты одного класса представлены синими кружочками, а объекты второго класса — красными крестиками. Справа от пространства признаков приведена сеть [2,1] из одного нейрона. За ней, на сине-красном квадратике, нарисована карта значений выхода нейрона при тех или иных входах ( x₁,x₂ пробегают значения от 0 до 1 с шагом 0.01). Если y=0 — то это синий цвет, если y=1 — то красный, а белый цвет соответствует значению y=0.5:

σ=0.2D

Справа от рисунков под чертой, в квадратных скобках даны параметры нейрона: [w,w₁,w₂]. В круглых скобках приведена длина |w| вектора нормали ω и среднее значение выхода и его волатильность σ_y (см. ниже). Ось x₁ пространства признаков направлена вправо, а ось x₂ — вниз. Поэтому вектор ω с положительными компонентами 1, w₂> направлен по диагонали вниз (он нарисован рядом с кружочком на прямой, содержащим номер нейрона 1).

Над чертой в таблице приведена среднеквадратичная ошибка Error такой сети. При этом строка Learn означает обучающую последовательность объектов, а Test — проверочную, которая не участвовала в обучении (тестовые объекты на графике пространства признаков изображены полупрозрачными). Колонка Miss содержит процент неправильно распознанных сетью объектов (отнесённых не к своему классу). Последняя строка kNear означает ошибку и процент ошибок в методе 10 ближайших соседей (он будет описан позднее).

В этом примере разброс признаков объектов каждого класса невелик. Классы легко разделяются гиперплоскостью (линией в 2-мерии). Сеть стремиться минимизировать ошибку к целевым значениям 0 или 1 на выходе, поэтому модуль вектора |w|=48 принимает сравнительно большое значение. В результате, даже недалеко расположенные от плоскости объекты (в обычном евклидовом смысле) получают большое по модулю значение d. Соответственно y=S(d) = 0 или 1. Такой нейрон мы будем называть уверенным. Чем больше |w|, тем более уверен в себе нейрон. На его карте выхода тонкая белая линия (область неуверенности) отделяет насыщенный синий цвет (один класс) от насыщенного красного цвета (второй класс).

Несколько иная ситуация во втором примере, где существует широкая область перекрытия объектов различных классов. Теперь нейрон не столь уверен в себе и длина вектора |w|=24 в 2 раза меньше:

σ=D σ=D

Приведём функции деформации расстояния (сигмоид) при длине вектора нормали, равной 1,2,5,10,100:

Так как входы нейрона нормированы на единицу, максимальное расстояние от точки x с координатами 1. x_n> в n-мерном кубе (его диагональ) равна корню из n. В 2-мерном пространстве признаков d_max=1.4. Если плоскость проходит через середину куба d_max

Уверенный нейрон — не всегда хороший нейрон. Если размерность пространства признаков n велика, а обучающих данных N мало, сеть состоящая из уверенных нейронов может оказаться переобученной и на тестовых объектах приводить к большой ошибке распознавания. Кроме этого самоуверенные нейроны медленнее обучаются. Подробнее мы остановимся на этих вопросах ниже.

В заключение сформулируем главный вывод, справедливый для пространств любой размерности:

2. Если два класса в пространстве признаков разделяются гиперплоскостью, то для их распознавания достаточно одного нейрона.

Полезность нейрона

В случае, если гиперплоскость нейрона не пересекает единичный гиперкуб в котором находятся признаки (или значения выходов предыдущих нейронов), то от такого нейрона обычно мало пользы. Он не разделяет на две части входные данные (которые всегда принадлежат интервалу [0 . 1]. Такой нейрон будет называться бесполезным.

Необходимо стремиться к тому, чтобы все нейроны сети были полезными. Иногда бесполезность появляется и для плоскости, пересекающей гиперкуб, если объекты любых классов оказываются с одной стороны этой плоскости.

Перед началом обучения параметры нейронов полагают равными случайным значениям. При этом нейрон может сразу оказаться бесполезным. Чтобы этого не произошло, можно использовать следующий алгоритм инициализации:

Компоненты вектора ω задаём случайным образом, например в диапазоне [-w . w], где w

1 — 10. Затем, внутри единичного гиперкуба (или в некоторой его центральной части), выбираем случайную точку x =01. x_0n>. Параметр сдвига задаём следующим образом: w = —ω·x = -(w₁x₀₁ + . + w_nx_0n). В результате гиперплоскость будет гарантированно проходить через гиперкуб.

Параметр сдвига стоит контролировать и в процессе обучения, так чтобы нейрон был всё время полезным. Здесь возможны два способа — геометрический и эмпирический. В эмпирическом вычисляется среднее значение выхода каждого нейрона по обучающим объектам. Если после прохождения через сеть всех обучающих примеров, средние значения некоторых нейронов близки к нулю или единице, то они считаются бесполезными. В этом случае их можно «встряхнуть» случайным образом (возможно с сохранением вектора ω, изменяя только параметр сдвига w).

На всех примерах в этом документе нейроны в сетях разукрашены в соответствии со значением их . Если = 0.5, то нейрон белый, если = 0 — синий, а если = 1 — красный. Насыщенный синий или красный цвета означают бесполезность нейрона. В первых двух примерах, единственный нейрон получился очень полезным (белым), так как объекты классов равновероятно находились справа и слева от линии (разделяющей гиперплоскости).

Кроме среднего значения выхода, важную роль играет волатильность нейрона σ_y, равная среднеквадратичным отклонениям его выхода от среднего значения . Чем волатильность меньше, тем менее полезен нейрон. Действительно, в этом случае, не зависимо от значений входов, он принимает одно и то же значение на выходе. Поэтому, без изменения выходных значений сети, такой нейрон можно выбросить, сдвинув соответствующим образом параметры нейронов, для которых бесполезный нейрон является входным.

Несколько выходов

Рассмотрим теперь 3 класса. Использовать один нейрон не очень удобно, поэтому, как было описано в начале документа, создадим сеть [2,3] с тремя выходами. Пусть классы локализованы в пространстве признаков следующим образом:

Каждый выходной нейрон отделяет «свой класс» от остальных двух. Например, первый сверху нейрон (на рисунке горизонтальная плоскость номер 1) распознаёт объекты, помеченные синими кружочками, выдавая на выходе 1, если объект находится с той стороны, куда направлен вектор ω (чёрточка рядом с номером плоскости).

Аналогично, второй нейрон распознаёт красные крестики, а третий — зелёные квадратики. В каждом случае векторы нормали направлены в сторону «своих» классов. Все нейроны сети достаточно уверенны в себе и вполне полезны. Их небольшая синева связана с тем, что против вектора нормали всегда расположено вдвое больше данных («чужих» двух классов), чем по вектору. Поэтому среднее значение каждого выхода смещено ниже нейтрального уровня 0.5.

Когда нужен скрытый слой

Перейдём теперь к чуть более сложной задаче. Пусть объекты двух классов (кружочки и крестики) сосредоточены по углам пространства признаков так, как на рисунке справа. Одной гиперплоскостью (линией) эти два класса разделить нельзя. Иногда такую задачу называют разделяющим ИЛИ ( xor). Эта логическая операция равна истине (единице) только, если один из аргументов равен истине, а второй лжи (нулю): «Маша любит или Колю или Васю, но не их обоих». На рисунке классу, помеченными кружками, на выходе сеть должна выдавать ноль, а классу крестика — единицу. Если объекты находятся точно в углах, то xor(0,0) = xor(1,1) = 0 и xor(0,1) = xor(1,0) = 1.

Чтобы провести классификацию, необходима нейронная сеть [2,2,1] с одним скрытым слоем. Ниже на первом графике (в осях признаков x₁ и x₂) показаны две гиперплоскости (линии A и B). Они соответствуют двум скрытым нейронам A и B. Значения выходов нейронов приведены на втором графике (оси y_A и y_B).

Оба крестика лежат по направлениям векторов нормалей плоскостей A и B. Поэтому расстояние от них к плоскостям будет положительным и, если нейроны достаточно уверены в себе, на их выходах y_A и y_B будет получаться единица (нижний правый угол плоскости y_A, y_B).

Кружок с признаками (0,0) из верхнего левого угла плоскости x₁, x₂ даст на выходах нейронов y_A

1 (этот объект лежит против вектора нормали плоскости A и по вектору нормали плоскости B). Второй кружок с признаками (1,1) даст на выходах нейронов значения y_A

0. Получившееся «деформированное» пространство признаков y_A и y_B (второй график) уже легко разделить одной плоскостью C, которая и будет выходным нейроном сети. Если вектор её нормали направлен так как указано на втором графике, то для обоих крестиков получится y

1, а для кружков y

Ниже приведен реальный пример нейронной сети, обученной распознавать два класса объектов, каждый из которых разбивается на два кластера:

3. Каждый слой сети преобразует входное пространство признаков в некоторое другое пространство, возможно, с иной размерностью. Такое нелинейное преобразование происходит до тех пор, пока классы не оказываются линейно разделимыми нейронами выходного слоя.

Нейроны как логические элементы

К анализу поведения нейронов можно подойти с позиций математической логики. Для этого сконцентрируемся на одном классе задачи xor, например на крестиках. Запишем логическое условие которому удовлетворяют все объекты этого класса. В примере выше: «любой крестик лежит по вектору плоскости A и по вектору плоскости B«. Это кратко можно выразить формулой A & B. Выходной нейрон » C» реализует такое логическое «И». Действительно, его плоскость прижата к правому нижнему углу квадрата в пространстве признаков с координатами (1,1). Поэтому для входов (поставляемых нейронами » A» и » B«) близких к единице, на выходе этого нейрона будет 1 (точнее его значение больше 0.5). Поэтому, как и положено, 1 & 1 = 1. Если хотя бы один из входов отличен от 1, то и выход будет нулевым (меньшим 0.5). Это справедливо и в пространстве произвольной размерности, где гиперплоскость нейрона, обеспечивающего логическое «И» прижата к углу гиперкуба с координатами (1,1. 1) (отсекает его от остального гиперкуба).

Если плоскость сместить в угол (0,0), сохранив направление нормали к углу (1,1), то такой нейрон будет логическим «ИЛИ». Его функция y=S(x₁,x₂) даёт S(0,0)=0 и в остальных случаях 1 (ниже первый рисунок):

В общем случае, плоскость нейрона, реализующего логическое «ИЛИ» отсекает угол (0,0. 0) n-мерного куба, а вектор его нормали направлен в сторону большего объём гиперкуба. В отличии от этого, стандартное логическое «И» (второй рисунок) имеет вектор нормали в сторону меньшего объёма.

Логическое «И» для нейрона с n входами описывается следующей функцией:

где параметр α — параметр, лежащий в диапазоне 0 (1,1. 1). Действительно, когда α=0 и x₁=. =x_n=1, имеем x₁+. +x_n-n=0. Чтобы этот нейрон обеспечивал логическое И, он должен давать отрицательное расстояние к «ближайшему» углу гиперкуба у которого одна координата равна нулю: (1. 1,0,1. 1). Это даёт ограничение α w характеризует длину нормали (чем он больше, тем более уверен в себе нейрон). Сигмоидная функция S(d) приведена в начале документа.

Аналогично записывается функция логического «ИЛИ» ( 0 y = S( w·(x₁+. +x_n-α) ), y = x₁ ∨ x₂ ∨ . ∨ x_n.

Ещё одна логическая функция отрицания реализуется при помощи вычитания. Обозначим её чертой над именем переменной. Тогда x = 1-x и, как обычно, 0 =1, 1 =0. Если один из входов нейронов имеет отрицание, то его функция выхода имеет вид:

Таким образом, одна из компонент вектора нормали меняет свой знак и плоскость нейрона сдвигается. Выше на третьем и четвёртом рисунках приведены различные отрицания перменных. Стоит в этих терминах получить логическое ИЛИ из логического И при помощи правила де-Моргана:

где восклицательный знак — ещё один способ обозначения логического отрицания.

Четыре варианта xor

В качестве упражнения, стоит проанализировать 4 различных реализаций бинарной функции xor при помощи нейронных сетей:

Последний ряд картинок — это карты выхода реально обученных нейронных сетей, имеющих разделяющие плоскости на первом скрытом слое такие, как приведено в первом ряду картинок.

Аппроксимация функции y=f(x)

При помощи нейронной сети с одним входом, одним выходом и достаточно большим скрытым слоем, можно аппроксимировать любую функцию y=f(x). Для доказательства, создадим сначала сеть, которая на выходе даёт 1, если вход лежит в диапазоне [a. b] и 0 — в противном случае.

Пусть σ(d) = S(ω·d) — сигмоидная функция, аргумент которой умножен на большое число ω, так что получается прямоугольная ступенька. При помощи двух таких ступенек, можно создать столбик единичной высоты:

Нормируем аппроксимируемую функцию y=f(x) на интервал [0. 1] как для её аргумента x, так и для значения y. Разобъём диапазон изменения x=[0. 1] на большое число интервалов (не обязательно равных). На каждом интервале функция должна меняется незначительно. Ниже приведено два таких интервала:

Каждая пара нейронов в скрытом слое реализует единичный столбик. Величина d равна w₁, если x∈(a,b) и w₂, если x∈(b,с). Если выходной нейрон является линейным сумматором, то можно положить w_i=f_i, где f_i — значения функции на каждом интервале. Если же выходной нейрон — обычный нелинейный элемент, то необходимо пересчитать веса w_i при помощи обратной к сигмоиду функции (последняя формула).

Аппроксимация функции на Phyton

Ниже приведен код на языке Phyton, который аппроксимирует функцию y=sin(pi*x):

В результате работы, при n=10 и n=100 получаются следующие результаты:

Нечёткая логика

Интерпретация нейронов как логических элементов в дальнейшем упростит анализ архитектуры нейронных сетей. Кроме этого, существует замечательная возможность реализовывать при помощи нейронных сетей системы, оперирующие с нечёткой логикой. В такой логике, кроме истины ( 1) и лжи ( 0) существует непрерывный диапазон истинностных значение от 0 до 1:

Сумка
симпотная Дорогая Красного
цвета Такая есть
у подруги Моя машина
красная У меня
депрессия Покупаю
эту сумку!

x₁ x₂ x₃ x₄ x₅ x₆ y

1.0 0.0 1.0 1.0 0.0 0.0 0.0

1.0 1.0 1.0 0.0 1.0 0.0 1.0

0.5 0.5 0.5 0.5 0.5 1.0 1.0

Пусть свойствами объектов являются бинарные значения («да», «нет»). А выход чёрного ящика y может принимать непрерывные значения. В ряде случаев они также равны 0 («нет») или 1 («да»). Однако при некоторых входах, выход может равняться, например, 0.5 («возможно»). Нейронная сеть, наученная на подобных примерах, будет выдавать как бинарные рекомендации, так и выражать степень своей неуверенности.

Ниже приведены функции, которые принято использовать в нечёткой логике и их аппроксимация (задача регрессии!) при помощи нейронной сети:

Источник

Источник

Лабораторная
работа №2
Линейная искусственная
нейронная сеть.
Правило обучения
Видроу-Хоффа.

Цель работы: Изучить обучение и
функционирование линейной ИНС при
решении задач прогнозирования.

1.Правило обучения
Видроу-Хоффа

Используется для обучения нейронной
сети, состоящей из распределительных
нейронов и одного выходного нейрона,
который имеет линейную функцию активации
(рис.1):

Рис. 1.Линейная сеть.

Такая сеть называется адаптивным
нейронным элементом или «ADALINE»
(Adaptive Linear Element). Его предложили в 1960 г.
Видроу (Widrow) и Хофф (Hoff). Выходное значение
такой сети определяется, как

.
(1.2)

Правило обучения Видроу Хоффа известно
под названием дельта правила
(delta rule). Оно предполагает минимизацию
среднеквадратичной ошибки нейронной
сети, которая для L входных образов
определяется следующим образом:

(1.3)

где
—
среднеквадратичная ошибка сети для
k-го образа;
и
—
соответственно выходное и эталонное
значение нейронной сети для k-го
образа.

Критерий (1.3) характеризуется тем, что
при малых ошибках ущерб является также
малой величиной, т. к.
меньше
чем величина отклонения
.
При больших ошибках ущерб возрастает,
так как
возрастает
с ростом величины ошибки.

Среднеквадратичная ошибка нейронной
сети для одного входного образа
определяется, как

(1.4)

Правило обучения Видроу-Хоффа базируется
на методе градиентного спуска в
пространстве весовых коэффициентов и
порогов нейронной сети. Согласно этому
правилу, весовые коэффициенты и пороги
нейронной сети необходимо изменять с
течением времени по следующим выражениям:

(1.5)

(1.6)

где
;
—
скорость или шаг обучения. Найдем
производные

среднеквадратичной ошибки
по
настраиваемым параметрам сети
и
.
Тогда

где x_j^k — j-ая
компонента k-го образа.

Отсюда получаем следующие выражения
для обучения нейронной сети по дельта
правилу:

(1.7)

(1.8)

где
.

Видроу и Хофф доказали [18], что данный
закон обучения всегда позволяет находить
весовые коэффициенты нейронного элемента
таким образом, чтобы минимизировать
среднеквадратичную ошибку сети независимо
от начальных значений весовых
коэффициентов.

Алгоритм обучения, в основе которого
лежит дельта правило состоит из следующих
шагов:

1. Задается скорость обучения
и
минимальная среднеквадратичная ошибка
сети
,
которой необходимо достичь в процессе
обучения.

2. Случайным образом инициализируются
весовые коэффициенты и порог нейронной
сети.

3. Подаются входные образы на нейронную
сеть и вычисляются векторы выходной
активности сети.

4. Производится изменение весовых
коэффициентов и порога нейронной сети
согласно выражениям (1.7) и (1.8).

5. Алгоритм продолжается до тех пор, пока
суммарная среднеквадратичная ошибка
сети не станет меньше заданной, т. е.
.

В алгоритме Видроу-Хоффа существует
проблема выбора значения шага обучения
.
Если коэффициент
слишком
мал, то процесс обучения является очень
длительным. В случае, когда шаг обучения
большой, процесс обучения может оказаться
расходящимся, то есть не привести к
решению задачи. Таким образом сходимость
алгоритма обучения не избавляет от
разумного выбора значения шага обучения.

1.13. Использование
линейной нейронной сети для прогнозирования

Способность нейронных сетей после
обучения к обобщению и пролонгации
результатов создает потенциальные
предпосылки для построения на базе их
различного рода прогнозирующих систем.
В данном разделе рассмотрим прогнозирование
временных рядов при помощи линейных
нейронных сетей. Пусть дан временной
ряд
на
промежутке
.
Тогда задача прогнозирования состоит
в том, чтобы найти продолжение временного
ряда на неизвестном промежутке, т. е.
необходимо определить
,
и
так далее (рис. 1.2):

Совокупность известных значений
временного ряда образуют обучающую
выборку, размерность которой равняется
m. Для прогнозирования временных
рядов используется метод «скользящего
окна». Он характеризуется длиной окна
n, которая равняется
количеству элементов ряда, одновременно
подаваемых на нейронную сеть. Это
определяет структуру нейронной сети,
которая состоит из n
распределительных нейронов и одного
выходного нейрона.

Такая модель соответствует линейной
авторегрессии и описывается следующим
выражением:

где
—
весовые коэффициенты нейронной сети;
—
оценка значения ряда
в
момент времени
.

Рис. 1.2. Прогнозирование временного
ряда.

Ошибка прогнозирования определяется,
как

.

Модель линейной авторегрессии формирует
значение ряда
,
как взвешенную сумму предыдущих значений
ряда. Обучающую выборку нейронной сети
можно представить в виде матрицы, строки
которой характеризуют векторы, подаваемые
на вход сети:

.

Это эквивалентно перемещению окна по
ряду
с
единичным шагом.

Таким образом для обучения нейронной
сети прогнозированию используется
выборка известных членов ряда. После
обучения сеть должна прогнозировать
временной ряд на упреждающий промежуток
времени.

Задание.

1. Написать на любом ЯВУ программу
моделирования прогнозирующей линейной
ИНС. Для тестирования использовать
функцию

Варианты заданий приведены в следующей
таблице:

№ варианта	a	b	d	Кол-во входов ИНС
1	1	5	0.1	3
2	2	6	0.2	4
3	3	7	0.3	5
4	4	8	0.4	3
5	1	9	0.5	4
6	2	5	0.6	5
7	3	6	0.1	3
8	4	7	0.2	4
9	1	8	0.3	5
10	2	9	0.4	3
11	3	5	0.5	4

Обучение и прогнозирование производить
на 30 и 15 значениях соответственно
табулируя функцию с шагом 0.1. Скорость
обучения выбирается студентом
самостоятельно, для чего моделирование
проводится несколько раз для разных .
Результаты оцениваются по двум критериям
— скорости обучения и минимальной
достигнутой ошибке. Необходимо заметить,
что эти критерии в общем случае являются
взаимоисключающими, и оптимальные
значения для каждого критерия достигаются
при разных .

2. Результаты представить в виде отчета
содержащего:

Титульный лист,
Цель работы,
Задание,
Результаты обучения: таблицу со
столбцами: эталонное значение, полученное
значение, отклонение; график изменения
ошибки в зависимости от итерации.
Результаты прогнозирования: таблицу
со столбцами: эталонное значение,
полученное значение, отклонение.
Выводы по лабораторной работе.

Результаты для пунктов 3 и 4 приводятся
для значения , при
котором достигается минимальная ошибка.
В выводах анализируются все полученные
результаты.

Контрольные вопросы.

ИНС какой архитектуры Вы использовали
в данной работе? Опишите принцип
построения этой ИНС.
Как функционирует используема Вами
ИНС?
Опишите (в общих чертах) алгоритм
обучения Вашей ИНС.
Как формируется обучающая выборка для
решения задачи прогнозирования?
Как выполняется многошаговое
прогнозирование временного ряда?
Предложите критерий оценки качества
результатов прогноза.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

оглавление

1 связанные термины

2 функция потерь

2.1 Определение

2.2 Среднеквадратичная ошибка

2.3 Ошибка перекрестной энтропии

2.4 данные партии

2.5 Зачем нужна функция потерь

3 Численное дифференцирование

3.1 Производная

3.2 частные производные

4 градиента

5 реализация корпуса

5.1dataset

5.2common

5.2.1functions.py:

5.2.2gradient.py：

5.3ch04

5.3.1two_layer_net.py

5.3.2train_neuralnet.py

Эта статья представляет собой краткое изложение «Введение в теорию глубокого обучения и реализацию на основе Python», автор — [ ] Сайто Ясуи.

1 связанные термины

В нейронных сетях данные очень важны, также очень важно извлечение функций данных.

«Количество функций»Это преобразователь, который может точно извлекать важные данные (важные данные) из входных данных (входное изображение).

Сравнение нейронной сети и машинного обучения выглядит следующим образом:

В машинном обучении данные обычно делятся наДанные обученияс участиемДанные испытанийДве части для обучения и экспериментов

ОбобщениеОтносится к способности обрабатывать ненаблюдаемые данные (данные не включаются в данные обучения). Получение способности обобщения — конечная цель машинного обучения.

Состояние переобучения только на определенный набор данных называетсяПереоснащение（over fitting）

2 функция потерь

2.1 Определение

Функция потерьЭто показатель «плохой степени» производительности нейронной сети, то есть степени, в которой текущая нейронная сеть не соответствует данным наблюдения, и насколько она непоследовательна. Использование «плохой производительности» в качестве индикатора может заставить людей чувствовать себя неестественно, но если вы умножите функцию потерь на отрицательное значение, это можно интерпретировать как «насколько плохая производительность», то есть «насколько хороша производительность».

2.2 Среднеквадратичная ошибка

Формат среднеквадратичной ошибки следующий:

[Примечание]: y k — это выходной сигнал нейронной сети, t k — это данные наблюдения, а k — размер данных.

Код реализован следующим образом:

import numpy as np


def mean_squared_error(y, t):
    return 0.5*np.sum((y-t)**2)


if __name__ == "__main__":
         # Используйте распознавание чисел, чтобы понять, что y - это прогнозируемые данные (с точки зрения вероятности), а t - реальные данные
         # Установите 2 как правильное решение
    t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
         # 2 имеет самую высокую вероятность и составляет 0,6
    y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
         # 7 имеет самую высокую вероятность 0,6
    y1 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]

         # Среднеквадратичная ошибка
    # r1 = mean_squared_error(np.array(y), np.array(t))
    # r2 = mean_squared_error(np.array(y1), np.array(t))
    # print(r1)  # 0.09750000000000003
    # print(r2)  # 0.5975
         # Мы обнаружили, что значение функции потерь в первом примере меньше, и разница между
         # Ошибка небольшая. Другими словами, среднеквадратичная ошибка показывает, что результат первого примера более согласуется с данными наблюдения.

2.3 Ошибка перекрестной энтропии

Формат функции потерь кросс-энтропийной ошибки следующий:

[Примечание]: log представляет собой натуральный логарифм с основанием e (log e). y k — выход нейронной сети, а t k — метка правильного решения.

Код реализован следующим образом:

import numpy as np

# Добавлена крошечная дельта значения. Это потому, что когда появляется np.log (0), np.log (0) становится отрицательным бесконечным -inf
 # Это приведет к сбою последующих вычислений. В качестве защитной меры добавление небольшого значения может предотвратить возникновение отрицательной бесконечности.
def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta))


if __name__ == "__main__":
         # Установите 2 как правильное решение
    t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
         # 2 имеет самую высокую вероятность и составляет 0,6
    y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
         # 7 имеет самую высокую вероятность 0,6
    y1 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]


         # Ошибка перекрестной энтропии
    r1 = cross_entropy_error(np.array(y), np.array(t))
    r2 = cross_entropy_error(np.array(y1), np.array(t))
    print(r1)  # 0.510825457099338
    print(r2)  # 2.302584092994546

2.4 данные партии

В приведенных выше примерах функций потерь рассматриваются все функции потерь для отдельных данных. Если требуется сумма функций потерь всех обучающих данных, взяв в качестве примера кросс-энтропийную ошибку, ее можно записать в виде следующей формулы:

[Примечание]: Предполагая, что имеется N данных, t nk представляет значение k-го элемента n-х данных (y nk — это выходной сигнал нейронной сети, t nk — это данные наблюдения).

Данные пакетной обработки, тогда как читать несколько частей данных случайным образом за раз? Вы можете использовать np.random.choice () NumPy, например, np.random.choice (60000, 10) случайным образом выберет 10 чисел от 0 до 59999.

Например:

import sys,os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

# print(x_train.shape)  # (60000, 784)
# print(t_train.shape)  # (60000, 10)

 # Произвольно рисуем 10 данных
train_size = x_train.shape[0]  # 60000
batch_size = 10
 # Случайно выбрать 10 чисел от 0 до 59999
 batch_mask = np.random.choice (train_size, batch_size) # случайным образом выбираем желаемое число из указанных чисел
# print(batch_mask)  # [40011 45133 49757 27590 11182 32214 23597 45193 56422 33356]
x_batch = x_train[batch_mask]  # (10, 784)
t_batch = t_train[batch_mask]  # (10, 10)

Можно добиться следующегоОдновременная обработка отдельных данных и пакетных данных(Данные вводятся централизованно) Функция двух наблюдений.

В коде реализована ошибка кросс-энтропии mini_batch:

def batch_cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
    batch_size = y.shape[0]
    return -np.sum(t * np.log(y + 1e-7))/batch_size

[Примечание]: y — выход нейронной сети, t — данные наблюдения. Когда размерность y равна 1, то есть, когда вычисляется ошибка кросс-энтропии отдельных данных, форму данных необходимо изменить. И, когда вводится мини-пакетом, нормализуйте с количеством пакетов, чтобы вычислить среднюю ошибку кросс-энтропии отдельных данных.

Когда данные мониторингаФорма этикетки(Не одна горячая, а метки типа «2» и «7»), ошибка перекрестной энтропии может быть достигнута с помощью следующего кода.

def batch_cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7))/batch_size

[Примечание]: для np.log (y [np.arange (batch_size), t]). np.arange (batch_size) сгенерирует массив от 0 до batch_size-1. Например, когда batch_size равно 5, np.arange (batch_size) сгенерирует массив NumPy [0, 1, 2, 3, 4]. Поскольку метка в t хранится в форме [2, 7, 0, 9, 4], y [np.arange (batch_size), t] может извлекать выходные данные нейронной сети, соответствующие правильной маркировке каждого данных (в В этом примере y [np.arange (batch_size), t] сгенерирует массив NumPy [y [0,2], y [1,7], y [2,0], y [3,9], y [ 4,4]]).

2.5 Зачем нужна функция потерь

1. При поиске оптимальных параметров (весов и смещений) при обучении нейронных сетей,Найдите параметр, чтобы сделать значение функции потерь как можно меньше. Чтобы найти место, где значение функции потерь является как можно меньшим, необходимо вычислить производную параметра (а точнее, градиент), а затем использовать эту производную в качестве руководства для постепенного обновления значения параметра.

2. Если значение производной отрицательное, значение функции потерь может быть уменьшено путем изменения весового параметра в положительном направлении; наоборот, если значение производной положительно, весовой параметр может быть изменен в отрицательном направлении для уменьшения Значение функции малых потерь. Однако, когда значение производной равно 0, независимо от того, в каком направлении изменяется весовой параметр, значение функции потерь не изменится, и обновление весового параметра здесь остановится.

3 Численное дифференцирование

3.1 Производная

Производная означает количество изменений в определенный момент (предел коэффициента приращения) и имеет следующий формат:

[Примечание]: левая часть знака равенства представляет собой производную от значения функции, а правая часть представляет степень изменения значения функции f (x) относительно независимой переменной x (представленной пределами)

Ошибка округления: Относится к ошибке в окончательном результате вычисления, вызванной пропуском значения точной части десятичной дроби (например, значения после восьмой десятичной точки).

Например:

print(np.float32(1e-50))  # 10^-50 = 0.0

[Примечание]: указанное выше значение h необходимо установить разумно, иначе это приведет к большой ошибке, вы можете изменить 1e-50 на 1e-4.

Помимо изменения значения h, вторая область, которая нуждается в улучшении, связана с различием функции f. Хотя разность между x + h и x функции f вычисляется в приведенной выше реализации, необходимо отметить, что это вычисление имеет ошибки с самого начала. «Истинная производная» соответствует наклону функции в точке x (называемой касательной), но производная, вычисленная в приведенной выше реализации, соответствует наклону между (x + h) и x.

Чтобы уменьшить эту ошибку, мы можем вычислить разницу функции f между (x + h) и (x — h). Поскольку этот метод расчета принимает x в качестве центра и вычисляет разницу между его левой и правой сторонами, его также называютЦентральная разница(Разница между (x + h) и x называется прямой разницей).

Производный код реализован следующим образом:

import numpy as np


 # Плохая реализация, примерная разница
def forward_numerical_diff(f, x):
    h = 10e-50
    # h = 1e-4  # 0.0001
    return (f(x+h) - f(x))/h


 # Центральное отличие
def center_numerical_diff(f, x):
    h = 1e-4  # 0.0001
    return (f(x+h) - f(x-h))/(2*h)


def fun(x):
    return 0.01*x**2 + 0.1*x


def fun2(x):
    # return x[0]**2 + x[1]**2
    return np.sum(x**2)


if __name__ == "__main__":
         # Аппроксимация производной при x = 5
    z = center_numerical_diff(fun, 5)  # 0.1999999999990898
         # Аппроксимация производной при x = 10
    z1 = center_numerical_diff(fun, 10)  # 0.2999999999986347

3.2 частные производные

Когда в функции несколько параметров, ищется частная производная функции.

Например:

Когда требуется частная производная от x0, рассматривайте x1 как константу. При поиске x1 также рассматривайте x0 как константу.

Остальные такие же, как и в предыдущем методе поиска производной.

4 градиента

Основная задача машинного обучения — найти оптимальные параметры во время обучения.Точно так же нейронная сеть должна также найти оптимальные параметры (веса и смещения) во время обучения. Упомянутый здесь оптимальный параметр относится к параметру, когда функция потерь принимает минимальное значение. Градиент представляет направление, в котором значение функции в каждой точке уменьшается в наибольшей степени.

Формат градиентного метода следующий:

Скорость обучения необходимо определить заранее до определенного значения, например 0,01 или 0,001. Приведенная выше формула обновляется один раз, и этот шаг будет повторяться. Другими словами, каждый шаг обновляет значение переменной в соответствии с приведенной выше формулой и постепенно уменьшает значение функции, повторяя этот шаг.

[Примечание]: η представляет собой количество обновлений, которое называется скоростью обучения при обучении нейронных сетей.

Код для поиска градиента реализован следующим образом:

import numpy as np


 # Определить функцию
def fun2(x):
    return x[0]**2 + x[1]**2


 # Найдите частную производную
def numerical_gradient(f, x):
    h = 1e-4  # 0.0001
         grad = np.zeros_like (x) # Сгенерировать тот же массив, что и x

    for idx in range(x.size):
        tmp_val = x[idx]
                 # f (x + h) вычисление
        x[idx] = tmp_val + h
                 fxh1 = f (x) # При вычислении x! = [3, 4], но [3 + h, 4]

                 # f (x-h) вычисление
        x[idx] = tmp_val - h
        fxh2 = f(x)
        grad[idx] = (fxh1 - fxh2)/(2*h)
                 x [idx] = tmp_val # значение восстановления
    return grad


 # Реализация метода градиентного спуска
 # f: функция для оптимизации, init_x: начальное значение, lr: скорость обучения, step_num: время повторения градиентного метода
def gradient_descent(f, init_x, lr=0.01, step_num=100):
    x = init_x
    for i in range(step_num):
                 grad = numeric_gradient (f, x) # Найти градиент функции
        x -= lr * grad
    return x


if __name__ == "__main__":
    x, y = numerical_gradient(fun2, np.array([3.0, 4.0]))
    # print(x)  # 6.00000000000378
    # print(y)  # 7.999999999999119

         # Установить начальное значение
    init_x = np.array([-3.0, 4.0])
    # m, n = gradient_descent(fun2, init_x=init_x, lr=0.1, step_num=100)
    # print(m)  # -6.111107928998789e-10
    # print(n)  # 8.148143905314271e-10

         # Скорость обучения слишком велика
    # m, n = gradient_descent(fun2, init_x=init_x, lr=10, step_num=100)
    # print(m)  # -25898374737328.363
    # print(n)  # -1295248616896.5398

         # Скорость обучения слишком мала
    m, n = gradient_descent(fun2, init_x=init_x, lr=1e-4, step_num=100)
    print(m)  # -2.9405901379497053
    print(n)  # 3.920786850599603
    '''
         Если скорость обучения слишком велика, она превратится в большое значение; и наоборот, если скорость обучения слишком мала, она в основном закончится без значительного обновления.
    '''

5 реализация корпуса

Документы, необходимые для реализации дела:

5.1dataset

Можно найти в предыдущей главе

5.2common

5.2.1functions.py:

Этот файл играет роль функции активации и функции потери.

# coding: utf-8
import numpy as np


def identity_function(x):
    return x


def step_function(x):
    return np.array(x > 0, dtype=np.int)


def sigmoid(x):
    return 1 / (1 + np.exp(-x))    


def sigmoid_grad(x):
    return (1.0 - sigmoid(x)) * sigmoid(x)
    

def relu(x):
    return np.maximum(0, x)


def relu_grad(x):
    grad = np.zeros(x)
    grad[x>=0] = 1
    return grad
    

def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T 

    x = x - np.max(x) #
    return np.exp(x) / np.sum(np.exp(x))


def sum_squared_error(y, t):
    return 0.5 * np.sum((y-t)**2)


def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
        
    if t.size == y.size:
        t = t.argmax(axis=1)
             
    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size


def softmax_loss(X, t):
    y = softmax(X)
    return cross_entropy_error(y, t)

5.2.2gradient.py：

Файл воспроизводит производную, градиент

# coding: utf-8
import numpy as np


 # Найти одномерную частную производную
def _numerical_gradient_1d(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)
    
    for idx in range(x.size):
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x) # f(x+h)
        
        x[idx] = tmp_val - h 
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
                 x [idx] = tmp_val # восстановление
        
    return grad


 # Найдите двумерную частную производную
def numerical_gradient_2d(f, X):
    if X.ndim == 1:
        return _numerical_gradient_1d(f, X)
    else:
        grad = np.zeros_like(X)
        
        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_1d(f, x)
        
        return grad


def numerical_gradient(f, x):
    h = 1e-4  # 0.0001
    grad = np.zeros_like(x)
         # flags: использовать внешние циклы, мультииндекс: каждая итерация может отслеживать один тип индекса
         # У объекта nditer есть еще один необязательный параметр op_flags. По умолчанию nditer будет рассматривать массив, который будет повторяться, как объект только для чтения.
         # Чтобы понять, что элементы массива стоит изменять при обходе массива, вы должны указать режим чтения-записи или только для записи.
         it = np.nditer (x, flags = ['multi_index'], op_flags = ['readwrite']) # итерация
    while not it.finished:
        idx = it.multi_index
        tmp_val = x[idx]
        x[idx] = tmp_val + h
        fxh1 = f(x) # f(x+h)
        
        x[idx] = tmp_val - h 
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
                 x [idx] = tmp_val # восстановление
        it.iternext()   
        
    return grad

5.3ch04

5.3.1two_layer_net.py

Этот документ создает двухуровневую сеть

# coding: utf-8
import sys, os
 sys.path.append (os.pardir) # путь загрузки
from common.functions import *
from common.gradient import numerical_gradient


class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
                 # Инициализация сети
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

    def predict(self, x):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
    
        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)
        
        return y
        
         # x: прогнозируемое значение, t: истинное значение
    def loss(self, x, t):
        y = self.predict(x)
        
        return cross_entropy_error(y, t)
    
    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        t = np.argmax(t, axis=1)
        
        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy
        
    
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)
        
        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
        
        return grads
        
    def gradient(self, x, t):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
        grads = {}
        
        batch_num = x.shape[0]
        
        # forward
        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)
        
        # backward
        dy = (y - t) / batch_num
        grads['W2'] = np.dot(z1.T, dy)
        grads['b2'] = np.sum(dy, axis=0)
        
        dz1 = np.dot(dy, W2.T)
        da1 = sigmoid_grad(a1) * dz1
        grads['W1'] = np.dot(x.T, da1)
        grads['b1'] = np.sum(da1, axis=0)

        return grads

5.3.2train_neuralnet.py

Используйте нейронные сети для обучения

# coding: utf-8
import sys, os
 sys.path.append (os.pardir) # путь загрузки
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from ch04.two_layer_net import TwoLayerNet

 # Прочитать набор данных
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

 iters_num = 10000 # количество итераций 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
         # Расчет градиента
    # grad = network.numerical_gradient(x_batch, t_batch)
    grad = network.gradient(x_batch, t_batch)
    
         # Обновление параметров
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]
    
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))

 # Рисование
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()

Получите окончательный результат

Источник

Выбор функции потерь для задач построения нейронных сетей

Время прочтения: 4 мин.

При построении нейронных сетей перед нами часто встаёт вопрос правильного выбора функции потерь, используемой для формирования соответствий между входными и выходными параметрами. Функция потерь отвечает за оценку того, насколько хорошо модель предсказывает реальное значение, и построение модели сводится к решению задачи минимизации значения этой функции на каждом этапе. И в зависимости от того, как выглядят наши данные, требуется использовать разные подходы.

В рамках данной статьи мы рассмотрим три функции потерь для нейронных сетей, решающих регрессионные задачи.

Mean Squared Error

Среднеквадратичная ошибка (MSE) — одна из основных функций расчёта отклонения. Для каждой точки вычисляется квадрат отклонения, после чего полученные значения суммируются и делятся на общее количество точек. Чем ближе полученное значение к нулю, тем точнее наша модель. Данный метод расчёта в значительной мере чувствителен к выбросам в выборке, или к выборкам где разброс значений очень большой. В основном, данная функция применяется для переменных, распределение которых близко к распределению Гаусса.

Mean Absolute Error

Средняя абсолютная ошибка (MAE) – это усреднённая сумма модулей разницы между реальным и предсказанным значениями. MAE во многом похожа на MSE, но она отличается меньшей чувствительностью к выбросам значений (так как не берётся квадрат отклонения).

Mean Squared Logarithmic Error

Среднеквадратичная логарифмическая ошибка (MSLE) – усреднённая сумма квадратов разностей между логарифмами значений. Благодаря большому гасящему эффекту логарифма она более применима к моделям, строящимся на данных, которые имеют большой разброс значений на несколько порядков.

Продемонстрируем как выбор функции потерь влияет на процесс построения нейронной сети. Для генерации данных будем использовать встроенную в scikit-learn функцию make_regression, а в качестве нейронной сети будет выступать многослойный перцептрон.

Код используемый для демонстрации:

from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# формирование датасета
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# нормализация
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# разделение
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# определение для модели
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss=вид функции потерь, optimizer=opt)
# расчёт
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# Оценка качества
train_mse = model.evaluate(trainX, trainy, verbose=0)
test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot Демонстрация результата
pyplot.title('Loss / Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()

В данном коде мы будем заменять только указанный вид функции потерь.
Результат для MSE:

model.compile(loss='mean_squared_error', optimizer=opt)

Полученное отклонение для модели:

Train: 0.000, Test: 0.001

Как видно из графика, модель показывает хорошую сходимость и низкое отклонение.

Результат для MSLE:

model.compile(loss=' mean_squared_logarithmic_error', optimizer=opt)

Полученное отклонение для модели:

Train: 0.165, Test: 0.184

По графику видно, что для данного набора данных MSLE сходится медленней чем MSE. С одной стороны, это может привести к тому что модель будет строиться медленней и получится хуже, с другой – использование MSE может привести к переобучению. Результат для MAE:

model.compile(loss='mean_absolute_error', optimizer=opt)

Полученное отклонение для модели:

Train: 0.002, Test: 0.002

Здесь мы можем увидеть, что результат сходится очень эффективно, но ошибка имеет нерегулярный характер. Так как используемый нами генератор строит гауссово распределение без выбросов, использование MAE не даёт значительных преимуществ.

Очевидно, что от выбора правильной функции потерь сильно зависит точность, качество и скорость построения модели, поэтому следует внимательно подходить к выбору опираясь как на используемую модель, так и на характеристики входных данных.

Источник

Содержание

Введение
1. Постановка задачи
2. Проектирование модели нейронной сети

2.1. Определение количества нейронов входного слоя
2.2. Проектирование скрытых слоев
2.3. Определение количества нейронов выходного слоя

3. Программирование

3.1. Подготовительная работа
3.2. Инициализация классов
3.3. Обучение нейронной сети
3.4. Доработка метода расчета градиента

4.Тестирование
Заключение
Программы, используемые в статье

Введение

В предыдущей статье «Нейросети — это просто» рассказано о принципах построения класса CNet для работы с полносвязными нейронными сетями средствами MQL5. В данной статье я хочу продемонстрировать пример применения данного класса в советнике и оценить работоспособность нашего класса в «полевых условиях».

1. Постановка задачи

Прежде чем приступить к построению нашего советника, мы должны определиться с целями и задачами, которые мы поставим перед нашей новой нейронной сетью. Несомненно, общей целью любого советника на финансовых рынках является получение прибыли. Однако, это довольно обобщенная цель. Мы же должны конкретизировать задачи для нейронной сети. Более того, мы должны понимать, как будем оценивать результаты работы нейронной сети.

И еще один аспект: ранее созданный класс CNet построен по принципам обучения с учителем, что предполагает наличие размеченных данных для обучающей выборки.

Глядя на график валютной пары, естественным желанием является совершать торговые операции на пиках, которые нам легко помечает стандартный индикатор фракталов Билла Вильямса. Но есть один нюанс, индикатор определяет пики по 3-м свечам и всегда дает сигнал с опозданием на 1 свечу, на которой часто может в последующем сформироваться обратный сигнал. А что, если поставить перед нейронной сетью задачу определять точки разворота до формирования третьей свечи? Данный подход нам даст как минимум одну свечу движения в направлении сделки.

Таким образом мы решаем вопрос с обучающей выборкой:

Для прямого прохода на вход нейронной сети будем подавать текущую рыночную ситуацию, а на выходе оценку вероятности формирования пика на последней закрытой свече.
Для обратного прохода после формирования очередной свечи проверяем наличие фрактала на предыдущей свече и подаем результат для корректировки весов.

Для оценки результатов работы сети можно использовать среднеквадратичную ошибку предсказания, процент правильного предсказания фракталов, процент пропущенных фракталов.

Теперь осталось решить вопрос, какие же исходные данные будем подавать на вход нашей нейронной сети. И тут давайте вспомним, что мы делаем сами, когда пытаемся оценить рыночную ситуацию по графику.

Первое, что советуют начинающему трейдеру — визуально оценить направление тренда по графику. Следовательно, мы должны оцифровать и передать на вход нейронной сети информацию о ценовых движениях. Я предлагаю передавать информацию о ценах открытия и закрытия, максимальной и минимальной цене, объемах и времени формирования.

Еще одним, наверное, самым популярным способом определения тренда и его силы являются индикаторы-осцилляторы. Применение таких индикаторов удобно еще и тем, что выходные данные индикаторов являются нормализованными. Недолго думая, для эксперимента я взял 4 стандартных индикатора RCI, CCI, ATR и MACD со стандартными параметрами. Я не проводил никакого дополнительного анализа по выбору индикаторов и подбора их параметров.

Возможно, кто-то скажет, что применение индикаторов бессмысленно, так как их данные строятся из пересчета ценовых данных свечей, которые мы уже передали на вход нейронной сети. Но все не совсем так. Значения индикаторов определяются из расчета данных нескольких свечей, что позволяет несколько расширить анализируемую выборку. Задачу же «определить их влияние на результат» мы возлагаем на процесс обучения нейронной сети.

Для возможности оценки динамики рынка будем подавать на вход нейронной сети всю информацию за некий исторический период.

2. Проектирование модели нейронной сети

2.1. Определение количества нейронов входного слоя

Приступая к проектированию самой нейронной сети, надо понимать количество нейронов во входном слое. Для этого мы оцениваем исходную информацию на каждой свече и умножаем на глубину анализируемой истории.

Предварительно обрабатывать данные индикаторов нет необходимости, они нормализованы и их количество индикаторных буферов известно (4 вышеупомянутых индикатора в сумме дают 5 значений). Следовательно, для приема данных индикаторов во входном слое необходимо создать 5 нейронов на каждую анализируемую свечу.

С ценовыми данными свечей ситуация немного другая. Визуально определяя тренд и его силу на графике, мы прежде всего смотрим направление свечей и их размер. И только потом, определяя начало тренда и вероятные точки разворота, обращаем внимание на уровень цены анализируемого инструмента. Следовательно, до подачи данных на вход нейронной сети мы должны их как-то нормализовать. Для себя я решил данную задачу в подаче на вход нейронной сети разности цен закрытия, максимума и минимума от цены открытия описываемой свечи. При таком подходе для описания свечи достаточно 3-х нейронов, а знак первого значения покажет направление свечи.

В различной литературе можно встретить описание влияния различных временных факторов на волатильность валют: сезонность, различия в динамике по дням недели, а также европейская, американская и азиатская торговые сессии по-разному влияют на курсы валют. Для анализа подобных факторов на вход нейронной сети подадим месяц, час и день недели формирования свечи. Я намеренно разбил время и дату образования свечи на составляющие, чтобы дать возможность нейронной сети обобщить и найти зависимости.

Дополнительно добавим информацию об объемах. Если ваш брокер предоставляет данные о реальных объемах, то укажем их, в противном случае укажем тиковые объемы.

Таким образом, для описания каждой свечи нам потребуется 12 нейронов. Умножив это количество на глубину анализируемой истории, получаем размер входного слоя нейронной сети.

2.2. Проектирование скрытых слоев

Следующим шагом нам предстоит спроектировать скрытые слои нашей нейронной сети. Выбор структуры сети (количество слоев и нейронов) является одной из наиболее сложных задач. Однослойный перцептрон хорошо справляется с линейным разделением классов. Двухслойные сети могут повторять извилистые нелинейные границы. Трёхслойные сети позволяют описать сложные многосвязные области. С ростом количества слоёв шире класс функций, которые реализует сеть, но при этом ухудшается ее сходимость и растут затраты на её обучение. Количество нейронов в каждом слое должно удовлетворять ожидаемой вариативности функций. На практике слишком простые сети неспособны в реальных условиях моделировать поведение с достаточной точностью, а слишком сложные сети обучаются на повторение не только целевой функции, но и шума.

В первой статье упоминался метод «5-почему» и я предлагаю продолжить данный эксперимент и создать сеть с 4-мя скрытыми слоями. Количество нейронов в первом скрытом слое я поставил равным 1000, но вполне допускаю и настраивание некой зависимости от глубины анализируемого периода. Воспользовавшись правилом Парето, будем уменьшать количество нейронов в каждом последующем слое на 70%. К вышесказанному добавим ограничение по количеству нейронов в скрытом слое не менее 20.

2.3. Определение количества нейронов выходного слоя

Количество нейронов выходного слоя зависит от поставленной задачи и подхода к ее решению. Для решения задач регрессии достаточно одного нейрона, который будет выдавать ожидаемое значение. Для решения задач классификации потребуется количество нейронов, равное ожидаемому количеству классов, каждый из которых будет выдавать вероятность отнесения исходного объекта к каждому классу. На практике класс объекта определяется по максимальной вероятности.

Для решения нашей задачи я предлагаю создать 2 варианта нейронных сетей и на практике оценить их применимость для решения задачи. В первом случае в выходном слое будет один нейрон. Значения в диапазоне 0.5…1.0 будут соответствовать фракталу на покупку, -0.5…-1.0 — сигналу на продажу, а в диапазоне -0.5…0.5 — отсутствию сигнала. Напомню, в предложенном решении в качестве функции активации используется гиперболический тангенс, выходные значения которого возможны в диапазоне от -1.0 до +1.0.

Во втором случае, в выходном слое создадим 3 нейрона (покупка, продажа, отсутствие сигнала). В данном варианте будем обучать нейронную сеть на получение результата в диапазоне 0.0 … 1.0, с получением в качестве результата вероятность появления фрактала. Определять сигнал будем по максимальной вероятности, а его направление по индексу нейрона с максимальной вероятностью.

3. Программирование

3.1. Подготовительная работа

Приступая к программированию, вначале добавим необходимые библиотеки:

NeuroNet.mqh — библиотека для создания нейронной сети из предыдущей статьи;
SymbolInfo.mqh — стандартная библиотека для получения информации об инструменте;
TimeSeries.mqh — стандартная библиотека для работы с тайм-сериями;
Volumes.mqh — стандартная библиотека для получения информации об объемах;
Oscilators.mqh — стандартная библиотека с классами индикаторов-осцилляторов.

#include "NeuroNet.mqh"
#include <TradeSymbolInfo.mqh>
#include <IndicatorsTimeSeries.mqh>
#include <IndicatorsVolumes.mqh>
#include <IndicatorsOscilators.mqh>

Следующим шагом пропишем параметры нашей программы, с помощью которых мы будем задавать параметры нейронной сети и индикаторов.



input int                  StudyPeriod =  10;            
input uint                 HistoryBars =  20;            
ENUM_TIMEFRAMES            TimeFrame   =  PERIOD_CURRENT;

input group                "---- RSI ----"
input int                  RSIPeriod   =  14;            
input ENUM_APPLIED_PRICE   RSIPrice    =  PRICE_CLOSE;   

input group                "---- CCI ----"
input int                  CCIPeriod   =  14;            
input ENUM_APPLIED_PRICE   CCIPrice    =  PRICE_TYPICAL; 

input group                "---- ATR ----"
input int                  ATRPeriod   =  14;            

input group                "---- MACD ----"
input int                  FastPeriod  =  12;            
input int                  SlowPeriod  =  26;            
input int                  SignalPeriod=  9;             
input ENUM_APPLIED_PRICE   MACDPrice   =  PRICE_CLOSE;

И объявим глобальные переменные, о функционале которых я расскажу по мере их использования.

CSymbolInfo         *Symb;
CiOpen              *Open;
CiClose             *Close;
CiHigh              *High;
CiLow               *Low;
CiVolumes           *Volumes;
CiTime              *Time;
CNet                *Net;
CArrayDouble        *TempData;
CiRSI               *RSI;
CiCCI               *CCI;
CiATR               *ATR;
CiMACD              *MACD;

double               dError;
double               dUndefine;
double               dForecast;
double               dPrevSignal;
datetime             dtStudied;
bool                 bEventStudy;

На этом подготовительная работа закончена и приступаем к инициализации классов.

3.2 Инициализация классов

Непосредственно инициализацию классов будем осуществлять в функции OnInit. Сначала создадим экземпляр класса работы с инструментами CSymbolInfo и обновим данные об инструменте графика.



int OnInit()
  {

   Symb=new CSymbolInfo();
   if(CheckPointer(Symb)==POINTER_INVALID || !Symb.Name(_Symbol))
      return INIT_FAILED;
   Symb.Refresh();

Затем создадим экземпляры тайм-серий. Каждый раз, создавая экземпляр очередного класса, проверяем успешность его создания и инициализируем. В случае ошибки выходим из функции с результатом INIT_FAILED.

   Open=new CiOpen();
   if(CheckPointer(Open)==POINTER_INVALID || !Open.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;

   Close=new CiClose();
   if(CheckPointer(Close)==POINTER_INVALID || !Close.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;

   High=new CiHigh();
   if(CheckPointer(High)==POINTER_INVALID || !High.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;

   Low=new CiLow();
   if(CheckPointer(Low)==POINTER_INVALID || !Low.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;

   Volumes=new CiVolumes();
   if(CheckPointer(Volumes)==POINTER_INVALID || !Volumes.Create(Symb.Name(),TimeFrame,VOLUME_TICK))
      return INIT_FAILED;

   Time=new CiTime();
   if(CheckPointer(Time)==POINTER_INVALID || !Time.Create(Symb.Name(),TimeFrame))
      return INIT_FAILED;

В представленном примере взяты тиковые объемы. Если же вы хотите использовать реальные объемы, то при вызове метода Volumes.Creare нужно будет заменить «VOLUME_TICK» на «VOLUME_REAL».

После объявления тайм-серий аналогичным способом создадим экземпляры классов для работы с индикаторами.

   RSI=new CiRSI();      
   if(CheckPointer(RSI)==POINTER_INVALID || !RSI.Create(Symb.Name(),TimeFrame,RSIPeriod,RSIPrice))
      return INIT_FAILED;

   CCI=new CiCCI();      
   if(CheckPointer(CCI)==POINTER_INVALID || !CCI.Create(Symb.Name(),TimeFrame,CCIPeriod,CCIPrice))
      return INIT_FAILED;

   ATR=new CiATR();      
   if(CheckPointer(ATR)==POINTER_INVALID || !ATR.Create(Symb.Name(),TimeFrame,ATRPeriod))
      return INIT_FAILED;

   MACD=new CiMACD();      
   if(CheckPointer(MACD)==POINTER_INVALID || !MACD.Create(Symb.Name(),TimeFrame,FastPeriod,SlowPeriod,SignalPeriod,MACDPrice))
      return INIT_FAILED;

Следующим шагом приступим к работе непосредственно с классом нейронной сети. Вначале нам нужно создать экземпляр класса. При инициализации класса CNet в параметрах конструктора передается ссылка на массив с указанием структуры сети. Здесь хочется сказать, что обучение нейронной сети процесс довольно трудозатратный как по вычислительным ресурсам, так и по времени. Поэтому, было бы, наверно, неправильно каждый раз при перезапуске программы обучать нашу нейронную сеть заново. И я применил небольшую хитрость, вначале объявляем экземпляр сети без указания структуры и пытаемся загрузить предварительно обученную сеть с локального хранилища (имя файла я вынес в #define).

#define FileName        Symb.Name()+"_"+EnumToString((ENUM_TIMEFRAMES)Period())+"_"+IntegerToString(HistoryBars,3)+"fr_ea"
...
...
...
...
   Net=new CNet(NULL);
   ResetLastError();
   if(CheckPointer(Net)==POINTER_INVALID || !Net.Load(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false))
     {
      printf("%s - %d -> Error of read %s prev Net %d",__FUNCTION__,__LINE__,FileName+".nnw",GetLastError());

Если не удалось загрузить данные предварительно обученной сети, то выводим в журнал сообщение с указанием кода ошибки и приступаем к созданию новой необученной сети. Вначале объявляем экземпляр класса CArrayInt, в котором укажем структуру нейронной сети, количество элементов указывает на количество слоев нейронной сети, а значение элементов указывает на количество нейронов в соответствующем слое.

      CArrayInt *Topology=new CArrayInt();
      if(CheckPointer(Topology)==POINTER_INVALID)
         return INIT_FAILED;

Как уже говорилось выше, во входном слое нам требуется 12 нейронов для описание каждой свечи. Поэтому, в первый элемент массива запишем произведение 12 на глубину анализируемой истории.

      if(!Topology.Add(HistoryBars*12))
         return INIT_FAILED;

Далее опишем скрытые слоя. Мы определили, что у нас будет 4 скрытых слоя с 1000 нейронов в первом скрытом слое и уменьшением числа нейронов на 70% в каждом последующем слое, но не менее 20 нейронов в одном слое. Внесение данных в массив организуем в цикле.

      int n=1000;
      bool result=true;
      for(int i=0;(i<4 && result);i++)
        {
         result=(Topology.Add(n) && result);
         n=(int)MathMax(n*0.3,20);
        }
      if(!result)
        {
         delete Topology;
         return INIT_FAILED;
        }

В выходном слое для построения модели регрессии укажем 1 нейрон.

      if(!Topology.Add(1))
         return INIT_FAILED;

Для модели классификации в нашем случае потребовалось бы указать значение 3 для выходного нейрона.

Далее удалим ранее созданный экземпляр класса CNet и создадим новый с указанием структуры создаваемой нейронной сети. После создания нового экземпляра нейронной сети удалим класс структуры сети, так как далее он больше не используется.

      delete Net;
      Net=new CNet(Topology);
      delete Topology;
      if(CheckPointer(Net)==POINTER_INVALID)
         return INIT_FAILED;

И зададим начальные значения переменных для сбора статистических данных:

dError — среднеквадратичное отклонение (ошибка)
dUndefine — процент ненайденных фракталов
dForecast — процент правильно предсказанных фракталов
dtStudied — дата свечи последнего обучения.

      dError=-1;
      dUndefine=0;
      dForecast=0;
      dtStudied=0;
     }

Напомню, задание структуры нейронной сети, создание нового экземпляра класса нейронной сети и инициализация статистических переменных осуществляется только если не была загружена предварительно обученная нейронная сеть из локального хранилища.
В заключение функции OnInit создадим экземпляр класса CArrayDouble(), который будем использовать для обмена информацией с нейронной сетью и запустим процесс обучения нейронной сети.

И здесь делюсь еще одним решением. В MQL5 нет асинхронного вызова функций. И если мы явно вызовем функцию обучения из функции OnInit, то терминал будет считать незавершенным процесс инициализации программы до момента завершения обучения. Поэтому, вместо прямого вызова функции мы создаем пользовательское событие, а непосредственно вызов функции обучения осуществляется из функции OnChartEvent. При создании события в параметре lparam укажем дату для начала обучения. Такой подход позволяет нам осуществить вызов функции и при этом завершить функцию OnInit.

   TempData=new CArrayDouble();
   if(CheckPointer(TempData)==POINTER_INVALID)
      return INIT_FAILED;

   bEventStudy=EventChartCustom(ChartID(),1,(long)MathMax(0,MathMin(iTime(Symb.Name(),PERIOD_CURRENT,(int)(100*Net.recentAverageSmoothingFactor*(dForecast>=70 ? 1 : 10))),dtStudied)),0,"Init");

   return(INIT_SUCCEEDED);
  }



void OnChartEvent(const int id,
                  const long &lparam,
                  const double &dparam,
                  const string &sparam)
  {

   if(id==1001)
     {
      Train(lparam);
      bEventStudy=false;
      OnTick();
     }
  }

И не забываем произвести очистку памяти в функции OnDeinit.



void OnDeinit(const int reason)
  {

   if(CheckPointer(Symb)!=POINTER_INVALID)
      delete Symb;

   if(CheckPointer(Open)!=POINTER_INVALID)
      delete Open;

   if(CheckPointer(Close)!=POINTER_INVALID)
      delete Close;

   if(CheckPointer(High)!=POINTER_INVALID)
      delete High;

   if(CheckPointer(Low)!=POINTER_INVALID)
      delete Low;

   if(CheckPointer(Time)!=POINTER_INVALID)
      delete Time;

   if(CheckPointer(Volumes)!=POINTER_INVALID)
      delete Volumes;

   if(CheckPointer(RSI)!=POINTER_INVALID)
      delete RSI;

   if(CheckPointer(CCI)!=POINTER_INVALID)
      delete CCI;

   if(CheckPointer(ATR)!=POINTER_INVALID)
      delete ATR;

   if(CheckPointer(MACD)!=POINTER_INVALID)
      delete MACD;

   if(CheckPointer(Net)!=POINTER_INVALID)
      delete Net;
   if(CheckPointer(TempData)!=POINTER_INVALID)
      delete TempData;
  }

3.3. Обучение нейронной сети

Для обучения нейронной сети создадим функцию Train, в параметры функции будем передавать дату начала периода обучения.

void Train(datetime StartTrainBar=0)

В начале функции объявим локальные переменные:

count — подсчет эпох обучения;
prev_un — процент не распознанных фракталов за предыдущую эпоху;
prev_for — процент правильных «предсказаний» фракталов в предыдущую эпоху;
prev_er — ошибка предыдущей эпохи;
bar_time — дата бара пересчета;
stop — флаг для отслеживания вызова принудительного завершения программы.

   int count=0;
   double prev_up=-1;
   double prev_for=-1;
   double prev_er=-1;
   datetime bar_time=0;
   bool stop=IsStopped();
   MqlDateTime sTime;

Далее, проверим, не выходит ли полученная в параметрах функции дата за пределы изначально заданного периода обучения.

   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year-=StudyPeriod;
   if(start_time.year<=0)
      start_time.year=1900;
   datetime st_time=StructToTime(start_time);
   dtStudied=MathMax(StartTrainBar,st_time);

Непосредственно обучение нейронной сети организуем в цикле do-while. В начале цикла пересчитаем количество исторических баров для обучения нейронной сети и сохраним статистические данные предыдущего прохода.

   do
     {
      int bars=(int)MathMin(Bars(Symb.Name(),TimeFrame,dtStudied,TimeCurrent())+HistoryBars,Bars(Symb.Name(),TimeFrame));
      prev_un=dUndefine;
      prev_for=dForecast;
      prev_er=dError;
      ENUM_SIGNAL bar=Undefine;

Затем скорректируем размер буферов и загрузим необходимые исторические данные.

      if(!Open.BufferResize(bars) || !Close.BufferResize(bars) || !High.BufferResize(bars) || !Low.BufferResize(bars) || !Time.BufferResize(bars) ||
         !RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars) || !Volumes.BufferResize(bars))
         break;
      Open.Refresh(OBJ_ALL_PERIODS);
      Close.Refresh(OBJ_ALL_PERIODS);
      High.Refresh(OBJ_ALL_PERIODS);
      Low.Refresh(OBJ_ALL_PERIODS);
      Volumes.Refresh(OBJ_ALL_PERIODS);
      Time.Refresh(OBJ_ALL_PERIODS);
      RSI.Refresh(OBJ_ALL_PERIODS);
      CCI.Refresh(OBJ_ALL_PERIODS);
      ATR.Refresh(OBJ_ALL_PERIODS);
      MACD.Refresh(OBJ_ALL_PERIODS);

Актуализируем флаг отслеживания принудительного завершения программы и объявим новый флаг, сигнализирующей о прохождении эпохи обучения (add_loop).

      stop=IsStopped();
      bool add_loop=false;

И организуем вложенный цикл обучения с перебором всех исторических данных. В начале цикла проверим достижения конца перебора исторических данных и при необходимости изменим флаг add_loop. А также выведем на график через функционал комментариев текущее состояние обучения нейронной сети. Таким образом мы сможем наблюдать за процессом обучения.

      for(int i=(int)(bars-MathMax(HistoryBars,0)-1); i>=0 && !stop; i--)
        {
         if(i==0)
            add_loop=true;
         string s=StringFormat("Study -> Era %d -> %.2f -> Undefine %.2f%% foracast %.2f%%n %d of %d -> %.2f%% nError %.2fn%s -> %.2f",count,dError,dUndefine,dForecast,bars-i+1,bars,(double)(bars-i+1.0)/bars*100,Net.getRecentAverageError(),EnumToString(DoubleToSignal(dPrevSignal)),dPrevSignal);
         Comment(s);

Затем проверим, было ли просчитано прогнозное состояние системы на предыдущем шаге цикла. Если да, то проведем корректировку весов в направлении правильного значения. Для этого очистим содержимое массива TempData, проверим сформировался ли фрактал на предыдущей свече и внесем правильное значение в массив TempData (ниже приведен код для нейронной сети регрессии с одним нейроном в выходном слое). После чего вызовем метод backProp нашей нейронной сети с передачей ссылки на массив TempData в качестве параметра. И актуализируем статистические данные в переменных dForecast (процент правильно предсказанных фракталов) и dUndefine (процент пропущенных фракталов).

         if(i<(int)(bars-MathMax(HistoryBars,0)-1) && i>1 && Time.GetData(i)>dtStudied && dPrevSignal!=-2)
           {
            TempData.Clear();
            bool sell=(High.GetData(i+2)<High.GetData(i+1) && High.GetData(i)<High.GetData(i+1));
            bool buy=(Low.GetData(i+2)<Low.GetData(i+1) && Low.GetData(i)<Low.GetData(i+1));
            TempData.Add(buy && !sell ? 1 : !buy && sell ? -1 : 0);
            Net.backProp(TempData);
            if(DoubleToSignal(dPrevSignal)!=Undefine)
              {
               if(DoubleToSignal(dPrevSignal)==DoubleToSignal(TempData.At(0)))
                  dForecast+=(100-dForecast)/Net.recentAverageSmoothingFactor;
               else
                  dForecast-=dForecast/Net.recentAverageSmoothingFactor;
               dUndefine-=dUndefine/Net.recentAverageSmoothingFactor;
              }
            else
              {
               if(sell || buy)
                  dUndefine+=(100-dUndefine)/Net.recentAverageSmoothingFactor;
              }
           }

После корректировки весовых коэффициентов нейронной сети посчитаем вероятность появления фрактала на текущем историческом баре (при i равном «0» посчитается вероятность формирования фрактала на текущем баре). Для этого очистим массив TempData и внесем в него текущие данные для входного слоя нейронной сети. При ошибке добавления данных или недостатке введенных данных выходим из цикла.

         TempData.Clear();
         int r=i+(int)HistoryBars;
         if(r>bars)
            continue;

         for(int b=0; b<(int)HistoryBars; b++)
           {
            int bar_t=r+b;
            double open=Open.GetData(bar_t);
            TimeToStruct(Time.GetData(bar_t),sTime);
            if(open==EMPTY_VALUE || !TempData.Add(Close.GetData(bar_t)-open) || !TempData.Add(High.GetData(bar_t)-open) || !TempData.Add(Low.GetData(bar_t)-open) ||
               !TempData.Add(Volumes.Main(bar_t)/1000) || !TempData.Add(sTime.mon) || !TempData.Add(sTime.hour) || !TempData.Add(sTime.day_of_week) ||
               !TempData.Add(RSI.Main(bar_t)) ||
               !TempData.Add(CCI.Main(bar_t)) || !TempData.Add(ATR.Main(bar_t)) || !TempData.Add(MACD.Main(bar_t)) || !TempData.Add(MACD.Signal(bar_t)))
                  break;
           }
         if(TempData.Total()<(int)HistoryBars*12)
            break;

После подготовки исходных данных запускаем метод feedForward и результаты работы нейронной сети записываем в переменную dPrevSignal. Ниже приведен код для нейронной сети регрессии с одним нейроном в выходном слое. С кодом для нейронной сети классификации с 3-мя нейронами в выходном слое можно ознакомиться во вложении к статье.

         Net.feedForward(TempData);
         Net.getResults(TempData);
         dPrevSignal=TempData[0];

Для визуализации работы нейронной сети на графике выведем метки прогнозных фракталов для последних 200 свечей.

         bar_time=Time.GetData(i);
         if(i<200)
           {
            if(DoubleToSignal(dPrevSignal)==Undefine)
               DeleteObject(bar_time);
            else
               DrawObject(bar_time,dPrevSignal,High.GetData(i),Low.GetData(i));
           }

И в заключении цикла перебора исторических данных актуализируем флаг принудительного завершения программы.

         stop=IsStopped();
        }

После обучения нейронной сети на всем объеме исторических данных увеличим счетчик эпох обучения и сохраним текущее состояние нейронной сети в локальный файл для возможности последующей загрузке при перезапуске программы.

      if(add_loop)
         count++;
      if(!stop)
        {
         dError=Net.getRecentAverageError();
         if(add_loop)
           {
            Net.Save(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false);
            printf("Era %d -> error %.2f %% forecast %.2f",count,dError,dForecast);
           }
         }

В заключении укажем условия выхода из цикла обучения. Это может быть получение сигнала с вероятностью достижения цели выше заранее заданного уровня, достижение целевого параметра ошибки, или же когда после очередной эпохи обучения статистические данные не изменяются или их изменение незначительное (обучение остановилось в локальном минимуме). Или же вы можете определить свои критерии выхода из процесса обучения.

     }
   while((!(DoubleToSignal(dPrevSignal)!=Undefine || dForecast>70) || !(dError<0.1 && MathAbs(dError-prev_er)<0.01 && MathAbs(dUndefine-prev_up)<0.1 && MathAbs(dForecast-prev_for)<0.1)) && !stop);

И перед выходом из функции обучения сохраним время последней свечи обучения.

   if(count>0)
     {
      dtStudied=bar_time;
     }
  }

3.4. Доработка метода расчета градиента.

Хочется обратить внимание на один момент, который был обнаружен в процессе тестирования. При обучении нейронной сети в некоторых случаях возникала ситуация с неконтролируемым ростом весовых коэффициентов нейронов скрытых слоев, что приводило к превышению максимально допустимых значений переменных и, как следствие, параличу всей нейронной сети. Такая ситуация складывалась в случаях, когда ошибка последующего слоя требовала с выхода нейронов значений, выходящих за пределы возможных значений функции активации. Решение было найдено в нормализации целевых значений нейронов. Скорректированный код метода расчета градиента приведен ниже.

void CNeuron::calcOutputGradients(double targetVals)
  {
   double delta=(targetVals>1 ? 1 : targetVals<-1 ? -1 : targetVals)-outputVal;
   gradient=(delta!=0 ? delta*CNeuron::activationFunctionDerivative(targetVals) : 0);
  }

С полным кодом всех методов и функции можно ознакомиться во вложении.

4.Тестирование

Тестовое обучение нейронной сети проводилось по паре EURUSD на таймфрейме H1. На вход нейронной сети подавались данные за 20 свечей. Обучение проводилось за период в 2 последних года. Для чистоты эксперимента на двух графиках одного терминала были запущены оба советника: с нейронными сетями регрессии (Fractal — с 1-м нейроном в выходном слое) и классификации (Fractal_2 — с 3-мя нейронами в выходном слое).

Первая эпоха обучения на 12432 барах потребовала 2 часа 20 минут. Оба советника показали схожие результаты с уровнем попадания чуть более 6%.

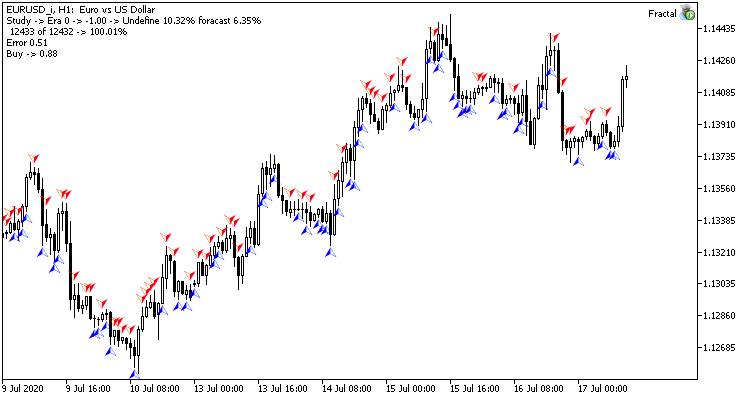
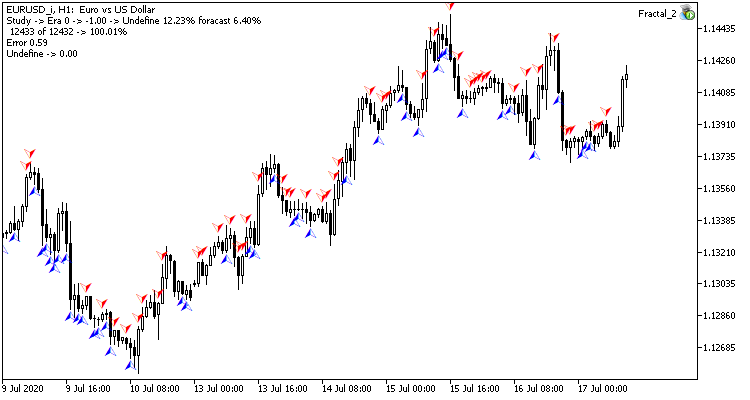
Первая эпоха максимально зависима от случайно выбранных на начальном этапе весовых коэффициентов нейронной сети.

После 35 эпох обучения разрыв в статистических показателях немного увеличился в пользу регрессионной модели нейронной сети:

Показатель	Нейронная сеть регрессии	Нейронная сеть классификации
Среднеквадратичная ошибка	0.68	0.78
Процент «попадания»	12.68%	11.22%
«Пропущенных» фракталов	20.22%	24.65%

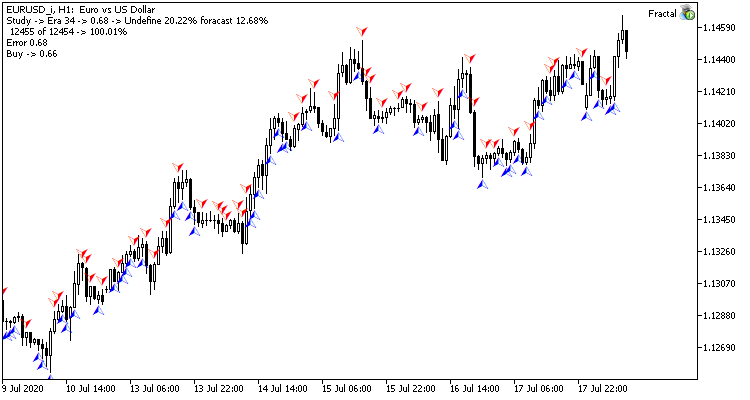
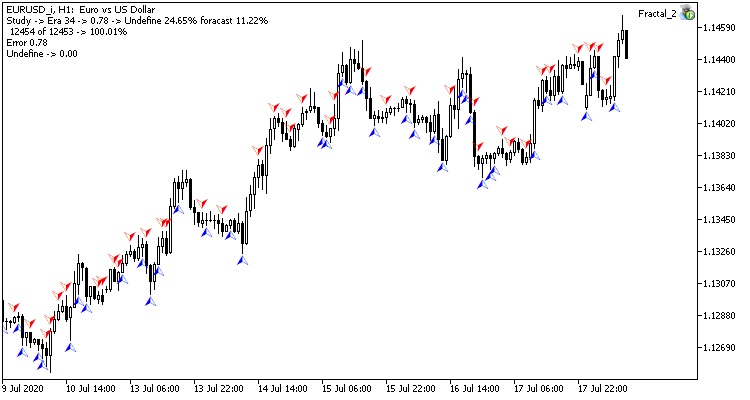
Результаты тестирования показывают, что оба варианта организации нейронной сети дают схожие результаты как по времени обучения, так и по точности предсказания. В тоже время полученные показатели говорят о необходимости дополнительных затрат времени и ресурсов на обучение. Желающие проанализировать динамику обучения нейронных сетей могут ознакомиться со скриншотами каждой эпохи обучения во вложении.

Заключение

В данной статье мы рассмотрели процесс построения, обучения и тестирования нейронной сети. Полученные результате говорят о существующем потенциале использования данной технологии. Однако процесс обучения нейронных сетей довольно затратный как по вычислительным ресурсам, так и по времени.

Программы, используемые в статье

#	Имя	Тип	Описание
	ExpertsNeuroNet_DNG
1	Fractal.mq5	Советник	Советник с нейронной сетью регрессии (1 нейрон в выходном слое)
2	Fractal_2.mq5	Советник	Советник с нейронной сетью классификации(3 нейрона в выходном слое)
3	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети (перцетрона)
	Files
4	Fractal	Директория	Содержит скриншоты тестирования нейронной сети регрессии
5	Fractal_2	Директория	Содержит скриншоты тестирования нейронной сети классификации

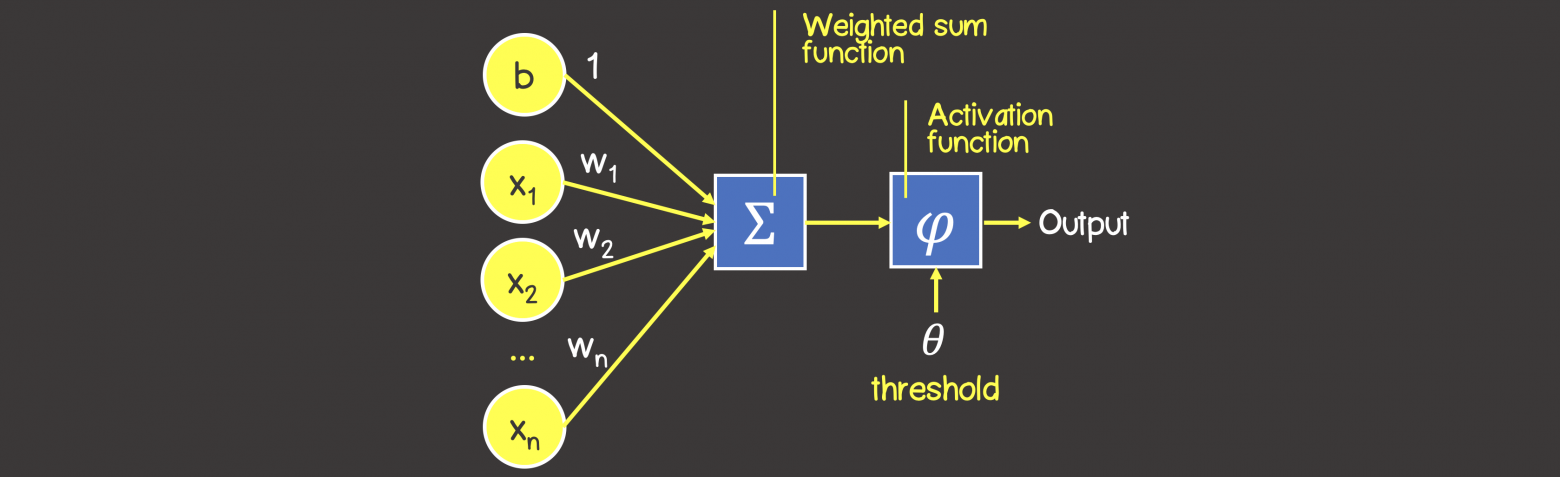
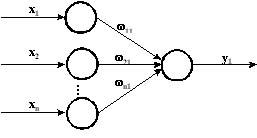
Источник

Нейронные сети

Персептрон

Заметка

Процесс обучения персептрона

Нейронные сети: 4. Обучение

Введение

Нейрон

Однослойная сеть

Усреднение градиента

Контроль уверенности нейрона

Двухслойная сеть

Обратное распространение ошибки

Нейронные сети: 1. Основы

Введение

Объекты и их признаки

Обучение с учителем

Нейрон

Сеть нейронов

Нейрон как гиперплоскость

Уверенность нейрона

Полезность нейрона

Несколько выходов

Когда нужен скрытый слой

Нейроны как логические элементы

Четыре варианта xor

Аппроксимация функции y=f(x)

Аппроксимация функции на Phyton

Нечёткая логика

Лабораторная работа №2 Линейная искусственная нейронная сеть. Правило обучения Видроу-Хоффа.

1.Правило обучения Видроу-Хоффа

Рис. 1.Линейная сеть.

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://studfile.net/html/2706/963/html_3f5EbOHSIW.cdKX/img-Ikypzj.png" width="123" height="45" />. (1.2)

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://studfile.net/html/2706/963/html_3f5EbOHSIW.cdKX/img-xBkZHJ.png" width="210" height="45" /> (1.3)

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://studfile.net/html/2706/963/html_3f5EbOHSIW.cdKX/img-I95qfr.png" width="139" height="38" /> (1.4)

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://studfile.net/html/2706/963/html_3f5EbOHSIW.cdKX/img-49A1X4.png" width="215" height="43" /> (1.5)

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://studfile.net/html/2706/963/html_3f5EbOHSIW.cdKX/img-2TtmZy.png" width="181" height="41" /> (1.6)

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://studfile.net/html/2706/963/html_3f5EbOHSIW.cdKX/img-Ty820n.png" width="236" height="29" /> (1.7)

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://studfile.net/html/2706/963/html_3f5EbOHSIW.cdKX/img-tfLVVg.png" width="189" height="29" /> (1.8)

1.13. Использование линейной нейронной сети для прогнозирования

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://studfile.net/html/2706/963/html_3f5EbOHSIW.cdKX/img-WHPjAu.png" width="197" height="45" />

Рис. 1.2. Прогнозирование временного ряда.

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://studfile.net/html/2706/963/html_3f5EbOHSIW.cdKX/img-xI3N6g.png" width="134" height="21" />.

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://studfile.net/html/2706/963/html_3f5EbOHSIW.cdKX/img-NTM4ab.png" width="298" height="89" />.

Задание.

1 связанные термины

2 функция потерь

2.1 Определение

2.2 Среднеквадратичная ошибка

2.3 Ошибка перекрестной энтропии

2.4 данные партии

2.5 Зачем нужна функция потерь

3 Численное дифференцирование

3.1 Производная

3.2 частные производные

4 градиента

5 реализация корпуса

5.1dataset

5.2common

5.2.1functions.py:

5.2.2gradient.py：

5.3ch04

5.3.1two_layer_net.py

5.3.2train_neuralnet.py

Выбор функции потерь для задач построения нейронных сетей

Содержание

Введение

1. Постановка задачи

2. Проектирование модели нейронной сети

2.1. Определение количества нейронов входного слоя

2.2. Проектирование скрытых слоев

2.3. Определение количества нейронов выходного слоя

3. Программирование

3.1. Подготовительная работа

3.2 Инициализация классов

3.3. Обучение нейронной сети

3.4. Доработка метода расчета градиента.

4.Тестирование

Заключение

Программы, используемые в статье

Лабораторная
работа №2
Линейная искусственная
нейронная сеть.
Правило обучения
Видроу-Хоффа.

1.Правило обучения
Видроу-Хоффа

.
(1.2)

(1.3)

(1.4)

(1.5)

(1.6)

(1.7)

(1.8)

1.13. Использование
линейной нейронной сети для прогнозирования

Рис. 1.2. Прогнозирование временного
ряда.

.

.