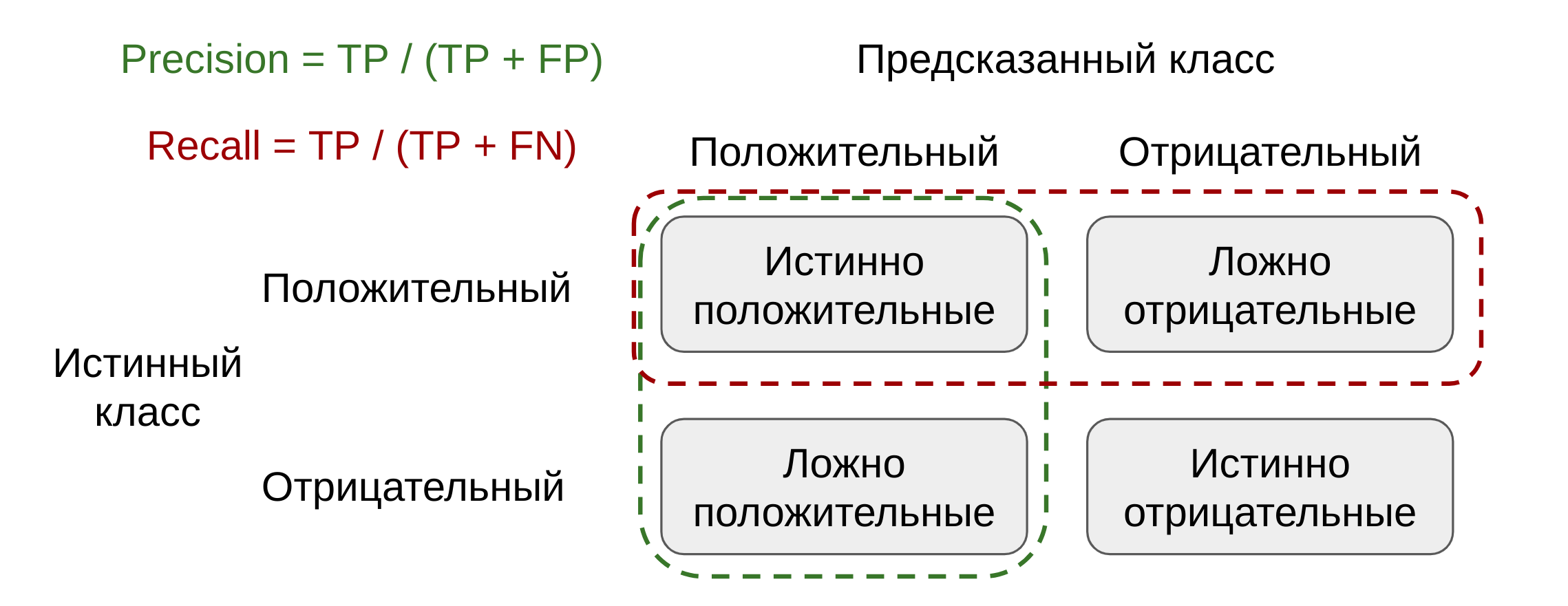
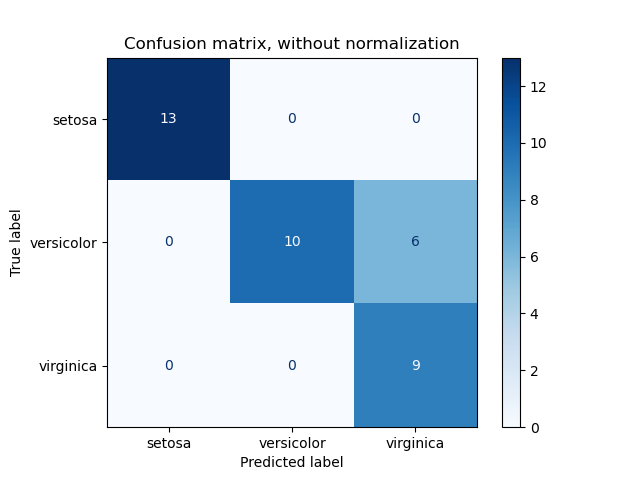
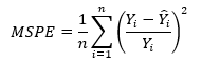From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
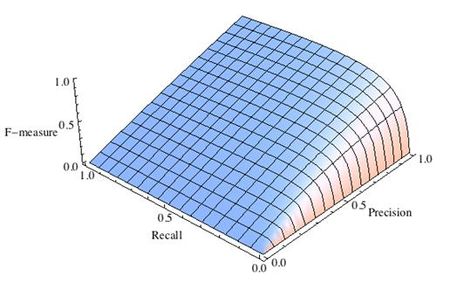
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
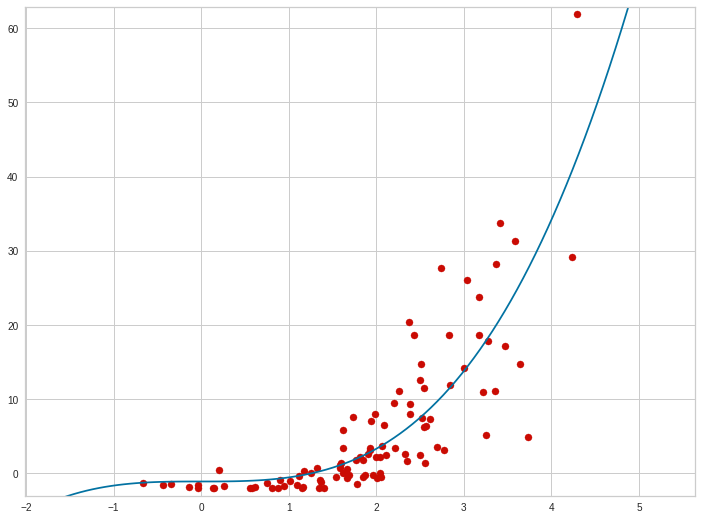
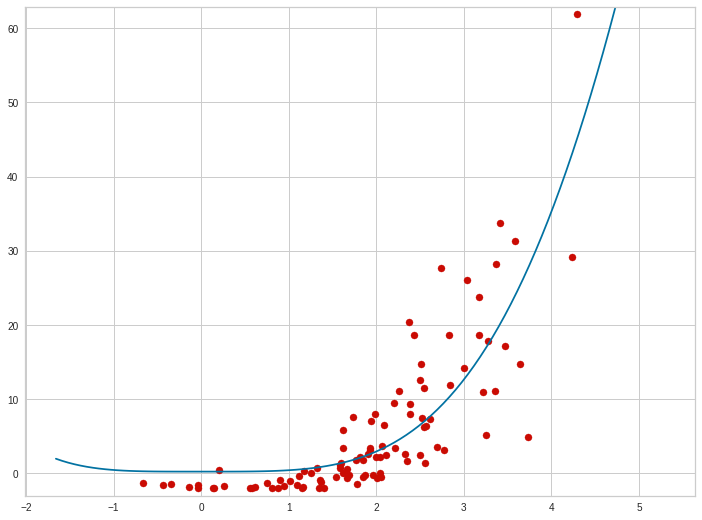
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
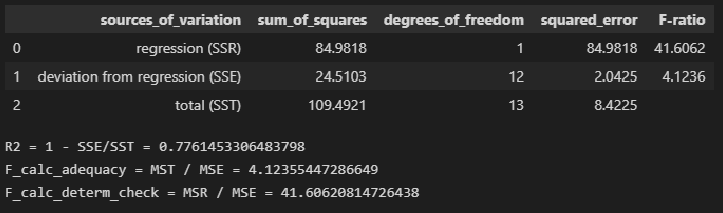
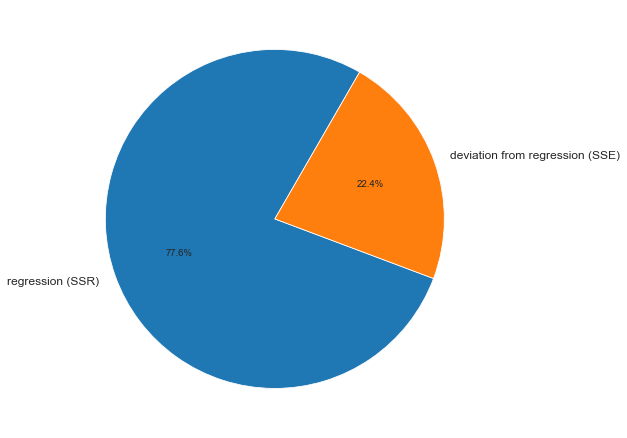
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
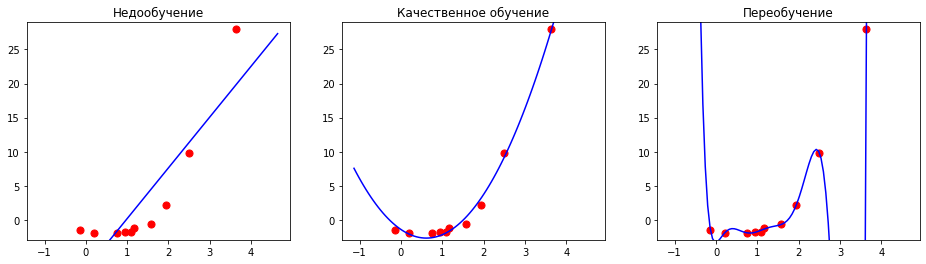
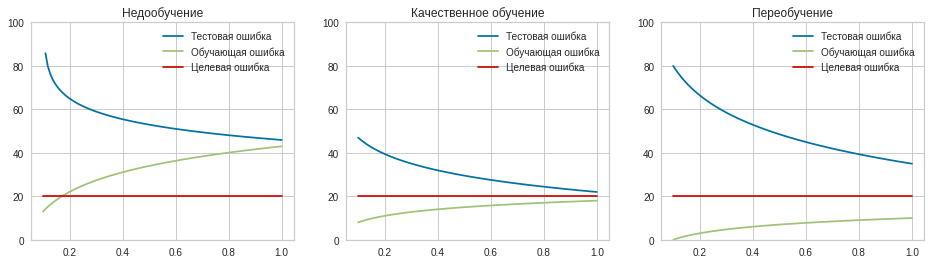
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
Для того чтобы модель линейной регрессии можно было применять на практике необходимо сначала оценить её качество. Для этих целей предложен ряд показателей, каждый из которых предназначен для использования в различных ситуациях и имеет свои особенности применения (линейные и нелинейные, устойчивые к аномалиям, абсолютные и относительные, и т.д.). Корректный выбор меры для оценки качества модели является одним из важных факторов успеха в решении задач анализа данных.
- Среднеквадратичная ошибка (Mean Squared Error)
- Корень из среднеквадратичной ошибки (Root Mean Squared Error)
- Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error)
- Cредняя абсолютная ошибка (Mean Absolute Error)
- Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error)
- Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error)
- Средняя абсолютная масштабированная ошибка (Mean absolute scaled error)
- Средняя относительная ошибка (Mean Relative Error)
- Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error
- R-квадрат
- Скорректированный R-квадрат
- Сравнение метрик
«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.
Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.
Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:
- Среднеквадратичная ошибка (MSE).
- Корень из среднеквадратичной ошибки (RMSE).
- Среднеквадратичная ошибка в процентах (MSPE).
- Средняя абсолютная ошибка (MAE).
- Средняя абсолютная ошибка в процентах (MAPE).
- Cимметричная средняя абсолютная процентная ошибка (SMAPE).
- Средняя абсолютная масштабированная ошибка (MASE)
- Средняя относительная ошибка (MRE).
- Среднеквадратичная логарифмическая ошибка (RMSLE).
- Коэффициент детерминации R-квадрат.
- Скорректированный коэффициент детеминации.
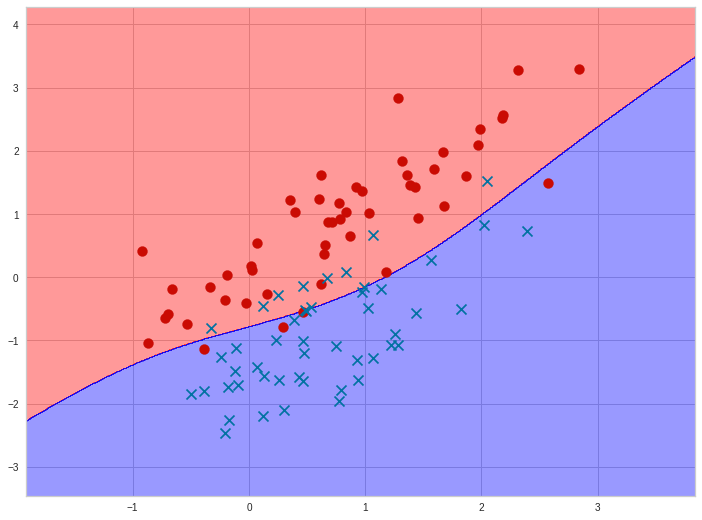
Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.
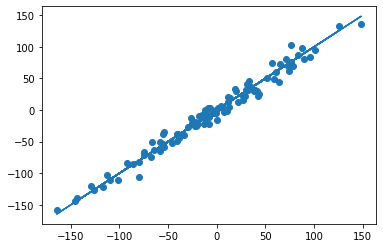
Рисунок 1. Линейная регрессия
Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.
Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — overline{y}.
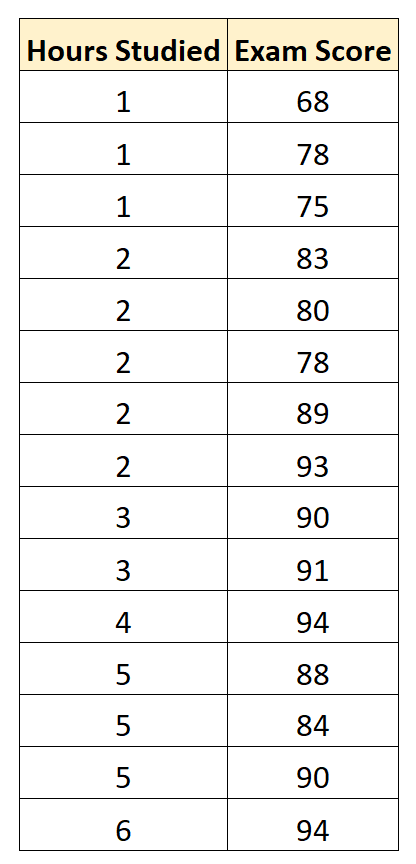
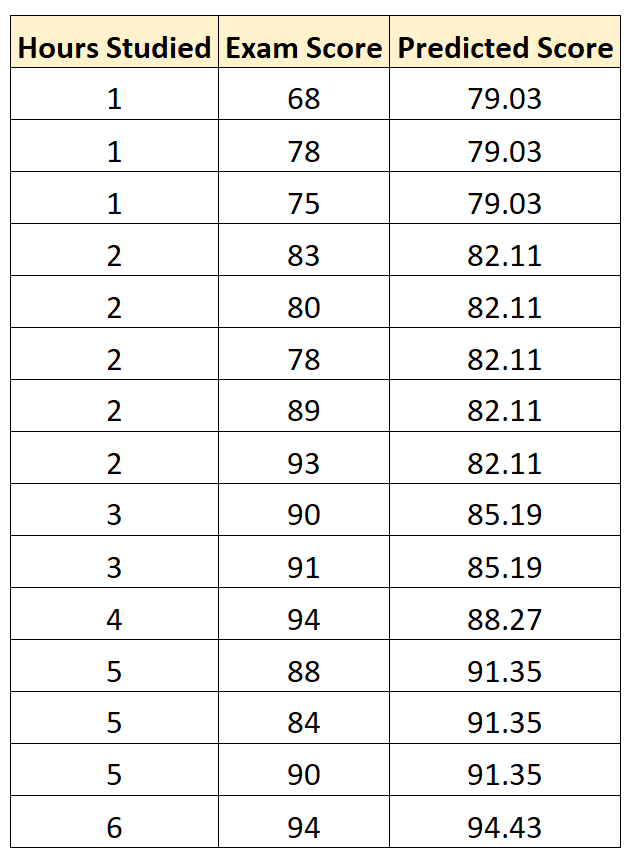
В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».
MSE
Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.
Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.
MSE рассчитывается по формуле:
MSE=frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y}_{i})^{2},
где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.
Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.
Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.
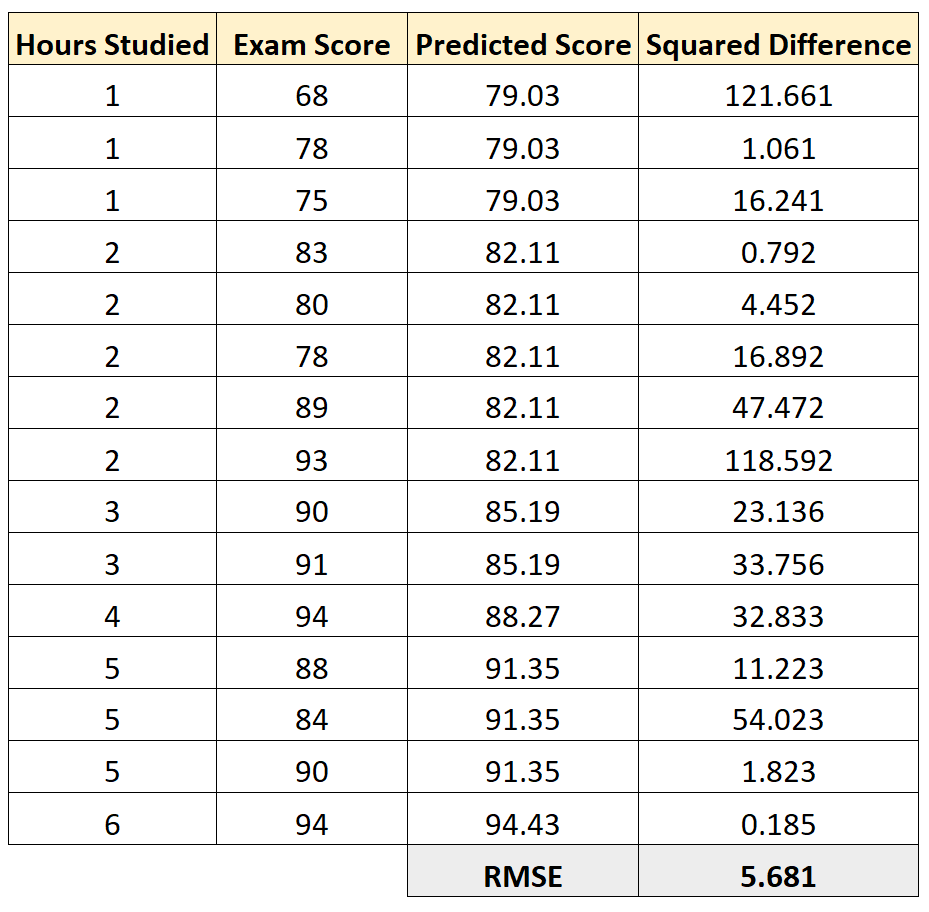
RMSE
Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:
RMSE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y_{i}})^{2}}
MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).
Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:
frac{partial RMSE}{partial widehat{y}_{i}}=frac{1}{2sqrt{MSE}}frac{partial MSE}{partial widehat{y}_{i}}
Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.
Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.
MSPE
Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:
MSPE=frac{100}{n}sumlimits_{i=1}^{n}left ( frac{y_{i}-widehat{y}_{i}}{y_{i}} right )^{2}
Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.
MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.
MAE
Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:
MAE=frac{1}{n}sumlimits_{i=1}^{n}left | y_{i}-widehat{y}_{i} right |
Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.
Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.
MAPE
Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:
MAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{left | y_{i} right |}
Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.
SMAPE
Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:
SMAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{(left | y_{i} right |+left | widehat{y}_{i} right |)/2}
Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.
Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и widehat{y}_{i}=90, то SMAPE=5.26.
Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).
MASE
Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:
MASE=frac{MAE_{i}}{MAE_{j}}
MASE симметрична и устойчива к выбросам.
MRE
Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:
MRE=frac{1}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y}_{i}right |}{left | y_{i} right |}
Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.
Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.
Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.
RMSLE
Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:
RMSLE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(log(widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}
Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.
Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.
R-квадрат
Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.
В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.
Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:
R^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}}
Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.
Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.
Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.
Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).
На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.
Скорректированный R-квадрат
Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.
В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).
Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:
R_{adj}^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}/(n-k)}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}/(n-1)}
где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.
Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.
Сравнение метрик
Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:
| Мера | Сильные стороны | Слабые стороны |
|---|---|---|
| MSE | Позволяет подчеркнуть большие отклонения, простота вычисления. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости. |
| RMSE | Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. |
| MSPE | Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер. | Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки. |
| MAPE | Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области. | Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю. |
| SMAPE | Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше. | Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения. |
| MASE | Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели. | Сложность интерпретации. |
| MRE | Позволяет оценить величину ошибки относительно значения целевой переменной. | Неприменима для наблюдений с нулевым значением выходной переменной. |
| RMSLE | Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше | Может быть затруднена интерпретация из-за нелинейности. |
| R-квадрат | Универсальность, простота интерпретации. | Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы. |
| R-квадрат скорр. | Корректно отражает вклад каждой переменной в модель. | Плохо работает, когда входные переменные зависимы. |
В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.
Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.
Другие материалы по теме:
Отбор переменных в моделях линейной регрессии
Репрезентативность выборочных данных
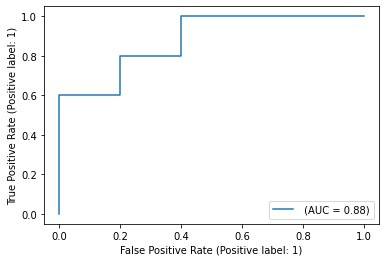
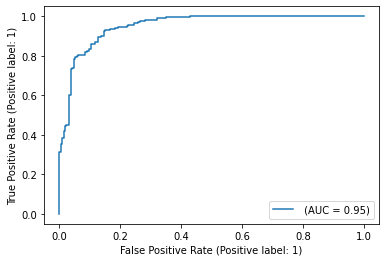
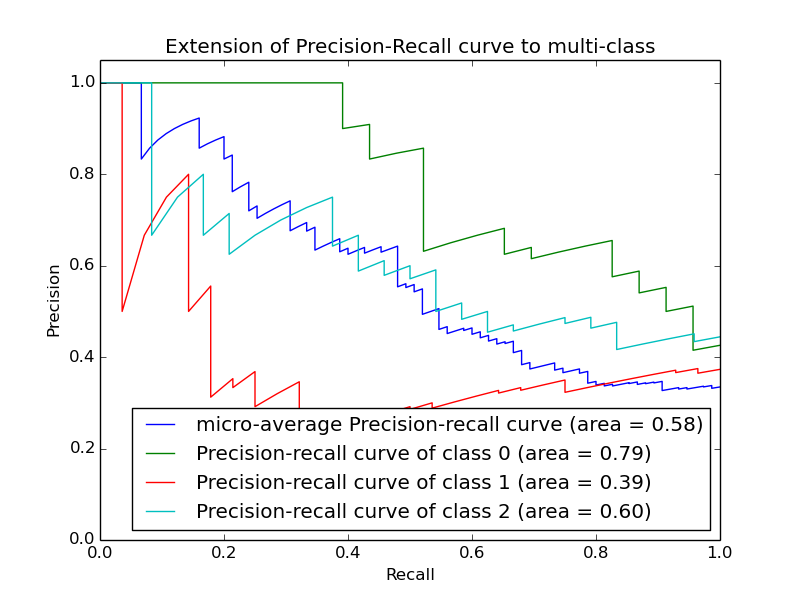
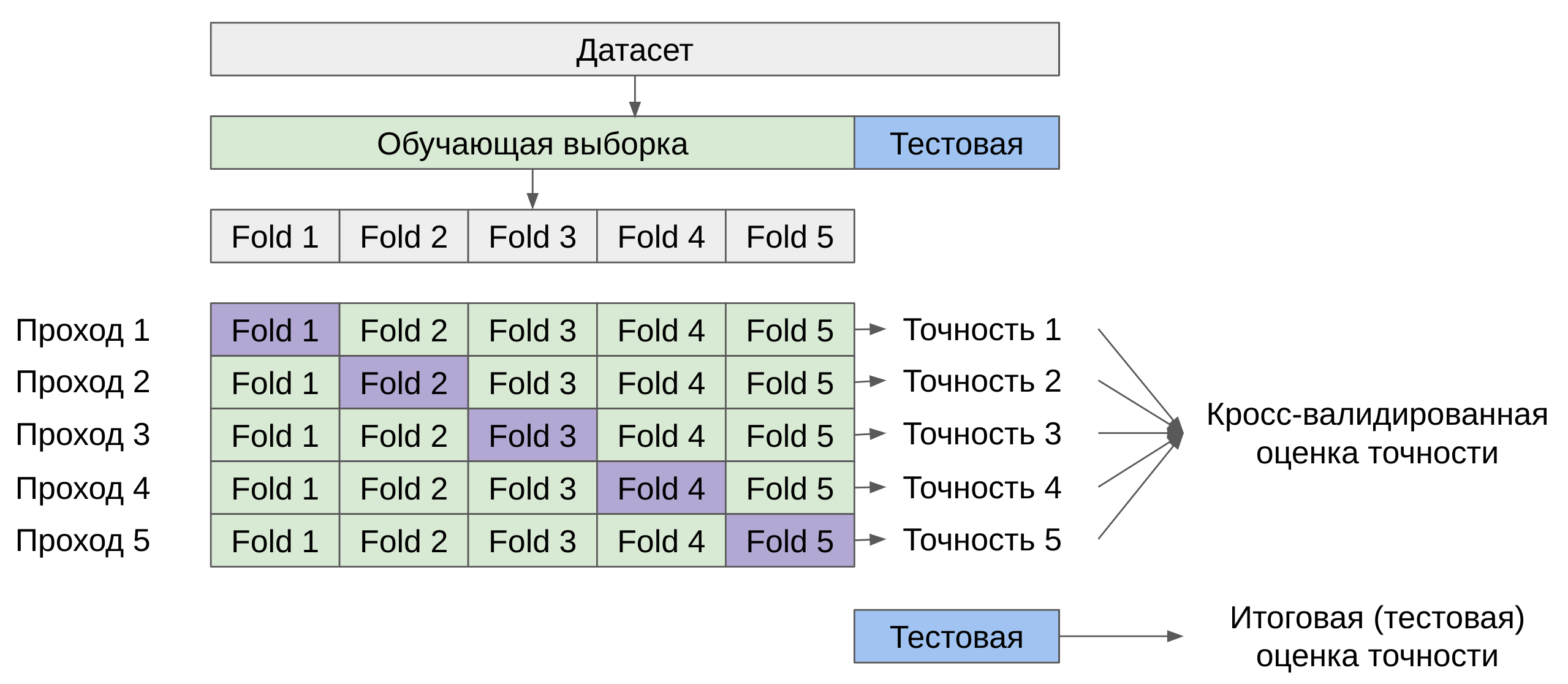
Логистическая регрессия и ROC-анализ — математический аппарат
АКТУАЛЬНОСТЬ ТЕМЫ
Общие положения
Про регрессионный анализ вообще, и его применение в DataScience написано очень много. Есть множество учебников, монографий, справочников и статей по прикладной статистике, огромное количество информации в интернете, примеров расчетов. Можно найти множество кейсов, реализованных с использованием средств Python. Казалось бы — что тут еще можно добавить?
Однако, как всегда, есть нюансы:
1. Регрессионный анализ — это прежде всего процесс, набор действий исследователя по определенному алгоритму: «подготовка исходных данных — построение модели — анализ модели — прогнозирование с помощью модели». Это ключевая особенность. Не представляет особой сложности сформировать DataFrame исходных данных и построить модель, запустить процедуру из библиотеки statsmodels. Однако подготовка исходных данных и последующий анализ модели требуют гораздо больших затрат человеко-часов специалиста и строк программного кода, чем, собственно, построение модели. На этих этапах часто приходится возвращаться назад, корректировать модель или исходные данные. Этому, к сожалению, во многих источниках, не удаляется достойного внимания, а иногда — и совсем не уделяется внимания, что приводит к превратному представлению о регрессионном анализе.
2. Далеко не во всех источниках уделяется должное внимание интерпретации промежуточных и финальных результатов. Специалист должен уметь интерпретировать каждую цифру, полученную в ходе работы над моделью.
3. Далеко не все процедуры на этапах подготовки исходных данных или анализа модели в источниках разобраны подробно. Например, про проверку значимости коэффициента детерминации найти информацию не представляет труда, а вот про проверку адекватности модели, построение доверительных интервалов регрессии или про специфические процедуры (например, тест Уайта на гетероскедастичность) информации гораздо меньше.
4. Своеобразная сложность может возникнуть с проверкой статистических гипотез: для отечественной литературы по прикладной статистике больше характерно проверять гипотезы путем сравнения расчетного значения критерия с табличным, а в иностранных источниках чаще определяется расчетный уровень значимости и сравнивается с заданным (чаще всего 0.05 = 1-0.95). В разных источниках информации реализованы разные подходы. Инструменты python (прежде всего библиотеки scipy и statsmodels) также в основном оперируют с расчетным уровнем значимости.
5. Ну и, наконец, нельзя не отметить, что техническая документация библиотеки statsmodels составлена, на мой взгляд, далеко не идеально: информация излагается путано, изобилует повторами и пропусками, описание классов, функций и свойств выполнено фрагментарно и количество примеров расчетов — явно недостаточно.
Поэтому я решил написать ряд обзоров по регрессионному анализу средствами Python, в которых акцент будет сделан на практических примерах, алгоритме действий исследователя, интерпретации всех полученных результатов, конкретных методических рекомендациях. Буду стараться по возможности избегать теории (хотя совсем без нее получится) — все-таки предполагается, что специалист DataScience должен знать теорию вероятностей и математическую статистику, хотя бы в рамках курса высшей математики для технического или экономического вуза.
В данном статье остановимся на самои простом, классическом, стереотипном случае — простой линейной регрессии (simple linear regression), или как ее еще принято называть — парной линейной регрессионной модели (ПЛРМ) — в ситуации, когда исследователя не подстерегают никакие подводные камни и каверзы — исходные данные подчиняются нормальному закону, в выборке отсутствуют аномальные значения, отсутствует ложная корреляция. Более сложные случаи рассмотрим в дальнейшем.
Для построение регрессионной модели будем пользоваться библиотекой statsmodels.
В данной статье мы рассмотрим по возможности полный набор статистических процедур. Некоторые из них (например, дескриптивная статистика или дисперсионный анализ регрессионной модели) могут показаться избыточными. Все так, но эти процедуры улучшают наше представление о процессе и об исходных данных, поэтому в разбор я их включил, а каждый исследователь сам вправе для себя определить, потребуются ему эти процедуры или нет.
Краткий обзор источников
Источников информации по корреляционному и регрессионному анализу огромное количество, в них можно просто утонуть. Поэтому позволю себе просто порекомендовать ряд источников, на мой взгляд, наиболее полезных:
-
Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. — М.: ФИЗМАТЛИТ, 2006. — 816 с.
-
Львовский Е.Н. Статистические методы построения эмпирических формул. — М.: Высшая школа, 1988. — 239 с.
-
Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа / пер с нем. — М.: Финансы и статистика, 1983. — 302 с.
-
Афифи А., Эйзен С. Статистический анализ. Подход с использованием ЭВМ / пер с англ. — М.: Мир, 1982. — 488 с.
-
Дрейпер Н., Смит Г. Прикладной регрессионный анализ. Книга 1 / пер.с англ. — М.: Финансы и статистика, 1986. — 366 с.
-
Айвазян С.А. и др. Прикладная статистика: Исследование зависимостей. — М.: Финансы и статистика, 1985. — 487 с.
-
Прикладная статистика. Основы эконометрики: В 2 т. 2-е изд., испр. — Т.2: Айвазян С.А. Основы эконометрики. — М.: ЮНИТИ-ДАНА, 2001. — 432 с.
-
Магнус Я.Р. и др. Эконометрика. Начальный курс — М.: Дело, 2004. — 576 с.
-
Носко В.П. Эконометрика. Книга 1. — М.: Издательский дом «Дело» РАНХиГС, 2011. — 672 с.
-
Брюс П. Практическая статистика для специалистов Data Science / пер. с англ. — СПб.: БХВ-Петербург, 2018. — 304 с.
-
Уатт Дж. и др. Машинное обучение: основы, алгоритмы и практика применения / пер. с англ. — СПб.: БХВ-Петербург, 2022. — 640 с.
Прежде всего следует упомянуть справочник Кобзаря А.И. [1] — это безусловно выдающийся труд. Ничего подобного даже близко не издавалось. Всем рекомендую иметь под рукой.
Есть очень хорошее практическое пособие [2] — для начинающих и практиков.>
Добротная работа немецких авторов [3]. Все разобрано подробно, обстоятельно, с примерами — очень хорошая книга. Примеры приведены из области экономики.
Еще одна добротная работа — [4], с примерами медико-биологического характера.
Работа [5] считается одним из наиболее полных изложений прикладного регрессионного анализа.
Более сложные работы — [6] (классика жанра), [7], [8], [9] — выдержаны на достаточно высоком математическом уровне, примеры из экономической области.
Свежие работы [10] (с примерами на языке R) и [11] (с примерами на python).
Cтатьи
Статей про регрессионный анализ в DataScience очень много, обращаю внимание на некоторые весьма полезные из них.
Серия статей «Python, корреляция и регрессия», охватывающая весь процесс регрессионного анализа:
-
первичная обработка данных, визуализация и корреляционный анализ;
-
регрессия;
-
теория матриц в регрессионном анализе, проверка адекватности, мультиколлинеарность;
-
прогнозирование с помощью регрессионных моделей.
Очень хороший обзор «Интерпретация summary из statsmodels для линейной регрессии». В этой статье даны очень полезные ссылки:
-
Statistical Models
-
Interpreting Linear Regression Through statsmodels .summary()
Статья «Регрессионные модели в Python».
Основные предпосылки (гипотезы) регрессионного анализа
Очень кратко — об этом написано тысячи страниц в учебниках — но все же вспомним некоторые основы теории.
Проверка исходных предпосылок является очень важным моментом при статистическом анализе регрессионной модели. Если мы рассматриваем классическую линейную регрессионную модель вида:
то основными предпосылками при использовании обычного метода наименьших квадратов (МНК) для оценки ее параметров являются:
-
Среднее значение (математическое ожидание) случайной составляющей равно нулю:
-
Дисперсия случайной составляющей является постоянной:
В случае нарушения данного условия мы сталкиваемся с явлением гетероскедастичности.
-
Значения случайной составляющей статистически независимы (некоррелированы) между собой:
В случае нарушения данного условия мы сталкиваемся с явлением автокорреляции.
-
Условие существования обратной матрицы
что эквивалентно одному из двух следующих условий:
то есть число наблюдений должно превышать число параметров.
-
Значения случайной составляющей некоррелированы со значениями независимых переменных:
-
Случайная составляющая имеет нормальный закон распределения (с математическим ожиданием равным нулю — следует из условия 1):
Более подробно — см.: [3, с.90], [4, с.147], [5, с.122], [6, с.208], [7, с.49], [8, с.68], [9, с.88].
Кроме гетероскедастичности и автокорреляции возможно возникновение и других статистических аномалий — мультиколлинеарности, ложной корреляции и т.д.
Доказано, что оценки параметров, полученные с помощью МНК, обладают наилучшими свойствами (несмещенность, состоятельность, эффективность) при соблюдении ряда условий:
-
выполнение приведенных выше исходных предпосылок регрессионного анализа;
-
число наблюдений на одну независимую переменную должно быть не менее 5-6;
-
должны отсутствовать аномальные значения (выбросы).
Кроме обычного МНК существуют и другие его разновидности (взвешенный МНК, обобщенный МНК), которые применяются при наличии статистических аномалий. Кроме МНК применяются и другие методы оценки параметров моделей. В этом обзоре мы эти вопросы рассматривать не будем.
Алгоритм проведения регрессионного анализа
Алгоритм действий исследователя при построении регрессионной модели (полевые работы мы, по понятным причинам, не рассматриваем — считаем, что исходные данные уже получены):
-
Подготовительный этап — постановка целей и задач исследования.
-
Первичная обработка исходных данных — об этом много написано в учебниках и пособиях по DataScience, сюда могут относится:
-
выявление нерелевантных признаков (признаков, которые не несут полезной информации), нетипичных данных (выбросов), неинформативных признаков (имеющих большое количество одинаковых значений) и работа с ними (удаление/преобразование);
-
выделение категориальных признаков;
-
работа с пропущенными значениями;
-
преобразование признаков-дат в формат datetime и т.д.
-
Визуализация исходных данных — предварительный графический анализ.
-
Дескриптивная (описательная) статистика — расчет выборочных характеристик и предварительные выводы о свойствах исходных данных.
-
Исследование закона распределения исходных данных и, при необходимости, преобразование исходных данных к нормальному закону распределения.
-
Выявление статистически аномальных значений (выбросов), принятие решения об их исключении.
Этапы 4, 5 и 6 могут быть при необходимости объединены.
-
Корреляционный анализ — исследование корреляционных связей между исходными данными; это разведка перед проведением регрессионного анализа.
-
Построение регрессионной модели:
-
выбор моделей;
-
выбор методов;
-
оценка параметров модели.
-
Статистический анализ регрессионной модели:
-
оценка ошибок аппроксимации (error metrics);
-
анализ остатков (проверка нормальности распределения остатков и гипотезы о равенстве нулю среднего значения остатков);
-
проверка адекватности модели;
-
проверка значимости коэффициента детерминации;
-
проверка значимости коэффициентов регрессии;
-
проверка мультиколлинеарности (для множественных регрессионных моделей; вообще мультиколлинеарные переменные выявляются еще на стадии корреляционного анализа);
-
проверка автокорреляции;
-
проверка гетероскедастичности.
Этапы 8 и 9 могут быть при необходимости повторяться несколько раз.
-
Сравнительный анализ нескольких регрессионных моделей, выбор наилучшей (при необходимости).
-
Прогнозирование с помощью регрессионной модели и оценка качества прогноза.
-
Выводы и рекомендации.
Само собой, этот алгоритм не есть истина в последней инстанции — в зависимости от особенностей исходных данных и вида модели могут возникать дополнительные задачи.
Применение пользовательских функций
Далее в обзоре мной будут использованы несколько пользовательских функций для решения разнообразных задач. Все эти функции созданы для облегчения работы и уменьшения размера программного кода. Данные функции загружается из пользовательского модуля my_module__stat.py, который доступен в моем репозитории на GitHub. Лично мне так удобнее работать, хотя каждый исследователь сам формирует себе инструменты по душе — особенно в части визуализации. Желающие могут пользоваться этими функциями, либо создать свои.
Итак, вот перечень данных функций:
-
graph_scatterplot_sns — функция позволяет построить точечную диаграмму средствами seaborn и сохранить график в виде png-файла;
-
graph_hist_boxplot_probplot_XY_sns — функция позволяет визуализировать исходные данные для простой линейной регрессии путем одновременного построения гистограммы, коробчатой диаграммы и вероятностного графика (для переменных X и Y) средствами seaborn и сохранить график в виде png-файла; имеется возможность выбирать, какие графики строить (h — hist, b — boxplot, p — probplot);
-
descriptive_characteristics — функция возвращает в виде DataFrame набор статистических характеристики выборки, их ошибок и доверительных интервалов;
-
detecting_outliers_mad_test — функция выполняет проверку наличия аномальных значений (выбросов) по критерию наибольшего абсолютного отклонения (более подробно — см.[1, с.547]);
-
norm_distr_check — проверка нормальности распределения исходных данных с использованием набора из нескольких статистических тестов;
-
corr_coef_check — функция выполняет расчет коэффициента линейной корреляции Пирсона, проверку его значимости и расчет доверительных интервалов; об этой функции я писал в своей статье.
-
graph_regression_plot_sns — — функция позволяет построить график регрессионной модели.
Ряд пользовательских функций мы создаем в процессе данного обзора (они тоже включены в пользовательский модуль my_module__stat.py):
-
regression_error_metrics — расчет ошибок аппроксимации регрессионной модели;
-
ANOVA_table_regression_model — вывод таблицы дисперсионного анализа регрессионной модели;
-
regression_model_adequacy_check — проверка адекватности регрессионной модели по критерию Фишера;
-
determination_coef_check — проверка значимости коэффициента детерминации по критерию Фишера;
-
regression_coef_check — проверка значимости коэффициентов регрессии по критеирю Стьюдента;
-
Goldfeld_Quandt_test, Breush_Pagan_test, White_test — проверка гетероскедастичности с использование тестов Голдфелда-Квандта, Бриша-Пэгана и Уайта соответственно;
-
regression_pair_predict — функция для прогнозирования с помощью парной регрессионной модели: рассчитывает прогнозируемое значение переменной Y по заданной модели, а также доверительные интервалы среднего и индивидуального значения для полученного прогнозируемого значения Y;
-
graph_regression_pair_predict_plot_sns — прогнозирование: построение графика регрессионной модели (с доверительными интервалами) и вывод расчетной таблицы с данными для заданной области значений X.
ПОСТАНОВКА ЗАДАЧИ
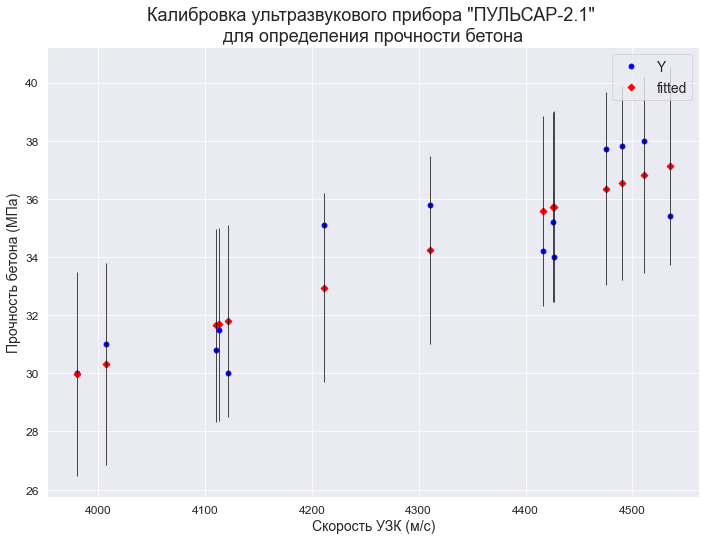
В качестве примера рассмотрим практическую задачу из области экспертизы промышленной безопасности — калибровку ультразвукового прибора для определения прочности бетона.
Итак, суть задачи: при обследовании несущих конструкций зданий и сооружений эксперт определяет прочность бетона с использованием ультразвукового прибора «ПУЛЬСАР-2.1», для которого необходимо предварительно построить градуировочную зависимость. Заключается это в следующем — производятся замеры с фиксацией следующих показателей:
-
X — показания ультразвукового прибора «ПУЛЬСАР-2.1» (м/с)
-
Y — результаты замера прочности бетона (методом отрыва со скалыванием) склерометром ИПС-МГ4.03.
Предполагается, что между показателями X и Y имеется линейная регрессионная зависимость, которая позволит прогнозировать прочность бетона на основании измерений, проведенных прибором «ПУЛЬСАР-2.1».
Были выполнены замеры фактической прочности бетона конструкций для бетонов одного вида с одним типом крупного заполнителя, с единой технологией производства. Для построения были выбраны 14 участков (не менее 12), включая участки, в которых значение косвенного показателя максимальное, минимальное и имеет промежуточные значения.
Настройка заголовков отчета:
# Общий заголовок проекта
Task_Project = 'Калибровка ультразвукового прибора "ПУЛЬСАР-2.1" nдля определения прочности бетона'
# Заголовок, фиксирующий момент времени
AsOfTheDate = ""
# Заголовок раздела проекта
Task_Theme = ""
# Общий заголовок проекта для графиков
Title_String = f"{Task_Project}n{AsOfTheDate}"
# Наименования переменных
Variable_Name_X = "Скорость УЗК (м/с)"
Variable_Name_Y = "Прочность бетона (МПа)"
# Константы
INCH = 25.4 # мм/дюйм
DecPlace = 5 # number of decimal places - число знаков после запятой
# Доверительная вероятность и уровень значимости:
p_level = 0.95
a_level = 1 - p_level Подключение модулей и библиотек:
# Стандартные модули и библиотеки
import os # загрузка модуля для работы с операционной системой
import sys
import platform
print('{:<35}{:^0}'.format("Текущая версия Python: ", platform.python_version()), 'n')
import math
from math import * # подключаем все содержимое модуля math, используем без псевдонимов
import numpy as np
#print ("Текущая версия модуля numpy: ", np.__version__)
print('{:<35}{:^0}'.format("Текущая версия модуля numpy: ", np.__version__))
from numpy import nan
import scipy as sci
print('{:<35}{:^0}'.format("Текущая версия модуля scipy: ", sci.__version__))
import scipy.stats as sps
import pandas as pd
print('{:<35}{:^0}'.format("Текущая версия модуля pandas: ", pd.__version__))
import matplotlib as mpl
print('{:<35}{:^0}'.format("Текущая версия модуля matplotlib: ", mpl.__version__))
import matplotlib.pyplot as plt
import seaborn as sns
print('{:<35}{:^0}'.format("Текущая версия модуля seaborn: ", sns.__version__))
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.graphics.api as smg
import statsmodels.stats.api as sms
from statsmodels.compat import lzip
print('{:<35}{:^0}'.format("Текущая версия модуля statsmodels: ", sm.__version__))
import statistics as stat # module 'statistics' has no attribute '__version__'
import sympy as sym
print('{:<35}{:^0}'.format("Текущая версия модуля sympy: ", sym.__version__))
# Настройки numpy
np.set_printoptions(precision = 4, floatmode='fixed')
# Настройки Pandas
pd.set_option('display.max_colwidth', None) # текст в ячейке отражался полностью вне зависимости от длины
pd.set_option('display.float_format', lambda x: '%.4f' % x)
# Настройки seaborn
sns.set_style("darkgrid")
sns.set_context(context='paper', font_scale=1, rc=None) # 'paper', 'notebook', 'talk', 'poster', None
# Настройки Mathplotlib
f_size = 8 # пользовательская переменная для задания базового размера шрифта
plt.rcParams['figure.titlesize'] = f_size + 12 # шрифт заголовка
plt.rcParams['axes.titlesize'] = f_size + 10 # шрифт заголовка
plt.rcParams['axes.labelsize'] = f_size + 6 # шрифт подписей осей
plt.rcParams['xtick.labelsize'] = f_size + 4 # шрифт подписей меток
plt.rcParams['ytick.labelsize'] = f_size + 4
plt.rcParams['legend.fontsize'] = f_size + 6 # шрифт легенды
# Пользовательские модули и библиотеки
Text1 = os.getcwd() # вывод пути к текущему каталогу
#print(f"Текущий каталог: {Text1}")
sys.path.insert(1, "D:REPOSITORYMyModulePython")
from my_module__stat import *ФОРМИРОВАНИЕ ИСХОДНЫХ ДАННЫХ
Показания ультразвукового прибора «ПУЛЬСАР-2.1» (м/с):
X = np.array([
4416, 4211, 4113, 4110, 4122,
4427, 4535, 4311, 4511, 4475,
3980, 4490, 4007, 4426
])Результаты замера прочности бетона (методом отрыва со скалыванием) прибором ИПС-МГ4.03:
Y = np.array([
34.2, 35.1, 31.5, 30.8, 30.0,
34.0, 35.4, 35.8, 38.0, 37.7,
30.0, 37.8, 31.0, 35.2
])Запишем данные в DataFrame:
calibrarion_df = pd.DataFrame({
'X': X,
'Y': Y})
display(calibrarion_df)
calibrarion_df.info()Сохраняем данные в csv-файл:
calibrarion_df.to_csv(
path_or_buf='data/calibrarion_df.csv',
mode='w+',
sep=';')Cоздаем копию исходной таблицы для работы:
dataset_df = calibrarion_df.copy()ВИЗУАЛИЗАЦИЯ ДАННЫХ
Границы значений переменных (при построении графиков):
(Xmin_graph, Xmax_graph) = (3800, 4800)
(Ymin_graph, Ymax_graph) = (25, 45)# Пользовательская функция
graph_scatterplot_sns(
X, Y,
Xmin=Xmin_graph, Xmax=Xmax_graph,
Ymin=Ymin_graph, Ymax=Ymax_graph,
color='orange',
title_figure=Task_Project,
x_label=Variable_Name_X,
y_label=Variable_Name_Y,
s=100,
file_name='graph/scatterplot_XY_sns.png')Существует универсальный набор графиков — гистограмма, коробчатая диаграмма, вероятностный график — которые позволяют исследователю сделать предварительные выводы о свойствах исходных данных.
Так как объем выборки невелик (n=14), строить гистограммы распределения переменных X и Y не имеет смысла, поэтому ограничимся построением коробчатых диаграмм и вероятностных графиков:
# Пользовательская функция
graph_hist_boxplot_probplot_XY_sns(
data_X=X, data_Y=Y,
data_X_min=Xmin_graph, data_X_max=Xmax_graph,
data_Y_min=Ymin_graph, data_Y_max=Ymax_graph,
graph_inclusion='bp', # выбираем для построения виды графиков: b - boxplot, p - probplot)
data_X_label=Variable_Name_X,
data_Y_label=Variable_Name_Y,
title_figure=Task_Project,
file_name='graph/hist_boxplot_probplot_XY_sns.png') Для сравнения характера распределений переменных X и Y возможно также построить совмещенную коробчатую диаграмму по стандартизованным данным:
# стандартизуем исходные данные
standardize_df = lambda X: ((X - np.mean(X))/np.std(X))
dataset_df_standardize = dataset_df.copy()
dataset_df_standardize = dataset_df_standardize.apply(standardize_df)
display(dataset_df_standardize)
# построим график
fig, axes = plt.subplots(figsize=(210/INCH, 297/INCH/2))
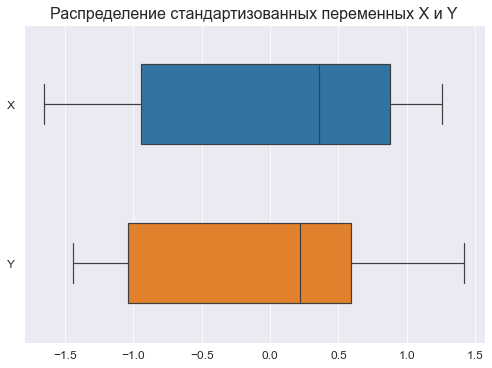
axes.set_title("Распределение стандартизованных переменных X и Y", fontsize = 16)
sns.boxplot(
data=dataset_df_standardize,
orient='h',
width=0.5,
ax=axes)
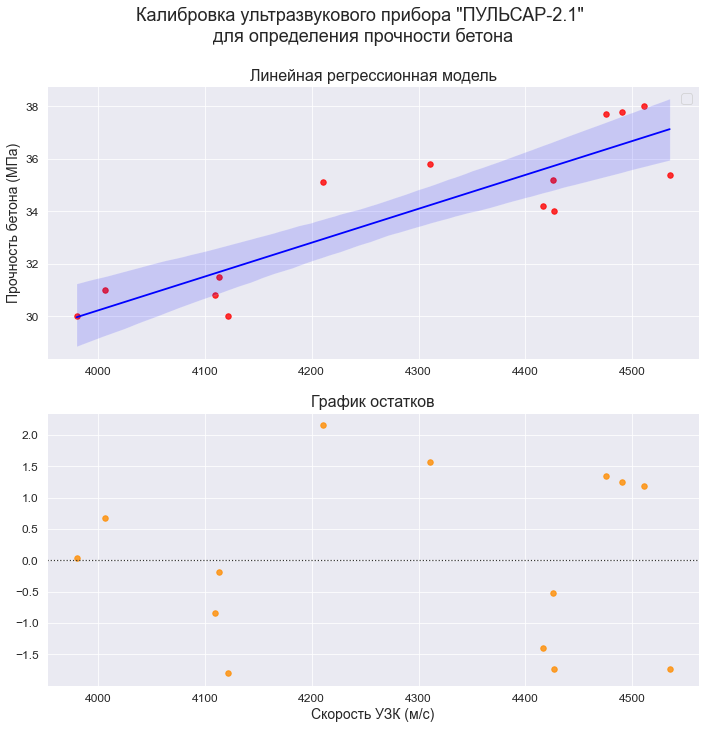
plt.show()Графический анализ позволяет сделать следующие выводы:
-
Отсутствие выбросов на коробчатых диаграммах свидетельствует об однородности распределения переменных.
-
Смещение медианы вправо на коробчатых диаграммах свидетельствует о левосторонней асимметрии распределения.
ДЕСКРИПТИВНАЯ (ОПИСАТЕЛЬНАЯ СТАТИСТИКА)
Собственно говоря, данный этап требуется проводить далеко не всегда, однако с помощью статистических характеристик выборки мы тоже можем сделать полезные выводы.
Описательная статистика исходных данных средствами библиотеки Pandas — самый простой вариант:
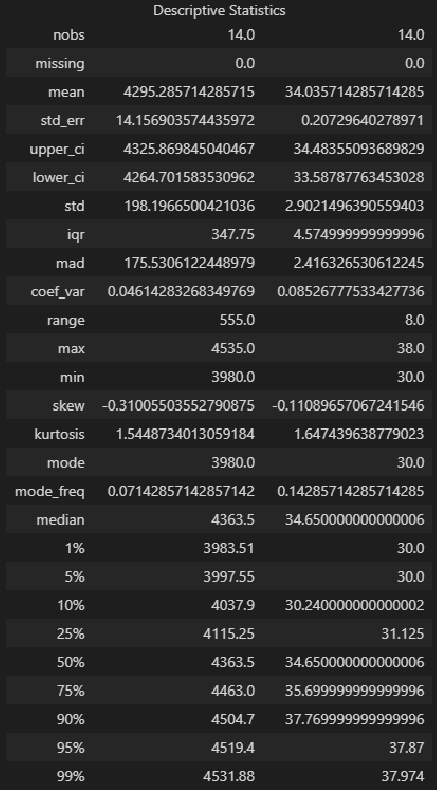
dataset_df.describe()Описательная статистика исходных данных средствами библиотеки statsmodels — более развернутый вариант, с большим количеством показателей:
from statsmodels.stats.descriptivestats import Description
result = Description(
dataset_df,
stats=["nobs", "missing", "mean", "std_err", "ci", "ci", "std", "iqr", "mad", "coef_var", "range", "max", "min", "skew", "kurtosis", "mode",
"median", "percentiles", "distinct", "top", "freq"],
alpha=a_level,
use_t=True)
display(result.summary())Описательная статистика исходных данных с помощью пользовательской функции descriptive_characteristics:
# Пользовательская функция
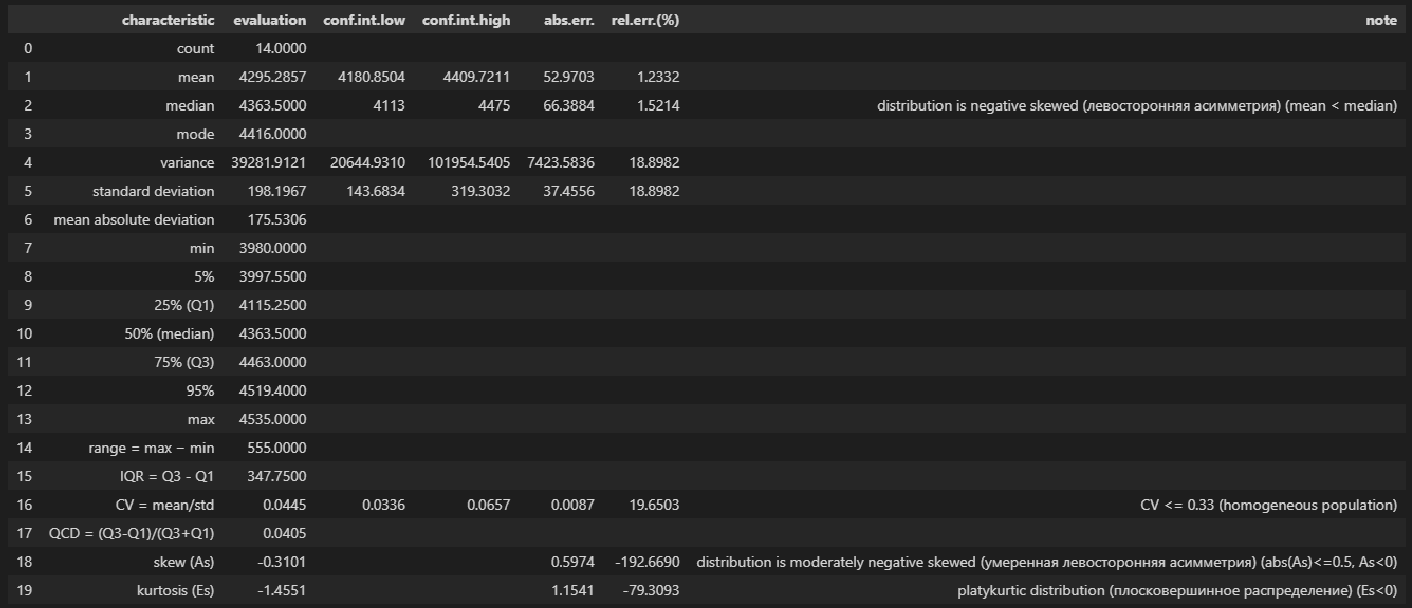
descriptive_characteristics(X)Выводы:
-
Сравнение показателей среднего арифметического (mean) и медианы (median) свидетельствует о левосторонней асимметрии (т.к.mean < median).
-
Значение коэффициента вариации CV = 0.0445 и доверительный интервал для него 0.0336 ≤ CV ≤ 0.0657 свидетельствует об однородности исходных данных (т.к. CV ≤ 0.33).
-
Значение показателя асимметрии skew (As) = -0.3101 свидетельствует об умеренной левосторонней асимметрии распределении (т.к. |As| ≤ 0.5, As < 0).
-
Значение показателя эксцесса kurtosis (Es) = -1.4551 свидетельствует о плосковершинном распределении (platykurtic distribution) (т.к. Es < 0).
# Пользовательская функция
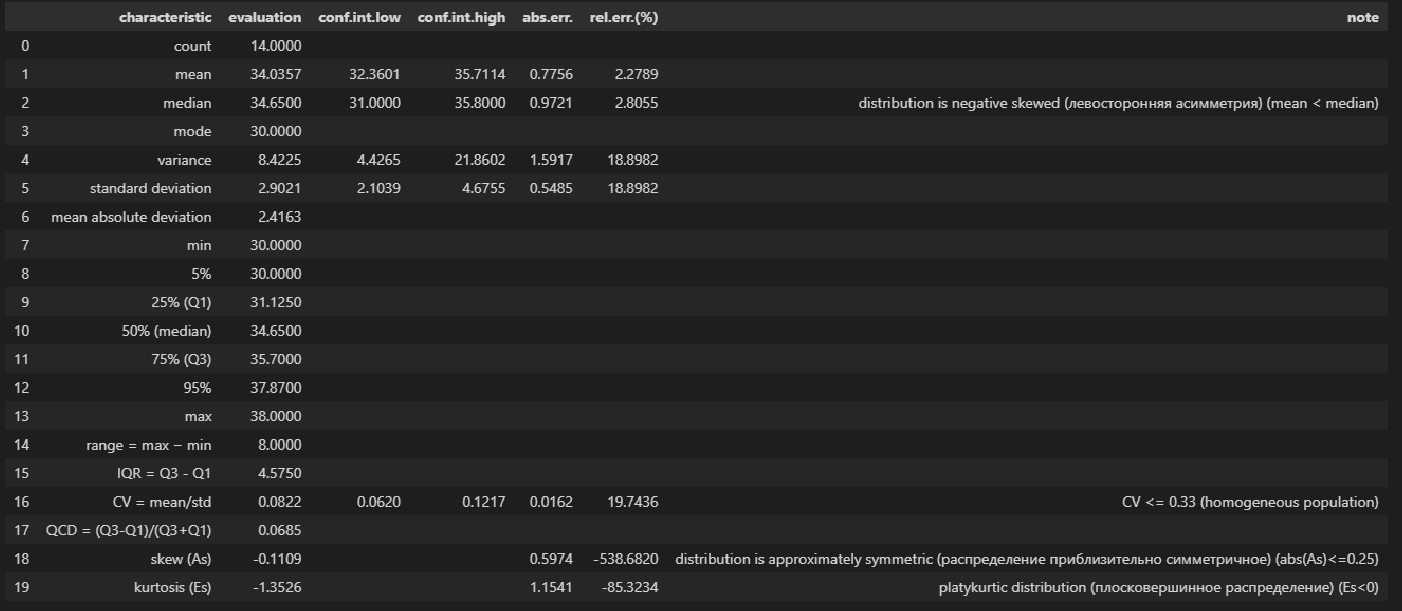
descriptive_characteristics(Y)Выводы:
-
Сравнение показателей среднего арифметического (mean) и медианы (median) свидетельствует о левосторонней асимметрии (т.к.mean < median).
-
Значение коэффициента вариации CV = 0.0822 и доверительный интервал для него 0.06202 ≤ CV ≤ 0.1217 свидетельствует об однородности исходных данных (т.к. CV ≤ 0.33).
-
Значение показателя асимметрии skew (As) = -0.1109 свидетельствует о приблизительно симметричном распределении (т.к. |As| ≤ 0.25).
-
Значение показателя эксцесса kurtosis (Es) = -1.3526 свидетельствует о плосковершинном распределении (platykurtic distribution) (т.к. Es < 0).
ПРОВЕРКА НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ
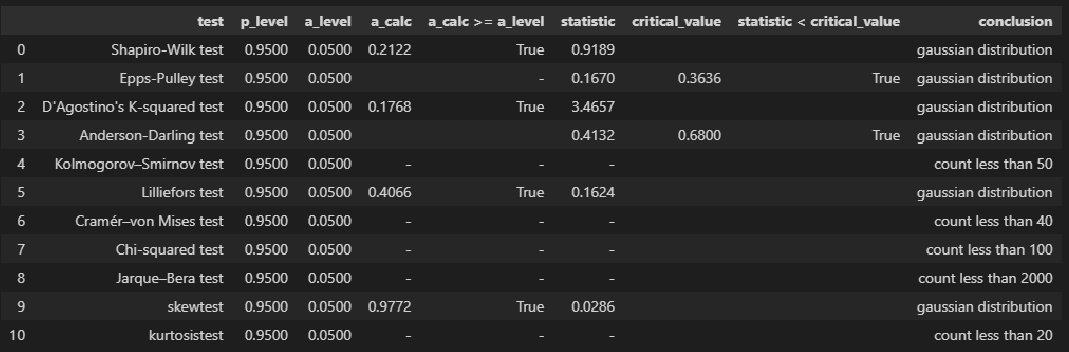
Для проверки нормальности распределения использована пользовательская функция norm_distr_check, которая объединяет в себе набор стандартных статистических тестов проверки нормальности. Все тесты относятся к стандартному инструментарию Pyton (библиотека scipy, модуль stats), за исключением теста Эппса-Палли (Epps-Pulley test); о том, как реализовать этот тест средствами Pyton я писал в своей статье https://habr.com/ru/post/685582/.
Примечание: для использования функции norm_distr_check в каталог с ipynb-файлом необходимо поместить папку table c файлом Tep_table.csv, который содержит табличные значения статистики критерия Эппса-Палли.
# пользовательская функция
norm_distr_check(X)# Пользовательская функция
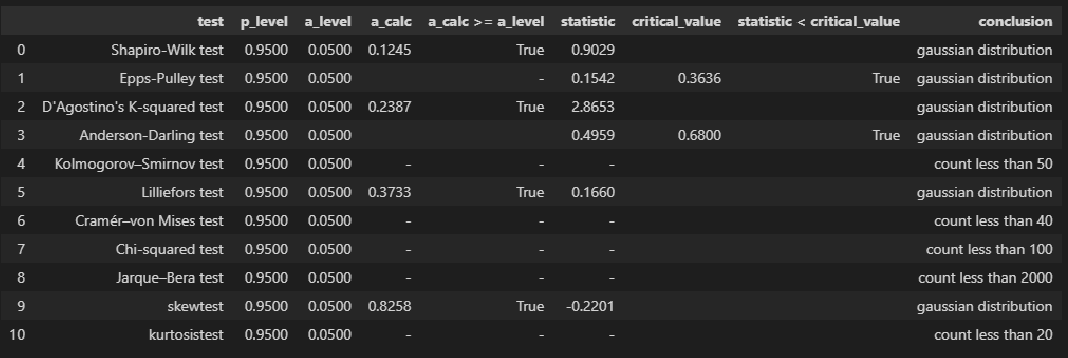
norm_distr_check (Y)Вывод: большинство статистических тестов позволяют принять гипотезу о нормальности распределения переменных X и Y.
ПРОВЕРКА АНОМАЛЬНЫХ ЗНАЧЕНИЙ (ВЫБРОСОВ)
Статистическую проверку аномальных значений (выбросов) не стоит путать с проверкой выбросов, которая проводится на этапе первичной обработки результатов наблюдений. Последняя проводится с целью отсеять явные ошибочные данные (например, в результате неправильно поставленной запятой величина показателя может увеличиться/уменьшиться на порядок); здесь же мы говорим о статистической проверке данных, которые уже прошли этап первичной обработки.
Имеется довольно много критериев для проверки аномальных значений (подробнее см.[1]); вообще данная процедура довольно неоднозначная:
-
критерии зависят от вида распределения;
-
мало данных о сравнительной мощности этих критериев;
-
даже в случае принятии гипотезы о нормальном распределении в выборке могут быть обнаружены аномальные значения и пр.
Кроме существует дилемма: если какие-то значения в выборке признаны выбросами — стоит или не стоит исследователю исключать их? Ведь каждое значение несет в себе информацию, причем иногда весьма ценную, а сильно отклоняющиеся от основного массива данные (которые не являются выбросами в смысле первичной обработки, но являются статистическим значимыми аномальными значениями) могут кардинально изменить статистический вывод.
В общем, о задаче выявления аномальных значений (выбросов) можно написать отдельно, а пока, в данном разборе, ограничимся проверкой аномальных значений по критерию наибольшего максимального отклонения (см.[1, с.547]) с помощью пользовательской функции detecting_outliers_mad_test. Данные функция возвращает DataFrame, которые включает список аномальных значений со следующими признаками:
-
value — проверяемое значение из выборки;
-
mad_calc и mad_table — расчетное и табличное значение статистики критерия;
-
outlier_conclusion — вывод (выброс или нет).
Обращаю внимание, что критерий наибольшего максимального отклонения можно использовать только для нормально распределенных данных.
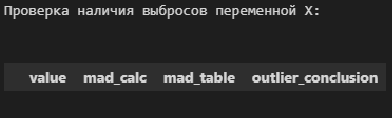
# пользовательская функция
print("Проверка наличия выбросов переменной X:n")
result = detecting_outliers_mad_test(X)
mask = (result['outlier_conclusion'] == 'outlier')
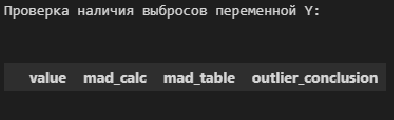
display(result[mask])# пользовательская функция
print("Проверка наличия выбросов переменной Y:n")
result = detecting_outliers_mad_test(Y)
mask = (result['outlier_conclusion'] == 'outlier')
display(result[mask])Вывод: в случае обеих переменных X и Y список пуст, следовательно, аномальных значений (выбросов) не выявлено.
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
Корреляционный анализ — это разведка перед построением регрессионной модели.
Выполним расчет коэффициента линейной корреляции Пирсона, проверку его значимости и построение доверительных интервалов с помощью пользовательской функции corr_coef_check (про эту функцию более подробно написано в моей статье https://habr.com/ru/post/683442/):
# пользовательская функция
display(corr_coef_check(X, Y, scale='Evans'))Выводы:
-
Значение коэффициента корреляции coef_value = 0.8900 свидетельствует о весьма сильной корреляционной связи (по шкале Эванса).
-
Коэффициент корреляции значим по критерию Стьюдента: t_calc ≥ t_table, a_calc ≤ a_level.
-
Доверительный интервал для коэффициента корреляции: 0.6621 ≤ coef_value ≤ 0.9625.
РЕГРЕССИОННЫЙ АНАЛИЗ
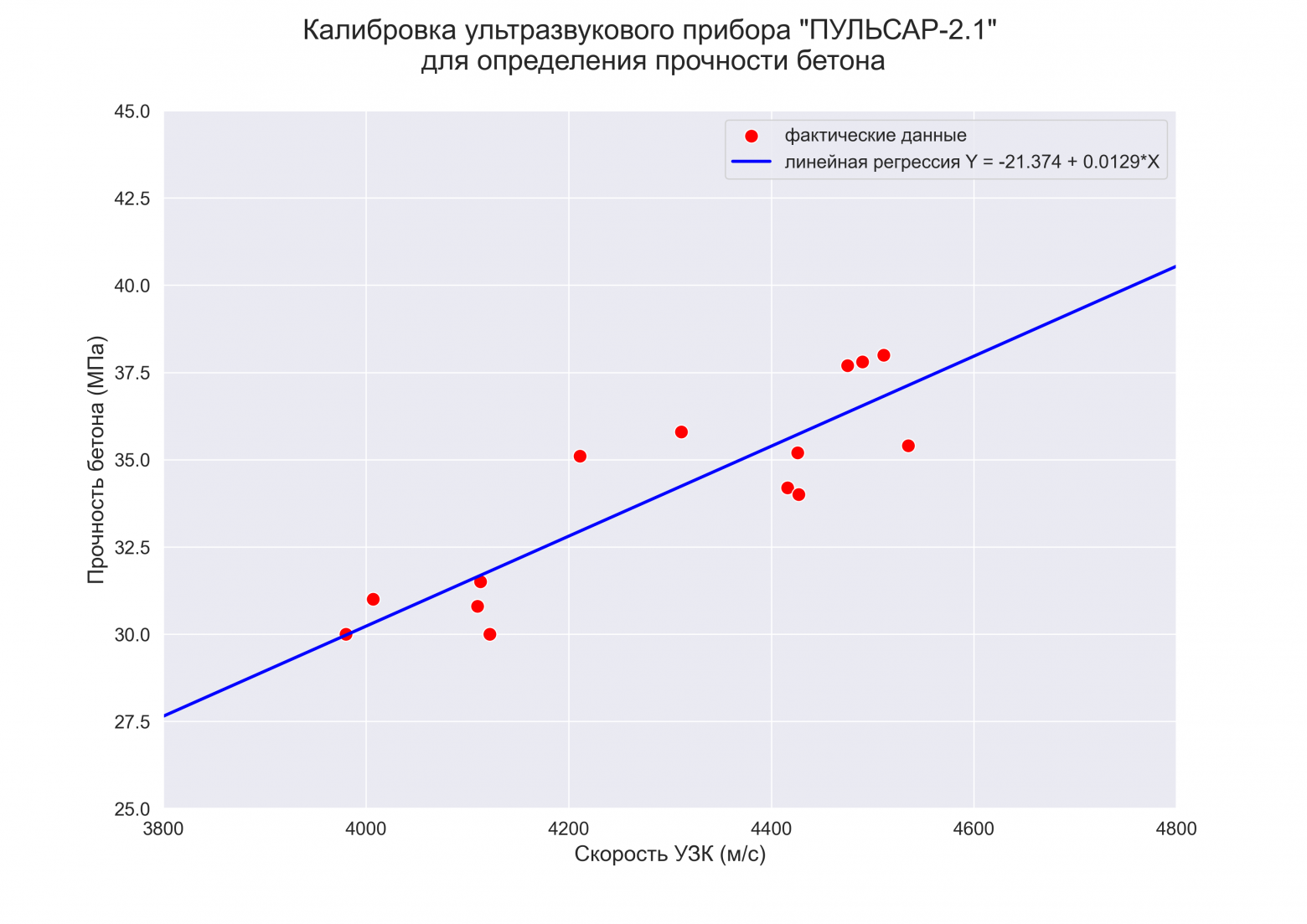
Предварительная визуализация
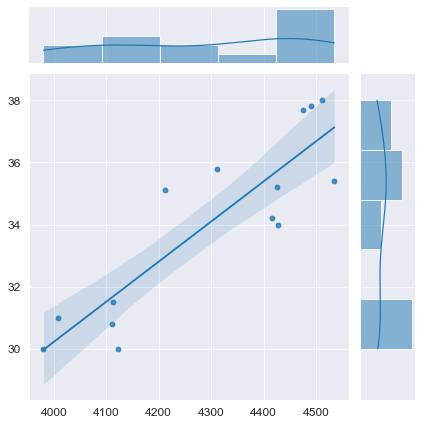
python позволяет выполнить предварительную визуализацию, например, с помощью функции jointplot библиотеки seaborn:
fig = plt.figure(figsize=(297/INCH, 210/INCH))
axes = sns.jointplot(
x=X, y=Y,
kind='reg',
ci=95)
plt.show()Построение модели
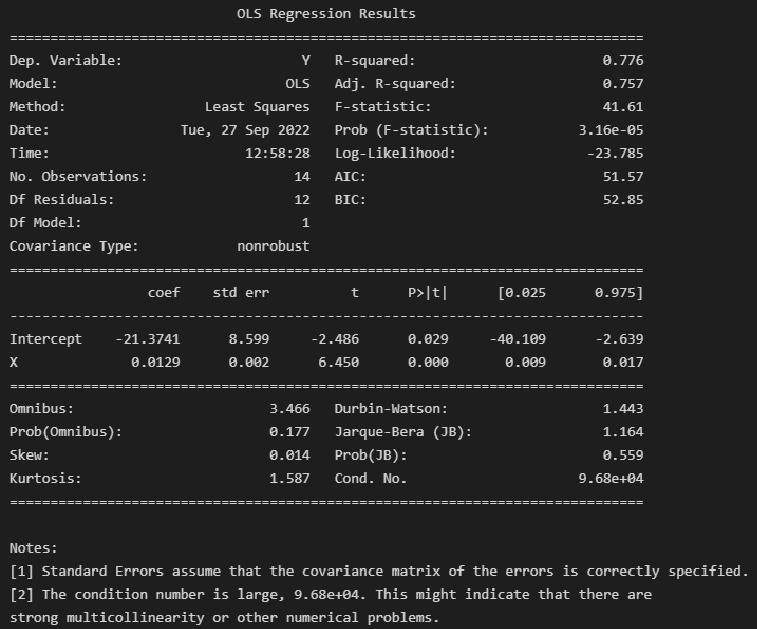
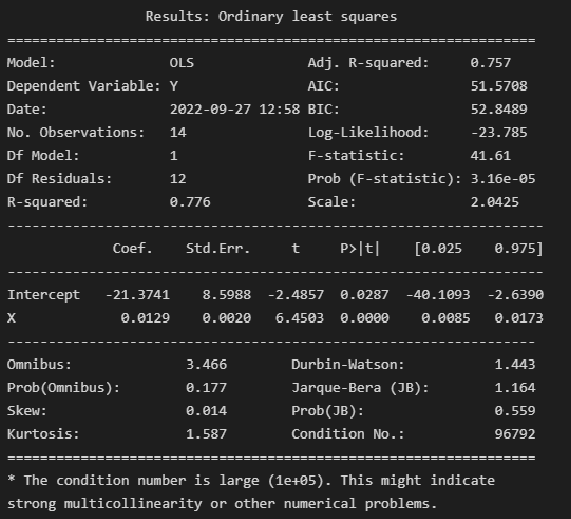
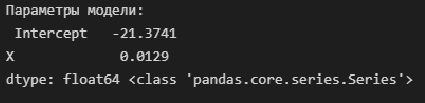
Выполним оценку параметров и анализ простой линейной регрессии (simple linear regression), используя библиотеку statsmodels (https://www.statsmodels.org/) и входящий в нее модуль линейной регрессии Linear Regression (https://www.statsmodels.org/stable/regression.html).
Данный модуль включает в себя классы, реализующие различные методы оценки параметров моделей линейной регрессии, в том числе:
-
класс OLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.OLS.html#statsmodels.regression.linear_model.OLS) — Ordinary Least Squares (обычный метод наименьших квадратов).
-
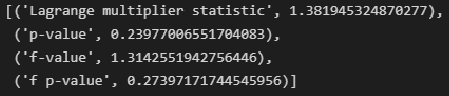
класс WLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.WLS.html#statsmodels.regression.linear_model.WLS) — Weighted Least Squares (метод взвешенных наименьших квадратов) (https://en.wikipedia.org/wiki/Weighted_least_squares), применяется, если имеет место гетероскедастичность данных (https://ru.wikipedia.org/wiki/Гетероскедастичность).
-
класс GLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.GLS.html#statsmodels.regression.linear_model.GLS) — Generalized Least Squares (обобщенный метод наименьших квадратов) (https://en.wikipedia.org/wiki/Generalized_least_squares), применяется, если существует определенная степень корреляции между остатками в модели регрессии.
-
класс GLSAR (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.GLSAR.html#statsmodels.regression.linear_model.GLSAR) — Generalized Least Squares with AR covariance structure (обобщенный метод наименьших квадратов, ковариационная структура с автокорреляцией — экспериментальный метод)
-
класс RecurciveLS (https://www.statsmodels.org/stable/examples/notebooks/generated/recursive_ls.html) — Recursive least squares (рекурсивный метод наименьших квадратов) (https://en.wikipedia.org/wiki/Recursive_least_squares_filter)
-
классы RollingOLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.rolling.RollingOLS.html#statsmodels.regression.rolling.RollingOLS) и RollingWLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.rolling.RollingWLS.html#statsmodels.regression.rolling.RollingWLS) — скользящая регрессия (https://www.statsmodels.org/stable/examples/notebooks/generated/rolling_ls.html, https://help.fsight.ru/ru/mergedProjects/lib/01_regression_models/rolling_regression.htm)
и т.д.
Так как исходные данные подчиняются нормальному закону распределения и аномальные значения (выбросы) отсутствуют, воспользуемся для оценки параметров обычным методом наименьших квадратов (класс OLS):
model_linear_ols = smf.ols(formula='Y ~ X', data=dataset_df)
result_linear_ols = model_linear_ols.fit()
print(result_linear_ols.summary())Альтернативная форма выдачи результатов:
print(result_linear_ols.summary2())Результаты построения модели мы получаем как класс statsmodels.regression.linear_model.RegressionResults (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.html#statsmodels.regression.linear_model.RegressionResults).
Экспресс-выводы, которые мы можем сразу сделать из результатов построения модели:
-
Коэффициенты регрессии модели Y = b0 + b1∙X:
-
Intercept = b0 = -21.3741
-
b1 = 0.0129
-
-
Коэффициент детерминации R-squared = 0.776, его скорректированная оценка Adj. R-squared = 0.757 — это означает, что регрессионная модуль объясняет 75.75% вариации переменной Y.
-
Проверка значимости коэффициента детерминации:
-
расчетное значение статистики критерия Фишера: F-statistic = 41.61
-
расчетный уровень значимости Prob (F-statistic) = 3.16e-05
-
так как значение Prob (F-statistic) < 0.05, то нулевая гипотеза R-squared = 0 НЕ ПРИНИМАЕТСЯ, т.е. коэффициент детерминации ЗНАЧИМ
-
-
Проверка значимости коэффициентов регрессии:
-
расчетный уровень значимости P>|t| не превышает 0.05 — это означает, что оба коэффициента регрессии значимы
-
об этом же свидетельствует то, что доверительный интервал для обоих коэффициентов регрессии ([0.025; 0.975]) не включает в себя точку 0
Также в таблице результатов содержится прочая информация по коэффициентам регрессии: стандартная ошибка Std.Err. расчетное значение статистики критерия Стьюдента t для проверки гипотезы о значимости.
-
-
Анализ остатков модели:
-
Тест Omnibus — про этот тест подробно написано в https://en.wikipedia.org/wiki/Omnibus_test, https://medium.com/swlh/interpreting-linear-regression-through-statsmodels-summary-4796d359035a, http://work.thaslwanter.at/Stats/html/statsModels.html.
Расчетное значение статистики критерия Omnibus = 3.466 — по сути расчетное значение F-критерия (см. https://en.wikipedia.org/wiki/Omnibus_test).
Prob(Omnibus) = 0.177 — показывает вероятность нормального распределения остатков (значение 1 указывает на совершенно нормальное распределение).
Учитывая, что в дальнейшем мы проверим нормальность распределения остатков по совокупности различных тестов, в том числе с достаточно высокой мощностью, и все тесты позволят принять гипотезу о нормальном распределении — в данном случае к тесту Omnibus возникают вопросы. С этим тестом нужно разбираться отдельно.
-
Skew = 0.014 и Kurtosis = 1.587 — показатели асимметрии и эксцесса остатков свидетельствуют, что распределение остатков практически симметричное, островершинное.
-
проверка нормальности распределения остатков по критерию Харке-Бера: расчетное значение статистики критерия Jarque-Bera (JB) = 1.164 и расчетный уровень значимости Prob(JB) = 0.559. К данным результатам также возникают вопросы, особенно, если учесть, что критерий Харке-Бера является асимптотическим, расчетное значение имеет распределение хи-квадрат, поэтому данный критерий рекомендуют применять только для больших выборок (см. https://en.wikipedia.org/wiki/Jarque–Bera_test). Проверку нормальности распределения остатков модели лучше проводить с использованием набора стандартных статистических тестов python (см. далее).
-
-
Проверка автокорреляции по критерию Дарбина-Уотсона: Durbin-Watson = 1.443.
Мы не будем здесь разбирать данный критерий, так как явление автокорреляции больше характерно для данных, выражаемых в виде временных рядов. Однако, для грубой оценки считается, что при расчетном значении статистики криетрия Дарбина=Уотсона а интервале [1; 2] автокорреляция отсутствует (см.https://en.wikipedia.org/wiki/Durbin–Watson_statistic).
Более подробно про критерий Дарбина-Уотсона — см. [1, с.659].
Прочая информация, которую можно извлечь из результатов построения модели:
-
Covariance Type — тип ковариации, подробнее см. https://habr.com/ru/post/681218/, https://towardsdatascience.com/simple-explanation-of-statsmodel-linear-regression-model-summary-35961919868b#:~:text=Covariance type is typically nonrobust,with respect to each other.
-
Scale — масштабный коэффициент для ковариационной матрицы (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.scale.html#statsmodels.regression.linear_model.RegressionResults.scale), равен величине Mean squared error (MSE) (cреднеквадратической ошибке), об подробнее см. далее, в разделе про ошибки аппроксимации моделей.
-
Показатели сравнения качества различных моделей:
-
Log-Likelihood — логарифмическая функция правдоподобия, подробнее см. https://en.wikipedia.org/wiki/Likelihood_function#Log-likelihood, https://habr.com/ru/post/433804/
-
AIC — информационный критерий Акаике (Akaike information criterion), подробнее см. https://en.wikipedia.org/wiki/Akaike_information_criterion
-
BIC — информационный критерий Байеса (Bayesian information criterion), подробнее см. https://en.wikipedia.org/wiki/Bayesian_information_criterion
В данной статье мы эти показатели рассматривать не будем, так как задача выбора одной модели из нескольких перед нами не стоит.
-
-
Число обусловленности Cond. No = 96792 используется для проверки мультиколлинеарности (считается, что мультиколлинеарность есть, если значение Cond. No > 30) (см. http://work.thaslwanter.at/Stats/html/statsModels.html). В нашем случае парной регрессионной модели о мультиколлинеарности речь не идет.
Далее будем извлекать данные из стандартного набора выдачи результатов и анализировать их более подробно. Последующие этапы вовсе не обязательно проводить в полном объеме при решении задач, но здесь мы рассмотрим их подробно.
Параметры и уравнение регрессионной модели
Извлечем параметры полученной модели — как свойство params модели:
print('Параметры модели: n', result_linear_ols.params, type(result_linear_ols.params))Имея параметры модели, можем формализовать уравнение модели Y = b0 + b1*X:
b0 = result_linear_ols.params['Intercept']
b1 = result_linear_ols.params['X']
Y_calc = lambda x: b0 + b1*xГрафик регрессионной модели
Для построения графиков регрессионных моделей можно воспользоваться стандартными возможностями библиотек statsmodels, seaborn, либо создать пользовательскую функцию — на усмотрение исследователя:
1. Построение графиков регрессионных моделей с использованием библиотеки statsmodels
С помощью функции statsmodels.graphics.plot_fit (https://www.statsmodels.org/stable/generated/statsmodels.graphics.regressionplots.plot_fit.html#statsmodels.graphics.regressionplots.plot_fit) — отображается график Y and Fitted vs.X (фактические и расчетные значения Y с доверительным интервалом для каждого значения Y):
fig, ax = plt.subplots(figsize=(297/INCH, 210/INCH))
fig = sm.graphics.plot_fit(
result_linear_ols, 'X',
vlines=True, # это параметр отвечает за отображение доверительных интервалов для Y
ax=ax)
ax.set_ylabel(Variable_Name_Y)
ax.set_xlabel(Variable_Name_X)
ax.set_title(Task_Project)
plt.show()С помощью функции statsmodels.graphics.plot_regress_exog (https://www.statsmodels.org/stable/generated/statsmodels.graphics.regressionplots.plot_regress_exog.html#statsmodels.graphics.regressionplots.plot_regress_exog) — отображается область 2х2, которая содержит:
-
предыдущий график Y and Fitted vs.X;
-
график остатков Residuals versus X;
-
график Partial regression plot — график частичной регрессии, пытается показать эффект добавления другой переменной в модель, которая уже имеет одну или несколько независимых переменных (более подробно см. https://en.wikipedia.org/wiki/Partial_regression_plot);
-
график CCPR Plot (Component-Component plus Residual Plot) — еще один способ оценить влияние одной независимой переменной на переменную отклика, принимая во внимание влияние других независимых переменных (более подробно — см. https://towardsdatascience.com/calculating-price-elasticity-of-demand-statistical-modeling-with-python-6adb2fa7824d, https://www.kirenz.com/post/2021-11-14-linear-regression-diagnostics-in-python/linear-regression-diagnostics-in-python/).
fig = plt.figure(figsize=(297/INCH, 210/INCH))
sm.graphics.plot_regress_exog(result_linear_ols, 'X', fig=fig)
plt.show()2. Построение графиков регрессионных моделей с использованием библиотеки seaborn
Воспользуемся модулем regplot библиотеки seaborn (https://seaborn.pydata.org/generated/seaborn.regplot.html). Данный модуль позволяет визуализировать различные виды регрессии:
-
линейную
-
полиномиальную
-
логистическую
-
взвешенную локальную регрессию (LOWESS — Locally Weighted Scatterplot Smoothing) (см. http://www.machinelearning.ru/wiki/index.php?title=Алгоритм_LOWESS, https://www.statsmodels.org/stable/generated/statsmodels.nonparametric.smoothers_lowess.lowess.html)
Более подробно про модуль regplot можно прочитать в статье: https://pyprog.pro/sns/sns_8_regression_models.html.
Есть более совершенный модуль lmplot (https://seaborn.pydata.org/generated/seaborn.lmplot.html), который объединяет в себе regplot и FacetGrid, но мы его здесь рассматривать не будем.
# создание рисунка (Figure) и области рисования (Axes)
fig = plt.figure(figsize=(297/INCH, 420/INCH/1.5))
ax1 = plt.subplot(2,1,1)
ax2 = plt.subplot(2,1,2)
# заголовок рисунка (Figure)
title_figure = Task_Project
fig.suptitle(title_figure, fontsize = 18)
# заголовок области рисования (Axes)
title_axes_1 = 'Линейная регрессионная модель'
ax1.set_title(title_axes_1, fontsize = 16)
# график регрессионной модели
order_mod = 1 # порядок модели
#label_legend_regr_model = 'фактические данные'
sns.regplot(
#data=dataset_df,
x=X, y=Y,
#x_estimator=np.mean,
order=order_mod,
logistic=False,
lowess=False,
robust=False,
logx=False,
ci=95,
scatter_kws={'s': 30, 'color': 'red'},
line_kws={'color': 'blue'},
#label=label_legend_regr_model,
ax=ax1)
ax1.set_ylabel(Variable_Name_Y)
ax1.legend()
# график остатков
title_axes_2 = 'График остатков'
ax2.set_title(title_axes_2, fontsize = 16)
sns.residplot(
#data=dataset_df,
x=X, y=Y,
order=order_mod,
lowess=False,
robust=False,
scatter_kws={'s': 30, 'color': 'darkorange'},
ax=ax2)
ax2.set_xlabel(Variable_Name_X)
plt.show()3. Построение графиков регрессионных моделей с помощью пользовательской функции
# Пользовательская функция
graph_regression_plot_sns(
X, Y,
regression_model=Y_calc,
Xmin=Xmin_graph, Xmax=Xmax_graph,
Ymin=Ymin_graph, Ymax=Ymax_graph,
title_figure=Task_Project,
x_label=Variable_Name_X,
y_label=Variable_Name_Y,
label_legend_regr_model=f'линейная регрессия Y = {b0:.3f} + {b1:.4f}*X',
s=80,
file_name='graph/regression_plot_lin.png')Статистический анализ регрессионной модели
1. Расчет ошибки аппроксимации (Error Metrics)
Ошибки аппроксимации (Error Metrics) позволяют получить общее представление о качестве модели, а также позволяют сравнивать между собой различные модели.
Создадим пользовательскую функцию, которая рассчитывает основные ошибки аппроксимации для заданной модели:
-
Mean squared error (MSE) или Mean squared deviation (MSD) — среднеквадратическая ошибка (https://en.wikipedia.org/wiki/Mean_squared_error):
-
Root mean square error (RMSE) или Root mean square deviation (RMSD) — квадратный корень из MSE (https://en.wikipedia.org/wiki/Root-mean-square_deviation):
-
Mean absolute error (MAE) — средняя абсолютная ошибка (https://en.wikipedia.org/wiki/Mean_absolute_error):
-
Mean squared prediction error (MSPE) — среднеквадратическая ошибка прогноза (среднеквадратическая ошибка в процентах) (https://en.wikipedia.org/wiki/Mean_squared_prediction_error):
-
Mean absolute percentage error (MAPE) — средняя абсолютная ошибка в процентах (https://en.wikipedia.org/wiki/Mean_absolute_percentage_error):
Про выбор метрики см. также https://machinelearningmastery.ru/how-to-select-the-right-evaluation-metric-for-machine-learning-models-part-2-regression-metrics-d4a1a9ba3d74/.
# Пользовательская функция
def regression_error_metrics(model, model_name=''):
model_fit = model.fit()
Ycalc = model_fit.predict()
n_fit = model_fit.nobs
Y = model.endog
MSE = (1/n_fit) * np.sum((Y-Ycalc)**2)
RMSE = sqrt(MSE)
MAE = (1/n_fit) * np.sum(abs(Y-Ycalc))
MSPE = (1/n_fit) * np.sum(((Y-Ycalc)/Y)**2)
MAPE = (1/n_fit) * np.sum(abs((Y-Ycalc)/Y))
model_error_metrics = {
'MSE': MSE,
'RMSE': RMSE,
'MAE': MAE,
'MSPE': MSPE,
'MAPE': MAPE}
result = pd.DataFrame({
'MSE': MSE,
'RMSE': RMSE,
'MAE': MAE,
'MSPE': "{:.3%}".format(MSPE),
'MAPE': "{:.3%}".format(MAPE)},
index=[model_name])
return model_error_metrics, result
(model_error_metrics, result) = regression_error_metrics(model_linear_ols, model_name='linear_ols')
display(result)В литературе по прикладной статистике нет единого мнения о допустимом размере относительных ошибок аппроксимации: в одних источниках допустимой считается ошибка 5-7%, в других она может быть увеличена до 8-10%, и даже до 15%.
Вывод: модель хорошо аппроксимирует фактические данные (относительная ошибка аппроксимации MAPE = 3.405% < 10%).
2. Дисперсионный анализ регрессионной модели (ДАРМ)
ДАРМ не входит в стандартную форму выдачи результатов Regression Results, однако я решил написать здесь о нем по двум причинам:
-
Именно анализ дисперсии регрессионной модели, разложение этой дисперсии на составляющие дает фундаментальное представление о сути регрессии, а термины, используемые при ДАРМ, применяются на последующих этапах анализа.
-
С терминами ДАРМ в литературе по прикладной статистике имеется некоторая путаница, в разных источниках они могут именоваться по-разному (см., например, [8, с.52]), поэтому, чтобы двигаться дальше, необходимо определиться с понятиями.
При ДАРМ общую вариацию результативного признака (Y) принято разделять на две составляющие — вариация, обусловленная регрессией и вариация, обусловленная отклонениями от регрессии (остаток), при этом в разных источниках эти термины могут именоваться и обозначаться по-разному, например:
-
Вариация, обусловленная регрессией — может называться Explained sum of squares (ESS), Sum of Squared Regression (SSR) (https://en.wikipedia.org/wiki/Explained_sum_of_squares, https://towardsdatascience.com/anova-for-regression-fdb49cf5d684), Sum of squared deviations (SSD).
-
Вариация, обусловленная отклонениями от регрессии (остаток) — может называться Residual sum of squares (RSS), Sum of squared residuals (SSR), Squared estimate of errors, Sum of Squared Error (SSE) (https://en.wikipedia.org/wiki/Residual_sum_of_squares, https://towardsdatascience.com/anova-for-regression-fdb49cf5d684); в отчественной практике также применяется термин остаточная дисперсия.
-
Общая (полная) вариация — может называться Total sum of squares (TSS), Sum of Squared Total (SST) (https://en.wikipedia.org/wiki/Partition_of_sums_of_squares, https://towardsdatascience.com/anova-for-regression-fdb49cf5d684).
Как видим, путаница знатная:
-
в разных источниках под SSR могут подразумеваться различные показатели;
-
легко перепутать показатели ESS и SSE;
-
в библиотеке statsmodel также есть смешение терминов: для показателя Explained sum of squares используется свойство ess, а для показателя Sum of squared (whitened) residuals — свойство ssr.
Мы будем пользоваться системой обозначений, принятой в большинстве источников — SSR (Sum of Squared Regression), SSE (Sum of Squared Error), SST (Sum of Squared Total). Стандартная таблица ДАРМ в этом случае имеет вид:
Примечания:
-
Здесь приведена таблица ДАРМ для множественной линейной регрессионной модели (МЛРМ), в нашем случае при ПЛРМ мы имеем частный случай p=1.
-
Показатели Fcalc-ad и Fcalc-det — расчетные значения статистики критерия Фишера при проверке адекватности модели и значимости коэффициента детерминации (об этом — см.далее).
Более подробно про дисперсионный анализ регрессионной модели — см.[4, глава 3].
Класс statsmodels.regression.linear_model.RegressionResults позволяет нам получить данные для ANOVA (см. https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.html#statsmodels.regression.linear_model.RegressionResults) как свойства класса:
-
Сумма квадратов, обусловленная регрессией / SSR (Sum of Squared Regression) — свойство ess.
-
Сумма квадратов, обусловленная отклонением от регрессии / SSE (Sum of Squared Error) — свойство ssr.
-
Общая (полная) сумма квадратов / SST (Sum of Squared Total) — свойство centered_tss.
-
Кол-во наблюдений / Number of observations — свойство nobs.
-
Число степеней свободы модели / Model degrees of freedom — равно числу переменных модели (за исключением константы, если она присутствует — свойство df_model.
-
Среднеквадратичная ошибка модели / Mean squared error the model — сумма квадратов, объясненная регрессией, деленная на число степеней свободы регрессии — свойство mse_model.
-
Среднеквадратичная ошибка остатков / Mean squared error of the residuals — сумма квадратов остатков, деленная на остаточные степени свободы — свойство mse_resid.
-
Общая среднеквадратичная ошибка / Total mean squared error — общая сумма квадратов, деленная на количество наблюдений — свойство mse_total.
Также имеется модуль statsmodels.stats.anova.anova_lm, который позволяет получить результаты ДАРМ (нескольких типов — 1, 2, 3):
# тип 1
print('The type of Anova test: 1')
display(sm.stats.anova_lm(result_linear_ols, typ=1))
# тип 2
print('The type of Anova test: 2')
display(sm.stats.anova_lm(result_linear_ols, typ=2))
# тип 3
print('The type of Anova test: 3')
display(sm.stats.anova_lm(result_linear_ols, typ=3))На мой взгляд, форма таблица результатов statsmodels.stats.anova.anova_lm не вполне удобна, поэтому сформируем ее самостоятельно, для чего создадим пользовательскую функцию ANOVA_table_regression_model:
# Пользовательская функция
def ANOVA_table_regression_model(model_fit):
n = int(model_fit.nobs)
p = int(model_fit.df_model)
SSR = model_fit.ess
SSE = model_fit.ssr
SST = model_fit.centered_tss
result = pd.DataFrame({
'sources_of_variation': ('regression (SSR)', 'deviation from regression (SSE)', 'total (SST)'),
'sum_of_squares': (SSR, SSE, SST),
'degrees_of_freedom': (p, n-p-1, n-1)})
result['squared_error'] = result['sum_of_squares'] / result['degrees_of_freedom']
R2 = 1 - result.loc[1, 'sum_of_squares'] / result.loc[2, 'sum_of_squares']
F_calc_adequacy = result.loc[2, 'squared_error'] / result.loc[1, 'squared_error']
F_calc_determ_check = result.loc[0, 'squared_error'] / result.loc[1, 'squared_error']
result['F-ratio'] = (F_calc_determ_check, F_calc_adequacy, '')
return result
result = ANOVA_table_regression_model(result_linear_ols)
display(result)
print(f"R2 = 1 - SSE/SST = {1 - result.loc[1, 'sum_of_squares'] / result.loc[2, 'sum_of_squares']}")
print(f"F_calc_adequacy = MST / MSE = {result.loc[2, 'squared_error'] / result.loc[1, 'squared_error']}")
print(f"F_calc_determ_check = MSR / MSE = {result.loc[0, 'squared_error'] / result.loc[1, 'squared_error']}")ДАРМ позволяет визуализировать вариацию:
fig, axes = plt.subplots(figsize=(210/INCH, 297/INCH/1.5))
axes.pie(
(result.loc[0, 'sum_of_squares'], result.loc[1, 'sum_of_squares']),
labels=(result.loc[0, 'sources_of_variation'], result.loc[1, 'sources_of_variation']),
autopct='%.1f%%',
startangle=60)
plt.show()На основании данных ДАРМ мы рассчитали ряд показателей (R2, Fcalc-ad и Fcalc-det), которые будут использоваться в дальнейшем.
3. Анализ остатков (проверка нормальности распределения остатков и гипотезы о равенстве нулю среднего значения остатков)
Проверка нормальности распределения остатков — один их важнейших этапов анализа регрессионной модели. Требование нормальности распределения остатков не требуется для отыскания параметров модели, но необходимо в дальнейшем для проверки статистических гипотез с использованием критериев Фишера и Стьюдента (проверка адекватности модели, значимости коэффициента детерминации, значимости коэффициентов регрессии) и построения доверительных интервалов [5, с.122].
Остатки регрессионной модели:
print('Остатки регрессионной модели:n', result_linear_ols.resid, type(result_linear_ols.resid))
res_Y = np.array(result_linear_ols.resid)statsmodels может выдавать различные преобразованные виды остатков (см. https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.resid_pearson.html, https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.wresid.html).
График остатков:
# Пользовательская функция
graph_scatterplot_sns(
X, res_Y,
Xmin=Xmin_graph, Xmax=Xmax_graph,
Ymin=-3.0, Ymax=3.0,
color='red',
#title_figure=Task_Project,
title_axes='Остатки линейной регрессионной модели', title_axes_fontsize=18,
x_label=Variable_Name_X,
y_label='ΔY = Y - Ycalc',
s=75,
file_name='graph/residuals_plot_sns.png')Проверка нормальности распределения остатков:
# Пользовательская функция
graph_hist_boxplot_probplot_sns(
data=res_Y,
data_min=-2.5, data_max=2.5,
graph_inclusion='bp',
data_label='ΔY = Y - Ycalc',
#title_figure=Task_Project,
title_axes='Остатки линейной регрессионной модели', title_axes_fontsize=16,
file_name='graph/residuals_hist_boxplot_probplot_sns.png') norm_distr_check(res_Y)Вывод: большинство статистических тестов позволяют принять гипотезу о нормальности распределения остатков.
Проверка гипотезы о равенстве нулю среднего значения остатков — так как остатки имеют нормальное распределение, воспользуемся критерием Стьюдента (функция scipy.stats.ttest_1samp, https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html):
sps.ttest_1samp(res_Y, popmean=0)Вывод: так как расчетный уровень значимости превышает заданный (0.05), то нулевая гипотеза о равенстве нулю остатков ПРИНИМАЕТСЯ.
4. Проверка адекватности модели
Суть проверки адекватности регрессионной модели заключается в сравнении полной дисперсии MST и остаточной дисперсии MSE — проверяется гипотеза о равенстве этих дисперсий по критерию Фишера. Если дисперсии различаются значимо, то модель считается адекватной. Более подробно про проверку адекватности регрессионной — см.[1, с.658], [2, с.49], [4, с.154].
Для проверки адекватности регрессионной модели создадим пользовательскую функцию regression_model_adequacy_check:
def regression_model_adequacy_check(
model_fit,
p_level: float=0.95,
model_name=''):
n = int(model_fit.nobs)
p = int(model_fit.df_model) # Число степеней свободы регрессии, равно числу переменных модели (за исключением константы, если она присутствует)
SST = model_fit.centered_tss # SST (Sum of Squared Total)
dfT = n-1
MST = SST / dfT
SSE = model_fit.ssr # SSE (Sum of Squared Error)
dfE = n - p - 1
MSE = SSE / dfE
F_calc = MST / MSE
F_table = sci.stats.f.ppf(p_level, dfT, dfE, loc=0, scale=1)
a_calc = 1 - sci.stats.f.cdf(F_calc, dfT, dfE, loc=0, scale=1)
conclusion_model_adequacy_check = 'adequacy' if F_calc >= F_table else 'adequacy'
# формируем результат
result = pd.DataFrame({
'SST': (SST),
'SSE': (SSE),
'dfT': (dfT),
'dfE': (dfE),
'MST': (MST),
'MSE': (MSE),
'p_level': (p_level),
'a_level': (a_level),
'F_calc': (F_calc),
'F_table': (F_table),
'F_calc >= F_table': (F_calc >= F_table),
'a_calc': (a_calc),
'a_calc <= a_level': (a_calc <= a_level),
'adequacy_check': (conclusion_model_adequacy_check),
},
index=[model_name]
)
return result
regression_model_adequacy_check(result_linear_ols, p_level=0.95, model_name='linear_ols')Вывод: модель является АДЕКВАТНОЙ.
5. Коэффициент детерминации и проверка его значимости
Различают несколько видов коэффициента детерминации:
-
Собственно обычный коэффициент детерминации:
Его значение может быть получено как свойство rsquared модели.
-
Скорректированный (adjusted) коэффициент детерминации — используется для того, чтобы была возможность сравнивать модели с разным числом признаков так, чтобы число регрессоров (признаков) не влияло на статистику R2, при его расчете используются несмещённые оценки дисперсий:
Его значение может быть получено как свойство rsquared_adj модели.
-
Обобщённый (extended) коэффициент детерминации — используется для сравнения моделей регрессии со свободным членом и без него, а также для сравнения между собой регрессий, построенных с помощью различных методов: МНК, обобщённого метода наименьших квадратов (ОМНК), условного метода наименьших квадратов (УМНК), обобщённо-условного метода наименьших квадратов (ОУМНК). В данном разборе ПЛРМ рассматривать этот коэффициент мы не будем.
Более подробно с теорией вопроса можно ознакомиться, например: http://www.machinelearning.ru/wiki/index.php?title=Коэффициент_детерминации), а также в [7].
Значения коэффициента детерминации и скорректированного коэффициента детерминации, извлеченные с помощью свойств rsquared и rsquared_adj модели.
print('R2 =', result_linear_ols.rsquared)
print('R2_adj =', result_linear_ols.rsquared_adj)Значимость коэффициента детерминации можно проверить по критерию Фишера [3, с.201-203; 8, с.83].
Расчетное значение статистики критерия Фишера может быть получено с помощью свойства fvalue модели:
print(f"result_linear_ols.fvalue = {result_linear_ols.fvalue}")Расчетный уровень значимости при проверке гипотезы по критерию Фишера может быть получено с помощью свойства f_pvalue модели:
print(f"result_linear_ols.f_pvalue = {result_linear_ols.f_pvalue}")Можно рассчитать уровень значимости самостоятельно (так сказать, для лучшего понимания и общей демонстрации возможностей) — для этого воспользуемся библиотекой scipy, модулем распределения Фишера scipy.stats.f, свойством cdf (функция распределения):
df1 = int(result_linear_ols.df_model)
df2 = int(result_linear_ols.nobs - result_linear_ols.df_model - 1)
F_calc = result_linear_ols.fvalue
a_calc = 1 - sci.stats.f.cdf(F_calc, df1, df2, loc=0, scale=1)
print(a_calc)Как видим, результаты совпадают.
Табличное значение статистики критерия Фишера получить с помощью Regression Results нельзя. Рассчитаем его самостоятельно — для этого воспользуемся библиотекой scipy, модулем распределения Стьюдента scipy.stats.f, свойством ppf (процентные точки):
F_table = sci.stats.f.ppf(p_level, df1, df2, loc=0, scale=1)
print(F_table)Для удобства создадим пользовательскую функцию determination_coef_check для проверки значимости коэффициента детерминации, которая объединяет все вышеперечисленные расчеты:
# Пользовательская функция
def determination_coef_check(
model_fit,
p_level: float=0.95):
a_level = 1 - p_level
R2 = model_fit.rsquared
R2_adj = model_fit.rsquared_adj
n = model_fit.nobs # объем выборки
p = model_fit.df_model # Model degrees of freedom. The number of regressors p. Does not include the constant if one is present.
F_calc = R2 / (1 - R2) * (n-p-1)/p
df1 = int(p)
df2 = int(n-p-1)
F_table = sci.stats.f.ppf(p_level, df1, df2, loc=0, scale=1)
a_calc = 1 - sci.stats.f.cdf(F_calc, df1, df2, loc=0, scale=1)
conclusion_determ_coef_sign = 'significance' if F_calc >= F_table else 'not significance'
# формируем результат
result = pd.DataFrame({
'notation': ('R2'),
'coef_value (R)': (sqrt(R2)),
'coef_value_squared (R2)': (R2),
'p_level': (p_level),
'a_level': (a_level),
'F_calc': (F_calc),
'df1': (df1),
'df2': (df2),
'F_table': (F_table),
'F_calc >= F_table': (F_calc >= F_table),
'a_calc': (a_calc),
'a_calc <= a_level': (a_calc <= a_level),
'significance_check': (conclusion_determ_coef_sign),
'conf_int_low': (''),
'conf_int_high': ('')
},
index=['Coef. of determination'])
return result
determination_coef_check(
result_linear_ols,
p_level=0.95)Вывод: коэффициент детерминации ЗНАЧИМ.
6. Коэффициенты регрессии и проверка их значимости
Ранее мы уже извлекли коэффициенты регрессии как параметры модели b0 и b1 (как свойство params модели). Также можно получить их значения, как свойство bse модели:
print(b0, b1)
print(result_linear_ols.bse, type(result_linear_ols.bse))Значимость коэффициентов регрессии можно проверить по критерию Стьюдента [3, с.203-212; 8, с.78].
Расчетные значения статистики критерия Стьюдента могут быть получены с помощью свойства tvalues модели:
print(f"result_linear_ols.tvalues = n{result_linear_ols.tvalues}")Расчетные значения уровня значимости при проверке гипотезы по критерию Стьюдента могут быть получены с помощью свойства pvalues модели:
print(f"result_linear_ols.pvalues = n{result_linear_ols.pvalues}")Доверительные интервалы для коэффициентов регрессии могут быть получены с помощью свойства conf_int модели:
print(result_linear_ols.conf_int(), 'n')Можно рассчитать уровень значимости самостоятельно (как ранее для критерия Фишера — для лучшего понимания и общей демонстрации возможностей) — для этого воспользуемся библиотекой scipy, модулем распределения Стьюдента scipy.stats.t, свойством cdf (функция распределения):
t_calc = result_linear_ols.tvalues
df = int(result_linear_ols.nobs - result_linear_ols.df_model - 1)
a_calc = 2*(1-sci.stats.t.cdf(abs(t_calc), df, loc=0, scale=1))
print(a_calc)Как видим, результаты совпадают.
Табличные значения статистики критерия Стьюдента получить с помощью Regression Results нельзя. Рассчитаем их самостоятельно — для этого воспользуемся библиотекой scipy, модулем распределения Стьюдента scipy.stats.t, свойством ppf (процентные точки):
t_table = sci.stats.t.ppf((1 + p_level)/2 , df)
print(t_table)Для удобства создадим пользовательскую функцию regression_coef_check для проверки значимости коэффициентов регрессии, которая объединяет все вышеперечисленные расчеты:
def regression_coef_check(
model_fit,
notation_coef: list='',
p_level: float=0.95):
a_level = 1 - p_level
# параметры модели (коэффициенты регрессии)
model_params = model_fit.params
# стандартные ошибки коэффициентов регрессии
model_bse = model_fit.bse
# проверка гипотезы о значимости регрессии
t_calc = abs(model_params) / model_bse
n = model_fit.nobs # объем выборки
p = model_fit.df_model # Model degrees of freedom. The number of regressors p. Does not include the constant if one is present.
df = int(n - p - 1)
t_table = sci.stats.t.ppf((1 + p_level)/2 , df)
a_calc = 2*(1-sci.stats.t.cdf(t_calc, df, loc=0, scale=1))
conclusion_ = ['significance' if elem else 'not significance' for elem in (t_calc >= t_table).values]
# доверительный интервал коэффициента регрессии
conf_int_low = model_params - t_table*model_bse
conf_int_high = model_params + t_table*model_bse
# формируем результат
result = pd.DataFrame({
'notation': (notation_coef),
'coef_value': (model_params),
'std_err': (model_bse),
'p_level': (p_level),
'a_level': (a_level),
't_calc': (t_calc),
'df': (df),
't_table': (t_table),
't_calc >= t_table': (t_calc >= t_table),
'a_calc': (a_calc),
'a_calc <= a_level': (a_calc <= a_level),
'significance_check': (conclusion_),
'conf_int_low': (conf_int_low),
'conf_int_high': (conf_int_high),
})
return result
regression_coef_check(
result_linear_ols,
notation_coef=['b0', 'b1'],
p_level=0.95)Вывод: коэффициенты регрессии b0 и b1 ЗНАЧИМЫ.
7. Проверка гетероскедастичности
Для проверка гетероскедастичности statsmodels предлагает нам следующие инструменты:
-
тест Голдфелда-Квандта (https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.het_goldfeldquandt.html#statsmodels.stats.diagnostic.het_goldfeldquandt) — теорию см. [8, с.178], также https://ru.wikipedia.org/wiki/Тест_Голдфелда_—_Куандта.
-
тест Бриша-Пэгана (Breush-Pagan test) (https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.het_breuschpagan.html#statsmodels.stats.diagnostic.het_breuschpagan) — теорию см.[8, с.179], также https://en.wikipedia.org/wiki/Breusch–Pagan_test.
-
тест Уайта (White test) (https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.het_white.html#statsmodels.stats.diagnostic.het_white) — теорию см.[8, с.177], а также https://ru.wikipedia.org/wiki/Тест_Уайта.
Тест Голдфелда-Квандта (Goldfeld–Quandt test)
# тест Голдфелда-Квандта (Goldfeld–Quandt test)
test = sms.het_goldfeldquandt(result_linear_ols.resid, result_linear_ols.model.exog)
test_result = lzip(['F_calc', 'p_calc'], test) # распаковка результатов теста
# расчетное значение статистики F-критерия
F_calc_tuple = test_result[0]
F_calc = F_calc_tuple[1]
print(f"Расчетное значение статистики F-критерия: F_calc = {round(F_calc, DecPlace)}")
# расчетный уровень значимости
p_calc_tuple = test_result[1]
p_calc = p_calc_tuple[1]
print(f"Расчетное значение доверительной вероятности: p_calc = {round(p_calc, DecPlace)}")
#a_calc = 1 - p_value
#print(f"Расчетное значение уровня значимости: a_calc = 1 - p_value = {round(a_calc, DecPlace)}")
# вывод
if p_calc < a_level:
conclusion_GQ_test = f"Так как p_calc = {round(p_calc, DecPlace)} < a_level = {round(a_level, DecPlace)}" +
", то дисперсии в подвыборках отличаются значимо, т.е. гипотеза о наличии гетероскедастичности ПРИНИМАЕТСЯ"
else:
conclusion_GQ_test = f"Так как p_calc = {round(p_calc, DecPlace)} >= a_level = {round(a_level, DecPlace)}" +
", то дисперсии в подвыборках отличаются незначимо, т.е. гипотеза о наличии гетероскедастичности ОТВЕРГАЕТСЯ"
print(conclusion_GQ_test)Для удобства создадим пользовательскую функцию Goldfeld_Quandt_test:
def Goldfeld_Quandt_test(
model_fit,
p_level: float=0.95,
model_name=''):
a_level = 1 - p_level
# реализация теста
test = sms.het_goldfeldquandt(model_fit.resid, model_fit.model.exog)
test_result = lzip(['F_statistic', 'p_calc'], test) # распаковка результатов теста
# расчетное значение статистики F-критерия
F_calc_tuple = test_result[0]
F_statistic = F_calc_tuple[1]
# расчетный уровень значимости
p_calc_tuple = test_result[1]
p_calc = p_calc_tuple[1]
# вывод
conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
result = pd.DataFrame({
'test': ('Goldfeld–Quandt test'),
'p_level': (p_level),
'a_level': (a_level),
'F_statistic': (F_statistic),
'p_calc': (p_calc),
'p_calc < a_level': (p_calc < a_level),
'heteroscedasticity_check': (conclusion_test)
},
index=[model_name])
return result
Goldfeld_Quandt_test(result_linear_ols, p_level=0.95, model_name='linear_ols')Тест Бриша-Пэгана (Breush-Pagan test)
# тест Бриша-Пэгана (Breush-Pagan test)
name = ["Lagrange multiplier statistic", "p-value", "f-value", "f p-value"]
test = sms.het_breuschpagan(result_linear_ols.resid, result_linear_ols.model.exog)
lzip(name, test)Для удобства создадим пользовательскую функцию Breush_Pagan_test:
def Breush_Pagan_test(
model_fit,
p_level: float=0.95,
model_name=''):
a_level = 1 - p_level
# реализация теста
test = sms.het_breuschpagan(model_fit.resid, model_fit.model.exog)
name = ['Lagrange_multiplier_statistic', 'p_calc_LM', 'F_statistic', 'p_calc']
test_result = lzip(name, test) # распаковка результатов теста
# расчетное значение статистики теста множителей Лагранжа
LM_calc_tuple = test_result[0]
Lagrange_multiplier_statistic = LM_calc_tuple[1]
# расчетный уровень значимости статистики теста множителей Лагранжа
p_calc_LM_tuple = test_result[1]
p_calc_LM = p_calc_LM_tuple[1]
# расчетное значение F-статистики гипотезы о том, что дисперсия ошибки не зависит от x
F_calc_tuple = test_result[2]
F_statistic = F_calc_tuple[1]
# расчетный уровень значимости F-статистики
p_calc_tuple = test_result[3]
p_calc = p_calc_tuple[1]
# вывод
conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
# вывод
conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
result = pd.DataFrame({
'test': ('Breush-Pagan test'),
'p_level': (p_level),
'a_level': (a_level),
'Lagrange_multiplier_statistic': (Lagrange_multiplier_statistic),
'p_calc_LM': (p_calc_LM),
'p_calc_LM < a_level': (p_calc_LM < a_level),
'F_statistic': (F_statistic),
'p_calc': (p_calc),
'p_calc < a_level': (p_calc < a_level),
'heteroscedasticity_check': (conclusion_test)
},
index=[model_name])
return result
Breush_Pagan_test(result_linear_ols, p_level=0.95, model_name='linear_ols')Тест Уайта (White test)
# тест Уайта (White test)
name = ["Lagrange multiplier statistic", "p-value", "f-value", "f p-value"]
test = sms.het_white(result_linear_ols.resid, result_linear_ols.model.exog)
lzip(name, test)Для удобства создадим пользовательскую функцию White_test:
def White_test(
model_fit,
p_level: float=0.95,
model_name=''):
a_level = 1 - p_level
# реализация теста
test = sms.het_white(model_fit.resid, model_fit.model.exog)
name = ['Lagrange_multiplier_statistic', 'p_calc_LM', 'F_statistic', 'p_calc']
test_result = lzip(name, test) # распаковка результатов теста
# расчетное значение статистики теста множителей Лагранжа
LM_calc_tuple = test_result[0]
Lagrange_multiplier_statistic = LM_calc_tuple[1]
# расчетный уровень значимости статистики теста множителей Лагранжа
p_calc_LM_tuple = test_result[1]
p_calc_LM = p_calc_LM_tuple[1]
# расчетное значение F-статистики гипотезы о том, что дисперсия ошибки не зависит от x
F_calc_tuple = test_result[2]
F_statistic = F_calc_tuple[1]
# расчетный уровень значимости F-статистики
p_calc_tuple = test_result[3]
p_calc = p_calc_tuple[1]
# вывод
conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
# вывод
conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
result = pd.DataFrame({
'test': ('White test'),
'p_level': (p_level),
'a_level': (a_level),
'Lagrange_multiplier_statistic': (Lagrange_multiplier_statistic),
'p_calc_LM': (p_calc_LM),
'p_calc_LM < a_level': (p_calc_LM < a_level),
'F_statistic': (F_statistic),
'p_calc': (p_calc),
'p_calc < a_level': (p_calc < a_level),
'heteroscedasticity_check': (conclusion_test)
},
index=[model_name])
return result
White_test(result_linear_ols, p_level=0.95, model_name='linear_ols')Объединим результаты всех тестов гетероскедастичность в один DataFrame:
Goldfeld_Quandt_test_df = Goldfeld_Quandt_test(result_linear_ols, p_level=0.95, model_name='linear_ols')
Breush_Pagan_test_df = Breush_Pagan_test(result_linear_ols, p_level=0.95, model_name='linear_ols')
White_test_df = White_test(result_linear_ols, p_level=0.95, model_name='linear_ols')
heteroscedasticity_tests_df = pd.concat([Breush_Pagan_test_df, White_test_df, Goldfeld_Quandt_test_df])
display(heteroscedasticity_tests_df)Выводы
Итак, мы провели статистический анализ регрессионной модели и установили:
-
исходные данные имеют нормальное распределение;
-
между переменными имеется весьма сильная корреляционная связь;
-
регрессионная модель хорошо аппроксимирует фактические данные;
-
остатки модели имеют нормальное распределение;
-
регрессионная модель адекватна по критерию Фишера;
-
коэффициент детерминации значим по критеию Фишера;
-
коэффициенты регрессии значимы по критерию Стьюдента;
-
гетероскедастичность отсутствует.
Применительно к рассматриваемой задаче выполнять проверку автокорреляции не имеет особого смысла из-за особенностей исходных данных (результаты замеров прочности бетона на разных участках здания).
Про статистический анализ регрессионных моделей с помощью statsmodels— см. еще https://www.statsmodels.org/stable/examples/notebooks/generated/regression_diagnostics.html.
Доверительные интервалы регрессионной модели
Для регрессионных моделей определяют доверительные интервалы двух видов [3, с.184-192; 4, с.172; 8, с.205-209]:
-
Доверительный интервал средних значений переменной Y.
-
Доверительный интервал индивидуальных значений переменной Y.
При этом размер доверительного интервала для индивидуальных значений больше, чем для средних значений.
Доверительные интервалы регрессионных моделей (ДИРМ) могут быть найдены разными способами:
-
непосредственно путем расчетов по формулам (см., например, https://habr.com/ru/post/558158/);
-
с использованием инструментария библиотеки statsmodels (см., например, https://www.stackfinder.ru/questions/17559408/confidence-and-prediction-intervals-with-statsmodels).
Разбререм более подробно способ с использованием библиотеки statsmodels. Прежде всего, с помощью свойства summary_table класса statsmodels.stats.outliers_influence.OLSInfluence (https://www.statsmodels.org/stable/generated/statsmodels.stats.outliers_influence.OLSInfluence.html?highlight=olsinfluence) мы можем получить таблицу данных, содержащую необходимую нам информацию:
-
Dep Var Population — фактические значения переменной Y;
-
Predicted Value — предсказанные значения переменной Y по по регрессионной модели;
-
Std Error Mean Predict — среднеквадратическая ошибка предсказанного среднего;
-
Mean ci 95% low и Mean ci 95% upp — границы доверительного интервала средних значений переменной Y;
-
Predict ci 95% low и Predict ci 95% upp — границы доверительного интервала индивидуальных значений переменной Y;
-
Residual — остатки регрессионной модели;
-
Std Error Residual — среднеквадратическая ошибка остатков;
-
Student Residual — стьюдентизированные остатки (подробнее см. http://statistica.ru/glossary/general/studentizirovannie-ostatki/);
-
Cook’s D — Расстояние Кука (Cook’s distance) — оценивает эффект от удаления одного (рассматриваемого) наблюдения; наблюдение считается выбросом, если Di > 4/n (более подробно — см.https://translated.turbopages.org/proxy_u/en-ru.ru.f584ceb5-63296427-aded8f31-74722d776562/https/en.wikipedia.org/wiki/Cook’s_distance, http://www.machinelearning.ru/wiki/index.php?title=Расстояние_Кука).
from statsmodels.stats.outliers_influence import summary_table
st, data, ss2 = summary_table(result_linear_ols, alpha=0.05)
print(st, 'n', type(st))В нашем случае критическое значение расстояния Кука равно:
print(f'D_crit = 4/n = {4/result_linear_ols.nobs}')то есть выбросов, смещающих оценки коэффициентов регрессии, не наблюдается.
Мы получили данные как класс statsmodels.iolib.table.SimpleTable. Свойство data преобразует данные в список. Далее для удобства работы преобразуем данные в DataFrame:
st_data_df = pd.DataFrame(st.data)Будем использовать данный DataFrame в дальнейшем, несколько преобразуем его:
-
изменим наименование столбцов (с цифр на названия показателей из таблицы summary_table)
-
удалим строки с текстовыми значениями
-
изменим индекс
-
добавим новый столбец — значения переменной X
-
отсортируем по возрастанию значений переменной X (это необходимо, чтобы графики границ доверительных интервалов выглядели как линии)
st_df = st_data_df.copy()
# изменим наименования столбцов
str = st_df.iloc[0,0:] + ' ' + st_df.iloc[1,0:]
st_df = st_df.rename(str, axis='columns')
# удалим строки 0, 1
st_df = st_df.drop([0,1])
# изменим индекс
st_df = st_df.set_index(np.arange(0, result_linear_ols.nobs))
# добавим новый столбец - значения переменной X
st_df.insert(1, 'X', X)
# отсортируем по возрастанию значений переменной X
st_df = st_df.sort_values(by='X')
display(st_df)С помощью полученных данных мы можем построить график регрессионной модели с доверительными интервалами:
# создание рисунка (Figure) и области рисования (Axes)
fig, axes = plt.subplots(figsize=(297/INCH, 210/INCH))
# заголовок рисунка (Figure)
title_figure = Task_Project
fig.suptitle(title_figure, fontsize = 16)
# заголовок области рисования (Axes)
title_axes = 'Линейная регрессионная модель'
axes.set_title(title_axes, fontsize = 14)
# фактические данные
sns.scatterplot(
x=st_df['X'], y=st_df['Dep Var Population'],
label='фактические данные',
s=50,
color='red',
ax=axes)
# график регрессионной модели
label_legend_regr_model=f'линейная регрессия Y = {b0:.3f} + {b1:.4f}*X'
sns.lineplot(
x=st_df['X'], y=st_df['Predicted Value'],
label=label_legend_regr_model,
color='blue',
ax=axes)
# доверительный интервал средних значений переменной Y
Mean_ci_low = st_df['Mean ci 95% low']
plt.plot(
st_df['X'], Mean_ci_low,
color='magenta', linestyle='--', linewidth=1,
label='доверительный интервал средних значений Y')
Mean_ci_upp = st_df['Mean ci 95% upp']
plt.plot(
st_df['X'], Mean_ci_upp,
color='magenta', linestyle='--', linewidth=1)
# доверительный интервал индивидуальных значений переменной Y
Predict_ci_low = st_df['Predict ci 95% low']
plt.plot(
st_df['X'], Predict_ci_low,
color='orange', linestyle='-.', linewidth=2,
label='доверительный интервал индивидуальных значений Y')
Predict_ci_upp = st_df['Predict ci 95% upp']
plt.plot(
st_df['X'], Predict_ci_upp,
color='orange', linestyle='-.', linewidth=2)
axes.set_xlabel(Variable_Name_X)
axes.set_ylabel(Variable_Name_Y)
axes.legend(prop={'size': 12})
plt.show()Однако, мы получили данные о границах доверительных интервалов регрессионной модели только в пределах области фактических значений переменной X. Как быть, если мы хотим распространить прогноз за пределы этой области?
Прогнозирование
Под прогнозированием мы в данном случае будем понимать определение значений переменной Y и доверительных интервалов для ее средних и индивидуальных значений при заданном X. По сути, нам предстоит построить аналог рассмотренной выше таблицы summary_table, только с другими значениями X, причем эти значения могут выходить за пределы тех значений, которые использовались нами для построения регрессии.
Методика расчета доверительных интервалов регрессионных моделей разобрана в статье «Python, корреляция и регрессия: часть 4» (https://habr.com/ru/post/558158/), всем рекомендую ознакомиться.
Найти прогнозные значения Y не представляет труда, так как ранее мы уже формализовали модель в виде лямбда-функции, а вот для построения доверительных интервалов придется выполнить расчеты по формулам. Для этого создадим пользовательскую функцию regression_pair_predict, которая в случае парной регрессии (pair regression) для заданного значения X возвращает:
-
прогнозируемое по регрессионной модели значение y_calc
-
доверительный интервал [y_calc_mean_ci_low, y_calc_mean_ci_upp] средних значений переменной Y
-
доверительный интервал [y_calc_predict_ci_low, y_calc_predict_ci_upp] индивидуальных значений переменной Y
Алгоритм расчета доверительных интервалов для множественной регрессии (multiple regression) отличается и в данном обзоре не рассматривается (рассмотрим в дальнейшем).
Про прогнозирование с помощью регрессионных моделей — см.также:
-
https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.predict.html?highlight=predict#statsmodels.regression.linear_model.RegressionResults.predict
-
How to Make Predictions Using Regression Model in Statsmodels
-
https://www.statsmodels.org/stable/examples/notebooks/generated/predict.html
def regression_pair_predict(
x_in,
model_fit,
regression_model,
p_level: float=0.95):
a_level = 1 - p_level
X = pd.DataFrame(model_fit.model.exog)[1].values # найти лучшее решение
Y = model_fit.model.endog
# вспомогательные величины
n = int(result_linear_ols.nobs)
SSE = model_fit.ssr # SSE (Sum of Squared Error)
dfE = n - p - 1
MSE = SSE / dfE # остаточная дисперсия
Xmean = np.mean(X)
SST_X = np.sum([(X[i] - Xmean)**2 for i in range(0, n)])
t_table = sci.stats.t.ppf((1 + p_level)/2 , dfE)
S2_y_calc_mean = MSE * (1/n + (x_in - Xmean)**2 / SST_X)
S2_y_calc_predict = MSE * (1 + 1/n + (x_in - Xmean)**2 / SST_X)
# прогнозируемое значение переменной Y
y_calc=regression_model(x_in)
# доверительный интервал средних значений переменной Y
y_calc_mean_ci_low = y_calc - t_table*sqrt(S2_y_calc_mean)
y_calc_mean_ci_upp = y_calc + t_table*sqrt(S2_y_calc_mean)
# доверительный интервал индивидуальных значений переменной Y
y_calc_predict_ci_low = y_calc - t_table*sqrt(S2_y_calc_predict)
y_calc_predict_ci_upp = y_calc + t_table*sqrt(S2_y_calc_predict)
result = y_calc, y_calc_mean_ci_low, y_calc_mean_ci_upp, y_calc_predict_ci_low, y_calc_predict_ci_upp
return resultСравним результаты расчета доверительных интервалов разными способами — с использованием функции regression_pair_predict и средствами statsmodels, для этого сформируем DaraFrame с новыми данными:
regression_pair_predict_df = pd.DataFrame(
[regression_pair_predict(elem, result_linear_ols, regression_model=Y_calc) for elem in st_df['X'].values],
columns=['y_calc', 'y_calc_mean_ci_low', 'y_calc_mean_ci_upp', 'y_calc_predict_ci_low', 'y_calc_predict_ci_upp'])
regression_pair_predict_df.insert(0, 'X', st_df['X'].values)
display(regression_pair_predict_df)Видим, что результаты расчетов идентичны, следовательно мы можем использовать функцию regression_pair_predict для прогнозирования.
def graph_regression_pair_predict_plot_sns(
model_fit,
regression_model_in,
Xmin=None, Xmax=None, Nx=10,
Ymin_graph=None, Ymax_graph=None,
title_figure=None, title_figure_fontsize=18,
title_axes=None, title_axes_fontsize=16,
x_label=None,
y_label=None,
label_fontsize=14, tick_fontsize=12,
label_legend_regr_model='', label_legend_fontsize=12,
s=50, linewidth_regr_model=2,
graph_size=(297/INCH, 210/INCH),
result_output=True,
file_name=None):
# фактические данные
X = pd.DataFrame(model_fit.model.exog)[1].values # найти лучшее решение
Y = model_fit.model.endog
X = np.array(X)
Y = np.array(Y)
# границы
if not(Xmin) and not(Xmax):
Xmin=min(X)
Xmax=max(X)
Xmin_graph=min(X)*0.99
Xmax_graph=max(X)*1.01
else:
Xmin_graph=Xmin
Xmax_graph=Xmax
if not(Ymin_graph) and not(Ymax_graph):
Ymin_graph=min(Y)*0.99
Ymax_graph=max(Y)*1.01
# формируем DataFrame данных
Xcalc = np.linspace(Xmin, Xmax, num=Nx)
Ycalc = regression_model_in(Xcalc)
result_df = pd.DataFrame(
[regression_pair_predict(elem, model_fit, regression_model=regression_model_in) for elem in Xcalc],
columns=['y_calc', 'y_calc_mean_ci_low', 'y_calc_mean_ci_upp', 'y_calc_predict_ci_low', 'y_calc_predict_ci_upp'])
result_df.insert(0, 'x_calc', Xcalc)
# заголовки графика
fig, axes = plt.subplots(figsize=graph_size)
fig.suptitle(title_figure, fontsize = title_figure_fontsize)
axes.set_title(title_axes, fontsize = title_axes_fontsize)
# фактические данные
sns.scatterplot(
x=X, y=Y,
label='фактические данные',
s=s,
color='red',
ax=axes)
# график регрессионной модели
sns.lineplot(
x=Xcalc, y=Ycalc,
color='blue',
linewidth=linewidth_regr_model,
legend=True,
label=label_legend_regr_model,
ax=axes)
# доверительный интервал средних значений переменной Y
Mean_ci_low = result_df['y_calc_mean_ci_low']
plt.plot(
result_df['x_calc'], Mean_ci_low,
color='magenta', linestyle='--', linewidth=1,
label='доверительный интервал средних значений Y')
Mean_ci_upp = result_df['y_calc_mean_ci_upp']
plt.plot(
result_df['x_calc'], Mean_ci_upp,
color='magenta', linestyle='--', linewidth=1)
# доверительный интервал индивидуальных значений переменной Y
Predict_ci_low = result_df['y_calc_predict_ci_low']
plt.plot(
result_df['x_calc'], Predict_ci_low,
color='orange', linestyle='-.', linewidth=2,
label='доверительный интервал индивидуальных значений Y')
Predict_ci_upp = result_df['y_calc_predict_ci_upp']
plt.plot(
result_df['x_calc'], Predict_ci_upp,
color='orange', linestyle='-.', linewidth=2)
axes.set_xlim(Xmin_graph, Xmax_graph)
axes.set_ylim(Ymin_graph, Ymax_graph)
axes.set_xlabel(x_label, fontsize = label_fontsize)
axes.set_ylabel(y_label, fontsize = label_fontsize)
axes.tick_params(labelsize = tick_fontsize)
#axes.tick_params(labelsize = tick_fontsize)
axes.legend(prop={'size': label_legend_fontsize})
plt.show()
if file_name:
fig.savefig(file_name, orientation = "portrait", dpi = 300)
if result_output:
return result_df
else:
return
graph_regression_pair_predict_plot_sns(
model_fit=result_linear_ols,
regression_model_in=Y_calc,
Xmin=Xmin_graph-300, Xmax=Xmax_graph+200, Nx=25,
Ymin_graph=Ymin_graph-5, Ymax_graph=Ymax_graph+5,
title_figure=Task_Project, title_figure_fontsize=16,
title_axes='Линейная регрессионная модель', title_axes_fontsize=14,
x_label=Variable_Name_X,
y_label=Variable_Name_Y,
label_legend_regr_model=f'линейная регрессия Y = {b0:.3f} + {b1:.4f}*X',
s=50,
result_output=True,
file_name='graph/regression_plot_lin.png')Выводы и рекомендации
Исследована зависимость показаний ультразвукового прибора «ПУЛЬСАР-2.1» (X) и результатов замера прочности бетона (методом отрыва со скалыванием) склерометром ИПС-МГ4.03 (Y).
Между переменными имеется весьма сильная линейная корреляционная связь. Получена регрессионная модель:
Y = b0 + b1∙X = -21.3741 + 0.0129∙X
Модель хорошо аппроксимирует фактические данные, является адекватной, значимой и может использоваться для предсказания прочности бетона.
Также построен график прогноза с доверительными интервалами.
ИТОГИ
Итак, мы рассмотрели все этапы регрессионного анализа в случае простой линейной регрессии (simple linear regression) с использованием библиотеки statsmodels на конкретном практическом примере; подробно остановились на статистическом анализа модели с проверкой гипотез; также предложен ряд пользовательских функций, облегчающих работу исследователя и уменьшающих размер программного кода.
Конечно, мы разобрали далеко не все вопросы анализа регрессионных моделей и возможности библиотеки statsmodels применительно к simple linear regression, в частности статистики влияния (Influence Statistics), инструмент Leverage, анализ стьюдентизированных остатков и пр. — это темы для отдельных обзоров.
Исходный код находится в моем репозитории на GitHub.
Надеюсь, данный обзор поможет специалистам DataScience в работе.
17 авг. 2022 г.
читать 2 мин
Регрессионный анализ — это метод, который мы можем использовать для понимания взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика .
Один из способов оценить, насколько хорошо регрессионная модель соответствует набору данных, — вычислить среднеквадратичную ошибку , которая представляет собой показатель, указывающий нам среднее расстояние между прогнозируемыми значениями из модели и фактическими значениями в наборе данных.
Чем ниже RMSE, тем лучше данная модель может «соответствовать» набору данных.
Формула для нахождения среднеквадратичной ошибки, часто обозначаемая аббревиатурой RMSE , выглядит следующим образом:
СКО = √ Σ(P i – O i ) 2 / n
куда:
- Σ — причудливый символ, означающий «сумма».
- P i — прогнозируемое значение для i -го наблюдения в наборе данных.
- O i — наблюдаемое значение для i -го наблюдения в наборе данных.
- n — размер выборки
В следующем примере показано, как интерпретировать RMSE для данной модели регрессии.
Пример: как интерпретировать RMSE для регрессионной модели
Предположим, мы хотим построить регрессионную модель, которая использует «учебные часы» для прогнозирования «экзаменационного балла» студентов на конкретном вступительном экзамене в колледж.
Мы собираем следующие данные для 15 студентов:
Затем мы используем статистическое программное обеспечение (например, Excel, SPSS, R, Python) и т. д., чтобы найти следующую подогнанную модель регрессии:
Экзаменационный балл = 75,95 + 3,08 * (часы обучения)
Затем мы можем использовать это уравнение, чтобы предсказать экзаменационную оценку каждого студента, исходя из того, сколько часов они учились:
Затем мы можем вычислить квадрат разницы между каждой прогнозируемой оценкой экзамена и фактической оценкой экзамена. Затем мы можем извлечь квадратный корень из среднего значения этих разностей:
RMSE для этой регрессионной модели оказывается равным 5,681 .
Напомним, что остатки регрессионной модели представляют собой разницу между наблюдаемыми значениями данных и значениями, предсказанными моделью.
Остаток = (P i – O i )
куда
- P i — прогнозируемое значение для i -го наблюдения в наборе данных.
- O i — наблюдаемое значение для i -го наблюдения в наборе данных.
И помните, что RMSE регрессионной модели рассчитывается как:
СКО = √ Σ(P i – O i ) 2 / n
Это означает, что RMSE представляет собой квадратный корень из дисперсии остатков.
Это значение полезно знать, поскольку оно дает нам представление о среднем расстоянии между наблюдаемыми значениями данных и прогнозируемыми значениями данных.
Это отличается от R-квадрата модели, который сообщает нам долю дисперсии переменной отклика, которая может быть объяснена предикторной переменной (переменными) в модели.
Сравнение значений RMSE из разных моделей
RMSE особенно полезен для сравнения соответствия различных моделей регрессии.
Например, предположим, что мы хотим построить регрессионную модель, чтобы предсказать результаты экзаменов студентов, и мы хотим найти наилучшую возможную модель среди нескольких потенциальных моделей.
Предположим, мы подгоняем три разные модели регрессии и находим соответствующие им значения RMSE:
- RMSE модели 1: 14,5
- RMSE модели 2: 16,7
- RMSE модели 3: 9,8
Модель 3 имеет самый низкий RMSE, что говорит нам о том, что она способна лучше всего соответствовать набору данных из трех потенциальных моделей.
Дополнительные ресурсы
Калькулятор среднеквадратичной ошибки
Как рассчитать RMSE в Excel
Как рассчитать RMSE в R
Как рассчитать RMSE в Python
Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):
Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:
Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:
Рассчитаем квадрат разницы между Y и Ỹ:
Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
- 1 Оценки качества классификации
- 1.1 Матрица ошибок (англ. Сonfusion matrix)
- 1.2 Аккуратность (англ. Accuracy)
- 1.3 Точность (англ. Precision)
- 1.4 Полнота (англ. Recall)
- 1.5 F-мера (англ. F-score)
- 1.6 ROC-кривая
- 1.7 Precison-recall кривая
- 2 Оценки качества регрессии
- 2.1 Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
- 2.2 Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
- 2.3 Коэффициент детерминации
- 2.4 Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
- 2.5 Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
- 2.6 Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
- 2.7 Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
- 3 Кросс-валидация
- 4 Примечания
- 5 См. также
- 6 Источники информации
Оценки качества классификации
Матрица ошибок (англ. Сonfusion matrix)
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов.
Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика () можно рассматривать как «сигнал тревоги», сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
- Кредитоспособный заёмщик распознается моделью как некредитоспособный и ему отказывается в кредите. Данный случай можно трактовать как «ложную тревогу».
- Некредитоспособный заёмщик распознаётся как кредитоспособный и ему ошибочно выдаётся кредит. Данный случай можно рассматривать как «пропуск цели».
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае «ложной тревоги» потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае «пропуска цели» можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить «пропуск цели», чем «ложную тревогу».
Поскольку с точки зрения логики задачи нам важнее правильно распознать некредитоспособного заёмщика с меткой , чем ошибиться в распознавании кредитоспособного, будем называть соответствующий исход классификации положительным (заёмщик некредитоспособен), а противоположный — отрицательным (заемщик кредитоспособен ). Тогда возможны следующие исходы классификации:
- Некредитоспособный заёмщик классифицирован как некредитоспособный, т.е. положительный класс распознан как положительный. Наблюдения, для которых это имеет место называются истинно-положительными (True Positive — TP).
- Кредитоспособный заёмщик классифицирован как кредитоспособный, т.е. отрицательный класс распознан как отрицательный. Наблюдения, которых это имеет место, называются истинно отрицательными (True Negative — TN).
- Кредитоспособный заёмщик классифицирован как некредитоспособный, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Наблюдения, для которых был получен такой исход классификации, называются ложно-положительными (False Positive — FP), а ошибка классификации называется ошибкой I рода.
- Некредитоспособный заёмщик распознан как кредитоспособный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Наблюдения, для которых был получен такой исход классификации, называются ложно-отрицательными (False Negative — FN), а ошибка классификации называется ошибкой II рода.
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
-
Истинно-положительный (True Positive — TP) Ложно-положительный (False Positive — FP) Ложно-отрицательный (False Negative — FN) Истинно-отрицательный (True Negative — TN)
Здесь — это ответ алгоритма на объекте, а — истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
# код для матрицы ошибок # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import confusion_matrix from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (англ. Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе # Для расчета матрицы ошибок сначала понадобится иметь набор прогнозов, чтобы их можно было сравнивать с фактическими целями y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687], # [ 1891, 3530]])
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.metrics import confusion_matrix
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
y_train_perfect_predictions = y_train_5 # притворись, что мы достигли совершенства
print(confusion_matrix(y_train_5, y_train_perfect_predictions))
# array([[54579, 0],
# [ 0, 5421]])
Аккуратность (англ. Accuracy)
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
# код для для подсчета аккуратности: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import accuracy_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(accuracy_score(y_train_5, y_train_pred)) # == (53892 + 3530) / (53892 + 3530 + 1891 +687) # 0.9570333333333333
Точность (англ. Precision)
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall)
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
# код для для подсчета точности и полноты: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import precision_score, recall_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(precision_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 687) print(recall_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 1891) # 0.8370879772350012 # 0.6511713705958311
F-мера (англ. F-score)
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
где принимает значения в диапазоне если вы хотите отдать приоритет точности, а при приоритет отдается полноте. При формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют ).
-
Рис.1 Сбалансированная F-мера,
-
Рис.2 F-мера c приоритетом точности,
-
Рис.3 F-мера c приоритетом полноты,
F-мера достигает максимума при максимальной полноте и точности, и близка к нулю, если один из аргументов близок к нулю.
F-мера является хорошим кандидатом на формальную метрику оценки качества классификатора. Она сводит к одному числу две других основополагающих метрики: точность и полноту. Имея «F-меру» гораздо проще ответить на вопрос: «поменялся алгоритм в лучшую сторону или нет?»
# код для подсчета метрики F-mera: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier from sklearn.metrics import f1_score mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распознавать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(f1_score(y_train_5, y_train_pred)) # 0.7325171197343846
ROC-кривая
Кривая рабочих характеристик (англ. Receiver Operating Characteristics curve).
Используется для анализа поведения классификаторов при различных пороговых значениях.
Позволяет рассмотреть все пороговые значения для данного классификатора.
Показывает долю ложно положительных примеров (англ. false positive rate, FPR) в сравнении с долей истинно положительных примеров (англ. true positive rate, TPR).
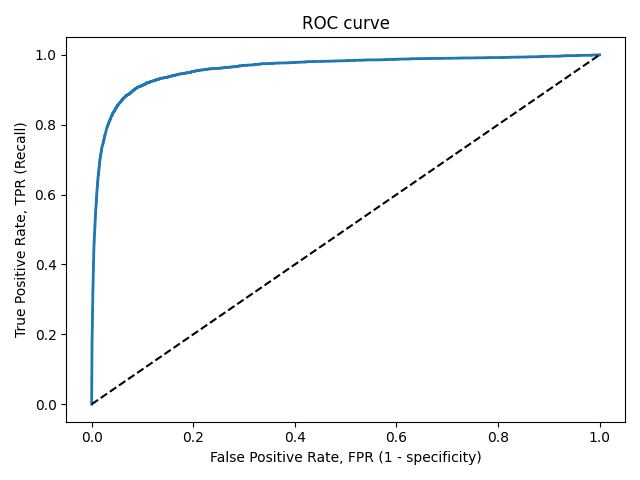
Доля FPR — это пропорция отрицательных образцов, которые были некорректно классифицированы как положительные.
- ,
где TNR — доля истинно отрицательных классификаций (англ. Тrие Negative Rate), представляющая собой пропорцию отрицательных образцов, которые были корректно классифицированы как отрицательные.
Доля TNR также называется специфичностью (англ. specificity). Следовательно, ROC-кривая изображает чувствительность (англ. seпsitivity), т.е. полноту, в сравнении с разностью 1 — specificity.
Прямая линия по диагонали представляет ROC-кривую чисто случайного классификатора. Хороший классификатор держится от указанной линии настолько далеко, насколько это
возможно (стремясь к левому верхнему углу).
Один из способов сравнения классификаторов предусматривает измерение площади под кривой (англ. Area Under the Curve — AUC). Безупречный классификатор будет иметь площадь под ROC-кривой (ROC-AUC), равную 1, тогда как чисто случайный классификатор — площадь 0.5.
# Код отрисовки ROC-кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import roc_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") fpr, tpr, thresholds = roc_curve(y_train_5, y_scores) def plot_roc_curve(fpr, tpr, label=None): plt.plot(fpr, tpr, linewidth=2, label=label) plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal plt.xlabel('False Positive Rate, FPR (1 - specificity)') plt.ylabel('True Positive Rate, TPR (Recall)') plt.title('ROC curve') plt.savefig("ROC.png") plot_roc_curve(fpr, tpr) plt.show()
Precison-recall кривая
Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь плохой алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма.
Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
Precison-recall (PR) кривая. Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)
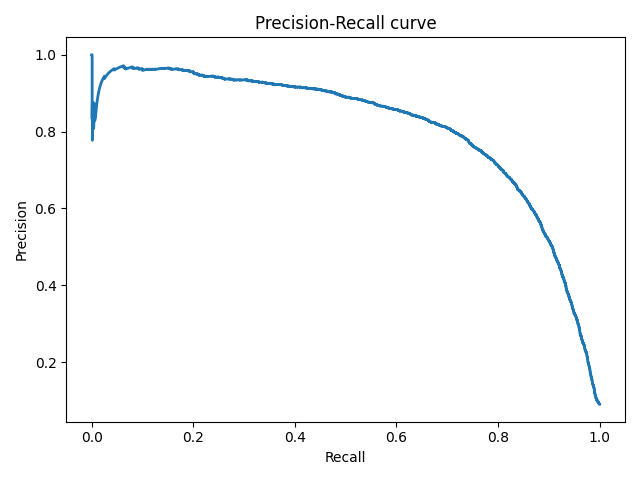
# Код отрисовки Precison-recall кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import precision_recall_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores) def plot_precision_recall_vs_threshold(precisions, recalls, thresholds): plt.plot(recalls, precisions, linewidth=2) plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall curve') plt.savefig("Precision_Recall_curve.png") plot_precision_recall_vs_threshold(precisions, recalls, thresholds) plt.show()
Оценки качества регрессии
Наиболее типичными мерами качества в задачах регрессии являются
Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
MSE применяется в ситуациях, когда нам надо подчеркнуть большие ошибки и выбрать модель, которая дает меньше больших ошибок прогноза. Грубые ошибки становятся заметнее за счет того, что ошибку прогноза мы возводим в квадрат. И модель, которая дает нам меньшее значение среднеквадратической ошибки, можно сказать, что что у этой модели меньше грубых ошибок.
- и
Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
Среднеквадратичный функционал сильнее штрафует за большие отклонения по сравнению со среднеабсолютным, и поэтому более чувствителен к выбросам. При использовании любого из этих двух функционалов может быть полезно проанализировать, какие объекты вносят наибольший вклад в общую ошибку — не исключено, что на этих объектах была допущена ошибка при вычислении признаков или целевой величины.
Среднеквадратичная ошибка подходит для сравнения двух моделей или для контроля качества во время обучения, но не позволяет сделать выводов о том, на сколько хорошо данная модель решает задачу. Например, MSE = 10 является очень плохим показателем, если целевая переменная принимает значения от 0 до 1, и очень хорошим, если целевая переменная лежит в интервале (10000, 100000). В таких ситуациях вместо среднеквадратичной ошибки полезно использовать коэффициент детерминации —
Коэффициент детерминации
Коэффициент детерминации измеряет долю дисперсии, объясненную моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что MAPE=11.4%, то это говорит о том, что ошибка составила 11,4% от фактических значений.
Основная проблема данной ошибки — нестабильность.
Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
Примерно такая же проблема, как и в MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня.
Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
MASE является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Обратите внимание, что в MASE мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе — обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тенденцию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.
Недостаток MASE в том, что её тяжело интерпретировать. Например, MASE=1.21 ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более.
Кросс-валидация
Хороший способ оценки модели предусматривает применение кросс-валидации (cкользящего контроля или перекрестной проверки).
В этом случае фиксируется некоторое множество разбиений исходной выборки на две подвыборки: обучающую и контрольную. Для каждого разбиения выполняется настройка алгоритма по обучающей подвыборке, затем оценивается его средняя ошибка на объектах контрольной подвыборки. Оценкой скользящего контроля называется средняя по всем разбиениям величина ошибки на контрольных подвыборках.
Примечания
- [1] Лекция «Оценивание качества» на www.coursera.org
- [2] Лекция на www.stepik.org о кросвалидации
- [3] Лекция на www.stepik.org о метриках качества, Precison и Recall
- [4] Лекция на www.stepik.org о метриках качества, F-мера
- [5] Лекция на www.stepik.org о метриках качества, примеры
См. также
- Оценка качества в задаче кластеризации
- Кросс-валидация
Источники информации
- [6] Соколов Е.А. Лекция линейная регрессия
- [7] — Дьяконов А. Функции ошибки / функционалы качества
- [8] — Оценка качества прогнозных моделей
- [9] — HeinzBr Ошибка прогнозирования: виды, формулы, примеры
- [10] — egor_labintcev Метрики в задачах машинного обучения
- [11] — grossu Методы оценки качества прогноза
- [12] — К.В.Воронцов, Классификация
- [13] — К.В.Воронцов, Скользящий контроль
Диагностика систем машинного обучения
115 мин на чтение
(169.722 символов)
Что такое метрики эффективности?
Для того, чтобы эффективно проводить обучение моделей необходимо иметь способ оценки, насколько хорошо та или иная модель выполняет свою работу — предсказывает значение целевой переменной. Кажется, мы уже что-то подобное изучали. У каждой модели есть функция ошибки, которая показывает, на сколько модель соответствует эмпирическим значениям. Однако, использование функции ошибки не очень удобно для оценки именно “качества” уже построенных моделей. Ведь эта функция специально создается для единственной цели — организации процесса обучения. Поэтому для оценки уже построенных моделей используется не функция ошибки, а так называемые метрики эффективности — специальные функции, которые показывают, насколько эффективна уже готовая, обученная модель.
Метрики эффективности на первый взгляд очень похожи на функции ошибки, ведь у них одна цель — отличать хорошие модели от плохих. Но делают они это по-разному, по-разному и применяются. К метрикам эффективности предъявляются совершенно другие требования, нежели к функциям ошибки. Поэтому давайте рассмотрим, для чего нужны и те и другие.
Функция ошибки нужна в первую очередь для формализации процесса обучения модели. То есть для того, чтобы подбирать параметры модели именно такими, чтобы модель как можно больше соответствовала реальным данным в обучающей выборке. Да, значение этой функции можно использовать как некоторую оценку качества модели уже после того, как она обучена, но это не удобно.
Функция ошибки нужна, чтобы формализовать отклонения предсказанных моделью значений от реальных. Например, в методе линейной регрессии функция ошибки (среднеквадратическое отклонение) используется для метода градиентного спуска. Поэтому функция ошибки обязательно должна быть везде дифференцируемой, мы это отдельно отмечали, когда говорили про метод градиентного спуска. Это требование — дифференцируемость — нужно исключительно для метода оптимизации, то есть для обучения модели.
Зато функция, которая используется для оценки качества модели совершенно не должна быть аналитической и гладкой. Ведь мы не будем вычислять ее производную, мы только вычислим ее один раз для того, чтобы понять, насколько хорошая модель получилась. Так что не любую метрику эффективности вообще физически возможно использовать как функцию ошибки — метод обучения может просто не сработать.
Кроме того, функция ошибки должна быть вычислительно простой, ведь ее придется считать много раз в процессе обучения — тысячи или миллионы раз. Это еще одно требование, которое совершенно необязательно для метрики эффективности. Она как раз может считаться довольно сложно, ведь вычислять ее приходится всего несколько раз.
Зато метрика эффективности должна быть понятной и интерпретируемой, в отличие от функции ошибки. Раньше мы подчеркивали, что само абсолютное значение функции ошибки ничего не показывает. Важно лишь, снижается ли оно в процессе обучения. И разные значения функции ошибки имеет смысл сравнивать только на одних и тех же данных. Что значит, если значение функции ошибки модели равно 35 000? Да ничего, только то, что эта модель хуже, чем та, у которой ошибка 32 000.
Для того, чтобы значение было более понятно, метрики эффективности зачастую выражаются в каких-то определенных единицах измерения — чеще всего в натуральных или в процентах. Натуральные единицы — это единицы измерения целевой переменной. Допустим, целевая переменная выражается в рублях. То есть, мы предсказываем некоторую стоимость. В таком случае будет вполне понятно, если качество этой модели мы тоже выразим в рублях. Например, так: модель в среднем ошибается на 500 рублей. И сразу становится ясно, насколько эта модель применима на практике.
Еще одно важное отличие. Как мы сказали, требования к функции ошибки определяются алгоритмом оптимизации. Который, в свою очередь зависит от типа модели. У линейной регрессии будет один алгоритм (и одна функция ошибки), а у, например, решающего дерева — другой алгоритм и совершенно другая функция ошибки. Это в частности значит, что функцию ошибки невозможно применять для сравнения нескольких разных моделей, обученных на одной и той же задаче.
И вот для этого как раз и нужны метрики эффективности. Они не зависят от типа модели, а выбираются исходя из задачи и тех вопросов, ответы на которые мы хотим получить. Например, в одной задаче качество модели лучше измерять через среднеквадратическую логарифмическую ошибку, а в другой — через медианную ошибку. Как раз в этом разделе мы посмотрим на примеры разных метрик эффективности, на их особенности и сферы применения.
Кстати, это еще означает, что в каждой конкретной задаче вы можете применять сразу несколько метрик эффективности, для более глубокого понимания работы модели. Зачастую так и поступают, ведь одна метрика не может дать полной информации о сильных и слабых сторонах модели. Тут исследователи ничем не ограничены. А вот функция ошибки обязательно должна быть только одна, ведь нельзя одновременно находить минимум сразу нескольких разных функций (на самом деле можно, но многокритериальная оптимизация — это гораздо сложнее и не используется для обучения моделей).
| Функция ошибки | Метрика эффективности |
|---|---|
| Используется для организации процесса обучения | Используется для оценки качества полученной модели |
| Используется для нахождения оптимума | Используется для сравнения моделей между собой |
| Должна быть быстро вычислимой | Должна быть понятной |
| Должна конструироваться исходя их типа модели | Должна выбираться исходя из задачи |
| Может быть только одна | Может быть несколько |
Еще раз определим, эффективность — это свойство модели машинного обучения давать предсказания значения целевой переменной, как можно ближе к реальным данным. Это самая главная характеристика модели. Но надо помнить, что исходя из задачи и ее условий, к моделям могут предъявляться и другие требования, как сказали бы в программной инженерии — нефункциональные. Типичный пример — скорость работы. Иногда маленький выигрыш в эффективности не стоит того, что модель стала работать в десять раз меньше. Другой пример — интерпретируемость модели. В некоторых областях важно не только сделать точное предсказание, но и иметь возможность обосновать его, провести анализ, выработать рекомендации по улучшению ситуации и так далее. Все эти нефункциональные требования — скорость обучения, скорость предсказания, надежность, робастность, федеративность, интерпретируемость — выходят за рамки данного пособия. Здесь мы сконцентрируемся на измерении именно эффективности модели.
Обратите внимание, что мы старательно избегаем употребления слова “точность” при описании качества работы модели. Хотя казалось бы, оно подходит как нельзя лучше. Дело в том, что “точностью” называют одну из метрик эффективности моделей классификации. Поэтому мы не хотим внести путаницу в термины.
Как мы говорили, метрики эффективности не зависят от самого типа модели. Для их вычисления обычно используется два вектора — вектор эмпирических значений целевой переменной (то есть тех, которые даны в датасете) и вектор теоретических значений (то есть тех, которые выдала модель). Естественно, эти вектора должны быть сопоставимы — на соответствующих местах должны быть значения целевой переменной, соответствующие одном у и тому же объекту. И, конечно, у них должна быть одинаковая длина. То есть метрика зависит от самих предсказаний, но не от модели, которая их выдала. Причем, большинство метрик устроены симметрично — если поменять местами эти два вектора, результат не изменится.
При рассмотрении метрик надо помнить следующее — чем выше эффективность модели, тем лучше. Но некоторые метрики устроены как измерение ошибки модели. В таком случае, конечно, тем ниже, тем лучше. Так что эффективность и ошибка модели — это по сути противоположные понятия. Так сложилось, что метрики регрессии чаще устроены именно как ошибки, а метрики классификации — как метрики именно эффективности. При использовании конкретной метрики на это надо обращать внимание.
Выводы:
- Метрики эффективности — это способ показать, насколько точно модель отражает реальный мир.
- Метрики эффективность должны выбираться исходя из задачи, которую решает модель.
- Функция ошибки и метрика эффективности — это разные вещи, к ним предъявляются разные требования.
- В задаче можно (и, зачастую, нужно) применять несколько метрик эффективности.
- Наряду с метриками эффективности есть и другие характеристики моделей — скорость обучения, скорость работы, надежность, робастность, интерпретируемость.
- Метрики эффективности вычисляются как правило из двух векторов — предсказанных (теоретических) значений целевой переменной и эмпирических (реальных) значений.
- Обычно метрики устроены таким образом, что чем выше значение, тем модель лучше.
Метрики эффективности для регрессии
Как мы говорили в предыдущем пункте, метрики зависят от конкретной задачи. А все задачи обучения с учителем разделяются на регрессию и классификацию. Совершенно естественно, что метрики для регрессии и для классификации будут разными.
Метрики эффективности для регрессии оценивают отклонение (расстояние) между предсказанными значениями и реальными. Кажется, что это очевидно, но метрики эффективности классификации устроены по-другому. Предполагается, что чем меньше каждое конкретное отклонение, тем лучше. Разница между разными метриками в том, как учитывать индивидуальные отклонения в общей метрике и в том, как агрегировать ряд значений в один интегральный показатель.
Все метрики эффективности моделей регрессии покажутся вам знакомыми, если вы изучали математическую статистику, ведь именно статистические методы легли в основу измерения эффективности моделей машинного обучения. Причем, метрики эффективности — это лишь самые простые статистические показатели, которые можно использовать для анализа качества модели. При желании можно и нужно задействовать более мощные статистические методы исследования данных. Например, можно проанализировать вид распределения отклонений, и сделать из этого вывод о необходимость корректировки моделей. Но в 99% случаев можно обойтись простым вычислением одной или двух рассматриваемых ниже метрик.
Так как метрики эффективности позволяют интерпретировать оценку качества модели, они зачастую неявно сравнивают данную модель с некоторой тривиальной. Тривиальна модель — это очень простая, даже примитивная модель, которая выдает предсказания оценки целевой переменной абсолютно без оглядки на эффективность и вообще соответствие реальным данным. Тривиальной моделью может выступать, например, предсказание для любого объекта среднего значения целевой переменной из обучающей выборки. Такие тривиальные модели нужны, чтобы оценить, насколько данная модель лучше или хуже них.
Естественно, мы хотим получить модель, которая лучше тривиальной. Причем, у нас есть некоторый идеал — модель, которая никогда не ошибается, то есть чьи предсказания всегда совпадают с реальными значениями. Поэтому реальная модель может быть лучше тривиальной только до этого предела. У такой идеальной модели, говорят, 100% эффективность или нулевая ошибка.
Но надо помнить, что в задачах регрессии модель предсказывает непрерывное значение. Это значит, что величина отклонения может быть неограниченно большой. Так что не бывает нижнего предела качества модели. Модель регрессии может быть бесконечно далекой от идеала, бесконечно хуже даже тривиальной модели. Поэтому ошибки моделей регрессии не ограничиваются сверху (или, что то же самое, эффективность моделей регрессии не ограничивается снизу).
Поэтому в задачах регрессии
Выводы:
- Метрики эффективности для регрессий обычно анализируют отклонения предсказанных значений от реальных.
- Большинство метрик пришло в машинное обучение из математической статистики.
- Результаты работы модели можно исследовать более продвинутыми статистическими методами.
- Обычно метрики сравнивают данную модель с тривиальной — моделью, которая всегда предсказывает среднее реальное значение целевой переменной.
- Модель могут быть точны на 100%, но плохи они могут быть без ограничений.
Коэффициент детерминации (r-квадрат)
Те, кто раньше хотя бы немного изучал математическую статистику, без труда узнают первую метрику эффективности моделей регрессии. Это так называемый коэффициент детерминации. Это доля дисперсии (вариации) целевой переменной, объясненная данной моделью. Данная метрика вычисляется по такой формуле:
[R^2(y, hat{y}) = 1 — frac
{sum_{i=1}^n (y_i — hat{y_i})^2}
{sum_{i=1}^n (y_i — bar{y_i})^2}]
где
$y$ — вектор эмпирических (истинных) значений целевой переменной,
$hat{y}$ — вектор теоретических (предсказанных) значений целевой переменной,
$y_i$ — эмпирическое значение целевой переменной для $i$-го объекта,
$hat{y_i}$ — теоретическое значение целевой переменной для $i$-го объекта,
$bar{y_i}$ — среднее из эмпирических значений целевой переменной для $i$-го объекта.
Если модель всегда предсказывает идеально (то есть ее предсказания всегда совпадают с реальностью, другими словами, теоретические значения — с эмпирическими), то числитель дроби в формуле будет равен 0, а значит, вся метрика будет равна 1. Если же мы рассмотрим тривиальную модель, которая всегда предсказывает среднее значение, то числитель будет равен знаменателю, дробь будет равна 1, а метрика — 0. Если модель хуже идеальной, но лучше тривиальной, то метрика будет в диапазоне от 0 до 1, причем чем ближе к 1 — тем лучше.
Если же модель предсказывает такие значения, что отклонения их от теоретических получаются больше, чем от среднего значения, то числитель будет больше знаменателя, а значит, что метрика будет принимать отрицательные значения. Запомните, что отрицательные значения коэффициента детерминации означают, что модель хуже, чем тривиальная.
В целом эта метрика показывает силу линейной связи между двумя случайными величинами. В нашем случае этими величинами выступают теоретические и эмпирические значения целевой переменной (то есть предсказанные и реальные). Если модель дает точные предсказания, то будет наблюдаться сильная связь (зависимость) между теоретическим значением и реальным, то есть высокая детерминация, близкая к 1. Если эе модель дает случайные предсказания, никак не связанные с реальными значениями, то связь будет отсутствовать.
Причем так как нас интересует, насколько значения совпадают, нам достаточно использовать именно линейную связь. Ведь когда мы оцениваем связь, например, одного из факторов в целевой переменной, то связь может быть нелинейной, и линейный коэффициент детерминации ее не покажет, то есть пропустит. Но в данному случае это не важно, так как наличие нелинейной связи означает, что предсказанные значения все-таки отклоняются от реальных. Такую линейную связь можно увидеть на графике, если построить диаграмму рассеяния между теоретическими и эмпирическими значениями, вот так:
1
2
3
4
5
6
from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(X, Y)
Y_ = reg.predict(X)
plt.scatter(Y, Y_)
plt.plot(Y, Y)
Здесь мы еще строим прямую $y = y$. Она нужна только для удобства. Вот как может выглядеть этот график:
Здесь мы видим, что точки немного отклоняются от центральной линии, но в целом ей следуют. Такая картина характерна для высокого коэффициента детерминации. А вот как может выглядеть менее точная модель:
И в целом, чем точки ближе к центральной линии, тем лучше модель и тем ближе коэффициент детерминации к 1.
В англоязычной литература эта метрика называется $R^2$, так как в определенных случаях она равна квадрату коэффициента корреляции. Пусть это название не вводит вас в заблуждение. Некоторые думаю, что раз метрика в квадрате, то она не может быть отрицательной. Это лишь условное название.
Пару слов об использовании метрик эффективности в библиотеке sklearn. Именно коэффициент детерминации чаще всего используется как метрика по умолчанию, которую можно посмотреть при помощи метода score() у модели регрессии. Обратите внимание, что этот метод принимает на вход саму обучающую выборку. Это сделано для единообразия с методами наподобие fit().
Но более универсально будет использовать эту метрику независимо от модели. Все метрики эффективности собраны в отдельный пакет metrics. Данная метрика называется r2_score. Обратите внимание, что при использовании этой функции ей надо передавать два вектора целевой переменной — сначала эмпирический, а вторым аргументом — теоретический.
1
2
3
4
5
6
7
8
from sklearn.metrics import r2_score
def r2(y, y_):
return 1 - ((y - y_)**2).sum() / ((y - y.mean())**2).sum()
print(reg.score(X, Y))
print(r2_score(Y, Y_))
print(r2(Y, Y_))
В данном коде мы еще реализовали самостоятельный расчет данной метрики, чтобы пояснить применение формулы выше. Можете самостоятельно убедиться, что три этих вызова напечатают одинаковые значения.
Коэффициент детерминации, или $R^2$ — это одна из немногих метрик эффективности для моделей регрессии, значение которой чем больше, тем лучше. Почти все остальные измеряют именно ошибку, что мы и увидим ниже. Еще это одна из немногих несимметричных метрик. Ведь если в формуле поменять теоретические и эмпирические значения, ее смысл и значение могут поменяться. Поэтому при использовании этой метрики нужно обязательно следить за порядком передачи аргументов.
При использовании этой метрики есть один небольшой подводный камень. Так как в знаменатели у этой формулы стоит вариация реального значения целевой переменной, важно следить, чтобы эта вариация присутствовала. Ведь если реальное значение целевой переменной будет одинаковым для всех объектов выборки, то вариация этой переменной будет равна 0. А значит, метрика будет не определена. Причем это единственная причина, почему эта метрика может быть неопределена. Надо понимать, что отсутствие вариации целевой переменной ставит под сомнение вообще целесообразность машинного обучения и моделирования в целом. Ведь что нам предсказывать если $y$ всегда один и тот же? С другой стороны, такая ситуация может случиться, например, при случайном разбиении выборки на обучающую и тестовую. Но об этом мы поговорим дальше.
Выводы:
- Коэффициент детерминации показывает силу связи между двумя случайными величинами.
- Если модель всегда предсказывает точно, метрика равна 1. Для тривиальной модели — 0.
- Значение метрики может быть отрицательно, если модель предсказывает хуже, чем тривиальная.
- Это одна из немногих несимметричных метрик эффективности.
- Эта метрика не определена, если $y=const$. Надо следить, чтобы в выборке присутствовали разные значения целевой переменной.
Средняя абсолютная ошибка (MAE)
Коэффициент детерминации — не единственная возможная характеристика эффективности моделей регрессии. Иногда полезно оценить отклонения предсказаний от истинных значений более явно. Как раз для этого служат сразу несколько метрик ошибок моделей регрессии. Самая простая из них — средняя абсолютная ошибка (mean absolute error, MAE). Она вычисляется по формуле:
[MAE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1} |y_i — hat{y_i}|]
Данная метрика действительно очень проста: это средняя величина разницы между предсказанными и реальными значениями целевой переменной. Причем эта разница берется по модулю, чтобы компенсировать возможные отрицательные отклонения. Мы уже рассматривали похожую функцию, когда говорили о конструировании функции ошибки для градиентного спуска. Но тогда мы отмели использование абсолютного значения, так как эта функция не везде дифференцируема. Но вот для метрики эффективности такого требования нет и MAE вполне можно использовать.
Если модель предсказывает идеально, то, естественно, все отклонения равны 0 и MAE в целом равна нулю. Но эта метрика не учитывает явно сравнение с тривиальной моделью — она просто тем хуже, чем больше. Ниже нуля она быть, конечно, не может.
Данная метрика выражается в натуральных единицах и имеет очень простой и понятный смысл — средняя ошибка модели. Степень применимости модели в таком случае можно очень просто понять исходя из предметной области. Например, наша модель ошибается в среднем на 500 рублей. Хорошо это или плохо? Зависит от размерности исходных данных. Если мы предсказываем цены на недвижимость — то модель прекрасно справляется с задачей. Если же мы моделируем цены на спички — то такая модель скорее всего очень неэффективна.
Использование данной метрики в пакете sklearn очень похоже на любую другую метрику, меняется только название:
1
2
3
4
5
>>> from sklearn.metrics import mean_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_absolute_error(y_true, y_pred)
0.5
Выводы:
- MAE показывает среднее абсолютное отклонение предсказанных значений от реальных.
- Чем выше значение MAE, тем модель хуже. У идеальной модели $MAE=0$
- MAE очень легко интерпретировать — на сколько в среднем ошибается модель.
Средний квадрат ошибки (MSE)
Средний квадрат ошибки (mean squared error, MSE) очень похож на предыдущую метрику, но вместо абсолютного значения (модуля) используется квадрат:
[MSE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1} (y_i — hat{y_i})^2]
Граничные случаи у этой метрики такие же, как у предыдущей — 0 у идеальной модели, а в остальном — чем больше, тем хуже. MSE у тривиальной модели будет равна дисперсии целевой переменной. Но это не то, чтобы очень полезно на практике.
Эта метрика используется во многих моделях регрессии как функция ошибки. Но вот как метрику эффективности ее применяют довольно редко. Дело в ее интерпретируемости. Ведь она измеряется в квадратах натуральной величины. А какой физический смысл имеют, например, рубли в квадрате? На самом деле никакого. Поэтому несмотря на то, что математически MAE и MSE в общем-то эквивалентны, первая более проста и понятна, и используется гораздо чаще.
Единственное существенное отличие данной метрики от предыдущей состоит в том, что она чуть больший “вес” в общей ошибке придает большим значениям отклонений. То есть чем больше значение отклонения, тем сильнее оно будет вкладываться в значение MSE. Это иногда бывает полезно, когда исходя из задачи стоит штрафовать сильные отклонения предсказанных значений от реальных. Но с другой стороны это свойство делает эту метрику чувствительной к аномалиям.
Пример расчета метрики MSE:
1
2
3
4
5
>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred, squared=False)
0.612...
Выводы:
- MAE показывает средний квадрат отклонений предсказанных значений от реальных.
- Чем выше значение MSE, тем модель хуже. У идеальной модели $MSE=0$
- MSE больше учитывает сильные отклонения, но хуже интерпретируется, чем MAE.
Среднеквадратичная ошибка (RMSE)
Если главная проблема метрики MSE в том, что она измеряется в квадратах натуральных величин, что что будет, если мы возьмем от нее квадратный корень? Тогда мы получим среднеквадратичную ошибку (root mean squared error, RMSE):
[RMSE(y, _hat{y}) = sqrt{frac{1}{n} sum_{i=0}^{n-1} (y_i — hat{y_i})^2}]
Использование данной метрики достаточно привычно при статистическом анализе данных. Однако, для интерпретации результатов машинного обучения она имеет те же недостатки, что и MSE. Главный из них — чувствительность к аномалиям. Поэтому при интерпретации эффективности моделей регрессии чаще рекомендуется применять метрику MAE.
Пример использования:
1
2
3
4
5
>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred)
0.375
Выводы:
- RMSE — это по сути корень из MSE. Выражается в тех же единицах, что и целевая переменная.
- Чаще применяется при статистическом анализа данных.
- Данная метрика очень чувствительна к аномалиям и выбросам.
Среднеквадратичная логарифмическая ошибка (MSLE)
Еще одна довольно редкая метрика — среднеквадратическая логарифмическая ошибка (mean squared logarithmic error, MSLE). Она очень похожа на MSE, но квадрат вычисляется не от самих отклонений, а от разницы логарифмов (про то, зачем там +1 поговорим позднее):
[MSLE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1} (
ln(1 + y_i) — ln(1 + hat{y_i})
)^2]
Данная материка имеет специфическую, но довольно полезную сферу применения. Она применяется в тех случаях, когда значения целевой переменной простираются на несколько порядков величины. Например, если мы анализируем доходы физических лиц, они могут измеряться от тысяч до сотен миллионов. Понятно, что при использовании более привычных метрик, таких как MSE, RMSE и даже MAE, отклонения в больших значениях, даже небольшие относительно, будут полностью доминировать над отклонениями в малых значениях.
Это приведет к тому, что оценка моделей в подобных задачах классическими метриками будет давать преимущество моделям, которые более точны в одной части выборки, но почти не будут учитывать ошибки в других частях выборки. Это может привести к несправедливой оценке моделей. А вот использование логарифма поможет сгладить это противоречие.
Чаще всего, величины с таким больших размахом, что имеет смысл использовать логарифмическую ошибку, возникают в тех задачах, которые моделируют некоторые естественные процессы, характеризующиеся экспоненциальным ростом. Например, моделирование популяций, эпидемий, финансов. Такие процессы часто порождают величины, распределенные по экспоненциальному закону. А они чаще всего имеют область значений от нуля до плюс бесконечности, то есть иногда могут обращаться в ноль.
Проблема в том, что логарифм от нуля не определен. Именно поэтому в формуле данной метрики присутствует +1. Это искусственный способ избежать неопределенности. Конечно, если вы имеете дело с величиной, которая может принимать значение -1, то у вас опять будут проблемы. Но на практике такие особые распределения не встречаются почти никогда.
Использование данной метрике в коде полностью аналогично другим:
1
2
3
4
5
>>> from sklearn.metrics import mean_squared_log_error
>>> y_true = [3, 5, 2.5, 7]
>>> y_pred = [2.5, 5, 4, 8]
>>> mean_squared_log_error(y_true, y_pred)
0.039...
Выводы:
- MSLE это среднее отклонение логарифмов реальных и предсказанных данных.
- Так же, идеальная модель имеет $MSLE = 0$.
- Данная метрика используется, когда целевая переменная простирается на несколько порядков величины.
- Еще эта метрика может быть полезна, если моделируется процесс в экспоненциальным ростом.
Среднее процентное отклонение (MAPE)
Все метрики, которые мы рассматривали до этого рассчитывали абсолютную величину отклонения. Но ведь отклонение в 5 единиц при истинном значении 5 и при значении в 100 — разные вещи. В первом случае мы имеем ошибку в 100%, а во втором — только в 5%. Очевидно, что первый и второй случай должны по-разному учитываться в ошибке. Для этого придумана средняя абсолютная процентная ошибка (mean absolute percentage error, MAPE). В ней каждое отклонение оценивается в процентах от истинного значения целевой переменной:
[MAPE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1}
frac{|y_i — hat{y_i}|}{max(epsilon, |y_i|)}]
Эта метрика имеет одно критическое преимущество над остальными — с ее помощью можно сравнивать эффективность моделей на разных обучающих выборках. Ведь если мы возьмем классические метрики (например, MAE), то размер отклонений будет очевидно зависеть от самих данных. А в двух разных выборках и средняя величина скорее всего будет разная. Поэтому метрики MAE, MSE, RMSE, MSLE не сопоставимы при сравнении предсказаний, сделанных на разных выборках.
А вот по метрике MAPE можно сравнивать разные модели, которые были обучены на разных данных. Это очень полезно, например, в научных публикациях, где метрика MAPE (и ее вариации) практически обязательны для описания эффективности моделей регрессии.Ведь если одна модель ошибается в среднем на 3,9%, а другая — на 3,5%, очевидно, что вторая более точна. А вот если оперировать той же MAE, так сказать нельзя. Ведь если одна модель ошибается в среднем на 500 рублей, а вторая — на 490, очевидно ли, что вторая лучше? Может, она даже хуже, просто в исходных данных величина целевой переменной во втором случае была чуть меньше.
При этом у метрики MAPE есть пара недостатков. Во-первых, она не определена, если истинное значение целевой переменной равно 0. Именно для преодоления этого в знаменателе формулы этой метрики присутствует $max(epsilon, |y_i|)$. $epsilon$ — это некоторое очень маленькое значение. Оно нужно только для того, чтобы избежать деления на ноль. Это, конечно, настоящий математический костыль, но позволяет без опаски применять эту метрику на практике.
Во-вторых, данная метрика дает преимущество более низким предсказаниям. Ведь если предсказание ниже, чем реальное значение, процентное отклонение может быть от 0% до 100%. В это же время если предсказание выше реального, то верхней границы нет, предсказание может быть больше и на 200%, и на 1000%.
В-третьих, эта метрика несимметрична. Ведь в этой формуле $y$ и $hat{y}$ не взаимозаменяемы. Это не большая проблема и может быть исправлена использованием симметричного варианта этой метрики, который называется SMAPE (symmetric mean absolute percentage error):
[MAPE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1}
frac{|y_i — hat{y_i}|}{max(epsilon, (|hat{y_i}|, |y_i|) / 2)}]
В русскоязычной литературе данная метрика часто называется относительной ошибкой, так как она учитывает отклонение относительно целевого значения. В английском названии метрики она называется абсолютной. Тут нет никакого противоречия, так как “абсолютный” здесь значит просто взятие по модулю.
С точки зрения использования в коде, все полностью аналогично:
1
2
3
4
5
>>> from sklearn.metrics import mean_absolute_percentage_error
>>> y_true = [1, 10, 1e6]
>>> y_pred = [0.9, 15, 1.2e6]
>>> mean_absolute_percentage_error(y_true, y_pred)
0.2666...
Выводы:
- Идея этой метрики — это чувствительность к относительным отклонениям.
- Данная модель выражается в процентах и имеет хорошую интерпретируемость.
- Идеальная модель имеет $MAPE = 0$. Верхний предел — не ограничен.
- Данная метрика отдает предпочтение предсказанию меньших значений.
Абсолютная медианная ошибка
Практически во всех ранее рассмотренных метриках используется среднее арифметическое для агрегации частных отклонений в общую величину ошибки. Иногда это может быть не очень уместно, если в выборке присутствует очень неравномерное распределение по целевой переменной. В таких случаях может быть целесообразно использование медианной ошибки:
[MedAE(y, _hat{y}) = frac{1}{n} median_{i=0}^{n-1}
|y_i — hat{y_i}|]
Эта метрика полностью аналогична MAE за одним исключением: вместо среднего арифметического подсчитывается медианное значение. Медиана — это такое значение в выборке, больше которого и меньше которого примерно половина объектов выборки (с точностью до одного объекта).
Эта метрика чаще всего применяется при анализе демографических и экономических данных. Ее особенность в том, что она не так чувствительна к выбросам и аномальным значениям, ведь они практически не влияют на медианное значение выборки, что делает эту метрику более надежной и робастной, чем абсолютная ошибка.
Пример использования:
1
2
3
4
5
>>> from sklearn.metrics import median_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> median_absolute_error(y_true, y_pred)
0.5
Выводы:
- Медианная абсолютная ошибка похожа на среднюю абсолютную, но более устойчива к аномалиям.
- Применяется в задачах, когда известно, что в данных присутствуют выбросы, аномальные , непоказательные значения.
- Эта метрика более робастная, нежели MAE.
Максимальная ошибка
Еще одна достаточно экзотическая, но очень простая метрика эффективности регрессии — максимальная ошибка:
[ME(y, _hat{y}) = max_{i=0}^{n-1}
|y_i — hat{y_i}|]
Как следует из названия, это просто величина максимального абсолютного отклонения предсказанных значений от теоретических. Особенность этой метрики в том, что она вообще не характеризует распределение отклонений в целом. Поэтому она практически никогда не применяется самостоятельно, в качестве единственной метрики.
Эта метрика именно вспомогательная. В сочетании с другими метриками, она может дополнительно охарактеризовать, насколько сильно модель может ошибаться в самом худшем случае. Опять же, в зависимости от задачи, это может быть важно. В некоторых задачах модель, которая в среднем ошибается пусть чуть больше, но при этом не допускает очень больших “промахов”, может быть предпочтительнее, чем более точная модель в среднем, но у которой встречаются сильные отклонения.
Применение этой метрики та же просто, как и других:
1
2
3
4
5
>>> from sklearn.metrics import max_error
>>> y_true = [3, 2, 7, 1]
>>> y_pred = [9, 2, 7, 1]
>>> max_error(y_true, y_pred)
6
Выводы:
- Максимальная ошибка показывает наихудший случай предсказания модели.
- В некоторых задачах важно, чтобы модель не ошибалась сильно, а небольшие отклонения не критичны.
- Зачастую эта метрика используется как вспомогательная совместно с другими.
Метрики эффективности для классификации
Приступим к рассмотрению метрик эффективности, которые применяются для оценки моделей классификации. Для начала ответим на вопрос, почему для них нельзя использовать те метрики, которые мы уже рассмотрели в предыдущей части? Дело в том, что метрики эффективности регрессии так или иначе оценивают расстояние от предсказанного значения до реального. Это подразумевает, что в значениях целевой переменной существует определенный порядок. Формально говоря, предполагается, что целевая переменная измеряется по относительной шкале. Это значит, что разница между значениями имеет какой-то смысл. Например, если мы ошиблись в предполагаемой цене товара на 10 рублей, это лучше, чем ошибка на 20 рублей. Причем, можно сказать, что это в два раза лучше.
Но вот целевые переменные, которые существуют в задачах классификации обычно не обладают таким свойством. Да, метки классов часто обозначают числами (класс 0, класс 1, класс 5 и так далее). И мы используем эти числа в качестве значения переменных в программе. Но это ничего не значит. Представим объект, принадлежащий 0 классу, что бы этот класс не значил. Допустим, мы предсказали 1 класс. Было бы хуже, если бы мы предсказали 2 класс. Можно ли сказать, что во втором случае модель ошиблась в два раза сильнее? В общем случае, нельзя. Что в первом, что во втором случае модель просто ошиблась. Имеет значение только разница между правильным предсказанием и неправильным. Отклонение в задачах классификации не играет роли.
Поэтому метрики эффективности для классификации оценивают количество правильно и неправильно классифицированных (иногда еще говорят, распознанных) объектов. При этом разные метрики, как мы увидим, концентрируются на разных соотношениях этих количеств, особенно в случае, когда классов больше двух, то есть имеет место задача множественной классификации.
Причем метрики эффективности классификации тоже нельзя применять для оценки регрессионных моделей. Дело в том, что в задачах регрессии почти никогда не встречается полное совпадение предсказанного и реального значения. Так как мы работам с непрерывным континуумом значений, вероятность такого совпадения равна, буквально, нулю. Поэтому по метрикам для классификации практически любая регрессионная модель будет иметь нулевую эффективность, даже очень хорошая и точная модель. Именно потому, что для метрик классификации даже самая небольшая ошибка уже считается как промах.
Как мы говорили ранее,для оценки конкретной модели можно использовать несколько метрик одновременно. Это хорошая практика для задач регрессии, но для классификации — это практически необходимость. Дело в том, что метрики классификации гораздо легче “обмануть” с помощью тривиальных моделей, особенно в случае несбалансированных классов (об этом мы поговорим чуть позже). Тривиальной моделью в задачах классификации может выступать модель, которая предсказывает случайный класс (такая используется чаще всего), либо которая предсказывает всегда какой-то определенный класс.
Надо обратить внимание, что по многим метрикам, ожидаемая эффективность моделей классификации сильно зависит от количества классов в задаче. Чем больше классов, тем на меньшую эффективность в среднем можно рассчитывать.Поэтому метрики эффективности классификации не позволяют сопоставить задачи, состоящие из разного количества классов. Это следует помнить при анализе моделей. Если точность бинарной классификации составляет 50%, это значит, что модель работает не лучше случайного угадывания. Но в модели множественной классификации из, допустим, 10 000 классов, точность 50% — это существенно лучше случайного гадания.
Еще обратим внимание, что некоторые метрики учитывают только само предсказание, в то время, как другие — степень уверенности модели в предсказании. Вообще, все модели классификации разделяются на логические и метрические. Логические методы классификации выдают конкретное значение класса, без дополнительной информации. Типичные примеры — дерево решений, метод ближайших соседей. Метрические же методы выдают степень уверенности (принадлежности) объекта к одному или, чаще, ко всем классам. Так, например, работает метод логистической регрессии в сочетании с алгоритмом “один против всех”. Так вот, в зависимости, от того, какую модель классификации вы используете, вам могут быть доступны разные метрики. Те метрики, которые оценивают эффективность классификации в зависимости от выбранной величины порога не могут работать с логическими методами. Поэтому, например, нет смысла строить PR-кривую для метода ближайших соседей. Остальные метрики, которые не используют порог, могут работать с любыми методами классификации.
Выводы:
- Метрики эффективности классификации подсчитывают количество правильно распознанных объектов.
- В задачах классификации почти всегда надо применять несколько метрик одновременно.
- Тривиальной моделью в задачах классификации считается та, которая предсказывает случайный класс, либо самый популярный класс.
- Качество бинарной классификации при прочих равных почти всегда будет сильно выше, чем для множественной.
- Вообще, чем больше в задаче классов, тем ниже ожидаемые значения эффективности.
- Некоторые метрики работают с метрическими методами, другие — со всеми.
Доля правильных ответов (accuracy)
Если попробовать самостоятельно придумать способ оценить качество модели классификации, ничего не зная о существующих метриках, скорее всего получится именно метрика точности (accuracy). Это самая простая и естественная метрика эффективности классификации. Она подсчитывается как количество объектов в выборке, которые были классифицированы правильно (то есть, для которых теоретическое и эмпирическое значение метки класса — целевой переменной — совпадает), разделенное на общее количество объектов выборки. Вот формула для вычисления точности классификации:
[acc(y, hat{y}) = frac{1}{n} sum_{i=0}^{n} 1(hat{y_i} = y_i)]
В этой формуле используется так называемая индикаторная функция $1()$. Эта функция равна 1 тогда, когда ее аргумент — истинное выражение, и 0 — если ложное. В данном случае она равна единице для всех объектов, у которых предсказанное значение равно реальному ($hat{y_i} = y_i$). Суммируя по всем объектам мы получим количество объектов, классифицированных верно. Перед суммой стоит множитель $frac{1}{n}$, где $n$ — количество объектов в выборке. То есть в итоге мы получаем долю правильных ответов исследуемой модели.
Значение данной метрики может быть выражено в долях единицы, либо в процентах, домножив значение на 100%. Чем выше значение accuracy, тем лучше модель классифицирует выборку, то есть тем лучше ответы модели соответствуют значениям целевой переменной, присутствующим в выборке. Если модель всегда дает правильные предсказания, то ее accuracy будет равн 1 (или 100%). Худшая модель, которая всегда предсказывает неверно будет иметь accuracy, равную нулю, причем это нижняя граница, хуже быть не может.
В дальнейшем, для обозначения названий метрик эффективности я буду использовать именно английские названия — accuracy, precision, recall. У каждого из этих слов есть перевод на русский, но так случилось, что в русскоязычных терминах существует путаница. Дело в том, что и accuracy и precision чаще всего переводятся словом “точность”. А это разные метрики, имеющие разный смысл и разные формулы. Accuracy еще называют “правильность”, precision — “прецизионность”. Причем у последнего термина есть несколько другое значение в метрологии. Поэтому, пока будем обозначать эти метрики изначальными названиями.
А вот accuracy тривиальной модели будет как раз зависеть от количества классов. Если мы имеем дело с бинарной классификацией, то модель будет ошибаться примерно в половине случаев. То есть ее accuracy будет 0,5. В общем же случае, если есть $m$ классов, то тривиальная модель, которая предсказывает случайный класс будет иметь accuracy в среднем около $frac{1}{m}$.
Но это в случае, если в выборке объекты разных классов встречаются примерно поровну. В реальности же часто встречаются несбалансированные выборки, в которых распределение объектов по классам очень неравномерно. Например, может быть такое, что объектов одного класса в десять раз больше, чем другого. В таком случае, accuracy тривиальной модели может быть как выше, так и ниже $1/m$. Вообще, метрика accuracy очень чувствительна к соотношению классов в выборке. И именно поэтому мы рассматриваем другие способы оценки качества моделей классификации.
Использование метрики accuracy в библиотеке sklearn ничем принципиальным не отличается от использования других численных метрик эффективности:
1
2
3
4
5
6
>>> import numpy as np
>>> from sklearn.metrics import accuracy_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> accuracy_score(y_true, y_pred)
0.5
В данном примере в задаче 4 класса (0, 1, 2, 3) и столько же объектов, по одному на каждый класс. Модель правильно классифицировала первый и третий объект, то есть половину. Поэтому ее accuracy составляет 0,5 или 50%.
Выводы:
- Точность (accuracy) — самая простая метрика качества классификации, доля правильных ответов.
- Может быть выражена в процентах и в долях единицы.
- Идеальная модель дает точность 1.0, тривиальная — 0.5, самая худшая — 0.0.
- Тривиальная модель в множественной сбалансированной задаче классификации дает точность 1/m.
- Метрика точности очень чувствительная к несбалансированности классов.
Метрики классификации для неравных классов (precision, recall, F1)
Как мы говорили ранее, метрика accuracy может быть чувствительна к несбалансированности классов. Рассмотрим типичный пример — диагностика заболевания. Допустим, в случайной выборке людей заболевание встречается один раз на 100 человек. То есть в выборке у нас может быть всего 1% объектов, принадлежащих положительному классу и 99% — отрицательному, то есть почти в 100 раз больше. Какая accuracy будет у абсолютно тривиальной модели, которая всегда предсказывает отрицательный класс? Такая модель будет права в 99% случаев и ошибаться только в 1%. То есть иметь accuracy 0,99. Естественно, ценность такой модели минимальна, несмотря на высокий показатель метрики. Поэтому в случае с сильно несбалансированными классами метрика accuracy не то, чтобы неверна, она непоказательна, то есть не дает хорошего представления о качественных характеристиках модели.
Для более полного описания модели используется ряд других метрик. Для того, чтобы понять, как они устроены и что показывают нужно разобраться с понятием ошибок первого и второго рода. Пока будем рассматривать случай бинарной классификации, а о том, как эти метрики обобщаются на множественные задачи, поговорим позднее. Итак, у нас есть задача бинарной классификации, объекты положительного и отрицательного класса. Идеальным примером для этого будет все та же медицинская диагностика.
По отношению к модели бинарной классификации все объекты выборки можно разделить на четыре непересекающихся множества. Истинноположительные (true positive, TP) — это те объекты, которые отнесены моделью к положительному классу и действительно ему принадлежат. Истинноотрицательные (true negative, TN) — соответственно те, которые правильно распознаны моделью как принадлежащие отрицательному классу. Ложноположительные объекты (FP, false positive) — это те, которые модель распознала как положительные, хотя на самом деле они отрицательные. В математической статистике такая ситуация называется ошибкой первого рода. И, наконец, ложноотрицательные значения (false negative, FN) — это те, которые ошибочно отнесены моделью к отрицательному классу, хотя на самом деле они принадлежат положительному.
В примере с медицинско диагностикой, ложноположительные объекты или ошибки первого рода — это здоровые пациенты, которых при диагностике ошибочно назвали больными. Ложноотрицательные, или ошибки второго рода, — это больные пациенты, которых диагностическая модель “пропустила”, ошибочно приняв за здоровых. Очевидно, что в этой задаче, как и во многих других, ошибки первого и второго рода не равнозначны. В медицинской диагностике, например, гораздо важнее распознать всех здоровых пациентов, то есть не допустить ложноотрицательных объектов или ошибок второго рода. Ошибки же первого рода, или ложноположительные предсказания, тоже нежелательны, но значительно меньше, чем ложноотрицательные.
Так вот, метрика accuracy учитывает и те и другие ошибки одинаково, абсолютно симметрично. В терминах наших четырех классов она может выражаться такой формулой:
[A = frac{TP + TN}{TP + TN + FP + FN}]
Обратите внимание, что если в модели переименовать положительный класс в отрицательный и наоборот, то это никак не повлияет на accuracy. Так вот, в зависимости от решаемой задачи, нам может быть необходимо воспользоваться другими метриками. Вообще, их существует большое количество, но на практике чаще других применяются метрики precision и recall.
Precision (чаще переводится как “точность”, “прецизионность”) — это доля объектов, плавильно распознанных как положительные из всех, распознанных как положительные. Считается этот показатель по следующей формуле: $P = frac{TP}{TP + FP}$. Как можно видеть, precision будет равен 1, если модель не делает ошибок первого рода, то есть не дает ложноположительных предсказаний. Причем ошибки второго рода (ложноотрицательные) вообще не влияют на величину precision, так как эта метрика рассматривает только объекты, отнесенные моделью к положительным.
Precision характеризует способность модели отличать положительный класс от отрицательного, не делать ложноположительных предсказаний. Ведь если мы будем всегда предсказывать отрицательный класс, precision будет не определен. А вот если модель будет всегда предсказывать положительный класс, то precision будет равен доли объектов этого класса в выборке. В нашем примере с медицинской диагностикой, модель, всех пациентов записывающая в больные даст precision всего 0,01.
Метрика recall (обычно переводится как “полнота” или “правильность”) — это доля положительных объектов выборки, распознанных моделью. То есть это отношение все тех же истинноположительных объектов к числу всех положительных объектов выборки: $R = frac{TP}{TP + FN}$. Recall будет равен 1 только в том случае, если модель не делает ошибок второго рода, то есть не дает ложноотрицательных предсказаний. А вот ошибки первого рода (ложноположительные) не влияют на эту метрику, так как она рассматривает только объекты, которые на самом деле принадлежат положительному классу.
Recall характеризует способность модели обнаруживать все объекты положительного класса. Если мы будем всегда предсказывать отрицательный класс, то данная метрика будет равна 0, а если всегда положительный — то 1. Метрика Recall еще называется полнотой, так как она характеризует полноту распознавания положительного класса моделью.
В примере с медицинской диагностикой нам гораздо важнее, как мы говорили, не делать ложноотрицательных предсказаний. Поэтому метрика recall будет для нас важнее, чем precision и даже accuracy. Однако, как видно из примеров, каждый из этих метрик легко можно максимизировать довольно тривиальной моделью. Если мы будет ориентироваться на recall, то наилучшей моделью будет считаться та, которая всегда предсказывает положительный класс. Если только на precision — то “выиграет” модель, которая всегда предсказывает наоборот, положительный. А если брать в расчет только accuracy, то при сильно несбалансированных классах модель, предсказывающая самый популярный класс. Поэтому эти метрики нелья использовать по отдельности, только сразу как минимум две из них.
Так как метрики precision и recall почти всегда используются совместно, часто возникает ситуация, когда есть две модели, у одной из которых выше precision, а у второй — recall. Возникает вопрос, как выбрать лучшую? Для такого случая можно посчитать среднее значение. Но для этих метрик больше подойдет среднее не арифметическое, а гармоническое, ведь оно равно 0, если хотя бы одно число равно 0. Эта метрика называется $F_1$:
[F_1 = frac{2 P R}{P + R} = frac{2 TP}{2 TP + FP + FN}]
Эта метрика полезна, если нужно одно число, которое в себе объединяет и precision и recall. Но эта формула подразумевает, что нам одинаково важны и то и другое. А как мы заметили раньше, часто одна из этих метрик важнее. Поэтому иногда используют обобщение метрики $F_1$, так называемое семейство F-метрик:
[F_{beta} = (1 + beta^2) frac{P R}{beta^2 P + R}]
Эта метрика имеет параметр $beta > 0$, который определяет, во сколько раз recall важнее precision. Если этот параметр больше единицы, то метрика будет полагать recall более важным. А если меньше — то важнее будет precision. Если же $beta = 1$, то мы получим уже известную нам метрику $F_1$. Все метрики из F-семейства измеряются от 0 до 1, причем чем значение больше, тем модель лучше.
1
2
3
4
5
6
7
8
9
>>> from sklearn import metrics
>>> y_pred = [0, 1, 0, 0]
>>> y_true = [0, 1, 0, 1]
>>> metrics.precision_score(y_true, y_pred)
1.0
>>> metrics.recall_score(y_true, y_pred)
0.5
>>> metrics.f1_score(y_true, y_pred)
0.66...
Выводы:
- Если классы в задаче не сбалансированы, то метрика точности не дает полного представления о качестве работы моделей.
- Для бинарной классификации подсчитывается количество истинно положительных, истинно отрицательных, ложно положительных и ложно отрицательных объектов.
- Precision — доля истинно положительных объектов во всех, распознанных как положительные.
- Precision характеризует способность модели не помечать положительные объекты как отрицательные (не делать ложно положительных прогнозов).
- Recall — для истинно положительных объектов во всех положительных.
- Recall характеризует способность модели выявлять все положительные объекты (не делать ложно отрицательных прогнозов).
- F1 — среднее гармоническое между этими двумя метриками. F1 — это частный случай. Вообще, семейство F-метрик — это взвешенное среднее гармоническое.
- Часто используют все вместе для более полной характеристики модели.
Матрица классификации
Матрица классификации — это не метрика сама по себе, но очень удобный способ “заглянуть” внутрь модели и посмотреть, насколько хорошо она классифицирует какую-то выборку объектов. Особенно удобна эта матрица в задачах множественной классификации, когда из-за большого количества классов численные метрики не всегда наглядно показывают, какие объекты к каким классам относятся.
С использованием библиотеки sklearn матрица классификации может быть сформирована всего одной строчкой кода:
1
2
3
4
5
6
7
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
В этой матрице по строкам располагаются истинные значения целевой переменной, то есть действительные значения классов. По столбцам же отмечены предсказанные классы. В самой матрице на пересечении строки и столбца отмечается число объектов, которые принадлежат данному действительному классу, но моделью были распознаны как объекты данного предсказанного класса.
Естественно, элементы, располагающиеся на главной диагонали, показывают объекты, которые были правильно распознаны моделью. Элементы же вне этой диагонали — это ошибки классификации. Поэтому чем лучше модель, тем выше должны быть значения по диагонали и тем меньше — вне ее. В идеале все элементы вне главной диагонали должны быть нулевыми.
Но гораздо удобнее представлять ее в графическом виде:
Источник: sklearn.
В таком виде матрица представляется в виде тепловой карты, в которой чем выше значение, тем насыщеннее оттенок цвета. Это позволяет при первом взгляде на матрицу понять, как часто она ошибается и в каких именно классах. В отличие от простых численных метрик, матрица классификации может дать информацию о паттернах распространенных ошибок, которые допускает данная модель.
Практически любое аномальное или тривиальное поведение модели будет иметь отражение в матрице классификации. Например, если модель чаще чем нужно предсказывает один класс, это сразу подсветит отдельный столбец в ней. Если же модель путает два класса, то есть не различает объекты этих классов, то в матрице будут подсвечены четыре элемента, располагающиеся в углах прямоугольника. Еще одно распространенное поведение модель — когда она распознает объекты одного класса, как объекты другого — подсветит один элемент вне главной диагонали.
Эта матрица очень наглядно показывает, как часто и в каких конкретно классах ошибается модель. Поэтому анализ этой матрицы может дать ценную информацию о путях увеличения эффективности моделей. Например, можно провести анализ ошибок на основе показаний данной матрицы — проанализировать объекты, на которых модель чаще всего ошибается. Может, будет выявлена какая-то закономерность, либо общая характеристика. Добавление информации о таких параметрах объектов к матрице атрибутов обычно очень сильно улучшает эффективность моделей.
Выводы:
- Матрица классификации, или матрица ошибок представляет собой количество объектов по двум осям — истинный класс и предсказанный класс.
- Обычно, истинный класс располагается по строкам, а предсказанный — по столбцам.
- Для идеальной модели матрица должна содержать ненулевые элементы только на главной диагонали.
- Матрица позволяет наглядно представить результаты классификации и увидеть, в каких случаях модель делает ошибки.
- Матрица незаменима при анализе ошибок, когда исследуется, какие объекты были неправильно классифицированы.
Метрики множественной классификации
Все метрики, о которых мы говорили выше рассчитываются в случае бинарной классификации, так как определяются через понятия ложноположительных, ложноотрицательных прогнозов. Но на практике чаще встречаются задачи множественной классификации. В них не определяется один положительный и один отрицательный класс, поэтому все рассуждения о precision и recall, казалось бы, не имеют смысла.
На самом деле, все рассмотренные метрики прекрасно обобщаются на случай множественных классов. Рассмотрим простой пример. У нас есть три класса — 0, 1 и 2. Есть пять объектов, каждый их которых принадлежит одному их этих трех классов. Истинные значения целевой переменной такие: $y = lbrace 0, 1, 2, 2, 0 rbrace$. Имеется модель, которая предсказывает классы этих объектов, соответственно так: $hat{y} = lbrace 0, 0, 2, 1, 0 rbrace$. Давайте рассчитаем известные нам метрики качества классификации.
С метрикой accuracy все просто. Модель правильно предсказала класс в трех случаях из пяти — первом, третьем и пятом. А в двух случаях — ошиблась. Поэтому метрика рассчитывается так: $A = 3 / 5 = 0.6$. То есть точность модели — 60%.
А вот precision и recall рассчитываются более сложно. В моделях множественной классификации эти метрики могут быть рассчитаны отдельно по каждому классу. Подход в этом случае очень похож на алгоритм “один против всех” — для каждого класса он предполагается положительным, а все остальные классы — отрицательными. Давайте рассчитаем эти метрики на нашем примере.
Возьмем нулевой класс. Его обозначим за 1, а все остальные — за 0. Тогда вектора эмпирических и теоретических значений целевой пременной станут выглядеть так:
$y = lbrace 1, 0, 0, 0, 1 rbrace$,
$hat{y} = lbrace 1, 1, 0, 0, 1 rbrace$.
Тогда $P = frac{TP}{TP + FP} = frac{2}{3} approx 0.67$, ведь у нас получается 2 истинноположительных предсказания (первый и пятый объекты) и одно ложноположительное (второй). $R = frac{TP}{TP + FN} = frac{2}{2} = 1$, ведь в модели нет ложноотрицательных прогнозов.
$F_1 = frac{2 P R}{P + R} = frac{2 TP}{2 TP + FP + FN} = frac{2 cdot 2}{2 cdot 2 + 1 + 0} = frac{4}{5} = 0.8$.
Аналогично рассчитываются метрики и по остальным классам. Например, для первого класса вектора целевой переменной будут такими:
$y = lbrace 0, 1, 0, 0, 0 rbrace$,
$hat{y} = lbrace 0, 0, 0, 1, 0 rbrace$. Обратите внимание, что в данном случае получается, что модель ни разу не угадала. Такое тоже бывает, и в таком случае, метрики будут нулевые. Для третьего класса попробуйте рассчитать метрики самостоятельно, а чуть ниже можно увидеть правильный ответ.
Конечно, при использовании библиотечный функций не придется рассчитывать все эти метрики вручную. В библиотеке sklearn для этого есть очень удобная функция — classification_report, отчет о классификации, которая как раз вычисляет все необходимые метрики и представляет результат в виде наглядной таблицы. Вот как будет выглядеть рассмотренный нами пример:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 0.50 0.67 2
accuracy 0.60 5
macro avg 0.56 0.50 0.49 5
weighted avg 0.67 0.60 0.59 5
Здесь мы видим несколько строк, соответствующих классам в нашей задаче. По каждому классу рассчитаны метрики precision, recall и $F_1$. Последний столбец называется support — это количество объектов данного класса в используемой выборке. Это тоже важный показатель, так как чем меньше объектов какого-то класса, тем хуже он обычно распознается.
Ниже приведены интегральные, то есть общие метрики эффективности модели. Это три последние строки таблицы. В первую очередь это accuracy — она всегда рассчитывается один раз. Обратите внимание, что в столбце support здесь везде стоит 5 — это общее число объектов выборки. Ниже приведены средние значения по метрикам precision, recall и $F_1$. Почему же строк две? Дело в том, что усреднять эти метрики можно по-разному.
Во-первых, можно взять обычное среднее арифметическое из метрик всех классов. Это называется macro average. Это самый простой способ, но у него есть одна проблема. Почему метрики очень малочисленных классов должны давать тот же вклад в итоговый результат, что и метрики очень многочисленных? Можно усреднить метрики используя в качестве весов долю каждого класса в выборке. Такое усреднение называется weighted average. Обратите внимание, что при усреднении метрика $F_1$ может получиться не между precision и recall.
Отчет о классификации — очень полезная функция, использование которой практически обязательно при анализе эффективности моделей классификации. Особенно для задач множественной классификации. Эта таблица может дать важную информацию о том, какие классы распознаются моделью лучше, какие — хуже, как это связано в численностью классов в выборке. Анализ этой таблицы может навести на необходимость определенных действий по повышению эффективности модели. Например, можно понять, какие данные полезно будет добавить в модель.
Выводы:
- Метрики для каждого класса рассчитываются, полагая данный класс положительным, а все остальные — отрицательными.
- Каждую метрику можно усреднить арифметически или взвешенно по классам. Весами выступают объемы классов.
- В модуле sklearn реализовано несколько алгоритмов усреднения они выбираются исходя их задачи.
- В случае средневзвешенного, F1-метрика может получиться не между P и R.
- Отчет о классификации содержит всю необходимую информацию в стандартной форме.
- Отчет показывает метрики для каждого класса, а так же объем каждого класса.
- Также отчет показывает средние и средневзвешенные метрики для всей модели.
- Отчет о классификации — обязательный элемент представления результатов моделирования.
- По отчету можно понять сбалансированность задачи, какие классы определяются лучше, какие — хуже.
PR-AUC
При рассмотрении разных моделей классификации мы упоминали о том, что они подразделяются на метрические и логические методы. Логические методы (дерево решений, k ближайших соседей) выдают конкретную метку класса,без какой-либо дополнительной информации. Метрические методы (логистическая регрессия, перцептрон, SVM) выдают принадлежность данного объекта к разным классам, присутствующим в задаче. При рассмотрении модели логистической регрессии мы говорили, что предсказывается положительный класс, если значение логистической функции больше 0,5.
Но это пороговое значение можно поменять. Что будет, если мы измени его на 0,6? Тогда мы для некоторых объектовы выборки изменим предсказание с положительного класса на отрицательный. То есть без изменения модели можно менять ее предсказания. Это значит, что изменятся и метрики модели, то есть ее эффективность.
Чем больше мы установим порог, тем чаще будем предсказывать отрицательный класс. Это значит, что в среднем, у модели будет меньше ложноположительных предсказаний, но может стать больше ложноотрицательных. Значит, у модели может увеличится precision, то упадет recall. В крайнем случае, если мы возьмем порог равный 1, мы всегда будем предсказывать отрицательный класс. Тогда у модели будет $P = 1, R = 0$. Если же, наоборот, возьмем в качестве порога 0, то мы всегда будем предсказывать отрицательный класс, а значит у модели будет $P = 0, R = 1$, так как она не будет давать ложноположительных прогнозов, но будут встречаться ложноотрицательные.
Это означает, что эффективность моделей метрической классификации зависит не только от того, как модель соотносится с данными, но и от значения порога. Из этого следует, кстати, что было бы не совсем правильно вообще сравнивать метрики двух разных моделей между собой. Ведь значение этих метрик будет зависеть не только от самих моделей, но и от порогов, которые они используют. Может, первая модель будет лучше, если немного изменить ее пороговое значение? Может, одна из метрик второй модели станет выше, если изменить ее порог.
Это все сильно затрудняет анализ метрических моделей классификации. Для сравнения разных моделей необходим способ “убрать” влияние порога, сравнить модели вне зависимости от его значения. И такой способ есть. Достаточно просто взять все возможные значения порога, посчитать метрики в каждом из них и затем усреднить. Для этого служит PR-кривая или кривая “precision-recall”:
Каждая точка на этом графике представляет собой значение precision и recall для конкретного значения порога. Для построения этого графика выбирают все возможные значение порога и отмечают на графике. Давайте рассмотрим простой пример из 10 точек. Истинные значения классов этих точек равны, соответственно, $y = lbrace 0, 0, 0, 0, 0, 1, 1, 1, 1, 1 rbrace$. Модель (сейчас совершенно неважно, какая) выдает следующие предсказания для этих объектов: $h(x) = lbrace 0.1, 0.2, 0.3, 0.45, 0.6, 0.4, 0.55, 0.7, 0.8, 0.9 rbrace$. Заметим, что модель немного ошибается для средних объектов, то есть она не будет достигать стопроцентной точности. Построим таблицу, в которой переберем некоторые значения порога и вычислим, к какому классу будет относиться объект при каждом значении порога:
| y | h(x) | 0,1 | 0,15 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0,1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,3 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,45 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0,4 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0,55 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0,7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0,8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0,9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
Можно сразу заметить, что чем выше порог, тем чаще предсказывается отрицательный класс. В крайних случаях модель всегда предсказывает либо положительный класс (при малых значениях порога), либо отрицательный (при больших).
Далее, для каждого значения порога рассчитаем количество истинно положительных, истинно отрицательных, ложноположительных и ложноотрицательных предсказаний. На основе этих данных легко рассчитать и метрики precision и recall. Запишем это в таблицу:
| y | h(x) | 0,1 | 0,15 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TP | 5 | 5 | 5 | 5 | 5 | 4 | 3 | 3 | 2 | 1 | 0 | |
| TN | 0 | 0 | 1 | 2 | 3 | 4 | 4 | 5 | 5 | 5 | 5 | |
| FP | 5 | 5 | 4 | 3 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | |
| FN | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 2 | 3 | 4 | 5 | |
| P | 0,50 | 0,50 | 0,56 | 0,63 | 0,71 | 0,80 | 0,75 | 1,00 | 1,00 | 1,00 | 1,00 | |
| R | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 0,80 | 0,60 | 0,60 | 0,40 | 0,20 | 0,00 |
При самом низком значении порога модель всегда предсказывает отрицательный класс, метрика recall равна 1, а метрика precision равна доли отрицательного класса в выборке. Причем ниже этого значения precision уже не опускается. Можно заметить, что в целом при повышении порога precision повышается, а recall понижается. В другом крайнем случае, когда порог равен 1, модель всегда предсказывает отрицательный класс, метрика recall равна 0, а precision — 1 (на самом деле эта метрика не определена, но считается равной именно 1, так как ее значение стремится к этому при повышении порога). За счет чего это происходит?
При повышении порога может произойти один из трех случаев. Первый заключается в том, что данное изменение может не влияет ни на одно предсказание. Так происходит, например, при повышении порога с 0,1 до 0,15. Оценка ни одного объекта не попадает в данный диапазон, поэтому ни одно предсказание не меняется. И, соответственно, не изменится ни одна метрика.
Если же повышение порога все-таки затрагивает один или несколько объектов, то изменение предсказания может произойти только с положительного на отрицательное. Допустим, для простоты, что повышение порога затрагивает только один объект. То есть мы изменяем предсказание по одному объекту с 1 на 0. Второй случай заключается в том, что это изменение правильное. То есть объект в действительности принадлежит отрицательному классу. Так происходит, например, при изменении порога с 0,15 до 0,2. В данном случае первый объект из ложноположительного стал истинно отрицательным. Такое изменение не влияет на recall, но повышает precision.
Третий случай заключается в том, что изменение предсказаные было неверным. То есть объект из истинно положительного стал ложноотрицательным. Это происходит, например, при изменении порога с 0,4 до 0,5 — в данном случае шестой объект становится классифицированным ошибочно. Уменьшение количества истинно положительных объектов снижает обе метрики — и precision и recall.
Таким образом можно заключить, что recall при повышении порога может оставаться неизменным или снижаться, а precision может как повышаться, так и понижаться, но в среднем будет повышаться за счет уменьшения доли ложноположительных предсказаний. Если изобразить рассмотренный пример на графике можно получить такую кривую:
PR-кривая не всегда монотонна, обе метрики могут изменяться как однонаправленно, так и разнонаправленно при изменении порогового значения. Но главный смысл этой кривой не в этом. При таком анализе очень просто обобщить эффективность модели вне зависимости от значения порога. Для этого нужно всего лишь найти площадь под графиком этой кривой. Эта метрика называется PR-AUC (area under the curve) или average precision (AP). Чем она выше, тем качественнее модель.
Давайте порассуждаем, ка будет вести себя идеальная модель. Крайние случаи, когда порога равны 0 и 1, значения метрик будут такими же, как и всегда. Но вот при любом другом значении порога модель будет классифицировать все объекты правильно. И обе метрики у нее будут равны 1. Таким образом, PR-кривая выродится в два отрезка, один из которых проходит из точки (0, 1) в точку (1, 1). и площадь под графиком будет равна 1. У самой худшей же модели метрики будут равны 0, так как она всегда будет предсказывать неверно. И площадь тоже будет равна 0.
У случайной модели, как можно догадаться, площадь под графиком будет равна 0,5. Поэтому метрика PR-AUC может использоваться для сравнения разных моделей метрической классификации вне зависимости от значения порога. Также эта метрика показывает соотношение данной модели и случайной. Если PR-AUC модели меньше 0,5, значит она хуже предсказывает класс, чем простое угадывание.
Выводы:
- Кривая precision-recall используется для методов метрической классификации, которые выдают вероятность принадлежности объекта данному классу.
- Дискретная классификации производится при помощи порогового значения.
- Чем больше порог, тем больше объектов модель будет относить к отрицательному классу.
- Повышение порога в среднем увеличивает precision модели, но понижает recall.
- PR-кривая используется чтобы выбрать оптимальное значение порога.
- PR-кривая нужна для того, чтобы сравнивать и оценивать модели вне зависимости от выбранного уровня порога.
- PR-AUC — площадь под PR-кривой, у лучшей модели — 1.0, у тривиальной — 0.5, у худшей — 0.0.
ROC_AUC
Помимо кривой PR есть еще один довольно популярный метод оценки эффективности метрических моделей классификации. Он использует тот же подход, что и PR-кривая, но немного другие координаты. ROC-кривая (receiver operating characteristic) — это график показывающий соотношение доли истинно положительных предсказаний и ложноположительных предсказаний в модели метрической классификации для разных значений порога.
В этой кривой используются два новых термина — доля истинно положительных и доля ложноположительных предсказаний. Доля истинно положительных предсказаний (TPR, true positive rate), как можно догадаться, это отношение количества объектов выборки, правильно распознанных как положительные, ко всем положительным объектам. Другими словами, это всего лишь иное название метрики recall.
А вот доля ложноположительных предсказаний (FPR, false positive rate) считается как отношение количества отрицательных объектов, неправильно распознанных как положительные, в общем количестве отрицательных объектов выборки:
[TPR = frac{TP}{TP + FN} = R \
FRP = frac{FP}{TN + FP} = 1 — S]
Обратите внимание, что FPR — мера ошибки модели. То есть, чем больше — тем хуже. У идеальной модели $FRP=0$, а у наихудшей — $FPR=1$. Для иллюстрации давайте рассчитаем эти метрики для нашего примера, который мы использовали выше (для дополнительной информации еще приведена метрика accuracy для каждого значения порога):
| y | h(x) | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TPR | 1,00 | 1,00 | 1,00 | 1,00 | 0,80 | 0,60 | 0,60 | 0,40 | 0,20 | 0,00 | |
| FPR | 1,00 | 0,80 | 0,60 | 0,40 | 0,20 | 0,20 | 0,00 | 0,00 | 0,00 | 0,00 | |
| A | 0,50 | 0,60 | 0,70 | 0,80 | 0,80 | 0,70 | 0,80 | 0,70 | 0,60 | 0,50 |
Можно заметить, что при увеличении порога обе эти метрики увеличиваются, начиная со значения 1 до нуля. Причем, движения этих двух показателей всегда однонаправленно. Давайте опять же разберемся, почему так. Если увеличение порога приводит к правильному изменению классификации, то есть изменению ложноположительного значения на истинно отрицательное, то это уменьшит FRP, но не затронет TRP. Если же изменение будет неверным, то есть истинно положительное значение поменялось на ложноотрицательное, это однозначно уменьшит TPR, при этом FRP либо уменьшится так же, либо останется неименным.
В итоге, кривая получается монотонной, причем она всегда проходит через центр координат и через точку (1, 1). В нашем примере кривая будет выглядеть так:
Более сложные данные могут выглядеть с большим количеством деталей, но общая форма и монотонность сохраняются:
Также, как и с кривой PR, важное значение имеет площадь под графиком. Эта метрика называется ROC-AUC и является одной из самых популярных метрик качества метрических моделей классификации. Ее главное преимущество перед другими метриками состоит в том, что она позволяет объективно сопоставить уровень качества разных моделей классификации, решающих одну и ту же задачу, но обученных на разных данных. Это приводит к частому использованию ROC-AUC, например, в научной литературе для представления результатов моделирования.
Существует множество споров, какая диагностическая кривая более адекватно измеряет качество классификации — ROC или PR. Считается, что PR-кривая больше ориентирована на задачи, в которых присутствует дисбаланс классов. Это задачи в которых объектов одного класса значительно больше чем другого, классы имеют разное толкование и, как следствие, ошибки первого и второго рода не равнозначны. Зачастую это модели бинарной классификации. ROC же дает более адекватную картину в задачах, где классов примерно поровну в выборке. Но для полного анализа модели все равно рекомендуется использовать оба метода.
В случае с множественной классификацией построение диагностических кривых происходит отдельно по каждому классу. Так же, как и при расчете метрик precision и recall, каждый класс поочередно полагается положительным, а остальные — отрицательными. Каждая такая частная кривая показывает качество распознавания конкретного класса. Поэтому кривые могут выглядеть примерно так:
Источник: sklearn.
На данном графике мы видим PR-кривую модели множественной классификации из 3 классов. Кроме отдельных значений precision и recall в каждой точке рассчитываются и усредненные значения. Так формируется кривая средних значений. Интегральная метрика качества модели классификации считается как площадь под кривой средних значений. Алгоритм построения ROC-кривой полностью аналогичен.
Выводы:
- ROC-кривая показывает качество бинарной классификации при разных значениях порога.
- В отличие от PR-кривой, ROC-кривая монотонна.
- Площадь под графиком ROC-кривой, ROC_AUC — одна из основных метрик качества классификационных моделей.
- ROC_AUC можно использовать для сравнения качества разных моделей, обученных на разных данных.
- ROC чаще используют для сбалансированных и множественных задач, PR — для несбалансированных.
- Кривые для множественной классификации строятся отдельно для каждого класса.
- Метрика AUC считается по кривой средних значений.
Топ k классов
Все метрики, которые мы обсуждали выше оперируют точным совпадением предсказанного класса с истинным. В некоторых особых задачах может быть полезно немного смягчить это условие. Как мы говорили, метрические методы классификации выдают больше информации — степень принадлежности объекта выборки каждому классу. Обычно, мы выбираем из них тот класс, который имеет наибольшую принадлежность. Но можно выбрать не один класс, а несколько. Таким образом можно рассматривать не единственный вариант класса для конкретного объекта, а 3, 5, 10 и так далее.
Другими словами можно говорить о том, находится ли истинный класс объекта среди 3, 5 или 10 классов, которые выбрала для него модель. Количество классов, которые мы рассматриваем, можно брать любым. В данной метрике оно обозначается k. Таким образом, можно построить метрику, которая оценивает долю объектов выборки, для которых истинный класс находится среди k лучших предсказаний модели:
[tka(y, hat{f}) = frac{1}{n} sum_{i=0}^{n-1}
sum_{j=1}^{k} 1(hat{f_{ij}} = y_i)]
где $hat{f_{ij}}$ — это j-й в порядке убывания уверенности модели класс i-го объекта.
Рассмотрим такой пример. Пусть у нас есть задача классификации из 3 классов. Мы оцениваем 4 объекта, которые имеют на самом деле такие классы:
$y = lbrace 0, 1, 2, 2 rbrace$.
1
2
3
>>> import numpy as np
>>> from sklearn.metrics import top_k_accuracy_score
>>> y_true = np.array([0, 1, 2, 2])
Модель предсказывает следующие вероятности для каждого объекта:
1
2
3
4
>>> y_score = np.array([[0.5, 0.2, 0.2],
... [0.4, 0.3, 0.2],
... [0.2, 0.4, 0.3],
... [0.7, 0.2, 0.1]])
То есть для первого объекта она выбирает первый класс, но немного предполагает и второй. А вот, например, последний, четвертый объект она уверенно относит тоже к первому классу. Давайте посчитаем метрику топ-2 для этой модели. Для этого для каждого объекта рассмотрим, какие 2 класса модель называет наиболее вероятными. Для первого — это 0 и 1, для второго — также 0 и 1, причем модель отдает предпочтение 0 классу, хотя на самом деле объект относится к 1 классу. Для третьего — уже 2 и 2 класс, причем класс 1 кажется модели более вероятным, для четвертого — так же наиболее вероятными модели кажутся 0 и 1 класс.
Если бы мы говорили об обычной accuracy, то для такой модели она была бы равна 0,25. Ведь только для первого объекта модель дала правильное предсказание наиболее вероятного класса. Но по метрике топ-2, для целых трех объектов истинный класс находится среди двух наиболее вероятных. Модель полностью ошибается только в последнем случае. Так что эта метрика равна 0,75. Это же подтверждают и автоматические расчеты:
1
2
>>> top_k_accuracy_score(y_true, y_score, k=2)
0.75
Как мы говорили, количество классов k можно взять любым. В частном случае $k=1$ эта метрика превращается в классическую accuracy. Чем больше возьмем k, тем выше будет значение данной метрики, но слабее условие. Так что брать очень большие k нет никакого смысла. В другом крайнем случае, когда k равно количеству классов, метрика будет равна 1 для любой модели.
Эта метрика имеет не очень много практического смысла. Ведь при прикладном применении моделей машинного обучения важен все-таки итоговый результат классификации. И если модель ошиблась, то модель ошиблась. Но эта метрика может пролить свет на внутреннее устройство модели, показать, насколько сильно она ошибается. Ведь одно дело, если модель иногда называет правильный ответ может и не наиболее вероятным, но в топ, скажем, 3. Совсем другое дело, если модель не находит правильный ответ и среди топ-10. Так что эта метрика может использоваться для диагностики моделей классификации и для поиска путей их совершенствования. Еще она бывает полезна, если две модели имеют равные значения метрики accuracy, но нужно понять, какая их них адекватнее имеющимся данным.
Такие проблемы часто возникают в задачах, где классов очень много. Например, в распознавании объектов на изображениях количество объектов может быть несколько тысяч. А в задачах обработки текста количество классов может определяться количеством слов в языке — сотни тысяч и миллионы (если учитывать разные формы слов). Естественно, что эффективность моделей классификации в таких задачах, измеренная обычными способами будет очень низкой. А данная метрика позволяет эффективно сравнивать и оценивать такие модели.
Выводы:
- Эта метрика — обобщение точности для случая, когда модель выдает вероятности отнесения к каждому классу.
- Вычисляется как доля объектов, для которых правильный класс попадает в список k лучших предсказанных классов.
- Чем больше k, тем выше метрика, но бесполезнее результат.
- Эта метрика часто применяется в задачах с большим количеством классов.
- Применимость этой метрики сильно зависит от характера задачи.
Проблема пере- и недообучения
Проблема Bias/Variance
При решении задачи методами машинного обучения всегда встает задача выбора вида модели. Как мы обсуждали в предыдущих главах, существует большое количество классов модели — достаточно вспомнить линейные модели, метод опорных векторов, перцептрон и другие. Каждая их этих моделей, будучи обученной на одном и том же наборе данных может давать разные результаты. Важно понимать, что мы не говорим о степени подстройки модели к данным. Даже если обучение прошло до конца, найдены оптимальные значения параметров, все равно модели могут и, скорее всего, будут различаться.
Причем многие классы моделей представляют собой не одно, а целое множество семейств функций. Например, та же логарифмическая регрессия — это не одна функция, а бесконечное количество — квадратичные, кубические, четвертой степени и так далее. Множество функций или моделей, имеющих единую форму, но различающуюся значениями параметров составляет так называемое параметрическое семейство функций. Так, все возможные линейные функции — это одно параметрическое семейство, все возможные квадратические — другое, а, например, множество всех возможных однослойных перцептронов с 5 нейронами во входном, 3 нейронами в скрытом и одном нейроне в выходном слое — третье семейство.
Таким образом можно говорить, что перед аналитиком стоит задача выбора параметрического семейства модели, которую он будет обучать на имеющихся данных. Причем разные семейства дадут модели разного уровня качества после обучения. К сожалению, очень сложно заранее предугадать, какое семейство моделей после завершения обучения даст наилучшее качество предсказания по данной выборке.
Что является главным фактором выбора этого семейства? Как показывает практика, самое существенное влияние на эффективность оказывает уровень сложности модели. Любое параметрическое семейство моделей имеет определенное количество степеней свободы, которое определяет то, насколько сложное и изменчивое поведение может демонстрировать получившаяся функция.
Сложность модели можно определять разными способами, но в контексте нашего рассуждения сложность однозначно ассоциируется с количеством параметров в модели. Чем больше параметров, тем больше у модели степеней свободы, возможности изменять свое поведение при разных значениях входных признаков. Конечно, это не означает полной эквивалентности разных типов моделей с одинаковым количеством параметров. Например, никто не говорит, что модель, скажем, регрессии по методу опорных векторов эквивалентна модели нейронной сети с тем же самым количеством весов. Главное, что модели со сходным уровнем сложности демонстрируют сходное поведение по отношению к конкретному набору данных.
Влияние уровня сложности на поведение модели относительно данных наиболее наглядно можно проследить на примере модели полиномиальной модели. Степень полинома — это очень показательная характеристика уровня сложности модели. Давайте рассмотрим три модели регрессии — линейную (которую можно рассматривать как полином первой степени), полином второй и восьмой степени. Мы обучили эти модели на одном и том же датасете и вот что получилось:
Следует отдельно заметить, что в каждом из представленных случаев модель обучалась до конца, то есть до схождения метода численной оптимизации параметров. То есть для каждой модели на графике представлены оптимальные значения параметров. Гладя на эти три графика и то, как эти линии ложатся в имеющиеся точки, можно заметить некоторое противоречие. Естественно предположить, что модель, изображенная на втором графике показывает наилучшее описание точек данных. Но по любой метрике качества третья модель будет показывать более высокий результат.
Человек, глядя на график третьей модели, сразу сделает вывод, что она “слишком” хорошо подстроилась под имеющиеся данные. Сравните это поведение с первым графиком, который демонстрирует самую низкую эффективность на имеющихся данных. Можно проследить, как именно сложность модели влияет на ее применимость. Если модель слишком простая, то она может не выявить имеющиеся сложные зависимости между признаками и целевой переменной. Говорят, что у простых моделей низкая вариативность (variance). Слишком же сложная модель имеет слишком высокую вариативность, что тоже не очень хорошо.
Те же самые рассуждения можно применить и к моделям классификации. Можно взглянуть на форму границы принятия решения для трех моделей разного уровня сложности, обученных на одних и тех же данных:
В данном случае мы видим ту же картину — слишком простая модель не может распознать сложную форму зависимости между факторами и целевой переменной. Такая ситуация называется недообучение. Обратите внимание, что недообучение не говорит о том, что модель не обучилась не до конца. Просто недостаток сложности, вариативности модели не дает ни одной возможной функции их этого параметрического семейства хорошо описывать данные.
Слишком сложные модели избыточно подстраиваются под малейшие выбросы в данных. Это увеличивает значение метрик эффективности, но снижает пригодность модели на практике, так как очевидно, что модель будет делать большие ошибки на новых данных из той же выборки. Такая ситуация называется переобучением. Переобучение — это очень коварная проблема моделей машинного обучения, ведь на “бумаге” все метрики показывают отличный результат.
Конечно, в общем случае не получится так наглядно увидеть то, как модель подстраивается под данные. Ведь в случае, когда данные имеют большую размерность, строить графики в проекции не даст представления об общей картине. Поэтому ситуацию пере- и недообучения довольно сложно обнаружить. Для этого нужно проводить отдельную диагностику.
Это происходит потому, что в практически любой выборке данных конкретное положение точек, их совместное распределение определяется как существенной зависимостью между признаками и целевой переменной, так и случайными отклонениями. Эти случайные отклонения, выбросы, аномалии не позволяют сделать однозначный вывод, что модель, которая лучше описывает имеющиеся данные, является лучшей в глобальном смысле.
Выводы:
- Прежде чем обучать модель, нужно выбрать ее вид (параметрическое семейство функций).
- Разные модели при своих оптимальных параметрах будут давать разный результат.
- Чем сложнее и вариативнее модель, тем больше у нее параметров.
- Простые модели быстрые, но им недостает вариативности, изменчивости, у них высокое смещение (bias).
- Сложные модели могут описывать больше зависимостей, но вычислительно более трудоемкие и имеют большую дисперсию (variance).
- Слишком вариативные (сложные) модели алгоритм может подстраиваться под случайный шум в данных — переобучение.
- Слишком смещенные (простые) модели алгоритм может пропустить связь признака и целевой переменной — недообучение.
- Не всегда модель, которая лучше подстраивается под данные (имеет более высокие метрики эффективности) лучше.
Обобщающая способность модели, тестовый набор
Как было показано выше, не всякая модель, которая показывает высокую эффективность на тех данных, на которых она обучалась, полезна на практике. Нужно всегда помнить, что модели машинного обучения строят не для того, чтобы точно описывать объекты из обучающего набора. На то он и обучающий набор, что мы уже знаем правильные ответы. Цель моделирования — создать модель, которая на примере этих данных формализует некоторые внутренние зависимости в данных для того, чтобы адекватно описывать новые объекты, которые модель не учитывала при обучении.
Полезность модели машинного обучения определяется именно способность описывать новые данные. Это называется обобщающей способностью модели. И как мы показали в предыдущей главе, эффективность модели на тех данных, на которых она обучается, не дает адекватного понимания этой самой обобщающей способности модели. Вместе с тем, обобщающая способность — это главный показатель качества модели машинного обучения и у нас должен быть способ ее измерять.
Конечно, мы не можем измерить эффективность модели на тех данных, которых у нас нет. Поэтому для того, чтобы иметь адекватное представление об уровне качества модели применяется следующий трюк: до начала обучения весь имеющийся датасет разбивают на две части. Первая часть носит название обучающая выборка (training set) и используется для подбора оптимальных параметров модели, то есть для ее обучения. Вторая часть — тестовый набор (test set) — используется только для оценки эффективности модели.
Такая эффективность, измеренная на “новых” данных — объектах, которые модель не видела при своем обучении — дает более объективную оценку обобщающей силы модели, то есть эффективности, которую модель будет показывать на неизвестных данных. В машинном обучении часто действует такое правило — никогда не оценивать эффективность модели на тех данных, на которых она обучалась. Не то, чтобы этого нельзя делать категорически (и в следующих главах мы это часто будем применять), просто нужно осознавать, что эффективность модели на обучающей выборки всегда будет завышенной, ведь модель подстроилась именно к этим данным, включая все их случайные колебания.
Надо помнить, что все рассуждения и выводы в этой и последующих главах носят чисто вероятностный характер. Так что в конкретном случае, тестовая эффективность вполне может оказаться даже выше, чем эффективность на обучающей выборке. Когда мы говорим о наборах данных и случайных процессах, все возможно. Но смысл в том, что распределение оценки эффективности модели, измеренное на обучающих данных имеет значимо более высокое математическое ожидание, чем “истинная” эффективность этой модели.
Для практического применения этого приема надо ответить на два вопроса: как делить выборку и сколько данных оставлять на тестовый датасет. Что касается способа деления, здесь чуть проще — практически всегда делят случайным образом. Случайное разбиение выгодно тем, что у каждого объекта датасета равная вероятность оказаться в обучающей или в тестовой выборке. Причем, эта вероятность независима для всех объектов выборки. Это делает все случайные ошибки выборки нормально распределенными, то есть их математическое ожидание равно нулю. Об этом мы еще поговорим в следующей главе.
Но этот способ не работает в случае со специальными наборами данных. Например с временными рядами. Ведь при разбиении выборки важно, чтобы сами объекты в тестовой выборке были независимы от объектов обучающей. В случае, если мы анализируем какое-то неупорядоченное множество объектов, это почти всегда выполняется. Но для временных рядов это не так. Объекты более позднего времени могут зависеть от предыдущих объектов. Так цена актива за текущий период однозначно зависит от цены актива за предыдущий. Поэтому нельзя допустить, чтобы в обучающей выборке оказались объекты более ранние, чем в обучающей. Поэтому такие временные ряды делят строго хронологически — в тестовую выборку попадает определенное количество последних по времени объектов. Но анализ временных рядов сам по себе довольно специфичен как статистическая дисциплина, и как раздел машинного обучения.
Что касается пропорции деления, то, опять же, как правило, выборку разделяют в соотношении 80/20. То есть если в исходном датасете, например, 1000 объектов, то случайно выбранные 800 из них образуют обучающую выборку, а оставшиеся 200 — тестовую. Но это соотношение “по умолчанию” в общем-то ничем не обосновано. Его можно изменять в любую сторону исходя из обстоятельств. Но для этого надо понимать, как вообще формируется эта пропорция и что на нее влияет.
Что будет, если на тестовую выборку оставить слишком много данных, скажем, 50% всего датасета? Очевидно, у нас останется мало данных для обучения. То есть модель будет обучена на всего лишь небольшой части объектов, которых может не хватить для того, чтобы модель “распознала” зависимости в данных. Вообще, чем больше данных для обучения, тем в целом лучше, так как на маленьком объеме большую роль играют те самые случайные колебания. Поэтому модель может переобучаться. И чем меньше данных, тем переобученнее и “случайнее” будет получившаяся модель. И это не проблема модели, это именно проблема нехватки данных. А чем больше точек данных, тем больше все эти случайные колебания будут усредняться и это сильно повысит качество обученной модели.
А что будет, если наоборот, слишком мало данных оставить на тестовую выборку? Скажем, всего 1% от имеющихся данных. Мы же сказали, что чем больше данных для обучения, тем лучше. Значит, но обучающую выборку надо оставить как можно большую часть датасета? Не совсем так. Да, обучение модели пройдет более полно. Но вот оценка ее эффективности будет не такой надежной. Ведь такие же случайные колебания будут присутствовать и в тестовой выборке. И если мы оценим эффективность модели на слишком маленьком количестве точек, случайные колебания этой оценки будут слишком большими. Другими словами мы получим оценку, в которой будет сильно не уверены. Истинная оценка эффективности может быть как сильно больше, так и сильно меньше получившегося уровня. То есть даже если модель обучается хорошо, мы этого никогда не узнаем с точностью.
То есть пропорция деления выборки на обучающуюся и тестовую является следствием компромисса между полнотой обучения и надежность оценки эффективности. Соотношение 80/20 является хорошим балансом — не сильно много, но и не сильно мало. Но это оптимально для среднего размера датасетов. Если у вас очень мало данных, то его можно немного увеличить в пользу тестовой выборки. Если же данных слишком много — то в пользу обучающей. Кроме того, при использовании кросс-валидации размер тестовой выборки тоже можно уменьшить.Но на практике очень редько используются соотношения больше, чем 70/30 или меньше чем 90/10 — такое значения уже считаются экстремальными.
Выводы:
- Цель разработки моделей машинного обучения — не описывать обучающий набор, а на его примере описывать другие объекты реального мира.
- Главное качество модели — описывать объекты, которых она не видела при обучении — обобщающая способность.
- Для того, чтобы оценить обобщающую способность модели нужно вычислить метрики эффективности на новых данных.
- Для этого исходный датасет разбивают на обучающую и тестовую выборки. Делить можно в любой пропорции, обычно 80-20.
- Чаще всего выборку делят случайным образом, но временные ряды — только в хронологической последовательности.
- Обучающая выборки используется для подбора параметров модели (обучения), а тестовая — для оценки ее эффективности.
- Никогда не оценивайте эффективность модели на тех же данных, на которых она училась — оценка получится слишком оптимистичная.
Кросс-валидация
Как мы говорили ранее, маленькая тестовая выборка проблемна тем, что большое влияние на результат оценки эффективности модели имеют случайные отклонения. Это становится меньше заметно при росте объема выборки, но полностью проблема не исчезает. Эта проблема состоит в том, что каждый раз разбивая датасет на две выборки, мы вносим случайные ошибки выборки. Эта случайная ошибка обоснована тем, что две получившиеся подвыборки наверняка будут демонстрировать немного разное распределение. Даже если взять простой пример. Возьмем группу людей и разделим ее случайным образом на две половины. В каждой половине посчитаем какую-нибудь статистику, например, средний рост. Будут ли в двух группах выборочные средние точно совпадать? Наверняка нет. Обосновано ли чем-то существенным такое различие? Тоже нет, это случайные отклонения, которые возникают при выборке объектов из какого-то множества.
Поэтому разбиение выборки на тестовую и обучающую вносит такие случайные колебания, из-за которых мы не можем быть полностью уверены в получившейся оценке эффективности модели. Допустим, мы получили тестовую эффективность 95% (непример, измеренную по метрике accuracy, но вообще это не важно). Можем ли мы быть уверены, что это абсолютно точный уровень эффективности? Нет, ведь как любая выборочная оценка, то есть статистика, рассчитанная на определенной выборке метрика эффективности представляет собой случайную величину с некоторым распределением. А у этого распределения есть математическое ожидание и дисперсия. Как мы говорили в предыдущей главе, случайное разделение выборки на тестовую и обучающую приводит к тому, что распределение этой величины имеет математическое ожидание, совпадающее с истинным уровнем эффективности модели. Но это именно математическое ожидание. И у этой случайной величины есть какая-то ненулевая дисперсия. Это значит, что при каждом измерении, выборочная оценка может отклоняться от матожидания, то есть быть произвольно больше или меньше.
Есть ли способ уменьшить эту дисперсию, то есть неопределенность при измерении эффективности модели? Да, очень простой. Нужно всего лишь повторить измерение несколько раз, а затем усреднить полученные значения. Так как математическое ожидание случайных отклонений всегда предполагается равным нулю, чем больше независимых оценок эффективности мы получим, тем ближе среднее этих оценок будет к математическом ожиданию распределения, то есть к истинному значению эффективности.
Проблема в том, что эти измерения должны быть независимы, то есть производиться на разных данных. Но кратное увеличение тестовой выборки имеет существенные недостатки — соответствующее уменьшение обучающей выборки. Поэтому так никогда не делают. Гораздо лучше повторить случайное разбиение датасета на обучающую и тестовую выборки еще раз и измерить метрику эффективности на другой тестовой выборки из того же изначального датасета.
К сожалению, это означает, что и обучающая выборка будет другая. То есть нам необходимо будет повторить обучение. Но зато после обучения мы получим новую, независимую оценку эффективности модели. Если мы повторим этот процесс несколько раз, мы сможем усреднить эти значения и получить гораздо более точную оценку эффективности модели.
Имейте в виду, что все, что мы говорим в этой части применимо к любой метрике эффективности или метрике ошибки модели. Чаще всего, на практике измеряют метрики accuracy для моделей классификации и $R^2$ для регрессии. Но вы можете использовать эти методики для оценки любых метрик качества моделей машинного обучения. Напомним, что они должны выбираться исходя из задачи.
Конечно, можно реализовать это случайное разбиение руками и повторить процедуру оценивания несколько раз, но на практике используют готовую схему, которая называется кросс-валидация или перекрестная проверка. Она заключается в том, что датасет заранее делят на несколько равных частей случайным образом. Затем каждая из этих частей выступает как тестовый набор, а остальные вместе взятые — как обучающий:
Источник: Towards Data Science.
На схеме части датасета изображены для наглядности непрерывными блоками, но на самом деле это именно случайные разбиения. Так что они буду в датасете “вперемешку”. Количество блоков, на которые делится выборка задает количество проходов или оценок. Это количество называется k. Обычно его берут равным 5 или трем. Это называется, 5-fold cross-validation. То есть на первом проходе блоки 1,2,3 и 4 в совокупность составляют обучающую выборку. Модель обучается на них, а затем ее эффективность измеряется на блоке 5. Во втором проходе та же модель заново обучается на данных их блоков 1,2,3 и 5, и ее эффективность измеряется на блоке 4. И таким образом мы получаем 5 независимых оценок эффективности модели. Они могут различаться из-за тех самых случайных оценок выборки. Но если посчитать их среднее, оно будет значительно ближе к истинному значению эффективности. Поэтому что статистика.
Количество проходов k еще определяет то, сколько раз будет повторяться обучение модели. Чем больше выбрать k, тем более надежными будут оценки, но вся процедура займет больше машинного времени. Это особенно актуально для моделей, которые сами по себе обучаются долго — например, глубокие нейронные сети. Надо помнить, что использование кросс-валидации сильно замедляет процесс обучения. Если же выбрать k слишком маленьким, то не будет главного эффекта кросс-валидации — усреднения индивидуальных оценок эффективности. Кроме того, чем больше k, тем меньшая часть выборки будет отводиться на тестовый набор. Поэтому k не стоит брать больше, скажем, 10, даже если у вас достаточно вычислительных мощностей.
Кросс-валидация никак не влияет на эффективность модели. Многие думают, что валидированные модели получаются более эффективными. Это не так, просто использование перекрестной проверки позволяет более точно и надежно измерить уже имеющуюся эффективность данной модели. И уж тем более кросс-валидация не может ускорить процесс обучения, совсем наоборот. Но несмотря на это, использование кросс-валидации с k равным 5 или, в крайнем случае, 3, совершенно обязательно в любом серьезном проекте по машинному обучению, ведь оценки, полученные без использования этой методики совершенно ненадежны.
В библиотеке sklearn, естественно, кросс-валидация реализована в виде готовых функций. Поэтому ее применение очень просто. В примере ниже используется кросс-валидация с количеством проходов по умолчанию для получения робастных оценок заранее выбранных метрик (precision и recall):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import recall_score
>>> scoring = ['precision_macro','recall_macro']
>>> clf =
svm.SVC(kernel='linear', C=1, random_state=0)
>>> scores =
cross_validate(clf, X, y, scoring=scoring)
>>> sorted(scores.keys())
['fit_time', 'score_time',
'test_precision_macro', 'test_recall_macro']
>>> scores['test_recall_macro']
array([0.96..., 1. ..., 0.96..., 0.96..., 1. ])
Такой код просто оценивает значение метрик. Но обратите внимание, что он возвращает не просто одно значение метрики, но целый вектор. Это именно те индивидуальные оценки. Из них очень легко получить средние и выборочную дисперсию. Эта выборочная дисперсия как раз и показывает степень уверенности в данной оценке — чем она ниже, тем уверенность больше, как доверенный интервал в статистике. Кроме такого явного использования кросс-валидации для оценки метрик, она зачастую встроена в большое количество функций, которые используют ее неявно. О некоторых таких функциях, осуществляющих оптимизацию гиперпараметров модели, пойдет речь чуть позже.
Выводы:
- Разбиение выборки на обучающую и тестовую может внести случайные ошибки.
- Нужно повторить разбиение несколько раз, посчитать метрики и усреднить.
- Кросс-валидация разбивает выборку на $k$ блоков, каждый из которых используется по очереди как тестовый.
- Сколько задать $k$, столько и будет проходов. Обычно берут 3 или 5.
- Чем больше $k$ тем надежнее оценка, но дольше ее получение, так как модель каждый раз заново обучается.
- Использование кросс-валидации обязательно для получения робастных оценок.
- В библиотеке sklearn кросс-валидация (CV) встроена во многие функции.
Кривые обучения
Как мы говорили раньше, не следует ориентироваться на эффективность модели, измеренную на обучающей выборке, ведь она получается слишком оптимистичной. Но эта обучающая эффективность все равно может дать интересную информацию о работе модели. А именно с ее помощью можно оценить, переобучается модель или недообучается. В этой главе мы расскажем об одном из самых наглядных способов диагностики моделей машинного обучения — кривых обучения.
Построение кривых обучения может быть проведено после разделения датасета на обучающую и тестовую выборки. Происходит это следующим образом. Тестовый набор фиксируется и каждый раз используется один и тот же. Из обучающего набора же сначала берут малую часть, скажем 10% от общего количества точек в нем. Обучают модель на этой малой части, а затем измеряют ее эффективность на этой части и на постоянной тестовой выборке. Первая оценка называется обучающая эффективность (training score), а вторая — тестовая эффективность (test score). Затем повторяют процесс с чуть большей частью обучающей выборки, например, 20%, затем еще с большей и так, пока мы не дойдем до полной обучающей выборки.
На каждом этапе мы измеряем обучающую эффективность (измеренную именно на той части данных, на которых модель училась, не на полной обучающей выборке) и тестовую эффективность. Таким образом мы получаем зависимость эффективности модели от размера обучающей выборки. Эти данные можно построить на графике. Это график и называется кривой обучения (learning curve). Такой график может выглядеть, например, так:
В данном случае, на графике мы видим всего пять точек на каждой кривой. Верхняя кривая показывает обучающую эффективность, нижняя — тестовую. Значит, мы использовали всего пять делений обучающей выборки на подвыборки разного размера. Это размер как раз и отложен на горизонтальной оси. Сколько таких разбиений брать? Если взять слишком мало, то не будет понятна форма графика, а именно она нам важна для диагностики. Если же взять слишком много — то построение кривой обучения займет много времени, так как каждая точка на графике — это заново обученная модель.
Давайте объясним форму этого графика. Слева, когда обучающая выборка мала, обучающая эффективность довольно высока. Это вполне понятно, ведь чем меньше данных, тем проще модели к ним подстроиться. Помните, что через любые две точки можно провести линию (то есть линейную регрессию)? Это, конечно, крайний случай, но в общем, чем меньше обучающая выборка, тем большую эффективность одной и той же модели (параметрического семейства функций) можно на ней ожидать. А вот тестовая эффективность довольно маленькая. Это тоже понятно. Ведь на маленькой выборке модель не смогла обнаружить зависимости в данных так, чтобы эффективно предсказывать значение целевой переменной в новых данных. То есть она подстроилась под конкретные точки без какой-либо обобщающей способности.
Сперва отметим, что обычно кривые обучения демонстрируют некоторые общие тенденции. Например, при малых объемах обучающей выборки, обучающая эффективность модели может быть очень большой. Ведь чем меньше данных, тем проще подобрать параметры любой, пусть даже простой модели, так, чтобы эта модель ошибалась меньше. В самом предельном случае, вспомните, что через любые две точки можно провести прямую. Это значит, что линейная регрессия, обученная на двух точках, всегда будет давать нулевую ошибку или полную, 100%-ю эффективность. То же можно сказать и про квадратичную функцию, обученную на трех точках. Но и в целом, чем меньше данных, тем меньше можно ожидать суммарную ошибку любого рассматриваемого класса моделей на этих данных.
Тестовая же эффективность модели, обученной на малом объеме выборки, скорее всего будет очень невысокой. Это тоже естественно. Ведь модель видела всего малую часть примеров и не может подстроиться под какие-то глобальные зависимости в данных. Поэтому в левой части кривых обучения почти всегда будет большой зазор.
При повышении объема обучающей выборки обучающая же эффективность будет падать. Это связано в тем, что чем больше данных, тем больше пространства для ошибки для конкретной модели. Поэтому чем больше точек описывает модель, тем хуже она это делает в среднем. Это неизбежно и не страшно. Важно то, что тестовая эффективность наоборот, растет. Это происходит потому, что чем больше данных, тем больше вероятность того, что модель подстроится под существенные связи между признаками и целевой переменной, и таким образом, повысит обобщающую способность, свою предсказательную силу.
В итоге, кривая обучения показывает, как изменяется эффективность модели по сравнению к конкретному набору данных. В частности, именно с помощью кривых обучения можно предположить пере- и недообучение модели, что является главной целью диагностики моделей машинного обучения. Например, взглянув на график кривой обучения, приведенный выше, можно ответить на вопрос, хватает ли модели данных для обучения. Для этого можно спросить, улучшится ли тестовая эффективность модели, если добавить в датасет больше точек. Для этого можно мысленно продолжить кривую обучения вправо.
При построении кривых обучения обращайте внимание на деления вертикальной оси. Если вы строите графики с использованием библиотечных инструментов, то они автоматически масштабируются по осям. Имейте в виду, что одна и та же кривая обучения может выглядеть при разном масштабе совершенно по-разному. А навык сопоставления разных кривых очень важен при диагностике моделей. Лучше всего вручную задавать масштаб вертикальной оси и использовать один и тот же для всех графиков в одной задаче.
Обратите внимание, что на графике помимо самих кривых обучения присутствуют еще какие-то полосы. Что они значат? Дело в том, что при построении кривых обучения очень часто применяется кросс-валидация, о которой мы говорили в предыдущей главе. Ведь разбиение выборки на тестовую и обучающую вносит случайные ошибки. Поэтому для построения на кривых обучения более надежных оценок всех измеряемых оценок эффективности процесс повторяют несколько раз и усредняют полученные оценки. Каждая точка на графике — это не просто оценка эффективности, это среднее из всех кросс-валидированных оценок. Именно поэтому, кстати, в легенде нижняя линяя называется не test score, а cross-validation score. А ширина полосы вокруг точки определяется величиной дисперсии этих оценок. Чем шире полоса, тем больше разброс оценки на разных проходах кросс-валидации и тем меньше мы уверены в значении этой оценки. При построении кривых обучения эта неопределенность почти всегда выше при малых объемах обучающей выборки (слева на графике) и меньше — справа.
Выводы:
- Кривая обучения — это зависимость эффективности модели от размера обучающей выборки.
- Для построения кривых обучения модель обучают много раз, каждый раз с другим размером обучающей выборки (от одного элемента до всех, что есть).
- При малых объемах обучающая эффективность будет очень большой, а тестовая — очень маленькой.
- При увеличении объема обучающей выборки они будут сходиться, но обычно тестовая эффективность всегда ниже обучающей.
- Кривые обучения позволяют увидеть, как быстро модель учится, хватает ли ей данных, а также обнаруживать пере- и недообучение.
- Кривые обучения часто используют кросс-валидацию.
Обнаружение пере- и недообучения
Как мы говорили, построение кривых обучения — это исключительно диагностическая процедура. Именно они позволяют нам предполагать, к чему более склонна модель, обученная на конкретном наборе данных — к переобучению или к недообучению. Это важно, так как подходы у повышению эффективности в этих двух случаях будут совершенно противоположными. Давайте предположим, как будут вести себя на кривых обучения переобученные и недообученные модели.
Что будет, если модель слишком проста для имеющихся данных? При увеличении количества объектов в обучающей выборке, эффективность, измеренная на ней же будет вначале заметно падать по причинам, описанным выше. Но постепенно она будет выходить на плато и больше не будет уменьшаться. Это связано с тем, что начиная с какого-то объема выборки в ней будут превалировать нелинейные зависимости, слишком сложные для данной модели. С ростом объема обучающей выборки неизбежно растет тестовая эффективность, но так как модель слишком проста и не может ухватить этих сложных зависимостей в данных, то ее тестовая эффективность не будет повышаться сильно. Причем при достаточном объеме обучающей выборки тестовая и обучающая эффективности будут достаточно близкими. Другими словами, простые модели одинаково работают как на старых, так и на новых данных, но одинаково плохо.
А что будет происходить со слишком сложной моделью для существующих данных? Ее показатели в левой части графика будут аналогичны — высокая обучающая и низкая тестовая эффективности. Причины все те же. Но вот с ростом объема обучающей выборки, разрыв между этими двумя показателями не будет сокращаться так сильно. Модель, обученная на полном датасете покажет высокую эффективность на обучающей выборке, но гораздо более низкую — на тестовой. Это же практически определение переобучения — низкая ошибка, но отсутствие обобщающей способности. Это происходит, как мы уже обсуждали, за счет того, что слишком сложная модель имеет достаточный запас вариативности, чтобы подстроиться под случайные отклонения в данных.
Таким образом, недообученные и переобученные модели демонстрируют совершенно разное поведение на кривых обучения. А значит, недообучение и переобучения можно выявить, проанализировав поведение модели на графике. Типичное переобучение характеризуется большим разрывом между тестовой и обучающей эффективность. Признак типичного недообучения — низкая эффективность как на тестовой, так и на обучающей выборке. Но на практике, конечно, диагностика моделей машинного обучения не такая простая.
На данном графике представлены абстрактные картины, наиболее характерные для недообучения, переобучения, и ситуации, когда сложность модели оптимальна — мы назовем ее качественное обучение. Именно анализируя схожесть кривой обучения исследуемой модели с этими “идеальными” случаями, можно сделать обоснованный вывод о наличии недо- или переобучения модели.
Как вы могли заметить, мы нигде не говорим о четких критериях. Недо- и переобученность моделей — это вообще относительные понятия. И кривые обучения измеряют их только косвенно. Поэтому диагностика не сводится к оценке какой-либо метрики или статистики. Нам нужно оценить общую форму графика кривых обучения, что не является точной наукой. Возникает множество вопросов. Например, мы говорили, что большой зазор между тестовой и обучающей эффективностью — это признак переобучения. Но какой зазор считать большим? Это вопрос интерпретации. Точно так же, что считать низким уровнем эффективности? 50%? Может, 75%? Вообще это очень зависит от самой задачи. В некоторых задачах 80% accuracy — это выдающийся результат, а в других — даже 99% считается недостаточной точностью.
Поэтому рассматривая один график кривой обучения очень сложно понять, особенно без опыта анализа моделей машинного обучения, на что мы смотрим — на слишком простую недообученную модель, или на слишком сложную — переобученную. Вообще, строго говоря, большой зазор между эффективностями модели указывает на присутствующую в модели вариативность (variance), а низкий,не 100%-й уровень обучающей эффективности — на наличие в модели смещения (bias). А любые модели в той или иной степени обладают этими характеристиками. Вопрос в их соотношении друг к другу и к конкретному набору данных.
Чтобы облегчить задачу диагностики модели очень часто эффективность данной модели рассматривают не абстрактно, а сравнивают с аналогами. Практически всегда выбор моделей осуществляется от простого к сложному — сначала строят очень простые модели. Их тестовая эффективность может задать некоторых базовый уровень, планку, по сравнению к которой уже можно готовить об улучшении эффективности у данной, более сложной модели, насколько это улучшение существенно и так далее. Кроме того, строя кривые обучения нескольких моделей можно получить сравнительное представление о том, как эти модели соотносятся между собой, какие из них более недообученные, какие — наоборот.
Ситуация еще очень осложняется тем, что на практике вы никогда не получите таких красивых и однозначных кривых обучения, как в учебнике. Положение точек на кривых обучения зависит, в том числе и от тех самых случайных отклонений в данных, которые так портят нам жизнь. Поэтому в реальности графики могут произвольно искривляться, быть немонотонными. Тестовая эффективность вообще может быть выше обучающей. Что это начит для диагностики? Да в общем-то, ничего, это лишь свидетельствует об особом характере имеющихся данных. И, естественно, чем меньше данных, тем более явно проявляются эти случайности и тем менее показательными будут графики.
Достаточно сильно от этих случайных колебаний помогает применение кросс-валидации. Так как усреднение случайности — это и есть цель перекрестной проверки, она может быть полезна и для “сглаживания” кривых обучения. Еще надо помнить, что во многих библиотеках по умолчанию кривые обучения строятся на основе всего нескольких точек, то есть всего пяти-десяти вариантов размера обучающей выборки. Если такой график не дает достаточной информации, можно попробовать построить кривую по большему количеству точек. Но при этом и случайные колебания тоже могут проявиться сильнее.
Вообще, все факторы, которые улучшают “читаемость” кривых обучения, одновременно сильно замедляют их построение — кросс-валидация, использование большей выборки, построение большего количества точек. Помните, что это приводит к кратному увеличению количества циклов обучения модели.
Как мы говорили, поведение модели в целом не зависит от выбранной метрики, которую вы используете для построения кривых обучения. Поэтому зачастую используют не метрики эффективности, а метрики ошибок. Поэтому графики кривых обучения выглядят “перевернутыми” — тестовая ошибка больше, чем обучающая и так далее. Следует помнить, что все сказанное выше остается справедливым в этом случае, только следует помнить, где у модели высокая эффективность и малая ошибка.
На этом графике вы видите тоже идеальные случаи, но выраженные в терминах величины ошибки, а не эффективности. Можно проследить те же тенденции, но как бы “отраженные” по вертикальной оси.
Как мы говорили, реальные наборы данных, имеющие случайные колебания, ненадежные зависимости, случайные ошибки выборки могут существенно искажать кривые обучения. Рассмотри пример, приближенный к реальности. Возьмем датасет, содержащий рукописные цифры и обучим на нем классификатор по методу опорных векторов с гауссовым ядром. Для примера возьмем значение параметра “гамма”, который задает масштабирование функции расстояния в ядре, равным 0,008. Построив кривые обучения для этой модели мы получаем следующий график:
Данный график, несмотря на свою сложную форму достаточно легко интерпретируется. Мы видим, что обучающая эффективность равна 1 при любых объемах обучающей выборки. То есть модель разделяет классы полностью идеально. Но вот тестовая эффективность всегда остается гораздо ниже. И хотя она растет при увеличении объема обучающей выборки, все равно, даже при использовании полного набора данных, остается большой разрыв между тестовой и обучающей эффективностями модели. Налицо явное и типичное переобучение.
Теперь давайте уменьшим параметр “гамма” в четыре раза. В методе опорных векторов это может ограничить вариативность модели. Получаем следующий график кривых обучения:
Видно, что общее поведение модели значительно улучшилось. Обратите внимание на масштаб вертикальной оси. На первом графике мы говорили о разнице между тестовой и обучающей эффективностью в примерно 0,3. На этом же графике разница сократилась до примерно 0,025 — больше, чем в 10 раз. Это говорит о том, что модель очень сильно увеличила свою обобщающую способность. Давайте теперь уменьшим параметр еще в сто раз и посмотрим на кривую обучения:
Поведение модели явно не улучшилось. Хотя, итоговая эффективность тоже получается достаточно высокой (около 0,9), она все равно значительно меньше, чем в предыдущем случае. Другими словами, дальнейшее сокращение “гаммы” не пошло модели на пользу. Низкая тестовая эффективность и небольшая разница между тестовой и обучающей эффективностью — типичные признаки недообучения.
Обратите внимание, что интерпретация графика кривых обучения и, соответственно, диагностика модели, приобретает гораздо больше смысла к контексте сравнения нескольких моделей. Третья модель дает относительно неплохой результат с тестовой эффективностью в 0,9. Эту модель вполне можно признать валидной и качественно обученной, если бы мы не знали, что мы можем достичь точности в 0,975 (вторая модель).
Для сравнения рассмотрим результаты анализа еще одной модели на тех же самых данных — наивного байесовского классификатора с гауссовым распределением:
Хотя график сильно отличается от любого из трех предыдущих, самое главное, на что следует обратить внимание — низкое значение обучающей эффективности на полном наборе данных. Это показывает, что даже если мы продолжим добавлять данные в обучающую выборку, максимум, на который мы можем рассчитывать — это что тестовая эффективность приблизится к обучающей, которая все равно недостаточная (в данном примере меньше 0,9). Это свидетельствует о недообученности модели.
Как мы говорили, недообучение и переобучение — это условные понятия, которые называют распространенные ситуации при использовании моделей машинного обучения. Недообучение — это когда у модели низкая вариация и высокое смещение. Переобучение — это наоборот, когда низкое смещение и высокая вариация. На самом деле эти свойства в моделях присутствуют всегда. Более тщательный анализ может сделать вывод, что последняя модель имеет как высокую вариацию (что выражается в сильной разнице между эффективностями), так и высокое смещение (об этом говорит низкое значение обучающей эффективности).
Выводы:
- При недообучении тестовая и обучающая эффективности будут достаточно близкими, но недостаточными.
- При переобучении тестовая и обучающая эффективности будут сильно различаться — тестовая будет значительно ниже.
- Пере- и недообучение — это относительные понятия.
- Более простые модели склонны к недообучению, более сложные — к переобучению.
- Диагностика пере- и недообучения очень важна, так как для повышения эффективности предпринимаются противоположные меры.
- Для построения можно использовать функцию ошибки, метрику эффективности или метрику ошибки, важна только динамика этих показателей.
- Диагностика моделей машинного обучения — это не точная наука, здесь нужно принимать в расчет и задачу, и выбор признаков и многие другие факторы.
Методы повышения эффективности моделей
Регуляризация
Как мы говорили, диагностика моделей нужна для поиска путей повышения ее эффективности. И мы выяснили, что пере- и недообучение моделей напрямую связаны с уровнем сложности моделей. Можно рассмотреть гипотетический график, на котором показан уровень ошибок моделей на конкретном наборе данных в зависимости от уровня сложности этой модели. Пока мы не сталкивались с тем, как можно плавно менять уровень сложности модели в рамках одного параметрического класса. Но представим, что речь идет о полиномиальной модели, а по горизонтали отложена степень этого полинома.
Если модель слишком проста, то уровень тестовых и обучающих ошибок будет высок и достаточно близок друг к другу. Мы говорили об этом (правда другими словами, в терминах эффективности) в предыдущей главе. По мере увеличения сложности разрыв между этими уровнями ошибок будет в среднем увеличиваться. Это происходит за счет более глубокой подстройки модели именно к обучающей выборке. Причем уровень ошибок на обучающей выборке будет в среднем падать за счет повышения вариативности модели. Но уровень ошибок не может опуститься ниже нуля. Поэтому либо с какого-то момента он стабилизируется, либо будет асимптотически приближаться к 0. А это значит, что уровень тестовой ошибки неизбежно рано или поздно начнет повышаться с ростом сложности модели. Таким образом, у уровня тестовой ошибки есть некоторое оптимальное значение.
Другими словами, для любого конкретного датасета существует некоторый оптимальный уровень сложности модели, который дает наименьшую ошибку на тестовой выборке. Модели, имеющие более низкую сложность будут недообучаться, а более высокую — переобучаться. Поэтому существует задача нахождения этого оптимального уровня сложности. К сожалению, это не получится сделать методом обучения, или любой другой численной оптимизации, так как изменение уровня сложности модели требует запуска ее обучения заново. Мы не можем непрерывно менять уровень сложности, как какой-то дополнительный параметр модели.
Изучив несколько видов моделей обучения с учителем легко сделать вывод, что сложность модели — это некоторое “встроенное” свойство, которое определяется видом самой модели, то есть параметрическим классом функций, которые аппроксимируются этой моделью. Некоторые модели просто сложнее чем другие. Например, многослойный перцептрон гораздо сложнее линейной регрессии, а глубокое дерево решений сложнее более мелкого.
Выше мы определяли уровень сложности модели через количество ее параметров. Но стоит сказать, что численное значение этих параметров тоже имеет значение. Рассмотрим для примера две модели — линейную ($y = b_0 + b_1 x$) и квадратичную ($y = b_0 + b_1 x + b_2 x^2$). Очевидно, вторая модель сложнее, так как у нее больше параметров. Квадратичная функция имеет больше степеней свободы и демонстрирует нелинейное поведение — рост функции на разных участках может сильно отличаться.
Но что, если параметр $b_2$ у квадратичной модели будет очень маленьким, скажем, $b_2 = 0.0001$. Если у нас есть функция, например, $y = -8 + 15 x + 0.0001 x^2$, то взглянув на ее график мы не отличим ее от линейной. Да, формально она будет относиться к классу квадратичных функций, но на практике она будет почти прямой линией. Рост функции на разных участках будет отличаться, но очень незначительно. Тем более, что нас интересует поведение функции не на всей числовой прямой а в окрестностях имеющихся точек данных. Если на этом участке функция ведет себя как линейная, то для прикладной задачи она и эквивалентна линейной.
То есть чем ближе параметр $b_2$ к нулю, тем эффективно ближе квадратичная модель к линейной. Так можно сказать про любой параметр любой модели обучения с учителем. Только в более сложных моделях связь между конкретным параметром и уровнем сложности не так очевидна, так в случае с полиномиальными функциями. Но в любом случае, чем меньше в модели параметров, существенно отклоняющихся от нуля, тем она проще. Причем, это обычно не распространяется на свободный коэффициент $b_0$, у него особая роль — его значение смещает все предсказания модели (поэтому он часто называется параметром смещения). Его отличие от нуля несущественно. На этом эффекте основан один очень полезный и распространенный на практике математический прием, который позволяет гибко и очень удобно управлять сложностью параметрических моделей машинного обучения. Этот прием называется регуляризация.
Допустим, у нас есть набор данных и мы не знаем, модель какого вида подойдет к нему лучше — линейная или квадратичная. При прочих равных, квадратичная модель всегда даст меньшую величину ошибки и поэтому будет предпочтительнее. Но мы уже видели, что малая ошибка — не всегда показатель качества модели. Если обычная функция ошибки, основанная на суммарном отклонении значений данных от модели (которую мы рассматривали до этого), не дает адекватной оценки качества модели, может стоит ее как-нибудь изменить?
Функция ошибки — это по сути система штрафов. Каждый раз, когда модель ошибается, к значению ошибки прибавляется величина, пропорциональная отклонению. Это — штраф за ошибку модели. Но может быть, мы можем штрафовать что-нибудь еще? Например, уровень сложности модели. Представьте, что мы добавляем к ошибке некоторые штрафы за высокие значения параметров модели. Тогда алгоритм обучения, который минимизирует именно функцию ошибки будет не так сильно отдавать сложным переобученным моделям. Небольшие ошибки модели могут быть скомпенсированы тем, что модель становится более простой.
Причем эти штрафы очень легко выражаются математически. Если штраф за ошибки модели — это некоторое математическое выражение, основанное на отклонениях предсказанных значений от эмпирических, то штрафы за сложность модели — это выражение, основанное на отклонениях параметров самой модели от нуля. Существует несколько конкретных реализаций регуляризации и о них мы поговорим чуть далее. Кстати, регуляризация обычно не затрагивает свободный коэффициент. Причины этого мы только что обсуждали — он не влияет на сложность модели.
В этом и состоит идея регуляризации — модификация функции ошибки таким образом, чтобы штрафовать сложные модели в пользу более простых. Да, достаточно странно складывать отклонения целевой переменной (которые могут быть выражены в натуральных единицах) и безразмерные параметры модели. Это может выглядеть, как сложение метров с красным. Регуляризация — это именно математический трюк. У нее нет физического значения, какой-то внятной интерпретации в терминах предметной области.Это лишь способ отдавать предпочтение моделям с низкими значениями параметров, ведь такие модели ведут себя как более простые и поэтому менее склонны к переобучению.
Можно заметить, что регуляризация — это способ искусственно понизить сложность модели. То есть при использовании регуляризации берут модель более сложную, которая в “чистом” виде будет явно переобучаться на имеющихся данных. Но за счет этих дополнительных штрафов, ее сложность принижают. Причем, самое удобное в регуляризации то, что она параметрическая. То есть соотношением “силы” штрафа за ошибки и штрафа за сложность легко управлять, введя множитель — так называемый параметр регуляризации. Чем он больше, тем сильнее штрафуются сложные модели, то есть даже большие ошибки модели могут быть скомпенсированы небольшим понижением сложности. Таким образом, возвращаясь к графику в начале главы, именно параметр регуляризации может быть отложен на нем по горизонтали.
Регуляризация настолько удобна и универсальна, что большинство библиотечных реализаций тех моделей, которые мы проходили раньше, уже реализуют встроенную регуляризацию. Причем это относится равно как к моделям классификации, так и к моделям регрессии, это прием не зависит от типа задачи обучения с учителем. За счет способности уменьшить сложность любой модели регуляризация является одним их основных способов борьбы с переобучением.
Обратите внимание, что мы в основном говорим именно о борьбе с переобучением. Борьба с недообучением в основном сводится к использованию более сложной модели. В настоящее время разработаны настолько сложные модели, что узким местом современного машинного обучения становятся вычислительные мощности и доступность данных.
Выводы:
- Регуляризация — это способ искусственно ограничить вариативность моделей.
- При использовании регуляризации можно применять более сложные модели и снижать склонность к переобучению.
- Регуляризация модифицирует функцию ошибки модели, добавляя в нее штрафы за повышение сложности.
- Основная идея регуляризации — отдавать предпочтение низким значениям параметров в модели.
- Регуляризация обычно не затрагивает свободный коэффициент $b_0$.
- Регуляризация обычно параметрическая, можно управлять ее степенью.
Ridge
Зачастую переобучение модели, которое является следствием большого количества параметров в модели, появляется потому, что в наборе данных присутствует много “лишних” атрибутов. Количество параметров любой модели обучения с учителем зависит от количества признаков в данных. Для борьбы с этим явлением используется регуляризация. Как мы говорили, регуляризация “штрафует” отклонения параметров модели (за исключением свободного) от нуля. Совершенно естественно формализовать это отклонение так же, как и в самой функции ошибки — как сумму квадратов этих значений. Такая модель называется гребневой регрессией (ridge regression). В ней функция ошибки принимает такой вид:
[J(vec{b}) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2 + lambda sum_{j=1}^{n} b_j^2]
Как мы можем видеть, что функция ошибки аналогична обычной модели регрессии, но имеет одно дополнительное слагаемое — регуляризационный член. Это сумма квадратов значений параметров модели (начиная с первого). Эта сумма умножается на специальный параметр — параметр регуляризации $lambda$. Он как раз отвечает за “силу” регуляризации модели. В передельном случае, когда $lambda = 0$, мы имеем обычную нерегуляризованную регрессию. Чем больше этот параметр, тем сравнительно больший вклад в ошибку дают отклонения параметров модели. То есть, чем больше этот параметр, тем более простые модели мы будем получать после обучения, при достижении минимума этой функции. Естественно, параметр регуляризации не может быть отрицательным, так как в таком случае мы наоборот, будем отдавать предпочтение более сложным моделям. А сложность, как и ошибка могут возрастать неограниченно.
Но если мы модифицируем функцию ошибки, то это влечет изменение и метода градиентного спуска. На самом деле он меняется незначительно. Вспомним, что градиентный спуск основан на вычислении частной производной функции ошибки по параметрам модели. Если взять свободный параметр, то вообще ничего не меняется, так как регуляризационный член от него не зависит:
[frac{partial}{partial b_0} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot frac{partial}{partial b_0} h_b(x_i)]
Если же рассматривать другие параметры модели, то в выражение производной добавится всего одно небольшое слагаемое:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x_i) + 2 lambda b_i]
Это слагаемое $2 lambda b_i$ как раз и будет учитывать значения параметров при выполнении шагов градиентного спуска в регуляризованной модели регрессии. В остальном метод обучения никак не меняется. Если мы рассматриваем линейную модель, то получается почти знакомое нам по предыдущим главам выражение:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot x_i + 2 lambda b_i]
Как мы уже говорили, этот прием может быть применен как к задачам классификации, так и к задачам регрессии. Но применяя регуляризованные модели на практике стоит быть внимательнее. Дело в том, что в некоторых моделях (например, в методе опорных векторов) регуляризация задается чуть иначе:
[J(vec{b}) = С frac{1}{m} sum_{i=1}^{m} cost(h_b(x_i) , y^{(i)}) + sum_{j=1}^{n} b_j^2]
Где $C$ — это тоже параметр регуляризации. Обратили внимание, что этот множитель стоит перед другим слагаемым — самой функцией ошибки? Численно, это эквивалентно предыдущей формализации, если полагать, что $C = frac{1}{lambda}$. Но стоит помнить, что в такой форме чем больше $C$, тем меньше регуляризации присутствует в модели.
Гребневую регрессию еще называют регрессией по L2-норме (L2 означает норма Лагранжа второго порядка) или регуляризацией Тихонова. Простыми словами это означает, что мы считаем сумму квадратов параметров.Гребневая регрессия полезна тем, что она может помочь повысить эффективность модели, если в данных присутствует большое количество мультиколлинеарных факторов, то есть атрибутов, которые очень сильно зависят друг от друга. Вообще, мультиколлинеарность в статистике — это в принципе не очень хорошее явление. В машинном обучении она опасна тем, что оптимальные параметры модели становятся гораздо менее устойчивыми, а значит обучение будет не очень надежным. Ну и вдобавок, большое количество признаков, как мы уже говорили, увеличивает количество параметров и порядок сложности модели, что приводит к переобучению. На практике мультиколлинеарные признаки можно обнаруживать и удалять из датасета руками, но гребневая регрессия может это делать автоматически.
Рассмотрим работу гребневой регрессии на примере. Для лучшего понимания того, как регуляризация влияет на получаемую модель, мы возьмем одни и те же данные и построим одну и ту же модель классификации с L2 регуляризацией, но с разными значениями параметра регуляризации. В качестве базовой модели мы используем полином пятой степени. Для начала классификация без регуляризации ($lambda=0$):
Мы видим достаточно сложную границу принятия решения и высокую точность модели — на этих данных эта модель показывает 0,91 accuracy. Давайте возьмем $lambda=2$:
За счет использования регуляризации точность модели немного снизилась и составила 0,89. Граница принятия решения тоже стала более гладкой и простой.
Обратите внимание, что расположение границы принятия решения полностью изменилось по сравнению с первой моделью. Ведь параметр регуляризации — это не то же самое, что и обычный параметр модели, коэффициент в функции. Один и тот же алгоритм, обученный с разными значениями параметра регуляризации даст две совершенно разные модели, не имеющие ничего общего. Поэтому нельзя, например, плавно менять параметр регуляризации и смотреть, как изменится граница принятия решения. И физического смысла параметр регуляризации никакого не несет. Это лишь численная переменная в алгоритме обучения, которая влияет на то, какая модель из определенного параметрического класса будет считаться оптимальной для данной задаче. В дальнейшем такие “сложные” параметры мы будем называть гиперпараметрами.
Увеличим регуляризацию еще больше и получим такую модель:
Точность снизилась еще больше — до 0,85. Очевидно, что точность регуляризованных моделей будет меньше, так как функция ошибки может “променять” точность на упрощение модели. Но в метриках эффективности сложность модели не учитывается, поэтому они падают. Ну и граница принятия решения тоже становится все более плоской.
Рассмотрим влияние регуляризации на модель регрессии. Для этого также возьмем один и тот же набор данных и будем строить на нем разные модели. Также будем использовать полиномиальные признаки пятой степени. Но на этот раз обратим внимание и на сами коэффициенты модели. Для начала посмотрим на модель практически без регуляризации ($lambda=0.1$):
Эта модель имеет точность 0,714 (по метрике r-квадрат) и следующие коэффициенты — 0, -2.84, -4.49, 8.03, -2.92, 0.34. Как видно, все полиномиальные признаки имеют влияние на модель, коэффициенты при них отличаются от нуля существенн. Теперь добавим регуляризацию ($lambda=1$):
Точность модели немного упала — до 0,712. Теперь взглянем на коэффициенты: 0, -2.51, -0.97, 4.48, -1.76, 0.22. Заметно, что все они сильно уменьшились (в абсолютном выражении), особенно третий и четвертый. Это как раз и есть влияние регуляризации — она стремится держать коэффициенты как можно более близкими к нулю, даже за счет понижения точности. А параметр регуляризации — это своего рода “обменный курс” между коэффициентами и точностью. Давайте поднимем его еще сильнее (до $lambda=100$):
Точность модели понизилась более существенно — до 0,698. А вот ее коэффициенты: 0, 0.13, 0.37, 0.49, -0.04, 0.01. По мере увеличения регуляризации ни один из коэффициентов не удалялся от нуля. А некоторые вплотную к нему приблизились. При этом заметим, что ни один коэффициент не стал нулем — гребневая регрессия даже с запредельным уровнем регуляризации стремится оставить в модели все имеющиеся признаки.
Выводы:
- $lambda > 0$ — параметр регуляризации.
- Чем он больше, тем сильнее штрафуются сложные модели.
- Этот прием может применяться как к классификации, так и к регрессии.
- Ridge еще называют регуляризацией по L2-норме. Она же — гребневая регрессия.
- Такая регуляризация делает параметры более робастными к мультиколлинеарности признаков.
Lasso
У гребневой регрессии есть один недостаток, проявляющий себя при работе с данным, в которых есть много “лишних” признаков — она всегда включает в модель все признаки. Но параметры у них могут быть близки к нулю, что затрудняет интерпретацию модели и не сокращает размерность задачи. На практике в данных могут присутствовать не просто мультиколлинеарные атрибуты, но и такие, которые имеют очень маленькое влияние на целевую переменную или не имеют его вообще. Включать их в модель не имеет никакого смысла.
Для решения этой проблемы существует так называемая лассо-регрессия. Она по своей формализации очень похожа на гребневую, но чуть по-другому учитывает значения параметров модели:
[J(vec{b}) = sum_{i=1}^{m} (h_b(x_i) — y_i)^2 + lambda sum_{j=1}^{n} mid b_j mid]
В данном случае говорят о регуляризации по L1-норме. За счет того, что функция абсолютного значения, которая используется здесь не везде дифференцируема, для обучения такой модели используется специальный метод координатного спуска (coordinate descent), а не градиентного. Но рассмотрение всех вариантов алгоритмов обучения выходит за рамки данного пособия. В остальном же использование лассо на практике абсолютно идентично другим моделям обучения с учителем.
Из-за своей специфической формализации, модель лассо стремиться обратить в ноль как можно больше параметров модели. Это значит, что если какой-то признак не оказывает сильного влияния на целевую переменную, то модель с L1-регуляризацией с большой долей вероятности “занулит” этот признак. Это бывает очень полезно в задачах, где в данных присутствует больше количество ненужной информации. Такие задачи еще часто называют разреженными. К ним часто относятся, например, задачи анализа текстов.
В таких задачах регрессия по методу лассо может использоваться для отбора признаков. Часто эта модель потом вообще не используется, а на оставшихся признаках строится какая-то другая модель обучения с учителем. Так лассо-регрессия может играть вспомогательную роль. Регрессию лассо поэтому часто называют методом понижения размерности — после ее применения в модели остаются (ненулевыми) только те признаки, которые действительно влияют на значение целевой переменной. Хотя это не совсем то, что называют понижением размерности в задачах обучения без учителя.
Также как и любая регуляризация, лассо управляет компромиссом между bias и variance модели за счет введения параметра регуляризации. Он имеет точно такой же смысл, как и в гребневой регрессии — чем он больше численно, тем более простые модели будет предпочитать этот алгоритм. Можно построить график зависимость обучающей и тестовой эффективностей модели от значения параметра регуляризации:
Здесь мы видим, что при малых значениях этого параметра наблюдается большая разница между эффективностями. ПО мере увеличения значения параметра регуляризации сложность, а следовательно и обучающая эффективность модели падают, а разница между ними сокращается. Тестовая же эффективность поначалу растет, но начиная в определенного значения параметра регуляризации (в районе $10^{-1}$) снова начинает снижаться. В левой части этого графика мы наблюдаем ситуацию переобучения, а в правой — недообучения. А примерно $10^{-1}$ — это оптимальное значение параметра регуляризации, при котором получается наиболее качественная модель линейной регрессии.
Давайте построим регрессию по методу лассо на тех же данных, на которых строили в предыдущей главе гребневую регрессию. На этот раз ограничимся одной моделью со средним уровнем регуляризации ($lambda=1$):
Обратим внимание на коэффициенты модели: 0, 0, 0, 0.55, 0, 0. Даже при таком небольшом значении параметра регуляризации модель оставила только один признак — признак третьей степени (что мы и видим на графике — это кубическая парабола, только масштабированная по вертикали). В этом и проявляется действие алгоритма лассо — он стремится как можно больше коэффициентов обратить в ноль.
Lasso, кстати, расшифровывается как least absolute shrinkage and selection operator, оператор наименьшего абсолютного сокращения и выбора.
В данном примере можно сделать вывод, что среди полиномиальных признаков только признак третьей степени оказывал сколь-нибудь существенное влияние на целевую переменную. Таким образом, регрессия по методу лассо работает как алгоритм отбора признаков. В дальнейшем можно используя только этот один признак строить и другие модели машинного обучения на данной задаче, или просто ввести его в датасет, таким образом лассо станет основой для инжиниринга признаков.
Выводы:
- Lasso еще называют регуляризацией по L1-норме.
- Lasso заставляет модель использовать меньше ненулевых коэффициентов.
- Фактически, эта регуляризация уменьшает количество признаков, от которых зависит модель.
- Может использоваться для отбора признаков.
- Полезна в задачах с разреженной матрицей признаков.
Elastic net
После прочтения двух предыдущих разделов может появиться вопрос: какой метод регуляризации лучше? Как всегда не существует универсального ответа. Это целиком зависит от данных. С разреженностью признаков лучше справляется лассо, а с мультиколлинеарностью — гребневая модель. Как всегда, когда есть два подхода, каждый со своими преимуществами, есть способ их скомбинировать. Рассмотрим модель, которая обычно называется elastic net или “эластичная сеть”:
[J(vec{b}) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2 +
lambda_1 sum_{j=1}^{n} | b_j | + lambda_2 sum_{j=1}^{n} b_j^2]
Как мы видим, функция ошибки такой модели комбинирует подходы гребневой и лассо-регрессии. То есть включает в себя регуляризацию и по L1 и по L2 нормам. Поэтому в этой модели присутствует целых два параметра регуляризации, причем они независимы друг от друга и задают не только соотношение регуляризации того или иного типа и классической функции ошибки, но и соотношение силы двух типов регуляризации между собой.
А между тем мы еще не говорили о том, как подбирать оптимальные значение параметров регуляризации. А ведь это достаточно серьезная проблема. Их не подберешь обычным методом обучения — это не просто параметры модели. Чуть позже мы назовем их гиперпараметрами. Но подбирать их можно только непосредственной проверкой, то есть подбором в классическом смысле. И это достаточно трудоемкий процесс, так как надо проверить потенциально бесконечное количество значений, причем еще хорошо бы использовать кросс-валидацию для надежности результатов.
А как быть с двумя гиперпараметрами. Обычно их значения подбираются “наивным” способом, в два прохода. Сначала находится оптимальный параметр $lambda_2$ для гребневой регрессии, а потом он фиксируется и подбирается наилучший параметр $lambda_1$ для лассо. Понятно, что они могут зависеть еще и друг от друга. И чуть позже мы изучим более вычислительно емкий, но правильный способ искать оптимальные значения гиперпараметров.
Давайте построим регрессию методом эластичной сети по уже известным нам данным из двух предыдущих глав. В данном случае используем $lambda_1 = lambda_2 = 10$:
Коэффициенты у модели следующие: 0, 0, 0, 0, 0.202, -0.016. Очень заметно совместное влияние двух регуляризаций. L1 выбирает только самые значимые признаки, оставляя у других коэффициенты равными нулю, а L2 еще приближает к нулю оставшиеся коэффициенты. В результате получается очень компактная модель, которая имеет только очень обоснованные коэффициенты.
Конечно, приведенные в данных главах модели не являются обязательно лучшими или оптимальными для решения данной задачи регрессии. Их цель — проиллюстрировать работу алгоритмов и для этого зачастую приходилось на максимум “выкручивать” регуляризацию. В реальности надо искать оптимальный уровень регуляризации, но об этом речь пойдет в следующих главах.
Выводы:
- По сути, это комбинация регуляризации по L1 и L2 нормам.
- Имеет два параметра, которые определяют соотношение соответствующих норм.
- Комбинирует достоинства предыдущих двух методов.
- Недостаток в необходимости задавать сразу два параметра регуляризации.
Методы борьбы с недообучением
В этой главе мы говорим о диагностике моделей машинного обучения в контексте диагностики недо- и переобучения. И мы много говорили о том, как обнаружить эти состояния модели. Так что же делать, если мы обнаружили, что наша модель недообучается. Сейчас поговорим о типичных путях повышения эффективности моделей. И начнем с более простого случая — недообучения.
В первую очередь напомним себе, что такое недообучение. Это ситуация, когда модель демонстрирует слишком большой bias по отношению к имеющимся данным. Модели не хватает вариативности, чтобы “ухватить” зависимости между признаками и целевой переменной. С точки зрения модели, их вообще нет. Простыми словами можно сказать, что модель слишком проста, примитивна для решения поставленной задачи. При этом может быть такое, что имеющиеся данные действительно не содержат необходимой информации, позволяющей надежно предсказать значение целевой переменной.
Поэтому при недообучении первое о чем нужно подумать: есть ли в датасете информация (признак или комбинация признаков), которые бы определяли значение целевой переменной. Если таких нет, то неважно, сколько точек данных, примеров мы соберем, модель всегда будет недообучаться. Неважно, насколько сложную модель мы будем использовать, она покажет случайных шум. Наиболее эффективный способ борьбы с недообучением — инжиниринг признаков. Необходимо ввести в модель признаки (или атрибуты, неважно, важно чтобы была нужная информация), которые позволят модели предсказать значение целевой переменной.
Помните, как мы решали задачу с полиномиальными признаками, как они превращали нерешаемую задачу классификации в линейно разделимую? Так может произойти в любой задаче. Может, одного свойства объекта нам и не хватает, чтобы превратить случайный перемешанный набор точек в многомерном пространстве в четкую и очевидную зависимость.
К сожалению, нет универсального алгоритма инжиниринга признаков. Это всегда творческая деятельность, которая требует, причем, глубокого знания предметной области. Иногда нужно просто вернуться на этап сбора данных и найти (или сгенерировать) больше информации. Иногда помогает вдумчивое и осмысленное преобразование имеющихся атрибутов. Главный вопрос, который надо себе задать: что в реальности влияет на целевую переменную? Затем собирать как можно больше информации об этом, добавлять ее в модель в виде признаков и надеяться, что это повысит эффективность моделей.
Если такой возможности нет, то очевидно, имеет смысл уменьшить степень регуляризации модели. Конечно, этот способ подходит только, если вы используете регуляризованные модели. Но как мы уже обсуждали выше, очень многие модели используют регуляризацию автоматически. А если она применяется, то можно легко манипулировать ее степенью. Понижение регуляризации приведет к тому, что после обучения мы получим более сложную и вариативную модель, что может исправить ситуацию с недообучением.
Другой очевидный способ — использование более сложных моделей в целом. Имеется в виду смена класса моделей. Если недообучается, например, модель линейной регрессии, стоит попробовать дерево решений. Если недообучилась логистическая — попробуйте многослойный перцептрон. Хотя, регуляризация обычно работает более эффективно, чем использование более сложной модели, она ограничена рамками одного параметрического класса функций.
Возможно стоит попытаться повторить обучение или увеличить количество итераций обучения. Возможна ситуация, когда существующего количества итераций недостаточно для схождения метода обучения к локальному минимуму функции ошибки. Это опять же может происходить вследствие того, что задача слишком сложна. В особо сложных случаях можно использовать предобученные модели. Это так называемое трансферное обучение — когда используют уже обученную модель на каком-то одном наборе данных для решения подобной задачи на другом датасете. Например, существуют так называемые глубокие языковые модели — огромные нейросети с миллиардами параметров, которые обучаются на гигантских корпусах текстов. Они используются для разнообразных задач текстовой аналитики. Конечно, каждый раз нецелесообразно обучать такую огромную модель с нуля — можно воспользоваться уже обученной и дообучить ее (или обучить, например, только последний слой нейронной сети) под собственную задачу. Трансферное обучение — отдельная и очень интересная дисциплина машинного обучения, но ее подробное рассмотрение выходит за рамки этого пособия.
Отдельно стоит сказать, что не поможет при недообучении. Вам вряд ли поможет увеличение объема выборки. Многие думают, что собрать больше данных — это универсальный рецепт эффективности. Это тоже не так. Хотя, большая по объему выборка особенно и не помешает, то есть не уменьшит эффективность модели, она увеличит вычислительную емкость. Другими словами, модель будет обучаться значительно дольше, но без видимого положительного эффекта по эффективности.
Обратите внимание, что мы здесь всегда имеем в виду эффективность, измеренную на тестовой выборке. А еще лучше — с использованием кросс-валидации. Эффективность на обучающей выборке нужна только для диагностики и анализа моделей.
Стоит помнить, что машинное обучение — это всегда итеративный процесс. Построив первую модель нужно ее исследовать и пытаться улучшить, увеличить эффективность. При этом возможно стоит попробовать множество разных видов моделей и способов обработки данных.
Выводы:
- Ввести в модель новые данные об объектах (атрибуты).
- Уменьшение степени регуляризации модели.
- Введение полиномиальных и других суррогатных признаков.
- В целом, инжиниринг признаков.
- Использование более сложных моделей.
- Увеличение количества итераций.
- Трансферное обучение.
Методы борьбы с переобучением
Переобучение на практике более частая и более коварная проблема потому, что несложно взять для решение конкретной задачи более сложную модель. Гораздо труднее заставить ее работать хорошо на новых данных. Проблему переобучения обнаружить сложнее и потому, что при этой ситуации модель работает вроде бы хорошо — дает низкую ошибку на данных. Но на других точках модель почему-то начинает ошибаться гораздо сильнее.
Опять же вспомним, что суть ситуации переобучения состоит в том, что модель оказывается слишком сложной для имеющихся данных и зависимостей в них. Поэтому вместо общих тенденций модель начинает обращать внимание на конкретное расположение точек в обучающей выборке, на случайные флуктуации, которые не несут смысловой нагрузки и не будут повторяться в новых данных.
Чем меньше данных присутствует в обучающей выборке, тем больше в них “шума” по отношению к полезному “сигналу” — информации о случайных колебаниях значений признаков по сравнению с информацией о тенденциях и реальных зависимостях. Поэтому неудивительно, что на малых объемах данных при прочих равных модели склонны к переобучению. Взгляните на график выше — даже человеку неочевидно, что точки выборки образуют линейную тенденцию — их просто слишком мало, чтобы показать эту тенденцию.
Самый действенный способ борьбы с переобучением — собрать больше обучающих примеров.
Если мы добавим больше точек, принадлежащих тому же распределению, мы неизбежно более четко увидим имеющуюся тенденцию. Все дело в том, что основное свойство случайных колебаний — их математическое ожидание равно нулю. То есть значение показателя может под воздействием неизвестных или неучтенных факторов отклоняться от “правильного” значения как в сторону увеличения, так и в сторону уменьшения. Причем вероятность этого примерно равна. И если мы рассматриваем одну точку данных, то сложно сказать, чем обосновано ее конкретное значение — существенными факторами или случайностью. Но если рассмотреть большое множество точек, можно увидеть, что они группируются вокруг некоторого среднего.
Другими словами, при увеличении количества точек обучающей выборки все случайные колебания будут усредняться — на каждое положительное отклонение найдется примерно равное отрицательное. А тенденция же будет, наоборот, усиливаться. В итоге и человеку и модели будет значительно легче эту тенденцию “ухватить”. Посмотрите, например, что будет, если к выборке, изображенной на рисунке выше добавить еще в 10 раз больше точек из того же распределения:
Теперь довольно очевидно, что на лицо линейная тенденция. И даже более сложная полиномиальная функция работает гораздо более эффективно на этих данных. Именно так добавление данных борется с переобучением моделей.
Причем необходимое количество данных зависит от вида тенденции и величины случайных отклонений. Чем более сложная, нелинейная тенденция в данных существует, чем тоньше зависимость целевой переменной от значения атрибутов, тем больше данных нужно для адекватной работы моделей. И чем больше по величине случайные отклонения, чем “сильнее” они размывают эту тенденцию, тем больше данных понадобится. Поэтому не существует какого-то оптимального объема данных, все зависит от конкретной задачи.
Как мы видели на примерах ранее, переобучение зачастую возникает вследствие того, что в модели присутствует большое количество параметров за счет большого количества лишних признаков в датасете. Именно для борьбы с этим используется регуляризация и в целом отбор признаков. Незначимые атрибуты лучше убирать из данных еще на этапе предварительного анализа и очистки данных. Чем меньше в данных будет лишних признаков, тем более четко и ясно будет прослеживаться та самая заветная тенденция.
Однако следует помнить, что регуляризация на практике работает лучше, чем ручное удаление признаков, так как подбор коэффициентов модели происходит автоматически. При этом регуляризация имеет свои недостатки — необходимость подбора параметра регуляризации. Поэтому стоит комбинировать эти способы — если какие-то признаки явно не влияют на целевую переменную — их стоит убрать при обработке данных, а если есть сомнения — то лучше оставить на усмотрение регуляризации.
Кроме того, следует помнить, что в других классах моделей могут применяться и иные способы управления сложностью модели, которые эффективно в чем-то похожи на регуляризацию. Например, в деревьях решений — это ограничение глубины дерева. Мы уже говорили об этом: чем больше слоев в дереве, тем сложнее получается модель. В нейронных сетях для подобного же используются Dropout-слои. Подробно мы не сможем рассказать про все эти способы, тем более что они специфичны для разных классов моделей. Но на практике они применяются примерно также, как и обычная регуляризация.
Как мы видим на втором графике даже после добавления большого количества точек более простая модель все равно описывает выборку лучше, так как полиномиальная модель имеет не очень понятные “хвосты” на концах распределения. Поэтому при обнаружении переобучения стоит задуматься об использовании более простого параметрического класса функций. Этот способ работает лучше в совокупности с увеличением объема выборки. Вообще, комбинация нескольких способов может быть более эффективной, чем применение только одного.
В глубоком обучении есть эмпирическое правило, которое гласит, что количество параметров модели должно быть в 2-3 раза меньше, чем количество примеров в обучающей выборке. Это ни в коем случае не универсальное правило и не гарантия от переобучения. Помните, вся зависит от задачи. Но можно помнить об этом ориентире. Если количество параметров больше, чем рекомендует это правило, вы практически точно получите переобученную модель.
Кроме того, не стоит забывать о ложных корреляциях в данных, которые тоже могут стать причиной переобучения. Хотя, ложные зависимости данных в силу их ограниченности — это явление несколько другой природы, на практике оно проявляет себя точно как переобучение — снижает обобщающую способность модели. Для устранения ложных корреляций необходимо хорошо разбираться в предметной области или привлекать для анализа данных экспертов.
Еще устраняют или сильно снижают переобучение так называемые ансамблевые модели, особенно основанные на методе бустинга. Ансамблевые модели это отдельная большая тема, которую мы не сможем рассмотреть в этой главе, про них можно написать отдельную книгу. Но если вкратце, ансамбль — это набор моделей, обученных на одном и том же наборе данных. Метод бустинга заключается в том, что каждая следующая модель в ансамбле исправляет или компенсирует ошибки предыдущей. В итоге мы получаем такую метамодель, которая может работать более эффективно, чем каждая модель ансамбля по отдельности.
Еще один способ избежать переобучения моделей — ранняя остановка обучения. Раньше мы говорили, что процесс обучения всегда продолжается до полной сходимости, то есть до нахождения оптимальных значений параметров по заданной функции ошибки. Но это не всегда так. В процессе обучения можно контролировать ту самую тестовую эффективность и остановить обучение тогда, когда она начнет падать. Этот способ часто применяется в обучении нейронных сетей, так как оно начинается с малых случайных значений весов (параметров) сети. Поэтому само обучение, то есть подбор весов, немного имеет эффект повышения значения коэффициентов, который противоположен регуляризации, то есть повышение степени сложности модели. Поэтому ранняя остановка обучения эффективно похожа на введение регуляризации в модель. Важно остановить обучение именно в тот момент, когда сложность модели начнет превышать оптимальное значение, после которого начинается переобучение. Это простой, но не очень универсальный способ.
Каждый способ борьбы с переобучением (впрочем как и с недообучением) имеет свои достоинства и недостатки. Не существует универсального алгоритма действий. Поэтому всегда надо исходить из поставленной задачи, а также руководствоваться всеми факторами: характер модели, нефункциональные требования, особенности набора данных, возможность собрать больше точек или атрибутов. При возможности стоит попробовать несколько разных способов увеличения эффективности моделей.
Выводы:
- Ввести в модель данные о новых объектах, использовать выборку большего объема.
- Убрать признаки из модели, использовать отбор признаков, устранить ложные корреляции.
- Увеличить степень регуляризации модели.
- Использовать более простые модели.
- Регуляризация обычно работает лучше уменьшения количества параметров.
- Можно использовать ансамблевые модели.
- Ранняя остановка обучения.
Анализ ошибок
Рассматривая алгоритмические и математические способы повышения эффективности работы моделей машинного обучения не стоит забывать и о самом простом, но в тоже время одном из самых эффективных — ручном анализе ошибок модели. После обучения модели, если она не достигает желаемого уровня эффективности стоит просто обратить внимание на те объекты, на которых она делает ошибки. Этот подход называется анализ ошибок и может дать достаточно неожиданную информацию о модели, данных и самой задаче.
В отдельных случаях анализ ошибок приводит к выводу, что модель работает хорошо. Например, очень известна задача по распознаванию рукописных цифр по картинке. Даже относительно простые модели справляются с ней очень хорошо, но могут не достигать стопроцентной эффективности. Вот пример картинки, которую простая модель может классифицировать неправильно:
Свидетельствует ли эта ошибка о том, что модель обучилась неправильно? Скорее нет, это свидетельствует о низком разрешении картинок и наличии некоторых двусмысленных объектов в обучающей выборке. Такую рукописную цифру и человек бы не распознал.
Кроме того, в данных могут присутствовать просто ошибки. Особенно это касается датасетов, размеченных вручную. Человек мог просто опечататься или ошибиться и в наборе данных появился объект с неправильным значением целевой переменной. На практике все случается и именно ручной анализ ошибок может выявить такую ситуацию.
Ручная проверка индивидуальных объектов, на которых модель работает неправильно часто подсказывает, какие общие характеристики имеют такие объекты или чем они отличаются от остальной выборки. Поняв эти особенности можно найти способы модифицировать признаки таким образом, чтобы лучше учитывать эти особенности. Например, анализируя модель распознавания человека по лицу можно придти к выводу о том, что такая модель значительно чаще ошибается на лицах с растительностью или на людях в очках. Это вполне объяснимо с логической точки зрения. Так что же делать в таком случае? Можно просто собрать больше точек данных, лиц с растительностью или очками. Это не только просто повысит эффективность модели, но и сделает ее более устойчивой к подобным особенностям в принципе.
При проведении анализа ошибок следует ориентироваться на ошибки, которые модель делает именно в тестовой выборке. В задачах классификации в первую очередь следует проанализировать ошибки в тех классах, в которых модель делает больше всего ошибок. Это очень заметно в отчете о классификации и в марице классификации. Обычно бывает, что модель постоянно относит объекты одного класса к какому-то другому. А в задачах регрессии очень логично обратить внимание на объекты, на которых модель ошибается сильнее всего в численном выражении.
Выводы:
- Анализ ошибок — это ручная проверка объектов, на которых модель делает ошибки.
- Анализ характеристик таких объектов может подсказать направление инжиниринга признаков.
- Можно сравнить эти объекты с остальной выборкой. Может, это аномалии.
- В задачах регрессии в первую очередь обращать внимание на объекты с самым высоким отклонением.
Выбор модели
Выводы:
- Задача выбора класса модели для решения определенной задачи.
- Очень сложно сказать априори какой класс модели будет работать лучше на конкретных данных.
- Следует учитывать нефункциональные требования к задаче.
- Обычно начинают с самых простых моделей — они быстро считаются и дают базовый уровень эффективности.
- По результатам диагностики простых моделей принимают решение о дальнейших действиях.
- Можно провести поиск по разным классам моделей для определения самых перспективных.
- Выбор модели — это творческий и исследовательский процесс.
- Есть подходы автоматизации выбора модели (AutoML), но они пока несовершенны.
- В исследовательских задачах модели сравниваются со state-of-the-art.
Гиперпараметры модели
Выводы:
- Гиперпараметр модели — это численное значение, которое влияет на работу модели, но не подбирается в процессе обучения.
- Примеры гиперпараметров — k в kNN, параметр регуляризации, степень полиномиальной регрессии, глубина дерева решения.
- У каждой модели множество гиперпараметров, которые можно посмотреть в документации.
- Гиперпараметры модели нужно задавать до начала обучения.
- Если значение гиперпараметра изменилось, то обучение надо начинать заново.
- Существуют скрытые гиперпараметры модели — степень полинома, количество нейронов и слоев, ядерная функция.
- Оптимизация гиперпараметров и задача выбора модели — одно и то же.
Поиск по сетке
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
tuned_parameters = [
{"kernel": ["rbf"],
"gamma": [1e-3, 1e-4],
"C": [1, 10, 100, 1000]},
{"kernel": ["linear"],
"C": [1, 10, 100, 1000]},
]
scores = ["precision", "recall"]
grid_search = GridSearchCV(SVC(), tuned_parameters,
scoring=scores).fit(X_train, y_train)
Выводы:
- Поиск по сетке — полный перебор всех комбинаций значений гиперпараметров для поиска оптимальных значений.
- Для его организации надо задать список гиперпараметров и их конкретных значений.
- Непрерывные гиперпараметры надо дискретизировать.
- Поиск по сетке имеет экспоненциальную сложность.
- Чем больше параметров и значений задать, тем лучше модель, но дольше поиск.
- Можно задать критерии поиска — целевые метрики.
Случайный поиск
1
2
3
4
5
6
7
8
9
10
11
12
clf = SGDClassifier(loss="hinge", penalty="elasticnet", fit_intercept=True)
param_dist = {
"average": [True, False],
"l1_ratio": stats.uniform(0, 1),
"alpha": loguniform(1e-2, 1e0),
}
n_iter_search = 15
random_search = RandomizedSearchCV(
clf, param_distributions=param_dist, n_iter=n_iter_search
).fit(X, y)
Выводы:
- Случайный поиск позволяет задать распределение гиперпараметра, в котором будет вестись поиск.
- Случайный поиск семплирует набор значений гиперпараметров из указанных распределений.
- Можно задать количество итераций поиска независимо от количества гиперпараметров.
- Добавление параметров не влияет на продолжительность поиска.
- Результат не гарантируется. Воспроизводимость можно настроить.
Сравнение эффективности моделей (валидационный набор)
Выводы:
- При сравнении нескольких моделей между собой возникает проблема оптимистичной оценки эффективности.
- Поэтому для исследования выбранной модели нужно использовать третью часть выборки — валидационную.
- В терминах существует путаница, главное — три непересекающиеся части выборки.
- Обучающая (train) используется для оптимизации параметров (обучения) модели.
- Валидационная (validation) — для оптимизации гиперпараметров и выбора модели.
- Тестовая (test, holdout) — для итоговой оценки качества, представления результатов.
- Во многих случаях использование кросс-валидации автоматически разбивает выборку. Поэтому тестовая играет роль валидационной.
- Есть проблема глобального переобучения моделей на известных датасетах.
Перевод
Ссылка на автора
Каждая модель машинного обучения пытается решить проблему с другой целью, используя свой набор данных, и, следовательно, важно понять контекст, прежде чем выбрать метрику. Обычно ответы на следующий вопрос помогают нам выбрать подходящий показатель:
- Тип задачи: регрессия? Классификация?
- Бизнес цель?
- Каково распределение целевой переменной?
Ну, в этом посте я буду обсуждать полезность каждой метрики ошибки в зависимости от цели и проблемы, которую мы пытаемся решить. Часть 1 фокусируется только на показателях оценки регрессии.
Метрики регрессии
- Средняя квадратическая ошибка (MSE)
- Среднеквадратическая ошибка (RMSE)
- Средняя абсолютная ошибка (MAE)
- R в квадрате (R²)
- Скорректированный R квадрат (R²)
- Среднеквадратичная ошибка в процентах (MSPE)
- Средняя абсолютная ошибка в процентах (MAPE)
- Среднеквадратичная логарифмическая ошибка (RMSLE)
Средняя квадратическая ошибка (MSE)
Это, пожалуй, самый простой и распространенный показатель для оценки регрессии, но, вероятно, наименее полезный. Определяется уравнением
гдеyᵢфактический ожидаемый результат иŷᵢэто прогноз модели.
MSE в основном измеряет среднеквадратичную ошибку наших прогнозов. Для каждой точки вычисляется квадратная разница между прогнозами и целью, а затем усредняются эти значения.
Чем выше это значение, тем хуже модель. Он никогда не бывает отрицательным, поскольку мы возводим в квадрат отдельные ошибки прогнозирования, прежде чем их суммировать, но для идеальной модели это будет ноль.
Преимущество:Полезно, если у нас есть неожиданные значения, о которых мы должны заботиться. Очень высокое или низкое значение, на которое мы должны обратить внимание.
Недостаток:Если мы сделаем один очень плохой прогноз, возведение в квадрат сделает ошибку еще хуже, и это может исказить метрику в сторону переоценки плохости модели. Это особенно проблематичное поведение, если у нас есть зашумленные данные (то есть данные, которые по какой-либо причине не совсем надежны) — даже в «идеальной» модели может быть высокий MSE в этой ситуации, поэтому становится трудно судить, насколько хорошо модель выполняет. С другой стороны, если все ошибки малы или, скорее, меньше 1, то ощущается противоположный эффект: мы можем недооценивать недостатки модели.
Обратите внимание, чтоесли мы хотим иметь постоянный прогноз, лучшим будетсреднее значение целевых значений.Его можно найти, установив производную нашей полной ошибки по этой константе в ноль, и найти ее из этого уравнения.
Среднеквадратическая ошибка (RMSE)
RMSE — это просто квадратный корень из MSE. Квадратный корень введен, чтобы масштаб ошибок был таким же, как масштаб целей.
Теперь очень важно понять, в каком смысле RMSE похож на MSE, и в чем разница.
Во-первых, они похожи с точки зрения их минимизаторов, каждый минимизатор MSE также является минимизатором для RMSE и наоборот, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора предсказаний, A и B, и скажем, что MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. И это также работает в противоположном направлении. ,
Что это значит для нас?
Это означает, что, если целевым показателем является RMSE, мы все равно можем сравнивать наши модели, используя MSE, поскольку MSE упорядочит модели так же, как RMSE. Таким образом, мы можем оптимизировать MSE вместо RMSE.
На самом деле, с MSE работать немного проще, поэтому все используют MSE вместо RMSE. Также есть небольшая разница между этими двумя моделями на основе градиента.
Это означает, что путешествие по градиенту MSE эквивалентно путешествию по градиенту RMSE, но с другой скоростью потока, и скорость потока зависит от самой оценки MSE.
Таким образом, хотя RMSE и MSE действительно схожи с точки зрения оценки моделей, они не могут быть сразу взаимозаменяемыми для методов на основе градиента. Возможно, нам нужно будет настроить некоторые параметры, такие как скорость обучения.
Средняя абсолютная ошибка (MAE)
В MAE ошибка рассчитывается как среднее абсолютных разностей между целевыми значениями и прогнозами. MAE — это линейная оценка, которая означает, чтовсе индивидуальные различия взвешены одинаковов среднем. Например, разница между 10 и 0 будет вдвое больше разницы между 5 и 0. Однако то же самое не верно для RMSE. Математически он рассчитывается по следующей формуле:
Что важно в этой метрике, так это то, что онанаказывает огромные ошибки, которые не так плохо, как MSE.Таким образом, он не так чувствителен к выбросам, как среднеквадратическая ошибка.
MAE широко используется в финансах, где ошибка в 10 долларов обычно в два раза хуже, чем ошибка в 5 долларов. С другой стороны, метрика MSE считает, что ошибка в 10 долларов в четыре раза хуже, чем ошибка в 5 долларов. MAE легче обосновать, чем RMSE.
Еще одна важная вещь в MAE — это его градиенты относительно прогнозов. Gradiend — это пошаговая функция, которая принимает -1, когда Y_hat меньше цели, и +1, когда она больше.
Теперь градиент не определен, когда предсказание является совершенным, потому что, когда Y_hat равен Y, мы не можем оценить градиент. Это не определено.
Таким образом, формально, MAE не дифференцируемо, но на самом деле, как часто ваши прогнозы точно измеряют цель. Даже если они это сделают, мы можем написать простое условие IF и вернуть ноль, если это так, и через градиент в противном случае. Также известно, что вторая производная везде нулевая и не определена в нулевой точке.
Обратите внимание, чтоесли мы хотим иметь постоянный прогноз, лучшим будетсрединное значение целевых значений.Его можно найти, установив производную нашей полной ошибки по этой константе в ноль, и найти ее из этого уравнения.
R в квадрате (R²)
А что если я скажу вам, что MSE для моих моделей предсказаний составляет 32? Должен ли я улучшить свою модель или она достаточно хороша? Или что, если мой MSE был 0,4? На самом деле, трудно понять, хороша наша модель или нет, посмотрев на абсолютные значения MSE или RMSE. Мы, вероятно, захотим измерить, как Во многом наша модель лучше, чем постоянная базовая линия.
Коэффициент детерминации, или R² (иногда читаемый как R-два), является еще одним показателем, который мы можем использовать для оценки модели, и он тесно связан с MSE, но имеет преимущество в том, чтобезмасштабное— не имеет значения, являются ли выходные значения очень большими или очень маленькими,R² всегда будет между -∞ и 1.
Когда R² отрицательно, это означает, что модель хуже, чем предсказание среднего значения.
MSE модели рассчитывается, как указано выше, в то время как MSE базовой линии определяется как:
гдеYс чертой означает среднее из наблюдаемогоyᵢ.
Чтобы сделать это более ясным, этот базовый MSE можно рассматривать как MSE, чтопростейшиймодель получит. Простейшей возможной моделью было бывсегдапредсказать среднее по всем выборкам. Значение, близкое к 1, указывает на модель с ошибкой, близкой к нулю, а значение, близкое к нулю, указывает на модель, очень близкую к базовой линии.
В заключение, R² — это соотношение между тем, насколько хороша наша модель, и тем, насколько хороша модель наивного среднего.
Распространенное заблуждение:Многие статьи в Интернете утверждают, что диапазон R² лежит между 0 и 1, что на самом деле не соответствует действительности. Максимальное значение R² равно 1, но минимальное может быть минус бесконечность.
Например, рассмотрим действительно дрянную модель, предсказывающую крайне отрицательное значение для всех наблюдений, даже если y_actual положительно. В этом случае R² будет меньше 0. Это крайне маловероятный сценарий, но возможность все еще существует.
MAE против MSE
Я заявил, что MAE более устойчив (менее чувствителен к выбросам), чем MSE, но это не значит, что всегда лучше использовать MAE. Следующие вопросы помогут вам решить:
Взять домой сообщение
В этой статье мы обсудили несколько важных метрик регрессии. Сначала мы обсудили среднеквадратичную ошибку и поняли, что наилучшей константой для нее является среднее целевое значение. Среднеквадратичная ошибка и R² очень похожи на MSE с точки зрения оптимизации. Затем мы обсудили среднюю абсолютную ошибку и когда люди предпочитают использовать MAE вместо MSE.
Спасибо за чтение, и я с нетерпением жду, чтобы услышать ваши вопросы 
P.SСледите за моей следующей статьей, которая изучает другие более продвинутые метрики регрессии. Если вы хотите больше узнать о мире машинного обучения, вы также можете подписаться на меня в Instagram, напишите мне напрямую или найди меня на linkedin, Я хотел бы услышать от вас.
Ресурсы:
[1] https://dmitryulyanov.github.io/about




![{displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0e1b3bac58f9ba2d2f4ff8b85b2e35a8f4bf78)

![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}\&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ac524a751828f971013e1297a33ca1cc4c38cd6)
![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]\&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}\&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864646cf4426e2b62a3caf9460382eec1a77fe4e)

![{displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4647a2cc4c8f9a4c90b628faad2dcf80c4aae84)



![{displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]\&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}\&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}\&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf22322412b8454c706d78671e5d94208675a6e0)