Standard Error of the Mean vs. Standard Deviation: An Overview
Standard deviation (SD) measures the amount of variability, or dispersion, from the individual data values to the mean. SD is a frequently-cited statistic in many applications from math and statistics to finance and investing.
Standard error of the mean (SEM) measures how far the sample mean (average) of the data is likely to be from the true population mean. The SEM is always smaller than the SD.
Standard deviation and standard error are both used in statistical studies, including those in finance, medicine, biology, engineering, and psychology. In these studies, the SD and the estimated SEM are used to present the characteristics of sample data and explain statistical analysis results.
However, even some researchers occasionally confuse the SD and the SEM. Such researchers should remember that the calculations for SD and SEM include different statistical inferences, each of them with its own meaning. SD is the dispersion of individual data values. In other words, SD indicates how accurately the mean represents sample data.
However, the meaning of SEM includes statistical inference based on the sampling distribution. SEM is the SD of the theoretical distribution of the sample means (the sampling distribution).
Key Takeaways
- Standard deviation (SD) measures the dispersion of a dataset relative to its mean.
- SD is used frequently in statistics, and in finance is often used as a proxy for the volatility or riskiness of an investment.
- The standard error of the mean (SEM) measures how much discrepancy is likely in a sample’s mean compared with the population mean.
- The SEM takes the SD and divides it by the square root of the sample size.
- The SEM will always be smaller than the SD.
Click Play to Learn the Difference Between Standard Error and Standard Deviation
Standard error estimates the likely accuracy of a number based on the sample size.
Standard error of the mean, or SEM, indicates the size of the likely discrepancy compared to that of the larger population.
Calculating SD and SEM
standard deviation
σ
=
∑
i
=
1
n
(
x
i
−
x
ˉ
)
2
n
−
1
variance
=
σ
2
standard error
(
σ
x
ˉ
)
=
σ
n
where:
x
ˉ
=
the sample’s mean
n
=
the sample size
begin{aligned} &text{standard deviation } sigma = sqrt{ frac{ sum_{i=1}^n{left(x_i — bar{x}right)^2} }{n-1} } \ &text{variance} = {sigma ^2 } \ &text{standard error }left( sigma_{bar x} right) = frac{{sigma }}{sqrt{n}} \ &textbf{where:}\ &bar{x}=text{the sample’s mean}\ &n=text{the sample size}\ end{aligned}
standard deviation σ=n−1∑i=1n(xi−xˉ)2variance=σ2standard error (σxˉ)=nσwhere:xˉ=the sample’s meann=the sample size
Standard Deviation
The formula for the SD requires a few steps:
- First, take the square of the difference between each data point and the sample mean, finding the sum of those values.
- Next, divide that sum by the sample size minus one, which is the variance.
- Finally, take the square root of the variance to get the SD.
Standard Error of the Mean
SEM is calculated simply by taking the standard deviation and dividing it by the square root of the sample size.
Standard error gives the accuracy of a sample mean by measuring the sample-to-sample variability of the sample means. The SEM describes how precise the mean of the sample is as an estimate of the true mean of the population.
As the size of the sample data grows larger, the SEM decreases vs. the SD. As the sample size increases, the sample mean estimates the true mean of the population with greater precision.
Increasing the sample size does not make the SD necessarily larger or smaller; it just becomes a more accurate estimate of the population SD.
A sampling distribution is a probability distribution of a sample statistic taken from a greater population. Researchers typically use sample data to estimate the population data, and the sampling distribution explains how the sample mean will vary from sample to sample. The standard error of the mean is the standard deviation of the sampling distribution of the mean.
Standard Error and Standard Deviation in Finance
In finance, the SEM daily return of an asset measures the accuracy of the sample mean as an estimate of the long-run (persistent) mean daily return of the asset.
On the other hand, the SD of the return measures deviations of individual returns from the mean. Thus, SD is a measure of volatility and can be used as a risk measure for an investment.
Assets with greater day-to-day price movements have a higher SD than assets with lesser day-to-day movements. Assuming a normal distribution, around 68% of daily price changes are within one SD of the mean, with around 95% of daily price changes within two SDs of the mean.
How Are Standard Deviation and Standard Error of the Mean Different?
Standard deviation measures the variability from specific data points to the mean. Standard error of the mean measures the precision of the sample mean to the population mean that it is meant to estimate.
Is the Standard Error Equal to the Standard Deviation?
No, the standard deviation (SD) will always be larger than the standard error (SE). This is because the standard error divides the standard deviation by the square root of the sample size.
If the sample size is one, they will be the same, but a sample size of one is rarely useful.
How Can You Compute the SE From the SD?
If you have the standard error (SE) and want to compute the standard deviation (SD) from it, simply multiply it by the square root of the sample size.
Why Do We Use Standard Error Instead of Standard Deviation?
What Is the Empirical Rule, and How Does It Relate to Standard Deviation?
A normal distribution is also known as a standard bell curve, since it looks like a bell in graph form. According to the empirical rule, or the 68-95-99.7 rule, 68% of all data observed under a normal distribution will fall within one standard deviation of the mean. Similarly, 95% falls within two standard deviations and 99.7% within three.
The Bottom Line
Investors and analysts measure standard deviation as a way to estimate the potential volatility of a stock or other investment. It helps determine the level of risk to the investor that is involved. When reading an analyst’s report, the level of riskiness of an investment may be labeled «standard deviation.»
Standard error of the mean is an indication of the likely accuracy of a number. The larger the sample size, the more accurate the number should be.
From Wikipedia, the free encyclopedia
For a value that is sampled with an unbiased normally distributed error, the above depicts the proportion of samples that would fall between 0, 1, 2, and 3 standard deviations above and below the actual value.
The standard error (SE)[1] of a statistic (usually an estimate of a parameter) is the standard deviation of its sampling distribution[2] or an estimate of that standard deviation. If the statistic is the sample mean, it is called the standard error of the mean (SEM).[1]
The sampling distribution of a mean is generated by repeated sampling from the same population and recording of the sample means obtained. This forms a distribution of different means, and this distribution has its own mean and variance. Mathematically, the variance of the sampling mean distribution obtained is equal to the variance of the population divided by the sample size. This is because as the sample size increases, sample means cluster more closely around the population mean.
Therefore, the relationship between the standard error of the mean and the standard deviation is such that, for a given sample size, the standard error of the mean equals the standard deviation divided by the square root of the sample size.[1] In other words, the standard error of the mean is a measure of the dispersion of sample means around the population mean.
In regression analysis, the term «standard error» refers either to the square root of the reduced chi-squared statistic or the standard error for a particular regression coefficient (as used in, say, confidence intervals).
Standard error of the sample mean[edit]
Exact value[edit]
Suppose a statistically independent sample of 




.
Practically this tells us that when trying to estimate the value of a population mean, due to the factor 
Estimate[edit]
The standard deviation 


.
As this is only an estimator for the true «standard error», it is common to see other notations here such as:
or alternately
.
A common source of confusion occurs when failing to distinguish clearly between:
Accuracy of the estimator[edit]
When the sample size is small, using the standard deviation of the sample instead of the true standard deviation of the population will tend to systematically underestimate the population standard deviation, and therefore also the standard error. With n = 2, the underestimate is about 25%, but for n = 6, the underestimate is only 5%. Gurland and Tripathi (1971) provide a correction and equation for this effect.[3] Sokal and Rohlf (1981) give an equation of the correction factor for small samples of n < 20.[4] See unbiased estimation of standard deviation for further discussion.
Derivation[edit]
The standard error on the mean may be derived from the variance of a sum of independent random variables,[5] given the definition of variance and some simple properties thereof. If 



which due to the Bienaymé formula, will have variance
where we’ve approximated the standard deviations, i.e., the uncertainties, of the measurements themselves with the best value for the standard deviation of the population. The mean of these measurements 
.
The variance of the mean is then
The standard error is, by definition, the standard deviation of 
.
For correlated random variables the sample variance needs to be computed according to the Markov chain central limit theorem.
Independent and identically distributed random variables with random sample size[edit]
There are cases when a sample is taken without knowing, in advance, how many observations will be acceptable according to some criterion. In such cases, the sample size 

[6]
If 




(since the standard deviation is the square root of the variance)
Student approximation when σ value is unknown[edit]
In many practical applications, the true value of σ is unknown. As a result, we need to use a distribution that takes into account that spread of possible σ’s.
When the true underlying distribution is known to be Gaussian, although with unknown σ, then the resulting estimated distribution follows the Student t-distribution. The standard error is the standard deviation of the Student t-distribution. T-distributions are slightly different from Gaussian, and vary depending on the size of the sample. Small samples are somewhat more likely to underestimate the population standard deviation and have a mean that differs from the true population mean, and the Student t-distribution accounts for the probability of these events with somewhat heavier tails compared to a Gaussian. To estimate the standard error of a Student t-distribution it is sufficient to use the sample standard deviation «s» instead of σ, and we could use this value to calculate confidence intervals.
Note: The Student’s probability distribution is approximated well by the Gaussian distribution when the sample size is over 100. For such samples one can use the latter distribution, which is much simpler.
Assumptions and usage[edit]
An example of how 


- Upper 95% limit
and
- Lower 95% limit
In particular, the standard error of a sample statistic (such as sample mean) is the actual or estimated standard deviation of the sample mean in the process by which it was generated. In other words, it is the actual or estimated standard deviation of the sampling distribution of the sample statistic. The notation for standard error can be any one of SE, SEM (for standard error of measurement or mean), or SE.
Standard errors provide simple measures of uncertainty in a value and are often used because:
- in many cases, if the standard error of several individual quantities is known then the standard error of some function of the quantities can be easily calculated;
- when the probability distribution of the value is known, it can be used to calculate an exact confidence interval;
- when the probability distribution is unknown, Chebyshev’s or the Vysochanskiï–Petunin inequalities can be used to calculate a conservative confidence interval; and
- as the sample size tends to infinity the central limit theorem guarantees that the sampling distribution of the mean is asymptotically normal.
Standard error of mean versus standard deviation[edit]
In scientific and technical literature, experimental data are often summarized either using the mean and standard deviation of the sample data or the mean with the standard error. This often leads to confusion about their interchangeability. However, the mean and standard deviation are descriptive statistics, whereas the standard error of the mean is descriptive of the random sampling process. The standard deviation of the sample data is a description of the variation in measurements, while the standard error of the mean is a probabilistic statement about how the sample size will provide a better bound on estimates of the population mean, in light of the central limit theorem.[7]
Put simply, the standard error of the sample mean is an estimate of how far the sample mean is likely to be from the population mean, whereas the standard deviation of the sample is the degree to which individuals within the sample differ from the sample mean.[8] If the population standard deviation is finite, the standard error of the mean of the sample will tend to zero with increasing sample size, because the estimate of the population mean will improve, while the standard deviation of the sample will tend to approximate the population standard deviation as the sample size increases.
Extensions[edit]
Finite population correction (FPC)[edit]
The formula given above for the standard error assumes that the population is infinite. Nonetheless, it is often used for finite populations when people are interested in measuring the process that created the existing finite population (this is called an analytic study). Though the above formula is not exactly correct when the population is finite, the difference between the finite- and infinite-population versions will be small when sampling fraction is small (e.g. a small proportion of a finite population is studied). In this case people often do not correct for the finite population, essentially treating it as an «approximately infinite» population.
If one is interested in measuring an existing finite population that will not change over time, then it is necessary to adjust for the population size (called an enumerative study). When the sampling fraction (often termed f) is large (approximately at 5% or more) in an enumerative study, the estimate of the standard error must be corrected by multiplying by a »finite population correction» (a.k.a.: FPC):[9]
[10]
which, for large N:
to account for the added precision gained by sampling close to a larger percentage of the population. The effect of the FPC is that the error becomes zero when the sample size n is equal to the population size N.
This happens in survey methodology when sampling without replacement. If sampling with replacement, then FPC does not come into play.
Correction for correlation in the sample[edit]
Expected error in the mean of A for a sample of n data points with sample bias coefficient ρ. The unbiased standard error plots as the ρ = 0 diagonal line with log-log slope −½.
If values of the measured quantity A are not statistically independent but have been obtained from known locations in parameter space x, an unbiased estimate of the true standard error of the mean (actually a correction on the standard deviation part) may be obtained by multiplying the calculated standard error of the sample by the factor f:
where the sample bias coefficient ρ is the widely used Prais–Winsten estimate of the autocorrelation-coefficient (a quantity between −1 and +1) for all sample point pairs. This approximate formula is for moderate to large sample sizes; the reference gives the exact formulas for any sample size, and can be applied to heavily autocorrelated time series like Wall Street stock quotes. Moreover, this formula works for positive and negative ρ alike.[11] See also unbiased estimation of standard deviation for more discussion.
See also[edit]
- Illustration of the central limit theorem
- Margin of error
- Probable error
- Standard error of the weighted mean
- Sample mean and sample covariance
- Standard error of the median
- Variance
References[edit]
- ^ a b c d Altman, Douglas G; Bland, J Martin (2005-10-15). «Standard deviations and standard errors». BMJ: British Medical Journal. 331 (7521): 903. doi:10.1136/bmj.331.7521.903. ISSN 0959-8138. PMC 1255808. PMID 16223828.
- ^ Everitt, B. S. (2003). The Cambridge Dictionary of Statistics. CUP. ISBN 978-0-521-81099-9.
- ^ Gurland, J; Tripathi RC (1971). «A simple approximation for unbiased estimation of the standard deviation». American Statistician. 25 (4): 30–32. doi:10.2307/2682923. JSTOR 2682923.
- ^ Sokal; Rohlf (1981). Biometry: Principles and Practice of Statistics in Biological Research (2nd ed.). p. 53. ISBN 978-0-7167-1254-1.
- ^ Hutchinson, T. P. (1993). Essentials of Statistical Methods, in 41 pages. Adelaide: Rumsby. ISBN 978-0-646-12621-0.
- ^ Cornell, J R, and Benjamin, C A, Probability, Statistics, and Decisions for Civil Engineers, McGraw-Hill, NY, 1970, ISBN 0486796094, pp. 178–9.
- ^ Barde, M. (2012). «What to use to express the variability of data: Standard deviation or standard error of mean?». Perspect. Clin. Res. 3 (3): 113–116. doi:10.4103/2229-3485.100662. PMC 3487226. PMID 23125963.
- ^ Wassertheil-Smoller, Sylvia (1995). Biostatistics and Epidemiology : A Primer for Health Professionals (Second ed.). New York: Springer. pp. 40–43. ISBN 0-387-94388-9.
- ^ Isserlis, L. (1918). «On the value of a mean as calculated from a sample». Journal of the Royal Statistical Society. 81 (1): 75–81. doi:10.2307/2340569. JSTOR 2340569. (Equation 1)
- ^ Bondy, Warren; Zlot, William (1976). «The Standard Error of the Mean and the Difference Between Means for Finite Populations». The American Statistician. 30 (2): 96–97. doi:10.1080/00031305.1976.10479149. JSTOR 2683803. (Equation 2)
- ^ Bence, James R. (1995). «Analysis of Short Time Series: Correcting for Autocorrelation». Ecology. 76 (2): 628–639. doi:10.2307/1941218. JSTOR 1941218.
Download Article
Download Article
After collecting data, oftentimes the first thing you need to do is analyze it. This usually entails finding the mean, the standard deviation, and the standard error of the data. This article will show you how it’s done.
Cheat Sheets
-
1
Obtain a set of numbers you wish to analyze. This information is referred to as a sample.
- For example, a test was given to a class of 5 students, and the test results are 12, 55, 74, 79 and 90.
Advertisement
-
1
Calculate the mean. Add up all the numbers and divide by the population size:[1]
- Mean (μ) = ΣX/N, where Σ is the summation (addition) sign, xi is each individual number, and N is the population size.
- In the case above, the mean μ is simply (12+55+74+79+90)/5 = 62.
-
1
Calculate the standard deviation. This represents the spread of the population.
Standard deviation = σ = sq rt [(Σ((X-μ)^2))/(N)].[2]
- For the example given, the standard deviation is sqrt[((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27.4. (Note that if this was the sample standard deviation, you would divide by n-1, the sample size minus 1.)
Advertisement
-
1
Calculate the standard error (of the mean). This represents how well the sample mean approximates the population mean. The larger the sample, the smaller the standard error, and the closer the sample mean approximates the population mean. Do this by dividing the standard deviation by the square root of N, the sample size.[3]
Standard error = σ/sqrt(n)[4]
- So for the example above, if this were a sampling of 5 students from a class of 50 and the 50 students had a standard deviation of 17 (σ = 21), the standard error = 17/sqrt(5) = 7.6.
Add New Question
-
Question
How do you find the mean given number of observations?
To find the mean, add all the numbers together and divide by how many numbers there are. e.g to find the mean of 1,7,8,4,2: 1+7+8+4+2 = 22/5 = 4.4.
-
Question
The standard error is calculated as 0.2 and the standard deviation of a sample is 5kg. Can it be said to be smaller or larger than the standard deviation?
The standard error (SE) must be smaller than the standard deviation (SD), because the SE is calculating by dividing the SD by something — i.e. making it smaller.
-
Question
How can I find out the standard deviation of 50 samples?
The results of all your figures (number plus number plus number etc.) divided by quantity of samples 50 =SD.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Calculations of the mean, standard deviation, and standard error are most useful for analysis of normally distributed data. One standard deviation about the central tendency covers approximately 68 percent of the data, 2 standard deviation 95 percent of the data, and 3 standard deviation 99.7 percent of the data. The standard error gets smaller (narrower spread) as the sample size increases.
Thanks for submitting a tip for review!
Advertisement
-
Check your math carefully. It is very easy to make mistakes or enter numbers incorrectly.
Advertisement
References
About This Article
Article SummaryX
The mean is simply the average of a set of numbers. You can work it out by adding up all the numbers and dividing the total by the amount of numbers. For example, if you wanted to find the average test score of 3 students who scored 74, 79, and 90, you’d add the 3 numbers together to get 243, then divide it by 3 to get 81. The standard error represents how well the sample mean approximates the population mean. All you need to do is divide the standard deviation by the square root of the sample size. For instance, if you were sampling 5 students from a class of 50 and the 50 students had a standard deviation of 17, you’d divide 17 by the square root of 5 to get 7.6. For more tips, including how to calculate the standard deviation, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 996,034 times.
Did this article help you?
Perhaps you’ve come across the terms “standard deviation” and “standard error” and are wondering what the difference is. What are they used for, and what do they actually mean for data analysts? Well, you’ve come to the right place. Keep reading for a beginner-friendly explanation.
When analyzing and interpreting data, you’re trying to find patterns and insights that can tell you something useful. For example, you might use data to better understand the spending habits of people who live in a certain city. In this case, it most likely wouldn’t be possible to collect the data you need from every single person living in that city—rather, you’d use a sample of data and then apply your findings to the general population. As part of your analysis, it’s important to understand how accurately or closely the sample data represents the whole population. In other words, how applicable are your findings?
This is where statistics like standard deviation and standard error come in. In this post, we’ll explain exactly what standard deviation and standard error mean, as well as the key differences between them. First, though, we’ll set the scene by briefly recapping the difference between descriptive and inferential statistics (as standard deviation is a descriptive statistic, while standard error an inferential statistic). Sound confusing? Don’t worry! All will become clear by the end of this post.
If you’re already familiar with descriptive vs inferential statistics, just use the clickable menu to skip ahead.
- Quick recap: What is the difference between descriptive and inferential statistics?
- What is standard deviation?
- How to calculate standard deviation
- What is standard error?
- How to calculate standard error
- Standard error vs standard deviation: What is the difference?
- Standard error vs standard deviation: When should you use them?
- Key takeaways and further reading
Are you ready to explore the difference between standard error and standard deviation? Let’s dive in.
1. What is the difference between descriptive and inferential statistics?
The first main difference between standard deviation and standard error is that standard deviation is a descriptive statistic while standard error is an inferential statistic. So what’s the difference?
Descriptive statistics are used to describe the characteristics or features of a dataset. This includes things like distribution(the frequency of different data points within a data sample—for example, how many people in the chosen population have brown hair, blonde hair, black hair, etc), measures of central tendency (the mean, median, and mode values), and variability (how the data is distributed—for example, looking at the minimum and maximum values within a dataset).
While descriptive statistics simply summarize your data, with inferential statistics, you’re making generalizations about a population (e.g. residents of New York City) based on a representative sample of data from that population. Inferential statistics are often expressed as a probability.
You can learn more about the difference between descriptive and inferential statistics in this guide, but for now, we’ll focus on the topic at hand: Standard deviation vs standard error.
So without further ado: What is standard deviation?
As already mentioned, standard deviation is a descriptive statistic, which means it helps you to describe or summarize your dataset. In simple terms, standard deviation tells you, on average, how far each value within your dataset lies from the mean. A high standard deviation means that the values within a dataset are generally positioned far away from the mean, while a low standard deviation indicates that the values tend to be clustered close to the mean. So, in a nutshell, it measures how much “spread” or variability there is within your dataset.
An example of standard deviation
Let’s illustrate this further with the help of an example. Suppose two shops X and Y have four employees each. In shop X, two employees earn $14 per hour and the other two earn $16 per hour. In shop Y, one employee earns $11 per hour, one earns $10 per hour, the third earns $19, and the fourth receives $20 per hour. The average hourly wage for each shop is $15, but you can see that some employees earn much closer to this average value than others.
For shop X, the employees’ wages are close to the average value of $15, with little variation (just one dollar difference either side), while for shop Y, the values are spread quite far apart from each other, and from the average. In this simple example, we can see this at a glance without doing any heavy calculations. But, in a more comprehensive and complex dataset, you’d calculate the standard deviation to tell you how far each individual value sits from the mean value.
We’ll look at how to calculate standard deviation in section three. For now, we’ll introduce two key concepts: Normal distribution and the empirical rule.
Normal distribution in standard deviation
Standard deviation can be interpreted by using normal distribution. In graph form, normal distribution is a bell-shaped curve which is used to display the distribution of independent and similar data values. In any normal distribution, data is symmetrical and distributed in fixed intervals around the mean. In terms of standard deviation, a graph (or curve) with a high, narrow peak and a small spread indicates low standard deviation, while a flatter, broader curve indicates high standard deviation.
What is the empirical rule?
If your dataset follows a normal distribution, you can interpret it using the empirical rule. The empirical rule states that almost all observed data will fall within three standard deviations of the mean:
- Around 68% of values fall within the first standard deviation of the mean
- Around 95% of values fall within the first two standard deviations of the mean
- Around 99.7% of values fall within the first three standard deviations of the mean
The empirical rule gives a quick overview of data and determines extreme values that don’t follow a pattern of normal distribution.
Now we know what standard deviation tells us, let’s take a look at how to calculate it.
3. How to calculate standard deviation
Now, you must be wondering about the formula used to calculate standard deviation. There are actually two formulas which can be used to calculate standard deviation depending on the nature of the data—are you calculating the standard deviation for population data or for sample data?
- Population data is when you have data for the entire group (or population) that you want to analyze. For example, if you’re collecting data on employees in your company and have data for all 100 employees, you are working with population data.
- Sample data is when you collect data from just a sample of the population you want to gather insights for. For example, if you wanted to collect data on residents of New York City, you’d likely get a sample rather than gathering data for every single person who lives in New York.
With that in mind, you can calculate standard deviation as follows:
How to calculate standard deviation for population data
To calculate standard deviation for population data, the formula is:

Where:
- refers to population standard deviation
- ∑ refers to sum of values
- xi refers to each value
- refers to population mean
- N refers to number of values in the sample
How to calculate standard deviation for sample data
To calculate standard deviation for sample data, you can use the following formula:
Where:
- s refers to sample standard deviation
- ∑ refers to sum of values
- xi refers to each value
- x̅ refers to sample mean
- N refers to number of values in the sample
At this stage, simply having the mathematical formula may not be all that helpful. Let’s take a look at the actual steps involved in calculating the standard deviation.
How to calculate the standard deviation (step by step)
Here we’ll break down the formula for standard deviation, step by step.
- Find the mean: Add up all the scores (or values) in your dataset and divide them by the total number of scores or data points.
- Calculate the deviation from the mean for each individual score or value: Subtract the mean value (from step one) from each individual value or score you have in your dataset. You’ll end up with a set of deviation values.
- Square each deviation from the mean: Multiply each deviation value you got in step two by itself. E.g. if the deviation value is 4, multiply it by 4.
- Find the sum of squares: Add up all of the squared deviations as calculated in step three. This will give you a single value known as the sum of squares.
- Find the variance: Divide the sum of the squares by n − 1 for sample data, or by N for population data. N denotes the total number of scores or values within your dataset, so if you collected data on thirty employees, N is thirty. This will give you a variance value.
- Find the square root of the variance: Calculate the square root of the variance (as calculated in step five). This gives you the standard deviation (SD).
Let’s further illustrate the step-by-step procedure of calculating standard deviation through an interesting example.
How to calculate standard deviation with an example (in Excel or Google Sheets)
Let’s imagine a group of fifteen employees took part in an assessment, and their employer wants to know how much variation there is in the test scores. Did all employees perform at a similar level, or was there a high standard deviation? The test scores are as follows:
Now let’s calculate the standard deviation for our dataset, following the step-by-step process laid out previously. We’ll use formulas in Google Sheets / Excel, but you can also calculate these values manually.
- Find the mean: Add all test scores together and divide the total score by the number of scores (1280 / 15 = 85.3). Your mean value is 85.3. In Google Sheets, we used the formula =SUM(A2:A16)/15
- Calculate the deviation from the mean for each score and then square this value: Subtract the mean value (85.3) from each test score, and then square it. In Google Sheets, we used the formula =(A2-85.3)^2 (and so on). 3
- Find the sum of the squares: Add up all of the squared deviations (in column B) to find the sum of the squares. In Google Sheets, we used the formula =SUM(B2:B16) to get the value 1139.35.
- Find the variance: Divide the sum of the squares by N (as we’re using population data). So: 1139.35 / 15 = 75.96.
- Find the square root of the variance to get the standard deviation: You can calculate the square root in Excel or Google Sheets using the following formula: =B18^0.5. In our example, the square root of 75.96 is 8.7.
So, for the employee test scores, the standard deviation is 8.7. This is low variance, indicating that all employees performed at a similar level.
4. What is standard error?
Standard error (or standard error of the mean) is an inferential statistic that tells you, in simple terms, how accurately your sample data represents the whole population. For example, if you conduct a survey of people living in New York, you’re collecting a sample of data that represents a segment of the entire population of New York. Different samples of the same population will give you different results, so it’s important to understand how applicable your findings are. So, when you take the mean results from your sample data and compare it with the overall population mean on a distribution, the standard error tells you what the variance is between the two means. In other words, how much would the sample mean vary if you were to repeat the same study with a different sample of people from the New York City population?
Just like standard deviation, standard error is a measure of variability. However, the difference is that standard deviationdescribes variability within a single sample, while standard error describes variability across multiple samples of a population. We’ll explore those differences in more detail in section six. For now, let’s continue to explore standard error.
Standard error can either be high or low. In the case of high standard error, your sample data does not accurately represent the population data; the sample means are widely spread around the population mean. In the case of low standard error, your sample is a more accurate representation of the population data, with the sample means closely distributed around the population mean.
What is the relationship between standard error (SE) and the sample size?
Sample size is inversely proportional to standard error, and so the standard error can be minimized by using a large sample size. As you can see from this graph, the larger the sample size, the lower the standard error.
5. How to calculate standard error
The computational method for calculating standard error is very similar to that of standard deviation, with a slight difference in formula. The exact formula you use will depend on whether or not the population standard deviation is known. It’s also important to note that the following formulas can only be applied to data samples containing more than 20 values.
So, if the population standard deviation is known, you can use this formula to calculate standard error:
Where:
- SE refers to standard error of all possible samples from a single population
- σ refers to population standard deviation
- n refers to the number of values in the sample
If the population standard deviation is not known, use this formula:
Where:
- SE refers to standard error of all possible samples from a single population
- s refers to sample standard deviation which is a point estimate of population standard deviation
- n refers to the number of values in the sample
How to calculate standard error (step by step)
Let’s break that process down step by step.
- Find the square root of your sample size (n)
- Find the standard deviation for your data sample (following the steps laid out in section three of this guide)
- Divide the sample standard deviation (as found in step 2) by the square root of your sample size (as calculated in step 1)
Let’s solve a problem step-by-step to show you how to calculate the standard error of mean by hand.
How to calculate standard error with an example
Suppose a large number of students from multiple schools participated in a design competition. From the whole population of students, evaluators chose a sample of 300 students for a second round. The mean of their competition scores is 650, while the sample standard deviation of scores is 220. Now let’s calculate the standard error.
- Find the square root of the sample size. In our example,n = 300, and you can calculate the square root in Excel or Google Sheets using the following formula: =300^0.5. So n= 17.32
- Find the standard deviation for your data sample. You can do this following the steps laid out in section three, but for now we’ll take it as known that the sample standard deviation S = 220.
- Divide the sample standard deviation by the square root of the sample size. So, in our example, 220 / 17.32 = 12.7. So, the standard error is 12.7.
When reporting the standard error, you would write (for our example): The mean test score is 650 ± 12.7 (SE).
6. Standard error vs standard deviation: What’s the difference?
Now we know what standard deviation and standard error are, let’s examine the differences between them. The key differences are:
- Standard deviation describes variability within a single sample, while standard error describes variability across multiple samples of a population.
- Standard deviation is a descriptive statistic that can be calculated from sample data, while standard error is an inferential statistic that can only be estimated.
- Standard deviation measures how much observations vary from one another, while standard error looks at how accurate the mean of a sample of data is compared to the true population mean.
- The formula for standard deviation calculates the square root of the variance, while the formula for standard error calculates the standard deviation divided by the square root of the sample size.
7. Standard error vs standard deviation: When should you use which?
With those differences in mind, when should you use standard deviation and when should you use standard error?
Standard deviation is useful when you need to compare and describe different data values that are widely scattered within a single dataset. Because standard deviation measures how close each observation is to the mean, it can tell you how precise the measurements are. So, if you have a dataset forecasting air pollution for a certain city, a standard deviation of 0.89 (i.e. a low standard deviation) shows you that the data is precise.
Standard error is useful if you want to test a hypothesis, as it allows you to gauge how accurate and precise your sample data is in relation to drawing conclusions about the actual overall population. For example, if you want to investigate the spending habits of everyone over 50 in New York City, using a sample of 500 people, standard error can tell you how “powerful” or applicable your findings are.
8. Key takeaways and further reading
In this guide, we’ve explained how to calculate standard error and standard deviation, and outlined the key differences between the two. In summary, standard deviation tells you how far each value lies from the mean within a single dataset, while standard error tells you how accurately your sample data represents the whole population.
Statistical concepts such as these form the very basis of data analytics, so it’s important to get your head around them if you’re considering a career in data analytics or data science. If you’d like to try your hand at analyzing real data, we can recommend this free introductory data analytics short course. And, for more useful guides, check out the following:
- What’s the difference between covariance and correlation?
- What is exploratory data analysis?
- What is multivariate data analysis?
Стандартное отклонение и стандартная ошибка: в чем разница?
17 авг. 2022 г.
читать 2 мин
В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .
Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.
Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.
Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.
Пример: стандартное отклонение против стандартной ошибки
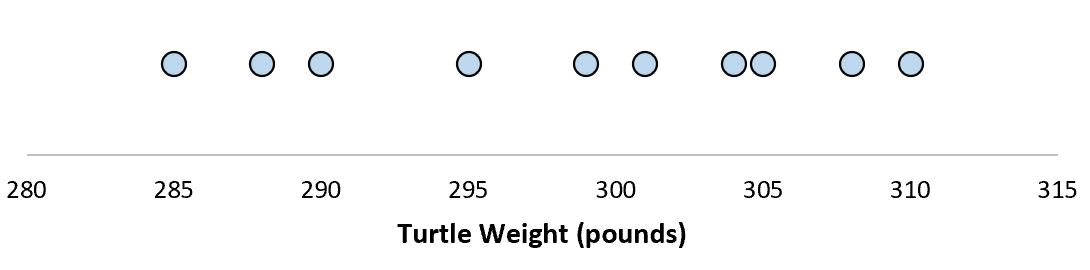
Предположим, мы измеряем вес 10 разных черепах.
Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:
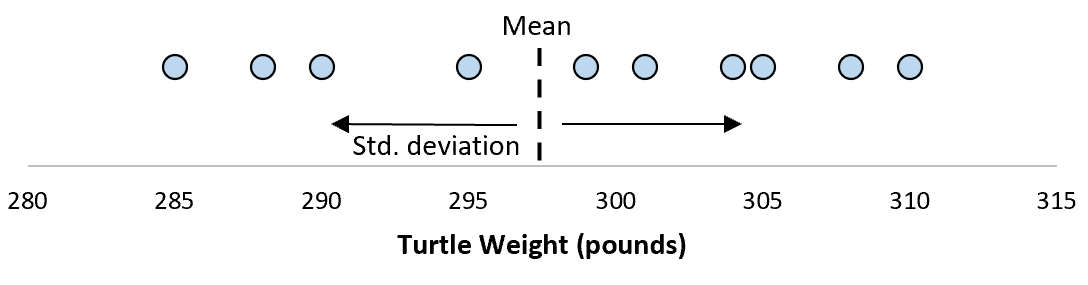
Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.
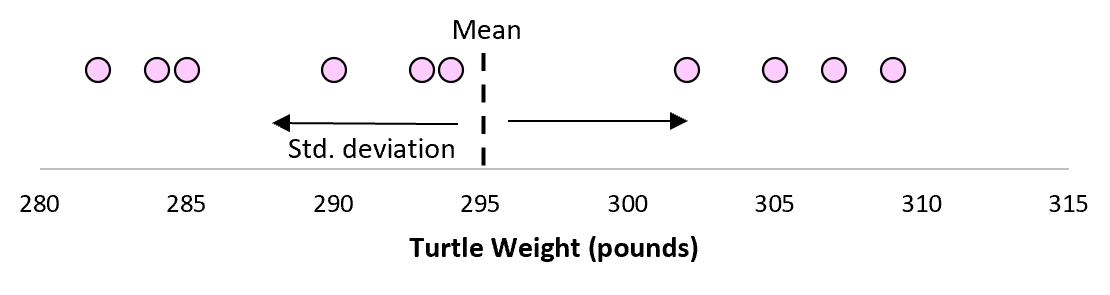
Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:
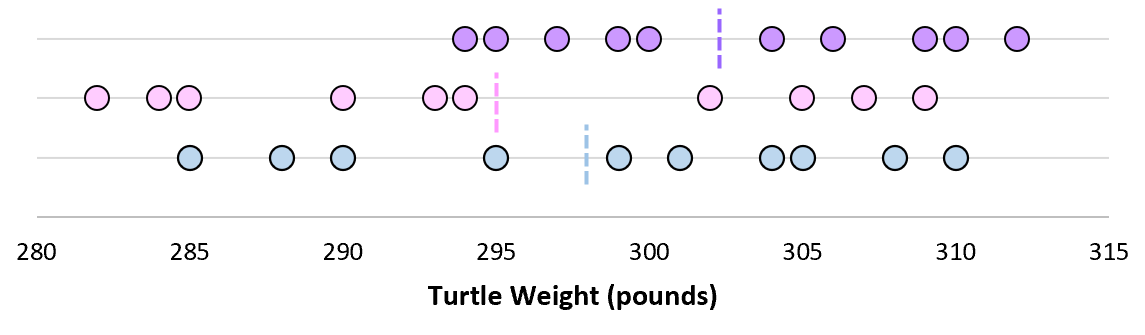
Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:
Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:
Стандартное отклонение этих средних значений известно как стандартная ошибка.
Формула для фактического расчета стандартной ошибки:
Стандартная ошибка = s/ √n
куда:
- s: стандартное отклонение выборки
- n: размер выборки
Какой смысл использовать стандартную ошибку?
Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.
Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.
Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:
Стандартная ошибка = s/ √n
Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.
Когда использовать стандартное отклонение против стандартной ошибки
Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .
Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .
В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.

Standard Error is used to measure the statistical accuracy of an estimate. It is primarily used in the process of testing hypothesis and estimating interval.
These are two important concepts of statistics, which are widely used in the field of research. The difference between standard deviation and standard error is based on the difference between the description of data and its inference.
- Comparison Chart
- Definition
- Key Differences
- Conclusion
Comparison Chart
| Basis for Comparison | Standard Deviation | Standard Error |
|---|---|---|
| Meaning | Standard Deviation implies a measure of dispersion of the set of values from their mean. | Standard Error connotes the measure of statistical exactness of an estimate. |
| Statistic | Descriptive | Inferential |
| Measures | How much observations vary from each other. | How precise the sample mean to the true population mean. |
| Distribution | Distribution of observation concerning normal curve. | Distribution of an estimate concerning normal curve. |
| Formula | Square root of variance | Standard deviation divided by square root of sample size. |
| Increase in sample size | Gives a more specific measure of standard deviation. | Decreases standard error. |
Definition of Standard Deviation
Standard Deviation, is a measure of the spread of a series or the distance from the standard. In 1893, Karl Pearson coined the notion of standard deviation, which is undoubtedly most used measure, in research studies.
It is the square root of the average of squares of deviations from their mean. In other words, for a given data set, the standard deviation is the root-mean-square-deviation, from arithmetic mean. For the whole population, it is indicated by Greek letter ‘sigma (σ)’, and for a sample, it is represented by Latin letter ‘s’.
Standard Deviation is a measure that quantifies the degree of dispersion of the set of observations. The farther the data points from the mean value, the greater is the deviation within the data set, representing that data points are scattered over a wider range of values and vice versa.
Definition of Standard Error
You might have observed that different samples, with identical size, drawn from the same population, will give diverse values of statistic under consideration, i.e. sample mean. Standard Error (SE) provides, the standard deviation in different values of the sample mean. It is used to make a comparison between sample means across the populations.
In short, standard error of a statistic is nothing but the standard deviation of its sampling distribution. It has a great role to play the testing of statistical hypothesis and interval estimation. It gives an idea of the exactness and reliability of the estimate. The smaller the standard error, the greater is the uniformity of the theoretical distribution and vice versa.
- Formula: Standard Error for sample mean = σ/√n
Where, σ is population standard deviation
Key Differences Between Standard Deviation and Standard Error
The points stated below are substantial so far as the difference between standard deviation is concerned:
- Standard Deviation is the measure which assesses the amount of variation in the set of observations. Standard Error gauges the accuracy of an estimate, i.e. it is the measure of variability of the theoretical distribution of a statistic.
- Standard Deviation is a descriptive statistic, whereas the standard error is an inferential statistic.
- Standard Deviation measures how far the individual values are from the mean value. On the contrary, how close the sample mean is to the population mean.
- Standard Deviation is the distribution of observations with reference to the normal curve. As against this, the standard error is the distribution of an estimate with reference to the normal curve.
- Standard Deviation is defined as the square root of the variance. Conversely, the standard error is described as the standard deviation divided by square root of sample size.
- When the sample size is raised, it provides a more particular measure of standard deviation. Unlike, standard error when the sample size is increased, the standard error tends to decrease.
Conclusion
By and large, the standard deviation is considered as one of the best measures of dispersion, which gauges the dispersion of values from the central value. On the other hand, the standard error is mainly used to check the reliability and accuracy of the estimate and so, the smaller the error, the greater is its reliability and accuracy.
Стандартное отклонение (SD), измеряет количество изменчивости или дисперсии, из отдельных значений данных, к среднему значению, в то время как стандартная ошибка среднего (SEM) мер, как далеко образец среднее (среднее) данных, вероятно, будет от истинного среднего значения населения. SEM всегда меньше SD.
Ключевые выводы
- Стандартное отклонение (SD) измеряет разброс набора данных относительно его среднего значения.
- Стандартная ошибка среднего (SEM) измеряет, насколько вероятно расхождение между средним значением выборки по сравнению со средним значением генеральной совокупности.
- SEM берет SD и делит его на квадратный корень из размера выборки.
SEM против SD
Стандартное отклонение и стандартная ошибка используются во всех типах статистических исследований, включая исследования в области финансов, медицины, биологии, инженерии, психологии и т. Д. В этих исследованиях стандартное отклонение (SD) и расчетная стандартная ошибка среднего (SEM) ) используются для представления характеристик данных выборки и объяснения результатов статистического анализа. Однако некоторые исследователи иногда путают SD и SEM. Таким исследователям следует помнить, что расчеты SD и SEM включают разные статистические выводы, каждый из которых имеет свое значение. SD – это разброс отдельных значений данных.
Другими словами, SD указывает, насколько точно среднее значение представляет данные выборки. Однако значение SEM включает статистический вывод, основанный на распределении выборки. SEM – это стандартное отклонение теоретического распределения выборочных средних (выборочное распределение).
Расчет стандартного отклонения
Формула SD требует нескольких шагов:
- Во-первых, возьмите квадрат разницы между каждой точкой данных и средним значением выборки, найдя сумму этих значений.
- Затем разделите эту сумму на размер выборки минус один, который представляет собой дисперсию.
- Наконец, извлеките квадратный корень из дисперсии, чтобы получить стандартное отклонение.
Стандартная ошибка среднего
SEM рассчитывается путем деления стандартного отклонения на квадратный корень из размера выборки.
Стандартная ошибка дает точность выборочного среднего путем измерения изменчивости выборочного среднего от образца к образцу. SEM описывает, насколько точное среднее значение выборки является оценкой истинного среднего значения совокупности. По мере увеличения размера выборки данных SEM уменьшается по сравнению с SD; следовательно, по мере увеличения размера выборки среднее значение выборки оценивает истинное среднее значение генеральной совокупности с большей точностью. Напротив, увеличение размера выборки не обязательно делает SD больше или меньше, это просто становится более точной оценкой SD населения.
Стандартная ошибка и стандартное отклонение в финансах
В финансах стандартная ошибка средней дневной доходности актива измеряет точность выборочного среднего как оценки долгосрочной (постоянной) средней дневной доходности актива.
С другой стороны, стандартное отклонение доходности измеряет отклонения индивидуальных доходов от среднего значения. Таким образом, SD является мерой волатильности и может использоваться в качестве меры риска для инвестиций. Активы с более высокими ежедневными движениями цен имеют более высокое SD, чем активы с меньшими ежедневными движениями. Предполагая нормальное распределение, около 68% дневных изменений цен находятся в пределах одного стандартного отклонения от среднего, при этом около 95% дневных изменений цен находятся в пределах двух стандартных значений среднего.