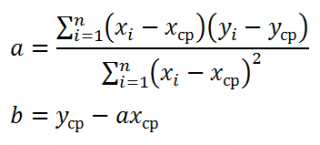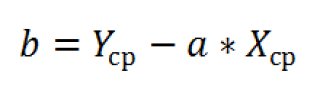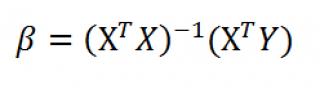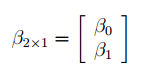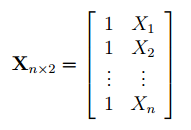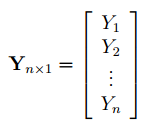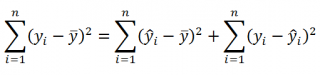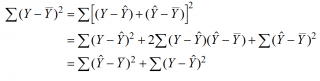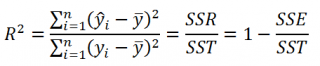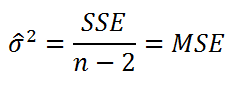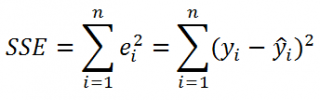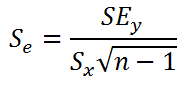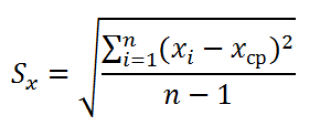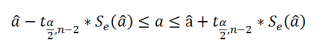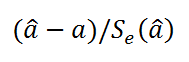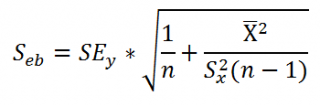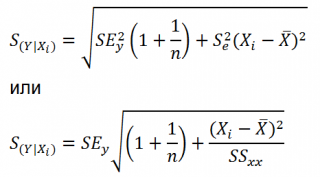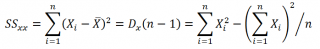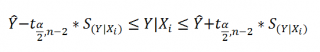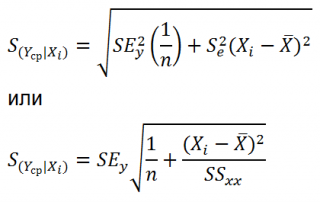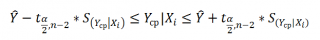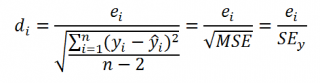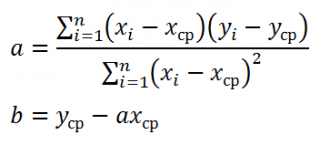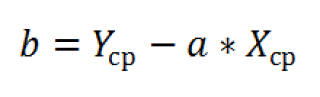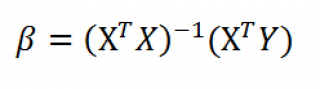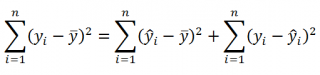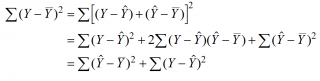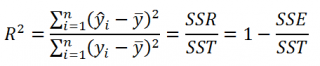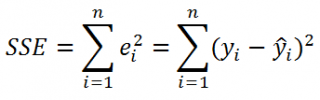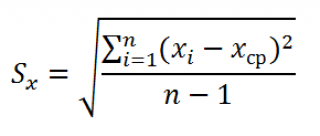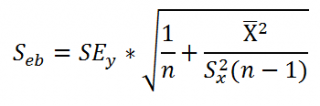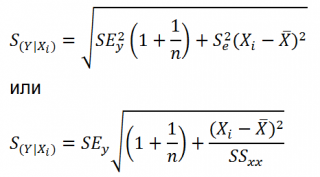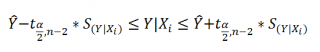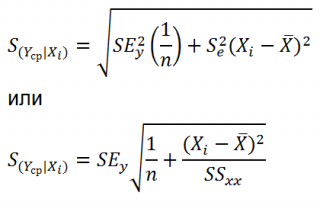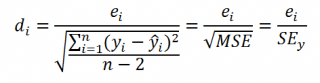Whenever we fit a linear regression model, the model takes on the following form:
Y = β0 + β1X + … + βiX +ϵ
where ϵ is an error term that is independent of X.
No matter how well X can be used to predict the values of Y, there will always be some random error in the model.
One way to measure the dispersion of this random error is by using the standard error of the regression model, which is a way to measure the standard deviation of the residuals ϵ.
This tutorial provides a step-by-step example of how to calculate the standard error of a regression model in Excel.
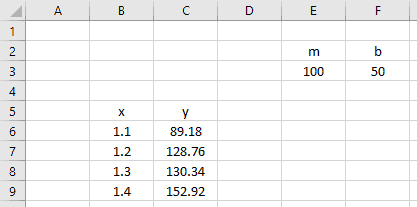
Step 1: Create the Data
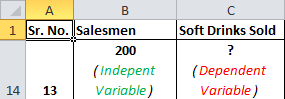
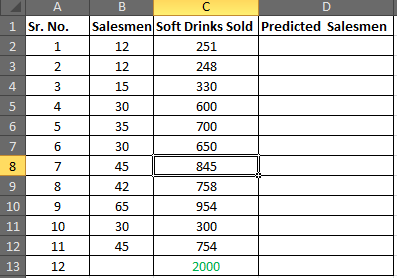
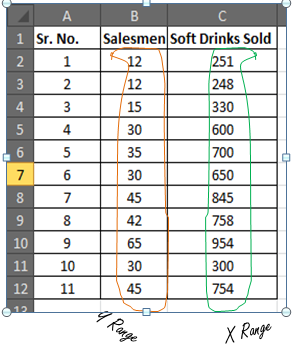
For this example, we’ll create a dataset that contains the following variables for 12 different students:
- Exam Score
- Hours Spent Studying
- Current Grade
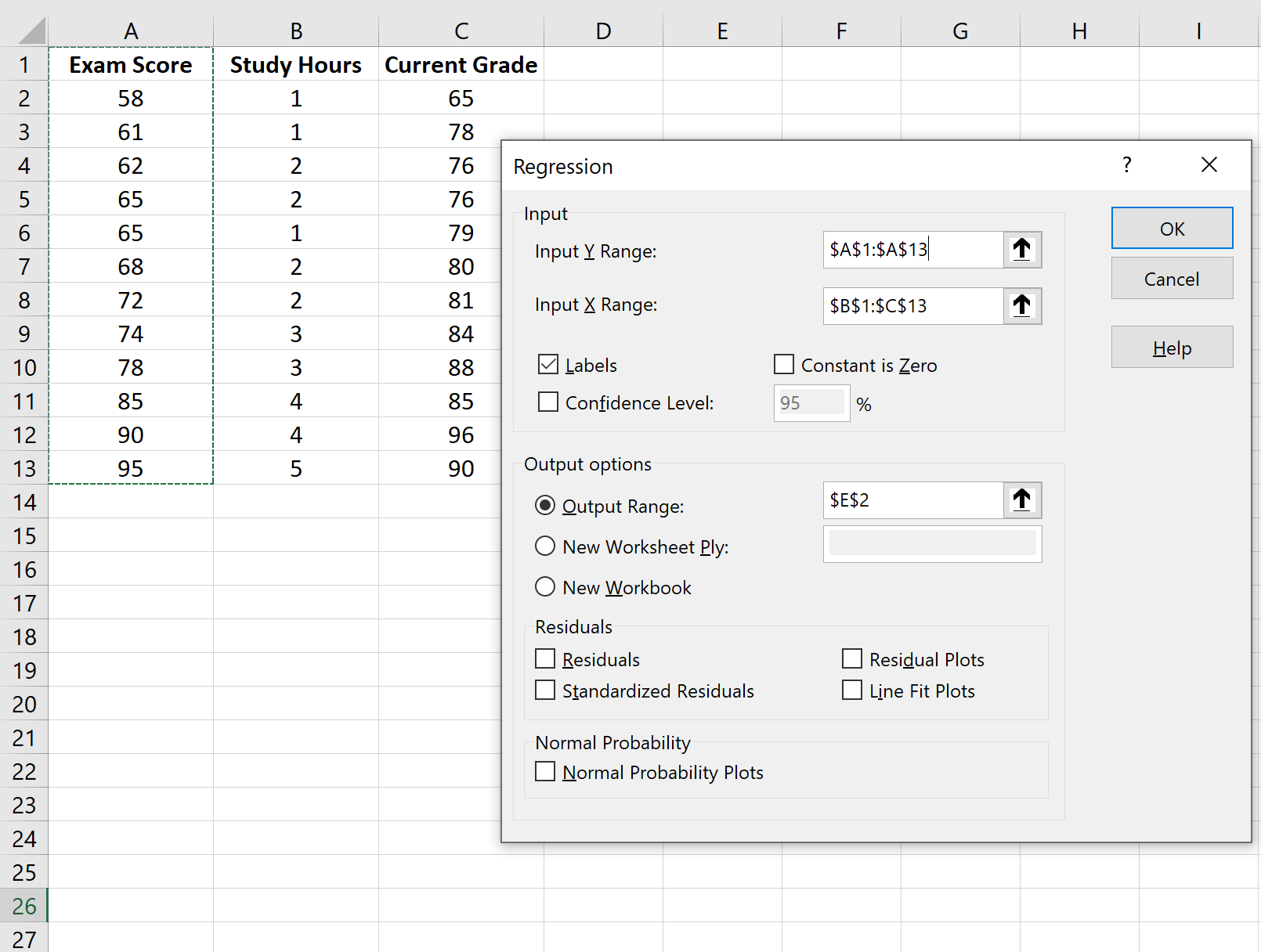
Step 2: Fit the Regression Model
Next, we’ll fit a multiple linear regression model using Exam Score as the response variable and Study Hours and Current Grade as the predictor variables.
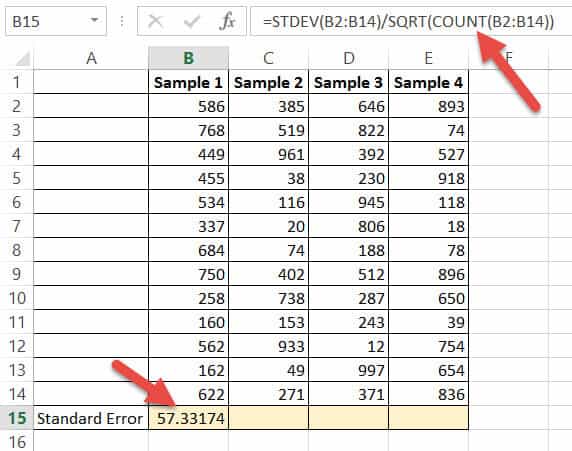
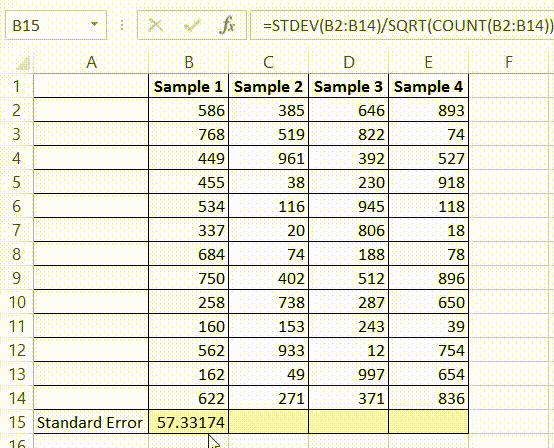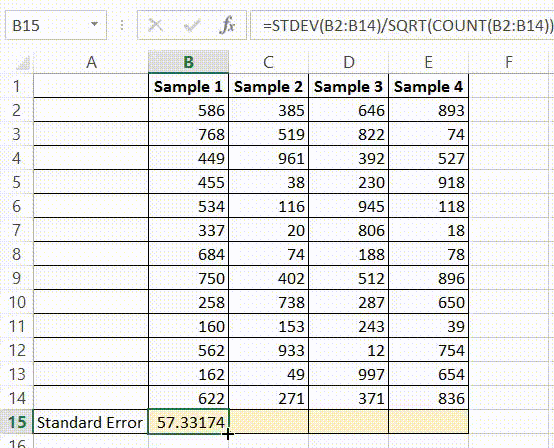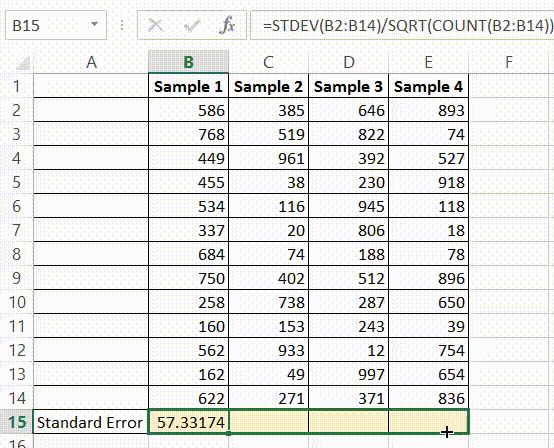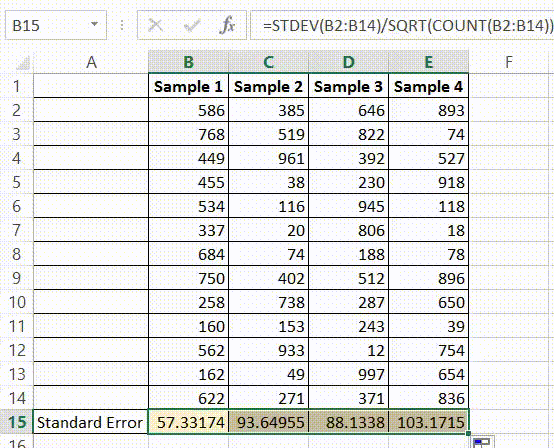
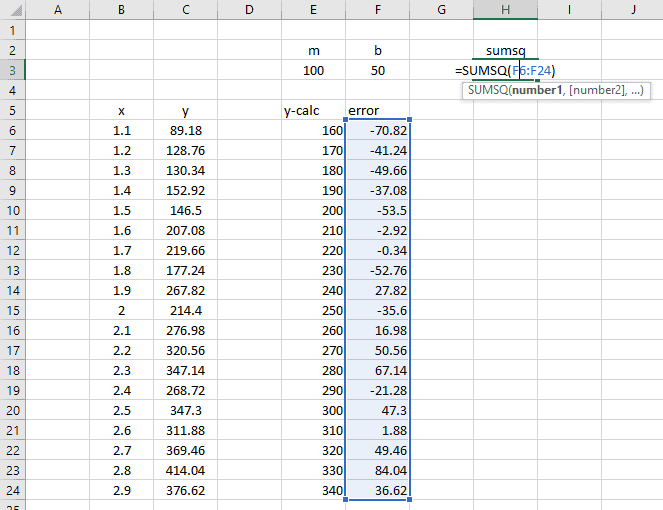
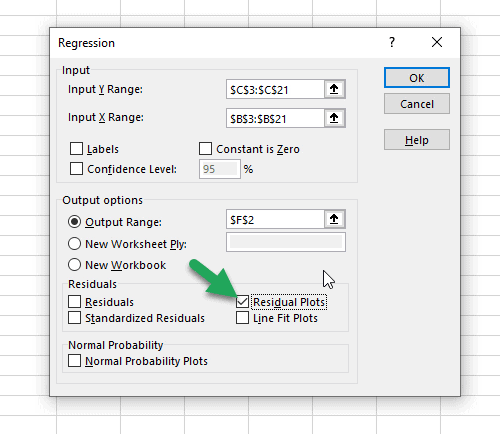
To do so, click the Data tab along the top ribbon and then click Data Analysis:
If you don’t see this option available, you need to first load the Data Analysis ToolPak.
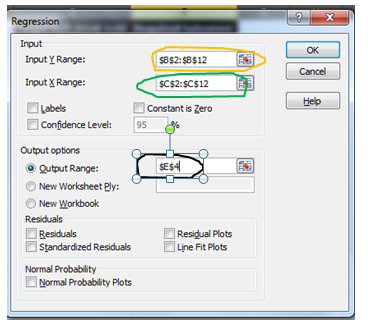
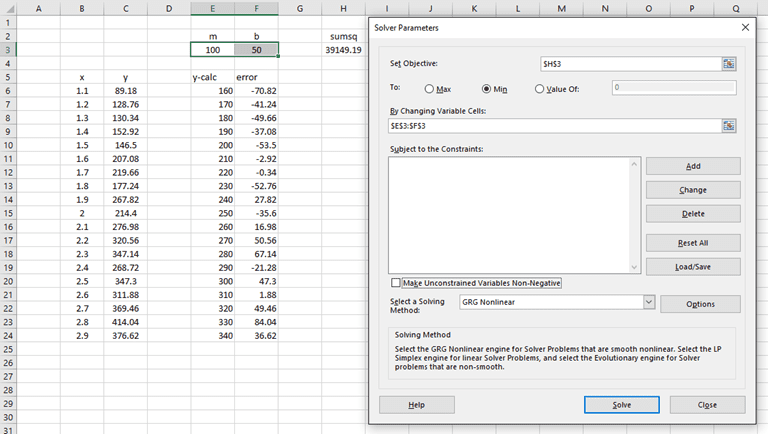
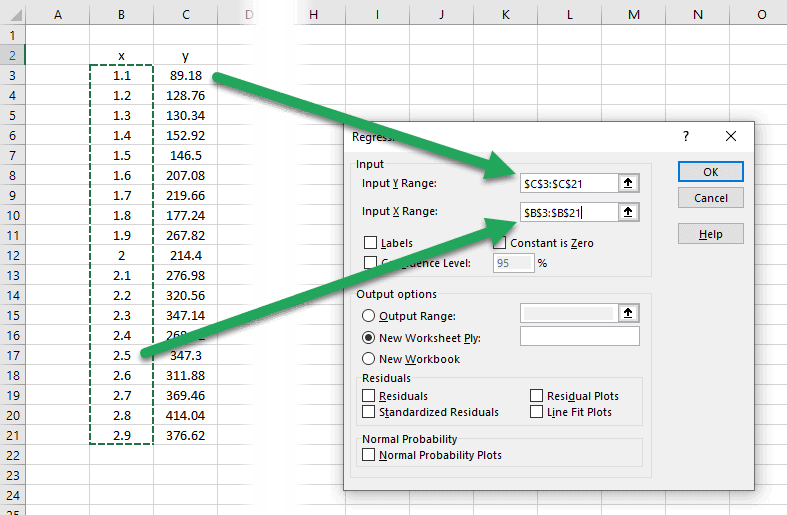
In the window that pops up, select Regression. In the new window that appears, fill in the following information:
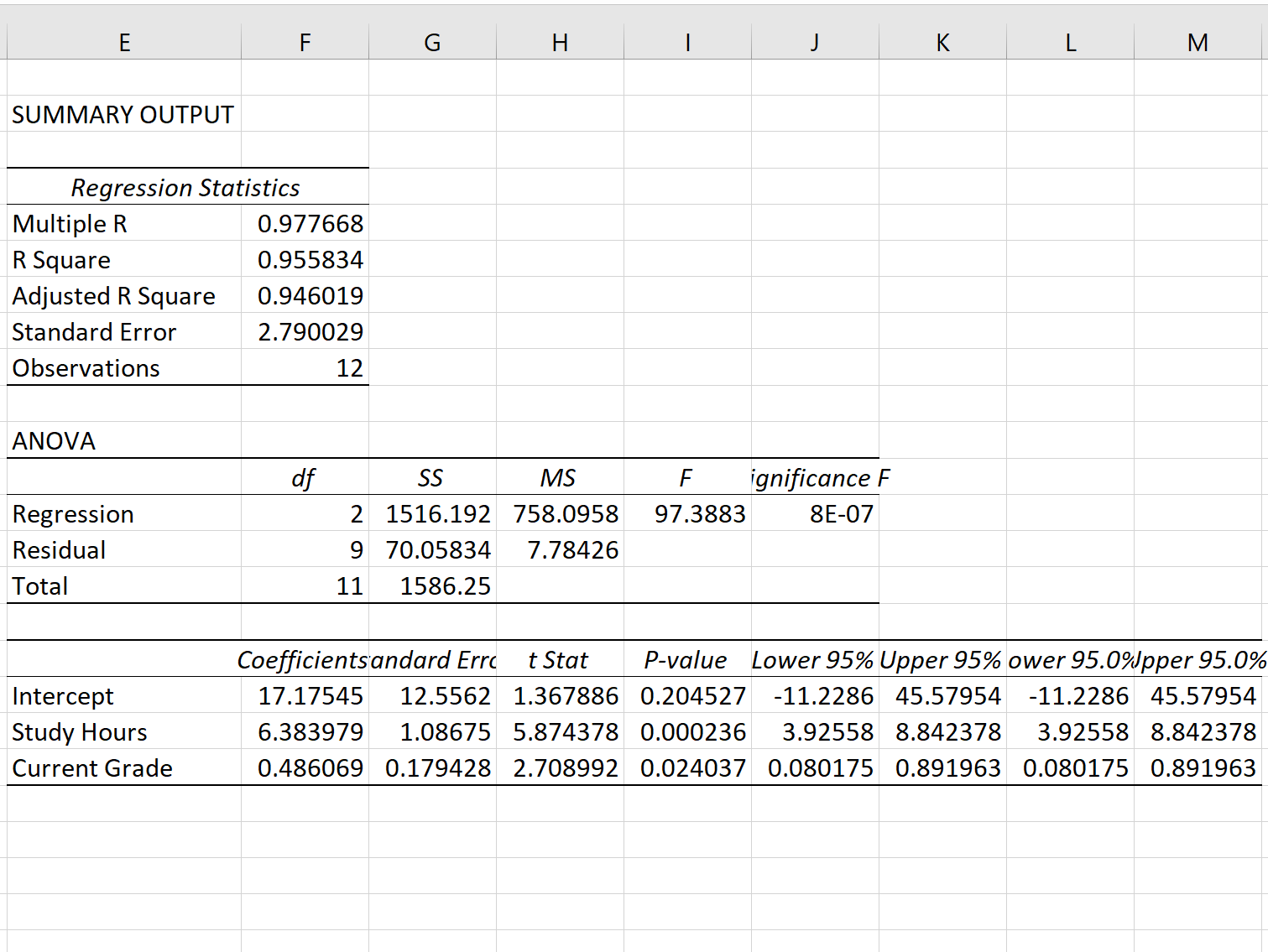
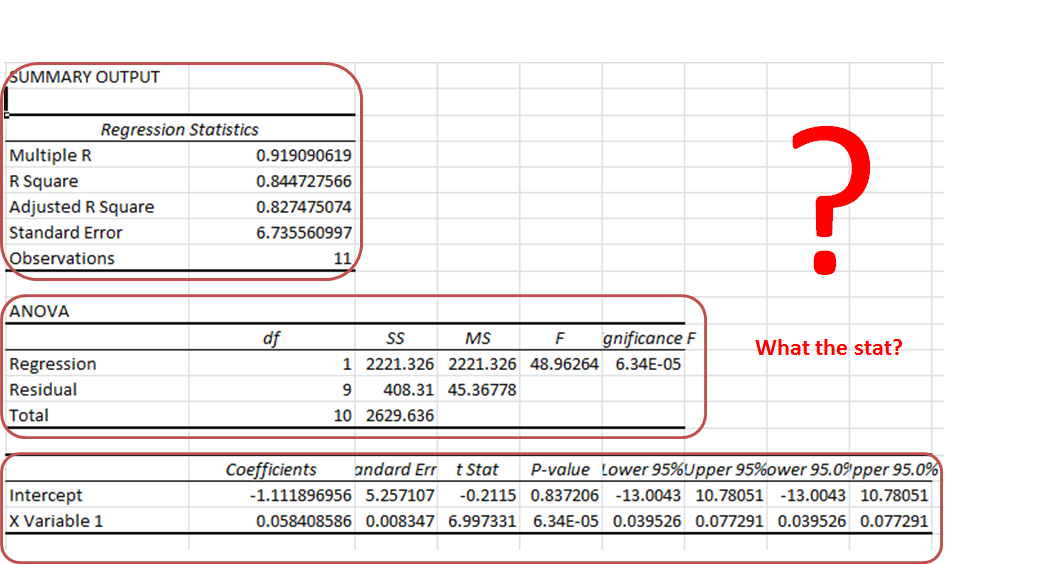
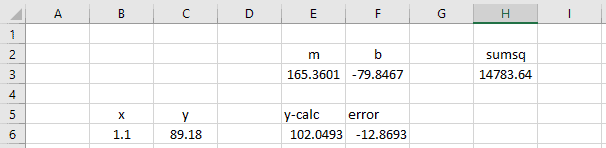
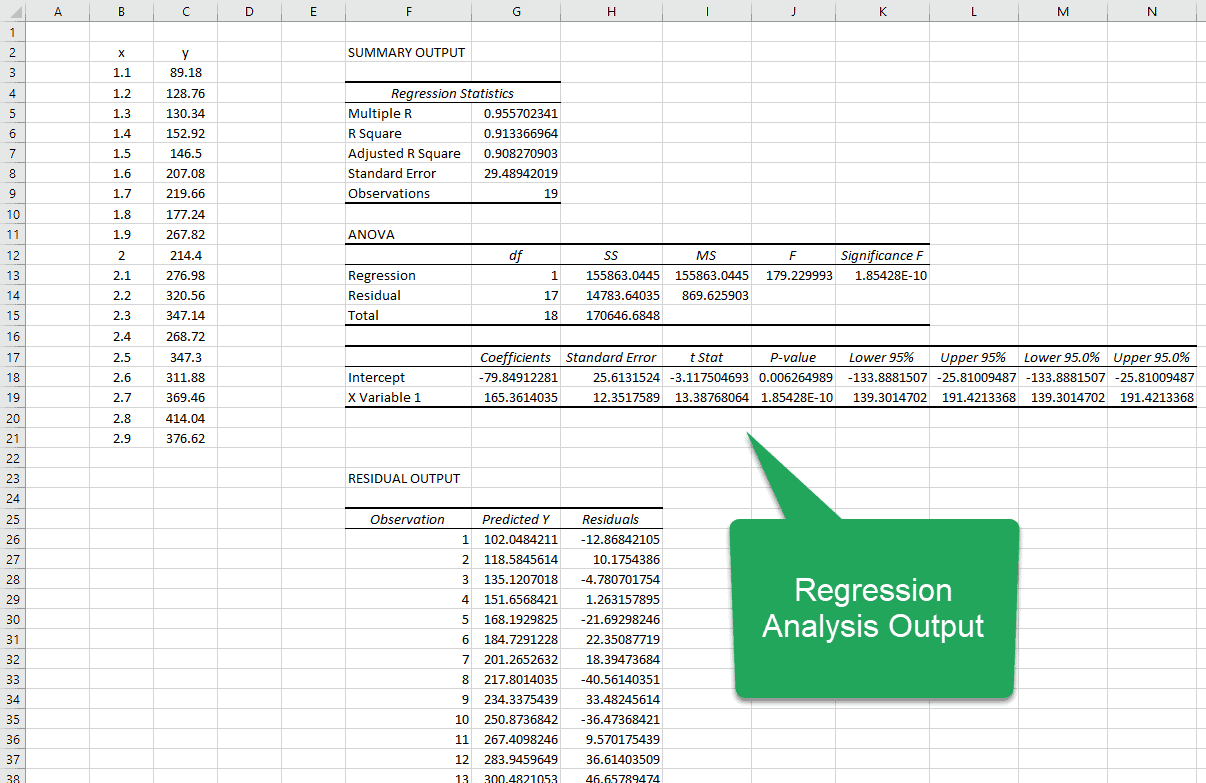
Once you click OK, the output of the regression model will appear:
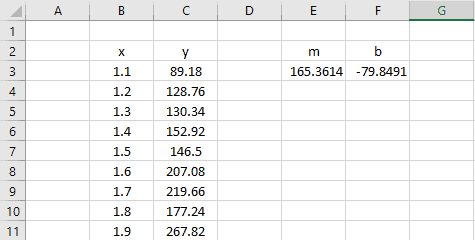
Step 3: Interpret the Standard Error of Regression
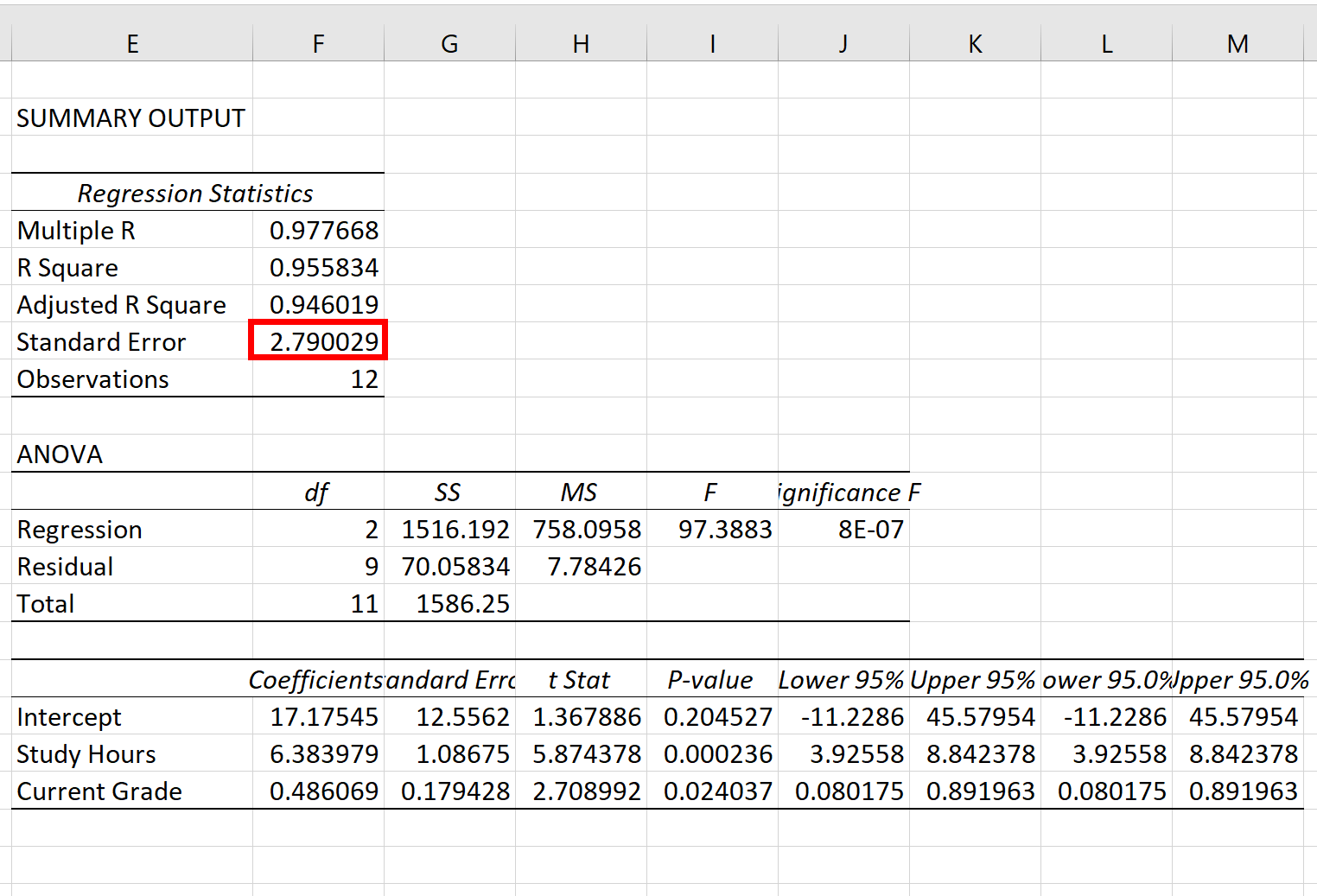
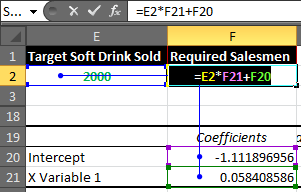
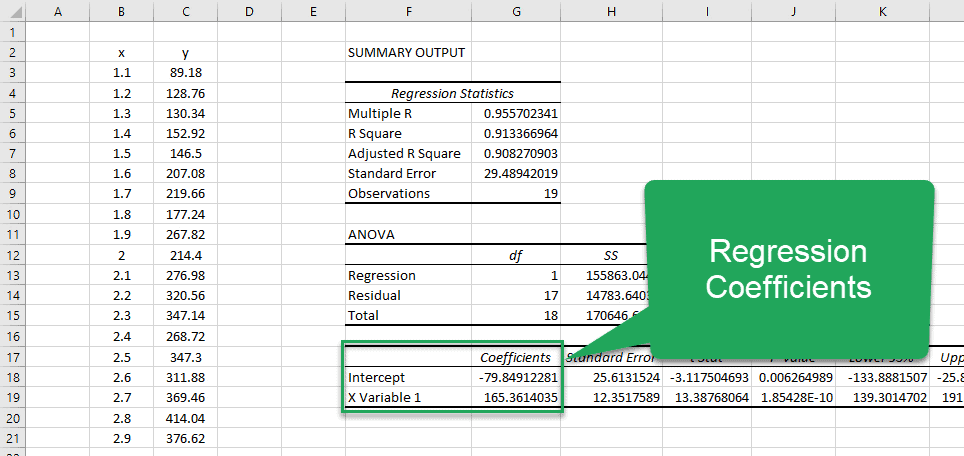
The standard error of the regression model is the number next to Standard Error:
The standard error of this particular regression model turns out to be 2.790029.
This number represents the average distance between the actual exam scores and the exam scores predicted by the model.
Note that some of the exam scores will be further than 2.79 units away from the predicted score while some will be closer. But, on average, the distance between the actual exam scores and the predicted scores is 2.790029.
Also note that a smaller standard error of regression indicates that a regression model fits a dataset more closely.
Thus, if we fit a new regression model to the dataset and ended up with a standard error of, say, 4.53, this new model would be worse at predicting exam scores than the previous model.
Additional Resources
Another common way to measure the precision of a regression model is to use R-squared. Check out this article for a nice explanation of the benefits of using the standard error of the regression to measure precision compared to R-squared.
17 авг. 2022 г.
читать 2 мин
Всякий раз, когда мы подбираем модель линейной регрессии , модель принимает следующую форму:
Y = β 0 + β 1 X + … + β i X +ϵ
где ϵ — член ошибки, не зависящий от X.
Независимо от того, насколько хорошо можно использовать X для предсказания значений Y, в модели всегда будет какая-то случайная ошибка.
Одним из способов измерения дисперсии этой случайной ошибки является использование стандартной ошибки регрессионной модели , которая представляет собой способ измерения стандартного отклонения остатков ϵ.
В этом руководстве представлен пошаговый пример расчета стандартной ошибки регрессионной модели в Excel.
Шаг 1: Создайте данные
В этом примере мы создадим набор данных, содержащий следующие переменные для 12 разных учащихся:
- Оценка экзамена
- Часы, потраченные на учебу
- Текущая оценка
Шаг 2: Подгонка регрессионной модели
Далее мы подгоним модель множественной линейной регрессии , используя экзаменационный балл в качестве переменной ответа и часы обучения и текущую оценку в качестве переменных-предикторов.
Для этого щелкните вкладку « Данные » на верхней ленте, а затем щелкните « Анализ данных» :
Если вы не видите эту опцию доступной, вам нужно сначала загрузить Data Analysis ToolPak .
В появившемся окне выберите Регрессия.В появившемся новом окне заполните следующую информацию:
Как только вы нажмете OK , появится результат регрессионной модели:
Шаг 3: Интерпретируйте стандартную ошибку регрессии
Стандартная ошибка модели регрессии — это число рядом со стандартной ошибкой :
Стандартная ошибка этой конкретной модели регрессии оказывается равной 2,790029 .
Это число представляет собой среднее расстояние между фактическими результатами экзаменов и оценками экзаменов, предсказанными моделью.
Обратите внимание, что некоторые экзаменационные баллы будут отличаться от прогнозируемого более чем на 2,79 единицы, в то время как некоторые будут ближе. Но в среднем расстояние между реальными экзаменационными баллами и прогнозируемыми составляет 2,790029 .
Также обратите внимание, что меньшая стандартная ошибка регрессии указывает на то, что модель регрессии более точно соответствует набору данных.
Таким образом, если мы подгоним новую регрессионную модель к набору данных и получим стандартную ошибку, скажем, 4,53 , эта новая модель будет хуже предсказывать результаты экзаменов, чем предыдущая модель.
Дополнительные ресурсы
Другим распространенным способом измерения точности регрессионной модели является использование R-квадрата. Прочтите эту статью , чтобы получить хорошее объяснение преимуществ использования стандартной ошибки регрессии для измерения точности по сравнению с R-квадратом.
Простая линейная регрессия в EXCEL
history 26 января 2019 г.
- Группы статей
- Статистический анализ
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В MS EXCEL имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Статья про Регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:
Примечание : Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место множественная регрессия .
Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.
Примечание : Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части — оценке неизвестных параметров линейной модели .
Немного теории и основные понятия
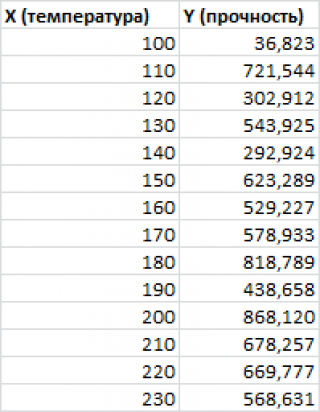
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.
Примером такой задачи может быть производственный процесс изготовления некого волокна, причем прочность этого волокна (Y) зависит только от рабочей температуры процесса в реакторе (Х), которая задается оператором.
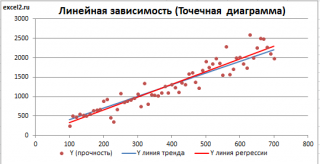
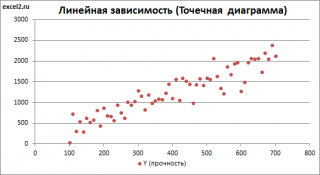
Построим диаграмму рассеяния (см. файл примера лист Линейный ), созданию которой посвящена отдельная статья . Вообще, построение диаграммы рассеяния для целей регрессионного анализа де-факто является стандартом.
СОВЕТ : Подробнее о построении различных типов диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .
Приведенная выше диаграмма рассеяния свидетельствует о возможной линейной взаимосвязи между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.
Примечание : Наличие даже такой очевидной линейной взаимосвязи не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие причинной взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.
Примечание : Как известно, уравнение прямой линии имеет вид Y = m * X + k , где коэффициент m отвечает за наклон линии ( slope ), k – за сдвиг линии по вертикали ( intercept ), k равно значению Y при Х=0.
Предположим, что мы можем зафиксировать переменную Х ( рабочую температуру процесса ) при некотором значении Х i и произвести несколько наблюдений переменной Y ( прочность нити ). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).
Полученные значения Y, при заданном Хi, будут колебаться вокруг некого значения . При увеличении количества измерений, среднее этих измерений, будет стремиться к математическому ожиданию случайной величины Y (при Х i ) равному μy(i)=Е(Y i ).
Подобные рассуждения можно привести для любого значения Хi.
Чтобы двинуться дальше, воспользуемся материалом из раздела Проверка статистических гипотез . В статье о проверке гипотезы о среднем значении генеральной совокупности в качестве нулевой гипотезы предполагалось равенство неизвестного значения μ заданному μ0.
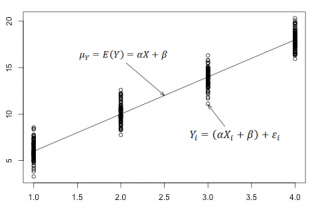
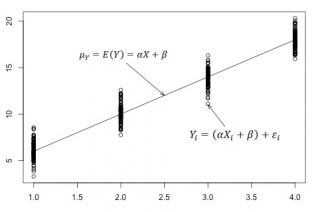
В нашем случае простой линейной регрессии в качестве нулевой гипотезы предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ y(i) =α* Х i +β. Уравнение μ y(i) =α* Х i +β можно переписать в обобщенном виде (для всех Х и μ y ) как μ y =α* Х +β.
Для наглядности проведем прямую линию соединяющую все μy(i).
Данная линия называется регрессионной линией генеральной совокупности (population regression line), параметры которой ( наклон a и сдвиг β ) нам не известны (по аналогии с гипотезой о среднем значении генеральной совокупности , где нам было неизвестно истинное значение μ).
Теперь сделаем переход от нашего предположения, что μy=a* Х + β , к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.
Уравнение Y=a*X+b+ε называют линейной регрессионной моделью . Часто Х еще называют независимой переменной (еще предиктором и регрессором , английский термин predictor , regressor ), а Y – зависимой (или объясняемой , response variable ). Так как регрессор у нас один, то такая модель называется простой линейной регрессионной моделью ( simple linear regression model ). α часто называют коэффициентом регрессии.
Предположения линейной регрессионной модели перечислены в следующем разделе.
Предположения линейной регрессионной модели
Чтобы модель линейной регрессии Yi=a*Xi+β+ε i была адекватной — требуется:
- Ошибки ε i должны быть независимыми переменными;
- При каждом значении Xi ошибки ε i должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε i ]=0);
- При каждом значении Xi ошибки ε i должны иметь равные дисперсии (обозначим ее σ 2 ).
Примечание : Последнее условие называется гомоскедастичность — стабильность, гомогенность дисперсии случайной ошибки e. Т.е. дисперсия ошибки σ 2 не должна зависеть от значения Xi.
Используя предположение о равенстве математического ожидания Е[ε i ]=0 покажем, что μy(i)=Е[Yi]:
Е[Yi]= Е[a*Xi+β+ε i ]= Е[a*Xi+β]+ Е[ε i ]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.
Дисперсия случайной переменной Y равна дисперсии ошибки ε, т.е. VAR(Y)= VAR(ε)=σ 2 . Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε i ).
Задачи регрессионного анализа
Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует регрессионная линия генеральной совокупности , т.е. μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений .
На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно a и b . Также часто используются обозначения â и b̂.
Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?
Первая задача регрессионного анализа – оценка неизвестных параметров ( estimation of the unknown parameters ). Подробнее см. раздел Оценки неизвестных параметров модели .
Вторая задача регрессионного анализа – Проверка адекватности модели ( model adequacy checking ).
Примечание : Оценки параметров модели обычно вычисляются методом наименьших квадратов (МНК), которому посвящена отдельная статья .
Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Неизвестные параметры простой линейной регрессионной модели Y=a*X+β+ε оценим с помощью метода наименьших квадратов (в статье про МНК подробно описано этот метод ).
Для вычисления параметров линейной модели методом МНК получены следующие выражения:
Таким образом, мы получим уравнение прямой линии Y= a *X+ b , которая наилучшим образом аппроксимирует имеющиеся данные.
Примечание : В статье про метод наименьших квадратов рассмотрены случаи аппроксимации линейной и квадратичной функцией , а также степенной , логарифмической и экспоненциальной функцией .
Оценку параметров в MS EXCEL можно выполнить различными способами:
Сначала рассмотрим функции НАКЛОН() , ОТРЕЗОК() и ЛИНЕЙН() .
Пусть значения Х и Y находятся соответственно в диапазонах C 23: C 83 и B 23: B 83 (см. файл примера внизу статьи).
Примечание : Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью Генерация данных для линейной регрессии в MS EXCEL ).
В MS EXCEL наклон прямой линии а ( оценку коэффициента регрессии ), можно найти по методу МНК с помощью функции НАКЛОН() , а сдвиг b ( оценку постоянного члена или константы регрессии ), с помощью функции ОТРЕЗОК() . В английской версии это функции SLOPE и INTERCEPT соответственно.
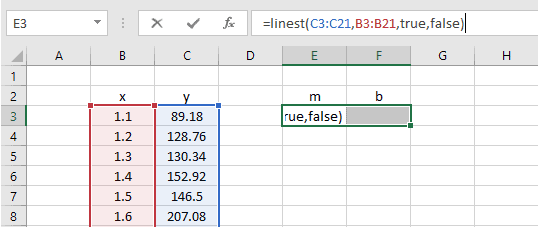
Аналогичный результат можно получить с помощью функции ЛИНЕЙН() , английская версия LINEST (см. статью об этой функции ).
Формула =ЛИНЕЙН(C23:C83;B23:B83) вернет наклон а . А формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) — сдвиг b . Здесь требуются пояснения.
Функция ЛИНЕЙН() имеет 4 аргумента и возвращает целый массив значений:
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Если 4-й аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН() возвращает только оценки параметров модели: a и b .
Примечание : Остальные значения, возвращаемые функцией ЛИНЕЙН() , нам потребуются при вычислении стандартных ошибок и для проверки значимости регрессии . В этом случае аргумент статистика должен иметь значение ИСТИНА.
Чтобы вывести сразу обе оценки:
- в одной строке необходимо выделить 2 ячейки,
- ввести формулу в Строке формул
- нажать CTRL+SHIFT+ENTER (см. статью про формулы массива ).
Если в Строке формул выделить формулу = ЛИНЕЙН(C23:C83;B23:B83) и нажать клавишу F9 , то мы увидим что-то типа <3,01279389265416;154,240057900613>. Это как раз значения a и b . Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».
Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу = ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83)) . При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция ТРАНСП() транспонировала строку в столбец ).
Чтобы разобраться в этом подробнее необходимо ознакомиться с формулами массива .
Чтобы не связываться с вводом формул массива , можно использовать функцию ИНДЕКС() . Формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1) или просто ЛИНЕЙН(C23:C83;B23:B83) вернет параметр, отвечающий за наклон линии, т.е. а . Формула =ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) вернет параметр b .
Оценка неизвестных параметров линейной модели (через статистики выборок)
Наклон линии, т.е. коэффициент а , можно также вычислить через коэффициент корреляции и стандартные отклонения выборок :
= КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))
Вышеуказанная формула математически эквивалентна отношению ковариации выборок Х и Y и дисперсии выборки Х:
И, наконец, запишем еще одну формулу для нахождения сдвига b . Воспользуемся тем фактом, что линия регрессии проходит через точку средних значений переменных Х и Y.
Вычислив средние значения и подставив в формулу ранее найденный наклон а , получим сдвиг b .
Оценка неизвестных параметров линейной модели (матричная форма)
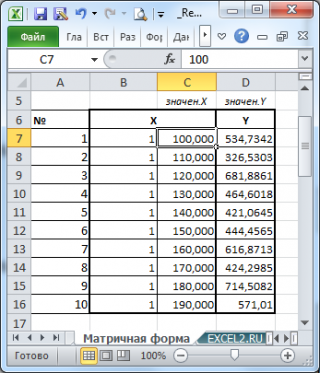
Также параметры линии регрессии можно найти в матричной форме (см. файл примера лист Матричная форма ).
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг b ), β1 (наклон a ).
Матрица Х равна:
Матрица Х называется регрессионной матрицей или матрицей плана . Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.
Матрица Х T – это транспонированная матрица Х . Она состоит соответственно из n столбцов и 2-х строк.
В формуле символом Y обозначен столбец значений переменной Y.
Чтобы перемножить матрицы используйте функцию МУМНОЖ() . Чтобы найти обратную матрицу используйте функцию МОБР() .
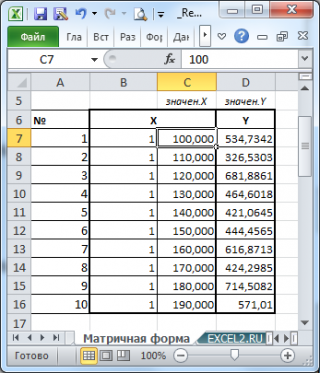
Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).
Слева от него достроим столбец с 1 для матрицы Х.
и введя ее как формулу массива в 2 ячейки, получим оценку параметров модели.
Красота применения матричной формы полностью раскрывается в случае множественной регрессии .
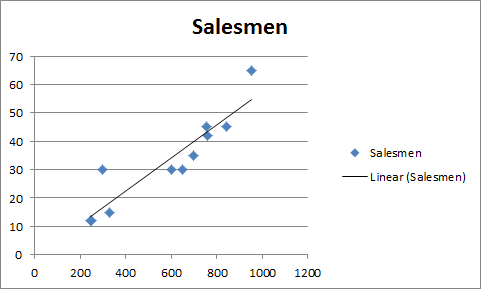
Построение линии регрессии
Для отображения линии регрессии построим сначала диаграмму рассеяния , на которой отобразим все точки (см. начало статьи ).
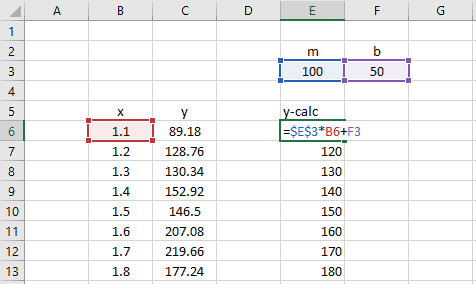
Для построения прямой линии используйте вычисленные выше оценки параметров модели a и b (т.е. вычислите у по формуле y = a * x + b ) или функцию ТЕНДЕНЦИЯ() .
Формула = ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23) возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца В2 .
Примечание : Линию регрессии можно также построить с помощью функции ПРЕДСКАЗ() . Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции ТЕНДЕНЦИЯ() работает только в случае одного регрессора. Функция ТЕНДЕНЦИЯ() может быть использована и в случае множественной регрессии (в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).
Как видно из диаграммы выше линия тренда и линия регрессии не обязательно совпадают: отклонения точек от линии тренда случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.
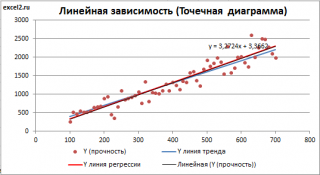
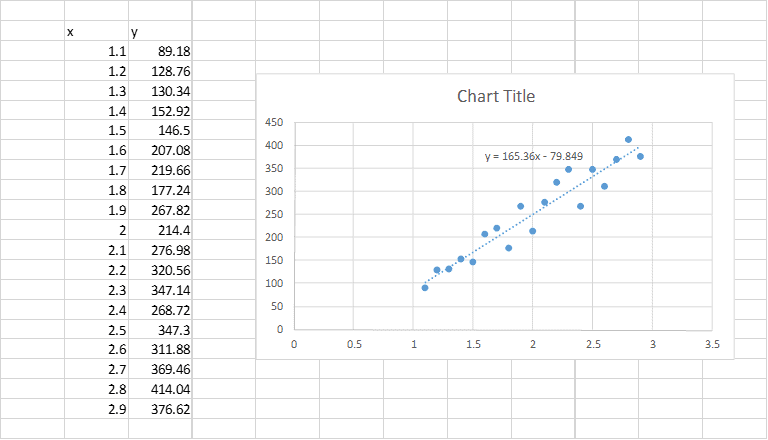
Линию регрессии можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента Линия тренда. Для этого выделите диаграмму, в меню выберите вкладку Макет , в группе Анализ нажмите Линия тренда , затем Линейное приближение. В диалоговом окне установите галочку Показывать уравнение на диаграмме (подробнее см. в статье про МНК ).
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами линией регрессии, а параметры уравнения a и b должны совпасть с параметрами уравнения отображенными на диаграмме.
Примечание: Для того, чтобы вычисленные параметры уравнения a и b совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был Точечная, а не График , т.к. тип диаграммы График не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; . Именно эти значения и берутся при расчете параметров линии тренда . Убедиться в этом можно если построить диаграмму График (см. файл примера ), а значения Хнач и Хшаг установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с a и b .
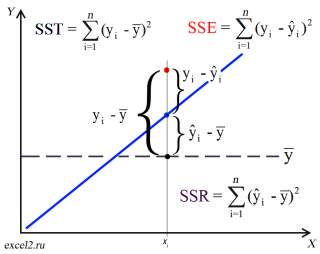
Коэффициент детерминации R 2
Коэффициент детерминации R 2 показывает насколько полезна построенная нами линейная регрессионная модель .
Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения регрессионной модели ). Очевидно, что лучшей оценкой для yi будет среднее значение ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).
Примечание : Далее будет использована терминология и обозначения дисперсионного анализа .
После построения регрессионной модели для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).
Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.
Очевидно, что используя регрессионную модель мы уменьшили первоначальную (полную) ошибку (yi — ȳ) на значение (ŷi — ȳ) до величины (yi — ŷi).
(yi — ŷi) – это оставшаяся, необъясненная ошибка.
Очевидно, что все три ошибки связаны выражением:
(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)
Можно показать, что в общем виде справедливо следующее выражение:
или в других, общепринятых в зарубежной литературе, обозначениях:
Total Sum of Squares = Regression Sum of Squares + Error Sum of Squares
Примечание : SS — Sum of Squares — Сумма Квадратов.
Как видно из формулы величины SST, SSR, SSE имеют размерность дисперсии (вариации) и соответственно описывают разброс (изменчивость): Общую изменчивость (Total variation), Изменчивость объясненную моделью (Explained variation) и Необъясненную изменчивость (Unexplained variation).
По определению коэффициент детерминации R 2 равен:
R 2 = Изменчивость объясненная моделью / Общая изменчивость.
Этот показатель равен квадрату коэффициента корреляции и в MS EXCEL его можно вычислить с помощью функции КВПИРСОН() или ЛИНЕЙН() :
R 2 принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.
Стандартная ошибка регрессии
Стандартная ошибка регрессии ( Standard Error of a regression ) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).
Теперь вспомним уравнение линейной регрессионной модели Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со средним значением μ и дисперсией σ 2 .
Оценив значение дисперсии σ 2 и вычислив из нее квадратный корень – получим Стандартную ошибку регрессии. Чем точки наблюдений на диаграмме рассеяния ближе находятся к прямой линии, тем меньше Стандартная ошибка.
Примечание : Вспомним , что при построении модели предполагается, что среднее значение ошибки ε равно 0, т.е. E[ε]=0.
Оценим дисперсию σ 2 . Помимо вычисления Стандартной ошибки регрессии эта оценка нам потребуется в дальнейшем еще и при построении доверительных интервалов для оценки параметров регрессии a и b .
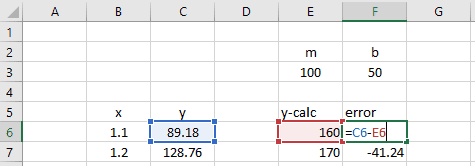
Для оценки дисперсии ошибки ε используем остатки регрессии — разности между имеющимися значениями yi и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.
Для оценки дисперсии σ 2 используют следующую формулу:
где SSE – сумма квадратов значений ошибок модели ε i =yi — ŷi ( Sum of Squared Errors ).
SSE часто обозначают и как SSres – сумма квадратов остатков ( Sum of Squared residuals ).
Оценка дисперсии s 2 также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов ошибок или MSRES (Mean Square of Residuals), т.е. среднее квадратов остатков . Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.
Примечание : Напомним, что когда мы использовали МНК для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на линии регрессии.
Математическое ожидание случайной величины MSE равно дисперсии ошибки ε, т.е. σ 2 .
Чтобы понять почему SSE выбрана в качестве основы для оценки дисперсии ошибки ε, вспомним, что σ 2 является также дисперсией случайной величины Y (относительно среднего значения μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi = a * Хi + b (значение уравнения регрессии при Х= Хi), то логично использовать именно SSE в качестве основы для оценки дисперсии σ 2 . Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество степеней свободы ( df – degrees of freedom ), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае простой линейной регрессии число степеней свободы равно n-2, т.к. при построении линии регрессии было оценено 2 параметра модели (на это было «потрачено» 2 степени свободы ).
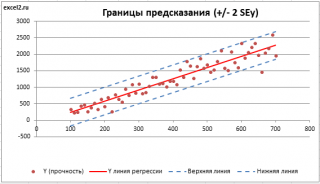
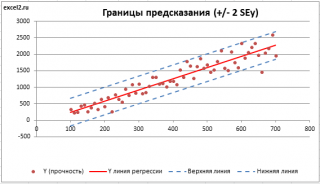
Итак, как сказано было выше, квадратный корень из s 2 имеет специальное название Стандартная ошибка регрессии ( Standard Error of a regression ) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см. этот раздел ). Если ошибки предсказания ε имеют нормальное распределение , то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от линии регрессии . SEy имеет размерность переменной Y и откладывается по вертикали. Часто на диаграмме рассеяния строят границы предсказания соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).
В MS EXCEL стандартную ошибку SEy можно вычислить непосредственно по формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))
или с помощью функции ЛИНЕЙН() :
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
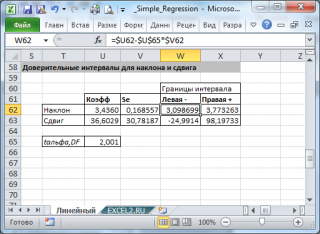
Стандартные ошибки и доверительные интервалы для наклона и сдвига
В разделе Оценка неизвестных параметров линейной модели мы получили точечные оценки наклона а и сдвига b . Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со средним значением и дисперсией . Но, чтобы перейти от точечных оценок к интервальным , необходимо вычислить соответствующие стандартные ошибки (т.е. стандартные отклонения ).
Стандартная ошибка коэффициента регрессии a вычисляется на основании стандартной ошибки регрессии по следующей формуле:
где Sx – стандартное отклонение величины х, вычисляемое по формуле:
где Sey – стандартная ошибка регрессии, т.е. ошибка предсказания значения переменой Y ( см. выше ).
В MS EXCEL стандартную ошибку коэффициента регрессии Se можно вычислить впрямую по вышеуказанной формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/ СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)
или с помощью функции ЛИНЕЙН() :
Формулы приведены в файле примера на листе Линейный в разделе Регрессионная статистика .
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
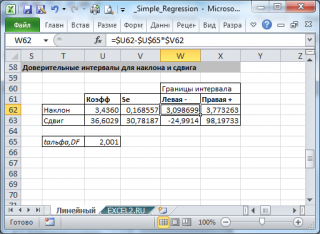
При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:
где — квантиль распределения Стьюдента с n-2 степенями свободы. Величина а с «крышкой» является другим обозначением наклона а .
Например для уровня значимости альфа=0,05, можно вычислить с помощью формулы =СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)
Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины
является t-распределением Стьюдента с n-2 степенью свободы (то же справедливо и для наклона b ).
Примечание : Подробнее о построении доверительных интервалов в MS EXCEL можно прочитать в этой статье Доверительные интервалы в MS EXCEL .
В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии. Здесь мы считаем, что коэффициент регрессии a имеет распределение Стьюдента с n-2 степенями свободы (n – количество наблюдений, т.е. пар Х и Y).
Примечание : Подробнее о построении доверительных интервалов с использованием t-распределения см. статью про построение доверительных интервалов для среднего .
Стандартная ошибка сдвига b вычисляется по следующей формуле:
В MS EXCEL стандартную ошибку сдвига Seb можно вычислить с помощью функции ЛИНЕЙН() :
При построении двухстороннего доверительного интервала для сдвига его границы определяются аналогичным образом как для наклона : b +/- t*Seb.
Проверка значимости взаимосвязи переменных
Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда коэффициент регрессии a равен 0.
Чтобы убедиться, что вычисленная нами оценка наклона прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют проверку гипотез . В качестве нулевой гипотезы Н 0 принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы Н 1 принимают, что a <>0.
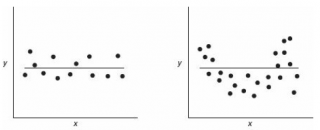
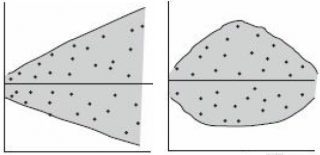
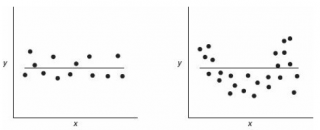
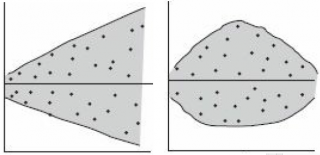
Ниже на рисунках показаны 2 ситуации, когда нулевую гипотезу Н 0 не удается отвергнуть.
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом коэффициент линейной корреляции равен 0.
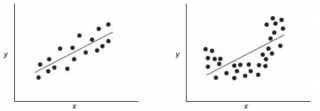
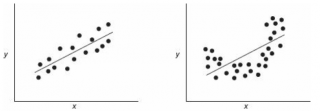
Ниже — 2 ситуации, когда нулевая гипотеза Н 0 отвергается.
На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).
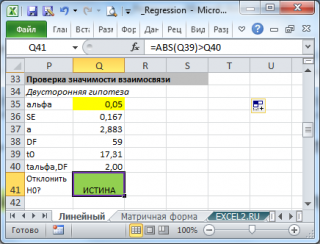
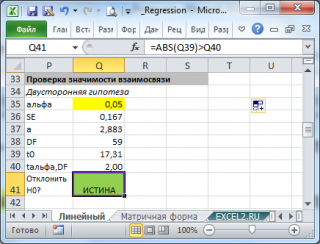
Для проверки гипотезы нам потребуется:
- Установить уровень значимости , пусть альфа=0,05;
- Рассчитать с помощью функции ЛИНЕЙН() стандартное отклонение Se для коэффициента регрессии (см. предыдущий раздел );
- Рассчитать число степеней свободы: DF=n-2 или по формуле = ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
- Вычислить значение тестовой статистики t 0 =a/S e , которая имеет распределение Стьюдента с числом степеней свободы DF=n-2;
- Сравнить значение тестовой статистики |t0| с пороговым значением t альфа ,n-2. Если значение тестовой статистики больше порогового значения, то нулевая гипотеза отвергается ( наклон не может быть объяснен лишь случайностью при заданном уровне альфа) либо
- вычислить p-значение и сравнить его с уровнем значимости .
В файле примера приведен пример проверки гипотезы:
Изменяя наклон тренда k (ячейка В8 ) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.
Примечание : Проверка значимости взаимосвязи эквивалентна проверке статистической значимости коэффициента корреляции . В файле примера показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью процедуры F-тест .
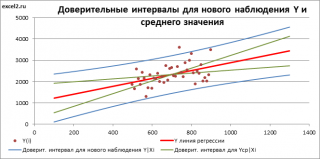
Доверительные интервалы для нового наблюдения Y и среднего значения
Вычислив параметры простой линейной регрессионной модели Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ= a * Хi + b
Ŷ также является точечной оценкой для среднего значения Yi при заданном Хi. Но, при построении доверительных интервалов используются различные стандартные ошибки .
Стандартная ошибка нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:
- неопределенность связанную со случайностью оценок параметров модели a и b ;
- случайность ошибки модели ε.
Учет этих неопределенностей приводит к стандартной ошибке S(Y|Xi), которая рассчитывается с учетом известного значения Xi.
где SS xx – сумма квадратов отклонений от среднего значений переменной Х:
В MS EXCEL 2010 нет функции, которая бы рассчитывала эту стандартную ошибку , поэтому ее необходимо рассчитывать по вышеуказанным формулам.
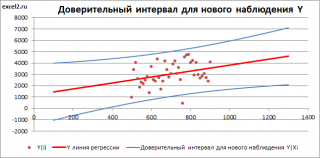
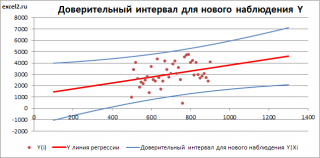
Доверительный интервал или Интервал предсказания для нового наблюдения (Prediction Interval for a New Observation) построим по схеме показанной в разделе Проверка значимости взаимосвязи переменных (см. файл примера лист Интервалы ). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х ср ), то интервал будет постепенно расширяться при удалении от Х ср .
Границы доверительного интервала для нового наблюдения рассчитываются по формуле:
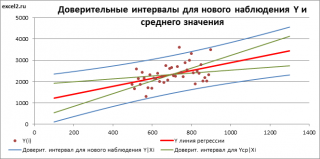
Аналогичным образом построим доверительный интервал для среднего значения Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае доверительный интервал будет уже, т.к. средние значения имеют меньшую изменчивость по сравнению с отдельными наблюдениями ( средние значения, в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).
Стандартная ошибка S(Yср|Xi) вычисляется по практически аналогичным формулам как и стандартная ошибка для нового наблюдения:
Как видно из формул, стандартная ошибка S(Yср|Xi) меньше стандартной ошибки S(Y|Xi) для индивидуального значения .
Границы доверительного интервала для среднего значения рассчитываются по формуле:
Проверка адекватности линейной регрессионной модели
Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел Предположения линейной регрессионной модели ).
Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках простой линейной модели n остатков имеют только n-2 связанных с ними степеней свободы . Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.
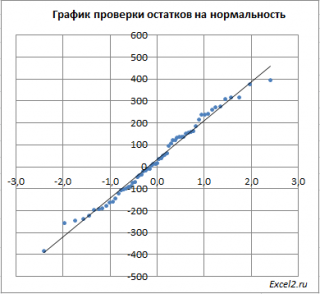
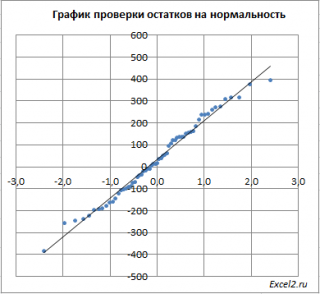
Чтобы проверить предположение о нормальности распределения ошибок строят график проверки на нормальность (Normal probability Plot).
В файле примера на листе Адекватность построен график проверки на нормальность . В случае нормального распределения значения остатков должны быть близки к прямой линии.
Так как значения переменной Y мы генерировали с помощью тренда , вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.
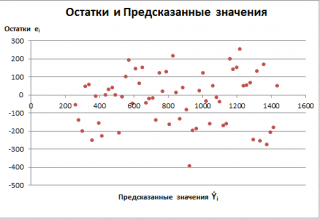
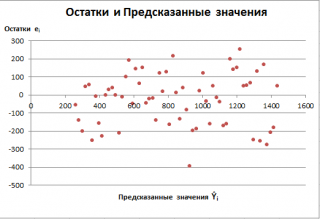
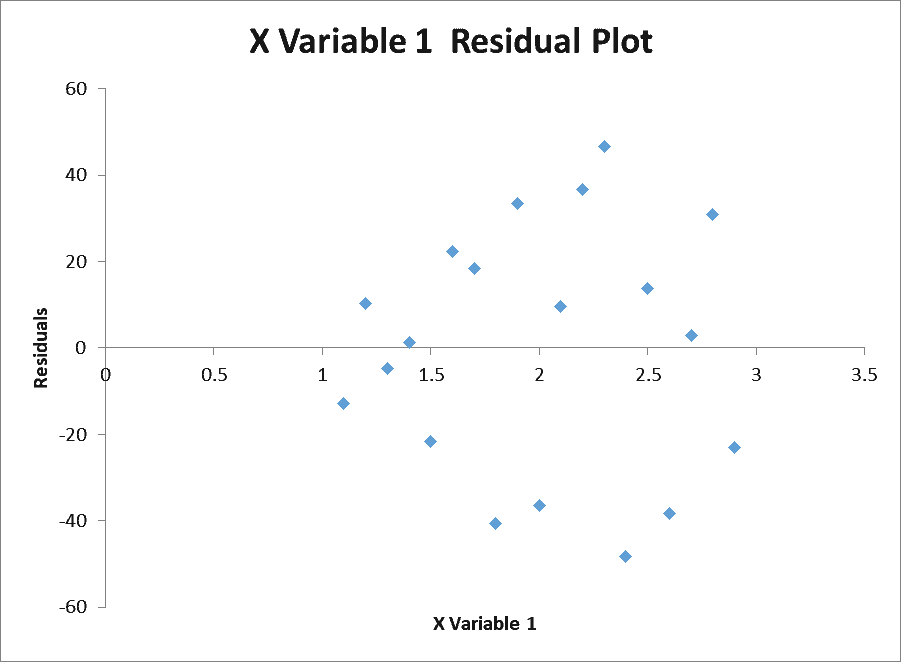
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор о нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.
В нашем случае точки располагаются примерно равномерно.
Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе Стандартная ошибка регрессии оценкой стандартного отклонения ошибок является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.
SEy можно вычислить с помощью функции ЛИНЕЙН() :
Иногда нормирование остатков производится на величину стандартного отклонения остатков (это мы увидим в статье об инструменте Регрессия , доступного в надстройке MS EXCEL Пакет анализа ), т.е. по формуле:
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.
Регрессионный анализ в Microsoft Excel
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
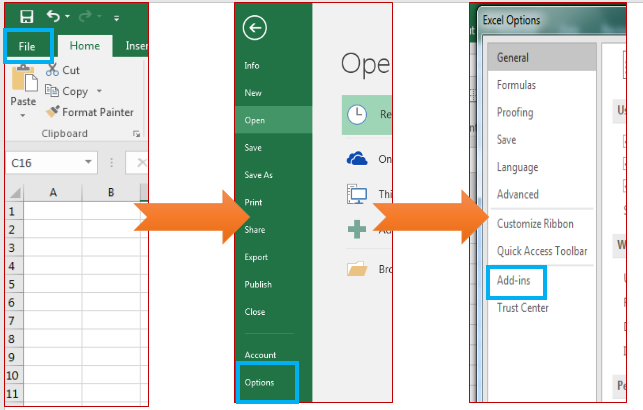
- Перемещаемся во вкладку «Файл».
Переходим в раздел «Параметры».
В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Линейная регрессия в программе Excel
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк . В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Помимо этой статьи, на сайте еще 12771 полезных инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Корреляционно-регрессионный анализ в Excel: инструкция выполнения
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
- линейной (у = а + bx);
- параболической (y = a + bx + cx 2 );
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
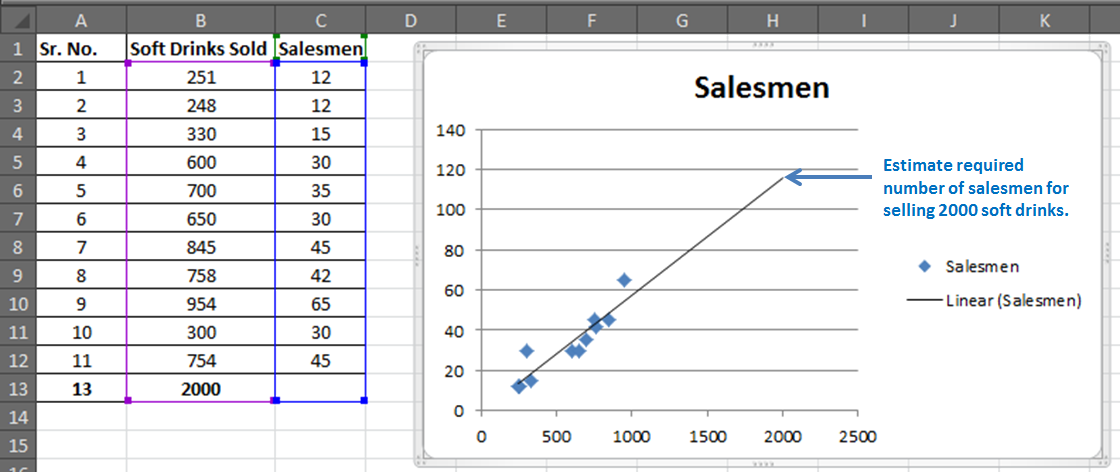
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
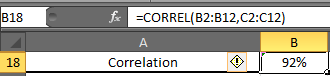
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
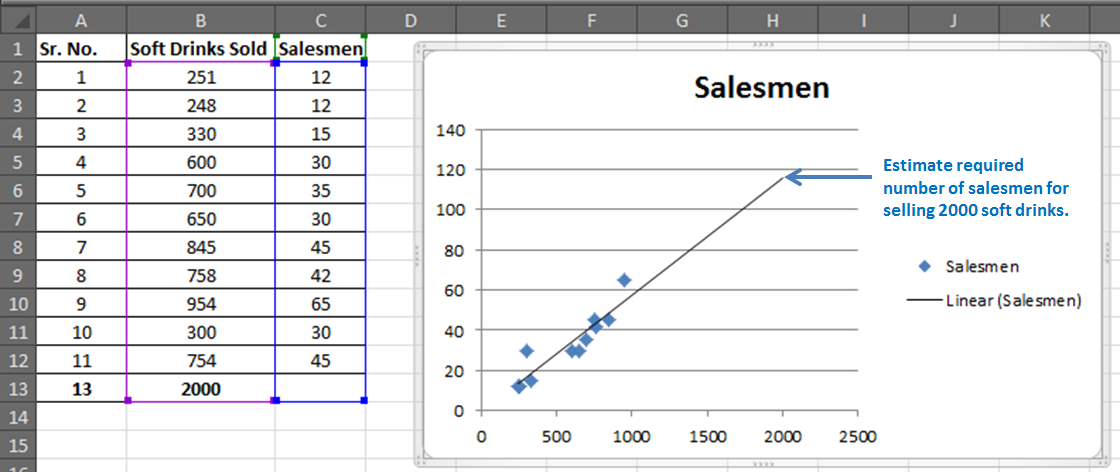
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
источники:
http://lumpics.ru/regression-analysis-in-excel/
http://exceltable.com/otchety/korrelyacionno-regressionnyy-analiz
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В
MS
EXCEL
имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.
Disclaimer
: Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей
Регрессионного анализа.
Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения
Регрессии
– плохая идея.
Статья про
Регрессионный анализ
получилась большая, поэтому ниже для удобства приведены ее разделы:
- Немного теории и основные понятия
- Предположения линейной регрессионной модели
- Задачи регрессионного анализа
- Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
- Оценка неизвестных параметров линейной модели (через статистики выборок)
- Оценка неизвестных параметров линейной модели (матричная форма)
- Построение линии регрессии
- Коэффициент детерминации
- Стандартная ошибка регрессии
- Стандартные ошибки и доверительные интервалы для наклона и сдвига
- Проверка значимости взаимосвязи переменных
- Доверительные интервалы для нового наблюдения Y и среднего значения
- Проверка адекватности линейной регрессионной модели
Примечание
: Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место
множественная регрессия
.
Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.
Примечание
: Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части —
оценке неизвестных параметров линейной модели
.
Немного теории и основные понятия
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.
Примером такой задачи может быть производственный процесс изготовления некого волокна, причем
прочность этого волокна
(Y) зависит только от
рабочей температуры процесса
в реакторе (Х), которая задается оператором.
Построим
диаграмму рассеяния
(см.
файл примера лист Линейный
), созданию которой
посвящена отдельная статья
. Вообще, построение
диаграммы рассеяния
для целей
регрессионного анализа
де-факто является стандартом.
СОВЕТ
: Подробнее о построении различных типов диаграмм см. статьи
Основы построения диаграмм
и
Основные типы диаграмм
.
Приведенная выше
диаграмма рассеяния
свидетельствует о возможной
линейной взаимосвязи
между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.
Примечание
: Наличие даже такой очевидной
линейной взаимосвязи
не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие
причинной
взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.
Примечание
: Как известно, уравнение прямой линии имеет вид
Y
=
m
*
X
+
k
, где коэффициент
m
отвечает за наклон линии (
slope
),
k
– за сдвиг линии по вертикали (
intercept
),
k
равно значению Y при Х=0.
Предположим, что мы можем зафиксировать переменную Х (
рабочую температуру процесса
) при некотором значении Х
i
и произвести несколько наблюдений переменной Y (
прочность нити
). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).
Полученные значения Y, при заданном Хi, будут колебаться вокруг некого
значения
. При увеличении количества измерений, среднее этих измерений, будет стремиться к
математическому ожиданию
случайной величины Y (при Х
i
) равному μy(i)=Е(Y
i
).
Подобные рассуждения можно привести для любого значения Хi.
Чтобы двинуться дальше, воспользуемся материалом из раздела
Проверка статистических гипотез
. В статье о
проверке гипотезы о среднем значении генеральной совокупности
в качестве
нулевой
гипотезы
предполагалось равенство неизвестного значения μ заданному μ0.
В нашем случае
простой линейной регрессии
в качестве
нулевой
гипотезы
предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ
y(i)
=α* Х
i
+β. Уравнение μ
y(i)
=α* Х
i
+β можно переписать в обобщенном виде (для всех Х и μ
y
) как μ
y
=α* Х +β.
Для наглядности проведем прямую линию соединяющую все μy(i).
Данная линия называется
регрессионной линией генеральной совокупности
(population regression line), параметры которой (
наклон
a и
сдвиг β
) нам не известны (по аналогии с
гипотезой о среднем значении генеральной совокупности
, где нам было неизвестно истинное значение μ).
Теперь сделаем переход от нашего предположения, что μy=a* Х +
β
, к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.
Уравнение Y=a*X+b+ε называют
линейной регрессионной моделью
. Часто Х еще называют
независимой переменной
(еще
предиктором
и
регрессором
, английский термин
predictor
,
regressor
), а Y –
зависимой
(или
объясняемой
,
response
variable
). Так как
регрессор
у нас один, то такая модель называется
простой линейной регрессионной моделью
(
simple
linear
regression
model
). α часто называют
коэффициентом регрессии.
Предположения линейной регрессионной модели перечислены в следующем разделе.
Предположения линейной регрессионной модели
Чтобы модель линейной регрессии Yi=a*Xi+β+ε
i
была адекватной — требуется:
-
Ошибки ε
i
должны быть независимыми переменными; -
При каждом значении Xi ошибки ε
i
должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε
i
]=0); -
При каждом значении Xi ошибки ε
i
должны иметь равные дисперсии (обозначим ее σ
2
).
Примечание
: Последнее условие называется
гомоскедастичность
— стабильность, гомогенность дисперсии случайной ошибки e. Т.е.
дисперсия
ошибки σ
2
не должна зависеть от значения Xi.
Используя предположение о равенстве математического ожидания Е[ε
i
]=0 покажем, что μy(i)=Е[Yi]:
Е[Yi]= Е[a*Xi+β+ε
i
]= Е[a*Xi+β]+ Е[ε
i
]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.
Дисперсия
случайной переменной Y равна
дисперсии
ошибки ε, т.е. VAR(Y)= VAR(ε)=σ
2
. Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε
i
).
Задачи регрессионного анализа
Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует
регрессионная линия генеральной совокупности
, т.е. μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений {X;Y}.
На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно
a
и
b
. Также часто используются обозначения â и b̂.
Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?
Таким образом:
Первая задача
регрессионного анализа
– оценка неизвестных параметров (
estimation
of
the
unknown
parameters
). Подробнее см. раздел
Оценки неизвестных параметров модели
.
Вторая задача
регрессионного анализа
–
Проверка адекватности модели
(
model
adequacy
checking
).
Примечание
: Оценки параметров модели обычно вычисляются
методом наименьших квадратов
(МНК),
которому посвящена отдельная статья
.
Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Неизвестные параметры
простой линейной регрессионной модели
Y=a*X+β+ε оценим с помощью
метода наименьших квадратов
(в
статье про МНК подробно описано этот метод
).
Для вычисления параметров линейной модели методом МНК получены следующие выражения:
Таким образом, мы получим уравнение прямой линии Y=
a
*X+
b
, которая наилучшим образом аппроксимирует имеющиеся данные.
Примечание
: В статье про
метод наименьших квадратов
рассмотрены случаи аппроксимации
линейной
и
квадратичной функцией
, а также
степенной
,
логарифмической
и
экспоненциальной функцией
.
Оценку параметров в MS EXCEL можно выполнить различными способами:
-
с помощью функций
НАКЛОН()
и
ОТРЕЗОК()
; -
с помощью функции
ЛИНЕЙН()
; см. статьюФункция MS EXCEL ЛИНЕЙН()
-
формулами через статистики выборок
;
-
в матричной форме
;
-
с помощью
инструмента Регрессия надстройки Пакет Анализа
.
Сначала рассмотрим функции
НАКЛОН()
,
ОТРЕЗОК()
и
ЛИНЕЙН()
.
Пусть значения Х и Y находятся соответственно в диапазонах
C
23:
C
83
и
B
23:
B
83
(см.
файл примера
внизу статьи).
Примечание
: Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью
Генерация данных для линейной регрессии в MS EXCEL
).
В MS EXCEL наклон прямой линии
а
(
оценку
коэффициента регрессии
), можно найти по
методу МНК
с помощью функции
НАКЛОН()
, а сдвиг
b
(
оценку
постоянного члена
или
константы регрессии
), с помощью функции
ОТРЕЗОК()
. В английской версии это функции SLOPE и INTERCEPT соответственно.
Аналогичный результат можно получить с помощью функции
ЛИНЕЙН()
, английская версия LINEST (см.
статью об этой функции
).
Формула
=ЛИНЕЙН(C23:C83;B23:B83)
вернет наклон
а
. А формула =
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2)
— сдвиг
b
. Здесь требуются пояснения.
Функция
ЛИНЕЙН()
имеет 4 аргумента и возвращает целый массив значений:
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Если 4-й аргумент
статистика
имеет значение ЛОЖЬ или опущен, то функция
ЛИНЕЙН()
возвращает только оценки параметров модели:
a
и
b
.
Примечание
: Остальные значения, возвращаемые функцией
ЛИНЕЙН()
, нам потребуются при вычислении
стандартных ошибок
и для
проверки значимости регрессии
. В этом случае аргумент
статистика
должен иметь значение ИСТИНА.
Чтобы вывести сразу обе оценки:
- в одной строке необходимо выделить 2 ячейки,
-
ввести формулу в
Строке формул
-
нажать
CTRL
+
SHIFT
+
ENTER
(см. статью проформулы массива
).
Если в
Строке формул
выделить формулу =
ЛИНЕЙН(C23:C83;B23:B83)
и нажать
клавишу F9
, то мы увидим что-то типа {3,01279389265416;154,240057900613}. Это как раз значения
a
и
b
. Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».
Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу =
ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83))
. При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция
ТРАНСП()
транспонировала строку в столбец
).
Чтобы разобраться в этом подробнее необходимо ознакомиться с
формулами массива
.
Чтобы не связываться с вводом
формул массива
, можно
использовать функцию ИНДЕКС()
. Формула =
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1)
или просто
ЛИНЕЙН(C23:C83;B23:B83)
вернет параметр, отвечающий за наклон линии, т.е.
а
. Формула
=ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2)
вернет параметр
b
.
Оценка неизвестных параметров линейной модели (через статистики выборок)
Наклон линии, т.е. коэффициент
а
, можно также вычислить через
коэффициент корреляции
и
стандартные отклонения выборок
:
=
КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))
Вышеуказанная формула математически эквивалентна отношению
ковариации
выборок Х и Y и
дисперсии
выборки Х:
=
КОВАРИАЦИЯ.В(B23:B83;C23:C83)/ДИСП.В(B23:B83)
И, наконец, запишем еще одну формулу для нахождения сдвига
b
. Воспользуемся тем фактом, что
линия регрессии
проходит через точку
средних значений
переменных Х и Y.
Вычислив
средние значения
и подставив в формулу ранее найденный наклон
а
, получим сдвиг
b
.
Оценка неизвестных параметров линейной модели (матричная форма)
Также параметры
линии регрессии
можно найти в матричной форме (см.
файл примера лист Матричная форма
).
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг
b
), β1 (наклон
a
).
Матрица Х равна:
Матрица
Х
называется
регрессионной матрицей
или
матрицей плана
. Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.
Матрица
Х
T
– это
транспонированная матрица
Х
. Она состоит соответственно из n столбцов и 2-х строк.
В формуле символом
Y
обозначен столбец значений переменной Y.
Чтобы
перемножить матрицы
используйте функцию
МУМНОЖ()
. Чтобы
найти обратную матрицу
используйте функцию
МОБР()
.
Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).
Слева от него достроим столбец с 1 для матрицы Х.
Записав формулу
=
МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП(B7:C16);(B7:C16))); МУМНОЖ(ТРАНСП(B7:C16);(D7:D16)))
и введя ее как
формулу массива
в 2 ячейки, получим оценку параметров модели.
Красота применения матричной формы полностью раскрывается в случае
множественной регрессии
.
Построение линии регрессии
Для отображения
линии регрессии
построим сначала
диаграмму рассеяния
, на которой отобразим все точки (см.
начало статьи
).
Для построения прямой линии используйте вычисленные выше оценки параметров модели
a
и
b
(т.е. вычислите
у
по формуле
y
=
a
*
x
+
b
) или функцию
ТЕНДЕНЦИЯ()
.
Формула =
ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23)
возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца
В2
.
Примечание
:
Линию регрессии
можно также построить с помощью функции
ПРЕДСКАЗ()
. Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции
ТЕНДЕНЦИЯ()
работает только в случае одного регрессора. Функция
ТЕНДЕНЦИЯ()
может быть использована и в случае
множественной регрессии
(в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).
Как видно из диаграммы выше
линия тренда
и
линия регрессии
не обязательно совпадают: отклонения точек от
линии тренда
случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.
Линию регрессии
можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента
Линия тренда.
Для этого выделите диаграмму, в меню выберите
вкладку Макет
, в
группе Анализ
нажмите
Линия тренда
, затем
Линейное приближение.
В диалоговом окне установите галочку
Показывать уравнение на диаграмме
(подробнее см. в
статье про МНК
).
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами
линией регрессии,
а параметры уравнения
a
и
b
должны совпасть с параметрами уравнения отображенными на диаграмме.
Примечание:
Для того, чтобы вычисленные параметры уравнения
a
и
b
совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был
Точечная, а не График
, т.к. тип диаграммы
График
не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; … Именно эти значения и берутся при расчете параметров
линии тренда
. Убедиться в этом можно если построить диаграмму
График
(см.
файл примера
), а значения
Хнач
и
Хшаг
установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с
a
и
b
.
Коэффициент детерминации R
2
Коэффициент детерминации
R
2
показывает насколько полезна построенная нами
линейная регрессионная модель
.
Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения
регрессионной модели
). Очевидно, что лучшей оценкой для yi будет
среднее значение
ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).
Примечание
: Далее будет использована терминология и обозначения
дисперсионного анализа
.
После построения
регрессионной модели
для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).
Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.
Очевидно, что используя
регрессионную модель
мы уменьшили первоначальную (полную) ошибку (yi — ȳ) на значение (ŷi — ȳ) до величины (yi — ŷi).
(yi — ŷi) – это оставшаяся, необъясненная ошибка.
Очевидно, что все три ошибки связаны выражением:
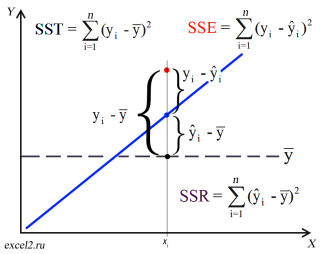
(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)
Можно показать, что в общем виде справедливо следующее выражение:
Доказательство:
или в других, общепринятых в зарубежной литературе, обозначениях:
SST
=
SSR
+
SSE
Что означает:
Total Sum of Squares
=
Regression Sum of Squares
+
Error Sum of Squares
Примечание
: SS — Sum of Squares — Сумма Квадратов.
Как видно из формулы величины SST, SSR, SSE имеют размерность
дисперсии
(вариации) и соответственно описывают разброс (изменчивость):
Общую изменчивость
(Total variation),
Изменчивость объясненную моделью
(Explained variation) и
Необъясненную изменчивость
(Unexplained variation).
По определению
коэффициент детерминации
R
2
равен:
R
2
=
Изменчивость объясненная моделью / Общая изменчивость.
Этот показатель равен квадрату
коэффициента корреляции
и в MS EXCEL его можно вычислить с помощью функции
КВПИРСОН()
или
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3)
R
2
принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.
Стандартная ошибка регрессии
Стандартная ошибка регрессии
(
Standard Error of a regression
) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).
Теперь вспомним уравнение
линейной регрессионной модели
Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со
средним значением
μ и
дисперсией
σ
2
.
Оценив значение
дисперсии
σ
2
и вычислив из нее квадратный корень – получим
Стандартную ошибку регрессии.
Чем точки наблюдений на диаграмме
рассеяния
ближе находятся к прямой линии, тем меньше
Стандартная ошибка.
Примечание
:
Вспомним
, что при построении модели предполагается, что
среднее значение
ошибки ε равно 0, т.е. E[ε]=0.
Оценим
дисперсию σ
2
. Помимо вычисления
Стандартной ошибки регрессии
эта оценка нам потребуется в дальнейшем еще и при построении
доверительных интервалов
для оценки параметров регрессии
a
и
b
.
Для оценки
дисперсии
ошибки ε используем
остатки регрессии
— разности между имеющимися значениями
yi
и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.
Для оценки
дисперсии σ
2
используют следующую формулу:
где SSE – сумма квадратов значений ошибок модели ε
i
=yi — ŷi (
Sum of Squared Errors
).
SSE часто обозначают и как SSres – сумма квадратов остатков (
Sum
of
Squared
residuals
).
Оценка
дисперсии
s
2
также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов
ошибок
или MSRES (Mean Square of Residuals), т.е. среднее квадратов
остатков
. Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.
Примечание
: Напомним, что когда
мы использовали МНК
для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на
линии регрессии.
Математическое ожидание
случайной величины MSE равно
дисперсии ошибки
ε, т.е.
σ
2
.
Чтобы понять почему SSE выбрана в качестве основы для оценки
дисперсии
ошибки ε, вспомним, что
σ
2
является также
дисперсией
случайной величины Y (относительно
среднего значения
μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi =
a
* Хi +
b
(значение
уравнения регрессии
при Х= Хi), то логично использовать именно SSE в качестве основы для оценки
дисперсии
σ
2
. Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество
степеней свободы
(
df
–
degrees
of
freedom
), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае
простой линейной регрессии
число степеней свободы
равно n-2, т.к. при построении
линии регрессии
было оценено 2 параметра модели (на это было «потрачено» 2
степени свободы
).
Итак, как сказано было выше, квадратный корень из s
2
имеет специальное название
Стандартная ошибка регрессии
(
Standard Error of a regression
) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см.
этот раздел
). Если ошибки предсказания ε имеют
нормальное распределение
, то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от
линии регрессии
. SEy имеет размерность переменной Y и откладывается по вертикали. Часто на
диаграмме рассеяния
строят
границы предсказания
соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).
В MS EXCEL
стандартную ошибку
SEy можно вычислить непосредственно по формуле:
=
КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))
или с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;2)
Примечание
: Подробнее о функции
ЛИНЕЙН()
см.
эту статью
.
Стандартные ошибки и доверительные интервалы для наклона и сдвига
В разделе
Оценка неизвестных параметров линейной модели
мы получили точечные оценки наклона
а
и сдвига
b
. Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со
средним значением
и
дисперсией
. Но, чтобы перейти от
точечных оценок
к
интервальным
, необходимо вычислить соответствующие
стандартные ошибки
(т.е.
стандартные отклонения
).
Стандартная ошибка коэффициента регрессии
a
вычисляется на основании
стандартной ошибки регрессии
по следующей формуле:
где Sx – стандартное отклонение величины х, вычисляемое по формуле:
где Sey –
стандартная ошибка регрессии,
т.е. ошибка предсказания значения переменой Y
(
см. выше
).
В MS EXCEL
стандартную ошибку коэффициента регрессии
Se можно вычислить впрямую по вышеуказанной формуле:
=
КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/ СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)
или с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);2;1)
Формулы приведены в
файле примера на листе Линейный
в разделе
Регрессионная статистика
.
Примечание
: Подробнее о функции
ЛИНЕЙН()
см.
эту статью
.
При построении
двухстороннего доверительного интервала
для
коэффициента регрессии
его границы определяются следующим образом:
где —
квантиль распределения Стьюдента
с n-2 степенями свободы. Величина
а
с «крышкой» является другим обозначением
наклона
а
.
Например для
уровня значимости
альфа=0,05, можно вычислить с помощью формулы
=СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)
Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины
является
t-распределением Стьюдента
с n-2 степенью свободы (то же справедливо и для наклона
b
).
Примечание
: Подробнее о построении
доверительных интервалов
в MS EXCEL можно прочитать в этой статье
Доверительные интервалы в MS EXCEL
.
В результате получим, что найденный
доверительный интервал
с вероятностью 95% (1-0,05) накроет истинное значение
коэффициента регрессии.
Здесь мы считаем, что
коэффициент регрессии
a
имеет
распределение Стьюдента
с n-2
степенями свободы
(n – количество наблюдений, т.е. пар Х и Y).
Примечание
: Подробнее о построении
доверительных интервалов
с использованием t-распределения см. статью про построение
доверительных интервалов
для среднего
.
Стандартная ошибка сдвига
b
вычисляется по следующей формуле:
В MS EXCEL
стандартную ошибку сдвига
Seb можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);2;2)
При построении
двухстороннего доверительного интервала
для
сдвига
его границы определяются аналогичным образом как для
наклона
:
b
+/- t*Seb.
Проверка значимости взаимосвязи переменных
Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда
коэффициент регрессии
a
равен 0.
Чтобы убедиться, что вычисленная нами оценка
наклона
прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют
проверку гипотез
. В качестве
нулевой гипотезы
Н
0
принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы
Н
1
принимают, что a <>0.
Ниже на рисунках показаны 2 ситуации, когда
нулевую гипотезу
Н
0
не удается отвергнуть.
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом
коэффициент линейной корреляции
равен 0.
Ниже — 2 ситуации, когда
нулевая гипотеза
Н
0
отвергается.
На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).
Для проверки гипотезы нам потребуется:
-
Установить
уровень значимости
, пусть альфа=0,05;
-
Рассчитать с помощью функции
ЛИНЕЙН()
стандартное отклонение
Se для
коэффициента регрессии
(см.предыдущий раздел
);
-
Рассчитать число степеней свободы: DF=n-2 или по формуле =
ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
-
Вычислить значение тестовой статистики t
0
=a/S
e
, которая имеетраспределение Стьюдента
с
числом степеней свободы
DF=n-2; -
Сравнить значение
тестовой статистики
|t0| с пороговым значением t
альфа
,n-2. Если значение
тестовой статистики
больше порогового значения, то
нулевая гипотеза
отвергается (
наклон
не может быть объяснен лишь случайностью при заданном уровне альфа) либо -
вычислить
p-значение
и сравнить его с
уровнем значимости
.
В
файле примера
приведен пример проверки гипотезы:
Изменяя
наклон
тренда k (ячейка
В8
) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.
Примечание
: Проверка значимости взаимосвязи эквивалентна
проверке статистической значимости коэффициента корреляции
. В
файле примера
показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью
процедуры F-тест
.
Доверительные интервалы для нового наблюдения Y и среднего значения
Вычислив параметры
простой линейной регрессионной модели
Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ=
a
* Хi +
b
Ŷ также является точечной оценкой для
среднего значения
Yi при заданном Хi. Но, при построении
доверительных интервалов
используются различные
стандартные ошибки
.
Стандартная ошибка
нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:
-
неопределенность связанную со случайностью оценок параметров модели
a
и
b
; - случайность ошибки модели ε.
Учет этих неопределенностей приводит к
стандартной ошибке
S(Y|Xi), которая рассчитывается с учетом известного значения Xi.
где SS
xx
– сумма квадратов отклонений от
среднего
значений переменной Х:
Примечание
: Se –
стандартная ошибка коэффициента регрессии
(
наклона
а
).
В
MS EXCEL 2010
нет функции, которая бы рассчитывала эту
стандартную ошибку
, поэтому ее необходимо рассчитывать по вышеуказанным формулам.
Доверительный интервал
или
Интервал предсказания для нового наблюдения
(Prediction Interval for a New Observation) построим по схеме показанной в разделе
Проверка значимости взаимосвязи переменных
(см.
файл примера лист Интервалы
). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х
ср
), то интервал будет постепенно расширяться при удалении от Х
ср
.
Границы
доверительного интервала
для
нового наблюдения
рассчитываются по формуле:
Аналогичным образом построим
доверительный интервал
для
среднего значения
Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае
доверительный интервал
будет уже, т.к.
средние значения
имеют меньшую изменчивость по сравнению с отдельными наблюдениями (
средние значения,
в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).
Стандартная ошибка
S(Yср|Xi) вычисляется по практически аналогичным формулам как и
стандартная ошибка
для нового наблюдения:
Как видно из формул,
стандартная ошибка
S(Yср|Xi) меньше
стандартной ошибки
S(Y|Xi) для индивидуального значения
.
Границы
доверительного интервала
для
среднего значения
рассчитываются по формуле:
Проверка адекватности линейной регрессионной модели
Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел
Предположения линейной регрессионной модели
).
Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках
простой линейной модели
n остатков имеют только n-2 связанных с ними
степеней свободы
. Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.
Чтобы проверить предположение о
нормальности распределения
ошибок строят
график проверки на нормальность
(Normal probability Plot).
В
файле примера на листе Адекватность
построен
график проверки на нормальность
. В случае
нормального распределения
значения остатков должны быть близки к прямой линии.
Так как значения переменной Y мы
генерировали с помощью тренда
, вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор
о
нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.
В нашем случае точки располагаются примерно равномерно.
Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе
Стандартная ошибка регрессии
оценкой
стандартного отклонения ошибок
является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.
SEy можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;2)
Иногда нормирование остатков производится на величину
стандартного отклонения
остатков (это мы увидим в статье об инструменте
Регрессия
, доступного в
надстройке MS EXCEL Пакет анализа
), т.е. по формуле:
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.
Most people use spreadsheets software such as Microsoft Excel to process their data and carry out their analysis tasks.
When performing an analysis of data, a number of statistical metrics come into play. Some of these include the means, the medians, standard deviations, and standard errors. These metrics help in understanding the true nature of the data.
In this article, I will show you two ways to calculate the Standard Error in Excel.
One of the methods involves using a formula and the other involves using a Data Analytics Tool Pack that usually comes with every copy of Excel.
So let’s get started!
What is Standard Error?
When working with real-world data, it is often not possible to work with data of the entire population. So we usually take random samples from the population and work with them.
The standard error of a sample tells how accurate its mean is in terms of the true population mean.
In other words, the standard error of a sample is its standard deviation from the population mean.
This helps analyze how accurately your sample’s mean represents the true population. It also helps analyze the amount of dispersion or variation between your different data samples.
How is Standard Error Calculated?
The Standard Error for a sample is usually calculated using the formula:
In this above formula:
- SE is Standard Error
- σ represents the Standard deviation of the sample
- n represents the sample size.
How to Find the Standard Error in Excel Using a Formula
Unfortunately, unlike the Standard Deviation, Excel does not have a built-in formula to calculate the Standard Error, at least not at the time of writing this tutorial.
However, you could use the above formula to easily and quickly calculate the standard error. Here are the steps you need to follow:
- Click on the cell where you want the Standard Error to appear and click on the formula bar next to the fx symbol just below your toolbar.
- Type the symbol ‘=’ in the formula bar. And type: =STDEV(
- Drag and select the range of cells that are part of your sample data. This will add the location of the range in your formula. So, if your sample data is in cells B2 to B14, you will see: =STDEV(B2:B14 in the formula bar.
- Close the bracket for the STDEV formula. So far, you have used the STDEV function to find the Standard deviation of your sample data.
- Next, we want to divide this Standard deviation by the square root of the sample size. So let’s continue with our formula. Click on the formula bar after the closing brackets of the STDEV formula and add a ‘/’ symbol to indicate that you want to divide the result of the STDEV function. So your formula so far is: =STDEV(B2:B14)/
- To find the square root of a number, we use the SQRT formula. So next, type SQRT(. Your formula bar will now have the formula: =STDEV(B2:B14)/SQRT(
- Finally, you want the sample size. For this, you need to use the COUNT function. So, type COUNT( after what you already have in your formula bar. Again, drag and select the range of cells that are part of your sample data and close the bracket for the COUNT formula. This will give you the number of cells in your selected range.
- Close the bracket for the SQRT function too. So your final formula should look like this: =STDEV(B2:B14)/SQRT(COUNT(B2:B14)) Notice there are two closing braces in the end. One is for the COUNT function, the other is for the SQRT function.
- That’s it! Press the return key on your keyboard and you got your sample’s Standard Error!
To find the Standard errors for the other samples, you can apply the same formula to these samples too.
If your samples are placed in columns adjacent to one another (as shown in the above image), you only need to drag the fill handle (located at the bottom left corner of your calculated cell) to the right.
This will copy the same formula to all the other cells on the right, and you will get standard errors for each of your samples!
How to Find the Standard Error in Excel Using the Data Analysis Toolpak
If you’re not in the mood to type complex formulae, there’s an easier way to find not just the Standard error, but practically all the statistical metrics you might need to analyze your sample data.
For this, you will need to install the Data Analysis Toolpak. This package gives you access to a variety of statistical functions, which include correlation functions, z-test, and t-test functions too.
Once you install the package, you can use the tool whenever you need to analyze data, without having to re-install it each time.
The Data Analysis Toolpak is free to use and comes along with your Excel package, but for simplicity, it does not appear in your standard toolbar. You need to activate it in order for it to be added to your toolbar.
The process of activating it is quite simple. Just follow these steps to install and activate your Data Analysis Toolpak:
- Click the File tab and click on Options. This will open the Options window for you.
- From here, click “Add-ins” from the left sidebar.
- From the list of Add-ins, select Analysis ToolPak.
- At the bottom of the window, click on the ‘Go’ button just next to Manage: Add-ins.
- Click the checkmark for Analysis ToolPak and click OK.
With this, your Data Analysis Toolpak will get added to your Excel Toolbar. When you click the Excel ‘Data’ tab, you should find a tool named “Data Analysis” at the far right of the Data toolbar (under the ‘Analysis’ group).
Now, to find out your Standard Error and other Statistical metrics, do the following:
- Click on the Data Analysis tool under the Data tab. This will open the Analysis Tools dialog box.
- Select “Descriptive Statistics” from the list on the left of the dialog box and click OK.
- Enter the location of the range of cells that contain your sample data into the “Input Range” box. You can also choose to drag and select the range of cells that you need too. If you have data for more than one sample arranged in adjacent columns, you can select the data in all the columns. You will get your results separately for each column.
- If your data has column headers, check the “Labels in first row” box.
- Select where you want your results to be displayed. It is safer to select “New Worksheet”. This will ensure that the details get displayed on a newly created worksheet, and will not disturb any data on your current worksheet.
- Select the checkbox next to “Summary Statistics” and click OK.
This will display all your analytical metrics in a new worksheet.
These metrics will also include the Standard Error for your selected sample data. If you had selected multiple data sets in multiple columns, you will get analytics for each column separately.
Conclusion
In this article, we discussed two ways in which you can find the Standard error for your sample data.
You can either create a formula to calculate it or use a data analytics tool, like the Data Analysis Toolpak that comes with Excel.
Either way, you will be able to use the Standard error information to analyze your sample data for further processing.
Hope you found this Excel tutorial useful!
Other Excel tutorials you may find useful:
- How to Convert Decimal to Fraction in Excel
- How to Square a Number in Excel
- How to Subtract Multiple Cells from One Cell in Excel
- How to Find Range in Excel
- How to Find Outliers in Excel
- How to Calculate IRR with Excel
- How to Calculate NPV in Excel (Net Present Value)
- How to Calculate Confidence Interval in Excel
- How to Get the p-Value in Excel?
- How to Find Z-score in Excel?
- How to Calculate Percentage Difference in Excel
- Calculate the Coefficient of Variation in Excel
- How to Calculate Mean Squared Error (MSE) in Excel?
In this article, I will show you how to perform a simple linear regression test in Microsoft Excel.
Not only will I show you how to perform the linear regression, but I’ll show you how to analyse the outputs of the regression test.
My example data
For this example, I just have two variables of data:
- Weight (kg)
- Height (cm)
I have these measures for 49 different participants; each row represents a different participant.
So, for the first participant, I can see that they had a weight of 51.24 kg and a height of 167.08 cm.
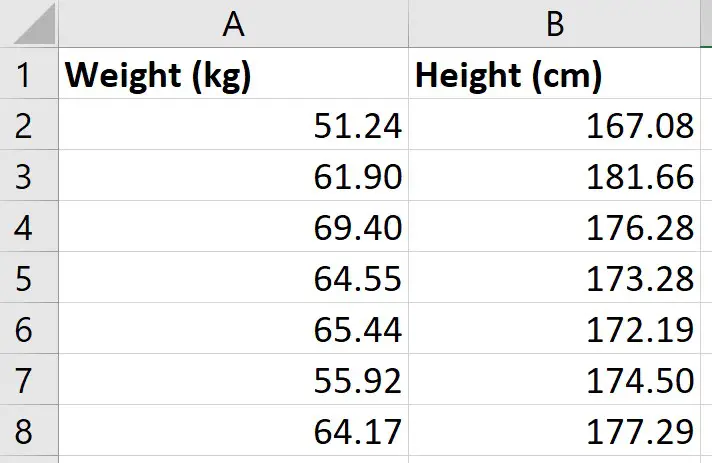
What I want to do is to perform a simple linear regression to see how well the measures of height in my sample can predict the measures of weight.
Installing the Analysis ToolPak
There are a few ways you can perform a linear regression in Excel, but perhaps the easiest method is to use the Analysis ToolPak. This is an add-on created by Microsoft to provide data analysis tools for statistical analyses.
Here are the intrustions for installing the Analysis Toolpak:
- Go to File>Options
- Then click on Add-ins
- At the bottom, you want to manage the Excel add-ins and click the Go button
- Then, ensure you tick the Analysis ToolPak add-in, and click OK
Now, when you click on the Data ribbon, you should see a Data Analysis button in a sub-section called Analyze

We are now ready to perform the linear regression in Excel.
Performing the linear regression in Excel
To perform the linear regression, click on the Data Analysis button.
Then, select Regression from the list.
You must then enter the following:
- Input Y Range – this is the data for the Y variable, otherwise known as the dependent variable. The Y variable is the one that you want to predict in the regression model. For me, this will be the weight data
- Input X Range – this is the data for the X variable, otherwise known as the independent variable. For me, this will be the height data
If you have highlighted the labels of the columns when selecting the data, then tick the Labels options. If you didn’t have any labels when you selected your data, then you should not tick this option.
The next option called Constant is Zero is used if you want the regression line to start at 0, otherwise known as the origin. Doing so would mean there is no Y intercept in the model. Generally, for linear regression, this option is not selected, so I will leave it unchecked for this example.
It is also possible to specify the confidence level for the test. By default, the results will return the 95% confidence intervals without having to change any options. However, if you want to use a different confidence level than 95%, then you need to select this option and enter the desired value here.
Output options
For the Output Options, you can specify where you want the regression results to be placed.
- Output Range – you can highlight where you want the results to be placed in that worksheet
- New Worksheet Ply – lets you place the results in a new worksheet
- New Workbook – lets you save the results in an entirely separate workbook
For my example, I’m going to select the second option and have the results placed in a new worksheet.
Residuals
The final set of options concerns the residuals in the analysis.
- Residuals – will return the list of predicted dependent values, based on the regression line, as well as the residual values for each point
- Standardized Residuals – will return the standardized residuals; these values can be useful when identifying potential outliers
- Residual Plots – will create a scatter graph where the residuals are plotted on the Y axis and the X variable is plotted on the X axis
- Line Fit Plots – will create another scatter graph where the Y and X variables are plotted, but it will also add the predicted Y values onto the graph
Finally, the Normal Probability Plots option plots another scatter plot, which is used to determine whether the Y variable data fits a normal distribution.
Interpretation of the linear regression results
Depending on the options selected in the set-up window, you will have quite a lot of information in the results sheet.
I’ll now break down the output and go through each in more detail.
- Summary Output table
- ANOVA table
- Coefficients table
- Residual Output table
- Residual plot
- Standardized Residuals
- Line Fits plot
- Normal Probability plot
Summary Output table
In the first table called Summary Output, there are some regression statistics from the test.
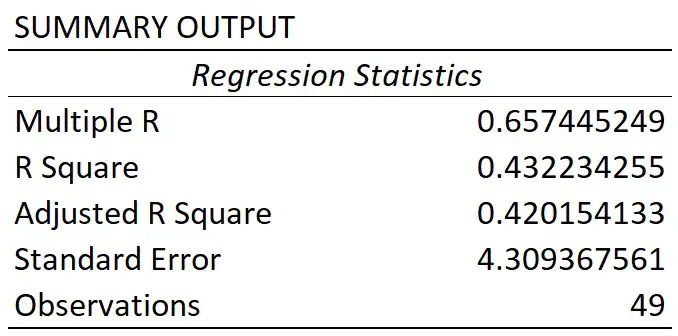
Multiple R
This is the absolute value of the correlation coefficient between the two variables of interest. Briefly, it is a value that tells you how strong the linear relationship is.
A value of 0.65 in this case indicates a fairly strong linear correlation between height and weight measures.
If you’re interested to learn more about correlation, then I suggest you refer to the What is Pearson Correlation post.
R square
You may sometimes see the R square being referred to as the coefficient of determination.
To get this value, you simple square the multiple R value.
The R square value tells you how much variance the dependent variable can be accounted for by the values of the independent variable. Researchers often multiple this value by 100 to get a percentage value.
So, for my example, I can say that 43% of the variance in weight can be accounted for by the height measures. The other 57% of the variance is therefore caused by other factors, such as measurements errors.
Adjusted R square
The adjusted R square takes into account the number of independent variables in the regression analysis, and corrects for bias.
Usually, this value is only relevant when you are performing multiple linear regression, where there are more than 1 independent variables in the model.
Standard error
The standard error of the regression is the average distance that the observed values fall from the regression line.
What’s useful about the standard error is that it is in the same units as the dependent variable. So, here my standard error is 4.31 kg, when rounded. This means, on average, my observed values were 4.31 kg from the regression line.
The smaller the standard error, the more precise the linear regression model is.
Observations
Finally, we have the number of observations. This is just the number of subjects in the test.
So, for my example, I had 49 participants.
ANOVA table
The main thing you will be concerned with when looking at this table is the value under the Significance F header; this is in fact the P value for the regression model.
To be able to interpret this, we need our hypotheses:
- Null hypothesis – there is no linear relationship between the height and weight measures
- Alternative hypothesis – there is a linear relationship between the height and weight measures
If my alpha was 0.05, this means I will reject the null and accept the alternative hypothesis if P≤0.05. The opposite will be true if P>0.05; in this case, I would fail to reject the null hypothesis.
As you can see, the P value (Significance F) for the model was considerably lower than my alpha value of 0.05. So, I can conclude that the linear regression model is significant.
Coefficients table
Let me now move on to the final table of results regarding the coefficients.

The first row displays the results for the intercept, this is the point where the line of best fit (regression line) crosses the Y axis when the value of X is zero.
The second row displays the results for the slope.
For a simple linear regression model, the most basic version of the equation is Y = m.X + b.

Using the information reported from the results, we can then say:
Y = 0.800264.X – 79.599
So, in this example, if we knew a participants height (in cm), we can predict their weight (in kg) by using this equation. For example, if a participant measured 175 cm, the model estimates their height to be 60.45 kg.
Looking back at the coefficient results table, we can see there are other columns which tells us the standard error, as well as the lower and upper 95% confidence intervals, or a different confidence interval if a different confidence level was entered. And these values are for the intercept and slope values.
You will also notice each also has a T-statistic. This value is used to compute the P value.
Again, to interpret this P value we need our hypotheses:
- Null hypothesis – the intercept or slope is 0
- Alternative hypothesis – the slope of the line is not 0
As you can see, both values are less than my alpha of 0.05. However, we usually ignore the P value for the intercept.
For the slope, this means that height is a significant variable that impacts weight in this case.
Residual options
So, that’s an overview of the regression model results, let me know cover the other outputs from the regression test.
Residual Output
If you selected to have the Residuals option during the regression set-up, you will have a table titled Residual Output.

For each observation from your data that was entered into the regression test, you will get a predicted value of Y based on the regression model.
For example, if you look at the first observation in my original data, you see this participant had a height of 167.08 cm. If I put this into the regression equation, along with the slope and intercept values, I get the predicted weight value of 54.10999 kg.
This is what the Predicted column represents; Excel does this for each of the observations.
Using the predicted values, Excel can then calculate the residuals.
A residual is simply the distance between the actual data point and the line of best fit.
For my first participant they had a height of 167.08 cm and a weight of 51.24 kg. As calculated above, the predicted weight value based on the model was 54.10999 kg. The residual for this point therefore is the difference between the actual weight value (51.24 kg), and the predicted weight value (54.10999 kg), which comes out at around -2.867 kg.
Excel then repeats this process for the rest of the observations.
Residual Plot
If you also selected the Residual Plots option in the Regression set-up window, you will also get a graph returned.
Here is my Residual Plot.
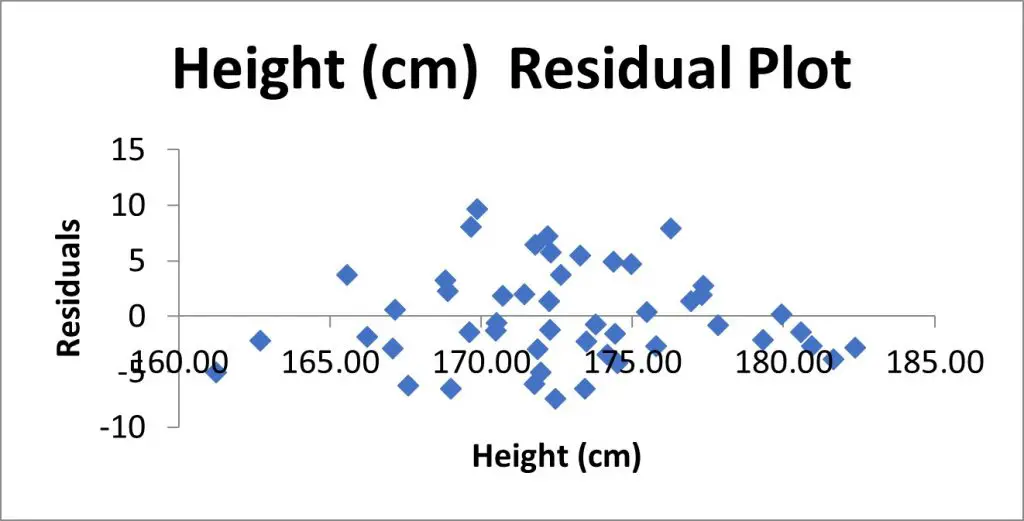
This is a scatter plot of the residuals on the Y axis and the values of the independent variable on the X axis.
Residual plots are useful to look at when investigating homogeneity of variance, which is an assumption of the linear regression test.
What you are looking for here is a random pattern to the graph; there should be roughly half the number of data points above 0 and below 0, and there vertical spread of the data points should be roughly constant the further along the X axis you go.
Standardized Residuals
If you selected the Standardized Residuals option in the regression options, you will also see a column called Standard Residuals in the residuals table.
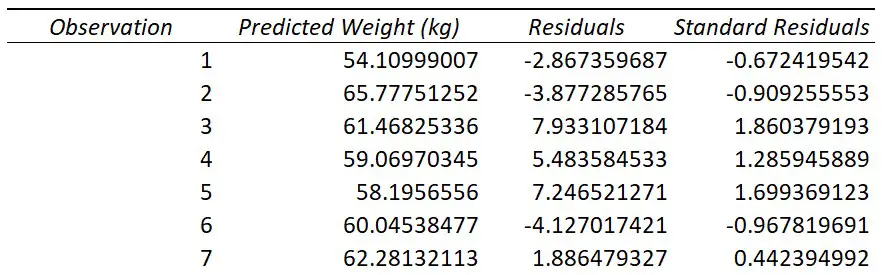
The standardized residual is the residual divided by an estimate of its standard deviation. You can think of them as Z scores.
These values are useful to look at when trying to identify potential outliers in your sample.
Generally, any standardized residuals with a value greater than 3 or -3 is a sign that it may be an outlier.
Line Fits Plot
If you selected to have the Line Fit Plots option, you will also see a scatter plot containing the data that was entered into the regression test.
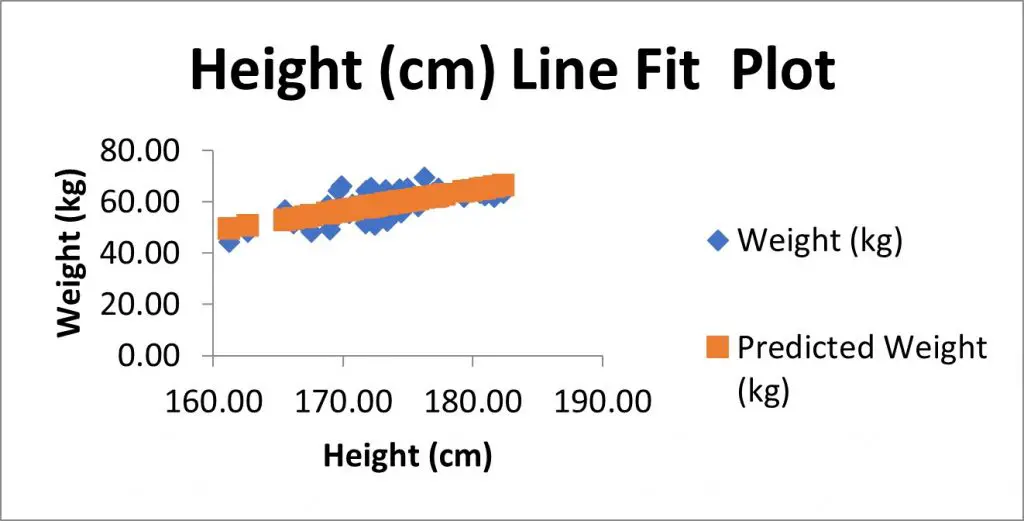
In my example, I have the height measures on the X axis and the weight measures on the Y axis.
There is also another set of data, as shown in orange here, which are in fact the predicted Y value based on the model. These are the Predicted values from the residuals table.
If instead of showing the Predicted values on the graph, but you instead wanted to plot the line of best fit (which will pass through the predicted values), then you could remove the predicted values from the graph.
To do this:
- Right-click on on the graph, and go to Select Data
- Highlight the predicted Y variable in the legend entry, select remove, and click Okay
- Select the graph, then go to Add Chart Element>Trendline, and select the Linear option
- If you also want to show the equation of the line, then double-click on the line
- Then, in the Format Trendline options that have opened to the right, scroll down and select Display Equation on Chart
Normal Probability plot
Finally, if you selected the Normal Probability plots option in the regression setup window, you will also see a table called Probability Output and a graph, called the Normal Probability Plot, which is a scatter plot of this data in the graph.
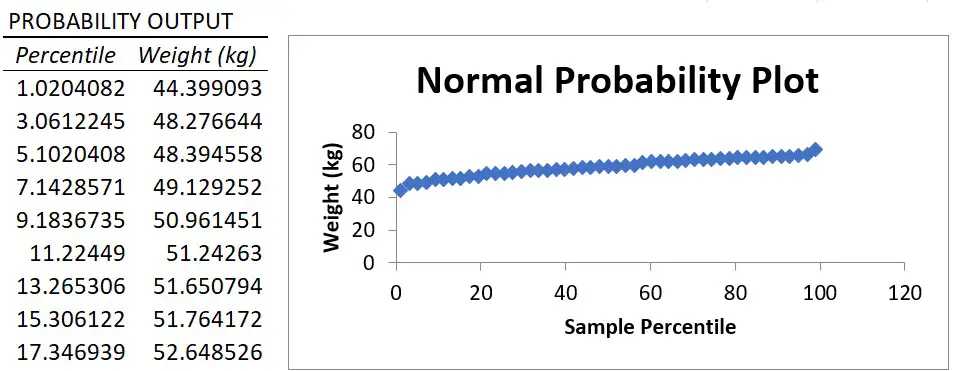
The X axis plots the percentile value ranging from 0 to 100 and the Y axis plots the Y variable data.
The normal probability plot is used to determine whether the data fits a normal distribution.
Essentially, what you are looking for is a straight line of data. And, as you can see, there is a nice straight line of data for my example, which suggests the weight data are normally distributed.
However, it’s worth noting that the Y variable does not actually have to be normally distributed when fitting a linear regression model. I’ll go into a bit more detail about the assumptions of linear regression in a future tutorial.
Wrapping up
You now know how to perform a simple linear regression test in Microsoft Excel, and how to interpret the output of results.
Microsoft Excel version used: 365 ProPlus
Regression is an Analysis Tool, which we use for analyzing large amounts of data and making forecasts and predictions in Microsoft Excel.
Want to predict the future? No, we are not going to learn astrology. We are into numbers and we will learn regression analysis in Excel today.
To predict future estimates, we will study:
- REGRESSION ANALYSIS USING EXCEL FUNCTIONS (MANUAL REGRESSION FINDING)
- REGRESSION ANALYSIS USING EXCEL’S ANALYSIS TOOLPAK ADD-IN
- REGRESSION CHART IN EXCEL
Let’s do it…
Scenario:
Let’s assume you sell soft drinks. How cool will it be if you can predict:
- How many soft drinks will be sold next year based on previous year’s data?
- Which fields need to be focused?
- And how can you increase your sales by changing your strategy?
It will be profitably awesome. Right?… I know. So let’s get started.
You have 11 records of salesmen and soft drinks sold.
Now based on this data you want to predict the number of salesmen required to achieve 2000 sales of soft drinks.
The regression equation is a tool to make such close estimates. To do so, we need to know Regression first.
REGRESSION ANALYSIS USING EXCEL FUNCTIONS (MANUAL REGRESSION FINDING)
This part will make you understand regression better than just telling excel regression procedure.
Introduction:
Simple Linear Regression:
The study of the relationship between two variables is called Simple Linear Regression. Where one variable depends on the other independent variable. The dependent variable is often called by names such as Driven, Response, and Target variable. And the independent variable is often pronounced as a Driving, Predictor or simply Independent variable. These names clearly describe them.
Now let’s compare this with your scenario. You want to know the number of salesmen required to achieve 2000 sales. So here, the dependent variable is the number of salesmen and the independent variable is sold soft drinks.
The independent variable is mostly denoted as x and dependent variable as y.
In our case, soft drinks are sold x and the number of salesmen is y.
If we want to know how many soft drinks will be sold if we appoint 200 salesmen, then the scenario will be vice-versa.
Moving On.
The “Simple” Math of Linear Regression Equation:
Well, it’s not simple. But Excel made it simple to do.
We need to predict the required number of salesmen for all 11 cases to get the 12th closest prediction.
Let’s say:
Soft Drink Sold is x
The number of Salesmen is y
The predicted y (number of salesmen) also called Regression Equation, would be
Now you must be wondering where the stat will you get the slope and intercept. Don’t worry, excel has functions for them. You do not need to learn how to find the slope and intercept it manually.
If you want, I will prepare a separate tutorial for that. Let me know in the comments section. These are some important data analytics tools.
Now let’s step into our calculation:
Step1: Prepare this small table
Step 2: Find the slope of the regression line
Excel Function for slopes is
=SLOPE(known_y’s,known_x’s)
Your known_y’s are in range B2:B12 and known_x’s are in range C2:C12
In cell B16, write the formula below
(Note: Slope is also called coefficient of x in the regression equation)
You will get 0.058409. Round up to 2 decimal digits and you will get 0.06.
Step 3: Find the Intercept of Regression Line
Excel function for the intercept is
=INTERCEPT(known_y’s, known_x’s)
We know what our known x’s and y’s
In cell B17, write down this formula
=INTERCEPT(B2:B12, C2:C12)
You will get a value of -1.1118969. Roundup to 2 decimal digits. You will get -1.11.
Our Linear Regression Equation is = x*0.06 + (-1.11). Now we can predict possible y depending on the target x easily.
Step 4: In D2 write the formula below
=C2*$B$16+$B$17 (Regression Equation)
You will get a value of 13.55.
Select D2 to D13 and press CTRL+D to fill down the formula in the range D2:D13
In cell D13 you have your required number of salesmen.
Hence, to achieve the target of 2000 Soft Drink Sales, you need an estimate of 115.71 salesmen or say 116 since it is illegal to cut humans into pieces.
Now using this you can easily conduct What-If analysis in excel. Just change the number of sales and it will show you many salesmen will it take to get that sales target achieved.
Play around it to find out:
How much workforce do you need to increase sales?
How many sales will increase if you increase your salesmen?
Make Your Estimate More Reliable:
Now you know that you need 116 salesmen to get 2000 sales done.
In analytics, nothing is just said and believed. You must give a percentage of reliability on your estimate. It is like giving a certificate of your equation.
Correlation Coefficient Formula:
The next thing you will be asked is how much these two variables are related. In static terms, you need to tell the coefficient of correlation.
Excel function for correlation is
In your case, known_x’s and Know_y’s are array1 and array2 irrespectively.
In B18 enter this formula
You will have 0.919090. Formate cell B2 into the percentage. Now have 92% of correlation.
Now, what this 92% means. It means, there 92% of chances of sales increase if you increase the number of salesmen and 92% of sales decrease if you decrease the number of salesmen. It is called Positive Correlation Coefficient.
R Squire (R^2) :
R Squire value tells you, by what percentage your regression equation is not a fluke. How much it is accurate by the data provided.
The Excel function for R squire is RSQ.
RSQ(known_y’s, Known_x’s)
In our case, we will get R squire value in cell B19.
In B19 enter this formula
So we have 84% of r Square value. Which is a very good explanation of our regression. It says that 84% of our data is just not by chance. Y (number of salesmen) is very much dependent on X (sales of soft drinks).
There are many other tests we can do on this data to ensure our regression. But manually it will be a complex and lengthy procedure. That is why excel provides Analysis Toolpak. Using this tool we can do this regression analysis in seconds.
REGRESSION IN EXCEL USING EXCEL’S ANALYSIS TOOLPAK ADD-IN
If you already know what regression equations are, and you just want your results quickly then this part is for you. But if you want to understand regression equations easily then scroll up to REGRESSION ANALYSIS USING EXCEL FUNCTIONS (MANUAL REGRESSION FINDING).
Excel provides a whole bunch of tools for analysis in its Analysis Toolpak. By default, it is not available in the Data tab. You need to add it. So let’s add it first.
Adding Analysis Toolpak to Excel 2016
If you don’t know where is data analysis in excel follow these steps
Step 1: Go to Excel Options: File? Options? Add-Ins
Step 2: Click on Add-Ins. You will see a list of available add-Ins.
Select Analysis ToolPak and at the bottom of the window, find manage. In manage select Excel Add-Ins and Click on GO.
Add-ins window will open. Here, select Analysis ToolPak. Then click the ok button.
Now you can access all functions of data analysis ToolPak from Data Tab.
Using Analysis ToolPak for Regression
Step 1: Go to the Data tab, Locate Data Analysis. Then click on it.
A dialogue box will pop up.
Step 2: Find ‘Regression’ in Analysis Tools list and hit the OK button.
The regression input window will pop up. You will see a number of available input options. But for now, we will just concentrate on Y Range and X Range, leaving everything else to default.
Step 4: Provide Inputs:
No. of Salesmen is Y
Sales of soft drinks are X
Hence
- Y Range= B2:B11
And
- X Range = C2:C11
For the output range, I have selected E4 on the same sheet. You may select a new worksheet to get results on a new worksheet in the same workbook or a complete new workbook. When you are done with your inputs, hit the OK button.
Results:
You will be served with a variety of information from your data. Don’t get overwhelmed. You don’t need to consume all the dishes.
We will only deal with those results which will help us to estimate the required number of salesmen
Step 5: We know the regression equation for estimation of y, that is
x*Slope+Intercept
We just need to locate Slope and Intercept in results.
And here they are.
The intercept Coefficient is clearly mentioned.
The slope is written as ‘X Variable 1’, some times also mentioned as the coefficient of X. Round up them and we will get -1.11 as Intercept and 0.06 as Slope.
Step 6: From results, we can drive the Regression equation. And that would be
=x*(0.06) + (-1.11)
Prepare this table in excel.
For now, x is 2000, which is in cell E2.
In Cell F2 enter this formula
=E2*F21+F20
You will get a result of 115.7052757.
Rounding it up will give us 116 of Required Salesmen.
So we have learned how to form the regression equation manually and using Analysis ToolPak. How can you use this equation to estimate future stats?
Now let’s understand the regression output given by Analysis Toolpak.
Understanding the Regression Output:
There is no benefit, if you do regression analysis using analysis tool pack in excel and can’t interpret its meaning.
Summary Section:
As the name suggests, it is a summary of the data.
-
- Multiple R: It tells how fit the regression equation is to the data. It is also called the correlation coefficient.
In our case, it is 0.919090619 or 0.92 (roundup). This means that there is a 92% chance of an increase in sales if we increase our salesmen count.
-
- R Square: It tells the reliability of found regression. It tells us how many observations are part of our line of regression. In our case, it is 0.844727566 or 0.85. It means that our regression is fit by 85%.
- Adjusted R Square: Theadjusted square is just a more testified version of R square. Mainly useful in Multiple Regression Analysis.
- Standard Error: While R. Squire tells you how many data points fall near the regression line, the standard error tells you how far a data point can go from the regression line.
In our case, it is 6.74.
- Observation: This is simply the number of observations, which is 11 in our example.
Anova Section:
This section is hardly used in linear regression.
- df. It is a degree of freedom. It is used when calculating regression manually.
- SS. Sum of squares. It is just a sum of squares of variances. Used to find R squire values.
- MS. This means squared value.
- And 5. F and Significance of F. If the significance of F (p-value of the slope) is less than the F test than you can discard the null hypothesis and prove your hypothesis. In simple language, you can conclude that there is some effect of x on y when changed.
In our case, F is 48.96264 and Significance of F is 0.000063. It means our regression fits the data.
Regression Section:
In this section, we have the two most important values for our regression equation.
- Intercept: We have an intercept here that tells where x-intercepts on Y. This is an important part of the regression equation. It is -1.11 in our case.
- X variable 1 (Slope). Also called the coefficient of x. It defines the tangent of the regression line.
REGRESSION CHART IN EXCEL
In excel, it is easy to plot a regression chart. Just follow these steps. To add Regression Chart in Excel 2016, 2013, and 2010 follow these simple steps.
Step 1. Have your known x’s in the first column and know y’s in the second.
In our case, we know Known_ x’s are Soft Drinks Sold. And known_y’s are Salesmen.
Step 2. Select your known x’s and y’s range.
Step 3: Go to the Insert tab and click on the scatter chart.
You will have a chart that looks like this.
Step 4. Add the trend line: Goto layout and locate the trendline option in the analysis section.
Under the Trendline option, click on Linear Trendline.
You will have your graph looking like this.
This is your regression graph.
Now if you add the data below and extend the selected data. You will see a change in your graph.
For our example, we added 2000 to the Soft Drink Sold and left the Salesmen blank. And when we extend the range of the graph, this is what we will have.
It will give the required number of salesmen for doing 2000 sales of soft drinks in graphical form. Which is slightly below 120 in the graph. And from our regression equation, we know it is 116.
In this article, I tried to cover everything under Excel Regression Analysis. I explained regression in excel 2016. Regression in excel 2010 and excel 2013 is same as in excel 2016.
For any further query on this topic, use the comments section. Ask a question, give an opinion or just mention my grammatical mistakes. Everything is welcome. Just don’t hesitate to use the comment section.
Related Data:
How to Use STDEV Function in Excel
How To Calculate MODE function in Excel
How To Calculate Mean function in Excel
How to Create Standard Deviation Graph
Descriptive Statistics in Microsoft Excel 2016
How to Use Excel NORMDIST Function
How to use the Pareto Chart and Analysis
Popular Articles:
50 Excel Shortcut to Increase Your Productivity
How to use the VLOOKUP Function in Excel
How to use the COUNTIF function in Excel 2016
How to use the SUMIF Function in Excel
With many things we try to do in Excel, there are usually multiple paths to the same outcome. Some paths are better than others depending on the situation. The same holds true for linear regression in Excel. There are four ways you can perform this analysis (without VBA). They are:
- Chart Trendlines
- LINEST function
- “Old School” regression using the Solver
- Linear regression with the Analysis Toolpak Add-In
Each of these linear regression methods has an appropriate time and place. Let’s take a look at each one individually.
Simple Linear Regression with Excel Charts
When you need to get a quick and dirty linear equation fit to a set of data, the best way is to simply create an XY-chart (or “Scatter Chart”) and throw in a quick trendline. Add the equation to the trendline and you have everything you need. You can go from raw data to having the slope and intercept of a best-fit line in 6 clicks (in Excel 2016).
Let’s say we have the data set below, and we want to quickly determine the slope and y-intercept of a best-fit line through it.
We’d follow these 6 steps (in Excel 2016):
- Select x- and y- data
- Open Insert Tab
- Select Scatter Chart
- Right-Click Data Series
- Select Add Trendline
- Check Display Equation on Chart
Now we know that the data set shown above has a slope of 165.4 and a y-intercept of -79.85.
Easy, right?
Linear Regression with the LINEST function
The chart trendline method is a quick way to perform a very simple linear regression and fit a curve to a series of data, but it has two significant downfalls.
The first is that the equation displayed on the chart cannot be used anywhere else. It’s essentially “dumb” text.
If you want to use that equation anywhere in your spreadsheet, you have to manually enter it. However, if you change the data set used to obtain the equation, that equation you manually entered will not update, leaving your spreadsheet with an erroneous equation.
The second issue is that sometimes the number of significant digits displayed in the formula on the chart is very limited. In fact, sometimes, you’ll only be able to see one or two significant digits. And that will lead to inaccuracy in the predicted values of y.
What we need for these situations is a function that can perform the same kind of simple linear regression done by the charting utility and output the coefficients to cells where we can use them in an equation. Of course, it also needs to return values with more significant digits.
The LINEST function does this perfectly. Given two sets of data, x and y, it will return the slope (m) and intercept (b) values that complete the equation
y = mx + b
The syntax of the function is as follows:
LINEST(known_y’s, [known_x’s], [const], [stats])
Where:
Known_y’s is the y-data you are attempting to fit
Known_x’s is the x-data you are attempting to fit
Const is a logical value specifying whether the intercept is forced to zero (FALSE) or not (TRUE)
Stats is a logical value that specifies whether regression statistics are returned
LINEST is an array function, so we need to enter it as an array formula, providing two cells to which it can return the values of m and b.
Let’s take a look at how LINEST could be used to determine the equation of a best-fit line for the data above.
Since LINEST will return two values, I start by selecting two adjacent cells on the worksheet.
Next, I enter the formula in the formula bar, rather than in the cell.
Finally, because it’s an array formula, I press CTRL+SHIFT+ENTER to calculate the cells.
The results are…
…exactly the same as those provided by the trendline method.
This was obviously more work than using a trendline, but the real advantage here is that the slope and y-intercept values have been output to a cell. That means we can use them dynamically in a calculation somewhere else in the spreadsheet.
Linear Regression Using Solver
This method is more complex than both of the previous methods. Fortunately, it will probably be unnecessary to ever use this method for simple linear regression. I’ve included it here because it provides some understanding into the way that the previous linear regression methods work. It will also introduce you to the possibilities for more complicated curve fitting using Excel.
- Enter “guess-values” for the slope and intercept of the equation
- Calculate new y-values based on those guess values
- Calculate the error between the calculated y-values and the y-data
- Use the Solver to find values of the slope and intercept that minimize the total error
Let’s start again with the x- and y- data we had before.
Next, enter some guess values for m and b into some cells on the worksheet.
Now create a new column of calculated y-values based on the m and b guess values and the known x-data.
Next, create an error column, calculating the difference between the y-data and calculated y-values.
Finally, create a new formula, calculating the sum of squares of the error column.
We will use the Solver to minimize this value – the sum of the squared errors. The reason why we use “sum of squares” instead of just “sum” is because we do not want an error of -100 in one cell to cancel out an error of 100 in another cell. We want each value in the error column to be driven to its minimum absolute value.
Now, let’s open up the Solver. If you have never used the Solver Add-In before, you must first enable it. Follow the steps here to enable the Solver.
After the Add-In has been loaded, you can open the Solver from the Data tab. You’ll find it way over on the right side of the ribbon:
With the Solver open, the setup for this is pretty straightforward.
- We want to minimize the objective, cell H3, or the sum of the squared errors.
- To do so, we will change variable cells E3 and F3, the slope and y-intercept of our linear equation.
- As a last step, uncheck the option to “Make Unconstrained Variables Non-Negative”.
When properly set up, the solver dialog should look like this:
When we click “Solve”, the Solver does its thing and finds that the values m = 165.36 and b = -79.85 define the best-fit line through the data. Exactly what was predicted by the chart trendline and LINEST.
Of course, this is totally expected. After all, we have just done “manually” what the Trendline tool and LINEST do automatically.
In the case of a simple linear regression like we have here, Solver is probably complete overkill. However, this is just the start. We can use this same concept to do more complex multiple linear regression or non-linear regression analysis in Excel. Using Solver, you can fit whatever kind of equation you can dream up to any set of data. But that’s a topic for a completely different post.
Regression Analysis in Excel with the Analysis Toolpak Add-In
The final method for performing linear regression in Excel is to use the Analysis Toolpak add-in. This add-in enables Excel to perform difficult statistical analysis, but it is not enabled by default in Excel installations.
Install the Analysis Toolpak Add-In
To enable the Analysis Toolpak, follow these steps:
- Open the File tab, then select Options in the lower left corner
- Click Add-Ins in the lower left of the Excel Options window
- In the Manage drop-down, select “Excel Add-Ins”
- Click Go
- Select Analysis Toolpak
- Click OK
The Analysis Toolpak will be available in the Data tab in the Analysis group (on the far right of the ribbon and next to Solver). It is labelled as “Data Analysis”.
Simple Linear Regression Analysis with the Analysis Toolpak
Open the Analsis Toolpak Add-In from the ribbon and scroll down until you see Regression. Select it and click OK.
When the regression window opens, you’ll be greeted by tons of options. We’ll cover those in a minute, but let’s just keep it simple for now.
First, place the cursor in the box for “Input Y Range”, and select the y-values or dependent variables.
Repeat this for the “Input X Range”.
We can choose to set the intercept, or constant, to zero. If this box is unchecked, the constant will be calculated similarly to our previous regression analyses.
Next, select where the output data should be stored. The regression tool generates a large table of statistics, so you may want to store them on a new worksheet. Or you can specify a specific output range cell on the current worksheet. This cell will become the upper right cell in the output table. In the example below, I chose cell F2.
Finally, the regression tool provides several options for examining the residuals. Residuals are the difference between the observed y-values and the predicted y-values. Generally, the residuals should be randomly distributed with no obvious trends, such as increasing or decreasing in value as the x-values increase.
To examine for this easily, we can choose to create a residual plot with the regression analysis by checking the box next to “Residual Plots”.
Finally, with everything set up, all that is left to do is click the OK button to generate the report.
This is what it should look like:
If you are looking for the coefficients that describe the best-fit line, you’ll have to go all the way down into the third table in the report. Here, you’ll see two rows:
- Intercept
- X Variable 1
The column in this table labeled “Coefficients” contains the values of the intercept and slope (X Variable 1). You can see that they match the values we obtained using the other methods. (Which is always nice to see!)
The plot of residuals is random, and there are no trends in the residuals:
The regression tool generates a lot of other data as well, so let’s look at some of the more important details:
Linear Regression Statistics
The first table in the report contains the Regression Statistics. These statistics are important because they tell us how well the line that results from the linear regression analysis fits the observed data.
Multiple R: This is the Pearson correlation coefficient that describes the correlation between the predicted values of Y and the observed values of Y. A value of 1 means that there is a perfect correlation between the two, and a value of 0 means that there is no correlation at all. In this analysis the value is 0.96, so there is a very strong correlation between the predicted and observed y-values.
R-Square: This is the coefficient of determination and it explains how much of the variation in the dependent variable can be explained by the equation. In this case, the R-Squared value is 0.91, so 91% of the variation is captured by the equation. That means the other 9% of the variation is not explained by the equation. It may be due to randomness or measurement error, for example.
Adjusted R-Square: This term is used for multiple linear regression and is useful in determining if a new term added to the model has helped to improve the prediction capability of the model or not. If an added term improves the model, this value increases. If an added term does not improve the model, this value decreases.
Standard Error: This is an estimate of how far the observed values are from the line that results from the regression analysis.
Observations: This is simply the number of observed data points.
Regression Coefficients
This is the third table in the report that contains a row for each of the coefficients and several columns:
- Coefficients
- Standard Error
- t Stat
- P-value
- Lower 95%
- Upper 95%
Coefficients: These are the coefficients on the variables that describe the line of best fit. In this example, we would assemble the coefficients into the equation:
Standard Error: This value tells us how much the observed values deviate from the best-fit line.
t Stat: This is the value you would use in a t-test.
P-value: This is the P-value used for the hypothesis test. If the P-value is low, we reject the null hypothesis.
Lower 95%: This is the lower bound of the 95% confidence interval.
Upper 95%: This is the upper bound of the 95% confidence interval.
Residual Output
The final table in the report lists the predicted value of y and the residual, or error between the predicted and observed value, for each value of x.
Regression Analysis Options
Performing a basic linear regression analysis with the Analysis Toolpak is straightforward, but there are many options to really expand its capability.
Labels: By selecting this option, the regression tool will use the cell value in the top row of the x-values as a label for the x-values.
Confidence Level: It’s possible to set a different confidence level in this field. The default is 95%.
Residuals: Choosing this option will add the residuals to the output table.
Standardized Residuals: When this option is selected, standardized residuals will be written to the worksheet.
Line Fit Plots: This will create a plot that includes the original observations and the predicted y-values. It is like adding a trendline to a plot.
Normal Probability Plot: This will plot the data against a normal distribution, which helps to determine whether the data is normally distributed.