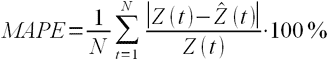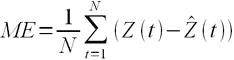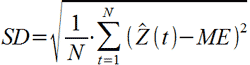Стандартное отклонение ошибки прогноза

Оценка ошибки прогнозирования временного ряда

Работая с научными публикациями, сталкиваюсь с различными показателями ошибок прогнозирования временных рядов. Среди всех встречающихся оценок ошибки прогнозирования стоит отметить две, которые в настоящее время, являются самыми популярными: MAE и MAPE.
Пусть ошибка есть разность:
     ,
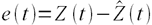
где Z(t) – фактическое значение временного ряда, а – прогнозное.
Тогда формулы для оценок ошибки прогнозирования временных рядов для N отчетов можно записать в следующем виде.

MAPE – средняя абсолютная ошибка в процентах

     
.

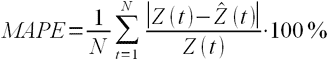
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.

Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.

MAE – средняя абсолютная ошибка

     
.

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.

После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.

Кроме указанных иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.

MSE – среднеквадратичная ошибка

     
.

RMSE – квадратный корень из среднеквадратичной ошибки

     
.

ME – средняя ошибка

     
.

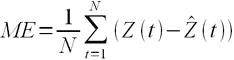
SD – стандартное отклонение

     
, где ME – есть средняя ошибка, определенная по формуле выше.

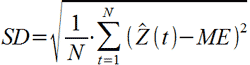
Связь точности и ошибки прогнозирования

Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.

Точность прогноза в % = 100% – MAPE

Величину точности оценивать не принято, говоря о прогнозировании всегда оценивают, то есть определяют значение именно ошибки прогноза, то есть величину MAPE и/или MAE. Однако нужно понимать, что если MAPE = 5%, то точность прогнозирования = 95%. Говоря о высокой точности, мы всегда говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности.

При этом величина MAPE является количественной оценкой именно ошибки, и эта величина нам ясно говорит и о точности прогнозирования, исходя из приведенной выше простой формулы. Таким образом, оценивая ошибку, мы всегда оцениваем точность прогнозирования.

Основной задачей при управлении запасами является определение объема пополнения, то есть, сколько необходимо заказать поставщику. При расчете этого объема используется несколько параметров — сколько будет продано в будущем, за какое время происходит пополнение, какие остатки у нас на складе и какое количество уже заказано у поставщика. То, насколько правильно мы определим эти параметры, будет влиять на то, будет ли достаточно товара на складе или его будет слишком много. Но наибольшее влияние на эффективность управления запасами влияет то, насколько точен будет прогноз. Многие считают, что это вообще основной вопрос в управлении запасами. Действительно, точность прогнозирования очень важный параметр. Поэтому важно понимать, как его оценивать. Это важно и для выявления причин дефицитов или неликвидов, и при выборе  программных продуктов для прогнозирования продаж и управления запасами.

В данной статье я представила несколько формул для расчета точности прогноза и ошибки прогнозирования. Кроме этого, вы сможете скачать файлы с примерами расчетов этого показателя.

Статистические методы

Для оценки прогноза продаж используются статистические оценки Оценка ошибки прогнозирования временного ряда. Самый простой показатель – отклонение факта от прогноза в количественном выражении.

В практике рассчитывают ошибку прогнозирования по каждой отдельной позиции, а также рассчитывают среднюю ошибку прогнозирования. Следующие распространенные показатели ошибки относятся именно  к показателям средних ошибок прогнозирования.

К ним относятся:

MAPE – средняя абсолютная ошибка в процентах

где Z(t) – фактическое значение временного ряда, а   – прогнозное.

Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE. 

Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.

MAE – средняя абсолютная ошибка

                                                                                                  .

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.

После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.

Кроме указанных методов иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.

ME – средняя ошибка

Встречается еще другое название этого показателя — Bias (англ. – смещение) демонстрирует величину отклонения, а также — в какую сторону прогноз продаж отклоняется от фактической потребности. Этот индикатор показывает, был ли прогноз оптимистичным или пессимистичным. То есть, отрицательное значение Bias говорит о том, что прогноз был завышен (реальная потребность оказалась ниже), и, наоборот, положительное значение о том, что прогноз был занижен. Цифровое значение показателя определяет величину отклонения (смещения).

MSE – среднеквадратичная ошибка

.

RMSE – квадратный корень из среднеквадратичной ошибки

.

.

SD – стандартное отклонение

где ME – есть средняя ошибка, определенная по формуле выше.

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже. Скачать пример расчета в Excel >>>

Связь точности и ошибки прогнозирования

В начале этого обсуждения разберемся с определениями.

Ошибка прогноза — апостериорная величина отклонения прогноза от действительного состояния объекта. Если говорить о прогнозе продаж, то это показатель отклонения фактических продаж от прогноза.

Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.

Точность прогноза в % = 100% – MAPE, встречается еще название этого показателя Forecast Accuracy. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности. Показатель точности прогноза выражается в процентах:

• Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно. Нужно сразу оговориться, что такого показателя никогда не будет, основное свойство прогноза в том, что он всегда ошибочен.
• Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.

Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда.  Говоря о высокой точности, мы говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Не имеет значения, что именно вы будете отслеживать, но важно, чтобы вы сравнивали модели прогнозирования или целевые показатели по одному показателю – ошибка прогноза или точность прогнозирования.

Ранее я использовала оценку MAPE, до тех пор пока не встретила формулу, которую рекомендует Валерий Разгуляев. 

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>

Оценка ошибки прогноза – формула Валерия Разгуляева (сайт http://upravlenie-zapasami.ru/)

Одной из самых используемых формул оценки ошибки прогнозирования является следующая формула:

где: P – это прогноз, а S – факт за тот же месяц. Однако у этой формулы есть серьезное ограничение — как оценить ошибку, если факт равен нулю? Возможный ответ, что в таком случае D = 100% – который означает, что мы полностью ошиблись. Однако простой пример показывает, что такой ответ — не верен:

Оказывается, что в варианте развития событий №2, когда мы лучше угадали спрос, чем в варианте №1, ошибка по данной формуле оказалась – больше. То есть ошиблась уже сама формула. Есть и другая проблема, если мы посмотрим на варианты №2 и №3, то увидим, что имеем дело с зеркальной ситуацией в прогнозе и факте, а ошибка при этом отличается – в разы!.. То есть при такой оценке ошибки прогноза нам лучше его заведомо делать менее точным, занижая показатель – тогда ошибка будет меньше!.. Хотя понятно, что чем точнее будет прогноз – тем лучше будет и закупка. Поэтому для расчёта ошибки Валерий Разгуляев рекомендует использовать следующую формулу:

В таком случае для тех же примеров ошибка рассчитается иначе:

Как мы видим, в варианте №1 ошибка становится равной 100%, причём это уже – не наше предположение, а чистый расчёт, который можно доверить машине. Зеркальные же варианты №2 и №3 – имеют и одинаковую ошибку, причём эта ошибка меньше ошибки самого плохого варианта №1. Единственная ситуация, когда данная формула не сможет дать однозначный ответ – это равенство знаменателя нулю. Но максимум из прогноза и факта равен нулю, только когда они оба равны нулю. В таком случае получается, что мы спрогнозировали отсутствие спроса, и его, действительно, не было – то есть ошибка тоже равна нулю – мы сделали совершенно точное предсказание.   

Визуальный метод – графический

Визуальный метод состоит в том, что мы на график выводим значение прогнозной модели и факта продаж по тем моделям, которые хотим сравнить. Далее  сравниваем визуально, насколько прогнозная модель близка к фактическим продажам. Давайте рассмотрим на примере. В таблице представлены две прогнозные модели, а также фактические продажи по этому товару за тот же период. Для наглядности мы также рассчитали ошибку прогнозирования по обеим моделям.  

По графикам очевидно, что модель 2 описывает лучше продажи этого товара. Оценка ошибки прогнозирования тоже это показывает – 65% и 31% ошибка прогнозирования по модели 1 и модели 2 соответственно.

Недостатком данного метода является то, что небольшую разницу между моделями сложно выявить — разницу в несколько процентов сложно оценить по диаграмме. Однако эти несколько процентов могут существенно улучшить качество прогнозирования и планирования пополнения запасов в целом.  

Использование формул ошибки прогнозирования на практике

Практический аспект оценки ошибки прогнозирования я вывела отдельным пунктом. Это связано с тем, что все статистические методы расчета показателя ошибки прогнозирования рассчитывают то, насколько мы ошиблись в прогнозе в количественных показателях. Давайте теперь обсудим, насколько такой показатель будет полезен в вопросах управления запасами. Дело в том, что основная цель управления запасами  — обеспечить продажи, спрос наших клиентов. И, в конечном счете, максимизировать доход и прибыль компании. А эти показатели оцениваются как раз  в стоимостном выражении. Таким образом, нам важно при оценке ошибки прогнозирования понимать какой вклад каждая позиция внесла в объем продаж в стоимостном выражении. Когда мы оцениваем ошибку прогнозирования в количественном выражении мы предполагаем, что каждый товар имеет одинаковый вес в общем объеме продаж, но на самом деле это не так – есть очень дорогие товары, есть товары, которые продаются в большом количестве, наша группа А, а есть не очень дорогие товары, есть товары которые вносят небольшой вклад в объем продаж. Другими словами большая ошибка прогнозирования по товарам группы А будет нам «стоить» дороже, чем низкая ошибка прогнозирования по товарам группы С, например. Для того, чтобы наша оценка ошибки прогнозирования была корректной, релевантной целям управления запасами, нам необходимо оценивать ошибку прогнозирования по всем товарам или по отдельной группе не по средними показателями, а средневзвешенными с учетом прогноза и факта в стоимостном выражении.

Пример расчета такой оценки Вы сможете увидеть в файле Excel.

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>

При этом нужно помнить, что для оценки ошибки прогнозирования по отдельным позициям мы рассчитываем по количеству, но вот если нам важно понять в целом ошибку прогнозирования по компании, например, для оценки модели, которую используем, то нам нужно рассчитывать не среднюю оценку по всем товарам, а средневзвешенную с учетом стоимостной оценки. Оценку можно брать по ценам себестоимости или ценам продажи, это не играет большой роли, главное, эти же цены (тип цен) использовать при всех расчетах.  

Для чего используется ошибка прогнозирования

В первую очередь, оценка ошибки прогнозирования нам необходима для оценки того, насколько мы ошибаемся при планировании продаж, а значит при планировании поставок товаров. Если мы все время прогнозируем продажи значительно больше, чем потом фактически продаем, то вероятнее всего у нас будет излишки товаров, и это невыгодно компании. В случае, когда мы ошибаемся в обратную сторону – прогнозируем продажи меньше чем фактические продажи, с большой вероятностью у нас будут дефициты и компания не дополучит прибыль. В этом случае ошибка прогнозирования служит индикатором качества планирования и качества управления запасами.

Индикатором того, что повышение эффективности возможно за счет улучшения качества прогнозирования. За счет чего можно улучшить качество прогнозирования мы не будем здесь рассматривать, но одним из вариантов является поиск другой модели прогнозирования, изменения параметров расчета, но вот насколько новая модель будет лучше, как раз поможет показатель ошибки прогнозирования или точности прогноза. Сравнение этих показателей по нескольким моделям поможет определить ту модель, которая дает лучше результат.

В идеальном случае, мы можем так подбирать модель для каждой отдельной позиции. В этом случае мы будем рассчитывать прогноз по разным товарам по разным моделям, по тем, которые дают наилучший вариант именно для конкретного товара.

Также этот показатель можно использовать при выборе автоматизированного инструмента для прогнозирования спроса и управления запасами. Вы можете сделать тестовые расчеты прогноза в предлагаемой программе и сравнить ошибку прогнозирования полученного прогноза с той, которая есть у вашей существующей модели. Если у предлагаемого инструмента ошибка прогнозирования меньше. Значит, этот инструмент можно рассматривать для применения в компании. Кроме этого, показатель точности прогноза или ошибки прогнозирования можно использовать как KPI сотрудников, которые отвечают за подготовку прогноза продаж или менеджеров по закупкам, в том случае, если они рассчитывают прогноз будущих продаж при расчете заказа.

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>

Если вы хотите повысить эффективность управления запасами и увеличить оборачиваемость товарных запасов, предлагаю изучить мастер-класс «Как увеличить оборачиваемость товарных запасов».

Источник: сайт http://uppravuk.net/  

Стандартное
отклонение для оценки обозначается S_e
и рассчитывается по формуле
среднеквадратичного отклонения:

.

Величина стандартного
отклонения характеризует точность
прогноза.

Вариант
5. Возвращаясь к данным нашего примера,
рассчитаем значение S_e:

Предположим,
необходимо оценить значение Y для
конкретного значения независимой
переменной, например, спрогнозировать
объем продаж при затратах на рекламу в
объеме 10 тыс. долл. Обычно при этом также
требуется оценить степень достоверности
результата, одним из показателей которого
является доверительный интервал для
Y.

Граница доверительного
интервала для Y при заданной величине
X рассчитывается следующим образом:

где
Х_p
– выбранное значение независимой
переменной, на основе которого выполняется
прогноз. Обратите внимание: t – это
критическое значение текущего уровня
значимости. Например, для уровня
значимости, равного 0,025 (что соответствует
уровню доверительности двухстороннего
критерия, равному 95%) и числа степеней
свободы, равного 10, критическое значение
t равно 2, 228 (см. Приложение II). Как можно
увидеть, доверительный интервал – это
интервал, ограниченный с двух сторон
граничными значениями предсказания
(зависимой переменной).

Вариант
6. Для нашего примера расходов на рекламу
в размере 10 тыс. долл. интервал предсказания
зависимой переменной (объема продаж) с
уровнем доверительности в 95% находится
в пределах [10,5951; 21,8361]. Его границы
определяются следующим образом (обратите
внимание, что в Варианте 2 Y’=16,2156):

Из приведенного
расчета имеем: для заданных расходов
на рекламу в объеме 10 тыс. долл., объем
продаж изменяется в диапазоне от 10,5951
до 21,8361 тыс. долл. При этом:
10,5951=16,2156-5,6205 и 21,8361=16,2156+5,6205.

3. Стандартное отклонение для коэффициента регрессии Sb и t-статистика

Значения
стандартного отклонения для коэффициентов
регрессии S_b
и значение статистики тесно взаимосвязаны.
S_b
рассчитываются как

Или в сокращенной
форме:

S_b
задает интервал, в который попадают.
Все возможные значения коэффициента
регрессии. t-статистика
(или t-значение)
– мера статистической значимости
влияния независимой переменной Х на
зависимую переменную Y
определяется путем деления оценки
коэффициента b
на его стандартное отклонение S_b.
Полученное значение затем сравнивается
с табличным (см. табл. В Приложении II).

Таким
образом, t-статистика
показывает, насколько велики величина
стандартного отклонения для коэффициента
регрессии (насколько оно больше нуля).
Практика показывает, что любое t-значение,
не принадлежащее интервалу [-2;2], является
приемлемым. Чем выше t-значение,
тем выше достоверность коэффициента
(т.е. точнее прогноз на его основе). Низкое
t-значение
свидетельствует о низкой прогнозирующей
силе коэффициента регрессии.

Вариант
7. S_b
для нашего примера равно:

t-статистика
определяется:

Так
как t=3,94>2,
можно заключить,
что
коэффициент
b
является
статистически
значимым.
Как
отмечалось раньше,
табличное
критическое
значение (уровень отсечения)
для 10 степеней свободы равно
2,228
(см.
табл.
в
Приложении
11).

Обратите
внимание:

—
t-значения
играют большую
роль для коэффициентов
множественной регрессии
(множественная
модель описывается
с помощью
нескольких
коэффициентов
b);

—
R²
характеризует
общее согласие (всего
«леса»
невязок
на
диаграмме
разброса),
в
то время как
t-значение
характеризует
отдельную
независимую переменную
(отдельное
«дерево»
невязок).

В
общем случае
табличное
t-значение
для
заданных
числа
степеней свободы и уровня
значимости используется,
чтобы:

—
установить
диапазон
предсказания:
верхнюю
и нижнюю границы
для прогнозируемого
значения при заданном значении
независимой
переменной;

-установить
доверительные
интервалы
для
коэффициентов
регрессии;

—
определить
уровень
отсечения
для t-теста.

РЕГРЕССИОННЫЙ
АНАЛИЗ С ПРИМЕНЕНИЕМ ЭЛЕКТРОННЫХ ТАБЛИЦ
MS EXCEL

Электронные
таблицы,
такие
как Excel,
имеют
встроенную
процедуру
регрессионного
анализа,
легкую
в
применении.

Регрессионный
анализ
с помощью
MS Ехсеl
требует
выполнения
следующих
действий:

—
выберите
пункт
меню
«Сервис
— Надстройки»;

—
в
появившемся
окне отметьте
галочкой
надстройку
Analysis
ToolPak
–
VBA нажмите
кнопку
ОК.

Если
в списке Analysis
ToolPak
—
VВА
отсутствует,
выйдите
из MS Ехсеl
и добавьте эту надстройку,
воспользовавшись
программой
установки Мiсrosоft
Office.
Затем
запустите Ехсеl
снова
и повторите
эти действия.
Убедившись,
что
надстройка
Analysis
ToolPak
—
VВА
доступна,
запустите
инструмент
регрессионного
анализа,
выполнив
следующие
действия:

—
выберите
пункт меню «Сервис
—
Анализ»
данных;

—
в появившемся окне выберите
пункт
«Регрессия»
и
нажмите
кнопку
ОК.
На
рисунке 16.3
показано окно ввода данных для
регрессионного
анализа.

Рисунок 16.3 – Окно
ввода данных для регрессионного анализа

Таблица
16.2
показывает
выходной
результат
регрессии,
содержащий
описанные
выше статистические
данные.

Примечание:
для
того чтобы получить
поточечный
график
(ХY график),
используйте
«Мастер
Диаграмм»
MS
Excel.

Получаем:
Y’
= 10,5386
+ 0,563197
Х (d
виде
Y’
=
а
+
bХ)
с R²=0,608373=60,84%.

Все
полученные
данные
ответствуют
данным,
рассчитанным
вручную.

Таблица 16.2 –
Результаты регрессионного анализа

в
электронных таблицах MS
Excel

Таблица
16.3 показывает выходной результат
регрессии, полученный с применением
популярного программного обеспечения
Minitab
для статистического анализа.

Таблица
16.3 – Результаты регрессионного анализа
Minitab

ВЫВОДЫ

C
помощью регрессионного анализа
устанавливается
зависимость
между
изменениями
независимых
переменных
и
значениями зависимой
переменной.
Регрессионный
анализ
— популярный
метод для прогнозирования
продаж.
В
этой
главе обсуждался
широко
распространенный
способ
оценки значений,
так
называемый
метод
наименьших
квадратов.
Метод
наименьших
квадратов
рассматривался
применительно
к
модели
простой
регрессии
Y
=
а
+ bх.
Обсуждались
различные
статистические
коэффициенты,
характеризующие
добротность
и надежность
уравнения
(согласие
модели)
и помогающие установить
доверительный
интервал.

Показано
применение
электронных
таблиц MS Ехсеl для
проведения
регрессионного
анализа
шаг за шагом.
С
помощью электронных
таблиц
можно не только составить
уравнение
регрессии,
но
и рассчитать статистические
коэффициенты.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Существует множество моделей прогноза, но как выбрать среди них ту, которая наиболее точно сделает прогноз?

Из данной статьи вы узнаете:

1. Какие способы оценки прогноза вы можете использовать?
2. Как выбрать оптимальную модель, которая поможет вам сделать максимально точный прогноз?
3. Как рассчитать показатель «Точность прогноза»?

Какие способы оценки прогнозной модели вы можете использовать:

1.  Оценить отношение фактических продаж к прогнозу;

2. Расчет показателя точность прогноза — оценка на сколько точно выбранная модель описывает анализируемые данные;

3. Графический анализ — строим график и визуально оцениваем адекватность модели прогноза относительно фактических продаж за последний период ;
 

1-й способ — Расчет отношения фактических продаж к прогнозу.

Сначала рассчитываем прогноз разными способами и оцениваем отношение фактических продаж к прогнозу. ВАЖНО протестировать модели не по одному товару или направлению продаж, а сразу взять 10 и более товарных позиций или направлений продаж и рассчитать прогноз по ним на минимум на 3 периода вперед (количество периодов и направления прогноза зависят от ваших задач. Если задача — сделать точный прогноз на 6 месяцев, то рассчитываем прогноз на 6 месяцев несколькими вариантами и оцениваем отношение факта к прогнозу по сумме полугода).

Рассчитаем прогноз 4 способами на полгода. Протестируем следующие модели:

1. Линейный тренд + сезонность — лист «Линейный» в приложенном файле (см. статью «Как рассчитать прогноз с учетом роста и сезонности в Excel»)

2. Логарифмический тренд + сезонность — лист «Логарифмический» в приложенном файле (см. статью «5 способов расчета значений логарифмического тренда»)

3. Скользящая средняя с сезонностью к 2-м месяцам — лист «Скользящая к 2-м» (см. статью «Как рассчитать прогноз по методу скользящей средней»);

4. Скользящяя средняя с сезонностью к 3-м месяцам — лист «Скользящая к 3-м»;

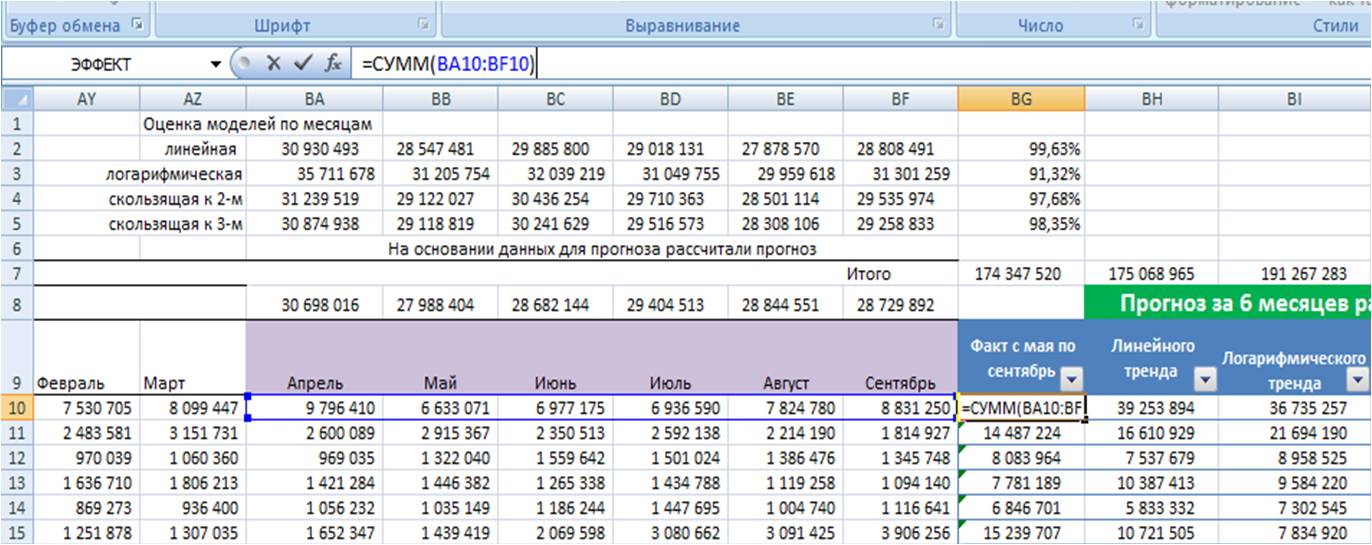
Для каждой из 4-х прогнозных моделей в листе «Оценка моделей»:

• Суммируем прогноз по каждой модели за 6 месяцев;

• Суммируем фактические продажи, которые мы будем сравнивать с прогнозом;

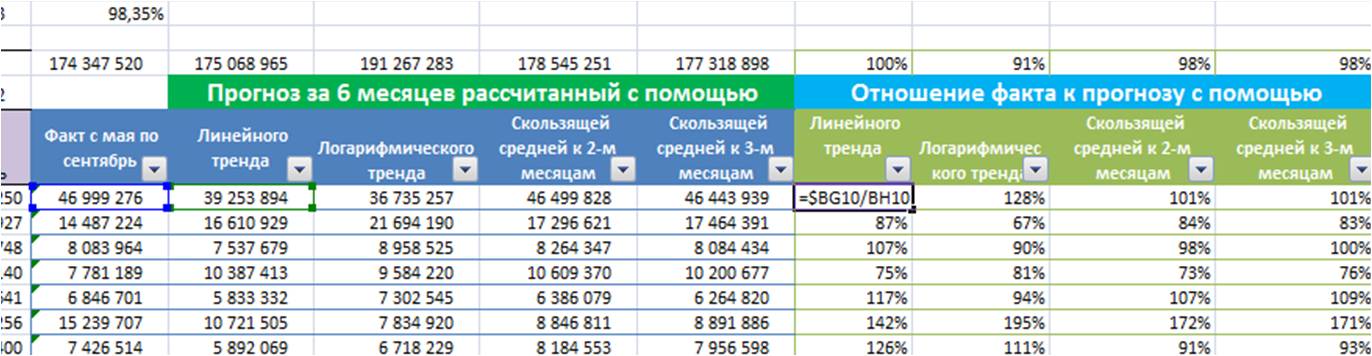
• Рассчитываем отношение факта к прогнозу по каждой позиции для каждой модели;

• Рассчитываем по каждой модели среднее отношение факта к прогнозу;

• Выбираем модель прогноза, которая по показателю «среднее отношение факта к прогнозу» оказалась максимально приближена к 100%;

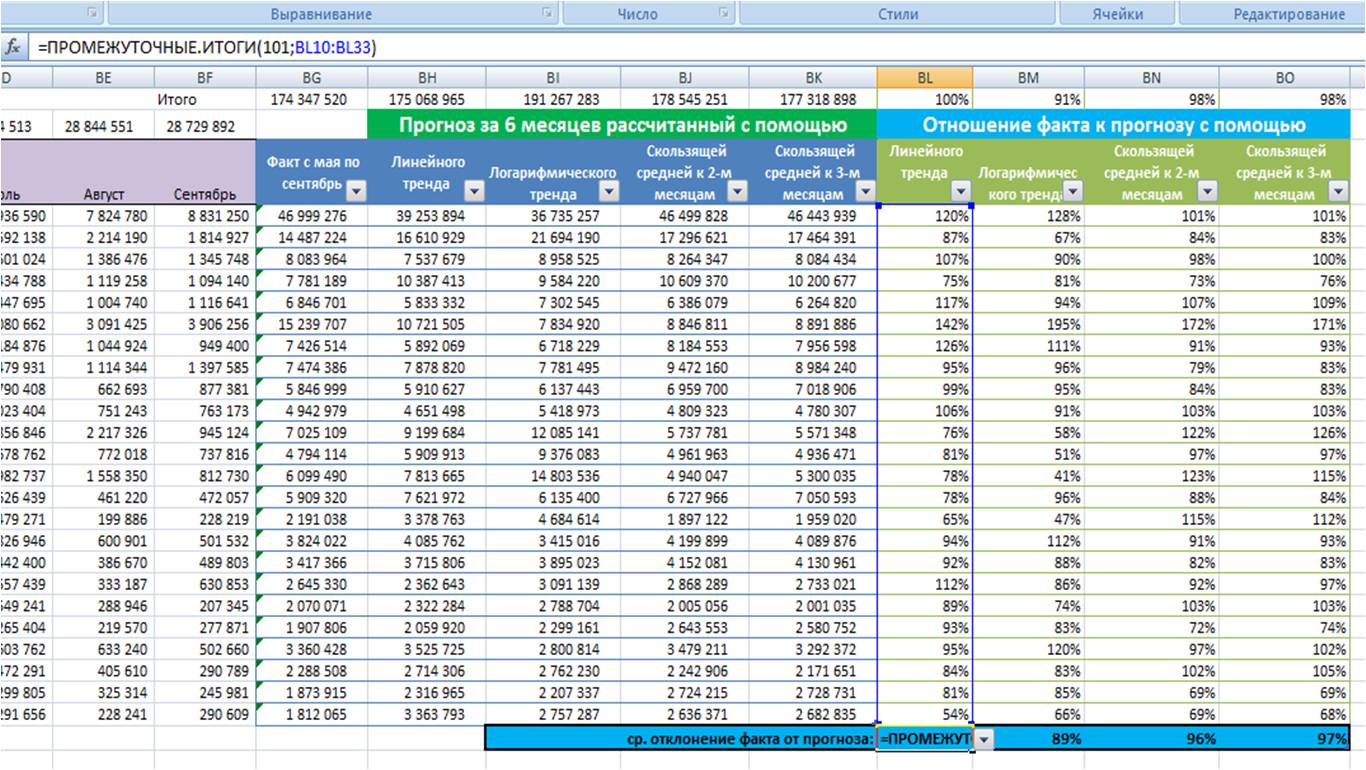
Для наших данных самой точной моделью оказалась скользящая средняя к 3-м месяцам с сезонностью, среднее отклонение факта от прогноза 97%.

Мы протестировали каждую модель прогноза на реальных данных и выбрали для себя оптимальную, которая в среднем показала минимальное отклонение от факлических продаж.

2-й способ оценки модели прогноза — расчет показателя точность прогноза.

Показатель точность прогноза показывает, на сколько точно выбранная модель прогноза описывает данные. Идея в том, чем точнее выбранная модель описывает фактические данные, тем точнее она сделает прогноз.

Как рассчитать точность прогноза? Рассмотрим на примере расчета для модели прогноза с линейным трендом и сезонностью.

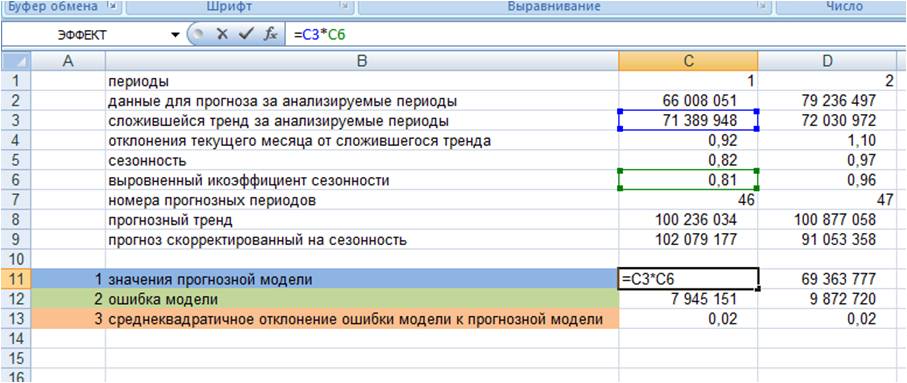
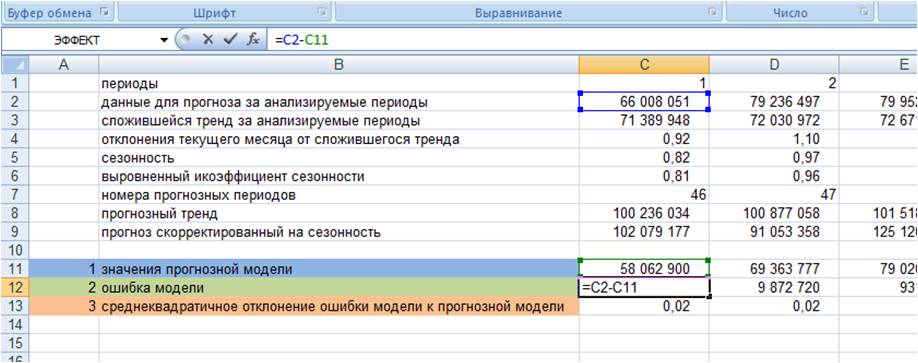
1. Рассчитываем значения прогнозной модели для каждого анализируемого момента времени в прошлом.

Для этого значения тренда для анализируемых периодов умножаем на выровненные коэффициенты сезонности (см. файл с примером)

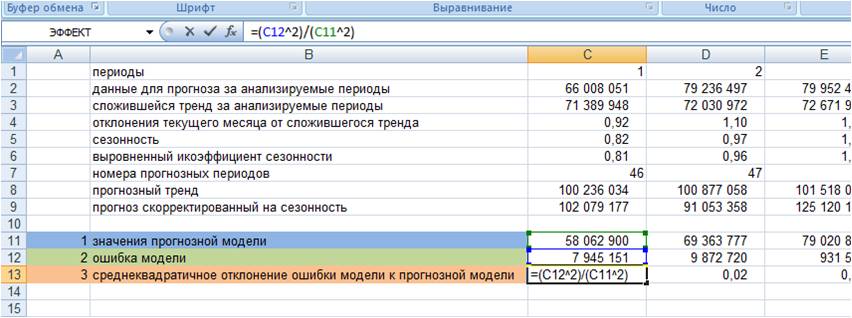
2. Рассчитываем ошибку прогнозной модели. Для этого за каждый период от фактических значений вычитаем значения прогнозной модели.

3. Рассчитываем квадратическое отклонение ошибки от значений прогнозной модели (см. файл с примером);

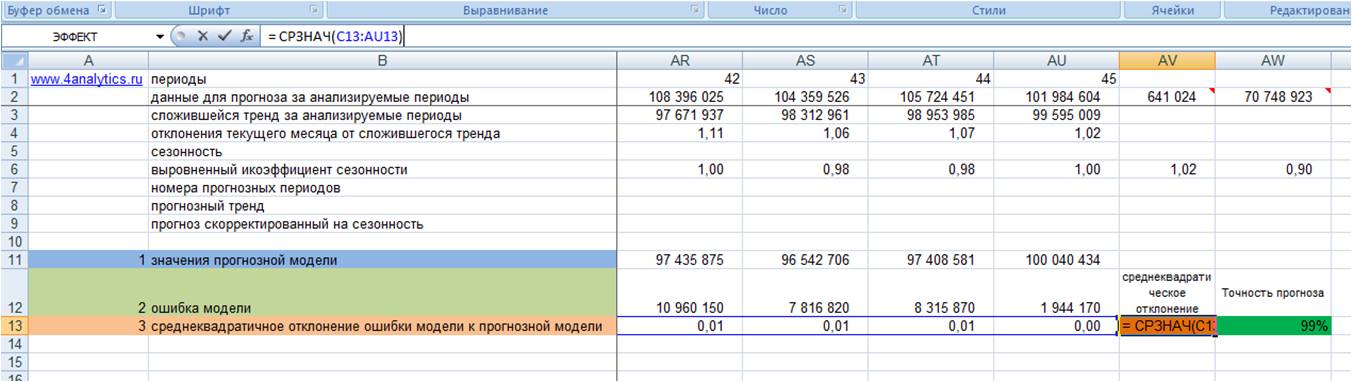
4. Рассчитываем среднее значение квадратического отклонения, т.е. среднеквадратическое отклонение

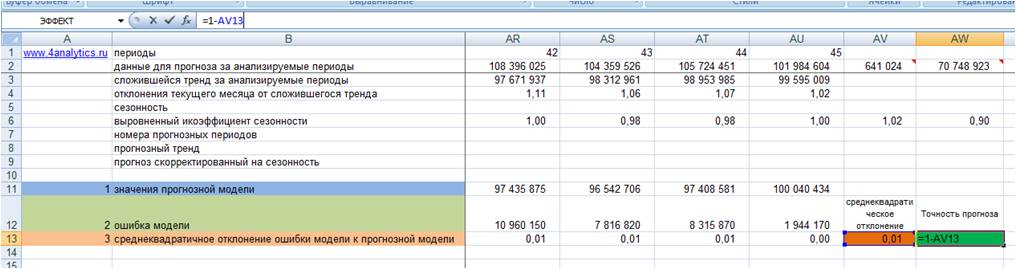
5. Точность прогноза = (1- среднеквадратическое отклонение ошибки прогнозной модели)*100 (см. файл с примером).

Показатель точности прогноза выражается в процентах:

• Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно.

• Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.

 Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда.

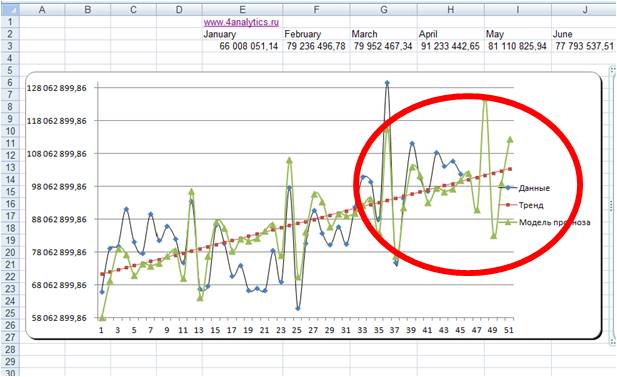
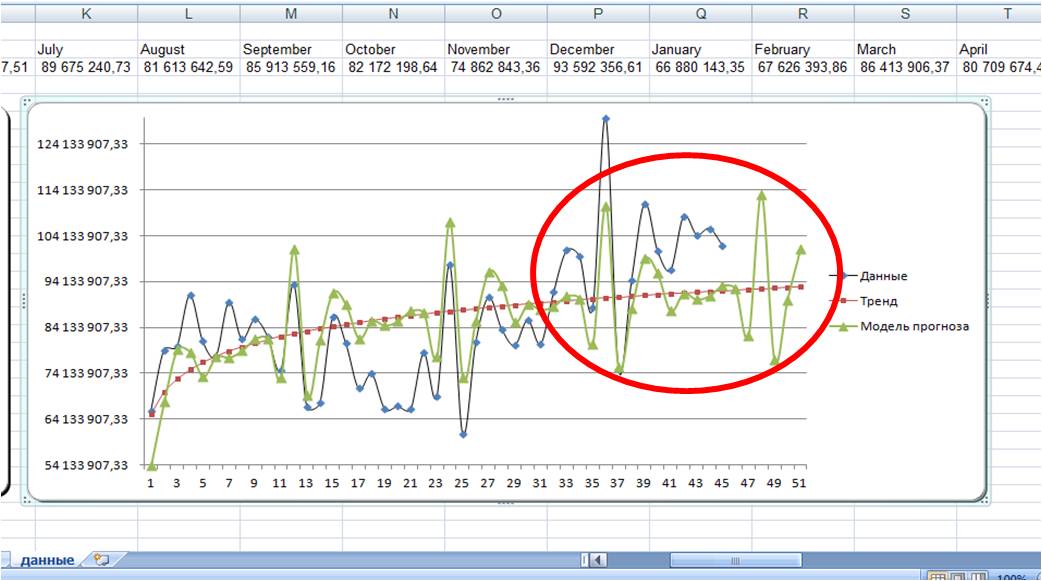
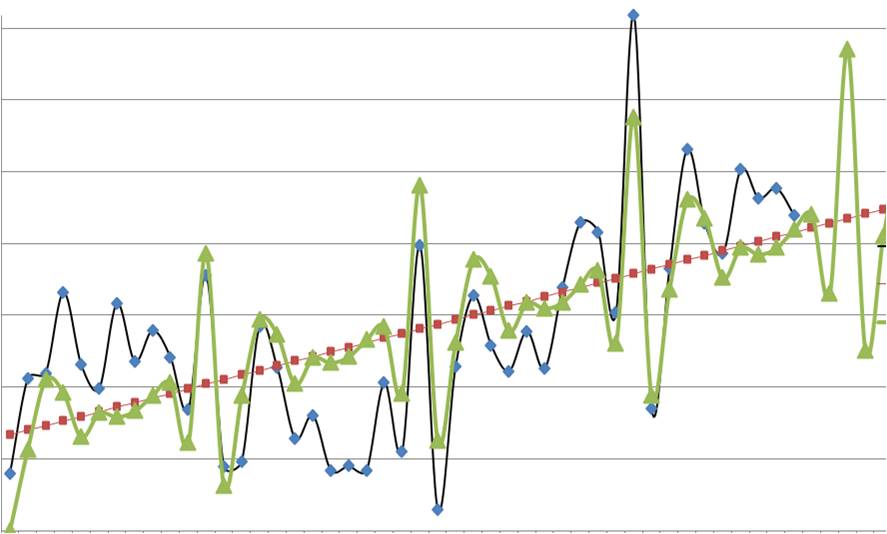
3. Способ оценки прогнозной модели — визуальный.

На график выводим анализируемые данные, тренд, значение модели и прогноз (см. вложенный файл). Обычно визуально видно, какая модель адекватнее строит прогноз . 3-й способ по своей сути схож с 1-м и вторым, только мы верим не цифрам, а тому что мы видим на графике.

Линейная модель:

Логарифмическая модель:

По последним периодам видно, что линейная модель более точно описывает данные за последние месяцы, и она, вероятнее всего, сделает более точный прогноз.

Какую модель прогноза выбрать?

1. Которая на основании тестирования на реальных данных для выбранного промежутка времени (месяца, 3-х месяцев, полугода, года) будет делать максимально точный прогноз, т.е. отношение факта к прогнозу будет близко к 1 или 100%.

2. Модель, которая будет максимально точно описывать фактические данные, т.е. показатель точность прогноза будет приближаться к 1, но не всегда модели точно описывающие данные делают адекватные прогнозы (это надо понимать и оценивать графически).

3. Модель, которой визуально вы больше доверяете с точки зрения описания входящих данных и продления прогнозной модели в будущее.

Для повышения точности прогноза я в своей практике стараюсь использовать 3 этих способа параллельно:

• По завершении прогнозного периода и в промежутках всегда оцениваю отношение фактических продаж к прогнозу.

• При построении прогноза анализирую показатель «среднеквадратическое отклонение» и рассчитываю показатель «точность прогноза» для оценки данных и модели.

• А также на график вывожу анализируемые данные и прогнозную модель, для визуального контроля.

Оценивая прогноз по факту или в промежуточные периоды в случае значительных отклонений фактических продаж от прогнозных, разбираю ситуацию и выясняю причины, в случае необходимости вношу корректировки в прогнозную модель.

С помощью программы Forecast4AC PRO вы можете рассчитать показатель точность прогноза автоматически.

Также Forecast4AC умеет автоматически выбирать оптимальную модель прогноза для каждого временного ряда.

+ одним нажатием строить график «Анализируемые данные + модель прогноза», на котором вы можете оценить, как соотносятся между собой:

• анализируемые данные;

• выбранный тренд;

• модель прогноза;

как в анализируемом периоде, так и в будущем. 

Точных прогнозов!

Статья полезная? Поделитесь с друзьями