Стандартное отклонение и стандартная ошибка: в чем разница?
17 авг. 2022 г.
читать 2 мин
В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .
Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.
Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.
Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.
Пример: стандартное отклонение против стандартной ошибки
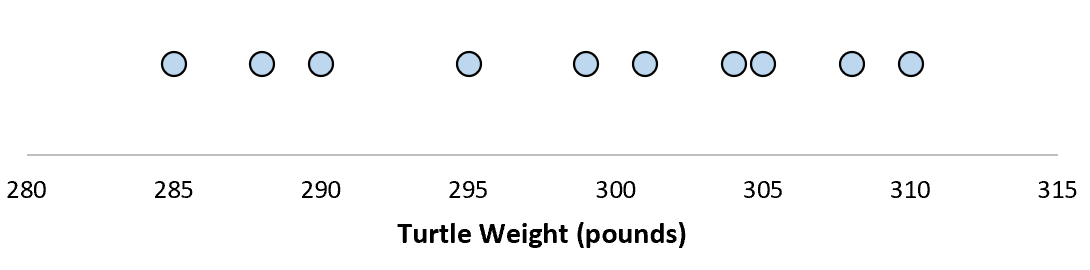
Предположим, мы измеряем вес 10 разных черепах.
Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:
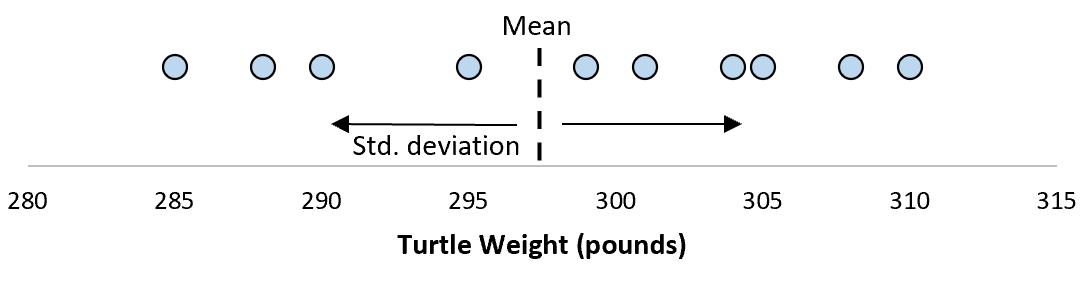
Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.
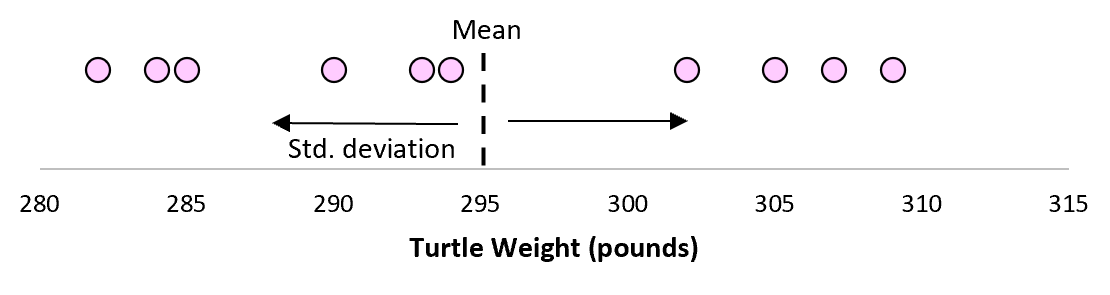
Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:
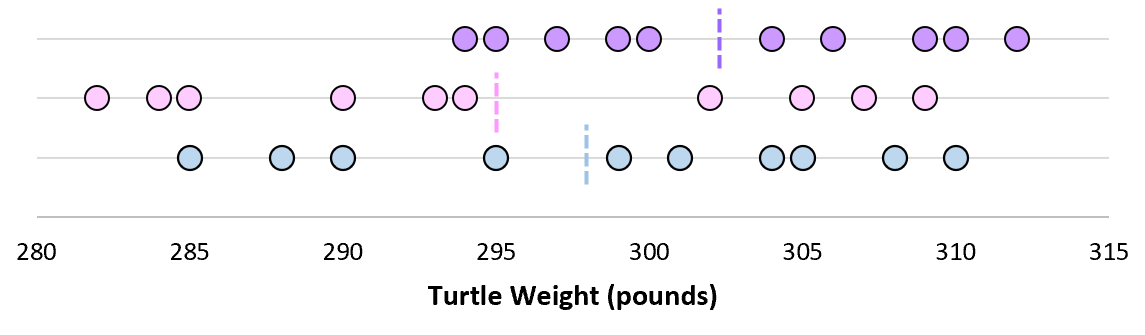
Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:
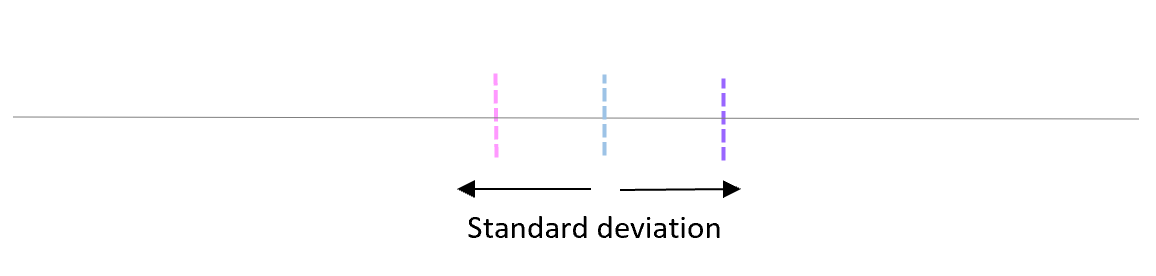
Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:
Стандартное отклонение этих средних значений известно как стандартная ошибка.
Формула для фактического расчета стандартной ошибки:
Стандартная ошибка = s/ √n
куда:
- s: стандартное отклонение выборки
- n: размер выборки
Какой смысл использовать стандартную ошибку?
Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.
Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.
Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:
Стандартная ошибка = s/ √n
Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.
Когда использовать стандартное отклонение против стандартной ошибки
Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .
Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .
В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.
Стандартные ошибки в форме Ньюи-Уеста или состоятельные при гетероскедастичности и автокорреляции стандартные ошибки (HAC s.e. — Heteroskedasticity and Autocorrelation consistent standard errors) — применяемая в эконометрике оценка ковариационной матрицы МНК-оценок (в частности и стандартных ошибок) параметров линейной модели регрессии, альтернативная стандартной (классической) оценке, которая состоятельна при гетероскедастичности и автокорреляции случайных ошибок модели (в отличие от несостоятельной в этом случае классической оценки и стандартных ошибок в форме Уайта).
Содержание
- 1 Сущность и формула
- 1.1 Замечание
- 2 См. также
- 3 Литература
Сущность и формула
Истинная ковариационная матрица МНК-оценок параметров линейной модели в общем случае равна:
где 

Поэтому для оценки ковариационной матрицы в классическом случае достаточно использовать оценку единственного параметра — дисперсии случайных ошибок: 
Данная оценка, как видно из формулы зависит от выбранной «ширины окна» L и весовых коэффициентов 

Существует также проблема выбора «ширины окна» L. Обычно рекомендуется следующая оценка
Замечание
Иногда приведенную формулу оценки ковариационной матрицы корректируют на множитель 
См. также
- Стандартные ошибки в форме Уайта
- Обобщенный метод наименьших квадратов
Литература
- Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. — М.: Дело, 2004. — 576 с.
- William H. Greene Econometric analysis. — New York: Pearson Education, Inc., 2003. — 1026 с.
Имея
прямую регрессии, необходимо оценить
насколько сильно точки исходных данных
отклоняются от прямой регрессии. Можно
выполнить оценку разброса, аналогичную
стандартному отклонению выборки. Этот
показатель, называемый стандартной
ошибкой оценки, демонстрирует величину
отклонения точек исходных данных от
прямой регрессии в направлении оси Y.
Стандартная ошибка оценки ()
вычисляется по следующей формуле.
Стандартная
ошибка оценки измеряет степень отличия
реальных значений Y от оцененной величины.
Для сравнительно больших выборок следует
ожидать, что около 67% разностей по модулю
не будет превышать
и около 95% модулей разностей будет не
больше 2.
Стандартная
ошибка оценки подобна стандартному
отклонению. Ее можно использовать для
оценки стандартного отклонения
совокупности. Фактически
оценивает стандартное отклонение
слагаемого ошибки
в статистической модели простой линейной
регрессии. Другими словами,
оценивает общее стандартное отклонение
нормального распределения значений Y,
имеющих математические ожидания
для каждого X.
Малая
стандартная ошибка оценки, полученная
при регрессионном анализе, свидетельствует,
что все точки данных находятся очень
близко к прямой регрессии. Если стандартная
ошибка оценки велика, точки данных могут
значительно удаляться от прямой.
2.3 Прогнозирование величины y
Регрессионную
прямую можно использовать для оценки
величины переменной Y
при данных значениях переменной X. Чтобы
получить точечный прогноз, или предсказание
для данного значения X, просто вычисляется
значение найденной функции регрессии
в точке X.
Конечно
реальные значения величины Y,
соответствующие рассматриваемым
значениям величины X, к сожалению, не
лежат в точности на регрессионной
прямой. Фактически они разбросаны
относительно прямой в соответствии с
величиной
.
Более того, выборочная регрессионная
прямая является оценкой регрессионной
прямой генеральной совокупности,
основанной на выборке из определенных
пар данных. Другая случайная выборка
даст иную выборочную прямую регрессии;
это аналогично ситуации, когда различные
выборки из одной и той же генеральной
совокупности дают различные значения
выборочного среднего.
Есть
два источника неопределенности в
точечном прогнозе, использующем уравнение
регрессии.
-
Неопределенность,
обусловленная отклонением точек данных
от выборочной прямой регрессии. -
Неопределенность,
обусловленная отклонением выборочной
прямой регрессии от регрессионной
прямой генеральной совокупности.
Интервальный
прогноз значений переменной Y
можно построить так, что при этом будут
учтены оба источника неопределенности.
Стандартная
ошибка прогноза
дает меру вариативности предсказанного
значения Y
около истинной величины Y
для данного значения X.
Стандартная ошибка прогноза равна:
Стандартная
ошибка прогноза зависит от значения X,
для которого прогнозируется величина
Y.
минимально, когда
,
поскольку тогда числитель в третьем
слагаемом под корнем в уравнении будет
0. При прочих неизменных величинах
большему отличию соответствует большее
значение стандартной ошибки прогноза.
Если
статистическая модель простой линейной
регрессии соответствует действительности,
границы интервала прогноза величины Y
равны:
где
— квантиль распределения Стьюдента с
n-2 степенями свободы ().
Если выборка велика (),
этот квантиль можно заменить соответствующим
квантилем нормального распределения.
Например, для большой выборки 95%-ный
интервал прогноза задается следующими
значениями:
Завершим
раздел обзором предположений, положенных
в основу статистической модели линейной
регрессии.
-
Для
заданного значения X генеральная
совокупность значений Y имеет нормальное
распределение относительно регрессионной
прямой совокупности. На практике
приемлемые результаты получаются
и
тогда, когда значения Y имеют
нормальное распределение лишь
приблизительно. -
Разброс
генеральной совокупности точек данных
относительно регрессионной прямой
совокупности остается постоянным всюду
вдоль этой прямой. Иными словами, при
возрастании значений X в точках данных
дисперсия генеральной совокупности
не увеличивается и не уменьшается.
Нарушение этого предположения называется
гетероскедастичностью. -
Слагаемые
ошибок
независимы между собой. Это предположение
определяет случайность выборки точек
Х-Y.
Если точки данных X-Y
записывались в течение некоторого
времени, данное предположение часто
нарушается. Вместо независимых данных,
такие последовательные наблюдения
будут давать серийно коррелированные
значения. -
В
генеральной совокупности существует
линейная зависимость между X и Y.
По аналогии с простой линейной регрессией
может рассматриваться и нелинейная
зависимость между X и У. Некоторые такие
случаи будут обсуждаться ниже.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Так как гетероскедастичность не приводит к смещению оценок коэффициентов, можно по-прежнему использовать МНК. Смещены и несостоятельны оказываются не сами оценки коэффициентов, а их стандартные ошибки, поэтому формула для расчета стандартных ошибок в условиях гомоскедастичности не подходит для случая гетероскедастичности.
Естественной идеей в этой ситуации является корректировка формулы расчета стандартных ошибок, чтобы она давала «правильный» (состоятельный) результат. Тогда можно снова будет корректно проводить тесты, проверяющие, например, незначимость коэффициентов, и строить доверительные интервалы. Соответствующие «правильные» стандартные ошибки называются состоятельными в условиях гетероскедастичности стандартными ошибками (heteroskedasticity consistent (heteroskedasticity robust) standard errors)1. Первоначальная формула для их расчета была предложена Уайтом, поэтому иногда их также называют стандартными ошибками в форме Уайта (White standard errors). Предложенная Уайтом состоятельная оценка ковариационной матрицы вектора оценок коэффициентов имеет вид:
(widehat{V}{left( widehat{beta} right) = n}left( {X^{‘}X} right)^{- 1}left( {frac{1}{n}{sumlimits_{s = 1}^{n}e_{s}^{2}}x_{s}x_{s}^{‘}} right)left( {X^{‘}X} right)^{- 1},)
где (x_{s}) – это s-я строка матрицы регрессоров X. Легко видеть, что эта формула более громоздка, чем формула (widehat{V}{left( widehat{beta} right) = left( {X^{‘}X} right)^{- 1}}S^{2}), которую мы вывели в третьей главе для случая гомоскедастичности. К счастью, на практике соответствующие вычисления не представляют сложности, так как возможность автоматически рассчитывать стандартные ошибки в форме Уайта реализована во всех современных эконометрических пакетах. Общепринятое обозначение для этой версии стандартных ошибок: «HC0». В работах (MacKinnon, White,1985) и (Davidson, MacKinnon, 2004) были предложены и альтернативные версии, которые обычно обозначаются в эконометрических пакетах «HC1», «HC2» и «HC3». Их расчетные формулы несколько отличаются, однако суть остается прежней: они позволяют состоятельно оценивать стандартные отклонения МНК-оценок коэффициентов в условиях гетероскедастичности.
Для случая парной регрессии состоятельная в условиях гетероскедастичности стандартная ошибка оценки коэффициента при регрессоре имеет вид:
(mathit{se}{left( widehat{beta_{2}} right) = sqrt{frac{1}{n}frac{frac{1}{n — 2}{sumlimits_{i = 1}^{n}{left( {x_{i} — overline{x}} right)^{2}e_{i}^{2}}}}{widehat{mathit{var}}(x)^{2}}.}})
Формальное доказательство состоятельности будет приведено в следующей главе. Пока же обсудим пример, иллюстрирующий важность использования робастных стандартных ошибок.
Пример 5.1. Оценка эффективности использования удобрений
В файле Agriculture в материалах к этому учебнику содержатся следующие данные 2010 года об урожайности яровой и озимой пшеницы в Спасском районе Пензенской области:
PRODP — урожайность в денежном выражении, в тысячах рублей с 1 га,
SIZE – размер пахотного поля, га,
LABOUR – трудозатраты, руб. на 1 га,
FUNG1 – фунгициды, протравители семян, расходы на удобрение в руб. на 1 га,
FUNG2 – фунгициды, во время роста, расходы на удобрение в руб. на 1 га,
GIRB – гербициды, расходы на удобрение в руб. на 1 га,
INSEC – инсектициды, расходы на удобрение в руб. на 1 га,
YDOB1 – аммофос, во время сева, расходы на удобрение в руб. на 1 га,
YDOB2 – аммиачная селитра, во время роста, расходы на удобрение в руб. на 1 га.
Представим, что вас интересует ответ на вопрос: влияет ли использование фунгицидов на урожайность поля?
(а) Оцените зависимость урожайности в денежном выражении от константы и переменных FUNG1, FUNG2, YDOB1, YDOB2, GIRB, INSEC, LABOUR. Запишите уравнение регрессии в стандартной форме, указав коэффициент детерминации и (в скобках под соответствующими коэффициентами) стандартные ошибки для случая гомоскедастичности. Какие из переменных значимы на 5-процентном уровне значимости?
(б) Решите предыдущий пункт заново, используя теперь состоятельные в условиях гетероскедастичности стандартные ошибки. Сопоставьте выводы по поводу значимости (при пятипроцентном уровне) переменных, характеризующих использование фунгицидов.
Решение:
(а) Оценим требуемое уравнение:
Модель 1: МНК, использованы наблюдения 1-200
Зависимая переменная: PRODP
| Коэффициент | Ст. ошибка | t-статистика | P-значение | ||
| const | -38,4019 | 7,5273 | -5,1017 | <0,00001 | *** |
| FUNG1 | 0,0445755 | 0,0487615 | 0,9142 | 0,36178 | |
| FUNG2 | 0,103625 | 0,049254 | 2,1039 | 0,03669 | ** |
| GIRB | 0,0776059 | 0,0523553 | 1,4823 | 0,13990 | |
| INSEC | 0,0782521 | 0,0484667 | 1,6146 | 0,10805 | |
| LABOUR | 0,0415064 | 0,00275277 | 15,0781 | <0,00001 | *** |
| YDOB1 | 0,0492168 | 0,0233328 | 2,1093 | 0,03621 | ** |
| YDOB2 | -0,0906824 | 0,025864 | -3,5061 | 0,00057 | *** |
| Сумма кв. остатков | 150575,6 | Ст. ошибка модели | 28,00443 | |
| R-квадрат | 0,801958 | Испр. R-квадрат | 0,794738 | |
| F(7, 192) | 111,0701 | Р-значение (F) | 5,08e-64 |
Переменные FUNG2, LABOUR, YDOB1 и YDOB2 значимы на пятипроцентном уровне значимости (причем LABOUR и YDOB2 — ещё и на однопроцентном).
Если представить те же самые результаты в форме уравнения, то получится вот так:
({widehat{mathit{PRODP}}}_{i} = {{- underset{(7,53)}{38,40}} + {underset{(0,05)}{0,04} ast {mathit{FUNG}1}_{i}} + {underset{(0,05)}{0,10} ast {mathit{FUNG}2}_{i}} +})
({{+ underset{(0,05)}{0,08}} ast mathit{GIRB}_{i}} + {underset{(0,05)}{0,08} ast mathit{INSEC}_{i}} + {underset{(0,003)}{0,04} ast mathit{LABOUR}_{i}} + {})
({{{+ underset{(0,02)}{0,05}} ast {mathit{YDOB}1}_{i}} — {underset{(0,03)}{0,09} ast {mathit{YDOB}2}_{i}}},{R^{2} = 0,802})
(б) При использовании альтернативных стандартных ошибок получим следующий результат:
Модель 2: МНК, использованы наблюдения 1-200
Зависимая переменная: PRODP
Робастные оценки стандартных ошибок (с поправкой на гетероскедастичность),
вариант HC1
| Коэффициент | Ст. ошибка | t-статистика | P-значение | ||
| const | -38,4019 | 7,40425 | -5,1865 | <0,00001 | *** |
| FUNG1 | 0,0445755 | 0,0629524 | 0,7081 | 0,47975 | |
| FUNG2 | 0,103625 | 0,0624082 | 1,6604 | 0,09846 | * |
| GIRB | 0,0776059 | 0,0623777 | 1,2441 | 0,21497 | |
| INSEC | 0,0782521 | 0,0536527 | 1,4585 | 0,14634 | |
| LABOUR | 0,0415064 | 0,00300121 | 13,8299 | <0,00001 | *** |
| YDOB1 | 0,0492168 | 0,0197491 | 2,4921 | 0,01355 | ** |
| YDOB2 | -0,0906824 | 0,030999 | -2,9253 | 0,00386 | *** |
| Сумма кв. остатков | 150575,6 | Ст. ошибка модели | 28,00443 | |
| R-квадрат | 0,801958 | Испр. R-квадрат | 0,794738 | |
| F(7, 192) | 119,2263 | Р-значение (F) | 2,16e-66 |
Оценки коэффициентов по сравнению с пунктом (а) не поменялись, что естественно: мы ведь по-прежнему используем обычный МНК. Однако стандартные ошибки теперь немного другие. В некоторых случаях это меняет выводы тестов на незначимость.
Переменные LABOUR, YDOB1 и YDOB2 значимы на пятипроцентном уровне значимости (причем LABOUR и YDOB2 — ещё и на однопроцентном).
Переменная FUNG2 перестала быть значимой на пятипроцентном уровне. Таким образом, при использовании корректных стандартных ошибок следует сделать вывод о том, что соответствующий вид удобрений не важен для урожайности. Обратите внимание, что если бы мы использовали «обычные» стандартные ошибки, то мы пришли бы к противоположному заключению (см. пункт (а)).
* * *
Важно подчеркнуть, что в реальных пространственных данных гетероскедастичность в той или иной степени наблюдается практически всегда. А даже если её и нет, то состоятельные в условиях гетероскедастичности стандартные ошибки по-прежнему будут… состоятельными (и будут близки к «обычным» стандартным ошибкам, посчитанным по формулам из третьей главы). Поэтому в современных прикладных исследованиях при оценке уравнений по умолчанию используются именно робастные стандартные ошибки, а не стандартные ошибки для случая гомоскедастичности. Мы настоятельно рекомендуем читателю поступать так же2. В нашем учебнике с этого момента и во всех последующих главах, если прямо не оговорено иное, для МНК-оценок параметров всегда используются состоятельные в условиях гетероскедастичности стандартные ошибки.
-
Поскольку довольно утомительно каждый раз произносить это название полностью в англоязычном варианте их часто называют просто robust standard errors, что на русском языке эконометристов превратилось в «робастные стандартные ошибки». Кому-то подобный англицизм, конечно, режет слух, однако в устной речи он и правда куда удобней своей длинной альтернативы.↩︎
-
Просто не забывайте включать соответствующую опцию в своем эконометрическом пакете.↩︎
Download Article
Download Article
After collecting data, oftentimes the first thing you need to do is analyze it. This usually entails finding the mean, the standard deviation, and the standard error of the data. This article will show you how it’s done.
Cheat Sheets
-
1
Obtain a set of numbers you wish to analyze. This information is referred to as a sample.
- For example, a test was given to a class of 5 students, and the test results are 12, 55, 74, 79 and 90.
Advertisement
-
1
Calculate the mean. Add up all the numbers and divide by the population size:[1]
- Mean (μ) = ΣX/N, where Σ is the summation (addition) sign, xi is each individual number, and N is the population size.
- In the case above, the mean μ is simply (12+55+74+79+90)/5 = 62.
-
1
Calculate the standard deviation. This represents the spread of the population.
Standard deviation = σ = sq rt [(Σ((X-μ)^2))/(N)].[2]
- For the example given, the standard deviation is sqrt[((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27.4. (Note that if this was the sample standard deviation, you would divide by n-1, the sample size minus 1.)
Advertisement
-
1
Calculate the standard error (of the mean). This represents how well the sample mean approximates the population mean. The larger the sample, the smaller the standard error, and the closer the sample mean approximates the population mean. Do this by dividing the standard deviation by the square root of N, the sample size.[3]
Standard error = σ/sqrt(n)[4]
- So for the example above, if this were a sampling of 5 students from a class of 50 and the 50 students had a standard deviation of 17 (σ = 21), the standard error = 17/sqrt(5) = 7.6.
Add New Question
-
Question
How do you find the mean given number of observations?
To find the mean, add all the numbers together and divide by how many numbers there are. e.g to find the mean of 1,7,8,4,2: 1+7+8+4+2 = 22/5 = 4.4.
-
Question
The standard error is calculated as 0.2 and the standard deviation of a sample is 5kg. Can it be said to be smaller or larger than the standard deviation?
The standard error (SE) must be smaller than the standard deviation (SD), because the SE is calculating by dividing the SD by something — i.e. making it smaller.
-
Question
How can I find out the standard deviation of 50 samples?
The results of all your figures (number plus number plus number etc.) divided by quantity of samples 50 =SD.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Calculations of the mean, standard deviation, and standard error are most useful for analysis of normally distributed data. One standard deviation about the central tendency covers approximately 68 percent of the data, 2 standard deviation 95 percent of the data, and 3 standard deviation 99.7 percent of the data. The standard error gets smaller (narrower spread) as the sample size increases.
Thanks for submitting a tip for review!
Advertisement
-
Check your math carefully. It is very easy to make mistakes or enter numbers incorrectly.
Advertisement
References
About This Article
Article SummaryX
The mean is simply the average of a set of numbers. You can work it out by adding up all the numbers and dividing the total by the amount of numbers. For example, if you wanted to find the average test score of 3 students who scored 74, 79, and 90, you’d add the 3 numbers together to get 243, then divide it by 3 to get 81. The standard error represents how well the sample mean approximates the population mean. All you need to do is divide the standard deviation by the square root of the sample size. For instance, if you were sampling 5 students from a class of 50 and the 50 students had a standard deviation of 17, you’d divide 17 by the square root of 5 to get 7.6. For more tips, including how to calculate the standard deviation, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 996,353 times.
Did this article help you?
Download Article
Download Article
After collecting data, oftentimes the first thing you need to do is analyze it. This usually entails finding the mean, the standard deviation, and the standard error of the data. This article will show you how it’s done.
Cheat Sheets
-
1
Obtain a set of numbers you wish to analyze. This information is referred to as a sample.
- For example, a test was given to a class of 5 students, and the test results are 12, 55, 74, 79 and 90.
Advertisement
-
1
Calculate the mean. Add up all the numbers and divide by the population size:[1]
- Mean (μ) = ΣX/N, where Σ is the summation (addition) sign, xi is each individual number, and N is the population size.
- In the case above, the mean μ is simply (12+55+74+79+90)/5 = 62.
-
1
Calculate the standard deviation. This represents the spread of the population.
Standard deviation = σ = sq rt [(Σ((X-μ)^2))/(N)].[2]
- For the example given, the standard deviation is sqrt[((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27.4. (Note that if this was the sample standard deviation, you would divide by n-1, the sample size minus 1.)
Advertisement
-
1
Calculate the standard error (of the mean). This represents how well the sample mean approximates the population mean. The larger the sample, the smaller the standard error, and the closer the sample mean approximates the population mean. Do this by dividing the standard deviation by the square root of N, the sample size.[3]
Standard error = σ/sqrt(n)[4]
- So for the example above, if this were a sampling of 5 students from a class of 50 and the 50 students had a standard deviation of 17 (σ = 21), the standard error = 17/sqrt(5) = 7.6.
Add New Question
-
Question
How do you find the mean given number of observations?
To find the mean, add all the numbers together and divide by how many numbers there are. e.g to find the mean of 1,7,8,4,2: 1+7+8+4+2 = 22/5 = 4.4.
-
Question
The standard error is calculated as 0.2 and the standard deviation of a sample is 5kg. Can it be said to be smaller or larger than the standard deviation?
The standard error (SE) must be smaller than the standard deviation (SD), because the SE is calculating by dividing the SD by something — i.e. making it smaller.
-
Question
How can I find out the standard deviation of 50 samples?
The results of all your figures (number plus number plus number etc.) divided by quantity of samples 50 =SD.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Calculations of the mean, standard deviation, and standard error are most useful for analysis of normally distributed data. One standard deviation about the central tendency covers approximately 68 percent of the data, 2 standard deviation 95 percent of the data, and 3 standard deviation 99.7 percent of the data. The standard error gets smaller (narrower spread) as the sample size increases.
Thanks for submitting a tip for review!
Advertisement
-
Check your math carefully. It is very easy to make mistakes or enter numbers incorrectly.
Advertisement
References
About This Article
Article SummaryX
The mean is simply the average of a set of numbers. You can work it out by adding up all the numbers and dividing the total by the amount of numbers. For example, if you wanted to find the average test score of 3 students who scored 74, 79, and 90, you’d add the 3 numbers together to get 243, then divide it by 3 to get 81. The standard error represents how well the sample mean approximates the population mean. All you need to do is divide the standard deviation by the square root of the sample size. For instance, if you were sampling 5 students from a class of 50 and the 50 students had a standard deviation of 17, you’d divide 17 by the square root of 5 to get 7.6. For more tips, including how to calculate the standard deviation, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 996,353 times.
Did this article help you?
Надежна ли ваша стандартная ошибка?
Перевод
Ссылка на автора
Практическое руководство по выбору правильной спецификации
Управляющее резюме
- Проблема:Стандартные ошибки по умолчанию (SE), сообщаемые Stata, R и Python, являются правильными только при очень ограниченных обстоятельствах. В частности, эти программы предполагают, что ваша ошибка регрессии распределена независимо и одинаково. На самом деле это не так, что приводит к серьезным ошибкам типа 1 и типа 2 в тестах гипотез.
- Лечение 1:если вы используете OLS, вы должны кластеризовать SE по двум параметрам: индивидуально по годам.
- Лечение 2:если вы используете FE (фиксированный эффект), вы должны кластеризовать SE только на 1 измерение: индивидуальное.
- коды: Вот это ссылка на коды Stata, R и SAS для реализации кластеризации SE.
Если вам интересно об этой проблеме, пожалуйста, продолжайте читать. В противном случае, увидимся в следующий раз 
План на день
В этом посте я собрал бы 69-страничный документ о здравой стандартной ошибке в чит-лист. Эта бумага Опубликованный профессором Митчеллом Петерсеном в 2009 году, на сегодняшний день собрал более 7 879 ссылок. Это остается библией для выбора правильной здравой стандартной ошибки.
Проблема
Обычная практика
В любом классе Stats 101 ваш профессор мог бы научить вас набирать «reg Y X» в Stata или R:
Вы приступаете к проверке своей гипотезы с указанными точечными оценками и стандартной ошибкой. Но в 99% случаев это было бы неправильно.
Ловушка
Чтобы OLS давал объективные и непротиворечивые оценки, нам нужно, чтобы термин ошибки epsilon был распределен независимо и одинаково:
Независимый означает, что никакие серийные или взаимные корреляции не допускаются:
- Последовательные корреляции:для одного и того же человека остатки в разные периоды времени коррелируют;
- Кросс-корреляция:различные индивидуальные остатки коррелируются внутри и / или между периодами.
Одинаковый означает, что все остатки имеют одну и ту же дисперсию (например, гомоскедастичность).
Визуализация проблемы
Давайте визуализируем i.i.d. предположение в дисперсионно-ковариационной матрице.
- Нет последовательной корреляции:все недиагональные записи в красных пузырьках должны быть 0;
- Нет взаимной корреляции:все диагональные записи должны быть одинаковыми — все записи в зеленых прямоугольниках должны быть 0;
- гомоскедастичность:диагональные записи должны быть одинаковыми константами.
Что не так, если вы используете SE по умолчанию без I.I.D. Ошибки?
Вывод выражения SE:
Стандартная ошибка по умолчанию — последняя строка в (3). Но чтобы получить от 1-й до последней строки, нам нужно сделать дополнительные предположения:
- Нам нужно предположение о независимости, чтобы переместить нас с 1-й строки на 2-ю в (3). Визуально все записи в зеленых прямоугольниках И все недиагональные записи в красных пузырьках должны быть 0.
- Нам нужно одинаково распределенное предположение, чтобы переместить нас со 2-й строки на 3-ю. Визуально все диагональные элементы должны быть точно такими же.
По умолчанию SE прав в ОЧЕНЬ ограниченных обстоятельствах!
Цена неправильного
Мы не знаем, будет ли заявленная SE переоценена или недооценена истинная SE. Таким образом, мы можем получить:
- Статистически значимый результат, когда эффекта нет в реальности. В результате команде разработчиков программного обеспечения и продукта может потребоваться несколько часов работы над каким-либо прототипом, который никак не повлияет на итоговую прибыль компании.
- Статистически незначимый результат, когда в действительности наблюдается значительный эффект. Это могло быть для тебя перерывом. Упущенная возможность Очень плохо
На самом деле ложный позитив более вероятен.Там нет недостатка в новичках машинного обучения студентов, заявляющих, что они нашли какой-то шаблон / сигнал, чтобы побить рынок. Однако после развертывания их модели работают катастрофически. Частично причина в том, что они никогда не думали о последовательной или взаимной корреляции остатков.
Когда это происходит, стандартная ошибка по умолчанию может быть в 11 раз меньше, чем истинная стандартная ошибка, что приводит к серьезной переоценке статистической значимости их сигнала.
Надежная стандартная ошибка на помощь!
Правильно заданная надежная стандартная ошибка избавит от смещения или, по крайней мере, улучшит его. Вооружившись серьезной стандартной ошибкой, вы можете безопасно перейти к этапу вывода.
Есть много надежных стандартных ошибок. Выбор неправильного средства может усугубить проблему!
Какую робастную стандартную ошибку я должен использовать?
Это зависит от дисперсионно-ковариантной структуры. Спросите себя, страдает ли ваш остаток от взаимной корреляции, последовательной корреляции или от того и другого? Напомним, что:
- Кросс-корреляция:в течение одного и того же периода времени разные индивидуальные остатки могут быть коррелированы;
- Последовательная корреляция:для одного и того же лица остатки за разные периоды времени могут быть коррелированы
Случай 1: Термин ошибки имеет отдельный конкретный компонент
Предположим, что это истинное состояние мира:
При условии независимости от отдельных лиц, правильная стандартная ошибка будет:
Сравните это с (3), у нас есть дополнительный член, который обведен красным. Превышение или недооценка сообщаемой стандартной ошибки OLS истинной стандартной ошибки зависит от знака коэффициентов корреляции, который затем увеличивается на число периодов времени T.
Где практическое руководство?
Основываясь на большем количестве теории и результатов моделирования, Петерсен показывает, что:
Вы не должны использовать:
- Стандартные ошибки Fama-MacBeth:он предназначен для работы с последовательной корреляцией, а не с перекрестной корреляцией между отдельными фирмами.
- Стандартные ошибки Ньюи-Уэста:он предназначен для учета последовательной корреляции неизвестной формы в остатках одного временного ряда.
Вы должны использовать:
- Стандартные кластерные ошибки:в частности, вы должны объединить вашу стандартную ошибку по фирмам. Обратитесь к концу поста для кодов.
Случай 2: Термин ошибки имеет компонент, зависящий от времени
Предположим, что это истинное состояние мира:
Правильная стандартная ошибка по существу такая же, как (7), если вы поменяете N и T.
Вы должны использовать:
- Стандартные ошибки Fama-MacBeth:так как это то, что он создан для Обратитесь к концу поста для кода Stata.
Случай 3: Термин «ошибка» имеет как твердое, так и временное влияние
Предположим, что это истинное состояние мира:
Вы должны использовать:
- Кластерная стандартная ошибка:кластеризацию следует проводить по двум параметрам — по годам. Обратите внимание, что это не настоящие стандартные ошибки, они просто создают менее предвзятую стандартную ошибку. Смещение становится более выраженным, когда в одном измерении всего несколько кластеров.
коды
Подробные инструкции и тестовые данные Stata, R и SAS от Petersen можно найти Вот, Для моей собственной записи я собираю список кода Stata здесь:
Случай 1: кластеризация по 1 измерению
Регресс зависимая_вариантная независимая_вариабельная, надежный кластер (cluster_variable)
Случай 2: Фама-Макбет
tsset firm_identifier time_identifier
fm independent_variable independent_variables, byfm (by_variable)
Случай 3: кластеризация по двум измерениям
cluster2 зависимая_ переменная independent_variables, fcluster (cluster_variable_one) tcluster (cluster_variable_two)
Случай 4: фиксированный эффект + кластеризация
xtreg variable_variable independent_variables, надежный кластер (cluster_variable_one)
Наслаждайтесь своим недавно найденным крепким миром!
До следующего раза 
Стандартное отклонение (SD), измеряет количество изменчивости или дисперсии, из отдельных значений данных, к среднему значению, в то время как стандартная ошибка среднего (SEM) мер, как далеко образец среднее (среднее) данных, вероятно, будет от истинного среднего значения населения. SEM всегда меньше SD.
Ключевые выводы
- Стандартное отклонение (SD) измеряет разброс набора данных относительно его среднего значения.
- Стандартная ошибка среднего (SEM) измеряет, насколько вероятно расхождение между средним значением выборки по сравнению со средним значением генеральной совокупности.
- SEM берет SD и делит его на квадратный корень из размера выборки.
SEM против SD
Стандартное отклонение и стандартная ошибка используются во всех типах статистических исследований, включая исследования в области финансов, медицины, биологии, инженерии, психологии и т. Д. В этих исследованиях стандартное отклонение (SD) и расчетная стандартная ошибка среднего (SEM) ) используются для представления характеристик данных выборки и объяснения результатов статистического анализа. Однако некоторые исследователи иногда путают SD и SEM. Таким исследователям следует помнить, что расчеты SD и SEM включают разные статистические выводы, каждый из которых имеет свое значение. SD – это разброс отдельных значений данных.
Другими словами, SD указывает, насколько точно среднее значение представляет данные выборки. Однако значение SEM включает статистический вывод, основанный на распределении выборки. SEM – это стандартное отклонение теоретического распределения выборочных средних (выборочное распределение).
Расчет стандартного отклонения
Формула SD требует нескольких шагов:
- Во-первых, возьмите квадрат разницы между каждой точкой данных и средним значением выборки, найдя сумму этих значений.
- Затем разделите эту сумму на размер выборки минус один, который представляет собой дисперсию.
- Наконец, извлеките квадратный корень из дисперсии, чтобы получить стандартное отклонение.
Стандартная ошибка среднего
SEM рассчитывается путем деления стандартного отклонения на квадратный корень из размера выборки.
Стандартная ошибка дает точность выборочного среднего путем измерения изменчивости выборочного среднего от образца к образцу. SEM описывает, насколько точное среднее значение выборки является оценкой истинного среднего значения совокупности. По мере увеличения размера выборки данных SEM уменьшается по сравнению с SD; следовательно, по мере увеличения размера выборки среднее значение выборки оценивает истинное среднее значение генеральной совокупности с большей точностью. Напротив, увеличение размера выборки не обязательно делает SD больше или меньше, это просто становится более точной оценкой SD населения.
Стандартная ошибка и стандартное отклонение в финансах
В финансах стандартная ошибка средней дневной доходности актива измеряет точность выборочного среднего как оценки долгосрочной (постоянной) средней дневной доходности актива.
С другой стороны, стандартное отклонение доходности измеряет отклонения индивидуальных доходов от среднего значения. Таким образом, SD является мерой волатильности и может использоваться в качестве меры риска для инвестиций. Активы с более высокими ежедневными движениями цен имеют более высокое SD, чем активы с меньшими ежедневными движениями. Предполагая нормальное распределение, около 68% дневных изменений цен находятся в пределах одного стандартного отклонения от среднего, при этом около 95% дневных изменений цен находятся в пределах двух стандартных значений среднего.
Предыдущий пост см. здесь.
Проверка статистических гипотез
Для статистиков и исследователей данных проверка статистической гипотезы представляет собой формальную процедуру. Стандартный подход к проверке статистической гипотезы подразумевает определение области исследования, принятие решения в отношении того, какие переменные необходимы для измерения предмета изучения, и затем выдвижение двух конкурирующих гипотез. Во избежание рассмотрения только тех данных, которые подтверждают наши субъективные оценки, исследователи четко констатируют свою гипотезу заранее. Затем, основываясь на данных, они применяют выборочные статистики с целью подтвердить либо отклонить эту гипотезу.
Проверка статистической гипотезы подразумевает использование тестовой статистики, т.е. выборочной величины, как функции от результатов наблюдений. Тестовая статистика (test statistic) — это вычисленная из выборочных данных величина, которая используется для оценивания прочности данных, подтверждающих нулевую статистическую гипотезу и служит для выявления меры расхождения между эмпирическими и гипотетическими значениями. Конкретные методы проверки называются тестами, например, z-тест, t-тест (соответственно z-тест Фишера, t-тест Студента) и т.д. в зависимости от применяемых в них тестовых статистик.
Примечание. В отечественной статистической науке используется «туманный» термин «статистика критерия». Туманный потому здесь мы снова наблюдаем мягкую подмену: вместо теста возникает критерий. Если уж на то пошло, то критерий — это принцип или правило. Например, выполняя z-тест, t-тест и т.д., мы соответственно используем z-статистику, t-статистику и т.д. в правиле отклонения гипотезы. Это хорошо резюмируется следующей ниже таблицей:
|
Тестирование гипотезы |
Тестовая статистика |
Правило отклонения гипотезы |
|
z-тесты |
z-статистика |
Если тестовая статистика ≥ z или ≤ -z, то отклонить нулевую гипотезу H0. |
|
t-тесты |
t-статистика |
Если тестовая статистика ≥ t или ≤ -t, то отклонить нулевую гипотезу H0. |
|
Анализ дисперсии (ANOVA) |
F-статистика |
Если тестовая статистика ≥ F, то отклонить нулевую гипотезу H0. |
|
Тесты хи-квадрат |
Статистика хи-квадрат |
Если тестовая статистика ≥ χ, то отклонить нулевую гипотезу H0. |
Для того, чтобы помочь сохранить поток посетителей веб-сайта, дизайнеры приступают к работе над вариантом веб-сайта с использованием всех новейших методов по поддержанию внимания аудитории. Мы хотели бы удостовериться, что наши усилия не напрасны, и поэтому стараемся увеличить время пребывания посетителей на обновленном веб-сайте.
Отсюда главный вопрос нашего исследования состоит в том, «приводит ли обновленный вид веб-сайта к увеличению времени пребывания на нем посетителей»? Мы принимаем решение проверить его относительно среднего значения времени пребывания. Теперь, мы должны изложить две наши гипотезы. По традиции считается, что изучаемые данные не содержат того, что исследователь ищет. Таким образом, консервативное мнение заключается в том, что данные не покажут ничего необычного. Все это называется нулевой гипотезой и обычно обозначается как H0.
При тестировании статистической гипотезы исходят из того, что нулевая гипотеза является истинной до тех пор, пока вес представленных данных, подтверждающих обратное, не сделает ее неправдоподобной. Этот подход к поиску доказательств «в обратную сторону» частично вытекает из простого психологического факта, что, когда люди пускаются на поиски чего-либо, они, как правило, это находят.
Затем исследователь формулирует альтернативную гипотезу, обозначаемую как H1. Она может попросту заключаться в том, что популяционное среднее отличается от базового уровня. Или же, что популяционное среднее больше или меньше базового уровня, либо больше или меньше на некоторую указанную величину. Мы хотели бы проверить, не увеличивает ли обновленный дизайн веб-сайта время пребывания, и поэтому нашей нулевой и альтернативной гипотезами будут следующие:
-
H0: Время пребывания для обновленного веб-сайта не отличается от времени пребывания для существующего веб-сайта
-
H1: Время пребывания для обновленного веб-сайта больше по сравнению с временем пребывания для существующего веб-сайта
Наше консервативное допущение состоит в том, что обновленный веб-сайт никак не влияет на время пребывания посетителей на веб-сайте. Нулевая гипотеза не обязательно должна быть «нулевой» (т.е. эффект отсутствует), но в данном случае, у нас нет никакого разумного оправдания, чтобы считать иначе. Если выборочные данные не поддержат нулевую гипотезу (т.е. если данные расходятся с ее допущением на слишком большую величину, чтобы носить случайный характер), то мы отклоним нулевую гипотезу и предложим альтернативную в качестве наилучшего альтернативного объяснения.
Указав нулевую и альтернативную гипотезы, мы должны установить уровень значимости, на котором мы ищем эффект.
Статистическая значимость
Проверка статистической значимости изначально разрабатывалась независимо от проверки статистических гипотез, однако сегодня оба подхода очень часто используются во взаимодействии друг с другом. Задача проверки статистической значимости состоит в том, чтобы установить порог, за пределами которого мы решаем, что наблюдаемые данные больше не поддерживают нулевую гипотезу.
Следовательно, существует два риска:
-
Мы можем принять расхождение как значимое, когда на самом деле оно возникло случайным образом
-
Мы можем приписать расхождение случайности, когда на самом деле оно показывает истинное расхождение с популяцией
Эти две возможности обозначаются соответственно, как ошибки 1-го и 2-го рода:
|
H0 ложная |
H0 истинная |
|
|
Отклонить H0 |
Истинноотрицательный исход |
Ошибка 1-го рода (ложноположительный исход) |
|
Принять H0 |
Ошибка 2-го рода (ложноотрицательный исход) |
Истинноположительный исход |
Чем больше мы уменьшаем риск совершения ошибок 1-го рода, тем больше мы увеличиваем риск совершения ошибок 2-го рода. Другими словами, с чем большей уверенностью мы хотим не заявлять о наличии расхождения, когда его нет, тем большее расхождение между выборками нам потребуется, чтобы заявить о статистической значимости. Эта ситуация увеличивает вероятность того, что мы проигнорируем подлинное расхождение, когда мы с ним столкнемся.
В статистической науке обычно используются два порога значимости. Это уровни в 5% и 1%. Расхождение в 5% обычно называют значимым, а расхождение в 1% — крайне значимым. В формулах этот порог часто обозначается греческой буквой α (альфа) и называется уровнем значимости. Поскольку, отсутствие эффекта по результатам эксперимента может рассматриваться как неуспех (эксперимента либо обновленного веб-сайта, как в нашем случае), то может возникнуть желание корректировать уровень значимости до тех пор, пока эффект не будет найден. По этой причине классический подход к проверке статистической значимости требует, чтобы мы устанавливали уровень значимости до того, как обратимся к нашим данным. Часто выбирается уровень в 5%, и поэтому мы на нем и остановимся.
Проверка обновленного дизайна веб-сайта
Веб-команда в AcmeContent была поглощена работой, конструируя обновленный веб-сайт, который будет стимулировать посетителей оставаться на нем в течение более длительного времени. Она употребила все новейшие методы и, в результате мы вполне уверены, что веб-сайт покажет заметное улучшение показателя времени пребывания.
Вместо того, чтобы запустить его для всех пользователей сразу, в AcmeContent хотели бы сначала проверить веб-сайт на небольшой выборке посетителей. Мы познакомили веб-команду с понятием искаженности выборки, и в результате там решили в течение одного дня перенаправлять случайные 5% трафика на обновленный веб-сайт. Результат с дневным трафиком был нам предоставлен одним текстовым файлом. Каждая строка показывает время пребывания посетителей. При этом, если посетитель пользовался исходным дизайном, ему присваивалось значение «0», и если он пользовался обновленным (и надеемся, улучшенным) дизайном, то ему присваивалось значение «1».
Выполнение z-теста
Ранее при тестировании с интервалами уверенности мы располагали лишь одним популяционным средним, с которым и выполнялось сравнение.
При тестировании нулевой гипотезы с помощью z-теста мы имеем возможность сравнивать две выборки. Посетители, которые видели обновленный веб-сайт, отбирались случайно, и данные для обеих групп были собраны в тот же день, чтобы исключить другие факторы с временной зависимостью.
Поскольку в нашем распоряжении имеется две выборки, то и стандартных ошибок у нас тоже две. Z-тест выполняется относительно объединенной стандартной ошибки, т.е. квадратного корня суммы дисперсий (вариансов), деленных на размеры выборок. Она будет такой же, что и результат, который мы получим, если взять стандартную ошибку обеих выборок вместе:
Здесь σ2a — это дисперсия выборки a, σ2b — дисперсия выборки b и соответственно na и nb — размеры выборок a и b. На Python объединенная стандартная ошибка вычисляется следующим образом:
def pooled_standard_error(a, b, unbias=False):
'''Объединенная стандартная ошибка'''
std1 = a.std(ddof=0) if unbias==False else a.std()
std2 = b.std(ddof=0) if unbias==False else b.std()
x = std1 ** 2 / a.count()
y = std2 ** 2 / b.count()
return sp.sqrt(x + y)С целью выявления того, является ли видимое нами расхождение неожиданно большим, можно взять наблюдавшиеся расхождения между средними значениями на объединенной стандартной ошибке. Эту статистическую величину принято обозначать переменной z:
Используя функции pooled_standard_error, которая вычисляет объединенную стандартную ошибку, z-статистику можно получить следующим образом:
def z_stat(a, b, unbias=False):
return (a.mean() - b.mean()) / pooled_standard_error(a, b, unbias)Соотношение z объясняет, насколько средние значения отличаются относительно величины, которую мы ожидаем при заданной стандартной ошибке. Следовательно, z-статистика сообщает нам о том, на какое количество стандартных ошибок расходятся средние значения. Поскольку стандартная ошибка имеет нормальное распределение вероятностей, мы можем связать это расхождение с вероятностью, отыскав z-статистику в нормальной ИФР:
def z_test(a, b):
return stats.norm.cdf([ z_stat(a, b) ])В следующем ниже примере z-тест используется для сравнения результативность двух веб-сайтов. Это делается путем группировки строк по номеру веб-сайта, в результате чего возвращается коллекция, в которой конкретному веб-сайту соответствует набор строк. Мы вызываем groupby('site')['dwell-time'] для конвертирования набора строк в набор значений времени пребывания. Затем вызываем функцию get_group с номером группы, соответствующей номеру веб-сайта:
def ex_2_14():
'''Сравнение результативности двух вариантов
дизайна веб-сайта на основе z-теста'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
print('a n: ', a.count())
print('b n: ', b.count())
print('z-статистика:', z_stat(a, b))
print('p-значение: ', z_test(a, b))a n: 284
b n: 16
z-статистика: -1.6467438180091214
p-значение: [0.04980536]Установление уровня значимости в размере 5% во многом аналогично установлению интервала уверенности шириной 95%. В сущности, мы надеемся убедиться, что наблюдавшееся расхождение попадает за пределы 95%-го интервала уверенности. Если это так, то мы можем утверждать, что нашли результат с 5%-ым уровнем значимости.
P-значение — это вероятность совершения ошибки 1-го рода в результате неправильного отклонения нулевой гипотезы, которая в действительности является истинной. Чем меньше p-значение, тем больше определенность в том, что нулевая гипотеза является ложной, и что мы нашли подлинный эффект.
Этот пример возвращает значение 0.0498, или 4.98%. Поскольку оно немногим меньше нашего 5% порога значимости, мы можем утверждать, что нашли нечто значимое.
Приведем еще раз нулевую и альтернативную гипотезы:
-
H0: Время пребывания на обновленном веб-сайте не отличается от времени пребывания на существующем веб-сайте
-
H1: Время пребывания на обновленном веб-сайте превышает время пребывания на существующем веб-сайте.
Наша альтернативная гипотеза состоит в том, что время пребывания на обновленном веб-сайте больше.
Мы готовы заявить о статистической значимости, и что время пребывания на обновленном веб-сайте больше по сравнению с существующим веб-сайтом, но тут есть одна трудность — чем меньше размер выборки, тем больше неопределенность в том, что выборочное стандартное отклонение совпадет с популяционным. Как показано в результатах предыдущего примера, наша выборка из обновленного веб-сайта содержит всего 16 посетителей. Столь малые выборки делают невалидным допущение о том, что стандартная ошибка нормально распределена.
К счастью, существует тест и связанное с ним распределение, которое моделирует увеличенную неопределенность стандартных ошибок для выборок меньших размеров.
t-распределение Студента
Популяризатором t-распределения был химик, работавший на пивоварню Гиннес в Ирландии, Уилльям Госсетт, который включил его в свой анализ темного пива Стаут.
В 1908 Уильям Госсет опубликовал статью об этой проверке в журнале Биометрика, но при этом по распоряжению своего работодателя, который рассматривал использованную Госсеттом статистику как коммерческую тайну, был вынужден использовать псевдоним. Госсет выбрал псевдоним «Студент».
В то время как нормальное распределение полностью описывается двумя параметрами — средним значением и стандартным отклонением, t-распределение описывается лишь одним параметром, так называемыми степенями свободы. Чем больше степеней свободы, тем больше t-распределение похоже на нормальное распределение с нулевым средним и стандартным отклонением, равным 1. По мере уменьшения степеней свободы, это распределение становится более широким с более толстыми чем у нормального распределения, хвостами.
Приведенный выше рисунок показывает, как t-распределение изменяется относительно нормального распределения при наличии разных степеней свободы. Более толстые хвосты для выборок меньших размеров соответствуют увеличенной возможности наблюдать более крупные отклонения от среднего значения.
Степени свободы
Степени свободы, часто обозначаемые сокращенно df от англ. degrees of freedom, тесно связаны с размером выборки. Это полезная статистика и интуитивно понятное свойство числового ряда, которое можно легко продемонстрировать на примере.
Если бы вам сказали, что среднее, состоящее из двух значений, равно 10 и что одно из значений равно 8, то Вам бы не потребовалась никакая дополнительная информация для того, чтобы суметь заключить, что другое значение равно 12. Другими словами, для размера выборки, равного двум, и заданного среднего значения одно из значений ограничивается, если другое известно.
Если напротив вам говорят, что среднее, состоящее из трех значений, равно 10, и первое значение тоже равно 10, то Вы были бы не в состоянии вывести оставшиеся два значения. Поскольку число множеств из трех чисел, начинающихся с 10, и чье среднее равно 10, является бесконечным, то прежде чем вы сможете вывести значение третьего, второе тоже должно быть указано.
Для любого множества из трех чисел ограничение простое: вы можете свободно выбрать первые два числа, но заключительное число ограничено. Степени свободы могут таким образом быть обобщены следующим образом: количество степеней свободы любой отдельной выборки на единицу меньше размера выборки.
При сопоставлении двух выборок степени свободы на две единицы меньше суммы размеров этих выборок, что равно сумме их индивидуальных степеней свободы.
t-статистика
При использовании t-распределения мы обращаемся к t-статистике. Как и z-статистика, эта величина количественно выражает степень маловероятности отдельно взятого наблюдавшегося отклонения. Для двухвыборочного t-теста соответствующая t-статистика вычисляется следующим образом:
Здесь Sa̅b̅ — это объединенная стандартная ошибка. Объединенная стандартная ошибка вычисляется таким же образом, как и раньше:
Однако это уравнение допускает наличие информации о популяционных параметрах σa и σb, которые можно аппроксимировать только на основе крупных выборок. t-тест предназначен для малых выборок и не требует от нас принимать допущения о поплуляционной дисперсии (вариансе).
Как следствие, объединенная стандартная ошибка для t-теста записывается как квадратный корень суммы стандартных ошибок:
На практике оба приведенных выше уравнения для объединенной стандартной ошибки дают идентичные результаты при заданных одинаковых входных последовательностях. Разница в математической записи всего лишь служит для иллюстрации того, что в условиях t-теста мы на входе зависим только от выборочных статистик. Объединенная стандартная ошибка может быть вычислена следующим образом:
def pooled_standard_error_t(a, b):
'''Объединенная стандартная ошибка для t-теста'''
return sp.sqrt(standard_error(a) ** 2 +
standard_error(b) ** 2)Хотя в математическом плане t-статистика и z-статистика представлены по-разному, на практике процедура вычисления обоих идентичная:
t_stat = z_stat
def ex_2_15():
'''Вычисление t-статистики
двух вариантов дизайна веб-сайта'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
return t_stat(a, b)-1.6467438180091214Различие между двумя выборочными показателями является не алгоритмическим, а концептуальным — z-статистика применима только тогда, когда выборки подчинены нормальному распределению.
t-тест
Разница в характере работы t-теста вытекает из распределения вероятностей, из которого вычисляется наше p-значение. Вычислив t-статистику, мы должны отыскать ее значение в t-распределении, параметризованном степенями свободы наших данных:
def t_test(a, b):
df = len(a) + len(b) - 2
return stats.t.sf([ abs(t_stat(a, b)) ], df)Значение степени свободы обеих выборок на две единицы меньше их размеров, и для наших выборок составляет 298.
Напомним, что мы выполняем проверку статистической гипотезы. Поэтому выдвинем нашу нулевую и альтернативную гипотезы:
-
H0: Эта выборка взята из популяции с предоставленным средним значением
-
H1: Эта выборка взята из популяции со средним значением большего размера
Выполним следующий ниже пример:
def ex_2_16():
'''Сравнение результативности двух вариантов
дизайна веб-сайта на основе t-теста'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
return t_test(a, b)array([ 0.05033241])Этот пример вернет p-значение, составляющее более 0.05. Поскольку оно больше α, равного 5%, который мы установили для проверки нулевой гипотезы, то мы не можем ее отклонить. Наша проверка с использованием t-теста значимого расхождения между средними значениями не обнаружила. Следовательно, наш едва значимый результат z-теста отчасти объясняется наличием слишком малой выборки.
Двухсторонние тесты
В нашей альтернативной гипотезе было принято неявное допущение, что обновленный веб-сайт будет работать лучше существующего. В процедуре проверки нулевой статистической гипотезы предпринимаются особые усилия для обеспечения того, чтобы при поиске статистической значимости мы не делали никаких скрытых допущений.
Проверки, при выполнении которых мы ищем только значимое количественное увеличение или уменьшение, называются односторонними и обычно не приветствуются, кроме случая, когда изменение в противоположном направлении было бы невозможным. Название термина «односторонний» обусловлено тем, что односторонняя проверка размещает всю α в одном хвосте распределения. Не делая проверок в другом направлении, проверка имеет больше мощности отклонить нулевую гипотезу в отдельно взятом направлении и, в сущности, понижает порог, по которому мы судим о результате как значимом.
Статистическая мощность — это вероятность правильного принятия альтернативной гипотезы. Она может рассматриваться как способность проверки обнаруживать эффект там, где имеется искомый эффект.
Хотя более высокая статистическая мощность выглядит желательной, она получается за счет наличия большей вероятности совершить ошибку 1-го рода. Правильнее было бы допустить возможность того, что обновленный веб-сайт может в действительности оказаться хуже существующего. Этот подход распределяет нашу α одинаково по обоим хвостам распределения и обеспечивает значимый результат, не искаженный под воздействием априорного допущения об улучшении работы обновленного веб-сайта.
В действительности в модуле stats библиотеки scipy уже предусмотрены функции для выполнения двухвыборочных t-проверок. Это функция stats.ttest_ind. В качестве первого аргумента мы предоставляем выборку данных и в качестве второго — выборку для сопоставления. Если именованный аргумент equal_var равен True, то выполняется стандартная независимая проверка двух выборок, которая предполагает равные популяционные дисперсии, в противном случае выполняется проверка Уэлша (обратите внимание на служебную функцию t_test_verbose, (которую можно найти среди примеров исходного кода в репо):
def ex_2_17():
'''Двухсторонний t-тест'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
return t_test_verbose(a, sample2=b, fn=stats.ttest_ind) #t-тест Уэлша{'p-значение': 0.12756432502462475,
'степени свободы ': 17.761382349686098,
'интервал уверенности': (76.00263198799597, 99.89877646270826),
'n1 ': 284,
'n2 ': 16,
'среднее x ': 87.95070422535211,
'среднее y ': 122.0,
'дисперсия x ': 10463.941024237296,
'дисперсия y ': 6669.866666666667,
't-статистика': -1.5985205593851322}По результатам t-теста служебная функция t_test_verbose возвращает много информации и в том числе p-значение. P-значение примерно в 2 раза больше того, которое мы вычислили для односторонней проверки. На деле, единственная причина, почему оно не совсем в два раза больше, состоит в том, что в модуле stats имплементирован легкий вариант t-теста, именуемый t-тестом Уэлша, который немного более робастен, когда две выборки имеют разные стандартные отклонения. Поскольку мы знаем, что для экспоненциальных распределений среднее значение и дисперсия тесно связаны, то этот тест немного более строг в применении и даже возвращает более низкую значимость.
Одновыборочный t-тест
Независимые выборки в рамках t-тестов являются наиболее распространенным видом статистического анализа, который обеспечивает очень гибкий и обобщенный способ установления, что две выборки представляют одинаковую либо разную популяцию. Однако в случаях, когда популяционное среднее уже известно, существует еще более простая проверка, представленная функцией библиотеки sciзy stats.ttest_1samp.
Мы передаем выборку и популяционное среднее относительно которого выполняется проверка. Так, если мы просто хотим узнать, не отличается ли обновленный веб-сайт значимо от существующего популяционного среднего времени пребывания, равного 90 сек., то подобную проверку можно выполнить следующим образом:
def ex_2_18():
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
b = groups.get_group(1)
return t_test_verbose(b, mean=90, fn=stats.ttest_1samp) {'p-значение ': 0.13789520958229415,
'степени свободы df ': 15.0,
'интервал уверенности': (78.4815276659039, 165.5184723340961),
'n1 ': 16,
'среднее x ': 122.0,
'дисперсия x ': 6669.866666666667,
't-статистика ': 1.5672973291495713}Служебная функция t_test_verbose не только возвращает p-значение для выполненной проверки, но и интервал уверенности для популяционного среднего. Интервал имеет широкий диапазон между 78.5 и 165.5 сек., и, разумеется, перекрывается 90 сек. нашего теста. Как раз он и объясняет, почему мы не смогли отклонить нулевую гипотезу.
Многократные выборки
В целях развития интуитивного понимания относительно того, каким образом t-тест способен подтвердить и вычислить эти статистики из столь малых данных, мы можем применить подход, который связан с многократными выборками, от англ. resampling. Извлечение многократных выборок основывается на допущении о том, что каждая выборка является лишь одной из бесконечного числа возможных выборок из популяции. Мы можем лучше понять природу того, какими могли бы быть эти другие выборки, и, следовательно, добиться лучшего понимания опорной популяции, путем извлечения большого числа новых выборок из нашей существующей выборки.
На самом деле существует несколько методов взятия многократных выборок, и мы обсудим один из самых простых — бутстрапирование. При бустрапировании мы генерируем новую выборку, неоднократно извлекая из исходной выборки случайное значение с возвратом до тех пор, пока не сгенерируем выборку, имеющую тот же размер, что и оригинал. Поскольку выбранные значения возвращаются назад после каждого случайного отбора, то в новой выборке то же самое исходное значение может появляться многократно. Это как если бы мы неоднократно вынимали случайную карту из колоды игральных карт и каждый раз возвращали вынутую карту назад в колоду. В результате время от времени мы будем иметь карту, которую мы уже вынимали.
Бутстраповская выборка, или бутстрап, — синтетический набор данных, полученный в результате генерирования повторных выборок (с возвратом) из исследуемой выборки, используемой в качестве «суррогатной популяции», в целях аппроксимации выборочного распределения статистики (такой как, среднее, медиана и др.).
В библиотеке pandas при помощи функции sample можно легко извлекать бутстраповские выборки и генерировать большое число многократных выборок. Эта функция принимает ряд опциональных аргументов, в т.ч. n (число элементов, которые нужно вернуть из числового ряда), axis (ось, из которой извлекать выборку) и replace (выборка с возвратом или без), по умолчанию равный False. После этой функции можно задать метод агрегирования, вычисляющий сводную статистику в отношении бутстраповских выборок:
def ex_2_19():
'''Построение графика синтетических времен пребывания
путем извлечения бутстраповских выборок'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
b = groups.get_group(1)
xs = [b.sample(len(b), replace=True).mean() for _ in range(1000)]
pd.Series(xs).hist(bins=20)
plt.xlabel('Бутстрапированные средние значения времени пребывания, сек.')
plt.ylabel('Частота')
plt.show()Приведенный выше пример наглядно показывает результаты на гистограмме:
Гистограмма демонстрирует то, как средние значения изменялись вместе с многократными выборками, взятыми из времени пребывания на обновленном веб-сайте. Хотя на входе имелась лишь одна выборка, состоящая из 16 посетителей, бутстрапированные выборки очень четко просимулировали стандартную ошибку изначальной выборки и позволили визуализировать интервал уверенности (между 78 и 165 сек.), вычисленный ранее в результате одновыборочного t-теста.
Благодаря бутстрапированию мы просимулировали взятие многократных выборок, при том, что у нас на входе имелась всего одна выборка. Этот метод обычно применяется для оценивания параметров, которые мы не способны или не знаем, как вычислить аналитически.
Проверка многочисленных вариантов дизайна
Было разочарованием обнаружить отсутствие статистической значимости на фоне увеличенного времени пребывания пользователей на обновленном веб-сайте. Хотя хорошо, что мы обнаружили это на малой выборке пользователей, прежде чем выкладывать его на всеобщее обозрение.
Не позволяя себя обескуражить, веб-команда AcmeContent берется за сверхурочную работу и создает комплект альтернативных вариантов дизайна веб-сайта. Беря лучшие элементы из других проектов, они разрабатывают 19 вариантов для проверки. Вместе с нашим изначальным веб-сайтом, который будет действовать в качестве контрольного, всего имеется 20 разных вариантов дизайна веб-сайта, куда посетители будут перенаправляться.
Вычисление выборочных средних
Веб-команда разворачивает 19 вариантов дизайна обновленного веб-сайта наряду с изначальным. Как отмечалось ранее, каждый вариант дизайна получает случайные 5% посетителей, и при этом наше испытание проводится в течение 24 часов.
На следующий день мы получаем файл, показывающий значения времени пребывания посетителей на каждом варианте веб-сайта. Все они были промаркированы числами, при этом число 0 соответствовало веб-сайту с исходным дизайном, а числа от 1 до 19 представляли другие варианты дизайна:
def ex_2_20():
df = load_data('multiple-sites.tsv')
return df.groupby('site').aggregate(sp.mean)Этот пример сгенерирует следующую ниже таблицу:
|
site |
dwell-time |
|
0 |
79.851064 |
|
1 |
106.000000 |
|
2 |
88.229167 |
|
3 |
97.479167 |
|
4 |
94.333333 |
|
5 |
102.333333 |
|
6 |
144.192982 |
|
7 |
123.367347 |
|
8 |
94.346939 |
|
9 |
89.820000 |
|
10 |
129.952381 |
|
11 |
96.982143 |
|
12 |
80.950820 |
|
13 |
90.737705 |
|
14 |
74.764706 |
|
15 |
119.347826 |
|
16 |
86.744186 |
|
17 |
77.891304 |
|
18 |
94.814815 |
|
19 |
89.280702 |
Мы хотели бы проверить каждый вариант дизайна веб-сайта, чтобы увидеть, не генерирует ли какой-либо из них статистически значимый результат. Для этого можно сравнить варианты дизайна веб-сайта друг с другом следующим образом, причем нам потребуется вспомогательный модуль Python itertools, который содержит набор функций, создающих итераторы для эффективной циклической обработки:
import itertools
def ex_2_21():
'''Проверка вариантов дизайна веб-сайта на основе t-теста
по принципу "каждый с каждым"'''
groups = load_data('multiple-sites.tsv').groupby('site')
alpha = 0.05
pairs = [list(x) # найти сочетания из n по k
for x in itertools.combinations(range(len(groups)), 2)]
for pair in pairs:
gr, gr2 = groups.get_group( pair[0] ), groups.get_group( pair[1] )
site_a, site_b = pair[0], pair[1]
a, b = gr['dwell-time'], gr2['dwell-time']
p_val = stats.ttest_ind(a, b, equal_var = False).pvalue
if p_val < alpha:
print('Варианты веб-сайта %i и %i значимо различаются: %f'
% (site_a, site_b, p_val))Однако это было бы неправильно. Мы скорее всего увидим статистическое расхождение между вариантами дизайна, показавшими себя в особенности хорошо по сравнению с вариантами, показавшими себя в особенности плохо, даже если эти расхождения носили случайный характер. Если вы выполните приведенный выше пример, то увидите, что многие варианты дизайна веб-сайта статистически друг от друга отличаются.
С другой стороны, мы можем сравнить каждый вариант дизайна веб-сайта с нашим текущим изначальным значением — средним значением времени пребывания, равным 90 сек., измеренным на данный момент для существующего веб-сайта:
def ex_2_22():
groups = load_data('multiple-sites.tsv').groupby('site')
alpha = 0.05
baseline = groups.get_group(0)['dwell-time']
for site_a in range(1, len(groups)):
a = groups.get_group( site_a )['dwell-time']
p_val = stats.ttest_ind(a, baseline, equal_var = False).pvalue
if p_val < alpha:
print('Вариант %i веб-сайта значимо отличается: %f'
% (site_a, p_val))В результате этой проверки будут идентифицированы два варианта дизайна веб-сайта, которые существенно отличаются:
Вариант 6 веб-сайта значимо отличается: 0.005534
Вариант 10 веб-сайта 10 значимо отличается: 0.006881Малые p-значения (меньше 1%) указывают на то, что существует статистически очень значимые расхождения. Этот результат представляется весьма многообещающим, однако тут есть одна проблема. Мы выполнили t-тест по 20 выборкам данных с уровнем значимости α, равным 0.05. Уровень значимости α определяется, как вероятность неправильного отказа от нулевой гипотезы. На самом деле после 20-кратного выполнения t-теста становится вероятным, что мы неправильно отклоним нулевую гипотезу по крайней мере для одного варианта веб-сайта из 20.
Сравнивая таким одновременным образом многочисленные страницы, мы делаем результаты t-теста невалидными. Существует целый ряд альтернативных технических приемов решения проблемы выполнения многократных сравнений в статистических тестах. Эти методы будут рассмотрены в следующем разделе.
Поправка Бонферрони
Для проведения многократных проверок используется подход, который объясняет увеличенную вероятность обнаружить значимый эффект в силу многократных испытаний. Поправка Бонферрони — это очень простая корректировка, которая обеспечивает, чтобы мы вряд ли совершили ошибки 1-го рода. Она выполняется путем настройки значения уровня значимости для тестов.
Настройка очень простая — поправка Бонферрони попросту делит требуемое значение α на число тестов. Например, если для теста имелось k вариантов дизайна веб-сайта, и α эксперимента равно 0.05, то поправка Бонферрони выражается следующим образом:
Она представляет собой безопасный способ смягчить увеличение вероятности совершения ошибки 1-го рода при многократной проверке. Следующий пример идентичен примеру ex-2-22, за исключением того, что значение α разделено на число групп:
def ex_2_23():
'''Проверка вариантов дизайна веб-сайта на основе t-теста
против исходного (0) с поправкой Бонферрони'''
groups = load_data('multiple-sites.tsv').groupby('site')
alpha = 0.05 / len(groups)
baseline = groups.get_group(0)['dwell-time']
for site_a in range(1, len(groups)):
a = groups.get_group(site_a)['dwell-time']
p_val = stats.ttest_ind(a, baseline, equal_var = False).pvalue
if p_val < alpha:
print('Вариант %i веб-сайта значимо отличается от исходного: %f'
% (site_a, p_val))Если вы выполните приведенный выше пример, то увидите, что при использовании поправки Бонферрони ни один из веб-сайтов больше не считается статистически значимым.
Метод проверки статистической значимости связан с поддержанием равновесия — чем меньше шансы совершения ошибки 1-го рода, тем больше риск совершения ошибки 2-го рода. Поправка Бонферрони очень консервативна, и весьма возможно, что из-за излишней осторожности мы пропускаем подлинное расхождение.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
В заключительном посте, посте №4, этой серии постов мы проведем исследование альтернативного подхода к проверке статистической значимости, который позволяет устанавливать равновесие между совершением ошибок 1-го и 2-го рода, давая нам возможность проверить все 20 вариантов веб-сайта одновременно.






![L=[4(n/100)^{2/9}]](https://dic.academic.ru/dic.nsf/ruwiki/dbb0a47f743bfd848533422845b186bc.png)





















