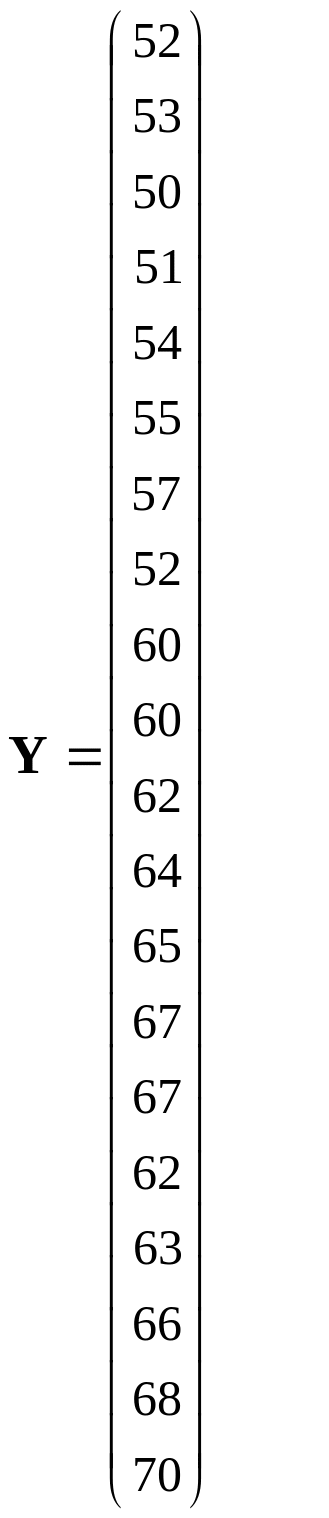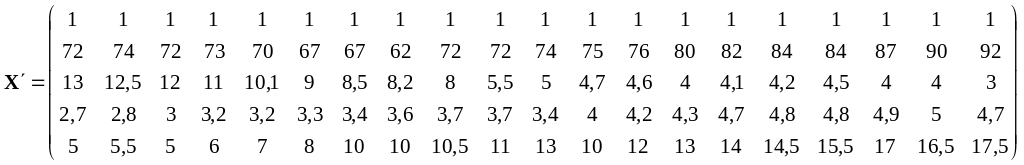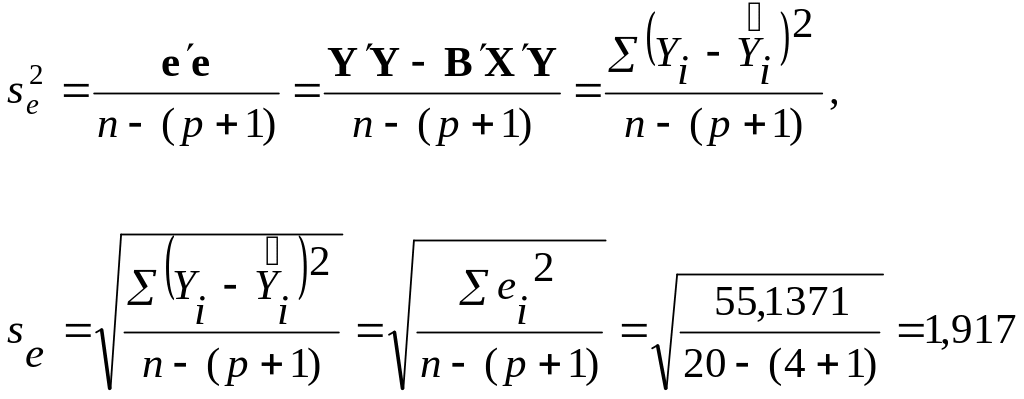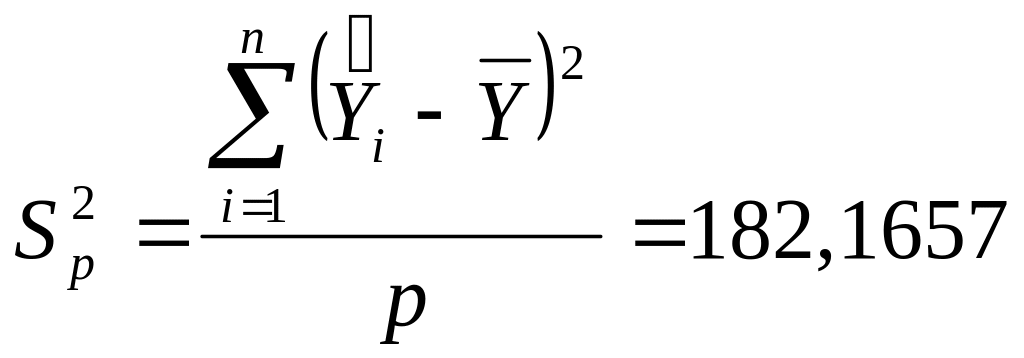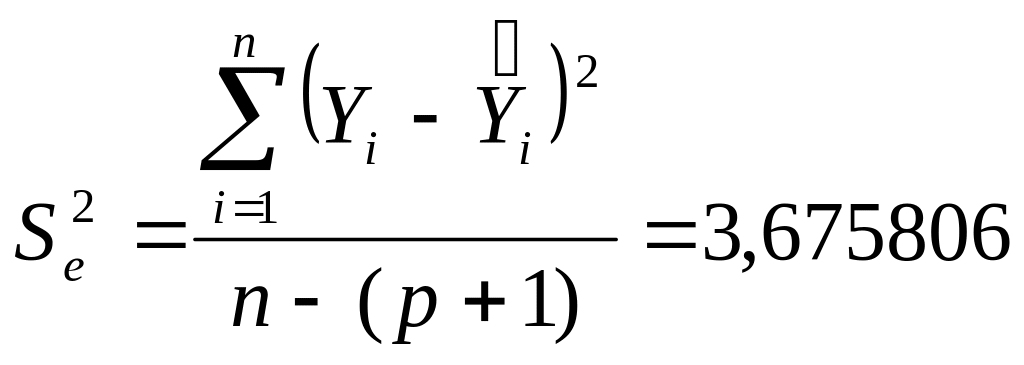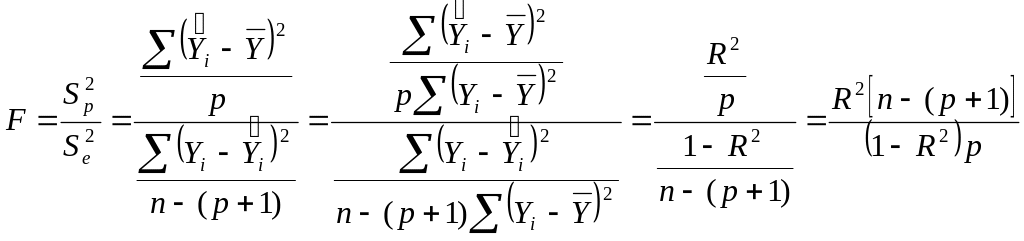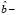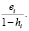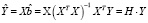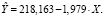-
Построение эконометрической модели производительности труда
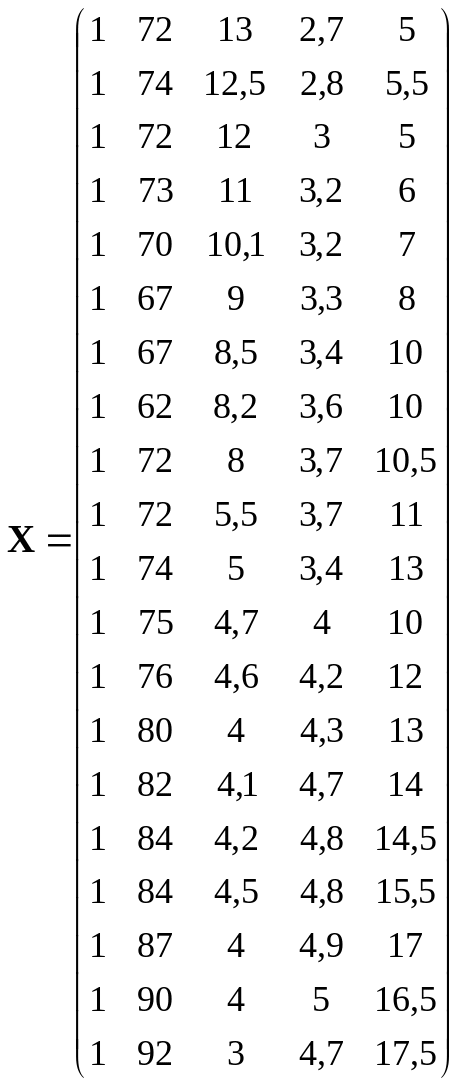
Введем обозначения: Y – зависимая
переменная, результативный признак –
производительность труда; Х1, Х2,
Х3, Х4 – независимые переменные
(объясняющие переменные, факторы), где
Х1 – фондовооруженность труда,
Х2 – коэффициент текучести рабочей
силы, Х3 – потери рабочего времени,
Х4 – стаж работы.
Модель производительности труда можно
представить в следующем виде:
-
линейная
функция Y = 0
+ 1X1 +
2X2 +
3X3 +
4X4 + ; -
степенная
функция
,
где
— стохастическая составляющая, учитывающая
влияние случайных факторов на уровень
производительности труда; j
– параметры модели.
Соответственно расчетные по выборочной
совокупности функции будут иметь вид:
-
=
b0 + b1X1 + b2X2
+ b3X3 + b4X4 ; -
,
здесь bj
– оценки параметров модели (j = 1,2,3,4).
Основываясь
на 20 наблюдениях, представленных в
табл.1, построим линейную модель методом
наименьших квадратов (МНК- модель).
Построение
линейной эконометрической модели на
основе матричного оператора 1МНК, пакет
Excel.
Матричный
оператор 1МНК имеет вид
,
где
,
— транспонированная матрица Х.
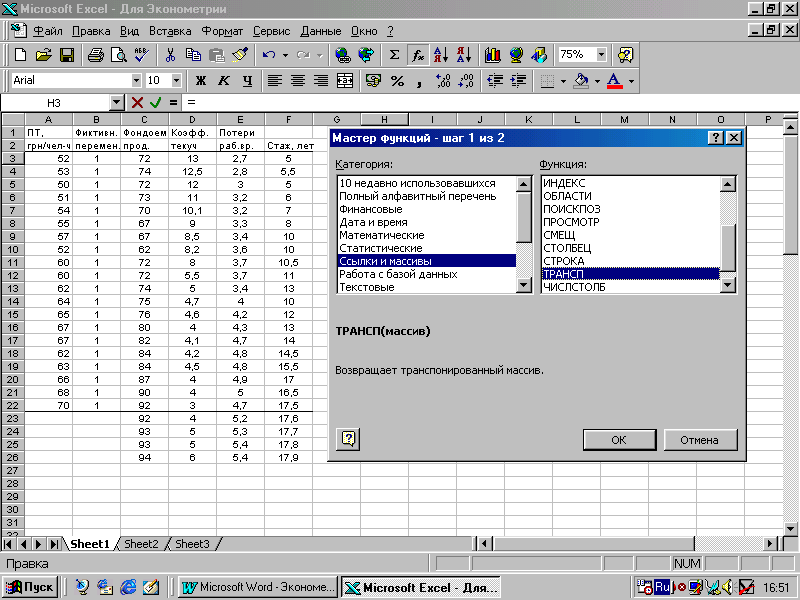
Для транспонирования матрицы Х
выполните следующие действия:
-
выделите
область пустых ячеек, состоящую из
(р+1) = 5 строк и n = 20 столбцов для вывода
результата, здесь р – количество
независимых переменных, n – количество
наблюдений; -
активизируйте
Мастер функций любым из способов:
-
в главном
меню выберите Вставка/Функция; -
на панели
инструментов Стандартная щелкните
по кнопке Вставка функции;
-
в раскрывшемся
окне выберите Категорию Ссылки и
массивы, Функцию – ТРАНСП (рис.1).
Щелкните по кнопке ОК; -
в
строке Массив появившегося окна
укажите диапазон ячеек, в которых
содержится матрица Х. Щелкните по
кнопке ОК;
Рис. 6.1
-
в левой
верхней ячейке выделенной области
появится первый элемент итоговой
таблицы. Чтобы раскрыть всю таблицу,
нажмите на клавишу <F2>, а затем – на
комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
Результат:
.
Произведение
матриц (X’X)
находим с помощью Мастера функций,
используя Категорию
Математические, функцию
МУМНОЖ:
-
выделите
область пустых ячеек, состоящую из
(р+1) = 5 строк и (р+1) = 5 столбцов для вывода
результата; -
в
окне МУМНОЖ в
строке Массив 1 укажите
диапазон ячеек, в которых содержится
матрица X‘
(первый сомножитель), а в строке Массив
2 – матрица Х
(второй сомножитель). Щелкните по кнопке
ОК; -
в левой
верхней ячейке выделенной области
появится первый элемент итоговой
таблицы. Чтобы раскрыть всю таблицу,
нажмите на клавишу <F2>, а затем – на
комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
Результат умножения матриц:
|
|
20 |
1525 |
139,9 |
77,4 |
221 |
||
|
1525 |
117509 |
10331 |
5995,4 |
17335 |
|||
|
(X’X) |
139,9 |
10331 |
1186,95 |
498,74 |
1307,7 |
||
|
77,4 |
5995,4 |
498,74 |
310,36 |
909,8 |
|||
|
221 |
17335 |
1307,7 |
909,8 |
2756,5 |
|||
|
Аналогично |
|||||||
|
|
15,5851 |
-0,0545 |
-0,5706 |
-1,6119 |
-0,104 |
||
|
-0,0545 |
0,00282 |
-0,0042 |
-0,0244 |
-0,0033 |
|||
|
(X’X)-1 |
-0,5706 |
-0,0042 |
0,04402 |
0,07434 |
0,02697 |
||
|
-1,6119 |
-0,0244 |
0,07434 |
0,98119 |
-0,0763 |
|||
|
-0,104 |
-0,0033 |
0,02697 |
-0,0763 |
0,04194 |
|||
|
|
1198 |
56,9124 |
|||||
|
92121 |
0,3375 |
||||||
|
(X’Y) |
8003,2 |
B |
(X’Y) |
-1,8406 |
|||
|
4716,5 |
-2,2722 |
||||||
|
13685 |
-0,0976 |
Таким образом, получили эконометрическую
модель:
= 56,912 + 0,338Х1 – 1,841Х2 – 2,272Х3
– 0,098Х4.
Подставив в модель исходные значения
Хij (i = 1,2,…,20; j = 1,2,3,4), получим
расчетные значения
.
Разность между фактическими и расчетными
значениями результирующего показателя
представляет собой остатки (еi
), являющиеся оценками значений
возмущения.
|
|
50,6616 |
1,33836 |
1,79122 |
|||||
|
51,9809 |
1,01908 |
1,03852 |
||||||
|
51,8206 |
-1,8206 |
3,31455 |
||||||
|
53,4467 |
-2,4467 |
5,98621 |
||||||
|
53,9931 |
0,00686 |
4,7E-05 |
||||||
|
54,6805 |
0,31949 |
0,10207 |
||||||
|
55,1784 |
1,82157 |
3,31813 |
||||||
|
53,5887 |
-1,5887 |
2,52395 |
||||||
|
57,0558 |
2,94423 |
8,66847 |
||||||
|
= |
61,6085 |
e |
-1,6085 |
е2 |
2,58722 |
|||
|
63,6903 |
-1,6903 |
2,85696 |
||||||
|
63,5094 |
0,49061 |
0,2407 |
||||||
|
63,3813 |
1,61865 |
2,62003 |
||||||
|
65,5109 |
1,4891 |
2,21743 |
||||||
|
64,9954 |
2,00462 |
4,01849 |
||||||
|
65,2103 |
-3,2103 |
10,3061 |
||||||
|
64,5605 |
-1,5605 |
2,4353 |
||||||
|
66,1197 |
-0,1197 |
0,01434 |
||||||
|
66,9538 |
1,04619 |
1,09451 |
||||||
|
70,0535 |
-0,0535 |
0,00286 |
||||||
|
Сумма |
55,1371 |
Найдем стандартную ошибку остатков
(модели) по формуле:
Определим стандартные ошибки оценок
параметров модели:
где
– диагональные элементы матрицы
(Х’X)-1.
,
,
,
,
.
Для проверки
статистической надежности (значимости)
оценок параметров модели найдем величину
t-статистики, используя формулу:
.
,
,
,
,
.
Построение
эконометрической модели с использованием
стандартной программы
«ЛИНЕЙН»:
Встроенная статистическая функция
ЛИНЕЙН определяет коэффициенты
линейной регрессии:
=
b0 + b1X1 + b2X2
+ b3X3 + … + bрXр.
Порядок вычислений следующий:
-
введите
исходные данные; -
выделите
область пустых ячеек, состоящую из 5
строк и (р + 1) столбцов (где р – количество
независимых переменных) для вывода
результатов регрессионной статистики; -
активизируйте
Мастер функций любым из способов:
-
в главном
меню выберите Вставка/Функция; -
на панели
инструментов Стандартная щелкните
по кнопке Вставка функции fx
-
в раскрывшемся
окне выберите Категорию Статистические,
Функцию – ЛИНЕЙН. Щелкните по
кнопке ОК; -
заполните
аргументы функции (рис. 2):
-
Известные
значения У – диапазон, содержащий
данные, характеризующие результативный
признак; -
Известные значения Х – диапазон,
содержащий данные, описывающие все
независимые переменные; -
Константа – логическое значение,
указывающее на наличие или отсутствие
свободного члена в уравнении; если
Константа = 1, то свободный член
рассчитывается обычным образом, если
Константа = 0, то свободный член = 0; -
Статистика
– логическое значение, которое указывает,
выводить дополнительную информацию
по регрессионному анализу или нет. Если
Статистика = 1, то дополнительная
информация выводится, если Статистика
= 0, то выводятся только оценки параметров
уравнения. Щелкните по кнопке ОК;
-
в левой
верхней ячейке выделенной области
появится первый элемент итоговой
таблицы. Чтобы раскрыть всю таблицу,
нажмите на клавишу <F2>, а затем – на
комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
Рис. 6.2. Мастер функций. Работа с функцией
ЛИНЕЙН
Дополнительная регрессионная статистика
будет выводиться в следующем виде
(табл. 6.2):
Таблица
6.2
|
Значение bр |
Значение bр-1 |
. . . |
Значение b2 |
Значение b1 |
Значение b0 |
|
Стандартная ошибка оценки bр |
Стандартная ошибка оценки bр-1 |
. . . |
Стандартная ошибка оценки b2 |
Стандартная ошибка оцен-ки b1 |
Стандартная ошибка оцен-ки b0 |
|
Коэффициент детерминации R2 |
Стандартная ошибка модели (остатков) |
#Н/Д |
#Н/Д |
#Н/Д |
#Н/Д |
|
F-статистика |
Число степеней свободы n-(p+1) |
#Н/Д |
#Н/Д |
#Н/Д |
#Н/Д |
|
Регрессионная сумма квадратов |
Остаточная сумма квадратов |
#Н/Д |
#Н/Д |
#Н/Д |
#Н/Д |
Функция ЛИНЕЙН используется и для
расчета оценок параметров моделей,
которые с помощью преобразования могут
быть сведены к линейному виду. Например,
степенная функция
путем логарифмирования превращается
в линейную по параметрам функцию:
ln
=
lnb0 + b1 lnX1 + b2 ln
X2 + b3 lnX3 + b4 lnX4,
или
Z = A + b1z1
+ b2z2 + b3z3 + b4z4,
где Z =
ln
,
zj = lnXj ( j = 1,2,3,4); А =
lnb0, т.е. b0 = exp(A) = eA,
где е – основание натурального логарифма.
Из способа преобразования видно, что
для вычисления коэффициентов степенной
функции с помощью ЛИНЕЙН следует в
строки Известные значения У и
Известные значения Х окна
рассматриваемой функции вводить
логарифмы исходных значений У и Х.
Для
рассматриваемого примера (модель
производительности труда) результат
применения функции ЛИНЕЙН выглядит
следующим образом:
Линейная модель
-
-0,09758
-2,27216
-1,8406
0,33749665
56,91243
0,392655
1,899119
0,402268
0,10189618
7,568861
0,929654
1,917239
#Н/Д
#Н/Д
#Н/Д
49,55804
15
#Н/Д
#Н/Д
#Н/Д
728,6629
55,13708
#Н/Д
#Н/Д
#Н/Д
Степенная модель
0,054165
-0,12441
-0,19206
0,197562
3,625281
0,06836
0,126229
0,057959
0,12589694
0,627738
0,9251
0,033461
#Н/Д
#Н/Д
#Н/Д
46,31687
15
#Н/Д
#Н/Д
#Н/Д
0,207431
0,016794
#Н/Д
#Н/Д
#Н/Д
b0 = exp(3,625281) = e3,625281 = 37,5353.
Таким образом, получили следующие
уравнения:
= 56,912 + 0,338Х1 – 1,841Х2 – 2,271Х3
– 0,098Х4;
=
37,5353 X10,198 X2-0,192
X3-0,124 X40,0541.
Однако следует иметь в виду, что
статистические характеристики степенной
модели определены через логарифмы, и
поэтому прямо использовать их для
сравнения с соответствующими
характеристиками линейной модели
(например, с целью выбора лучшей модели)
нельзя. Необходимо привести их в
сопоставимый вид. Это касается всех
функций, при преобразовании которых к
линейному виду изменялась (преобразовывалась)
зависимая переменная Y.
С учетом
пересчета, который выполняется с
применением соответствующих формул
(3), (5), для степенной функции получили:
R2= 0,9242; Se = 1,9906.
Построение эконометрической модели
с помощью инструмента Анализа
Данных / Регрессия
Порядок действий:
-
проверьте
доступ к Пакету анализа. При его
отсутствии в главном меню выберите
Сервис/Надстройки. Установите
флажок Пакет анализа. Щелкните по
кнопке ОК; -
в главном
меню выберите Сервис/Анализ данных
/Регрессия. Щелкните по кнопке ОК; -
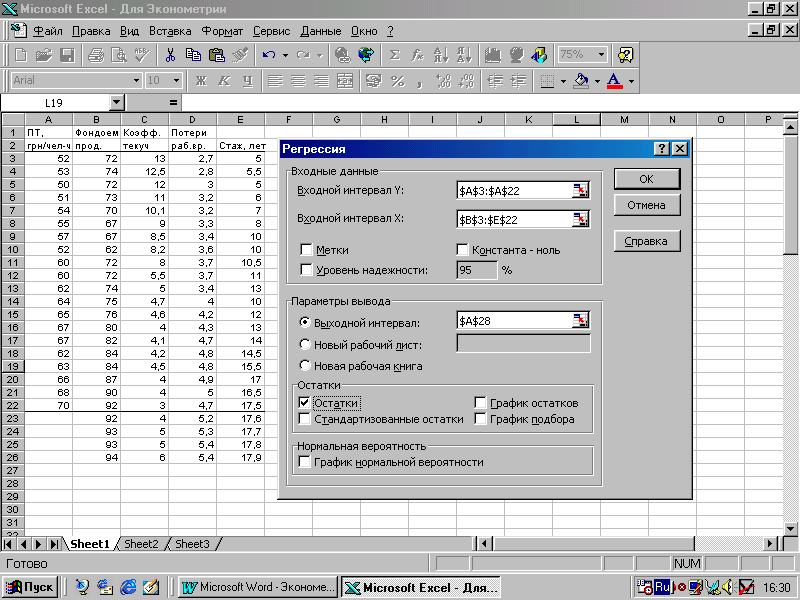
заполните
диалоговое окно ввода данных (фактических
значений всех показателей, если
рассчитываются оценки параметров
линейной модели, и логарифмы фактических
значений, если речь идет о степенной
функции) и параметров вывода (рис.3):
-
Входной
интервал У – диапазон, содержащий
данные результативного признака ; -
Входной
интервал Х – диапазон, содержащий
данные независимых переменных; -
Метки –
флажок, который указывает, содержит
ли первая строка название столбцов или
нет;
Рис.6.3
-
Константа
– ноль – флажок, указывающий на
наличие или отсутствие свободного
члена в уравнении; -
Выходной
интервал – достаточно указать левую
верхнюю ячейку будущего диапазона; -
Новый
рабочий лист – можно задать произвольное
имя нового листа.
Если необходимо получить информацию и
графики остатков, установите соответствующие
флажки в диалоговом окне. Щелкните по
кнопке ОК.
Результаты регрессионного анализа для
линейной модели ПТ (табл.63):
Таблица 3.
|
ВЫВОД ИТОГОВ |
||||||
|
Регрессионная |
||||||
|
Множественный |
0,96418574 |
|||||
|
R-квадрат |
0,92965414 |
|||||
|
Нормированный |
0,91089525 |
|||||
|
Стандартная |
1,91723904 |
|||||
|
Наблюдения |
20 |
|||||
|
Дисперсионный |
||||||
|
Источники |
df |
SS |
MS |
F |
Значимость |
|
|
Регрессия |
4 |
728,6629171 |
182,1657 |
49,558 |
1,8E-08 |
|
|
Остаток |
15 |
55,1370829 |
3,675806 |
|||
|
Итого |
19 |
783,8 |
||||
|
Оценки параметров модели и их |
||||||
|
Коэффициенты |
Станд.ошиб- ка |
t-стат. |
P-Значение. |
Нижн.95% |
Верх.95% |
|
|
Y-пересечение |
56,9124321 |
7,568860683 |
7,519287 |
1,8E-06 |
40,77978 |
73,04509 |
|
Переменная X 1 |
0,33749665 |
0,101896176 |
3,312162 |
0,00474 |
0,12031 |
0,554683 |
|
Переменная X 2 |
-1,8406011 |
0,402267501 |
-4,57557 |
0,00036 |
-2,69801 |
-0,98319 |
|
Переменная X 3 |
-2,2721556 |
1,899118933 |
-1,19643 |
0,2501 |
-6,32003 |
1,775723 |
|
Переменная X 4 |
-0,0975842 |
0,392655308 |
-0,24852 |
0,8071 |
-0,93451 |
0,739341 |
|
ВЫВОД ОСТАТКА |
||||||
|
Наблюдение |
Предсказан-ное |
Остатки |
||||
|
1 |
50,6616359 |
1,338364147 |
||||
|
2 |
51,9809221 |
1,019077932 |
||||
|
3 |
51,8205903 |
-1,820590278 |
||||
|
4 |
53,4466727 |
-2,446672748 |
||||
|
5 |
53,9931396 |
0,006860385 |
||||
|
6 |
54,6805111 |
0,319488857 |
||||
|
7 |
55,1784278 |
1,821572197 |
||||
|
8 |
53,5886938 |
-1,58869375 |
||||
|
9 |
57,0557729 |
2,944227141 |
||||
|
10 |
61,6084835 |
-1,608483531 |
||||
|
11 |
63,6902557 |
-1,690255734 |
||||
|
12 |
63,5093919 |
0,490608139 |
||||
|
13 |
63,3813492 |
1,618650827 |
||||
|
14 |
65,5108967 |
1,489103278 |
||||
|
15 |
64,9953835 |
2,004616485 |
||||
|
16 |
65,2103091 |
-3,210309068 |
||||
|
17 |
64,5605446 |
-1,560544572 |
||||
|
18 |
66,1197433 |
-0,119743273 |
||||
|
19 |
66,9538098 |
1,046190244 |
||||
|
20 |
70,0534667 |
-0,053466676 |
Результаты расчетов по этой программе
дают наибольшее количество характеристик
взаимосвязи. Рассмотрим эти характеристики
подробнее.
Регрессионная статистика
-
R = 0,9642 –
коэффициент корреляции; -
R2 =
0,9296 – не скорректированный коэффициент
детерминации (без учета числа степеней
свободы) оценивает долю вариации
результата за счет введенных в модель
факторов в общей вариации Y. Здесь эта
доля составляет 92,96% и указывает на
весьма высокую степень обусловленности
вариации результата вариацией факторов,
иными словами – на очень тесную связь
факторов и результата. -
=
0,9109 – скорректированный коэффициент
детерминации определяет тесноту связи
с учетом числа степеней свободы общей
и остаточной дисперсии. Он дает оценку,
не зависящую от количества независимых
переменных (факторов) модели, и поэтому
может сравниваться по разным моделям
с разным количеством факторов. Связь
между не скорректированным и
скорректированным коэффициентами
детерминации определяется по формуле:
.
Оба коэффициента
(R2,
)
указывают на весьма высокую (более 91%)
детерминированность результата Y в
модели факторами Х1, Х2, Х3,
Х4.
-
se =
1,9172 – стандартная ошибка остатков; -
n = 20 –
количество наблюдений.
Дисперсионный анализ включает пять
столбцов:
-
(df
) – степени свободы, т.е. число
свободы независимого варьирования
признака. Число степеней свободы связано
с числом единиц совокупности n и с
числом определяемых по ней оценок. Для
условий рассматриваемого примера число
степеней свободы:
для регрессии
р = 4; для остатка n – (р + 1) = 20 – (4 +
1) = 15; общее n – 1 = 20 – 1 = 19;
-
(SS)
– суммы квадратов
отклонений:
— регрессии (объясненная);
—
остаточная (не объясненная);
— общая (зависимой переменной);
-
(MS)
– дисперсия на одну
степень свободы:
— регрессий (объясненная);
— остатков (не объясненная);
-
(F) –
фактическое значение F-критерия:
=
49,558;
-
(Значимость
F) – уровень значимости F-критерия
= 1,8E-08
= 0,00000018.
Коэффициент детерминации R2 равен
0,9296, что указывает на сильную зависимость
между независимыми переменными и
производительностью труда. Можно
использовать F-статистику, чтобы
определить, является ли этот результат
(с таким высоким значение R2)
случайным. Величина
применяется для обозначения вероятности
ошибочного вывода о том, что имеется
сильная взаимозависимость.
Предположим, что на самом деле нет
взаимосвязи между переменными, а просто
были выбраны редкие 20 наблюдений, для
которых статистический анализ вывел
сильную взаимозависимость.
Оценку надежности уравнения
регрессии в целом и коэффициента
детерминации дает F-критерий Фишера.
Его расчетное (фактическое) значение
F = 49,558 сравнивается с табличным, которое
при уровне значимости
= 5% и при числе степеней свободы v1
= р = 4, v2 = n-(р+1) = 15 составляет 3,06.
Если фактическое значение превышает
табличное, то с вероятностью 0,95 гипотеза
о ненадежности уравнения отвергается
и утверждается статистическая значимость
модели и коэффициента детерминации.
Или, что то же самое, из таблицы
дисперсионного анализа следует, что
вероятность случайно получить такое
значение F-критерия (F = 49,558) составляет
Р = 0,00000018, что не превышает
допустимый уровень значимости 5% (величину
= 0,05). Следовательно,
полученное значение не случайно, оно
сформировалось под влиянием существенных
факторов, то есть, подтверждается
статистическая значимость всей модели
и коэффициента детерминации.
Оценки
параметров модели и их
значимость
Этот блок результатов содержит 9 столбцов.
Первый и второй – название и величина
оценок параметров модели:
Y
– пересечение – b0
= 56,9124321; переменная Х1
– b1
= 0,33749665;
переменная
Х2
– b2
= -1,8406011; переменная Х3
– b3
= -2,2721556;
переменная
Х4
– b4
= -0,0975842.
Таким образом,
получена модель:
= 56,912 + 0,338Х1 – 1,841Х2 – 2,272Х3
– 0,098Х4.
Величины bj (j = 1,2,3,4) показывают,
насколько изменится результат с
увеличением значения некоторого фактора
на единицу и при неизменной величине
остальных факторов. Так, увеличение Х1
(фондовооруженность труда) на 1
тыс.грн/чел. при прочих равных условиях
будет способствовать росту производительности
труда на 0,338 (тыс.грн./чел.-ч)/(тыс.грн/чел).
Если же Х2 (коэффициент текучести
кадров) увеличится на 1%, а другие факторы
не изменятся, то величина производительности
труда уменьшится на 1,841(тыс.грн./чел.-ч)/%.
Рост Х3 (потери рабочего времени)
на единицу (1%) также отрицательно
воздействует на производительность
труда: уменьшает ее на 2,271(тыс.грн./чел.-ч)/%
при прочих равных условиях.
Направленность воздействия первых трех
из рассмотренных факторов на
производительность труда не противоречит
экономическому смыслу, тогда как влияние
четвертого фактора – стаж работы –
вызывает сомнение: казалось бы, чем
дольше человек работает, тем лучше у
него навыки и тем выше производительность;
а b4
= -0,0975842 показывает, что увеличение стажа
на 1 год, хотя и незначительно, снижает
уровень производительности труда.
Сравнивать силу влияния отдельных
факторов на величину результирующего
показателя, сопоставляя коэффициенты,
не следует, так как эти коэффициенты
зависят от единиц измерения каждого
показателя. С целью выявления наиболее
влияющих показателей необходимо перейти
к уравнению в стандартизованном масштабе,
в котором в качестве единицы измерения
влияния всех факторов выступает среднее
квадратичное отклонение.
Третий
столбец содержит стандартные ошибки
оценок параметров модели:
=
7,568886;
= 0,101896;
=
0,402267;
= 1,899119;
=0,392655.
Они показывают,
какая доля значения данной характеристики
сформировалась под влиянием случайных
факторов. Эти величины (см.(7)) используются
для расчета t-критерия Стьюдента, значения
которого для различных оценок представлены
в четвертом столбце.
Четвертый
столбец – t-критерий:
t0 = 7,519287; t1 = 3,312162; t2
= -4,57557; t3 = -1,19643; t4 =
-0,24852.
Если значения t-критерия больше 2–3, то
можно сделать вывод о существенности
данного параметра, который формируется
под воздействием неслучайных величин.
Для более обоснованных выводов используем
результаты, находящиеся в пятом столбце.
Пятый столбец – уровень значимости
– показатель вероятности случайных
значений параметров регрессии:
0 = 0,0000018; 1
= 0,00474; 2 =
0,00036; 3 =
0,2501; 4 =
0,8071.
Если j меньше
принятого нами уровня (обычно 0,1; 0,05 или
0,01; это соответствует 10%, 5% или 1%
вероятности), то делают вывод о неслучайной
природе данного значения оценки, т.е. о
том, что оценки параметров достоверны
(статистически значимы). В противном
случае принимается гипотеза о случайной
природе значения коэффициента регрессии.
Поскольку 3
= 0,2501 и 4 =
0,8071 больше 0,005, то делаем вывод, что
соответствующие оценки b3
и b4
– недостоверны. Это позволяет
рассматривать факторы Х3 и Х4
как неинформативные и ставить под
сомнение необходимость включения их в
модель.
Возникшее противоречие (F-критерий
утверждает достоверность модели в
целом, а t-критерий – недостоверность
отдельных оценок) обычно определяется
существующей между независимыми
переменными мультиколлинеарностью.
Оставшиеся
четыре столбца с вероятностью 0,95
определяют верхние и нижние границы
оценок параметров модели, т.е. позволяют
осуществить интервальное оценивание
параметров. (Поскольку находящиеся в
этих столбцах величины повторяют друг
друга, то здесь приведены только 6 и 7
столбцы).
Интервальное
оценивание параметра модели j
выполняется следующим образом:
bj
t ,
или bj —
t
j
bj +
t .
Так, например, для 0
:
для
= 5% и 20 – 5 = 15 степеней свободы табличное
значение (двустороннее) t
= 2,13,
тогда
t =
7,568886 2,131 = 16,1293;
56,9124321 – 16,1293
0
56,9124321+ 16,1293; 40,78
0
73,04;
0,12031
1
0,554683;
-2,69801 2
-0,98319;
-6,32003
3
1,775723;
-0,93451 4
0,739341.
Таким
образом, с вероятностью 0,95, увеличение
фондовооруженности труда на одну единицу
обеспечит прирост производительности
труда не ниже 0,12031 и не выше 0,554683
тыс.грн./чел.-ч. Аналогично интерпретируются
остальные доверительные интервалы.
Доверительные
интервалы для третьего и четвертого
параметров включают нулевое значение,
что еще раз подтверждает сделанный
ранее вывод о недостоверности их оценок.
Вывод
остатков
В этом блоке
результатов приводятся расчетные
значения зависимой переменной и остатки,
которые определяются как разность между
фактическими значениями зависимой
переменной и расчетными.
Программа
Анализ данных/Регрессия позволяет
вывести и графики «подбора», т.е.
зависимости результативного признака
от каждого из факторов, а также графики
остатков для парных зависимостей. Для
вывода графиков следует в окне Регрессия
поставить соответствующие флажки.
|
|
Макеты страниц
После того как мы кратко обсудили наиболее важные проблемы, связанные с идентификацией и предпосылками построения эконометрических моделей, можно заняться вопросами оценивания параметров этих моделей. Разработан ряд методов оценивания. Их выбор определяется в основном видом модели и возможностями идентификации. Далее мы рассмотрим различные методы оценивания, не вдаваясь в особые подробности и не приводя доказательств, а делая основной упор на возможности их применения.
I. Метод наименьших квадратов.
1. Применение к модели из взаимозависимых переменных. Для множественной регрессии, о которой говорилось в разделе 2.7, предполагалась независимость между объясняющими переменными и возмущениями (см. предпосылку 5 в разделе 2.9). Эта предпосылка означала также отсутствие многосторонней связи (как функциональной, так и стохастической) между зависимой и объясняющими переменными.
В различных уравнениях эконометрической модели со взаимозависимыми переменными (см. формулу 







Если метод наименьших квадратов применяется к первому уравнению (12.2), то оценка его параметров производится так же, как в случае множественной регрессии (см. раздел 2.7). При этом минимизируется в направлении к 




Несмотря на это противоречие, практика показывает, что при оценивании эконометрической модели со взаимозависимыми переменными методом наименьших квадратов во многих случаях достигается удовлетворительная точность. Кроме того, метод обладает рядом свойств (робастность относительно мультиколлинеарности и ошибок спецификации, простота вычислительной процедуры, возможность обработки небольшого числа наблюдений), которые оказываются полезными при оценивании эконометрической модели.
Продемонстрируем применение метода наименьших квадратов к модели со взаимозависимыми переменными на формальном числовом примере 






Таблица 20. Отклонения значений переменных модели (12.7) от их средних

Оценки параметров регрессии получим в соответствии с (2.64):

Произведем следующие операции:

Подставив в 

Аналогично представим второе уравнение (12.7) в виде множественной регрессии:

Выполнив соответствующие вычисления, получим МНК-оценку уравнения (12.31):

Оценки параметров указывают воздействия объясняющих переменных на 


2. Применение к рекурсивным моделям. Будем исходить из рекурсивной модели вида (12.17). Применение метода наименьших квадратов дает состоятельные оценки, если соблюдается определенная последовательность вычислительной процедуры. Вначале следует оценить первое уравнение, в правой части которого содержатся только предопределенные переменные. Если установлены параметры первого уравния, то из значений переменной 





Если поочередность в оценивании параметров рекурсивной модели Не соблюдается, то обычный метод наименьших квадратов дает несостоятельные оценки. Таким образом, если для оценки произвольно отбирается любое уравнение, то это приводит к тем же результатам, что и при модели со взаимозависимыми переменными.
3. Применение к системе независимых уравнений. Поскольку в Этих моделях не возникают многосторонние зависимости между эндогенными переменными, каждое уравнение можно отдельно оценивать с Помощью метода наименьших квадратов, как в случае множественной регрессии. Если соблюдаются предпосылки, введенные в разделе 2.9, то оценки параметров будут обладать свойствами, указанными там же.
II. Косвенный метод наименьших квадратов.
Метод наименьших квадратов может применяться к системе одновременных уравнений, которые полностью или только точно идентифицируемы. Конечно, этот метод не может непосредственно применяться при оценивании параметров структурных уравнений, так как они не учитывают одновременных соотношений между совместно зависимыми переменными. Модель вначале представляется в приведенной форме. Это возможно при предположении, что модель полная. Применяя метод наименьших квадратов к каждому полученному уравнению, оценивают все параметры системы в приведенной форме. Так как по предположению все структурные уравнения точно идентифицируемы, на следующем этапе однозначно определяются структурные параметры по параметрам приведенной формы. Итак, структурные параметры оцениваются косвенно через параметры приведенной формы. Поэтому мы говорим о косвенном методе наименьших квадратов. Если соблюдаются предпосылки из раздела 2.9, то оценки, полученные с помощью косвенного метода наименьших квадратов, состоятельны. Метод неприменим, если модель состоит из сверхидентифицированных структурных уравнений, так как тогда структурные параметры не могут быть вычислены однозначно по параметрам приведенной формы. Это большой недостаток косвенного метода наименьших квадратов, так как практически во всех эконометрических моделях содержатся сверх-идентифицированные структурные уравнения.
Мы покажем применение косвенного метода наименьших квадратов, используя данные табл. 20. Так как значения переменных приведены в виде отклонений от их средних, структурная форма модели (12.7) упрощается:

Приведенная форма этой модели имеет вид:

Каждое уравнение приведенной формы (12.33) необходимо оценить отдельно по методу наименьших квадратов в соответствии с (2.64). Выполним следующие операции с матрицами и векторами:

В итоге получим оценки уравнений в приведенной форме (12.33):

Так как оба структурных уравнения точно идентифицируемы (см. раздел 12.4), параметры структурной формы однозначно определяются по параметрам приведенной формы на основе системы уравнений (см. (12.11)):

В результате получим оценки:

Таким образом, структурные уравнения (12.32) имеют вид:

По этим уравнениям мы можем сделать следующие выводы:
1. Параметры приведенной формы (12.33) отражают общее воздействие предопределенных переменных на совместно зависимые переменные 
а) Параметр 
В — непосредственное воздействие, 

Параметр 

б) Благодаря существующим одновременным соотношениям между 




Воздействие денежных доходов населения 



Эти воздействия нельзя обнаружить по структурной форме модели (12.32).
2. Параметры структурной формы (12.32) отражают непосредственное воздействие переменных (см. раздел 12.3). При сравнении 




3. При сравнении результатов применения обычного и косвенного методов наименьших квадратов к структурным уравнениям (12.30) и (12.31) обнаруживается четкое различие по всем параметрам:

III. Двухшаговый метод наименьших квадратов.
В связи с тем что обычный метод наименьших квадратов не всегда дает удовлетворительные оценки моделей из систем одновременных уравнений, были разработаны методы оценивания, которые учитывают многосторонние связи совместно зависимых переменных. Мы остановимся лишь на наиболее часто применяемом двухшаговом методе наименьших квадратов.
Двухшаговый метод наименьших квадратов является обобщением метода наименьших квадратов. Он представляет собой обычный метод наименьших квадратов для оценивания параметров структурного уравнения в два этапа. Вначале мы изложим основную идею метода, а затем проиллюстрируем применение этого метода на примере. Отправной точкой является структурное уравнение модели (12.4), которое запишем в следующем виде:

где 


кроме того, в 








Y в правой части (12.34) матрицей оценок 
Итак, первый этап применения двухшагового метода наименьших квадратов заключается в определении матрицы значений регрессий 


Однако для построения приведенной формы (12.35) должны быть заданы все предопределенные переменные модели (см. раздел 12.3).
Матрица значений регрессий Y получается из (12.35) путем известного преобразования:

Значения регрессий матрицы Y независимы от возмущающих переменных приведенной и структурной форм, так как они являются линейными функциями только от предопределенных переменных. Таким образом, отдельные уравнения (12.36) представляют собой множественную регрессию, для которой выполняется предпосылка 5 из раздела 2.9.
Метод наименьших квадратов может применяться для оценивания параметров матрицы С. В соответствии с (2.64) имеем:

Подставляя (12.37) в (12.36), получим матрицу значений регрессий:

Таким образом, задача, поставленная на первом этапе применения метода, выполнена.
На втором этапе матрицу Y в (12.34) заменяют матрицей Y.
При этом следует учитывать, что по 

или, учитывая, что

В полученном уравнении в правой части находятся только предопреде ленные переменные, так как матрица 



Двукратное (в два этапа) применение метода наименьших квадратов можно представить в виде одной формулы. Для этого образуем систему нормальных уравнений для уравнения регрессии (12.40). Если мы положим, что

то (12.40) можно представить в виде:

Тогда в соответствии с (2.63) из раздела 2.7 мы получим систему нормальных уравнений:

Подставив (12.41) в (12.43), приходим к выражению:

Используя (12.38) для 

Формула (12.45) представляет собой результат применения двухшагового метода наименьших квадратов к 
Легко видеть, что матрица значений регрессий 
этапе применения метода, не содержится в (12.45) в явном виде. В нее входят только матрицы и векторы наблюдений. Преимущество двухшагового метода заключается, во-первых, в том, что он применим к сверхидентифицированным уравнениям, и, во-вторых, в том, что нерассмотренные нами структурные уравнения модели не должны быть точно специфицированы. Разумеется, должны быть известны все предопределенные переменные модели и указаны результаты наблюдений над ними. Недостаток метода состоит в том, что в оценках содержатся не остатки 


Пример
Воспользуемся снова примером-моделью (12.32) и оценим первое уравнение 















Для оценок параметров 

По данным табл. 20 получим промежуточные результаты:

Подставив в (12.47) эти промежуточные результаты, найдем численные значения искомых параметров:

Таким образом, оценка первого уравнения (12.32) по двухшаговому методу наименьших квадратов имеет вид:

Сравнивая последнее выражение с уравнением, полученным косвенным методом наименьших квадратов (см. с. 263), замечаем, что они совпадают. Это объясняется тем, что первое уравнение модели (12.32) точно идентифицируемо. В случае точно идентифицируемых уравнений модели оценки косвенного и двухшагового методов наименьших квадратов совпадают.
Аналогичным способом можно оценить второе уравнение модели (12.32). Получим результат, идентичный оценке уравнения по косвенному методу наименьших квадратов, так как второе уравнение модели также точно идентифицируемо.
Разработан также ряд других методов оценивания систем одновременных уравнений, среди которых прежде всего следует назвать трехшаговый метод наименьших квадратов, метод максимального правдоподобия с ограниченной и с полной информацией, метод оценок класса 
Оглавление
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ
- 1. ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЕ ОСНОВЫ РЕГРЕССИОННОГО И КОРРЕЛЯЦИОННОГО АНАЛИЗА
- 1.2. ПОНЯТИЕ РЕГРЕССИИ
- 1.3. ПОНЯТИЕ КОРРЕЛЯЦИИ
- 1.4. ЗАДАЧИ КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО АНАЛИЗА
- 1.5. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ, ВЫБОРКА, СРЕДНЕЕ, ВЫБОРОЧНАЯ ДИСПЕРСИЯ, КОВАРИАЦИЯ. СВОЙСТВА ОЦЕНОК
- 1.6. РАСПРЕДЕЛЕНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ДИСПЕРСИЯ
- 1.7. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, «хи-квадрат»-РАСПРЕДЕЛЕНИЕ, t-РАСПРЕДЕЛЕНИЕ, F-РАСПРЕДЕЛЕНИЕ
- 1.8. ИСТОРИЯ РАЗВИТИЯ КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО АНАЛИЗА
- 2. ЛИНЕЙНАЯ РЕГРЕССИЯ
- 2.1. ДИАГРАММА РАССЕЯНИЯ
- 2.2. МЕТОД ЧАСТНЫХ СРЕДНИХ
- 2.3. ПРОСТАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ
- 2.4. ПОСТРОЕНИЕ РЕГРЕССИОННОЙ ПРЯМОЙ С ПОМОЩЬЮ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ (по несгруппированным данным)
- 2.5. СОПРЯЖЕННЫЕ РЕГРЕССИОННЫЕ ПРЯМЫЕ
- 2.6. ПОСТРОЕНИЕ РЕГРЕССИОННОЙ ПРЯМОЙ ПО СГРУППИРОВАННЫМ ДАННЫМ
- 2.7. ЛИНЕЙНАЯ МНОЖЕСТВЕННАЯ РЕГРЕССИЯ
- 2.8. ЛИНЕЙНАЯ ЧАСТНАЯ РЕГРЕССИЯ
- 2.9. ИСХОДНЫЕ ПРЕДПОСЫЛКИ РЕГРЕССИОННОГО АНАЛИЗА И СВОЙСТВА ОЦЕНОК
- 2.10. ПОСЛЕДОВАТЕЛЬНОСТЬ ПРОВЕДЕНИЯ РЕГРЕССИОННОГО АНАЛИЗА И ЕГО ПРИМЕНЕНИЕ В ЭКОНОМИКЕ
- 3. ОЦЕНКА ТОЧНОСТИ РЕГРЕССИОННОГО АНАЛИЗА
- 3.2. КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ ДЛЯ ПРОСТОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
- 3.3. КОЭФФИЦИЕНТ МНОЖЕСТВЕННОЙ ДЕТЕРМИНАЦИИ
- 3.4. КОЭФФИЦИЕНТ ЧАСТНОЙ ДЕТЕРМИНАЦИИ
- 3.5. КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ МЕЖДУ ОБЪЯСНЯЮЩИМИ ПЕРЕМЕННЫМИ
- 3.6. СТАНДАРТНЫЕ ОШИБКИ ОЦЕНОК
- 4. ЛИНЕЙНАЯ КОРРЕЛЯЦИЯ
- 4.1. ПРОСТАЯ ЛИНЕЙНАЯ КОРРЕЛЯЦИЯ ПРИ НЕСГРУППИРОВАННЫХ ДАННЫХ
- 4.2. ПРОСТАЯ ЛИНЕЙНАЯ КОРРЕЛЯЦИЯ ПРИ СГРУППИРОВАННЫХ ДАННЫХ
- 4.3. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТАМИ КОРРЕЛЯЦИИ, РЕГРЕССИИ И ДЕТЕРМИНАЦИИ
- 4.4. ЛИНЕЙНАЯ МНОЖЕСТВЕННАЯ КОРРЕЛЯЦИЯ
- 4.5. ЧАСТНАЯ КОРРЕЛЯЦИЯ
- 4.6. СООТНОШЕНИЯ МЕЖДУ КОЭФФИЦИЕНТАМИ МНОЖЕСТВЕННОЙ И ЧАСТНОЙ КОРРЕЛЯЦИИ, РЕГРЕССИИ И ДЕТЕРМИНАЦИИ
- 4.7. ВЛИЯНИЕ НЕУЧТЕННЫХ ФАКТОРОВ НА КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
- 5. НЕЛИНЕЙНАЯ РЕГРЕССИЯ
- 5.1. ПРОСТАЯ НЕЛИНЕЙНАЯ РЕГРЕССИЯ ПРИ НЕСГРУППИРОВАННЫХ ДАННЫХ
- 5.2. ПРОСТАЯ НЕЛИНЕЙНАЯ РЕГРЕССИЯ ПРИ СГРУППИРОВАННЫХ ДАННЫХ
- 5.3. МНОЖЕСТВЕННАЯ НЕЛИНЕЙНАЯ РЕГРЕССИЯ
- 6. НЕЛИНЕЙНАЯ КОРРЕЛЯЦИЯ
- 6.1. ПРОСТАЯ НЕЛИНЕЙНАЯ КОРРЕЛЯЦИЯ ПРИ НЕСГРУППИРОВАННЫХ ДАННЫХ
- 6.2. ПРОСТАЯ НЕЛИНЕЙНАЯ КОРРЕЛЯЦИЯ ПРИ СГРУППИРОВАННЫХ ДАННЫХ
- 6.3. МНОЖЕСТВЕННАЯ НЕЛИНЕЙНАЯ КОРРЕЛЯЦИЯ
- 7. ЧАСТНЫЕ ВОПРОСЫ КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО АНАЛИЗА
- 7.1. КОЭФФИЦИЕНТ РАНГОВОЙ КОРРЕЛЯЦИИ СПИРМЭНА
- 7.2. КОЭФФИЦИЕНТ РАНГОВОЙ КОРРЕЛЯЦИИ КЕНДЭЛА
- 7.3. ИНДЕКС ФЕХНЕРА
- 7.4. КОРРЕЛЯЦИОННОЕ ОТНОШЕНИЕ
- 7.5. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМ КОЭФФИЦИЕНТОМ КОРРЕЛЯЦИИ, ИНДЕКСОМ КОРРЕЛЯЦИИ И КОРРЕЛЯЦИОННЫМ ОТНОШЕНИЕМ
- 7.6. УПРОЩЕННЫЕ СПОСОБЫ ОЦЕНИВАНИЯ ПАРАМЕТРОВ РЕГРЕССИИ И КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
- 7.7. КОРРЕЛЯЦИЯ И РЕГРЕССИЯ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН
- 7.8. КОЭФФИЦИЕНТ КОНКОРДАЦИИ
- 8. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ПРОВЕРКА ЗНАЧИМОСТИ
- 8.1. РАСПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ РЕГРЕССИИ И КОРРЕЛЯЦИИ
- 8.2. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ ПАРАМЕТРОВ РЕГРЕССИИ И ГЕНЕРАЛЬНОГО КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
- 8.3. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ УСЛОВНОГО МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
- 8.4. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ ОТДЕЛЬНЫХ ЗНАЧЕНИЙ ЗАВИСИМОЙ ПЕРЕМЕННОЙ у
- 8.5. ПРОВЕРКА ЗНАЧИМОСТИ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
- 8.6. ПРОВЕРКА ЗНАЧИМОСТИ КОЭФФИЦИЕНТА ДЕТЕРМИНАЦИИ
- 8.7. ПРОВЕРКА ЗНАЧИМОСТИ ОЦЕНОК ПАРАМЕТРОВ РЕГРЕССИИ
- 8.8. ПРОВЕРКА ЛИНЕЙНОСТИ РЕГРЕССИИ
- 9. МУЛЬТИКОЛЛИНЕАРНОСТЬ
- 10. ТИПИЧНЫЙ ПРИМЕР
- 11. РЕГРЕССИЯ И КОРРЕЛЯЦИЯ ВРЕМЕННЫХ РЯДОВ
- 11.1. МОДЕЛЬ РЕГРЕССИИ ВРЕМЕННОГО РЯДА
- 11.2. АВТОКОРРЕЛЯЦИЯ ПЕРЕМЕННЫХ
- 11.3. АВТОКОРРЕЛЯЦИЯ ВОЗМУЩЕНИЙ
- 12. ОДНОВРЕМЕННЫЕ УРАВНЕНИЯ В РЕГРЕССИОННОМ АНАЛИЗЕ
- 12.2. ПЕРЕМЕННЫЕ В ЭКОНОМЕТРИЧЕСКОЙ МОДЕЛИ
- 12.3. ВИДЫ ЭКОНОМЕТРИЧЕСКИХ МОДЕЛЕЙ
- 12.4. ПРОБЛЕМА ИДЕНТИФИКАЦИИ
- 12.5. ПРЕДПОСЫЛКИ ПОСТРОЕНИЯ ЭКОНОМЕТРИЧЕСКИХ МОДЕЛЕЙ
- 12.6. МЕТОДЫ ОЦЕНИВАНИЯ ЭКОНОМЕТРИЧЕСКИХ МОДЕЛЕЙ
- 13. АССОЦИАЦИЯ И КОНТИНГЕНЦИЯ
- 13.1. КОЭФФИЦИЕНТ АССОЦИАЦИИ
- 13.2. КОЭФФИЦИЕНТ КОНТИНГЕНЦИИ (СОПРЯЖЕННОСТИ)
- 13.3. ДВУХСТРОЧЕЧНАЯ КОРРЕЛЯЦИЯ
- ПРИЛОЖЕНИЕ
- ЛИТЕРАТУРА
К ВОПРОСУ ОБ ОЦЕНКЕ КАЧЕСТВА ЭКОНОМЕТРИЧЕСКИХ МОДЕЛЕЙ
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Орлова И.В.
1
1 ФГОБУ ВО «Финансовый университет при Правительстве РФ»
В работе рассматриваются вопросы оценки качества моделей, выбора оптимальных моделей. Анализируются подходы к проверке адекватности регрессионных моделей, предназначенных для прогнозирования. Рассматриваются возможности Excel для проверки спецификации модели с помощью метода Салкевера при моделировании зависимости количества безработных в России от заявленной потребности в работниках по данным за период с 2001 по 2020 г. Для оценки адекватности модели и выбора лучшей модели используется перекрестная проверка с последовательным исключением одного наблюдения. При этом исследуются два способа реализации метода перекрестной проверки. В первом случае критерий перекрестной проверки CV может быть механически вычислен путем выполнения n регрессий, в которых каждый раз пропускается одно наблюдение, а все остальные используются для прогнозирования его значения. Другой способ, менее трудоемкий, связан с использованием так называемой матрицы шляп для вычисления критерия перекрестной проверки CV. Этот метод включен в свободно распространяемую программу Gretl. Применение метода перекрёстной проверки продемонстрировано на примере моделирования зависимости рождаемости (число родившихся на 1000 чел.) от индекса потребительских цен на товары и услуги 2020 г. на данных 16 регионов РФ за 2020 г. В заключении приведены выводы относительно применения инструментария для оценки адекватности моделей.
регрессия
адекватность модели
перекрестная проверка
программа Gretl
1. Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование: учебное пособие. 3-e изд., перераб. и доп. М.: Вузовский учебник: Инфра-М, 2019. 389 с.
2. Демидова О.А., Малахов Д.И. Эконометрика: учебник и практикум для вузов. М.: Юрайт, 2022. 334 с.
3. Грин У.Г. Эконометрический анализ. Кн. 1 / пер. с англ.; под науч. ред. С.С. Синельникова, М.Ю. Турунцевой. М.: Издательский дом «Дело» РАНХиГС, 2016. 760 с.
4. Кеннеди П. Путеводитель по эконометрике / пер. с англ.; под науч. ред. В.П. Носко. М.: Издательский дом «Дело» РАНХиГС, 2016. 528 с.
5. Айвазян С.А., Фантаццини Д. Эконометрика – 2: продвинутый курс с приложениями в финансах: учебник. М.: Магистр, НИЦ ИНФРА-М, 2018. 944 с.
6. Бабешко Л.О., Бич М.Г., Орлова И.В. Эконометрика и эконометрическое моделирование. 2-е изд., испр. и доп. М.: ООО «Научно-издательский центр ИНФРА-М», 2021. 385 с. DOI: 10.12737/1141216.
7. Единый архив экономических и социологических данных. URL: http://sophist.hse.ruhttps://urait.ru/bcode/ 380873 (дата обращения: 05.02.2022).
8. Бабешко Л.О. Эконометрическое моделирование спроса на электроэнергию: проверка адекватности // Фундаментальные исследования. 2018. № 12–1. С. 47–52.
9. Salkever, David S. The use of dummy variables to compute predictions, prediction errors, and confidence intervals. Journal of Econometrics, Elsevie. 1976. Vol. 4 (4). P. 393–397.
10. Kurt S. Riedel. A Sherman – Morrison – Woodbury Identity for Rank Augmenting Matrices with Application to Centering”, SIAM Journal on Matrix Analysis and Applications. 1992. No. 13. P. 659-662. DOI: 10.1137/0613040 preprint MR1152773.
11. Естественное движение населения в разрезе субъектов Российской Федерации за январь – февраль 2020 года. URL: https://www.gks.ru/free_doc/2019/demo/edn12-19.htm (дата обращения: 05.02.2022).
12. Федеральная служба государственной статистики. URL: https://www.gks.ru/dbscripts/cbsd_internal/DBInet.cgi?pl=1902001(дата обращения: 05.02.2022).
При эконометрическом моделировании весьма важными являются вопросы оценки качества построенных моделей, выбора оптимальных моделей. Существуют различные подходы к решению этих вопросов. Будем рассматривать проблемы, связанные только с оценкой качества линейных регрессионных моделей. Пусть спецификация регрессионной модели имеет вид
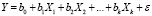
где Y – эндогенная (зависимая) переменная, k – количество регрессоров, ε – случайная составляющая эндогенной переменной (случайное возмущение), которая не может быть объяснена значениями объясняющих переменных 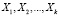
Обычно считают, что «модель считается хорошей со статистической точки зрения, если она адекватна и достаточно точна» [1, с. 310]. Если вопросы оценки точности модели, как правило, не вызывают разночтений, то по оценке адекватности не существует единого мнения. Существует распространённое мнение, что проверка адекватности модели означает проверку гипотезы о равенстве нулю всех коэффициентов регрессии (Н0: b1 = b2 =…bk = 0), т.е. проверяется значимость модели регрессии в целом [2, 3]. Если основная гипотеза Н0 принимается, то модель считается неадекватной. Если же основная гипотеза отклоняется, то модель можно считать адекватной только после проверки выполнения предпосылок МНК относительно остатков: равенство нулю математического ожидания, гомоскедастичность, случайность и независимость, соответствие нормальному закону распределения. Если эти предпосылки не выполняются, то модель признается неадекватной.
Другое представление об адекватности модели заключается в проверке качества прогнозов, получаемых на базе обучающей выборки путем сравнения этих прогнозов с реальными значениями из контролирующей выборки [4–6]. При этом следует иметь в виду, что такая проверка осуществляется только при выполнении предпосылок МНК.
Подход, когда модель обучается на одном образце данных («обучающем наборе») и оценивается вне выборки на так называемом «тестовом наборе», известен как перекрестная проверка (cross-validation, сокращенно CV).
Целью работы является анализ разных подходов к оценке адекватности и выбору линейных регрессионных моделей, предназначенных для прогнозирования, и исследование инструментария для проведения перекрестной проверки моделей, построенных на пространственных наблюдениях.
Материалы и методы исследования
Использование интервальных прогнозов для проверки спецификации модели. Если значения эндогенной переменной из контролирующей выборки попадают в прогнозные интервалы, то спецификация модели подтверждается.
Исследуем зависимость количества безработных в среднем в млн чел в России от заявленной потребности в работниках (в тыс. чел.) [7].
По данным (табл. 1) за период с 2001 по 2019 г. (обучающая выборка) построена регрессионная модель зависимости количества безработных в среднем (Y) от заявленной потребности в работниках – X: 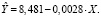
Для оценки прогноза 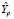
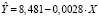
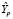
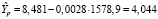
Ошибка прогноза sp, необходимая для вычисления доверительного интервала 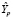
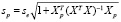
где 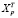
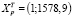
НГр = 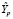
ВГр = 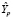
Так как значение эндогенной переменной из контролирующей выборки Y(2020), равное 4,3, попадает в 95%-ый доверительный интервал (3,07 5,02), то модель признаётся адекватной.
Таблица 1
Исходные данные
|
T |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
|
X |
971 |
958,8 |
941,8 |
923,5 |
915 |
1006,9 |
1206,5 |
|
Y |
6,4 |
5,7 |
6,1 |
6 |
5,6 |
5,3 |
4,6 |
|
T |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
2014 |
|
X |
1351,9 |
1015,8 |
1109,7 |
1341,6 |
1536,4 |
1713,5 |
1856,4 |
|
Y |
4,8 |
6,3 |
5,6 |
5 |
4,2 |
4,1 |
3,9 |
|
T |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
|
|
X |
1292,5 |
1291,5 |
1487,2 |
1593,7 |
1626,4 |
1578,9 |
|
|
Y |
4,2 |
4,3 |
4 |
3,7 |
3,5 |
4,3 |
Рис. 1. Вычисление ошибки прогноза sp в Excel
Рис. 2. Оценка параметров модели с фиктивной переменной: 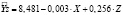
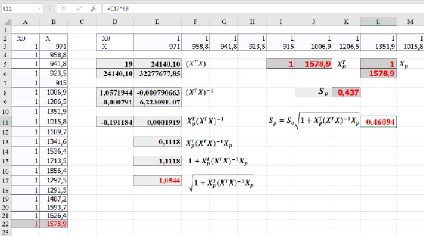
Для вычисления стандартных ошибок прогнозов воспользуемся методом Салкевера [8, 9]. В этом методе для оценки стандартной ошибки прогноза на момент t = n + 1 в матрицу регрессоров добавляется строка Xn+1 и столбец фиктивных переменных Z, содержащий нули для всех наблюдений, кроме (n + 1)-го, в котором фиктивная переменная равна 1. На рис. 2 приведена таблица исходных данных и результаты оценки параметров модели с фиктивной переменной. Стандартная ошибка оценки параметра при фиктивной переменной равна стандартной ошибке прогноза. В нашем случае она равна sp = 0,461.
Использование перекрестной проверки для оценки адекватности модели и выбора лучшей модели
Рассмотрим применение одного из самых простых методов перекрестной проверки LOOCV (Leave One Out Cross Validation) – перекрестная проверка с исключением одного наблюдения. В LOOCV каждое наблюдение рассматривается как контролирующий набор, а остальные (n–1) наблюдений – как обучающий набор. Подгонка модели и прогнозирование повторяется n раз. Критерий перекрестной проверки CV может быть вычислен путем выполнения n регрессий, в которых каждый раз пропускается одно наблюдение, а все остальные используются для прогнозирования его значения. Сумма n квадратов ошибок прогноза – это и есть CV – та статистика, которая используется для оценки качества модели. Однако в вычислении n регрессий нет необходимости. Эту статистику можно найти иначе, воспользовавшись так называемой матрицей шляп H от английского слова hat. Матрица H равна
H = X (XT X)–1 XT . (2)
Покажем, как ошибку прогноза i-го наблюдения зависимой переменной по уравнению регрессии без i-го наблюдения можно вычислить, зная лишь ошибку прогноза этого наблюдения по уравнению регрессии с полным набором наблюдений и диагональные элементы матрицы H.
Пусть X, Y – матрица регрессоров и вектор значений зависимой переменной, X[i], Y[i] получены из X, Y после удаления из них i-го наблюдения, 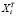
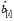
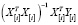
Тогда ошибка прогноза i-го наблюдения, вычисленная по регрессии без i-го наблюдения, равна 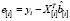
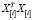
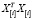
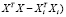
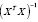
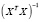
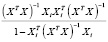
Но произведение 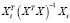
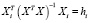
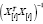
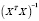
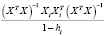
Учитывая также, что 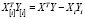
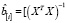
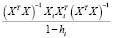
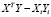
= 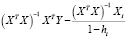
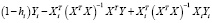
= 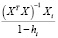
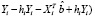
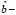
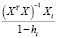
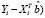
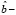
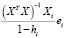
где 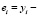
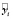
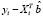
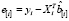
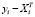
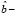
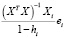
= 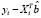
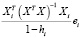
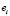
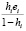
Таким образом, получили, что ошибка прогноза i-го наблюдения по регрессии без i-го наблюдения e[i] равна e[i] = ei / (1 – hi). Полученная формула существенно упрощает процедуру вычисления критерия перекрестной проверки CV,
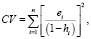
где hi – диагональный элемент матрицы H.
Для пояснения смысла матрицы Н запишем предсказываемые моделью значения эндогенной переменной Y в виде
или, в координатной форме,
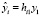
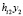
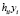
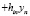
Диагональные элементы матрицы H изменяются от нуля до единицы и в сумме равны числу параметров модели m. Показатель hii (диагональный элемент hii матрицы H отражает расстояние между точкой с координатами Xi и центром данных. Если значение hi близко к нулю, то это означает, что i-я точка Xi располагается недалеко от центра, если hi близка к единице, то i-я точка является удаленной. Считается, что наблюдение оказывает существенное влияние на параметры модели, если 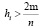
Результаты исследования и их обсуждение
Применим метод LOOCV для выбора лучшей модели при моделировании зависимости рождаемости (число родившихся на 1000 чел.) [11] от индекса цен (Индексы потребительских цен на товары и услуги 2020 г.) по данным 16 регионов РФ [12].
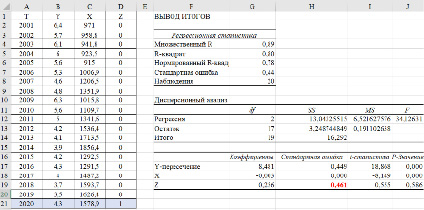
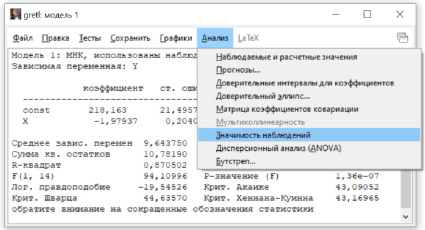
Построенная по всем наблюдениям (табл. 2) модель имеет вид:
Из приведенного протокола (рис. 3) можно сделать вывод, что параметры модели значимы, коэффициент детерминации достаточно высокий 0,87. Для выбранных регионов увеличение индекса цен на один процент приводит в среднем к уменьшению числа родившихся примерно на два человека.
Для оценки качества этой модели построено 16 уравнений регрессии, в каждом из которых последовательно удалялось по одному наблюдению. Оценки параметров этих моделей, прогноз на 16-е наблюдение, ошибка прогноза и квадрат ошибки приведены в табл. 2. Сумма квадратов ошибок – это и есть CV – равна 14,824.
Другой подход к вычислению статистики CV с помощью Н матрицы приведен в табл. 3 и 4. В табл. 3 приведен фрагмент матрицы Н, вычисленной с помощью матричных преобразований по формуле (2).
Таблица 2
Исходные данные и результаты перекрестной проверки по 16 моделям
|
№ |
Регион |
X |
Y |
b1 |
b0 |
Y^ |
e |
e^2 |
|
|
1 |
Тульская область |
106,1 |
7,4 |
-1,946 |
214,656 |
8,229 |
-0,8 |
0,687 |
|
|
2 |
Пензенская область |
106,12 |
7,4 |
-1,946 |
214,745 |
8,187 |
-0,8 |
0,619 |
|
|
3 |
Ивановская область |
105,79 |
7,6 |
-1,949 |
215,064 |
8,857 |
-1,3 |
1,581 |
|
|
4 |
Саратовская область |
106,69 |
7,7 |
-2,041 |
224,634 |
6,847 |
0,9 |
0,727 |
|
|
5 |
Рязанская область |
106,01 |
7,9 |
-1,962 |
216,414 |
8,371 |
-0,5 |
0,221 |
|
|
6 |
Новгородская область |
105,57 |
8,2 |
-1,966 |
216,866 |
9,271 |
-1,1 |
1,146 |
|
|
7 |
Воронежская область |
106,93 |
8,2 |
-2,160 |
237,051 |
6,091 |
2,1 |
4,447 |
|
|
8 |
Курская область |
105,77 |
8,3 |
-1,967 |
216,884 |
8,844 |
-0,5 |
0,296 |
|
|
9 |
Липецкая область |
106,14 |
8,3 |
-1,990 |
219,285 |
8,048 |
0,3 |
0,063 |
|
|
10 |
Республика Карелия |
106,06 |
8,5 |
-1,991 |
219,347 |
8,204 |
0,3 |
0,087 |
|
|
11 |
Республика Татарстан |
104,78 |
10,6 |
-1,985 |
218,751 |
10,779 |
-0,2 |
0,032 |
|
|
12 |
Ханты-Мансийский автономный округ |
103,89 |
12,3 |
-2,001 |
220,460 |
12,575 |
-0,3 |
0,076 |
|
|
13 |
Тюменская область |
104,22 |
12,3 |
-1,949 |
214,981 |
11,809 |
0,5 |
0,241 |
|
|
14 |
Ямало-Ненецкий автономный округ |
103,36 |
12,9 |
-2,079 |
228,768 |
13,832 |
-0,9 |
0,869 |
|
|
15 |
Республика Алтай |
104,16 |
13,3 |
-1,882 |
207,809 |
11,781 |
1,5 |
2,306 |
|
|
16 |
Республика Саха (Якутия) |
103,95 |
13,4 |
-1,889 |
208,604 |
12,207 |
1,2 |
1,423 |
|
|
14,824 |
Рис. 3. Оценка параметров модели регрессии зависимости рождаемости от индекса цен на данных 16 регионов РФ
В табл. 4 приведены остатки, полученные при построении модели регрессии по всем наблюдениям, диагональные элементы матрицы Н и CV критерий.
Метод перекрестной проверки с исключением одного наблюдения реализован в Gretl. При анализе построенной модели (рис. 3) в меню следует выбрать значимость наблюдений (рис. 4) и в качестве дополнительной информации для команды leverage будет получен критерий CV (табл. 5).
Таблица 3
Фрагмент матрицы Н
|
1 |
2 |
3 |
4 |
… |
13 |
14 |
15 |
16 |
|
|
1 |
0,093 |
0,094 |
0,081 |
0,117 |
… |
0,017 |
-0,018 |
0,014 |
0,006 |
|
2 |
0,094 |
0,095 |
0,081 |
0,119 |
… |
0,015 |
-0,021 |
0,013 |
0,004 |
|
3 |
0,081 |
0,081 |
0,073 |
0,095 |
… |
0,035 |
0,015 |
0,034 |
0,029 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
13 |
0,017 |
0,015 |
0,035 |
-0,019 |
… |
0,131 |
0,183 |
0,135 |
0,148 |
|
14 |
-0,018 |
-0,021 |
0,015 |
-0,082 |
… |
0,183 |
0,276 |
0,190 |
0,212 |
|
15 |
0,014 |
0,013 |
0,034 |
-0,024 |
… |
0,135 |
0,190 |
0,139 |
0,152 |
|
16 |
0,006 |
0,004 |
0,029 |
-0,039 |
… |
0,148 |
0,212 |
0,152 |
0,168 |
Таблица 4
Вычисление критерия перекрестной проверки на основе матрицы Н
|
№ |
Остатки |
hi |
CV |
|
1 |
-0,752 |
0,093 |
0,687 |
|
2 |
-0,712 |
0,095 |
0,619 |
|
3 |
-1,165 |
0,073 |
1,581 |
|
4 |
0,716 |
0,160 |
0,727 |
|
5 |
-0,430 |
0,086 |
0,221 |
|
6 |
-1,001 |
0,065 |
1,146 |
|
7 |
1,691 |
0,198 |
4,447 |
|
8 |
-0,505 |
0,072 |
0,296 |
|
9 |
0,227 |
0,097 |
0,063 |
|
10 |
0,269 |
0,090 |
0,087 |
|
11 |
-0,165 |
0,080 |
0,032 |
|
12 |
-0,226 |
0,177 |
0,076 |
|
13 |
0,427 |
0,131 |
0,241 |
|
14 |
-0,675 |
0,276 |
0,869 |
|
15 |
1,308 |
0,139 |
2,306 |
|
16 |
0,993 |
0,168 |
1,423 |
|
14,8237 |
Рис. 4. Оценка параметров модели регрессии в Gretl и выбор вида анализа построенной модели
Таблица 5
Вычисление критерия перекрестной проверки в Gretl
Остатки леверидж Воздействие DFFITS
u 0<=h<=1 u*h/(1-h)
1 -0,7518 0,093 -0,07728 -0,286
2 -0,71221 0,095 -0,074644 -0,273
3 -1,1654 0,073 -0,09197 -0,402
4 0,71603 0,160 0,1365 0,386
5 -0,42994 0,086 -0,040616 -0,153
6 -1,0009 0,065 -0,069815 -0,316
7 1,6911 0,198 0,41773 1,260
8 -0,50499 0,072 -0,039302 -0,163
9 0,22738 0,097 0,024302 0,086
10 0,26903 0,090 0,02662 0,098
11 -0,16457 0,080 -0,014278 -0,056
12 -0,22621 0,177 -0,048696 -0,127
13 0,42698 0,131 0,064405 0,197
14 -0,67528 0,276* -0,25712 -0,554
15 1,3082 0,139 0,21044 0,687
16 0,99255 0,168 0,20025 0,569
(‘*’ указывает на точку левериджа)
Критерий перекрестной проверки = 14,8237
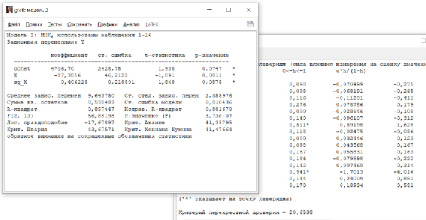
Затем в Gretl была построена двухфакторная модель, спецификация которой имеет вид:
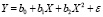
После оценки параметров модели в Gretl был вычислен критерий перекрестной проверки CV. Несмотря на то, что коэффициент детерминации двухфакторной модели 0,88 больше коэффициента детерминации однофакторной модели (0,87), а стандартная ошибка меньше (0,81 против 0,88), критерий перекрестной проверки CV, равный 20,65, больше значения CV для однофакторной модели, равного 14,82. В качестве лучшей модели для прогнозирования выбираем однофакторную модель.
Рис. 5. Оценка параметров и критерия перекрестной проверки двухфакторной модели
Заключение
Рассмотрев некоторые аспекты оценки качества линейных регрессионных моделей, а именно проблему проверки адекватности моделей, можно сделать следующие выводы.
Оценка качества моделей регрессии должна выполняться по нескольким направлениям: оценка значимости всего уравнения регрессии, оценка значимости параметров модели регрессии, оценка точности модели, проверка выполнения предпосылок МНК, и только при положительных результатах по этим пунктам осуществлять проверку качества прогнозов, получаемых на базе обучающей выборки путем сравнения этих прогнозов с реальными значениями из контролирующей выборки, т.е. проверять адекватность модели, ее способность к построению точных прогнозов.
В качестве инструментария могут использоваться различные методы перекрестной проверки, реализованные в R или Gretl, а при небольших выборках можно использовать Excel.
Библиографическая ссылка
Орлова И.В. К ВОПРОСУ ОБ ОЦЕНКЕ КАЧЕСТВА ЭКОНОМЕТРИЧЕСКИХ МОДЕЛЕЙ // Фундаментальные исследования. – 2022. – № 3.
– С. 92-99;
URL: https://fundamental-research.ru/ru/article/view?id=43220 (дата обращения: 13.02.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)