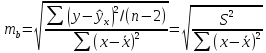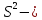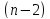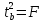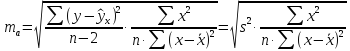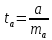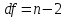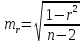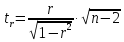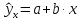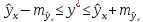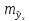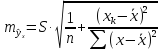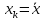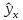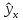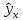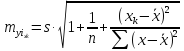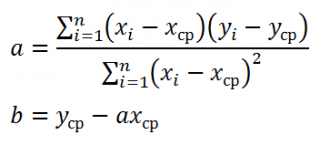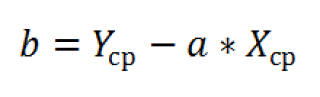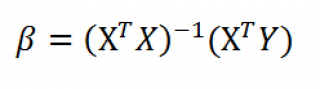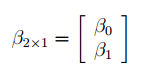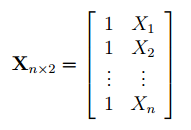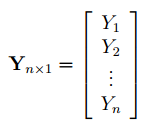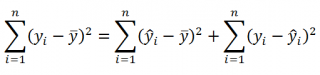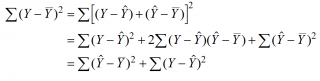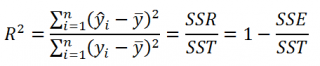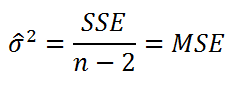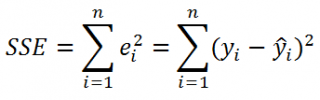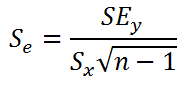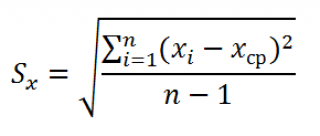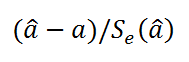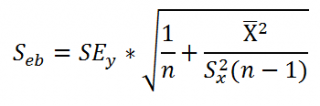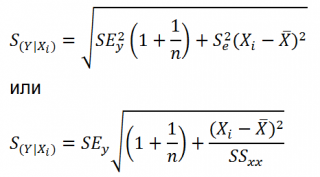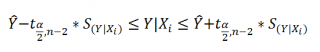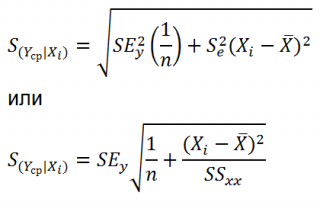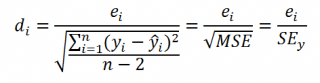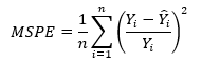Стандартные ошибки параметров линейной регрессии формула

В
линейной регрессии обычно оценивается
значимость не только уравнения в целом,
но и отдельных его параметров. С этой
целью по каждому из параметров определяется
его стандартная ошибка: т_b
и
т_а.

Стандартная
ошибка коэффициента регрессии параметра
b
рассчитывается
по формуле:

Где

остаточная дисперсия на одну степень
свободы.

Отношение
коэффициента регрессии к его стандартной
ошибке дает t-статистику,
которая подчиняется статистике Стьюдента
при

степенях
свободы. Эта статистика применяется
для проверки статистической значимости
коэффициента регрессии и для расчета
его доверительных интервалов.

Для
оценки значимости коэффициента регрессии
его величину сравнивают с его стандартной
ошибкой, т.е. определяют фактическое
значение t-критерия
Стьюдента:
,
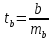
которое затем сравнивают с табличным
значением при определенном уровне
значимостиα
и
числе степе­ней свободы
.

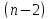
Справедливо
равенство

Доверительный
интервал для коэффициента регрессии
определяется как
.

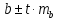
Стандартная
ошибка параметра а
определяется
по формуле

Процедура
оценивания значимости данного параметра
не отличается от рассмотренной выше
для коэффициента регрессии: вычисляется
t-критерий:

Его
величина сравнивается с табличным
значением при

степенях свободы.

Значимость
линейного коэффициента корреляции
проверяется на основе величины ошибки
коэффициента корреляции m_r:

Фактическое
значение t-критерия
Стьюдента определяется как

Данная
формула свидетельствует, что в парной
линейной регрессии
,
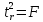
ибо как уже указывалось,
.
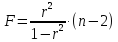
Кроме того,,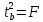
следовательно,.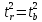

Таким
образом, проверка гипотез о значимости
коэффициентов регрессии и корреляции
равносильна проверке гипотезы о
значимости линейного уравнения регрессии.

Рассмотренную
формулу оценки коэффициента корреляции
рекомендуется применять при большом
числе наблюдений, а также если r
не близко к +1 или –1.

2.3 Интервальный прогноз на основе линейного уравнения регрессии

В
прогнозных расчетах по уравнению
регрессии определяется предсказываемое
y_р
значение
как точечный прогноз
_х
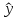
при
х_р
= х_k
т.
е. путем подстановки в линейное уравнение
регрессии

соответствующего
значения х.
Однако
точечный прогноз явно нереален, поэтому
он дополняется расчетом стандартной
ошибки
_х,
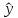
т.
е.
,
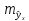
и
соответственно мы получаем интервальную
оценку прогнозного значения у*:

Считая,
что прогнозное значение фактора х_р
= х_k
получим
следующую формулу расчета стандартной
ошибки предсказываемого по линии
регрессии значения, т. е.

имеет выражение:

Рассмотренная
формула стандартной ошибки предсказываемого
среднего значения у
при
заданном значении х_k
характеризует
ошибку положения линии регрессии.
Величина стандартной ошибки
достигает
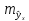
минимума при
и
возрастает по мере того, как «удаляется»
от
в любом направлении. Иными словами, чем
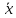
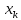
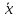
больше разность междуи,
тем больше ошибка,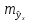
с
которой предсказывается среднее значение
у
для
заданного значения
.
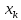
Можно ожидать наилучшие результаты
прогноза, если признак-фактор х находится
в центре области наблюдений х, и нельзя
ожидать хороших результатов прогноза
при удалении.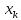
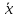
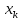
от. Если же значение.
оказывается за пределами наблюдаемых
значенийх,
используемых при построении линейной
регрессии, то результаты прогноза
ухудшаются в зависимости от того,
насколько
.
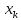
отклоняется от области наблюдаемых
значений факторах.

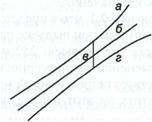
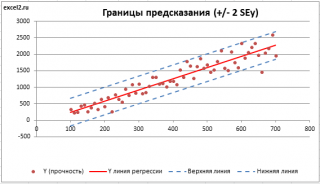
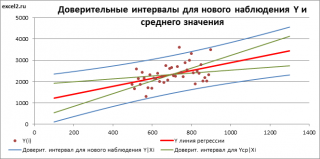
На
графике, приведенном на рис. 1, доверительные
границы для

представляют
собой гиперболы, расположенные по обе
стороны от линии регрессии. Рис. 1
показывает, как изменяются пределы в
зависимости от изменения
.:
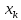
две гиперболы по обе стороны от линии
регрессии определяют 95 %-ные доверительные
интервалы для среднего значенияу
при
заданном значении х.

Однако
фактические значения у
варьируют
около среднего значения
.
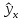
Индивидуальные
значения у
могут
отклоняться от


на
величину случайной ошибки ε, дисперсия
которой оценивается как остаточная
дисперсия на одну степень свободы
.
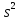
Поэтому ошибка предсказываемого
индивидуального значенияу
должна включать не только стандартную
ошибку
,
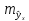
но и случайную ошибкуs.

Рис.
1. Доверительный интервал линии регрессии:

а
— верхняя
доверительная граница; б
— линия
регрессии;

в
— доверительный
интервал для

при
;

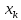
г
— нижняя
доверительная граница.

Средняя
ошибка прогнозируемого индивидуального
значения у
составит:

При
прогнозировании на основе уравнения
регрессии следует помнить, что величина
прогноза зависит не только от стандартной
ошибки индивидуального значения у,
но
и от точности прогноза значения фактора
х.
Его
величина может задаваться на основе
анализа других моделей исходя из
конкретной ситуации, а также анализа
динамики данного фактора.

Рассмотренная
формула средней ошибки индивидуального
значения признака у
может
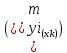
быть использована также для оценки
существенности различия предсказываемого
значения и некоторого гипотетического
значения.

11

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В

MS

EXCEL

имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.

Disclaimer

: Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей

Регрессионного анализа.

Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения

Регрессии

– плохая идея.

Статья про

Регрессионный анализ

получилась большая, поэтому ниже для удобства приведены ее разделы:

• Немного теории и основные понятия
• Предположения линейной регрессионной модели
• Задачи регрессионного анализа
• Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
• Оценка неизвестных параметров линейной модели (через статистики выборок)
• Оценка неизвестных параметров линейной модели (матричная форма)
• Построение линии регрессии
• Коэффициент детерминации
• Стандартная ошибка регрессии
• Стандартные ошибки и доверительные интервалы для наклона и сдвига
• Проверка значимости взаимосвязи переменных
• Доверительные интервалы для нового наблюдения Y и среднего значения
• Проверка адекватности линейной регрессионной модели

Примечание

: Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место

множественная регрессия

.

Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.

Примечание

: Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части —

оценке неизвестных параметров линейной модели

.

Немного теории и основные понятия

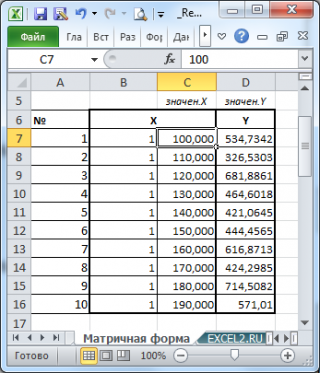
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.

Примером такой задачи может быть производственный процесс изготовления некого волокна, причем

прочность этого волокна

(Y) зависит только от

рабочей температуры процесса

в реакторе (Х), которая задается оператором.

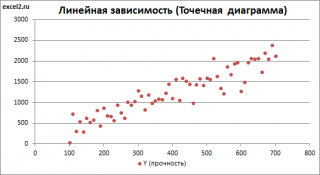
Построим

диаграмму рассеяния

(см.

файл примера лист Линейный

), созданию которой

посвящена отдельная статья

. Вообще, построение

диаграммы рассеяния

для целей

регрессионного анализа

де-факто является стандартом.

СОВЕТ

: Подробнее о построении различных типов диаграмм см. статьи

Основы построения диаграмм

и

Основные типы диаграмм

.

Приведенная выше

диаграмма рассеяния

свидетельствует о возможной

линейной взаимосвязи

между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.

Примечание

: Наличие даже такой очевидной

линейной взаимосвязи

не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие

причинной

взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.

Примечание

: Как известно, уравнение прямой линии имеет вид

Y

=

m

*

X

+

k

, где коэффициент

m

отвечает за наклон линии (

slope

),

k

– за сдвиг линии по вертикали (

intercept

),

k

равно значению Y при Х=0.

Предположим, что мы можем зафиксировать переменную Х (

рабочую температуру процесса

) при некотором значении Х

_i

и произвести несколько наблюдений переменной Y (

прочность нити

). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).

Полученные значения Y, при заданном Хi, будут колебаться вокруг некого

значения

. При увеличении количества измерений, среднее этих измерений, будет стремиться к

математическому ожиданию

случайной величины Y (при Х

_i

) равному μy(i)=Е(Y

_i

).

Подобные рассуждения можно привести для любого значения Хi.

Чтобы двинуться дальше, воспользуемся материалом из раздела

Проверка статистических гипотез

. В статье о

проверке гипотезы о среднем значении генеральной совокупности

в качестве

нулевой

гипотезы

предполагалось равенство неизвестного значения μ заданному μ0.

В нашем случае

простой линейной регрессии

в качестве

нулевой

гипотезы

предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ

_y(i)

=α* Х

_i

+β. Уравнение μ

_y(i)

=α* Х

_i

+β можно переписать в обобщенном виде (для всех Х и μ

_y

) как μ

_y

=α* Х +β.

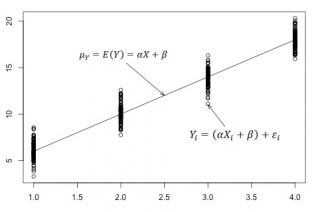
Для наглядности проведем прямую линию соединяющую все μy(i).

Данная линия называется

регрессионной линией генеральной совокупности

(population regression line), параметры которой (

наклон

a и

сдвиг β

) нам не известны (по аналогии с

гипотезой о среднем значении генеральной совокупности

, где нам было неизвестно истинное значение μ).

Теперь сделаем переход от нашего предположения, что μy=a* Х +

β

, к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.

Уравнение Y=a*X+b+ε называют

линейной регрессионной моделью

. Часто Х еще называют

независимой переменной

(еще

предиктором

и

регрессором

, английский термин

predictor

,

regressor

), а Y –

зависимой

(или

объясняемой

,

response

variable

). Так как

регрессор

у нас один, то такая модель называется

простой линейной регрессионной моделью

(

simple

linear

regression

model

). α часто называют

коэффициентом регрессии.

Предположения линейной регрессионной модели перечислены в следующем разделе.

Предположения линейной регрессионной модели

Чтобы модель линейной регрессии Yi=a*Xi+β+ε

_i

была адекватной — требуется:

• Ошибки ε
  
  _i
  
  должны быть независимыми переменными;
• При каждом значении Xi ошибки ε
  
  _i
  
  должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε
  
  _i
  
  ]=0);
• При каждом значении Xi ошибки ε
  
  _i
  
  должны иметь равные дисперсии (обозначим ее σ
  
  ²
  
  ).

Примечание

: Последнее условие называется

гомоскедастичность

— стабильность, гомогенность дисперсии случайной ошибки e. Т.е.

дисперсия

ошибки σ

²

не должна зависеть от значения Xi.

Используя предположение о равенстве математического ожидания Е[ε

_i

]=0 покажем, что μy(i)=Е[Yi]:

Е[Yi]= Е[a*Xi+β+ε

_i

]= Е[a*Xi+β]+ Е[ε

_i

]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.

Дисперсия

случайной переменной Y равна

дисперсии

ошибки ε, т.е. VAR(Y)= VAR(ε)=σ

²

. Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε

_i

).

Задачи регрессионного анализа

Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует

регрессионная линия генеральной совокупности

, т.е.  μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений {X;Y}.

На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно

a

и

b

. Также часто используются обозначения â и b̂.

Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?

Таким образом:

Первая задача

регрессионного анализа

– оценка неизвестных параметров (

estimation

of

the

unknown

parameters

). Подробнее см. раздел

Оценки неизвестных параметров модели

.

Вторая задача

регрессионного анализа

–

Проверка адекватности модели

(

model

adequacy

checking

).

Примечание

: Оценки параметров модели обычно вычисляются

методом наименьших квадратов

(МНК),

которому посвящена отдельная статья

.

Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)

Неизвестные параметры

простой линейной регрессионной модели

Y=a*X+β+ε оценим с помощью

метода наименьших квадратов

(в

статье про МНК подробно описано этот метод

).

Для вычисления параметров линейной модели методом МНК получены следующие выражения:

Таким образом, мы получим уравнение прямой линии Y=

a

*X+

b

, которая наилучшим образом аппроксимирует имеющиеся данные.

Примечание

: В статье про

метод наименьших квадратов

рассмотрены случаи аппроксимации

линейной

и

квадратичной функцией

, а также

степенной

,

логарифмической

и

экспоненциальной функцией

.

Оценку параметров в MS EXCEL можно выполнить различными способами:

• с помощью функций
  
  НАКЛОН()
  
  и
  
  ОТРЕЗОК()
  
  ;
• с помощью функции
  
  ЛИНЕЙН()
  
  ; см. статью

  Функция MS EXCEL ЛИНЕЙН()

• формулами через статистики выборок

  ;

• в матричной форме

  ;

• с помощью

  инструмента Регрессия надстройки Пакет Анализа

  .

Сначала рассмотрим функции

НАКЛОН()

,

ОТРЕЗОК()

и

ЛИНЕЙН()

.

Пусть значения Х и Y находятся соответственно в диапазонах

C

23:

C

83

и

B

23:

B

83

(см.

файл примера

внизу статьи).

Примечание

: Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью

Генерация данных для линейной регрессии в MS EXCEL

).

В MS EXCEL наклон прямой линии

а

(

оценку

коэффициента регрессии

), можно найти по

методу МНК

с помощью функции

НАКЛОН()

, а сдвиг

b

(

оценку

постоянного члена

или

константы регрессии

), с помощью функции

ОТРЕЗОК()

. В английской версии это функции SLOPE и INTERCEPT соответственно.

Аналогичный результат можно получить с помощью функции

ЛИНЕЙН()

, английская версия LINEST (см.

статью об этой функции

).

Формула

=ЛИНЕЙН(C23:C83;B23:B83)

вернет наклон

а

. А формула =

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2)

— сдвиг

b

. Здесь требуются пояснения.

Функция

ЛИНЕЙН()

имеет 4 аргумента и возвращает целый массив значений:

ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])

Если 4-й аргумент

статистика

имеет значение ЛОЖЬ или опущен, то функция

ЛИНЕЙН()

возвращает только оценки параметров модели:

a

и

b

.

Примечание

: Остальные значения, возвращаемые функцией

ЛИНЕЙН()

, нам потребуются при вычислении

стандартных ошибок

и для

проверки значимости регрессии

. В этом случае аргумент

статистика

должен иметь значение ИСТИНА.

Чтобы вывести сразу обе оценки:

• в одной строке необходимо выделить 2 ячейки,
• ввести формулу в

  Строке формул

• нажать
  
  CTRL
  
  +
  
  SHIFT
  
  +
  
  ENTER
  
  (см. статью про

  формулы массива

  ).

Если в

Строке формул

выделить формулу =

ЛИНЕЙН(C23:C83;B23:B83)

и нажать

клавишу F9

, то мы увидим что-то типа {3,01279389265416;154,240057900613}. Это как раз значения

a

и

b

. Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».

Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу =

ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83))

. При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция

ТРАНСП()

транспонировала строку в столбец

).

Чтобы разобраться в этом подробнее необходимо ознакомиться с

формулами массива

.

Чтобы не связываться с вводом

формул массива

, можно

использовать функцию ИНДЕКС()

. Формула =

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1)

или просто

ЛИНЕЙН(C23:C83;B23:B83)

вернет параметр, отвечающий за наклон линии, т.е.

а

. Формула

=ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2)

вернет параметр

b

.

Оценка неизвестных параметров линейной модели (через статистики выборок)

Наклон линии, т.е. коэффициент

а

, можно также вычислить через

коэффициент корреляции

и

стандартные отклонения выборок

:

=

КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))

Вышеуказанная формула математически эквивалентна отношению

ковариации

выборок Х и Y и

дисперсии

выборки Х:

=

КОВАРИАЦИЯ.В(B23:B83;C23:C83)/ДИСП.В(B23:B83)

И, наконец, запишем еще одну формулу для нахождения сдвига

b

. Воспользуемся тем фактом, что

линия регрессии

проходит через точку

средних значений

переменных Х и Y.

Вычислив

средние значения

и подставив в формулу ранее найденный наклон

а

, получим сдвиг

b

.

Оценка неизвестных параметров линейной модели (матричная форма)

Также параметры

линии регрессии

можно найти в матричной форме (см.

файл примера лист Матричная форма

).

В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг

b

), β1 (наклон

a

).

Матрица Х равна:

Матрица

Х

называется

регрессионной матрицей

или

матрицей плана

. Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.

Матрица

Х

^T

– это

транспонированная матрица

Х

. Она состоит соответственно из n столбцов и 2-х строк.

В формуле символом

Y

обозначен столбец значений переменной Y.

Чтобы

перемножить матрицы

используйте функцию

МУМНОЖ()

. Чтобы

найти обратную матрицу

используйте функцию

МОБР()

.

Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).

Слева от него достроим столбец с 1 для матрицы Х.

Записав формулу

=

МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП(B7:C16);(B7:C16))); МУМНОЖ(ТРАНСП(B7:C16);(D7:D16)))

и введя ее как

формулу массива

в 2 ячейки, получим оценку параметров модели.

Красота применения матричной формы полностью раскрывается в случае

множественной регрессии

.

Построение линии регрессии

Для отображения

линии регрессии

построим сначала

диаграмму рассеяния

, на которой отобразим все точки (см.

начало статьи

).

Для построения прямой линии используйте вычисленные выше оценки параметров модели

a

и

b

(т.е. вычислите

у

по формуле

y

=

a

*

x

+

b

) или функцию

ТЕНДЕНЦИЯ()

.

Формула =

ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23)

возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца

В2

.

Примечание

:

Линию регрессии

можно также построить с помощью функции

ПРЕДСКАЗ()

. Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции

ТЕНДЕНЦИЯ()

работает только в случае одного регрессора. Функция

ТЕНДЕНЦИЯ()

может быть использована и в случае

множественной регрессии

(в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).

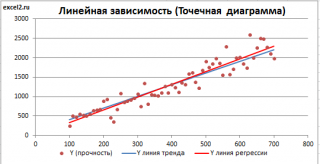
Как видно из диаграммы выше

линия тренда

и

линия регрессии

не обязательно совпадают: отклонения точек от

линии тренда

случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.

Линию регрессии

можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента

Линия тренда.

Для этого выделите диаграмму, в меню выберите

вкладку Макет

, в

группе Анализ

нажмите

Линия тренда

, затем

Линейное приближение.

В диалоговом окне установите галочку

Показывать уравнение на диаграмме

(подробнее см. в

статье про МНК

).

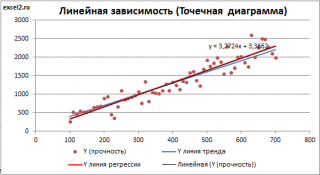
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами

линией регрессии,

а параметры уравнения

a

и

b

должны совпасть с параметрами уравнения отображенными на диаграмме.

Примечание:

Для того, чтобы вычисленные параметры уравнения

a

и

b

совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был

Точечная, а не График

, т.к. тип диаграммы

График

не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; … Именно эти значения и берутся при расчете параметров

линии тренда

. Убедиться в этом можно если построить диаграмму

График

(см.

файл примера

), а значения

Хнач

и

Хшаг

установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с

a

и

b

.

Коэффициент детерминации R

²

Коэффициент детерминации

R

²

показывает насколько полезна построенная нами

линейная регрессионная модель

.

Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения

регрессионной модели

). Очевидно, что лучшей оценкой для yi будет

среднее значение

ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).

Примечание

: Далее будет использована терминология и обозначения

дисперсионного анализа

.

После построения

регрессионной модели

для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).

Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.

Очевидно, что используя

регрессионную модель

мы уменьшили первоначальную (полную) ошибку (yi — ȳ)  на значение (ŷi — ȳ)  до величины (yi — ŷi).

(yi — ŷi) – это оставшаяся, необъясненная ошибка.

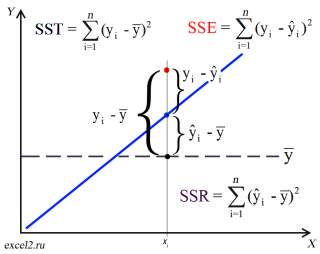
Очевидно, что все три ошибки связаны выражением:

(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)

Можно показать, что в общем виде справедливо следующее выражение:

Доказательство:

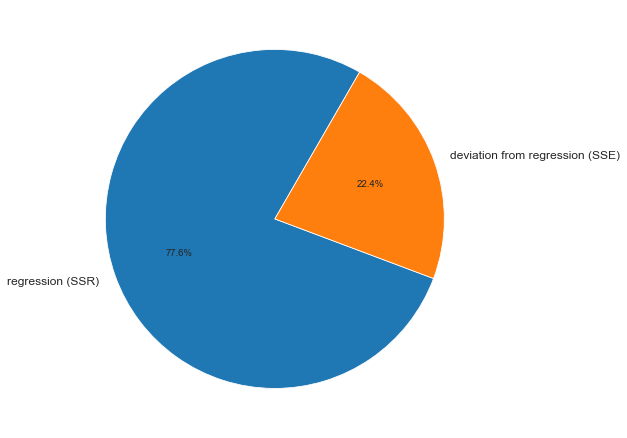
или в других, общепринятых в зарубежной литературе, обозначениях:

SST

=

SSR

+

SSE

Что означает:

Total Sum of Squares

=

Regression Sum of Squares

+

Error Sum of Squares

Примечание

: SS — Sum of Squares — Сумма Квадратов.

Как видно из формулы величины SST, SSR, SSE имеют размерность

дисперсии

(вариации) и соответственно описывают разброс (изменчивость):

Общую изменчивость

(Total variation),

Изменчивость объясненную моделью

(Explained variation) и

Необъясненную изменчивость

(Unexplained variation).

По определению

коэффициент детерминации

R

²

равен:

R

²

=

Изменчивость объясненная моделью / Общая изменчивость.

Этот показатель равен квадрату

коэффициента корреляции

и в MS EXCEL его можно вычислить с помощью функции

КВПИРСОН()

или

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3)

R

₂

принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.

Стандартная ошибка регрессии

Стандартная ошибка регрессии

(

Standard Error of a regression

) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).

Теперь вспомним уравнение

линейной регрессионной модели

Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со

средним значением

μ и

дисперсией

σ

²

.

Оценив значение

дисперсии

σ

²

и вычислив из нее квадратный корень – получим

Стандартную ошибку регрессии.

Чем точки наблюдений на диаграмме

рассеяния

ближе находятся к прямой линии, тем меньше

Стандартная ошибка.

Примечание

:

Вспомним

, что при построении модели предполагается, что

среднее значение

ошибки ε равно 0, т.е. E[ε]=0.

Оценим

дисперсию σ

²

. Помимо вычисления

Стандартной ошибки регрессии

эта оценка нам потребуется в дальнейшем еще и при построении

доверительных интервалов

для оценки параметров регрессии

a

и

b

.

Для оценки

дисперсии

ошибки ε используем

остатки регрессии

— разности между имеющимися значениями

yi

и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.

Для оценки

дисперсии σ

²

используют следующую формулу:

где SSE – сумма квадратов значений ошибок модели ε

_i

=yi — ŷi (

Sum of Squared Errors

).

SSE часто обозначают и как SSres – сумма квадратов остатков (

Sum

of

Squared

residuals

).

Оценка

дисперсии

s

²

также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов

ошибок

или MSRES (Mean Square of Residuals), т.е. среднее квадратов

остатков

. Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.

Примечание

: Напомним, что когда

мы использовали МНК

для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на

линии регрессии.

Математическое ожидание

случайной величины MSE равно

дисперсии ошибки

ε, т.е.

σ

²

.

Чтобы понять почему SSE выбрана в качестве основы для оценки

дисперсии

ошибки ε, вспомним, что

σ

²

является также

дисперсией

случайной величины Y (относительно

среднего значения

μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi =

a

* Хi +

b

(значение

уравнения регрессии

при Х= Хi), то логично использовать именно SSE в качестве основы для оценки

дисперсии

σ

²

. Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество

степеней свободы

(

df

–

degrees

of

freedom

), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае

простой линейной регрессии

число степеней свободы

равно n-2, т.к. при построении

линии регрессии

было оценено 2 параметра модели (на это было «потрачено» 2

степени свободы

).

Итак, как сказано было выше, квадратный корень из s

²

имеет специальное название

Стандартная ошибка регрессии

(

Standard Error of a regression

) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см.

этот раздел

). Если ошибки предсказания ε имеют

нормальное распределение

, то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от

линии регрессии

. SEy имеет размерность переменной Y и откладывается по вертикали. Часто на

диаграмме рассеяния

строят

границы предсказания

соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).

В MS EXCEL

стандартную ошибку

SEy можно вычислить непосредственно по формуле:

=

КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))

или с помощью функции

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;2)

Примечание

: Подробнее о функции

ЛИНЕЙН()

см.

эту статью

.

Стандартные ошибки и доверительные интервалы для наклона и сдвига

В разделе

Оценка неизвестных параметров линейной модели

мы получили точечные оценки наклона

а

и сдвига

b

. Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со

средним значением

и

дисперсией

. Но, чтобы перейти от

точечных оценок

к

интервальным

, необходимо вычислить соответствующие

стандартные ошибки

(т.е.

стандартные отклонения

).

Стандартная ошибка коэффициента регрессии

a

вычисляется на основании

стандартной ошибки регрессии

по следующей формуле:

где Sx – стандартное отклонение величины х, вычисляемое по формуле:

где Sey –

стандартная ошибка регрессии,

т.е. ошибка предсказания значения переменой Y

(

см. выше

).

В MS EXCEL

стандартную ошибку коэффициента регрессии

Se можно вычислить впрямую по вышеуказанной формуле:

=

КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/  СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)

или с помощью функции

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);2;1)

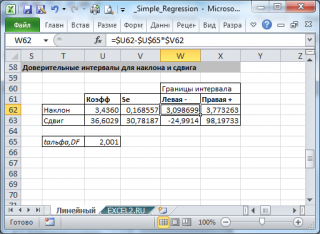
Формулы приведены в

файле примера на листе Линейный

в разделе

Регрессионная статистика

.

Примечание

: Подробнее о функции

ЛИНЕЙН()

см.

эту статью

.

При построении

двухстороннего доверительного интервала

для

коэффициента регрессии

его границы определяются следующим образом:

где  —

квантиль распределения Стьюдента

с n-2 степенями свободы. Величина

а

с «крышкой» является другим обозначением

наклона

а

.

Например для

уровня значимости

альфа=0,05, можно вычислить с помощью формулы

=СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)

Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины

является

t-распределением Стьюдента

с n-2 степенью свободы (то же справедливо и для наклона

b

).

Примечание

: Подробнее о построении

доверительных интервалов

в MS EXCEL можно прочитать в этой статье

Доверительные интервалы в MS EXCEL

.

В результате получим, что найденный

доверительный интервал

с вероятностью 95% (1-0,05) накроет истинное значение

коэффициента регрессии.

Здесь мы считаем, что

коэффициент регрессии

a

имеет

распределение Стьюдента

с n-2

степенями свободы

(n – количество наблюдений, т.е. пар Х и Y).

Примечание

: Подробнее о построении

доверительных интервалов

с использованием t-распределения см. статью про построение

доверительных интервалов

для среднего

.

Стандартная ошибка сдвига

b

вычисляется по следующей формуле:

В MS EXCEL

стандартную ошибку сдвига

Seb можно вычислить с помощью функции

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);2;2)

При построении

двухстороннего доверительного интервала

для

сдвига

его границы определяются аналогичным образом как для

наклона

:

b

+/- t*Seb.

Проверка значимости взаимосвязи переменных

Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.

Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда

коэффициент регрессии

a

равен 0.

Чтобы убедиться, что вычисленная нами оценка

наклона

прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют

проверку гипотез

. В качестве

нулевой гипотезы

Н

₀

принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы

Н

₁

принимают, что a <>0.

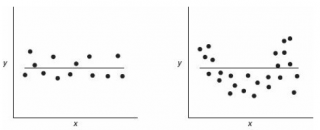
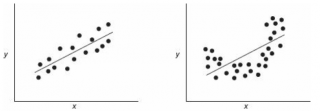
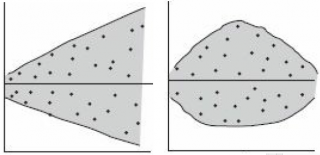
Ниже на рисунках показаны 2 ситуации, когда

нулевую гипотезу

Н

₀

не удается отвергнуть.

На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом

коэффициент линейной корреляции

равен 0.

Ниже — 2 ситуации, когда

нулевая гипотеза

Н

₀

отвергается.

На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).

Для проверки гипотезы нам потребуется:

• Установить

  уровень значимости

  , пусть альфа=0,05;

• Рассчитать с помощью функции
  
  ЛИНЕЙН()
  
  стандартное отклонение
  
  Se для
  
  коэффициента регрессии
  
  (см.

  предыдущий раздел

  );

• Рассчитать число степеней свободы: DF=n-2 или по формуле =
  
  ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
  
• Вычислить значение тестовой статистики t
  
  ₀
  
  =a/S
  
  _e
  
  , которая имеет

  распределение Стьюдента

  с
  
  числом степеней свободы
  
  DF=n-2;

• Сравнить значение
  
  тестовой статистики
  
  |t0| с пороговым значением t
  
  _альфа
  
  ,n-2. Если значение
  
  тестовой статистики
  
  больше порогового значения, то
  
  нулевая гипотеза
  
  отвергается (
  
  наклон
  
  не может быть объяснен лишь случайностью при заданном уровне альфа) либо
• вычислить
  
  p-значение
  
  и сравнить его с
  
  уровнем значимости
  
  .

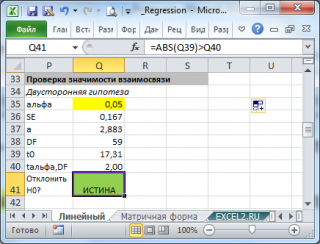
В

файле примера

приведен пример проверки гипотезы:

Изменяя

наклон

тренда k (ячейка

В8

) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.

Примечание

: Проверка значимости взаимосвязи эквивалентна

проверке статистической значимости коэффициента корреляции

. В

файле примера

показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью

процедуры F-тест

.

Доверительные интервалы для нового наблюдения Y и среднего значения

Вычислив параметры

простой линейной регрессионной модели

Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ=

a

* Хi +

b

Ŷ также является точечной оценкой для

среднего значения

Yi при заданном Хi. Но, при построении

доверительных интервалов

используются различные

стандартные ошибки

.

Стандартная ошибка

нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:

• неопределенность связанную со случайностью оценок параметров модели
  
  a
  
  и
  
  b
  
  ;
• случайность ошибки модели ε.

Учет этих неопределенностей приводит к

стандартной ошибке

S(Y|Xi), которая рассчитывается с учетом известного значения Xi.

где SS

_xx

– сумма квадратов отклонений от

среднего

значений переменной Х:

Примечание

: Se –

стандартная ошибка коэффициента регрессии

(

наклона

а

).

В

MS EXCEL 2010

нет функции, которая бы рассчитывала эту

стандартную ошибку

, поэтому ее необходимо рассчитывать по вышеуказанным формулам.

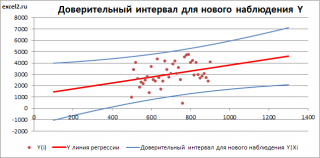
Доверительный интервал

или

Интервал предсказания для нового наблюдения

(Prediction Interval for a New Observation) построим по схеме показанной в разделе

Проверка значимости взаимосвязи переменных

(см.

файл примера лист Интервалы

). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х

_ср

), то интервал будет постепенно расширяться при удалении от Х

_ср

.

Границы

доверительного интервала

для

нового наблюдения

рассчитываются по формуле:

Аналогичным образом построим

доверительный интервал

для

среднего значения

Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае

доверительный интервал

будет уже, т.к.

средние значения

имеют меньшую изменчивость по сравнению с отдельными наблюдениями (

средние значения,

в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).

Стандартная ошибка

S(Yср|Xi) вычисляется по практически аналогичным формулам как и

стандартная ошибка

для нового наблюдения:

Как видно из формул,

стандартная ошибка

S(Yср|Xi) меньше

стандартной ошибки

S(Y|Xi) для индивидуального значения

.

Границы

доверительного интервала

для

среднего значения

рассчитываются по формуле:

Проверка адекватности линейной регрессионной модели

Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел

Предположения линейной регрессионной модели

).

Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках

простой линейной модели

n остатков имеют только n-2 связанных с ними

степеней свободы

. Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.

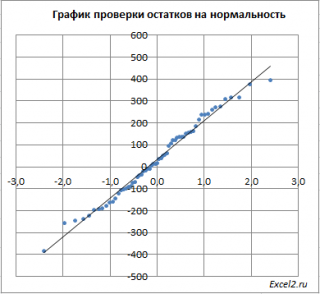
Чтобы проверить предположение о

нормальности распределения

ошибок строят

график проверки на нормальность

(Normal probability Plot).

В

файле примера на листе Адекватность

построен

график проверки на нормальность

. В случае

нормального распределения

значения остатков должны быть близки к прямой линии.

Так как значения переменной Y мы

генерировали с помощью тренда

, вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.

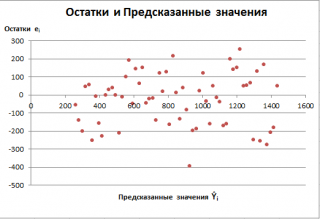
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор

о

нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.

В нашем случае точки располагаются примерно равномерно.

Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе

Стандартная ошибка регрессии

оценкой

стандартного отклонения ошибок

является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.

SEy можно вычислить с помощью функции

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;2)

Иногда нормирование остатков производится на величину

стандартного отклонения

остатков (это мы увидим в статье об инструменте

Регрессия

, доступного в

надстройке MS EXCEL Пакет анализа

), т.е. по формуле:

Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.

АКТУАЛЬНОСТЬ ТЕМЫ

Общие положения

Про регрессионный анализ вообще, и его применение в DataScience написано очень много. Есть множество учебников, монографий, справочников и статей по прикладной статистике, огромное количество информации в интернете, примеров расчетов. Можно найти множество кейсов, реализованных с использованием средств Python. Казалось бы — что тут еще можно добавить?

Однако, как всегда, есть нюансы:

1. Регрессионный анализ — это прежде всего процесс, набор действий исследователя по определенному алгоритму: «подготовка исходных данных — построение модели — анализ модели — прогнозирование с помощью модели». Это ключевая особенность. Не представляет особой сложности сформировать DataFrame исходных данных и построить модель, запустить процедуру из библиотеки statsmodels. Однако подготовка исходных данных и последующий анализ модели требуют гораздо больших затрат человеко-часов специалиста и строк программного кода, чем, собственно, построение модели. На этих этапах часто приходится возвращаться назад, корректировать модель или исходные данные. Этому, к сожалению, во многих источниках, не удаляется достойного внимания, а иногда — и совсем не уделяется внимания, что приводит к превратному представлению о регрессионном анализе.

2. Далеко не во всех источниках уделяется должное внимание интерпретации промежуточных и финальных результатов. Специалист должен уметь интерпретировать каждую цифру, полученную в ходе работы над моделью.

3. Далеко не все процедуры на этапах подготовки исходных данных или анализа модели в источниках разобраны подробно. Например, про проверку значимости коэффициента детерминации найти информацию не представляет труда, а вот про проверку адекватности модели, построение доверительных интервалов регрессии или про специфические процедуры (например, тест Уайта на гетероскедастичность) информации гораздо меньше.

4. Своеобразная сложность может возникнуть с проверкой статистических гипотез: для отечественной литературы по прикладной статистике больше характерно проверять гипотезы путем сравнения расчетного значения критерия с табличным, а в иностранных источниках чаще определяется расчетный уровень значимости и сравнивается с заданным (чаще всего 0.05 = 1-0.95). В разных источниках информации реализованы разные подходы. Инструменты python (прежде всего библиотеки scipy и statsmodels) также в основном оперируют с расчетным уровнем значимости.

5. Ну и, наконец, нельзя не отметить, что техническая документация библиотеки statsmodels составлена, на мой взгляд, далеко не идеально: информация излагается путано, изобилует повторами и пропусками, описание классов, функций и свойств выполнено фрагментарно и количество примеров расчетов — явно недостаточно.

Поэтому я решил написать ряд обзоров по регрессионному анализу средствами Python, в которых акцент будет сделан на практических примерах, алгоритме действий исследователя, интерпретации всех полученных результатов, конкретных методических рекомендациях. Буду стараться по возможности избегать теории (хотя совсем без нее получится) — все-таки предполагается, что специалист DataScience должен знать теорию вероятностей и математическую статистику, хотя бы в рамках курса высшей математики для технического или экономического вуза.

В данном статье остановимся на самои простом, классическом, стереотипном случае — простой линейной регрессии (simple linear regression), или как ее еще принято называть — парной линейной регрессионной модели (ПЛРМ) — в ситуации, когда исследователя не подстерегают никакие подводные камни и каверзы — исходные данные подчиняются нормальному закону, в выборке отсутствуют аномальные значения, отсутствует ложная корреляция. Более сложные случаи рассмотрим в дальнейшем.

Для построение регрессионной модели будем пользоваться библиотекой statsmodels.

В данной статье мы рассмотрим по возможности полный набор статистических процедур. Некоторые из них (например, дескриптивная статистика или дисперсионный анализ регрессионной модели) могут показаться избыточными. Все так, но эти процедуры улучшают наше представление о процессе и об исходных данных, поэтому в разбор я их включил, а каждый исследователь сам вправе для себя определить, потребуются ему эти процедуры или нет.

Краткий обзор источников

Источников информации по корреляционному и регрессионному анализу огромное количество, в них можно просто утонуть. Поэтому позволю себе просто порекомендовать ряд источников, на мой взгляд, наиболее полезных:

1. Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. — М.: ФИЗМАТЛИТ, 2006. — 816 с.

2. Львовский Е.Н. Статистические методы построения эмпирических формул. — М.: Высшая школа, 1988. — 239 с.

3. Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа / пер с нем. — М.: Финансы и статистика, 1983. — 302 с.

4. Афифи А., Эйзен С. Статистический анализ. Подход с использованием ЭВМ / пер с англ. — М.: Мир, 1982. — 488 с.

5. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. Книга 1 / пер.с англ. — М.: Финансы и статистика, 1986. — 366 с.

6. Айвазян С.А. и др. Прикладная статистика: Исследование зависимостей. — М.: Финансы и статистика, 1985. — 487 с.

7. Прикладная статистика. Основы эконометрики: В 2 т. 2-е изд., испр. — Т.2: Айвазян С.А. Основы эконометрики. — М.: ЮНИТИ-ДАНА, 2001. — 432 с.

8. Магнус Я.Р. и др. Эконометрика. Начальный курс — М.: Дело, 2004. — 576 с.

9. Носко В.П. Эконометрика. Книга 1. — М.: Издательский дом «Дело» РАНХиГС, 2011. — 672 с.

10. Брюс П. Практическая статистика для специалистов Data Science / пер. с англ. — СПб.: БХВ-Петербург, 2018. — 304 с.

11. Уатт Дж. и др. Машинное обучение: основы, алгоритмы и практика применения / пер. с англ. — СПб.: БХВ-Петербург, 2022. — 640 с.

Прежде всего следует упомянуть справочник Кобзаря А.И. [1] — это безусловно выдающийся труд. Ничего подобного даже близко не издавалось. Всем рекомендую иметь под рукой.

Есть очень хорошее практическое пособие [2] — для начинающих и практиков.>

Добротная работа немецких авторов [3]. Все разобрано подробно, обстоятельно, с примерами — очень хорошая книга. Примеры приведены из области экономики.

Еще одна добротная работа — [4], с примерами медико-биологического характера.

Работа [5] считается одним из наиболее полных изложений прикладного регрессионного анализа.

Более сложные работы — [6] (классика жанра), [7], [8], [9] — выдержаны на достаточно высоком математическом уровне, примеры из экономической области.

Свежие работы [10] (с примерами на языке R) и [11] (с примерами на python).

Cтатьи

Статей про регрессионный анализ в DataScience очень много, обращаю внимание на некоторые весьма полезные из них.

Серия статей «Python, корреляция и регрессия», охватывающая весь процесс регрессионного анализа:

• первичная обработка данных, визуализация и корреляционный анализ;

• регрессия;

• теория матриц в регрессионном анализе, проверка  адекватности, мультиколлинеарность;

• прогнозирование с помощью регрессионных моделей.

Очень хороший обзор «Интерпретация summary из statsmodels для линейной регрессии». В этой статье даны очень полезные ссылки:

• Statistical Models

• Interpreting Linear Regression Through statsmodels .summary()

Статья «Регрессионные модели в Python».

Основные предпосылки (гипотезы) регрессионного анализа

Очень кратко — об этом написано тысячи страниц в учебниках — но все же вспомним некоторые основы теории.

Проверка исходных предпосылок является очень важным моментом при статистическом анализе регрессионной модели. Если мы рассматриваем классическую линейную регрессионную модель вида:

то основными предпосылками при использовании обычного метода наименьших квадратов (МНК) для оценки ее параметров являются:

1. Среднее значение (математическое ожидание) случайной составляющей равно нулю:

1. Дисперсия случайной составляющей является постоянной:

В случае нарушения данного условия мы сталкиваемся с явлением гетероскедастичности.

1. Значения случайной составляющей статистически независимы (некоррелированы) между собой:

В случае нарушения данного условия мы сталкиваемся с явлением автокорреляции.

1. Условие существования обратной матрицы

что эквивалентно одному из двух следующих условий:

то есть число наблюдений должно превышать число параметров.

1. Значения случайной составляющей некоррелированы со значениями независимых переменных:

1. Случайная составляющая имеет нормальный закон распределения (с математическим ожиданием равным нулю — следует из условия 1):

Более подробно — см.: [3, с.90], [4, с.147], [5, с.122], [6, с.208], [7, с.49], [8, с.68], [9, с.88].

Кроме гетероскедастичности и автокорреляции возможно возникновение и других статистических аномалий — мультиколлинеарности, ложной корреляции и т.д.

Доказано, что оценки параметров, полученные с помощью МНК, обладают наилучшими свойствами (несмещенность, состоятельность, эффективность) при соблюдении ряда условий:

• выполнение приведенных выше исходных предпосылок регрессионного анализа;

• число наблюдений на одну независимую переменную должно быть не менее 5-6;

• должны отсутствовать аномальные значения (выбросы).

Кроме обычного МНК существуют и другие его разновидности (взвешенный МНК, обобщенный МНК), которые применяются при наличии статистических аномалий. Кроме МНК применяются и другие методы оценки параметров моделей. В этом обзоре мы эти вопросы рассматривать не будем.

Алгоритм проведения регрессионного анализа

Алгоритм действий исследователя при построении регрессионной модели (полевые работы мы, по понятным причинам, не рассматриваем — считаем, что исходные данные уже получены):

1. Подготовительный этап — постановка целей и задач исследования.

2. Первичная обработка исходных данных — об этом много написано в учебниках и пособиях по DataScience, сюда могут относится:

• выявление нерелевантных признаков (признаков, которые не несут полезной информации), нетипичных данных (выбросов), неинформативных признаков (имеющих большое количество одинаковых значений) и работа с ними (удаление/преобразование);

• выделение категориальных признаков;

• работа с пропущенными значениями;

• преобразование признаков-дат в формат datetime и т.д.

1. Визуализация исходных данных — предварительный графический анализ.

2. Дескриптивная (описательная) статистика — расчет выборочных характеристик и предварительные выводы о свойствах исходных данных.

3. Исследование закона распределения исходных данных и, при необходимости, преобразование исходных данных к нормальному закону распределения.

4. Выявление статистически аномальных значений (выбросов), принятие решения об их исключении.

   Этапы 4, 5 и 6 могут быть при необходимости объединены.

5. Корреляционный анализ — исследование корреляционных связей между исходными данными; это разведка перед проведением регрессионного анализа.

6. Построение регрессионной модели:

• выбор моделей;

• выбор методов;

• оценка параметров модели.

1. Статистический анализ регрессионной модели:  

• оценка ошибок аппроксимации (error metrics);

• анализ остатков (проверка нормальности распределения остатков и гипотезы о равенстве нулю среднего значения остатков);

• проверка адекватности модели;

• проверка значимости коэффициента детерминации;

• проверка значимости коэффициентов регрессии;

• проверка мультиколлинеарности (для множественных регрессионных моделей; вообще мультиколлинеарные переменные выявляются еще на стадии корреляционного анализа);

• проверка автокорреляции;

• проверка гетероскедастичности.

   Этапы 8 и 9 могут быть при необходимости повторяться несколько раз.

1. Сравнительный анализ нескольких регрессионных моделей, выбор наилучшей (при необходимости).

2. Прогнозирование с помощью регрессионной модели и оценка качества прогноза.

3. Выводы и рекомендации.

Само собой, этот алгоритм не есть истина в последней инстанции — в зависимости от особенностей исходных данных и вида модели могут возникать дополнительные задачи.

Применение пользовательских функций

Далее в обзоре мной будут использованы несколько пользовательских функций для решения разнообразных задач. Все эти функции созданы для облегчения работы и уменьшения размера программного кода. Данные функции загружается из пользовательского модуля my_module__stat.py, который доступен в моем репозитории на GitHub. Лично мне так удобнее работать, хотя каждый исследователь сам формирует себе инструменты по душе — особенно в части визуализации. Желающие могут пользоваться этими функциями, либо создать свои.

Итак, вот перечень данных функций:

• graph_scatterplot_sns — функция позволяет построить точечную диаграмму средствами seaborn и сохранить график в виде png-файла;

• graph_hist_boxplot_probplot_XY_sns  — функция позволяет визуализировать исходные данные для простой линейной регрессии путем одновременного построения гистограммы, коробчатой диаграммы и вероятностного графика (для переменных X и Y) средствами seaborn и сохранить график в виде png-файла; имеется возможность выбирать, какие графики строить (h — hist, b — boxplot, p — probplot);

• descriptive_characteristics — функция возвращает в виде DataFrame набор статистических характеристики выборки, их ошибок и доверительных интервалов;

• detecting_outliers_mad_test — функция выполняет проверку наличия аномальных значений (выбросов) по критерию наибольшего абсолютного отклонения (более подробно — см.[1, с.547]);

• norm_distr_check — проверка нормальности распределения исходных данных с использованием набора из нескольких статистических тестов;

• corr_coef_check — функция выполняет расчет коэффициента линейной корреляции Пирсона, проверку его значимости и расчет доверительных интервалов; об этой функции я писал в своей статье.

• graph_regression_plot_sns —  — функция позволяет построить график регрессионной модели.

Ряд пользовательских функций мы создаем в процессе данного обзора (они тоже включены в пользовательский модуль my_module__stat.py):

• regression_error_metrics — расчет ошибок аппроксимации регрессионной модели;

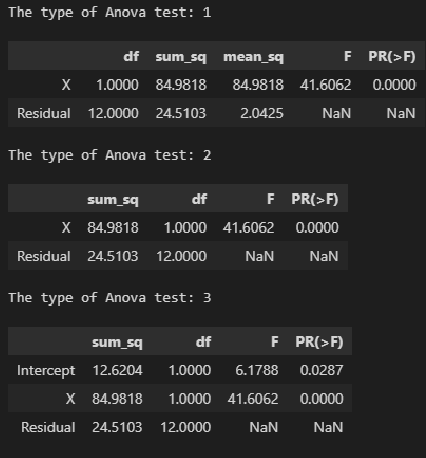
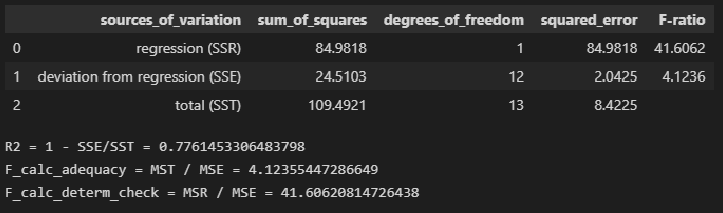
• ANOVA_table_regression_model — вывод таблицы дисперсионного анализа регрессионной модели;

• regression_model_adequacy_check — проверка адекватности регрессионной модели по критерию Фишера;

• determination_coef_check — проверка значимости коэффициента детерминации по критерию Фишера;

• regression_coef_check — проверка значимости коэффициентов регрессии по критеирю Стьюдента;

• Goldfeld_Quandt_test, Breush_Pagan_test, White_test — проверка гетероскедастичности с использование тестов Голдфелда-Квандта, Бриша-Пэгана и Уайта соответственно;

• regression_pair_predict — функция для прогнозирования с помощью парной регрессионной модели: рассчитывает прогнозируемое значение переменной Y по заданной модели, а также доверительные интервалы среднего и индивидуального значения для полученного прогнозируемого значения Y;

• graph_regression_pair_predict_plot_sns — прогнозирование: построение графика регрессионной модели (с доверительными интервалами) и вывод расчетной таблицы с данными для заданной области значений X.

ПОСТАНОВКА ЗАДАЧИ

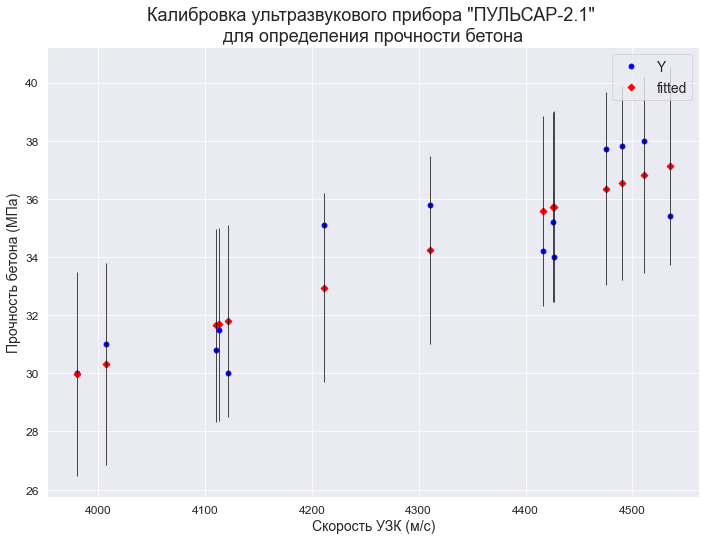
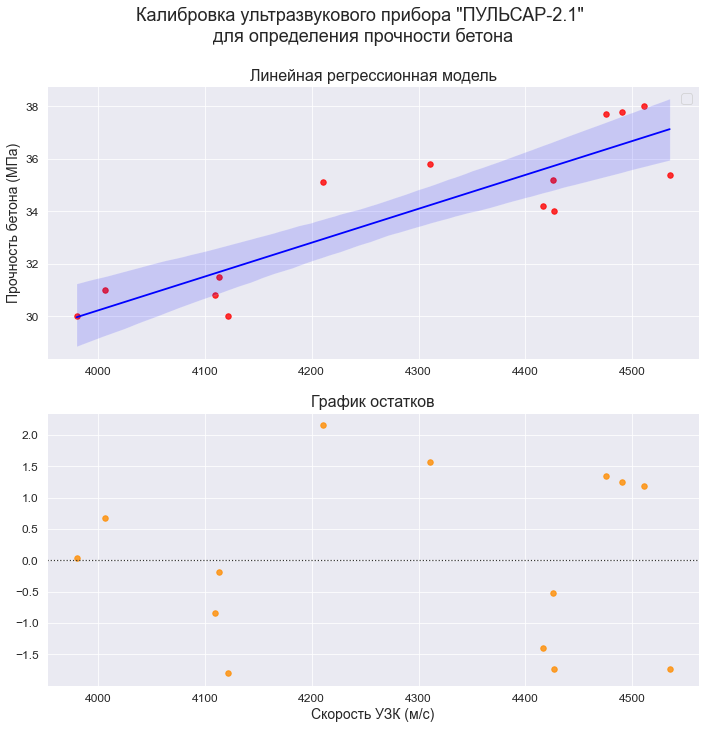
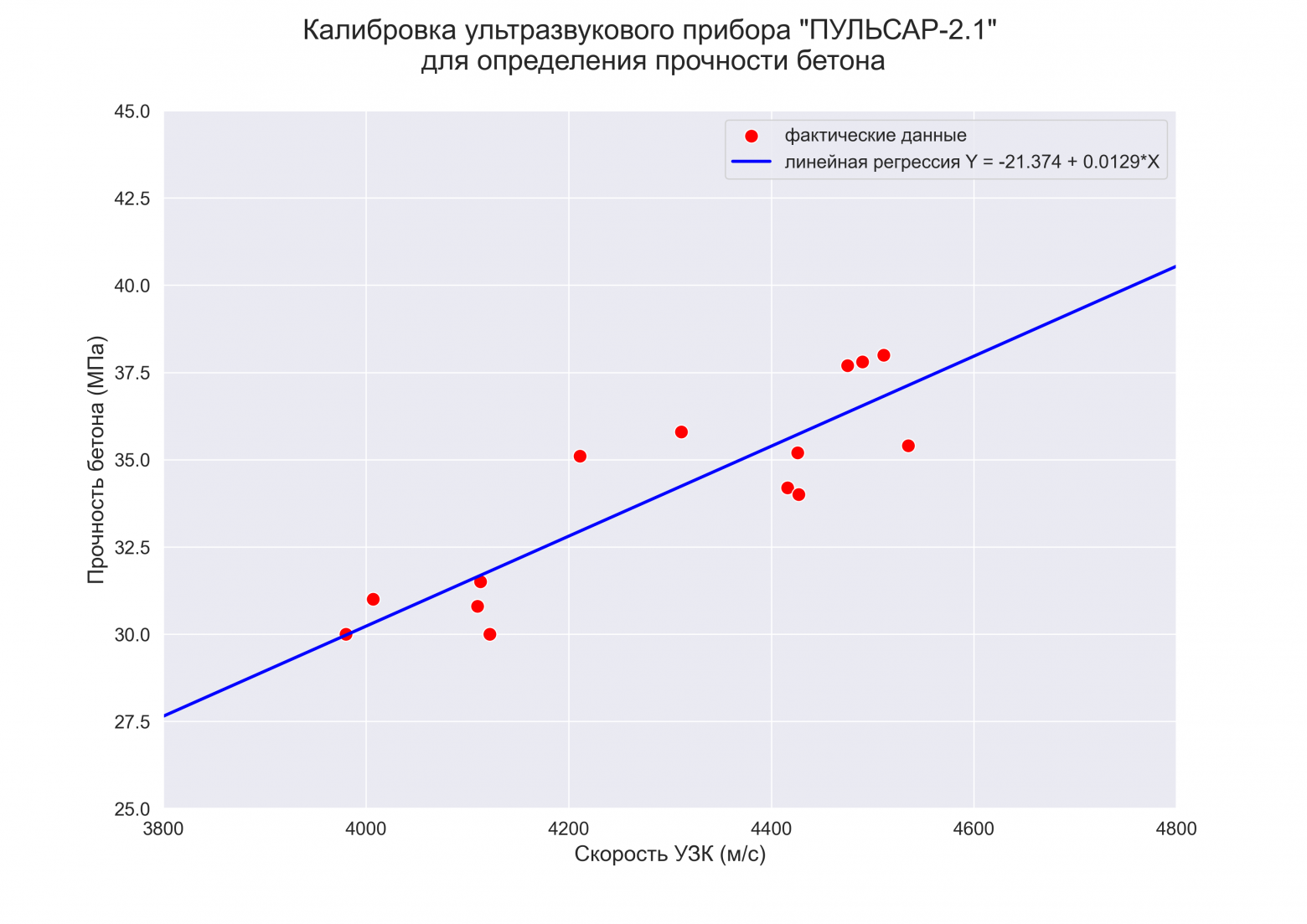
В качестве примера рассмотрим практическую задачу из области экспертизы промышленной безопасности — калибровку ультразвукового прибора для определения прочности бетона.

Итак, суть задачи: при обследовании несущих конструкций зданий и сооружений эксперт определяет прочность бетона с использованием ультразвукового прибора «ПУЛЬСАР-2.1», для которого необходимо предварительно построить градуировочную зависимость. Заключается это в следующем — производятся замеры с фиксацией следующих показателей:

• X — показания ультразвукового прибора «ПУЛЬСАР-2.1» (м/с)

• Y — результаты замера прочности бетона (методом отрыва со скалыванием) склерометром ИПС-МГ4.03.

Предполагается, что между показателями X и Y имеется линейная регрессионная зависимость, которая позволит прогнозировать прочность бетона на основании измерений, проведенных прибором «ПУЛЬСАР-2.1».

Были выполнены замеры фактической прочности бетона конструкций для бетонов одного вида с одним типом крупного заполнителя, с единой технологией производства. Для построения были выбраны 14 участков (не менее 12), включая участки, в которых значение косвенного показателя максимальное, минимальное и имеет промежуточные значения.

Настройка заголовков отчета:

# Общий заголовок проекта
Task_Project = 'Калибровка ультразвукового прибора "ПУЛЬСАР-2.1" nдля определения прочности бетона'

# Заголовок, фиксирующий момент времени
AsOfTheDate = ""

  # Заголовок раздела проекта
Task_Theme = ""

# Общий заголовок проекта для графиков
Title_String = f"{Task_Project}n{AsOfTheDate}"

# Наименования переменных
Variable_Name_X = "Скорость УЗК (м/с)"
Variable_Name_Y = "Прочность бетона (МПа)"

# Константы
INCH = 25.4    # мм/дюйм
  DecPlace = 5    # number of decimal places - число знаков после запятой

# Доверительная вероятность и уровень значимости:
p_level = 0.95
a_level = 1 - p_level   

Подключение модулей и библиотек:

# Стандартные модули и библиотеки

import os    # загрузка модуля для работы с операционной системой
import sys
import platform
print('{:<35}{:^0}'.format("Текущая версия Python: ", platform.python_version()), 'n')

import math
from math import *    # подключаем все содержимое модуля math, используем без псевдонимов

import numpy as np
#print ("Текущая версия модуля numpy: ", np.__version__)
print('{:<35}{:^0}'.format("Текущая версия модуля numpy: ", np.__version__))
from numpy import nan

import scipy as sci
print('{:<35}{:^0}'.format("Текущая версия модуля scipy: ", sci.__version__))
import scipy.stats as sps

import pandas as pd
print('{:<35}{:^0}'.format("Текущая версия модуля pandas: ", pd.__version__))

import matplotlib as mpl
print('{:<35}{:^0}'.format("Текущая версия модуля matplotlib: ", mpl.__version__))
import matplotlib.pyplot as plt

import seaborn as sns
print('{:<35}{:^0}'.format("Текущая версия модуля seaborn: ", sns.__version__))

import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.graphics.api as smg
import statsmodels.stats.api as sms
from statsmodels.compat import lzip
print('{:<35}{:^0}'.format("Текущая версия модуля statsmodels: ", sm.__version__))

import statistics as stat    # module 'statistics' has no attribute '__version__'

import sympy as sym
print('{:<35}{:^0}'.format("Текущая версия модуля sympy: ", sym.__version__))

# Настройки numpy
np.set_printoptions(precision = 4, floatmode='fixed')

# Настройки Pandas
pd.set_option('display.max_colwidth', None)    # текст в ячейке отражался полностью вне зависимости от длины
pd.set_option('display.float_format', lambda x: '%.4f' % x)

# Настройки seaborn
sns.set_style("darkgrid")
sns.set_context(context='paper', font_scale=1, rc=None)    # 'paper', 'notebook', 'talk', 'poster', None

# Настройки Mathplotlib
f_size = 8    # пользовательская переменная для задания базового размера шрифта
plt.rcParams['figure.titlesize'] = f_size + 12    # шрифт заголовка
plt.rcParams['axes.titlesize'] = f_size + 10      # шрифт заголовка
plt.rcParams['axes.labelsize'] = f_size + 6       # шрифт подписей осей
plt.rcParams['xtick.labelsize'] = f_size + 4      # шрифт подписей меток
plt.rcParams['ytick.labelsize'] = f_size + 4
plt.rcParams['legend.fontsize'] = f_size + 6      # шрифт легенды

# Пользовательские модули и библиотеки

Text1 = os.getcwd()    # вывод пути к текущему каталогу
#print(f"Текущий каталог: {Text1}")

sys.path.insert(1, "D:REPOSITORYMyModulePython")

from my_module__stat import *

ФОРМИРОВАНИЕ ИСХОДНЫХ ДАННЫХ

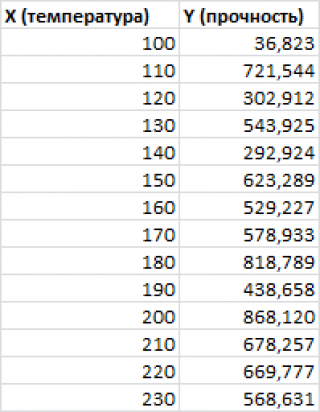
Показания ультразвукового прибора «ПУЛЬСАР-2.1» (м/с):

X = np.array([
    4416, 4211, 4113, 4110, 4122,
    4427, 4535, 4311, 4511, 4475,
    3980, 4490, 4007, 4426
    ])

Результаты замера прочности бетона (методом отрыва со скалыванием) прибором ИПС-МГ4.03:

Y = np.array([
    34.2, 35.1, 31.5, 30.8, 30.0,
    34.0, 35.4, 35.8, 38.0, 37.7,
    30.0, 37.8, 31.0, 35.2
    ])

Запишем данные в DataFrame:

calibrarion_df = pd.DataFrame({
    'X': X,
    'Y': Y})
display(calibrarion_df)
calibrarion_df.info()

Сохраняем данные в csv-файл:

calibrarion_df.to_csv(
    path_or_buf='data/calibrarion_df.csv',
    mode='w+',
    sep=';')

Cоздаем копию исходной таблицы для работы:

dataset_df = calibrarion_df.copy()

ВИЗУАЛИЗАЦИЯ ДАННЫХ

Границы значений переменных (при построении графиков):

(Xmin_graph, Xmax_graph) = (3800, 4800)
(Ymin_graph, Ymax_graph) = (25, 45)

# Пользовательская функция
graph_scatterplot_sns(
    X, Y,
    Xmin=Xmin_graph, Xmax=Xmax_graph,
    Ymin=Ymin_graph, Ymax=Ymax_graph,
    color='orange',
    title_figure=Task_Project,
    x_label=Variable_Name_X,
    y_label=Variable_Name_Y,
    s=100,
    file_name='graph/scatterplot_XY_sns.png')

Существует универсальный набор графиков — гистограмма, коробчатая диаграмма, вероятностный график — которые позволяют исследователю сделать предварительные выводы о свойствах исходных данных.

Так как объем выборки невелик (n=14), строить гистограммы распределения переменных X и Y не имеет смысла, поэтому ограничимся построением коробчатых диаграмм и вероятностных графиков:

# Пользовательская функция
graph_hist_boxplot_probplot_XY_sns(
    data_X=X, data_Y=Y,
    data_X_min=Xmin_graph, data_X_max=Xmax_graph,
    data_Y_min=Ymin_graph, data_Y_max=Ymax_graph,  
    graph_inclusion='bp',    # выбираем для построения виды графиков: b - boxplot, p - probplot)
    data_X_label=Variable_Name_X,
    data_Y_label=Variable_Name_Y,
    title_figure=Task_Project,
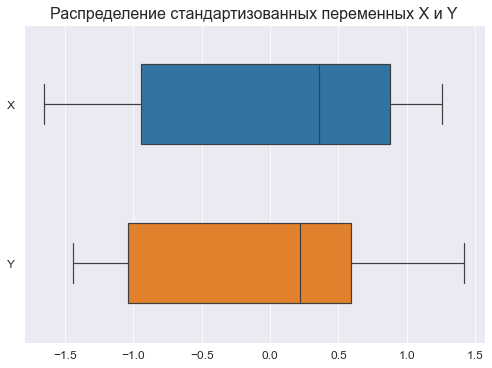
    file_name='graph/hist_boxplot_probplot_XY_sns.png')    

Для сравнения характера распределений переменных X и Y возможно также построить совмещенную коробчатую диаграмму по стандартизованным данным:

# стандартизуем исходные данные
standardize_df = lambda X: ((X - np.mean(X))/np.std(X))

dataset_df_standardize = dataset_df.copy()
dataset_df_standardize = dataset_df_standardize.apply(standardize_df)
display(dataset_df_standardize)

# построим график
fig, axes = plt.subplots(figsize=(210/INCH, 297/INCH/2))
axes.set_title("Распределение стандартизованных переменных X и Y", fontsize = 16)
sns.boxplot(
    data=dataset_df_standardize,    
    orient='h',
    width=0.5,
    ax=axes)
plt.show()

Графический анализ позволяет сделать следующие выводы:

1. Отсутствие выбросов на коробчатых диаграммах свидетельствует об однородности распределения переменных.

2. Смещение медианы вправо на коробчатых диаграммах свидетельствует о левосторонней асимметрии распределения.

ДЕСКРИПТИВНАЯ (ОПИСАТЕЛЬНАЯ СТАТИСТИКА)

Собственно говоря, данный этап требуется проводить далеко не всегда, однако с помощью статистических характеристик выборки мы тоже можем сделать полезные выводы.

Описательная статистика исходных данных средствами библиотеки Pandas — самый простой вариант:

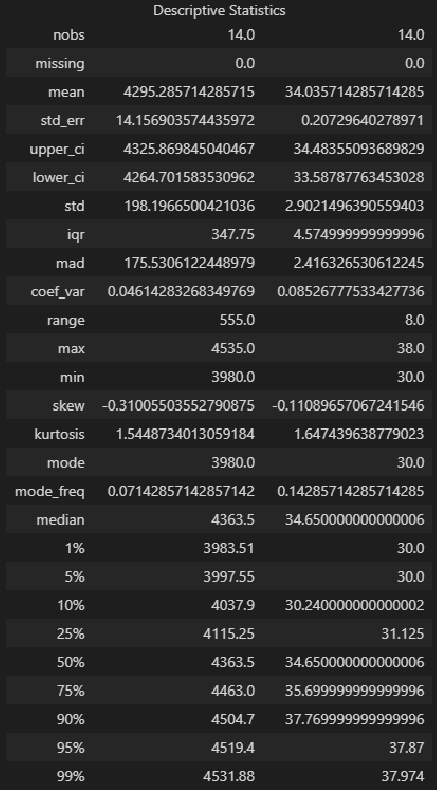
dataset_df.describe()

Описательная статистика исходных данных средствами библиотеки statsmodels — более развернутый вариант, с большим количеством показателей:

from statsmodels.stats.descriptivestats import Description
result = Description(
    dataset_df,
    stats=["nobs", "missing", "mean", "std_err", "ci", "ci", "std", "iqr", "mad", "coef_var", "range", "max", "min", "skew", "kurtosis", "mode",
           "median", "percentiles", "distinct", "top", "freq"],
    alpha=a_level,
    use_t=True)
display(result.summary())

Описательная статистика исходных данных с помощью пользовательской функции descriptive_characteristics:

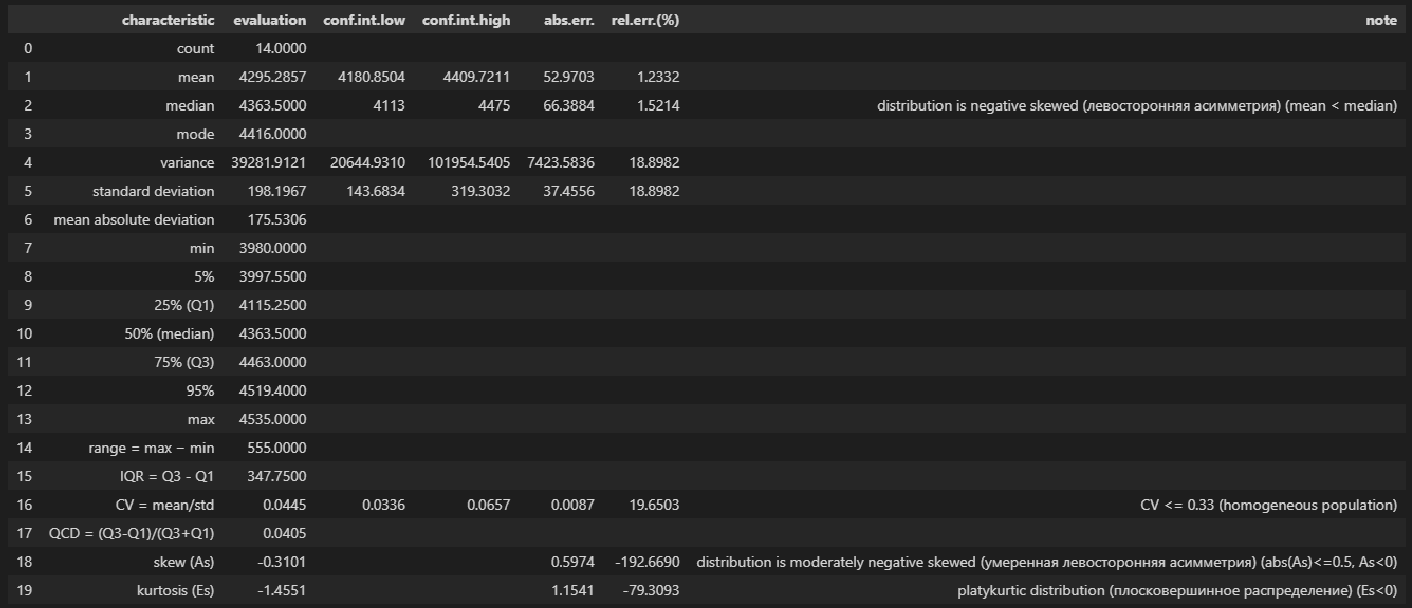
# Пользовательская функция
descriptive_characteristics(X)

Выводы:

1. Сравнение показателей среднего арифметического (mean) и медианы (median) свидетельствует о левосторонней асимметрии (т.к.mean < median).

2. Значение коэффициента вариации CV = 0.0445 и доверительный интервал для него 0.0336 ≤ CV ≤ 0.0657 свидетельствует об однородности исходных данных (т.к. CV ≤ 0.33).

3. Значение показателя асимметрии skew (As) = -0.3101 свидетельствует об умеренной левосторонней асимметрии распределении (т.к. |As| ≤ 0.5, As < 0).

4. Значение показателя эксцесса kurtosis (Es) = -1.4551 свидетельствует о плосковершинном распределении (platykurtic distribution) (т.к. Es < 0).

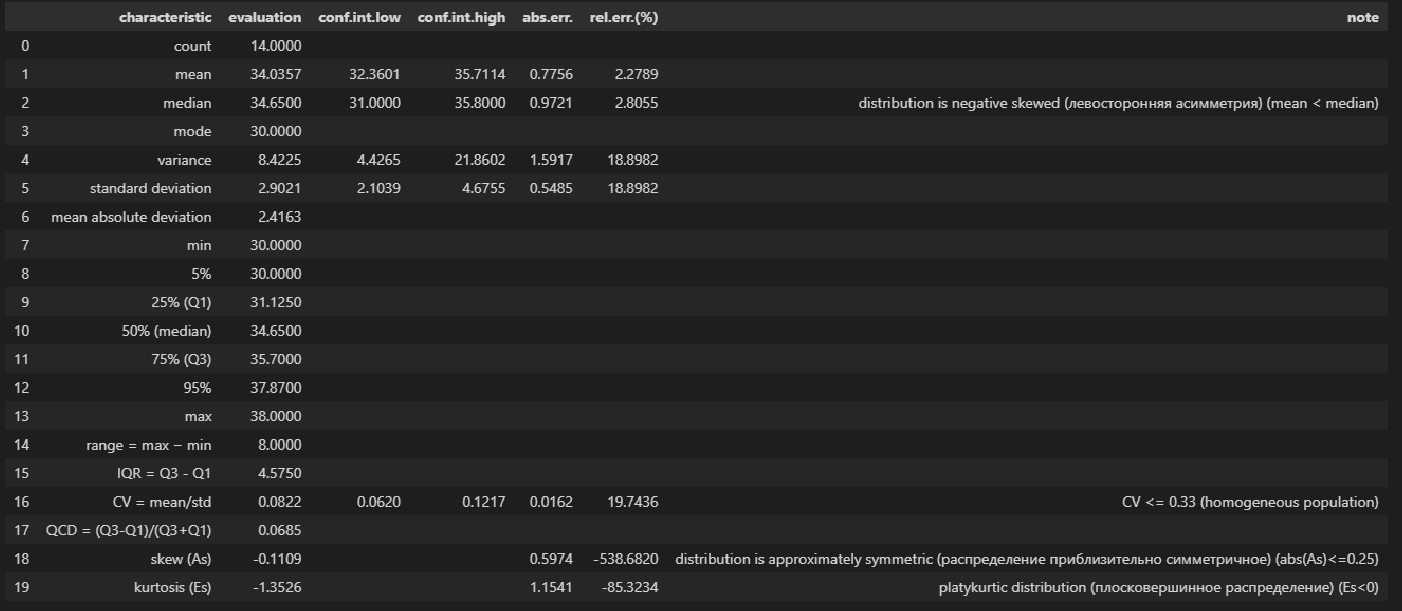
# Пользовательская функция
descriptive_characteristics(Y)

Выводы:

1. Сравнение показателей среднего арифметического (mean) и медианы (median) свидетельствует о левосторонней асимметрии (т.к.mean < median).

2. Значение коэффициента вариации CV = 0.0822 и доверительный интервал для него 0.06202 ≤ CV ≤ 0.1217 свидетельствует об однородности исходных данных (т.к. CV ≤ 0.33).

3. Значение показателя асимметрии skew (As) = -0.1109 свидетельствует о приблизительно симметричном распределении (т.к. |As| ≤ 0.25).

4. Значение показателя эксцесса kurtosis (Es) = -1.3526 свидетельствует о плосковершинном распределении (platykurtic distribution) (т.к. Es < 0).

ПРОВЕРКА НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ

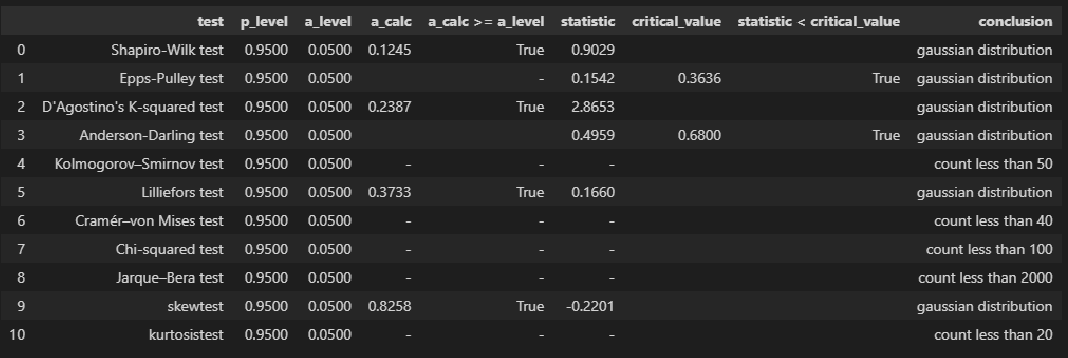
Для проверки нормальности распределения использована пользовательская функция norm_distr_check, которая объединяет в себе набор стандартных статистических тестов проверки нормальности. Все тесты относятся к стандартному инструментарию Pyton (библиотека scipy, модуль stats), за исключением теста Эппса-Палли (Epps-Pulley test); о том, как реализовать этот тест средствами Pyton я писал в своей статье https://habr.com/ru/post/685582/.

Примечание: для использования функции norm_distr_check в каталог с ipynb-файлом необходимо поместить папку table c файлом Tep_table.csv, который содержит табличные значения статистики критерия Эппса-Палли.

# пользовательская функция
norm_distr_check(X)

# Пользовательская функция
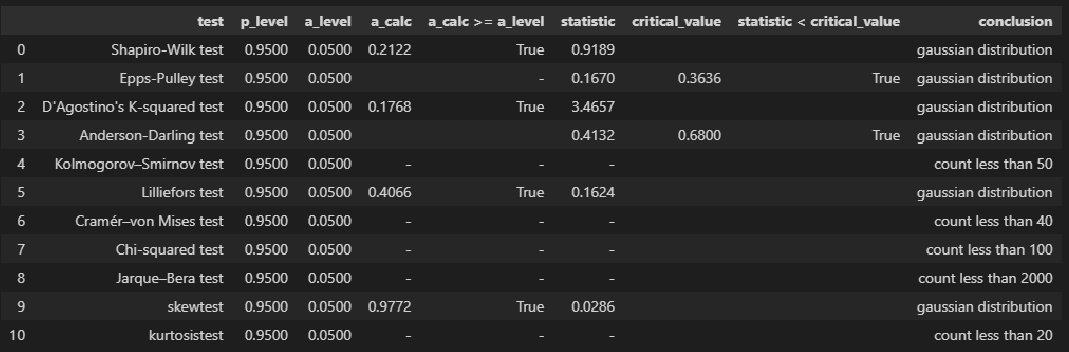
norm_distr_check (Y)

Вывод: большинство статистических тестов позволяют принять гипотезу о нормальности распределения переменных X и Y.

ПРОВЕРКА АНОМАЛЬНЫХ ЗНАЧЕНИЙ (ВЫБРОСОВ)

Статистическую проверку аномальных значений (выбросов) не стоит путать с проверкой выбросов, которая проводится на этапе первичной обработки результатов наблюдений. Последняя проводится с целью отсеять явные ошибочные данные (например, в результате неправильно поставленной запятой величина показателя может увеличиться/уменьшиться на порядок); здесь же мы говорим о статистической проверке данных, которые уже прошли этап первичной обработки.

Имеется довольно много критериев для проверки аномальных значений (подробнее см.[1]); вообще данная процедура довольно неоднозначная:

• критерии зависят от вида распределения;

• мало данных о сравнительной мощности этих критериев;

• даже в случае принятии гипотезы о нормальном распределении в выборке могут быть обнаружены аномальные значения и пр.

Кроме существует дилемма: если какие-то значения в выборке признаны выбросами — стоит или не стоит исследователю исключать их? Ведь каждое значение несет в себе информацию, причем иногда весьма ценную, а сильно отклоняющиеся от основного массива данные (которые не являются выбросами в смысле первичной обработки, но являются статистическим значимыми аномальными значениями) могут кардинально изменить статистический вывод.

В общем, о задаче выявления аномальных значений (выбросов) можно написать отдельно, а пока, в данном разборе, ограничимся проверкой аномальных значений по критерию наибольшего максимального отклонения (см.[1, с.547]) с помощью пользовательской функции detecting_outliers_mad_test. Данные функция возвращает DataFrame, которые включает список аномальных значений со следующими признаками:

• value — проверяемое значение из выборки;

• mad_calc и mad_table — расчетное и табличное значение статистики критерия;

• outlier_conclusion — вывод (выброс или нет).

Обращаю внимание, что критерий наибольшего максимального отклонения можно использовать только для нормально распределенных данных.

# пользовательская функция
print("Проверка наличия выбросов переменной X:n")
result = detecting_outliers_mad_test(X)
mask = (result['outlier_conclusion'] == 'outlier')
display(result[mask])

# пользовательская функция
print("Проверка наличия выбросов переменной Y:n")
result = detecting_outliers_mad_test(Y)
mask = (result['outlier_conclusion'] == 'outlier')
display(result[mask])

Вывод: в случае обеих переменных X и Y список пуст, следовательно, аномальных значений (выбросов) не выявлено.

КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

Корреляционный анализ — это разведка перед построением регрессионной модели.

Выполним расчет коэффициента линейной корреляции Пирсона, проверку его значимости и построение доверительных интервалов с помощью пользовательской функции corr_coef_check (про эту функцию более подробно написано в моей статье https://habr.com/ru/post/683442/):

# пользовательская функция
display(corr_coef_check(X, Y, scale='Evans'))

Выводы:

1. Значение коэффициента корреляции coef_value = 0.8900 свидетельствует о весьма сильной корреляционной связи (по шкале Эванса).

2. Коэффициент корреляции значим по критерию Стьюдента: t_calc ≥ t_table, a_calc ≤ a_level.

3. Доверительный интервал для коэффициента корреляции: 0.6621 ≤ coef_value ≤ 0.9625.

РЕГРЕССИОННЫЙ АНАЛИЗ

Предварительная визуализация

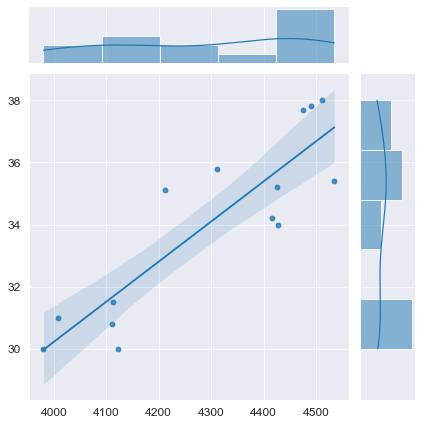
python позволяет выполнить предварительную визуализацию, например, с помощью функции jointplot библиотеки seaborn:

fig = plt.figure(figsize=(297/INCH, 210/INCH))
axes = sns.jointplot(
    x=X, y=Y,
    kind='reg',
    ci=95)
plt.show()

Построение модели

Выполним оценку параметров и анализ простой линейной регрессии (simple linear regression), используя библиотеку statsmodels (https://www.statsmodels.org/) и входящий в нее модуль линейной регрессии Linear Regression (https://www.statsmodels.org/stable/regression.html).

Данный модуль включает в себя классы, реализующие различные методы оценки параметров моделей линейной регрессии, в том числе:

• класс OLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.OLS.html#statsmodels.regression.linear_model.OLS) — Ordinary Least Squares (обычный метод наименьших квадратов).

• класс WLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.WLS.html#statsmodels.regression.linear_model.WLS) — Weighted Least Squares (метод взвешенных наименьших квадратов) (https://en.wikipedia.org/wiki/Weighted_least_squares), применяется, если имеет место гетероскедастичность данных (https://ru.wikipedia.org/wiki/Гетероскедастичность).

• класс GLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.GLS.html#statsmodels.regression.linear_model.GLS) — Generalized Least Squares (обобщенный метод наименьших квадратов) (https://en.wikipedia.org/wiki/Generalized_least_squares), применяется, если существует определенная степень корреляции между остатками в модели регрессии.

• класс GLSAR (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.GLSAR.html#statsmodels.regression.linear_model.GLSAR) — Generalized Least Squares with AR covariance structure (обобщенный метод наименьших квадратов, ковариационная структура с автокорреляцией — экспериментальный метод)

• класс RecurciveLS (https://www.statsmodels.org/stable/examples/notebooks/generated/recursive_ls.html) — Recursive least squares (рекурсивный метод наименьших квадратов) (https://en.wikipedia.org/wiki/Recursive_least_squares_filter)

• классы RollingOLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.rolling.RollingOLS.html#statsmodels.regression.rolling.RollingOLS) и RollingWLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.rolling.RollingWLS.html#statsmodels.regression.rolling.RollingWLS) — скользящая регрессия (https://www.statsmodels.org/stable/examples/notebooks/generated/rolling_ls.html, https://help.fsight.ru/ru/mergedProjects/lib/01_regression_models/rolling_regression.htm)

  и т.д.

Так как исходные данные подчиняются нормальному закону распределения и аномальные значения (выбросы) отсутствуют, воспользуемся для оценки параметров обычным методом наименьших квадратов (класс OLS):

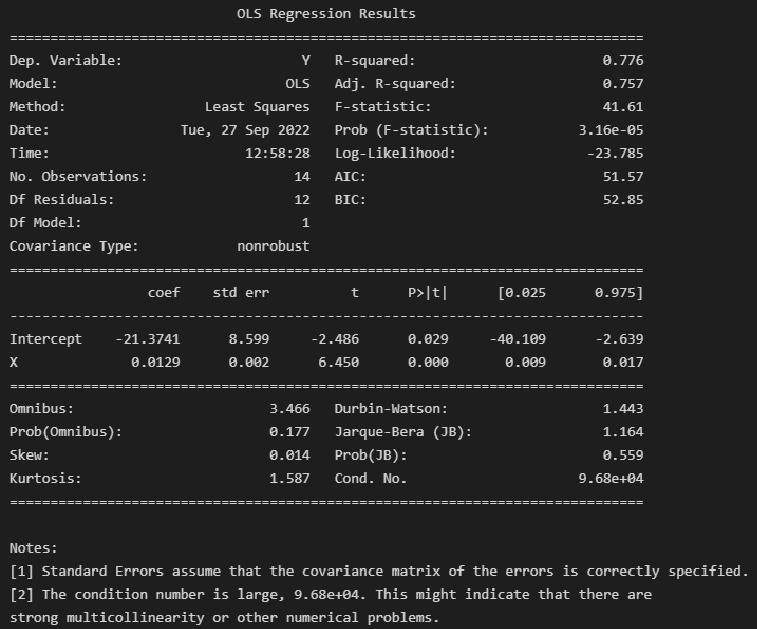
model_linear_ols = smf.ols(formula='Y ~ X', data=dataset_df)
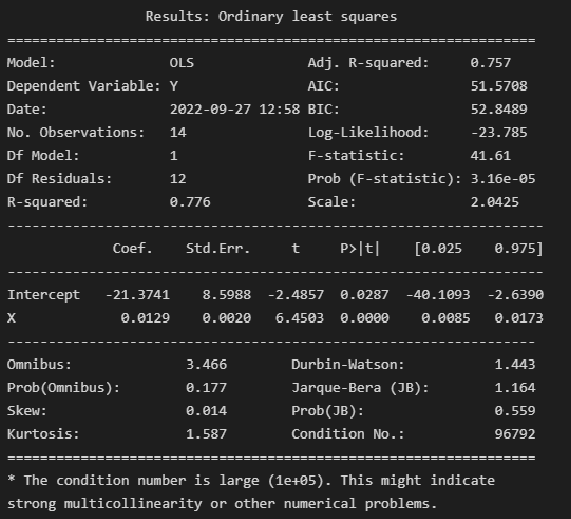
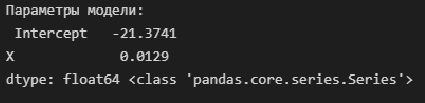
result_linear_ols = model_linear_ols.fit()
print(result_linear_ols.summary())

Альтернативная форма выдачи результатов:

print(result_linear_ols.summary2())

Результаты построения модели мы получаем как класс statsmodels.regression.linear_model.RegressionResults (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.html#statsmodels.regression.linear_model.RegressionResults).

Экспресс-выводы, которые мы можем сразу сделать из результатов построения модели:

1. Коэффициенты регрессии модели Y = b0 + b1∙X:

   • Intercept = b0 = -21.3741

   • b1 = 0.0129

2. Коэффициент детерминации R-squared = 0.776, его скорректированная оценка Adj. R-squared = 0.757 — это означает, что регрессионная модуль объясняет 75.75% вариации переменной Y.

3. Проверка значимости коэффициента детерминации:

   • расчетное значение статистики критерия Фишера: F-statistic = 41.61

   • расчетный уровень значимости Prob (F-statistic) = 3.16e-05

   • так как значение Prob (F-statistic) < 0.05, то нулевая гипотеза R-squared = 0 НЕ ПРИНИМАЕТСЯ, т.е. коэффициент детерминации ЗНАЧИМ

4. Проверка значимости коэффициентов регрессии:

   • расчетный уровень значимости P>|t| не превышает 0.05 — это означает, что оба коэффициента регрессии значимы

   • об этом же свидетельствует то, что доверительный интервал для обоих коэффициентов регрессии ([0.025; 0.975]) не включает в себя точку 0

   Также в таблице результатов содержится прочая информация по коэффициентам регрессии: стандартная ошибка Std.Err. расчетное значение статистики критерия Стьюдента t для проверки гипотезы о значимости.

5. Анализ остатков модели:

   • Тест Omnibus — про этот тест подробно написано в https://en.wikipedia.org/wiki/Omnibus_test, https://medium.com/swlh/interpreting-linear-regression-through-statsmodels-summary-4796d359035a, http://work.thaslwanter.at/Stats/html/statsModels.html.

     Расчетное значение статистики критерия Omnibus = 3.466 — по сути расчетное значение F-критерия (см. https://en.wikipedia.org/wiki/Omnibus_test).

     Prob(Omnibus) = 0.177 — показывает вероятность нормального распределения остатков (значение 1 указывает на совершенно нормальное распределение).

     Учитывая, что в дальнейшем мы проверим нормальность распределения остатков по совокупности различных тестов, в том числе с достаточно высокой мощностью, и все тесты позволят принять гипотезу о нормальном распределении — в данном случае к тесту Omnibus возникают вопросы. С этим тестом нужно разбираться отдельно.

   • Skew = 0.014 и Kurtosis = 1.587 — показатели асимметрии и эксцесса остатков свидетельствуют, что распределение остатков практически симметричное, островершинное.

   • проверка нормальности распределения остатков по критерию Харке-Бера: расчетное значение статистики критерия Jarque-Bera (JB) = 1.164 и расчетный уровень значимости Prob(JB) = 0.559. К данным результатам также возникают вопросы, особенно, если учесть, что критерий Харке-Бера является асимптотическим, расчетное значение имеет распределение хи-квадрат, поэтому данный критерий рекомендуют применять только для больших выборок (см. https://en.wikipedia.org/wiki/Jarque–Bera_test). Проверку нормальности распределения остатков модели лучше проводить с использованием набора стандартных статистических тестов python (см. далее).

6. Проверка автокорреляции по критерию Дарбина-Уотсона: Durbin-Watson = 1.443.

   Мы не будем здесь разбирать данный критерий, так как явление автокорреляции больше характерно для данных, выражаемых в виде временных рядов. Однако, для грубой оценки считается, что при расчетном значении статистики криетрия Дарбина=Уотсона а интервале [1; 2] автокорреляция отсутствует (см.https://en.wikipedia.org/wiki/Durbin–Watson_statistic).

   Более подробно про критерий Дарбина-Уотсона — см. [1, с.659].

Прочая информация, которую можно извлечь из результатов построения модели:

1. Covariance Type — тип ковариации, подробнее см. https://habr.com/ru/post/681218/, https://towardsdatascience.com/simple-explanation-of-statsmodel-linear-regression-model-summary-35961919868b#:~:text=Covariance type is typically nonrobust,with respect to each other.

2. Scale — масштабный коэффициент для ковариационной матрицы (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.scale.html#statsmodels.regression.linear_model.RegressionResults.scale), равен величине Mean squared error (MSE) (cреднеквадратической ошибке), об подробнее см. далее, в разделе про ошибки аппроксимации моделей.

3. Показатели сравнения качества различных моделей:

   • Log-Likelihood — логарифмическая функция правдоподобия, подробнее см. https://en.wikipedia.org/wiki/Likelihood_function#Log-likelihood, https://habr.com/ru/post/433804/

   • AIC — информационный критерий Акаике (Akaike information criterion), подробнее см. https://en.wikipedia.org/wiki/Akaike_information_criterion

   • BIC — информационный критерий Байеса (Bayesian information criterion), подробнее см. https://en.wikipedia.org/wiki/Bayesian_information_criterion

   В данной статье мы эти показатели рассматривать не будем, так как задача выбора одной модели из нескольких перед нами не стоит.

4. Число обусловленности Cond. No = 96792 используется для проверки мультиколлинеарности (считается, что мультиколлинеарность есть, если значение Cond. No > 30) (см. http://work.thaslwanter.at/Stats/html/statsModels.html). В нашем случае парной регрессионной модели о мультиколлинеарности речь не идет.

Далее будем извлекать данные из стандартного набора выдачи результатов и анализировать их более подробно. Последующие этапы вовсе не обязательно проводить в полном объеме при решении задач, но здесь мы рассмотрим их подробно.

Параметры и уравнение регрессионной модели

Извлечем параметры полученной модели — как свойство params модели:

print('Параметры модели: n', result_linear_ols.params, type(result_linear_ols.params))

Имея параметры модели, можем формализовать уравнение модели Y = b0 + b1*X:

b0 = result_linear_ols.params['Intercept']
b1 = result_linear_ols.params['X']
Y_calc = lambda x: b0 + b1*x

График регрессионной модели

Для построения графиков регрессионных моделей можно воспользоваться стандартными возможностями библиотек statsmodels, seaborn, либо создать пользовательскую функцию — на усмотрение исследователя:

1. Построение графиков регрессионных моделей с использованием библиотеки statsmodels

С помощью функции statsmodels.graphics.plot_fit (https://www.statsmodels.org/stable/generated/statsmodels.graphics.regressionplots.plot_fit.html#statsmodels.graphics.regressionplots.plot_fit) — отображается график Y and Fitted vs.X (фактические и расчетные значения Y с доверительным интервалом для каждого значения Y):

fig, ax = plt.subplots(figsize=(297/INCH, 210/INCH))
fig = sm.graphics.plot_fit(
    result_linear_ols, 'X',
    vlines=True,    # это параметр отвечает за отображение доверительных интервалов для Y
    ax=ax)
ax.set_ylabel(Variable_Name_Y)
ax.set_xlabel(Variable_Name_X)
ax.set_title(Task_Project)
plt.show()

С помощью функции statsmodels.graphics.plot_regress_exog (https://www.statsmodels.org/stable/generated/statsmodels.graphics.regressionplots.plot_regress_exog.html#statsmodels.graphics.regressionplots.plot_regress_exog) — отображается область 2х2, которая содержит:

• предыдущий график Y and Fitted vs.X;

• график остатков Residuals versus X;

• график Partial regression plot — график частичной регрессии, пытается показать эффект добавления другой переменной в модель, которая уже имеет одну или несколько независимых переменных (более подробно см. https://en.wikipedia.org/wiki/Partial_regression_plot);

• график CCPR Plot (Component-Component plus Residual Plot) — еще один способ оценить влияние одной независимой переменной на переменную отклика, принимая во внимание влияние других независимых переменных (более подробно — см. https://towardsdatascience.com/calculating-price-elasticity-of-demand-statistical-modeling-with-python-6adb2fa7824d, https://www.kirenz.com/post/2021-11-14-linear-regression-diagnostics-in-python/linear-regression-diagnostics-in-python/).

fig = plt.figure(figsize=(297/INCH, 210/INCH))
sm.graphics.plot_regress_exog(result_linear_ols, 'X', fig=fig)
plt.show()

2. Построение графиков регрессионных моделей с использованием библиотеки seaborn

Воспользуемся модулем regplot библиотеки seaborn (https://seaborn.pydata.org/generated/seaborn.regplot.html). Данный модуль позволяет визуализировать различные виды регрессии:

• линейную

• полиномиальную

• логистическую

• взвешенную локальную регрессию (LOWESS — Locally Weighted Scatterplot Smoothing) (см. http://www.machinelearning.ru/wiki/index.php?title=Алгоритм_LOWESS, https://www.statsmodels.org/stable/generated/statsmodels.nonparametric.smoothers_lowess.lowess.html)

Более подробно про модуль regplot можно прочитать в статье: https://pyprog.pro/sns/sns_8_regression_models.html.

Есть более совершенный модуль lmplot (https://seaborn.pydata.org/generated/seaborn.lmplot.html), который объединяет в себе regplot и FacetGrid, но мы его здесь рассматривать не будем.

# создание рисунка (Figure) и области рисования (Axes)
fig = plt.figure(figsize=(297/INCH, 420/INCH/1.5))
ax1 = plt.subplot(2,1,1)
ax2 = plt.subplot(2,1,2)
# заголовок рисунка (Figure)
title_figure = Task_Project
fig.suptitle(title_figure, fontsize = 18)
# заголовок области рисования (Axes)
title_axes_1 = 'Линейная регрессионная модель'
ax1.set_title(title_axes_1, fontsize = 16)
# график регрессионной модели
order_mod = 1    # порядок модели
#label_legend_regr_model = 'фактические данные'
sns.regplot(
    #data=dataset_df,
    x=X, y=Y,
    #x_estimator=np.mean,
    order=order_mod,
    logistic=False,
    lowess=False,
    robust=False,
    logx=False,
    ci=95,
    scatter_kws={'s': 30, 'color': 'red'},
    line_kws={'color': 'blue'},
    #label=label_legend_regr_model,
    ax=ax1)
ax1.set_ylabel(Variable_Name_Y)
ax1.legend()
# график остатков
title_axes_2 = 'График остатков'
ax2.set_title(title_axes_2, fontsize = 16)
sns.residplot(
    #data=dataset_df,
    x=X, y=Y,
    order=order_mod,
    lowess=False,
    robust=False,
    scatter_kws={'s': 30, 'color': 'darkorange'},
    ax=ax2)
ax2.set_xlabel(Variable_Name_X)

plt.show()

3. Построение графиков регрессионных моделей с помощью пользовательской функции

# Пользовательская функция
graph_regression_plot_sns(
    X, Y,
    regression_model=Y_calc,
    Xmin=Xmin_graph, Xmax=Xmax_graph,
    Ymin=Ymin_graph, Ymax=Ymax_graph,
    title_figure=Task_Project,
    x_label=Variable_Name_X,
    y_label=Variable_Name_Y,
    label_legend_regr_model=f'линейная регрессия Y = {b0:.3f} + {b1:.4f}*X',
    s=80,
    file_name='graph/regression_plot_lin.png')

Статистический анализ регрессионной модели

1. Расчет ошибки аппроксимации (Error Metrics)

Ошибки аппроксимации (Error Metrics) позволяют получить общее представление о качестве модели, а также позволяют сравнивать между собой различные модели.

Создадим пользовательскую функцию, которая рассчитывает основные ошибки аппроксимации для заданной модели:

• Mean squared error (MSE) или Mean squared deviation (MSD) — среднеквадратическая ошибка (https://en.wikipedia.org/wiki/Mean_squared_error):

• Root mean square error (RMSE) или Root mean square deviation (RMSD) — квадратный корень из MSE (https://en.wikipedia.org/wiki/Root-mean-square_deviation):

• Mean absolute error (MAE) — средняя абсолютная ошибка (https://en.wikipedia.org/wiki/Mean_absolute_error):

• Mean squared prediction error (MSPE) — среднеквадратическая ошибка прогноза (среднеквадратическая ошибка в процентах) (https://en.wikipedia.org/wiki/Mean_squared_prediction_error):

• Mean absolute percentage error (MAPE) — средняя абсолютная ошибка в процентах (https://en.wikipedia.org/wiki/Mean_absolute_percentage_error):

Про выбор метрики см. также https://machinelearningmastery.ru/how-to-select-the-right-evaluation-metric-for-machine-learning-models-part-2-regression-metrics-d4a1a9ba3d74/.

# Пользовательская функция
def regression_error_metrics(model, model_name=''):
    model_fit = model.fit()
    Ycalc = model_fit.predict()
    n_fit = model_fit.nobs
    Y = model.endog
    
    MSE = (1/n_fit) * np.sum((Y-Ycalc)**2)
    RMSE = sqrt(MSE)
    MAE = (1/n_fit) * np.sum(abs(Y-Ycalc))
    MSPE = (1/n_fit) *  np.sum(((Y-Ycalc)/Y)**2)
    MAPE = (1/n_fit) *  np.sum(abs((Y-Ycalc)/Y))
        
    model_error_metrics = {
        'MSE': MSE,
        'RMSE': RMSE,
        'MAE': MAE,
        'MSPE': MSPE,
        'MAPE': MAPE}
    
    result = pd.DataFrame({
        'MSE': MSE,
        'RMSE': RMSE,
        'MAE': MAE,
        'MSPE': "{:.3%}".format(MSPE),
        'MAPE': "{:.3%}".format(MAPE)},
        index=[model_name])        
        
    return model_error_metrics, result

(model_error_metrics, result) = regression_error_metrics(model_linear_ols, model_name='linear_ols')
display(result)

В литературе по прикладной статистике нет единого мнения о допустимом размере относительных ошибок аппроксимации: в одних источниках допустимой считается ошибка 5-7%, в других она может быть увеличена до 8-10%, и даже до 15%.

Вывод: модель хорошо аппроксимирует фактические данные (относительная ошибка аппроксимации MAPE = 3.405% < 10%).

2. Дисперсионный анализ регрессионной модели (ДАРМ)

ДАРМ не входит в стандартную форму выдачи результатов Regression Results, однако я решил написать здесь о нем по двум причинам:

1. Именно анализ дисперсии регрессионной модели, разложение этой дисперсии на составляющие дает фундаментальное представление о сути регрессии, а термины, используемые при ДАРМ, применяются на последующих этапах анализа.

2. С терминами ДАРМ в литературе по прикладной статистике имеется некоторая путаница, в разных источниках они могут именоваться по-разному (см., например, [8, с.52]), поэтому, чтобы двигаться дальше, необходимо определиться с понятиями.

При ДАРМ общую вариацию результативного признака (Y) принято разделять на две составляющие — вариация, обусловленная регрессией и вариация, обусловленная отклонениями от регрессии (остаток), при этом в разных источниках эти термины могут именоваться и обозначаться по-разному, например:

1. Вариация, обусловленная регрессией — может называться Explained sum of squares (ESS), Sum of Squared Regression (SSR) (https://en.wikipedia.org/wiki/Explained_sum_of_squares, https://towardsdatascience.com/anova-for-regression-fdb49cf5d684), Sum of squared deviations (SSD).

2. Вариация, обусловленная отклонениями от регрессии (остаток) — может называться Residual sum of squares (RSS), Sum of squared residuals (SSR), Squared estimate of errors, Sum of Squared Error (SSE) (https://en.wikipedia.org/wiki/Residual_sum_of_squares, https://towardsdatascience.com/anova-for-regression-fdb49cf5d684); в отчественной практике также применяется термин остаточная дисперсия.

3. Общая (полная) вариация — может называться Total sum of squares (TSS), Sum of Squared Total (SST) (https://en.wikipedia.org/wiki/Partition_of_sums_of_squares, https://towardsdatascience.com/anova-for-regression-fdb49cf5d684).

Как видим, путаница знатная:

• в разных источниках под SSR могут подразумеваться различные показатели;

• легко перепутать показатели ESS и SSE;

• в библиотеке statsmodel также есть смешение терминов: для показателя Explained sum of squares используется свойство ess, а для показателя Sum of squared (whitened) residuals — свойство ssr.

Мы будем пользоваться системой обозначений, принятой в большинстве источников — SSR (Sum of Squared Regression), SSE (Sum of Squared Error), SST (Sum of Squared Total). Стандартная таблица ДАРМ в этом случае имеет вид:

Примечания:

1. Здесь приведена таблица ДАРМ для множественной линейной регрессионной модели (МЛРМ), в нашем случае при ПЛРМ мы имеем частный случай p=1.

2. Показатели Fcalc-ad и Fcalc-det — расчетные значения статистики критерия Фишера при проверке адекватности модели и значимости коэффициента детерминации (об этом — см.далее).

Более подробно про дисперсионный анализ регрессионной модели — см.[4, глава 3].

Класс statsmodels.regression.linear_model.RegressionResults позволяет нам получить данные для ANOVA (см. https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.html#statsmodels.regression.linear_model.RegressionResults) как свойства класса:

1. Сумма квадратов, обусловленная регрессией / SSR (Sum of Squared Regression) — свойство ess.

2. Сумма квадратов, обусловленная отклонением от регрессии / SSE (Sum of Squared Error) — свойство ssr.

3. Общая (полная) сумма квадратов / SST (Sum of Squared Total) — свойство centered_tss.

4. Кол-во наблюдений / Number of observations — свойство nobs.

5. Число степеней свободы модели / Model degrees of freedom — равно числу переменных модели (за исключением константы, если она присутствует — свойство df_model.

6. Среднеквадратичная ошибка модели / Mean squared error the model — сумма квадратов, объясненная регрессией, деленная на число степеней свободы регрессии — свойство mse_model.

7. Среднеквадратичная ошибка остатков / Mean squared error of the residuals — сумма квадратов остатков, деленная на остаточные степени свободы — свойство mse_resid.

8. Общая среднеквадратичная ошибка / Total mean squared error — общая сумма квадратов, деленная на количество наблюдений — свойство mse_total.

Также имеется модуль statsmodels.stats.anova.anova_lm, который позволяет получить результаты ДАРМ (нескольких типов — 1, 2, 3):

# тип 1
print('The type of Anova test: 1')
display(sm.stats.anova_lm(result_linear_ols, typ=1))

# тип 2
print('The type of Anova test: 2')
display(sm.stats.anova_lm(result_linear_ols, typ=2))

# тип 3
print('The type of Anova test: 3')
display(sm.stats.anova_lm(result_linear_ols, typ=3))

На мой взгляд, форма таблица результатов statsmodels.stats.anova.anova_lm не вполне удобна, поэтому сформируем ее самостоятельно, для чего создадим пользовательскую функцию ANOVA_table_regression_model:

# Пользовательская функция
def ANOVA_table_regression_model(model_fit):
    n = int(model_fit.nobs)
    p = int(model_fit.df_model)
    SSR = model_fit.ess
    SSE = model_fit.ssr
    SST = model_fit.centered_tss

    result = pd.DataFrame({
        'sources_of_variation': ('regression (SSR)', 'deviation from regression (SSE)', 'total (SST)'),
        'sum_of_squares': (SSR, SSE, SST),
        'degrees_of_freedom': (p, n-p-1, n-1)})
    result['squared_error'] = result['sum_of_squares'] / result['degrees_of_freedom']
    R2 = 1 - result.loc[1, 'sum_of_squares'] / result.loc[2, 'sum_of_squares']
    F_calc_adequacy = result.loc[2, 'squared_error'] / result.loc[1, 'squared_error']
    F_calc_determ_check = result.loc[0, 'squared_error'] / result.loc[1, 'squared_error']
    result['F-ratio'] = (F_calc_determ_check, F_calc_adequacy, '')
    
    return result

result = ANOVA_table_regression_model(result_linear_ols)
display(result)
print(f"R2 = 1 - SSE/SST = {1 - result.loc[1, 'sum_of_squares'] / result.loc[2, 'sum_of_squares']}")
print(f"F_calc_adequacy = MST / MSE = {result.loc[2, 'squared_error'] / result.loc[1, 'squared_error']}")
print(f"F_calc_determ_check = MSR / MSE = {result.loc[0, 'squared_error'] / result.loc[1, 'squared_error']}")

ДАРМ позволяет визуализировать вариацию:

fig, axes = plt.subplots(figsize=(210/INCH, 297/INCH/1.5))
axes.pie(
    (result.loc[0, 'sum_of_squares'], result.loc[1, 'sum_of_squares']), 
    labels=(result.loc[0, 'sources_of_variation'], result.loc[1, 'sources_of_variation']),
    autopct='%.1f%%',
    startangle=60)
plt.show()

На основании данных ДАРМ мы рассчитали ряд показателей (R2, Fcalc-ad и Fcalc-det), которые будут использоваться в дальнейшем.

3. Анализ остатков (проверка нормальности распределения остатков и гипотезы о равенстве нулю среднего значения остатков)

Проверка нормальности распределения остатков — один их важнейших этапов анализа регрессионной модели. Требование нормальности распределения остатков не требуется для отыскания параметров модели, но необходимо в дальнейшем для проверки статистических гипотез с использованием критериев Фишера и Стьюдента (проверка адекватности модели, значимости коэффициента детерминации, значимости коэффициентов регрессии) и построения доверительных интервалов [5, с.122].

Остатки регрессионной модели:

print('Остатки регрессионной модели:n', result_linear_ols.resid, type(result_linear_ols.resid))
res_Y = np.array(result_linear_ols.resid)

statsmodels может выдавать различные преобразованные виды остатков (см. https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.resid_pearson.html, https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.wresid.html).

График остатков:

# Пользовательская функция
graph_scatterplot_sns(
    X, res_Y,
    Xmin=Xmin_graph, Xmax=Xmax_graph,
    Ymin=-3.0, Ymax=3.0,
    color='red',
    #title_figure=Task_Project,
    title_axes='Остатки линейной регрессионной модели', title_axes_fontsize=18,
    x_label=Variable_Name_X,
    y_label='ΔY = Y - Ycalc',
    s=75,
    file_name='graph/residuals_plot_sns.png')

Проверка нормальности распределения остатков:

# Пользовательская функция
graph_hist_boxplot_probplot_sns(
    data=res_Y,
    data_min=-2.5, data_max=2.5,
    graph_inclusion='bp',
    data_label='ΔY = Y - Ycalc',
    #title_figure=Task_Project,
    title_axes='Остатки линейной регрессионной модели', title_axes_fontsize=16,
    file_name='graph/residuals_hist_boxplot_probplot_sns.png')    

norm_distr_check(res_Y)

Вывод: большинство статистических тестов позволяют принять гипотезу о нормальности распределения остатков.

Проверка гипотезы о равенстве нулю среднего значения остатков — так как остатки имеют нормальное распределение, воспользуемся критерием Стьюдента (функция scipy.stats.ttest_1samp, https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html):

sps.ttest_1samp(res_Y, popmean=0)

Вывод: так как расчетный уровень значимости превышает заданный (0.05), то нулевая гипотеза о равенстве нулю остатков ПРИНИМАЕТСЯ.

4. Проверка адекватности модели

Суть проверки адекватности регрессионной модели заключается в сравнении полной дисперсии MST и остаточной дисперсии MSE — проверяется гипотеза о равенстве этих дисперсий по критерию Фишера. Если дисперсии различаются значимо, то модель считается адекватной. Более подробно про проверку адекватности регрессионной — см.[1, с.658], [2, с.49], [4, с.154].

Для проверки адекватности регрессионной модели создадим пользовательскую функцию regression_model_adequacy_check:

def regression_model_adequacy_check(
    model_fit,
    p_level: float=0.95,
    model_name=''):
    
    n = int(model_fit.nobs)
    p = int(model_fit.df_model)    # Число степеней свободы регрессии, равно числу переменных модели (за исключением константы, если она присутствует)
    
    SST = model_fit.centered_tss    # SST (Sum of Squared Total)
    dfT = n-1
    MST = SST / dfT

    SSE = model_fit.ssr    # SSE (Sum of Squared Error)
    dfE = n - p - 1
    MSE = SSE / dfE
    
    F_calc = MST / MSE
    F_table = sci.stats.f.ppf(p_level, dfT, dfE, loc=0, scale=1)
    a_calc = 1 - sci.stats.f.cdf(F_calc, dfT, dfE, loc=0, scale=1)
    conclusion_model_adequacy_check = 'adequacy' if F_calc >= F_table else 'adequacy'
    
    # формируем результат            
    result = pd.DataFrame({
        'SST': (SST),
        'SSE': (SSE),
        'dfT': (dfT),
        'dfE': (dfE),
        'MST': (MST),
        'MSE': (MSE),
        'p_level': (p_level),
        'a_level': (a_level),
        'F_calc': (F_calc),
        'F_table': (F_table),
        'F_calc >= F_table': (F_calc >= F_table),
        'a_calc': (a_calc),
        'a_calc <= a_level': (a_calc <= a_level),
        'adequacy_check': (conclusion_model_adequacy_check),
        },
        index=[model_name]
        )
    
    return result

regression_model_adequacy_check(result_linear_ols, p_level=0.95, model_name='linear_ols')

Вывод: модель является АДЕКВАТНОЙ.

5. Коэффициент детерминации и проверка его значимости

Различают несколько видов коэффициента детерминации:

1. Собственно обычный коэффициент детерминации:

   

Его значение может быть получено как свойство rsquared модели.

1. Скорректированный (adjusted) коэффициент детерминации — используется для того, чтобы была возможность сравнивать модели с разным числом признаков так, чтобы число регрессоров (признаков) не влияло на статистику R2, при его расчете используются несмещённые оценки дисперсий:

   

Его значение может быть получено как свойство rsquared_adj модели.

1. Обобщённый (extended) коэффициент детерминации — используется для сравнения моделей регрессии со свободным членом и без него, а также для сравнения между собой регрессий, построенных с помощью различных методов: МНК, обобщённого метода наименьших квадратов (ОМНК), условного метода наименьших квадратов (УМНК), обобщённо-условного метода наименьших квадратов (ОУМНК). В данном разборе ПЛРМ рассматривать этот коэффициент мы не будем.

Более подробно с теорией вопроса можно ознакомиться, например: http://www.machinelearning.ru/wiki/index.php?title=Коэффициент_детерминации), а также в [7].

Значения коэффициента детерминации и скорректированного коэффициента детерминации, извлеченные с помощью свойств rsquared и rsquared_adj модели.

print('R2 =', result_linear_ols.rsquared)
print('R2_adj =', result_linear_ols.rsquared_adj)

Значимость коэффициента детерминации можно проверить по критерию Фишера [3, с.201-203; 8, с.83].

Расчетное значение статистики критерия Фишера может быть получено с помощью свойства fvalue модели:

print(f"result_linear_ols.fvalue = {result_linear_ols.fvalue}")

Расчетный уровень значимости при проверке гипотезы по критерию Фишера может быть получено с помощью свойства f_pvalue модели:

print(f"result_linear_ols.f_pvalue = {result_linear_ols.f_pvalue}")

Можно рассчитать уровень значимости самостоятельно (так сказать, для лучшего понимания и общей демонстрации возможностей) — для этого воспользуемся библиотекой scipy, модулем распределения Фишера scipy.stats.f, свойством cdf (функция распределения):

df1 = int(result_linear_ols.df_model)
df2 = int(result_linear_ols.nobs - result_linear_ols.df_model - 1)
F_calc = result_linear_ols.fvalue
a_calc = 1 - sci.stats.f.cdf(F_calc, df1, df2, loc=0, scale=1)
print(a_calc)

Как видим, результаты совпадают.

Табличное значение статистики критерия Фишера получить с помощью Regression Results нельзя. Рассчитаем его самостоятельно — для этого воспользуемся библиотекой scipy, модулем распределения Стьюдента scipy.stats.f, свойством ppf (процентные точки):

F_table = sci.stats.f.ppf(p_level, df1, df2, loc=0, scale=1)
print(F_table)

Для удобства создадим пользовательскую функцию determination_coef_check для проверки значимости коэффициента детерминации, которая объединяет все вышеперечисленные расчеты:

# Пользовательская функция
def determination_coef_check(
    model_fit,
    p_level: float=0.95):
    
    a_level = 1 - p_level
    
    R2 = model_fit.rsquared
    R2_adj = model_fit.rsquared_adj
    n = model_fit.nobs    # объем выборки
    p = model_fit.df_model    # Model degrees of freedom. The number of regressors p. Does not include the constant if one is present.
    
    F_calc = R2 / (1 - R2) * (n-p-1)/p
    df1 = int(p)
    df2 = int(n-p-1)
    F_table = sci.stats.f.ppf(p_level, df1, df2, loc=0, scale=1)
    a_calc = 1 - sci.stats.f.cdf(F_calc, df1, df2, loc=0, scale=1)
    conclusion_determ_coef_sign = 'significance' if F_calc >= F_table else 'not significance'
        
    # формируем результат            
    result = pd.DataFrame({
        'notation': ('R2'),
        'coef_value (R)': (sqrt(R2)),
        'coef_value_squared (R2)': (R2),
        'p_level': (p_level),
        'a_level': (a_level),
        'F_calc': (F_calc),
        'df1': (df1),
        'df2': (df2),
        'F_table': (F_table),
        'F_calc >= F_table': (F_calc >= F_table),
        'a_calc': (a_calc),
        'a_calc <= a_level': (a_calc <= a_level),
        'significance_check': (conclusion_determ_coef_sign),
        'conf_int_low': (''),
        'conf_int_high': ('')
        },
        index=['Coef. of determination'])
    return result

determination_coef_check(
    result_linear_ols,
    p_level=0.95)

Вывод: коэффициент детерминации ЗНАЧИМ.

6. Коэффициенты регрессии и проверка их значимости

Ранее мы уже извлекли коэффициенты регрессии как параметры модели b0 и b1 (как свойство params модели). Также можно получить их значения, как свойство bse модели:

print(b0, b1)
print(result_linear_ols.bse, type(result_linear_ols.bse))

Значимость коэффициентов регрессии можно проверить по критерию Стьюдента [3, с.203-212; 8, с.78].

Расчетные значения статистики критерия Стьюдента могут быть получены с помощью свойства tvalues модели:

print(f"result_linear_ols.tvalues = n{result_linear_ols.tvalues}")

Расчетные значения уровня значимости при проверке гипотезы по критерию Стьюдента могут быть получены с помощью свойства pvalues модели:

print(f"result_linear_ols.pvalues = n{result_linear_ols.pvalues}")

Доверительные интервалы для коэффициентов регрессии могут быть получены с помощью свойства conf_int модели:

print(result_linear_ols.conf_int(), 'n')

Можно рассчитать уровень значимости самостоятельно (как ранее для критерия Фишера — для лучшего понимания и общей демонстрации возможностей) — для этого воспользуемся библиотекой scipy, модулем распределения Стьюдента scipy.stats.t, свойством cdf (функция распределения):

t_calc = result_linear_ols.tvalues
df = int(result_linear_ols.nobs - result_linear_ols.df_model - 1)
a_calc = 2*(1-sci.stats.t.cdf(abs(t_calc), df, loc=0, scale=1))
print(a_calc)

Как видим, результаты совпадают.

Табличные значения статистики критерия Стьюдента получить с помощью Regression Results нельзя. Рассчитаем их самостоятельно — для этого воспользуемся библиотекой scipy, модулем распределения Стьюдента scipy.stats.t, свойством ppf (процентные точки):

t_table = sci.stats.t.ppf((1 + p_level)/2 , df)
print(t_table)

Для удобства создадим пользовательскую функцию regression_coef_check для проверки значимости коэффициентов регрессии, которая объединяет все вышеперечисленные расчеты:

def regression_coef_check(
    model_fit,
    notation_coef: list='',
    p_level: float=0.95):
    
    a_level = 1 - p_level
    
    # параметры модели (коэффициенты регрессии)
    model_params = model_fit.params
    # стандартные ошибки коэффициентов регрессии
    model_bse = model_fit.bse
    # проверка гипотезы о значимости регрессии
    t_calc = abs(model_params) / model_bse
    n = model_fit.nobs    # объем выборки
    p = model_fit.df_model    # Model degrees of freedom. The number of regressors p. Does not include the constant if one is present.
    df = int(n - p - 1)
    t_table = sci.stats.t.ppf((1 + p_level)/2 , df)
    a_calc = 2*(1-sci.stats.t.cdf(t_calc, df, loc=0, scale=1))
    conclusion_ = ['significance' if elem else 'not significance' for elem in (t_calc >= t_table).values]
        
    # доверительный интервал коэффициента регрессии
    conf_int_low = model_params - t_table*model_bse
    conf_int_high = model_params + t_table*model_bse
    
    # формируем результат            
    result = pd.DataFrame({
        'notation': (notation_coef),
        'coef_value': (model_params),
        'std_err': (model_bse),
        'p_level': (p_level),
        'a_level': (a_level),
        't_calc': (t_calc),
        'df': (df),
        't_table': (t_table),
        't_calc >= t_table': (t_calc >= t_table),
        'a_calc': (a_calc),
        'a_calc <= a_level': (a_calc <= a_level),
        'significance_check': (conclusion_),
        'conf_int_low': (conf_int_low),
        'conf_int_high': (conf_int_high),
        })
    
    return result

regression_coef_check(
    result_linear_ols,
    notation_coef=['b0', 'b1'],
    p_level=0.95)

Вывод: коэффициенты регрессии b0 и b1 ЗНАЧИМЫ.

7. Проверка гетероскедастичности

Для проверка гетероскедастичности statsmodels предлагает нам следующие инструменты:

• тест Голдфелда-Квандта (https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.het_goldfeldquandt.html#statsmodels.stats.diagnostic.het_goldfeldquandt) — теорию см. [8, с.178], также https://ru.wikipedia.org/wiki/Тест_Голдфелда_—_Куандта.

• тест Бриша-Пэгана (Breush-Pagan test) (https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.het_breuschpagan.html#statsmodels.stats.diagnostic.het_breuschpagan) — теорию см.[8, с.179], также https://en.wikipedia.org/wiki/Breusch–Pagan_test.

• тест Уайта (White test) (https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.het_white.html#statsmodels.stats.diagnostic.het_white) — теорию см.[8, с.177], а также https://ru.wikipedia.org/wiki/Тест_Уайта.

  Тест Голдфелда-Квандта (Goldfeld–Quandt test)

# тест Голдфелда-Квандта (Goldfeld–Quandt test)
test = sms.het_goldfeldquandt(result_linear_ols.resid, result_linear_ols.model.exog)
test_result = lzip(['F_calc', 'p_calc'], test)    # распаковка результатов теста
# расчетное значение статистики F-критерия
F_calc_tuple = test_result[0]
F_calc = F_calc_tuple[1]
print(f"Расчетное значение статистики F-критерия: F_calc = {round(F_calc, DecPlace)}")
# расчетный уровень значимости
p_calc_tuple = test_result[1]
p_calc = p_calc_tuple[1]
print(f"Расчетное значение доверительной вероятности: p_calc = {round(p_calc, DecPlace)}")
#a_calc = 1 - p_value
#print(f"Расчетное значение уровня значимости: a_calc = 1 - p_value = {round(a_calc, DecPlace)}")
# вывод
if p_calc < a_level:
    conclusion_GQ_test = f"Так как p_calc = {round(p_calc, DecPlace)} < a_level = {round(a_level, DecPlace)}" + 
        ", то дисперсии в подвыборках отличаются значимо, т.е. гипотеза о наличии гетероскедастичности ПРИНИМАЕТСЯ"
else:
    conclusion_GQ_test = f"Так как p_calc = {round(p_calc, DecPlace)} >= a_level = {round(a_level, DecPlace)}" + 
        ", то дисперсии в подвыборках отличаются незначимо, т.е. гипотеза о наличии гетероскедастичности ОТВЕРГАЕТСЯ"
print(conclusion_GQ_test)

Для удобства создадим пользовательскую функцию Goldfeld_Quandt_test:

def Goldfeld_Quandt_test(
    model_fit,
    p_level: float=0.95,
    model_name=''):
    
    a_level = 1 - p_level
    
    # реализация теста
    test = sms.het_goldfeldquandt(model_fit.resid, model_fit.model.exog)
    test_result = lzip(['F_statistic', 'p_calc'], test)    # распаковка результатов теста
    # расчетное значение статистики F-критерия
    F_calc_tuple = test_result[0]
    F_statistic = F_calc_tuple[1]
    # расчетный уровень значимости
    p_calc_tuple = test_result[1]
    p_calc = p_calc_tuple[1]
    # вывод
    conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
    
    result = pd.DataFrame({
        'test': ('Goldfeld–Quandt test'),
        'p_level': (p_level),
        'a_level': (a_level),
        'F_statistic': (F_statistic),
        'p_calc': (p_calc),
        'p_calc < a_level': (p_calc < a_level),
        'heteroscedasticity_check': (conclusion_test)
        },
        index=[model_name])
    
    return result

Goldfeld_Quandt_test(result_linear_ols, p_level=0.95, model_name='linear_ols')

Тест Бриша-Пэгана (Breush-Pagan test)

# тест Бриша-Пэгана (Breush-Pagan test)
name = ["Lagrange multiplier statistic", "p-value", "f-value", "f p-value"]
test = sms.het_breuschpagan(result_linear_ols.resid, result_linear_ols.model.exog)
lzip(name, test)

Для удобства создадим пользовательскую функцию Breush_Pagan_test:

def Breush_Pagan_test(
    model_fit,
    p_level: float=0.95,
    model_name=''):
    
    a_level = 1 - p_level
    
    # реализация теста
    test = sms.het_breuschpagan(model_fit.resid, model_fit.model.exog)
    name = ['Lagrange_multiplier_statistic', 'p_calc_LM', 'F_statistic', 'p_calc']
    test_result = lzip(name, test)    # распаковка результатов теста
    # расчетное значение статистики теста множителей Лагранжа
    LM_calc_tuple = test_result[0]
    Lagrange_multiplier_statistic = LM_calc_tuple[1]
    # расчетный уровень значимости статистики теста множителей Лагранжа
    p_calc_LM_tuple = test_result[1]
    p_calc_LM = p_calc_LM_tuple[1]
    # расчетное значение F-статистики гипотезы о том, что дисперсия ошибки не зависит от x
    F_calc_tuple = test_result[2]
    F_statistic = F_calc_tuple[1]
    # расчетный уровень значимости F-статистики
    p_calc_tuple = test_result[3]
    p_calc = p_calc_tuple[1]
    # вывод
    conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'

    # вывод
    conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
    
    result = pd.DataFrame({
        'test': ('Breush-Pagan test'),
        'p_level': (p_level),
        'a_level': (a_level),
        'Lagrange_multiplier_statistic': (Lagrange_multiplier_statistic),
        'p_calc_LM': (p_calc_LM),
        'p_calc_LM < a_level': (p_calc_LM < a_level),
        'F_statistic': (F_statistic),
        'p_calc': (p_calc),
        'p_calc < a_level': (p_calc < a_level),
        'heteroscedasticity_check': (conclusion_test)
        },
        index=[model_name])
    
    return result

Breush_Pagan_test(result_linear_ols, p_level=0.95, model_name='linear_ols')

Тест Уайта (White test)

# тест Уайта (White test)
name = ["Lagrange multiplier statistic", "p-value", "f-value", "f p-value"]
test = sms.het_white(result_linear_ols.resid, result_linear_ols.model.exog)
lzip(name, test)

Для удобства создадим пользовательскую функцию White_test:

def White_test(
    model_fit,
    p_level: float=0.95,
    model_name=''):
    
    a_level = 1 - p_level
    
    # реализация теста
    test = sms.het_white(model_fit.resid, model_fit.model.exog)
    name = ['Lagrange_multiplier_statistic', 'p_calc_LM', 'F_statistic', 'p_calc']
    test_result = lzip(name, test)    # распаковка результатов теста
    # расчетное значение статистики теста множителей Лагранжа
    LM_calc_tuple = test_result[0]
    Lagrange_multiplier_statistic = LM_calc_tuple[1]
    # расчетный уровень значимости статистики теста множителей Лагранжа
    p_calc_LM_tuple = test_result[1]
    p_calc_LM = p_calc_LM_tuple[1]
    # расчетное значение F-статистики гипотезы о том, что дисперсия ошибки не зависит от x
    F_calc_tuple = test_result[2]
    F_statistic = F_calc_tuple[1]
    # расчетный уровень значимости F-статистики
    p_calc_tuple = test_result[3]
    p_calc = p_calc_tuple[1]
    # вывод
    conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'

    # вывод
    conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
    
    result = pd.DataFrame({
        'test': ('White test'),
        'p_level': (p_level),
        'a_level': (a_level),
        'Lagrange_multiplier_statistic': (Lagrange_multiplier_statistic),
        'p_calc_LM': (p_calc_LM),
        'p_calc_LM < a_level': (p_calc_LM < a_level),
        'F_statistic': (F_statistic),
        'p_calc': (p_calc),
        'p_calc < a_level': (p_calc < a_level),
        'heteroscedasticity_check': (conclusion_test)
        },
        index=[model_name])
    
    return result

White_test(result_linear_ols, p_level=0.95, model_name='linear_ols')

Объединим результаты всех тестов гетероскедастичность в один DataFrame:

Goldfeld_Quandt_test_df = Goldfeld_Quandt_test(result_linear_ols, p_level=0.95, model_name='linear_ols')
Breush_Pagan_test_df = Breush_Pagan_test(result_linear_ols, p_level=0.95, model_name='linear_ols')
White_test_df = White_test(result_linear_ols, p_level=0.95, model_name='linear_ols')

heteroscedasticity_tests_df = pd.concat([Breush_Pagan_test_df, White_test_df, Goldfeld_Quandt_test_df])
display(heteroscedasticity_tests_df)

Выводы

Итак, мы провели статистический анализ регрессионной модели и установили:

• исходные данные имеют нормальное распределение;

• между переменными имеется весьма сильная корреляционная связь;

• регрессионная модель хорошо аппроксимирует фактические данные;

• остатки модели имеют нормальное распределение;

• регрессионная модель адекватна по критерию Фишера;

• коэффициент детерминации значим по критеию Фишера;

• коэффициенты регрессии значимы по критерию Стьюдента;

• гетероскедастичность отсутствует.

Применительно к рассматриваемой задаче выполнять проверку автокорреляции не имеет особого смысла из-за особенностей исходных данных (результаты замеров прочности бетона на разных участках здания).

Про статистический анализ регрессионных моделей с помощью statsmodels— см. еще https://www.statsmodels.org/stable/examples/notebooks/generated/regression_diagnostics.html.

Доверительные интервалы регрессионной модели

Для регрессионных моделей определяют доверительные интервалы двух видов [3, с.184-192; 4, с.172; 8, с.205-209]:

1. Доверительный интервал средних значений переменной Y.

2. Доверительный интервал индивидуальных значений переменной Y.

При этом размер доверительного интервала для индивидуальных значений больше, чем для средних значений.

Доверительные интервалы регрессионных моделей (ДИРМ) могут быть найдены разными способами:

• непосредственно путем расчетов по формулам (см., например, https://habr.com/ru/post/558158/);

• с использованием инструментария библиотеки statsmodels (см., например, https://www.stackfinder.ru/questions/17559408/confidence-and-prediction-intervals-with-statsmodels).

Разбререм более подробно способ с использованием библиотеки statsmodels. Прежде всего, с помощью свойства summary_table класса statsmodels.stats.outliers_influence.OLSInfluence (https://www.statsmodels.org/stable/generated/statsmodels.stats.outliers_influence.OLSInfluence.html?highlight=olsinfluence) мы можем получить таблицу данных, содержащую необходимую нам информацию:

• Dep Var Population — фактические значения переменной Y;

• Predicted Value — предсказанные значения переменной Y по по регрессионной модели;

• Std Error Mean Predict — среднеквадратическая ошибка предсказанного среднего;

• Mean ci 95% low и Mean ci 95% upp — границы доверительного интервала средних значений переменной Y;

• Predict ci 95% low и Predict ci 95% upp — границы доверительного интервала индивидуальных значений переменной Y;

• Residual — остатки регрессионной модели;

• Std Error Residual — среднеквадратическая ошибка остатков;

• Student Residual — стьюдентизированные остатки (подробнее см. http://statistica.ru/glossary/general/studentizirovannie-ostatki/);

• Cook’s D — Расстояние Кука (Cook’s distance) — оценивает эффект от удаления одного (рассматриваемого) наблюдения; наблюдение считается выбросом, если Di > 4/n (более подробно — см.https://translated.turbopages.org/proxy_u/en-ru.ru.f584ceb5-63296427-aded8f31-74722d776562/https/en.wikipedia.org/wiki/Cook’s_distance, http://www.machinelearning.ru/wiki/index.php?title=Расстояние_Кука).

from statsmodels.stats.outliers_influence import summary_table
st, data, ss2 = summary_table(result_linear_ols, alpha=0.05)
print(st, 'n', type(st))

В нашем случае критическое значение расстояния Кука равно:

print(f'D_crit = 4/n = {4/result_linear_ols.nobs}')

то есть выбросов, смещающих оценки коэффициентов регрессии, не наблюдается.

Мы получили данные как класс statsmodels.iolib.table.SimpleTable. Свойство data преобразует данные в список. Далее для удобства работы преобразуем данные в DataFrame:

  st_data_df = pd.DataFrame(st.data)

Будем использовать данный DataFrame в дальнейшем, несколько преобразуем его:

• изменим наименование столбцов (с цифр на названия показателей из таблицы summary_table)

• удалим строки с текстовыми значениями

• изменим индекс

• добавим новый столбец — значения переменной X

• отсортируем по возрастанию значений переменной X (это необходимо, чтобы графики границ доверительных интервалов выглядели как линии)

st_df = st_data_df.copy()
# изменим наименования столбцов
str = st_df.iloc[0,0:] + ' ' + st_df.iloc[1,0:]
st_df = st_df.rename(str, axis='columns')
# удалим строки 0, 1
st_df = st_df.drop([0,1])
# изменим индекс
st_df = st_df.set_index(np.arange(0, result_linear_ols.nobs))
# добавим новый столбец - значения переменной X
st_df.insert(1, 'X', X)
# отсортируем по возрастанию значений переменной X
st_df = st_df.sort_values(by='X')

display(st_df)

С помощью полученных данных мы можем построить график регрессионной модели с доверительными интервалами:

# создание рисунка (Figure) и области рисования (Axes)
fig, axes = plt.subplots(figsize=(297/INCH, 210/INCH))
# заголовок рисунка (Figure)
title_figure = Task_Project
fig.suptitle(title_figure, fontsize = 16)
# заголовок области рисования (Axes)
title_axes = 'Линейная регрессионная модель'
axes.set_title(title_axes, fontsize = 14)
# фактические данные
sns.scatterplot(
    x=st_df['X'], y=st_df['Dep Var Population'],
    label='фактические данные',
    s=50,
    color='red',
    ax=axes)
# график регрессионной модели
label_legend_regr_model=f'линейная регрессия Y = {b0:.3f} + {b1:.4f}*X'
sns.lineplot(
    x=st_df['X'], y=st_df['Predicted Value'],
    label=label_legend_regr_model,
    color='blue',
    ax=axes)
# доверительный интервал средних значений переменной Y
Mean_ci_low = st_df['Mean ci 95% low']
plt.plot(
    st_df['X'], Mean_ci_low,
    color='magenta', linestyle='--', linewidth=1,
    label='доверительный интервал средних значений Y')
Mean_ci_upp = st_df['Mean ci 95% upp']
plt.plot(
    st_df['X'], Mean_ci_upp,
    color='magenta', linestyle='--', linewidth=1)
# доверительный интервал индивидуальных значений переменной Y
Predict_ci_low = st_df['Predict ci 95% low']
plt.plot(
    st_df['X'], Predict_ci_low,
    color='orange', linestyle='-.', linewidth=2,
    label='доверительный интервал индивидуальных значений Y')
Predict_ci_upp = st_df['Predict ci 95% upp']
plt.plot(
    st_df['X'], Predict_ci_upp,
    color='orange', linestyle='-.', linewidth=2)

axes.set_xlabel(Variable_Name_X)
axes.set_ylabel(Variable_Name_Y)
axes.legend(prop={'size': 12})
plt.show()

Однако, мы получили данные о границах доверительных интервалов регрессионной модели только в пределах области фактических значений переменной X. Как быть, если мы хотим распространить прогноз за пределы этой области?

Прогнозирование

Под прогнозированием мы в данном случае будем понимать определение значений переменной Y и доверительных интервалов для ее средних и индивидуальных значений при заданном X. По сути, нам предстоит построить аналог рассмотренной выше таблицы summary_table, только с другими значениями X, причем эти значения могут выходить за пределы тех значений, которые использовались нами для построения регрессии.

Методика расчета доверительных интервалов регрессионных моделей разобрана в статье «Python, корреляция и регрессия: часть 4» (https://habr.com/ru/post/558158/), всем рекомендую ознакомиться.

Найти прогнозные значения Y не представляет труда, так как ранее мы уже формализовали модель в виде лямбда-функции, а вот для построения доверительных интервалов придется выполнить расчеты по формулам. Для этого создадим пользовательскую функцию regression_pair_predict, которая в случае парной регрессии (pair regression) для заданного значения X возвращает:

• прогнозируемое по регрессионной модели значение y_calc

• доверительный интервал [y_calc_mean_ci_low, y_calc_mean_ci_upp] средних значений переменной Y

• доверительный интервал [y_calc_predict_ci_low, y_calc_predict_ci_upp] индивидуальных значений переменной Y

Алгоритм расчета доверительных интервалов для множественной регрессии (multiple regression) отличается и в данном обзоре не рассматривается (рассмотрим в дальнейшем).

Про прогнозирование с помощью регрессионных моделей — см.также:

• https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.predict.html?highlight=predict#statsmodels.regression.linear_model.RegressionResults.predict

• How to Make Predictions Using Regression Model in Statsmodels

• https://www.statsmodels.org/stable/examples/notebooks/generated/predict.html

def regression_pair_predict(
    x_in,
    model_fit,
    regression_model,
    p_level: float=0.95):
    
    a_level = 1 - p_level
    
    X = pd.DataFrame(model_fit.model.exog)[1].values    # найти лучшее решение
    Y = model_fit.model.endog
    
    # вспомогательные величины
    n = int(result_linear_ols.nobs)
    SSE = model_fit.ssr    # SSE (Sum of Squared Error)
    dfE = n - p - 1
    MSE = SSE / dfE    # остаточная дисперсия
    
    Xmean = np.mean(X)
    SST_X = np.sum([(X[i] - Xmean)**2 for i in range(0, n)])
    
    t_table = sci.stats.t.ppf((1 + p_level)/2 , dfE)
    S2_y_calc_mean = MSE * (1/n + (x_in - Xmean)**2 / SST_X)
    S2_y_calc_predict = MSE * (1 + 1/n + (x_in - Xmean)**2 / SST_X)
        
    # прогнозируемое значение переменной Y
    y_calc=regression_model(x_in)
    # доверительный интервал средних значений переменной Y
    y_calc_mean_ci_low = y_calc - t_table*sqrt(S2_y_calc_mean)
    y_calc_mean_ci_upp = y_calc + t_table*sqrt(S2_y_calc_mean)
    # доверительный интервал индивидуальных значений переменной Y
    y_calc_predict_ci_low = y_calc - t_table*sqrt(S2_y_calc_predict)
    y_calc_predict_ci_upp = y_calc + t_table*sqrt(S2_y_calc_predict)
    
    result = y_calc, y_calc_mean_ci_low, y_calc_mean_ci_upp, y_calc_predict_ci_low, y_calc_predict_ci_upp
    
    return result

Сравним результаты расчета доверительных интервалов разными способами — с использованием функции regression_pair_predict и средствами statsmodels, для этого сформируем DaraFrame с новыми данными:

regression_pair_predict_df = pd.DataFrame(
    [regression_pair_predict(elem, result_linear_ols, regression_model=Y_calc) for elem in st_df['X'].values],
    columns=['y_calc', 'y_calc_mean_ci_low', 'y_calc_mean_ci_upp', 'y_calc_predict_ci_low', 'y_calc_predict_ci_upp'])
regression_pair_predict_df.insert(0, 'X', st_df['X'].values)
display(regression_pair_predict_df)

Видим, что результаты расчетов идентичны, следовательно мы можем использовать функцию regression_pair_predict для прогнозирования.

def graph_regression_pair_predict_plot_sns(
    model_fit,
    regression_model_in,
    Xmin=None, Xmax=None, Nx=10,
    Ymin_graph=None, Ymax_graph=None,
    title_figure=None, title_figure_fontsize=18,
    title_axes=None, title_axes_fontsize=16,
    x_label=None,
    y_label=None,
    label_fontsize=14, tick_fontsize=12, 
    label_legend_regr_model='', label_legend_fontsize=12,
    s=50, linewidth_regr_model=2,
    graph_size=(297/INCH, 210/INCH),
    result_output=True,
    file_name=None):
    
    # фактические данные
    X = pd.DataFrame(model_fit.model.exog)[1].values    # найти лучшее решение
    Y = model_fit.model.endog
    X = np.array(X)
    Y = np.array(Y)
    
    # границы
    if not(Xmin) and not(Xmax):
        Xmin=min(X)
        Xmax=max(X)
        Xmin_graph=min(X)*0.99
        Xmax_graph=max(X)*1.01
    else:
        Xmin_graph=Xmin
        Xmax_graph=Xmax
    
    if not(Ymin_graph) and not(Ymax_graph):
        Ymin_graph=min(Y)*0.99
        Ymax_graph=max(Y)*1.01       
    
    # формируем DataFrame данных
    Xcalc = np.linspace(Xmin, Xmax, num=Nx)
    Ycalc = regression_model_in(Xcalc)
    
    result_df = pd.DataFrame(
        [regression_pair_predict(elem, model_fit, regression_model=regression_model_in) for elem in Xcalc],
        columns=['y_calc', 'y_calc_mean_ci_low', 'y_calc_mean_ci_upp', 'y_calc_predict_ci_low', 'y_calc_predict_ci_upp'])
    result_df.insert(0, 'x_calc', Xcalc)
            
    # заголовки графика
    fig, axes = plt.subplots(figsize=graph_size)
    fig.suptitle(title_figure, fontsize = title_figure_fontsize)
    axes.set_title(title_axes, fontsize = title_axes_fontsize)
    
    # фактические данные
    sns.scatterplot(
        x=X, y=Y,
        label='фактические данные',
        s=s,
        color='red',
        ax=axes)
    
    # график регрессионной модели
    sns.lineplot(
        x=Xcalc, y=Ycalc,
        color='blue',
        linewidth=linewidth_regr_model,
        legend=True,
        label=label_legend_regr_model,
        ax=axes)
    
    # доверительный интервал средних значений переменной Y
    Mean_ci_low = result_df['y_calc_mean_ci_low']
    plt.plot(
        result_df['x_calc'], Mean_ci_low,
        color='magenta', linestyle='--', linewidth=1,
        label='доверительный интервал средних значений Y')
    
    Mean_ci_upp = result_df['y_calc_mean_ci_upp']
    plt.plot(
        result_df['x_calc'], Mean_ci_upp,
        color='magenta', linestyle='--', linewidth=1)
    
    # доверительный интервал индивидуальных значений переменной Y
    Predict_ci_low = result_df['y_calc_predict_ci_low']
    plt.plot(
        result_df['x_calc'], Predict_ci_low,
        color='orange', linestyle='-.', linewidth=2,
        label='доверительный интервал индивидуальных значений Y')
    
    Predict_ci_upp = result_df['y_calc_predict_ci_upp']
    plt.plot(
        result_df['x_calc'], Predict_ci_upp,
        color='orange', linestyle='-.', linewidth=2)
    
        
    axes.set_xlim(Xmin_graph, Xmax_graph)
    axes.set_ylim(Ymin_graph, Ymax_graph)        
    axes.set_xlabel(x_label, fontsize = label_fontsize)
    axes.set_ylabel(y_label, fontsize = label_fontsize)
    axes.tick_params(labelsize = tick_fontsize)
    #axes.tick_params(labelsize = tick_fontsize)
    axes.legend(prop={'size': label_legend_fontsize})
        
    plt.show()
    if file_name:
        fig.savefig(file_name, orientation = "portrait", dpi = 300)
        
    if result_output:
        return result_df
    else:
        return

graph_regression_pair_predict_plot_sns(
    model_fit=result_linear_ols,
    regression_model_in=Y_calc,
    Xmin=Xmin_graph-300, Xmax=Xmax_graph+200, Nx=25,
    Ymin_graph=Ymin_graph-5, Ymax_graph=Ymax_graph+5,
    title_figure=Task_Project, title_figure_fontsize=16,
    title_axes='Линейная регрессионная модель', title_axes_fontsize=14,
    x_label=Variable_Name_X,
    y_label=Variable_Name_Y,
    label_legend_regr_model=f'линейная регрессия Y = {b0:.3f} + {b1:.4f}*X',
    s=50,
    result_output=True,
    file_name='graph/regression_plot_lin.png')

Выводы и рекомендации

Исследована зависимость показаний ультразвукового прибора «ПУЛЬСАР-2.1» (X) и результатов замера прочности бетона (методом отрыва со скалыванием) склерометром ИПС-МГ4.03 (Y).

Между переменными имеется весьма сильная линейная корреляционная связь. Получена регрессионная модель:

Y = b0 + b1∙X = -21.3741 + 0.0129∙X

Модель хорошо аппроксимирует фактические данные, является адекватной, значимой и может использоваться для предсказания прочности бетона.

Также построен график прогноза с доверительными интервалами.

ИТОГИ

Итак, мы рассмотрели все этапы регрессионного анализа в случае простой линейной регрессии (simple linear regression) с использованием библиотеки statsmodels на конкретном практическом примере; подробно остановились на статистическом анализа модели с проверкой гипотез; также предложен ряд пользовательских функций, облегчающих работу исследователя и уменьшающих размер программного кода.

Конечно, мы разобрали далеко не все вопросы анализа регрессионных моделей и возможности библиотеки statsmodels применительно к simple linear regression, в частности статистики влияния (Influence Statistics), инструмент Leverage, анализ стьюдентизированных остатков и пр. — это темы для отдельных обзоров.

Исходный код находится в моем репозитории на GitHub.

Надеюсь, данный обзор поможет специалистам DataScience в работе.

Стандартная ошибка оценки по уравнению регрессии

Стандартная ошибка оценки, также известная как стандартная ошибка уравнения регрессии, определяется следующим образом (см. (6.23)) [c.280]

Стандартная ошибка уравнения регрессии, Эта статистика SEE представляет собой стандартное отклонение фактических значений теоретических значений У. [c.650]

Что такое стандартная ошибка уравнения регрессии ).Какие допущения лежат в основе парной регрессии 10. Что такое множественная регрессия [c.679]

Следующий этап корреляционного анализа — расчет уравнения связи (регрессии). Решение проводится обычно шаговым способом. Сначала в расчет принимается один фактор, который оказывает наиболее значимое влияние на результативный показатель, потом второй, третий и т.д. И на каждом шаге рассчитываются уравнение связи, множественный коэффициент корреляции и детерминации, /»»-отношение (критерий Фишера), стандартная ошибка и другие показатели, с помощью которых оценивается надежность уравнения связи. Величина их на каждом шаге сравнивается с предыдущей. Чем выше величина коэффициентов множественной корреляции, детерминации и критерия Фишера и чем ниже величина стандартной ошибки, тем точнее уравнение связи описывает зависимости, сложившиеся между исследуемыми показателями. Если добавление следующих факторов не улучшает оценочных показателей связи, то надо их отбросить, т.е. остановиться на том уравнении, где эти показатели наиболее оптимальны. [c.149]

Прогнозное значение ур определяется путем подстановки в уравнение регрессии ух =а + Ьх соответствующего (прогнозного) значения хр. Вычисляется средняя стандартная ошибка прогноза [c.9]

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка ть и та. [c.53]

В прогнозных расчетах по уравнению регрессии определяется предсказываемое (ур) значение как точечный прогноз ух при хр =хь т. е. путем подстановки в уравнение регрессии 5 = а + b х соответствующего значения х. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки ух, т. е. Шух, и соответственно интервальной оценкой прогнозного значения (у ) [c.57]

Чтобы понять, как строится формула для определения величин стандартной ошибки ух, обратимся к уравнению линейной регрессии ух = а + b х. Подставим в это уравнение выражение параметра а [c.57]

При прогнозировании на основе уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от точности прогноза значения фактора х. Его величина может задаваться на основе анализа других моделей исходя из конкретной ситуации, а также из анализа динамики данного фактора. [c.61]

В скобках указаны стандартные ошибки параметров уравнения регрессии. [c.327]

В скобках указаны стандартные ошибки параметров уравнения регрессии. Определим по этому уравнению расчетные значения >>, ,, а затем параметры уравнения регрессии (7.44). Получим следующие результаты [c.328]

На каждом шаге рассматриваются уравнение регрессии, коэффициенты корреляции и детерминации, F-критерий, стандартная ошибка оценки и другие оценочные показатели. После каждого шага перечисленные оценочные показатели сравниваются с [c.39]

Проблемы с методологией регрессии. Методология регрессии — это традиционный способ уплотнения больших массивов данных и их сведения в одно уравнение, отражающее связь между мультипликаторами РЕ и финансовыми фундаментальными переменными. Но данный подход имеет свои ограничения. Во-первых, независимые переменные коррелируют друг с другом . Например, как видно из таблицы 18,2, обобщающей корреляцию между коэффициентами бета, ростом и коэффициентами выплат для всех американских фирм, быстрорастущие фирмы обычно имеют большой риск и низкие коэффициенты выплат. Обратите внимание на отрицательную корреляцию между коэффициентами выплат и ростом, а также на положительную корреляцию между коэффициентами бета и ростом. Эта мультиколлинеарность делает мультипликаторы регрессии ненадежными (увеличивает стандартную ошибку) и, возможно, объясняет ошибочные знаки при коэффициентах и крупные изменения этих мультипликаторов в разные периоды. Во-вторых, регрессия основывается на линейной связи между мультипликаторами РЕ и фундаментальными переменными, и данное свойство, по всей вероятности, неадекватно. Анализ остаточных явлений, связанных с корреляцией, может привести к трансформациям независимых переменных (их квадратов или натуральных логарифмов), которые в большей степени подходят для объяснения мультипликаторов РЕ. В-третьих, базовая связь между мультипликаторами РЕ и финансовыми переменными сама по себе не является стабильной. Если же эта связь смещается из года в год, то прогнозы, полученные из регрессионного уравнения, могут оказаться ненадежными для более длительных периодов времени. По всем этим причинам, несмотря на полезность регрессионного анализа, его следует рассматривать только как еще один инструмент поиска подлинного значения ценности. [c.649]

На рисунке 16.6 явно просматривается четкая линейная зависимость объема частного потребления от величины располагаемого дохода. Уравнение парной линейной регрессии, оцененное по этим данным, имеет вид С= -217,6 + 1,007 Yf Стандартные ошибки для свободного члена и коэффициента парной регрессии равны, соответственно, 28,4 и 0,012, а -статистики — -7,7 и 81 9. Обе они по модулю существенно превышают 3, следовательно, их статистическая значимость весьма высока. Впрочем, несмотря на то, что здесь удалось оценить статистически значимую линейную функцию потребления, в ней нарушены сразу две предпосылки Кейнса — уровень автономного потребления С0 оказался отрицательным, а предель- [c.304]

Стандартные ошибки свободного члена и коэффициента регрессии равны, соответственно, 84,7 и 0,46 их /-статистики — (-21,4 и 36,8). По абсолютной величине /-статистики намного превышают 3, и это свидетельствует о высокой надежности оцененных коэффициентов. Коэффициент детерминации /Р уравнения равен 0,96, то есть объяснено 96% дисперсии объема потребления. И в то же время уже по рисунку видно, что оцененная рефессия не очень хоро- [c.320]

Эта стандартная ошибка S у, равная 0,65, указывает отклонение фактических данных от прогнозируемых на основании использования воздействующих факторов j i и Х2 (влияние среди покупателей бабушек с внучками и высокопрофессионального вклада Шарика). В то же время мы располагаем обычным стандартным отклонением Sn, равным 1,06 (см. табл.8), которое было рассчитано для одной переменной, а именно сами текущие значения уги величина среднего арифметического у, которое равно 6,01. Легко видеть, что S у tTa6n. В противном случае доверять полученной оценке параметра нет оснований. [c.139]

Для определения профиля посетителей магазинов местного торгового центра, не имеющих определенной цели (browsers), маркетологи использовали три набора независимых переменных демографические, покупательское поведение психологические. Зависимая переменная представляет собой индекс посещения магазина без определенной цели, индекс (browsing index). Методом ступенчатой включающей все три набора переменных, выявлено, что демографические факторы — наиболее сильные предикторы, определяющие поведение покупателей, не преследующих конкретных целей. Окончательное уравнение регрессии, 20 из 36 возможных переменных, включало все демографические переменные. В следующей таблице приведены коэффициенты регрессии, стандартные ошибки коэффициентов, а также их уровни значимости. [c.668]

Смотреть страницы где упоминается термин Стандартная ошибка уравнения регрессии

Маркетинговые исследования Издание 3 (2002) — [ c.650 ]

Лекции по дисциплине «Эконометрика» (заочное отделение) (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4

Параметр формально является значением Y при X = 0. Он может не иметь экономического содержания. Интерпретировать можно лишь знак при параметре . Если > 0, то относительное изменение результата происходит мед­леннее, чем изменение фактора. Иными словами, вариация по фактору X выше вариации для результата Y. Также считают, что включает в себя неучтенные в модели факторы.

По итогам 2008 года были собраны данные по прибыли и оборачиваемости оборотных средств 500 торговых предприятий г. Челябинска. Результаты наблюдения сведены в таблицу.

Годовая прибыль предприятия, млн. руб.

Годовая оборачиваемость оборотных средств, раз

Требуется построить зависимость прибыли предприятий от оборачиваемости оборотных средств и оценить качество полученного уравнения.

Пусть y – прибыль предприятия, x – оборачиваемость оборотных средств.

На основе исходных данных были рассчитаны следующие показатели:

Уровень доверия возьмем q=0,95 или 95%.

1. Стандартные ошибки оценок , . намного больше =0,39, следовательно, низкая точность коэффициента . очень мала по сравнению с , следовательно, высокая точность коэффициента .

2. Интервальные оценки коэффициентов уравнения регрессии.

n – 2 = 500 – 2 = 498;

α: → → очень низкая точность коэффициента;

β: → → высокая точность коэффициента.

3. Значимость коэффициентов регрессии.

= >1,96 → коэффициент значим;

= >1,96 → коэффициент значим.

4. Стандартная ошибка регрессии. Se=0,91, по сравнению со средним значением =34,5 ошибка невысокая, точность уравнения хорошая.

5. Коэффициент детерминации. R2 = rxy2=0,782=0,6084 не очень близко к 1, качество подгонки среднее.

6. Средняя ошибка аппроксимации. A=11%, качество подгонки уравнения среднее.

Экономическая интерпретация: при увеличении оборачиваемости оборотных средств предприятия на 1 раз в год средняя годовая прибыль увеличится на 5,86 млн. руб.

Тема 6. Нелинейная парная регрессия

Часто на практике между зависимой и независимыми переменными существует нелинейная форма взаимосвязи. В этом случае существует два выхода:

1) подобрать к анализируемым переменным преобразование, которое бы позволило представить существующую зависимость в виде линейной функции;

2) применить нелинейный метод наименьших квадратов.

Основные нелинейные регрессионные модели и приведение их к линейной форме

1. Экспоненциальное уравнение .

Если прологарифмировать левую и правую части данного уравнения, то получится

.

Это уравнение является линейным, но вместо y в левой части стоит ln y.

В данном случае параметр β1 имеет следующий экономический смысл: при увеличении переменной x на единицу переменная y в среднем увеличится примерно на 100·β% (более точно: y увеличится в раз).

2. Логарифмическое уравнение .

Переход к линейному уравнению осуществляется заменой переменной x на X=lnx..

Параметр β1 имеет следующий экономический смысл: для увеличения y на единицу необходимо увеличить переменную x в раз, т. е. примерно на .

3. Гиперболическое уравнение .

В этом случае необходимо сделать замену переменных x на . Для гиперболической зависимости нет простой интерпретации коэффициента регрессии β1.

4. Степенное уравнение .

Прологарифмировав левую и правую части данного уравнения, получим

.

Заменив соответствующие ряды их логарифмами, получится линейная регрессия.

Экономический смысл параметра β1: если значение переменной x увеличить на 1%, то y увеличится на β1%.

5. Показательное уравнение (β1>0, β1≠1).

Прологарифмировав левую и правую части уравнения, получим

.

Проведя замены Y=ln y и B1=ln β1, получится линейная регрессия.

Экономический смысл параметра β1: при увеличении переменной x на единицу переменная y в среднем увеличится в β1 раз.

Тема 7. Множественная линейная регрессия: определение и оценка параметров

1. Понятие множественной линейной регрессии

Модель множественной линейной регрессии является обобщением парной линейной регрессии и представляет собой следующее выражение:

, t=1. n,

где yt – значение зависимой переменной для наблюдения t,

xit – значение i-й независимой переменной для наблюдения t,

εt – значение случайной ошибки для наблюдения t,

n – число наблюдений,

m – число независимых переменных x.

2. Матричная форма записи множественной линейной регрессии

Уравнение множественной линейной регрессии можно записать в матричной форме:

,

где , , , .

3. Основные предположения

2. для всех наблюдений;

3. = const для всех наблюдений;

4. ;

В случае выполнения вышеперечисленных гипотез модель называется нормальной линейной регрессионной.

4. Метод наименьших квадратов

Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК): .

Чтобы найти минимум этой функции необходимо вычислить производные по каждому из параметров и приравнять их к нулю, в результате получается система уравнений, решение которой в матричном виде следующее:

→ .

,

5. Теорема Гаусса-Маркова

Если выполнены предположения 1-5 из пункта 3, то оценки , полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе линейных несмещенных оценок, то есть являются несмещенными, состоятельными и эффективными.

Тема 8. Множественная линейная регрессия: оценка качества

1. Общая схема проверки качества парной регрессии

Адекватность модели – остатки должны удовлетворять условиям теоремы Гаусса-Маркова.

Основные показатели качества коэффициентов регрессии:

1. Стандартные ошибки оценок (анализ точности определения оценок).

2. Интервальные оценки коэффициентов уравнения регрессии (построение доверительных интервалов).

3. Значимость коэффициентов регрессии (проверка гипотез относительно коэффициентов регрессии).

Основные показатели качества уравнения регрессии в целом:

1. Стандартная ошибка регрессии Se (анализ точности уравнения регрессии).

2. Значимость уравнения регрессии в целом (проверка гипотезы относительно всех коэффициентов регрессии).

3. Коэффициент детерминации R2 (проверка качества подгонки уравнения к исходным данным).

4. Скорректированный коэффициент детерминации R2adj (проверка качества подгонки уравнения к исходным данным).

5. Средняя ошибка аппроксимации (проверка качества подгонки уравнения к эмпирическим данным).

2. Стандартные ошибки оценок

Стандартные ошибки коэффициентов регрессии – это средние квадратические отклонения коэффициентов регрессии от их истинных значений.

,

где

— диагональные элементы матрицы ,

.

Стандартная ошибка является оценкой среднего квадратического отклонения коэффициента регрессии от его истинного значения. Чем меньше стандартная ошибка тем точнее оценка.

3. Интервальные оценки коэффициентов множественной линейной регрессии

Доверительные интервалы для коэффициентов регрессии определяются следующим образом:

1. Выбирается уровень доверия q (0,9; 0,95 или 0,99).

2. Рассчитывается уровень значимости g = 1 – q.

3. Рассчитывается число степеней свободы n – m – 1, где n – число наблюдений, m – число независимых переменных.

4. Определяется критическое значение t-статистики (tкр) по таблицам распределения Стьюдента на основе g и n – m – 1.

5. Рассчитывается доверительный интервал для параметра :

.

Доверительный интервал показывает, что истинное значение параметра с вероятностью q находится в данных пределах.

Чем меньше доверительный интервал относительно коэффициента, тем точнее полученная оценка.

4. Значимость коэффициентов регрессии

Процедура оценки значимости коэффициентов осуществляется аналогичной парной регрессии следующим образом:

1. Рассчитывается значение t-статистики для коэффициента регрессии по формуле .

2. Выбирается уровень доверия q ( 0,9; 0,95 или 0,99).

3. Рассчитывается уровень значимости g = 1 – q.

4. Рассчитывается число степеней свободы n – m – 1, где n – число наблюдений, m – число независимых переменных.

5. Определяется критическое значение t-статистики (tкр) по таблицам распределения Стьюдента на основе g и n – m – 1.

6. Если , то коэффициент является значимым на уровне значимости g. В противном случае коэффициент не значим (на данном уровне g).

t-тесты обеспечивают проверку значимости предельного вклада каждой переменной при допущении, что все остальные переменные уже включены в модель.

5. Стандартная ошибка регрессии

Стандартная ошибка регрессии Se показывает, насколько в среднем фактические значения зависимой переменной y отличаются от ее расчетных значений

.

Используется как основная величина для измерения качества модели (чем она меньше, тем лучше).

Значения Se в однотипных моделях с разным числом наблюдений и (или) переменных сравнимы.

6. Оценка значимости уравнения регрессии в целом

Уравнение значимо, если есть достаточно высокая вероятность того, что существует хотя бы один коэффициент, отличный от нуля.

Имеются альтернативные гипотезы:

Если принимается гипотеза H0, то уравнение статистически незначимо. В противном случае говорят, что уравнение статистически значимо.

Значимость уравнения регрессии в целом осуществляется с помощью F-статистики.

Оценка значимости уравнения регрессии в целом основана на тождестве дисперсионного анализа:

Þ

TSS – общая сумма квадратов отклонений

ESS – объясненная сумма квадратов отклонений

RSS – необъясненная сумма квадратов отклонений

F-статистика представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы)

n – число выборочных наблюдений, m – число независимых переменных.

При отсутствии линейной зависимости между зависимой и независимой переменными F-статистика имеет F-распределение Фишера-Снедекора со степенями свободы k1 = m, k2 = n – m –1.

Процедура оценки значимости уравнения осуществляется следующим образом:

7. Рассчитывается значение F-статистики по формуле .

8. Выбирается уровень доверия q ( 0,9; 0,95 или 0,99).

9. Рассчитывается уровень значимости g = 1 – q.

10. Рассчитывается число степеней свободы n – m – 1, где n – число наблюдений, m – число независимых переменных.

11. Определяется критическое значение F-статистики (Fкр) по таблицам распределения Фишера на основе g и n – m – 1.

12. Если , то уравнение является значимым на уровне значимости g. В противном случае уравнение не значимо (на данном уровне g).

В парной регрессии F-статистика равна квадрату t-статистики: , а значимость коэффициента регрессии и значимость уравнения в целом эквивалентны.

Качество оценки уравнения можно проверить путем расчета коэффициента детерминации R2, который показывает степень соответствия найденного уравнения экспериментальным данным.

.

Коэффициент R2 показывает долю дисперсии переменной y, объясненную регрессией, в общей дисперсии y.

Коэффициент детерминации лежит в пределах 0 £ R2 £ 1.

Чем ближе R2 к 1, тем выше качество подгонки уравнения к статистическим данным.

Чем ближе R2 к 0, тем ниже качество подгонки уравнения к статистическим данным.

Коэффициенты R2 в разных моделях с разным числом наблюдений и переменных несравнимы.

8. Скорректированный коэффициент детерминации R2adj

Низкое значение R2 не свидетельствует о плохом качестве модели, и может объясняться наличием существенных факторов, не включенных в модель

R2 всегда увеличивается с включением новой переменной. Поэтому его необходимо корректировать, и рассчитывают скорректированный коэффициент детерминации

Если R2adj выходит за пределы интервала [0;1], то его использовать нельзя.

Если при добавлении новой переменной в модель увеличивается не только R2, но и R2adj, то можно считать, что вклад этой переменной в повышение качества модели существенен.

9. Средняя ошибка аппроксимации

Средняя ошибка аппроксимации (средняя абсолютная процентная ошибка) – показывает в процентах среднее отклонение расчетных значений зависимой переменной от фактических значений yi

Если A ≤ 10%, то качество подгонки уравнения считается хорошим. Чем меньше значение A, тем лучше.

10. Использование показателей качества коэффициентов и уравнения регрессии для интерпретации и корректировки модели

В случае незначимости уравнения, необходимо устранить ошибки модели. Наиболее распространенными являются следующие ошибки:

— неправильно выбран вид функции регрессии;

— в модель включены незначимые регрессоры;

— в модели отсутствуют значимые регрессоры.

После устранения ошибок требуется заново оценить параметры уравнения и его качество, продолжая этот процесс до тех пор, пока качество уравнения не станет удовлетворительным. Если после поделанных процедур, мы не достигли требуемого уровня значимости, то необходимо устранять другие ошибки (спецификации, классификации, наблюдения и т. д., см. тему 3, п. 6).

11. Интерпретация множественной линейной регрессии

Коэффициент регрессии при переменной xi показывает, на сколько увеличится среднее значение зависимой переменной y при увеличении xi на 1, при условии постоянства других переменных.

В апреле 2006 года были собраны данные по стоимости 200 двухкомнатных квартир в Металлургическом районе г. Челябинска, их жилой площади, площади кухни и расстоянии до центра города (пл. Революции). Результаты наблюдения сведены в таблицу.

Оценка результатов линейной регрессии

Введение

Модель линейной регрессии

Итак, пусть есть несколько независимых случайных величин X1, X2, . Xn (предикторов) и зависящая от них величина Y (предполагается, что все необходимые преобразования предикторов уже сделаны). Более того, мы предполагаем, что зависимость линейная, а ошибки рапределены нормально, то есть

где I — единичная квадратная матрица размера n x n.

Итак, у нас есть данные, состоящие из k наблюдений величин Y и Xi и мы хотим оценить коэффициенты. Стандартным методом для нахождения оценок коэффициентов является метод наименьших квадратов. И аналитическое решение, которое можно получить, применив этот метод, выглядит так: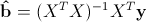

где b с крышкой — оценка вектора коэффициентов, y — вектор значений зависимой величины, а X — матрица размера k x n+1 (n — количество предикторов, k — количество наблюдений), у которой первый столбец состоит из единиц, второй — значения первого предиктора, третий — второго и так далее, а строки соответствуют имеющимся наблюдениям.

Функция summary.lm() и оценка получившихся результатов

Теперь рассмотрим пример построения модели линейной регрессии в языке R:

Таблица gala содержит некоторые данные о 30 Галапагосских островах. Мы будем рассматривать модель, где Species — количество разных видов растений на острове линейно зависит от нескольких других переменных.

Рассмотрим вывод функции summary.lm().
Сначала идет строка, которая напоминает, как строилась модель.
Затем идет информация о распределении остатков: минимум, первая квартиль, медиана, третья квартиль, максимум. В этом месте было бы полезно не только посмотреть на некоторые квантили остатков, но и проверить их на нормальность, например тестом Шапиро-Уилка.
Далее — самое интересное — информация о коэффициентах. Здесь потребуется немного теории.
Сначала выпишем следующий результат:

при этом сигма в квадрате с крышкой является несмещенной оценкой для реальной сигмы в квадрате. Здесь b — реальный вектор коэффициентов, а эпсилон с крышкой — вектор остатков, если в качестве коэффициентов взять оценки, полученные методом наименьших квадратов. То есть при предположении, что ошибки распределены нормально, вектор коэффициентов тоже будет распределен нормально вокруг реального значения, а его дисперсию можно несмещенно оценить. Это значит, что можно проверять гипотезу на равенство коэффициентов нулю, а следовательно проверять значимость предикторов, то есть действительно ли величина Xi сильно влияет на качество построенной модели.
Для проверки этой гипотезы нам понадобится следующая статистика, имеющая распределение Стьюдента в том случае, если реальное значение коэффициента bi равно 0: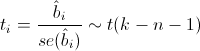

где
— стандартная ошибка оценки коэффициента, а t(k-n-1) — распределение Стьюдента с k-n-1 степенями свободы.

Теперь все готово для продолжения разбора вывода функции summary.lm().
Итак, далее идут оценки коэффициентов, полученные методом наименьших квадратов, их стандартные ошибки, значения t-статистики и p-значения для нее. Обычно p-значение сравнивается с каким-нибудь достаточно малым заранее выбранным порогом, например 0.05 или 0.01. И если значение p-статистики оказывается меньше порога, то гипотеза отвергается, если же больше, ничего конкретного, к сожалению, сказать нельзя. Напомню, что в данном случае, так как распределение Стьюдента симметричное относительно 0, то p-значение будет равно 1-F(|t|)+F(-|t|), где F — функция распределения Стьюдента с k-n-1 степенями свободы. Также, R любезно обозначает звездочками значимые коэффициенты, для которых p-значение достаточно мало. То есть, те коэффициенты, которые с очень малой вероятностью равны 0. В строке Signif. codes как раз содержится расшифровка звездочек: если их три, то p-значение от 0 до 0.001, если две, то оно от 0.001 до 0.01 и так далее. Если никаких значков нет, то р-значение больше 0.1.

В нашем примере можно с большой уверенностью сказать, что предикторы Elevation и Adjacent действительно с большой вероятностью влияют на величину Species, а вот про остальные предикторы ничего определенного сказать нельзя. Обычно, в таких случаях предикторы убирают по одному и смотрят, насколько изменяются другие показатели модели, например BIC или Adjusted R-squared, который будет разобран далее.

Значение Residual standart error соответствует просто оценке сигмы с крышкой, а степени свободы вычисляются как k-n-1.

А теперь самая важные статистики, на которые в первую очередь стоит смотреть: R-squared и Adjusted R-squared:

где Yi — реальные значения Y в каждом наблюдении, Yi с крышкой — значения, предсказанные моделью, Y с чертой — среднее по всем реальным значениям Yi.

Начнем со статистики R-квадрат или, как ее иногда называют, коэффициента детерминации. Она показывает, насколько условная дисперсия модели отличается от дисперсии реальных значений Y. Если этот коэффициент близок к 1, то условная дисперсия модели достаточно мала и весьма вероятно, что модель неплохо описывает данные. Если же коэффициент R-квадрат сильно меньше, например, меньше 0.5, то, с большой долей уверенности модель не отражает реальное положение вещей.

Однако, у статистики R-квадрат есть один серьезный недостаток: при увеличении числа предикторов эта статистика может только возрастать. Поэтому, может показаться, что модель с большим количеством предикторов лучше, чем модель с меньшим, даже если все новые предикторы никак не влияют на зависимую переменную. Тут можно вспомнить про принцип бритвы Оккама. Следуя ему, по возможности, стоит избавляться от лишних предикторов в модели, поскольку она становится более простой и понятной. Для этих целей была придумана статистика скорректированный R-квадрат. Она представляет собой обычный R-квадрат, но со штрафом за большое количество предикторов. Основная идея: если новые независимые переменные дают большой вклад в качество модели, значение этой статистики растет, если нет — то наоборот уменьшается.

Для примера рассмотрим ту же модель, что и раньше, но теперь вместо пяти предикторов оставим два:

Как можно увидеть, значение статистики R-квадрат снизилось, однако значение скорректированного R-квадрат даже немного возросло.

Теперь проверим гипотезу о равенстве нулю всех коэффициентов при предикторах. То есть, гипотезу о том, зависит ли вообще величина Y от величин Xi линейно. Для этого можно использовать следующую статистику, которая, если гипотеза о равенстве нулю всех коэффициентов верна, имеет распределение Фишера c n и k-n-1 степенями свободы:

Значение F-статистики и p-значение для нее находятся в последней строке вывода функции summary.lm().

Заключение

В этой статье были описаны стандартные методы оценки значимости коэффициентов и некоторые критерии оценки качества построенной линейной модели. К сожалению, я не касался вопроса рассмотрения распределения остатков и проверки его на нормальность, поскольку это увеличило бы статью еще вдвое, хотя это и достаточно важный элемент проверки адекватности модели.
Очень надеюсь что мне удалось немного расширить стандартное представление о линейной регрессии, как об алгоритме который просто оценивает некоторый вид зависимости, и показать, как можно оценить его результаты.