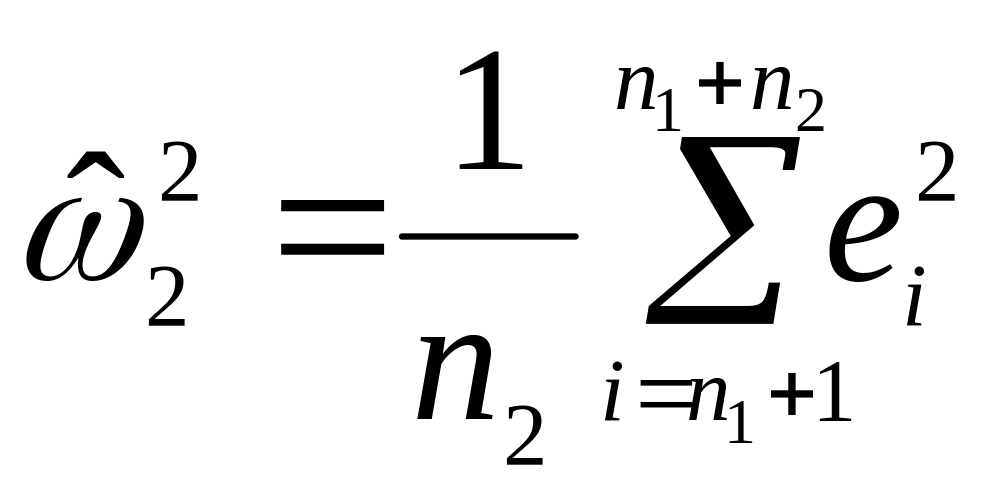Так как гетероскедастичность не приводит к смещению оценок коэффициентов, можно по-прежнему использовать МНК. Смещены и несостоятельны оказываются не сами оценки коэффициентов, а их стандартные ошибки, поэтому формула для расчета стандартных ошибок в условиях гомоскедастичности не подходит для случая гетероскедастичности.
Естественной идеей в этой ситуации является корректировка формулы расчета стандартных ошибок, чтобы она давала «правильный» (состоятельный) результат. Тогда можно снова будет корректно проводить тесты, проверяющие, например, незначимость коэффициентов, и строить доверительные интервалы. Соответствующие «правильные» стандартные ошибки называются состоятельными в условиях гетероскедастичности стандартными ошибками (heteroskedasticity consistent (heteroskedasticity robust) standard errors)1. Первоначальная формула для их расчета была предложена Уайтом, поэтому иногда их также называют стандартными ошибками в форме Уайта (White standard errors). Предложенная Уайтом состоятельная оценка ковариационной матрицы вектора оценок коэффициентов имеет вид:
(widehat{V}{left( widehat{beta} right) = n}left( {X^{‘}X} right)^{- 1}left( {frac{1}{n}{sumlimits_{s = 1}^{n}e_{s}^{2}}x_{s}x_{s}^{‘}} right)left( {X^{‘}X} right)^{- 1},)
где (x_{s}) – это s-я строка матрицы регрессоров X. Легко видеть, что эта формула более громоздка, чем формула (widehat{V}{left( widehat{beta} right) = left( {X^{‘}X} right)^{- 1}}S^{2}), которую мы вывели в третьей главе для случая гомоскедастичности. К счастью, на практике соответствующие вычисления не представляют сложности, так как возможность автоматически рассчитывать стандартные ошибки в форме Уайта реализована во всех современных эконометрических пакетах. Общепринятое обозначение для этой версии стандартных ошибок: «HC0». В работах (MacKinnon, White,1985) и (Davidson, MacKinnon, 2004) были предложены и альтернативные версии, которые обычно обозначаются в эконометрических пакетах «HC1», «HC2» и «HC3». Их расчетные формулы несколько отличаются, однако суть остается прежней: они позволяют состоятельно оценивать стандартные отклонения МНК-оценок коэффициентов в условиях гетероскедастичности.
Для случая парной регрессии состоятельная в условиях гетероскедастичности стандартная ошибка оценки коэффициента при регрессоре имеет вид:
(mathit{se}{left( widehat{beta_{2}} right) = sqrt{frac{1}{n}frac{frac{1}{n — 2}{sumlimits_{i = 1}^{n}{left( {x_{i} — overline{x}} right)^{2}e_{i}^{2}}}}{widehat{mathit{var}}(x)^{2}}.}})
Формальное доказательство состоятельности будет приведено в следующей главе. Пока же обсудим пример, иллюстрирующий важность использования робастных стандартных ошибок.
Пример 5.1. Оценка эффективности использования удобрений
В файле Agriculture в материалах к этому учебнику содержатся следующие данные 2010 года об урожайности яровой и озимой пшеницы в Спасском районе Пензенской области:
PRODP — урожайность в денежном выражении, в тысячах рублей с 1 га,
SIZE – размер пахотного поля, га,
LABOUR – трудозатраты, руб. на 1 га,
FUNG1 – фунгициды, протравители семян, расходы на удобрение в руб. на 1 га,
FUNG2 – фунгициды, во время роста, расходы на удобрение в руб. на 1 га,
GIRB – гербициды, расходы на удобрение в руб. на 1 га,
INSEC – инсектициды, расходы на удобрение в руб. на 1 га,
YDOB1 – аммофос, во время сева, расходы на удобрение в руб. на 1 га,
YDOB2 – аммиачная селитра, во время роста, расходы на удобрение в руб. на 1 га.
Представим, что вас интересует ответ на вопрос: влияет ли использование фунгицидов на урожайность поля?
(а) Оцените зависимость урожайности в денежном выражении от константы и переменных FUNG1, FUNG2, YDOB1, YDOB2, GIRB, INSEC, LABOUR. Запишите уравнение регрессии в стандартной форме, указав коэффициент детерминации и (в скобках под соответствующими коэффициентами) стандартные ошибки для случая гомоскедастичности. Какие из переменных значимы на 5-процентном уровне значимости?
(б) Решите предыдущий пункт заново, используя теперь состоятельные в условиях гетероскедастичности стандартные ошибки. Сопоставьте выводы по поводу значимости (при пятипроцентном уровне) переменных, характеризующих использование фунгицидов.
Решение:
(а) Оценим требуемое уравнение:
Модель 1: МНК, использованы наблюдения 1-200
Зависимая переменная: PRODP
| Коэффициент | Ст. ошибка | t-статистика | P-значение | ||
| const | -38,4019 | 7,5273 | -5,1017 | <0,00001 | *** |
| FUNG1 | 0,0445755 | 0,0487615 | 0,9142 | 0,36178 | |
| FUNG2 | 0,103625 | 0,049254 | 2,1039 | 0,03669 | ** |
| GIRB | 0,0776059 | 0,0523553 | 1,4823 | 0,13990 | |
| INSEC | 0,0782521 | 0,0484667 | 1,6146 | 0,10805 | |
| LABOUR | 0,0415064 | 0,00275277 | 15,0781 | <0,00001 | *** |
| YDOB1 | 0,0492168 | 0,0233328 | 2,1093 | 0,03621 | ** |
| YDOB2 | -0,0906824 | 0,025864 | -3,5061 | 0,00057 | *** |
| Сумма кв. остатков | 150575,6 | Ст. ошибка модели | 28,00443 | |
| R-квадрат | 0,801958 | Испр. R-квадрат | 0,794738 | |
| F(7, 192) | 111,0701 | Р-значение (F) | 5,08e-64 |
Переменные FUNG2, LABOUR, YDOB1 и YDOB2 значимы на пятипроцентном уровне значимости (причем LABOUR и YDOB2 — ещё и на однопроцентном).
Если представить те же самые результаты в форме уравнения, то получится вот так:
({widehat{mathit{PRODP}}}_{i} = {{- underset{(7,53)}{38,40}} + {underset{(0,05)}{0,04} ast {mathit{FUNG}1}_{i}} + {underset{(0,05)}{0,10} ast {mathit{FUNG}2}_{i}} +})
({{+ underset{(0,05)}{0,08}} ast mathit{GIRB}_{i}} + {underset{(0,05)}{0,08} ast mathit{INSEC}_{i}} + {underset{(0,003)}{0,04} ast mathit{LABOUR}_{i}} + {})
({{{+ underset{(0,02)}{0,05}} ast {mathit{YDOB}1}_{i}} — {underset{(0,03)}{0,09} ast {mathit{YDOB}2}_{i}}},{R^{2} = 0,802})
(б) При использовании альтернативных стандартных ошибок получим следующий результат:
Модель 2: МНК, использованы наблюдения 1-200
Зависимая переменная: PRODP
Робастные оценки стандартных ошибок (с поправкой на гетероскедастичность),
вариант HC1
| Коэффициент | Ст. ошибка | t-статистика | P-значение | ||
| const | -38,4019 | 7,40425 | -5,1865 | <0,00001 | *** |
| FUNG1 | 0,0445755 | 0,0629524 | 0,7081 | 0,47975 | |
| FUNG2 | 0,103625 | 0,0624082 | 1,6604 | 0,09846 | * |
| GIRB | 0,0776059 | 0,0623777 | 1,2441 | 0,21497 | |
| INSEC | 0,0782521 | 0,0536527 | 1,4585 | 0,14634 | |
| LABOUR | 0,0415064 | 0,00300121 | 13,8299 | <0,00001 | *** |
| YDOB1 | 0,0492168 | 0,0197491 | 2,4921 | 0,01355 | ** |
| YDOB2 | -0,0906824 | 0,030999 | -2,9253 | 0,00386 | *** |
| Сумма кв. остатков | 150575,6 | Ст. ошибка модели | 28,00443 | |
| R-квадрат | 0,801958 | Испр. R-квадрат | 0,794738 | |
| F(7, 192) | 119,2263 | Р-значение (F) | 2,16e-66 |
Оценки коэффициентов по сравнению с пунктом (а) не поменялись, что естественно: мы ведь по-прежнему используем обычный МНК. Однако стандартные ошибки теперь немного другие. В некоторых случаях это меняет выводы тестов на незначимость.
Переменные LABOUR, YDOB1 и YDOB2 значимы на пятипроцентном уровне значимости (причем LABOUR и YDOB2 — ещё и на однопроцентном).
Переменная FUNG2 перестала быть значимой на пятипроцентном уровне. Таким образом, при использовании корректных стандартных ошибок следует сделать вывод о том, что соответствующий вид удобрений не важен для урожайности. Обратите внимание, что если бы мы использовали «обычные» стандартные ошибки, то мы пришли бы к противоположному заключению (см. пункт (а)).
* * *
Важно подчеркнуть, что в реальных пространственных данных гетероскедастичность в той или иной степени наблюдается практически всегда. А даже если её и нет, то состоятельные в условиях гетероскедастичности стандартные ошибки по-прежнему будут… состоятельными (и будут близки к «обычным» стандартным ошибкам, посчитанным по формулам из третьей главы). Поэтому в современных прикладных исследованиях при оценке уравнений по умолчанию используются именно робастные стандартные ошибки, а не стандартные ошибки для случая гомоскедастичности. Мы настоятельно рекомендуем читателю поступать так же2. В нашем учебнике с этого момента и во всех последующих главах, если прямо не оговорено иное, для МНК-оценок параметров всегда используются состоятельные в условиях гетероскедастичности стандартные ошибки.
-
Поскольку довольно утомительно каждый раз произносить это название полностью в англоязычном варианте их часто называют просто robust standard errors, что на русском языке эконометристов превратилось в «робастные стандартные ошибки». Кому-то подобный англицизм, конечно, режет слух, однако в устной речи он и правда куда удобней своей длинной альтернативы.↩︎
-
Просто не забывайте включать соответствующую опцию в своем эконометрическом пакете.↩︎
1. Статистика критерия Дарбина-Уотсона вычисляется по формуле DW = ________, где еk – остатки в наблюдениях авторегрессионной схемы первого порядка:
2. Фиктивная переменная взаимодействия – фиктивная переменная, предназначенная для
установления влияния на регрессию __________событий:
1) одновременного наступления нескольких независимых
2) степени взаимосвязи возможных
3) наступления одного из нескольких взаимосвязанных
4) наступления одного из нескольких независимых
5) циклических
3. Если две переменные независимы, то их теоретическая ковариация равна:
1) ½
2) 0
3) 2
4) 1
5) -1
4. В вторегрессионной схеме первого порядка зависимость между последовательными случайными членами описывается формулой u k+1 = ________, где а ρ – константа, ε k+1 – новый случайный член:
1) −1 +1 + k k ρu ε
2) +1 + k k ρu ε
3) +1 + k k u ρε
4) k +1 ρε
5) +1 − k k ρu ε
5. Для того, чтобы установить влияние какого-либо события на коэффициент линейной
регрессии при нефиктивной переменной, в модель включают:
1) фиктивную переменную взаимодействия
2) лаговую переменную
3) лишнюю переменную
4) фиктивную переменную для коэффициента наклона
5) циклическую
6. Наиболее частая причина положительной автокорреляции заключается в постоянной направленности воздействия _____________ переменных:
1) не включенных в уравнение
2) лишних
3) сезонных
4) фиктивных
5) циклических
7. Близко к линии регрессии находится наблюдение, для которого теоретическое распределение случайного члена имеет:
1) асимметрию, равную 0
2) нулевое среднее значение
3) большое стандартное отклонение
4) малое стандартное отклонение
5) наибольшее среднее значение
8. Модель множественной регрессии имеет вид: y =
9. Если независимые переменные имеют ярко выраженный временной тренд, то они оказываются:
1) имеющими большое влияние:
2) малозначимыми
3) тесно коррелированными
4) слабо коррелированными
5) некоррелированными
10. Если предположение о природе гетероскедастичности верно, то дисперсия случайного
члена для первых наблюдений в упорядоченном ряду будет ________ для последних:
1) больше, чем
2) такая же, как
3) ниже, чем
4) равно 0
5) равно 1
11. Автокорреляция первого порядка – ситуация, когда коррелируют случайные члены регрессии в __________ наблюдениях:
1) последовательных
2) k первых и k последних
3) нечетных
4) четных
5) первых
12. Число степеней свободы для уравнения множественной (m-мерной) регрессии при достаточном числе наблюдений n составляет:
1) n-m-1
2) n-m+1
3) n-m
4)m/n
5) n+m+1
13. Стандартные ошибки, вычисленные при гетероскедастичности:
1) завышены по сравнению с истинными значениями
2) занижены по сравнению с истинными значениями
3) соответствуют истинным значениям
4) не имеют математического смысла
5) являются случайными
14. В авторегрессионной схеме первого порядка предполагается, что значение ε в каждом
наблюдении:
1) не зависит от его значения во всех других наблюдениях
2) зависит от его значения в предыдущих наблюдениях
3) зависит от его значения во всех других наблюдениях
4) зависит от его значения в первом наблюдении
5) равны 0
15. Из перечисленного: 1) число объясняющих переменных, 2) количество наблюдений в выборке, 3) конкретные значения переменных − критические значения статистики Дарбина-Уотсона зависят от:
1) 3
2) 1, 2
3) 1, 2, 3
4) 1, 3
5) 2
16. Множественный регрессионный анализ является ________ парного регрессионного анализа:
1) развитием
2) противоположностью
3) частным случаем
4) подобием
5) эквивалентностью
17. Критерий Дарбина-Уотсона –метод обнаружения _________ с помощью статистики Дарбина-Уотсона:
1) гетероскедастичности ошибки
2) сезонных колебаний
3) мультиколлинеарности
4) автокорреляции
5) гомоскедастичности
18. Процесс выбора необходимых переменных для регрессии переменных и отбрасывание
лишних переменных называется:
1) унификацией переменных
2) моделированием
3) спецификацией переменных
4) прогнозированием
5) подгонкой
19. Условие гомоскедастичности означает, что вероятность того, что случайный член при-
мет какое-либо конкретное значение _________ наблюдений:
1) зависит от времени проведения
2) одинакова для всех
3) зависит от номера
4) зависит от числа
5) от характера
20. Положительная автокорреляция –ситуация, когда случайный член регрессии в сле-
дующем наблюдении ожидается:
1) противоположного знака по сравнению с настоящим наблюдением
2) того же знака, что и в первом наблюдении
3) того же знака, что и в настоящем наблюдении
4) противоположного знака по сравнению с первым наблюдением
5) равным 0
From Wikipedia, the free encyclopedia
The topic of heteroskedasticity-consistent (HC) standard errors arises in statistics and econometrics in the context of linear regression and time series analysis. These are also known as heteroskedasticity-robust standard errors (or simply robust standard errors), Eicker–Huber–White standard errors (also Huber–White standard errors or White standard errors),[1] to recognize the contributions of Friedhelm Eicker,[2] Peter J. Huber,[3] and Halbert White.[4]
In regression and time-series modelling, basic forms of models make use of the assumption that the errors or disturbances ui have the same variance across all observation points. When this is not the case, the errors are said to be heteroskedastic, or to have heteroskedasticity, and this behaviour will be reflected in the residuals 
Heteroskedasticity-consistent standard errors that differ from classical standard errors may indicate model misspecification. Substituting heteroskedasticity-consistent standard errors does not resolve this misspecification, which may lead to bias in the coefficients. In most situations, the problem should be found and fixed.[5] Other types of standard error adjustments, such as clustered standard errors or HAC standard errors, may be considered as extensions to HC standard errors.
History[edit]
Heteroskedasticity-consistent standard errors are introduced by Friedhelm Eicker,[6][7] and popularized in econometrics by Halbert White.
Problem[edit]
Consider the linear regression model for the scalar Y.
where 


The ordinary least squares (OLS) estimator is
where 



If the sample errors have equal variance 

where 
When the error terms do not have constant variance (i.e., the assumption of ![{displaystyle mathbb {E} [mathbf {u} mathbf {u} ^{top }]=sigma ^{2}mathbf {I} _{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c38bd674a3bee8eb6338750d7cf3d8ca9ea6911)
where ![{displaystyle mathbf {Sigma } =mathbb {V} [mathbf {u} ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a0f375e230fb618630294094fa481afa28f375a)
While the OLS point estimator remains unbiased, it is not «best» in the sense of having minimum mean square error, and the OLS variance estimator ![{displaystyle {hat {mathbb {V} }}left[{widehat {boldsymbol {beta }}}_{mathrm {OLS} }right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc59a54a62987ab2c5d320a2382371a6d6d0f0e4)
For any non-linear model (for instance logit and probit models), however, heteroskedasticity has more severe consequences: the maximum likelihood estimates of the parameters will be biased (in an unknown direction), as well as inconsistent (unless the likelihood function is modified to correctly take into account the precise form of heteroskedasticity).[8][9] As pointed out by Greene, “simply computing a robust covariance matrix for an otherwise inconsistent estimator does not give it redemption.”[10]
Solution[edit]
If the regression errors 



where as above 

Also often discussed in the literature (including White’s paper) is the covariance matrix 

where
and
Thus,
and
Precisely which covariance matrix is of concern is a matter of context.
Alternative estimators have been proposed in MacKinnon & White (1985) that correct for unequal variances of regression residuals due to different leverage.[11] Unlike the asymptotic White’s estimator, their estimators are unbiased when the data are homoscedastic.
Of the four widely available different options, often denoted as HC0-HC3, the HC3 specification appears to work best, with tests relying on the HC3 estimator featuring better power and closer proximity to the targetted size, especially in small samples. The larger the sample, the smaller the difference between the different estimators.[12]
An alternative to explicitly modelling the heteroskedasticity is using a resampling method such as the Wild Bootstrap. Given that the studentized Bootstrap, which standardizes the resampled statistic by its standard error, yields an asymptotic refinement,[13] heteroskedasticity-robust standard errors remain nevertheless useful.
Instead of accounting for the heteroskedastic errors, most linear models can be transformed to feature homoskedastic error terms (unless the error term is heteroskedastic by construction, e.g. in a Linear probability model). One way to do this is using Weighted least squares, which also features improved efficiency properties.
See also[edit]
- Delta method
- Generalized least squares
- Generalized estimating equations
- Weighted least squares, an alternative formulation
- White test — a test for whether heteroskedasticity is present.
- Newey–West estimator
- Quasi-maximum likelihood estimate
Software[edit]
- EViews: EViews version 8 offers three different methods for robust least squares: M-estimation (Huber, 1973), S-estimation (Rousseeuw and Yohai, 1984), and MM-estimation (Yohai 1987).[14]
- Julia: the
CovarianceMatricespackage offers several methods for heteroskedastic robust variance covariance matrices.[15] - MATLAB: See the
hacfunction in the Econometrics toolbox.[16] - Python: The Statsmodel package offers various robust standard error estimates, see statsmodels.regression.linear_model.RegressionResults for further descriptions
- R: the
vcovHC()command from the sandwich package.[17][18] - RATS: robusterrors option is available in many of the regression and optimization commands (linreg, nlls, etc.).
- Stata:
robustoption applicable in many pseudo-likelihood based procedures.[19] - Gretl: the option
--robustto several estimation commands (such asols) in the context of a cross-sectional dataset produces robust standard errors.[20]
References[edit]
- ^ Kleiber, C.; Zeileis, A. (2006). «Applied Econometrics with R» (PDF). UseR-2006 conference. Archived from the original (PDF) on April 22, 2007.
- ^ Eicker, Friedhelm (1967). «Limit Theorems for Regression with Unequal and Dependent Errors». Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Vol. 5. pp. 59–82. MR 0214223. Zbl 0217.51201.
- ^ Huber, Peter J. (1967). «The behavior of maximum likelihood estimates under nonstandard conditions». Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Vol. 5. pp. 221–233. MR 0216620. Zbl 0212.21504.
- ^ White, Halbert (1980). «A Heteroskedasticity-Consistent Covariance Matrix Estimator and a Direct Test for Heteroskedasticity». Econometrica. 48 (4): 817–838. CiteSeerX 10.1.1.11.7646. doi:10.2307/1912934. JSTOR 1912934. MR 0575027.
- ^ King, Gary; Roberts, Margaret E. (2015). «How Robust Standard Errors Expose Methodological Problems They Do Not Fix, and What to Do About It». Political Analysis. 23 (2): 159–179. doi:10.1093/pan/mpu015. ISSN 1047-1987.
- ^ Eicker, F. (1963). «Asymptotic Normality and Consistency of the Least Squares Estimators for Families of Linear Regressions». The Annals of Mathematical Statistics. 34 (2): 447–456. doi:10.1214/aoms/1177704156.
- ^ Eicker, Friedhelm (January 1967). «Limit theorems for regressions with unequal and dependent errors». Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics. 5 (1): 59–83.
- ^ Giles, Dave (May 8, 2013). «Robust Standard Errors for Nonlinear Models». Econometrics Beat.
- ^ Guggisberg, Michael (2019). «Misspecified Discrete Choice Models and Huber-White Standard Errors». Journal of Econometric Methods. 8 (1). doi:10.1515/jem-2016-0002.
- ^ Greene, William H. (2012). Econometric Analysis (Seventh ed.). Boston: Pearson Education. pp. 692–693. ISBN 978-0-273-75356-8.
- ^ MacKinnon, James G.; White, Halbert (1985). «Some Heteroskedastic-Consistent Covariance Matrix Estimators with Improved Finite Sample Properties». Journal of Econometrics. 29 (3): 305–325. doi:10.1016/0304-4076(85)90158-7. hdl:10419/189084.
- ^ Long, J. Scott; Ervin, Laurie H. (2000). «Using Heteroscedasticity Consistent Standard Errors in the Linear Regression Model». The American Statistician. 54 (3): 217–224. doi:10.2307/2685594. ISSN 0003-1305.
- ^ C., Davison, Anthony (2010). Bootstrap methods and their application. Cambridge Univ. Press. ISBN 978-0-521-57391-7. OCLC 740960962.
- ^ «EViews 8 Robust Regression».
- ^ CovarianceMatrices: Robust Covariance Matrix Estimators
- ^ «Heteroskedasticity and autocorrelation consistent covariance estimators». Econometrics Toolbox.
- ^ sandwich: Robust Covariance Matrix Estimators
- ^ Kleiber, Christian; Zeileis, Achim (2008). Applied Econometrics with R. New York: Springer. pp. 106–110. ISBN 978-0-387-77316-2.
- ^ See online help for
_robustoption andregresscommand. - ^ «Robust covariance matrix estimation» (PDF). Gretl User’s Guide, chapter 19.
Further reading[edit]
- Freedman, David A. (2006). «On The So-Called ‘Huber Sandwich Estimator’ and ‘Robust Standard Errors’«. The American Statistician. 60 (4): 299–302. doi:10.1198/000313006X152207. S2CID 6222876.
- Hardin, James W. (2003). «The Sandwich Estimate of Variance». In Fomby, Thomas B.; Hill, R. Carter (eds.). Maximum Likelihood Estimation of Misspecified Models: Twenty Years Later. Amsterdam: Elsevier. pp. 45–74. ISBN 0-7623-1075-8.
- Hayes, Andrew F.; Cai, Li (2007). «Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation». Behavior Research Methods. 39 (4): 709–722. doi:10.3758/BF03192961. PMID 18183883.
- King, Gary; Roberts, Margaret E. (2015). «How Robust Standard Errors Expose Methodological Problems They Do Not Fix, and What to Do About It». Political Analysis. 23 (2): 159–179. doi:10.1093/pan/mpu015.
- Wooldridge, Jeffrey M. (2009). «Heteroskedasticity-Robust Inference after OLS Estimation». Introductory Econometrics : A Modern Approach (Fourth ed.). Mason: South-Western. pp. 265–271. ISBN 978-0-324-66054-8.
- Buja, Andreas, et al. «Models as approximations-a conspiracy of random regressors and model deviations against classical inference in regression.» Statistical Science (2015): 1. pdf
From Wikipedia, the free encyclopedia
The topic of heteroskedasticity-consistent (HC) standard errors arises in statistics and econometrics in the context of linear regression and time series analysis. These are also known as heteroskedasticity-robust standard errors (or simply robust standard errors), Eicker–Huber–White standard errors (also Huber–White standard errors or White standard errors),[1] to recognize the contributions of Friedhelm Eicker,[2] Peter J. Huber,[3] and Halbert White.[4]
In regression and time-series modelling, basic forms of models make use of the assumption that the errors or disturbances ui have the same variance across all observation points. When this is not the case, the errors are said to be heteroskedastic, or to have heteroskedasticity, and this behaviour will be reflected in the residuals 
Heteroskedasticity-consistent standard errors that differ from classical standard errors may indicate model misspecification. Substituting heteroskedasticity-consistent standard errors does not resolve this misspecification, which may lead to bias in the coefficients. In most situations, the problem should be found and fixed.[5] Other types of standard error adjustments, such as clustered standard errors or HAC standard errors, may be considered as extensions to HC standard errors.
History[edit]
Heteroskedasticity-consistent standard errors are introduced by Friedhelm Eicker,[6][7] and popularized in econometrics by Halbert White.
Problem[edit]
Consider the linear regression model for the scalar Y.
where 


The ordinary least squares (OLS) estimator is
where 



If the sample errors have equal variance 

where 
When the error terms do not have constant variance (i.e., the assumption of ![{displaystyle mathbb {E} [mathbf {u} mathbf {u} ^{top }]=sigma ^{2}mathbf {I} _{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c38bd674a3bee8eb6338750d7cf3d8ca9ea6911)
where ![{displaystyle mathbf {Sigma } =mathbb {V} [mathbf {u} ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a0f375e230fb618630294094fa481afa28f375a)
While the OLS point estimator remains unbiased, it is not «best» in the sense of having minimum mean square error, and the OLS variance estimator ![{displaystyle {hat {mathbb {V} }}left[{widehat {boldsymbol {beta }}}_{mathrm {OLS} }right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc59a54a62987ab2c5d320a2382371a6d6d0f0e4)
For any non-linear model (for instance logit and probit models), however, heteroskedasticity has more severe consequences: the maximum likelihood estimates of the parameters will be biased (in an unknown direction), as well as inconsistent (unless the likelihood function is modified to correctly take into account the precise form of heteroskedasticity).[8][9] As pointed out by Greene, “simply computing a robust covariance matrix for an otherwise inconsistent estimator does not give it redemption.”[10]
Solution[edit]
If the regression errors 



where as above 

Also often discussed in the literature (including White’s paper) is the covariance matrix 

where
and
Thus,
and
Precisely which covariance matrix is of concern is a matter of context.
Alternative estimators have been proposed in MacKinnon & White (1985) that correct for unequal variances of regression residuals due to different leverage.[11] Unlike the asymptotic White’s estimator, their estimators are unbiased when the data are homoscedastic.
Of the four widely available different options, often denoted as HC0-HC3, the HC3 specification appears to work best, with tests relying on the HC3 estimator featuring better power and closer proximity to the targetted size, especially in small samples. The larger the sample, the smaller the difference between the different estimators.[12]
An alternative to explicitly modelling the heteroskedasticity is using a resampling method such as the Wild Bootstrap. Given that the studentized Bootstrap, which standardizes the resampled statistic by its standard error, yields an asymptotic refinement,[13] heteroskedasticity-robust standard errors remain nevertheless useful.
Instead of accounting for the heteroskedastic errors, most linear models can be transformed to feature homoskedastic error terms (unless the error term is heteroskedastic by construction, e.g. in a Linear probability model). One way to do this is using Weighted least squares, which also features improved efficiency properties.
See also[edit]
- Delta method
- Generalized least squares
- Generalized estimating equations
- Weighted least squares, an alternative formulation
- White test — a test for whether heteroskedasticity is present.
- Newey–West estimator
- Quasi-maximum likelihood estimate
Software[edit]
- EViews: EViews version 8 offers three different methods for robust least squares: M-estimation (Huber, 1973), S-estimation (Rousseeuw and Yohai, 1984), and MM-estimation (Yohai 1987).[14]
- Julia: the
CovarianceMatricespackage offers several methods for heteroskedastic robust variance covariance matrices.[15] - MATLAB: See the
hacfunction in the Econometrics toolbox.[16] - Python: The Statsmodel package offers various robust standard error estimates, see statsmodels.regression.linear_model.RegressionResults for further descriptions
- R: the
vcovHC()command from the sandwich package.[17][18] - RATS: robusterrors option is available in many of the regression and optimization commands (linreg, nlls, etc.).
- Stata:
robustoption applicable in many pseudo-likelihood based procedures.[19] - Gretl: the option
--robustto several estimation commands (such asols) in the context of a cross-sectional dataset produces robust standard errors.[20]
References[edit]
- ^ Kleiber, C.; Zeileis, A. (2006). «Applied Econometrics with R» (PDF). UseR-2006 conference. Archived from the original (PDF) on April 22, 2007.
- ^ Eicker, Friedhelm (1967). «Limit Theorems for Regression with Unequal and Dependent Errors». Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Vol. 5. pp. 59–82. MR 0214223. Zbl 0217.51201.
- ^ Huber, Peter J. (1967). «The behavior of maximum likelihood estimates under nonstandard conditions». Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Vol. 5. pp. 221–233. MR 0216620. Zbl 0212.21504.
- ^ White, Halbert (1980). «A Heteroskedasticity-Consistent Covariance Matrix Estimator and a Direct Test for Heteroskedasticity». Econometrica. 48 (4): 817–838. CiteSeerX 10.1.1.11.7646. doi:10.2307/1912934. JSTOR 1912934. MR 0575027.
- ^ King, Gary; Roberts, Margaret E. (2015). «How Robust Standard Errors Expose Methodological Problems They Do Not Fix, and What to Do About It». Political Analysis. 23 (2): 159–179. doi:10.1093/pan/mpu015. ISSN 1047-1987.
- ^ Eicker, F. (1963). «Asymptotic Normality and Consistency of the Least Squares Estimators for Families of Linear Regressions». The Annals of Mathematical Statistics. 34 (2): 447–456. doi:10.1214/aoms/1177704156.
- ^ Eicker, Friedhelm (January 1967). «Limit theorems for regressions with unequal and dependent errors». Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics. 5 (1): 59–83.
- ^ Giles, Dave (May 8, 2013). «Robust Standard Errors for Nonlinear Models». Econometrics Beat.
- ^ Guggisberg, Michael (2019). «Misspecified Discrete Choice Models and Huber-White Standard Errors». Journal of Econometric Methods. 8 (1). doi:10.1515/jem-2016-0002.
- ^ Greene, William H. (2012). Econometric Analysis (Seventh ed.). Boston: Pearson Education. pp. 692–693. ISBN 978-0-273-75356-8.
- ^ MacKinnon, James G.; White, Halbert (1985). «Some Heteroskedastic-Consistent Covariance Matrix Estimators with Improved Finite Sample Properties». Journal of Econometrics. 29 (3): 305–325. doi:10.1016/0304-4076(85)90158-7. hdl:10419/189084.
- ^ Long, J. Scott; Ervin, Laurie H. (2000). «Using Heteroscedasticity Consistent Standard Errors in the Linear Regression Model». The American Statistician. 54 (3): 217–224. doi:10.2307/2685594. ISSN 0003-1305.
- ^ C., Davison, Anthony (2010). Bootstrap methods and their application. Cambridge Univ. Press. ISBN 978-0-521-57391-7. OCLC 740960962.
- ^ «EViews 8 Robust Regression».
- ^ CovarianceMatrices: Robust Covariance Matrix Estimators
- ^ «Heteroskedasticity and autocorrelation consistent covariance estimators». Econometrics Toolbox.
- ^ sandwich: Robust Covariance Matrix Estimators
- ^ Kleiber, Christian; Zeileis, Achim (2008). Applied Econometrics with R. New York: Springer. pp. 106–110. ISBN 978-0-387-77316-2.
- ^ See online help for
_robustoption andregresscommand. - ^ «Robust covariance matrix estimation» (PDF). Gretl User’s Guide, chapter 19.
Further reading[edit]
- Freedman, David A. (2006). «On The So-Called ‘Huber Sandwich Estimator’ and ‘Robust Standard Errors’«. The American Statistician. 60 (4): 299–302. doi:10.1198/000313006X152207. S2CID 6222876.
- Hardin, James W. (2003). «The Sandwich Estimate of Variance». In Fomby, Thomas B.; Hill, R. Carter (eds.). Maximum Likelihood Estimation of Misspecified Models: Twenty Years Later. Amsterdam: Elsevier. pp. 45–74. ISBN 0-7623-1075-8.
- Hayes, Andrew F.; Cai, Li (2007). «Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation». Behavior Research Methods. 39 (4): 709–722. doi:10.3758/BF03192961. PMID 18183883.
- King, Gary; Roberts, Margaret E. (2015). «How Robust Standard Errors Expose Methodological Problems They Do Not Fix, and What to Do About It». Political Analysis. 23 (2): 159–179. doi:10.1093/pan/mpu015.
- Wooldridge, Jeffrey M. (2009). «Heteroskedasticity-Robust Inference after OLS Estimation». Introductory Econometrics : A Modern Approach (Fourth ed.). Mason: South-Western. pp. 265–271. ISBN 978-0-324-66054-8.
- Buja, Andreas, et al. «Models as approximations-a conspiracy of random regressors and model deviations against classical inference in regression.» Statistical Science (2015): 1. pdf
43
Тема:
ОБОБЩЕННЫЙ
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
И
ЕГО ВАРИАНТЫ В СЛУЧАЕ ГЕТЕРОСКЕДАСТИЧНОСТИ
План лекции
-
Обобщенный метод
наименьших квадратов -
Метод взвешенных
наименьших квадратов -
Стандартные ошибки
и их корректировка -
Тесты на
гетероскедастичность
1. Классическая регрессионная модель
(1.1)
Строится в предположении выполнения ряда условий, в том числе
3а.
,
3b.
.
Если выполнение первого условия не
вызывает сомнения, то надеяться на
выполнение второго условия имеет смысл
только тогда, когда выборочные наблюдения
достаточно однородны. В практике
построения регрессионных моделей, часто
встречаются ситуации, в которых
нереалистичность этого предположения
становится очевидной. Наблюдения либо
коррелированны между собой, либо их
дисперсии не равны постоянной величине.
Случай неравенства дисперсий в
эконометрике называется гетероскедастичностью
(в отличие от гомоскедастичности –
равенства дисперсий). В этом случае
возникает необходимость в построении
регрессионных моделей без предположения,
что выполняется условие 3b.
Выясним, что происходит, если в основе
построения множественной регрессии
положены следующие гипотезы:
1.
— спецификация модели;
2.
— детерминированная матрица, имеющая
максимальный ранг m+1;
3а.
,
3b.
,
где матрица
положительно определена.
Модель, которая строится в предположении
выполнения данных условий, называется
обобщенной регрессией. Она отличается
от классической только условием 3b.
Если для ее построения применить МНК,
то полученные оценки вектора
(4.1.2)
обладают следующими
свойствами:
-
они в силу условия
3а несмещенные, так как
;
-
их ковариационная
матрица равна
Как
правило, матрица
неизвестна и ковариационную матрицу
заменяют оценкой
,
(4.1.3)
где
.
Проверим оценку ковариационной матрицы на несмещенность, для чего вычислим ее математическое ожидание
.
(4.1.4)
В свою очередь,
(4.1.5)
.
Здесь использован
тот факт, что
,
так как
и
матрица
обладает
свойствами:
,
,
.
Таким
образом, математическое ожидание
ковариационной матрицы может быть
записано в виде
,
(4.1.6)
что
в общем случае не совпадает с
.
Следовательно,
оценка матрицы ковариации вектора
,
полученная с помощью обычного МНК,
является смещенной и требуется в данной
ситуации применять модифицированный
МНК. Способ модификации дает теорема
Айткена. В соответствии с этой теоремой
для обобщенной регрессионной модели
оценка
(4.1.7)
имеет
наименьшую матрицу ковариаций в классе
линейных несмещенных оценок вектора
.
Таким
образом, для применения обобщенного
метода наименьших квадратов (ОМНК),
также как и для получения оценки
ковариационной матрицы, необходимо
знать матрицу
,
которая на практике чаще всего не
известна. Самый простой способ, позволяющий
справиться с этой проблемой положен в
основу так называемого доступного
обобщенного метода наименьших квадратов,
суть которого в том, что сначала каким
либо образом получают оценку матрицы
,
а затем эту оценку используют вместо
матрицы.
2.
4.2.1. Неоднородность дисперсии.
Частным случаем обобщенного метода
наименьших квадратов является метод
взвешенных наименьших квадратов. Его
обычно применяют для построения моделей
с гетероскедастичностью. Предположения,
лежащие в основе построения этой модели,
выглядят следующим образом.
1.
— спецификация модели;
2.
— детерминированная матрица, имеющая
максимальный ранг m+1;
3а.
,
3b.
,
где матрица
диагональная с неравными элементами.
В
некоторых случаях удобно считать, что
элементы ковариационной матрицы
представимы в виде
,
а весовые коэффициенты
нормированы так, что
.
Если
для всех t
=1, 2, . . . , n
, то модель с гетероскедастичностью
сводится к классической.
Применение
формулы (4.1.7) для расчета оценок
регрессионного уравнения в условиях
гетероскедастичности эквивалентно
минимизации взвешенной суммы квадратов
.
Последнее выражение позволяет понять
содержательный смысл метода взвешенных
наименьших квадратов. Как было показано
выше, применение стандартного МНК к
неоднородным данным дает неэффективные
оценки. Причина в том, что не учитывается
зависящий от дисперсии уровень
статистического вклада каждого
слагаемого. «Взвешивание» каждого
отклонения с помощью величины
,
предусмотренное в методе взвешенных
наименьших квадратов, устраняет
неоднородность, причем более точным
наблюдениям (с меньшей дисперсией)
придается «больший вес».
В практических расчетах применяют
различные приемы для устранения эффектов
гетероскедастичности в зависимости
от того, что принимается за оценку
неизвестной дисперсии.
4.2.2. Пропорциональность дисперсии
независимой переменной. Если есть
основания считать, что дисперсия ошибки
прямо пропорциональна квадрату одной
из независимых переменных модели, т.е.
,
то путем деления на эту независимую
переменную всех (зависимой и независимых)
переменных модели случай гетероскедастичности
сводится к классической модели.
В более сложном случае можно считать,
что дисперсия зависит от нескольких
независимых переменных, например
и
.
Тогда
моделирование осуществляется в три
этапа с использованием идей доступного
МНК. На первом этапе с помощью стандартного
МНК строится регрессия
,
и
вычисляются остатки, квадраты которых
принимаются за оценки
.
На втором этапе для этих оценок строится
регрессия, расчетные значения которой
используются для получения весовых
коэффициентов, применяемых в методе
взвешенных наименьших квадратов на
завершающем этапе построения модели.
4.2.3. Двухуровневая дисперсия.
Встречаются ситуации, когда данные
неоднородны по дисперсии, но их можно
разделить на две группы однородных.
Пусть, например, в первой группе
наблюдение с дисперсией
для t=1,
,
а во второй —
наблюдений
с дисперсией
для
.
Значения
и
неизвестны.
Для этого случая также можно предложить
многоэтапную процедуру оценивания
коэффициентов регрессии на основе
доступного МНК.
На первом этапе стандартным МНК получают
коэффициенты обычной регрессии и с ее
помощью рассчитывают остатки
.
На втором этапе в соответствии с
группировкой данных строят оценки
неизвестных значений дисперсий
,
.
На следующем этапе все переменные первых
уравнений делятся на
,
а остальные – на
.
К преобразованным уравнения применяется
обычный МНК, завершающий построение
модели.
Этот подход к построению регрессии в
условиях гетероскедастичностью с
двухуровневой дисперсией допускает
обобщение на случай, когда дисперсия
имеет не два, а несколько различных
уровней.
3. Как было показано выше, применение
обычного МНК для оценки вектора параметров
в
условиях гетероскедастичности позволяет
получить несмещенные состоятельные
оценки этого вектора, но стандартные
ошибки полученных оценок смещены.
Проблема их корректировки возникает
потому, что большинство компьютерных
пакетов при оценивании коэффициентов
регрессии вычисляют стандартные ошибки
этих коэффициентов по формуле обычного
МНК, т.е.
,
и, следовательно, эффект гетероскедастичности
в них не учитывается. Рассмотрим два
способа, позволяющих получить стандартные
ошибки с поправкой на гетероскедастичность.
4.3.1. Стандартные ошибки в форме Уайта.
В этой форме стандартные ошибки
вычисляются тогда, когда матрица
ковариаций вектора ошибок
диагональна, т.е.
,
.
Учитывая, что оценка МНК может быть
представлена в виде
,
ковариационная
матрица записывается следующим образом
.
(4.3.1.1)
Распишем произведение матриц через
сумму
,
где
— s-ая вектор-строка
матрицы регрессоров.
Уайт показал, что замена неизвестных
величин
на остатки в квадрате
позволяют получить состоятельную оценку
матрицы ковариаций оценок коэффициентов
регрессии в виде следующего выражения
.
(4.3.1.2)
Рассчитанные
по это формуле ошибки называются
стандартными ошибками в форме Уайта.
4.3.2. Стандартные
ошибки в форме Невье-Веста. Если
ненулевые элементы
матрицы
стоят не только на главной диагонали,
но и на соседних диагоналях, отстающих
от главной не более, чем на L
(при
,
),
то выражение
,
(4.3.2.1)
как
показали Невье-Вест дает состоятельную
оценку матрицы ковариаций оценок
коэффициентов регрессии. В формулу
(4.3.2.1) включены весовые коэффициенты
,
от выбора которых зависят стандартные
ошибки. Существует несколько способов
выбора этих весовых коэффициентов.
Простейший случай
следует
исключить из рассмотрения, так как при
таком выборе весовых коэффициентов
может оказаться, что матрица (4.3.2.1) не
является неотрицательно определенной.
Обычно рассматривают два способа,
предложенные Бартлеттом
1)
;
и
Парзеном:
2)
.
В
большинстве случаев рекомендуется
использовать весовые коэффициенты
Парзена.
Рассчитанные по формуле (4.3.2.1) стандартные
отклонения принято называть стандартными
ошибками в форме Невье-Веста или
стандартными ошибками с учетом
гетероскедастичности и автокорреляции.
4. Наличие гетероскедастичности не
является очевидным фактом. Поэтому при
построении регрессионных моделей
возникает вопрос о тестировании на
гетероскедастичность. Как правило, в
этих тестах проверяется нуль-гипотеза
против альтернативной гипотезы
предположение
н выполняется.
4.4.1. Тест Уайта. В этом тесте
используется идея, состоящая в том, что
наличие гетероскедастичности является
следствием взаимосвязи дисперсии ошибок
с регрессорами. Тест построен на проверке
этой взаимосвязи без использования
каких-либо предположений относительно
структуры гетероскедастичности.
Последовательность проверке в соответствии
с тестом Уайта состоит в следующем.
Сначала с помощью обычного МНК строится
регрессионная модель и находятся остатки
,
.
После чего строится регрессия квадратов
этих остатков на все регрессоры, их
квадраты и попарные произведения. В
предположении, что гипотеза
имеет место, величина
асимптотически имеет распределение
,
где
— коэффициент детерминации, а m
— число регрессоров второй модели.
Если
,
то
отвергается. Тест универсален и может
применяться в любых ситуациях. Однако,
в тех случаях, когда гипотеза
отвергается, с помощью этого теста не
удается установить структурную форму
гетероскедастичности и, поэтому либо
применяется другой тест, либо используются
стандартные ошибки в форме Уайта.
4.4.2. Тест Голдфельда-Куандта. Тест
используется в тех случаях, когда есть
основания предполагать, что дисперсия
ошибки зависит от некоторой независимой
переменной. Краткое описание теста
выглядит так:
1) данные упорядочиваются по убыванию
той независимой переменной, от которой
в соответствии с предположением зависит
дисперсия ошибки;
2)
наблюдений,
расположенных в средине упорядоченного
ряда, исключаются (
рекомендуется
брать равным четверти общего числа
наблюдений);
3) по первым
и
последним
строятся
независимо друг от друга два регрессионных
уравнения и с их помощью рассчитываются
соответствующие вектора остатков
и
;
4) из полученных остатков рассчитывается
статистика
.
Если верна гипотеза
,
то
имеет распределение Фишера с
степенями
свободы. Если статистика больше табличного
значения, то гипотеза
отвергается.
Этот тест можно использовать в тех
случаях, когда есть предположение, что
дисперсия принимает два значения
(двухуровневая дисперсия).
4.4.3. Тест Бреуша-Пагана. Тест
рекомендуется применять, если априори
предполагается, что дисперсия есть
линейная функция от некоторых
дополнительных переменных, т.е.
,
,
где
—
вектор независимых переменных;
— неизвестные параметры.
Проверка с помощью этого теста
осуществляется так:
1) строится обычная регрессия и с ее
помощью рассчитываются компоненты
вектора остатков
;
2) полученные остатки используются для
получения оценки дисперсии
;
3) строится регрессионное уравнение
,
для
которого рассчитывается объясненная
часть вариации, т.е. сумма квадратов
отклонений расчетных значений от
среднего значения, обозначаемая обычно
RSS;
4) статистика RSS/2 сравнивается
с табличным значением
и, если RSS/2 превосходит
табличное значение, то нуль-гипотеза
(отсутствие гетероскедастичности)
отбрасывается. Возможность такой
проверки обеспечивается результатом,
установленным Бреушем и Паганом, в
соответствии с которым при выполнении
гипотезы
величина RSS/2 асимптотически
имеет распределение
.
В тех случаях, когда среди расчетных
значений уравнения регрессии, построенного
в п. 3), имеется много отрицательных,
можно рекомендовать использовать вместо
линейной зависимости экспоненциальную
форму гетероскедастичности
,
.
Использование
экспоненциальной формы приводит к
замене линейной регрессии п. 3) на
регрессию
.
Вопрос 1. Модель множественной регрессии с тремя объясняющими переменными без свободного коэффициента имеет вид: y =
- Ответ: b1x1 + b2x2 + b3x3
Вопрос 2. При автокорреляции оценка коэффициентов регрессии становится:
- Ответ: неэффективной
Вопрос 3. Cитуация, при которой нулевая гипотеза была отвергнута, хотя была истинной, носит название:
- Ответ: ошибки I рода
Вопрос 4. При использовании уровня значимости, равного 5%, истинная гипотеза отвергается в __________________ случаев.
- Ответ: 5%
Вопрос 5. Для идентификации АР и СС моделей сначала делают оценки
- Ответ: автокорреляционной функции
Вопрос 6. Значение статистики Дарбина-Уотсона находится между значениями
- Ответ: 0 и 4
Вопрос 7. Пересмотр оценок в методе Кокрана-Оркатта выполняется до тех пор, пока не будет __________________ оценок.
- Ответ: получена требуемая точность
Вопрос 8. Способ оценивания (estimator) — общее правило для получения __________________ какого-либо параметра по данным выборки.
- Ответ: приближенного численного значения
Вопрос 9. Явление, когда строгая линейная зависимость между переменными приводит к невозможности применения МНК, называется:
- Ответ: полной коллинеарностью
Вопрос 10. Выборочная дисперсия зависимой переменной регрессии равна __________________ объясненной дисперсии зависимой переменной и необъясненной дисперсии зависимой переменной.
- Ответ: сумме
Вопрос 11. Четвертое условие Гаусса-Маркова состоит в том, что для любого k cov (uk, хk) равна:
- Ответ: 0
Вопрос 12. Эластичность y по x рассчитывается __________________ величины относительного изменения y на величину относительного изменения x.
- Ответ: делением
Вопрос 13. Если выборка достаточно полно отражает изучаемые параметры генеральной совокупности, то ее называют:
- Ответ: репрезентативной
Вопрос 14. Целью эконометрики является получение количественных выводов о свойствах экономических явлений и процессов по данным
- Ответ: выборки
Вопрос 15. Если все наблюдения лежат на линии регрессии, то коэффициент детерминации R2 для модели парной регрессии равен:
- Ответ: единице
Вопрос 16. Если две переменные независимы, то их теоретическая ковариация равна:
- Ответ: 0
Вопрос 17. Обычно прогнозы, получаемые с помощью моделей Бокса-Дженкинса, оказываются на практике __________________ прогнозов, построенных по макроэкономическим моделям.
- Ответ: не хуже
Вопрос 18. Весовые коэффициенты в методе скользящего среднего
- Ответ: всегда больше нуля
Вопрос 19. Если вычисленное значение статистики Спирмена превысит некое критическое значение, то принимается решение о:
- Ответ: наличии гетероскедастичности
Вопрос 20. Отклонение еi в i-м наблюдении yi от регрессии с двумя объясняющими переменными:
- Ответ: ei = yi — a — b1x1 — b2x2
Вопрос 21. Положительная автокорреляция — ситуация, когда случайный член регрессии в следующем наблюдении ожидается:
- Ответ: того же знака, что и в настоящем наблюдении
Вопрос 22. При построении отдельных уравнений регрессии для каждого из 4-х кварталов сумма сезонных отклонений должна равняться:
- Ответ: 0
Вопрос 23. Коэффициент Тейла лежит в пределах
- Ответ: от 0 до 1
Вопрос 24. Множественный регрессионный анализ является __________________ парного регрессионного анализа.
- Ответ: развитием
Вопрос 25. При положительной автокорреляции DW
- Ответ:
Вопрос 26. Процесс Юла описывается моделью
- Ответ: АР (2)
Вопрос 27. Эконометрический инструментарий базируется на методах и моделях
- Ответ: математической статистики
Вопрос 28. Если из экономических соображений известно, что b >= b0, то нулевая гипотеза отвергается только при:
- Ответ: t > tкрит
Вопрос 29. При вычислении t-статистики применяется распределение
- Ответ: Стьюдента
Вопрос 30. Аналитические методы выделения неслучайной составляющей основаны на допущении, что …
- Ответ: известен общий вид неслучайной составляющей
Вопрос 31. Наблюдение зависимой переменной регрессии в предшествующий момент, используемое как объясняющая переменная, называется __________________ переменной.
- Ответ: лаговой
Вопрос 32. Явление, когда нестрогая линейная зависимость между объясняющими переменными в модели множественной регрессии приводит к получению ненадежных оценок регрессии, называют:
- Ответ: мультиколлинеарностью
Вопрос 33. Для модели парной регрессии оценки, полученные по МНК, являются несмещенными, эффективными, состоятельными, если …
- Ответ: выполнены условия Гаусса-Маркова
Вопрос 34. Если элементы набора данных не являются статистически независимыми, то речь идет о:
- Ответ: временном ряде
Вопрос 35. Метод наименьших квадратов — метод нахождения оценок параметров регрессии, основанный на минимизации __________________ квадратов остатков всех наблюдений.
- Ответ: суммы
Вопрос 36. Тест Бокса-Кокса (решетчатый поиск) — прямой компьютерный метод выбора наилучших значений __________________ модели в заданных исследователем пределах с заданным шагом (решеткой).
- Ответ: параметров нелинейной
Вопрос 37. Уравнение y = a + bx, где a и b — оценки параметров a и b, полученные в результате оценивания модели y = a + bx + u по данным выборки, называется уравнением
- Ответ: линейной регрессии
Вопрос 38. Фиктивную переменную для коэффициента наклона вводят как __________________ фиктивной переменной, отвечающей за исследуемую категорию, и интересующей нефиктивной переменной.
- Ответ: произведение
Вопрос 39. Ситуация, когда не отвергнута ложная гипотеза, называется:
- Ответ: ошибкой II рода
Вопрос 40. Доверительный интервал в 99% __________________ интервал в 95%.
- Ответ: шире, чем
Вопрос 41. В множественном регрессионном анализе коэффициент детерминации определяет ____________________________________ регрессией.
- Ответ: долю дисперсии y, объясненную
Вопрос 42. Гетероскедастичность заключается в том, что дисперсия случайного члена регрессии __________________ наблюдений.
- Ответ: зависит от номера
Вопрос 43. Третье условие Гаусса-Маркова состоит в том, что cov (ui, uj) = 0, если …
- Ответ: i ¹ j
Вопрос 44. В модели множественной регрессии всегда желательно присутствие хотя бы одной __________________ переменной для того, чтобы обеспечить надлежащий уровень достоверности оценок.
- Ответ: нефиктивной
Вопрос 45. Зависимая переменная может быть представлена как фиктивная в случае, если она
- Ответ: является качественной по своему характеру
Вопрос 46. Множество наблюдений, составляющих часть генеральной совокупности, называется:
- Ответ: выборкой
Вопрос 47. Сглаживание временного ряда означает устранение
- Ответ: случайных остатков
Вопрос 48. Если автокорреляция отсутствует, то DW»:
- Ответ: 2
Вопрос 49. В методе скользящего среднего веса определяется с помощью:
- Ответ: МНК
Вопрос 50. Отличие одностороннего теста от двустороннего заключается в том, что он имеет только
- Ответ: одно критическое значение
Вопрос 51. Сумма квадратов остатков всех наблюдений — __________________ сумма квадратов отклонений.
- Ответ: остаточная
Вопрос 52. F-статистика для __________________ является в точности квадратом t-статистики для rx, y.
- Ответ: коэффициента детерминации
Вопрос 53. Для уравнения регрессии у=4+2х и наблюденных данных х=4, у=14 остаток в наблюдении равен:
- Ответ: 2
Вопрос 54. Фиктивная переменная для коэффициента наклона предназначена для установление влияния категории на:
- Ответ: коэффициент при нефиктивной переменной
Вопрос 55. Для линейного регрессионного анализа требуется линейность
- Ответ: только по параметрам
Вопрос 56. Второе условие Гаусса-Маркова заключается в том, что …
- Ответ: s2 (ui) — не зависит от i
Вопрос 57. Любой набор категорий можно описать некоторой совокупностью __________________ переменных.
- Ответ: фиктивных
Вопрос 58. В экономике отрицательная автокорреляция встречается __________________ положительная.
- Ответ: гораздо реже, чем
Вопрос 59. Итерационные методы — компьютерные __________________ методы поиска наилучших значений параметров нелинейной модели.
- Ответ: сходящиеся
Вопрос 60. Коэффициент Тейла основан на расчете
- Ответ: среднеквадратичного значения ошибки прогноза приростов
Вопрос 61. Процесс СС (2) имеет автокорреляционную функцию, которая:
- Ответ: обращается в ноль после некоторой точки
Вопрос 62. Набор категорий представляет собой конечный набор __________________ событий.
- Ответ: взаимоисключающих
Вопрос 63. Авторегрессионная схема называется схемой первого порядка, если описываемое __________________ равно 1.
- Ответ: максимальное запаздывание
Вопрос 64. В модели АР (1) частная автокорреляционная функция случайных остатков, разделенных двумя тактами времени, равна:
- Ответ: 0
Вопрос 65. Для выполнения теста Чоу используется распределение
- Ответ: Фишера
Вопрос 66. Коэффициент детерминации равен __________________ выборочной корреляции между y и a + bx.
- Ответ: квадрату
Вопрос 67. Если в регрессионную модель включена лишняя переменная, то оценки коэффициентов оказываются, как правило, …
- Ответ: неэффективными
Вопрос 68. Для производственного процесса, описываемого функцией Кобба-Дугласа, увеличение капитала (К) и труда (i) в 4 раза приводит к увеличению объема выпуска (у):
- Ответ: в 4 раза
Вопрос 69. Коэффициент ранговой корреляции имеет дисперсию
- Ответ: 1/ (n — 1)
Вопрос 70. Коэффициент Тейла служит критерием
- Ответ: успешности сделанного прогноза
Вопрос 71. Метод скользящего среднего относятся к __________________ методам выделения неслучайной составляющей.
- Ответ: алгоритмическим
Вопрос 72. На первом этапе применения теста Голдфелда-Квандта в выборке все наблюдения
- Ответ: Упорядочиваются по возрастанию х
Вопрос 73. Регрессором в уравнении парной линейной регрессии называется:
- Ответ: объясняющая переменная
Вопрос 74. Число степеней свободы (верхнее и нижнее) для отношения RSS2 / RSS1 в тесте Голдфелда-Квандта равно:
- Ответ: n’ — k — 1
Вопрос 75. Доля объясненной дисперсии зависимой переменной в общей выборочной дисперсии y выражается коэффициентом
- Ответ: детерминации
Вопрос 76. Значение оценки является:
- Ответ: случайной величиной
Вопрос 77. Для регрессии второго порядка y = 12+7x1-3x2 отклонение от регрессии наблюдения (х1=2, х2=1, y=20) равно:
- Ответ: е=3
Вопрос 78. Критерий восходящих и нисходящих серий позволяет:
- Ответ: выявить неслучайную составляющую
Вопрос 79. На больших временах процесс формирования значений временного ряда находится под воздействием __________________ факторов.
- Ответ: долговременных и циклических
Вопрос 80. Критерий серий, основанный на медиане, позволяет:
- Ответ: выявить неслучайную составляющую
Вопрос 81. Близко к линии регрессии находится наблюдение, для которого теоретическое распределение случайного члена имеет
- Ответ: малое стандартное отклонение
Вопрос 82. Марковский процесс описывается моделью
- Ответ: АР (1)
Вопрос 83. Метод Кокрана-Оркатта — компьютерный итерационный метод устранения
- Ответ: автокорреляции
Вопрос 84. Второе условие Гаусса-Маркова предполагает, что дисперсия случайного члена __________________ в каждом наблюдении.
- Ответ: постоянна
Вопрос 85. Как правило в эталонной категории
- Ответ: все фиктивные переменные равны 0
Вопрос 86. Коэффициент наклона в уравнении линейной регрессии показывает __________________ изменяется y при увеличении x на одну единицу.
- Ответ: на сколько единиц
Вопрос 87. Оценка параметров в лаговой структуре Койка делается:
- Ответ: решетчатым методом
Вопрос 88. Эффективная оценка — несмещенная оценка, имеющая __________________ среди всех несмещенных оценок.
- Ответ: наименьшую дисперсию
Вопрос 89. В критерии серий, основанном на медиане, протяженность самой длинной серии временного ряда 5, 1, 4, 2 равна:
- Ответ: 1
Вопрос 90. Выборочная дисперсия расчетных значений величины y называется __________________ дисперсией зависимой переменной.
- Ответ: объясненной
Вопрос 91. Свойства коэффициентов регрессии как случайных величин зависят от свойств __________________ уравнения.
- Ответ: остаточного члена
Вопрос 92. Модель Бокса-Дженкинса — это модель …
- Ответ: АРПСС
Вопрос 93. Исследование соотношения между спросом на реальные денежные остатки и ожидаемым изменением уровня цен описывается моделью
- Ответ: Кейгана
Вопрос 94. Оценка ρ, полученная МНК для авторегрессионной схемы первого порядка рассчитывается по формуле __________________, ek — остатки в наблюдениях.
- Ответ: cov (ek-1, ek) / var (ek-1)
Вопрос 95. Фиктивные переменные включаются в модель множественной регрессии, если необходимо установить влияние каких-либо __________________ факторов.
- Ответ: дискретных
Вопрос 96. Для проверки нулевой гипотезы H0: b= b0 применяется тест
- Ответ: Стьюдента
Вопрос 97. Дисперсии оценок а и b __________________ дисперсии остаточного члена s2 (u).
- Ответ: прямо пропорциональны
Вопрос 98. Категория — это событие, которое определенно __________________ в каждом наблюдении.
- Ответ: либо происходит, либо нет
Вопрос 99. Область принятия гипотезы — множество значений __________________, при попадании в которое нулевая гипотеза не отвергается.
- Ответ: оценок параметра
Вопрос 100. Ловушка dummy trap приводит к:
- Ответ: полной коллинеарности
Вопрос 101. Модель Линтнера основывается на предположении, что желаемый объем дивидендов
- Ответ: пропорционален прибыли
Вопрос 102. Детерминированная переменная может рассматриваться как предельный вариант случайной переменной, принимающей свое единственное значение с вероятностью
- Ответ: 1
Вопрос 103. Показатель выборочной ковариации позволяет выразить связь между двумя переменными
- Ответ: единым числом
Вопрос 104. Эконометрика — часть экономической науки, занимающаяся разработкой и применением __________________ методов анализа экономических процессов.
- Ответ: математических
Вопрос 105. Статистика Дарбина-Уотсона проверяет нулевую гипотезу Но:
- Ответ: отсутствие автокорреляции
Вопрос 106. Зависимость объемов введенных основных фондов от капитальных вложений описывается:
- Ответ: регрессионной моделью с распределенными лагами
Вопрос 107. Для того, чтобы установить влияние категории на коэффициент регрессии при нефиктивной переменной, в модель включают:
- Ответ: фиктивную переменную для коэффициента наклона
Вопрос 108. При отрицательной автокорреляции DW
- Ответ: >2
Вопрос 109. На экзамене в группе из 15 студентов 4 человека получили отличную оценку, 8 человек — оценку хорошо, 3 человека — оценку удовлетворительно. Средний бал по группе равен:
- Ответ: 4,06
Вопрос 110. При использования обычного МНК наблюдению высокого качества придается вес __________________ наблюдению низкого качества.
- Ответ: такой же как
Вопрос 111. Фиктивная переменная взаимодействия — это __________________ фиктивных переменных.
- Ответ: произведение
Вопрос 112. При попадании оценки в критическое значение:
- Ответ: сохраняется неопределенность в отношении гипотезы
Вопрос 113. Модель Кейгана — модель, описывающая гиперинфляцию с помощью модели
- Ответ: адаптивных ожиданий
Вопрос 114. При проведении теста Голдфелда-Квандта из рассмотрения исключаются __________________ наблюдений.
- Ответ: средние (n — 2n’)
Вопрос 115. Фиктивные переменные, предназначены для обозначения различных лет, кварталов, месяцев и т.п. — это __________________ фиктивные переменные.
- Ответ: сезонные
Вопрос 116. Теоретическая ковариация двух случайных величин определяется как математическое ожидание __________________ отклонений этих величин от их средних значений.
- Ответ: произведения
Вопрос 117. В модели парной регрессии у* = 4 + 2х изменение х на 2 единицы вызывает изменение у на __________________ единиц.
- Ответ: 4
Вопрос 118. Вероятности, с которыми случайная величина принимает свои значения, называют __________________ случайной величины.
- Ответ: законом распределения
Вопрос 119. Мерой разброса значений случайной величины служит:
- Ответ: дисперсия
Вопрос 120. При снижении уровня значимости риск совершить ошибку I рода
- Ответ: уменьшается
Вопрос 121. Фиктивная переменная — переменная, принимающая в каждом наблюдении значения:
- Ответ: 0 или 1
Вопрос 122. На больших временах __________________ факторы описываются монотонной функцией.
- Ответ: долговременные
Вопрос 123. Необходимость применения специальных статистических методов для обработки экономической информации вызвана __________________ данных.
- Ответ: стохастической природой
Вопрос 124. При использовании метода Монте-Карло результаты наблюдения генерируются с помощью
- Ответ: датчика случайных чисел
Вопрос 125. Для отношения RSS2/RSS1 в рамках теста Голдфелда-Квандта проводят тест
- Ответ: Фишера
Вопрос 126. В парном регрессионном анализе коэффициент детерминации R2 равен:
- Ответ: rх;у2
Вопрос 127. Подбор порядка аппроксимирующего полинома производится при помощи
- Ответ: метода последовательных разностей
Вопрос 128. Функция цены — функция, где аргументом является __________________, а значением функции — цена ошибки.
- Ответ: род ошибки
Вопрос 129. Если нулевая гипотеза Н0: β = β0, то альтернативная гипотеза Н1 — это:
- Ответ: β≠β0
Вопрос 130. Невыполнение 2 и 3 условий Гаусса-Маркова, приводит к потере свойства __________________ оценок.
- Ответ: эффективности
Вопрос 131. Эксперимент по методу Монте-Карло — искусственный, контролируемый эксперимент, проводимый для проверки и сравнения эффективности различных
- Ответ: статистических методов
Вопрос 132. Нижний индекс переменной (t-s) означает, что она является:
- Ответ: лаговой
Вопрос 133. Автокорреляция первого порядка — ситуация, когда случайный член uк коррелирует с:
- Ответ: Uк-1
Вопрос 134. Для применения теста Зарембки необходимо
- Ответ: преобразование масштаба наблюдений у
Вопрос 135. Если элементы набора данных не являются одинаково распределенными, то речь идет о:
- Ответ: временном ряде
Вопрос 136. Нелинейная модель у = f (x), в которой возможна замена переменной z = g (x), приводящая получившуюся модель y = F (z) — к линейной, называется моделью, нелинейной по:
- Ответ: переменным
Вопрос 137. Гетероскедастичность приводит к __________________ оценок параметров регрессии по МНК.
- Ответ: неэффективности
Вопрос 138. Число степеней свободы для уравнения множественной (m-мерной) регрессии при достаточном числе наблюдений n составляет:
- Ответ: n — m — 1
Вопрос 139. В критерии восходящих и нисходящих серий, общее число серий временного ряда 5, 7, 6, 4, 3, 1 равно:
- Ответ: 2
Вопрос 140. Ловушка dummy trap — выбор совокупности фиктивных переменных, сумма которых
- Ответ: константа
Вопрос 141. Оценка параметра находится __________________ доверительного интервала.
- Ответ: в центре
Вопрос 142. Данные по определенному показателю, полученные для разных однотипных объектов, называются:
- Ответ: перекрестными
Вопрос 143. При увеличении размера выборки оценка математического ожидания
- Ответ: становится более точной
Вопрос 144. При стремлении размера выборки к бесконечности стандартное отклонение математического ожидания стремится к:
- Ответ: 0
Вопрос 145. Доля числа исходов, благоприятствующих данному событию, в общем числе равновероятных исходов называется __________________ этого события.
- Ответ: вероятностью
Вопрос 146. Нижнее число степеней свободы F-cтатистики в случае парной регрессии равно:
- Ответ: n-2
Вопрос 147. Автокорреляционная функция принимает значения в пределах
- Ответ: от -1 до 1
Вопрос 148. Фиктивная переменная взаимодействия — фиктивная переменная, предназначенная для установления влияния на регрессию __________________ событий.
- Ответ: одновременного наступления нескольких независимых
Вопрос 149. Метод Зарембки процедура выбора между линейной и __________________ моделями:
- Ответ: логарифмической
Вопрос 150. Функция спектральной плотности позволяет установить:
- Ответ: частоты колебаний
Вопрос 151. При проведении теста Голдфелда-Квандта предполагается, что стандартное отклонение остаточного члена регрессии растет с __________________ переменной.
- Ответ: ростом объясняющей
Вопрос 152. Ранг наблюдения переменной — номер наблюдения переменной в упорядоченной __________________ последовательности.
- Ответ: по возрастанию значений наблюдаемой величины
Вопрос 153. Коэффициенты при сезонных фиктивных переменных показывают __________________ при смене сезона.
- Ответ: численную величину изменения, происходящего
Вопрос 154. При высоком уровне значимости проблема заключается в высоком риске допущения
- Ответ: ошибки II рода
Вопрос 155. Тест ранговой корреляции Спирмена — тест на:
- Ответ: гетероскедастичность
Вопрос 156. Статистика для теста ранговой корреляции Спирмена имеет __________________ распределение.
- Ответ: нормальное
Вопрос 157. МНК дает __________________ для данной выборки значение коэффициента детерминации R2.
- Ответ: максимальное
Вопрос 158. Функция Кобба-Дугласа имеет вид Y =
- Ответ: AKa L1-a
Вопрос 159. Процесс АР (2) имеет автокорреляционную функцию, которая:
- Ответ: имеет бесконечную протяженность
Вопрос 160. Утверждение о том, что неизвестный параметр модели принадлежит другому заданному множеству В, АÇВ = Æ, называется:
- Ответ: альтернативной гипотезой
Вопрос 161. Эконометрика получает количественные зависимости для экономических соотношений, основываясь в первую очередь на:
- Ответ: данных
Вопрос 162. Строгая линейная зависимость между переменными — ситуация, когда __________________ двух переменных равна 1 или -1.
- Ответ: выборочная корреляция
Вопрос 163. При рассмотрении спектральной плотности ограничиваются значениями ω, лежащими в пределах
- Ответ: от 0 до π
Вопрос 164. Функция Кобба-Дугласа называется:
- Ответ: производственной функцией
Вопрос 165. Утверждение о том, что неизвестный параметр модели принадлежит заданному множеству А, называется:
- Ответ: нулевой гипотезой
Вопрос 166. Проверка гипотезы Н0: R2 = 0 происходит с помощью теста
- Ответ: Фишера
Вопрос 167. Спектральная плотность может принимать __________________ значения.
- Ответ: только положительные
Вопрос 168. В модели множественной регрессии за изменение __________________ регрессии отвечает несколько объясняющих переменных.
- Ответ: одной зависимой переменной
Вопрос 169. Функция потерь, используемая при выборе между несмещенной и эффективной оценкой, определяет стоимость неточности как функцию
- Ответ: размера ошибки
Вопрос 170. Для уравнения регрессии у = 3х — 2 прогнозное значение зависимой переменной, если объясняющая переменная равна 4, — это:
- Ответ: 10
Вопрос 171. Тест Глейзера устанавливает наличие __________________ связи между стандартным отклонением остаточного члена регрессии и объясняющей переменной.
- Ответ: нелинейной
Вопрос 172. Чем больше число наблюдений, тем __________________ зона неопределенности для критерия Дарбина-Уотсона.
- Ответ: уже
Вопрос 173. Остаток в i-ом наблюдении по модели парной регрессии y=a+bx равен:
- Ответ: yi — (a + bxi)
Вопрос 174. Модель парной регрессии — __________________ модель зависимости между двумя переменными.
- Ответ: линейная
Вопрос 175. Граничное значение области принятия гипотезы с p%-ной вероятностью совершить ошибку I рода определяется __________________ при p-процентном уровне значимости.
- Ответ: критическим значением теста
Вопрос 176. Спецификация запаздываний применительно к переменным в модели называется:
- Ответ: лаговой структурой
Вопрос 177. Если независимые переменные имеют ярко выраженный временной тренд, то они оказываются:
- Ответ: тесно коррелированными
Вопрос 178. Первое условие Гаусса-Маркова заключается в том, что __________________ для любого i.
- Ответ: М (ui) = 0
Вопрос 179. В критерии восходящих и нисходящих серий, длина самой длинной серии временного ряда 1, 5, 4, 1, 6 равна:
- Ответ: 2
Вопрос 180. Идентификация модели СС (2) сводится к решению системы двух __________________ уравнений.
- Ответ: нелинейных
Вопрос 181. Выборочная дисперсия как оценка теоретической дисперсии имеет __________________ смещение.
- Ответ: отрицательное
Вопрос 182. Функция спроса y = a xb pg n может быть линеаризована посредством
- Ответ: логарифмирования
Вопрос 183. Оценка стандартного отклонения случайной величины, полученная по данным выборки, называется стандартной __________________ случайной величины.
- Ответ: ошибкой
Вопрос 184. Оценивание каждого параметра в уравнении регрессии поглощает __________________ свободы в выборке.
- Ответ: одну степень
Вопрос 185. Выборочная корреляция является __________________ теоретической корреляции.
- Ответ: оценкой
Вопрос 186. Точность оценок по МНК улучшается, если увеличивается:
- Ответ: количество наблюдений
Вопрос 187. При добавлении объясняющей переменной в уравнение регрессии коэффициент детерминации
- Ответ: не уменьшается
Вопрос 188. В критерии серий, основанном на медиане, общее число серий временного ряда 1, 3, 5, 4, 2 равно:
- Ответ: 3
Вопрос 189. Для функции Кобба-Дугласа у=100к1/3*i2/3 эластичность выпуска продукции по капиталу равна:
- Ответ: 1/3
Вопрос 190. В процессе формирования значений всякого временного ряда всегда участвуют __________________ факторы.
- Ответ: случайные
Вопрос 191. Первый шаг метода Зарембки заключается в вычислении __________________ y по выборке.
- Ответ: среднего геометрического
Вопрос 192. Плоскость регрессии y = a + b1x1 + b2x2 — двумерная плоскость в __________________ пространстве.
- Ответ: трехмерном
Вопрос 193. Для функции y = 4x0,2, эластичность равна:
- Ответ: 0,2
Вопрос 194. Поправка Прайса-Уинстена — метод спасения __________________ в автокорреляционной схеме первого порядка.
- Ответ: первого наблюдения
Вопрос 195. В лаговой структуре Койка надо оценить только:
- Ответ: три параметра
Вопрос 196. Наилучший способ устранения автокорреляции — установление ответственного за нее фактора и включение соответствующей __________________ переменной в регрессию.
- Ответ: объясняющей
Вопрос 197. Автокорреляция представляет тем большую проблему, чем
- Ответ: меньше интервал между наблюдениями
Вопрос 198. Проблема, связанная со смещением оценки коэффициентов регрессии, в одном случае, или с утратой эффективности этих оценок в другом случае неправильной спецификации переменных, перестает существовать, если коэффициент парной корреляции между переменными равен:
- Ответ: 0
Вопрос 199. Выборочная дисперсия остатков в наблюдениях Var (y — (a + bx)) называется __________________ дисперсией зависимой переменной.
- Ответ: необъясненной
Вопрос 200. Тест ранговой корреляции Спирмена — тест, устанавливающий, имеет ли стандартное отклонение остаточного члена регрессии нестрогую линейную зависимость с __________________ переменной.
- Ответ: объясняющей
Вопрос 201. Если совокупность значений случайной величины представляет собой конечный или счетный набор возможных чисел, то случайная величина называется:
- Ответ: дискретной
Вопрос 202. Стандартные ошибки, вычисленные при гетероскедастичности
- Ответ: занижены по сравнению с истинными значениями
Вопрос 203. Логарифмическое преобразование позволяет осуществить переход от нелинейной модели y = 5x2u к модели
- Ответ: ln y = ln 5 + 2 ln x + ln u
Вопрос 204. Для одностороннего критерия нулевой гипотезы Н0: β =β0 альтернативная гипотеза Н1:
- Ответ: β > β
Вопрос 205. Для функции Кобба-Дугласа у=80К3/4*i1/4 эластичность выпуска продукции по труду равна:
- Ответ: 1/4
Вопрос 206. Если опущена переменная, которая должна входить в регрессионную модель, то оценки коэффициентов регрессии оказываются:
- Ответ: смещенными
Вопрос 207. Если между двумя переменными существует строгая положительная линейная зависимость, то коэффициент корреляции между ними принимает значение, равное:
- Ответ: единице
Вопрос 208. Процесс выбора необходимых для регрессии переменных и отбрасывание лишних переменных называется:
- Ответ: спецификацией переменных
Вопрос 209. Результаты проверки гипотезы H0: b = b0 представляются на __________________ значимости.
- Ответ: двух уровнях
Вопрос 210. Всю совокупность реализаций случайной величины называют __________________ совокупностью.
- Ответ: генеральной
Вопрос 211. Остатки значений log y __________________ остатков значений y.
- Ответ: значительно меньше
Вопрос 212. Общая (ТSS), объясненная (ESS) и необъясненная (RSS) суммы квадратов отклонений находятся в следующих соотношениях
- Ответ: TSS = RSS + ESS
Вопрос 213. Если F-статистика Фишера превысит критическое значение Fкрит, то регрессия считается:
- Ответ: значимой
Вопрос 214. Число степеней свободы для t-статистики равно числу наблюдений в выборке __________________ количество оцениваемых коэффициентов.
- Ответ: минус
Вопрос 215. Если коэффициент Тейла равен нулю, то …
- Ответ: прогноз сделан успешно
Вопрос 216. Верхнее число степеней свободы F-cтатистики в случае парной регрессии равно:
- Ответ: одному
Вопрос 217. Автокорреляция — нарушение __________________ условия Гаусса-Маркова.
- Ответ: третьего
Вопрос 218. Совокупность фиктивных переменных — некоторое количество фиктивных переменных, предназначенное для описания
- Ответ: набора категорий
Вопрос 219. Стандартное отклонение случайной величины характеризует среднее ожидаемое расстояние между наблюдениями этой случайной величины и ее:
- Ответ: математическим ожиданием
Вопрос 220. В авторегрессионной схеме первого порядка uкн = рuк + ek предполагается, что значение ek в каждом наблюдении:
- Ответ: не зависит от его значений во всех других наблюдениях
Вопрос 221. Цель регрессионного анализа состоит в объяснении поведения
- Ответ: зависимой переменной
Вопрос 222. Разность между математическим ожиданием оценки и истинным значением оцениваемого параметра называют:
- Ответ: смещением
Вопрос 223. В авторегрессионной схеме первого порядка зависимость между последовательными случайными членами описывается формулой uk+1 = __________________, где ρ — константа, ek+1 — новый случайный член.
- Ответ: ρuk + e k+1
Вопрос 224. В функции Кобба-Дугласа вида log Y = a + b1 log k + b2 log l (k — индекс затрат капитала, l — индекс затрат труда) роль замещающей переменной для показателя технического прогресса играет:
- Ответ: log k
Вопрос 225. Наиболее частая причина положительной автокорреляции заключается в постоянной направленности воздействия __________________ переменных.
- Ответ: не включенных в уравнение
Вопрос 226. Для линеаризации функции Кобба-Дугласа необходимо предварительно обе части уравнения
- Ответ: разделить на L
Вопрос 227. О наличии данной частоты в спектре временного ряда свидетельствует __________________ спектральной плотности.
- Ответ: пик на графике
Вопрос 228. При добавлении еще одной переменной в уравнение регрессии коэффициент детерминации:
- Ответ: не уменьшается
Вопрос 229. Стандартные отклонения коэффициентов регрессии обратно пропорциональны величине _________, где n – число наблюдений:
- Ответ: n
Вопрос 230. Зависимая переменная может быть представлена как фиктивная в случае если она:
- Ответ: трудноизмерима
Вопрос 231. Тест Фишера является:
- Ответ: односторонним
Вопрос 232. Выборочная корреляция является __________оценкой теоретической корреляции:
- Ответ: состоятельной
Вопрос 233. Определение отдельного вклада каждой из независимых переменных в объясненную дисперсию в случае их коррелированности является ___________ задачей:
- Ответ: невыполнимой
Вопрос 234. Условие гомоскедастичности означает, что вероятность того, что случайный член примет какое-либо конкретное значение _________ наблюдений:
- Ответ: одинакова для всех
Вопрос 235. Значения t-статистики для фиктивных переменных незначимо отличается от:
- Ответ: 0
Вопрос 236. Из перечисленных факторов: 1) число объясняющих переменных, 2) количество наблюдений в выборке, 3)конкретные значения переменных, критические значения статистики Дарбина-Уотсона зависят от:
- Ответ: 1, 2
Вопрос 237. Значение статистики DW находится между значениями:
- Ответ: 0 и 4
Вопрос 238. Наблюдение зависимой переменной регрессии в предшествующий момент, используемое как объясняющая переменная, называется:
- Ответ: лаговой
Вопрос 239. Чем больше число наблюдений, тем __________ зона неопределенности для критерия Дарбина-Уотсона:
- Ответ: уже
Вопрос 240. МНК автоматически дает ___________ для данной выборки значение коэффициента детерминации R2:
- Ответ: максимальное
Вопрос 241. В авторегрессионной схеме первого порядка предполагается, что значение в каждом наблюдении:
- Ответ: не зависит от его значения во всех других наблюдениях
Вопрос 242. Линия регрессии _______ через точку ( , ) :
- Ответ: всегда проходит
Вопрос 243. Если предположение о природе гетероскедастичности верно, то дисперсия случайного члена для первых наблюдений в упорядоченном ряду будет ________ для последних:
- Ответ: ниже, чем
Вопрос 244. Стандартные ошибки, вычисленные при гетероскедастичности:
- Ответ: занижены по сравнению с истинными значениями
Вопрос 245. Критерий Дарбина-Уотсона –метод обнаружения _________ с помощью статистики Дарбина-Уотсона:
- Ответ: автокорреляции
Вопрос 246. Параметры множественной регрессии ?1 , ?2 ,… ?м показывают _________ соответствующих экономических факторов:
- Ответ: степень влияния
Вопрос 247. Во множественном регрессионном анализе коэффициент детерминации определяет _______регрессией:
- Ответ: долю дисперсии y, объясненную
Вопрос 248. Сумма квадратов отклонений величины y от своего выборочного значения _____ сумма квадратов отклонений:
- Ответ: общая
Вопрос 249. Фиктивная переменная взаимодействия – фиктивная переменная, предназначенная для
- Ответ: одновременного наступления нескольких независимых
Вопрос 250. Автокорреляция первого порядка – ситуация, когда коррелируют случайные члены регрессии в __________ наблюдениях:
- Ответ: последовательных
Вопрос 251. Фиктивная переменная – переменная, принимающая в каждом наблюдении:
- Ответ: только два значения 0 или 1
Вопрос 252. Для того, чтобы установить влияние какого-либо события на коэффициент линейной регрессии при нефиктивной переменной, в модель включают:
- Ответ: фиктивную переменную для коэффициента наклона
Вопрос 253. Оценка параметра для модели множественной регрессии в случае двух независимых переменных вычисляется по формуле: а =
- Ответ: 1 1 2 2 y ? b x ? b x
Вопрос 254. Процесс выбора необходимых переменных для регрессии переменных и отбрасывание лишних переменных называется:
- Ответ: спецификацией переменных
Вопрос 255. Из перечисленного: 1) число объясняющих переменных, 2) количество наблюдений в выборке, 3) конкретные значения переменных критические значения статистики Дарбина-Уотсона зависят от:
- Ответ: 1, 2
Вопрос 256. Число степеней свободы для уравнения m-мерной регрессии при достаточном числе наблюдений n составляет:
- Ответ: n-m-1
Вопрос 257. Наилучший способ устранения автокорреляции – установление ответственного за нее фактора и включение соответствующей ___________ переменной в регрессию:
- Ответ: объясняющей
Вопрос 258. Строгая линейная зависимость между переменными – ситуация, когда ________ двух переменных равна 1 или -1:
- Ответ: выборочная корреляция
Вопрос 259. Значение статистики Дарбина-Уотсона находится между значениями:
- Ответ: 0 и 4
Стандартные ошибки, согласующиеся с гетероскедастичностью
Из Википедии, бесплатной энциклопедии
Перейти к навигации
Перейти к поиску
Тема стандартных ошибок, согласующихся с гетероскедастичностью ( HC ), возникает в статистике и эконометрике в контексте линейной регрессии и анализа временных рядов . Они также известны как стандартные ошибки, устойчивые к гетероскедастичности (или просто устойчивые стандартные ошибки ), стандартные ошибки Эйкера – Хубера – Уайта (также стандартные ошибки Хубера – Уайта или стандартные ошибки Уайта ) [1], чтобы признать вклад Фридхельма Эйкера , [ 2] Питер Дж. Хубер , [3] и Халберт Уайт . [4]
При моделировании регрессии и временных рядов в базовых формах моделей используется предположение, что ошибки или возмущения u i имеют одинаковую дисперсию во всех точках наблюдения. Если это не так, ошибки считаются гетероскедастичными или имеют гетероскедастичность , и это поведение будет отражено в остатках.оценивается по подобранной модели. Стандартные ошибки, согласованные с гетероскедастичностью, используются для подбора модели, которая действительно содержит гетероскедастические остатки. Первый такой подход был предложен Хубером (1967), и с тех пор были разработаны дальнейшие усовершенствованные процедуры для данных поперечного сечения, данных временных рядов и оценки GARCH .
Стандартные ошибки, соответствующие гетероскедастичности, которые отличаются от классических стандартных ошибок, могут указывать на неправильную спецификацию модели. Подстановка стандартных ошибок, согласующихся с гетероскедастичностью, не устраняет эту ошибку спецификации, которая может привести к смещению коэффициентов. В большинстве случаев проблему следует найти и устранить. [5] Другие типы корректировок стандартных ошибок, такие как кластерные стандартные ошибки , могут рассматриваться как расширения стандартных ошибок HC.
История
Гетероскедастичности-последовательной стандартные ошибки вводятся Фредхелм Эикер , [6] [7] и популяризировал в эконометрике по Halbert White .
Проблема
Рассмотрим модель линейной регрессии
где X — вектор независимых переменных, а β — вектор-столбец k × 1 параметров, подлежащих оценке.
В обычных наименьших квадратов (МНК) оценщик
куда обозначает матрицу сложенных значения, наблюдаемые в данных.
Если ошибки выборки имеют одинаковую дисперсию σ 2 и некоррелированы , то оценка β методом наименьших квадратов является СИНИМ (наилучшая линейная несмещенная оценка), а ее дисперсия оценивается с помощью
куда — остатки регрессии.
Когда члены ошибки не имеют постоянной дисперсии (т. Е. Допущение неверно), оценщик OLS теряет свои желаемые свойства. Формулу дисперсии теперь нельзя упростить:
куда
Хотя точечная оценка OLS остается несмещенной, она не «лучшая» в смысле наличия минимальной среднеквадратичной ошибки, а оценка дисперсии OLS не дает последовательной оценки дисперсии оценок OLS.
Однако для любой нелинейной модели (например, логит- модели и пробит- модели) гетероскедастичность имеет более серьезные последствия: оценки максимального правдоподобия параметров будут смещены (в неизвестном направлении), а также непоследовательны (если функция правдоподобия не определена). изменен для правильного учета точной формы гетероскедастичности). [8] [9] Как указал Грин , «простое вычисление устойчивой ковариационной матрицы для иначе несовместимой оценки не дает ей выгоды». [10]
Решение
Если ошибки регрессии независимы, но имеют различные дисперсии σ i 2 , то который можно оценить с помощью . Это дает оценку Уайта (1980), часто называемую HCE (оценка, согласованная с гетероскедастичностью):
где, как указано выше обозначает матрицу сложенных значения из данных. Оценка может быть получена с помощью обобщенного метода моментов (GMM).
Также в литературе (в том числе в статье Уайта) часто обсуждается ковариационная матрица принадлежащий -согласованное предельное распределение:
куда
а также
Таким образом,
а также
Какая именно ковариационная матрица вызывает беспокойство, зависит от контекста.
Альтернативные оценки были предложены в MacKinnon & White (1985), которые корректируют неравные дисперсии остатков регрессии из-за разного кредитного плеча . [11] В отличие от асимптотической оценки Уайта, их оценки несмещены, когда данные гомоскедастичны.
См. Также
- Дельта-метод
- Обобщенный метод наименьших квадратов
- Обобщенные оценочные уравнения
- Взвешенный метод наименьших квадратов , альтернативная формулировка
- Белый тест — тест на наличие гетероскедастичности.
- Оценка Ньюи – Уэста
- Оценка квази-максимального правдоподобия
Программное обеспечение
- EViews : EViews версии 8 предлагает три различных метода для робастных наименьших квадратов: M-оценка (Huber, 1973), S-оценка (Rousseeuw and Yohai, 1984) и MM-оценка (Yohai 1987). [12]
- MATLAB : см.
hacФункцию в наборе инструментов эконометрики. [13] - Python : пакет Statsmodel предлагает различные надежные стандартные оценки ошибок, дополнительные описания см. В statsmodels.regression.linear_model.RegressionResults
- R :
vcovHC()команда из пакета сэндвичей . [14] [15] - Крысы : robusterrors опция доступна во многих регрессии и оптимизации команд ( linreg , НМНК и т.д.).
- Stata :
robustопция, применимая во многих процедурах, основанных на псевдо-правдоподобии. [16] - Гретль : опция
--robustдля нескольких команд оценки (например,ols) в контексте набора данных сечения дает устойчивые стандартные ошибки. [17]
Ссылки
- ^ Kleiber, C .; Зейлис, А. (2006). «Прикладная эконометрика с R» (PDF) . Конференция UseR-2006 . Архивировано из оригинального (PDF) 22 апреля 2007 года.
- ^ Эйкер, Фридхельм (1967). «Предельные теоремы для регрессии с неравными и зависимыми ошибками» . Труды Пятого симпозиума Беркли по математической статистике и вероятности . 5 . С. 59–82. Руководство по ремонту 0214223 . Zbl 0217.51201 .
- ^ Хубер, Питер Дж. (1967). «Поведение оценок максимального правдоподобия в нестандартных условиях» . Труды Пятого симпозиума Беркли по математической статистике и вероятности . 5 . С. 221–233. Руководство по ремонту 0216620 . Zbl 0212.21504 .
- ^ White, Halbert (1980). «Матрица оценки согласованной с гетероскедастичностью ковариации и прямой тест на гетероскедастичность». Econometrica . 48 (4): 817–838. CiteSeerX 10.1.1.11.7646 . DOI : 10.2307 / 1912934 . JSTOR 1912934 . Руководство по ремонту 0575027 .
- ^ Король, Гэри; Робертс, Маргарет Э. (2015). «Насколько надежные стандартные ошибки выявляют методологические проблемы, которые они не исправляют, и что с этим делать» . Политический анализ . 23 (2): 159–179. DOI : 10,1093 / панорамирование / mpu015 . ISSN 1047-1987 .
- ^ Эйкер, Ф. (1963). «Асимптотическая нормальность и непротиворечивость оценок наименьших квадратов для семейств линейных регрессий» . Летопись математической статистики . 34 (2): 447–456. DOI : 10.1214 / АОМ / 1177704156 .
- ^ Eicker, Friedhelm (январь 1967). «Предельные теоремы для регрессий с неравными и зависимыми ошибками» . Труды Пятого симпозиума Беркли по математической статистике и вероятности, Том 1: Статистика . 5 (1): 59–83.
- ↑ Джайлз, Дэйв (8 мая 2013 г.). «Робастные стандартные ошибки для нелинейных моделей» . Эконометрика Beat .
- ^ Гуггисберг, Майкл (2019). «Неправильно указанные модели дискретного выбора и стандартные ошибки Хубера-Уайта». Журнал эконометрических методов . 8 (1). DOI : 10,1515 / ДСР-2016-0002 .
- ^ Грин, Уильям Х. (2012). Эконометрический анализ (седьмое изд.). Бостон: образование Пирсона. С. 692–693. ISBN 978-0-273-75356-8.
- ^ Маккиннон, Джеймс Г .; Белый, Халберт (1985). «Некоторые гетероскедастично-согласованные матричные оценки ковариаций с улучшенными свойствами конечной выборки». Журнал эконометрики . 29 (3): 305–325. DOI : 10.1016 / 0304-4076 (85) 90158-7 . hdl : 10419/189084 .
- ^ «EViews 8 робастная регрессия» .
- ^ «Гетероскедастичность и автокорреляционные согласованные оценки ковариации» . Панель инструментов эконометрики .
- ^ сэндвич: робастные оценщики ковариационной матрицы
- ^ Клейбер, Кристиан; Зейлейс, Ахим (2008). Прикладная эконометрика с R . Нью-Йорк: Спрингер. С. 106–110. ISBN 978-0-387-77316-2.
- ^ См. Интерактивную справку по
_robustпараметрам иregressкомандам. - ^ «Робастная оценка ковариационной матрицы» (PDF) . Руководство пользователя Gretl, глава 19 .
Дальнейшее чтение
- Фридман, Дэвид А. (2006). «О так называемой« сэндвичевой оценке Хубера »и« устойчивых стандартных ошибках » ». Американский статистик . 60 (4): 299–302. DOI : 10.1198 / 000313006X152207 . S2CID 6222876 .
- Хардин, Джеймс У. (2003). «Оценка дисперсии сэндвича». В Fomby, Thomas B .; Хилл, Р. Картер (ред.). Оценка максимальной вероятности моделей с ошибками: двадцать лет спустя . Амстердам: Эльзевир. С. 45–74. ISBN 0-7623-1075-8.
- Хейс, Эндрю Ф .; Цай, Ли (2007). «Использование оценок стандартной ошибки, согласованной с гетероскедастичностью, в регрессии OLS: введение и программная реализация» . Методы исследования поведения . 39 (4): 709–722. DOI : 10.3758 / BF03192961 . PMID 18183883 .
- Кинг, Гэри ; Робертс, Маргарет Э. (2015). «Насколько надежные стандартные ошибки выявляют методологические проблемы, которые они не исправляют, и что с этим делать» . Политический анализ . 23 (2): 159–179. DOI : 10,1093 / панорамирование / mpu015 .
- Вулдридж, Джеффри М. (2009). «Гетероскедастичность-робастный вывод после оценки МНК». Вводная эконометрика: современный подход (четвертое изд.). Мейсон: Юго-Западный. С. 265–271. ISBN 978-0-324-66054-8.
- Буя, Андреас и др. «Модели как приближения — заговор случайных регрессоров и модельных отклонений против классического вывода в регрессии». Статистическая наука (2015): 1. pdf
Стандартные ошибки в форме Уайта или состоятельные при гетероскедастичности стандартные ошибки (HC s.e. — Heteroskedasticity consistent standard errors) — применяемая в эконометрике оценка ковариационной матрицы МНК-оценок (в частности и стандартных ошибок) параметров линейной модели регрессии, альтернативная стандартной (классической) оценке, которая состоятельна при гетероскедастичности случайных ошибок модели (в отличие от несостоятельной в этом случае классической оценки).
Содержание
- 1 Сущность и формула
- 1.1 Замечание
- 2 См. также
- 3 Литература
Сущность и формула
Истинная ковариационная матрица МНК-оценок параметров линейной модели в общем случае равна:
где V — ковариационная матрца случайных ошибок. В случае, если нет гетероскедастичности и автокорреляции (то есть когда 
Поэтому для оценки ковариационной матрицы в классическом случае достаточно использовать оценку единственного параметра — дисперсии случайных ошибок: 
В общем случае, однако, необходима некоторая оценка неизвестной ковариационной матрицы. В частности, если предполагается наличие гетероскедастичности при отсутствии автокорреляции, ковариционная матрица случайных ошибок является диагональной и все диагональные элементы 
Уайт (White, 1980) показал, что если использовать в этой формуле вместо неизвестных дисперсий ошибок квадраты остатков регрессии, то получается состоятельная оценка:
Необходимо отметить, что данная оценка является состоятельной только при отсутствии автокорреляции случайных ошибок (то есть как и было описано — в случае диагональной ковариационной матрицы случайных ошибок). В случае, если имеется еще и автокорреляция, то можно использовать стандартные ошибки в форме Ньюи-Уеста.
Замечание
Иногда приведенную формулу оценки ковариационной матрицы корректируют на множитель 
См. также
- Стандартные ошибки в форме Ньюи-Уеста
- Обобщенный метод наименьших квадратов
Литература
- Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. — М.: Дело, 2004. — 576 с.
- William H. Greene Econometric analysis. — New York: Pearson Education, Inc., 2003. — 1026 с.



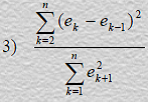
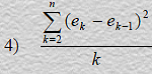
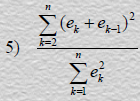


![{displaystyle {hat {mathbb {V} }}left[{widehat {boldsymbol {beta }}}_{mathrm {OLS} }right]=s^{2}(mathbf {X} ^{top }mathbf {X} )^{-1},quad s^{2}={frac {sum _{i}{widehat {varepsilon }}_{i}^{2}}{n-k}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd3f9d86ee8777e0132005ee7b87df048a68faf2)
![{displaystyle mathbb {V} left[{widehat {boldsymbol {beta }}}_{mathrm {OLS} }right]=mathbb {V} {big [}(mathbf {X} ^{top }mathbf {X} )^{-1}mathbf {X} ^{top }mathbf {y} {big ]}=(mathbf {X} ^{top }mathbf {X} )^{-1}mathbf {X} ^{top }mathbf {Sigma } mathbf {X} (mathbf {X} ^{top }mathbf {X} )^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2eb6038998637f73772725897a122b21a316afdc)
![{displaystyle {begin{aligned}{hat {mathbb {V} }}_{text{HCE}}{big [}{widehat {boldsymbol {beta }}}_{text{OLS}}{big ]}&={frac {1}{n}}{bigg (}{frac {1}{n}}sum _{i}mathbf {x} _{i}mathbf {x} _{i}^{top }{bigg )}^{-1}{bigg (}{frac {1}{n}}sum _{i}mathbf {x} _{i}mathbf {x} _{i}^{top }{widehat {varepsilon }}_{i}^{2}{bigg )}{bigg (}{frac {1}{n}}sum _{i}mathbf {x} _{i}mathbf {x} _{i}^{top }{bigg )}^{-1}\&=(mathbf {X} ^{top }mathbf {X} )^{-1}(mathbf {X} ^{top }operatorname {diag} ({widehat {varepsilon }}_{1}^{2},ldots ,{widehat {varepsilon }}_{n}^{2})mathbf {X} )(mathbf {X} ^{top }mathbf {X} )^{-1},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08d4969a485cdb096fa33d08f7ae04e9d737321b)

![{displaystyle mathbf {Omega } =mathbb {E} [mathbf {X} mathbf {X} ^{top }]^{-1}mathbb {V} [mathbf {X} {boldsymbol {varepsilon }}]operatorname {mathbb {E} } [mathbf {X} mathbf {X} ^{top }]^{-1},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35f99e141af80fcd8b22b13dc813519750b87466)

![{displaystyle {widehat {mathbf {Omega } }}_{n}=ncdot {hat {mathbb {V} }}_{text{HCE}}[{widehat {boldsymbol {beta }}}_{text{OLS}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff3af664b1167a553ee899c04356bf8a94df127f)
![{displaystyle {widehat {mathbb {V} }}[mathbf {X} {boldsymbol {varepsilon }}]={frac {1}{n}}sum _{i}mathbf {x} _{i}mathbf {x} _{i}^{top }{widehat {varepsilon }}_{i}^{2}={frac {1}{n}}mathbf {X} ^{top }operatorname {diag} ({widehat {varepsilon }}_{1}^{2},ldots ,{widehat {varepsilon }}_{n}^{2})mathbf {X} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1acd9bb6f131b50940af0e03ee47a684d0a76f8)