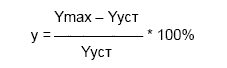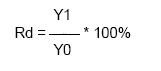Максимальная
динамическая ошибка
– наибольшее
отклонение регулируемой переменной от
заданного значения Узад:
.
(3.1)
В
устойчивой САР максимальным является
первое отклонение. Таким образом,
показатель
характеризует динамическую точность
регулирования [14].
Время
регулирования
tp
–промежуток времени от момента нанесения
возмущающего воздействия до момента,
начиная с которого отклонение регулируемой
переменной от установившегося значения
становится и остается меньше наперед
заданного значения ].
Остаточное
отклонение (остаточная неравномерность)
—
абсолютная статическая ошибка
регулирования, определяемая как разность
между установившимся значением
регулируемой величины и ее заданным
значением:
=Ууст
– Узад.
(3.2)
Показатель
характеризует точность регулирования
в статическом режиме [5].
Во
всех системах регулирования обязательно
имеется статическая ошибка. Ее можно
уменьшать путем увеличения общего
коэффициента усиления регулятора.
Однако она все равно остается, так как
увеличение коэффициента усиления
регулятора всегда ограничено.
Причиной
статической ошибки системы регулирования
является то, что в равновесном состоянии
регулятора положение регулирующего
органа жестко связано с величиной
регулируемой величины [6].
Система
регулирования, которая по принципу
своего действия обладает статической
ошибкой, называется статической
системой, а
регулятор в этом случае называется
статическим
регулятором.
Статический регулятор осуществляет
следующий закон регулирования:
y
= kрегх,
(3.3)
где
х
– отклонение регулируемой величины, у
– регулирующее воздействие регулятора
на объект.
Система
автоматического регулирования, не
обладающая статической ошибкой,
называется астатической
системой автоматического
регулирования,
а регулятор называется астатическим
регулятором [3].
3.2. Критерии устойчивости сар
Понятие
устойчивости САР связано с способностью
системы возвращаться в состояние
равновесия после исчезновения внешних
сил, которые вывели ее из этого состояния.
Устойчивость
систем автоматического управления
является одним из важнейших условий их
работоспособности, так как устойчивость
включает в себя требование затухания
переходных процессов во времени.
Очевидно, что система с расходящимся
процессом была бы неработоспособной.
Рассмотрим
дифференциальное уравнение движения
линеаризованной системы автоматического
регулирования, записанное для регулируемой
величины у(t)
при наличии управляющего воздействия
g(t)
и при равенстве нулю возмущающих
воздействий (см. формулу (2.4)):
.(3.4)
Процесс
регулирования определяется решением
дифференциального уравнения, как сумма
двух решений – частного решения
неоднородного уравнения (3.4)
с правой частью и общего решения уравнения
(3.4)
без правой части [1].
Характеристическое
уравнение САР имеет вид:
.
(3.5)
Корни
характеристического уравнения (3.5)
определяются только видом левой части
уравнения (3.4).
Постоянные интегрирования определяются
также и видом правой части. Поэтому
быстрота затухания и форма переходного
процесса определяются как левой, так и
правой частями исходного дифференциального
уравнения. Однако поскольку в понятие
устойчивости входит только факт наличия
или отсутствия затухания переходного
процесса (независимо от быстроты
затухания и формы переходного процесса),
то устойчивость линейной системы не
зависит от вида правой части
дифференциального уравнения (3.4)
и определяется только характеристическим
уравнением (3.5)
[13].
Так
как получающаяся при решении линейного
дифференциального уравнения (3.4) формула
переходного процесса содержит составляющие
в виде экспонент от вещественных частей
корней характеристического уравнения
САР (3.5) (см. главу 2), то для того, чтобы
САР была устойчивой и переходный процесс
затухал, необходимо, чтобы вещественные
части корней были отрицательными.
Следовательно,
для устойчивости линейной САР необходимо,
чтобы все корни лежали слева от мнимой
оси, в левой полуплоскости комплексных
чисел. Если хотя бы один корень окажется
справа от мнимой оси, то система будет
неустойчивой. Система будет находиться
на границе устойчивости при наличии:
нулевого корня
();
пары чисто мнимых корней
;
бесконечного корня
().
Во всех трех случаях предполагается,
что все остальные корни имеют отрицательные
вещественные части.
Необходимым
(но не достаточным) условием устойчивости
САР является положительность всех
коэффициентов характеристического
уравнения [7]. Это означает, что система
является неустойчивой, если хотя бы
один из коэффициентов характеристического
уравнения отрицателен. Если все
коэффициенты характеристического
уравнения положительны, то требуются
дополнительные исследования САР на
устойчивость с помощью критериев
устойчивости Гурвица, Михайлова или
Найквиста [3].
В
программе «SAU»
для определения устойчивости САР
используется критерий устойчивости
Гурвица, как наиболее удобный с точки
зрения компьютерной реализации. В методе
Гурвица для характеристического
уравнения (3.5) составляется квадратная
матрица коэффициентов, содержащая n
строк и n
столбцов:

(3.6)
Критерий
устойчивости сводится к тому, что при
а0>0
должны быть больше нуля все n
определителей Гурвица, получаемых из
квадратной матрицы коэффициентов.
Определители
Гурвица составляются по следующему
правилу:
;
;
(3.7)
Последний
определитель включает в себя всю матрицу.
Но так как в последнем столбце матрицы
все элементы, кроме нижнего, равны нулю,
то последний определитель Гурвица
выражается через предпоследний следующим
образом:
.
(3.8)
Однако
в устойчивой системе предпоследний
определитель тоже должен быть
положительным. Поэтому условие
положительности последнего определителя
сводится к условию
,
т.е. к положительности свободного члена
характеристического уравнения [1].
Условия
нахождения системы на границе устойчивости
можно получить, приравнивая к нулю
последний определитель ()
при положительности всех остальных
определителей. Как следует из (3.8),
это условие распадается на два условия:
и
.
Первое
условие соответствует границе устойчивости
первого типа (апериодическая граница
устойчивости), а второе – границе
устойчивости второго типа (колебательная
граница устойчивости).
Для
уравнения второго порядка необходимым
и достаточным условием устойчивости
является положительность всех
коэффициентов характеристического
уравнения. Для уравнений более высокого
порядка необходимо исследование с
помощью составления определителей
Гурвица и проверки их на положительность.
Существенным
недостатком критерия Гурвица является
то, что для уравнений высоких порядков
в лучшем случае можно получить ответ о
том, устойчива или неустойчива система
автоматического регулирования. При
этом в случае неустойчивой системы
критерий не дает ответа на то, каким
образом надо изменять параметры системы,
чтобы сделать ее устойчивой. Это
обстоятельство привело к поискам других
критериев, которые более удобны в
инженерной практике.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Статическая ошибка
Cтраница 4
Статической ошибкой САР называется значение отклонения регулируемой величины ( или ее среднего значения) от заданного значения в установившемся режиме.
[46]
Абсолютной статической ошибкой называют разность между каким-либо установившимся значением регулируемой величины и ее номинальным значением.
[48]
Чтобы статическая ошибка была равна нулю при действии возмущения, регулятор должен включать одно интегрирующее звено.
[49]
Термин статическая ошибка, применявшийся в начале для следящих систем по положению, был затем распространен на более широкий класс систем управления.
[50]
Хотя статическая ошибка имеет главенствующее значение, следует учитывать и динамические ошибки сельсинов. Они вызываются тем, что магнитные потоки, создающиеся в сельсинах, пересекаются обмоткой ротора. Если соединить сельсин-датчик с сельсин-трансформатором при нулевом положении и возбудить сельсин-датчик от источника переменного тока обычным образом, то выходная величина сельсин-трансформатора будет равна нулю, при отсутствии статической ошибки и остаточного напряжения в машинах. Это будет справедливо для любого углового положения соединенных валов.
[51]
Если статическая ошибка Дл: 0 во всей зоне регулирования, то такие регуляторы называются астатическими, если Д О, то статическими. Следовательно, астатическими регуляторами называются такие, у которых при различных постоянных значениях внешнего воздействия на объект ( например, изменение нагрузки) отклонение регулируемой величины от заданного значения по окончании процесса регулирования становится равным нулю.
[52]
Если статическая ошибка САР в состоянии покоя равна пулю для любых внешних возмущений, то система называется астатической. К астатическим системам мы также отнесем системы, в которых статическая ошибка меньше некоторой наперед заданной величины зоны нечувствительности и не зависит от величин приложенных возмущений. Если статическая погрешность САР в состоянии покоя отлична от нуля и зависит от величины внешних воздействий, то система называется статической.
[53]
Когда статическая ошибка магнитного компаса заведомо велика, азимутальную коррекцию по магнитной стрелке целесообразно отключать. Например, при использовании прибора на самолете азимутальную коррекцию при длительных виражах самолета отключают и определяют курс непосредственно по гироскопу направления. В качестве магнитного компаса в авиационных гиромагнитных компасах широко применяются феррозондовые датчики магнитного поля, рассмотренные выше.
[54]
Если статическая ошибка исследуемых цепей САР равна нулю, то регулируемые величины р2 и фз ( рис. 4 — 5 а) будут совершать колебания около тех уровней, которые регуляторы 2 и 3 стремятся поддерживать при отсутствии гармонических колебаний. Это облегчает стабилизацию системы и в случае объектов без самовыравнивания позволяет построить частотные характеристики без нарушения технологического процесса.
[56]
Ввиду статической ошибки и наличия ограничений теряет смысл выбор параметров настроек П — регулято-ра с точки зрения минимальной среднеквадратичной ошибки, получения переходного процесса заданной формы или минимального времени регулирования.
[57]
Величина статической ошибки зависит как от настройки регулятора, так и от характеристики и режима работы объекта.
[58]
Снятие статической ошибки, имеющей место в процессе регулирования пропорциональными регуляторами, достигается механизмом изодрома, который сообщает регулирующему органу дополнительное перемещение во времени.
[59]
Страницы:
1
2
3
4
Глава 8. Типовые законы регулирования. Одноконтурные САР
8.1. Основные типы автоматических регуляторов
Регулятор на основе усилительного звена называется П-регулятором (пропорциональный). Его положительной характеристикой является высокое быстродействие: при отклонении регулируемой величины от заданного значения регулятор выдает регулирующее воздействие, пропорциональное величине отклонения x, что обеспечивает быструю компенсацию возмущения. Существенным недостатком П-регулятора является наличие статической ошибки в переходном процессе АСР с П-регулятором (рис. 37). Статическая ошибка возникает потому, что у П-регулятора между регулируемой величиной x и регулирующим воздействием xр существует зависимость, однозначно определяемая коэффициентом K. Поэтому генерировать регулирующее воздействие xр для компенсации возмущения xв П-регулятор может только путем изменения регулируемой величины x, что и создает статическую ошибку.
Регулятор на основе интегрирующего звена (48) называется И‑регулятором:
Если xвых усилительного звена (П-регулятор) однозначно определяется величиной правой части уравнения, что является причиной возникновения статической погрешности в АСР с П-регулятором, то правая часть уравнения (48) интегрирующего звена (И-регулятор) определяет не величину, а скорость изменения xвых. Величина xвых будет изменяться до тех пор, пока правая часть уравнения (48) не станет равна нулю, т. е. пока регулируемая величина x при наличии возмущения xв не вернется к заданному значению. Следовательно, в АСР с И-регулятором не возникает статическая погрешность.
Однако у И-регулятора имеется свой недостаток сравнительно с П-регулятором: в случае возникновения возмущения регулирующее воздействие П-регулятора меняется быстрее, чем у И-регулятора с его конечной скоростью, что замедляет процесс компенсации возмущения и ухудшает критерии качества регулирования (рис. 40).
Рис. 40. Переходные процессы в АСР с П- и И-регуляторами
Таким образом, П-регулятор обеспечивает высокое быстродействие (что уменьшает динамическую ошибку), но не может обеспечить при наличии возмущения заданное значение регулируемой величины (статическая ошибка). И-регулятор, наоборот, не создает статическую ошибку, но вследствие относительно медленного изменения xр имеет большую динамическую ошибку.
Сравнивая характеристики П- и И-регуляторов можно сделать вывод: если включить усилительное и интегрирующие звенья параллельно, то автоматический регулятор будет лишен указанных недостатков. Такой регулятор называется ПИ-регулятором (рис. 41).
Рис. 41. Принципиальная схема АСР с ПИ-регулятором
Действительно, быстродействие ПИ-регулятора обеспечивает усилительное звено, а статическую ошибку снимает интегрирующее звено. Для управления производственными процессами чаще всего используются ПИ-регуляторы.
Кривая разгона идеального ПИ-регулятора показана на рис. 42 .
Уравнение ПИ-регулятора при нулевых начальных условиях имеет вид:

Отношение коэффициентов Kp1/Kp определяет степень влияния интегрирующей части, и его обратная величина называется временем изодрома Tи.

Время изодрома – это время, в течение которого интегрирующее звено изменяет регулирующее воздействие xр ПИ-регулятора на величину Dxр, равную предварительному изменению Dxр усилительного звена (рис. 42). Поэтому иногда время изодрома называют временем удвоения.
Рис. 42. График кривой разгона идеального ПИ-регулятора:
а – скачкообразное изменение входного воздействия x;
б – реакция (кривая разгона) ПИ-регулятора xр
Уравнение ПИ-регулятора можно записать как
откуда передаточная функция
Амплитудно-фазовая характеристика:

В том случае, если рассмотренные регуляторы не обеспечивают требуемое качество регулирования, необходимо увеличить интенсивность процесса компенсации возмущения. Этого можно достигнуть увеличением регулирующего воздействия, которое в свою очередь определяется коэффициентом усиления автоматического регулятора Kp
. Однако ниже будет показано, что увеличение коэффициента усиления регулятора в АСР приводит к тому, что в системе начинают генерироваться незатухающие колебания.
В связи с этим представляет интерес рассмотреть алгоритм, который реализует дифференцирующее звено.
Входной величиной любого регулятора является кривая разгона регулируемой величины (рис. 27), которая определяется величиной возмущения и передаточной функцией объекта регулирования (9). В свою очередь, регулирующее воздействие xp (рис. 27) определяется кривой разгона x и передаточной функцией регулятора.
На рис. 43 показана реакция дифференцирующего звена (Д‑регулятора) на входное воздействие в виде кривой разгона в соответствии с уравнением (51).
Рис. 43. Реакция дифференцирующего звена на кривую разгона
а –изменение входного воздействия x в виде кривой разгона;
б – реакция xр дифференцирующего звена
Из рис. 43,а следует, что дифференцирующее звено обеспечивает большее регулирующее воздействие в начале переходного процесса. Это означает, что дифференцирующий регулятор активно компенсирует возмущение и исключает возникновение незатухающих колебаний.
Если включить дифференцирующее звено параллельно ПИ‑регулятору (рис. 44), то получим ПИД-регулятор, обеспечивающий интенсивную компенсацию возмущений. При этом недостаток дифференцирующего звена (при Хвх = const, Хвых = 0 ) компенсируется усилительным и интегрирующим звеньями.
Рис. 44. Принципиальная схема АСР с ПИД-регулятором
На рис. 45 показана кривая разгона ПИД-регулятора.
Рис. 45. Кривая разгона ПИД-регулятора
На рис. 46 показаны переходные процессы на с различными регуляторами. ПИД-регулятор уменьшает динамическую ошибку сравнительно с ПИ-регулятором на 25–30%. Также можно объединить дифференцирующее звено с усилительным звеном и улучшить показатели П-регулятора, получив ПД-регулятор.

Все пять типов рассмотренных автоматических регуляторов имеют общую особенность своего функционирования – обеспечивают стабилизацию регулируемой величины после окончания переходного процесса.
8.2. Критерии качества регулирования
Качество процесса регулирования в АСР характеризуют следующие показатели (критерии) (рис. 16):
Рис. 16. Показатели качества регулирования:
1 – переходной процесс без статической ошибки;
2 – переходной процесс со статической ошибкой
1. Максимальное отклонение в процессе регулирования от заданного значения (динамическая ошибка) ΔХдин.
2. Статическая ошибка ΔХст — возможные отклонения от заданного значения по окончании переходного процесса при использовании некоторых типов регуляторов (подробнее такие АСР рассмотрены ниже).
3. Длительность переходного процесса Тр – период времени с момента начала отклонения регулируемого параметра от задания до возвращения его к заданному значению с определенной степенью точности регулирования ±Δ.
Например, если ±Δ=±25%, это означает, что для заданного значения температуры в 100 °С процесс регулирования будет завершен при достижении диапазона (100 ± 2,5) °С.
4. Степень затухания показывает характер затухания переходного процесса регулирования:
Для того, чтобы переходный процесс затухал за 2 ¸ 3 периода колебаний, степень затухания должна быть равна

5. Степень колебательности процесса m определяет характер колебательности процесса и равна отношению действительной части корня характеристического уравнения к коэффициенту при его мнимой части. Степень колебательности связана со степенью затухания следующим соотношением:
6. Интегральный квадратичный критерий – критерий, определяющий площадь под кривой переходного процесса, возведенной в квадрат (рис. 17):
Уменьшение интегрального критерия соответствует ускорению процесса регулирования.
Рис. 17. Интегральный квадратичный критерий качества регулирования
Однако все приведенные шесть критериев качества не определяют величину потерь производства при отклонениях регулируемой величины от оптимального значения в переходных процессах регулирования. Для определения таких потерь можно использовать экономический критерий.
7. Экономический критерий рассмотрим на примере, регулирования температуры химического реактора θ, когда степень превращения Q в реакторе определяется температурой (рис. 18а).
Разделим переходной процесс на равные интервалы времени Δt и запишем значения θ
в этих точках по графику (18, б). На графике (18, а) для этих температур определим уменьшение степени превращения вследствие отклонения от оптимального режима, а затем сделаем расчет потерь исходных продуктов для каждого интервала Δθ, суммируем эти потери для всего переходного процесса и представим потери в денежном выражении.
Рис. 18. Экономический критерий качества регулирования:
а – зависимость степени превращения Q от температуры θ;
б – переходный процесс регулирования температуры
Совместно со специалистом по технологии или по его заданию необходимо определить, какой из указанных критериев для рассматриваемой АСР является превалирующим, и задать максимально допустимую величину этого критерия, т. е. определить, какое качество регулирования должна обеспечить проектируемая АСР.
8.3. Выбор закона регулирования
При выборе регулятора следует определиться с группой регулирующих устройств – непрерывного, релейного или импульсного действия. Такой выбор ориентировочно может быть сделан по величине отношения запаздывания к постоянной времени объекта τ/Tоб:
· при отношении τ/Tоб меньше 0.2 целесообразно использовать регулятор релейного действия;
· если отношение τ/Tоб от 0.2 до 1.0, то нужно использовать регулятор непрерывного действия;
· при отношении τ/Tоб больше единицы можно использовать регулятор импульсного действия, или специальные регуляторы, например, регулятор («предиктор») Смита.
Затем необходимо определиться с типом регулятора, т.е. выбрать определенный закон регулирования: П-, И-, ПИ-, ПД- или ПИД-закон
8.4. Методы расчета одноконтурных САР
Как указывалось выше, качество автоматического регулирования определяется свойствами системы в целом, т. е. суммарными свойствами объекта и регулятора. Поскольку объект обычно является неизменяемой частью системы, то обеспечить определенные свойства системы, а следовательно и заданное качество регулирования, можно соответствующим подбором свойств автоматического регулятора, что зависит от параметров его настройки. В свою очередь, параметры настройки являются коэффициентами передачи в уравнении автоматического регулятора.
Таким образом, параметры настройки автоматического регулятора определяются свойствами объекта регулирования, т. е. величинами τоб, Тоб, Коб.
8.4.1. Расчет по «приближенным» формулам
Приближенные формулы для расчета параметров настройки автоматических регуляторов (Kр – коэффициент усиления; Tи – время изодрома; Тд – время дифференцирования) сведены в следующую таблицу:
Таблица 8.1. Формулы для приближенного расчета
параметров настройки регуляторов

Формулы сгруппированы в столбцы в зависимости от характера переходного процесса, который желательно получить, используя рассчитанный таким образом регулятор: апериодический или с перерегулированием в 20 %. В формулы входят следующие свойства объекта регулирования: Коб – коэффициент усиления; Тоб – постоянная времени; τоб – время запаздывания (полного).
Рис. 53. Кривые разгона:
1 – фактическая кривая разгона промышленного объекта;
2 – аппроксимированная (приближенная) кривая разгона
Необходимо отметить, что для пневматических регуляторов требуется определять не Kp, а диапазон дросселирования:
Рассмотрим методику более точного определения параметров настройки на примере расчета наиболее «популярного» регулятора – ПИ-регулятора.
8.4.2. Метод незатухающих колебаний
(метод Циглера-Никольса)
При использовании метода незатухающих колебаний [6], который иногда также называется по именам авторов методом Циглера-Никольса, поиск оптимальных параметров настройки осуществляется по величине критического коэффициента усиления П-регулятора и величине периода автоколебательного процесса.
Рис. 54. К поиску параметров настройки методом Циглера-Никольса
Расчет параметров настройки регуляторов проводится в два этапа.
1. На исследуемом объекте устанавливается П-регулятор и, последовательно увеличивая коэффициент усиления (уменьшая диапазон дросселирования), АСР выводится в режим незатухающих колебаний (автоколебаний на границе устойчивости). При этом фиксируется величина коэффициента усиления П-регулятора Ккрр и период незатухающих автоколебаний Т (рис. 54).
2. На втором этапе по величинам Кркр и Т определяются параметры настройки П-, ПИ- и ПИД-регуляторов:
Метод незатухающих колебаний не требует сложных вычислений, но имеет свои характерные недостатки:
· получить Кркр и Т можно только на действующем объекте, оснащенном АСР с П-регулятором;
· не все объекты химической технологии допускают режим автоколебаний;
· практически трудно уловить момент начала автоколебаний.
Данные недостатки имеют место лишь при настройке регулятора методом Циглера-Никольса непосредственно на действующем объекте. Если заменить реальный объект его математической моделью, данный метод лишается указанных недостатков, кроме того, моделирование позволяет на порядок ускорить процесс поиска параметров настройки. Но для выполнения моделирования требуется достаточно точное математическое описание объекта регулирования, а получить его удается не всегда.
8.4.3. Метод расширенных частотных характеристик
Уравнение ПИ-регулятора (65) или (66):
Передаточная функция ПИ-регулятора:

Знак «минус» указывает, что действие регулятора направлено против возмущения.
Из передаточной функции получаем амплитудно-фазовую характеристику ПИ-регулятора путем замены p на iw:

Так как по формуле Эйлера


с затуханием за три периода
Заменив iw на комплексную переменную (-mw+iw), получаем расширенную амплитудно-фазовую характеристику (РАФХ)Ю

Расширенными такие характеристики называются потому, что они как бы «расширены» по отношению к обычной АФХ (рис. 56).
Предположим, что объект регулирования имеет передаточную функцию второго порядка следующего вида:

Для дальнейшего математического моделирования АСР передаточную функцию необходимо преобразовать:

Рис. 56. АФХ объекта регулирования с самовыравниванием:
1 – обычная; 2 – расширенная
Расширенная амплитудно-фазовая характеристика объекта регулирования при замене p на (-mw+iw) будет иметь вид:



Где Rоб(m,w) -расширенная амплитудно-частотная характеристика объекта; Fоб(m,w) -расширенная фазочастотная харктеристика объекта. Величина 40w в выражении для Fоб (m,w) опеделяет угол в радианах и для пересчета в градусы неоходимо 40w умножить на 57,3
Условием нахождения замкнутой АСР на границе устойчивости является уравнение:

Аналогично, исходным уравнением для получения заданной степени колебательности m, а следовательно, определенной степени затухания y, является соотношение:
Это соотношение двух комплексных чисел возможно в том случае, если произведение модулей РАФХ равно единице, а аргументы (фазы) равны между собой, т. е.

Решая эти уравнения относительно S0 и Kp, получаем:


Обычно принимают степень колебательности m = 0,221, что соответствует степени затухания ψ=0,75 и обеспечивает затухание процесса регулирования примерно за три периода. Тогда

Уравнения для определения параметров настройки ПИ-регулятора можно преобразовать:


Подставляя в приведенные уравнения численные значения частоты w от 0 до значения, когда S0 становится отрицательной величиной, строим на плоскости параметров настройки кривую равной степени колебательности


Пример кривых равной степени колебательности в плоскости параметров настройки ПИ-регулятора показан на рис. 57. Графики процессов регулирования с различными параметрами настройки ПИ-регулятора при m = 0,221 показаны на рис. 58. Все процессы регулирования, показанные на рис. 58, реализованы ПИ-регулятором с параметрами настройки, полученными по кривой равной степени колебательности в точках 1, 2, 3, 4 (рис. 57), и все имеют m = 0,221, т. е. затухают примерно за три периода, но обладают существенно различным характером.
В связи с этим возникает задача определения оптимальных параметров настройки на кривой равной степени колебательности.
Рис. 57. Кривые равной степени колебательности
В качестве критерия оптимальности выбираем продолжительность переходного процесса – время регулирования (т. е. быстродействие АСР) и отсутствие постоянной или врéменной статической ошибки. Это исключает из рассмотрения параметры настройки в точке 4 (параметры настройки П-регулятора) и в точке 3 (врéменная статическая ошибка) (рис. 58).
Рис. 58. Графики процессов регулирования для ПИ-регулятора
с различными параметрами настройки в точках 1, 2, 3 и 4
при степени колебательности m =0,221
Быстродействие автоматического регулятора прежде всего зависит от величины регулирующего воздействия, которое для ПИ-регулятора, как следует из уравнения (65), прямо пропорционально величине коэффициента усиления Kp и обратно пропорционально времени изодрома Tи. Расчеты показывают, что если двигаться по кривой равной степени колебательности вправо, то величина регулирующего воздействия при прочих равных условиях сначала возрастает и достигает максимального значения на кривой равной степени колебательности вблизи ее вершины, когда
а затем начинает уменьшаться в связи с резким увеличением Tи (рис. 57).
Рис. 59. Выбор оптимальных параметров настройки
Таким образом, оптимальные параметры настройки ПИ-регулятора находятся в точке 2 на кривой равной степени колебательности (рис. 59).
Источник
Плютто В. П., Дубровский И. И. Элементы теории управления химико-технологическими процессами и системами. Конспект лекций: Учеб. пособие – М.: РХТУ им. Д. И. Менделеева, 2003. – 127 с.
К системам автоматического регулирования (САР) предъявляются требования не только
устойчивости процессов регулирования. Для работоспособности системы не менее необходимо, чтобы процесс автоматического регулирования осуществлялся при обеспечении определенных показателей качества процесса управления.
Если исследуемая САР является устойчивой, возникает вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям обьекта управления.На практике качество регулирования определяется визуально по графику переходной характеристики. Однако, имеются точные но более сложные математические методы, дающие конкретные числовые значения (которые не рассматриваются в данной методике).
Классификация показателей качества состоит из нескольких групп:
- прямые — определяемые непосредственно по переходной характеристике процесса,
- корневые — определяемые по корням характеристического полинома,
- частотные — по частотным характеристикам,
- интегральные — получаемые путем интегрирования функций.
Прямыми показателями качества процесса управления, определяемые непосредственно по
переходной характеристике являются:
- Установившееся значение выходной величины Yуст,
- Степень затухания ?,
- Время достижения первого максимума tmax,
- Время регулирования tp,
- Ошибка регулирования Ест (статистическая или среднеквадратическая составляющие),
- Перерегулирование у,
- Динамический коэффициент регулирования Rd,
- Показатель колебательности М.
Например, переходная характеристика, снятая на объекте управления при отработке ступенчатого воздействия, имеет колебательный вид и представлена на рис.1.
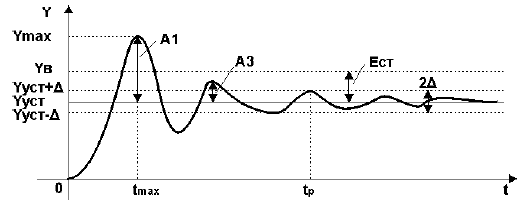
Рисунок 1 — Определение показателей качества по переходной характеристике
Установившееся значение выходной величины Yуст
Установившееся значение выходной величины Yуст определяется по переходной характеристике,представленной на рис.1.
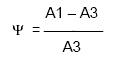
Степень затухания ?
Степень затухания ? определяется по формуле:
где А1 и А3 — соответственно 1-я и 3-я амплитуды переходной характеристики рис.1.
Время достижения первого максимума tmax
Время достижения первого максимума tmax определяется по переходной характеристике,представленной на рис.1.
Время регулирования tp
Время регулирования tp определяется согласно рис.1 следующим образом:Находится допустимое отклонение Д, например, задано Д = 5%Yуст и строится «зона» толщиной 2 Д(см. рис.1). Время tp соответствует последней точке пересечения Y(t) с данной границей. То есть время,когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.
Настройки регулятора необходимо выбирать так, чтобы обеспечить минимально возможное значение общего времени регулирования, либо минимальное значение первой полуволны переходного процесса.
В непрерывных системах с типовыми регуляторами это время бывает минимальным при так называемых оптимальных апериодических переходных процессах. Дальнейшего уменьшения времени регулирования до абсолютного минимума можно достичь при использовании специальных оптимальных по быстродействию систем регулирования.
Ошибка регулирования Ест
Статическая ошибка регулирования Ест = Ув — Ууст, где Ув — входная величина (см. рис.1).В некоторых САР наблюдается ошибка, которая не исчезает даже по истечении длительногоинтервала времени — это статическая ошибка регулирования Ест. Данная ошибка не должна превышатьнекоторой наперед заданной величины. У регуляторов с интегральной составляющей ошибки в установившемся состоянии теоретическиравны нулю, но практически незначительные ошибки могут существовать из-за наличия зоннечувствительности в элементах системы.
Перерегулирование у
Величина перерегулирования у зависит от вида отрабатываемого сигнала.При отработке ступенчатого воздействия (по сигналу задания) – см. рис.1 величина перерегулирования у определяется по формуле:
где значения величин Ymax и Yуст определяются согласно рис.1.
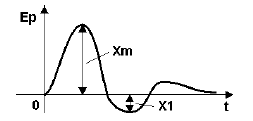
При отработке возмущающего воздействия, величина перерегулирования у определяется изсоотношения:
где значения величин Xm и X1 определяются согласно рис. 2.
Рисунок 2 — График переходного процесса при отработке возмущения
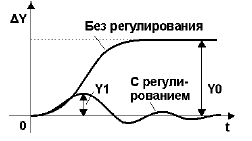
Динамический коэффициент регулирования Rd
Динамический коэффициент регулирования Rd определяется из формулы:
где значения величин Y1 и Y0 определяются согласно рис. 3.
Рисунок 3 — К понятию динамического коэффициента регулирования
Величина динамического коэффициента Rd характеризует степень воздействия регулятора напроцесс, т.е. степень понижения динамического отклонения в системе с регулятором и без него.
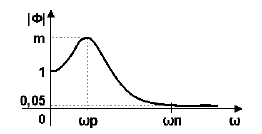
Показатель колебательности М
Показатель колебательности M характеризует величину максимума модуля частотной передаточной функции замкнутой системы (на частоте резонанса) и, тем самым, характеризует колебательные свойства системы. Показатель колебательности наглядно иллюстрируется на рисунке 4.
Рисунок 4 — График модуля частотной передаточной функции замкнутой системы
Условно считается, что значение М=1,5-1,6 является оптимальным для промышленных САР, т.к. вэтом случае у обеспечивается в районе от 20% до 40%. При увеличении значения M колебательность всистеме возрастает.
В некоторых случаях нормируется полоса пропускания системы щп, которая соответствует уровню усиления в замкнутой системе 0,05. Чем больше полоса пропускания, тем больше быстродействие замкнутой системы. Однако при этом повышается чувствительность системы к шумам в канале измерения и возрастает дисперсия ошибки регулирования.
Качество регулирования характеризует способность устойчивой системы обеспечивать требуемую точность регулирования в установившихся и переходных режимах.
СодержаниеСвернуть
- Общие понятия
- Оценка качества регулирования в установившихся режимах
- Методы оценки качества в переходных режимах. Диаграмма Вышнеградского
- Способы улучшения качества переходных процессов САР
- Конструкции устройств гибких обратных связей
Общие понятия
К непосредственным показателям качества регулирования относятся:
- на установившихся режимах — величина статической ошибки регулирования;
- на переходных режимах (см. рис. 1 Схема регулятора скорости и его характеристики) — показатели переходных процессов;
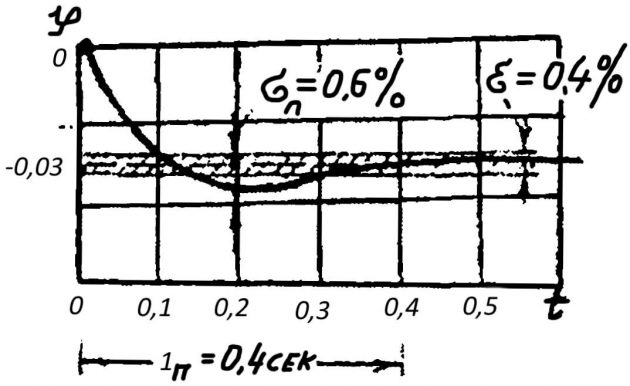
- максимальное отклонение регулируемой величины Δymax от прежнего установившегося значения, величина перерегулирования δn и длительность переходного процесса tn т.е. время до вхождения регулируемой величины в заданную зону. Для реальных систем такой зоной принимается зона нечувствительности.
Непосредственные показатели качества могут быть получены с помощью прямых методов исследования, т.е. непосредственно решением систем дифференциальных уравнений. Современные ЭЦВМ позволяют получить необходимую точность при решении нелинейных дифференциальных уравнений высокого порядка. На основании этого решения можно определить Δymax, δn и tn заданным требованиям. Однако точный ответ на вопросы качества регулирования требуется, как правило, при проектировании систем и, прежде всего, систем с высокими требованиями по качеству, осуществление выполнения которых зачастую сопряжено с конструктивными сложностями регулятора и специальных корректирующих устройств.
В ряде случаев, например, при настройке регуляторов, требуется знать способы изменения статизма, уменьшения или увеличения показателей Δymax, δn и tn по сравнению с имеемыми в системе. На этот вопрос можно ответить, изучая качество регулирования с помощью приближенных или косвенных методов оценки качества.
Оценка качества регулирования в установившихся режимах
Качество регулирования в установившихся режимах работы системы оценивается величиной статической ошибки υ:
υ=ymp–y
где:
- у — текущее, уmp — заданное значение регулируемой величины.
Величина ошибки υ равна отклонению регулируемой величины от заданного значения и может быть обусловлена как принятым законом регулирования, так и особенностями структурной Методы исследования линейных систем автоматического регулирования. Структурные схемы и передаточные функциисхемы системы. При оценке величины ошибки линейных САР не учитываются нечувствительность и непрямолинейность статических характеристик реальных систем, обусловленных зазорами, сухим трением и другими нелинейностями.
Для систем стабилизации, задача которых уменьшать отклонение регулируемой величины от заданного значения уmp, целесообразно в качестве выходной величины принимать это отклонение, считая уmp за ноль отсчета. Статическая ошибка системы будет υ = -у.
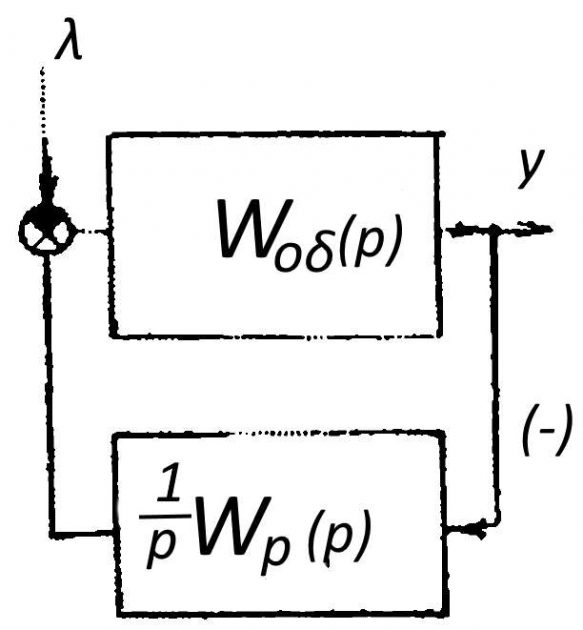
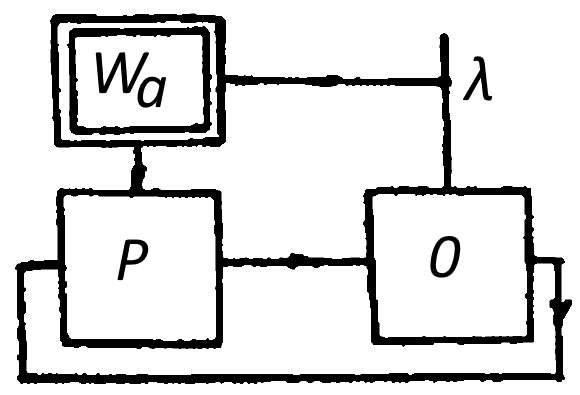
Если в качестве входной величины системы (рис. 1) принять нагрузку λ, то значение статической ошибки может быть получено из выражения для передаточной функции замкнутой системы Ф(p):
υ=–y=—Ф(p)λ при p=0, где Ф(p)=y(p)/λ(p) с учетом знака λ.
Максимальную статическую ошибку υmax получим, подставив λ = 1:
υmax=Ф(p)p=0=+δ.
Таким образом, величина максимальной статической ошибки САР стабилизации численно равна наклону статической Методы исследования линейных систем автоматического регулирования. Структурные схемы и передаточные функциихарактеристики САР.
Допустим, что регулятор САР состоит из позиционных звеньев (П-регулятор).
Определим ошибку для этого случая:
υmax=Wоб(p)/1+Wоб(p)Wp(p)p=0=kоб/1+kобk(p),
где:
- kоб и kp — коэффициенты передачи объекта и регулятора.
Обычно kобkp » 1, поэтому υmax = ≈ 1/kp.
Таким образом, максимальная статическая ошибка САР, регулятор которой состоит из позиционных звеньев, обратно пропорциональна коэффициенту усиления регулятора.
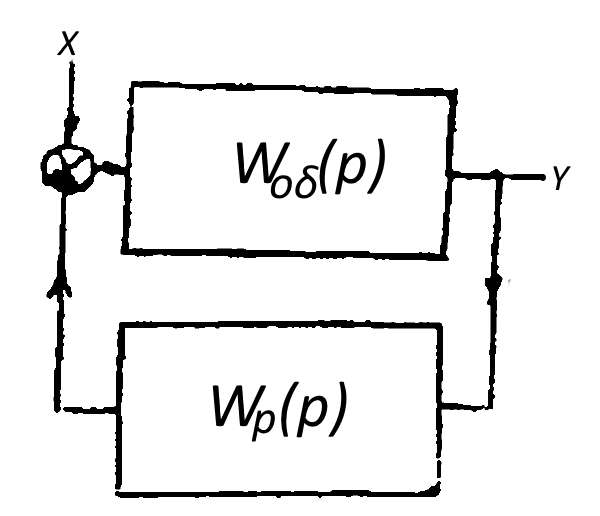
Рассмотрим также случай, когда в числе звеньев регулятора имеется одно последовательно соединенное интегрирующее звено (рис. 2), которым может быть, например, сервомотор, не охваченный обратной связью (И — регулятор):
где:
- 1/p × Wp(p) — передаточная функция регулятора;
- Wp(p) — передаточная функция остальных звеньев.
В этом случае коэффициент усиления регулятора равен бесконечности, а САР является астатической (δ = 0). Следовательно, повышение точности САР на установившихся режимах может быть достигнуто увеличением коэффициента усиления регулятора.
Предлагается к прочтению: Океанотехника прошлого
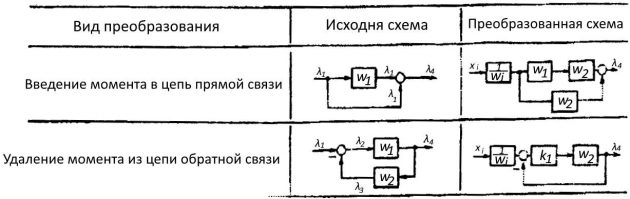
Для упрощения анализа влияния элементов на работу САР возможно произвести преобразование структурных схем.
Методы оценки качества в переходных режимах. Диаграмма Вышнеградского
Для оценки качества переходных процессов используются прямые оценки, определяемые путем расчета переходных процессов при стандартных входных воздействиях, и косвенные оценки. Различают ступенчатое (скачкообразное) воздействие — наиболее часто используемый метод для систем стабилизации, импульсное воздействие, гармоническое (синусоидальное) воздействие, случайное воздействие.
Случайное воздействие наиболее часто встречается в практике. Однако ступенчатое воздействие (единичный скачок) приводит к наибольшему отклонению выходной величины и поэтому является основным используемым методом оценки качества переходных процессов.
Разработаны различные методы позволяющие по прямым и косвенным признакам судить о качестве переходных процессов линейной САР.
Интегральные оценки качеств. Интегральной оценкой качества может служить площадь под кривой переходного процесса
∫0∞xdτ
где:
x=xp–xp0
где:
- х — отклонение xp от ее значения в новом установившемся режиме.
В колебательных системах используется квадратичная интегральная оценка
I=∫0∞x2dt
,
которая не зависит от закона отклонений. Для улучшенной интегральной оценки
I=∫0∞(x2+T2·x2)dt
, где T — заранее заданная постоянная величина.
Приближенное построение переходной характеристики h(t) можно осуществить, если рассчитать вещественную часть АФХ замкнутой системы P(ω) = ReФ(ω). Заменяя кривую Р(ω) трапециями, путем несложных расчетов получают h(t) — метод, трапециедальных частотных характеристик, разработанный профессором Солодов-пиковым.
Можно доказать, что по виду Р(ω) можно судить о характере переходного процесса — h(t). Например, конечное Ремонт автоматики, регуляторов частоты вращения и систем регулированиязначение регулируемой величины будет соответствовать у = δ = Ф(jω)ω = 0. Так как Ф(ω) = P(ω) + jQ(ω), где Q(ω) — нечетная функция от ω, то при ω = 0 равном нулю,
Ф(0)=P(0)=δ.
Можно также доказать, что начальное значение регу-лируемой величины будет равно Р(ω) при ω → ∞.
О качестве переходных процессов можно судить по расположению корней характеристического уравнения на плоскости корней. Так, например, наличие комплексных корней, расположенных близко к мнимой оси, свидетельствует о колебательности системы.
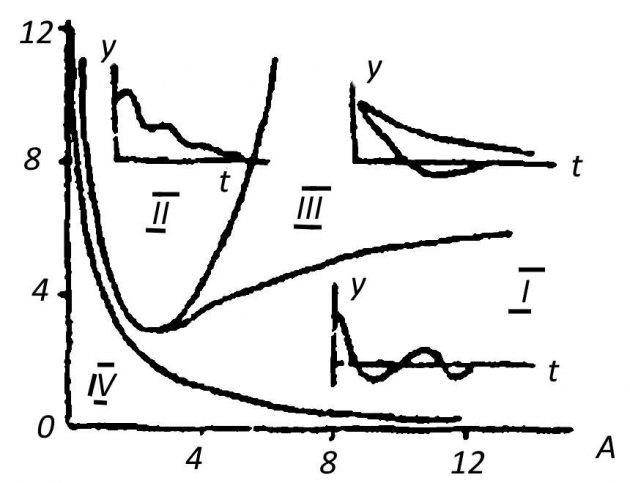
Наглядное представление о качестве переходных процессов и устойчивости линейной системы 3-го порядка дает диаграмма И.А. Вышнеградского, построенная в координатах А и В, где А и В постоянные нормированного уравнения 3-го порядка вида:
a1d3ydt3+a1d2ydt2+a3y=0,
A=a1a20a33; B=a2a0a323.
На рис. 3 показаны 3 области, соответствующие устойчивому решению уравнения, однако характер переходных процессов во всех областях различный: III — со-ответствует затуханию процесса по экспоненте, в области II — на экспоненту накладываются колебания, а в области I — процесс носит затухающий колебательный характер. При АВ < 1 процесс неустойчив.
I, II, III – области устойчивости САР; IV – область неустойчивости САР
При исследовании систем регулирования с помощью АФХ разомкнутой системы удобно использовать частотные критерии качества: Расчет судовой электроэнергетической системызапас устойчивости по модулю (амплитуде) и запас устойчивости по фазе.
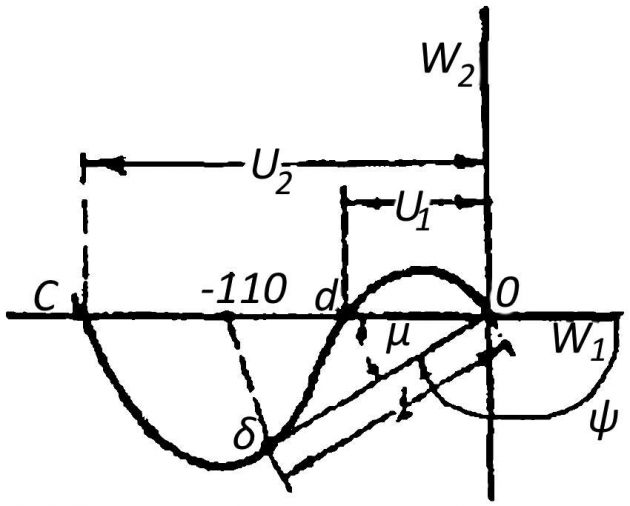
Запасом устойчивости по модулю называется величина, определяемая в общем случае для устойчивой САР по выражениям:
L1=20lg1U1∂δ и L2=20lgU2∂δ,
где:
- U1 и U2 — расстояния от начала координат до точек пересечения АФХ с отрицательной полуосью абсцисс (рис. 4).
Запасом устойчивости по фазе называется вели-чина μ = 180 + ψ, где:
- ψ — аргумент передаточной функции при модуле, равном единице.
Запасы устойчивости по модулю и фазе могут быть косвенно связаны с видом переходного процесса. Так, например, уменьшение демпфирования в звеньях системы, приводящие к увеличению колебательности процесса, как правило, приводит к уменьшению запасов устойчивости по модулю и фазе. В хорошо демпфированных системах запас устойчивости по модулю составляет 6-20∂δ, а запас устойчивости по фазе 30-60°.
Системное программное обеспечение на судахЦифровые вычислительные машины имеют большие возможности в решении линейных и нелинейных дифференциальных уравнений высокого порядка. Этим, в известной степени, можно объяснить, что приближенные и косвенные методы исследования качества переходных процессов, разработанные для линеаризованных систем, в настоящее время не имеют широкого применения. ЭВМ позволяют легко решать те же задачи путем прямого интегрирования нелинейных уравнений, что более важно, т. к. в любой реальной САР имеют место нелинейности, оказывающие существенное влияние на качество регулирования.
Способы улучшения качества переходных процессов САР
Поясним вначале на примере конкретной САР влияние на показатели переходного процесса быстродействия регулятора, оцениваемое величиной, обратно пропорциональной его постоянной времени Тp, при описании регулятора дифференциальным уравнением 1-го порядка, принято, что Kp = 30. Объект регулирования принят также инерционным звеном 1-го порядка, Тоб = 5с.
На рис. 5 приведены результаты исследования рассматриваемой системы при изменении значения Тp. Уменьшение быстродействия регулятора путем увеличения Тp приводит к тому, что регулирующее воздействие Z принимает значение, компенсирующее набрасываемую нагрузку λ = 1, позже. К этому времени регулируемая величина y успевает отклониться от прежнего установившегося значения на большую величину Δymax. Новое установившееся значение при сохранении Kp = const остается неизменным. При уменьшении Тp, значения Δymax и δn снижаются. Заметим, что снижение Тp ниже определенных пределов может быть конструктивно сложной задачей.
а) Kp = Kp1 = 30, Тp = Тp1 = 0,5 с; б) Kp2 = Kp1, Tp2 » Tp1, Тоб = 5с; в) Tp3 = Tp1, Kp3 = 50
В регуляторах прямого действия чувствительные элементы должны иметь работоспособность, достаточную для передвижения регулирующего органа, а это, как правило, приводит к увеличению Тp.
Эффект по уменьшению величины Δymax может быть достигнут путем увеличения Кp. Одновременно растет колебательность δn. Из предыдущего известно, что устойчивая САР с ростом Кp может стать неустойчивой.
Читайте также: Организация труда вахтенного ПКМ
Вместе с тем, имеются способы улучшения качества переходных процессов, которые позволяют решать задачи улучшения качества, без ухудшения устойчивости. К ним относится
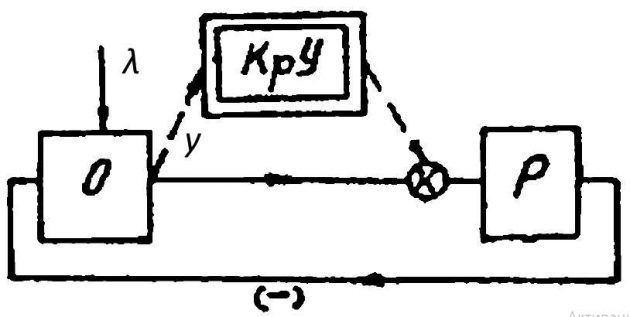
Применение принципа комбинированного регулирования. Пусть имеется САР, включающая объект и регулятор, действующий по отклонению регулируемой величины (рис. 6). С целью повышения точности регулирования используем принцип комбинированного регулирования и введем устройство, осуществляющее регулирование по возмущению (нагрузке) с коэффициентом передачи Кк.
Будем считать, что все ПФ соответствуют позиционным звеньям.
Передаточная функция замкнутой системы, после решения системы алгебраических уравнений:
Zк=Wк(p)λ,
μ=Z–λ,Z=Zp+Zк; y=Wоб(p)μ
Zp=–Wp(p)·y
примет вид
Ф(p)=+Wоб(p)[Wк(p)–11+Wоб(p)Wp(p)
при P = 0 наклон регуляторной характеристики определяется выражением:
1/Kp–Kк/KP.
Увеличивая Kк можно уменьшить наклон статической характеристики САР. На устойчивость системы и ее колебательность это влиять не будет, так как устойчивость определяется характеристическим уравнением, которое может быть получено, если полином знаменателя ПФ приравнять нулю. В полином знаменателя выражение Wк(p) не входит.
Коррекция введением производных. Для улучшения качества регулирования в систему могут быть введены дополнительные корректирующие звенья, например, по производным от возмущающего воздействия или регулируемой величины. SOS, Мэйдэй и другие международные сигналы о бедствииДействие сигнала производной по возмущению, если этот сигнал подавать с помощью специального устройства на регулирующий орган, в известной степени аналогично рассмотренному выше случаю. Отличие состоит в том, что сигнал по производной не действует на установившихся режимах и не изменяет статизма САР, но может повысить точность регулирования, снизив Δymax, в переходных режимах.
Рассмотрим действие коррекции по производной регулируемой величины, подаваемой на вход регулятора — (рис. 7), состоящего из позиционных звеньев, с помощью специального устройства, реализующего сигнал где:
- YK — выходная величина корректирующего устройства;
- K — его коэффициент передачи.
В переходном режиме, в первый момент переходного процесса, когда значение у еще мало, значение dy/dt может быть более существенно. Увеличивая коэффициент передачи, можно получить значение
KpY+Kdydt≫KpY.
В результате регулирующей орган будет передвигаться быстрее, восстанавливая требуемое значение регулируемой величины, значение Δymax — уменьшается. При значительном увеличении К колебательность может возрасти.
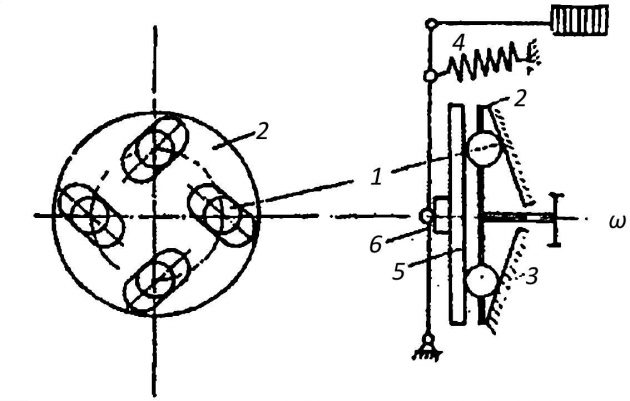
На рис. 8 представлена Элементы автоматических систем суднасхема чувствительного элемента регулятора скорости дизелей типа Д-6 и Д-12, в случае, если дизель используется для привода генераторов, когда к САР скорости вращения предъявляются высокие требования к показателям переходных процессов.
Чувствительный элемент частоты вращения — шаровые грузы 1, вращаются вместе с диском 2, приводимым во вращение от дизеля и имеющим продольные прорези, в которых могут передвигаться шары. При вращении диска шары перекатываются по неподвижной конусообразной поверхности 3 и под действием центробежных сил, приведенных к осевому направлению, преодолевают давление основной пружины 4 регулятора, воздействую-щей через рычаг 6 на тарельчатую муфту 5, прижимающую шары к неподвижной поверхности. При изменении частоты вращения баланс между центробежными силами грузов F и силой пружины изменяется и происходит передвижение муфты, вместе с ней рычага 6, передвигающего рейку топливных насосов. Прорези диска в модификации регулятора, предназначенного для ДГ, располагаются не радиально, как для варианта дизеля, работающего на винт, а под наклоном к радиусу. В этом случае при возникновении углового ускорения ε = dω/dt возникает противоположно направленная ему сила инерции шаров Fε = – mεε (где m — масса шара). Составляющая этой силы, направленная вдоль прорези — F1 вызывает передвижение шаров, также как и центробежная сила инерции F, но может действовать, опережая действие силы F, если ускорение возникнет, а изменение ω еще не произойдет.
Таким образом, передаточная функция такого чувствительного элемента (регулятора скорости прямого действия) будет иметь вид
Wp(p)=kp+kpT2ip2+T2p+1.
При точном выводе уравнения можно показать, что стремление в приведенной конструкции к увеличению действия 2-го импульса регулятора — по ускорению, величина постоянной времени Т1 растет, что нежелательно, т.к. увеличивает инерционность регулятора скорости.
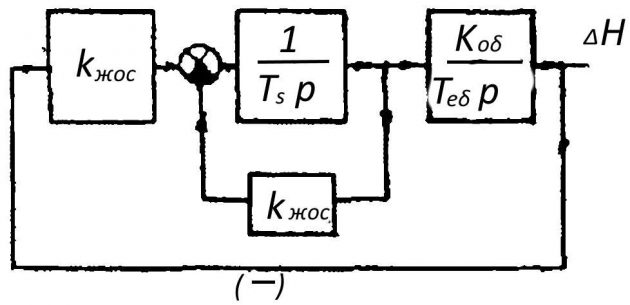
Введение внутренних жестких и гибких обратных связей. Рассмотрим влияние жесткой обратной связи на примере схемы регулирования уровня воды в емкости (см. рис. 1 Схема уровня воды).
На рис. 9 представлена структурная схема этой системы. Интегрирующее звено — сервомотор, охвачен жесткой обратной связью с коэффициентом передачи kжос = АО/ОВ, где ОА и ОВ — плечи рычага 3 (на рис. 1 Схема уровня воды).
Передаточная функция сервомотора, охваченного отрицательной обратной связью примет вид:
Ws(P)=1/Tsp1+1Tsp+kжос=1Tsp+kжос.
Интегрирующее звено, охваченное ЖОС, превратилось в инерционное. Коэффициент передачи этого звена равен 1/Kжос.
Увеличивая Kжос можно уменьшить коэффициент усиления регулятора и увеличить наклон статической характеристики САР. Запас устойчивости такой системы по модулю и фазе возрастет. Жесткие обратные связи действуют в установившихся и переходных режимах.
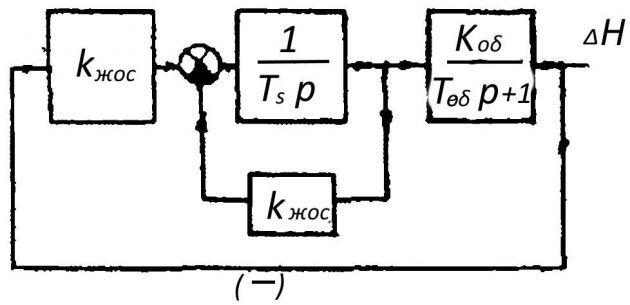
В отличие от жестких гибкие или изодромные обратные связи имеют передаточную функцию вида:
Wгос(p)=KiTiPTip+1,
и действуют только в переходных режимах, так как при Р = 0
Wгос(p)=0.
Для анализа влияния гибкой обратной на качество переходных процессов рассмотрим случай, когда величина Ti велика и поэтому в первый период переходного процесса
Tidxвыхdt≫Xвых.
Очевидно, что передаточная функция гибкой обратной связи примет виц W(р ) = Кj; т.е. в первый период переходного процесса, гибкая обратная связь действует подобно жесткой обратной связи с коэффициентом усиления Kj.
Это интерсно: Мировой Океан и океанотехника. Характеристики морских льдов, течений и волн
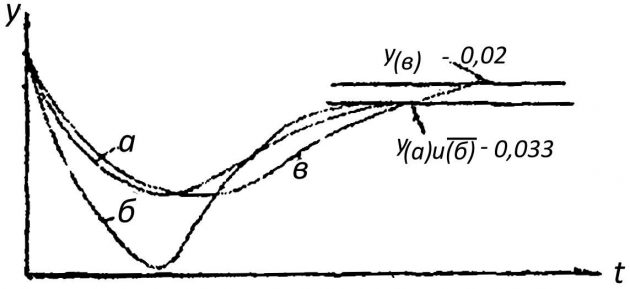
Таким образом, коэффициент усиления звена, охваченного гибкой обратной связью, временно уменьшается. Этим можно достичь уменьшения колебательности системы, без влияния на ее статизм. Однако при больших Kj может увеличиться величина перерегулирования и возрасти длительность переходного процесса (см. рис. 10, кривая 3).
1 – при отсутствии обратной связи; 2 – при включении ГОС; 3 – при значительном увеличении коэффициента усиления обратной связи
Конструкции устройств гибких обратных связей
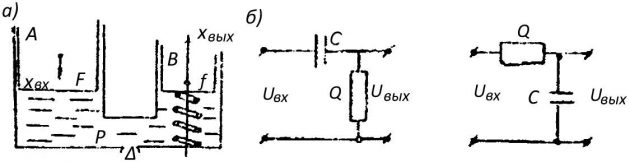
Гидравлические обратные связи. Устройство гидравлической обратной связи рассмотрим на примере изодрома — рис. 11, а. Изодром включает ведущий поршень А, ведомый поршень В, на который действует пружина, и иглу изодрома С, прикрывающую отверстие, ведущее в полость изодрома. Входной координатой xвх принимается относительное перемещение поршня А, выходной xвых — поршня В, который передает это движение последующим элементом регулятора. Очевидно, что характер движения поршня В зависит от скорости перемещения поршня А и положения иглы изодрома С. Если поршень А прекратит движение, то под действием избыточного давления или разрежения жидкость будет поступать в полость изодрома через отверстие, прикрываемое иглой С до тех пор, пока поршень В не займет положения, соответствующее разжатой пружине.
а) – гидравлической; б) – электрической, где F и f- площади поршней А и В, р – давление жидкости, а – коэффициент пропорциональности, Q – расход через отверстие
Таким образом, поршень В всегда занимает одно и то же установившееся положение.
Для случая ламинарного истечения жидкости через перепускное отверстие изодрома уравнение неразрывности имеет вид:
Q=ap=Fdxвхdt–fdxвыхdt
Если пренебречь силами гидравлического трения и передвигающихся частей, приложенных к ведомому поршеньку, которые малы по сравнению с силами давления масла, действующими на него, то уравнение его движения примет вид:
pt=cxвых,
где:
- с — Основы взаимодействия дизеля и устройств автоматического регулированияжесткость пружины ведомого поршенька.
Опуская вывод и приводя эти уравнения к относи-тельным координатам, получим:
(Tjp+1)dxвыхdt=KjTjdxвхdt,
где:
Tj=f2acc,Kj=Fxвыхномf+aKfxвыхном.
Изменением положения иглы изодромной обратной связи можно изменять ее постоянную времени: при завинчивании иглы постоянная времени увеличивается. Кроме того Tj можно изменить за счет жесткости с пружины ведомого поршенька. Увеличение коэффициента передачи изодромной обратной связи достигается за счет увеличения F/f.
Электрические гибкие и жесткие обратные связи. Гибкие и жесткие обратные связи электрического типа широко используются, например, в системах регулирования напряжения генераторов. На рис. 11, б представлена электрическая схема, состоящая из емкости С и сопротивления R. Найдем uвых = RI, где I — ток в цепи uвх = Uc + RI, где uc — падение напряжения на емкости С;
Исключив из этих уравнений uc и I, получим дифференциальное уравнение
Tduвыхdt+uвых=Tduвхdt,
где:
- T = RC.
Полученному уравнению соответствует передаточная функция гибкой обратной связи.
Таким образом, для осуществления гибкой обратной связи необходимо последовательное включение емкости и сопротивления. Такого типа связи используются, на-пример, в регуляторах напряжения генераторов со статической системой возбуждения. Электрическая жесткая обратная связь включает в себя только активное сопротивление; изменяя величину этого сопротивления, можно изменять коэффициент усиления жесткой обратной связи.
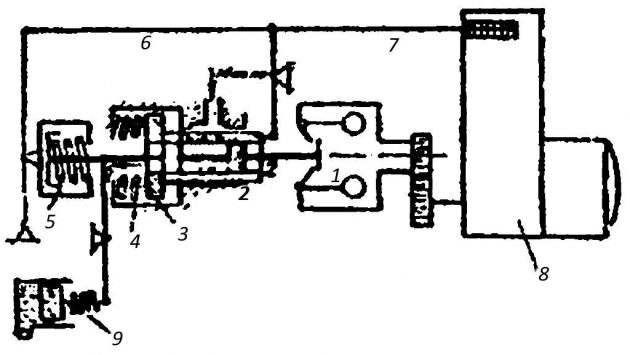
На рис. 12 представлена Основы взаимодействия дизеля и устройств автоматического регулированиясхема регулятора скорости непрямого действия двигателей типа М-401-А и др. В варианте главного судового дизеля этот всережимный регулятор (ВРН) не имеет жесткой обратной связи. В период переходного процесса грузы измерителя 1 изменяют свое положение, перемещая золотник 2. Пружина катаракта 9 временно увеличивает степень неравномерности измерителя, обеспечивая устойчивость системы. Передвижение золотника 2 приводит к тому, что масло под давлением либо попадает под сервопоршень 3, либо через то же окно во втулке сервопоршня идет на слив, в результате чего сервопоршень передвигается, следуя за золотником и перемещая рейку топливных насосов.
1 – грузы измерителя; 2 – золотник; 3 – сервомотор; 4 – пружина сервомотора; 5 – пружина измерителя; 6 – жесткая обратная связь; 7 — рычаг связи регулятора с рейкой; 8 – двигатель; 9 – пружина катаракта
При выводе передаточных функций звеньев можно ориентироваться на уже приведенном выше уравнении измерителя скорости, сервомотора, входной величиной которого является разность координат чувствительного элемента и сервомотора (η-z) и объекта регулирования — дизеля.
Передаточная функция упруго-присоединенного катаракта может быть получена из его дифференциального уравнения, которое приводится в п. VIII, 2. В передаточной функции чувствительного элемента пренебрегается влиянием T2ч и Тk из-за их малости. Кроме того, влиянием ЖОС на динамику из-за его малости также пренебрегаем.
Читайте также: Монтаж судовых двигателей внутреннего сгорания
Требуется определить показатели переходных процессов при набросе 100% нагрузки. Постоянные уравнений заданы: Система дифференциальных уравнений и передаточные функции регулятора (без ЖОС) примут вид:
Ta=2,51c, Ts=0,016c,Ti=0,037c,
δc=0,044,
δ=0,33.
- 1Уравнение и передаточная функция объекта:
Ta·p·φ=μ–λ, Wоб(p)=1Ta·p
- Уравнение чувствительного элемента
η=1δ·φ+1δc·l
- Уравнение и передаточная функция упруго присоединенного катаракта:
Tc·dldτ=η–l,Wc(p)=1Tc·p+1
- Уравнение и передаточная функция сервомотора:
Ts·pz+z=η,Wc(p)=1Ts·p+1
- Уравнение основной обратной связи:
μ=–z,
где:
- η, l, z — координаты чувствительного элемента, упруго присоединенного катаракта и сервомотора соответственно.
На рис. 13 показан график переходного процесса, полученный путем решения системы уравнений на ПЭВМ.
Сноски