Статистические гипотезы основные понятия критерии проверки ошибки при проверке гипотез - Исправление ошибок и поиск оптимальных решений проблем

5.1 Основные понятия, используемые при проверке гипотез

5.1.1 Статистические гипотезы

Статистическая
гипотеза – любое предположение,
касающееся неизвестного распределения
случайных величин (элементов),
соответствующее некоторым представлениям
об изучаемом явлении. В частном случае
это может быть утверждение о значениях
параметров распределения генеральной
совокупности.

Различают
нулевую и альтернативную гипотезы.
Нулевая гипотеза – гипотеза, подлежащая
проверке. Альтернативная гипотеза –
каждая допустимая гипотеза, отличная
от нулевой. Нулевую гипотезу обозначают
Н₀,
альтернативную
–
Н₁
(от
Hypothesis – «гипотеза» (англ.)).

Конкретная
задача проверки статистической гипотезы
полностью описана, если заданы нулевая
и альтернативная гипотезы. При обработке
реальных данных большое значение имеет
правильный выбор гипотез. Принимаемые
предположения, например, нормальность
распределения, должны быть тщательно
обоснованы, в частности, статистическими
методами. Необходимо помнить, что в
подавляющем большинстве конкретных
прикладных задач распределение
результатов наблюдений в той или иной
степени отлично от нормального.

5.1.2 Уровень значимости и мощность критерия. Ошибки при проверке гипотез

При
проверке статистической гипотезы
возможны ошибки. Есть два рода ошибок.

Ошибка
первого рода заключается в том, что
отвергают нулевую гипотезу, в то время
как в действительности эта гипотеза
верна. Вероятность ошибки первого рода
называется уровнем значимости и
обозначается α.

Ошибка
второго рода состоит в том, что принимают
нулевую гипотезу, в то время как в
действительности эта гипотеза неверна.

Обычно
используют не вероятность ошибки второго
рода, а ее дополнение до 1. Эта величина
носит название мощности критерия. Итак,
мощность критерия – это вероятность
того, что нулевая гипотеза будет
отвергнута, когда альтернативная
гипотеза верна.

Понятия
уровня значимости и мощности критерия
объединяются в понятии функции мощности
критерия – функции, определяющей
вероятность того, что нулевая гипотеза
будет отвергнута.

Наглядным
способом интерпретации ошибок является
их графическое представление.

Предположим,
что проверяется гипотеза Н0:
о равенстве среднего значения генеральной
совокупности заданной величине(известной, например, из предыдущих
экспериментов).

Для
этого берется выборка объема n, находится
ее среднее арифметическое
и по его величине судят о справедливости
гипотезы Н0.

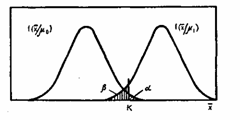
Распределение
среднего арифметического
при условии, что верна гипотеза Н0, будет.
Это распределение качественно представлено
на рис. 4.1.

Распределение
среднего арифметического
при условии, что верна альтернативная
гипотеза Н1:,
буде уже другим —.

Будем
считать, что гипотеза Н0 отвергается,
если выборочное среднее арифметическое
окажется больше некоторого критического
значения, т. е.,
как показано на рис.

Рис.
6.1. Ошибки первого и второго рода

Область
непринятия гипотезы Н0 называется
критической областью критерия. Она
показана па рисунке наклонной штриховкой.
Уровень значимости будет соответствовать
площади критической области.

Вероятность
ошибки второго рода
будет равна площади под кривой
распределения,
показанной на рисунке. вертикальной
штриховкой.

Величина
называется мощностью критерия.

Исследователь
всегда должен формулировать гипотезу
и задавать уровень значимости до
получения экспериментальных данных,
по которым эта гипотеза будет проверяться.

При
выборе уровня значимости исследователь
исходит из практических соображений,
отвечая на вопрос: какую вероятность
ошибки он считает допустимой для его
конкретной задачи?

Обычно
считают достаточным уровень значимости
0,05 (5%), иногда 1% или 10%, редко 0,1%.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

План:

1. Статистические гипотезы. Основные понятия.

2. Гипотезы о законе распределения.

3. Гипотезы о числовом значении генерального
среднего и дисперсии.

1.
Статистические гипотезы. Основные понятия.

Статистическая гипотеза— это утверждение о виде неизвестного
распределения или параметрах известного распределения. Статистические гипотезы
проверяются по результатам выборки статистическими методами в ходе эксперимента
(эмпирическим путем) с помощью статистических критериев.

В тех случаях, когда
известен закон, но неизвестны значения его параметров (дисперсия или
математическое ожидание) в конкретной ситуации, статистическую гипотезу
называют параметрической.

Например, предположение
об ожидаемом среднем доходе по акциям или разбросе дохода являются
параметрическими гипотезами.

Когда закон
распределения генеральной совокупности не известен, но есть основания
предположить, каков его конкретный вид, выдвигаемые гипотезы о виде его
распределения называются непараметрическими.

Например, можно
выдвинуть гипотезу, что число дневных продаж в магазине или доход населения
подчинены нормальному закону распределения.

По содержанию статистические гипотезы можно классифицировать:

1.
Гипотезы о типе вероятностного закона
распределения случайной величины, характеризующего явление или процесс.

2.
Гипотезы об однородности двух или более
обрабатываемых выборок. Изучаемое свойство исследуется с помощью двух или более генеральных
совокупностей. Гипотеза в этом случае может заключаться в следующем: исследуемые
выборочные характеристики различаются между собой статистически значимо или
нет.

3.
Гипотезы о свойствах числовых значений
параметров исследуемой генеральной совокупности. Больше ли значения параметров
некоторого заданного номинала или меньше и т.д.

4.
Гипотезы о вероятностной зависимости двух
или более признаков, характеризующих различные свойства рассматриваемого
явления или процесса. При этом определяется характер этой зависимости.

Гипотезы бывают простые (содержащие одно предположение) и сложные (содержащие несколько предположений).

Выдвинутую гипотезу называют основной или нулевой и обозначают H₀
. Противоречащую ей гипотезу называют альтернативной или конкурирующей и обозначают
H₁.

Под статистическим
критерием понимают однозначно определенное правило, устанавливающее
условие, при котором проверяемая гипотеза отвергается либо не отвергается.

Пример:

Увеличение числа заболевших некоторым
заболеванием дает возможность выдвинуть гипотезу о наличии эпидемии. Для сравнения
доли заболевших в обычных и экстремальных условиях используются статистические
данные, на основании которых делается вывод о том, является ли данное массовое
заболевание эпидемией. Предполагается, что существует некоторый критерий-
уровень доли заболевших, критический для этого заболевания, который
устанавливается по ранее имевшимся случаям.

Различают три вида критериев:

1.
Параметрические критерии—
критерии значимости, которые служат для проверки гипотез о параметрах
распределения генеральной совокупности при известном виде распределения.

2.
Критерии согласия—
позволяют проверить гипотезы о соответствии распределений генеральной
совокупности известной теоретической модели.

3.
Непараметрические критерии—
используются в гипотезах, когда не требуется знаний о конкретном виде
распределения.

Проверка
параметрических гипотез проводится на основе критериев значимости., а
непараметрических- критериев согласия.

Задача проверки
статистических гипотез сводится к исследованию генеральной совокупности по
выборке. Множество возможных значений элементов выборки может быть разделено на
два непересекающихся подмножества- критическую область и область принятия
гипотезы.

Областью принятия гипотезы или областью допустимых значений I_доп

называют совокупность значений критерия,
при которых эту гипотезу принимают.

Критической областью
I_кр называют множество значений критерия, при
котором гипотезу отвергают.

Наблюдаемые значения критерия (статистика)
K_набл
называют такое значение критерия, которое
находится по данным выборки.

Границы критической области, отделяющие ее от
области принятия гипотезы, называют критическими точками и обозначают
K_кр.

Для определения
критической области задается уровень значимости
—
некая малая вероятность попадания критерия в критическую область.

Уровень значимости— вероятность принятия
конкурирующей гипотезы, тогда как справедлива основная.

С помощью уровня
значимости определяются границы критической области.

Основной принцип проверки статистических гипотез
состоит в следующем: если наблюдаемое значение статистики критерия попадает (не
попадает) в критическую область, то гипотеза H₀

отвергается (принимается), а гипотеза H₁

принимается (отвергается) в качестве одного из
возможных решений с формулировкой «гипотеза
H₀ противоречит (не противоречит) выборочным
данным на уровне значимости
».

В зависимости от
содержания альтернативной гипотезы осуществляется выбор критической области:
левосторонней, правосторонней, двусторонней. Если смысл исследования заключается
в доказательстве конкретного изменения наблюдаемого параметра (его уменьшения
или увеличения), то говорят об односторонней критической области. Если смысл
исследования- выявить различия в изучаемых параметрах, но характер их
отклонения от контрольных (или теоретических) не известен, то говорят о
двусторонней критической области.

Однако, принятие той
или иной гипотезы не дает оснований утверждать, что она верна. Результат
проверки статистической гипотезы лишь устанавливают на определенном уровне
значимости ее соответствие (несоответствие) результатам эксперимента.

При проверке
статистических гипотез возможны следующие ошибки:

1.
Отвергнута правильная
H₀, а принята неправильная гипотеза
H₁ — ошибка
первого рода.

2. Отвергнута правильная альтернативная
гипотеза
H₁ и
принята неправильная нулевая гипотеза H₀
—
ошибка второго рода.

Заметим, что уровень значимости —
есть вероятность ошибки первого рода. Ошибка первого рода называется
-риском. Обычно они задаются
некоторыми конкретными значениями: 0,05; 0,01; 0,005; 0,001. Ошибки второго
рода называются -риском, а вероятность ее
допустить обозначается
(вероятность того, что принята гипотеза
H₀
, когда на самом деле справедлива
альтернативная гипотеза H₁
.

Можно доказать, что с
уменьшением ошибок первого рода одновременно увеличиваются ошибки второго рода
и наоборот. Поэтому, на практике пытаются подбирать значения параметров
и
опытным путем в целях минимизации суммарного
эффекта от возможных ошибок. При принятии управленческих решений для
одновременного уменьшения ошибок первого и второго рода самым действенным
средством является увеличение объема выборки, что согласуется с законом больших
чисел.

На бытовом уровне
ошибки второго рода могут иметь более трагические последствия, чем ошибки
первого рода.

2. Гипотеза о законе распределения. Критерий согласия Пирсона (
X²
-критерий).

Критериями согласия называют критерии, в
которых гипотеза определяет закон распределения либо полностью, либо с
точностью до небольшого числа параметров.

Причины расхождения
результатов эксперимента и теоретических характеристик могут быть вызваны малым
объемом выборки, неудачным способом группировки наблюдений, ошибками в
выборе гипотезы о виде распределения
генеральной совокупности и др.

Рассмотрим
универсальный критерий согласия Пирсона. Проверка гипотезы о том, что
эмпирическая частота мало отличается от соответствующей теоретической частоты,
осуществляется с помощью величины X²
—
меры расхождения между ними.

Для произвольной
выборки, когда распределение непрерывно или число различных вариант велико, все
пространство наблюдаемых вариант делят на конечное число непересекающихся
областей, в каждой из которых подсчитывают наблюдаемую частоту и теоретическую
вероятность.

Для применения критерия
согласия Пирсона необходимо:

1. Вычислить значение статистики по формуле:
, где
p_i –вероятность
принятия значения
x_i, n_i.
— эмпирическая частота для
соответствующего
x_i. n— объем выборки. s— число вариант выборки.

2.
По
соответствующей таблице распределения Пирсона найти критическое значение , где k = s –
r
– 1 – число степеней свободы, s—
число различных вариант или интервалов группировки, r— число неизвестных параметров
предполагаемого теоретического распределения,
— выбранный уровень значимости. Это
значит, что строится правосторонний интервал.

3.
Если
,
то основная гипотеза отвергается, в противном случае- принимается, т.е. чем
больше отклонение, тем меньше согласованы теоретическое и эмпирическое
распределение. Поэтому принято использовать только правостороннюю критическую
область.

Расчетная таблица имеет вид:

Интервалы

Середины
i-го
интервала x_i

Эмпирические
частоты n_i

Вероятности p_i

Теоретические
частоты np_i

Пример:

По таблице
эмпирического распределения изменения в процентах темпа роста акций проверьте
гипотезу о нормальном распределении выборки.

Интервалы	(-2; -1)	(-1; 0)	(0; 1)	(1; 2)	Итого
n_i	7	14	18	11	50
p_i	0,157	0,341	0,341	0,157	1

Решение:

Гипотезу о нормальном
распределении проверим по критерию Пирсона.

Интервалы	Эмпирические частоты n_i	Вероятности p_i	Теоретические частоты np_i
(-2; -1)	7	0,157	7,85	0,7225	0,092
(-1; 0)	14	0,341	17,05	9,3025	0,546
(0; 1)	18	0,341	17,05	0,9025	0,053
(1; 2)	11	0,157	7,85	9,925	1,264
Итого					=1,955

По таблице найдем
при =0,05
и k = s – r – 1 = 4 – 2 – 1 = 1. s = 4 – число
интервалов. r
= 2- число параметров теоретического (нормального) распределения.

Имеем . Т.к. 1,955 < 3,841, то
, т.е. гипотеза о нормальном
распределении подтверждается.

3. Гипотезы о числовом значении генерального
среднего и дисперсии.

Установление двусторонней критической
области на уровне значимости
для
проверки гипотезы соответствует отысканию соответствующего доверительного
интервала с надежностью
.

Рассмотрим условия применения некоторых
статистических гипотез.

Тип гипотезы H₀	Границы критической области на уровне значимости	Статистика наблюдений
О числовом значении генерального среднего нормального распределения M(X) = m = , с известным среднеквадратическим отклонением.
О числовом значении генерального среднего нормального распределения M(X) = m = m₀, с неизвестной среднеквадратическим отклонением	Распределение Стьюдента
О числовом значении дисперсии нормального распределения , или	Распределение Пирсона

Пример:

Результаты исследований в течение 35 лет
показали, что среднее изменение доходности векселей равно 5,5 %. Полагая, что
изменение доходности подчиняется нормальному закону распределения с
среднеквадратическим отклонением равным 2 %, на уровне значимости
, решите: можно ли принять 6 % в качестве нормативного процента
(математического ожидания) изменения доходности.

Решение:

По условию задачи
нулевая гипотеза
. Так как
, то в качестве альтернативной гипотезы
возьмем гипотезу:
, которой соответствует левосторонняя
критическая область с интервалом.

Найдем границы
критической области:

По таблице значений
функции Ф(х) найдем
, т.е. левосторонняя критическая область
лежит в интервале.

Найдем статистику
наблюдений:
.

Имеем:, нет основания отвергать нулевую
гипотезу. Значит, в качестве нормативного процента можно принять 6 %.

Пример:

Точность работы
программы проверяют по дисперсии контролируемого количества символов в коде,
которая не должна превышать 0,1. По выборке из 15 сообщений вычислена
исправленная оценка дисперсии 0,22. При
уровне значимости 0,05 проверьте, обеспечивает ли программа необходимую
точность.

Решение:

Имеем: n = 15, s² = 0,22
, ,
.

Сформулируем гипотезу о
числовом значении дисперсии:

H₀ — программа обеспечивает необходимую точность
;

H₁ —
программа не обеспечивает необходимую точность
.

Определим статистику: .

Найдем границы
критической области:
.

Поскольку 30,8 >
23,7;
, принимаем гипотезу H₁, т.к.
H₀ противоречит опытным данным. Вывод: программа
не обеспечивает необходимую точность.

Источник

Критерии проверки статистических гипотез

Понятие статистической гипотезы

Статистической гипотезой (гипотезой) называется любое утверждение об изучаемом законе распределения или характеристиках случайных величин.

Пример статистических гипотез:

Генеральная совокупность распределена по нормальному закону.
Дисперсии двух нормально распределенных совокупностей равны между собой.

Нулевая гипотеза (Н₀) — предположение о том, что между параметрами генеральных совокупностей нет различий, то есть эти различия носят не систематический, а случайный характер.

Пример1. Нулевая гипотеза записывается следующим образом:

H₀: µ₁=µ₂ (нулевая гипотеза заключается в том, что генеральное среднее одной совокупности равно генеральному среднему другой совокупности).

Альтернативная гипотеза (Н₁) – предположение о том, что между параметрами генеральных совокупностей есть достоверные различия.

Пример 2. Альтернативные гипотезы записываются следующим образом:

H₁: µ₁_≠µ₂ (нулевая гипотеза заключается в том, что генеральное среднее одной совокупности не равно генеральному среднему другой совокупности).
H₁: µ₁>µ₂(нулевая гипотеза заключается в том, что генеральное среднее одной совокупности больше генерального среднего другой совокупности).
H₁: µ_1<µ₂(нулевая гипотеза заключается в том, что генеральное среднее одной совокупности меньше генерального среднего другой совокупности).

Ошибки при проверке гипотез

Ошибки, допускаемые при проверке статистических гипотез, делятся на два типа:

ошибки первого рода;
ошибки второго рода.

Ошибка первого рода – отклонение гипотезы Н₀, когда она верна. Вероятность ошибки первого рода обозначается α и называется уровнем значимости.

Ошибка второго рода – принятие гипотезы Н₀, когда верна альтернативная гипотеза. Вероятность ошибки второго рода обозначается β.

Классификация критериев значимости (критериев проверки статистических гипотез)

Для проверки правдоподобия статистической гипотезы используют критерий значимости – метод проверки статистической гипотезы.

Необходимо отметить, что до получения исследователем экспериментальных данных необходимо сформулировать статистическую гипотезу и задать уровень значимости α. При выборе уровня значимости исследователь должен исходить из практических соображений, отвечая на вопрос: какую вероятность ошибки он считает допустимой. В области физической культуры и спорта чаще всего задают уровень значимости α=0,05.

Критерии проверки статистических гипотез (критерии значимости) можно разделить на три большие группы:

Критерии согласия;
Параметрические критерии;
Непараметрические критерии.

Критерии согласия называются критерии значимости, применяемые для проверки гипотезы о законе распределения генеральной совокупности, из которой взята выборка. Для проверки статистической гипотезы чаще всего используются следующие критерии согласия: критерий Шапиро-Уилки, критерий хи-квадрат, критерий Колмогорова-Смирнова.

Параметрические критерии – критерии значимости, которые служат для проверки гипотез о параметрах распределений (чаще всего нормального). Такими критериями являются: t-критерий Стьюдента (независимые выборки), t-критерий Стьюдента (связанные выборки), F-критерий Фишера (независимые выборки).

Непараметрические критерии – критерии значимости, которые для проверки статистических гипотез не использует предположений о распределении генеральной совокупности. В качестве примера таких критериев можно назвать критерий Манна-Уитни и критерий Вилкоксона.

Литература

Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.

Источник

В современном мире мы обладаем все большим и большим объемом данных о событиях, происходящих вокруг. Зачастую у нас появляются вопросы, на которые хотелось бы быстро ответить на основе имеющейся информации, для этого как нельзя лучше подходит процесс, связанный с проверкой статистических гипотез. Однако, многие считают, что это занятие подразумевает под собой большое число вычислений и в принципе довольно сложно для понимания. На самом деле, алгоритм проверки гипотез достаточно прост, а для осуществления расчетов с каждым годом появляется все больше и больше готовых инструментальных средств, не требующих от человека глубоких познаний в области. Далее я попытаюсь показать, что мало того, что процесс проверки гипотез может быть полезным, так и осуществляется достаточно быстро и без серьезных усилий.

Статистические гипотезы и области их применения

Статистическая гипотеза — это предположение о каких-либо характеристиках случайной величины. Например: существенно ли изменение числа AI-стартапов в Европе в два разных года и т. д.

Проверка статистических гипотез является важнейшим классом задач математической статистики. С помощью данного инструмента можно подтвердить или отвергнуть предположение о свойствах случайной величины путем применения методов статистического анализа для элементов выборки. Если в предыдущем предложении какие-либо термины являются не совсем понятными, ниже можно найти пояснение на простом языке.

Случайная величина — это величина, которая в зависимости от той или иной ситуации принимает конкретные значения с определенными вероятностями. Примеры: отметка на экзамене; результат игры в кости; количество AI-стартапов по странам Европы. В общем, почти все что угодно!

Генеральная совокупность — совокупность всех объектов для анализа. Например: все AI-стартапы в Европе в 2019-м году.

Выборка — часть данных из генеральной совокупности. Например: официально зарегистрированные AI-стартапы в некоторых странах Европы в 2019-м году.

Статистический анализ — использование различных методов для того, чтобы определить свойства генеральной совокупности по выборке.

Для проверки статистических гипотез зачастую применяются статистические тесты, о которых будет рассказано далее.

Алгоритм проверки статистической гипотезы

В обобщенном виде алгоритм выглядит таким образом:

Формулировка основной (H0) и альтернативной (H1) гипотез
Выбор уровня значимости
Выбор статистического критерия
Определения правила принятия решения
Итоговое принятие решения на основе исходной выборки данных

Данные шаги являются унифицированными и схему можно использовать почти во всех случаях. Далее подробнее рассмотрим пример работы данного алгоритма на конкретных данных.

Пример проверки статистической гипотезы

Итак, как вы, наверное, догадались по вышеприведенным примерам, будем проверять гипотезу о том, что имеется существенное различие между числом созданных европейских AI-стартапов в 2019-м и 2020-м годах. Пример достаточно простой, чтобы было проще разобраться в ходе работы алгоритма.

Рисунок 1 — исходные данные

Сначала обратим внимание на исходную выборку (рис. 1): датасет представлен для 30-ти Европейских стран, внесены только официально зарегистрированные в стране стартапы. Данные количественные по двум годам. Стоит отметить, что выборки — парные, то есть мы наблюдаем один и тот же показатель для одних и тех же стран с разницей в год.

Сразу стоит отметить, что будут проверены две статистические гипотезы подряд. Для того, чтобы применять критерий для сравнения средних выборок двух лет нужно сначала определить закон распределения данных. Таким образом, шаг 1 — проверка статистической гипотезы о законе распределения данных. Шаг 2 — проверка статистической гипотезы о равенстве между средними.

Проверка гипотезы о законе распределения

Для данных 2019-го года проверим нормальность распределения.

H0: случайная величина распределена нормально

H1: случайная величина не распределена нормально
Пусть уровень значимости alpha = 0.05 (как и в 95-ти процентах статистических тестов). Определение уровня значимости достойно отдельного поста, так что не будем заострять на нем внимание.
Будет использован критерий Шапиро-Уилка.
На этом шаге необходимо разобраться, как работает критерий. В данном случае рассчитывается следующая статистика — функция от нашей выборки:

$W=frac{{{b}^{2}}}{{{S}^{2}}}$ , ${{S}^{2}}={{sumlimits_{i=1}^{n}{({{X}_{i}}-overline{X})}}^{2}}$ , $b=sumlimits_{i=1}^{k}{{{a}_{n,i}}}({{X}_{(n-i+1)}}-{{X}_{(i)}})$ , ;

Как видно, формула не слишком простая, плюс существует непростой механизм определения параметра a, поэтому в таких случаях проще пользоваться онлайн-калькуляторами для расчета статистики. Я, например, воспользуюсь хорошим статистическим онлайн-ресурсом — https://www.statskingdom.com/320ShapiroWilk.html.

Итак, калькулятор показал нам, что p-value = 1.20005e-9 , W = 0.435974; Что же делать дальше? Есть два варианта:

Можно сравнить статистику W с критическим значением Wкрит. Критическое значение чаще всего приведено в готовых таблицах (по строкам/столбцам там отмечен объем выборки и уровень значимости, а на пересечении как раз-таки и лежит Wкрит.). Если W>Wкрит., то не отвергаем H0 и наоборот. Но это не очень удобно, поэтому чаще используется второй способ.

Можно сравнить p-value с alpha (выбран на 2-ом шаге). Если p-value < alpha, то отвергаем H0. Если нет, то НЕ отвергаем H0. В нашем случае p-value < alpha, следовательно с 95%-ой уверенностью отвергаем H0.
H0 отклонена, распределение выборочных данных за 2019-й год не подчинено нормальному закону распределения.

Для данных 2020-го года проверим нормальность распределения. Здесь шаги абсолютно те же самые. Получилось, что p-value = 3.41343e-9. Значение p-value < alpha, следовательно отвергаем H0.

Таким образом, значения в обеих выборках распределены не нормально. Для сравнения средних в двух годах будем использовать критерий Вилкоксона.

Проверка гипотезы о различии в числе AI-стартапов в европейских странах для 2019-го и 2020-го годов

H0: отсутствует статистически значимое различие между числом AI-стартапов в Европе в двух годах.

H1: признается статистическая значимость изменения показателя числа AI-стартапов в Европе между 2019-м и 2020-м годами.
Пусть уровень значимости alpha = 0.05.
Будет использован критерий Вилкоксона.
На этом шаге необходимо разобраться, как работает критерий. Безусловно, для данного критерия также существуют онлайн-калькуляторы, но его достаточно просто посчитать и вручную. Алгоритм очень прост:

Шаг 1 — Для каждой страны нужно вычислить разность между значениями двух лет.

Шаг 2 — Далее понять, какие из разностей являются типичными, то есть соответствуют преобладающему по частоте направлению изменения показателя.

Шаг 3 — Далее в порядке возрастания проранжировать разности пар по их абсолютным значениям. Меньшему абсолютному значению разности приписывается меньший ранг.

Шаг 4 — Рассчитать сумму рангов, соответствующих нетипичным сдвигам. Это и будет значением T-критерия.

Пример расчета для двенадцати стран приведен на рисунке ниже (рис. 2). Не пугайтесь, приведенные ранги рассчитаны по всем 30-ти элементам выборки, двенадцать стран приведены лишь для иллюстрации. Проведя такой расчет по всем 30-ти странам и сложив ранги для стран с нетипичными изменениями, получилось, что T = 28.

Сравним T и Tкрит.=163. T < Tкрит, значит с 95-ой уверенностью изменение числа стартапов статистически значимо.
H0 отвергается, различия между числом европейских AI-стартапов в 2019-м и 2020-м годах существенны.

Рисунок 2 — пример расчета критерия Вилкоксона

Разнообразие статистических критериев

Как мы увидели на примере, важным шагом в проверке статистической гипотезы является выбор критерия. В примере выше я использовала лишь два статистических критерия, но по факту их гораздо больше, так сказать, на все случаи жизни. Данные критерии важно знать и четко нужно осознавать, когда и какой можно применить. Многие из них направлены на сравнение центров распределений случайных величин, например, сравнение средних, медиан, равенство параметра распределения какому-либо числу и т. д. В основном они делятся на параметрические (знаем закон распределения случайной величины) и непараметрические.

Для вашего удобства внизу (рис. 3) приведена таблица с основными, с моей точки зрения, критериями сравнения центров распределения и их классификацией. Надеюсь, она будет вам полезна, ее можно дополнять и расширять по вашему желанию.

Рисунок 3 — классификация статистических критериев

Источник