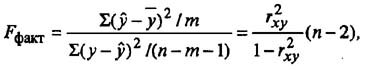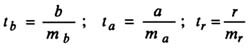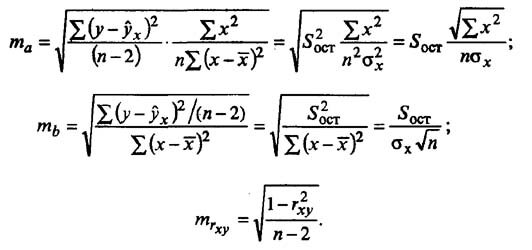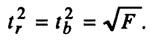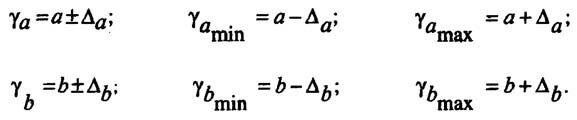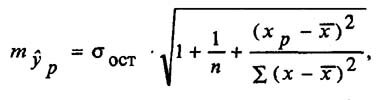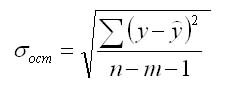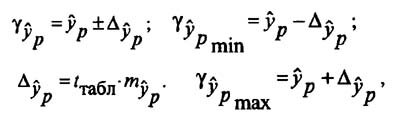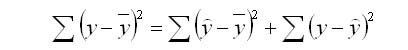Сумма квадратов ошибок формула - Исправление ошибок и поиск оптимальных решений проблем

Линейная регрессия используется для поиска линии, которая лучше всего «соответствует» набору данных.

Мы часто используем три разных значения суммы квадратов , чтобы измерить, насколько хорошо линия регрессии действительно соответствует данным:

1. Общая сумма квадратов (SST) – сумма квадратов разностей между отдельными точками данных (y i ) и средним значением переменной ответа ( y ).

SST = Σ(y i – y ) 2

2. Регрессия суммы квадратов (SSR) – сумма квадратов разностей между прогнозируемыми точками данных (ŷ i ) и средним значением переменной ответа ( y ).

SSR = Σ(ŷ i – y ) 2

3. Ошибка суммы квадратов (SSE) – сумма квадратов разностей между предсказанными точками данных (ŷ i ) и наблюдаемыми точками данных (y i ).

SSE = Σ(ŷ i – y i ) 2

Между этими тремя показателями существует следующая зависимость:

SST = SSR + SSE

Таким образом, если мы знаем две из этих мер, мы можем использовать простую алгебру для вычисления третьей.

SSR, SST и R-квадрат

R-квадрат , иногда называемый коэффициентом детерминации, является мерой того, насколько хорошо модель линейной регрессии соответствует набору данных. Он представляет собой долю дисперсии переменной отклика , которая может быть объяснена предикторной переменной.

Значение для R-квадрата может варьироваться от 0 до 1. Значение 0 указывает, что переменная отклика вообще не может быть объяснена предикторной переменной. Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.

Используя SSR и SST, мы можем рассчитать R-квадрат как:

R-квадрат = SSR / SST

Например, если SSR для данной модели регрессии составляет 137,5, а SST — 156, тогда мы рассчитываем R-квадрат как:

R-квадрат = 137,5/156 = 0,8814

Это говорит нам о том, что 88,14% вариации переменной отклика можно объяснить переменной-предиктором.

Расчет SST, SSR, SSE: пошаговый пример

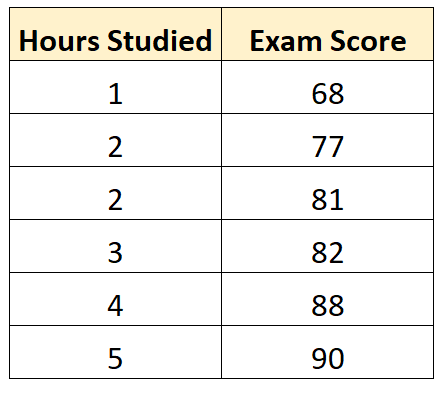
Предположим, у нас есть следующий набор данных, который показывает количество часов, отработанных шестью разными студентами, а также их итоговые оценки за экзамены:

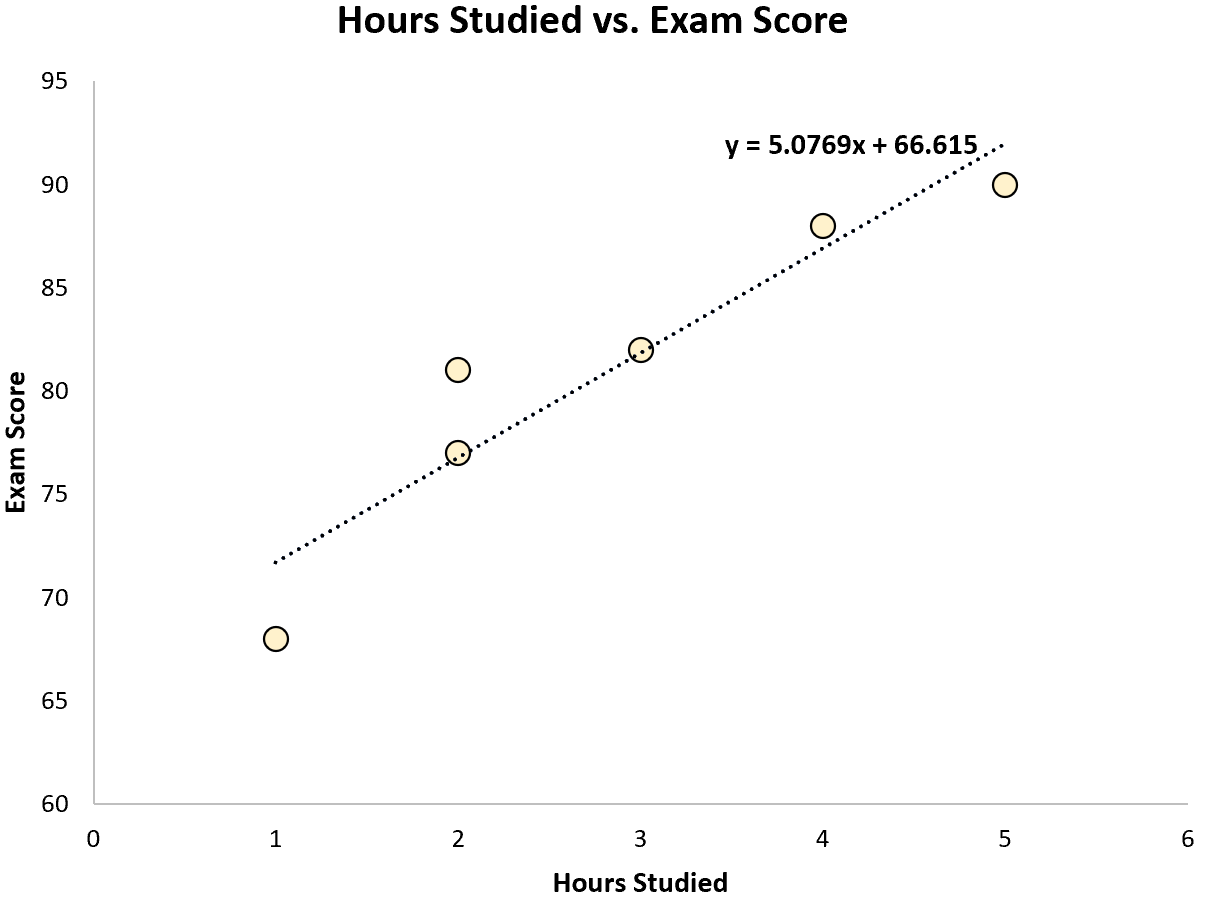
Используя некоторое статистическое программное обеспечение (например, R , Excel , Python ) или даже вручную , мы можем найти, что линия наилучшего соответствия:

Оценка = 66,615 + 5,0769 * (часы)

Как только мы узнаем строку уравнения наилучшего соответствия, мы можем использовать следующие шаги для расчета SST, SSR и SSE:

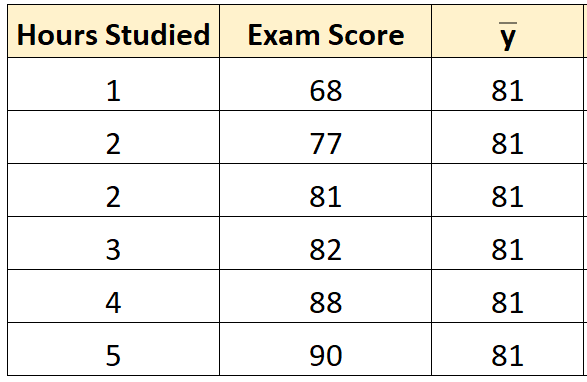
Шаг 1: Рассчитайте среднее значение переменной ответа.

Среднее значение переменной отклика ( y ) оказывается равным 81 .

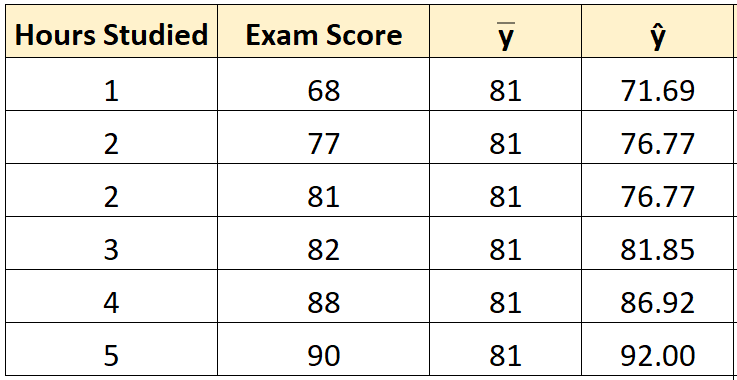
Шаг 2: Рассчитайте прогнозируемое значение для каждого наблюдения.

Затем мы можем использовать уравнение наилучшего соответствия для расчета прогнозируемого экзаменационного балла () для каждого учащегося.

Например, предполагаемая оценка экзамена для студента, который учился один час, такова:

Оценка = 66,615 + 5,0769*(1) = 71,69 .

Мы можем использовать тот же подход, чтобы найти прогнозируемый балл для каждого ученика:

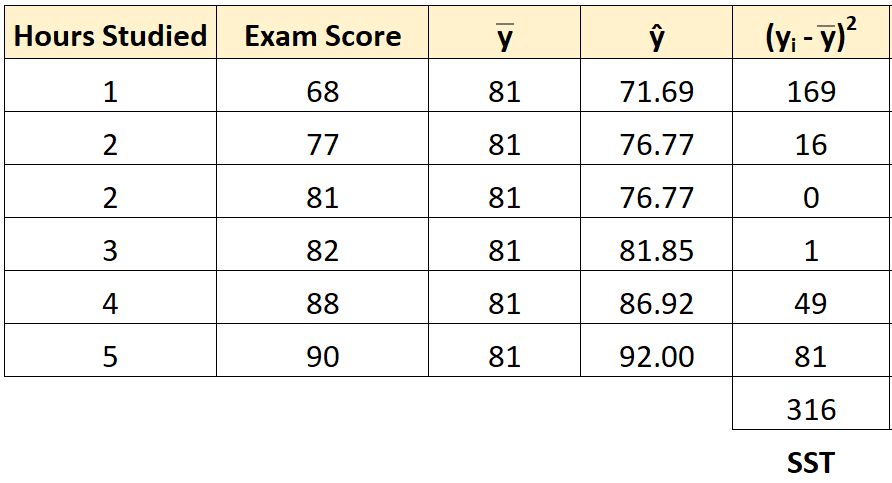
Шаг 3: Рассчитайте общую сумму квадратов (SST).

Далее мы можем вычислить общую сумму квадратов.

Например, сумма квадратов для первого ученика равна:

(y i – y ) 2 = (68 – 81) 2 = 169 .

Мы можем использовать тот же подход, чтобы найти общую сумму квадратов для каждого ученика:

Сумма квадратов получается 316 .

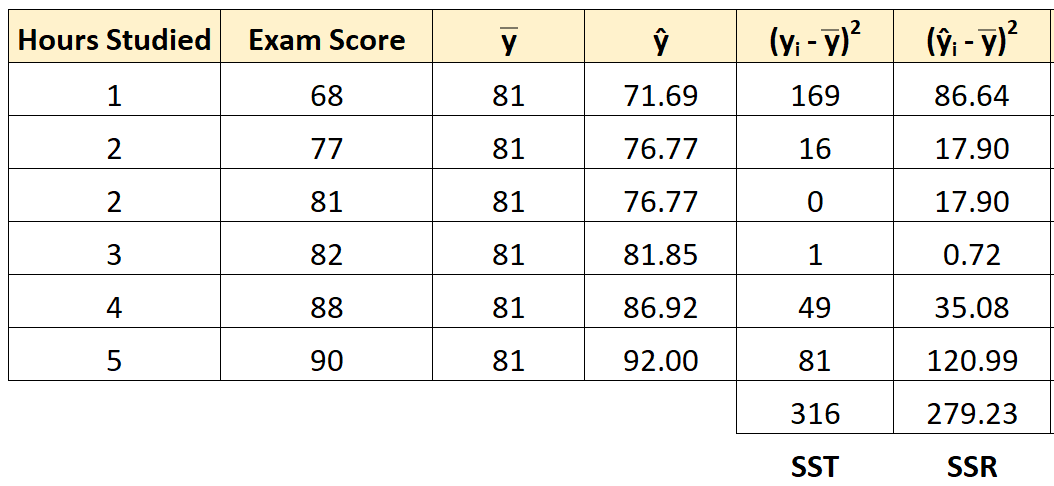
Шаг 4: Рассчитайте регрессию суммы квадратов (SSR).

Далее мы можем вычислить сумму квадратов регрессии.

Например, сумма квадратов регрессии для первого ученика равна:

(ŷ i – y ) 2 = (71,69 – 81) 2 = 86,64 .

Мы можем использовать тот же подход, чтобы найти сумму квадратов регрессии для каждого ученика:

Сумма квадратов регрессии оказывается равной 279,23 .

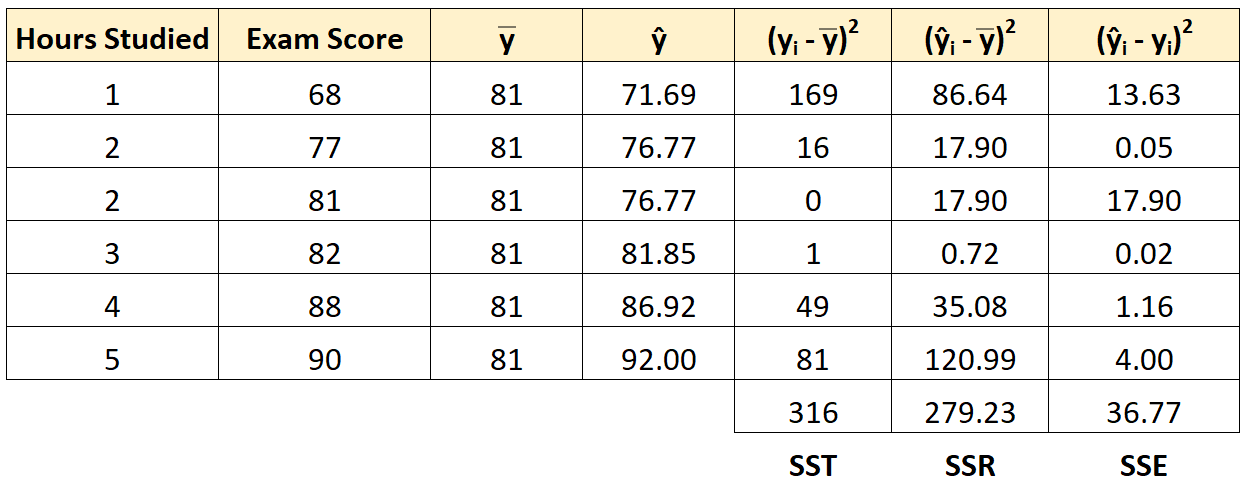
Шаг 5: Рассчитайте ошибку суммы квадратов (SSE).

Далее мы можем вычислить сумму квадратов ошибок.

Например, ошибка суммы квадратов для первого ученика:

(ŷ i – y i ) 2 = (71,69 – 68) 2 = 13,63 .

Мы можем использовать тот же подход, чтобы найти сумму ошибок квадратов для каждого ученика:

Мы можем проверить, что SST = SSR + SSE

SST = SSR + SSE
316 = 279,23 + 36,77

Мы также можем рассчитать R-квадрат регрессионной модели, используя следующее уравнение:

R-квадрат = SSR / SST
R-квадрат = 279,23/316
R-квадрат = 0,8836

Это говорит нам о том, что 88,36% вариаций в экзаменационных баллах можно объяснить количеством часов обучения.

Дополнительные ресурсы

Вы можете использовать следующие калькуляторы для автоматического расчета SST, SSR и SSE для любой простой линии линейной регрессии:

Калькулятор ТПН
Калькулятор ССР
Калькулятор SSE

Источник

Download Article

The sum of squared errors, or SSE, is a preliminary statistical calculation that leads to other data values. When you have a set of data values, it is useful to be able to find how closely related those values are. You need to get your data organized in a table, and then perform some fairly simple calculations. Once you find the SSE for a data set, you can then go on to find the variance and standard deviation.

1

Create a three column table. The clearest way to calculate the sum of squared errors is begin with a three column table. Label the three columns as , , and ${text{Deviation}}^{2}$ .^[1]
2
Fill in the data. The first column will hold the values of your measurements. Fill in the column with the values of your measurements. These may be the results of some experiment, a statistical study, or just data provided for a math problem.^[2]
- In this case, suppose you are working with some medical data and you have a list of the body temperatures of ten patients. The normal body temperature expected is 98.6 degrees. The temperatures of ten patients are measured and give the values 99.0, 98.6, 98.5, 101.1, 98.3, 98.6, 97.9, 98.4, 99.2, and 99.1. Write these values in the first column.
Advertisement
3

Calculate the mean. Before you can calculate the error for each measurement, you must calculate the mean of the full data set.^[3]
4
Calculate the individual error measurements. In the second column of your table, you need to fill in the error measurements for each data value. The error is the difference between the measurement and the mean.^[4]
- For the given data set, subtract the mean, 98.87, from each measured value, and fill in the second column with the results. These ten calculations are as follows:
5
Calculate the squares of the errors. In the third column of the table, find the square of each of the resulting values in the middle column. These represent the squares of the deviation from the mean for each measured value of data.^[5]
- For each value in the middle column, use your calculator and find the square. Record the results in the third column, as follows:
6
Add the squares of errors together. The final step is to find the sum of the values in the third column. The desired result is the SSE, or the sum of squared errors.^[6]
- For this data set, the SSE is calculated by adding together the ten values in the third column:

1
Label the columns of the spreadsheet. You will create a three column table in Excel, with the same three headings as above.
- In cell A1, type in the heading “Value.”
- In cell B1, enter the heading “Deviation.»
- In cell C1, enter the heading “Deviation squared.”
2

Enter your data. In the first column, you need to type in the values of your measurements. If the set is small, you can simply type them in by hand. If you have a large data set, you may need to copy and paste the data into the column.
3
Find the mean of the data points. Excel has a function that will calculate the mean for you. In some vacant cell underneath your data table (it really doesn’t matter what cell you choose), enter the following:^[7]
- =Average(A2:___)
- Do not actually type a blank space. Fill in that blank with the cell name of your last data point. For example, if you have 100 points of data, you will use the function:
  - =Average(A2:A101)
  - This function includes data from A2 through A101 because the top row contains the headings of the columns.
- When you press Enter or when you click away to any other cell on the table, the mean of your data values will automatically fill the cell that you just programmed.
4
Enter the function for the error measurements. In the first empty cell in the “Deviation” column, you need to enter a function to calculate the difference between each data point and the mean. To do this, you need to use the cell name where the mean resides. Let’s assume for now that you used cell A104.^[8]
- The function for the error calculation, which you enter into cell B2, will be:
  - =A2-$A$104. The dollar signs are necessary to make sure that you lock in cell A104 for each calculation.
5
Enter the function for the error squares. In the third column, you can direct Excel to calculate the square that you need.^[9]
- In cell C2, enter the function
  - =B2^2
6
Copy the functions to fill the entire table. After you have entered the functions in the top cell of each column, B2 and C2 respectively, you need to fill in the full table. You could retype the function in every line of the table, but this would take far too long. Use your mouse, highlight cells B2 and C2 together, and without letting go of the mouse button, drag down to the bottom cell of each column.
- If we are assuming that you have 100 data points in your table, you will drag your mouse down to cells B101 and C101.
- When you then release the mouse button, the formulas will be copied into all the cells of the table. The table should be automatically populated with the calculated values.
7
Find the SSE. Column C of your table contains all the square-error values. The final step is to have Excel calculate the sum of these values.^[10]
- In a cell below the table, probably C102 for this example, enter the function:
  - =Sum(C2:C101)
- When you click Enter or click away into any other cell of the table, you should have the SSE value for your data.

1
Calculate variance from SSE. Finding the SSE for a data set is generally a building block to finding other, more useful, values. The first of these is variance. The variance is a measurement that indicates how much the measured data varies from the mean. It is actually the average of the squared differences from the mean.^[11]
- Because the SSE is the sum of the squared errors, you can find the average (which is the variance), just by dividing by the number of values. However, if you are calculating the variance of a sample set, rather than a full population, you will divide by (n-1) instead of n. Thus:
  - Variance = SSE/n, if you are calculating the variance of a full population.
  - Variance = SSE/(n-1), if you are calculating the variance of a sample set of data.
- For the sample problem of the patients’ temperatures, we can assume that 10 patients represent only a sample set. Therefore, the variance would be calculated as:
2
Calculate standard deviation from SSE. The standard deviation is a commonly used value that indicates how much the values of any data set deviate from the mean. The standard deviation is the square root of the variance. Recall that the variance is the average of the square error measurements.^[12]
- Therefore, after you calculate the SSE, you can find the standard deviation as follows:
  - ${text{Standard Deviation}}={sqrt {{frac {{text{SSE}}}{n-1}}}}$
- For the data sample of the temperature measurements, you can find the standard deviation as follows:
3
Use SSE to measure covariance. This article has focused on data sets that measure only a single value at a time. However, in many studies, you may be comparing two separate values. You would want to know how those two values relate to each other, not only to the mean of the data set. This value is the covariance.^[13]
- The calculations for covariance are too involved to detail here, other than to note that you will use the SSE for each data type and then compare them. For a more detailed description of covariance and the calculations involved, see Calculate Covariance.
- As an example of the use of covariance, you might want to compare the ages of the patients in a medical study to the effectiveness of a drug in lowering fever temperatures. Then you would have one data set of ages and a second data set of temperatures. You would find the SSE for each data set, and then from there find the variance, standard deviations and covariance.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To calculate the sum of squares for error, start by finding the mean of the data set by adding all of the values together and dividing by the total number of values. Then, subtract the mean from each value to find the deviation for each value. Next, square the deviation for each value. Finally, add all of the squared deviations together to get the sum of squares for error. To learn how to calculate the sum of squares for error using Microsoft Excel, scroll down!

Did this summary help you?

Thanks to all authors for creating a page that has been read 489,304 times.

Did this article help you?

Источник

Download Article

1

Create a three column table. The clearest way to calculate the sum of squared errors is begin with a three column table. Label the three columns as , , and ${text{Deviation}}^{2}$ .^[1]
2
Fill in the data. The first column will hold the values of your measurements. Fill in the column with the values of your measurements. These may be the results of some experiment, a statistical study, or just data provided for a math problem.^[2]
- In this case, suppose you are working with some medical data and you have a list of the body temperatures of ten patients. The normal body temperature expected is 98.6 degrees. The temperatures of ten patients are measured and give the values 99.0, 98.6, 98.5, 101.1, 98.3, 98.6, 97.9, 98.4, 99.2, and 99.1. Write these values in the first column.
Advertisement
3

Calculate the mean. Before you can calculate the error for each measurement, you must calculate the mean of the full data set.^[3]
4
Calculate the individual error measurements. In the second column of your table, you need to fill in the error measurements for each data value. The error is the difference between the measurement and the mean.^[4]
- For the given data set, subtract the mean, 98.87, from each measured value, and fill in the second column with the results. These ten calculations are as follows:
5
Calculate the squares of the errors. In the third column of the table, find the square of each of the resulting values in the middle column. These represent the squares of the deviation from the mean for each measured value of data.^[5]
- For each value in the middle column, use your calculator and find the square. Record the results in the third column, as follows:
6
Add the squares of errors together. The final step is to find the sum of the values in the third column. The desired result is the SSE, or the sum of squared errors.^[6]
- For this data set, the SSE is calculated by adding together the ten values in the third column:

1
Label the columns of the spreadsheet. You will create a three column table in Excel, with the same three headings as above.
- In cell A1, type in the heading “Value.”
- In cell B1, enter the heading “Deviation.»
- In cell C1, enter the heading “Deviation squared.”
2

Enter your data. In the first column, you need to type in the values of your measurements. If the set is small, you can simply type them in by hand. If you have a large data set, you may need to copy and paste the data into the column.
3
Find the mean of the data points. Excel has a function that will calculate the mean for you. In some vacant cell underneath your data table (it really doesn’t matter what cell you choose), enter the following:^[7]
- =Average(A2:___)
- Do not actually type a blank space. Fill in that blank with the cell name of your last data point. For example, if you have 100 points of data, you will use the function:
  - =Average(A2:A101)
  - This function includes data from A2 through A101 because the top row contains the headings of the columns.
- When you press Enter or when you click away to any other cell on the table, the mean of your data values will automatically fill the cell that you just programmed.
4
Enter the function for the error measurements. In the first empty cell in the “Deviation” column, you need to enter a function to calculate the difference between each data point and the mean. To do this, you need to use the cell name where the mean resides. Let’s assume for now that you used cell A104.^[8]
- The function for the error calculation, which you enter into cell B2, will be:
  - =A2-$A$104. The dollar signs are necessary to make sure that you lock in cell A104 for each calculation.
5
Enter the function for the error squares. In the third column, you can direct Excel to calculate the square that you need.^[9]
- In cell C2, enter the function
  - =B2^2
6
Copy the functions to fill the entire table. After you have entered the functions in the top cell of each column, B2 and C2 respectively, you need to fill in the full table. You could retype the function in every line of the table, but this would take far too long. Use your mouse, highlight cells B2 and C2 together, and without letting go of the mouse button, drag down to the bottom cell of each column.
- If we are assuming that you have 100 data points in your table, you will drag your mouse down to cells B101 and C101.
- When you then release the mouse button, the formulas will be copied into all the cells of the table. The table should be automatically populated with the calculated values.
7
Find the SSE. Column C of your table contains all the square-error values. The final step is to have Excel calculate the sum of these values.^[10]
- In a cell below the table, probably C102 for this example, enter the function:
  - =Sum(C2:C101)
- When you click Enter or click away into any other cell of the table, you should have the SSE value for your data.

1
Calculate variance from SSE. Finding the SSE for a data set is generally a building block to finding other, more useful, values. The first of these is variance. The variance is a measurement that indicates how much the measured data varies from the mean. It is actually the average of the squared differences from the mean.^[11]
- Because the SSE is the sum of the squared errors, you can find the average (which is the variance), just by dividing by the number of values. However, if you are calculating the variance of a sample set, rather than a full population, you will divide by (n-1) instead of n. Thus:
  - Variance = SSE/n, if you are calculating the variance of a full population.
  - Variance = SSE/(n-1), if you are calculating the variance of a sample set of data.
- For the sample problem of the patients’ temperatures, we can assume that 10 patients represent only a sample set. Therefore, the variance would be calculated as:
2
Calculate standard deviation from SSE. The standard deviation is a commonly used value that indicates how much the values of any data set deviate from the mean. The standard deviation is the square root of the variance. Recall that the variance is the average of the square error measurements.^[12]
- Therefore, after you calculate the SSE, you can find the standard deviation as follows:
  - ${text{Standard Deviation}}={sqrt {{frac {{text{SSE}}}{n-1}}}}$
- For the data sample of the temperature measurements, you can find the standard deviation as follows:
3
Use SSE to measure covariance. This article has focused on data sets that measure only a single value at a time. However, in many studies, you may be comparing two separate values. You would want to know how those two values relate to each other, not only to the mean of the data set. This value is the covariance.^[13]
- The calculations for covariance are too involved to detail here, other than to note that you will use the SSE for each data type and then compare them. For a more detailed description of covariance and the calculations involved, see Calculate Covariance.
- As an example of the use of covariance, you might want to compare the ages of the patients in a medical study to the effectiveness of a drug in lowering fever temperatures. Then you would have one data set of ages and a second data set of temperatures. You would find the SSE for each data set, and then from there find the variance, standard deviations and covariance.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

Did this summary help you?

Thanks to all authors for creating a page that has been read 489,304 times.

Did this article help you?

Источник

Решаем уравнение простой линейной регрессии

Время прочтения
23 мин

Просмотры 23K

В статье рассматривается несколько способов определения математического уравнения линии простой (парной) регрессии.

Все рассматриваемые здесь способы решения уравнения основаны на методе наименьших квадратов. Обозначим способы следующим образом:

Аналитическое решение
Градиентный спуск
Стохастический градиентный спуск

Для каждого из способов решения уравнения прямой, в статье приведены различные функции, которые в основном делятся на те, которые написаны без использования библиотеки NumPy и те, которые для проведения расчетов применяют NumPy. Считается, что умелое использование NumPy позволит сократить затраты на вычисления.

Весь код, приведенный в статье, написан на языке python 2.7 с использованием Jupyter Notebook. Исходный код и файл с данными выборки выложен на гитхабе

Статья в большей степени ориентирована как на начинающих, так и на тех, кто уже понемногу начал осваивать изучение весьма обширного раздела в искусственном интеллекте — машинного обучения.

Для иллюстрации материала используем очень простой пример.

Условия примера

У нас есть пять значений, которые характеризуют зависимость Y от X (Таблица №1):

Таблица №1 «Условия примера»

Будем считать, что значения $x_i$ — это месяц года, а $y_i$ — выручка в этом месяце. Другими словами, выручка зависит от месяца года, а $x_i$ — единственный признак, от которого зависит выручка.

Пример так себе, как с точки зрения условной зависимости выручки от месяца года, так и с точки зрения количества значений — их очень мало. Однако такое упрощение позволит, что называется на пальцах, объяснить, не всегда с легкостью, усваиваемый новичками материал. А также простота чисел позволит без весомых трудозатрат, желающим, порешать пример на «бумаге».

Предположим, что приведенная в примере зависимость, может быть достаточно хорошо аппроксимирована математическим уравнением линии простой (парной) регрессии вида:

где $x$ — это месяц, в котором была получена выручка, $Y$ — выручка, соответствующая месяцу, $a$ и $b$ — коэффициенты регрессии оцененной линии.

Отметим, что коэффициент $b$ часто называют угловым коэффициентом или градиентом оцененной линии; представляет собой величину, на которую изменится $Y$ при изменении $x$ .

Очевидно, что наша задача в примере — подобрать в уравнении такие коэффициенты $a$ и $b$ , при которых отклонения наших расчетных значений выручки по месяцам от истинных ответов, т.е. значений, представленных в выборке, будут минимальны.

Метод наименьших квадратов

В соответствии с методом наименьших квадратов, отклонение стоит рассчитывать, возводя его в квадрат. Подобный прием позволяет избежать взаимного погашения отклонений, в том случае, если они имеют противоположные знаки. Например, если в одном случае, отклонение составляет +5 (плюс пять), а в другом -5 (минус пять), то сумма отклонений взаимно погасится и составит 0 (ноль). Можно и не возводить отклонение в квадрат, а воспользоваться свойством модуля и тогда у нас все отклонения будут положительными и будут накапливаться. Мы не будем останавливаться на этом моменте подробно, а просто обозначим, что для удобства расчетов, принято возводить отклонение в квадрат.

Вот так выглядит формула, с помощью которой мы определим наименьшую сумму квадратов отклонений (ошибки):

$ERR(x)=sumlimits_{i=1}^n(a + bx_i - y_i)^2 = sumlimits_{i=1}^n(f(x_i)-y_i)^2 rightarrow min$

где — это функция аппроксимации истинных ответов (то есть посчитанная нами выручка),

$y_i$ — это истинные ответы (предоставленная в выборке выручка),

$i$ — это индекс выборки (номер месяца, в котором происходит определение отклонения)

Продифференцируем функцию, определим уравнения частных производных и будем готовы перейти к аналитическому решению. Но для начала проведем небольшой экскурс о том, что такое дифференцирование и вспомним геометрический смысл производной.

Дифференцирование

Дифференцированием называется операция по нахождению производной функции.

Для чего нужна производная? Производная функции характеризует скорость изменения функции и указывает нам ее направление. Если производная в заданной точке положительна, то функция возрастает, в обратном случае — функция убывает. И чем больше значение производной по модулю, тем выше скорость изменения значений функции, а также круче угол наклона графика функции.

Например, в условиях декартовой системы координат, значение производной в точке M(0,0) равное +25 означает, что в заданной точке, при смещении значения $x$ вправо на условную единицу, значение $y$ возрастает на 25 условных единиц. На графике это выглядит, как достаточно крутой угол подъема значений $y$ с заданной точки.

Другой пример. Значение производной равное -0,1 означает, что при смещении $x$ на одну условную единицу, значение $y$ убывает всего лишь на 0,1 условную единицу. При этом, на графике функции, мы можем наблюдать едва заметный наклон вниз. Проводя аналогию с горой, то мы как будто очень медленно спускаемся по пологому склону с горы, в отличие от предыдущего примера, где нам приходилось брать очень крутые вершины:)

Таким образом, проведя дифференцирование функции $ERR(x)=sumlimits_{i=1}^n(a + bx_i - y_i)^2$ по коэффициентам $a$ и $b$ , определим уравнения частных производных 1-го порядка. После определения уравнений, мы получим систему из двух уравнений, решив которую мы сможем подобрать такие значения коэффициентов $a$ и $b$ , при которых значения соответствующих производных в заданных точках изменяются на очень и очень малую величину, а в случае с аналитическим решением не изменяются вовсе. Другими словами, функция ошибки при найденных коэффициентах достигнет минимума, так как значения частных производных в этих точках будут равны нулю.

Итак, по правилам дифференцирования уравнение частной производной 1-го порядка по коэффициенту $a$ примет вид:

$2na + 2bsumlimits_{i=1}^nx_i - 2sumlimits_{i=1}^ny_i = 2(na + bsumlimits_{i=1}^nx_i - sumlimits_{i=1}^ny_i)$

уравнение частной производной 1-го порядка по $b$ примет вид:

$2asumlimits_{i=1}^nx_i + 2bsumlimits_{i=1}^nx^2_i - 2sumlimits_{i=1}^nx_iy_i = 2sumlimits_{i=1}^nx_i(a +bsumlimits_{i=1}^nx_i - sumlimits_{i=1}^ny_i)$

В итоге мы получили систему уравнений, которая имеет достаточно простое аналитическое решение:

begin{equation*}
begin{cases}
na + bsumlimits_{i=1}^nx_i — sumlimits_{i=1}^ny_i = 0
\
sumlimits_{i=1}^nx_i(a +bsumlimits_{i=1}^nx_i — sumlimits_{i=1}^ny_i) = 0
end{cases}
end{equation*}

Прежде чем решать уравнение, предварительно загрузим, проверим правильность загрузки и отформатируем данные.

Загрузка и форматирование данных

Необходимо отметить, что в связи с тем, что для аналитического решения, а в дальнейшем для градиентного и стохастического градиентного спуска, мы будем применять код в двух вариациях: с использованием библиотеки NumPy и без её использования, то нам потребуется соответствующее форматирование данных (см. код).

Код загрузки и обработки данных

# импортируем все нужные нам библиотеки
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import math
import pylab as pl
import random

# графики отобразим в Jupyter
%matplotlib inline

# укажем размер графиков
from pylab import rcParams
rcParams['figure.figsize'] = 12, 6

# отключим предупреждения Anaconda
import warnings
warnings.simplefilter('ignore')

# загрузим значения
table_zero = pd.read_csv('data_example.txt', header=0, sep='t')

# посмотрим информацию о таблице и на саму таблицу
print table_zero.info()
print '********************************************'
print table_zero
print '********************************************'

# подготовим данные без использования NumPy

x_us = []
[x_us.append(float(i)) for i in table_zero['x']]
print x_us
print type(x_us)
print '********************************************'

y_us = []
[y_us.append(float(i)) for i in table_zero['y']]
print y_us
print type(y_us)
print '********************************************'

# подготовим данные с использованием NumPy

x_np = table_zero[['x']].values
print x_np
print type(x_np)
print x_np.shape
print '********************************************'

y_np = table_zero[['y']].values
print y_np
print type(y_np)
print y_np.shape
print '********************************************'

Визуализация

Теперь, после того, как мы, во-первых, загрузили данные, во-вторых, проверили правильность загрузки и наконец отформатировали данные, проведем первую визуализацию. Часто для этого используют метод pairplot библиотеки Seaborn. В нашем примере, ввиду ограниченности цифр нет смысла применять библиотеку Seaborn. Мы воспользуемся обычной библиотекой Matplotlib и посмотрим только на диаграмму рассеяния.

Код диаграммы рассеяния

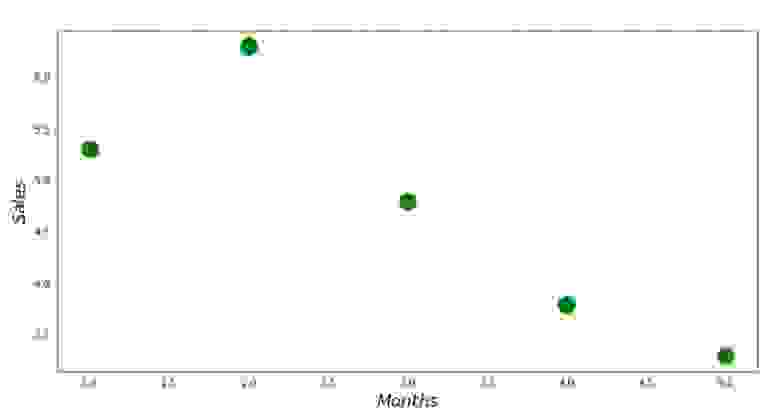
print 'График №1 "Зависимость выручки от месяца года"'

plt.plot(x_us,y_us,'o',color='green',markersize=16)
plt.xlabel('$Months$', size=16)
plt.ylabel('$Sales$', size=16)
plt.show()

График №1 «Зависимость выручки от месяца года»

Аналитическое решение

Воспользуемся самыми обычными инструментами в python и решим систему уравнений:

begin{equation*}
begin{cases}
na + bsumlimits_{i=1}^nx_i — sumlimits_{i=1}^ny_i = 0
\
sumlimits_{i=1}^nx_i(a +bsumlimits_{i=1}^nx_i — sumlimits_{i=1}^ny_i) = 0
end{cases}
end{equation*}

По правилу Крамера найдем общий определитель, а также определители по $a$ и по $b$ , после чего, разделив определитель по $a$ на общий определитель — найдем коэффициент $a$ , аналогично найдем коэффициент $b$ .

Код аналитического решения

# определим функцию для расчета коэффициентов a и b по правилу Крамера
def Kramer_method (x,y):
        # сумма значений (все месяца)
    sx = sum(x)
        # сумма истинных ответов (выручка за весь период)
    sy = sum(y)
        # сумма произведения значений на истинные ответы
    list_xy = []
    [list_xy.append(x[i]*y[i]) for i in range(len(x))]
    sxy = sum(list_xy)
        # сумма квадратов значений
    list_x_sq = []
    [list_x_sq.append(x[i]**2) for i in range(len(x))]
    sx_sq = sum(list_x_sq)
        # количество значений
    n = len(x)
        # общий определитель
    det = sx_sq*n - sx*sx
        # определитель по a
    det_a = sx_sq*sy - sx*sxy
        # искомый параметр a
    a = (det_a / det)
        # определитель по b
    det_b = sxy*n - sy*sx
        # искомый параметр b
    b = (det_b / det)
        # контрольные значения (прооверка)
    check1 = (n*b + a*sx - sy)
    check2 = (b*sx + a*sx_sq - sxy)
    return [round(a,4), round(b,4)]

# запустим функцию и запишем правильные ответы
ab_us = Kramer_method(x_us,y_us)
a_us = ab_us[0]
b_us = ab_us[1]
print '33[1m' + '33[4m' + "Оптимальные значения коэффициентов a и b:"  + '33[0m' 
print 'a =', a_us
print 'b =', b_us
print

# определим функцию для подсчета суммы квадратов ошибок
def errors_sq_Kramer_method(answers,x,y):
    list_errors_sq = []
    for i in range(len(x)):
        err = (answers[0] + answers[1]*x[i] - y[i])**2
        list_errors_sq.append(err)
    return sum(list_errors_sq)

# запустим функцию и запишем значение ошибки
error_sq = errors_sq_Kramer_method(ab_us,x_us,y_us)
print '33[1m' + '33[4m' + "Сумма квадратов отклонений" + '33[0m'
print error_sq
print

# замерим время расчета
# print '33[1m' + '33[4m' + "Время выполнения расчета суммы квадратов отклонений:" + '33[0m'
# % timeit error_sq = errors_sq_Kramer_method(ab,x_us,y_us)

Вот, что у нас получилось:

Итак, значения коэффициентов найдены, сумма квадратов отклонений установлена. Нарисуем на гистограмме рассеяния прямую линию в соответствии с найденными коэффициентами.

Код линии регрессии

# определим функцию для формирования массива рассчетных значений выручки
def sales_count(ab,x,y):
    line_answers = []
    [line_answers.append(ab[0]+ab[1]*x[i]) for i in range(len(x))]
    return line_answers

# построим графики
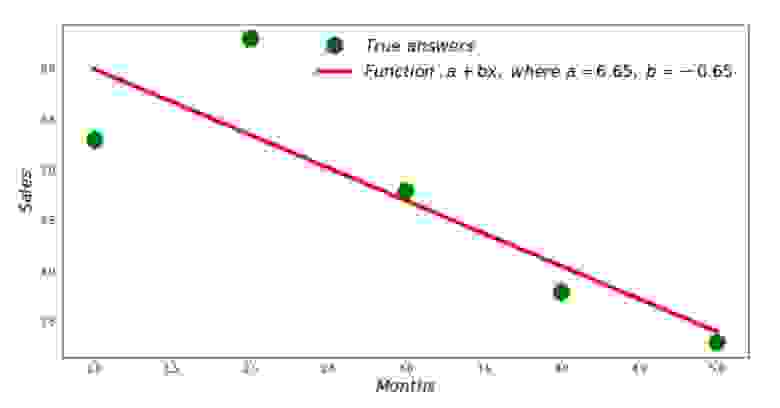
print 'Грфик№2 "Правильные и расчетные ответы"'
plt.plot(x_us,y_us,'o',color='green',markersize=16, label = '$True$ $answers$')
plt.plot(x_us, sales_count(ab_us,x_us,y_us), color='red',lw=4,
         label='$Function: a + bx,$ $where$ $a='+str(round(ab_us[0],2))+',$ $b='+str(round(ab_us[1],2))+'$')
plt.xlabel('$Months$', size=16)
plt.ylabel('$Sales$', size=16)
plt.legend(loc=1, prop={'size': 16})
plt.show()

График №2 «Правильные и расчетные ответы»

Можно посмотреть на график отклонений за каждый месяц. В нашем случае, какой-либо значимой практической ценности мы из него не вынесем, но удовлетворим любопытство в том, насколько хорошо, уравнение простой линейной регрессии характеризует зависимость выручки от месяца года.

Код графика отклонений

# определим функцию для формирования массива отклонений в процентах
def error_per_month(ab,x,y):
    sales_c = sales_count(ab,x,y)
    errors_percent = []
    for i in range(len(x)):
        errors_percent.append(100*(sales_c[i]-y[i])/y[i])
    return errors_percent

# построим график
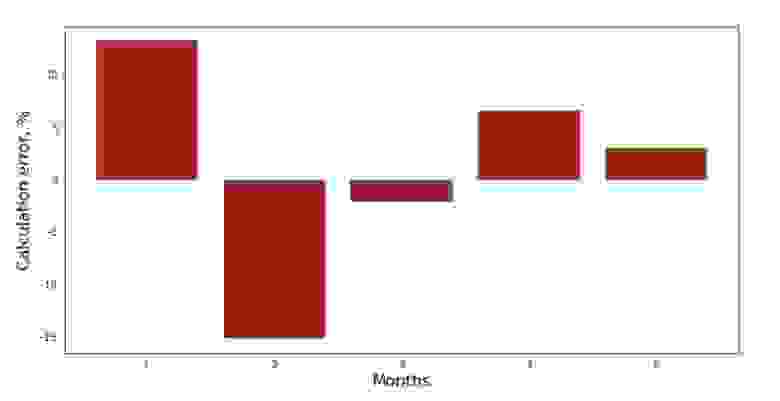
print 'График№3 "Отклонения по-месячно, %"'
plt.gca().bar(x_us, error_per_month(ab_us,x_us,y_us), color='brown')
plt.xlabel('Months', size=16)
plt.ylabel('Calculation error, %', size=16)
plt.show()

График №3 «Отклонения, %»

Не идеально, но нашу задачу мы выполнили.

Напишем функцию, которая для определения коэффициентов $a$ и $b$ использует библиотеку NumPy, точнее — напишем две функции: одну с использованием псевдообратной матрицы (не рекомендуется на практике, так как процесс вычислительно сложный и нестабильный), другую с использованием матричного уравнения.

Код аналитического решения (NumPy)

# для начала добавим столбец с не изменяющимся значением в 1. 
# Данный столбец нужен для того, чтобы не обрабатывать отдельно коэффицент a
vector_1 = np.ones((x_np.shape[0],1))
x_np = table_zero[['x']].values # на всякий случай приведем в первичный формат вектор x_np
x_np = np.hstack((vector_1,x_np))

# проверим то, что все сделали правильно
print vector_1[0:3]
print x_np[0:3]
print '***************************************'
print

# напишем функцию, которая определяет значения коэффициентов a и b с использованием псевдообратной матрицы
def pseudoinverse_matrix(X, y):
    # задаем явный формат матрицы признаков
    X = np.matrix(X)
    # определяем транспонированную матрицу
    XT = X.T
    # определяем квадратную матрицу
    XTX = XT*X
    # определяем псевдообратную матрицу
    inv = np.linalg.pinv(XTX)
    # задаем явный формат матрицы ответов
    y = np.matrix(y)
    # находим вектор весов
    return (inv*XT)*y

# запустим функцию
ab_np = pseudoinverse_matrix(x_np, y_np)
print ab_np
print '***************************************'
print

# напишем функцию, которая использует для решения матричное уравнение
def matrix_equation(X,y):
    a = np.dot(X.T, X)
    b = np.dot(X.T, y)
    return np.linalg.solve(a, b)

# запустим функцию
ab_np = matrix_equation(x_np,y_np)
print ab_np

Сравним время, которое было затрачено на определение коэффициентов $a$ и $b$ , в соответствии с 3-мя представленными способами.

Код для вычисления времени расчетов

print '33[1m' + '33[4m' + "Время выполнения расчета коэффициентов без использования библиотеки NumPy:" + '33[0m'
% timeit ab_us = Kramer_method(x_us,y_us)
print '***************************************'
print
print '33[1m' + '33[4m' + "Время выполнения расчета коэффициентов с использованием псевдообратной матрицы:" + '33[0m'
%timeit ab_np = pseudoinverse_matrix(x_np, y_np)
print '***************************************'
print
print '33[1m' + '33[4m' + "Время выполнения расчета коэффициентов с использованием матричного уравнения:" + '33[0m'
%timeit ab_np = matrix_equation(x_np, y_np)

На небольшом количестве данных, вперед выходит «самописная» функция, которая находит коэффициенты методом Крамера.

Теперь можно перейти к другим способам нахождения коэффициентов $a$ и $b$ .

Градиентный спуск

Для начала определим, что такое градиент. По-простому, градиент — это отрезок, который указывает направление максимального роста функции. По аналогии с подъемом в гору, то куда смотрит градиент, там и есть самый крутой подъем к вершине горы. Развивая пример с горой, вспоминаем, что на самом деле нам нужен самый крутой спуск, чтобы как можно быстрее достичь низины, то есть минимума — места где функция не возрастает и не убывает. В этом месте производная будет равна нулю. Следовательно, нам нужен не градиент, а антиградиент. Для нахождения антиградиента нужно всего лишь умножить градиент на -1 (минус один).

Обратим внимание на то, что функция может иметь несколько минимумов, и опустившись в один из них по предложенному далее алгоритму, мы не сможем найти другой минимум, который возможно находится ниже найденного. Расслабимся, нам это не грозит! В нашем случае мы имеем дело с единственным минимумом, так как наша функция $sumlimits_{i=1}^n(a + bx_i - y_i)^2$ на графике представляет собой обычную параболу. А как мы все должны прекрасно знать из школьного курса математики — у параболы существует только один минимум.

После того, как мы выяснили для чего нам потребовался градиент, а также то, что градиент — это отрезок, то есть вектор с заданными координатами, которые как раз являются теми самыми коэффициентами $a$ и $b$ мы можем реализовать градиентный спуск.

Перед запуском, предлагаю прочитать буквально несколько предложений об алгоритме спуска:

Определяем псевдослучайным образом координаты коэффициентов и . В нашем примере, мы будем определять коэффициенты вблизи нуля. Это является распространённой практикой, однако для каждого случая может быть предусмотрена своя практика.
От координаты вычитаем значение частной производной 1-го порядка в точке . Так, если производная будет положительная, то функция возрастает. Следовательно, отнимая значение производной, мы будем двигаться в обратную сторону роста, то есть в сторону спуска. Если производная отрицательна, значит функция в этой точке убывает и отнимая значение производной мы двигаемся в сторону спуска.
Проводим аналогичную операцию с координатой : вычитаем значение частной производной в точке .
Для того, чтобы не перескочить минимум и не улететь в далекий космос, необходимо установить размер шага в сторону спуска. В общем и целом, можно написать целую статью о том, как правильнее установить шаг и как его менять в процессе спуска, чтобы снизить затраты на вычисления. Но сейчас перед нами несколько иная задача, и мы научным методом «тыка» или как говорят в простонародье, эмпирическим путем, установим размер шага.
После того, как мы из заданных координат и вычли значения производных, получаем новые координаты и . Делаем следующий шаг (вычитание), уже из рассчитанных координат. И так цикл запускается вновь и вновь, до тех пор, пока не будет достигнута требуемая сходимость.

Все! Теперь мы готовы отправиться на поиски самого глубокого ущелья Марианской впадины. Приступаем.

Код для градиентного спуска

# напишем функцию градиентного спуска без использования библиотеки NumPy. 
# Функция на вход принимает диапазоны значений x,y, длину шага (по умолчанию=0,1), допустимую погрешность(tolerance)
def gradient_descent_usual(x_us,y_us,l=0.1,tolerance=0.000000000001):
    # сумма значений (все месяца)
    sx = sum(x_us)
    # сумма истинных ответов (выручка за весь период)
    sy = sum(y_us)
    # сумма произведения значений на истинные ответы
    list_xy = []
    [list_xy.append(x_us[i]*y_us[i]) for i in range(len(x_us))]
    sxy = sum(list_xy)
    # сумма квадратов значений
    list_x_sq = []
    [list_x_sq.append(x_us[i]**2) for i in range(len(x_us))]
    sx_sq = sum(list_x_sq)
    # количество значений
    num = len(x_us)
    # начальные значения коэффициентов, определенные псевдослучайным образом
    a = float(random.uniform(-0.5, 0.5))
    b = float(random.uniform(-0.5, 0.5))
    # создаем массив с ошибками, для старта используем значения 1 и 0
    # после завершения спуска стартовые значения удалим
    errors = [1,0]
    # запускаем цикл спуска
    # цикл работает до тех пор, пока отклонение последней ошибки суммы квадратов от предыдущей, не будет меньше tolerance
    while abs(errors[-1]-errors[-2]) > tolerance:
        a_step = a - l*(num*a + b*sx - sy)/num
        b_step = b - l*(a*sx + b*sx_sq - sxy)/num
        a = a_step
        b = b_step
        ab = [a,b]
        errors.append(errors_sq_Kramer_method(ab,x_us,y_us))
    return (ab),(errors[2:])

# запишем массив значений 
list_parametres_gradient_descence = gradient_descent_usual(x_us,y_us,l=0.1,tolerance=0.000000000001)


print '33[1m' + '33[4m' + "Значения коэффициентов a и b:" + '33[0m'
print 'a =', round(list_parametres_gradient_descence[0][0],3)
print 'b =', round(list_parametres_gradient_descence[0][1],3)
print


print '33[1m' + '33[4m' + "Сумма квадратов отклонений:" + '33[0m'
print round(list_parametres_gradient_descence[1][-1],3)
print



print '33[1m' + '33[4m' + "Количество итераций в градиентном спуске:" + '33[0m'
print len(list_parametres_gradient_descence[1])
print

Мы погрузились на самое дно Марианской впадины и там обнаружили все те же значения коэффициентов $a$ и $b$ , что собственно и следовало ожидать.

Совершим еще одно погружение, только на этот раз, начинкой нашего глубоководного аппарата будут иные технологии, а именно библиотека NumPy.

Код для градиентного спуска (NumPy)

# перед тем определить функцию для градиентного спуска с использованием библиотеки NumPy, 
# напишем функцию определения суммы квадратов отклонений также с использованием NumPy
def error_square_numpy(ab,x_np,y_np):
    y_pred = np.dot(x_np,ab)
    error = y_pred - y_np
    return sum((error)**2)

# напишем функцию градиентного спуска с использованием библиотеки NumPy. 
# Функция на вход принимает диапазоны значений x,y, длину шага (по умолчанию=0,1), допустимую погрешность(tolerance)
def gradient_descent_numpy(x_np,y_np,l=0.1,tolerance=0.000000000001):
    # сумма значений (все месяца)
    sx = float(sum(x_np[:,1]))
    # сумма истинных ответов (выручка за весь период)
    sy = float(sum(y_np))
    # сумма произведения значений на истинные ответы
    sxy = x_np*y_np
    sxy = float(sum(sxy[:,1]))
    # сумма квадратов значений
    sx_sq = float(sum(x_np[:,1]**2))
    # количество значений
    num = float(x_np.shape[0])
    # начальные значения коэффициентов, определенные псевдослучайным образом
    a = float(random.uniform(-0.5, 0.5))
    b = float(random.uniform(-0.5, 0.5))
    # создаем массив с ошибками, для старта используем значения 1 и 0
    # после завершения спуска стартовые значения удалим
    errors = [1,0]
    # запускаем цикл спуска
    # цикл работает до тех пор, пока отклонение последней ошибки суммы квадратов от предыдущей, не будет меньше tolerance
    while abs(errors[-1]-errors[-2]) > tolerance:
        a_step = a - l*(num*a + b*sx - sy)/num
        b_step = b - l*(a*sx + b*sx_sq - sxy)/num
        a = a_step
        b = b_step
        ab = np.array([[a],[b]])
        errors.append(error_square_numpy(ab,x_np,y_np))
    return (ab),(errors[2:])

# запишем массив значений 
list_parametres_gradient_descence = gradient_descent_numpy(x_np,y_np,l=0.1,tolerance=0.000000000001)

print '33[1m' + '33[4m' + "Значения коэффициентов a и b:" + '33[0m'
print 'a =', round(list_parametres_gradient_descence[0][0],3)
print 'b =', round(list_parametres_gradient_descence[0][1],3)
print


print '33[1m' + '33[4m' + "Сумма квадратов отклонений:" + '33[0m'
print round(list_parametres_gradient_descence[1][-1],3)
print

print '33[1m' + '33[4m' + "Количество итераций в градиентном спуске:" + '33[0m'
print len(list_parametres_gradient_descence[1])
print

Значения коэффициентов $a$ и $b$ неизменны.

Посмотрим на то, как изменялась ошибка при градиентном спуске, то есть как изменялась сумма квадратов отклонений с каждым шагом.

Код для графика сумм квадратов отклонений

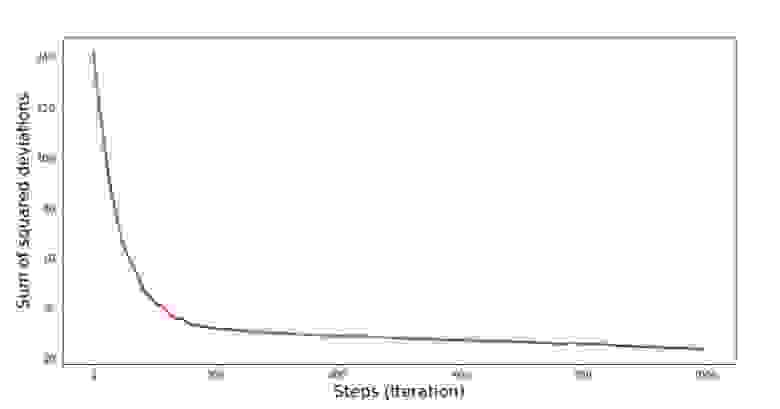
print 'График№4 "Сумма квадратов отклонений по-шагово"'
plt.plot(range(len(list_parametres_gradient_descence[1])), list_parametres_gradient_descence[1], color='red', lw=3)
plt.xlabel('Steps (Iteration)', size=16)
plt.ylabel('Sum of squared deviations', size=16)
plt.show()

График №4 «Сумма квадратов отклонений при градиентном спуске»

На графике мы видим, что с каждым шагом ошибка уменьшается, а спустя какое-то количество итераций наблюдаем практически горизонтальную линию.

Напоследок оценим разницу во времени исполнения кода:

Код для определения времени вычисления градиентного спуска

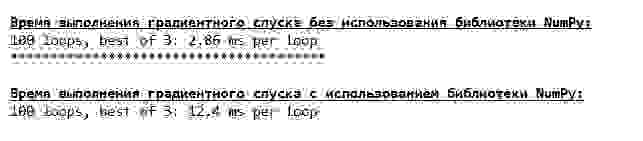
print '33[1m' + '33[4m' + "Время выполнения градиентного спуска без использования библиотеки NumPy:" + '33[0m'
%timeit list_parametres_gradient_descence = gradient_descent_usual(x_us,y_us,l=0.1,tolerance=0.000000000001)
print '***************************************'
print

print '33[1m' + '33[4m' + "Время выполнения градиентного спуска с использованием библиотеки NumPy:" + '33[0m'
%timeit list_parametres_gradient_descence = gradient_descent_numpy(x_np,y_np,l=0.1,tolerance=0.000000000001)

Возможно мы делаем что-то не то, но опять простая «самописная» функция, которая не использует библиотеку NumPy опережает по времени выполнения расчетов функцию, использующую библиотеку NumPy.

Но мы не стоим на месте, а двигаемся в сторону изучения еще одного увлекательного способа решения уравнения простой линейной регрессии. Встречайте!

Стохастический градиентный спуск

Для того, чтобы быстрее понять принцип работы стохастического градиентного спуска, лучше определить его отличия от обычного градиентного спуска. Мы, в случае с градиентным спуском, в уравнениях производных от $a$ и $a$ использовали суммы значений всех признаков и истинных ответов, имеющихся в выборке (то есть суммы всех $x_i$ и $y_i$ ). В стохастическом градиентном спуске мы не будем использовать все значения, имеющиеся в выборке, а вместо этого, псевдослучайным образом выберем так называемый индекс выборки и используем его значения.

Например, если индекс определился за номером 3 (три), то мы берем значения $x_3=3$ и , далее подставляем значения в уравнения производных и определяем новые координаты. Затем, определив координаты, мы опять псевдослучайным образом определяем индекс выборки, подставляем значения, соответствующие индексу в уравнения частных производных, по новому определяем координаты $a$ и $a$ и т.д. до

~~позеленения~~

сходимости. На первый взгляд, может показаться, как это вообще может работать, однако работает. Правда стоит отметить, что не с каждым шагом уменьшается ошибка, но тенденция безусловно имеется.

Каковы преимущества стохастического градиентного спуска перед обычным? В случае, если у нас размер выборки очень велик и измеряется десятками тысяч значений, то значительно проще обработать, допустим случайную тысячу из них, нежели всю выборку. Вот в этом случае и запускается стохастический градиентный спуск. В нашем случае мы конечно же большой разницы не заметим.

Смотрим код.

Код для стохастического градиентного спуска

# определим функцию стох.град.шага
def stoch_grad_step_usual(vector_init, x_us, ind, y_us, l):
#     выбираем значение икс, которое соответствует случайному значению параметра ind 
# (см.ф-цию stoch_grad_descent_usual)
    x = x_us[ind]
#     рассчитывыаем значение y (выручку), которая соответствует выбранному значению x
    y_pred = vector_init[0] + vector_init[1]*x_us[ind]
#     вычисляем ошибку расчетной выручки относительно представленной в выборке
    error = y_pred - y_us[ind]
#     определяем первую координату градиента ab
    grad_a = error
#     определяем вторую координату ab
    grad_b = x_us[ind]*error
#     вычисляем новый вектор коэффициентов
    vector_new = [vector_init[0]-l*grad_a, vector_init[1]-l*grad_b]
    return vector_new


# определим функцию стох.град.спуска
def stoch_grad_descent_usual(x_us, y_us, l=0.1, steps = 800):
#     для самого начала работы функции зададим начальные значения коэффициентов
    vector_init = [float(random.uniform(-0.5, 0.5)), float(random.uniform(-0.5, 0.5))]
    errors = []
#     запустим цикл спуска
# цикл расчитан на определенное количество шагов (steps)
    for i in range(steps):
        ind = random.choice(range(len(x_us)))
        new_vector = stoch_grad_step_usual(vector_init, x_us, ind, y_us, l)
        vector_init = new_vector
        errors.append(errors_sq_Kramer_method(vector_init,x_us,y_us))
    return (vector_init),(errors)


# запишем массив значений 
list_parametres_stoch_gradient_descence = stoch_grad_descent_usual(x_us, y_us, l=0.1, steps = 800)

print '33[1m' + '33[4m' + "Значения коэффициентов a и b:" + '33[0m'
print 'a =', round(list_parametres_stoch_gradient_descence[0][0],3)
print 'b =', round(list_parametres_stoch_gradient_descence[0][1],3)
print


print '33[1m' + '33[4m' + "Сумма квадратов отклонений:" + '33[0m'
print round(list_parametres_stoch_gradient_descence[1][-1],3)
print

print '33[1m' + '33[4m' + "Количество итераций в стохастическом градиентном спуске:" + '33[0m'
print len(list_parametres_stoch_gradient_descence[1])

Смотрим внимательно на коэффициенты и ловим себя на вопросе «Как же так?». У нас получились другие значения коэффициентов $a$ и $b$ . Может быть стохастический градиентный спуск нашел более оптимальные параметры уравнения? Увы, нет. Достаточно посмотреть на сумму квадратов отклонений и увидеть, что при новых значениях коэффициентов, ошибка больше. Не спешим отчаиваться. Построим график изменения ошибки.

Код для графика суммы квадратов отклонений при стохастическом градиентном спуске

print 'График №5 "Сумма квадратов отклонений по-шагово"'
plt.plot(range(len(list_parametres_stoch_gradient_descence[1])), list_parametres_stoch_gradient_descence[1], color='red', lw=2)
plt.xlabel('Steps (Iteration)', size=16)
plt.ylabel('Sum of squared deviations', size=16)
plt.show()

График №5 «Сумма квадратов отклонений при стохастическом градиентном спуске»

Посмотрев на график, все становится на свои места и сейчас мы все исправим.

Итак, что же произошло? Произошло следующее. Когда мы выбираем случайным образом месяц, то именно для выбранного месяца наш алгоритм стремится уменьшить ошибку в расчете выручки. Затем выбираем другой месяц и повторяем расчет, но ошибку уменьшаем уже для второго выбранного месяца. А теперь вспомним, что у нас первые два месяца существенно отклоняются от линии уравнения простой линейной регрессии. Это значит, что когда выбирается любой из этих двух месяцев, то уменьшая ошибку каждого из них, наш алгоритм серьезно увеличивает ошибку по всей выборке. Так что же делать? Ответ простой: надо уменьшить шаг спуска. Ведь уменьшив шаг спуска, ошибка так же перестанет «скакать» то вверх, то вниз. Вернее, ошибка «скакать» не перестанет, но будет это делать не так прытко:) Проверим.

Код для запуска SGD с меньшим шагом

# запустим функцию, уменьшив шаг в 100 раз и увеличив количество шагов соответсвующе 
list_parametres_stoch_gradient_descence = stoch_grad_descent_usual(x_us, y_us, l=0.001, steps = 80000)

print '33[1m' + '33[4m' + "Значения коэффициентов a и b:" + '33[0m'
print 'a =', round(list_parametres_stoch_gradient_descence[0][0],3)
print 'b =', round(list_parametres_stoch_gradient_descence[0][1],3)
print


print '33[1m' + '33[4m' + "Сумма квадратов отклонений:" + '33[0m'
print round(list_parametres_stoch_gradient_descence[1][-1],3)
print



print '33[1m' + '33[4m' + "Количество итераций в стохастическом градиентном спуске:" + '33[0m'
print len(list_parametres_stoch_gradient_descence[1])

print 'График №6 "Сумма квадратов отклонений по-шагово"'
plt.plot(range(len(list_parametres_stoch_gradient_descence[1])), list_parametres_stoch_gradient_descence[1], color='red', lw=2)
plt.xlabel('Steps (Iteration)', size=16)
plt.ylabel('Sum of squared deviations', size=16)
plt.show()

График №6 «Сумма квадратов отклонений при стохастическом градиентном спуске (80 тыс. шагов)»

Значения коэффициентов улучшились, но все равно не идеальны. Гипотетически это можно поправить таким образом. Выбираем, например, на последних 1000 итерациях значения коэффициентов, с которыми была допущена минимальная ошибка. Правда нам для этого придется записывать еще и сами значения коэффициентов. Мы не будем этого делать, а лучше обратим внимание на график. Он выглядит гладким, и ошибка как будто уменьшается равномерно. На самом деле это не так. Посмотрим на первые 1000 итераций и сравним их с последними.

Код для графика SGD (первые 1000 шагов)

print 'График №7 "Сумма квадратов отклонений по-шагово. Первые 1000 итераций"'
plt.plot(range(len(list_parametres_stoch_gradient_descence[1][:1000])), 
         list_parametres_stoch_gradient_descence[1][:1000], color='red', lw=2)
plt.xlabel('Steps (Iteration)', size=16)
plt.ylabel('Sum of squared deviations', size=16)
plt.show()

print 'График №7 "Сумма квадратов отклонений по-шагово. Последние 1000 итераций"'
plt.plot(range(len(list_parametres_stoch_gradient_descence[1][-1000:])), 
         list_parametres_stoch_gradient_descence[1][-1000:], color='red', lw=2)
plt.xlabel('Steps (Iteration)', size=16)
plt.ylabel('Sum of squared deviations', size=16)
plt.show()

График №7 «Сумма квадратов отклонений SGD (первые 1000 шагов)»

График №8 «Сумма квадратов отклонений SGD (последние 1000 шагов)»

В самом начале спуска мы наблюдаем достаточно равномерное и крутое уменьшение ошибки. На последних итерациях мы видим, что ошибка ходит вокруг да около значения в 1,475 и в некоторые моменты даже равняется этому оптимальному значению, но потом все равно уходит ввысь… Повторюсь, можно записывать значения коэффициентов $a$ и $b$ , а потом выбрать те, при которых ошибка минимальна. Однако у нас возникла проблема посерьезнее: нам пришлось сделать 80 тыс. шагов (см. код), чтобы получить значения, близкие к оптимальным. А это, уже противоречит идее об экономии времени вычислений при стохастическом градиентном спуске относительно градиентного. Что можно поправить и улучшить? Не трудно заметить, что на первых итерациях мы уверенно идем вниз и, следовательно, нам стоит оставить большой шаг на первых итерациях и по мере продвижения вперед шаг уменьшать. Мы не будем этого делать в этой статье — она и так уже затянулась. Желающие могут и сами подумать, как это сделать, это не сложно

Теперь выполним стохастический градиентный спуск, используя библиотеку NumPy (и не будем спотыкаться о камни, которые мы выявили раннее)

Код для стохастического градиентного спуска (NumPy)

# для начала напишем функцию градиентного шага
def stoch_grad_step_numpy(vector_init, X, ind, y, l):
    x = X[ind]
    y_pred = np.dot(x,vector_init)
    err = y_pred - y[ind]
    grad_a = err
    grad_b = x[1]*err
    return vector_init - l*np.array([grad_a, grad_b])

# определим функцию стохастического градиентного спуска
def stoch_grad_descent_numpy(X, y, l=0.1, steps = 800):
    vector_init = np.array([[np.random.randint(X.shape[0])], [np.random.randint(X.shape[0])]])
    errors = []
    for i in range(steps):
        ind = np.random.randint(X.shape[0])
        new_vector = stoch_grad_step_numpy(vector_init, X, ind, y, l)
        vector_init = new_vector
        errors.append(error_square_numpy(vector_init,X,y))
    return (vector_init), (errors)

# запишем массив значений 
list_parametres_stoch_gradient_descence = stoch_grad_descent_numpy(x_np, y_np, l=0.001, steps = 80000)

print '33[1m' + '33[4m' + "Значения коэффициентов a и b:" + '33[0m'
print 'a =', round(list_parametres_stoch_gradient_descence[0][0],3)
print 'b =', round(list_parametres_stoch_gradient_descence[0][1],3)
print


print '33[1m' + '33[4m' + "Сумма квадратов отклонений:" + '33[0m'
print round(list_parametres_stoch_gradient_descence[1][-1],3)
print



print '33[1m' + '33[4m' + "Количество итераций в стохастическом градиентном спуске:" + '33[0m'
print len(list_parametres_stoch_gradient_descence[1])
print

Значения получились почти такими же, как и при спуске без использования NumPy. Впрочем, это логично.

Узнаем сколько же времени занимали у нас стохастические градиентные спуски.

Код для определения времени вычисления SGD (80 тыс. шагов)

print '33[1m' + '33[4m' +
"Время выполнения стохастического градиентного спуска без использования библиотеки NumPy:"
+ '33[0m'
%timeit list_parametres_stoch_gradient_descence = stoch_grad_descent_usual(x_us, y_us, l=0.001, steps = 80000)
print '***************************************'
print

print '33[1m' + '33[4m' +
"Время выполнения стохастического градиентного спуска с использованием библиотеки NumPy:"
+ '33[0m'
%timeit list_parametres_stoch_gradient_descence = stoch_grad_descent_numpy(x_np, y_np, l=0.001, steps = 80000)

Чем дальше в лес, тем темнее тучи: опять «самописная» формула показывает лучший результат. Все это наводит на мысли о том, что должны существовать еще более тонкие способы использования библиотеки NumPy, которые действительно ускоряют операции вычислений. В этой статье мы о них уже не узнаем. Будет о чем подумать на досуге:)

Резюмируем

Перед тем как резюмировать, хотелось бы ответить на вопрос, который скорее всего, возник у нашего дорогого читателя. Для чего, собственно, такие «мучения» со спусками, зачем нам ходить по горе вверх и вниз (преимущественно вниз), чтобы найти заветную низину, если в наших руках такой мощный и простой прибор, в виде аналитического решения, который мгновенно телепортирует нас в нужное место?

Ответ на этот вопрос лежит на поверхности. Сейчас мы разбирали очень простой пример, в котором истинный ответ $y_i$ зависит от одного признака $x_i$ . В жизни такое встретишь не часто, поэтому представим, что у нас признаков 2, 30, 50 или более. Добавим к этому тысячи, а то и десятки тысяч значений для каждого признака. В этом случае аналитическое решение может не выдержать испытания и дать сбой. В свою очередь градиентный спуск и его вариации будут медленно, но верно приближать нас к цели — минимуму функции. А на счет скорости не волнуйтесь — мы наверняка еще разберем способы, которые позволят нам задавать и регулировать длину шага (то есть скорость).

А теперь собственно краткое резюме.

Во-первых, надеюсь, что изложенный в статье материал, поможет начинающим «дата сайнтистам» в понимании того, как решать уравнения простой (и не только) линейной регрессии.

Во-вторых, мы рассмотрели несколько способов решения уравнения. Теперь, в зависимости от ситуации, мы можем выбрать тот, который лучше всего подходит для решения поставленной задачи.

В-третьих, мы увидели силу дополнительных настроек, а именно длины шага градиентного спуска. Этим параметром нельзя пренебрегать. Как было подмечено выше, с целью сокращения затрат на проведение вычислений, длину шага стоит изменять по ходу спуска.

В-четвертых, в нашем случае, «самописные» функции показали лучший временной результат вычислений. Вероятно, это связано с не самым профессиональным применением возможностей библиотеки NumPy. Но как бы то ни было, вывод напрашивается следующий. С одной стороны, иногда стоит подвергать сомнению устоявшиеся мнения, а с другой — не всегда стоит все усложнять — наоборот иногда эффективнее оказывается более простой способ решения задачи. А так как цель у нас была разобрать три подхода в решении уравнения простой линейной регрессии, то использование «самописных» функций нам вполне хватило.

Предыдущая работа автора — «Исследуем утверждение центральной предельной теоремы с помощью экспоненциального распределения»
Следующая работа автора — «Приводим уравнение линейной регрессии в матричный вид»

Литература (или что-то вроде того)

1. Линейная регрессия

http://statistica.ru/theory/osnovy-lineynoy-regressii/

2. Метод наименьших квадратов

mathprofi.ru/metod_naimenshih_kvadratov.html

3. Производная

www.mathprofi.ru/chastnye_proizvodnye_primery.html

4. Градиент

mathprofi.ru/proizvodnaja_po_napravleniju_i_gradient.html

5. Градиентный спуск

habr.com/ru/post/471458

habr.com/ru/post/307312

artemarakcheev.com//2017-12-31/linear_regression

6. Библиотека NumPy

docs.scipy.org/doc/numpy-1.10.1/reference/generated/numpy.linalg.solve.html

docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.linalg.pinv.html

pythonworld.ru/numpy/2.html

Источник

Линейная регрессия

Перевод

Ссылка на автора

Введение

Недавно я написал об оценке максимального правдоподобия в своей продолжающейся серии статей об основах машинного обучения:

Оценка максимального правдоподобия

Основы машинного обучения (часть 2)

towardsdatascience.com

В этом посте мы узнали, что значит «моделировать» данные, а затем, как использовать MLE, чтобы найти параметры нашей модели. В этом посте мы собираемся погрузиться в линейную регрессию, одну из наиболее важных моделей в статистике, и научимся формировать ее с точки зрения MLE. Решение представляет собой прекрасный математический пример, который, как и большинство моделей MLE, богат интуицией. Я предполагаю, что вы получили представление о словаре, который я рассмотрел в других сериях (плотности вероятностей, условные вероятности, функция вероятности, данные iid и т. Д.). Если вы видите здесь что-то, что вас не устраивает, проверьте Вероятность а также MLE сообщения из этой серии для ясности.

Модель

Мы используем линейную регрессию, когда наши данные имеют линейную связь между независимыми переменными (нашими функциями) и зависимой переменной (нашей целью). В посте MLE мы увидели некоторые данные, которые тоже выглядели примерно так:

Мы заметили, что между x и y существует линейная зависимость, но она не идеальна. Мы думаем об этих недостатках как о результате некоторой ошибки или шумового процесса. Представьте, что проведете линию прямо через облако точек. Ошибка для каждой точки — это расстояние от точки до нашей линии. Мы хотели бы явно включить эти ошибки в нашу модель. Один из способов сделать это — предположить, что ошибки распределены из гауссовского распределения со средним значением 0 и некоторой неизвестной дисперсией σ². Gaussian кажется хорошим выбором, потому что наши ошибки выглядят симметричными относительно линии, и маленькие ошибки более вероятны, чем большие. Мы пишем нашу линейную модель с гауссовым шумом так:

Линейная модель с гауссовским шумовым членом.

Термин ошибки взят из нашего гауссовского алгоритма, а затем вычисленный нами у вычисляется путем добавления ошибки к выходным данным линейного уравнения. Эта модель имеет три параметра: наклон и пересечение нашей линии и дисперсию распределения шума. Наша главная цель — найти наилучшие параметры для наклона и пересечения нашей линии.

Функция правдоподобия

Чтобы применить максимальное правдоподобие, нам сначала нужно вывести функцию правдоподобия. Во-первых, давайте перепишем нашу модель сверху как единое условное распределение, заданное x:

Для данного x, y взят из гауссовского центра по нашей линии.

Это эквивалентно проталкиванию нашего x через уравнение линии, а затем добавлению шума от среднего гауссова 0.

Теперь мы можем записать условное распределение y для заданного x в терминах этого гауссиана. Это просто уравнение функции плотности вероятности распределения Гаусса с нашим линейным уравнением вместо среднего значения:

PDF из y с учетом х и нашей линейной модели.

Точка с запятой в условном распределении действует как запятая, но это полезное обозначение для отделения наших наблюдаемых данных от параметров.

Каждая точка является независимой и одинаково распределенной (iid), поэтому мы можем записать функцию правдоподобия относительно всех наших наблюдаемых точек как произведение каждой отдельной плотности вероятности. Поскольку σ² одинаково для каждой точки данных, мы можем вычленить термин гауссианы, который не включает x или y из произведения:

Вероятность нашего сбора данных X.

Log-правдоподобие:

Следующий шаг в MLE — найти параметры, которые максимизируют эту функцию. Чтобы упростить наше уравнение, давайте возьмем журнал нашей вероятности. Напомним, что максимизация логарифмической вероятности такая же, как максимизация вероятности, поскольку логарифм является монотонным. Натуральный логарифм вычитается по экспоненте, превращает произведения в суммы бревен и делится на вычитание бревен; так что наша логарифмическая вероятность выглядит намного проще:

Вывод логарифмической вероятности для нашей модели.

Сумма квадратов ошибок:

Чтобы еще кое-что прояснить, давайте запишем вывод нашей строки как одно значение:

Оценка Y от нашей линии.

Теперь наша логарифмическая вероятность может быть записана как:

Упрощенное логарифмическое уравнение правдоподобия.

Чтобы убрать отрицательные знаки, давайте вспомним, что максимизация числа — это то же самое, что минимизация отрицания числа. Поэтому вместо того, чтобы максимизировать вероятность, давайте минимизируем отрицательную логарифмическую вероятность:

Минимизируйте отрицательное логарифмическое правдоподобие.

Наша конечная цель — найти параметры нашей линии. Чтобы минимизировать отрицательное логарифмическое правдоподобие по отношению к линейным параметрам (θs), мы можем представить, что наш дисперсионный член является фиксированной константой.

Удаление любых констант, которые не включают наши θs, не изменит решение Поэтому мы можем выбросить любые постоянные термины и изящно написать то, что мы пытаемся минимизировать, как:

Сумма квадратов ошибок.

Оценка максимального правдоподобия для нашей линейной модели — это линия, которая минимизирует сумму квадратов ошибок! Это прекрасный результат, и вы увидите, что минимизация квадратичных ошибок повсеместно встречается в машинном обучении и статистике.

Решение для параметров

Мы пришли к выводу, что оценки максимального правдоподобия для нашего наклона и перехвата можно найти путем минимизации суммы квадратов ошибок. Давайте расширим нашу цель минимизации и используемякак наш индекс над нашимNТочки данных:

Квадрат в формуле SSE делает его квадратичным с одним минимумом. Минимум можно найти, взяв производную по каждому из параметров, установив ее равной 0 и решив для параметров по очереди.

Перехват:

Давайте начнем с решения для перехвата. Взятие частной производной по отношению к перехвату и проработка дает нам:

Производная SSE относительно перехвата нашей линии.

Горизонтальные полосы над переменными показывают среднее значение этих переменных. Мы использовали тот факт, что сумма значений переменных равна среднему значению этих значений, умноженному на количество значений, которые у нас есть. Установка производной равной 0 и решение для перехвата дает нам:

MLE для перехвата.

Это довольно аккуратный результат. Это уравнение линии со средствами х и у вместо этих переменных. Перехват по-прежнему зависит от наклона, поэтому нам нужно найти его дальше.

Склон:

Мы начнем с частной производной SSE относительно нашего наклона. Мы включаем наше решение для перехвата и используем алгебру, чтобы изолировать термин наклона:

Производная SSE относительно наклона нашей линии.

Установка этого значения равным 0 и решение для наклона дает нам:

Хотя технически мы закончили, мы можем использовать некоторую причудливую алгебру, чтобы переписать это, не используяN:

MLE оценка наклона.

Собираем все вместе:

Мы можем использовать эти производные уравнения, чтобы написать простую функцию в python для решения параметров для любой линии, заданной как минимум двумя точками:

def find_line(xs, ys):
    """Calculates the slope and intercept"""        # number of points
    n = len(xs)    # calculate means
    x_bar = sum(xs)/n
    y_bar = sum(ys)/n
            # calculate slope
    num = 0
    denom = 0
    for i in range(n):
        num += (xs[i]-x_bar)*(ys[i]-y_bar)
        denom += (xs[i]-x_bar)**2
    slope = num/denom
        # calculate intercept
    intercept = y_bar - slope*x_bar
        return slope, intercept

Используя этот код, мы можем поместить строку в наши исходные данные (см. Ниже). Это максимальная оценка правдоподобия для наших данных. Линия минимизирует сумму квадратов ошибок, поэтому этот метод линейной регрессии часто называют обычными наименьшими квадратами.

Решение MLE для нашей модели линейной регрессии.

Последние мысли

Я хотел написать этот пост главным образом для того, чтобы подчеркнуть связь между минимизацией суммы квадратов ошибок и подходом оценки максимального правдоподобия к линейной регрессии. Большинство людей сначала учатся решать линейную регрессию путем минимизации квадратичной ошибки, но, как правило, не понимают, что это происходит из вероятностной модели с запечатленными в допущениях (например, гауссовых распределенных ошибок).

Существует более элегантное решение для нахождения параметров этой модели, но для этого требуется линейная алгебра. Я планирую вернуться к линейной регрессии после того, как расскажу о линейной алгебре в своей серии основ, и покажу, как ее можно использовать для подбора более сложных кривых, таких как полиномы и экспоненты.

Увидимся в следующий раз!

Источник

Все курсы > Оптимизация > Занятие 4 (часть 2)

Во второй части занятия перейдем к практике.

Продолжим работать в том же ноутбуке⧉

Сквозной пример

Данные и постановка задачи

Обратимся к хорошо знакомому нам датасету недвижимости в Бостоне.

boston = pd.read_csv(‘/content/boston.csv’)

При этом нам нужно будет решить две основные задачи:

Задача 1. Научиться оценивать качество модели не только с точки зрения метрики, но и исходя из рассмотренных ранее допущений модели. Эту задачу мы решим в три этапа.

Этап 1. Построим базовую (baseline) модель линейной регрессии с помощью класса LinearRegression библиотеки sklearn и оценим, насколько выполняются рассмотренные выше допущения.
Этап 2. Попробуем изменить данные таким образом, чтобы модель в большей степени соответствовала этим критериям.
Этап 3. Обучим еще одну модель и посмотрим, как изменится результат.

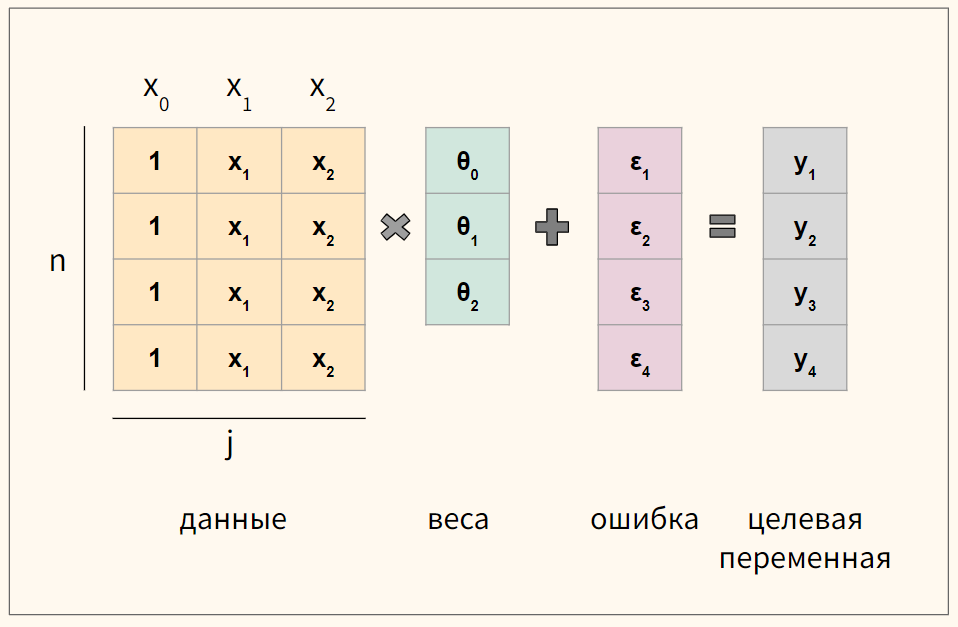
Задача 2. С нуля построить модель множественной линейной регрессии и сравнить прогноз с результатом, полученным при решении первой задачи. При этом обучение модели мы реализуем двумя способами, а именно, через:

Метод наименьших квадратов
Метод градиентного спуска

Разделение выборки

Мы уже не раз говорили про важность разделения выборки на обучаущую и тестовую части. Сегодня же, с учетом того, что нам предстоит изучить много нового материала, мы опустим этот этап и будем обучать и тестировать модель на одних и тех же данных.

Исследовательский анализ данных

Теперь давайте более внимательно посмотрим на имеющиеся у нас данные. Как вы вероятно заметили, все признаки в этом датасете количественные, за исключением переменной CHAS.

RangeIndex: 506 entries, 0 to 505

Data columns (total 14 columns):

# Column Non-Null Count Dtype

— —— ————— ——

0 CRIM 506 non-null float64

1 ZN 506 non-null float64

2 INDUS 506 non-null float64

3 CHAS 506 non-null float64

4 NOX 506 non-null float64

5 RM 506 non-null float64

6 AGE 506 non-null float64

7 DIS 506 non-null float64

8 RAD 506 non-null float64

9 TAX 506 non-null float64

10 PTRATIO 506 non-null float64

11 B 506 non-null float64

12 LSTAT 506 non-null float64

13 MEDV 506 non-null float64

dtypes: float64(14)

memory usage: 55.5 KB

# мы видим, что переменная CHAS категориальная

boston.CHAS.value_counts()

0.0 471

1.0 35

Name: CHAS, dtype: int64

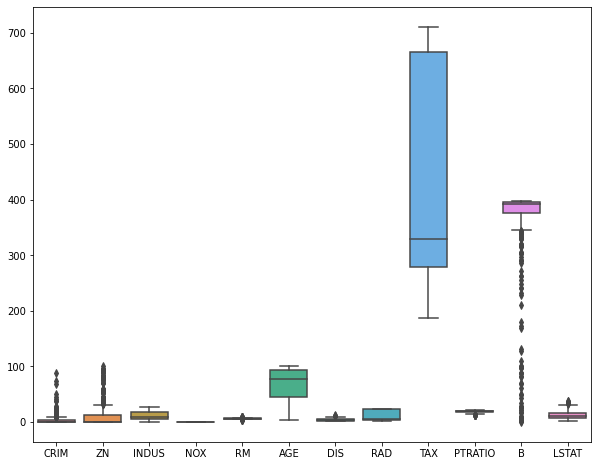
Посмотрим на распределение признаков с помощью boxplots.

plt.figure(figsize = (10, 8))

sns.boxplot(data = boston.drop(columns = [‘CHAS’, ‘MEDV’]))

plt.show()

Посмотрим на распределение целевой переменной.

def box_density(x):

# создадим два подграфика

f, (ax_box, ax_kde) = plt.subplots(nrows = 2, # из двух строк

ncols = 1, # и одного столбца

sharex = True, # оставим только нижние подписи к оси x

gridspec_kw = {‘height_ratios’: (.15, .85)}, # зададим разную высоту строк

figsize = (10,8)) # зададим размер графика

# в первом подграфике построим boxplot

sns.boxplot(x = x, ax = ax_box)

ax_box.set(xlabel = None)

# во втором — график плотности распределения

sns.kdeplot(x, fill = True)

# зададим заголовок и подписи к осям

ax_box.set_title(‘Распределение переменной’, fontsize = 17)

ax_kde.set_xlabel(‘Переменная’, fontsize = 15)

ax_kde.set_ylabel(‘Плотность распределения’, fontsize = 15)

plt.show()

box_density(boston.iloc[:, —1])

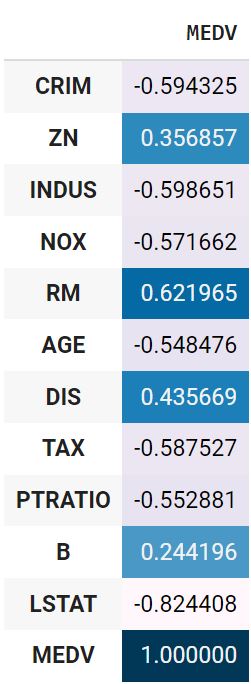
Посмотрим на корреляцию количественных признаков с целевой переменной.

boston.drop(columns = ‘CHAS’).corr().MEDV.to_frame().style.background_gradient()

Используем точечно-бисериальную корреляцию для оценки взамосвязи переменной CHAS и целевой переменной.

def pbc(continuous, binary):

# преобразуем количественную переменную в массив Numpy

continuous_values = np.array(continuous)

# классы качественной переменной превратим в нули и единицы

binary_values = np.unique(binary, return_inverse = True)[1]

# создадим две подгруппы количественных наблюдений

# в зависимости от класса дихотомической переменной

group0 = continuous_values[np.argwhere(binary_values == 0).flatten()]

group1 = continuous_values[np.argwhere(binary_values == 1).flatten()]

# найдем средние групп,

mean0, mean1 = np.mean(group0), np.mean(group1)

# а также длины групп и всего датасета

n0, n1, n = len(group0), len(group1), len(continuous_values)

# рассчитаем СКО количественной переменной

std = continuous_values.std()

# подставим значения в формулу

return (mean1 — mean0) / std * np.sqrt( (n1 * n0) / (n * (n—1)) )

pbc(boston.MEDV, boston.CHAS)

Обработка данных

Пропущенные значения

Посмотрим, есть ли пропущенные значения.

CRIM 0

ZN 0

INDUS 0

CHAS 0

NOX 0

RM 0

AGE 0

DIS 0

RAD 0

TAX 0

PTRATIO 0

B 0

LSTAT 0

MEDV 0

dtype: int64

Выбросы

Удалим выбросы.

from sklearn.ensemble import IsolationForest

clf = IsolationForest(max_samples = 100, random_state = 42)

clf.fit(boston)

boston[‘anomaly’] = clf.predict(boston)

boston = boston[boston.anomaly == 1]

boston = boston.drop(columns = ‘anomaly’)

boston.shape

При удалении выбросов важно помнить, что полное отсутствие вариантивности в данных не позволит выявить взаимосвязи.

Масштабирование признаков

Приведем признаки к одному масштабу (целевую переменную трогать не будем).

boston.iloc[:, :—1] = (boston.iloc[:, :—1] — boston.iloc[:, :—1].mean()) / boston.iloc[:, :—1].std()

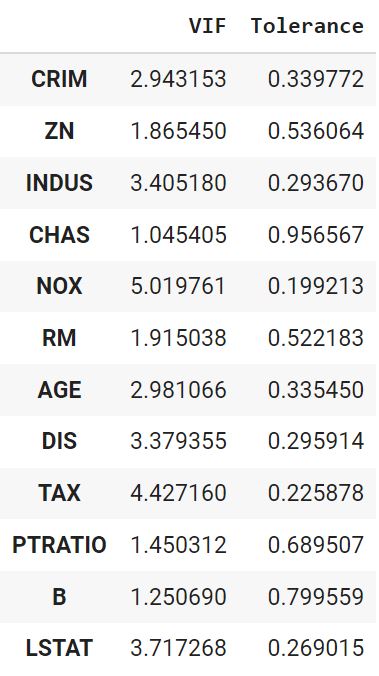
Замечу, что метод наименьших квадратов не требует масштабирования признаков, градиентному спуску же напротив необходимо, чтобы все значения находились в одном диапазоне (подробнее в дополнительных материалах).

Кодирование категориальных переменных

После стандартизации переменная CHAS также сохранила только два значения.

boston.CHAS.value_counts()

-0.182581 389

5.463391 13

Name: CHAS, dtype: int64

Ее можно не трогать.

Построение модели

Создадим первую пробную (baseline) модель с помощью библиотеки sklearn.

baseline-модель

X = boston.drop(‘MEDV’, axis = 1)

y = boston[‘MEDV’]

from sklearn.linear_model import LinearRegression

model = LinearRegression()

y_pred = model.fit(X, y).predict(X)

Оценка качества

Диагностика модели, метрики качества и функции потерь

Вероятно, вы заметили, что мы использовали MSE и для обучения модели, и для оценки ее качества. Возникает вопрос, есть ли отличие между функцией потерь и метрикой качества модели.

Функция потерь и метрика качества могут совпадать, а могут и не совпадать. Важно понимать, что у них разное назначение.

Функция потерь — это часть алгоритма, нам важно, чтобы эта функция была дифференцируема (у нее была производная)
Производная метрики качества нас не интересует. Метрика качества должна быть адекватна решаемой задаче.

MSE, RMSE, MAE, MAPE

MSE и RMSE

Для оценки качества RMSE предпочтительнее, чем MSE, потому что показывает насколько ошибается модель в тех же единицах измерения, что и целевая переменная. Например, если диапазон целевой переменной от 80 до 100, а RMSE 20, то в среднем модель ошибается на 20-25 процентов.

В качестве практики напишем собственную функцию.

# параметр squared = True возвращает MSE

# параметр squared = False возвращает RMSE

def mse(y, y_pred, squared = True):

mse = ((y — y_pred) ** 2).sum() / len(y)

if squared == True:

return mse

else:

return np.sqrt(mse)

mse(y, y_pred), mse(y, y_pred, squared = False)

(9.980044349414223, 3.1591208190593507)

Сравним с sklearn.

from sklearn.metrics import mean_squared_error

# squared = False дает RMSE

mean_squared_error(y, y_pred, squared = False)

MAE

Приведем формулу.

$$ MAE = frac{sum |y-hat{y}|}{n} $$

Средняя абсолютная ошибка представляет собой среднее арифметическое абсолютной ошибки $varepsilon = |y-hat{y}| $ и использует те же единицы измерения, что и целевая переменная.

def mae(y, y_pred):

return np.abs(y — y_pred).sum() / len(y)

from sklearn.metrics import mean_absolute_error

mean_absolute_error(y, y_pred)

MAE часто используется при оценке качества моделей временных рядов.

MAPE

Средняя абсолютная ошибка в процентах (mean absolute percentage error) по сути выражает MAE в процентах, а не в абсолютных величинах, представляя отклонение как долю от истинных ответов.

$$ MAPE = frac{1}{n} sum vert frac{y-hat{y}}{y} vert $$

Это позволяет сравнивать модели с разными единицами измерения между собой.

def mape(y, y_pred):

return 1/len(y) * np.abs((y — y_pred) / y).sum()

from sklearn.metrics import mean_absolute_percentage_error

mean_absolute_percentage_error(y, y_pred)

Коэффициент детерминации

В рамках вводного курса в ответах на вопросы к занятию по регрессии мы подробно рассмотрели коэффициент детерминации ($R^2$), его связь с RMSE, а также зачем нужен скорректированный $R^2$. Как мы знаем, если использовать, например, класс LinearRegression, то эта метрика содержится в методе .score().

Также можно использовать функцию r2_score() модуля metrics.

from sklearn.metrics import r2_score

r2_score(y, y_pred)

Для скорректированного $R^2$ напишем собственную функцию.

def r_squared(x, y, y_pred):

r2 = 1 — ((y — y_pred)** 2).sum()/((y — y.mean()) ** 2).sum()

n, k = x.shape

r2_adj = 1 — ((y — y_pred)** 2).sum()/((y — y.mean()) ** 2).sum()

return r2, r2_adj

(0.7965234359550825, 0.7965234359550825)

Диагностика модели

Теперь проведем диагностику модели в соответствии со сделанными ранее допущениями.

Анализ остатков и прогнозных значений

Напишем диагностическую функцию, которая сразу выведет несколько интересующих нас графиков и метрик, касающихся остатков и прогнозных значений.

from scipy.stats import probplot

from statsmodels.graphics.tsaplots import plot_acf

from statsmodels.stats.stattools import durbin_watson

def diagnostics(y, y_pred):

residuals = y — y_pred

residuals_mean = np.round(np.mean(y — y_pred), 3)

f, ((ax_rkde, ax_prob), (ax_ry, ax_auto), (ax_yy, ax_ykde)) = plt.subplots(nrows = 3,

ncols = 2,

figsize = (12, 18))

# в первом подграфике построим график плотности остатков

sns.kdeplot(residuals, fill = True, ax = ax_rkde)

ax_rkde.set_title(‘Residuals distribution’, fontsize = 14)

ax_rkde.set(xlabel = f‘Residuals, mean: {residuals_mean}’)

ax_rkde.set(ylabel = ‘Density’)

# во втором — график нормальной вероятности остатков

probplot(residuals, dist = ‘norm’, plot = ax_prob)

ax_prob.set_title(‘Residuals probability plot’, fontsize = 14)

# в третьем — график остатков относительно прогноза

ax_ry.scatter(y_pred, residuals)

ax_ry.set_title(‘Predicted vs. Residuals’, fontsize = 14)

ax_ry.set(xlabel = ‘y_pred’)

ax_ry.set(ylabel = ‘Residuals’)

# в четвертом — автокорреляцию остатков

plot_acf(residuals, lags = 30, ax = ax_auto)

ax_auto.set_title(‘Residuals Autocorrelation’, fontsize = 14)

ax_auto.set(xlabel = f‘Lags ndurbin_watson: {durbin_watson(residuals).round(2)}’)

ax_auto.set(ylabel = ‘Autocorrelation’)

# в пятом — сравним прогнозные и фактические значения

ax_yy.scatter(y, y_pred)

ax_yy.plot([y.min(), y.max()], [y.min(), y.max()], «k—«, lw = 1)

ax_yy.set_title(‘Actual vs. Predicted’, fontsize = 14)

ax_yy.set(xlabel = ‘y_true’)

ax_yy.set(ylabel = ‘y_pred’)

# в шестом — сравним распределение истинной и прогнозной целевой переменных

sns.kdeplot(y, fill = True, ax = ax_ykde, label = ‘y_true’)

sns.kdeplot(y_pred, fill = True, ax = ax_ykde, label = ‘y_pred’)

ax_ykde.set_title(‘Actual vs. Predicted Distribution’, fontsize = 14)

ax_ykde.set(xlabel = ‘y_true and y_pred’)

ax_ykde.set(ylabel = ‘Density’)

ax_ykde.legend(loc = ‘upper right’, prop = {‘size’: 12})

plt.tight_layout()

plt.show()

Разберем полученную информацию.

В целом остатки модели распределены нормально с нулевым средним значением
Явной гетероскедастичности нет, хотя мы видим, что дисперсия не всегда равномерна
Присутствует умеренная отрицательная корреляция
График y_true vs. y_pred показывает насколько сильно прогнозные значения отклоняются от фактических. В идеальной модели (без шума, т.е. без случайных колебаний) точки должны были би стремиться находиться на диагонали, в более реалистичной модели нам бы хотелось видеть, что точки плотно сосредоточены вокруг диагонали.
Распределение прогнозных значений в целом повторяет распределение фактических.

Мультиколлинеарность

Отдельно проведем анализ на мультиколлинеарность. Напишем соответствующую функцию.

def vif(df, features):

vif, tolerance = {}, {}

# пройдемся по интересующим нас признакам

for feature in features:

# составим список остальных признаков, которые будем использовать

# для построения регрессии

X = [f for f in features if f != feature]

# поместим текущие признаки и таргет в X и y

X, y = df[X], df[feature]

# найдем коэффициент детерминации

r2 = LinearRegression().fit(X, y).score(X, y)

# посчитаем tolerance

tolerance[feature] = 1 — r2

# найдем VIF

vif[feature] = 1 / (tolerance[feature])

# выведем результат в виде датафрейма

return pd.DataFrame({‘VIF’: vif, ‘Tolerance’: tolerance})

vif(df = X.drop(‘CHAS’, axis = 1), features = X.drop(‘CHAS’, axis = 1).columns)

Дополнительная обработка данных

Попробуем дополнительно улучшить некоторые из диагностических показателей.

VIF

Уберем признак с наибольшим VIF (RAD) и посмотрим, что получится.

vif(df = X, features = [‘CRIM’,

‘ZN’,

‘INDUS’,

‘CHAS’,

‘NOX’,

‘RM’,

‘AGE’,

‘DIS’,

‘TAX’,

‘PTRATIO’,

‘B’,

‘LSTAT’])

Показатели пришли в норму. Окончательно удалим RAD.

boston.drop(columns = ‘RAD’, inplace = True)

Преобразование данных

Применим преобразование Йео-Джонсона.

from sklearn.preprocessing import PowerTransformer

pt = PowerTransformer()

boston = pd.DataFrame(pt.fit_transform(boston),

columns = boston.columns)

Отбор признаков

Посмотрим на линейную корреляцию Пирсона количественных признаков и целевой переменной.

boston_t.drop(columns = ‘CHAS’).corr().MEDV.to_frame().style.background_gradient()

Также рассчитаем точечно-бисериальную корреляцию.

pbc(boston_t.MEDV, boston_t.CHAS)

Удалим признаки с наименьшей корреляцией, а именно ZN, CHAS, DIS и B.

boston.drop(columns = [‘ZN’, ‘CHAS’, ‘DIS’, ‘B’], inplace = True)

Повторное моделирование и диагностика

Повторное моделирование

Выполним повторное моделирование.

X = boston_t.drop(columns = [‘ZN’, ‘CHAS’, ‘DIS’, ‘B’, ‘MEDV’])

y = boston_t.MEDV

from sklearn.linear_model import LinearRegression

model = LinearRegression()

y_pred = model.fit(X, y).predict(X)

Оценка качества и диагностика

Оценим качество. Так как мы преобразовали целевую переменную, показатель RMSE не будет репрезентативен. Воспользуемся MAPE и $R^2$.

(0.7546883769637166, 0.7546883769637166)

Отклонение прогнозного значения от истинного снизилось. $R^2$ немного уменьшился, чтобы бывает, когда мы пытаемся привести модель к соответствию допущениям. Проведем диагностику.

Распределение остатков немного улучшилось, при этом незначительно усилилась их отрицательная автокорреляция. Распределение целевой переменной стало менее островершинным.

Данные можно было бы продолжить анализировать и улучшать, однако в рамках текущего занятия перейдем к механике обучения модели.

Коэффициенты

Выведем коэффициенты для того, чтобы сравнивать их с результатами построенных с нуля моделей.

model.intercept_, model.coef_

(9.574055157844797e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]))

Обучение модели

Теперь когда мы поближе познакомились с понятием регрессии, разобрали функции потерь и изучили допущения, при которых модель может быть удачной аппроксимацией данных, пора перейти к непосредственному созданию алгоритмов.

Векторизация уравнения

Для удобства векторизуем приведенное выше уравнение множественной линейной регрессии

$$ y = begin{bmatrix} y_1 \ y_2 \ vdots \ y_n end{bmatrix} X = begin{bmatrix} x_0 & x_1 & ldots & x_j \ x_0 & x_1 & ldots & x_j \ vdots & vdots & vdots & vdots \ x_{0} & x_{1} & ldots & x_{n,j} end{bmatrix}, theta = begin{bmatrix} theta_0 \ theta_1 \ vdots \ theta_n end{bmatrix}, varepsilon = begin{bmatrix} varepsilon_1 \ varepsilon_2 \ vdots \ varepsilon_n end{bmatrix} $$

где n — количество наблюдений, а j — количество признаков.

Обратите внимание, что мы создали еще один столбец данных $ x_0 $, который будем умножать на сдвиг $ theta_0 $. Его мы заполним единицами.

В результате такого несложного преобразования значение сдвига не изменится, но мы сможем записать уравнение через умножение матрицы на вектор.

$$ y = Xtheta + varepsilon $$

Кроме того, как мы увидим ниже, так нам не придется искать отдельную производную для коэффициента $ theta_0 $.

Схематично для модели с четырьмя наблюдениями (n = 4) и двумя признаками (j = 2) получаются вот такие матрицы.

Функция потерь

Как мы уже говорили, чтобы подобрать оптимальные коэффициенты $theta$, нам нужен критерий или функция потерь. Логично измерять отклонение прогнозного значения от истинного.

$$ varepsilon = Xtheta-y $$

При этом опять же просто складывать отклонения или ошибки мы не можем. Положительные и отрицательные значения будут взаимоудаляться. Для решения этой проблемы можно, например, использовать модуль и это приводит нас к абсолютной ошибке или L1 loss.

Абсолютная ошибка, L1 loss

При усреднении на количество наблюдений мы получаем среднюю абсолютную ошибку (mean absolute error, MAE).

$$ MAE = frac{sum{|y-Xtheta|}}{n} = frac{sum{|varepsilon|}}{n} $$

Приведем пример такой функции на Питоне.

def L1(y_true, y_pred):

return np.sum(np.abs(y_true — y_pred)) / y_true.size

Помимо модуля ошибку можно возводить в квадрат.

Квадрат ошибки, L2 loss

В этом случай говорят про сумму квадратов ошибок (sum of squared errors, SSE) или сумму квадратов остатков (sum of squared residuals, SSR или residual sum of squares, RSS).

$$ SSE = sum (y-Xtheta)^2 $$

Как мы уже знаем, на практике вместо SSE часто используется MSE, или вернее half MSE для удобства нахождения производной.

$$ MSE = frac{1}{2n} sum (y-theta X)^2 $$

Ниже код на Питоне.

def L2(y_true, y_pred):

return np.sum((y_true — y_pred) ** 2) / y_true.size

На практике у обеих функций есть сильные и слабые стороны. Рассмотрим L1 loss (MAE) и L2 loss (MSE) на графике.

# для построения графиков мы используем x вместо y_true, y_pred

# в качестве входящего значения

def mse(x):

return x ** 2

def mae(x):

return np.abs(x)

plt.figure(figsize = (10, 8))

x_vals = np.arange(—3, 3, 0.01)

plt.plot(x_vals, mae(x_vals), label = ‘MAE’)

plt.plot(x_vals, mse(x_vals), label = ‘MSE’)

plt.legend(loc = ‘upper center’, prop = {‘size’: 14})

plt.grid()

plt.show()

Очевидно, при отклонении от точки минимума из-за возведения в квадрат L2 значительно быстрее увеличивает ошибку, поэтому если в данных есть выбросы при суммированнии они очень сильно влияют на этот показатель, хотя де-факто большая часть значений такого уровня потерь не дали бы.

Функция L1 не дает такой большой ошибки на выбросах, однако ее сложно дифференцировать, в точке минимума ее производная не определена.

Функция Хьюбера

Рассмотрим функцию Хьюбера (Huber loss), которая объединяет сильные стороны вышеупомянутых функций и при этом лишена их недостатков. Посмотрим на формулу.

$$ L_{delta}= left{begin{matrix} frac{1}{2}(y-hat{y})^{2} & if | y-hat{y} | < delta\ delta (|y-hat{y}|-frac1 2 delta) & otherwise end{matrix}right. $$

Представим ее на графике.

plt.figure(figsize = (10, 8))

def huber(x, delta = 1.):

huber_mse = 0.5 * np.square(x)

huber_mae = delta * (np.abs(x) — 0.5 * delta)

return np.where(np.abs(x) <= delta, huber_mse, huber_mae)

x_vals = np.arange(—3, 3, 0.01)

plt.plot(x_vals, mae(x_vals), label = ‘MAE’)

plt.plot(x_vals, mse(x_vals), label = ‘MSE’)

plt.plot(x_vals, huber(x_vals, delta = 2), label = ‘Huber’)

plt.legend(loc = ‘upper center’, prop = {‘size’: 14})

plt.grid()

plt.show()

Также приведем код этой функции.

def huber(y_pred, y_true, delta = 1.0):

# пропишем обе части функции потерь

huber_mse = 0.5 * (y_true — y_pred) ** 2

huber_mae = delta * (np.abs(y_true — y_pred) — 0.5 * delta)

# выберем одну из них в зависимости от дельта

return np.where(np.abs(y_true — y_pred) <= delta, huber_mse, huber_mae)

На сегодняшнем занятии мы, как и раньше, в качестве функции потерь используем MSE.

Метод наименьших квадратов

Нормальные уравнения

Для множественной линейной регрессии коэффициенты находятся по следующей формуле

$$ theta = (X^TX)^{-1}X^Ty $$

Разберем эту формулу подробнее. Сумму квадратов остатков (SSE) можно переписать как произведение вектора $ hat{varepsilon} $ на самого себя, то есть $ SSE = varepsilon^{T} varepsilon$. Помня, что $varepsilon = y-Xtheta $ получаем (не забывая транспонировать)

$$ (y-Xtheta)^T(y-Xtheta) $$

Раскрываем скобки

$$ y^Ty-y^T(Xtheta)-(Xtheta)^Ty+(Xtheta)^T(Xtheta) $$

Заметим, что $A^TB = B^TA$, тогда

$$ y^Ty-(Xtheta)^Ty-(Xtheta)^Ty+(Xtheta)^T(Xtheta)$$

$$ y^Ty-2(Xtheta)^Ty+(Xtheta)^T(Xtheta) $$

Вспомним, что $(AB)^T = A^TB^T$, тогда

$$ y^Ty-2theta^TX^Ty+theta^TX^TXtheta $$

Теперь нужно найти частные производные этих функций

$$ nabla_{theta} J(theta) = y^Ty-2theta^TX^Ty+theta^TX^TXtheta $$

После дифференцирования мы получаем следующую производную

$$ -2X^Ty+2X^TXtheta $$

Как мы помним, оптимум функции находится там, где производная равна нулю.

$$ -2X^Ty+2X^TXtheta = 0 $$

$$ -X^Ty+X^TXtheta = 0 $$

$$ X^TXtheta = X^Ty $$

Выражение выше называется нормальным уравнением (normal equation). Решив его для $theta$ мы найдем аналитическое решение минимизации суммы квадратов отклонений.

$$ theta = (X^TX)^{-1}X^Ty $$

По теореме Гаусса-Маркова, оценка через МНК является наиболее оптимальной (обладающей наименьшей дисперсией) среди всех методов построения модели.

Код на Питоне

Перейдем к созданию класса линейной регрессии наподобие LinearRegression библиотеки sklearn. Вначале напишем функцию гипотезы (т.е. функцию самой модели), снабдив ее еще одной функцией, которая добавляет столбец из единиц к признакам.

$$ h_{theta}(x) = theta X $$

def add_ones(x):

# важно! метод .insert() изменяет исходный датафрейм

return x.insert(0,‘x0’, np.ones(x.shape[0]))

def h(x, theta):

x = x.copy()

add_ones(x)

return np.dot(x, theta)

Перейдем к функции, отвечающей за обучение модели.

$$ theta = (X^TX)^{-1}X^Ty $$

# строчную `x` используем внутри функций и методов класса

# заглавную `X` вне функций и методов

def fit(x, y):

x = x.copy()

add_ones(x)

xT = x.transpose()

inversed = np.linalg.inv(np.dot(xT, x))

thetas = inversed.dot(xT).dot(y)

return thetas

Обучим модель и выведем коэффициенты.

thetas = fit(X, y)

thetas[0], thetas[1:]

(9.3718435789647e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]))

Примечание. Замечу, что не все матрицы обратимы. В этом случае можно найти псевдообратную матрицу (pseudoinverse). Для этого в Numpy есть функция np.linalg.pinv().

Сделаем прогноз.

y_pred = h(X, thetas)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Создание класса

Объединим код в класс.

class ols():

def __init__(self):

self.thetas = None

def add_ones(self, x):

return x.insert(0,‘x0’, np.ones(x.shape[0]))

def fit(self, x, y):

x = x.copy()

self.add_ones(x)

xT = x.T

inversed = np.linalg.inv(np.dot(xT, x))

self.thetas = inversed.dot(xT).dot(y)

def predict(self, x):

x = x.copy()

self.add_ones(x)

return np.dot(x, self.thetas)

Создадим объект класса и обучим модель.

model = ols()

model.fit(X, y)

Выведем коэффициенты.

model.thetas[0], model.thetas[1:]

(9.3718435789647e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]))

Сделаем прогноз.

y_pred = model.predict(X)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Оценка качества

Оценим качество через MAPE и $R^2$.

(0.7546883769637167, 0.7546883769637167)

Мы видим, что результаты аналогичны.

Метод градиентного спуска

В целом с этим методом мы уже хорошо знакомы. В качестве упражнения давайте реализуем этот алгоритм на Питоне для многомерных данных.

Нахождение градиента

Покажем расчет градиента на схеме.

В данном случае мы берем датасет из четырех наблюдений и двух признаков ($x_1$ и $x_2$) и соответственно используем три коэффициента ($theta_0, theta_1, theta_2$).

Пошаговое построение модели

Начнем с функции гипотезы.

$$ h_{theta}(x) = theta X $$

def h(x, thetas):

return np.dot(x, thetas)

Объявим функцию потерь.

$$ J({theta_j}) = frac{1}{2n} sum (y-theta X)^2 $$

def objective(x, y, thetas, n):

return np.sum((y — h(x, thetas)) ** 2) / (2 * n)

Объявим функцию для расчета градиента.

$$ frac{partial}{partial theta_j} J(theta) = -x_j(y — Xtheta) times frac{1}{n} $$

где j — индекс признака.

def gradient(x, y, thetas, n):

return np.dot(—x.T, (y — h(x, thetas))) / n

Напишем функцию для обучения модели.

$$ theta_j := theta_j-alpha frac{partial}{partial theta_j} J(theta) $$

Символ := означает, что левая часть равенства определяется правой. По сути, с каждой итерацией мы обновляем веса, умножая коэффициент скорости обучения на градиент.

def fit(x, y, iter = 20000, learning_rate = 0.05):

x, y = x.copy(), y.copy()

# функцию add_ones() мы объявили выше

add_ones(x)

thetas, n = np.zeros(x.shape[1]), x.shape[0]

loss_history = []

for i in range(iter):

loss_history.append(objective(x, y, thetas, n))

grad = gradient(x, y, thetas, n)

thetas -= learning_rate * grad

return thetas, loss_history

Обучим модель, выведем коэффициенты и достигнутый (минимальный) уровень ошибки.

thetas, loss_history = fit(X, y, iter = 50000, learning_rate = 0.05)

thetas[0], thetas[1:], loss_history[—1]

(9.493787734953824e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]),

0.1226558115181417)

Полученный результат очень близок к тому, что было найдено методом наименьших квадратов.

Прогноз

Сделаем прогноз.

def predict(x, thetas):

x = x.copy()

add_ones(x)

return np.dot(x, thetas)

y_pred = predict(X, thetas)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Создание класса

Объединим написанные функции в класс.

class gd():

def __init__(self):

self.thetas = None

self.loss_history = []

def add_ones(self, x):

return x.insert(0,‘x0’, np.ones(x.shape[0]))

def objective(self, x, y, thetas, n):

return np.sum((y — self.h(x, thetas)) ** 2) / (2 * n)

def h(self, x, thetas):

return np.dot(x, thetas)

def gradient(self, x, y, thetas, n):

return np.dot(—x.T, (y — self.h(x, thetas))) / n

def fit(self, x, y, iter = 20000, learning_rate = 0.05):

x, y = x.copy(), y.copy()

self.add_ones(x)

thetas, n = np.zeros(x.shape[1]), x.shape[0]

# объявляем переменную loss_history (отличается от self.loss_history)

loss_history = []

for i in range(iter):

loss_history.append(self.objective(x, y, thetas, n))

grad = self.gradient(x, y, thetas, n)

thetas -= learning_rate * grad

# записываем обратно во внутренние атрибуты, чтобы передать методу .predict()

self.thetas = thetas

self.loss_history = loss_history

def predict(self, x):

x = x.copy()

self.add_ones(x)

return np.dot(x, self.thetas)

Создадим объект класса, обучим модель, выведем коэффициенты и сделаем прогноз.

model = gd()

model.fit(X, y, iter = 50000, learning_rate = 0.05)

model.thetas[0], model.thetas[1:], model.loss_history[—1]

(9.493787734953824e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]),

0.1226558115181417)

y_pred = model.predict(X)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Оценка качества

(0.7546883769637167, 0.7546883769637167)

Теперь рассмотрим несколько дополнительных соображений, касающихся построения модели линейной регрессии.

Диагностика алгоритма

Работу алгоритма можно проверить с помощью кривой обучения (learning curve).

Ошибка постоянно снижается
Алгоритм остановится, после истечения заданного количества итераций
Можно задать пороговое значение, после которого он остановится (например, $10^{-1}$)

Построим кривую обучения.

plt.plot(loss_history)

plt.show()

plt.plot(loss_history[:100])

plt.show()

Она также позволяет выбрать адекватный коэффициент скорости обучения.

Подведем итог

Сегодня мы подробно рассмотрели модель множественной линейной регрессиии. В частности, мы поговорили про построение гипотезы, основные функции потерь, допущения модели линейной регрессии, метрики качества и диагностику модели.

Кроме того, мы узнали как изнутри устроены метод наименьших квадратов и метод градиентного спуска и построили соответствующие модели на Питоне.

Отдельно замечу, что, изучив скорректированный коэффициент детерминации, мы начали постепенно обсуждать способы усовершенствования базовых алгоритмов и метрик. На последующих занятиях мы продолжим этот путь в двух направлениях: познакомимся со способами регуляризации функции потерь и начнем создавать более сложные алгоритмы оптимизации.

Но прежде предлагаю в деталях изучить уже знакомый нам алгоритм логистической регрессии.

Дополнительные материалы к занятию.

Источник

	Основные показатели качества:
1.	Коэффициент детерминации R2
2.	Скорректированный коэффициент детерминации
		R	2
3.	Значение F-статистики

4.Сумма квадратов остатков (RSS)

5.Стандартная ошибка регрессии Se

6.Прочие показатели: средняя ошибка аппроксимации, индекс множественной корреляции и т.д.

Коэффициент

детерминации R2

Коэффициент R2 показывает долю объясненной вариации зависимой переменной:

2	1	ei2
R
( yi
y)2

R2 всегда увеличивается с включением новой переменной

3.	F-статистика	для
проверки	качества

уравнения регрессии

F-статистика представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую

переменную)

к остаточной сумме квадратов (в расчете на одну степень свободы)

ESS

F m

RSS

n m 1

n – число выборочных наблюдений, m – число объясняющих переменных

F-статистика для проверки

значимости коэффициента

F-статистика рассчитывается на основе коэффициента детерминации

F	ESS / m		(ESS / TSS) / m		R2 / m
RSS /(n m 1)	(RSS / TSS) /(n m 1)	(1 R2 ) /(n m 1)

Для проверки значимости F-статистики используются таблицы F-распределения с m и (n–m–1) степеней свободы

Сумма квадратов остатков RSS

Является оценкой необъясненной части вариации зависимой переменной

RSS ei2

i 1

Используется как основная минимизируемая величина в МНК, а также для расчета других показателей

Стандартная ошибка регрессии Se

Является оценкой величины квадрата ошибки, приходящейся на одну степень свободы модели

ei2

Используется как основная величина для измерения качества модели (чем она меньше, тем лучше)

Индекс множественной корреляции

Тесноту совместного влияния факторов на результат характеризует индекс (показатель)

множественной корреляции:

		S2
R Ryx x	1	R2
e
Sy2
1	m

Диапазон значений лежит от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака Y со всем набором объясняющих факторов Xi

4. Расчет прогноза. Средняя ошибка прогноза, доверительные интервалы прогноза.

Под прогнозом по множественной регрессионной модели понимается оценка значения зависимой переменной для значений объясняющих переменных, которых нет в исходных наблюдениях. Как и в случае парной модели, различают точечный и интервальный прогнозы.

Точечный прогноз по уравнению регрессии осуществляется путем подстановки значений регрессоров в уравнение регрессии. В дополнение к точечному прогнозу можно определить (по аналогии с парным случаем) границы возможного изменения прогнозируемого показателя, т.е. с заданным уровнем значимости вычислить доверительный интервал для прогнозируемого значения зависимой переменной .

4. Расчет прогноза. Средняя ошибка прогноза, доверительные интервалы прогноза.


Y p t	; k	S	(X p )	Yp Y p t	S
	2	y	2	; k y(X p )
k n m 1,	Y p y(Xp ) b0 bj xpj

S	S 1 XTp (XT X) 1 Xp
y	(X p )

Соседние файлы в папке Лекции

Источник

Средняя случайная ошибка разностей двух выборочных средних оценок, как показано в гл. 7, есть корень квадратный из суммы квадратов ошибок каждой из средних, т. е.
[c.328]

Для проверки этой гипотезы разделим эмпирические данные на две группы по 350 точек с 1-й по 350-ю и с 467-й по 816-ю точки. Серединные точки с 351-й по 466-ю (14.2% от объема выборки) исключаем для лучшего разграничения между группами. Рассчитаем суммы квадратов ошибок для каждой из этих групп [c.152]

При сложении планируемых величин для нескольких работ суммарная ошибка составляет квадратичный корень из суммы квадратов ошибок по каждому виду работы.
[c.42]

Кумулятивная сумма квадратов ошибок Se 100 104 273 .498 982 [c.24]

В табл. 1.2 дана типичная схема построения с помощью экспоненциально взвешенного среднего целочисленного прогноза ежемесячного спроса на некоторый товар. Значение константы экспоненциального сглаживания а была выбрано равным 0,2. На практике чаще всего а необходимо брать из интервала от 0,1 до 0,2. В некоторых программах для ЭВМ пользователю предоставляется возможность найти значение а исходя из минимума суммы квадратов ошибок. Для коротких временных рядов (как в табл, 1,2) более значимым представляется выбор начальной оценки прогноза.
[c.25]

Покажите, что для данных из табл. 1.2 с начальным условием щ-г — 70 при а, = 0,If 0,3 и 0,4 значения суммы квадратов ошибок будут соответственно равны 2615, 2357 и 2212, Причина достаточно высокого оптимального значения а объясняется повышением спроса на товар, начиная с октября и далее.
[c.26]

Теперь вместо составления и вычисления суммы квадратов ошибок, как при нахождении дисперсии, определим другую меру разброса, известную под названием среднее абсолютное отклонение ошибки (MAD,). Из названия следует, что среднее абсолютное отклонение есть просто абсолютное значение ошибки (отклонения). В гл. 1 было рассмотрено экспоненциально взвешенное среднее в качестве одной из форм среднего, поэтому нет причин не вычислять среднее абсолютное отклонение опять по формуле экспоненциально взвешенного среднего абсолютных значений ошибок [c.42]

Сумма квадратов ошибок 2е [c.56]

Используя данные табл. 5.1, при а = 0,2 по методу адаптивной скорости реакции (с лагом и без лага) постройте прогноз значений показателя покажите, что сумма квадратов ошибок прогноза по этим двум методам соответственно рав на 3176 и 1986.
[c.65]

Критерий F в (13.20) при у = 0 имеет / -распределение с 1, (// — / — J) степенями свободы. Гипотезы НА и Нв проверяются так же, как в п. 13.3.2, только сумма квадратов ошибок определяется как СКе = ОСК — СКг и имеет на одну степень свободы меньше, чем в табл. 13.3.
[c.387]

Кумулятивная сумма квадратов ошибок Se,2 1 1,04 4,43 6,74 9,91 10,09
[c.125]

Метод адаптивного сглаживания Брауна. Согласно второму методу Брауна, предполагается, что если ряд значений спроса можно описать некоторой моделью, то желательно применить регрессионный анализ на основе взвешенной регрессии, т. е. большее внимание необходимо уделять той информации, которая поступает позже. Данный метод основывается на простом способе вычисления оценок по методу минимизации взвешенной суммы квадратов ошибок прогноза в случае линейно-аддитивного тренда. Оценка по взвешенному методу наименьших квадратов равна [c.127]

На практике пригодность определяется функцией пригодности — блоком программы, который рассчитывает показатель относительной привлекательности решения. Функция может быть запрограммирована для определения пригодности именно так, как пожелает трейдер например, пригодность можно определять как общую прибыль за вычетом максимального падения капитала. Функция расходов устроена аналогично, но чем выше ее значение, тем хуже работает система. Сумма квадратов ошибок, часто вычисляемая при использовании систем с нейронными сетями или линейной регрессией, может служить примером функции расходов.
[c.48]

Анализ (в смысле. математический или комплексный анализ) является расширением классического исчисления. Аналитические оптимизаторы используют наработанные методы, в особенности методы дифференциального исчисления и исследования аналитических функций для решения практических задач. В некоторых случаях анализ дает прямой (без перебора вариантов) ответ на задачу оптимизации. Так происходит при использовании множественной регрессии, где решение находится с помощью нескольких матричных вычислений. Целью множественной регрессии является подбор таких весов регрессии, при которых минимизируется сумма квадратов ошибок. В других случаях требуется перебор вариантов, например невозможно определить напрямую веса связей в нейронной сети, их требуется оценивать при помощи алгоритма обратного распространения.
[c.57]

Сумма квадратов ошибок. Значения расстояний всех точек до линии регрессии возводят в квадрат и суммируют, получая сумму квадратов ошибок, которая является показателем общей ошибки
[c.650]

Задавшись затем значением р, мы получим оценки р , р и р2, i процесс такого последовательного оценивания можно продолжать до ех пор, пока не будет достигнута сходимость с выбранной заранее точ-юстью. Некоторые эконометрики предпочитают комбинировать поиск итеративной процедурой, применяя поиск для решетки с очень широкими относительно р ячейками и выбирая в качестве начального значе-П1я р для итеративной процедуры тот узел решетки, который обеспе-шл наименьшее значение суммы квадратов ошибок.
[c.318]

По аналогии с моделью регрессии для оценки качества построения модели или для выбора наилучшей модели можно применять сумму квадратов полученных абсолютных ошибок. Для данной аддитивной модели сумма квадратов абсолютных ошибок равна 1,10. По отношению к общей сумме квадратов отклонений уровней ряда от его среднего уровня, равной 71,59, эта величина составляет чуть более 1,5% [c.245]

Численные значения ошибки приведены в гр. 7 табл. 5.14. Если временной ряд ошибок не содержит автокорреляции, его можно использовать вместо исходного ряда для изучения его взаимосвязи с другими временными рядами. Для того чтобы сравнить мультипликативную модель и другие модели временного ряда, можно по аналогии с аддитивной моделью использовать сумму квадратов абсолютных ошибок. Абсолютные ошибки в мультипликативной модели определяются как
[c.250]

В данной модели сумма квадратов абсолютных ошибок составляет 207,40. Общая сумма квадратов отклонений фактических уровней этого ряда от среднего значения равна 5023. Таким образом, доля объясненной дисперсии уровней ряда равна (1 — 207,40/5023) = 0,959, или 95,9%.
[c.250]

Остаточная сумма квадратов по аддитивной модели (сумма квадратов абсолютных ошибок) была рассчитана ранее (табл. 5.10) и составляет 1,10. Следовательно, модель регрессии с фиктивными переменными описывает динамику временного ряда потребления электроэнергии лучше, чем аддитивная модель.
[c.255]

Сумма квадратов абсолютных ошибок = 1,0981 [c.27]

Сумма квадратов абсолютных ошибок S Е = 1,0981
[c.28]

Для его вычисления отклонения по итоговым показателям по каждому признаку в отдельности возводятся в квадрат, полученные величины умножаются на соответствующие частоты, произведения суммируются, сумма делится на все число случаев, результаты уменьшаются на квадраты ошибок и из полученных чисел извлекается квадратный корень.
[c.270]

Главная причина зависимости меры разброса от квадратов ошибок, а, например, не просто от суммы ошибок в том, что возведение в квадрат делает результат положительным вне зависимости от того, была ли первоначальная ошибка отрицательной или положительной. Для большинства прогнозов сумма ошибок стремится к нулю, т. е. положительные и отрицательные ошибки компенсируют одна другую. Вот почему сумма ошибок не может служить удовлетворительной мерой разброса.
[c.42]

Метод, используемый чаще других для нахождения параметров уравнения регрессии и известный как метод наименьших квадратов, дает наилучшие линейные несмещенные оценки. Он называется так потому, что при расчете параметров прямой линии, которая наиболее соответствует фактическим данным, с помощью этого метода стараются найти линию, минимизирующую сумму квадратов значений ошибок или расхождений между величинами Y, которые рассчитаны по уравнению прямой и обозначаются Y, и фактическими наблюдениями. Это показано на рис. 6.2.
[c.265]

После построения сети следует этап ее обучения (тренировки). На этапе обучения происходит подбор коэффициентов в формулах (2.4.1), (2.4.2) для нейронов сети. Эту процедуру можно назвать контролируемым обучением на вход сети подается вектор исходных данных, а сигнал на выходе сравнивается с известным результатом. Целью обучения является минимизация функции ошибок или невязки на множестве примеров путем выбора значений коэффициентов сети. Обычно в качестве меры погрешности берется средняя квадратичная ошибка, которая определяется как сумма квадратов разностей между истинной величиной выхода d k и полученными на сети значениями по всем Р примерам
[c.144]

В ряде случаев проблема мультиколлинеарности может быть решена изменением спецификации модели либо изменением формы модели, либо добавлением объясняющих переменных, которые не учтены в первоначальной модели, но существенно влияющие на зависимую переменную. Если данный метод имеет основания, то его использование уменьшает сумму квадратов отклонений, тем самым сокращая стандартную ошибку регрессии. Это приводит к уменьшению стандартных ошибок коэффициентов.
[c.252]

Сумма квадратов остатков е2 = е е является естественным кандидатом на оценку дисперсии ошибок а1 (конечно, с некоторым поправочным коэффициентом, зависящим от числа степеней свободы) [c.73]

Формально это записывается как минимизация суммы квадратов отклонений (ошибок) функции регрессии и исходных точек
[c.112]

Эти два выражения показывают, как возникает ковариация между [52 и Рз в СИЛУ присутствия 2ыу в каждом из выражений для ошибок Р2 и (33. Положительное и большое значение ос приводит, как мы видим, к большим противоположным значениям ошибок J32 и(33- Если (32 оценивает значение р 2 снизу, то р3 оценивает значение ps сверху, и наоборот. Очень важным является то обстоятельство, что стандартные ошибки могут служить одним из индикаторов наличия мульти-коллинеарности. Формула (5.84) показывает, что истинное значение стандартной ошибки возрастает с увеличением а, однако эта формула содержит неизвестный параметр а . В оцененной величине стандартной ошибки значение а заменяется на Ее2/(п — /г), где 2е2 — сумма квадратов остатков после подгонки уравнения регрессии к эмпирическим данным. Как было показано в (5.19),
[c.162]

Рис. А.4. Блок-схема вычисления мер точности прогноза 1) суммы квадратов ошибок 2) среднего квадрата ошибок 3) средней ошибки 4) среднеа45сол отной процентной ошибки 5) средней лроцентной

Рис. А.4. <a href="/info/19143">Блок-схема</a> вычисления мер точности прогноза 1) суммы квадратов ошибок 2) <a href="/info/5384">среднего квадрата</a> ошибок 3) средней ошибки 4) среднеа45сол отной процентной ошибки 5) средней лроцентной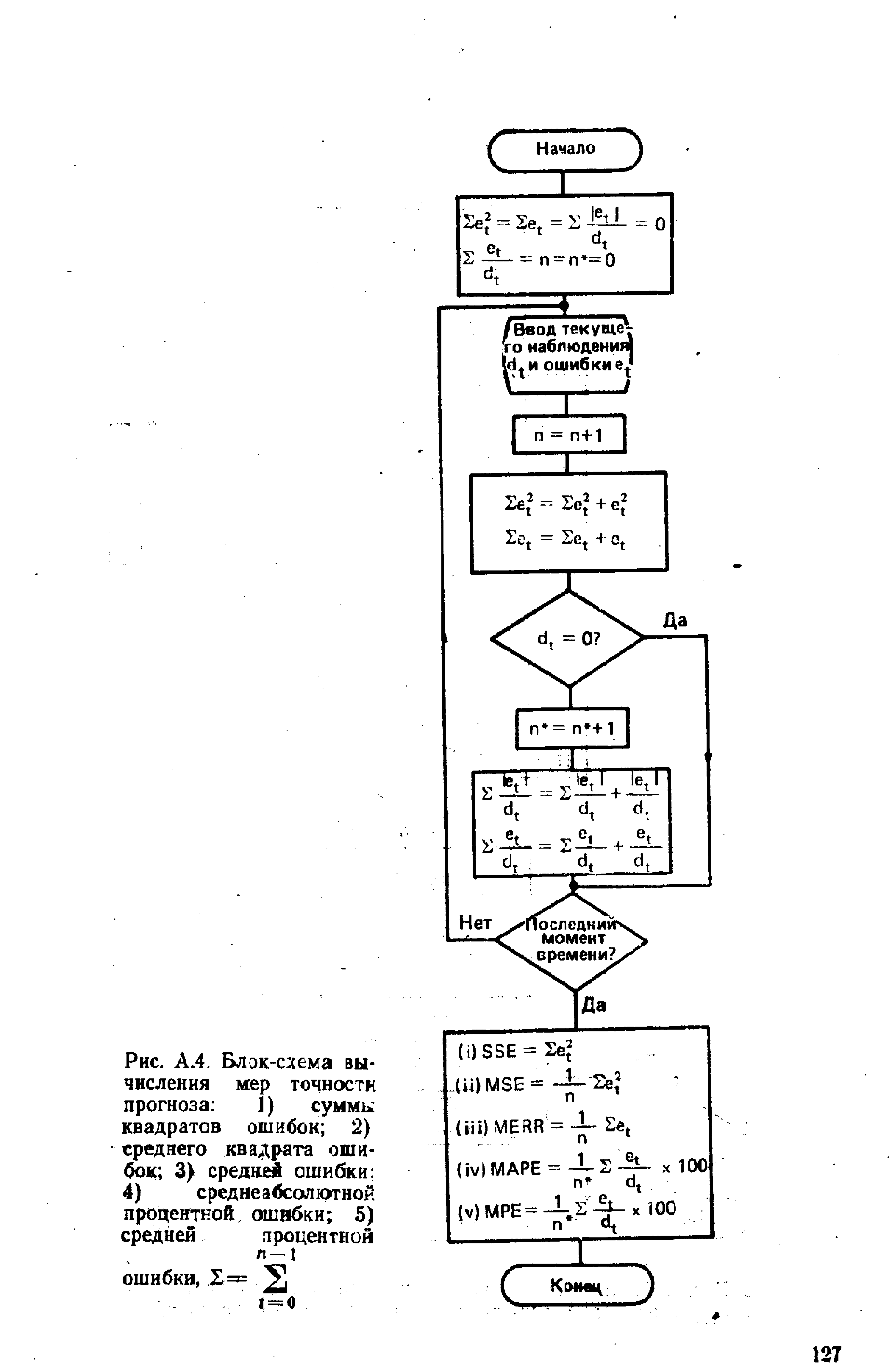

Статистика ошибок. Следующая немаловажная разработка сетевых решений заключается в определении того, что использовать в качестве статистики ошибок (отклонений) для апробации и для тестирования. Мерой измерения ошибок (отклонений) может служить разность между точно вычисленным каким-то статистическим значением ошибок, например их скользящей средней, и выходными данными нейросети. Эта разность должна быть определена для каждого из событий в тестовом множестве, просуммирована и затем разделена на число событий в тесте. Это стандартная мера ошибок, которая называется средней ошибкой . Другие способы вычисления ошибки включают в себя среднее значение абсолютных ошибок, сумму квадратов ошибок или же квадратный корень ошибок (Root-mean-squared — RMS). После того как будет выбрана нейросетевая модель, ее следует апробировать еще раз на определенных временных промежутках. Следующий этап исследования должен заключаться в модификации вхо-
[c.134]

Частные производные от суммы квадратов разности по данному весу довольно легко вычисляются и оказываются пропорциональными расчетным ошибкам, полученным в ходе данной итерации. При этом расчетная ошибка нейрона выходного слоя пропорциональна фактической ошибке на его выходе, а расчетная ошибка нейрона слоя, предшествующего выходному, пропорциональна сумме ошибок всех нейронов выходного слоя, умноженных на соответствующие синаптические веса. Поэтому сначала вычисляют ошибки выходного слоя и определяют приращение весов его связей, а затем вычисляют ошибки предыдущего слоя и вычисляются веса его связей и так корректируются все веса по направлению от входа к выходу. Поэтому такой алгоритм и назван
[c.132]

При выполнении предпосылок 1)-4) относительно ошибок е( оценки параметров множественной линейной регрессии являются несмещенными, состоятельными и эффективными. Отклонение зависимой переменной у ву-м наблюдении от линии регрессии, ер записывается следующим образом е = у — а0 — atx — a fl -. .. — amxjm. Обозначим сумму квадратов этих величин, которую нужно минимизировать в соответствии с методом наименьших квадратов, через Q.
[c.308]

Возникает естественный вопрос, при каких обстоятельствах можно пользоваться описанным выше методом. Ниже будут описаны некоторые процедуры, позволяющие выявлять гетероскеда-стичность того или иного рода (тесты на гетероскедастичность). Здесь мы ограничимся лишь практическими рекомендациями. Если есть предположение о зависимости ошибок от одной из независимых переменных, то целесообразно расположить наблюдения в порядке возрастания значений этой переменной, а затем провести обычную регрессию и получить остатки. Если размах их колебаний тоже возрастает (это хорошо заметно при обычном визуальном исследовании), то это говорит в пользу исходного предположения. Тогда надо сделать описанное выше преобразование, вновь провести регрессию и исследовать остатки. Если теперь их колебание имеет неупорядоченный характер, то это может служить показателем того, что коррекция на гетероскедастичность прошла успешно. Естественно, следует сравнивать и другие параметры регрессии (значимость оценок, сумму квадратов отклонений и т. п.) и только тогда принимать окончательное решение, какая из моделей более приемлема.
[c.170]

Пусть теперь Е( ) = О Q, где Q — вещественная, симметрическая положительно определенная матрица (структура ковариации ошибок). Обобщенный метод наименьших квадратов (ОМНК), приводящий к оценкам класса BLUE, означает минимизацию взвешенной суммы квадратов отклонений [c.27]

Чтобы сделать определенным анализ системы уравнений, предполагаемой уравнением (3.25), допустим, что NS — это положения ПВ, NR — положения сейсмоприемни-ков, NG — положения ОСТ. Определим кратность как NF. Задача состоит в том, чтобы разложить наблюденные времена пробега, оцененные (пикированные) по данным ( уй) на составляющие, как определено в правой части уравнения (3.25). Количество пиков времени (или отдельных уравнений) равно NG x NF. Количество неизвестных равно NS + NR + NG + NG. Обычно NG x NF > NS + NR + NG + NG количество уравнений превышает количество неизвестных. Это задача наименьших квадратов, в которой мы должны минимизировать сумму энергии ошибок наименьших квадратов между наибольшими пиками t ijh и смоделированными временами t [c.49]

Источник

Расчет F-критерия Фишера онлайн

Быстрая навигация по странице:

Понятие F-критерия Фишера

F-критерий Фишера – это один из важных статистических критериев, используемых при проверке значимости как уравнения регрессии в целом, так и отдельных его коэффициентов. Для оценки статистической значимости отдельных коэффициентов уравнения множественной регрессии используют так называемые частные F-критерий Фишера. Критическое значение данного критерия при проведении анализа определяется по специальным таблицам, а также может быть определено при помощи специальных функций в различных компьютерных программах. Например, в MS Excel для этого может быть использована функция FРАСПОБР.

Размещено на www.rnz.ru

Формулы расчета F-критерия Фишера

В общем виде F-критерий Фишера рассчитывается по следующей формуле:

F = S 2 _факт / S 2 _ост;
где: S 2 _факт — факторная дисперсия;
S 2 _ост — остаточная дисперсия

Соответствующие виды дисперсий определяются по следующим формулам:

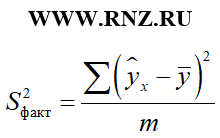
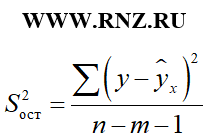
формула расчета факторной дисперсии

формула расчета остаточной дисперсии

В приведенных формулах n – это число наблюдений, m – число параметров при переменной x (то есть количество факторов в модели регрессии).

При этом необходимо обратить внимание на то, что в зависимости от типа исследуемой модели регрессии применяемая формула определения F-критерия Фишера может изменяться. Например, для расчета F-критерия Фишера для парной линейной регрессии может использоваться следующая формула:

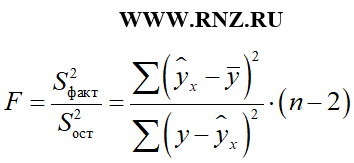
формула расчета F-критерия Фишера для парной линейной регрессии

При использовании коэффициента детерминации расчет F-критерия Фишера для парной линейной регрессии может быть выполнен по такой формуле:

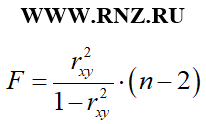
формула расчета F-критерия Фишера через коэффициент детерминации

Для парной нелинейной модели регрессии расчет F-критерия Фишера может быть осуществлен через связь с индексом детерминации по следующей формуле:

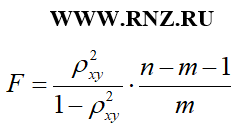
формула расчета F-критерия Фишера для парной нелинейной модели регрессии через индекс детерминации

Описания параметров n и m приведено выше.

Для уравнения множественной регрессии F-критерий Фишера рассчитывается по следующей формуле:

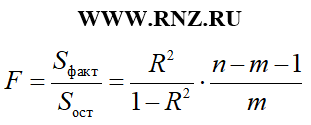
формула расчета F-критерия Фишера для уравнения множественной регрессии

В процессе исследования уравнения множественной регрессии кроме общего F-критерий Фишера могут быть рассчитаны частные F-критерии. В случае анализа уравнения с двумя регрессорами (переменными) вычисление частных F-критериев может быть выполнено по следующим формулам:

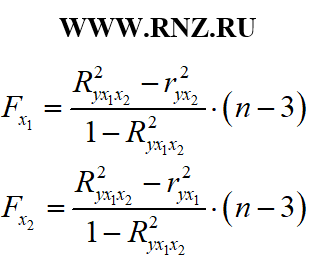
формула расчета частных F-критериев Фишера для уравнения множественной регрессии

Значимость F-критерия Фишера

Для определения статистической значимости рассчитанного значения F-критерия Фишера его сравнивают с критическим или табличным значением. При этом табличное значение определяется на основе числа наблюдений, степеней свободы и заданного уровня значимости следующим образом: Fтабл (a; k₁; k₂), где k₁ = m – это количество факторов в построенной регрессионной модели, а k₂ = n – m – 1 (n – число наблюдений). Для частного F-критерия k₁ = 1, k₂ = n – m – 1 (n – число наблюдений).

Интерпретация F — критерия Фишера для уравнения регрессии в целом следующая: в том случае, когда фактическая величина F — критерия Фишера больше табличного показателя, то уравнение регрессии в целом является статистически значимым.

Интерпретация частного F — критерия Фишера следующая: в том случае, когда рассчитанная величина частного F_xi превышает критическое значение, то дополнительное включение фактора x_i в регрессионную модель статистически оправданно и коэффициент регрессии b_i при соответствующем факторе x_i статистически значим. Но если рассчитанная величина F_xi меньше табличного, то дополнительное включение в модель фактора x_i не оправдано, т.к. данный фактор, как и коэффициент регрессии при нём является статистически незначимым.

Пример расчета F-критерия Фишера

Приведем условные примеры расчета F-критерия Фишера

Пример №1. Предположим, что исследуется регрессия с одним фактором (парная), на основе 30-ти наблюдений, в которой коэффициент детерминации составил 0,77. Тогда по приведённой выше формуле фактическое значение F-критерия Фишера составит: F = 0,77/(1-0,77)*(30-2) = 93,74. Для определения значимости его нужно сравнить с табличным значением. Предположим, что используется уровень значимости α = 0.05. Тогда критическая величины F_табл(0,05; 1; 30-1-1) = 4,2. Так как F > F_табл, то полученное уравнение регрессии является статистически значимым.

Пример №2. Предположим, что исследуется множественная регрессия с тремя факторами, на основе 40 наблюдений, в которой коэффициент множественной детерминации составил 0,89. Тогда по приведённой выше формуле фактическое значение F-критерия Фишера для уравнения множественной регрессии составит: F = (0,89/(1-0,89))*((40-3-1)/3) = 97,09. Для определения значимости его нужно сравнить с табличным значением. Предположим, что используется уровень значимости α = 0.05. Тогда критическая величины F_табл(0,05; 3; 40-3-1) = 2,87. Так как F > F_табл, то полученное уравнение множественной регрессии является статистически значимым.

Онлайн-калькулятор F-критерия Фишера

Представляем онлайн калькулятор расчета F-критерия Фишера, используя который, Вы можете самостоятельно определить значения соответствующего показателя. При заполнении приведенной формы калькулятора внимательно соблюдайте размерность полей, что позволит выполнить и точно выполнить вычисления. В приведенной форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как это работает и посмотреть, как правильно заполнять поля. Для определения значений соответствующих показателей по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить вычисления». При заполнении формы соблюдайте размерность показателей! Дробные числа записываются с точной, а не запятой!

Калькулятор позволяет вычислить значение F-критерия Фишера на основе коэффициента детерминации (первый вариант) или на основе показателей сумм квадратов отклонений, т.е. используя элементы дисперсионного анализа. Выберите необходимый способ и выполните соответствующие вычисления. Для проверки статистической значимости используется уровень значимости α = 0.05.

Онлайн-калькулятор расчета значения F-критерия Фишера:

1-й вариант: на основе значения коэффициент (индекса) детерминации

2-й вариант: на основе сумм квадратов отклонений

Критерий Фишера и критерий Стьюдента в эконометрике

С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.

Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

где n — число наблюдений;
m — число параметров при факторе х.

F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.

Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.

Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.

Таблицы по нахождению критерия Фишера и Стьюдента

Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.

Табличное значение критерия Фишера вычисляют следующим образом:

Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
На пересечении столбца k1 и строки k2 находят значение критерия Фишера

Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).

Критерии Стьюдента

Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.

Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:

Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:

Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.

Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так

Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт

Видео лекциий по расчету критериев Фишера и Стьюдента

Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео

Лекция 1. Критерии и Гипотезы

Лекция 2. Критерии и Гипотезы

Лекция 3. Критерии и Гипотезы

Определение доверительных интервалов

Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:

Формулы для нахождения доверительных интервалов выглядят так

Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза

и находится доверительный интервал

Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:

общая сумма квадратов отклонений (TSS)

сумма квадратов отклонений, обусловленная регрессией (RSS)

остаточная сумма квадратов отклонений (ESS)

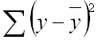
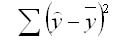
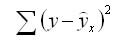
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R 2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.

F-тест качества спецификации множественной регрессионной модели

Цель этой статьи — рассказать о роли степеней свободы в статистическом анализе, вывести формулу F-теста для отбора модели при множественной регрессии.

1. Роль степеней свободы (degree of freedom) в статистике

Имея выборочную совокупность, мы можем лишь оценивать числовые характеристики совокупности, параметры выбранной модели. Так не имеет смысла говорить о среднеквадратическом отклонении при наличии лишь одного наблюдения. Представим линейную регрессионную модель в виде:

Сколько нужно наблюдений, чтобы построить линейную регрессионную модель? В случае двух наблюдений можем получить идеальную модель (рис.1), однако есть в этом недостаток. Причина в том, что сумма квадратов ошибки (MSE) равна нулю и не можем оценить оценить неопределенность коэффициентов . Например не можем построить доверительный интервал для коэффициента наклона по формуле:

А значит не можем сказать ничего о целесообразности использования коэффициента в данной регрессионной модели. Необходимо по крайней мере 3 точки. А что же, если все три точки могут поместиться на одну линию? Такое может быть. Но при большом количестве наблюдений маловероятна идеальная линейная зависимость между зависимой и независимыми переменными (рис. 1).

Рисунок 1 — простая линейная регрессия

Количество степеней свободы — количество значений, используемых при расчете статистической характеристики, которые могут свободно изменяться. С помощью количества степеней свободы оцениваются коэффициенты модели и стандартные ошибки. Так, если имеется n наблюдений и нужно вычислить дисперсию выборки, то имеем n-1 степеней свободы.

Мы не знаем среднее генеральной совокупности, поэтому оцениваем его средним значением по выборке. Это стоит нам одну степень свободы.

Представим теперь что имеется 4 выборочных совокупностей (рис.3).

Рисунок 3

Каждая выборочная совокупность имеет свое среднее значение, определяемое по формуле . И каждое выборочное среднее может быть оценено . Для оценки мы используем 2 параметра , а значит теряем 2 степени свободы (нужно знать 2 точки). То есть количество степеней свобод Заметим, что при 2 наблюдениях получаем 0 степеней свободы, а значит не можем оценить коэффициенты модели и стандартные ошибки.

Таким образом сумма квадратов ошибок имеет (SSE, SSE — standard error of estimate) вид:

Стоит упомянуть, что в знаменателе стоит n-2, а не n-1 в связи с тем, что среднее значение оценивается по формуле . Квадратные корень формулы (4) — ошибка стандартного отклонения.

В общем случае количество степеней свободы для линейной регрессии рассчитывается по формуле:

где n — число наблюдений, k — число независимых переменных.

2. Анализ дисперсии, F-тест

При выполнении основных предположений линейной регрессии имеет место формула:

где ,

В случае, если имеем модель по формуле (1), то из предыдущего раздела знаем, что количество степеней свободы у SSTO равно n-1. Количество степеней свободы у SSE равно n-2. Таким образом количество степеней свободы у SSR равно 1. Только в таком случае получаем равенство .

Масштабируем SSE и SSR с учетом их степеней свободы:

Получены хи-квадрат распределения. F-статистика вычисляется по формуле:

Формула (9) используется при проверке нулевой гипотезы при альтернативной гипотезе в случае линейной регрессионной модели вида (1).

3. Выбор линейной регрессионной модели

Известно, что с увеличением количества предикторов (независимых переменных в регрессионной модели) исправленный коэффициент детерминации увеличивается. Однако с ростом количества используемых предикторов растет стоимость модели (под стоимостью подразумевается количество данных которые нужно собрать). Однако возникает вопрос: “Какие предикторы разумно использовать в регрессионной модели?”. Критерий Фишера или по-другому F-тест позволяет ответить на данный вопрос.

Определим “полную” модель: (10)

Определим “укороченную” модель: (11)

Вычисляем сумму квадратов ошибок для каждой модели:

(12)

(13)

Определяем количество степеней свобод

(14)

Нулевая гипотеза — “укороченная” модель мало отличается от “полной (удлиненной) модели”. Поэтому выбираем “укороченную” модель. Альтернативная гипотеза — “полная (удлиненная)” модель объясняет значимо большую долю дисперсии в данных по сравнению с “укороченной” моделью.

Коэффициент детерминации из формулы (6):

Из формулы (15) выразим SSE(F):

SSTO одинаково как для “укороченной”, так и для “длинной” модели. Тогда (14) примет вид:

Поделим числитель и знаменатель (14a) на SSTO, после чего прибавим и вычтем единицу в числителе.

Используя формулу (15) в конечном счете получим F-статистику, выраженную через коэффициенты детерминации.

3 Проверка значимости линейной регрессии

Данный тест очень важен в регрессионном анализе и по существу является частным случаем проверки ограничений. Рассмотрим ситуацию. У линейной регрессионной модели всего k параметров (Сейчас среди этих k параметров также учитываем ).Рассмотрим нулевую гипотеза — об одновременном равенстве нулю всех коэффициентов при предикторах регрессионной модели (то есть всего ограничений k-1). Тогда “короткая модель” имеет вид . Следовательно. Используя формулу (14.в), получим

Заключение

Показан смысл числа степеней свободы в статистическом анализе. Выведена формула F-теста в простом случае(9). Представлены шаги выбора лучшей модели. Выведена формула F-критерия Фишера и его запись через коэффициенты детерминации.

Можно посчитать F-статистику самому, а можно передать две обученные модели функции aov, реализующей ANOVA в RStudio. Для автоматического отбора лучшего набора предикторов удобна функция step.

Надеюсь вам было интересно, спасибо за внимание.

При выводе формул очень помогли некоторые главы из курса по статистике STAT 501

источники:

http://univer-nn.ru/ekonometrika/kriterij-fishera-i-kriterij-styudenta-v-ekonometrike/

http://habr.com/ru/post/592677/

Источник