Data Science Tutorial
PySpark Machine Learning Tutorial for Beginners
Snowflake Data Warehouse Tutorial for Beginners with Examples
Jupyter Notebook Tutorial — A Complete Beginners Guide
Best Python NumPy Tutorial for Beginners
Tableau Tutorial for Beginners -Step by Step Guide
MLOps Python Tutorial for Beginners -Get Started with MLOps
Alteryx Tutorial for Beginners to Master Alteryx in 2021
Free Microsoft Power BI Tutorial for Beginners with Examples
Theano Deep Learning Tutorial for Beginners
Computer Vision Tutorial for Beginners | Learn Computer Vision
Python Pandas Tutorial for Beginners — The A-Z Guide
NumPy Python Tutorial for Beginners
Hadoop Online Tutorial – Hadoop HDFS Commands Guide
MapReduce Tutorial–Learn to implement Hadoop WordCount Example
Hadoop Hive Tutorial-Usage of Hive Commands in HQL
Hive Tutorial-Getting Started with Hive Installation on Ubuntu
Learn Java for Hadoop Tutorial: Inheritance and Interfaces
Learn Java for Hadoop Tutorial: Classes and Objects
Learn Java for Hadoop Tutorial: Arrays
Apache Spark Tutorial — Run your First Spark Program
Best PySpark Tutorial for Beginners-Learn Spark with Python
R Tutorial- Learn Data Visualization with R using GGVIS
Neural Network Training Tutorial
Python List Tutorial
MatPlotLib Tutorial
Decision Tree Tutorial
Neural Network Tutorial
Performance Metrics for Machine Learning Algorithms
R Tutorial: Data.Table
SciPy Tutorial
Step-by-Step Apache Spark Installation Tutorial
Introduction to Apache Spark Tutorial
R Tutorial: Importing Data from Web
R Tutorial: Importing Data from Relational Database
R Tutorial: Importing Data from Excel
Introduction to Machine Learning Tutorial
Machine Learning Tutorial: Linear Regression
Machine Learning Tutorial: Logistic Regression
Support Vector Machine Tutorial (SVM)
K-Means Clustering Tutorial
dplyr Manipulation Verbs
Introduction to dplyr package
Importing Data from Flat Files in R
Principal Component Analysis Tutorial
Pandas Tutorial Part-3
Pandas Tutorial Part-2
Pandas Tutorial Part-1
Tutorial- Hadoop Multinode Cluster Setup on Ubuntu
Data Visualizations Tools in R
R Statistical and Language tutorial
Introduction to Data Science with R
Apache Pig Tutorial: User Defined Function Example
Apache Pig Tutorial Example: Web Log Server Analytics
Impala Case Study: Web Traffic
Impala Case Study: Flight Data Analysis
Hadoop Impala Tutorial
Apache Hive Tutorial: Tables
Flume Hadoop Tutorial: Twitter Data Extraction
Flume Hadoop Tutorial: Website Log Aggregation
Hadoop Sqoop Tutorial: Example Data Export
Hadoop Sqoop Tutorial: Example of Data Aggregation
Apache Zookepeer Tutorial: Example of Watch Notification
Apache Zookepeer Tutorial: Centralized Configuration Management
Hadoop Zookeeper Tutorial for Beginners
Hadoop Sqoop Tutorial
Hadoop PIG Tutorial
Hadoop Oozie Tutorial
Hadoop NoSQL Database Tutorial
Hadoop Hive Tutorial
Hadoop HDFS Tutorial
Hadoop hBase Tutorial
Hadoop Flume Tutorial
Hadoop 2.0 YARN Tutorial
Hadoop MapReduce Tutorial
Big Data Hadoop Tutorial for Beginners- Hadoop Installation
Data Science Tutorial
PySpark Machine Learning Tutorial for Beginners
Snowflake Data Warehouse Tutorial for Beginners with Examples
Jupyter Notebook Tutorial — A Complete Beginners Guide
Best Python NumPy Tutorial for Beginners
Tableau Tutorial for Beginners -Step by Step Guide
MLOps Python Tutorial for Beginners -Get Started with MLOps
Alteryx Tutorial for Beginners to Master Alteryx in 2021
Free Microsoft Power BI Tutorial for Beginners with Examples
Theano Deep Learning Tutorial for Beginners
Computer Vision Tutorial for Beginners | Learn Computer Vision
Python Pandas Tutorial for Beginners — The A-Z Guide
NumPy Python Tutorial for Beginners
Hadoop Online Tutorial – Hadoop HDFS Commands Guide
MapReduce Tutorial–Learn to implement Hadoop WordCount Example
Hadoop Hive Tutorial-Usage of Hive Commands in HQL
Hive Tutorial-Getting Started with Hive Installation on Ubuntu
Learn Java for Hadoop Tutorial: Inheritance and Interfaces
Learn Java for Hadoop Tutorial: Classes and Objects
Learn Java for Hadoop Tutorial: Arrays
Apache Spark Tutorial — Run your First Spark Program
Best PySpark Tutorial for Beginners-Learn Spark with Python
R Tutorial- Learn Data Visualization with R using GGVIS
Neural Network Training Tutorial
Python List Tutorial
MatPlotLib Tutorial
Decision Tree Tutorial
Neural Network Tutorial
Performance Metrics for Machine Learning Algorithms
R Tutorial: Data.Table
SciPy Tutorial
Step-by-Step Apache Spark Installation Tutorial
Introduction to Apache Spark Tutorial
R Tutorial: Importing Data from Web
R Tutorial: Importing Data from Relational Database
R Tutorial: Importing Data from Excel
Introduction to Machine Learning Tutorial
Machine Learning Tutorial: Linear Regression
Machine Learning Tutorial: Logistic Regression
Support Vector Machine Tutorial (SVM)
K-Means Clustering Tutorial
dplyr Manipulation Verbs
Introduction to dplyr package
Importing Data from Flat Files in R
Principal Component Analysis Tutorial
Pandas Tutorial Part-3
Pandas Tutorial Part-2
Pandas Tutorial Part-1
Tutorial- Hadoop Multinode Cluster Setup on Ubuntu
Data Visualizations Tools in R
R Statistical and Language tutorial
Introduction to Data Science with R
Apache Pig Tutorial: User Defined Function Example
Apache Pig Tutorial Example: Web Log Server Analytics
Impala Case Study: Web Traffic
Impala Case Study: Flight Data Analysis
Hadoop Impala Tutorial
Apache Hive Tutorial: Tables
Flume Hadoop Tutorial: Twitter Data Extraction
Flume Hadoop Tutorial: Website Log Aggregation
Hadoop Sqoop Tutorial: Example Data Export
Hadoop Sqoop Tutorial: Example of Data Aggregation
Apache Zookepeer Tutorial: Example of Watch Notification
Apache Zookepeer Tutorial: Centralized Configuration Management
Hadoop Zookeeper Tutorial for Beginners
Hadoop Sqoop Tutorial
Hadoop PIG Tutorial
Hadoop Oozie Tutorial
Hadoop NoSQL Database Tutorial
Hadoop Hive Tutorial
Hadoop HDFS Tutorial
Hadoop hBase Tutorial
Hadoop Flume Tutorial
Hadoop 2.0 YARN Tutorial
Hadoop MapReduce Tutorial
Big Data Hadoop Tutorial for Beginners- Hadoop Installation
Основы линейной регрессии
Время прочтения
13 мин
Просмотры 108K
Здравствуй, Хабр!
Цель этой статьи — рассказать о линейной регрессии, а именно собрать и показать формулировки и интерпретации задачи регрессии с точки зрения математического анализа, статистики, линейной алгебры и теории вероятностей. Хотя в учебниках эта тема изложена строго и исчерпывающе, ещё одна научно-популярная статья не помешает.
! Осторожно, трафик! В статье присутствует заметное число изображений для иллюстраций, часть в формате gif.
Содержание
- Введение
- Метод наименьших квадратов
- Математический анализ
- Статистика
- Теория вероятностей
- Мультилинейная регрессия
- Линейная алгебра
- Произвольный базис
- Заключительные замечания
- Проблема выбора размерности
- Численные методы
- Реклама и заключение
Введение
Есть три сходных между собой понятия, три сестры: интерполяция, аппроксимация и регрессия.
У них общая цель: из семейства функций выбрать ту, которая обладает определенным свойством.
Интерполяция — способ выбрать из семейства функций ту, которая проходит через заданные точки. Часто функцию затем используют для вычисления в промежуточных точках. Например, мы вручную задаем цвет нескольким точкам и хотим чтобы цвета остальных точек образовали плавные переходы между заданными. Или задаем ключевые кадры анимации и хотим плавные переходы между ними. Классические примеры: интерполяция полиномами Лагранжа, сплайн-интерполяция, многомерная интерполяция (билинейная, трилинейная, методом ближайшего соседа и т.д). Есть также родственное понятие экстраполяции — предсказание поведения функции вне интервала. Например, предсказание курса доллара на основании предыдущих колебаний — экстраполяция.


В этой статье мы рассмотрим линейную регрессию. Это означает, что семейство функций, из которых мы выбираем, представляет собой линейную комбинацию наперед заданных базисных функций
Цель регрессии — найти коэффициенты этой линейной комбинации, и тем самым определить регрессионную функцию (которую также называют моделью). Отмечу, что линейную регрессию называют линейной именно из-за линейной комбинации базисных функций — это не связано с самыми базисными функциями (они могут быть линейными или нет).
Регрессия с нами уже давно: впервые метод опубликовал Лежандр в 1805 году, хотя Гаусс пришел к нему раньше и успешно использовал для предсказания орбиты «кометы» (на самом деле карликовой планеты) Цереры. Существует множество вариантов и обобщений линейной регрессии: LAD, метод наименьших квадратов, Ridge регрессия, Lasso регрессия, ElasticNet и многие другие.
Метод наименьших квадратов
Начнём с простейшего двумерного случая. Пусть нам даны точки на плоскости и мы ищем такую аффинную функцию

.
Как видно из иллюстрации, расстояние от точки до прямой можно понимать по-разному, например геометрически — это длина перпендикуляра. Однако в контексте нашей задачи нам нужно функциональное расстояние, а не геометрическое. Нас интересует разница между экспериментальным значением и предсказанием модели для каждого поэтому измерять нужно вдоль оси
.
Первое, что приходит в голову, в качестве функции потерь попробовать выражение, зависящее от абсолютных значений разниц . Простейший вариант — сумма модулей отклонений
приводит к Least Absolute Distance (LAD) регрессии.
Впрочем, более популярная функция потерь — сумма квадратов отклонений регрессанта от модели. В англоязычной литературе она носит название Sum of Squared Errors (SSE)
Метод наименьших квадратов (по англ. OLS) — линейная регрессия c в качестве функции потерь.
Такой выбор прежде всего удобен: производная квадратичной функции — линейная функция, а линейные уравнения легко решаются. Впрочем, далее я укажу и другие соображения в пользу .
Математический анализ
Простейший способ найти — вычислить частные производные по
и
, приравнять их нулю и решить систему линейных уравнений
Значения параметров, минимизирующие функцию потерь, удовлетворяют уравнениям
которые легко решить
Мы получили громоздкие и неструктурированные выражения. Сейчас мы их облагородим и вдохнем в них смысл.
Статистика
Полученные формулы можно компактно записать с помощью статистических эстиматоров: среднего , вариации
(стандартного отклонения), ковариации
и корреляции
Перепишем как
где это нескорректированное (смещенное) стандартное выборочное отклонение, а
— ковариация. Теперь вспомним, что коэффициент корреляции (коэффициент корреляции Пирсона)
и запишем
Теперь мы можем оценить все изящество дескриптивной статистики, записав уравнение регрессионной прямой так
Во-первых, это уравнение сразу указывает на два свойства регрессионной прямой:
Во-вторых, теперь становится понятно, почему метод регрессии называется именно так. В единицах стандартного отклонения отклоняется от своего среднего значения меньше чем
, потому что
. Это называется регрессией(от лат. regressus — «возвращение») по отношению к среднему. Это явление было описано сэром Фрэнсисом Гальтоном в конце XIX века в его статье «Регрессия к посредственности при наследовании роста». В статье показано, что черты (такие как рост), сильно отклоняющиеся от средних, редко передаются по наследству. Характеристики потомства как бы стремятся к среднему — на детях гениев природа отдыхает.
Возведя коэффициент корреляции в квадрат, получим коэффициент детерминации . Квадрат этой статистической меры показывает насколько хорошо регрессионная модель описывает данные.
, равный
, означает что функция идеально ложится на все точки — данные идеально скоррелированны. Можно доказать, что
показывает какая доля вариативности в данных объясняется лучшей из линейных моделей. Чтобы понять, что это значит, введем определения
— вариация исходных данных (вариация точек
).
— вариация остатков, то есть вариация отклонений от регрессионной модели — от
нужно отнять предсказание модели и найти вариацию.
— вариация регрессии, то есть вариация предсказаний регрессионной модели в точках
(обратите внимание, что среднее предсказаний модели совпадает с
).
Дело в том, что вариация исходных данных разлагается в сумму двух других вариаций: вариации случайного шума (остатков) и вариации, которая объясняется моделью (регрессии)
или
Как видим, стандартные отклонения образуют прямоугольный треугольник.
Мы стремимся избавиться от вариативности, связанной с шумом и оставить лишь вариативность, которая объясняется моделью, — хотим отделить зерна от плевел. О том, насколько это удалось лучшей из линейных моделей, свидетельствует , равный единице минус доля вариации ошибок в суммарной вариации
или доле объясненной вариации (доля вариации регрессии в полной вариации)
равен косинусу угла в прямоугольном треугольнике
. Кстати, иногда вводят долю необъясненной вариации
и она равна квадрату синуса в этом треугольнике. Если коэффициент детерминации мал, возможно мы выбрали неудачные базисные функции, линейная регрессия неприменима вовсе и т.п.
Теория вероятностей
Ранее мы пришли к функции потерь из соображений удобства, но к ней же можно прийти с помощью теории вероятностей и метода максимального правдоподобия (ММП). Напомню вкратце его суть. Предположим, у нас есть
независимых одинаково распределенных случайных величин (в нашем случае — результатов измерений). Мы знаем вид функции распределения (напр. нормальное распределение), но хотим определить параметры, которые в нее входят (например
и
). Для этого нужно вычислить вероятность получить
датапоинтов в предположении постоянных, но пока неизвестных параметров. Благодаря независимости измерений, мы получим произведение вероятностей реализации каждого измерения. Если мыслить полученную величину как функцию параметров (функция правдоподобия) и найти её максимум, мы получим оценку параметров. Зачастую вместо функции правдоподобия используют ее логарифм — дифференцировать его проще, а результат — тот же.
Вернемся к задаче простой регрессии. Допустим, что значения нам известны точно, а в измерении
присутствует случайный шум (свойство слабой экзогенности). Более того, положим, что все отклонения от прямой (свойство линейности) вызваны шумом с постоянным распределением (постоянство распределения). Тогда
где — нормально распределенная случайная величина
Исходя из предположений выше, запишем функцию правдоподобия
и ее логарифм
Таким образом, максимум правдоподобия достигается при минимуме
что дает основание принять ее в качестве функции потерь. Кстати, если
мы получим функцию потерь LAD регрессии
которую мы упоминали ранее.
Подход, который мы использовали в этом разделе — один из возможных. Можно прийти к такому же результату, используя более общие свойства. В частности, свойство постоянства распределения можно ослабить, заменив на свойства независимости, постоянства вариации (гомоскедастичность) и отсутствия мультиколлинеарности. Также вместо ММП эстимации можно воспользоваться другими методами, например линейной MMSE эстимацией.
Мультилинейная регрессия
До сих пор мы рассматривали задачу регрессии для одного скалярного признака , однако обычно регрессор — это
-мерный вектор
. Другими словами, для каждого измерения мы регистрируем
фич, объединяя их в вектор. В этом случае логично принять модель с
независимыми базисными функциями векторного аргумента —
степеней свободы соответствуют
фичам и еще одна — регрессанту
. Простейший выбор — линейные базисные функции
. При
получим уже знакомый нам базис
.
Итак, мы хотим найти такой вектор (набор коэффициентов) , что
Знак «» означает, что мы ищем решение, которое минимизирует сумму квадратов ошибок
Последнее уравнение можно переписать более удобным образом. Для этого расположим в строках матрицы (матрицы информации)
Тогда столбцы матрицы отвечают измерениям
-ой фичи. Здесь важно не запутаться:
— количество измерений,
— количество признаков (фич), которые мы регистрируем. Систему можно записать как
Квадрат нормы разности векторов в правой и левой частях уравнения образует функцию потерь
которую мы намерены минимизировать
Продифференцируем финальное выражение по (если забыли как это делается — загляните в Matrix cookbook)
приравняем производную к и получим т.н. нормальные уравнения
Если столбцы матрицы информации линейно независимы (нет идеально скоррелированных фич), то матрица
имеет обратную (доказательство можно посмотреть, например, в видео академии Хана). Тогда можно записать
где
псевдообратная к . Понятие псевдообратной матрицы введено в 1903 году Фредгольмом, она сыграла важную роль в работах Мура и Пенроуза.
Напомню, что обратить и найти
можно только если столбцы
линейно независимы. Впрочем, если столбцы
близки к линейной зависимости, вычисление
уже становится численно нестабильным. Степень линейной зависимости признаков в
или, как говорят, мультиколлинеарности матрицы
, можно измерить числом обусловленности — отношением максимального собственного значения к минимальному. Чем оно больше, тем ближе
к вырожденной и неустойчивее вычисление псевдообратной.
Линейная алгебра
К решению задачи мультилинейной регрессии можно прийти довольно естественно и с помощью линейной алгебры и геометрии, ведь даже то, что в функции потерь фигурирует норма вектора ошибок уже намекает, что у задачи есть геометрическая сторона. Мы видели, что попытка найти линейную модель, описывающую экспериментальные точки, приводит к уравнению
Если количество переменных равно количеству неизвестных и уравнения линейно независимы, то система имеет единственное решение. Однако, если число измерений превосходит число признаков, то есть уравнений больше чем неизвестных — система становится несовместной, переопределенной. В этом случае лучшее, что мы можем сделать — выбрать вектор , образ которого
ближе остальных к
. Напомню, что множество образов или колоночное пространство
— это линейная комбинация вектор-столбцов матрицы
—
-мерное линейное подпространство (мы считаем фичи линейно независимыми), линейная оболочка вектор-столбцов
. Итак, если
принадлежит
, то мы можем найти решение, если нет — будем искать, так сказать, лучшее из нерешений.
Если в дополнение к векторам мы рассмотрим все вектора им перпендикулярные, то получим еще одно подпространство и сможем любой вектор из
разложить на две компоненты, каждая из которых живет в своем подпространстве. Второе, перпендикулярное пространство, можно характеризовать следующим образом (нам это понадобится в дальнейшем). Пускай
, тогда
равен нулю в том и только в том случае, если перпендикулярен всем
, а значит и целому
. Таким образом, мы нашли два перпендикулярных линейных подпространства, линейные комбинации векторов из которых полностью, без дыр, «покрывают» все
. Иногда это обозначают c помощью символа ортогональной прямой суммы
где . В каждое из подпространств можно попасть с помощью соответствующего оператора проекции, но об этом ниже.
Теперь представим в виде разложения
Если мы ищем решение , то естественно потребовать, чтобы
была минимальна, ведь это длина вектора-остатка. Учитывая перпендикулярность подпространств и теорему Пифагора
но поскольку, выбрав подходящий , я могу получить любой вектор колоночного пространства, то задача сводится к
а останется в качестве неустранимой ошибки. Любой другой выбор
сделает ошибку только больше.
Если теперь вспомнить, что , то легко видеть
что очень удобно, так как у нас нет, а вот
— есть. Вспомним из предыдущего параграфа, что
имеет обратную при условии линейной независимости признаков и запишем решение
где уже знакомая нам псевдообратная матрица. Если нам интересна проекция
, то можно записать
где — оператор проекции на колоночное пространство.
Выясним геометрический смысл коэффициента детерминации.
Заметьте, что фиолетовый вектор пропорционален первому столбцу матрицы информации
, который состоит из одних единиц согласно нашему выбору базисных функций. В RGB треугольнике
Так как этот треугольник прямоугольный, то по теореме Пифагора
Это геометрическая интерпретация уже известного нам факта, что
Мы знаем, что
а значит
Красиво, не правда ли?
Произвольный базис
Как мы знаем, регрессия выполняется на базисных функциях и её результатом есть модель
но до сих пор мы использовали простейшие , которые просто ретранслировали изначальные признаки без изменений, ну разве что дополняли их постоянной фичей
. Как можно было заметить, на самом деле ни вид
, ни их количество ничем не ограничены — главное, чтобы функции в базисе были линейно независимы. Обычно, выбор делается исходя из предположений о природе процесса, который мы моделируем. Если у нас есть основания полагать, что точки
ложатся на параболу, а не на прямую, то стоит выбрать базис
. Количество базисных функций может быть как меньшим, так и большим, чем количество изначальных фич.
Если мы определились с базисом, то дальше действуем следующим образом. Мы формируем матрицу информации
записываем функцию потерь
и находим её минимум, например с помощью псевдообратной матрицы
или другим методом.
Заключительные замечания
Проблема выбора размерности
На практике часто приходится самостоятельно строить модель явления, то есть определяться сколько и каких нужно взять базисных функций. Первый порыв «набрать побольше» может сыграть злую шутку: модель окажется слишком чувствительной к шумам в данных (переобучение). С другой стороны, если излишне ограничить модель, она будет слишком грубой (недообучение).
Есть два способа выйти из ситуации. Первый: последовательно наращивать количество базисных функций, проверять качество регрессии и вовремя остановиться. Или же второй: выбрать функцию потерь, которая определит число степеней свободы автоматически. В качестве критерия успешности регрессии можно использовать коэффициент детерминации, о котором уже упоминалось выше, однако, проблема в том, что монотонно растет с ростом размерности базиса. Поэтому вводят скорректированный коэффициент
где — размер выборки,
— количество независимых переменных. Следя за
, мы можем вовремя остановиться и перестать добавлять дополнительные степени свободы.
Вторая группа подходов — регуляризации, самые известные из которых Ridge(/гребневая/Тихоновская регуляризация), Lasso(
регуляризация) и Elastic Net(Ridge+Lasso). Главная идея этих методов: модифицировать функцию потерь дополнительными слагаемыми, которые не позволят вектору коэффициентов
неограниченно расти и тем самым воспрепятствуют переобучению
где и
— параметры, которые регулируют «силу» регуляризации. Это обширная тема с красивой геометрией, которая заслуживает отдельного рассмотрения. Упомяну кстати, что для случая двух переменных при помощи вероятностной интерпретации можно получить Ridge и Lasso регрессии, удачно выбрав априорное распределения для коэффициента
Численные методы
Скажу пару слов, как минимизировать функцию потерь на практике. SSE — это обычная квадратичная функция, которая параметризируется входными данными, так что принципиально ее можно минимизировать методом скорейшего спуска или другими методами оптимизации. Разумеется, лучшие результаты показывают алгоритмы, которые учитывают вид функции SSE, например метод стохастического градиентного спуска. Реализация Lasso регрессии в scikit-learn использует метод координатного спуска.
Также можно решить нормальные уравнения с помощью численных методов линейной алгебры. Эффективный метод, который используется в scikit-learn для МНК — нахождение псевдообратной матрицы с помощью сингулярного разложения. Поля этой статьи слишком узки, чтобы касаться этой темы, за подробностями советую обратиться к курсу лекций К.В.Воронцова.
Реклама и заключение
Эта статья — сокращенный пересказ одной из глав курса по классическому машинному обучению в Киевском академическом университете (преемник Киевского отделения Московского физико-технического института, КО МФТИ). Автор статьи помогал в создании этого курса. Технически курс выполнен на платформе Google Colab, что позволяет совмещать формулы, форматированные LaTeX, исполняемый код Python и интерактивные демонстрации на Python+JavaScript, так что студенты могут работать с материалами курса и запускать код с любого компьютера, на котором есть браузер. На главной странице собраны ссылки на конспекты, «рабочие тетради» для практик и дополнительные ресурсы. В основу курса положены следующие принципы:
- все материалы должны быть доступны студентам с первой пары;
- лекция нужны для понимания, а не для конспектирования (конспекты уже готовы, нет смысла их писать, если не хочется);
- конспект — больше чем лекция (материала в конспектах больше, чем было озвучено на лекции, фактически конспекты представляют собой полноценный учебник);
- наглядность и интерактивность (иллюстрации, фото, демки, гифки, код, видео с youtube).
Если хотите посмотреть на результат — загляните на страничку курса на GitHub.
Надеюсь вам было интересно, спасибо за внимание.
Содержание:
Регрессионный анализ:
Регрессионным анализом называется раздел математической статистики, объединяющий практические методы исследования корреляционной зависимости между случайными величинами по результатам наблюдений над ними. Сюда включаются методы выбора модели изучаемой зависимости и оценки ее параметров, методы проверки статистических гипотез о зависимости.
Пусть между случайными величинами X и Y существует линейная корреляционная зависимость. Это означает, что математическое ожидание Y линейно зависит от значений случайной величины X. График этой зависимости (линия регрессии Y на X) имеет уравнение
Линейная модель пригодна в качестве первого приближения и в случае нелинейной корреляции, если рассматривать небольшие интервалы возможных значений случайных величин.
Пусть параметры линии регрессии 
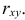
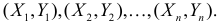
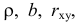
Неизвестная нам линия регрессии 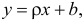

Такие значения 
Решения этой системы уравнений дают оценки называемые оценками по методу наименьших квадратов.
и
Известно, что оценки по методу наименьших квадратов являются несмещенными и, более того, среди всех несмещенных оценок обладают наименьшей дисперсией. Для оценки коэффициента корреляции можно воспользоваться тем, что 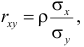
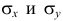
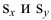
По методу наименьших квадратов можно находить оценки параметров линии регрессии и при нелинейной корреляции. Например, для линии регрессии вида 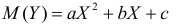
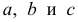
Пример:
По данным наблюдений двух случайных величин найти коэффициент корреляции и уравнение линии регрессии Y на X
Решение. Вычислим величины, необходимые для использования формул (3.7.1)–(3.7.3):
По формулам (3.7.1) и (3.7.2) получим
Итак, оценка линии регрессии имеет вид 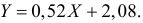
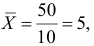
Аналогично, 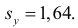
Ответ.
Пример:
Получена выборка значений величин X и Y
Для представления зависимости между величинами предполагается использовать модель 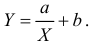
Решение. Рассмотрим сначала задачу оценки параметров этой модели в общем виде. Линия 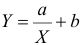
Необходимые условия экстремума приводят к системе из двух уравнений:
Откуда
Решения системы уравнений (3.7.4) и (3.7.5) и будут оценками по методу наименьших квадратов для параметров
На основе опытных данных вычисляем:
В итоге получаем систему уравнений (?????) и (?????) в виде
Эта система имеет решения
Ответ.
Если наблюдений много, то результаты их обычно группируют и представляют в виде корреляционной таблицы.
В этой таблице 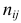
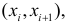
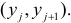
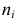
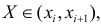
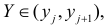
Если величины дискретны, то вместо интервалов указывают отдельные значения этих величин. Для непрерывных случайных величин представителем каждого интервала считают его середину и полагают, что 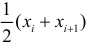
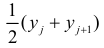
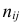
При больших значениях X и Y можно для упрощения вычислений перенести начало координат и изменить масштаб по каждой из осей, а после завершения вычислений вернуться к старому масштабу.
Пример:
Проделано 80 наблюдений случайных величин X и Y. Результаты наблюдений представлены в виде таблицы. Найти линию регрессии Y на X. Оценить коэффициент корреляции.
Решение. Представителем каждого интервала будем считать его середину. Перенесем начало координат и изменим масштаб по каждой оси так, чтобы значения X и Y были удобны для вычислений. Для этого перейдем к новым переменным 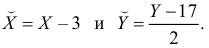
Чтобы иметь представление о виде линии регрессии, вычислим средние значения 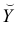
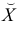
Нанесем эти значения на координатную плоскость, соединив для наглядности их отрезками прямой (рис. 3.7.1).
По виду полученной ломанной линии можно предположить, что линия регрессии Y на X является прямой. Оценим ее параметры. Для этого сначала вычислим с учетом группировки данных в таблице все величины, необходимые для использования формул (3.31–3.33):
Тогда
В новом масштабе оценка линии регрессии имеет вид 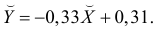
Для оценки 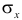
Подобным же образом можно оценить 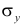
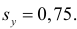
Вернемся к старому масштабу:
Коэффициент корреляции пересчитывать не нужно, так как это величина безразмерная и от масштаба не зависит.
Ответ.
Пусть некоторые физические величины X и Y связаны неизвестной нам функциональной зависимостью 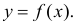
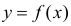
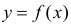
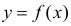
Регрессионный анализ
Основные положения регрессионного анализа:
Основная задача регрессионного анализа — изучение зависимости между результативным признаком Y и наблюдавшимся признаком X, оценка функции регрессий.
Предпосылки регрессионного анализа:
- Y — независимые случайные величины, имеющие постоянную дисперсию;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
можно представить в виде
Выражение (2.1), как уже упоминалось в п. 1.2, называется функцией регрессии (или модельным уравнением регрессии) Y на X. Оценке в этом выражении подлежат параметры 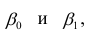
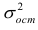
Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака; Остаточная дисперсия может служить для оценки точности подбора вида функции регрессии (модельного уравнения регрессии), полноты набора признаков, включенных в анализ. Оценки параметров функции регрессии находят, используя метод наименьших квадратов.
В данном вопросе рассмотрен линейный регрессионный анализ. Линейным он называется потому, что изучаем лишь те виды зависимостей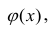
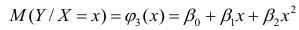
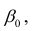
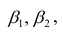
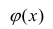
Важное место в линейном регрессионном анализе занимает так называемая «нормальная регрессия». Она имеет место, если сделать предположения относительно закона распределения случайной величины Y. Предпосылки «нормальной регрессии»:
- Y — независимые случайные величины, имеющие постоянную дисперсию и распределенные по нормальному закону;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
можно представить в виде (2.1).
В этом случае оценки коэффициентов регрессии — несмещённые с минимальной дисперсией и нормальным законом распределения. Из этого положения следует что при «нормальной регрессии» имеется возможность оценить значимость оценок коэффициентов регрессии, а также построить доверительный интервал для коэффициентов регрессии и условного математического ожидания M(YX=x).
Линейная регрессия
Рассмотрим простейший случай регрессионного анализа — модель вида (2.1), когда зависимость 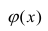
по переменным. Оценки параметров модели (2.1) 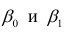
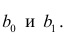
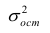
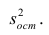
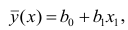
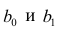
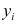
Составим систему нормальных уравнений: первое уравнение
откуда
второе уравнение
откуда
Итак,
Оценки, полученные по способу наименьших квадратов, обладают минимальной дисперсией в классе линейных оценок. Решая систему (2.2) относительно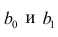
Остаётся получить оценку параметра 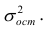
где т — количество наблюдений.
Еслит велико, то для упрощения расчётов наблюдавшиеся данные принята группировать, т.е. строить корреляционную таблицу. Пример построения такой таблицы приведен в п. 1.5. Формулы для нахождения коэффициентов регрессии по сгруппированным данным те же, что и для расчёта по несгруппированным данным, но суммы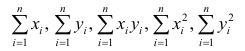
где 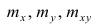
Нелинейная регрессия
Рассмотрим случай, когда зависимость нелинейна по переменным х, например модель вида
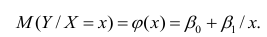
На рис. 2.1 изображено поле корреляции. Очевидно, что зависимость между Y и X нелинейная и её графическим изображением является не прямая, а кривая. Оценкой выражения (2.6) является уравнение регрессии
где 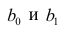
Принцип нахождения коэффициентов тот же — метод наименьших квадратов, т.е.
или
Дифференцируя последнее равенство по 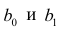
В общем случае нелинейной зависимости между переменными Y и X связь может выражаться многочленом k-й степени от x:
Коэффициенты регрессии определяют по принципу наименьших квадратов. Система нормальных уравнений имеет вид
Вычислив коэффициенты системы, её можно решить любым известным способом.
Оценка значимости коэффициентов регрессии. Интервальная оценка коэффициентов регрессии
Проверить значимость оценок коэффициентов регрессии — значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициента регрессии, соблюдая предпосылки «нормальной регрессии». В этом случае вычисляемая для проверки нулевой гипотезы 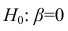
имеет распределение Стьюдента с к= n-2 степенями свободы (b — оценка коэффициента регрессии, 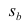
коэффициента регрессии, иначе стандартная ошибка оценки). По уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (см. табл. 1 приложений) критическое значение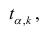
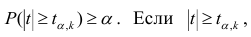
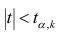
Оценки среднеквадратического отклонения коэффициентов регрессии вычисляют по следующим формулам:
где 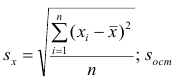
формуле (2.5).
Доверительный интервал для значимых параметров строят по обычной схеме. Из условия
где а — уровень значимости, находим
Интервальная оценка для условного математического ожидания
Линия регрессии характеризует изменение условного математического ожидания результативного признака от вариации остальных признаков.
Точечной оценкой условного математического ожидания 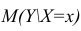
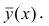
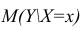
построить доверительный интервал в точке
Известно, что 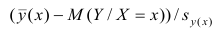
Стьюдента с k=n—2 степенями свободы. Найдя оценку среднеквадратического отклонения для условного среднего, можно построить доверительный интервал для условного математического ожидания
Оценку дисперсии условного среднего вычисляют по формуле
или для интервального ряда
Доверительный интервал находят из условия
где а — уровень значимости. Отсюда
Доверительный интервал для условного математического ожидания можно изобразить графически (рис, 2.2).
Из рис. 2.2 видно, что в точке 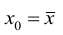
Проверка значимости уравнения регрессии
Оценить значимость уравнения регрессии — значит установить, соответствует ли математическая, модель, выражающая зависимость между Y и X, экспериментальным данным. Для оценки значимости в предпосылках «нормальной регрессии» проверяют гипотезу 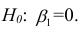
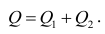
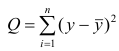
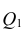
X) и 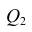
Для проверки нулевой гипотезы вычисляют статистику 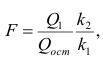
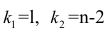
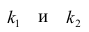
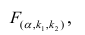
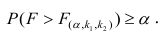
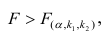
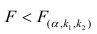
Многомерный регрессионный анализ
В случае, если изменения результативного признака определяются действием совокупности других признаков, имеет место многомерный регрессионный анализ. Пусть результативный признак У, а независимые признаки 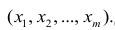
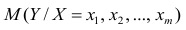
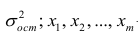
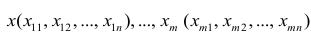
Оценке подлежат параметры 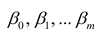
Заменив параметры их оценками, запишем уравнение регрессии
Коэффициенты в этом выражении находят методом наименьших квадратов.
Исходными данными для вычисления коэффициентов 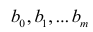

Как и в двумерном случае, составляют систему нормальных уравнений
которую можно решить любым способом, известным из линейной алгебры. Рассмотрим один из них — способ обратной матрицы. Предварительно преобразуем систему уравнений. Выразим из первого уравнения значение 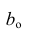
Подставим в остальные уравнения системы вместо 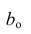
Пусть С — матрица коэффициентов при неизвестных параметрах 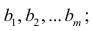
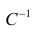
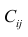
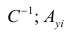
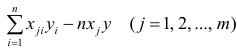
запишем окончательные выражения для параметров:
Оценкой остаточной дисперсии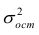
где 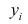
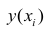
Если выборка получена из нормально распределенной генеральной совокупности, то, аналогично изложенному в п. 2.4, можно проверить значимость оценок коэффициентов регрессии, только в данном случае статистику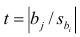
где 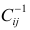
го столбца;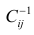
При заданном уровне значимости а и числе степеней свободы к=n— m—1 по табл. 1 приложений находят критическое значение 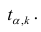
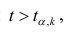
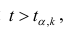
Для значимых коэффициентов регрессии целесообразно построить доверительные интервалы по формуле (2.10). Для оценки значимости уравнения регрессии следует проверить нулевую гипотезу о том, что все коэффициенты регрессии (кроме свободного члена) равны нулю: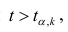
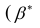
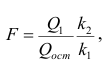
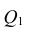
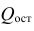
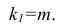
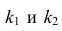
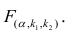
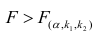
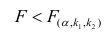
Факторный анализ
Основные положения. В последнее время всё более широкое распространение находит один из новых разделов многомерного статистического анализа — факторный анализ. Первоначально этот метод
разрабатывался для объяснения многообразия корреляций между исходными параметрами. Действительно, результатом корреляционного анализа является матрица коэффициентов корреляций. При малом числе параметров можно произвести визуальный анализ этой матрицы. С ростом числа параметра (10 и более) визуальный анализ не даёт положительных результатов. Оказалось, что всё многообразие корреляционных связей можно объяснить действием нескольких обобщённых факторов, являющихся функциями исследуемых параметров, причём сами обобщённые факторы при этом могут быть и неизвестны, однако их можно выразить через исследуемые параметры.
Один из основоположников факторного анализа Л. Терстоун приводит такой пример: несколько сотен мальчиков выполняют 20 разнообразных гимнастических упражнений. Каждое упражнение оценивают баллами. Можно рассчитать матрицу корреляций между 20 упражнениями. Это большая матрица размером 20><20. Изучая такую матрицу, трудно уловить закономерность связей между упражнениями. Нельзя ли объяснить скрытую в таблице закономерность действием каких-либо обобщённых факторов, которые в результате эксперимента непосредственно, не оценивались? Оказалось, что обо всех коэффициентах корреляции можно судить по трём обобщённым факторам, которые и определяют успех выполнения всех 20 гимнастических упражнений: чувство равновесия, усилие правого плеча, быстрота движения тела.
Дальнейшие разработки факторного анализа доказали, что этот метод может быть с успехом применён в задачах группировки и классификации объектов. Факторный анализ позволяет группировать объекты со сходными сочетаниями признаков и группировать признаки с общим характером изменения от объекта к объекту. Действительно, выделенные обобщённые факторы можно использовать как критерии при классификации мальчиков по способностям к отдельным группам гимнастических упражнений.
Методы факторного анализа находят применение в психологии и экономике, социологии и экономической географии. Факторы, выраженные через исходные параметры, как правило, легко интерпретировать как некоторые существенные внутренние характеристики объектов.
Факторный анализ может быть использован и как самостоятельный метод исследования, и вместе с другими методами многомерного анализа, например в сочетании с регрессионным анализом. В этом случае для набора зависимых переменных наводят обобщённые факторы, которые потом входят в регрессионный анализ в качестве переменных. Такой подход позволяет сократить число переменных в регрессионном анализе, устранить коррелированность переменных, уменьшить влияние ошибок и в случае ортогональности выделенных факторов значительно упростить оценку значимости переменных.
Представление, информации в факторном анализе
Для проведения факторного анализа информация должна быть представлена в виде двумерной таблицы чисел размерностью 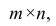
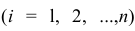
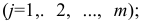
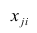
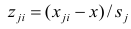
Основная модель факторного анализа. Основная модель факторного анализа имеет вид
где 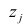
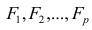
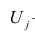
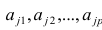
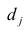
Модель предполагает, что каждый из j признаков, входящих в исследуемый набор и заданных в стандартной форме, может быть представлен в виде линейной комбинации небольшого числа общих факторов 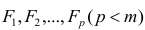
Термин «общий фактор» подчёркивает, что каждый такой фактор имеет существенное значение для анализа всех признаков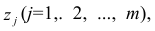
Термин «характерный фактор» показывает, что он относится только к данному j-му признаку. Это специфика признака, которая не может быть, выражена через факторы
Факторные нагрузки 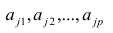
Для j-го признака и i-го объекта модель (2.19) можно записать в. виде
где 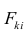
Дисперсию признака 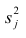
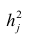
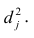
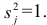
Если общие и характерные факторы не коррелируют между собой, то дисперсию j-го признака можно представить в виде
где 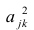
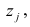
Полный вклад k-го фактора в суммарную дисперсию признаков
Вклад общих факторов в суммарную дисперсию
Факторное отображение
Используя модель (2.19), запишем выражения для каждого из параметров:
Коэффициенты системы (2,21) — факторные нагрузки — можно представить в виде матрицы, каждая строка которой соответствует параметру, а столбец — фактору.
Факторный анализ позволяет получить не только матрицу отображений, но и коэффициенты корреляции между параметрами и
факторами, что является важной характеристикой качества факторной модели. Таблица таких коэффициентов корреляции называется факторной структурой или просто структурой.
Коэффициенты отображения можно выразить через выборочные парные коэффициенты корреляции. На этом основаны методы вычисления факторного отображения.
Рассмотрим связь между элементами структуры и коэффициентами отображения. Для этого, учитывая выражение (2.19) и определение выборочного коэффициента корреляции, умножим уравнения системы (2.21) на соответствующие факторы, произведём суммирование по всем n наблюдениям и, разделив на n, получим следующую систему уравнений:
где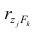
м фактором;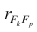
Если предположить, что общие факторы между собой, не коррелированы, то уравнения (2.22) можно записать в виде
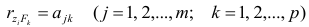
элементам структуры.
Введём понятие, остаточного коэффициента корреляции и остаточной корреляционной матрицы. Исходной информацией для построения факторной модели (2.19) служит матрица выборочных парных коэффициентов корреляции. Используя построенную факторную модель, можно снова вычислить коэффициенты корреляции между признаками и сравнись их с исходными Коэффициентами корреляции. Разница между ними и есть остаточный коэффициент корреляции.
В случае независимости факторов имеют место совсем простые выражения для вычисляемых коэффициентов корреляции между параметрами: для их вычисления достаточно взять сумму произведений коэффициентов отображения, соответствующих наблюдавшимся признакам:
где 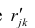
и к-м признаком. Остаточный коэффициент корреляции
Матрица остаточных коэффициентов корреляции называется остаточной матрицей или матрицей остатков
где 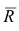
Результаты факторного анализа удобно представить в виде табл. 2.10.
Здесь суммы квадратов нагрузок по строкам — общности параметров, а суммы квадратов нагрузок по столбцам — вклады факторов в суммарную дисперсию параметров. Имеет место соотношение
Определение факторных нагрузок
Матрицу факторных нагрузок можно получить различными способами. В настоящее время наибольшее распространение получил метод главных факторов. Этот метод основан на принципе последовательных приближений и позволяет достичь любой точности. Метод главных факторов предполагает использование ЭВМ. Существуют хорошие алгоритмы и программы, реализующие все вычислительные процедуры.
Введём понятие редуцированной корреляционной матрицы или просто редуцированной матрицы. Редуцированной называется матрица выборочных коэффициентов корреляции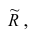
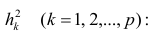
Редуцированная и полная матрицы связаны соотношением
где D — матрица характерностей.
Общности, как правило, неизвестны, и нахождение их в факторном анализе представляет серьезную проблему. Вначале определяют (хотя бы приближённо) число общих факторов, совокупность, которых может с достаточной точностью аппроксимировать все взаимосвязи выборочной корреляционной матрицы. Доказано, что число общих факторов (общностей) равно рангу редуцированной матрицы, а при известном ранге можно по выборочной корреляционной матрице найти оценки общностей. Числа общих факторов можно определить априори, исходя из физической природы эксперимента. Затем рассчитывают матрицу факторных нагрузок. Такая матрица, рассчитанная методом главных факторов, обладает одним интересным свойством: сумма произведений каждой пары её столбцов равна нулю, т.е. факторы попарно ортогональны.
Сама процедура нахождения факторных нагрузок, т.е. матрицы А, состоит из нескольких шагов и заключается в следующем: на первом шаге ищут коэффициенты факторных нагрузок при первом факторе так, чтобы сумма вкладов данного фактора в суммарную общность была максимальной:
Максимум 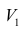
где 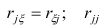
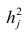
Затем рассчитывают матрицу коэффициентов корреляции с учётом только первого фактора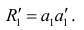
На втором шаге определяют коэффициенты нагрузок при втором факторе так, чтобы сумма вкладов второго фактора в остаточную общность (т.е. полную общность без учёта той части, которая приходится на долю первого фактора) была максимальной. Сумма квадратов нагрузок при втором факторе
Максимум 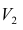
где 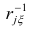
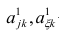
Факторный анализ учитывает суммарную общность. Исходная суммарная общность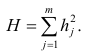
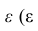
Адекватность факторной модели оценивается по матрице остатков (если величины её коэффициентов малы, то модель считают адекватной).
Такова последовательность шагов для нахождения факторных нагрузок. Для нахождения максимума функции (2.24) при условии (2.25) используют метод множителей Лагранжа, который приводит к системе т уравнений относительно m неизвестных
Метод главных компонент
Разновидностью метода главных факторов является метод главных компонент или компонентный анализ, который реализует модель вида
где m — количество параметров (признаков).
Каждый из наблюдаемых, параметров линейно зависит от m не коррелированных между собой новых компонент (факторов) 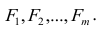
Если для дальнейшего анализа оставить все найденные т компонент, то тем самым будет использована вся информация, заложенная в корреляционной матрице. Однако это неудобно и нецелесообразно. На практике обычно оставляют небольшое число компонент, причём количество их определяется долей суммарной дисперсии, учитываемой этими компонентами. Существуют различные критерии для оценки числа оставляемых компонент; чаще всего используют следующий простой критерий: оставляют столько компонент, чтобы суммарная дисперсия, учитываемая ими, составляла заранее установленное число процентов. Первая из компонент должна учитывать максимум суммарной дисперсии параметров; вторая — не коррелировать с первой и учитывать максимум оставшейся дисперсии и так до тех пор, пока вся дисперсия не будет учтена. Сумма учтённых всеми компонентами дисперсий равна сумме дисперсий исходных параметров. Математический аппарат компонентного анализа полностью совпадает с аппаратом метода главных факторов. Отличие только в исходной матрице корреляций.
Компонента (или фактор) через исходные переменные выражается следующим образом:
где 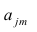
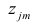
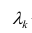
компонент.
Для иллюстрации возможностей факторного анализа покажем, как, используя метод главных компонент, можно сократить размерность пространства независимых переменных, перейдя от взаимно коррелированных параметров к независимым факторам, число которых р
Следует особо остановиться на интерпретации результатов, т.е. на смысловой стороне факторного анализа. Собственно факторный анализ состоит из двух важных этапов; аппроксимации корреляционной матрицы и интерпретации результатов. Аппроксимировать корреляционную матрицу, т.е. объяснить корреляцию между параметрами действием каких-либо общих для них факторов, и выделить сильно коррелирующие группы параметров достаточно просто: из корреляционной матрицы одним из методов
факторного анализа непосредственно получают матрицу нагрузок — факторное решение, которое называют прямым факторным решением. Однако часто это решение не удовлетворяет исследователей. Они хотят интерпретировать фактор как скрытый, но существенный параметр, поведение которого определяет поведение некоторой своей группы наблюдаемых параметров, в то время как, поведение других параметров определяется поведением других факторов. Для этого у каждого параметра должна быть наибольшая по модулю факторная нагрузка с одним общим фактором. Прямое решение следует преобразовать, что равносильно повороту осей общих факторов. Такие преобразования называют вращениями, в итоге получают косвенное факторное решение, которое и является результатом факторного анализа.
Приложения
Значение t — распределения Стьюдента
Понятие о регрессионном анализе. Линейная выборочная регрессия. Метод наименьших квадратов (МНК)
Основные задачи регрессионного анализа:
- Вычисление выборочных коэффициентов регрессии
- Проверка значимости коэффициентов регрессии
- Проверка адекватности модели
- Выбор лучшей регрессии
- Вычисление стандартных ошибок, анализ остатков
Построение простой регрессии по экспериментальным данным.
Предположим, что случайные величины 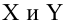
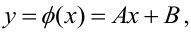
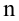
Диаграмма рассеяния (разброса, рассеивания)
Выборочное уравнение прямой линии регрессии 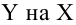
Задача: подобрать 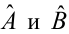
Для того, что бы провести прямую 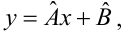
чтобы
Постулаты регрессионного анализа, которые должны выполняться при использовании МНК.
подчинены нормальному закону распределения.
- Дисперсия
постоянна и не зависит от номера измерения.
- Результаты наблюдений
в разных точках независимы.
- Входные переменные
независимы, неслучайны и измеряются без ошибок.
Введем функцию ошибок 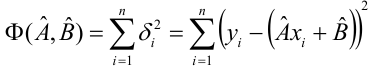
Решив систему, получим искомые значения
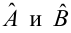
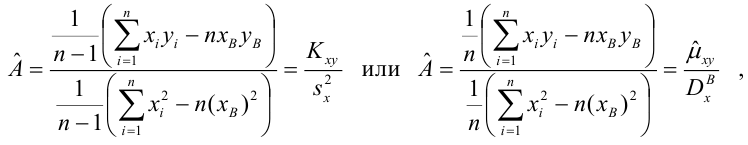
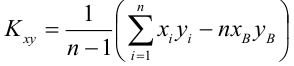
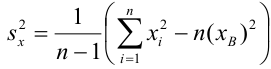
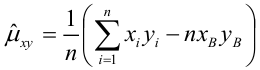
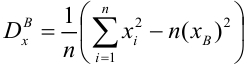
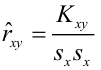
Коэффициент детерминации
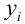
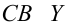
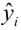
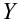
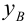
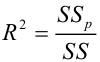
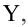
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это используется для доказательства адекватности модели (качества регрессии). Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 0,5 (в этом случае коэффициент множественной корреляции превышает по модулю 0,7). Модели с коэффициентом детерминации выше 0,8 можно признать достаточно хорошими (коэффициент корреляции превышает 0,9). Подтверждение адекватности модели проводится на основе дисперсионного анализа путем проверки гипотезы о значимости коэффициента детерминации.
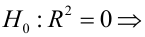
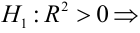
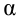
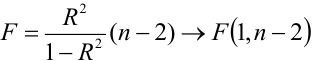
Критическая область — правосторонняя;
Если 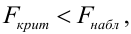
Мощность статистического критерия. Функция мощности
Определение. Мощностью критерия 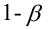
Задача: построить критическую область таким образом, чтобы мощность критерия была максимальной.
Определение. Наилучшей критической областью (НКО) называют критическую область, которая обеспечивает минимальную ошибку второго рода
Пример:
По паспортным данным автомобиля расход топлива на 100 километров составляет 10 литров. В результате измерения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки были проведены испытания 25 автомобилей с модернизированным двигателем; выборочная средняя расхода топлива по результатам испытаний составила 9,3 литра. Предполагая, что выборка получена из нормально распределенной генеральной совокупности с математическим ожиданием 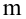
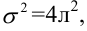
3) Уровень значимости
4) Статистический критерий
5) Критическая область — левосторонняя
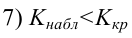
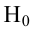
Пример:
В условиях примера 1 предположим, что наряду с 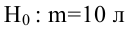
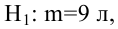
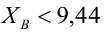
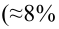
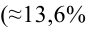
Определение. Пусть проверяется 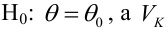
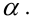
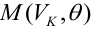
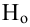
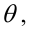
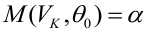
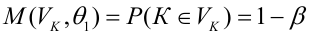
Пример:
Построить график функции мощности из примера 2 для

Пример:
Какой минимальный объем выборки следует взять в условии примера 2 для того, чтобы обеспечить
Лемма Неймана-Пирсона.
При проверке простой гипотезы 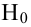
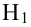
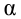
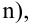
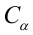
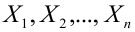
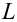
Пример:
Случайная величина 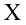
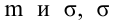
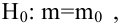
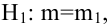
Решение:
Ошибка первого рода:
НКО:
Пример:
Для зависимости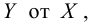
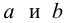
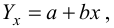
Решение. Воспользуемся предыдущими результатами
Согласно формуле (24), уравнение регрессии будет иметь вид 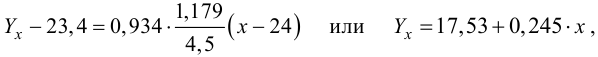
Для выяснения значимости уравнения регрессии вычислим суммы 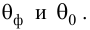
Из (27) и (28) по данным таблицы получим
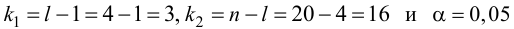
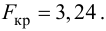
Вычислим статистику
Так как 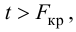
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
29. Линейная регрессия
Рассмотрим двумерную случайную величину (X, Y), где X и Y – зависимые случайные величины.
Представим приближенно одну случайную величину как функцию другой. Точное соответствие невозможно. Будем считать, что эта функция линейная.
Для определения этой функции остается только найти постоянные величины a и b.
Определение. Функция G(X) называется Наилучшим приближением случайной величины Y в смысле метода наименьших квадратов, если математическое ожидание

Теорема. Линейная средняя квадратическая регрессия Y На Х вычисляется по формуле:
В этой формуле Mx=M(X), My=M(Y), 
Величина 
Прямая, уравнение которой

Называется Прямой сренеквадратической регрессии Y На Х.
Величина 
Видно, что если R=±1, то остаточная дисперсия равна нулю, и, следовательно, ошибка равна нулю и случайная величина Y точно представляется линейной функцией от случайной величины Х.
Прямая среднеквадратичной регрессии Х на Y определяется аналогично по формуле:
Прямые среднеквадратичной регрессии пересекаются в точке (Тх, ту), которую называют Центром совместного распределения Случайных величин Х И Y.
Корреляционная таблица
Пример 1 . По данной корреляционной таблице построить прямые регрессии с X на Y и с Y на X . Найти соответствующие коэффициенты регрессии и коэффициент корреляции между X и Y .
| y/x | 15 | 20 | 25 | 30 | 35 | 40 |
| 100 | 2 | 2 | ||||
| 120 | 4 | 3 | 10 | 3 | ||
| 140 | 2 | 50 | 7 | 10 | ||
| 160 | 1 | 4 | 3 | |||
| 180 | 1 | 1 |
Решение:
Уравнение линейной регрессии с y на x будем искать по формуле
а уравнение регрессии с x на y, использовав формулу:
где x x , y — выборочные средние величин x и y, σx, σy — выборочные среднеквадратические отклонения.
Находим выборочные средние:
x = (15(1 + 1) + 20(2 + 4 + 1) + 25(4 + 50) + 30(3 + 7 + 3) + 35(2 + 10 + 10) + 40(2 + 3))/103 = 27.961
y = (100(2 + 2) + 120(4 + 3 + 10 + 3) + 140(2 + 50 + 7 + 10) + 160(1 + 4 + 3) + 180(1 + 1))/103 = 136.893
Выборочные дисперсии:
σ 2 x = (15 2 (1 + 1) + 20 2 (2 + 4 + 1) + 25 2 (4 + 50) + 30 2 (3 + 7 + 3) + 35 2 (2 + 10 + 10) + 40 2 (2 + 3))/103 — 27.961 2 = 30.31
σ 2 y = (100 2 (2 + 2) + 120 2 (4 + 3 + 10 + 3) + 140 2 (2 + 50 + 7 + 10) + 160 2 (1 + 4 + 3) + 180 2 (1 + 1))/103 — 136.893 2 = 192.29
Откуда получаем среднеквадратические отклонения:
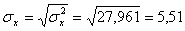
Определим коэффициент корреляции:
где ковариация равна:
Cov(x,y) = (35•100•2 + 40•100•2 + 25•120•4 + 30•120•3 + 35•120•10 + 40•120•3 + 20•140•2 + 25•140•50 + 30•140•7 + 35•140•10 + 15•160•1 + 20•160•4 + 30•160•3 + 15•180•1 + 20•180•1)/103 — 27.961 • 136.893 = -50.02
Запишем уравнение линий регрессии y(x):
и уравнение x(y):
Построим найденные уравнения регрессии на чертеже, из которого сделаем следующие вывод:
1) обе линии проходят через точку с координатами (27.961; 136.893)
2) все точки расположены близко к линиям регрессии.
Пример 2 . По данным корреляционной таблицы найти условные средние y и x . Оценить тесноту линейной связи между признаками x и y и составить уравнения линейной регрессии y по x и x по y . Сделать чертеж, нанеся его на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
Корреляционная таблица:
| X / Y | 2 | 4 | 6 | 8 | 10 |
| 1 | 5 | 4 | 2 | 0 | 0 |
| 2 | 0 | 6 | 3 | 3 | 0 |
| 3 | 0 | 0 | 1 | 2 | 3 |
| 5 | 0 | 0 | 0 | 0 | 1 |
Уравнение линейной регрессии с y на x имеет вид:
Уравнение линейной регрессии с x на y имеет вид:
найдем необходимые числовые характеристики.
Выборочные средние:
x = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 5.53
y = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 1.93
Дисперсии:
σ 2 x = (2 2 (5) + 4 2 (4 + 6) + 6 2 (2 + 3 + 1) + 8 2 (3 + 2) + 10 2 (3 + 1))/30 — 5.53 2 = 6.58
σ 2 y = (1 2 (5 + 4 + 2) + 2 2 (6 + 3 + 3) + 3 2 (1 + 2 + 3) + 5 2 (1))/30 — 1.93 2 = 0.86
Откуда получаем среднеквадратические отклонения:
σx = 2.57 и σy = 0.93
и ковариация:
Cov(x,y) = (2•1•5 + 4•1•4 + 6•1•2 + 4•2•6 + 6•2•3 + 8•2•3 + 6•3•1 + 8•3•2 + 10•3•3 + 10•5•1)/30 — 5.53 • 1.93 = 1.84
Определим коэффициент корреляции:
Запишем уравнения линий регрессии y(x):
и вычисляя, получаем:
yx = 0.28 x + 0.39
Запишем уравнения линий регрессии x(y):
и вычисляя, получаем:
xy = 2.13 y + 1.42
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (5.53; 1.93) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=30-m-1 = 28 находим tкрит:
tкрит (n-m-1;α/2) = (28;0.025) = 2.048
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
Пример 3 . Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице. Необходимо:
1. Вычислить групповые средние i и j x y, построить эмпирические линии регрессии.
2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции; на уровне значимости α= 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, оценить рост производительности труда при степени автоматизации производства 43%.
Скачать решение
Пример . По корреляционной таблице рассчитать ковариацию и коэффициент корреляции, построить прямые регрессии.
Пример 4 . Найти выборочное уравнение прямой Y регрессии Y на X по данной корреляционной таблице.
Решение находим с помощью калькулятора.
Скачать
Пример №4
Пример 5 . С целью анализа взаимного влияния прибыли предприятия и его издержек выборочно были проведены наблюдения за этими показателями в течение ряда месяцев: X — величина месячной прибыли в тыс. руб., Y — месячные издержки в процентах к объему продаж.
Результаты выборки сгруппированы и представлены в виде корреляционной таблицы, где указаны значения признаков X и Y и количество месяцев, за которые наблюдались соответствующие пары значений названных признаков.
Решение.
Пример №5
Пример №6
Пример №7
Пример 6 . Данные наблюдений над двумерной случайной величиной (X, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X. Построить график уравнения регрессии и показать точки (x;y)б рассчитанные по таблице данных.
Решение.
Скачать решение
Пример 7 . Дана корреляционная таблица для величин X и Y, X- срок службы колеса вагона в годах, а Y — усредненное значение износа по толщине обода колеса в миллиметрах. Определить коэффициент корреляции и уравнения регрессий.
| X / Y | 0 | 2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 | 42 |
| 0 | 3 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 25 | 108 | 44 | 8 | 2 | 0 | 0 | 0 | 0 | 0 |
| 2 | 30 | 50 | 60 | 21 | 5 | 5 | 0 | 0 | 0 | 0 |
| 3 | 1 | 11 | 33 | 32 | 13 | 2 | 3 | 1 | 0 | 0 |
| 4 | 0 | 5 | 5 | 13 | 13 | 7 | 2 | 0 | 0 | 0 |
| 5 | 0 | 0 | 1 | 2 | 12 | 6 | 3 | 2 | 1 | 0 |
| 6 | 0 | 1 | 0 | 1 | 0 | 0 | 2 | 1 | 0 | 1 |
| 7 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
Решение.
Скачать решение
Пример 8 . По заданной корреляционной таблице определить групповые средние количественных признаков X и Y. Построить эмпирические и теоретические линии регрессии. Предполагая, что между переменными X и Y существует линейная зависимость:
- Вычислить выборочный коэффициент корреляции и проанализировать степень тесноты и направления связи между переменными.
- Определить линии регрессии и построить их графики.
Скачать
Уравнение линейной средней квадратической регрессии
Регрессионный анализ позволяет приближенно определить форму связи между результативным и факторными признаками, а также решить вопрос о том, значима ли эта связь. Вид функции, с помощью которой приближенно выражается форма связи, выбирают заранее, исходя из содержательных соображений или визуального анализа данных. Математическое решение задачи основано на методе наименьших квадратов.
Суть метода наименьших квадратов. Рассмотрим содержание метода на конкретном примере. Пусть имеются данные о сборе хлеба на душу населения по совокупности черноземных губерний. От каких факторов зависит величина этого сбора? Вероятно, определяющее влияние на величину сбора хлеба оказывает величина посева и уровень урожайности. Рассмотрим сначала зависимость величины сбора хлеба на душу населения от размера посева на душу ( столбцы 1 и 2 табл .4 ) Попытаемся представить интересующую нас зависимость с помощью прямой линии. Разумеется, такая линия может дать только приближенное представление о форме реальной статистической связи. Постараемся сделать это приближение наилучшим. Оно будет тем лучше, чем меньше исходные данные будут отличаться от соответствующих точек, лежащих на линии. Степень близости может быть выражена величиной суммы квадратов отклонении, реальных значений от, расположенных на прямой. Использование именно квадратов отклонений (не просто отклонений) позволяет суммировать отклонения различных знаков без их взаимного погашения и дополнительно обеспечивает сравнительно большее внимание, уделяемое большим отклонениям. Именно этот критерий (минимизация суммы квадратов отклонений) положен в основу метода наименьших квадратов.
В вычислительном аспекте метод наименьших квадратов сводится к составлению и решению системы так называемых нормальных уравнений. Исходным этапом для этого является подбор вида функции, отображающей статистическую связь.
Тип функции в каждом конкретном случае можно подобрать путем прикидки на графике исходных данных подходящей, т. е. достаточно хорошо приближающей эти данные, линии. В нашем случае связь между сбором хлеба на душу и величиной посева на душу может быть изображена с помощью прямой линии ( рис. 14 ) и записана в виде
где у—величина сбора хлеба на душу (результативный признак или зависимая переменная); x—величина посева на душу (факторный признак или независимая переменная); a o и a 1 — параметры уравнения, которые могут быть найдены методом наименьших квадратов.
Для нахождения искомых параметров нужно составить систему уравнений, которая в данном случае будет иметь вид
Полученная система может быть решена известным из школьного курса методом Гаусса. Искомые параметры системы из двух нормальных уравнений можно вычислить и непосредственно с помощью последовательного использования нижеприведенных формул:
где y i — i-e значение результативного признака; x i — i-e значение факторного признака; и — средние арифметические результативного и факторного признаков соответственно; n— число значений признака y i , или, что то же самое, число значений признака x i .
Пример 9. Найдем уравнение линейной связи между величиной сбора хлеба (у) и размером посева (х) по данным табл. 4. Проделав необходимые вычисления, получим из (6.17):
Таким образом, уравнение связи, или, как принято говорить, уравнение регрессии, выглядит следующим образом:
Интерпретация коэффициента регрессии. Уравнение регрессии не только определяет форму анализируемой связи, но и показывает, в какой степени изменение одного признака сопровождается изменением другого признака.
Коэффициент при х, называемый коэффициентом регрессии, показывает, на какую величину в среднем изменяется результативный признак у при изменении факторного признака х на единицу.
В примере 9 коэффициент регрессии получился равным 24,58. Следовательно, с увеличением посева, приходящегося на душу, на одну десятину сбор хлеба на душу населения в среднем увеличивается на 24,58 пуда.
Средняя и предельная ошибки коэффициента регрессии. Поскольку уравнения регрессии рассчитываются, как правило, для выборочных данных, обязательно встают вопросы точности и надежности полученных результатов. Вычисленный коэффициент регрессии, будучи выборочным, с некоторой точностью оценивает соответствующий коэффициент регрессии генеральной совокупности. Представление об этой точности дает средняя ошибка коэффициента регрессии ( ), рассчитываемая по формуле
у i , — i-e значение результативного признака; ŷ i — i-e выравненное значение, полученное из уравнения (6.15); x i —i-e значение факторного признака; σ x —среднее квадратическое отклонение х; n — число значений х или, что то же самое, значений у; m—число факгорных признаков (независимых переменных).
В формуле (6.18), в частности, формализовано очевидное положение: чем больше фактические значения отклоняются от выравненных, тем большую ошибку следует ожидать; чем меньше число наблюдений, на основе которых строится уравнение, тем больше будет ошибка.
Средняя ошибка коэффициента регрессии является основой для расчета предельной ошибки. Последняя показывает, в каких пределах находится истинное значение коэффициента регрессии при заданной надежности результатов. Предельная ошибка коэффициента регрессии вычисляется аналогично предельной ошибке средней арифметической (см. гл. 5), т. е. как t где t—величина, числовое значение которой определяется в зависимости от принятого уровня надежности.
Пример 10. Найти среднюю и предельную ошибки коэффициента регрессии, полученного в примере 9.
Для расчета прежде всего подсчитаем выравненные значения ŷ i для чего в уравнение регрессии, полученное в примере 9, подставим конкретные значения x i :
ŷ i = 17,6681 +24,5762*0,91 = 40,04 и т. д.
Затем вычислим отклонения фактических значений у i , от выравненных и их квадраты
Далее, подсчитав средний по черноземным губерниям посев на душу ( =0,98), отклонения фактических значений x i от этой средней, квадраты отклонений и среднее квадратическое отклонение , получим все необходимые составляющие формул (618) и (619):
Таким образом, средняя ошибка коэффициента регрессии равна 2,89, что составляет 12% от вычисленного коэффициента
Задавшись уровнем надежности, равным 0,95, найдем по табл. 1 приложения соответствующее ему значение t=1,96, рассчитаем предельную ошибку 1,96*2,89=5,66 и пределы коэффициента регрессии для принятого уровня надежности ( В случае малых выборок величина t находится из табл. 2 приложения. ). Нижняя граница коэффициента регрессии равна 24,58-5,66=18,92, а верхняя граница 24,58+5,66=30,24
Средняя квадратическая ошибка линии регрессии. Уравнение регрессии представляет собой функциональную связь, при которой по любому значению х можно однозначно определить значение у. Функциональная связь лишь приближенно отражает связь реальную, причем степень этого приближения может быть различной и зависит она как от свойств исходных данных, так и от выбора вида функции, по которой производится выравнивание.
На рис. 15 представлены два различных случая взаимоотношения между двумя признаками. В обоих случаях предполагаемая связь описывается одним и тем же уравнением, но во втором случае соотношение между признаками х и у достаточно четко выражено и уравнение, по-видимому, довольно хорошо описывает это соотношение, тогда как в первом случае сомнительно само наличие сколько-нибудь закономерного соотношения между признаками. И в том, и в другом случаях, несмотря на их существенное различие, метод наименьших квадратов дает одинаковое уравнение, поскольку этот метод нечувствителен к потенциальным возможностям исходного материала вписаться в ту или иную схему. Кроме того, метод наименьших квадратов применяется для расчета неизвестных параметров заранее выбранного вида функции, и вопрос о выборе наиболее подходящего для конкретных данных вида функции в рамках этого метода не ставится и не решается. Таким образом, при пользовании методом наименьших квадратов открытыми остаются два важных вопроса, а именно: существует ли связь и верен ли выбор вида функции, с помощью которой делается попытка описать форму связи.
Чтобы оценить, насколько точно уравнение регрессии описывает реальные соотношения между переменными, нужно ввести меру рассеяния фактических значений относительно вычисленных с помощью уравнения. Такой мерой служит средняя квадратическая ошибка регрессионного уравнения, вычисляемая по приведенной выше формуле (6.19).
Пример 11. Определить среднюю квадратическую ошибку уравнения, полученного в примере 9.
Промежуточные расчеты примера 10 дают нам среднюю квадратическую ошибку уравнения. Она равна 4,6 пуда.
Этот показатель аналогичен среднему квадратическому отклонению для средней. Подобно тому, как по величине среднего квадратического отклонения можно судить о представительности средней арифметической (см. гл. 5), по величине средней квадратической ошибки регрессионного уравнения можно сделать вывод о том, насколько показательна для соотношения между признаками та связь, которая выявлена уравнением. В каждом конкретном случае фактическая ошибка может оказаться либо больше, либо меньше средней. Средняя квадратическая ошибка уравнения показывает, насколько в среднем мы ошибемся, если будем пользоваться уравнением, и тем самым дает представление о точности уравнения. Чем меньше σ y.x , тем точнее предсказание линии регрессии, тем лучше уравнение регрессии описывает существующую связь. Показатель σ y.x позволяет различать случаи, представленные на рис. 15. В случае б) он окажется значительно меньше, чем в случае а). Величина σ y.x зависит как от выбора функции, так и от степени описываемой связи.
Варьируя виды функций для выравнивания и оценивая результаты с помощью средней квадратической ошибки, можно среди рассматриваемых выбрать лучшую функцию, функцию с наименьшей средней ошибкой. Но существует ли связь? Значимо ли уравнение регрессии, используемое для отображения предполагаемой связи? На эти вопросы отвечает определяемый ниже критерий значи-мости регрессии.
Мерой значимости линии регрессии может служить следующее соотношение:
где ŷ i —i-e выравненное значение; —средняя арифметическая значений y i ; σ y.x —средняя квадратическая ошибка регрессионного уравнения, вычисляемая по формуле (6.19); n—число сравниваемых пар значений признаков; m—число факторных признаков.
Действительно, связь тем больше, чем значительнее мера рассеяния признака, обусловленная регрессией, превосходит меру рассеяния отклонений фактических значений от выравненных.
Соотношение (6.20) позволяет решить вопрос о значимости регрессии. Регрессия значима, т. е. между признаками существует линейная связь, если для данного уровня значимости вычисленное значение F ф [m,n-(m+1)] превышает критическое значение F кр [m,n-(m+1)], стоящее на пересечении m-го столбца и [n—(m+1)]-й строки специальной таблицы ( см. табл. 4 приложения ).
Пример 12. Выясним, связаны ли сбор хлеба на душу населения и посев на душу населения линейной зависимостью.
Воспользуемся F-критерием значимости регрессии. Подставив в формулу (6.20) данные табл. 4 и результат примера 10, получим
Обращаясь к таблице F-распределения для Р=0,95 (α=1—Р=0,5) и учитывая, что n=23, m =1, в табл. 4А приложения на пересечения 1-го столбца и 21-й строки находим критическое значение F кр , равное 4,32 при степени надежности Р=0,95. Поскольку вычисленное значение F ф существенно превосходит по величине F кр , то обнаруженная линейная связь существенна, т. е. априорная гипотеза о наличии линейной связи подтвердилась. Вывод сделан при степени надежности P=0,95. Между прочим, вывод в данном случае останется прежним, если надежность повысить до Р=0,99 (соответствующее значение F кр =8,02 по табл. 4Б приложения для уровня значимости α=0,01).
Коэффициент детерминации. С помощью F-критерия мы Установили, что существует линейная зависимость между величиной сбора хлеба и величиной посева на душу. Следовательно, можно утверждать, что величина сбора хлеба, приходящегося на душу, линейно зависит от величины посева на душу. Теперь уместно поставить уточняющий вопрос — в какой степени величина посева на душу определяет величину сбора хлеба на душу? На этот вопрос можно ответить, рассчитав, какая часть вариации результативного признака может быть объяснена влиянием факторного признака.
Оно показывает долю разброса, учитываемого регрессией, в общем разбросе результативного признака и носит название коэффициента детерминации. Этот показатель, равный отношению факторной вариации к полной вариации признака, позволяет судить о том, насколько «удачно» выбран вид функции ( Отметим, что по смыслу коэффициент детерминации в регрессионном анализе соответствует квадрату корреляционного отношения для корреляционной таблицы (см. § 2). ). Проведя расчеты, основанные на одних и тех же исходных данных, для нескольких типов функций, мы можем из них выбрать такую, которая дает наибольшее значение R 2 и, следовательно, в большей степени, чем другие функции, объясняет вариацию результативного признака. Действительно, при расчете R 2 для одних и тех же данных, но разных функций знаменатель выражения (6.21) остается неизменным, а числитель показывает ту часть вариации результативного признака, которая учитывается выбранной функцией. Чем больше R 2 , т. е. чем больше числитель, тем больше изменение факторного признака объясняет изменение результативного признака и тем, следовательно, лучше уравнение регрессии, лучше выбор функции.
Наконец, отметим, что введенный ранее, при изложении методов корреляционного анализа, коэффициент детерминации совпадает с определенным здесь показателем, если выравнивание производится По прямой линии. Но последний показатель (R 2 ) имеет более широкий спектр применения и может использоваться в случае связи, отличной от линейной ( см. § 4 данной главы ).
Пример 13. Рассчитать коэффициент детерминации для уравнения, полученного в примере 9.
Вычислим R 2 , воспользовавшись формулой (6.21) и данными табл. 4:
Итак, уравнение регрессии почти на 78% объясняет колебания сбора хлеба на душу. Это немало, но, По-видимому, можно улучшить модель введением в нее еще одного фактора.
Случай двух независимых переменных. Простейший случай множественной регрессии. В предыдущем изложении регрессионного анализа мы имели дело с двумя признаками — результативным и факторным. Но на результат действует обычно не один фактор, а несколько, что необходимо учитывать для достаточно полного анализа связей.
В математической статистике разработаны методы множественной регрессии ( Регрессия называется множественной, если число независимых переменных, учтенных в ней, больше или равно двум. ), позволяющие анализировать влияние на результативный признак нескольких факторных. К рассмотрению этих методов мы и переходим.
Возвратимся к примеру 9. В нем была определена форма связи между величиной сбора хлеба на душу и размером посева на душу. Введем в анализ еще один фактор — уровень урожайности (см. столбец З табл. 4). Без сомнения, эта переменная влияет на сбор хлеба на душу. Но в какой степени влияет? Насколько обе независимые переменные определяют сбор хлеба на душу в черноземных губерниях? Какая из переменных — посев на душу или урожайность — оказывает определяющее влияние на сбор хлеба? Попытаемся ответить на эти вопросы.
После добавления второй независимой переменной уравнение регрессии будет выглядеть так:
где у—сбор хлеба на душу; х 1 —размер посева на душу; x 2 —урожай с десятины (в пудах); а 0 , а 1 , а 2 —параметры, подлежащие определению.
Для нахождения числовых значений искомых параметров, как и в случае одной независимой переменной, пользуются методом наименьших квадратов. Он сводится к составлению и решению системы нормальных уравнений, которая имеет вид
Когда система состоит из трех и более нормальных уравнений, решение ее усложняется. Существуют стандартные программы расчета неизвестных параметров регрессионного уравнения на ЭВМ. При ручном счете можно воспользоваться известным из школьного курса методом Гаусса.
Пример 14. По данным табл. 4 описанным способом найдем параметры a 0 , а 1 , а 2 уравнения (6.22). Получены следующие результаты: a 2 =0,3288, a 1 =28,7536, a 0 =-0,2495.
Таким образом, уравнение множественной регрессии между величиной сбора хлеба на душу населения (у), размером посева на душу (x 1 ) и уровнем урожайности (х 2 ) имеет вид:
у=-0,2495+28,7536x 1 +0,3288x 2 .
Интерпретация коэффициентов уравнения множественной регрессии. Коэффициент при х 1 в полученном уравнении отличается от аналогичного коэффициента в уравнении примера 9.
Коэффициент при независимой переменной в уравнении простой регрессии отличается от коэффициента при соответствующей переменной в уравнении множественной регрессии тем, что в последнем элиминировано влияние всех учтенных в данном уравнении признаков.
Коэффициенты уравнения множественной регрессии поэтому называются частными или чистыми коэффициентами регрессии.
Частный коэффициент множественной регрессии при х 1 показывает, что с увеличением посева на душу на 1 дес. и при фиксированной урожайности сбор хлеба на душу населения вырастает в среднем на 28,8 пуда. Частный коэффициент при x 2 показывает, что при фиксированном посеве на душу увеличение урожая на единицу, т. е. на 1 пуд с десятины, вызывает в среднем увеличение сбора хлеба на душу на 0,33 пуда. Отсюда можно сделать вывод, что увеличение сбора хлеба в черноземных губерниях России идет, в основном, за счет расширения посева и в значительно меньшей степени—за счет повышения урожайности, т. е. экстенсивная форма развития зернового хозяйства является господствующей.
Введение переменной х 2 в уравнение позволяет уточнить коэффициент при х 1 . Конкретно, коэффициент оказался выше (28,8 против 24,6), когда в изучаемой связи вычленилось влияние урожайности на сбор хлеба.
Однако выводы, полученные в результате анализа коэффициентов регрессии, не являются пока корректными, поскольку, во-первых, не учтена разная масштабность факторов, во-вторых, не выяснен вопрос о значимости коэффициента a 2 .
Величина коэффициентов регрессии изменяется в зависимости от единиц измерения, в которых представлены переменные. Если переменные выражены в разном масштабе измерения, то соответствующие им коэффициенты становятся несравнимыми. Для достижения сопоставимости коэффициенты регрессии исходного уравнения стандартизуют, взяв вместо исходных переменных их отношения к собственным средним квадратическим отклонениям. Тогда уравнение (6.22) приобретает вид
Сравнивая полученное уравнение с уравнением (6.22), определяем стандартизованные частные коэффициенты уравнения, так называемые бета-коэффициенты, по формулам:
где β 1 и β 2 —бета-коэффициенты; а 1 и а 2 —коэффициенты регрессии исходного уравнения; σ у , , и — средние квадратические отклонения переменных у, х 1 и х 2 соответственно.
Вычислив бета-коэффициенты для уравнения, полученного в примере 14:
видим, что вывод о преобладании в черноземной полосе россии экстенсивной формы развития хозяйства над интенсивной остается в силе, так как β 1 значительно больше, чем β 2 .
Оценка точности уравнения множественной регрессии.
Точность уравнения множественной регрессии, как и в случае уравнения с одной независимой переменной, оценивается средней квадратической ошибкой уравнения. Обозначим ее , где подстрочные индексы указывают, что результативным признаком в уравнении является у, а факторными признаками х 1 и x 2 . Для расчета средней квадратической ошибки уравнения множественной регрессии применяется приведенная выше формула (6.19).
Пример 15. Оценим точность полученного в примере 14 уравнения регрессии.
Воспользовавшись формулой (6.19) и данными табл. 4, вычислим среднюю квадратическую ошибку уравнения:
Оценка полезности введения дополнительной переменной. Точность уравнения регрессии тесно связана с вопросом ценности включения дополнительных членов в это уравнение.
Сравним средние квадратические ошибки, рассчитанные для уравнения с одной переменной х 1 (пример 11) и для уравнения с двумя независимыми переменными х 1 и х 2 . Включение в уравнение новой переменной (урожайности) уменьшило среднюю квадратическую ошибку почти вдвое.
Можно провести сравнение ошибок с помощью коэффициентов вариации
где σ f —средняя квадратическая ошибка регрессионного уравнения; —средняя арифметическая результативного признака.
Для уравнения, содержащего одну независимую переменную:
Для уравнения, содержащего две независимые переменные:
Итак, введение независимой переменной «урожайность» уменьшило среднюю квадратическую ошибку до величины порядка 7,95% среднего значения зависимой переменной.
Наконец, по формуле (6.21) рассчитаем коэффициент детерминации
Он показывает, что уравнение регрессии на 81,9% объясняет колебания сбора хлеба на душу населения. Сравнивая полученный результат (81,9%) с величиной R 2 для однофакторного уравнения (77,9%), видим, что включение переменной «урожайность» заметно увеличило точность уравнения.
Таким образом, сравнение средних квадратических ошибок уравнения, коэффициентов вариации, коэффициентов детерминации, рассчитанных до и после введения независимой переменной, позволяет судить о полезности включения этой переменной в уравнение. Однако следует быть осторожными в выводах при подобных сравнениях, поскольку увеличение R 2 или уменьшение σ и V σ не всегда имеют приписываемый им здесь смысл. Так, увеличение R 2 может объясняться тем фактом, что число рассматриваемых параметров в уравнении приближается к числу объектов наблюдения. Скажем, весьма сомнительными будут ссылки на увеличение R 2 или уменьшение σ, если в уравнение вводится третья или четвертая независимая переменная и уравнение строится на данных по шести, семи объектам.
Полезность включения дополнительного фактора можно оценить с помощью F-критерия.
Частный F-критерий показывает степень влияния дополнительной независимой переменной на результативный признак и может использоваться при решении вопроса о добавлении в уравнение или исключении из него этой независимой переменной.
Разброс признака, объясняемый уравнением регрессии (6.22), можно разложить на два вида: 1) разброс признака, обусловленный независимой переменной х 1 , и 2) разброс признака, обусловленный независимой переменной x 2 , когда х 1 уже включена в уравнение. Первой составляющей соответствует разброс признака, объясняемый уравнением (6.15), включающим только переменную х 1 . Разность между разбросом признака, обусловленным уравнением (6.22), и разбросом признака, обусловленным уравнением (6.15), определит ту часть разброса, которая объясняется дополнительной независимой переменной x 2 . Отношение указанной разности к разбросу признака, регрессией не объясняемому, представляет собой значение частного критерия. Частный F-критерий называется также последовательным, если статистические характеристики строятся при последовательном добавлении переменных в регрессионное уравнение.
Пример 16. Оценить полезность включения в уравнение регрессии дополнительной переменной «урожайность» (по данным и результатам примеров 12 и 15).
Разброс признака, объясняемый уравнением множественной регрессии и рассчитываемый как сумма квадратов разностей выравненных значений и их средней, равен 1623,8815. Разброс признака, объясняемый уравнением простой регрессии, составляет 1545,1331.
Разброс признака, регрессией не объясняемый, определяется квадратом средней квадратической ошибки уравнения и равен 10,9948 (см. пример 15).
Воспользовавшись этими характеристиками, рассчитаем частный F-критерий
С уровнем надежности 0,95 (α=0,05) табличное значение F (1,20), т. е. значение, стоящее на пересечении 1-го столбца и 20-й строки табл. 4А приложения, равно 4,35. Рассчитанное значение F ф значительно превосходит табличное, и, следовательно, включение в уравнение переменной «урожайность» имеет смысл.
Таким образом, выводы, сделанные ранее относительно коэффициентов регрессии, вполне правомерны.
Важным условием применения к обработке данных метода множественной регрессии является отсутствие сколько-нибудь значительной взаимосвязи между факторными признаками. При практическом использовании метода множественной регрессии, прежде чем включать факторы в уравнение, необходимо убедиться в том, что они независимы.
Если один из факторов зависит линейно от другого, то система нормальных уравнений, используемая для нахождения параметров уравнения, не разрешима. Содержательно этот факт можно толковать так: если факторы х 1 и x 2 связаны между собой, то они действуют на результативный признак у практически как один фактор, т. е. сливаются воедино и их влияние на изменение у разделить невозможно. Когда между независимыми переменными уравнения множественной регрессии имеется линейная связь, следствием которой является неразрешимость системы нормальных уравнений, то говорят о наличии мультиколлинеарности.
На практике вопрос о наличии или об отсутствии мультиколлинеарности решается с помощью показателей взаимосвязи. В случае двух факторных признаков используется парный коэффициент корреляции между ними: если этот коэффициент по абсолютной величине превышает 0,8, то признаки относят к числу мультиколлинеарных. Если число факторных признаков больше двух, то рассчитываются множественные коэффициенты корреляции. Фактор признается мультиколлинеарным, если множественный коэффициент корреляции, характеризующий совместное влияние на этот фактор остальных факторных признаков, превзойдет по величине коэффициент множественной корреляции между результативным признаком и совокупностью всех независимых переменных.
Самый естественный способ устранения мультиколлинеарности — исключение одного из двух линейно связанных факторных признаков. Этот способ прост, но не всегда приемлем, так как подлежащий исключению фактор может оказывать на зависимую переменную особое влияние. В такой ситуации применяются более сложные методы избавления от мультиколлинеарности ( См.: Мот Ж. Статистические предвидения и решения на предприятии. М., 1966; Ковалева Л. Н. Многофакторное прогнозирование на основе рядов динамики. М., 1980. ).
Выбор «наилучшего» уравнения регрессии. Эта проблема связана с двойственным отношением к вопросу о включении в регрессионное уравнение независимых переменных. С одной стороны, естественно стремление учесть все возможные влияния на результативный признак и, следовательно, включить в модель полный набор выявленных переменных. С другой стороны, возрастает сложность расчетов и затраты, связанные с получением максимума информации, могут оказаться неоправданными. Нельзя забывать и о том, что для построения уравнения регрессии число объектов должно в несколько раз превышать число независимых переменных. Эти противоречивые требования приводят к необходимости компромисса, результатом которого и является «наилучшее» уравнение регрессии. Существует несколько методов, приводящих к цели: метод всех возможных регрессий, метод исключения, метод включения, шаговый регрессионный и ступенчатый регрессионный методы.
Метод всех возможных регрессий заключается в переборе и сравнении всех потенциально возможных уравнений. В качестве критерия сравнения используется коэффициент детерминации R 2 . «Наилучшим» признается уравнение с наибольшей величиной R 2 . Метод весьма трудоемок и предполагает использование вычислительных машин.
Методы исключения и включения являются усовершенствованными вариантами предыдущего метода. В методе исключения в качестве исходного рассматривается регрессионное уравнение, включающее все возможные переменные. Рассчитывается частный F-критерий для каждой из переменных, как будто бы она была последней переменной, введенной в регрессионное уравнение. Минимальная величина частного F-критерия (F min ) сравнивается с критической величиной (F кр ), основанной на заданном исследователем уровне значимости. Если F min >F кр , то уравнение остается без изменения. Если F min кр , то переменная, для которой рассчитывался этот частный F-критерий, исключается. Производится перерасчет уравнения регрессии для оставшихся переменных, и процедура повторяется для нового уравнения регрессии. Исключение из рассмотрения уравнений с незначимыми переменными уменьшает объем вычислений, что является достоинством этого метода по сравнению с предыдущим.
Метод включения состоит в том, что в уравнение включаются переменные по степени их важности до тех пор, пока уравнение не станет достаточно «хорошим». Степень важности определяется линейным коэффициентом корреляции, показывающим тесноту связи между анализируемой независимой переменной и результативным признаком: чем теснее связь, тем больше информации о результирующем признаке содержит данный факторный признак и тем важнее, следовательно, введение этого признака в уравнение.
Процедура начинается с отбора факторного признака, наиболее тесно связанного с результативным признаком, т. е. такого факторного признака, которому соответствует максимальный по величине парный линейный коэффициент корреляции. Далее строится линейное уравнение регрессии, содержащее отобранную независимую переменную. Выбор следующих переменных осуществляется с помощью частных коэффициентов корреляции, в которых исключается влияние вошедших в модель факторов. Для каждой введенной переменной рассчитывается частный F-критерий, по величине которого судят о том, значим ли вклад этой переменной. Как только величина частного F-критерия, относящаяся к очередной переменной, оказывается незначимой, т. е. эффект от введения этой переменной становится малозаметным, процесс включения переменных заканчивается. Метод включения связан с меньшим объемом вычислений, чем предыдущие методы. Но при введении новой переменной нередко значимость включенных ранее переменных изменяется. Метод включения этого не учитывает, что является его недостатком. Модификацией метода включения, исправляющей этот недостаток, является шаговый регрессионный метод.
Шаговый регрессионный метод кроме процедуры метода включения содержит анализ переменных, включенных в уравнение на предыдущей стадии. Потребность в таком анализе возникает в связи с тем, что переменная, обоснованно введенная в уравнение на ранней стадии, может оказаться лишней из-за взаимосвязи ее с переменными, позднее включенными в уравнение. Анализ заключается в расчете на каждом этапе частных F-критериев для каждой переменной уравнения и сравнении их с величиной F кр , точкой F-распределения, соответствующей заданному исследователем уровню значимости. Частный F-критерий показывает вклад переменной в вариацию результативного признака в предположении, что она вошла в модель последней, а сравнение его с F кр позволяет судить о значимости рассматриваемой переменной с учетом влияния позднее включенных факторов. Незначимые переменные из уравнения исключаются.
Рассмотренные методы предполагают довольно большой объем вычислений и практически неосуществимы без ЭВМ. Для реализации ступенчатого регрессионного метода вполне достаточно малой вычислительной техники.
Ступенчатый регрессионный метод включает в себя такую последовательность действий. Сначала выбирается наиболее тесно связанная с результативным признаком переменная и составляется уравнение регрессии. Затем находят разности фактических и выравненных значений и эти разности (остатки) рассматриваются как значения результативной переменной. Для остатков подбирается одна из оставшихся независимых переменных и т. д. На каждой стадии проверяется значимость регрессии. Как только обнаружится незначимость, процесс прекращается и окончательное уравнение получается суммированием уравнений, полученных на каждой стадии за исключением последней.
Ступенчатый регрессионный метод менее точен, чем предыдущие, но не столь громоздок. Он оказывается полезным в случаях, когда необходимо внести содержательные правки в уравнение. Так, для изучения факторов, влияющих на цены угля в Санкт-Петербурге в конце XIX— начале XX в., было получено уравнение множественной регрессии. В него вошли следующие переменные: цены угля в Лондоне, добыча угля в России и экспорт из России. Здесь не обосновано появление в модели такого фактора, как добыча угля, поскольку Санкт-Петербург работал исключительно на импортном угле. Модели легко придать экономический смысл, если независимую переменную «добыча» заменить независимой переменной «импорт». Формально такая замена возможна, поскольку между импортом и добычей существует тесная связь. Пользуясь ступенчатым методом, исследователь может совершить эту замену, если предпочтет содержательно интерпретируемый фактор.
§ 4. Нелинейная регрессия и нелинейная корреляция
Построение уравнений нелинейной регрессии. До сих пор мы, в основном, изучали связи, предполагая их линейность. Но не всегда связь между признаками может быть достаточно хорошо представлена линейной функцией. Иногда для описания существующей связи более пригодными, а порой и единственно возможными являются более сложные нелинейные функции. Ограничимся рассмотрением наиболее простых из них.
Одним из простейших видов нелинейной зависимости является парабола, которая в общем виде может быть представлена функцией (6.2):
Неизвестные параметры а 0 , а 1 , а 2 находятся в результате решения следующей системы уравнений:
Дает ли преимущества описание связи с помощью параболы по сравнению с описанием, построенным по гипотезе линейности? Ответ на этот вопрос можно получить, рассчитав последовательный F-критерий, как это делалось в случае множественной регрессии (см. пример 16).
На практике для изучения связей используются полиномы более высоких порядков (3-го и 4-го порядков). Составление системы, ее решение, а также решение вопроса о полезности повышения порядка функции для этих случаев аналогичны описанным. При этом никаких принципиально новых моментов не возникает, но существенно увеличивается объем расчетов.
Кроме класса парабол для анализа нелинейных связей можно применять и другие виды функций. Для расчета неизвестных параметров этих функций рекомендуется использовать метод наименьших квадратов, как наиболее мощный и широко применяемый.
Однако метод наименьших квадратов не универсален, поскольку он может использоваться только при условии, что выбранные для выравнивания функции линейны по отношению к своим параметрам. Не все функции удовлетворяют этому условию, но большинство применяемых на практике с помощью специальных преобразований могут быть приведены к стандартной форме функции с линейными параметрами.
Рассмотрим некоторые простейшие способы приведения функций с нелинейными параметрами к виду, который позволяет применять к ним метод наименьших квадратов.
Функция не является линейной относительно своих параметров.
Прологарифмировав обе части приведенного равенства
получим функцию, линейную относительно своих новых параметров:
Кроме логарифмирования для приведения функций к нужному виду используют обратные величины.
с помощью следующих переобозначений:
может быть приведена к виду
Подобные преобразования расширяют возможности использования метода наименьших квадратов, увеличивая число функций, к которым этот метод применим.
Измерение тесноты связи при криволинейной зависимости. Рассмотренные ранее линейные коэффициенты корреляции оценивают тесноту взаимосвязи при линейной связи между признаками. При наличии криволинейной связи указанные меры связи не всегда приемлемы. Разберем подобную ситуацию на примере.
Пример 17. В 1-м и 2-м столбцах табл. 5 приведены значения результативного признака у и факторного признака х (данные условные). Поставив вопрос о тесноте связи между ними, рассчитаем парный линейный коэффициент корреляции по формуле (6.3). Он оказался равным нулю, что свидетельствует об отсутствии линейной связи. Тем не менее связь между признаками существует, более того, она является функциональной и имеет вид
Для измерения тесноты связи при криволинейной зависимости используется индекс корреляции, вычисляемый по формуле
где у i —i-e значение результативного признака; ŷ i —i-e выравненное значение этого признака; —среднее арифметическое значение результативного признака.
Числитель формулы (6.27) характеризует разброс выравненных значений результативного признака. Поскольку изменения выравненных, т. е. вычисленных по уравнению регрессии, значений признака происходят только в результате изменения факторного признака х. то числитель измеряет разброс результативного признака, обусловленный влиянием на него факторного признака. Знаменатель же измеряет разброс признака-результата, который определен влиянием на него всех факторов, в том числе и учтенного. Таким образом, индекс корреляции оценивает участие данного факторного признака в общем действии всего комплекса факторов, вызывающих колеблемость результативного признака, тем самым определяя тесноту зависимости признака у от признака х. При этом, если признак х не вызывает никаких изменений признака у, то числитель и, следовательно, индекс корреляции равны 0. Если же линия регрессии полностью совпадает с фактическими данными, т. е. признаки связаны функционально, как в примере 17, то индекс корреляции равен 1. В случае линейной зависимости между х и у индекс корреляции численно равен линейному коэффициенту корреляции г. Квадрат индекса корреляции совпадает с введенным ранее (6.21) коэффициентом детерминации. Если же вопрос о форме связи не ставится, то роль коэффициента детерминации играет квадрат корреляционного отношения η 2 y/x (6.12).
Таковы основные принципы и условия, методика и техника применения корреляционного и регрессионного анализа. Их подробное рассмотрение обусловлено тем, что они являются высокоэффективными и потому очень широко применяемыми методами анализа взаимосвязей в объективном мире природы и общества. Корреляционный и регрессионный анализ широко и успешно применяются и в исторических исследованиях.
источники:
http://math.semestr.ru/math/corel.php
http://masters.donntu.org/2005/kita/tokarev/library/linreg.htm
Основы линейной регрессии
Что такое регрессия?
Линия регрессии
Метод наименьших квадратов
Предположения линейной регрессии
Аномальные значения (выбросы) и точки влияния
Гипотеза линейной регрессии
Оценка качества линейной регрессии: коэффициент детерминации R2
Применение линии регрессии для прогноза
Простые регрессионные планы
Пример: простой регрессионный анализ
Что такое регрессия?
Рассмотрим две непрерывные переменные x=(x1, x2, .., xn), y=(y1, y2, …, yn).
Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.
Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.
Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).
Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).
Линия регрессии
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
Y=a+bx.
x называется независимой переменной или предиктором.
Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»
- a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
- b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
- a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.
Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Метод наименьших квадратов
Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).
Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).
Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).
Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.
Предположения линейной регрессии
Итак, для каждой наблюдаемой величины остаток равен разнице
и соответствующего предсказанного
Каждый остаток может быть положительным или отрицательным.
Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:
- Остатки нормально распределены с нулевым средним значением;
Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или
и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).
Аномальные значения (выбросы) и точки влияния
«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).
Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.
И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).
При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.
Гипотеза линейной регрессии
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.
Если угловой коэффициент линии равен нулю, между и
нет линейного соотношения: изменение
не влияет на
Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:
Вычислить статистику критерия, равную отношению , которая подчиняется
распределению с
степенями свободы, где
стандартная ошибка коэффициента
,
— оценка дисперсии остатков.
Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.
Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :
где процентная точка
распределения со степенями свободы
что дает вероятность двустороннего критерия
Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.
Для больших выборок, скажем, мы можем аппроксимировать
значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
Оценка качества линейной регрессии: коэффициент детерминации R2
Из-за линейного соотношения и
мы ожидаем, что
изменяется, по мере того как изменяется
, и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.
Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.
Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R2 (в парной линейной регрессии это величина r2, квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.
Разность представляет собой процент дисперсии который нельзя объяснить регрессией.
Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.
Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования значения по значению
в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).
Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение
путем подстановки этого значения
в уравнение линии регрессии.
Итак, если прогнозируем
как
Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины
в популяции.
Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
Простые регрессионные планы
Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P, например, 7, 4 и 9, а план включает эффект первого порядка P, то матрица плана X будет иметь вид
а регрессионное уравнение с использованием P для X1 выглядит как
Y = b0 + b1P
Если простой регрессионный план содержит эффект высшего порядка для P, например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:
а уравнение примет вид
Y = b0 + b1P2
Сигма-ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X. При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X, а работать только с регрессионным уравнением.
Пример: простой регрессионный анализ
Этот пример использует данные, представленные в таблице:

Рис. 3. Таблица исходных данных.
Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

Рис. 4. Таблица спецификаций переменных.
Задача исследования
Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 (Pt_Poor) как зависимую переменную.
Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 (Pop_Chng) как переменную-предиктор.
Просмотр результатов
Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.
На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374. Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p<.05. Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.
Распределение переменных
Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor.

Рис. 6. Гистограмма переменной Pt_Poor.
Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»

Рис. 7. Гистограмма переменной Pt_Poor.
Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.
Диаграмма рассеяния
Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.

Рис. 8. Диаграмма рассеяния.
Диаграмма рассеяния показывает явную отрицательную корреляцию (-.65) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.
Критерии значимости

Рис. 9. Таблица, содержащая критерии значимости.
Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor, p<.001.
Итог
На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.
Связанные определения:
Линейная регрессия
Матрица плана
Общая линейная модель
Регрессия
В начало
Содержание портала
В предыдущих заметках предметом анализа часто становилась отдельная числовая переменная, например, доходность взаимных фондов, время загрузки Web-страницы или объем потребления безалкогольных напитков. В настоящей и следующих заметках мы рассмотрим методы предсказания значений числовой переменной в зависимости от значений одной или нескольких других числовых переменных. [1]
Материал будет проиллюстрирован сквозным примером. Прогнозирование объема продаж в магазине одежды. Сеть магазинов уцененной одежды Sunflowers на протяжении 25 лет постоянно расширялась. Однако в настоящее время у компании нет систематического подхода к выбору новых торговых точек. Место, в котором компания собирается открыть новый магазин, определяется на основе субъективных соображений. Критериями выбора являются выгодные условия аренды или представления менеджера об идеальном местоположении магазина. Представьте, что вы — руководитель отдела специальных проектов и планирования. Вам поручили разработать стратегический план открытия новых магазинов. Этот план должен содержать прогноз годового объема продаж во вновь открываемых магазинах. Вы полагаете, что торговая площадь непосредственно связана с объемом выручки, и хотите учесть этот факт в процессе принятия решения. Как разработать статистическую модель, позволяющую прогнозировать годовой объем продаж на основе размера нового магазина?
Как правило, для предсказания значений переменной используется регрессионный анализ. Его цель — разработать статистическую модель, позволяющую предсказывать значения зависимой переменной, или отклика, по значениям, по крайней мере одной, независимой, или объясняющей, переменной. В настоящей заметке мы рассмотрим простую линейную регрессию — статистический метод, позволяющий предсказывать значения зависимой переменной Y по значениям независимой переменной X. В последующих заметках будет описана модель множественной регрессии, предназначенная для предсказания значений независимой переменной Y по значениям нескольких зависимых переменных (Х1, Х2, …, Xk). [2]
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Виды регрессионных моделей
В заметке Представление числовых данных в виде таблиц и диаграмм для иллюстрации зависимости между переменными X и Y использовалась диаграмма разброса. На ней значения переменной X откладывались по горизонтальной оси, а значения переменной Y — по вертикальной. Зависимость между двумя переменными может быть разной: от самой простой до крайне сложной. Пример простейшей (линейной) зависимости показан на рис. 1.
Рис. 1. Положительная линейная зависимость
Простая линейная регрессия:
(1) Yi = β0 + β1Xi + εi
где β0 — сдвиг (длина отрезка, отсекаемого на координатной оси прямой Y), β1 — наклон прямой Y, εi— случайная ошибка переменной Y в i-м наблюдении.
В этой модели наклон β1 представляет собой количество единиц измерения переменной Y, приходящихся на одну единицу измерения переменной X. Эта величина характеризует среднюю величину изменения переменной Y (положительного или отрицательного) на заданном отрезке оси X. Сдвиг β0 представляет собой среднее значение переменной Y, когда переменная X равна 0. Последний компонент модели εi является случайной ошибкой переменной Y в i-м наблюдении. Выбор подходящей математической модели зависит от распределения значений переменных X и Y на диаграмме разброса. Различные виды зависимости переменных показаны на рис. 2.
Рис. 2. Диаграммы разброса, иллюстрирующие разные виды зависимостей
На панели А значения переменной Y почти линейно возрастают с увеличением переменной X. Этот рисунок аналогичен рис. 1, иллюстрирующему положительную зависимость между размером магазина (в квадратных футах) и годовым объемом продаж. Панель Б является примером отрицательной линейной зависимости. Если переменная X возрастает, переменная Y в целом убывает. Примером этой зависимости является связь между стоимостью конкретного товара и объемом продаж. На панели В показан набор данных, в котором переменные X и Y практически не зависят друг от друга. Каждому значению переменной X соответствуют как большие, так и малые значения переменной Y. Данные, приведенные на панели Г, демонстрируют криволинейную зависимость между переменными X и Y. Значения переменной Y возрастают при увеличении переменной X, однако скорость роста после определенных значений переменной X падает. Примером положительной криволинейной зависимости является связь между возрастом и стоимостью обслуживания автомобилей. По мере старения машины стоимость ее обслуживания сначала резко возрастает, однако после определенного уровня стабилизируется. Панель Д демонстрирует параболическую U-образную форму зависимости между переменными X и Y. По мере увеличения значений переменной X значения переменной Y сначала убывают, а затем возрастают. Примером такой зависимости является связь между количеством ошибок, совершенных за час работы, и количеством отработанных часов. Сначала работник осваивается и делает много ошибок, потом привыкает, и количество ошибок уменьшается, однако после определенного момента он начинает чувствовать усталость, и число ошибок увеличивается. На панели Е показана экспоненциальная зависимость между переменными X и Y. В этом случае переменная Y сначала очень быстро убывает при возрастании переменной X, однако скорость этого убывания постепенно падает. Например, стоимость автомобиля при перепродаже экспоненциально зависит от его возраста. Если перепродавать автомобиль в течение первого года, его цена резко падает, однако впоследствии ее падение постепенно замедляется.
Мы кратко рассмотрели основные модели, которые позволяют формализовать зависимости между двумя переменными. Несмотря на то что диаграмма разброса чрезвычайно полезна при выборе математической модели зависимости, существуют более сложные и точные статистические процедуры, позволяющие описать отношения между переменными. В дальнейшем мы будем рассматривать лишь линейную зависимость.
Вывод уравнения простой линейной регрессии
Вернемся к сценарию, изложенному в начале главы. Наша цель — предсказать объем годовых продаж для всех новых магазинов, зная их размеры. Для оценки зависимости между размером магазина (в квадратных футах) и объемом его годовых продаж создадим выборки из 14 магазинов (рис. 3).
Рис. 3. Площади и годовые объемы продаж 14 магазинов сети Sunflowers: (а) исходные данные; (б) диаграмма разброса
Анализ рис. 3 показывает, что между площадью магазина X и годовым объемом продаж Y существует положительная зависимость. Если площадь магазина увеличивается, объем продаж возрастает почти линейно. Таким образом, наиболее подходящей для исследования является линейная модель. Остается лишь определить, какая из линейных моделей точнее остальных описывает зависимость между анализируемыми переменными.
Метод наименьших квадратов
Данные, представленные на рис. 1а, получены для случайной выборки магазинов. Если верны некоторые предположения (об этом чуть позже), в качестве оценки параметров генеральной совокупности (β0 и β1) можно использовать сдвиг b0 и наклон b1 прямой Y. Таким образом, уравнение простой линейной регрессии принимает следующий вид:
где — предсказанное значение переменной Y для i-гo наблюдения, Xi — значение переменной X в i-м наблюдении.
Для того чтобы предсказать значение переменной Y, в уравнении (2) необходимо определить два коэффициента регрессии — сдвиг b0 и наклон b1 прямой Y. Вычислив эти параметры, проведем прямую на диаграмме разброса. Затем исследователь может визуально оценить, насколько близка регрессионная прямая к точкам наблюдения. Простая линейная регрессия позволяет найти прямую линию, максимально приближенную к точкам наблюдения. Критерии соответствия можно задать разными способами. Возможно, проще всего минимизировать разности между фактическими значениями Yi, и предсказанными значениями . Однако, поскольку эти разности могут быть как положительными, так и отрицательными, следует минимизировать сумму их квадратов.
Поскольку = b0 + b1Xi, сумма квадратов принимает следующий вид:
Параметры b0 и b1 неизвестны. Таким образом, сумма квадратов разностей является функцией, зависящей от сдвига b0 и наклона b1 выборки Y. Для того чтобы найти значения параметров b0 и b1, минимизирующих сумму квадратов разностей, применяется метод наименьших квадратов. При любых других значениях сдвига b0 и наклона b1 сумма квадратов разностей между фактическими значениями переменной Y и ее наблюдаемыми значениями лишь увеличится.
До того, как Excel взял на себя всю рутинную работу, вычисления по методу наименьших квадратов были очень трудоемкими. Excel позволяет решать подобные задачи двумя способами. Во-первых, можно воспользоваться Пакетом анализа (строка Регрессия). Результаты представлены на рис. 4. Во-вторых, можно, выделив точки на графике (как на рис. 3б), кликнуть правой кнопкой мыши и выбрать Добавить линию тренда. Далее можно выбрать вид линии тренда (в нашем случае – Линейная), отформатировать линию, показать на графике уравнение и величину достоверности аппроксимации (R2) (рис. 5).
Рис. 4. Результаты решения задачи о зависимости между площадями и годовыми объемами продаж в магазинах сети Sunflower (получены с помощью Пакета анализа Excel)
Рис. 5. Диаграмма разброса и линия регрессии (тренда) в задаче о выборе магазина
Как следует из рис. 4 и 5, b0 = 0,9645, а b1 = 1,6699. Таким образом, уравнение линейной регрессии для этих данных имеет следующий вид: = 0,9645 + 1,6699Xi. Вычисленный наклон b1 = +1,6699. Это означает, что при возрастании переменной X на единицу среднее значение переменной Y возрастает на 1,6699 единиц. Иначе говоря, увеличение площади магазина на один квадратный фут приводит к увеличению годового объема продаж на 1,67 тыс. долл. Таким образом, наклон представляет собой долю годового объема продаж, зависящую от размера магазина. Вычисленный сдвиг b0 = +0,9645 (млн. долл.). Эта величина представляет собой среднее значение переменной Y при X = 0. Поскольку площадь магазина не может равняться нулю, сдвиг можно считать долей годового дохода, зависящей от других факторов. Следует отметить, однако, что сдвиг переменной Y выходит за пределы диапазона переменной X. Следовательно, к интерпретации параметра b0 необходимо относиться внимательно.
Пример 1. Один экономист решил предсказать изменение индекса 500 наиболее активно покупаемых акций на Нью-Йоркской фондовой бирже, публикуемого агентством Standard and Poor, на основе показателей экономики США за 50 лет. В результате он получил следующее уравнение линейной регрессии: Ŷi = –5,0 + 7Хi. Какой смысл имеют параметры сдвига b0 и наклона b1.
Решение. Сдвиг регрессии b0 равен –5,0. Это значит, что если рост экономики США равен нулю, индекс акций за год снизится на 5%. Наклон b1 равен 7. Следовательно, при увеличении темпов роста экономики на 1% индекс акций возрастает на 7%.
Пример 2. Вернемся к сценарию, изложенному в начале заметки. Применим модель линейной регрессии для прогноза объема годовых продаж во всех новых магазинах в зависимости от их размеров. Предположим, что площадь магазина равна 4000 квадратных футов. Какой среднегодовой объем продаж можно прогнозировать?
Решение. Подставим значение X = 4 (тыс. кв. футов) в уравнение линейной регрессии: = 0,9645 + 1,6699Xi = 0,9645 + 1,6699*4 = 7,644 млн. долл. Итак, прогнозируемый среднегодовой объем продаж в магазине, площадь которого равна 4000 кв. футов, составляет 7 644 000 долл.
Прогнозирование в регрессионном анализе: интерполяция и экстраполяция
Применяя регрессионную модель для прогнозирования, необходимо учитывать лишь допустимые значения независимой переменной. В этот диапазон входят все значения переменной X, начиная с минимальной и заканчивая максимальной. Таким образом, предсказывая значение переменной Y при конкретном значении переменной X, исследователь выполняет интерполяцию между значениями переменной X в диапазоне возможных значений. Однако экстраполяция значений за пределы этого интервала не всегда релевантна. Например, пытаясь предсказать среднегодовой объем продаж в магазине, зная его площадь (рис. 3а), мы можем вычислять значение переменной Y лишь для значений X от 1,1 до 5,8 тыс. кв. футов. Следовательно, прогнозировать среднегодовой объем продаж можно лишь для магазинов, площадь которых не выходит за пределы указанного диапазона. Любая попытка экстраполяции означает, что мы предполагаем, будто линейная регрессия сохраняет свой характер за пределами допустимого диапазона.
Оценки изменчивости
Вычисление сумм квадратов. Для того чтобы предсказать значение зависимой переменной по значениям независимой переменной в рамках избранной статистической модели, необходимо оценить изменчивость. Существует несколько способов оценки изменчивости. Первый способ использует общую сумму квадратов (total sum of squares — SST), позволяющую оценить колебания значений Yi вокруг среднего значения . В регрессионном анализе полная вариация, представляющая собой полную сумму квадратов, разделяется на объяснимую вариацию, или сумму квадратов регрессии (regression sum of squares — SSR), и необъяснимую вариацию, или сумму квадратов ошибок (error sum of squares — SSE). Объяснимая вариация характеризует взаимосвязь между переменными X и Y, а необъяснимая зависит от других факторов (рис. 6).
Рис. 6. Оценки изменчивости в модели регрессии
Сумма квадратов регрессии (SSR) представляет собой сумму квадратов разностей между Ŷi (предсказанным значением переменной Y) и (средним значением переменной Y). Сумма квадратов ошибок (SSE) является частью вариации переменной Y, которую невозможно описать с помощью регрессионной модели. Эта величина зависит от разностей между наблюдаемыми и предсказанными значениями.
Полная сумма квадратов (SST) равна сумме квадратов регрессии плюс сумма квадратов ошибок:
(3) SST = SSR + SSE
Полная сумма квадратов (SST) равна сумме квадратов разностей между наблюдаемыми значениями переменной Y и ее средним значением:
Сумма квадратов регрессии (SSR) равна сумме квадратов разностей между предсказанными значениями переменной Y и ее средним значением:
Сумма квадратов ошибок (SSE) равна сумме квадратов разностей между наблюдаемыми и предсказанными значениями переменной Y:
Суммы квадратов, вычисленные с помощью программы Пакета анализа Excel при решении задачи о сети магазинов Sunflowers, представлены на рис. 4.
Полная сумма квадратов разностей равна SST = 116,9543. Эта величина состоит из суммы квадратов регрессии (SSR) равной 105,7476, и суммы квадратов ошибок (SSE), равной 11,2067.
Коэффициент смешанной корреляции. Величины SSR, SSE и SST не имеют очевидной интерпретации. Однако отношение суммы квадратов регрессии (SSR) к полной сумме квадратов (SST) представляет собой оценку полезности регрессионного уравнения. Это отношение называется коэффициентом смешанной корреляции r2:
Коэффициент смешанной корреляции оценивает долю вариации переменной Y, которая объясняется независимой переменной X в регрессионной модели. В задаче о сети магазинов Sunflowers SSR = 105,7476 и SST = 116,9543. Следовательно, r2 = 105,7476 / 116,9543 = 0,904. Таким образом, 90,4% вариации годового объема продаж объясняется изменчивостью площади магазинов, измеренной в квадратных футах. Данная величина r2 свидетельствует о сильной положительной линейной взаимосвязи между двумя переменными, поскольку применение регрессионной модели снижает изменчивость прогнозируемых годовых объемов продаж на 90,4%. Только 9,6% изменчивости годовых объемов продаж в выборке магазинов объясняются другими факторами, не учтенными в регрессионной модели.
Коэффициент смешанной корреляции в задаче о сети магазинов Sunflowers представлен в таблице Регрессионная статистика на рис. 4.
Среднеквадратичная ошибка оценки. Хотя метод наименьших квадратов позволяет вычислить линию, минимизирующую отклонение от наблюдаемых значений, наличие суммы квадратов ошибок (SSE) свидетельствует о том, что линейная регрессия не дает абсолютной точности прогноза, если, конечно, точки наблюдения не лежат на регрессионной прямой. Однако ожидать этого так же неестественно, как предполагать, что все выборочные значения точно равны их среднему арифметическому. Следовательно, необходима статистика, которая позволила бы оценить отклонение предсказанных значений переменной Y от ее реальных значений, аналогично тому, как стандартное отклонение, введенное ранее, позволяет оценить колебание данных вокруг их средней величины. Стандартное отклонение наблюдаемых значений переменной Y от ее регрессионной прямой называется среднеквадратичной ошибкой оценки. Отклонение реальных данных от регрессионной прямой в задаче о сети магазинов Sunflowers показано на рис. 5.
Среднеквадратичная ошибка оценки
где Yi — фактическое значение переменной Y при заданном значении Xi, Ŷi — предсказанное значение переменной Y при заданном значении Xi, SSE — сумма квадратов ошибок.
Поскольку SSE = 11,2067, по формуле (8) получаем:
Таким образом, среднеквадратичная ошибка оценки равна 0,9664 млн. долл. (т.е. 966 400 долл.). Этот параметр также рассчитывается Пакетом анализа (см. рис. 4). Среднеквадратичная ошибка оценки характеризует отклонение реальных данных от линии регрессии. Она измеряется в тех же единицах, что и переменная Y. По смыслу среднеквадратичная ошибка очень похожа на стандартное отклонение. В то время как стандартное отклонение характеризует разброс данных вокруг их среднего значения, среднеквадратичная ошибка позволяет оценить колебание точек наблюдения вокруг регрессионной прямой. Cреднеквадратичная ошибка оценки позволяет обнаружить статистически значимую зависимость, существующую между двумя переменными, и предсказать значения переменной Y.
Предположения
Обсуждая методы проверки гипотез и дисперсионного анализа, мы не раз подчеркивали важность условий, которые должны обеспечивать корректность сделанных выводов. Поскольку и регрессионный, и дисперсионный анализ используют линейную модель, условия их применения приблизительно одинаковы:
- Ошибка должна иметь нормальное распределение.
- Вариация данных вокруг линии регрессии должна быть постоянной.
- Ошибки должны быть независимыми.
Первое предположение, о нормальном распределении ошибок, требует, чтобы при каждом значении переменной X ошибки линейной регрессии имели нормальное распределение (рис. 7). Как и t— и F-критерий дисперсионного анализа, регрессионный анализ довольно устойчив к нарушениям этого условия. Если распределение ошибок относительно линии регрессии при каждом значении X не слишком сильно отличается от нормального, выводы относительно линии регрессии и коэффициентов регрессии изменяются незначительно.
Рис. 7. Предположение о нормальном распределении ошибок
Второе условие заключается в том, что вариация данных вокруг линии регрессии должна быть постоянной при любом значении переменной X. Это означает, что величина ошибки как при малых, так и при больших значениях переменной X должна изменяться в одном и том же интервале (см. рис. 7). Это свойство очень важно для метода наименьших квадратов, с помощью которого определяются коэффициенты регрессии. Если это условие нарушается, следует применять либо преобразование данных, либо метод наименьших квадратов с весами.
Третье предположение, о независимости ошибок, заключается в том, что ошибки регрессии не должны зависеть от значения переменной X. Это условие особенно важно, если данные собираются на протяжении определенного отрезка времени. В этих ситуациях ошибки, присущие конкретному отрезку времени, часто коррелируют с ошибками, характерными для предыдущего периода.
Анализ остатков
Чуть выше при решении задачи о сети магазинов Sunflowers мы использовали модель линейной регрессии. Рассмотрим теперь анализ ошибок — графический метод, позволяющий оценить точность регрессионной модели. Кроме того, с его помощью можно обнаружить потенциальные нарушения условий применения регрессионного анализа.
Оценка пригодности эмпирической модели. Остаток, или оценка ошибки еi, представляет собой разность между наблюдаемым (Yi) и предсказанным (Ŷi) значениями зависимой переменной при заданном значении Xi.
(9) ei = Yi – Ŷi
Для оценки пригодности эмпирической модели регрессии остатки откладываются по вертикальной оси, а значения Xi — по горизонтальной. Если эмпирическая модель пригодна, график не должен иметь ярко выраженной закономерности. Если же модель регрессии не пригодна, на рисунке проявится зависимость между значениями Xi и остатками еi.
Рассмотрим примеры (рис. 8). Панель А иллюстрирует возрастание переменной Y при увеличении переменной X. Однако зависимость между этими переменными носит нелинейный характер, поскольку скорость возрастания переменной Y падает при увеличении переменной X. Таким образом, для аппроксимации зависимости между этими переменными лучше подойдет квадратичная модель. Особенно ярко квадратичная зависимость между величинами Xi и ei проявляется на панели Б. Графическое изображение остатков позволяет отфильтровать или удалить линейную зависимость между переменными X и Y и выявить недостаточную точность модели простой линейной регрессии. Таким образом, в данной ситуации вместо простой линейной модели должна применяться квадратичная модель, обладающая более высокой точностью.
Рис. 8. Исследование эмпирической модели простой линейной регрессии
Вернемся к задаче о сети магазинов Sunflowers и посмотрим, хорошо ли подходит простая линейная регрессия для ее решения. Соответствующие данные и расчеты приведены на рис. 9а (формулы можно посмотреть в Excel-файле). Построим диаграмму разброса, откладывая по вертикальной оси остатки ei, а по горизонтальной — независимую переменную Xi (рис. 9б). Несмотря на большой разброс остатков, между ei и Хi нет ярко выраженной зависимости. Остатки одинаково часто принимают как положительные, так и отрицательные значения. Это позволяет сделать вывод, что модель линейной регрессии пригодна для решения задачи о сети магазинов Sunflowers.
Рис. 9. Остатки ei, вычисленные при решении задачи о сети магазинов Sunflowers
Значения остатков (таблица на рис. 9а) и график остатков (аналог рис. 9б) можно получить непосредственно в процедуре Регрессия Пакета анализа. Просто поставьте соответствующие галки (рис. 10).
Рис. 10. Остатки ei и график остатков полученные с помощью Пакета анализа
Проверка условий. График остатков позволяет оценить вариации ошибок. На рис. 10 нет особых различий между ошибками, соответствующими разным значениям Xi. Следовательно, вариации ошибок при разных значениях Хi приблизительно одинаковы. Рассмотрим гипотетическую ситуацию, в которой это условие не выполняется (рис. 11). На этом рисунке изображен эффект веера: при возрастании значений Хi ошибки увеличиваются. Таким образом, изменчивость значений Yi при разных значениях Хi является непостоянной.
Рис. 11. Пример нарушения условия независимости вариаций ошибок от Xi
Нормальность. Чтобы проверить предположение о нормальном распределении ошибок, построим график нормального распределения на основе точечного графика, на вертикальной оси которого отложены значения остатков, а на горизонтальной оси — соответствующие квантили стандартизованного нормального распределения (подробнее см. Проверка гипотезы о нормальном распределении). Для построения такого графика значения остатков должны быть упорядочены по возрастанию (рис. 12). График нормального распределения может быть построен одним кликом с помощью Пакета анализа Excel – просто поставьте соответствующую галочку в окне Регрессия (см. рис. 10, самый низ окна Регрессия – опция График нормальной вероятности).
Рис. 12. График нормального распределения для остатков
Без визуализации данных (с помощью гистограммы, диаграммы «ствол и листья», блочной диаграммы или графика как на рис. 12) проверить предположение о нормальном распределении ошибок очень трудно. Данные, изображенные на рис. 12, не слишком сильно отличаются от нормального распределения. Устойчивость регрессионного анализа и небольшой объем выборки позволяют утверждать, что условие о нормальном распределении ошибок нарушается незначительно.
Независимость. Предположение о независимости ошибок также проверяется с помощью графика остатков. Данные, собранные на протяжении некоторого периода времени, иногда демонстрируют эффект автокорреляции между последовательными наблюдениями. В таких ситуациях остатки зависят от значений предыдущих остатков. Подобная связь между остатками нарушает предположение о независимости ошибок. Эффект автокорреляции хорошо выявляется на графике. Кроме того, его можно измерить с помощью процедуры Дурбина-Уотсона (см. ниже). Если данные о размерах магазинов и объемах продаж собирались в течение одного и того же периода времени, гипотезу об их независимости проверять не имеет смысла.
Измерение автокорреляции: статистика Дурбина–Уотсона
Одним из основных предположений о регрессионной модели является гипотеза о независимости ее ошибок. Если данные собираются в течение определенного отрезка времени, это условие часто нарушается, поскольку остаток в определенный момент времени может оказаться приблизительно равным предыдущим остаткам. Такое поведение остатков называется автокорреляцией. Если набор данных обладает свойством автокорреляции, корректность регрессионной модели становится весьма сомнительной.
Распознавание автокорреляции с помощью графика остатков. Для выявления автокорреляции необходимо упорядочить остатки по времени и построить их график. Если данные обладают положительной автокорреляцией, на графике возникнут кластеры остатков, имеющие одинаковый знак. В случае отрицательной автокорреляции остатки будут скачкообразно принимать то положительные, то отрицательные значения. Этот вид автокорреляции очень редко встречается в регрессионном анализе, поэтому мы рассмотрим лишь положительную автокорреляцию. Проиллюстрируем ее следующим примером. Предположим, что менеджер магазина, доставляющего товары на дом, пытается предсказать объем продаж по количеству клиентов, совершивших покупки в течение 15 недель (рис. 13).
Рис. 13. Количество клиентов и объемы продаж за 15 недель
Поскольку данные собирались на протяжении 15 последовательных недель в одном и том же магазине, необходимо определить, наблюдается ли эффект автокорреляции. Построим регрессию с использованием Пакета анализа; включим вывод Остатков, но не будем включать График остатков (рис. 14).
Рис. 14. Параметры линейной регрессии, полученные с использованием Пакета анализа
Анализ рис. 14 показывает, что r2 = 0,657. Это значит, что 65,7% вариации объемов продаж объясняется изменчивостью количества клиентов. Кроме того, сдвиг b0 переменной Y равен –16,032, а наклон b1 = 0,0308. Однако, прежде чем применять эту модель, необходимо выполнить анализ остатков. Поскольку данные собирались на протяжении 15 последовательных недель, их следует отобразить на графике в том же порядке (рис. 15).
Рис. 15. Зависимость остатков от времени
Анализ рис. 15 показывает, что остатки циклически колеблются вверх и вниз. Эта цикличность является явным признаком автокорреляции. Следовательно, гипотезу о независимости остатков следует отклонить.
Статистика Дурбина-Уотсона. Автокорреляцию можно выявить и измерить с помощью статистики Дурбина-Уотсона. Эта статистика оценивает корреляцию между соседними остатками:
где еi — остаток, соответствующий i-му периоду времени.
Чтобы лучше понять статистику Дурбина-Уотсона, рассмотрим ее составные части. Числитель представляет собой сумму квадратов разностей между соседними остатками, начиная со второго и заканчивая n-м наблюдением. Знаменатель является суммой квадратов остатков. Вот, что по этому поводу написано в Википедии:
где ρ1 – коэффициент автокорреляции; если ρ1 = 0 (нет автокорреляции), D ≈ 2; если ρ1 ≈ 1 (положительная автокорреляции), D ≈ 0; если ρ1 = -1 (отрицательная автокорреляции), D ≈ 4.
На практике применение критерия Дурбина-Уотсона основано на сравнении величины D с критическими теоретическими значениями dL и dU для заданного числа наблюдений n, числа независимых переменных модели k (для простой линейной регрессии k = 1) и уровня значимости α. Если D < dL, гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция); если D > dU, гипотеза не отвергается (то есть автокорреляция отсутствует); если dL < D < dU, нет достаточных оснований для принятия решения. Когда расчётное значение D превышает 2, то с dL и dU сравнивается не сам коэффициент D, а выражение (4 – D).
Для вычисления статистики Дурбина-Уотсона в Excel обратимся к нижней таблице на рис. 14 Вывод остатка. Числитель в выражении (10) вычисляется с помощью функции =СУММКВРАЗН(массив1;массив2), а знаменатель =СУММКВ(массив) (рис. 16).
Рис. 16. Формулы расчета статистики Дурбина-Уотсона
В нашем примере D = 0,883. Основной вопрос заключается в следующем — какое значение статистики Дурбина-Уотсона следует считать достаточно малым, чтобы сделать вывод о существовании положительной автокорреляции? Необходимо соотнести значение D с критическими значениями (dL и dU), зависящими от числа наблюдений n и уровня значимости α (рис. 17).
Рис. 17. Критические значения статистики Дурбина-Уотсона (фрагмент таблицы)
Таким образом, в задаче об объеме продаж в магазине, доставляющем товары на дом, существуют одна независимая переменная (k = 1), 15 наблюдений (n = 15) и уровень значимости α = 0,05. Следовательно, dL= 1,08 и dU = 1,36. Поскольку D = 0,883 < dL= 1,08, между остатками существует положительная автокорреляция, метод наименьших квадратов применять нельзя.
Проверка гипотез о наклоне и коэффициенте корреляции
Выше регрессия применялась исключительно для прогнозирования. Для определения коэффициентов регрессии и предсказания значения переменной Y при заданной величине переменной X использовался метод наименьших квадратов. Кроме того, мы рассмотрели среднеквадратичную ошибку оценки и коэффициент смешанной корреляции. Если анализ остатков подтверждает, что условия применимости метода наименьших квадратов не нарушаются, и модель простой линейной регрессии является адекватной, на основе выборочных данных можно утверждать, что между переменными в генеральной совокупности существует линейная зависимость.
Применение t-критерия для наклона. Проверяя, равен ли наклон генеральной совокупности β1 нулю, можно определить, существует ли статистически значимая зависимость между переменными X и Y. Если эта гипотеза отклоняется, можно утверждать, что между переменными X и Y существует линейная зависимость. Нулевая и альтернативная гипотезы формулируются следующим образом: Н0: β1 = 0 (нет линейной зависимости), Н1: β1 ≠ 0 (есть линейная зависимость). По определению t-статистика равна разности между выборочным наклоном и гипотетическим значением наклона генеральной совокупности, деленной на среднеквадратичную ошибку оценки наклона:
(11) t = (b1 – β1) / Sb1
где b1 – наклон прямой регрессии по выборочным данным, β1 – гипотетический наклон прямой генеральной совокупности, , а тестовая статистика t имеет t-распределение с n – 2 степенями свободы.
Проверим, существует ли статистически значимая зависимость между размером магазина и годовым объемом продаж при α = 0,05. t-критерий выводится наряду с другими параметрами при использовании Пакета анализа (опция Регрессия). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к t-статистике – на рис. 18.
Рис. 18. Результаты применения t-критерия, полученные с помощью Пакета анализа Excel
Поскольку число магазинов n = 14 (см. рис.3), критическое значение t-статистики при уровне значимости α = 0,05 можно найти по формуле: tL =СТЬЮДЕНТ.ОБР(0,025;12) = –2,1788, где 0,025 – половина уровня значимости, а 12 = n – 2; tU =СТЬЮДЕНТ.ОБР(0,975;12) = +2,1788.
Поскольку t-статистика = 10,64 > tU = 2,1788 (рис. 19), нулевая гипотеза Н0 отклоняется. С другой стороны, р-значение для Х = 10,6411, вычисляемое по формуле =1-СТЬЮДЕНТ.РАСП(D3;12;ИСТИНА), приближенно равно нулю, поэтому гипотеза Н0 снова отклоняется. Тот факт, что р-значение почти равно нулю, означает, что если бы между размерами магазинов и годовым объемом продаж не существовало реальной линейной зависимости, обнаружить ее с помощью линейной регрессии было бы практически невозможно. Следовательно, между средним годовым объемом продаж в магазинах и их размером существует статистически значимая линейная зависимость.
Рис. 19. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, и 12 степенях свободы
Применение F-критерия для наклона. Альтернативным подходом к проверке гипотез о наклоне простой линейной регрессии является использование F-критерия. Напомним, что F-критерий применяется для проверки отношения между двумя дисперсиями (подробнее см. Однофакторный дисперсионный анализ). При проверке гипотезы о наклоне мерой случайных ошибок является дисперсия ошибки (сумма квадратов ошибок, деленная на количество степеней свободы), поэтому F-критерий использует отношение дисперсии, объясняемой регрессией (т.е. величины SSR, деленной на количество независимых переменных k), к дисперсии ошибок (MSE = SYX2).
По определению F-статистика равна среднему квадрату отклонений, обусловленных регрессией (MSR), деленному на дисперсию ошибки (MSE): F = MSR/MSE, где MSR = SSR / k, MSE = SSE/(n– k – 1), k – количество независимых переменных в регрессионной модели. Тестовая статистика F имеет F-распределение с k и n – k – 1 степенями свободы.
При заданном уровне значимости α решающее правило формулируется так: если F > FU, нулевая гипотеза отклоняется; в противном случае она не отклоняется. Результаты, оформленные в виде сводной таблицы дисперсионного анализа, приведены на рис. 20.
Рис. 20. Таблица дисперсионного анализа для проверки гипотезы о статистической значимости коэффициента регрессии
Аналогично t-критерию F-критерий выводится в таблицу при использовании Пакета анализа (опция Регрессия). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к F-статистике – на рис. 21.
Рис. 21. Результаты применения F-критерия, полученные с помощью Пакета анализа Excel
F-статистика равна 113,23, а р-значение близко к нулю (ячейка Значимость F). Если уровень значимости α равен 0,05, определить критическое значение F-распределения с одной и 12 степенями свободы можно по формуле FU =F.ОБР(1-0,05;1;12) = 4,7472 (рис. 22). Поскольку F = 113,23 > FU = 4,7472, причем р-значение близко к 0 < 0,05, нулевая гипотеза Н0 отклоняется, т.е. размер магазина тесно связан с его годовым объемом продаж.
Рис. 22. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, с одной и 12 степенями свободы
Доверительный интервал, содержащий наклон β1. Для проверки гипотезы о существовании линейной зависимости между переменными можно построить доверительный интервал, содержащий наклон β1 и убедиться, что гипотетическое значение β1 = 0 принадлежит этому интервалу. Центром доверительного интервала, содержащего наклон β1, является выборочный наклон b1, а его границами — величины b1 ± tn–2Sb1
Как показано на рис. 18, b1 = +1,670, n = 14, Sb1 = 0,157. t12 =СТЬЮДЕНТ.ОБР(0,975;12) = 2,1788. Следовательно, b1 ± tn–2Sb1 = +1,670 ± 2,1788 * 0,157 = +1,670 ± 0,342, или + 1,328 ≤ β1 ≤ +2,012. Таким образом, наклон генеральной совокупности с вероятностью 0,95 лежит в интервале от +1,328 до +2,012 (т.е. от 1 328 000 до 2 012 000 долл.). Поскольку эти величины больше нуля, между годовым объемом продаж и площадью магазина существует статистически значимая линейная зависимость. Если бы доверительный интервал содержал нуль, между переменными не было бы зависимости. Кроме того, доверительный интервал означает, что каждое увеличение площади магазина на 1 000 кв. футов приводит к увеличению среднего объема продаж на величину от 1 328 000 до 2 012 000 долларов.
Использование t-критерия для коэффициента корреляции. Ранее был введен коэффициент корреляции r, представляющий собой меру зависимости между двумя числовыми переменными. С его помощью можно установить, существует ли между двумя переменными статистически значимая связь. Обозначим коэффициент корреляции между генеральными совокупностями обеих переменных символом ρ. Нулевая и альтернативная гипотезы формулируются следующим образом: Н0: ρ = 0 (нет корреляции), Н1: ρ ≠ 0 (есть корреляция). Проверка существования корреляции:
где r = +, если b1 > 0, r = –
, если b1 < 0. Тестовая статистика t имеет t-распределение с n – 2 степенями свободы.
В задаче о сети магазинов Sunflowers r2 = 0,904, а b1— +1,670 (см. рис. 4). Поскольку b1 > 0, коэффициент корреляции между объемом годовых продаж и размером магазина равен r = +√0,904 = +0,951. Проверим нулевую гипотезу, утверждающую, что между этими переменными нет корреляции, используя t-статистику:
При уровне значимости α = 0,05 нулевую гипотезу следует отклонить, поскольку t = 10,64 > 2,1788. Таким образом, можно утверждать, что между объемом годовых продаж и размером магазина существует статистически значимая связь.
При обсуждении выводов, касающихся наклона генеральной совокупности, доверительные интервалы и критерии для проверки гипотез являются взаимозаменяемыми инструментами. Однако вычисление доверительного интервала, содержащего коэффициент корреляции, оказывается более сложным делом, поскольку вид выборочного распределения статистики r зависит от истинного коэффициента корреляции.
Оценка математического ожидания и предсказание индивидуальных значений
В этом разделе рассматриваются методы оценки математического ожидания отклика Y и предсказания индивидуальных значений Y при заданных значениях переменной X.
Построение доверительного интервала. В примере 2 (см. выше раздел Метод наименьших квадратов) регрессионное уравнение позволило предсказать значение переменной Y при заданном значении переменной X. В задаче о выборе места для торговой точки средний годовой объем продаж в магазине площадью 4000 кв. футов был равен 7,644 млн. долл. Однако эта оценка математического ожидания генеральной совокупности является точечной. Ранее для оценки математического ожидания генеральной совокупности была предложена концепция доверительного интервала. Аналогично можно ввести понятие доверительного интервала для математического ожидания отклика при заданном значении переменной X:
где 
= b0 + b1Xi – предсказанное значение переменное Y при X = Xi, SYX – среднеквадратичная ошибка, n – объем выборки, Xi — заданное значение переменной X, µY|X=Xi – математическое ожидание переменной Y при Х = Хi, SSX =
Анализ формулы (13) показывает, что ширина доверительного интервала зависит от нескольких факторов. При заданном уровне значимости возрастание амплитуды колебаний вокруг линии регрессии, измеренное с помощью среднеквадратичной ошибки, приводит к увеличению ширины интервала. С другой стороны, как и следовало ожидать, увеличение объема выборки сопровождается сужением интервала. Кроме того, ширина интервала изменяется в зависимости от значений Xi. Если значение переменной Y предсказывается для величин X, близких к среднему значению , доверительный интервал оказывается уже, чем при прогнозировании отклика для значений, далеких от среднего.
Допустим, что, выбирая место для магазина, мы хотим построить 95%-ный доверительный интервал для среднего годового объема продаж во всех магазинах, площадь которых равна 4000 кв. футов:
Следовательно, средний годовой объем продаж во всех магазинах, площадь которых равна 4 000 кв. футов, с 95% -ной вероятностью лежит в интервале от 6,971 до 8,317 млн. долл.
Вычисление доверительного интервала для предсказанного значения. Кроме доверительного интервала для математического ожидания отклика при заданном значении переменной X, часто необходимо знать доверительный интервал для предсказанного значения. Несмотря на то что формула для вычисления такого доверительного интервала очень похожа на формулу (13), этот интервал содержит предсказанное значение, а не оценку параметра. Интервал для предсказанного отклика YX=Xi при конкретном значении переменной Xi определяется по формуле:
Предположим, что, выбирая место для торговой точки, мы хотим построить 95%-ный доверительный интервал для предсказанного годового объема продаж в магазине, площадь которого равна 4000 кв. футов:
Следовательно, предсказанный годовой объем продаж в магазине, площадь которого равна 4000 кв. футов, с 95%-ной вероятностью лежит в интервале от 5,433 до 9,854 млн. долл. Как видим, доверительный интервал для предсказанного значения отклика намного шире, чем доверительный интервал для его математического ожидания. Это объясняется тем, что изменчивость при прогнозировании индивидуальных значений намного больше, чем при оценке математического ожидания.
Подводные камни и этические проблемы, связанные с применением регрессии
Трудности, связанные с регрессионным анализом:
- Игнорирование условий применимости метода наименьших квадратов.
- Ошибочная оценка условий применимости метода наименьших квадратов.
- Неправильный выбор альтернативных методов при нарушении условий применимости метода наименьших квадратов.
- Применение регрессионного анализа без глубоких знаний о предмете исследования.
- Экстраполяция регрессии за пределы диапазона изменения объясняющей переменной.
- Путаница между статистической и причинно-следственной зависимостями.
Широкое распространение электронных таблиц и программного обеспечения для статистических расчетов ликвидировало вычислительные проблемы, препятствовавшие применению регрессионного анализа. Однако это привело к тому, что регрессионный анализ стали применять пользователи, не обладающие достаточной квалификацией и знаниями. Откуда пользователям знать об альтернативных методах, если многие из них вообще не имеют ни малейшего понятия об условиях применимости метода наименьших квадратов и не умеют проверять их выполнение?
Исследователь не должен увлекаться перемалыванием чисел — вычислением сдвига, наклона и коэффициента смешанной корреляции. Ему нужны более глубокие знания. Проиллюстрируем это классическим примером, взятым из учебников. Анскомб показал, что все четыре набора данных, приведенных на рис. 23, имеют одни и те же параметры регрессии (рис. 24).
Рис. 23. Четыре набора искусственных данных
Рис. 24. Регрессионный анализ четырех искусственных наборов данных; выполнен с помощью Пакета анализа (кликните на рисунке, чтобы увеличить изображение)
Итак, с точки зрения регрессионного анализа все эти наборы данных совершенно идентичны. Если бы анализ был на этом закончен, мы потеряли бы много полезной информации. Об этом свидетельствуют диаграммы разброса (рис. 25) и графики остатков (рис. 26), построенные для этих наборов данных.
Рис. 25. Диаграммы разброса для четырех наборов данных
Диаграммы разброса и графики остатков свидетельствуют о том, что эти данные отличаются друг от друга. Единственный набор, распределенный вдоль прямой линии, — набор А. График остатков, вычисленных по набору А, не имеет никакой закономерности. Этого нельзя сказать о наборах Б, В и Г. График разброса, построенный по набору Б, демонстрирует ярко выраженную квадратичную модель. Этот вывод подтверждается графиком остатков, имеющим параболическую форму. Диаграмма разброса и график остатков показывают, что набор данных В содержит выброс. В этой ситуации необходимо исключить выброс из набора данных и повторить анализ. Метод, позволяющий обнаруживать и исключать выбросы из наблюдений, называется анализом влияния. После исключения выброса результат повторной оценки модели может оказаться совершенно иным. Диаграмма разброса, построенная по данным из набора Г, иллюстрирует необычную ситуацию, в которой эмпирическая модель значительно зависит от отдельного отклика (Х8 = 19, Y8 = 12,5). Такие регрессионные модели необходимо вычислять особенно тщательно. Итак, графики разброса и остатков являются крайне необходимым инструментом регрессионного анализа и должны быть его неотъемлемой частью. Без них регрессионный анализ не заслуживает доверия.
Рис. 26. Графики остатков для четырех наборов данных
Как избежать подводных камней при регрессионном анализе:
- Анализ возможной взаимосвязи между переменными X и Y всегда начинайте с построения диаграммы разброса.
- Прежде чем интерпретировать результаты регрессионного анализа, проверяйте условия его применимости.
- Постройте график зависимости остатков от независимой переменной. Это позволит определить, насколько эмпирическая модель соответствует результатам наблюдения, и обнаружить нарушение постоянства дисперсии.
- Для проверки предположения о нормальном распределении ошибок используйте гистограммы, диаграммы «ствол и листья», блочные диаграммы и графики нормального распределения.
- Если условия применимости метода наименьших квадратов не выполняются, используйте альтернативные методы (например, модели квадратичной или множественной регрессии).
- Если условия применимости метода наименьших квадратов выполняются, необходимо проверить гипотезу о статистической значимости коэффициентов регрессии и построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика.
- Избегайте предсказывать значения зависимой переменной за пределами диапазона изменения независимой переменной.
- Имейте в виду, что статистические зависимости не всегда являются причинно-следственными. Помните, что корреляция между переменными не означает наличия причинно-следственной зависимости между ними.
Резюме. Как показано на структурной схеме (рис. 27), в заметке описаны модель простой линейной регрессии, условия ее применимости и способы проверки этих условий. Рассмотрен t-критерий для проверки статистической значимости наклона регрессии. Для предсказания значений зависимой переменной использована регрессионная модель. Рассмотрен пример, связанный с выбором места для торговой точки, в котором исследуется зависимость годового объема продаж от площади магазина. Полученная информация позволяет точнее выбрать место для магазина и предсказать его годовой объем продаж. В следующих заметках будет продолжено обсуждение регрессионного анализа, а также рассмотрены модели множественной регрессии.
Рис. 27. Структурная схема заметки
Предыдущая заметка Критерий согласия «хи-квадрат»
Следующая заметка Введение в множественную регрессию
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 792–872
[2] Если зависимая переменная является категорийной, необходимо применять логистическую регрессию.
Для того чтобы модель линейной регрессии можно было применять на практике необходимо сначала оценить её качество. Для этих целей предложен ряд показателей, каждый из которых предназначен для использования в различных ситуациях и имеет свои особенности применения (линейные и нелинейные, устойчивые к аномалиям, абсолютные и относительные, и т.д.). Корректный выбор меры для оценки качества модели является одним из важных факторов успеха в решении задач анализа данных.
- Среднеквадратичная ошибка (Mean Squared Error)
- Корень из среднеквадратичной ошибки (Root Mean Squared Error)
- Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error)
- Cредняя абсолютная ошибка (Mean Absolute Error)
- Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error)
- Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error)
- Средняя абсолютная масштабированная ошибка (Mean absolute scaled error)
- Средняя относительная ошибка (Mean Relative Error)
- Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error
- R-квадрат
- Скорректированный R-квадрат
- Сравнение метрик
«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.
Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.
Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:
- Среднеквадратичная ошибка (MSE).
- Корень из среднеквадратичной ошибки (RMSE).
- Среднеквадратичная ошибка в процентах (MSPE).
- Средняя абсолютная ошибка (MAE).
- Средняя абсолютная ошибка в процентах (MAPE).
- Cимметричная средняя абсолютная процентная ошибка (SMAPE).
- Средняя абсолютная масштабированная ошибка (MASE)
- Средняя относительная ошибка (MRE).
- Среднеквадратичная логарифмическая ошибка (RMSLE).
- Коэффициент детерминации R-квадрат.
- Скорректированный коэффициент детеминации.
Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.
Рисунок 1. Линейная регрессия
Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.
Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — overline{y}.
В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».
MSE
Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.
Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.
MSE рассчитывается по формуле:
MSE=frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y}_{i})^{2},
где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.
Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.
Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.
RMSE
Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:
RMSE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y_{i}})^{2}}
MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).
Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:
frac{partial RMSE}{partial widehat{y}_{i}}=frac{1}{2sqrt{MSE}}frac{partial MSE}{partial widehat{y}_{i}}
Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.
Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.
MSPE
Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:
MSPE=frac{100}{n}sumlimits_{i=1}^{n}left ( frac{y_{i}-widehat{y}_{i}}{y_{i}} right )^{2}
Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.
MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.
MAE
Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:
MAE=frac{1}{n}sumlimits_{i=1}^{n}left | y_{i}-widehat{y}_{i} right |
Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.
Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.
MAPE
Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:
MAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{left | y_{i} right |}
Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.
SMAPE
Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:
SMAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{(left | y_{i} right |+left | widehat{y}_{i} right |)/2}
Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.
Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и widehat{y}_{i}=90, то SMAPE=5.26.
Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).
MASE
Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:
MASE=frac{MAE_{i}}{MAE_{j}}
MASE симметрична и устойчива к выбросам.
MRE
Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:
MRE=frac{1}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y}_{i}right |}{left | y_{i} right |}
Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.
Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.
Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.
RMSLE
Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:
RMSLE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(log(widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}
Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.
Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.
R-квадрат
Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.
В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.
Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:
R^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}}
Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.
Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.
Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.
Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).
На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.
Скорректированный R-квадрат
Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.
В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).
Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:
R_{adj}^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}/(n-k)}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}/(n-1)}
где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.
Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.
Сравнение метрик
Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:
| Мера | Сильные стороны | Слабые стороны |
|---|---|---|
| MSE | Позволяет подчеркнуть большие отклонения, простота вычисления. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости. |
| RMSE | Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. |
| MSPE | Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер. | Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки. |
| MAPE | Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области. | Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю. |
| SMAPE | Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше. | Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения. |
| MASE | Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели. | Сложность интерпретации. |
| MRE | Позволяет оценить величину ошибки относительно значения целевой переменной. | Неприменима для наблюдений с нулевым значением выходной переменной. |
| RMSLE | Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше | Может быть затруднена интерпретация из-за нелинейности. |
| R-квадрат | Универсальность, простота интерпретации. | Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы. |
| R-квадрат скорр. | Корректно отражает вклад каждой переменной в модель. | Плохо работает, когда входные переменные зависимы. |
В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.
Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.
Другие материалы по теме:
Отбор переменных в моделях линейной регрессии
Репрезентативность выборочных данных
Логистическая регрессия и ROC-анализ — математический аппарат
Регрессионный
и корреляционный анализ позволяет
установить и оценить зависимость
изучаемой случайной величины Y от одной
или нескольких других величин X,
и делать прогнозы значений Y. Параметр
Y, значение которого нужно предсказывать,
является зависимой переменной. Параметр
X, значения которого нам известны заранее
и который влияет на значения Y, называется
независимой переменной. Например, X –
количество внесенных удобрений, Y –
снимаемый урожай; X – величина затрат
компании на рекламу своего товара, Y –
объем продаж этого товара и т.д.
Корреляционная
зависимость Y от X – это функциональная
зависимость:
|
|
|
|
где |
|
Уравнение
(26) называется уравнением регрессии Y
на X, функция f(x)
– регрессией Y на X, а ее график – линией
регрессии Y на X.
Основная
задача регрессионного анализа –
установление формы корреляционной
связи, то есть вида функции регрессии
(линейная, квадратичная, показательная
и т.д.).
Метод
наименьших квадратов позволяет определить
коэффициенты уравнения регрессии таким
образом, чтобы точки, построенные по
исходным данным (xi,
yi),
лежали как можно ближе к точкам линии
регрессии. Формально это записывается
как минимизация суммы квадратов
отклонений (ошибок) функции регрессии
и исходных точек.
|
|
|
|
где |
n |
В
регрессионном анализе предполагается,
что математическое ожидание случайной
величины ε равно нулю и ее дисперсия
одинакова для всех наблюдаемых значений
Y. Отсюда следует, что рассеяние данных
возле линии регрессии должно быть
одинаково при всех значениях параметра
X.
В случае, показанном
на рисунке 1.12 данные распределяются
вдоль линии регрессии неравномерно,
поэтому метод наименьших квадратов в
этом случае неприменим.
Основная
задача корреляционного анализа – оценка
тесноты (силы) корреляционной связи.
Теснота корреляционной зависимости Y
от X оценивается по величине рассеяния
значений параметра Y вокруг условного
среднего
.
Большое рассеяние говорит о слабой
зависимости Y от X, либо об ее отсутствии
и, наоборот, малое рассеяние указывает
на наличие достаточно сильной зависимости.
Рисунок
1.11 – Понятие отклонения ε для случая
линейной регрессии
Рисунок 1.12 –
Неравномерное распределение исходных
точек вдоль линии регрессии
Коэффициент
детерминации r2
показывает,
на сколько процентов (r2*100%)
найденная функция регрессии описывает
связь между исходными значениями
параметров Y и X:
|
|
|
|
где |
|
Рисунок 1.13 –
Графическая интерпретация коэффициента
детерминации для случая линейной
регрессии
Соответственно,
величина (1- r2)*100%
показывает, сколько процентов вариации
параметра Y обусловлены факторами, не
включенными в регрессионную модель.
При высоком (r2
≥ 75%) значение
коэффициента детерминации можно делать
прогноз y*=f(x*)
для конкретного значения x*.
Для проведения
регрессионного анализа и прогнозирования
необходимо:
1)
построить
график
исходных данных и попытаться зрительно,
приближенно определить характер
зависимости;
2)
выбрать
вид функции
регрессии, которая может описывать
связь исходных данных;
3)
определить
численные коэффициенты
функции регрессии;
4)
оценить
силу
найденной регрессионной зависимости
на основе коэффициента детерминации
r2;
5)
сделать
прогноз
(при r2
≥ 75%) или
сделать вывод о невозможности
прогнозирования с помощью найденной
регрессионной зависимости. При этом не
рекомендуется использовать модель
регрессии для тех значений независимого
параметра X,
которые не принадлежат интервалу,
заданному в исходных данных.
Линейная
регрессия. Коэффициенты
линейной регрессии y=a0
+a1x
вычисляются по следующим формулам (все
суммы берутся по n парам исходных данных):
|
|
|
|
Для
удобства вычислений используют
вспомогательную таблицу (таблица 1.14),
в которой рассчитываются необходимые
суммы.
Таблица 1.14
Вспомогательная
таблица для линейной функции
|
Заголовки данных |
|
|
|
|
|
|
|
|
Промежуточные |
|||||||
|
… |
… |
… |
… |
… |
… |
… |
|
|
Сумма ( |
Пример
1.5. Некоторая
фирма занимается поставками различных
грузов на короткие расстояния внутри
города. Перед менеджером стоит задача
оценить стоимость таких услуг, зависящую
от затраченного на поставку времени. В
качестве наиболее важного фактора,
влияющего на время поставки, менеджер
выбрал пройденное расстояние. Были
собраны исходные данные о десяти
поставках (таблица 1.15).
Таблица
1.15
Исходные данные
для примера 1.5
|
Расстояние, миль |
3,5 |
2,4 |
4,9 |
4,2 |
3,0 |
1,3 |
1,0 |
3,0 |
1,5 |
4,1 |
|
Время, мин |
16 |
13 |
19 |
18 |
12 |
11 |
8 |
14 |
9 |
16 |
Необходимо
построить график исходных данных,
определить по нему характер зависимости
между расстоянием и затраченным временем,
проанализировать применимость метода
наименьших квадратов, построить уравнение
регрессии, проанализировать силу
регрессионной связи и сделать прогноз
времени поездки на 2 мили.
Решение.
На рисунке
1.14 построены исходные данные по десяти
поездкам.
Помимо
расстояния на время поставки влияют
пробки на дорогах, время суток, дорожные
работы, квалификация водителя, вид
транспорта. Построенные точки не
находятся точно на линии, что обусловлено
описанными выше факторами. Но эти точки
собраны вокруг прямой линии, поэтому
можно предположить линейную связь между
параметрами. Все исходные точки равномерно
распределены вдоль предполагаемой
прямой линии, что позволяет применить
метод наименьших квадратов.
Вычислим суммы,
необходимые для расчета коэффициентов
линейной регрессии, коэффициента
детерминации с помощью таблицы 1.16.
Рисунок 1.14 – График
исходных данных для примера 1.5
Таблица 1.16
Вспомогательная
таблица для примера 1.5
|
|
|
|
|
|
|
|
|
3,5 |
16 |
12,25 |
56,00 |
15,223 |
2,634129 |
5,76 |
|
2,4 |
13 |
5,76 |
31,2 |
12,297 |
1,697809 |
0,36 |
|
4,9 |
19 |
24,01 |
93,1 |
18,947 |
28,59041 |
29,16 |
|
4,2 |
18 |
17,64 |
75,60 |
17,085 |
12,14523 |
19,36 |
|
3,0 |
12 |
9,00 |
36,00 |
13,893 |
0,085849 |
2,56 |
|
1,3 |
11 |
1,69 |
14,30 |
9,371 |
17,88444 |
6,76 |
|
1,0 |
8 |
1,00 |
8,00 |
8,573 |
25,27073 |
31,36 |
|
3,0 |
14 |
9,00 |
42,00 |
13,893 |
0,085849 |
0,16 |
|
1,5 |
9 |
2,25 |
13,50 |
9,903 |
13,66781 |
21,16 |
|
4,1 |
16 |
16,81 |
65,60 |
16,819 |
10,36169 |
5,76 |
|
∑=28,9 |
∑=136 |
∑=99,41 |
∑=435,30 |
— |
112,4242 |
122,4 |
По формулам (29)
вычислим коэффициенты линейной регрессии:
;
.
Таким образом,
искомая регрессионная зависимость
имеет вид:
(30)
Наклон
линии регрессии а1=2,66
минут на милю – это количество минут,
приходящееся на одну милю расстояния.
Координата точки пересечения прямой с
осью Y а0=5,913
минут – это время, которое не зависит
от пройденного расстояния, а обуславливается
всеми остальными возможными факторами,
явно не учтенными при анализе.
По формуле (28)
вычислим коэффициент детерминации:
или
91,8%.
Таким
образом, линейная модель объясняет
91,8% вариации времени доставки. Не
объясняется 100% — 91,8% = 8,2% вариации времени
поездки, которые обусловлены остальными
факторами, влияющими на время поставки,
но не включенными в линейную модель
регрессии.
Поскольку
коэффициент детерминации имеет достаточно
высокое значение и расстояние 2 мили,
для которого надо сделать прогноз,
находится в пределах диапазона исходных
данных (см. таблицу 1.15), то мы можем
использовать полученное уравнение
линейной регрессии (30) для прогнозирования:
y* (2 мили) =
5,913+2,660*2 = 11,2 минут.
При
прогнозах на расстояния, не входивших
в диапазон исходных данных, нельзя
гарантировать справедливость модели
(30). Это объясняется тем, что связь между
временем и расстоянием может изменяться
по мере увеличения расстояния. На время
дальних перевозок могут влиять новые
факторы такие, как использование
скоростных шоссе, остановки на отдых,
обед и т.п.
Приблизительным,
но самым простым и наглядным способом
проверки удовлетворительности
регрессионной модели является графическое
представление отклонений (рисунок
1.15).
Рисунок 1.15 – График
отклонений в примере 1.5
Отложим
отклонений
по оси Y, для каждого значения
.
Если регрессионная модель близка к
реальной зависимости, то отклонения
будут носить случайный характер и их
сумма будет близка к нулю. В рассмотренном
примере.
Нелинейная
регрессия.
Рассмотрим
наиболее простые случаи нелинейной
регрессии: гиперболу, экспоненту и
параболу. При нахождении коэффициентов
гиперболы и экспоненты используют прием
приведения нелинейной регрессионной
зависимости к линейному виду. Это
позволяет использовать для вычисления
коэффициентов функции регрессии формулы
(29).
Гипербола.
При нахождении гиперболы
вводят новую переменную
,
тогда уравнение гиперболы принимает
линейный вид.
После этого используют формулы (29) для
нахождений линейной функции, но вместо
значенийxi
используются
значения
;
.
При
проведении вычислений во вспомогательную
таблицу вносятся соответствующие
колонки.
Экспонента.
Для приведения к линейному виду экспоненты
проведем логарифмирование
;
;
.
Введем
переменные
и
,
тогда,
откуда следует, что можно применять
формулы (29), в которых вместо значенийyi
надо
использовать ln
yi
;
.
При
этом мы получим численные значения
коэффициентов b0
и b1,
от которых надо перейти к a0
и a1,
используемых в модели экспоненты. Исходя
из введенных обозначений и определения
логарифма, получаем
,
.
Парабола.
Для нахождения коэффициентов параболы
необходимо решить линейную систему из
трех уравнений

,
Оценка
силы нелинейной регрессионной связи.
Силы регрессионной связи для гиперболы
и параболы определяется непосредственно
по формуле (28). При вычислении коэффициента
детерминации экспоненты все значения
параметра Y
(исходные, регрессионные, среднее)
необходимо заменить на их логарифмы,
например,
— на
и т.д.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #



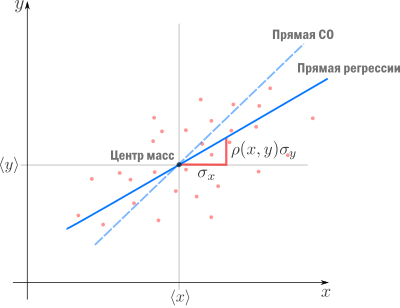


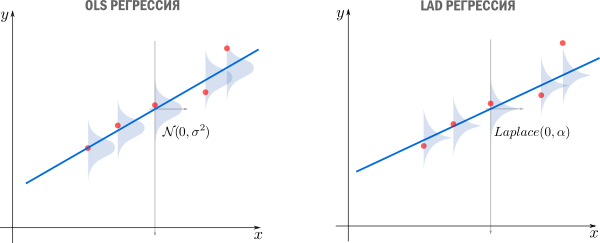
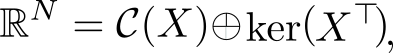

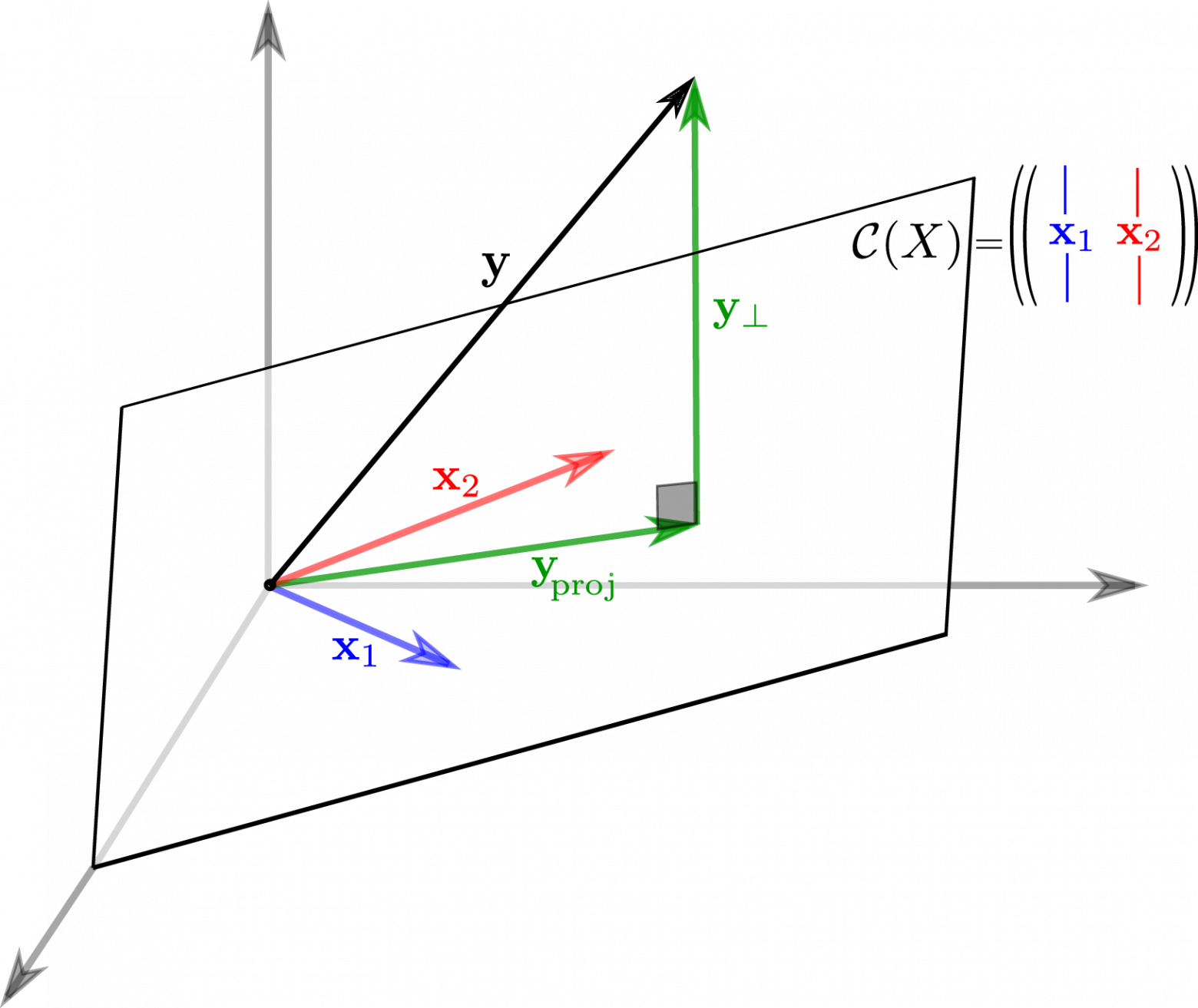

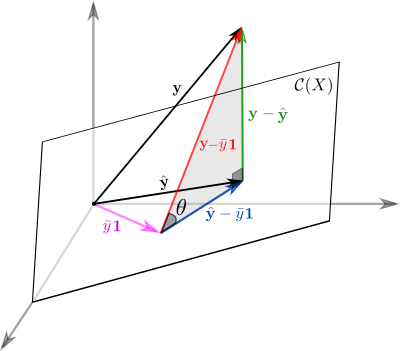

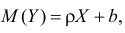
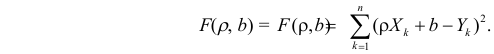
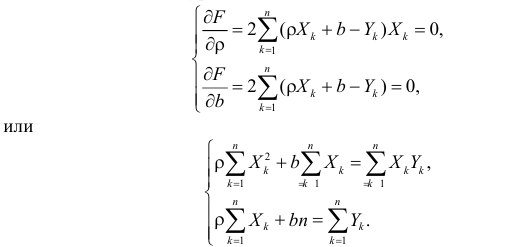
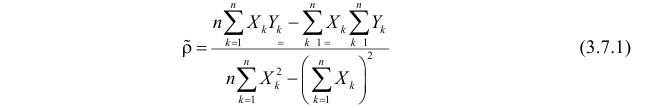
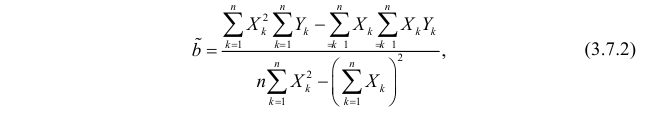
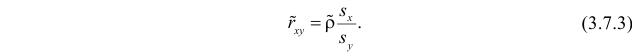
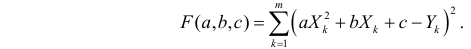

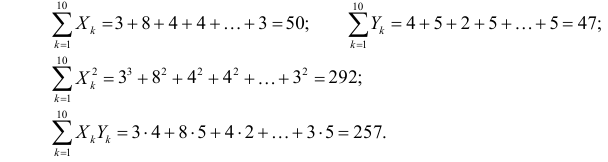
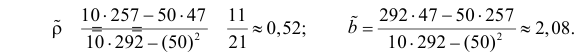
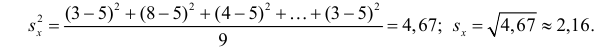
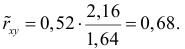
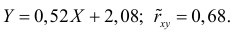

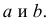
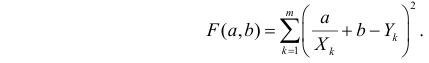
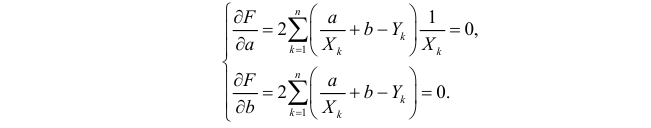
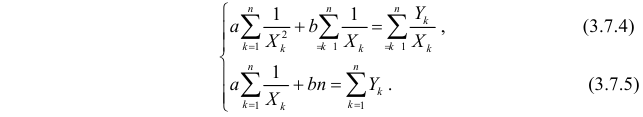
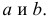
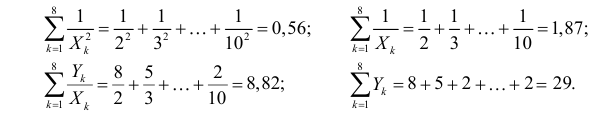
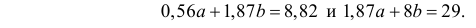
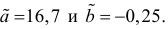
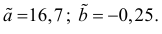

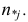



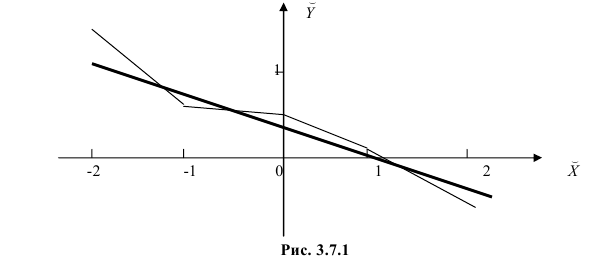
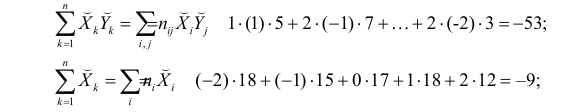
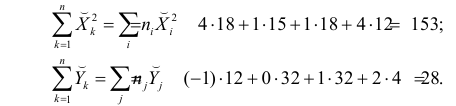
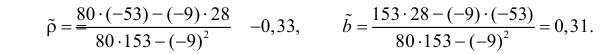
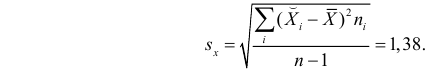
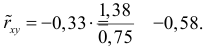
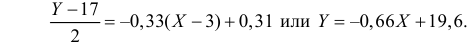
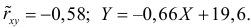
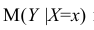 можно представить в виде
можно представить в виде 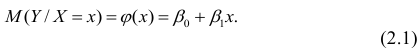
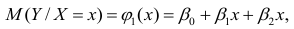
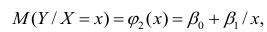
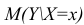 можно представить в виде (2.1).
можно представить в виде (2.1).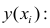
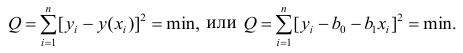
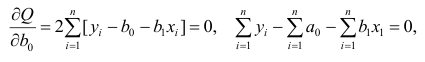
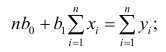
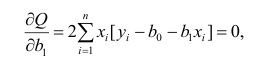
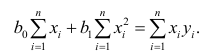
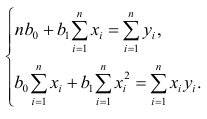
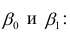
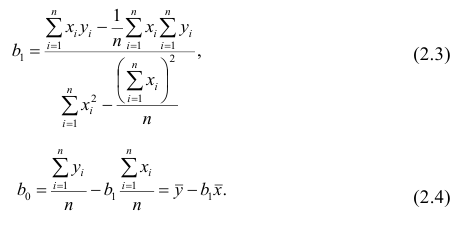
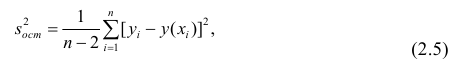
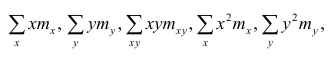
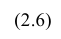
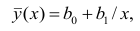
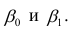
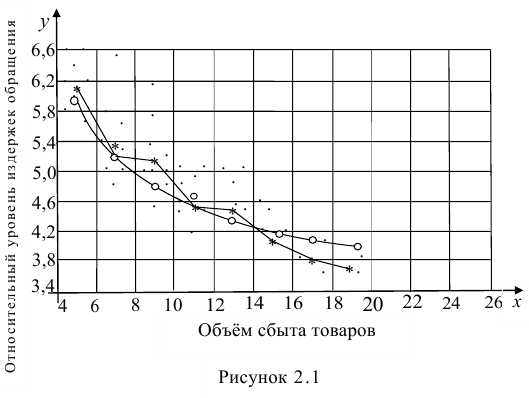
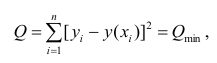
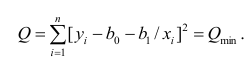
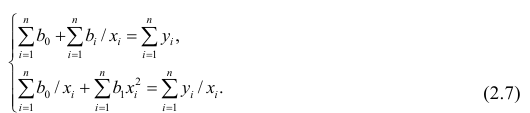
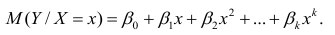
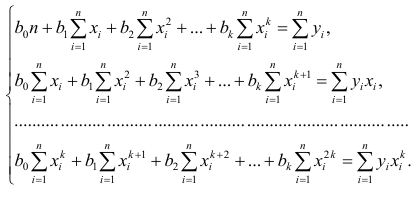

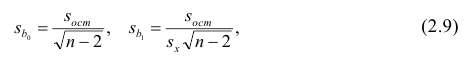
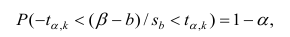

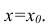
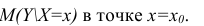
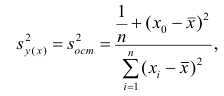
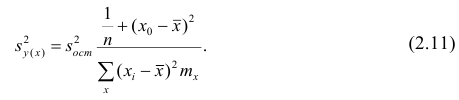
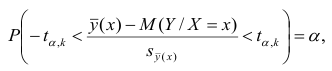
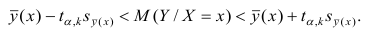
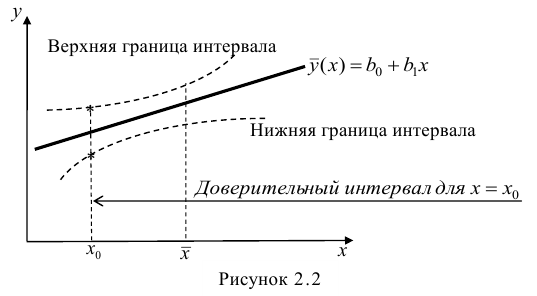
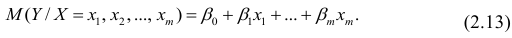
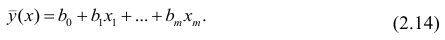
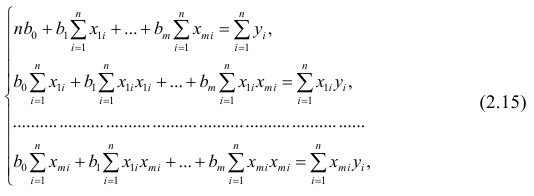
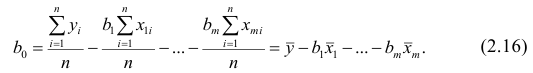
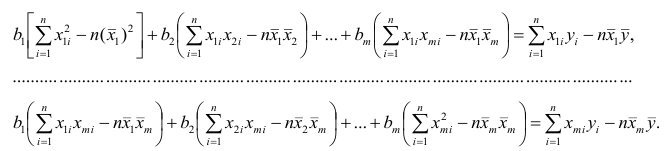
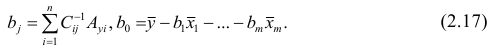
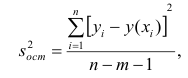
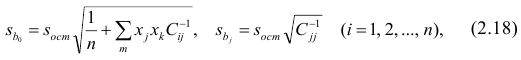
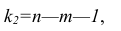
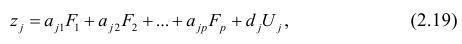
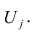
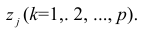
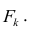
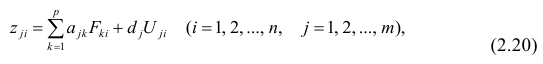
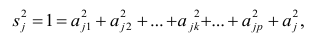
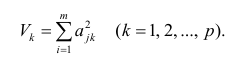
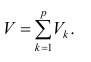
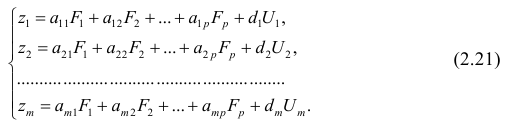
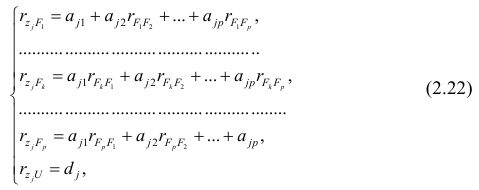
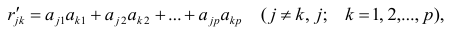
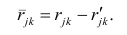
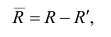

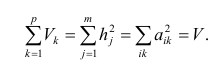
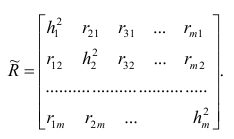


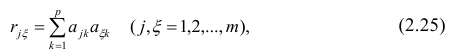

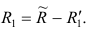

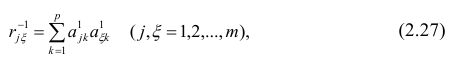
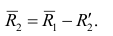
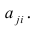
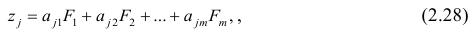
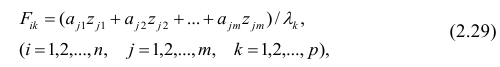
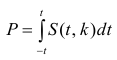
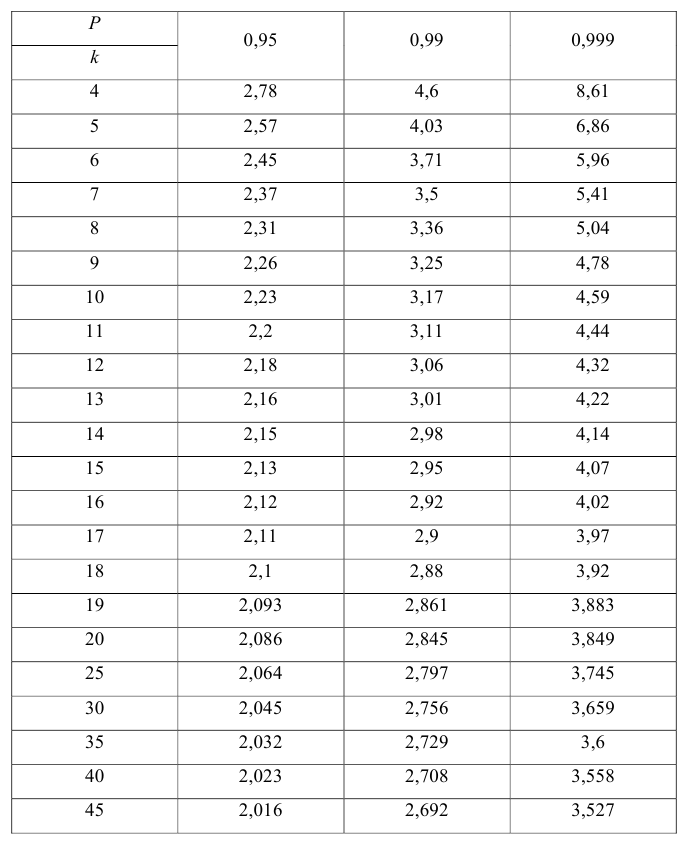
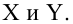
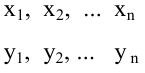
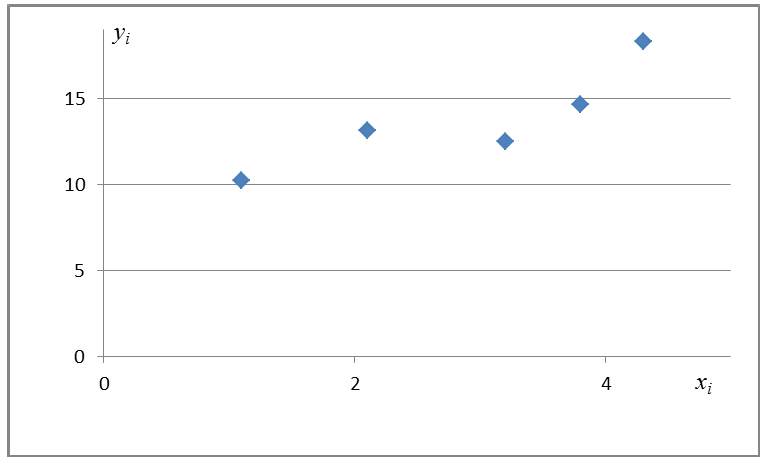
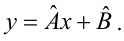
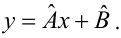
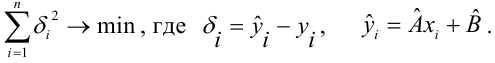
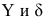 подчинены нормальному закону распределения.
подчинены нормальному закону распределения.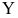 постоянна и не зависит от номера измерения.
постоянна и не зависит от номера измерения.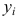 в разных точках независимы.
в разных точках независимы.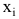 независимы, неслучайны и измеряются без ошибок.
независимы, неслучайны и измеряются без ошибок.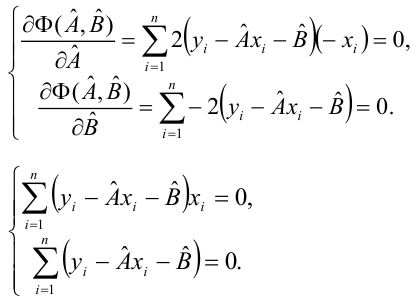
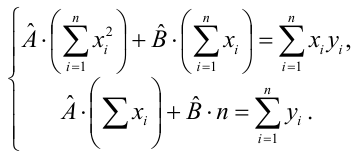
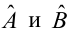
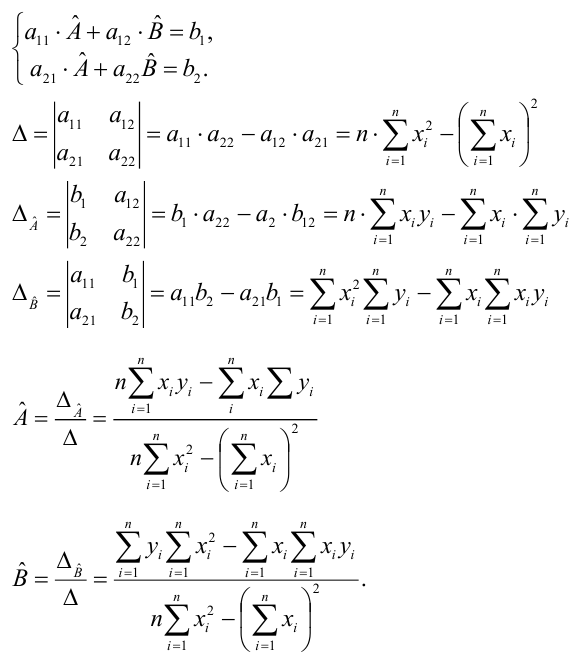
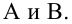
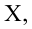
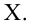
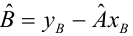
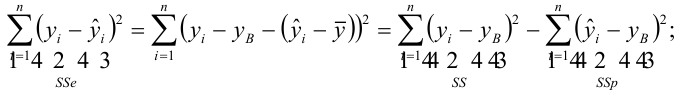
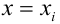
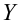
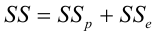
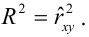
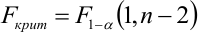
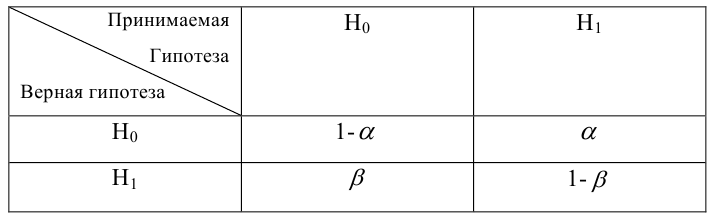
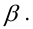
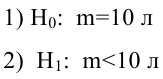
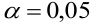
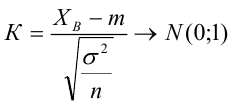
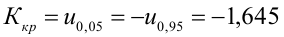
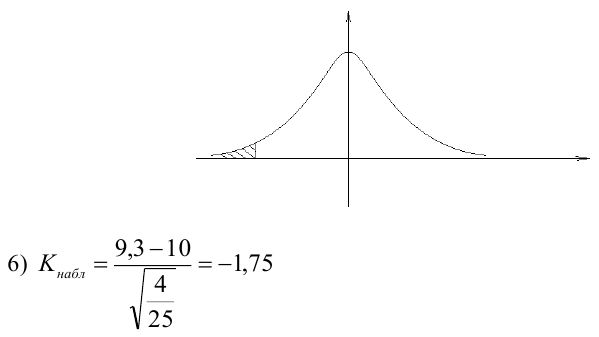
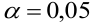
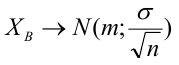
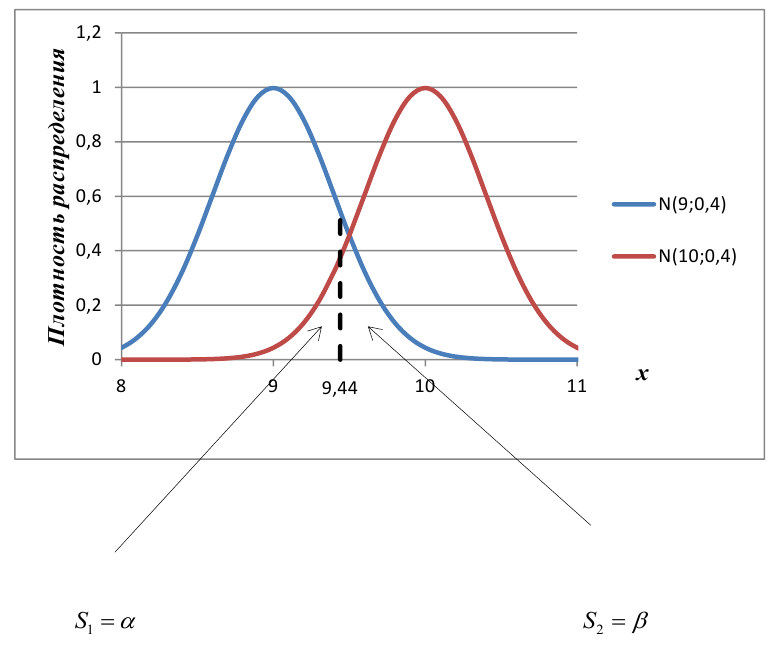
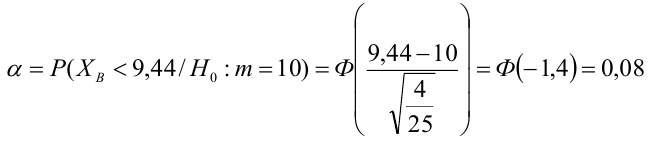
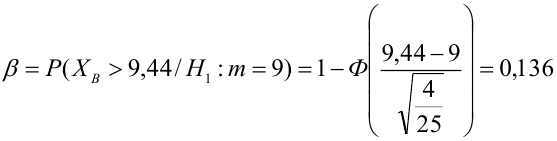
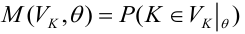
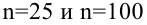
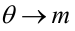
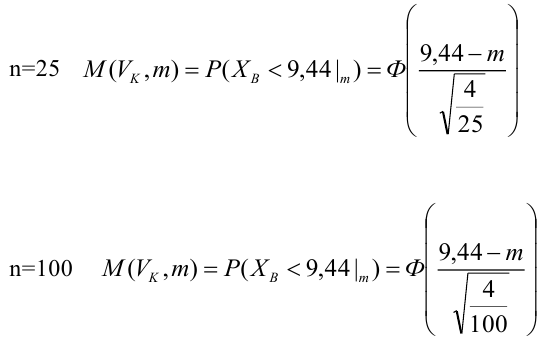
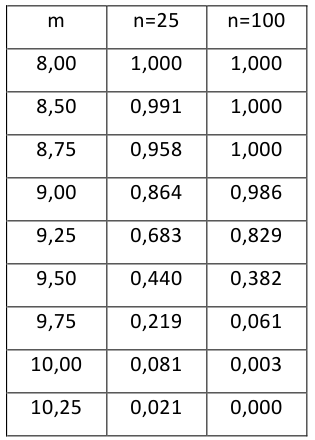
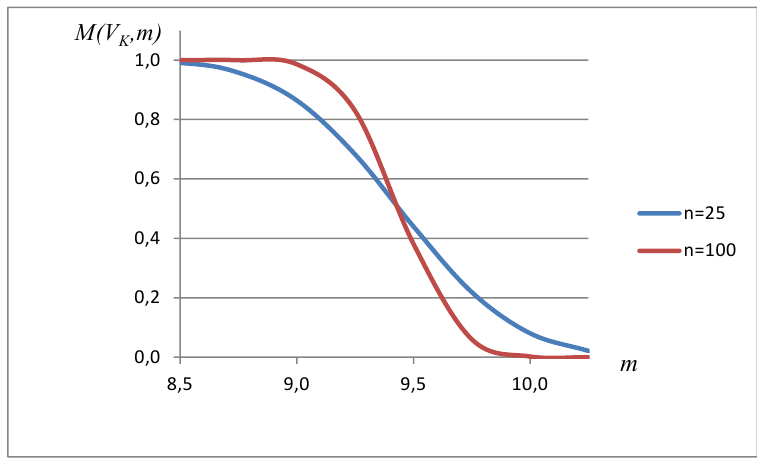
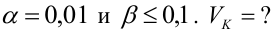
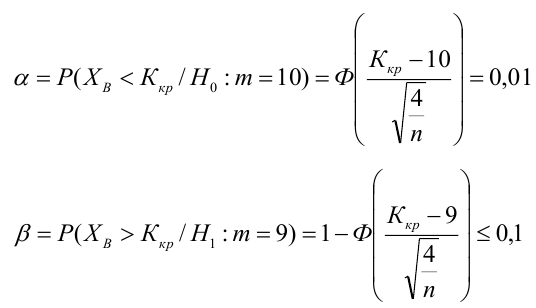
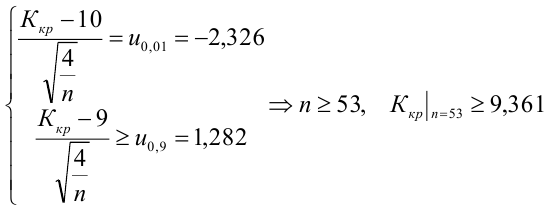
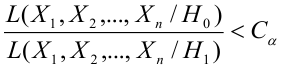
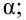
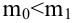
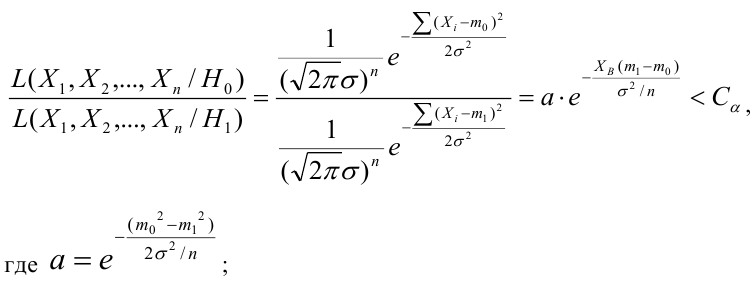
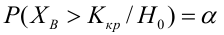
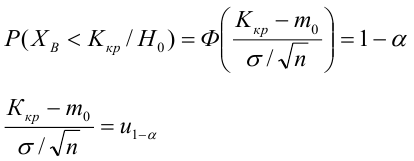
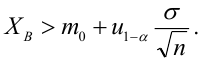
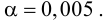
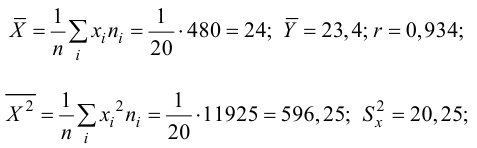
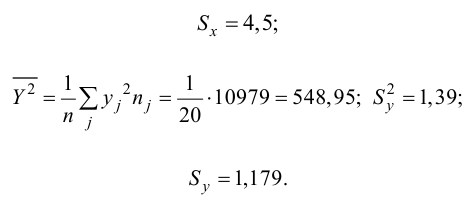
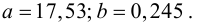
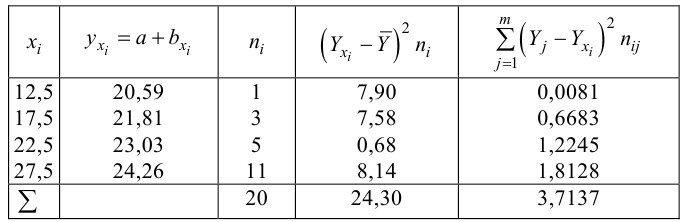
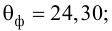
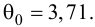
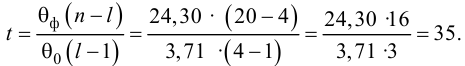
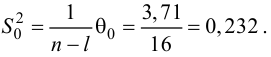



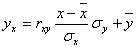
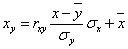
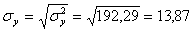
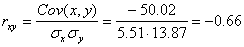
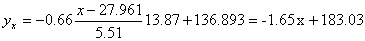
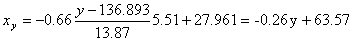

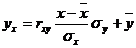
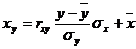
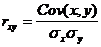
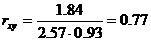
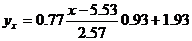
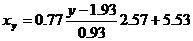
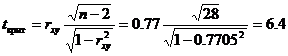

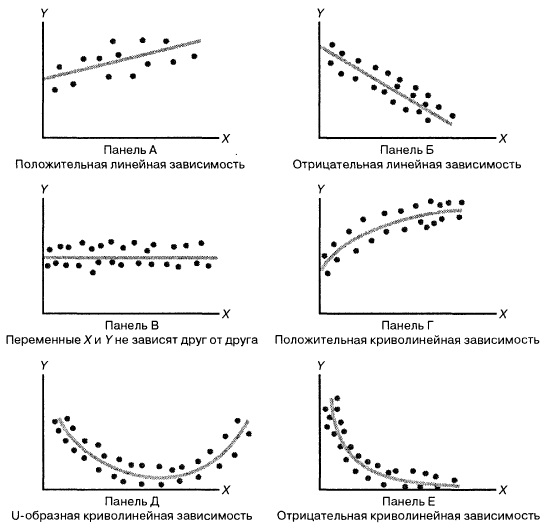


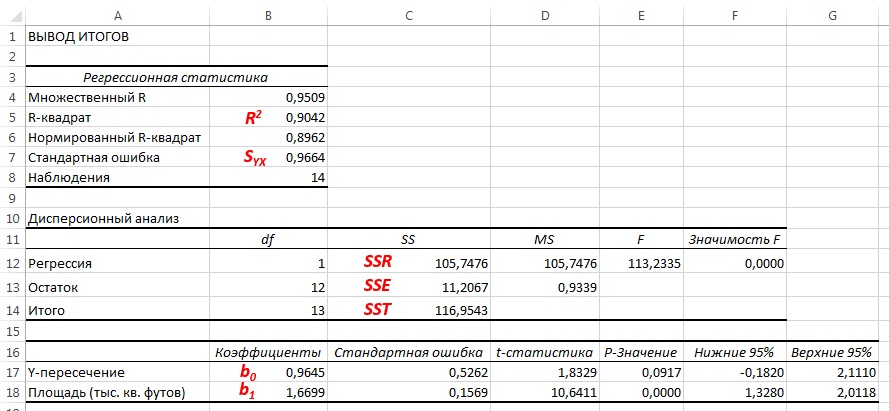
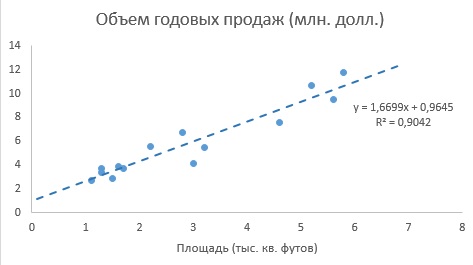





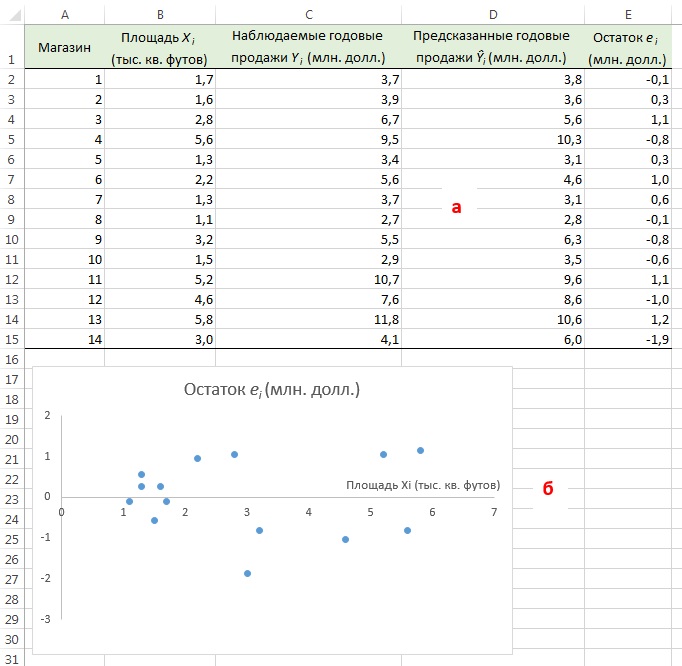




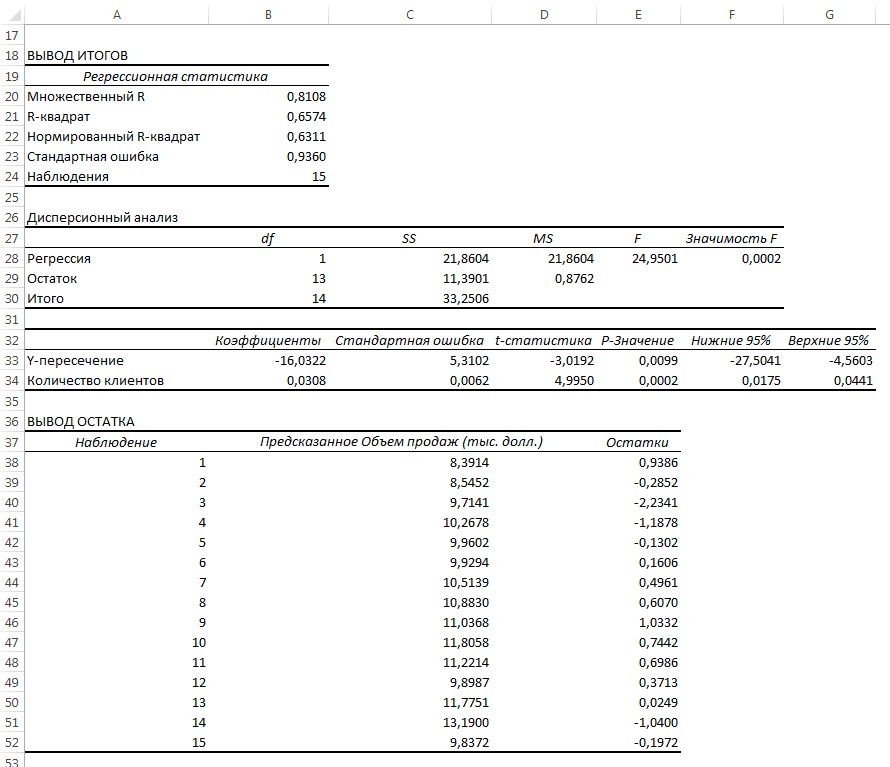



















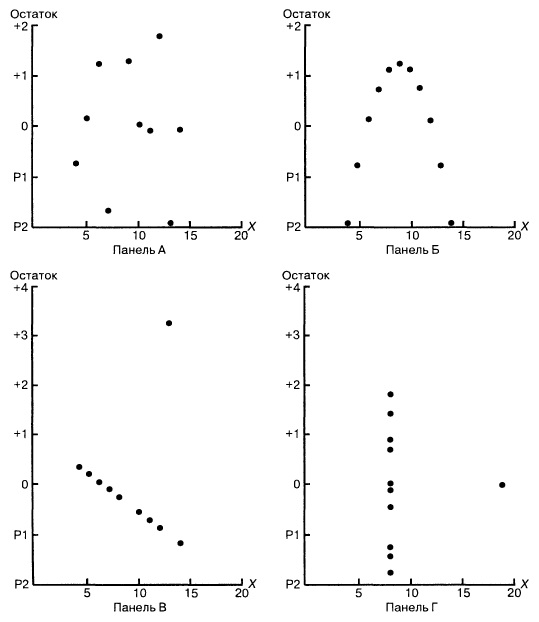
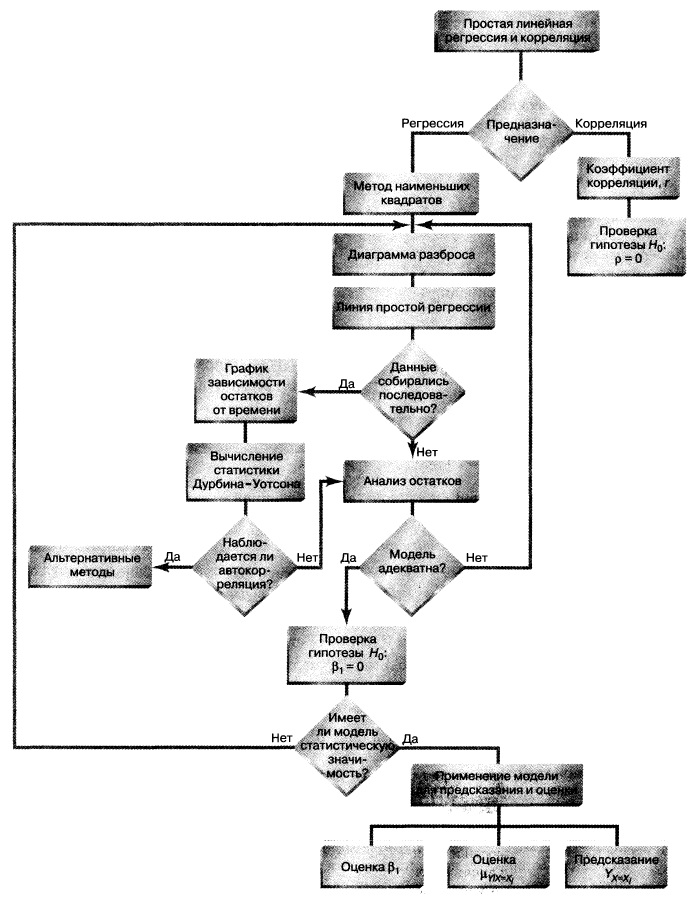


 (28)
(28)