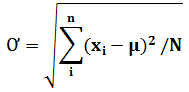The margin of error formula

From Wikipedia, the free encyclopedia

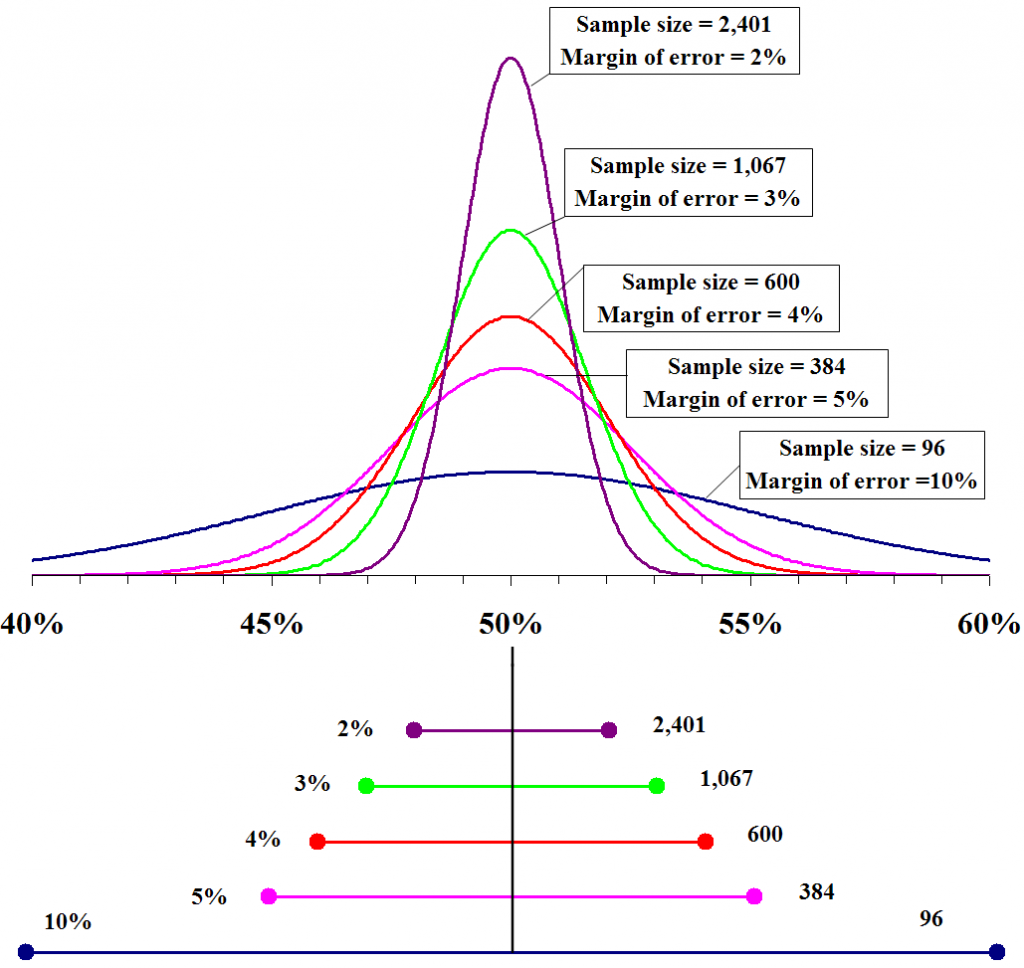
Probability densities of polls of different sizes, each color-coded to its 95% confidence interval (below), margin of error (left), and sample size (right). Each interval reflects the range within which one may have 95% confidence that the true percentage may be found, given a reported percentage of 50%. The margin of error is half the confidence interval (also, the radius of the interval). The larger the sample, the smaller the margin of error. Also, the further from 50% the reported percentage, the smaller the margin of error.

The margin of error is a statistic expressing the amount of random sampling error in the results of a survey. The larger the margin of error, the less confidence one should have that a poll result would reflect the result of a census of the entire population. The margin of error will be positive whenever a population is incompletely sampled and the outcome measure has positive variance, which is to say, the measure varies.

The term margin of error is often used in non-survey contexts to indicate observational error in reporting measured quantities.

Concept[edit]

Consider a simple yes/no poll as a sample of respondents drawn from a population reporting the percentage of yes responses. We would like to know how close is to the true result of a survey of the entire population , without having to conduct one. If, hypothetically, we were to conduct poll over subsequent samples of respondents (newly drawn from ), we would expect those subsequent results ${displaystyle p_{1},p_{2},ldots }$ to be normally distributed about . The margin of error describes the distance within which a specified percentage of these results is expected to vary from .

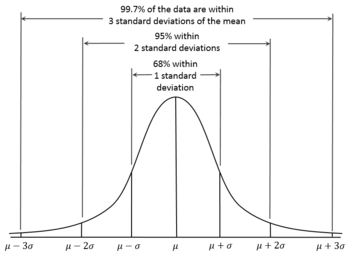
According to the 68-95-99.7 rule, we would expect that 95% of the results ${displaystyle p_{1},p_{2},ldots }$ will fall within about two standard deviations ( ${displaystyle pm 2sigma _{P}}$ ) either side of the true mean . This interval is called the confidence interval, and the radius (half the interval) is called the margin of error, corresponding to a 95% confidence level.

Generally, at a confidence level gamma , a sample sized of a population having expected standard deviation sigma has a margin of error

${displaystyle MOE_{gamma }=z_{gamma }times {sqrt {frac {sigma ^{2}}{n}}}}$

where ${displaystyle z_{gamma }}$ denotes the quantile (also, commonly, a z-score), and ${displaystyle {sqrt {frac {sigma ^{2}}{n}}}}$ is the standard error.

Standard deviation and standard error[edit]

We would expect the normally distributed values ${displaystyle p_{1},p_{2},ldots }$ to have a standard deviation which somehow varies with . The smaller , the wider the margin. This is called the standard error ${displaystyle sigma _{overline {p}}}$ .

For the single result from our survey, we assume that , and that all subsequent results ${displaystyle p_{1},p_{2},ldots }$ together would have a variance ${displaystyle sigma _{P}^{2}=P(1-P)}$ .

${displaystyle {text{Standard error}}=sigma _{overline {p}}approx {sqrt {frac {sigma _{P}^{2}}{n}}}approx {sqrt {frac {p(1-p)}{n}}}}$

Note that corresponds to the variance of a Bernoulli distribution.

Maximum margin of error at different confidence levels[edit]

For a confidence level gamma , there is a corresponding confidence interval about the mean ${displaystyle mu pm z_{gamma }sigma }$ , that is, the interval ${displaystyle [mu -z_{gamma }sigma ,mu +z_{gamma }sigma ]}$ within which values of should fall with probability gamma . Precise values of ${displaystyle z_{gamma }}$ are given by the quantile function of the normal distribution (which the 68-95-99.7 rule approximates).

Note that ${displaystyle z_{gamma }}$ is undefined for , that is, ${displaystyle z_{1.00}}$ is undefined, as is ${displaystyle z_{1.10}}$ .

	${displaystyle z_{gamma }}$			${displaystyle z_{gamma }}$
0.68	0.994457883210	0.999	3.290526731492
0.90	1.644853626951	0.9999	3.890591886413
0.95	1.959963984540	0.99999	4.417173413469
0.98	2.326347874041	0.999999	4.891638475699
0.99	2.575829303549	0.9999999	5.326723886384
0.995	2.807033768344	0.99999999	5.730728868236
0.997	2.967737925342	0.999999999	6.109410204869

Since ${displaystyle max sigma _{P}^{2}=max P(1-P)=0.25}$ at p=0.5 , we can arbitrarily set , calculate ${displaystyle sigma _{P}}$ , ${displaystyle sigma _{overline {p}}}$ , and ${displaystyle z_{gamma }sigma _{overline {p}}}$ to obtain the maximum margin of error for at a given confidence level gamma and sample size , even before having actual results. With

${displaystyle MOE_{95}(0.5)=z_{0.95}sigma _{overline {p}}approx z_{0.95}{sqrt {frac {sigma _{P}^{2}}{n}}}=1.96{sqrt {frac {.25}{n}}}=0.98/{sqrt {n}}=pm 3.1%}$

${displaystyle MOE_{99}(0.5)=z_{0.99}sigma _{overline {p}}approx z_{0.99}{sqrt {frac {sigma _{P}^{2}}{n}}}=2.58{sqrt {frac {.25}{n}}}=1.29/{sqrt {n}}=pm 4.1%}$

Also, usefully, for any reported ${displaystyle MOE_{95}}$

${displaystyle MOE_{99}={frac {z_{0.99}}{z_{0.95}}}MOE_{95}approx 1.3times MOE_{95}}$

Specific margins of error[edit]

If a poll has multiple percentage results (for example, a poll measuring a single multiple-choice preference), the result closest to 50% will have the highest margin of error. Typically, it is this number that is reported as the margin of error for the entire poll. Imagine poll reports ${displaystyle p_{a},p_{b},p_{c}}$ as

${displaystyle MOE_{95}(P_{a})=z_{0.95}sigma _{overline {p_{a}}}approx 1.96{sqrt {frac {p_{a}(1-p_{a})}{n}}}=0.89/{sqrt {n}}=pm 2.8%}$

(as in the figure above)

${displaystyle MOE_{95}(P_{b})=z_{0.95}sigma _{overline {p_{b}}}approx 1.96{sqrt {frac {p_{b}(1-p_{b})}{n}}}=0.87/{sqrt {n}}=pm 2.7%}$

${displaystyle MOE_{95}(P_{c})=z_{0.95}sigma _{overline {p_{c}}}approx 1.96{sqrt {frac {p_{c}(1-p_{c})}{n}}}=0.27/{sqrt {n}}=pm 0.8%}$

As a given percentage approaches the extremes of 0% or 100%, its margin of error approaches ±0%.

Comparing percentages[edit]

Imagine multiple-choice poll reports ${displaystyle p_{a},p_{b},p_{c}}$ as . As described above, the margin of error reported for the poll would typically be ${displaystyle MOE_{95}(P_{a})}$ , as ${displaystyle p_{a}}$ is closest to 50%. The popular notion of statistical tie or statistical dead heat, however, concerns itself not with the accuracy of the individual results, but with that of the ranking of the results. Which is in first?

If, hypothetically, we were to conduct poll over subsequent samples of respondents (newly drawn from ), and report result ${displaystyle p_{w}=p_{a}-p_{b}}$ , we could use the standard error of difference to understand how ${displaystyle p_{w_{1}},p_{w_{2}},p_{w_{3}},ldots }$ is expected to fall about ${displaystyle {overline {p_{w}}}}$ . For this, we need to apply the sum of variances to obtain a new variance, ${displaystyle sigma _{P_{w}}^{2}}$ ,

${displaystyle sigma _{P_{w}}^{2}=sigma _{P_{a}-P_{b}}^{2}=sigma _{P_{a}}^{2}+sigma _{P_{b}}^{2}-2sigma _{P_{a},P_{b}}=p_{a}(1-p_{a})+p_{b}(1-p_{b})+2p_{a}p_{b}}$

where ${displaystyle sigma _{P_{a},P_{b}}=-P_{a}P_{b}}$ is the covariance of ${displaystyle P_{a}}$ and ${displaystyle P_{b}}$ .

Thus (after simplifying),

${displaystyle {text{Standard error of difference}}=sigma _{overline {w}}approx {sqrt {frac {sigma _{P_{w}}^{2}}{n}}}={sqrt {frac {p_{a}+p_{b}-(p_{a}-p_{b})^{2}}{n}}}=0.029,P_{w}=P_{a}-P_{b}}$

${displaystyle MOE_{95}(P_{a})=z_{0.95}sigma _{overline {p_{a}}}approx pm {3.1%}}$

${displaystyle MOE_{95}(P_{w})=z_{0.95}sigma _{overline {w}}approx pm {5.8%}}$

Note that this assumes that $P_{{c}}$ is close to constant, that is, respondents choosing either A or B would almost never chose C (making ${displaystyle P_{a}}$ and ${displaystyle P_{b}}$ close to perfectly negatively correlated). With three or more choices in closer contention, choosing a correct formula for ${displaystyle sigma _{P_{w}}^{2}}$ becomes more complicated.

Effect of finite population size[edit]

The formulae above for the margin of error assume that there is an infinitely large population and thus do not depend on the size of population , but only on the sample size . According to sampling theory, this assumption is reasonable when the sampling fraction is small. The margin of error for a particular sampling method is essentially the same regardless of whether the population of interest is the size of a school, city, state, or country, as long as the sampling fraction is small.

In cases where the sampling fraction is larger (in practice, greater than 5%), analysts might adjust the margin of error using a finite population correction to account for the added precision gained by sampling a much larger percentage of the population. FPC can be calculated using the formula^[1]

${displaystyle operatorname {FPC} ={sqrt {frac {N-n}{N-1}}}}$

…and so, if poll were conducted over 24% of, say, an electorate of 300,000 voters,

${displaystyle MOE_{95}(0.5)=z_{0.95}sigma _{overline {p}}approx {frac {0.98}{sqrt {72,000}}}=pm 0.4%}$

${displaystyle MOE_{95_{FPC}}(0.5)=z_{0.95}sigma _{overline {p}}{sqrt {frac {N-n}{N-1}}}approx {frac {0.98}{sqrt {72,000}}}{sqrt {frac {300,000-72,000}{300,000-1}}}=pm 0.3%}$

Intuitively, for appropriately large ,

${displaystyle lim _{nto 0}{sqrt {frac {N-n}{N-1}}}approx 1}$

${displaystyle lim _{nto N}{sqrt {frac {N-n}{N-1}}}=0}$

In the former case, is so small as to require no correction. In the latter case, the poll effectively becomes a census and sampling error becomes moot.

References[edit]

^ Isserlis, L. (1918). «On the value of a mean as calculated from a sample». Journal of the Royal Statistical Society. Blackwell Publishing. 81 (1): 75–81. doi:10.2307/2340569. JSTOR 2340569. (Equation 1)

Sources[edit]

Sudman, Seymour and Bradburn, Norman (1982). Asking Questions: A Practical Guide to Questionnaire Design. San Francisco: Jossey Bass. ISBN 0-87589-546-8
Wonnacott, T.H.; R.J. Wonnacott (1990). Introductory Statistics (5th ed.). Wiley. ISBN 0-471-61518-8.

External links[edit]

«Errors, theory of», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Weisstein, Eric W. «Margin of Error». MathWorld.

Источник

What is a Margin of Error?

A margin of error is a statistical measurement that accounts for the difference between actual and projected results in a random survey sample. In simpler terms, the margin of error allows you to gauge the level of unpredictability in data and research outcomes.

For example, let’s say a researcher gives the mean estimate for a survey as 50 with a margin of error of ±5. This means that the actual mean, when calculated, could be any value from 45–55.

The margin of error of a data set directly influences the confidence level of the investigator in the research outcomes. Typically, if your research outcome or survey results have a higher margin of error, it means that the data sets might be unreliable. On the other hand, a lower margin of error indicates that the results truly represent the research population.

Importance of Margin of Error in Surveys, Research, and Polls

1. Margin of Error Helps You Achieve Reliable Outcomes in Research

Margin of error accounts for any disparities between results from the research sample and the target population. Typically, the higher the margin of error, the greater the difference between actual and estimated outcomes, further suggesting that the survey results are less likely to be true for the entire population.

2. It Helps the Researcher Determine How Representative the Sample Is

A low margin of error shows that the sample population closely represents the population of interest in a systematic investigation.

When dealing with a large population of interest, it is impossible to collect data from every variable. So, the researcher has to select a sample population that represents all the subgroups in the original population of interest.

If the sample population excludes some of the groups, then the final results of the poll, survey, or research will not reflect the actual outcome of the original population.

3. Margin of Error Helps You Determine the Confidence Level and Confidence Interval of Your Data Sets

When you know the margin of error of your survey and the value of your observed score, you can easily determine your data set’s confidence interval. Confidence interval is a statistical range of the possible values of a parameter. In contrast, confidence level measures the accuracy rate of your research outcomes of survey results based on the available data.

How to Calculate the Margin of Error

To determine the margin of error of your data sets, you need to ensure that the selected research sample truly represents your population of interest. This starts from identifying the right population of interest to applying the appropriate sampling technique.

Once you have a well-representative sample, you can go ahead to calculate the margin of error using the following formula:

Where;

P-hat = Sample Proportion

n = Sample Size

z = Z-Score

Here’s an example of how to apply this formula to your data.

Let’s say you conducted a poll on how many people use Snapchat for business. Out of 1,000 respondents, 450 chose “yes.” You also have a confidence level of 90%.

Step 1: Determine P-hat

P-hat = Numbers of respondents who chose yes ÷ Total number of respondents

P-hat = 450 ÷ 1000 = 0.45 or 45%

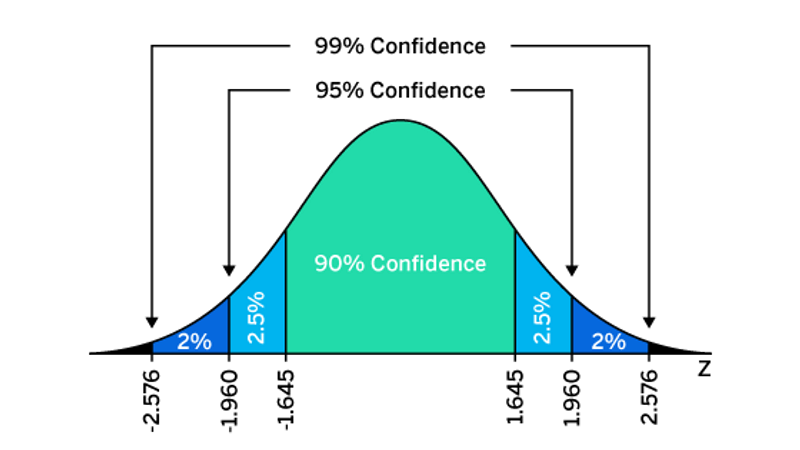
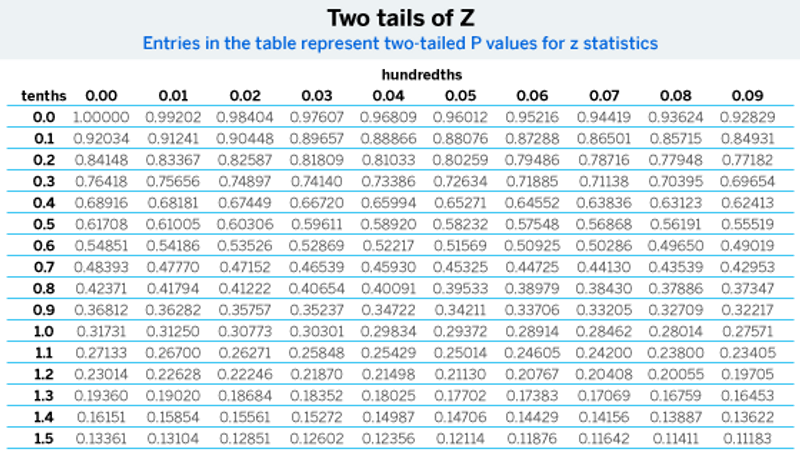
Step 2: Find the Z-Score of the corresponding confidence level. Using this Z-Score table, the Z-score of 90 is 1.645.

Step 3: Apply the Margin of Error formula.

Margin of Error = Z-score × [√P-hat (1–P-hat)] ÷ n]

1.645 × [√(0.45 × 0.55) ÷ 1000]

Margin of Error = 2.6%

Alternatively, you can calculate the margin of error using the standard deviation of your data. This means:

Margin of Error = Z-Score × (S ÷ √n)

If you’d rather not bother with manual calculations, you can use this margin of error calculator to determine the value for your data set.

How to Interpret Margin of Error

What does it mean when your data has a margin of error to a certain percentage? More importantly, how do you interpret this in layman terms to an audience that isn’t “statistics savvy?”

The first thing you should communicate is that margin of error accounts for the maximum difference between outcomes from your sample size and that of the population of interest. So, if you have a margin of error of ±3%, it means the actual results from your target population could be 3% more or less than the estimated value.

For example, suppose your survey shows that 62% of your sample size smoke cigarettes. When you extrapolate this data to the actual population, you would have to add and subtract the margin of error, which means the actual data would fall between 59% and 65%.

Related Statistical Variables in Margin of Error

1. Arithmetic Mean

Arithmetic mean is a statistical measure of distribution that accounts for the average of all the variables in a data set. In other words, arithmetic mean allows you to find the central value of a finite set of variables.

Often, you’d need the mean of your day sets for calculating the measure of error, especially if you need to determine the standard deviation of your data first.

Arithmetic Mean Formula

Arithmetic Mean = Sum of all Variables ÷ Number of Variables

Suppose you have a date set with the following values: 13, 5, 19, 7, 12.

Arithmetic Mean = (13+5+19+7+12) ÷ 5 = 11.2

Importance of Arithmetic Mean

It helps to reduce the margin of error of your data sets, leading to more reliable results.
It allows you to determine the central frequency of a distribution of data.

2. Confidence Intervals vs. Confidence Levels

Confidence interval and confidence level are often used interchangeably, but they do not mean the same thing. Let’s look at some key differences.

Definition

A confidence interval is a range of results from a poll, experiment, or survey that the researcher expects to contain the population parameter of interest. Typically, researchers use the confidence interval of observation to determine whether a parameter will fall between a pair of values around the mean.

On the other hand, the confidence level is the degree of certainty or probability that a survey will produce the same results repeatedly. Theoretically, a confidence level is a measure of accuracy for research outcomes and survey results.

Measurement

Confidence levels are measured in percentages, while confidence intervals are measured in ranges. This means that the confidence level of a data set can be 90% while the confidence interval is 45±50.

Formula

Confidence Interval (C.I) = X ± Z × (S÷√n)

Where;

X = Arithmetic Mean

Z = Confidence Level Value

S = Sample Standard Deviation

n = Sample Size

Since you cannot calculate the confidence level of any observation, most researchers choose an estimated value based on the type of research, sampling technique, and the like. Many times, this ends up as 95%.

Advantages of Confidence of Interval

Confidence interval attaches a measure of accuracy to your sample data. It also helps you to evaluate the reliability of the different variables in an observation.

Advantages of Confidence Level

Like confidence intervals, confidence level allows you to measure the level of accuracy of your data. In addition, it helps you to know if the sample mean is a good or poor representation of the population mean.

3. Standard Deviation

The standard deviation of observation is the amount of variation or dispersion of values around its mean. In other words, it tells you how far apart each value or variable lies from the mean of the same data set. Typically, the higher the standard deviation, the more dispersed the data is.

Understanding standard deviation is an essential part of calculating the margin of error for your data. If you do not have the value for your sample data proportion, you can use standard deviation to determine the margin of error.

Standard Deviation Formula

Where;

s = sample standard deviation

∑ = sum of…

X = each value

x̅ = sample mean

n = number of values in the sample

Importance of Standard of Deviation

It gives you a clear idea of the distribution of data in your observation.
Standard Deviation measures the spread of individual data points.

4. Population Size vs. Sample Size

Also referred to as population of interest, population size is the entire group with the measurable quality or parameter your research is based on. For example, if you’re researching birds of prey in Africa, your population size would be all kinds of birds of prey on the continent.

The sample size is the subset of your population of interest who become direct participants in the research. For example, out of all the birds of prey, you could narrow your research to the African Hawk Eagle in Angola.

5. Critical Value

A critical value is the split point in hypothesis testing that determines whether the researcher accepts or rejects the null hypothesis. When plotted on a graph, the critical value separates the variables into several sections, including the rejection regions. When calculating the margin of error, researchers use the critical value to determine the applicable ranges within the data sets.

Importance of Critical Value

It maps out the range of a confidence interval of observation.
Critical value plays a vital role in significant testing.

6. Z-score

Z-score or standard score accounts for the difference between a given data point and the mean in an observation. It accounts for the standardization of the different data points in the distribution, allowing you to compare scores on other variables.

Importance of Z-Score

It allows you to compare variables from different distributions.
Z-score allows the researcher to calculate the probability of a score occurring within a typical data set.

Margin of Error vs. Standard Error

Because of their similarities, it’s pretty easy for students and researchers to mistake the margin of error for standard error and vice versa. In this section, we’ll look at some key differences between standard error and margin of error. Let’s start with their definitions.

Definition

A margin of error is a statistical measure that accounts for the degree of error received from the outcome of your research sample. On the other hand, standard error measures the accuracy of the representation of the population sample to the mean using the standard deviation of the data set.

Purpose

The purpose of the standard error is to measure the spread of random variables within your data set, while the goal of the margin of error is to estimate how much allowable difference can exist between the research population and sample size.

Formula

Margin of Error = Z-score × [√P-hat (1–P-hat)] ÷ n]

Margin of Error = Z-Score × (S ÷ √n)

Where;

P-hat = Sample Proportion

n = Sample Size

z = Z-Score

S = Standard Deviation

Standard Error = Sample Standard Deviation ÷ √number of samples

Factors That Affect Margin of Error

From all we’ve discussed so far, you should already have a fair idea of the factors that primarily affect the margin of error. These factors are confidence level, sample size, and standard deviation.

It follows that increasing or decreasing any of them will have a dominant effect on the value of margin of error for your data. For example, if your sample size goes from 1,000 to 10,000, your margin of error might increase or reduce to a similar magnitude.

How to Reduce Margin of Error

Since a lower margin means a higher level of accuracy in your research results and sample, it follows that many researchers strive to reduce the margin of error in their systematic investigation. But how do you do this? Here are some ideas you can test out.

Choose a larger sample that allows you to make more observations within your data set. This way, you can have a more exact estimate for the population parameter you’re measuring.
Lower your confidence interval to have a more precise margin of error.
Adopt a one-sided confidence interval which has a smaller margin of error than a two-sided confidence interval.
Reduce the variability within your data sets, so you have more homogeneous values.

Real-Life Applications of Margin of Error

Whether in polling, market research, or simple data collection, a margin of error works in the same way—helping you determine the accuracy of your sample in relation to the actual population of interest. Let’s consider specific applications.

Polling

In polling, a margin of error allows you to accurately extrapolate results for one option to a broader population, with minimal inaccuracy. Here’s what we mean.

Let’s say you conduct a popularity poll for two candidates. Based on the data, you peg the margin of error for Candidate A at 3%. It means there’s a close approximation between the results and the actual popularity of the candidate in the population of interest. So, you can accurately predict future variables using present polling results.

Market Research

In market research, the margin of error shows the level of confidence an organization should have in the data collected from surveys. As mentioned earlier, the higher the margin of error, the less confident you should be in the research samples and, ultimately, the results obtained.

Conclusion

In this article, we’ve discussed the margin of error and its influence on the outcomes of any systematic investigation. Since research is based on collecting samples from a population of interest, you must account for variations between your sample data and the target audience. Calculating the margin of error of your observation is the most effective way to achieve this.

Источник

What is the Margin of Error?

The margin of Error is a statistical expression that is used to determine the percentage point by which the result arrived will differ from the value of the entire population, and it is calculated by dividing the standard deviation of the population by the sample size and lastly multiplying the resultant with the critical factor.

A higher error indicates a high chance that the result of the sample reported may not be the true reflection of the whole population.

What is the Margin of Error?
- The margin of Error Formula
- The margin of Error Calculation (Step by Step)
- Example
- The margin of Error Calculator
- Relevance and Uses
- Recommended Articles

The formula for the margin of error is calculated by multiplying a critical factor (for a certain confidence level) with the population standard deviation. Then the result is divided by the square root of the number of observations in the sample.

Mathematically, it is represented as,

Margin of Error = Z * ơ / √n

You are free to use this image on your website, templates, etc., Please provide us with an attribution linkArticle Link to be Hyperlinked
For eg:
Source: Margin of Error (wallstreetmojo.com)

where

z = critical factor
ơ = population standard deviation
n = sample size

The margin of Error Calculation (Step by Step)

Follow the below steps:

Firstly, gather the statistical observations to form a data set called the population. Now, calculate the mean of the population. Next, compute the population standard deviation based on each observation, the population means, and the number of observations of the population, as shown below.
Next, determine the number of observations in the sample, denoted by n. Remember that sample size is less than equal to the total population, i.e., n ≤ N.
Next, determine the critical factor or the z-scoreThe Z-score of raw data refers to the score generated by measuring how many standard deviations above or below the population mean the data, which helps test the hypothesis under consideration. In other words, it is the distance of a data point from the population mean that is expressed as a multiple of the standard deviation.read more based on the desired confidence level, and it is denoted by z.
Next, finally, the margin error is calculated by multiplying the critical factor for the desired confidence level and the population standard deviation, and then the result is divided by the square root of the sample size as shown above.

Example

You can download this Margin of Error Formula Excel Template here – Margin of Error Formula Excel Template

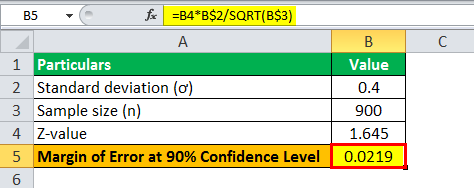
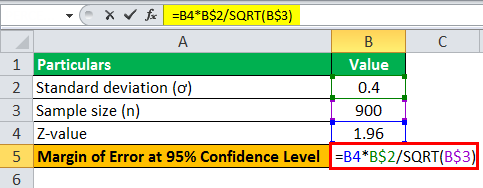
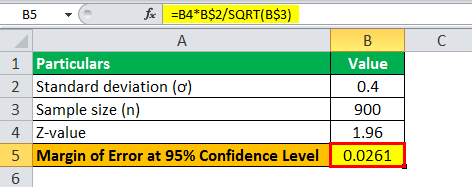
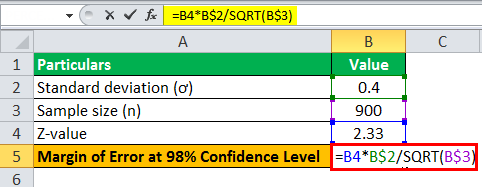
Let us take the example of 900 students who were part of a survey, and it was found that the average GPA of the population was 2.7, with a population standard deviation of 0.4. Calculate the margin of error for

90% confidence level
95% confidence level
98% confidence level
99% confidence level

We are going to use the following data for the calculation.

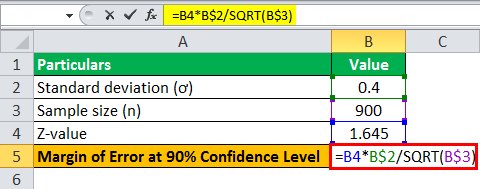
For a 90% Confidence Level

For a 90% confidence level, the critical factor or z-value is 1.645 i.e. z = 1.645

Therefore, the error at a 90% confidence level can be made using above the formula as,

= 1.645 * 0.4 / √900

Margin Error at 90% confidence level will be-

Error = 0.0219

For a 95% Confidence Level

For a 95% confidence level, the critical factor or z-value is 1.96 i.e. z = 1.96

Therefore, the calculation of margin of error at a 95% confidence level can be done using the above the formula as,

= 1.96 * 0.4 / √900

Margin Error at 95% confidence level will be-

Error = 0.0261

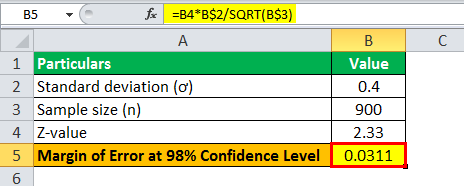
For a 98% confidence level

For a 98% confidence level, the critical factor or z-value is 2.33 i.e. z = 2.33

Therefore, the calculation of margin of error at a 98% confidence level can be done using the above the formula as,

= 2.33 * 0.4 / √900

Margin Error at 98% confidence level will be-

Error = 0.0311

Therefore, the error for the sample at 98% confidence level is 0.0311.

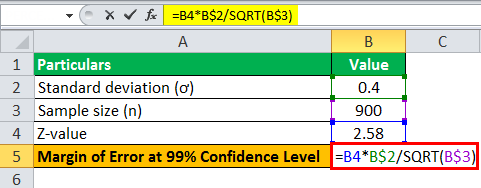
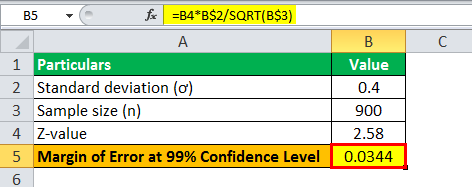
For a 99% confidence level

For a 99% confidence level, the critical factor or z-value is 2.58 i.e. z = 2.58

Therefore, the calculation of margin at a 99% confidence level can be done using the above the formula as,

= 2.58 * 0.4 / √900

Margin Error at 99% confidence level will be-

Error = 0.0344

Consequently, it can be seen that the error of a sample increases with the increase in confidence level.

The margin of Error Calculator

You can use the following calculator.

z
σ
n
Margin of Error Formula =

Margin of Error Formula =

Relevance and Uses

The margin of error equation can be seen as a way of measuring the effectiveness of the survey. It is essential to understand this concept because it indicates how much one can expect that survey results reflect the true view of the overall population. It should be kept in mind that a survey uses a smaller group of people (also known as survey respondents) to represent a much larger population (also known as the target marketA target market consists of different groups of individuals, households, and organizations towards which a company aims to offer its products and services.read more. A higher margin indicates that the survey results may stray from the actual views of the total population. On the other hand, a smaller margin indicates that the results are close to the true reflection of the total population, which builds more confidence in the survey.

Margin of Error Formula

In statistic, we calculate the confidence interval to see where the value of the data of sample statistic will fall. The range of values which are below and above the sample statistic in a confidence interval is known as Margin of Error. In other words, it is basically the degree of error in the sample statistic. Higher the margin of error, lesser will the confidence in the results because the degree of deviation in these results is very high. As its name suggests, the margin of error is a range of values above and below the actual results. For example, if we get a response in a survey wherein 70% people have responded “good” and margin of error is 5%, this means that in general, 65% to 75% of the population think that the answer is “good”.

The formula for Margin of Error –

Margin of Error = Z * S / √n

Where:

Z – Z score
S – Standard Deviation of a population
n – Sample Size

Another formula for calculating the margin of error is:

Margin of Error = Z * √((p * (1 – p)) / n)

Where:

p – Sample Proportion (fraction of sample which is a success)

Now to find the desired z score, you need to know the confidence interval of the sample because the Z score is dependent on that. Below table is given to see the relation of a confidence interval and z score:

Confidence Interval	Z – Score
80%	1.28
85%	1.44
90%	1.65
95%	1.96
99%	2.58

Once you know the confidence interval, you can use the corresponding z value and calculate the margin of error from there.

Examples of Margin of Error Formula (With Excel Template)

Let’s take an example to understand the calculation of Margin of Error in a better manner.

You can download this Margin of Error Template here – Margin of Error Template

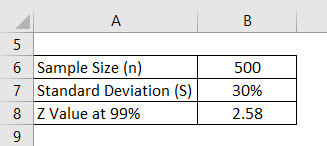
Margin of Error Formula – Example #1

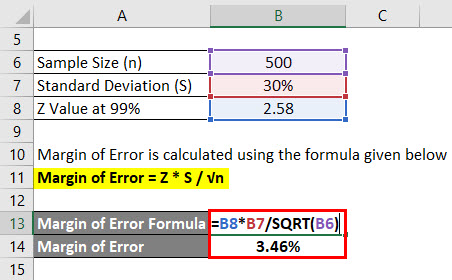
Let’s say we are conducting a survey to see what the grade score which university students are getting is. We have selected 500 students randomly and asked their grade score. The average of that is 2.4 out of 4 and the standard deviation is say 30%. Assume the confidence interval is 99%. Calculate the margin of error.

Solution:

Margin of Error is calculated using the formula given below

Margin of Error = Z * S / √n

Margin of Error = 2.58 * 30% / √(500)
Margin of Error = 3.46%

This means that with 99% confidence, the average grade of students is 2.4 plus or minus 3.46%.

Margin of Error Formula – Example #2

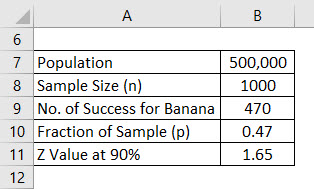
Let say you are launching a new health product in the market but you are confused which flavor will people like. You are confused between banana flavor and vanilla flavor and have decided to conduct a survey. Your population for that is 500,000 which is your target market and out of that you decided to ask the opinion of 1000 people and that will the sample. Assume that a confidence interval is 90%. Calculate the margin of error.

Solution:

Once the survey is done, you came to know that 470 people liked the banana flavor and 530 has asked for vanilla flavor.

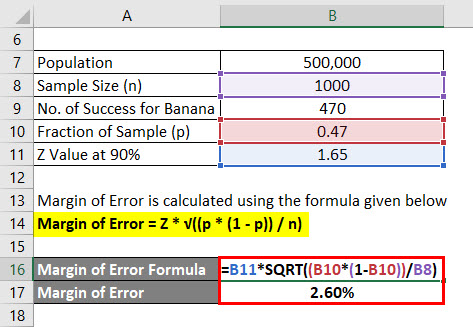
Margin of Error is calculated using the formula given below

Margin of Error = Z * √((p * (1 – p)) / n)

Margin of Error = 1.65 * √((0.47 * (1 – 0.47)) / 1000)
Margin of Error = 2.60%

So we can say that with 90% confidence that 47% of all people liked banana flavor plus or minus 2.60%.

Explanation

As discussed above, the margin of error helps us understand whether the sample size of your survey is appropriate or not. In case the margin error is too big, it can be the case that our sample size is too small and we need to increase that so that sample results match more closely with population results.

There are some scenarios where the margin of error will not be of much use and will not help us in tracking the error:

If the questions of the survey are not designed and do not help in getting the required answer
If the people who are responding to the survey have some bias regarding the product for which the survey is being done, then also, the result not be very accurate
If the sample chosen itself is the proper representative of the population, in that case also, results will be way off.

Also, one big assumption here is that the population is normally distributed. So if the sample size is too small and the population distribution is not normal, z score cannot be calculated and we will not be able to find the margin of error.

Relevance and Uses of Margin of Error Formula

Whenever we use sample data to find some relevant answer for the population set, there is some uncertainty and chances that the result might deviate from the actual result. The margin of error will tell us that what is the level of deviation is there is the sample output. We need to minimize the margin of error so that our sample results depict the actual story of population data. So lower the margin of error, the better will be the results. The margin of error complements and completes the statistical information which we have. For example, if a survey finds that 48% of the people prefer spending time at home during the weekend, we cannot be so precise and there are some missing elements in that information. When we introduced a margin of error here, say, 5%, then the outcome will be interpreted as 43-53% people liked the idea of being at home during the weekend, which makes complete sense.

Margin of Error Formula Calculator

You can use the following Margin of Error Calculator

Margin of Error

0 x	0	=	0

0

Introduction

While you are learning statistics, you will often have to focus on a sample rather than the entire population. This is because it is extremely costly, difficult and time-consuming to study the entire population. The best you can do is to take a random sample from the population – a sample that is a ‘true’ representative of it. You then carry out some analysis using the sample and make inferences about the population.

Since the inferences are made about the population by studying the sample taken, the results cannot be entirely accurate. The degree of accuracy depends on the sample taken – how the sample was selected, what the sample size is, and other concerns. Common sense would say that if you increase the sample size, the chances of error will be less because you are taking a greater proportion of the population. A larger sample is likely to be a closer representative of the population than a smaller one.

Let’s consider an example. Suppose you want to study the scores obtained in an examination by students in your college. It may be time-consuming for you to study the entire population, i.e. all students in your college. Hence, you take out a sample of, say, 100 students and find out the average scores of those 100 students. This is the sample mean. Now, when you use this sample mean to infer about the population mean, you won’t be able to get the exact population means. There will be some “margin of error”.

You will now learn the answers to some important questions: What is margin of error, what are the method of calculating margins of error, how do you find the critical value, and how to decide on t-score vs z-scores. Thereafter, you’ll be given some margin of error practice problems to make the concepts clearer.

What is Margin of Error?

The margin of error can best be described as the range of values on both sides (above and below) the sample statistic. For example, if the sample average scores of students are 80 and you make a statement that the average scores of students are 80 ± 5, then here 5 is the margin of error.

Calculating Margins of Error

For calculating margins of error, you need to know the critical value and sample standard error. This is because it’s calculated using those two pieces of information.

The formula goes like this:

margin of error = critical value * sample standard error.

How do you find the critical value, and how to calculate the sample standard error? Below, we’ll discuss how to get these two important values.

How do You find the Critical Value?

For finding critical value, you need to know the distribution and the confidence level. For example, suppose you are looking at the sampling distribution of the means. Here are some guidelines.

If the population standard deviation is known, use z distribution.
If the population standard deviation is not known, use t distribution where degrees of freedom = n-1 (n is the sample size). Note that for other sampling distributions, degrees of freedom can be different and should be calculated differently using appropriate formula.
If the sample size is large, then use z distribution (following the logic of Central Limit Theorem).

It is important to know the distribution to decide what to use – t-scores vs z-scores.

Caution – when your sample size is large and it is not given that the distribution is normal, then by Central Limit Theorem, you can say that the distribution is normal and use z-score. However, when the sample size is small and it is not given that the distribution is normal, then you cannot conclude anything about the normality of the distribution and neither z-score nor t-score can be used.

When finding the critical value, confidence level will be given to you. If you are creating a 90% confidence interval, then confidence level is 90%, for 95% confidence interval, the confidence level is 95%, and so on.

Here are the steps for finding critical value:

Step 1: First, find alpha (the level of significance). alpha =1 – Confidence level.

For 95% confidence level, alpha =0.05

For 99% confidence level, alpha =0.01

Step 2: Find the critical probability p*. Critical probability will depend on whether we are creating a one-sided confidence interval or a two-sided confidence interval.

For two-sided confidence interval, p*=1-dfrac { alpha }{ 2 }

For one-sided confidence interval, p*=1-alpha

Then you need to decide on using t-scores vs z-scores. Find a z-score having a cumulative probability of p*. For a t-statistic, find a t-score having a cumulative probability of p* and the calculated degrees of freedom. This will be the critical value. To find these critical values, you should use a calculator or respective statistical tables.

Sample Standard Error

Sample standard error can be calculated using population standard deviation or sample standard deviation (if population standard deviation is not known). For sampling distribution of means:

Let sample standard deviation be denoted by s, population standard deviation is denoted by sigma and sample size be denoted by n.

text {Sample standard error}=dfrac { sigma }{ sqrt { n } }, if sigma is known

text {Sample standard error}=dfrac { s }{ sqrt { n } }, if sigma is not known

Depending on the sampling distributions, the sample standard error can be different.

Having looked at everything that is required to create the margin of error, you can now directly calculate a margin of error using the formula we showed you earlier:

Margin of error = critical value * sample standard error.

Some Relationships

1. Confidence level and marginal of error

As the confidence level increases, the critical value increases and hence the margin of error increases. This is intuitive; the price paid for higher confidence level is that the margin of errors increases. If this was not so, and if higher confidence level meant lower margin of errors, nobody would choose a lower confidence level. There are always trade-offs!

2. Sample standard deviation and margin of error

Sample standard deviation talks about the variability in the sample. The more variability in the sample, the higher the chances of error, the greater the sample standard error and margin of error.

3. Sample size and margin of error

This was discussed in the Introduction section. It is intuitive that a greater sample size will be a closer representative of the population than a smaller sample size. Hence, the larger the sample size, the smaller the sample standard error and therefore the smaller the margin of error.

Image Source: Wikimedia Commons

Margin of Error Practice Problems

Example 1

25 students in their final year were selected at random from a high school for a survey. Among the survey participants, it was found that the average GPA (Grade Point Average) was 2.9 and the standard deviation of GPA was 0.5. What is the margin of error, assuming 95% confidence level? Give correct interpretation.

Step 1: Identify the sample statistic.

Since you need to find the confidence interval for the population mean, the sample statistic is the sample mean which is the average GPA = 2.9.

Step 2: Identify the distribution – t, z, etc. – and find the critical value based on whether you need a one-sided confidence interval or a two-sided confidence interval.

Since population standard deviation is not known and the sample size is small, use a t distribution.

text {Degrees of freedom}=n-1=25-1=24.

alpha=1-text {Confidence level}=1-0.95=0.05

Let the critical probability be p*.

For two-sided confidence interval,

p*=1-dfrac { alpha }{ 2 } =1-dfrac { 0.05 }{ 2 } =0.975.

The critical t value for cumulative probability of 0.975 and 24 degrees of freedom is 2.064.

Step 3: Find the sample standard error.

text{Sample standard error}=dfrac { s }{ sqrt { n } } =dfrac { 0.5 }{ sqrt { 25 } } =0.1

Step 4: Find margin of error using the formula:

Margin of error = critical value * sample standard error

= 2.064 * 0.1 = 0.2064

Interpretation: For a 95% confidence level, the average GPA is going to be 0.2064 points above and below the sample average GPA of 2.9.

Example 2

400 students in Princeton University are randomly selected for a survey which is aimed at finding out the average time students spend in the library in a day. Among the survey participants, it was found that the average time spent in the university library was 45 minutes and the standard deviation was 10 minutes. Assuming 99% confidence level, find the margin of error and give the correct interpretation of it.

Step 1: Identify the sample statistic.

Since you need to find the confidence interval for the population mean, the sample statistic is the sample mean which is the mean time spent in the university library = 45 minutes.

Step 2: Identify the distribution – t, z, etc. and find the critical value based on whether the need is a one-sided confidence interval or a two-sided confidence interval.

The population standard deviation is not known, but the sample size is large. Therefore, use a z (standard normal) distribution.

alpha=1-text{Confidence level}=1-0.99=0.01

Let the critical probability be p*.

For two-sided confidence interval,

p*=1-dfrac { alpha }{ 2 } =1-dfrac { 0.01 }{ 2 } =0.995.

The critical z value for cumulative probability of 0.995 (as found from the z tables) is 2.576.

Step 3: Find the sample standard error.

text{Sample standard error}=dfrac { s }{ sqrt { n } } =dfrac { 10 }{ sqrt { 400 } } =0.5

Step 4: Find margin of error using the formula:

Margin of error = critical value * sample standard error

= 2.576 * 0.5 = 1.288

Interpretation: For a 99% confidence level, the mean time spent in the library is going to be 1.288 minutes above and below the sample mean time spent in the library of 45 minutes.

Example 3

Consider a similar set up in Example 1 with slight changes. You randomly select X students in their final year from a high school for a survey. Among the survey participants, it was found that the average GPA (Grade Point Average) was 3.1 and the standard deviation of GPA was 0.7. What should be the value of X (in other words, how many students you should select for the survey) if you want the margin of error to be at most 0.1? Assume 95% confidence level and normal distribution.

Step 1: Find the critical value.

alpha=1-text{Confidence level}=1-0.95=0.05

Let the critical probability be p*.

For two-sided confidence interval,

p*=1-dfrac { alpha }{ 2 } =1-dfrac { 0.05 }{ 2 } =0.975.

The critical z value for cumulative probability of 0.975 is 1.96.

Step 3: Find the sample standard error in terms of X.

text{Sample standard error}=dfrac { s }{ sqrt { X } }=dfrac { 0.7 }{ sqrt { X } }

Step 4: Find X using margin of error formula:

Margin of error = critical value * sample standard error

0.1=1.96*dfrac { 0.7 }{ sqrt { X } }

This gives X=188.24.

Thus, a sample of 189 students should be taken so that the margin of error is at most 0.1.

Conclusion

The margin of error is an extremely important concept in statistics. This is because it is difficult to study the entire population and the sampling is not free from sampling errors. The margin of error is used to create confidence intervals, and most of the time the results are reported in the form of a confidence interval for a population parameter rather than just a single value. In this article, you made a beginning by learning answering questions like what is margin of error, what is the method of calculating margins of errors, and how to interpret these calculations. You also learned to decide whether to use t-scores vs z-scores and gained information about finding critical values. Now you know how to use margin of error for constructing confidence intervals, which are widely used in statistics and econometrics.

Let’s put everything into practice. Try this Statistics practice question:

Looking for more Statistics practice?

You can find thousands of practice questions on Albert.io. Albert.io lets you customize your learning experience to target practice where you need the most help. We’ll give you challenging practice questions to help you achieve mastery in Statistics.

Start practicing here.

Are you a teacher or administrator interested in boosting Statistics student outcomes?

Learn more about our school licenses here.

Источник

In this article we will give you all the vital information on the “margin of error in statistics” This is very vast to compile in just one small article but still we will give you all the essential information just give complete reading to this piece of compilation.

We will be covering all these questions like what is the margin of error in statistics, How to Calculate Margin of Error, How to Calculate Margin of Error: Steps, Some Relationships, Margin of Error Calculation and some more related information/formulas.

What is a margin Error?

The range of values below and above the sample statistic in a confidence interval is called the margin of error. We can also define confidence interval as the way to show the uncertainty with a certain static. for Example from a poll result we get that 98% of confidence interval of 4.88 and 5.26. And if the poll is repeat again using the same parameter and technique. Then we will definitely get results in the interval 4.88 to 5.26 98% of the times.

What is Margin of Error Percentage ?

Margin of error is defined as the difference between true population. And the estimated population from poll result is called “Error percentage of margin”. We can calculate margin of error using these formulas given below :

Margin of error = Product of Critical value and Standard deviation or Margin of error = Product of Critical value and Standard error of the statistic.

How to calculate the margin of error: Steps

Step 1

Calculate the critical value.

Step 2

Calculate the standard deviation or the standard Error.

Step 3

Calculate the Product of critical value with standard deviation or the standard Error. For example critical value= 1.5 and Standard deviation=0.06 then the margin of error calculation will be ‭0.09‬.

calculate using t-distribution calculator on this site find the t-score and the variance and standard deviation calculator will calculator will find the standard deviation from sample.

Margin of Error for a Proportion

To calculator proportion we need sample proportion, sample size and z-score

Where Z is the Z-score.

is the Sample proportion.

n is sample space.

For Example.

A group of people did a survey on 1000 scientists and 380 of thought that climate change was not caused by human pollution. Find the MoE for a 90% confidence interval

Calculate P-hat

Calculate P-hat(sample proportion) by dividing the no. of people who agreed climate change was not caused by human pollution. It means that they answered according to the statement in this example 38% scientist responded positively.

Calculate Z-Score

Calculate the z-score that goes with confidence interval. you’ll need to reference this critical values. A 90% confidence interval has a z-score of 1.64.

Use Margin of Error Formula

Using the formula of the margin of error find the value.

=1.64√[{0.38(0.62)}1000]

=1.64*0.0153=0.0252

Get the Result

Calculate the percentage of the step 3 and then we get thee value of the margin of error is 2.52%.

Statistics aren’t accurate Use of margin of Error

It is a very useful method for estimating any value in this method like Calculations assuming random sampling, Different confidence levels plays an important role and also effect of sample size matters a lot. And as the heading the static are never accurate use of margin of error provide better resolution to the estimated result from any polls or survey.
Also this process is easy to estimate as we don’t have to cover the entire size of the things rather we just have to focus on the small sample part of the entire thing and this small sample represents the entire thing. Besides, this way the cost of surveying the entire population.

Conclusion

Now you might be quite confident about the margin of error in statistics. Next time don’t get into trouble while talking about the margin of error in statistics.

Furthermore, get the best math assignment help from the most reliable math assignment helpers in the world.

What is margin of error?

Margin of error is information that’s provided alongside the results of a piece of research, such as a poll, survey, or a scientific study. You’ll recognize it because it’s expressed with a plus and minus sign together, e.g. + or -1%

Researchers use this to provide additional information that helps you interpret their results and to understand how the study was carried out. The figure tells you that the true result may differ from the percentage figure provided, and how much more or less than the stated percentage the reality might be.

Margin of error provides a clearer understanding of what a survey’s estimate of a population characteristic means. A plus or minus 2 percentage points means that if we ask this question using a simple random sample 100 times, 95 of those times it would come out at the estimated value plus or minus 2 points.

The larger your random sample (the more responses you get), the smaller your margin of error will be and the more confidence you’ll have that your sample results are reliable.

Find out how big your sample size should be with our free calculator

When is margin of error used?

Margin of error is used when you have a random or probability sample.

That means the survey respondents have been selected at random from your population as a whole and every population member has a known, non-zero probability of being included.

It’s not appropriate if the sample has been selected in a non-random way, for example when you use an opt-in research panel.

A research panel sample is typically a quota sample, where participants are selected because they have particular characteristics. Additionally, the respondents volunteer for the panel in return for benefits, so they are not randomly selected from the population size at large.

So although it is a popularly known term, it has a specific application in survey research and it won’t always be relevant to your market research data.

Here are a couple of scenarios:

A sports team has a complete list of everyone who has purchased tickets to their games in the past year. If they randomly select a sample of that population for a survey, they can calculate the margin of error on the percent of people who reported being a fan of the team.
An organization has a complete list of employees. They poll a simple random sample of these employees on whether they preferred an additional day of leave or a small bonus payment. They can report the margin of error on the percentage preferring each option.

Other kinds of error

Margin of error accounts for the level of confidence you have in your results, and the amount of sampling error you expect based on the size of the sample. But there are other kinds of survey errors that may influence your results too.

These include:

Coverage error

Where your sampling frame doesn’t cover the population you are interested in.

Non-response error

This happens when certain respondents don’t take part in your survey.

Measurement error

This can arise from problems with the questionnaire.

To learn about other sources of error, check out our guide to random and non-random sampling error.

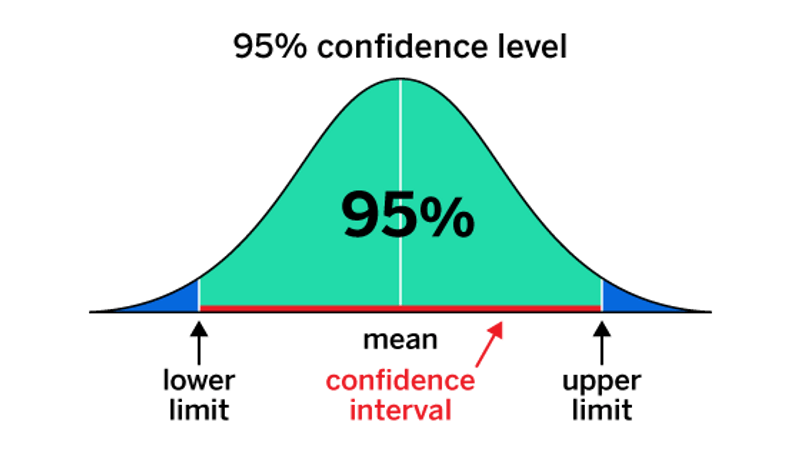
What is a confidence interval?

A confidence interval (CI) is a range of values that include a population value within a degree of confidence.

The values are typically shown in the results as a % value when a population mean sits between a lower and upper limit. Researchers use a CI to measure how accurately the survey sample resembles the overall population.

That’s because it’s almost impossible to find a sample that 100% matches the characteristics of the total population.

Researchers can choose a CI of any level, but a 95% CI is the most common.

This means researchers can be 95% certain that the results contain the actual mean value of the total population. This can be demonstrated using a normal distribution:

Using the graph above, you can see that if the probability of population mean value is between 1.96 and -1.96 standard deviations (sometimes called the z score), the sample mean is 95% (hence the 95% CI).

This is the most common industry formula for calculating the CI. However, when the costs of an error are extremely high, e.g. a multi-million dollar decision is at stake, the confidence interval should be kept small. This can be done by increasing the sample size.

How do you calculate margin of error?

Margin of Error Calculator

Confidence Interval:

Population Size:

Sample Size:

Margin of Error:

Margin of error is calculated using a formula:

Z * √((p * (1 – p)) / n)

Where

Z* is the Z*-value for your selected confidence level, which you’ll look up in a table of Z scores:

p is the sample proportion

n is the sample size

The sample proportion is the number within the sample that has the characteristic you’re interested in. It’s a decimal number representing a percentage, so while you’re doing the calculation it’s expressed in hundredths. For a 5% sample proportion, it would be 0.05.

The most commonly used confidence level is 95%, so we’ll use that for an example calculation. The Z*-value for a 95% confidence level is 1.96.

We’ll set our sample size at 1000. Next, we’ll follow the process to calculate the margin of error.

How to calculate margin of error with your survey data

Subtract p from 1. If p is 0.05, then 1-p = 0.95.
Multiply 1-p by p. So that’s 0.05 x 0.95 – which gives you 0.0475.
Divide the result (0.0475) by the sample size n. So 0.0475 divided by 1000 = 0.0000475.
Now we need the square root of that value, which is 0.0068920. This is the standard error.
Finally, we multiply that number by the Z*-value for our CI, which is 1.96. So 0.0068920 x 1.96 = 0.0134395. That’s a margin of error of just over 1%.

Let’s try it with a real-world example.

Imagine you are a business surveying your current customers. You’ve run a study with a randomly selected sample of 1,000 people from your CRM list. The results tell you that of these 1,000 customers, 52% (520 people) are happy with their latest purchase, but 48% (480 people) are not – yikes. You want to add a margin of error to these results when you report them to your shareholders.

We’ll assume you want a 95% level of confidence, so the z*-value you’re working with is once again 1.96.

The number of customers who are happy with their latest purchase was 520, so that’s the number you’ll use to work out the sample proportion. 520 (p) / 1,000 (n) = 0.52

1-p is 0.48
0.52 (p) x 0.48 (1-p) = 0.2496
0.2496 / 1,000 = 0.0002496
The square root of 0.0002496 = 0.0157987
0.0157987 x 1.96 (the z*-value) = 0.0309654, or in other words, 3.1% (when you round it up).

You can now report with 95% confidence that 52% of your customers were happy with their latest purchase, + or – 3.1%

There are a couple of conditions for using this formula. They are:

n x p must equal 10 or more
n x (1-p) must equal 10 or more

Usually, survey research involves quite high numbers of people in a sample, so unless you have a very small sample, or the sample proportion within your sample is very small, there won’t be a problem. If you’re getting numbers below 10 for either of these checks, you may need to increase your sample size.

Determining your sample size

Choosing the right sized sample is a critical part of creating a survey that will give you reliable results, especially when you’re using the data to make critical business decisions.

Determining sample size is based on the number of people you will need to represent the full population. For example, using 2,000 people as a representative sample of the UK workforce.

If you choose a sample that’s too small, you won’t get reliable results. The larger the sample, the smaller the margin of error. Of course, larger sample sizes mean costlier research, so ultimately there’s a trade off.

Determining the size of your sample is a relatively straightforward process:

Calculate margin of error

Your margin for error (also referred to as confidence interval) essentially determines how confident you can be that your sample will represent the same results you’d get if you were able to survey the total population.

If you used the margin of error formula mentioned above — Z * √((p * (1 – p)) / n) — and the associated z score table, you have your own margin of error calculator.

Understanding your confidence level

Your confidence level determines how certain you would be that the actual mean falls within your margin of error — and that if you were to repeat your survey multiple times, you’d still get the same results.

The lower your sample size, the lower your confidence level will be. The higher the sample size, the higher your confidence level.

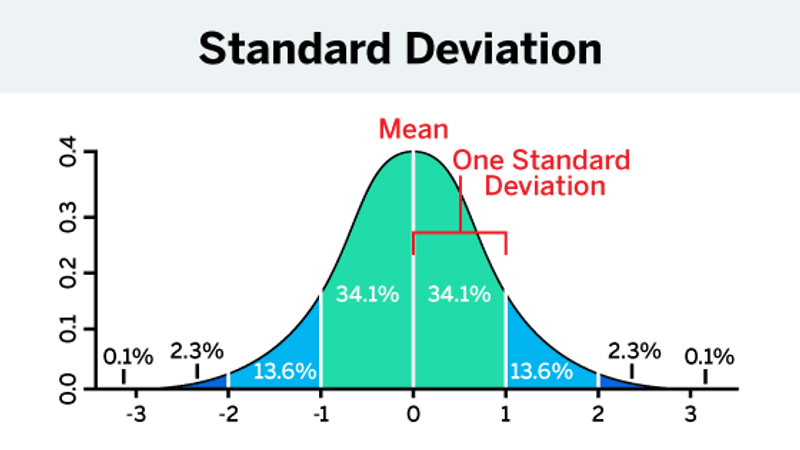
What’s the standard deviation likely to be?

In a population, standard deviation helps you to understand how the completed responses will differ from each other, as well as how they’ll deviate from the mean number.

A low standard deviation means that the values are clustered around the mean number, whereas a high standard deviation means they are spread across a range, with some small and large outlying figures.

What’s the total population size?

Population size is the main factor in determining the sample size you need to get the desired confidence level in your results.

The ‘population’ represents the whole group that you want to understand through your research, while the sample size is the number of people you need to survey to get a representative sample of that whole.

How to reduce the margin of error in your survey results

Reducing your margin of error is an essential part of increasing the reliability of your surveys and ensuring you’re generating better, more accurate results.

There are several ways you can reduce the margin error, some are more practical and will depend on a few variables around your project.

Reduce the variables

It stands to reason the more variables you have in your study the higher the chances that errors will creep into your study.

Reducing the variables in the way you gather your sample or complete your survey can also help to reduce the standard variation, meaning the margin of error will be lower.

Increase the total number in your sample

Often the easiest way to reduce the margin for error is to increase the size of the sample. Having a larger group complete your surveys statistically means you’ll be more likely to generate a representative response for your study and reduce the margin of error.

Use a lower confidence level

A lower confidence level provides you with a more precise margin of error – however you should be wary about this as lowering the confidence level reduces the confidence that your survey will accurately represent the overall population.

Use a single-sided confidence interval

Unlike a two-sided CI, a single-sided interval has a smaller margin of error, because it only shows if one of your parameters is above or below the cut-off value on one side i.e. it will only tell you if the parameter is above or below (it won’t show both).

You can use this method to reduce your margin for error if you’re confident the parameter will fall on one side of the cut-off value.

How Qualtrics can help

No matter the survey, research project or poll, Qualtrics CoreXM has the tools and capabilities you need to derive insight from data — and go from insight to action.

Used by more than 13,000 customers, Qualtrics CoreXM brings your survey, research, and polls into one platform, rather than multiple tools, enabling you to scale your activities, improve data quality, and uncover new opportunities.

With CoreXM, get insights faster through automation, reduce project costs and admin by consolidating your tools, and increase project impact by leveraging best-in-class survey methodologies and tools.

From simple polling and internal feedback surveys for strategy to gleaning customer, product, brand, and market insights, Qualtrics CoreXM empowers every department to carry out and benefit from research.

And if you want to get even more from your research, take advantage of Qualtrics’ Research Services and a network of experienced partners. Through trainer experts, unlock cost and time savings, while benefiting from flexible service options that let you choose how much or how little support you need.

Источник

Many times political polls and other applications of statistics state their results with a margin of error. It is not uncommon to see that an opinion poll states that there is support for an issue or candidate at a certain percentage of respondents, plus and minus a certain percentage. It is this plus and minus term that is the margin of error. But how is the margin of error calculated? For a simple random sample of a sufficiently large population, the margin or error is really just a restatement of the size of the sample and the level of confidence being used.

The Formula for the Margin of Error

In what follows we will utilize the formula for the margin of error. We will plan for the worst case possible, in which we have no idea what the true level of support is the issues in our poll. If we did have some idea about this number, possibly through previous polling data, we would end up with a smaller margin of error.

The formula we will use is: E = z_α/2/(2√ n)

The Level of Confidence

The first piece of information we need to calculate the margin of error is to determine what level of confidence we desire. This number can be any percentage less than 100%, but the most common levels of confidence are 90%, 95%, and 99%. Of these three the 95% level is used most frequently.

If we subtract the level of confidence from one, then we will obtain the value of alpha, written as α, needed for the formula.

The Critical Value

The next step in calculating the margin or error is to find the appropriate critical value. This is indicated by the term z_α/2 in the above formula. Since we have assumed a simple random sample of a large population, we can use the standard normal distribution of z-scores.

Suppose that we are working with a 95% level of confidence. We want to look up the z-score z*for which the area between -z* and z* is 0.95. From the table, we see that this critical value is 1.96.

We could have also found the critical value in the following way. If we think in terms of α/2, since α = 1 — 0.95 = 0.05, we see that α/2 = 0.025. We now search the table to find the z-score with an area of 0.025 to its right. We would end up with the same critical value of 1.96.

Other levels of confidence will give us different critical values. The greater the level of confidence, the higher the critical value will be. The critical value for a 90% level of confidence, with a corresponding α value of 0.10, is 1.64. The critical value for a 99% level of confidence, with a corresponding α value of 0.01, is 2.54.

Sample Size

The only other number that we need to use the formula to calculate the margin of error is the sample size, denoted by n in the formula. We then take the square root of this number.

Due to the location of this number in the above formula, the larger the sample size that we use, the smaller the margin of error will be. Large samples are therefore preferable to smaller ones. However, since statistical sampling requires resources of time and money, there are constraints to how much we can increase the sample size. The presence of the square root in the formula means that quadrupling the sample size will only half the margin of error.

A Few Examples

To make sense of the formula, let’s look at a couple of examples.

What is the margin of error for a simple random sample of 900 people at a 95% level of confidence?
By use of the table we have a critical value of 1.96, and so the margin of error is 1.96/(2 √ 900 = 0.03267, or about 3.3%.
What is the margin of error for a simple random sample of 1600 people at a 95% level of confidence?
At the same level of confidence as the first example, increasing the sample size to 1600 gives us a margin of error of 0.0245 or about 2.5%.

Источник

In statistics, margin of error is used to assess how precise some estimate is of a population proportion or a population mean.

We use typically use margin of error when calculating confidence intervals for population parameters.

The following examples show how to calculate and interpret margin of error for a population proportion and a population mean.

Example 1: Interpret Margin of Error for Population Proportion

We use the following formula to calculate a confidence interval for a population proportion:

Confidence Interval = p +/- z*(√p(1-p) / n)

where:

p: sample proportion
z: the chosen z-value
n: sample size

The portion of the equation that comes after the +/- sign represents the margin of error:

Margin of Error = z*(√p(1-p) / n)

For example, suppose we want to estimate the proportion of residents in a county that are in favor of a certain law. We select a random sample of 100 residents and ask them about their stance on the law.

Here are the results:

Sample size n = 100
Proportion in favor of law p = 0.56

Suppose we would like to calculate a 95% confidence interval for the true proportion of residents in the county that are in favor of the law.

Using the formula above, we calculate the margin of error to be:

Margin of Error = z*(√p(1-p) / n)
Margin of Error = 1.96*(√.56(1-.56) / 100)
Margin of Error = .0973

We can then calculate the 95% confidence interval to be:

Confidence Interval = p +/- z*(√p(1-p) / n)
Confidence Interval = .56 +/- .0973
Confidence Interval = [.4627, .6573]

The 95% confidence interval for the proportion of residents in the county who are in favor of the law turns out to be [.4627, .6573].

This means we’re 95% confident that the true proportion of residents who support the law is between 46.27% and 65.73%.

The proportion of residents in the sample who were in favor of the law was 56%, but by subtracting and adding the margin of error to this sample proportion we’re able to construct a confidence interval.

This confidence interval represents a range of values that are highly likely to contain the true proportion of residents in the county who are in favor of the law.

Example 2: Interpret Margin of Error for Population Mean

We use the following formula to calculate a confidence interval for a population mean:

Confidence Interval = x +/- z*(s/√n)

where:

x: sample mean
z: the z-critical value
s: sample standard deviation
n: sample size

The portion of the equation that comes after the +/- sign represents the margin of error:

Margin of Error = z*(s/√n)

For example, suppose we want to estimate the mean weight of a population of dolphins. We collect a random sample of dolphins with the following information:

Sample size n = 40
Sample mean weight x = 300
Sample standard deviation s = 18.5

Using the formula above, we calculate the margin of error to be:

Margin of Error = z*(s/√n)
Margin of Error = 1.96*(18.5/√40)
Margin of Error = 5.733

We can then calculate the 95% confidence interval to be:

Confidence Interval = x +/- z*(s/√n)
Confidence Interval = 300 +/- 5.733
Confidence Interval =[294.267, 305.733]

The 95% confidence interval for the mean weight of dolphins in this population turns out to be [294.267, 305.733].

This means we’re 95% confident that the true mean weight of dolphins in this population is between 294.267 pounds and 305.733 pounds.

The mean weight of dolphins in the sample was 300 pounds, but by subtracting and adding the margin of error to this sample mean we’re able to construct a confidence interval.

This confidence interval represents a range of values that are highly likely to contain the true mean weight of dolphins in this population.

Additional Resources

The following tutorials provide additional information about margin of error:

Margin of Error vs. Standard Error: What’s the Difference?
How to Find Margin of Error in Excel
How to Find Margin of Error on a TI-84 Calculator

Источник

Concept[edit]

Standard deviation and standard error[edit]

Maximum margin of error at different confidence levels[edit]

Specific margins of error[edit]

Comparing percentages[edit]

Effect of finite population size[edit]

See also[edit]

References[edit]

Sources[edit]

External links[edit]

What is a Margin of Error?

Importance of Margin of Error in Surveys, Research, and Polls

1. Margin of Error Helps You Achieve Reliable Outcomes in Research

2. It Helps the Researcher Determine How Representative the Sample Is

3. Margin of Error Helps You Determine the Confidence Level and Confidence Interval of Your Data Sets

How to Calculate the Margin of Error

How to Interpret Margin of Error

Related Statistical Variables in Margin of Error

1. Arithmetic Mean

Arithmetic Mean Formula

Importance of Arithmetic Mean

2. Confidence Intervals vs. Confidence Levels

Definition

Measurement

Formula

Advantages of Confidence of Interval

Advantages of Confidence Level

3. Standard Deviation

Standard Deviation Formula

Importance of Standard of Deviation

4. Population Size vs. Sample Size

5. Critical Value

Importance of Critical Value

Importance of Z-Score

Margin of Error vs. Standard Error

Factors That Affect Margin of Error

How to Reduce Margin of Error

Real-Life Applications of Margin of Error

What is the Margin of Error?

Table of contents