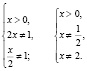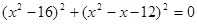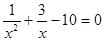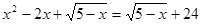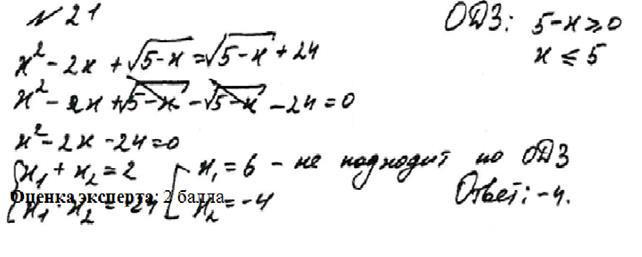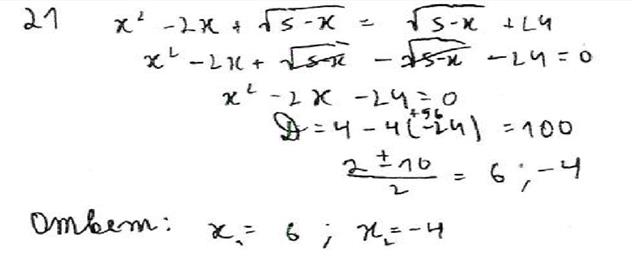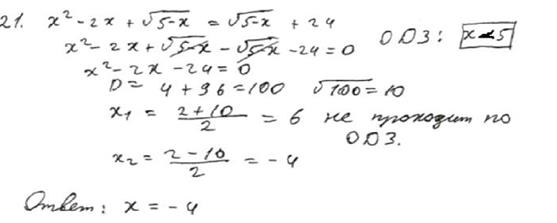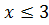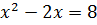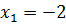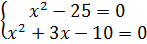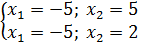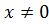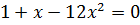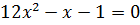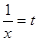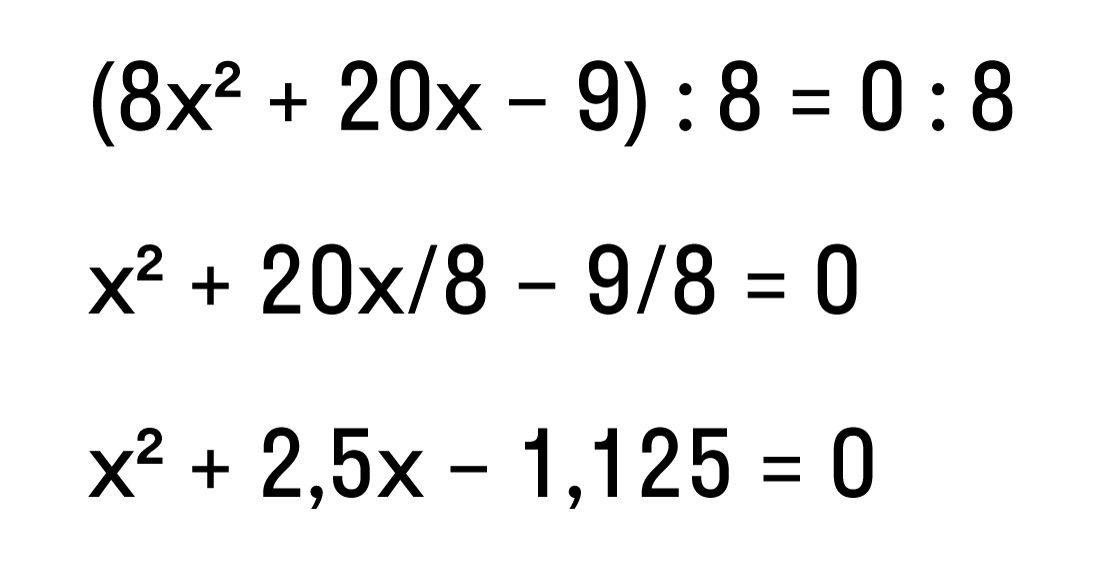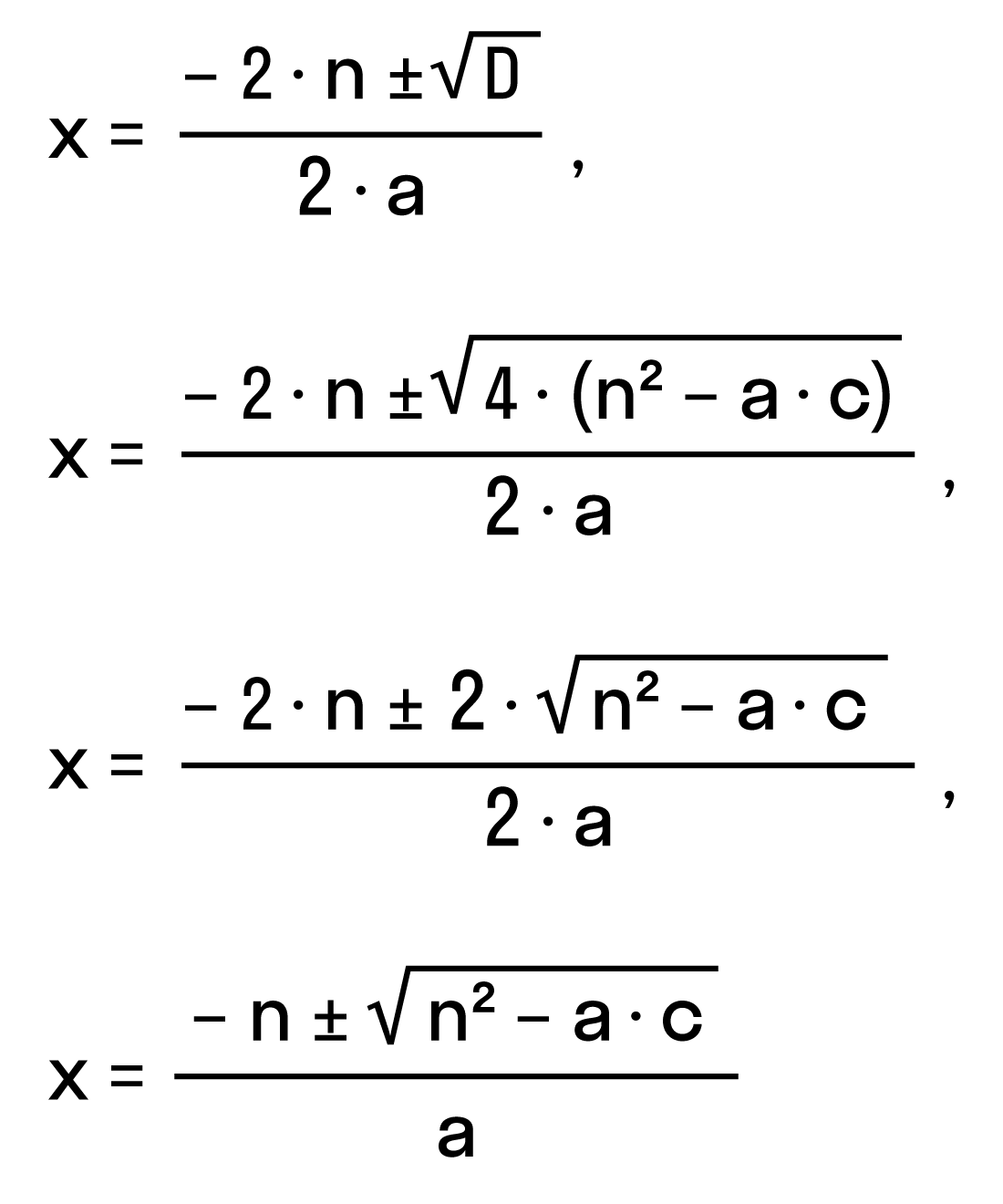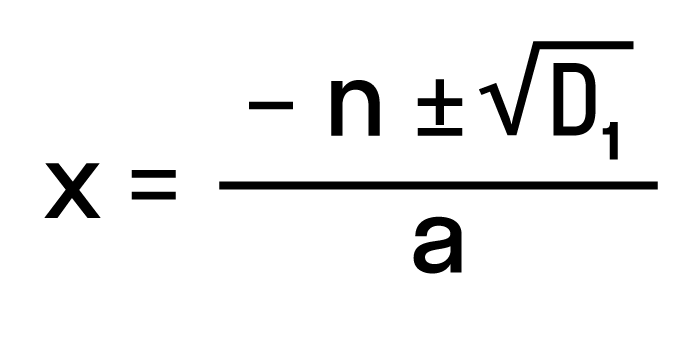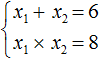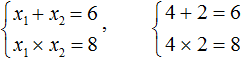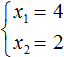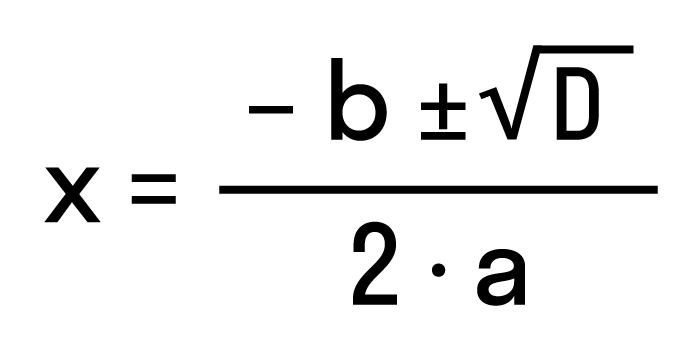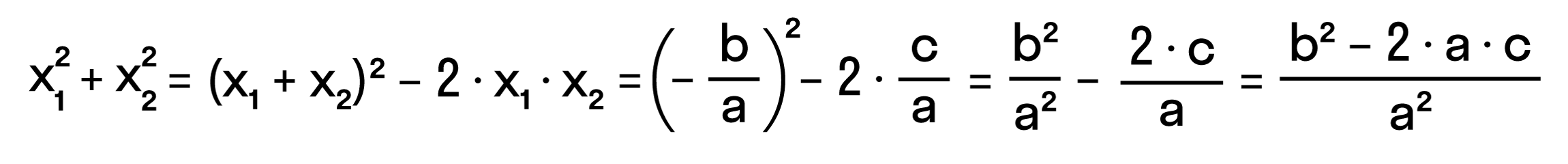Как избежать типичных ошибок, возникающих при выполнении заданий ЕГЭ по математике
Дземяшкевич Е.В., преподаватель математики
(Факультет довузовской подготовки ТулГУ)
Чтобы подготовиться к ЕГЭ по математике, необходимо уже сегодня перестать комплексовать и паниковать перед предстоящим единым экзаменом. Уже сейчас можно сказать, что на ЕГЭ можно получить вполне приличное количество баллов: время для форсированной подготовки еще не потеряно. Конечно, ЕГЭ — это не легко и просто, но и не безнадежно. Важно, чтобы школьник сам честно сформулировал для себя планируемый результат обучения. Это вовсе не означает, что выпускник, наметивший себе «3», может получить только «3» и не более, напротив, ориентируясь на намеченный результат, может и должен получить на один балл выше. Ученики, ориентированные на получение «4», должны помнить, что если постараться, то можно получить и «5».
Но не всегда так получается. Возможны ошибки при решении заданий, недостатки при подготовке, которые приводят к низким результатам ЕГЭ.
Для устранения недостатков в подготовке учеников к ЕГЭ по математике, необходимо совершенствовать процесс преподавания: активнее включать в учебный процесс идеи дифференцированного обучения; использовать практические разработки по индивидуализации обучения (создание индивидуальных модулей обучения), учитывать рекомендации психологов по организации усвоения и пр.).
Поговорим подробнее об ошибках, которые возможны при выполнении заданий ЕГЭ. Рассмотрим важные темы, встречающиеся на экзамене по математике.
| Тема | Ошибки | Рекомендации |
|---|---|---|
| преобразование иррациональных выражений | При кажущейся простоте этого задания, решаемость его далека от 100%. Сложно заставить себя при выполнении этих заданий сделать проверку. Казалось бы, все свойства действий с корнями просты. Вроде всё просто. Только не все выпускники могут вычислить или, не обращая внимания на степень корня, извлекают корень квадратный. | Не торопясь, выполнить все действия на черновике (обязательно записать все этапы решения). |
| преобразование показательных выражений | Выполнить проверку показательного выражения сложно | Не торопясь, выполнить все действия на черновике (обязательно записать все этапы решения); можно составить аналогичное задание и попытаться найти закономерность. |
| преобразование логарифмических выражений | Особенность темы заключается в том, что большинство одиннадцатиклассников узнают о логарифмах только в ноябре-декабре. Времени на «присвоение знаний» нет. Многие выпускники бояться решать задания с логарифмами, несмотря на то, что все свойства логарифмов они знают. Самое сложное при выполнении этих заданий – выполнить проверку. | Не торопясь, выполнить все действия на черновике (обязательно записать все этапы решения). |
| линейные уравнения | Решают все, правда, если a 0. Как только уравнение решается автоматически, возможны ошибки. Например, . Что это? Невнимательность? Досадная ошибка? | При решении линейных уравнений никто не застрахован от ошибок. Обязательно выполняем проверку. |
| квадратные уравнения | Очень большой процент ошибок приходится на квадратные уравнения. Ошибки начинаются с вычисления дискриминанта. В формулах для вычисления корней есть ошибки для –b и 2a. Не стоит упоминать про формулу «четного коэффициента» — много ошибок, особенно у сильных учеников. Важно повторить теорему Виета. | Не стоит пренебрегать проверкой корней с помощью теоремы Виета или подстановкой: она занимает меньше времени, чем полная проверка всего решения сложного задания. |
| дробно-рациональные уравнения | Школьники решают очень тяжело. Серьезные проблемы возникают при решении такого уравнения: даже записывая такое формальное условие- знаменатель не равен нулю – они о нем тут же забывают. | Чтобы избежать многих ошибок, проверка нужна обязательно: подстановка и удовлетворение условию «знаменатель не равен нулю». Обязательно включать в каждую домашнюю работу хотя бы одно задание на решение дробно рационального уравнения |
| рациональные неравенства | Линейные: чаще всего при делении на отрицательное число, неравенство вида: |
© Факультет довузовской подготовки Тульского государственного университета
300012, город Тула, проспект Ленина, 84, кор. 8, 3-й учебный корпус ТулГУ
(4872) 25-46-83, 25-46-84, 717-535
Тульский государственный университет
300012, город Тула, проспект Ленина, 92
(4872) 33-24-10, 35-34-44
Приемная комиссия ТулГУ: (4872) 332-332
Для того, чтобы мы могли качественно предоставить Вам услуги, мы используем cookies, которые сохраняются на Вашем компьютере (сведения о местоположении; ip-адрес; источник, откуда пришел на сайт пользователь, эта же информация используется для обработки статистических данных использования сайта посредством интернет-сервисов Google Analytics и Яндекс.Метрика). Продолжая использовать сайт, Вы соглашаетесь на использовании cookies. Отключить cookies Вы можете в настройках своего браузера.
Лист продвижения по отработке типичных ошибок при подготовке к ОГЭ по математике в 9 классе по теме «Решение квадратных уравнений».
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Лист продвижения по теме «Решение квадратных уравнений»
Отработка типичных ошибок допускаемых при решении квадратных уравнений
Кодификаторы проверяемых элементов содержания и требований к уровню подготовки обучающихся.
Проверяемые элементы содержания
Код проверяемого элемента
Проверяемые элементы содержания
Квадратное уравнение. Формула корней квадратного уравнения. Теорема Виета
Решение уравнений, сводящихся к квадратным алгебраическими преобразованиями и подстановкой
Проверяемые требования к уровню подготовки
Проверяемые элементы содержания
Метапред метный результат
Код проверяемого требования
Проверяемые предметные требования к результатам обучения
Овладение символьным языком алгебры, приемами выполнения тождественных преобразований выражений, решения уравнений, систем уравнений, неравенств и систем неравенств; умения моделировать реальные ситуации на языке алгебры, исследовать построенные модели с использованием аппарата алгебры, интерпретировать полученный результат
Решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных
уравнений и несложные нелинейные системы
Планируемые результаты освоения раздела «Квадратные уравнения»
определение квадратного уравнения (полного, неполного, приведенного), биквадратного уравнения
определять вид квадратного уравнения
формулу корней квадратного уравнения
записать квадратное уравнение в общем виде
вторую формула корней квадратного уравнения
определять коэффициенты квадратного уравнения
определение и формулу нахождения дискриминанта
находить дискриминант, определять число корней квадратного уравнения в зависимости от дискриминанта
теорему Виета и обратную ей теорему
не приведённое квадратное уравнение преобразовывать в приведённое
алгоритмы решения неполных квадратных уравнений и полных квадратных уравнений
решать квадратные уравнения по формуле корней квадратного уравнения
формулу разложения квадратного трехчлена
распознавать неполные квадратные уравнения и решать их, используя соответствующие приёмы
алгоритм решения биквадратных уравнений
использовать теорему Виета и обратную ей теорему для отыскания корней (подбором) и для проверки корней
выполнять разложение на множители квадратного трехчлена
составлять квадратное уравнение по условию задачи и решать текстовые задачи
решать биквадратные уравнения
свободно владеть соответствующей терминологией
осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач
использовать знаково-символические средства и модели при решении учебно-практических задач
Лист продвижения по теме «Решение квадратных уравнений»
9 класс (отработка типичных ошибок)
определять вид квадратного уравнения (полное, неполное, приведенное)
определять коэффициенты квадратного уравнения
находить дискриминант, определять число корней квадратного уравнения в зависимости от дискриминанта
решать квадратные уравнения по формуле корней квадратного уравнения
распознавать неполные квадратные уравнения и решать их, используя соответствующие приёмы
не приведённое квадратное уравнение преобразовывать в приведённое
использовать теорему Виета и обратную ей теорему
свободно владеть соответствующей терминологией
осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач
«-» — не усвоил, не могу выполнить
«!» — сомневаюсь, нужна тренировка
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 696 человек из 76 регионов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 858 человек из 78 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 46 человек из 20 регионов
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 843 580 материалов в базе
Материал подходит для УМК
«Алгебра», Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др.
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 09.12.2020
- 173
- 12
- 09.12.2020
- 137
- 0
- 09.12.2020
- 111
- 0
- 09.12.2020
- 123
- 0
- 09.12.2020
- 165
- 2
- 09.12.2020
- 88
- 2
- 09.12.2020
- 109
- 3
- 09.12.2020
- 170
- 9
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 09.12.2020 265
- DOCX 21.9 кбайт
- 27 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Караваева Юлия Геннадьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 9 месяцев
- Подписчики: 0
- Всего просмотров: 2646
- Всего материалов: 4
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Инфофорум о буллинге в школе: итоги и ключевые идеи
Время чтения: 6 минут
Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу
Время чтения: 1 минута
С 1 сентября в российских школах будут исполнять гимн России
Время чтения: 1 минута
Госдума рассматривает проект о регулировании «продленок» в школах
Время чтения: 1 минута
Эвакуированные в Россию из ДНР и ЛНР дети смогут поступить в вузы по квоте
Время чтения: 1 минута
Российские школьники начнут изучать историю с первого класса
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Трудности при изучении темы « Квадратные уравнения» в 8 классе.
Трудности при изучении темы « Квадратные уравнения» в 8 классе. Традиционные ошибки, допускаемые учащимися при изучении этой темы.
Акулова О.Н., учитель математики высшей категории МАОУ «СОШ №7» г. Гая Оренбургской области
Прежде, чем приступить к изучению данной темы, мы должны знать трудности изучения темы и те традиционные ошибки, которые допускают учащиеся при изучении данной темы.
Во первых, ученики часто применяют нерациональные приемы решения и излишне подробно записывают процесс преобразования данного уравнения к простейшему виду. Выучив формулу решения полного квадратного уравнения, учащиеся, нередко, применяют ее и в случае решения квадратных уравнений с четным коэффициентом при неизвестном в первой степени. Таким образом, большее внимание в процессе обучения следует уделять рациональным способам вычисления корней.
Наиболее часто встречающиеся ошибки в работах учеников 8-го класса при решении квадратных уравнений, относятся к операциям с буквенными коэффициентами. На вопрос, что называется коэффициентом, получаем один ответ: числовой множитель, стоящий перед буквенным выражением. Этот факт подтверждает, что при оперировании с буквами ученики 8-го класса не всегда видят их конкретный смысл. Если бы ученики были приучены контролировать свою работу, они придавали (хотя бы мысленно) численные значения буквам и сами вскрывали свои ошибки. Следовательно, при обучении большее внимание следует обращать на нахождение числовых значений алгебраических выражений и на аналогию в выполнении алгебраических и арифметических действий; тем самым, учащиеся будут привыкать смотреть на буквенное выражение не только как на объект для тождественных преобразований, но и как на функцию входящих в него букв.
Теорема Виета при изучении квадратных урав нений является наиболее сложной темой. Нередко ее смысл учащиеся усваивают формально и не мо гут применить теорему на практике. Для проверки понимания теоремы и знаний по данной теме, ре комендуется предлагать следующие обучающие- воп росы.
Известно, что сумма двух искомых чисел и их произведение — целые числа. Могут ли эти искомые числа быть дробными? Объясните на примерах.
Известно, что сумма и произведение корней квадратного уравнения — целые числа. Могут ли корни этого уравнения быть дробными числами?
Объясните на примерах.
Известно, что сумма корней квадратного урав нения (или сумма двух чисел) — число дробное, а произведение этих чисел — число целое. Могут ли
корни этого уравнения быть целыми числами?
Известно, что сумма корней и их произведе ние — числа дробные. Могут ли корни данного урав нения быть целыми числами. Приведите примеры для различных случаев.
Дано полное квадратное уравнение неприведенного вида, свободный член и коэффициенты которого не имеют общего множителя. Какими числами может выражаться сумма и произведение его корней? Приведите примеры неприведенных полных квадрат ных уравнений для случая:
а)когда и сумма, и произведение их корней выра жаются дробными числами;
б)когда только сумма или только произведение выражается дробным числом.
Могут ли в указанных случаях оба корня быть целыми?
Изучая ошибки по рассматриваемой теме, мы пришли к выводу, что теорему Виета целесообразно изучать индуктивным путем, исходя из рассмотрения приведен ного квадратного уравнения вида x 2 +рх+ q = 0. Затем перейти к рассмотрению этого вопроса для неприве денного квадратного уравнения вида ах 2 + b х + с = 0 и установить соотношение (- b / a )= p и ( c / a )= q
Исследование корней квадратного уравнения по его дискриминанту и коэффициентам, исследование вопроса, будут ли корни данного квадратного уравне ния действительными, различными или равными или среди действительных чисел нет корня данного урав нения, не затрудняет учащихся. Обычно, допускае мая ошибка состоит в том, что за дискриминант при нимают не подкоренное выражение, а квадратный корень из дискриминанта, то есть считают, что D =√( b 2 -4 ac ) или D 1 =√(( b /2) 2 — q ) при исследовании корней уравнения школьники часто применяют не рациональный прием, который состоит в том, что для ответа на вопросы: будут ли корни данного квадратного уравнения действительными числами, будут ли они различны или равны, учащиеся вычисляют дискриминант, хотя достаточно только установить его
знак. Заметим еще, что не всегда учащиеся умеют самостоятельно указать квадратное уравнение, заве домо имеющее действительные корни без нахождения числовой величины его дискриминанта. Только после приведения нескольких аналогичных примеров квадратных уравнений с отрицательным свободным членом и наводящего вопроса, учащиеся могут сделать вывод, что в этих случаях всегда D > 0 (сказывается недостаточный навык вычитания отрицательного числа). При определении знаков корней квадратного уравнения не всегда можно получить полное, последова тельное, доведенное до логического конца объясне ние процесса исследования без наводящих (и даже подсказывающих) вопросов учителя.
Четкость речи, как известно, связана с осознанно стью соответствующей мысли. Поэтому при объяснении данного вопроса учитель должен дать четкий об разец рассуждений. Прежде всего надо указать, что о знаках корней можно говорить лишь тогда, когда они существуют (во множестве действительных чисел).
Надо убедиться в неотрицательности дискриминанта, причем для этого не следует доводить до конца вычисления, достаточно убедиться, что он не отрица телен (в случае, когда свободный член квадратного уравнения отрицателен, а коэффициент при х 2 поло жителен, не надо вычислять дискриминант — он положителен). Затем рассмотреть на примерах все четыре возможных случая: оба корня уравнения отрицательные, положительные, один из корней отрица тельный, положительный. Выводы следует оформить таблицей.
Вопрос об оперировании с абсолютными величи нами остается слабым местом в знаниях учащихся 8-го класса. Особое внимание надо обратить на тот факт, что сравнение абсолютных величин корней не легко усваивается школьниками. Следует лишний раз подчеркнуть, что, например, число может быть записано в виде | + 6 |; + 6; | — 6 |; 6. Для достижения хо роших результатов можно рекомендовать систему уп ражнений с использованием наглядности.
Расположите в порядке возрастания (убывания) ряд чисел, среди которых имеются положительные, отрицательные числа и нуль. Покажите на числовой прямой числа : — 2,5; 4; — 3; + 2; — 0,1; 1/2; -3/4; — 1/3.
Расположите в порядке возрастания или убы вания абсолютные величины тех же чисел. Сделайте выводы.
Найдите сумму, разность, произведение, част ное абсолютных величин двух чисел, если компонен тами действий служат различные действительные числа в различных комбинациях, не исключая и нуля.
Составление квадратного уравнения по формуле (х — х 1 )(х — х 2 )=0 подготавливает учеников к даль нейшему изучению теории алгебраических уравнений. Уже первые примеры на квадратные уравнения- учащиеся решают разложением левой его части на линейные множители, делают необходимые выводы и устанавливают связи между различными вопросами одной и той же темы.
К изучению данного учебного материала учащихся следует готовить, начиная с 5-го класса:
При изучении квадрата числа, натуральной степени учащиеся выполняли такие задания: Найти значение выражения D = b 2 -4 ac , если a =2, b =5, c =4. При изучении десятичных дробей, обыкновенных дробей, отрицательных чисел – a , b , c меняются.
Знание квадратов натуральных чисел от 1 до 20 нужно проверять на протяжении всех лет обучения математики.
К работе по схеме учащиеся готовятся, начиная с устного счета, по цепочке, с указанием порядка действий, с помощью стрелок, по элементарным программам при работе с микрокалькулятором, при прохождении многих тем учащиеся учатся выполнять те, или другие преобразования по алгоритму. У учащихся должны быть отработаны навыки решения линейных уравнений.
источники:
http://infourok.ru/list-prodvizheniya-po-otrabotke-tipichnyh-oshibok-pri-podgotovke-k-oge-po-matematike-v-9-klasse-po-teme-reshenie-kvadratnyh-urav-4647347.html
http://www.prodlenka.org/metodicheskie-razrabotki/120609-trudnosti-pri-izuchenii-temykvadratnye-uravn
Инфоурок
›
Алгебра
›Другие методич. материалы›Лист продвижения по отработке типичных ошибок при подготовке к ОГЭ по математике в 9 классе по теме «Решение квадратных уравнений».
Скачать материал
Скачать материал


- Курс добавлен 16.12.2022


- Сейчас обучается 124 человека из 44 регионов


- Сейчас обучается 901 человек из 82 регионов


Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 119 809 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы

- 09.12.2020
- 163
- 0

«Разработка урока алгебры в 7 классе»
- Учебник: «Алгебра», Мордкович А.Г., Николаев Н.П.
- Тема: § 30. Разложение многочленов на множители с помощью формул сокращенного умножения
- 09.12.2020
- 154
- 0




- 09.12.2020
- 204
- 9
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Педагогическая риторика в условиях реализации ФГОС»
-
Курс профессиональной переподготовки «Организация и предоставление туристских услуг»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс повышения квалификации «Психодинамический подход в консультировании»
-
Курс профессиональной переподготовки «Управление сервисами информационных технологий»
-
Курс профессиональной переподготовки «Организация системы менеджмента транспортных услуг в туризме»
-
Курс повышения квалификации «Финансовые инструменты»
-
Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»
-
Настоящий материал опубликован пользователем Караваева Юлия Геннадьевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 7 лет и 7 месяцев
- Подписчики: 0
- Всего просмотров: 2939
-
Всего материалов:
4
01.04.2015
Квадратные уравнения — одна из важных тем современной школы. квадратные уравнения встречаются при решении текстовых задач, заданий прикладного характера, которые являются неотъемлемой частью контрольно-измерительных материалов ОГЭ и ЕГЭ. Статья раскрывает вопрос о приёмах преодоления трудностей при решении учащимися квадратных уравнений.
Оценить
2788
Содержимое разработки
Трудности при изучении темы « Квадратные уравнения» в 8 классе. Традиционные ошибки, допускаемые учащимися при изучении этой темы.
Акулова О.Н., учитель математики высшей категории МАОУ «СОШ №7» г. Гая Оренбургской области
Прежде, чем приступить к изучению данной темы, мы должны знать трудности изучения темы и те традиционные ошибки, которые допускают учащиеся при изучении данной темы.
Во первых, ученики часто применяют нерациональные приемы решения и излишне подробно записывают процесс преобразования данного уравнения к простейшему виду. Выучив формулу решения полного квадратного уравнения, учащиеся, нередко, применяют ее и в случае решения квадратных уравнений с четным коэффициентом при неизвестном в первой степени. Таким образом, большее внимание в процессе обучения следует уделять рациональным способам вычисления корней.
Наиболее часто встречающиеся ошибки в работах учеников 8-го класса при решении квадратных уравнений, относятся к операциям с буквенными коэффициентами. На вопрос, что называется коэффициентом, получаем один ответ: числовой множитель, стоящий перед буквенным выражением. Этот факт подтверждает, что при оперировании с буквами ученики 8-го класса не всегда видят их конкретный смысл. Если бы ученики были приучены контролировать свою работу, они придавали (хотя бы мысленно) численные значения буквам и сами вскрывали свои ошибки. Следовательно, при обучении большее внимание следует обращать на нахождение числовых значений алгебраических выражений и на аналогию в выполнении алгебраических и арифметических действий; тем самым, учащиеся будут привыкать смотреть на буквенное выражение не только как на объект для тождественных преобразований, но и как на функцию входящих в него букв.
Теорема Виета при изучении квадратных уравнений является наиболее сложной темой. Нередкоее смысл учащиеся усваивают формально и не могут применить теорему на практике. Для проверки понимания теоремы и знаний по данной теме, рекомендуется предлагать следующие обучающие-вопросы.
Известно, что сумма двух искомых чисел и ихпроизведение — целые числа. Могут ли эти искомыечисла быть дробными? Объясните на примерах.
Известно, что сумма и произведение корнейквадратного уравнения — целые числа. Могут ли корни этого уравнения быть дробными числами?
Объясните на примерах.
Известно, что сумма корней квадратного уравнения (или сумма двух чисел) — число дробное, а произведение этих чисел — число целое. Могут ли
корни этого уравнения быть целыми числами?
Известно, что сумма корней и их произведение — числа дробные. Могут ли корни данного уравнения быть целыми числами. Приведите примеры для различных случаев.
Дано полное квадратное уравнение неприведенного вида, свободный член и коэффициенты которого не имеют общего множителя. Какими числами может выражаться сумма и произведение его корней? Приведите примеры неприведенных полных квадратных уравнений для случая:
а)когда и сумма, и произведение их корней выражаются дробными числами;
б)когда только сумма или только произведениевыражается дробным числом.
Могут ли в указанных случаях оба корня бытьцелыми?
Изучая ошибки по рассматриваемой теме, мы пришли к выводу, что теорему Виета целесообразно изучать индуктивным путем, исходя из рассмотрения приведенного квадратного уравнения вида x2+рх+q=0. Затем перейти к рассмотрению этого вопроса для неприведенного квадратного уравнения вида ах2 + bх + с = 0 и установить соотношение (-b/a)=p и (c/a)=q
Исследование корней квадратного уравнения по его дискриминанту и коэффициентам, исследование вопроса, будут ли корни данного квадратного уравнения действительными, различными или равными или среди действительных чисел нет корня данного уравнения, не затрудняет учащихся. Обычно, допускаемая ошибка состоит в том, что за дискриминант принимают не подкоренное выражение, а квадратныйкорень из дискриминанта, то есть считают, чтоD=√(b2-4ac) или D1=√((b/2)2—q)при исследовании корнейуравнения школьники часто применяют нерациональный прием, который состоит в том, что дляответа на вопросы: будут ли корни данного квадратного уравнения действительными числами, будут ли они различны или равны, учащиеся вычисляют дискриминант, хотя достаточно только установить его
знак. Заметим еще, что не всегда учащиеся умеют самостоятельно указать квадратное уравнение, заведомо имеющее действительные корни без нахождения числовой величины его дискриминанта. Только после приведения нескольких аналогичных примеров квадратных уравнений с отрицательным свободным членом и наводящего вопроса, учащиеся могут сделать вывод, что в этих случаях всегда D > 0 (сказывается недостаточный навык вычитания отрицательного числа). При определении знаков корней квадратного уравнения не всегда можно получить полное, последовательное, доведенное до логического конца объяснение процесса исследования без наводящих (и даже подсказывающих) вопросов учителя.
Четкость речи, как известно, связана с осознанностью соответствующей мысли. Поэтому при объяснении данного вопроса учитель должен дать четкий образец рассуждений. Прежде всего надо указать, что о знаках корней можно говорить лишь тогда, когда они существуют (во множестве действительных чисел).
Надо убедиться в неотрицательности дискриминанта, причем для этого не следует доводить до конца вычисления, достаточно убедиться, что он не отрицателен (в случае, когда свободный член квадратного уравнения отрицателен, а коэффициент при х2положителен, не надо вычислять дискриминант — он положителен). Затем рассмотреть на примерах все четыре возможных случая: оба корня уравнения отрицательные, положительные, один из корней отрицательный, положительный. Выводы следует оформитьтаблицей.
Вопрос об оперировании с абсолютными величинами остается слабым местом в знаниях учащихся8-го класса. Особое внимание надо обратить на тот факт, что сравнение абсолютных величин корней не легко усваивается школьниками. Следует лишний раз подчеркнуть, что, например, число может быть записано в виде | + 6 |; + 6; | — 6 |; 6. Для достижения хороших результатов можно рекомендовать систему упражнений с использованием наглядности.
Расположите в порядке возрастания (убывания) ряд чисел, среди которых имеются положительные,отрицательные числа и нуль. Покажите на числовой прямой числа : — 2,5; 4; — 3; + 2; — 0,1; 1/2; -3/4; — 1/3.
Расположите в порядке возрастания или убывания абсолютные величины тех же чисел. Сделайте выводы.
Найдите сумму, разность, произведение, частное абсолютных величин двух чисел, если компонентами действий служат различные действительныечисла в различных комбинациях, не исключая и нуля.
Составление квадратного уравнения по формуле(х—х1)(х—х2)=0 подготавливает учеников к дальнейшему изучению теории алгебраических уравнений.Уже первые примеры на квадратные уравнения- учащиеся решают разложением левой его части на линейные множители, делают необходимые выводы и устанавливают связи между различными вопросами одной и той же темы.
К изучению данного учебного материала учащихся следует готовить, начиная с 5-го класса:
При изучении квадрата числа, натуральной степени учащиеся выполняли такие задания: Найти значение выраженияD=b2-4ac, если a=2, b=5, c =4. При изучении десятичных дробей, обыкновенных дробей, отрицательных чисел – a,b,c меняются.
Знание квадратов натуральных чисел от 1 до 20 нужно проверять на протяжении всех лет обучения математики.
К работе по схеме учащиеся готовятся, начиная с устного счета, по цепочке, с указанием порядка действий, с помощью стрелок, по элементарным программам при работе с микрокалькулятором, при прохождении многих тем учащиеся учатся выполнять те, или другие преобразования по алгоритму. У учащихся должны быть отработаны навыки решения линейных уравнений.

«Свидетельство участника экспертной комиссии»
Оставляйте комментарии к работам коллег и получите документ
БЕСПЛАТНО!
Впервые квадратные уравнения сумели решить математики древнего Египта. Вавилоняне умели решать неполные квадратные уравнения, так же частные виды полных квадратных уравнений около 2 тысяч лет до нашей эры. Древнегреческие математики умели решать некоторые виды квадратных уравнений, сводя их к геометрическим построениям. Примеры решения уравнений без использования геометрических знаний дает Диофант Александрийский (3 век). Диофант в своих книгах «Арифметика» изложил способ решения полных квадратных уравнений, однако эти книги не сохранились. В Европе формулы для решения квадратных уравнений были впервые изложены итальянским математиком Леонардо Фибоначчи в 1202 году.

х2 + bх + с = 0 при всевозможных вариациях знаков и коэффициентов b и с.
Франсуа Виет вывел формулы квадратного уравнения в общем виде, однако он работал только с положительными числами.
Тарталья, Кардано, Бомбелли – итальянские ученые, которые среди первых в XVI веке учитывают кроме положительных еще и отрицательные корни.
Выводом формулы решения квадратных уравнений общего вида занимался Виет. Одно свое утверждение он высказывал лишь для положительных корней (отрицательных чисел он не признавал).
После трудов нидерландского математика Альберта Жирара, а также Декарта и Ньютона, методы решения квадратных уравнений приняли современный вид.
Квадратные уравнения
1. Вспомним уже знакомые способы решения и исследования квадратных уравнений:
- выделение полного квадрата;
- по формуле корней для квадратного уравнения;
- по теореме Виета;
- на основании свойств квадратичной функции.
В процессе решения уравнений необходимо следить за множеством допустимых значений неизвестного, т.к. оно может изменяться. В случае его расширения следует проверять найденное решение, не является ли оно посторонним для данного уравнения. В случае, если произошло сужение, необходимо убедиться, не являются ли потерянные значения неизвестных решениями данного уравнения. Процесс нахождения выпавших решений не всегда легко выполним, поэтому желательно избегать сужение множества допустимых значений неизвестных уравнения.
2. Типичные ошибки при решении уравнений.
По правилам можно преобразовывать исходное уравнение в равносильное ему, при этом, вы знаете, что: обе части уравнения можно делить или умножать на одно и то же, отличное от нуля, число.
1) Если уравнение имеет вид f(х) · g(х) = p(х) · g(х), то деление обеих частей на одинаковый множитель g(x), как правило, недопустимо. Данное действие может привести к потере корней: могут быть потеряны корни уравнения g(х) = 0, если ни существуют.
Пример 1.
Решить уравнение 2(х – 3) = (х – 3)(х + 5).
Решение.
Здесь нельзя сокращать на множитель (х – 3).
2(х – 3) – (х – 3)(х + 5) = 0, вынесем общую скобку:
(х – 3)(-х – 3) = 0, теперь
х – 3 = 0 или -х – 3 = 0;
х = 3 или х = -3.
Ответ: -3; 3.
2) Уравнение вида f(х) / g(х) = 0 можно заменить системой:
{f(x) = 0,
{g(x) ≠ 0.
Она равносильна исходному уравнению.
Или можно решить уравнение f(x) = 0, а уже затем исключить найденных корней те, которые обращают в нуль знаменатель g(x).
Встречаются дробно-рациональные уравнения, которые сводятся к квадратным уравнениям.
Пример 2.
Решить уравнение: (х + 3) / (х – 3) + (х – 3) / (х + 3) = 10/3 + 36/(х – 3)(х + 3).
Решение.
Умножив обе части уравнения на общий знаменатель и заменив исходное уравнение целым, получим равносильную систему:
{3(х + 3)2 + 3(х – 3)2 = 10(х – 3)(х + 3) + 3 · 36;
{(х – 3)(х +3) ≠ 0.
В результате получим два корня: х = 3 или х = -3, но х ≠ 3 и х ≠ -3.
Ответ: уравнение корней не имеет.
Пример 3.
Решить уравнение: (х + 5)(х2 + 4х — 5)/(х + 5)(х + 2) = 0.
Решение.
Часто ограничиваются таким решением:
(х2 + 4х – 5) / (х + 2) = 0.
{х = -5, х = 1,
{х ≠ -2.
Ответ: -5; 1.
Правильный ответ: 1.
Пример 4.
При выполнении распространенных заданий на исследование квадратного уравнения следующего вида: «Не вычисляя действительных корней х1 и х2 уравнения 2х2 + 3х + 2 = 0, найти значение х12 + х22» банальная невнимательность приводит к грубой ошибке.
Действительно, по теореме Виета,
х12 + х22 = (х1 + х2)2 – х1х2 = (-3/2)2 – 2 · 1 = 1/4.
Однако, теоремой можно было воспользоваться при существовании действительных корней. В данном примере D < 0 и корней нет.
Ответ: значение х12 + х22 не существует.
Пример 5.
Вычислить отрицательный коэффициент b и корни уравнения х2 + bх – 1 = 0, если с увеличением каждого из этих корней на единицу они становятся корнями уравнения х2 – b2х – b = 0.
Решение.
Пусть х1 и х2 – корни уравнения х2 + bх – 1 = 0. Тогда по т. Виета
х1 + х2 = -b и х1х2 = -1 (*). С другой стороны, по условию
(х1 + 1) + (х2 + 1) = b2 и (х1 + 1)(х2 + 1) = -b.
Перепишем:
х1 + х2 = b2 – 2 и (х1 + 1)(х2 + 1) = -b.
Теперь, учитывая условия (*), получим b2 – 2 = -b, следовательно,
b1 = -2, b2 = 1. По условию подходит b1 = -2.
Значит, исходное уравнение имеет вид х2 – 2х – 1 = 0, корнями являются числа х1,2 = 1 ± √2.
Ответ: b1 = -2, х1,2 = 1 ± √2.
Уравнения, приводимые к квадратным. Биквадратные уравнения
Уравнения вида ах4 + bх2 + c = 0, где а ≠ 0, называются биквадратными уравнениями с одной переменной.
Для решения биквадратного уравнения нужно сделать подстановку х2 = t, найти корни t1 и t2 квадратного уравнения аt2 + bt + c = 0 и решить уравнения х2 = t1 и х2 = t2. Они имеют решения лишь в случае, когда t1,2 ≥ 0.
Пример 1.
Решить уравнение х4 + 5х2 – 36 = 0.
Решение.
Подстановка: х2 = t.
t2 + 5t – 36 = 0. По т. Виета t1 = -9 и t2 = 4.
х2 = -9 или х2 = 4.
Ответ: В первом уравнении корней нет, из второго: х = ±2.
Пример 2.
Решить уравнение (2х – 1)4 – 25(2х – 1)2 + 144 = 0.
Решение.
Подстановка: (2х – 1)2 = t.
t2 – 25t + 144 = 0. По т. Виета t1 = 9 и t2 = 16.
(2х – 1)2 = 9 или (2х – 1)2 = 16.
2х – 1 = ±3 или 2х – 1 = ±4.
Из первого уравнения два корня: х = 2 и х = -1, из второго тоже: х = 2,5 и х = -1,5.
Ответ: -1,5; -1; 2; 2,5.
Таким образом, процесс решения любых уравнений состоит в последовательной замене данного уравнения другим, равносильным ему и более простым уравнением.
Остались вопросы? Не знаете, как решать уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Задание «Проблемы,
типичные ошибки учащихся»
Вспоминается расхожая истина – умные люди
учатся на чужих ошибках. В математике приходится учиться, в основном, на
собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь
необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее
использовать.
Обидно получать плохие оценки из-за ошибок
«на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря
знака, скобки, необоснованное изменение чисел, пропуски переменных и
всевозможные ляпы. Сами ученики порой не могут объяснить, чем вызваны эти
ошибки.
Решая
уравнения и неравенства учащиеся допускают типичные ошибки:
·
Незнание
правил, определений, формул.
·
Непонимание
правил, определений, формул.
·
Неумение
применять правила, определения, формулы.
·
Неверное
применение формул.
·
Невнимательное
чтение условия и вопроса задания.
·
Вычислительные
ошибки.
·
Логические
ошибки
·
Раскрытие
скобок и применение формул сокращенного умножения.
Какие же проблемы, трудности общего
характера возникают у учащихся при изучении математики ( их несомненно можно
отнести и к трудностям, которые возникают у уч-ся при изучении темы «Уравнения
и неравенства»):
·
Пропуски
занятий приводят к незнанию материала, пробелам в знаниях.
·
Поверхностное,
невдумчивое восприятие нового материала приводят к непониманию его.
·
Недостаточная
мозговая деятельность приводит к неумению применять правила, определения и
формулы .
·
Неряшливый,
неаккуратный почерк ученика приводит к досадным ошибкам. Учащиеся не
всегда сами понимают, что именно они написали.
·
Усталость. Чрезмерная
нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и,
как следствие, к многочисленным ошибкам.
·
Кратковременное
или полное переключение внимания с одной деятельности на другую (учебную или
внеучебную) приводит к утрате только что воспринятого материала, приходится все
начинать сначала.
·
Скорость
работы. Низкая
скорость выполнения мыслительных операций часто мешает ученику контролировать
себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь
одной частью задания удаляет из «оперативной памяти» информацию о другой, в
которой допускается не вынужденная ошибка. Скорость работы определяется
физиологией конкретного школьника и навыками выполнения тех или иных операций.
·
Мотивация.
Следствие низкой мотивации – потеря внимания и ошибка.
Ошибки, допускаемые обучающимися при решении уравнений
и неравенств, самые разнообразные: от неверного оформления решения до
ошибок логического характера.
1. Самая типичная ошибка состоит в том, что учащиеся
при решении уравнений и неравенств без дополнительных пояснений используют
преобразования, нарушающие равносильность, что приводит к потере корней
и появлению посторонних корней.
Предлагаю на конкретных примерах рассмотреть ошибки
подобного рода и определить способы их предупреждения и исправления, но прежде
всего хочу обратить внимание на следующую мысль: не надо бояться
приобрести посторонние корни, их можно отбросить путем проверки ,надо бояться
потерять корни.
а) Решить уравнение:
log3(5 – x) = 3 – log3(–1 – x).
Это уравнение учащиеся очень часто решают следующим
образом.
log3(5 – x) = 3 –
log3(–1 – x), log3(5 – x) + log3(–1 – x) = 3, log3((5 – x)(
–1 – x)) = 3, (5 – x)( –1 – x) = 33, x2 – 4x –
32 = 0,
х1 = –4; x2 = 8.
Учащиеся часто, не проводя дополнительных рассуждений,
записывают оба числа в ответ. Но как показывает проверка, число
x = 8 не является корнем исходного уравнения, так как при
x = 8 левая и правая части уравнения теряют смысл. Проверка
показывает, что число x = –4 является корнем заданного
уравнения.
б) Решить уравнение
Область определения исходного уравнения задается системой
Для решения заданного уравнения перейдем к логарифму
по основанию x, получим
Мы видим, что левая и правая части этого последнего
уравнения при x = 1 не определены, но это число является корнем
исходного уравнения (убедиться в этом можно путем непосредственной
подстановки). Таким образом, формальный переход к новому основанию привел
к потере корня. Чтобы избежать потери корня x = 1, следует
указать, что новое основание должно быть положительным числом, отличным от
единицы, и рассмотреть отдельно случай x = 1.
2. Целая группа ошибок, вернее сказать недочетов, состоит
в том, что учащиеся не уделяют должного внимания нахождению области
определения уравнений, хотя именно она в ряде случаев есть ключ
к решению.
3. Типичной ошибкой учащихся является то, что они не
владеют на нужном уровне определениями понятий, формулами, формулировками
теорем, алгоритмами. Хочу подтвердить сказанное следующим примером.
Решить уравнение
Ученик предлагает следующее ошибочное решение этого
уравнения:
х = –2.
Поверка показывает, что х = –2 не является
корнем исходного уравнения.
Напрашивается вывод, что заданное уравнение корней не
имеет.
Однако это не так. Выполнив подстановку х =
–4 в заданное уравнение, мы можем убедиться, что это корень.
Предлагаю проанализировать, почему произошла потеря
корня.
В исходном уравнении выражения х и х +
3 могут быть одновременно оба отрицательными или оба положительными, но
при переходе к уравнению эти же выражения
могут быть только положительными. Следовательно, произошло сужение области
определения, что и привело к потере корней.
Чтобы избежать потери корня, можно поступить следующим
образом: перейти в исходном уравнении от логарифма суммы к логарифму
произведения. Возможно в этом случае появление посторонних корней, но от
них, путем подстановки, можно освободиться.
4. Многие ошибки, допускаемые при решении уравнений
и неравенств, являются следствием того, что учащиеся очень часто пытаются
решать задачи по шаблону, то есть привычным путем. Предлагаю рассмотреть
это на следующем примере.
Решить неравенство
Попытка решать это неравенство привычными
алгоритмическими способами не приведет к ответу. Решение здесь должно
состоять в оценке значений каждого слагаемого левой части неравенства
на области определения неравенства.
Найдем область определения неравенства:
Для всех x из
промежутка (9;10] выражение имеет
положительные значения (значения показательной функции всегда положительны).
Для всех x из
промежутка (9;10] выражение ( x – 9) имеет положительные значения,
а выражение lg(x – 9) имеет значения отрицательные или ноль, тогда
выражение
– (x – 9)
lg(x – 9) положительно или равно нулю.
Окончательно имеем x∈
(9;10]. Хочу заметить, что при таких значениях переменной каждое слагаемое,
стоящее в левой части неравенства, положительно (второе слагаемое может
быть равно нулю), а значит их сумма всегда больше нуля. Следовательно,
решением исходного неравенства является промежуток (9;10].
5. Одна из ошибок связана с графическим решением
уравнений.
Решить уравнение
Некоторые учащиеся, решая это уравнение графически (хочу
отметить, что его другими элементарными способами решить нельзя), получают лишь
один корень (он является абсциссой точки, лежащей на прямой y = x),
ибо графики функций
и
−
это графики взаимно обратных функций.
На самом деле исходное уравнение имеет три корня: один из
них является абсциссой точки, лежащей на биссектрисе первого координатного
угла y = x, другой корень и третий корень
Убедиться
в справедливости сказанного можно непосредственной подстановкой чисел и
в заданное уравнение.
Этот пример удачно иллюстрирует следующий вывод:
графическое решение уравнения f(x) = g(x) “безупречно”, если обе функции «разномонотонны»
(одна из них возрастает, а другая – убывает), и недостаточно
математически корректно в случае одномонотонных функций (обе либо
одновременно убывают, либо одновременно возрастают).
6. Ряд типичных ошибок связан с тем, что учащиеся не
совсем корректно решают уравнения и неравенства на основе функционального
подхода. Остановлюсь на типичных ошибки такого рода.
а) Решить уравнение xх = x.
Функция, стоящая в левой части уравнения, –
показательно-степенная и раз так, то на основание степени следует
наложить такие ограничения: x > 0, x ≠ 1. Прологарифмируем обе
части заданного уравнения:
или
Откуда имеем x = 1.
Логарифмирование не привело к сужению области
определения исходного уравнения. Но тем не менее произошла потеря двух корней
уравнения; непосредственным усмотрением мы находим, что x =
1 и x = –1 являются корнями исходного уравнения.
7. При решении неравенств с помощью подстановки мы
всегда сначала решаем новое неравенство относительно новой переменной,
и лишь в его решении делаем переход к старой переменной.
Школьники очень часто ошибочно делают обратный переход
раньше.Этого делать не следует.
8.Хочу привести пример еще одной ошибки, связанной
с решением неравенств.
Решите неравенство
.
Привожу ошибочное решение, которое очень часто
предлагают учащиеся.
Возведем обе части исходного неравенства в квадрат.
Будем иметь:
,
откуда получаем неверное числовое неравенство , что позволяет сделать
вывод: заданное неравенство не имеет решений.
Однако полученный вывод неверен, например, при
х = 1000 имеем
,
,
.
Полученное числовое неравенство верно, а значит
х = 1000 является решением.
Значит, заданное неравенство имеет решение, и, следовательно,
приведенное выше решение ошибочно.
Привожу правильное решение. Найдем область определения
исходного неравенства. Она задается системой
или
откуда
.
Ясно, что на интервале (10;1000) нет решений, ибо
левая часть заданного неравенства при любом х из этого интервала не имеет
смысла.
Рассмотрим два случая.
а) , откуда х > 100. С учетом области определения
исходного неравенства имеем промежуток . Для всех х из этого промежутка левая часть
исходного неравенства неотрицательна (как значение арифметического квадратного
корня), а правая часть – отрицательна. Делаем вывод о том, что – решение заданного
неравенства.
б) , откуда
. С учетом области определения исходного неравенства имеем
промежуток .
Для всех х из промежутка имеют смысл обе
части неравенства и они имеют неотрицательные значения, значит обе части
заданного неравенства мы можем возвести в квадрат. Будем иметь: , откуда
. Это неверное числовое
неравенство позволяет сделать вывод: значения х из промежутка решениями исходного неравенства не
являются.
Ответ: .
9. Типичная ошибка при решении уравнений, неравенств
и их систем состоит в том, что неверно преобразовываются выражения.
Большинство
ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение
некоторых вычислительных операций до автоматизма несколько снижает вероятность
их появления.
Необходимо
осуществлять процесс обучения правилам с помощью специальной модели с
использованием приема, активизирующего рефлексивную деятельность учащихся по
предупреждению и исправлению ошибок, которые возникают в результате формального
усвоения правил.
Самостоятельная
работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ
собственных действий по решению конкретной задачи, что оказывает благоприятное
влияние на качество получаемых знаний и стимулирует развитие логического
мышления.
Пример
неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет
его корни по хорошо известной формуле, не обращая внимания на недопустимые
значения sin x.
Для
исправления и предупреждения многих ошибок важно сформировать у школьников навыки
самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой
оценки ожидаемого результата.
Каждый
учитель знает, что планомерное и систематическое повторение и есть основной
помощник в ликвидации пробелов, а, следовательно, и ошибок.
Систематические проверки чужих записей
формируют у ученика привычку критически относиться к своему решению. Для этого
подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления
ошибок самими учащимися под руководством учителя можно сделать поучительным для
учащихся.
Самоконтроль
Для исправления и предупреждения многих
ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят
из двух частей:
а) умения обнаружить ошибку;
б) умения её объяснить и исправить.
В процессе обучения применяются несколько
приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и
своевременно их исправить. К ним относятся:
·
проверка
вычисления и тождественного преобразования путём выполнения обратного действия
или преобразования;
·
проверка
правильности решения задач путём составления и решения задач, обратных к
данной;
·
оценка
результата решения задачи с точки зрения здравого смысла;
·
проверка
аналитического решения графическим способом.
Способы
исправления и предупреждения ошибок
Свести
ошибки к минимуму способствуют следующие профилактические меры:
- Тексты письменных заданий должны быть
удобными для восприятия: грамотно сформулированными, хорошо читаемыми. - Активная устная отработка основных
ЗУН, регулярный разбор типичных ошибок. - При объяснении нового материала
предугадать ошибку и подобрать систему заданий на отработку правильного усвоения
понятия. Акцентировать внимание на каждом элементе формулы, выполнение
разнотипных заданий позволит свести ошибочность к минимуму. - Подбирать задания, вызывающие
интерес, формирующие устойчивое внимание. - Прочному
усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для
запоминания, четкие алгоритмы, следуя которым заведомо придешь к
намеченной цели.
Каждый
учитель знает, что планомерное и систематическое повторение и есть основной
помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как
ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и
понимание последующего невозможно без знания предыдущего, отсюда неизбежность
повторения на каждом уроке. При объяснении нового материала следует использовать
ряд определений и теорем, которые были изучены ранее.
- Авторы
- Файлы
- Ключевые слова
- Литература
Беляева Е.Р.
1
1 МБОУ ШР «СОШ №2»
подготовка к огэ по математике
анализ ошибок
уравнения
1. Марков С.Н., Осипенко Л.А., Лапшина Е.С. Результаты государственной итоговой аттестации в форме основного государственного экзамена по математике в Иркутской области в 2017 году. Методические рекомендации. – И: ГАУ ДПО ИРО, 2017. – 23с.
2. Лапшина Е. С., Марков С. Н., Осипенко Л. А. Результаты государственной итоговой аттестации в форме основного государственного экзамена по математике в Иркутской области в 2018 году. Методические рекомендации.– И: ГАУ ДПО ИРО, 2018. – 42 с.
3. Гаер М. А., Лапшина Е. С., Марков С. Н. Результаты государственной итоговой аттестации в форме основного государственного экзамена по математике в Иркутской области в 2019 году. Методические рекомендации. – И: ГАУ ДПО ИРО, 2019. – 38 с.
Введение
Структура Контрольно-измерительных материалов ОГЭ отвечает цели построения системы дифференцированного обучения математике в современной школе. Дифференциация обучения направлена на решение двух задач: формирования у всех обучающихся базовой математической подготовки, составляющей функциональную основу общего образования, и одновременного создания условий, способствующих получению частью обучающихся подготовки повышенного уровня, достаточной для активного использования математики во время дальнейшего обучения, прежде всего при изучении её в средней школе на профильном уровне.
Чтобы быть зачисленным в профильный 10 класс на базе нашего учебного учреждения, необходимо сдать успешно экзамены по итогу 9-го класса. Успешно для меня – это значит на «отлично». Критерии оценивания экзамена по математике таковы: чтобы получить отметку «отлично», необходимо набрать минимум 22 балла. Это становится возможным лишь тогда, когда выпускник приступает к решению заданий с развёрнутым ответом с №20 — №25.
Со слов сверстников, я знаю, что не все педагоги, работающие в общеобразовательных школах, рассматривают с обучающимися задания повышенного уровня сложности, анализ типичных ошибок, которые допускают выпускники прошлых лет.
Мой вклад в решение данного проблемного вопроса заключается в том, что я предлагаю своим ровесникам, на основании моей работы, рассмотреть типичные ошибки выпускников, и самостоятельно закрепить материал, подготовиться к экзамену с помощью предложенных заданий. Мной были проанализированы КИМы с 2016-2019 годы.
Обзор литературы
Вопрос типичных ошибок, которые допускают выпускники, в тех или иных заданиях, особенно 2 части, рассматривается педагогами на совещаниях по итогам ГИА. Я не нашла ни одной исследовательской работы по данному направлению, которая была бы предложена учащимися. В основном данный проблемный вопрос представлен в виде педагогических статей.
По рекомендации своего руководителя основным источником исследования стали «Методические рекомендации результатов государственной итоговой аттестации в форме основного государственного экзамена по математике в Иркутской области», которые издаются Государственным автономным учреждением дополнительного профессионального образования Иркутской области «Институт развития образования Иркутской области».
Цель
Анализ типичных ошибок выпускников в решении задания №20 (2 часть) по теме «Уравнения».
Методы исследования
1.Поисковый.
2. Анализ, синтез (отбор необходимой информации, обобщение)
3.Практический
Результаты исследования
Спецификация контрольно измерительных материалов ОГЭ по математике.
Я рассмотрела спецификацию контрольных измерительных материалов для проведения ОГЭ. И сделала вывод, что задание №20 проверяет умение учащегося выполнять преобразования алгебраических выражений, решать уравнения. Задание №20 относится к повышенному уровню сложности и оценивается на 2 балла. Задания, оцениваемые в 2 балла, считаются выполненными верно, если обучающийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется полный балл, соответствующий данному заданию. Если в решении допущена ошибка, не имеющая принципиального характера и не влияющая на общую правильность хода решения, то участнику выставляется 1 балл.
Задание №20 подразделяется на:
-алгебраические выражения;
-уравнения;
-неравенства;
-системы неравенств;
-системы уравнений.
На данном этапе мной рассмотрены и представлены в работе:
Уравнения:
· Иррациональные.
· Дробно-рациональные.
· Уравнения, приводимые к квадратным.
· Применение свойств при решении уравнений.
Таблица 1
Основная статистика по выполнению задания №20 учащимися 9-х классов Иркутской области.
|
№ задания |
Содержание задания |
Процент участников, набравших максимальный балл по заданию |
|||
|
2016 |
2017 |
2018 |
2019 |
||
|
21 * |
Решить уравнение или систему уравнений |
6,4 |
21,1 |
10,6 |
14,8 |
*До 2020 года задание №20 значилось под №21. Изменения произошли в контрольно-измерительных материалах в 2020-2021 учебном году.
Приведённая статистика говорит о том, что в среднем лишь 13% выпускников справляются с заданием №20. [3:19]
Содержание задания №20 по годам. Типичные ошибки выпускников.
2016 год
Решите уравнение:
Поскольку приём использования в решении уравнений свойств отрабатывается в школе редко, с заданием справились лишь 6,4% учащихся Иркутской области.
2017 год
Решите уравнение:
Типичные ошибки выпускников:
1.Вычислительные ошибки
2.Ошибки в формуле нахождения корней квадратного уравнения
3.Распостранённая ошибка в представлении ответа. Множество из двух корней уравнения описывалось как упорядоченная пара 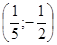
4.Обучающиеся записывали корни в виде десятичных дробей и отбрасывали из ответа те из них, которые имели ненулевой период.
О критериях оценивания:
Решение, в котором была допущена вычислительная ошибка, но с ее учетом доведенное до конца, оценивалось в 1 балл.
Подчеркну, что ошибка в формуле нахождения корней квадратного уравнения не является вычислительной, и за ее допущение ставится 0 баллов.
Правильное решение с ошибкой в форме представления ответа – 1 балл.
Появление лишних корней в ответе в результате логической (не вычислительной) ошибки – 0 баллов.[1:15]
2018 год
Решите уравнение:
Типичные ошибки выпускников:
1) Основные ошибки в решении задачи 21 связаны с областью допустимых значений переменной, входящей в уравнение. Ошибка, как правило, заключалась либо в неэквивалентном преобразовании уравнения, произведенном без учета ограничения на область допустимых значений переменной, либо в неправильном определении (возможно, описании) области допустимых значений. Ошибки такого рода не относятся к вычислительным. Решение в таком случае оценивается в 0 баллов.
2) Вычислительные ошибки.
О критериях оценивания:
Решение, в котором была допущена вычислительная ошибка, но с ее
учетом доведенное до конца, оценивалось в 1 балл.
Подчеркну, что ошибка в определении области допустимых значений переменной не является вычислительной и за ее допущение ставится 0 баллов.
Появление лишних корней в ответе в результате логической (не вычислительной) ошибки – 0 баллов. [2:15]
Рисунок 1
Вывод: данное уравнение решено верно. Обучающийся получил максимальное количество баллов.
Рисунок 2
Вывод: в данном примере решения уравнения учащийся не определил ОДЗ и не учёл его при ответе. Оценка эксперта 0 баллов.
Рисунок 3
Вывод: здесь учащимся определена область допустимых значений, но неправильно: упущен случай равенства 5. Оценка эксперта 0 баллов.
2019 год
Решите уравнение:
Типичные ошибки выпускников:
1.Вычислительные ошибки
2.Второй класс ошибок касается применения метода введения вспомогательной неизвестной при решении уравнения. [3:20]
Рисунок 4
Вывод: уравнение выпускником решено верно. Оценка эксперта 2 балла.
Банк заданий №20
Тщательно разобравшись в решении новых для меня уравнений, сделав анализ типичных ошибок выпускников, предлагаю небольшой банк заданий, который поможет моим сверстникам отработать задание №20.
Иррациональные уравнения (2019 год)
Решите уравнение:
Решение:
Поскольку подкоренное выражение не может быть меньше нуля, по свойству арифметического корня, область допустимых значений ограничивается выражением 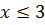
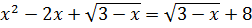
при уничтожении корней получаем:
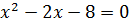
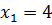
Решением искомого уравнения является только 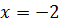
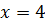
Ответ: 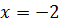
Решите уравнения самостоятельно:
a) 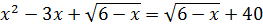
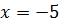
b)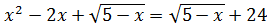
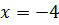
c) 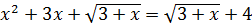
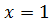
d) 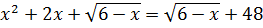
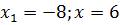
Применение свойств при решении уравнений (2016 год)
Решите уравнение: 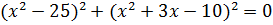
Решение:
Квадрат любого числа неотрицателен. Сумма двух неотрицательных чисел равна нулю, только если они оба равны нулю. Получаем систему уравнений:
Так как системе удовлетворяет только 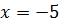
Ответ: 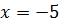
Решите уравнения самостоятельно:
a) 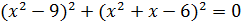
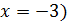
b) 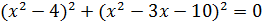
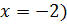
c) 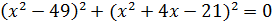
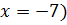
d) 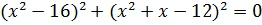
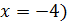
Дробно-рациональные уравнения (2017 год)
Решите уравнение:
Решение:
Так как на ноль делить нельзя, обозначаем область допустимых значений 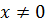
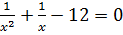
Решением через дискриминант получаем:
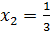
Сверим корни с ОДЗ, не входят. Соответственно в ответе записываем оба корня.
Ответ: 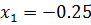
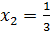
Второй способ: замена переменной
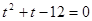
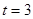
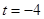
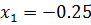
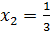
Второй способ решения был предложен составителями экзаменационных материалов. Его применяет подавляющее большинство обучающихся.
Решите уравнения самостоятельно:
a) 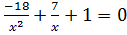
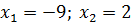
b) 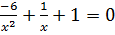
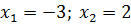
c) 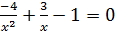
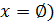
d) 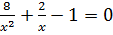
Библиографическая ссылка
Беляева Е.Р. АНАЛИЗ ТИПИЧНЫХ ОШИБОК В РЕШЕНИИ УРАВНЕНИЙ, ПРЕДЛАГАЕМЫХ В КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫХ МАТЕРИАЛАХ ОГЭ. ЗАДАНИЕ №20. МАТЕМАТИКА // Международный школьный научный вестник. – 2021. – № 2.
;
URL: https://school-herald.ru/ru/article/view?id=1423 (дата обращения: 13.02.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, которое содержит переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.
А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Квадратные уравнения могут иметь два корня, один корень или не иметь корней.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b2 − 4ac. А вот свойства дискриминанта:
- если D < 0, корней нет;
- если D = 0, есть один корень;
- если D > 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Разобраться в теме еще быстрее с помощью опытного преподавателя можно
на курсах по математике в онлайн-школе Skysmart.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.
Давайте-ка на примерах — вот у нас есть два уравнения:
- x2 — 2x + 6 = 0
- x2 — x — 1/4 = 0
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x2 ), а значит уравнение называется приведенным.
- 2x2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Запоминаем!
У преобразованного уравнения те же корни, что и у первоначального. Ну или вообще нет корней.
Пример 1. Превратим неприведенное уравнение: 8x2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x2 + 2,5x — 1,125 = 0.
Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
| Для самых любопытных объясняем откуда появились такие названия: |
|---|
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. |
Решение неполных квадратных уравнений
Как мы уже знаем, есть три вида неполных квадратных уравнений:
- ax2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
- ax2 + c = 0, при b = 0;
- ax2 + bx = 0, при c = 0.
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.
Как решить уравнение ax2 = 0
Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax2 = 0.
Уравнение ax2 = 0 равносильно x2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x2 = 0 является нуль, так как 02 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax2 = 0 имеет единственный корень x = 0.
Пример 1. Решить −6x2 = 0.
Как решаем:
- Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
- По шагам решение выглядит так:
−6x2 = 0
x2 = 0
x = √0
x = 0
Ответ: 0.
Как решить уравнение ax2 + с = 0
Обратим внимание на неполные квадратные уравнения вида ax2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax2 + c = 0:
- перенесем c в правую часть: ax2 = — c,
- разделим обе части на a: x2 = — c/а.
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.
Если — c/а < 0, то уравнение x2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = — c/а не является верным.
Если — c/а > 0, то корни уравнения x2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = — c/а. Ура, больше у этого уравнения нет корней.
| В двух словах |
|---|
|
Неполное квадратное уравнение ax2 + c = 0 равносильно уравнению х2= -c/a, которое:
|
Пример 1. Найти решение уравнения 8x2 + 5 = 0.
Как решать:
- Перенесем свободный член в правую часть:
8x2 = — 5
- Разделим обе части на 8:
x2 = — 5/8
- В правой части осталось число со знаком минус, значит у данного уравнения нет корней.
Ответ: уравнение 8x2 + 5 = 0 не имеет корней.
Как решить уравнение ax2 + bx = 0
Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Неполное квадратное уравнение ax2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:
-
Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
-
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное квадратное уравнение ax2 + bx = 0 имеет два корня:
- x = 0;
- x = −b/a.
Пример 1. Решить уравнение 0,5x2 + 0,125x = 0
Как решать:
- Вынести х за скобки
х(0,5x + 0,125) = 0
- Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
- Решить линейное уравнение:
0,5x = −0,125,
х = −0,125/0,5 - Разделить:
х = −0,25
- Значит корни исходного уравнения — 0 и −0,25.
Ответ: х = 0 и х = −0,25.
Как разложить квадратное уравнение
С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:
Формула разложения квадратного трехчлена
Если x1 и x2 — корни квадратного трехчлена ax2 + bx + c, то справедливо равенство ax2 + bx + c = a (x − x1) (x − x2).
Дискриминант: формула корней квадратного уравнения
Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:
где D = b2 − 4ac — дискриминант квадратного уравнения.
Эта запись означает:
,
.
Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.
Алгоритм решения квадратных уравнений по формулам корней
Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax2 + bx + c = 0:
- вычислить его значение дискриминанта по формуле D = b2−4ac;
- если дискриминант отрицательный, зафиксировать, что действительных корней нет;
- если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
- если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!
Примеры решения квадратных уравнений
Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.
Пример 1. Решить уравнение −4x2 + 28x — 49 = 0.
Как решаем:
- Найдем дискриминант: D = 282 — 4(-4)(-49) = 784 — 784 = 0
- Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
- Найдем корень
х = — 28/2(-4)
х = 3,5
Ответ: единственный корень 3,5.
Пример 2. Решить уравнение 54 — 6x2 = 0.
Как решаем:
- Произведем равносильные преобразования. Умножим обе части на −1
54 — 6x2 = 0 | *(-1)
6x2 — 54 = 0
- Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
6x2 = 54
х2 = 9
х = ±√9
х1 = 3, х2 = — 3
Ответ: два корня 3 и — 3.
Пример 3. Решить уравнение x2— х = 0.
Как решаем:
- Преобразуем уравнение так, чтобы появились множители
х(х — 1) = 0
х₁ = 0, х₂ = 1
Ответ: два корня 0 и 1.
Пример 4. Решить уравнение x2— 10 = 39.
Как решаем:
- Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
x2— 10 = 39
x2= 39 + 10
x2= 49
х = ±√49
х₁ = 7, х₂ = −7
Ответ: два корня 7 и −7.
Пример 5. Решить уравнение 3x2— 4x+94 = 0.
Как решаем:
- Найдем дискриминант по формуле
D = (-4)2 — 4 * 3 * 94 = 16 — 1128 = −1112
- Дискриминант отрицательный, поэтому корней нет.
Ответ: корней нет.
В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.
Формула корней для четных вторых коэффициентов
Рассмотрим частный случай. Формула решения корней квадратного уравнения 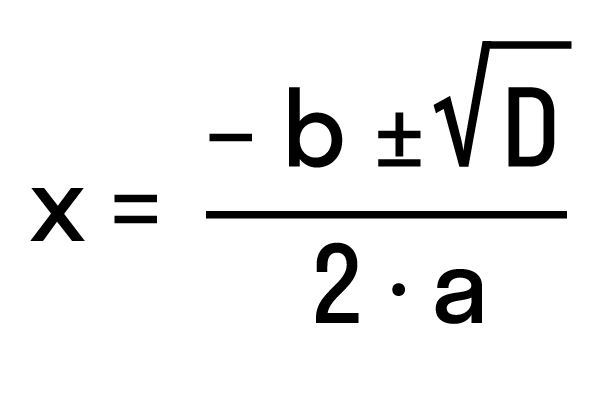
Например, нам нужно решить квадратное уравнение ax2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)2— 4ac = 4n2 — 4ac = 4(n2— ac) и подставим в формулу корней:
Для удобства вычислений обозначим выражение n2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:
где D1 = n2— ac.
Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.
Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
- вычислить D1= n2— ac;
- если D1< 0, значит действительных корней нет;
- если D1= 0, значит можно вычислить единственный корень уравнения по формуле x = -n/a;
- если же D1> 0, значит можно найти два действительных корня по формуле
Формула Виета
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Теорема Виета
Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Если дано x2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x2 + 4x + 3 = 0.
Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:
Обратная теорема Виета
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x2 + bx + c = 0.
Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.
Пример 1. Решить при помощи теоремы Виета: x2 − 6x + 8 = 0.
Как решаем:
- Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
- Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.
Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам:
- Значит числа 4 и 2 — корни уравнения x2 − 6x + 8 = 0. p>
Упрощаем вид квадратных уравнений
Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.
Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x2 — 4 x — 6 = 0, чем 1100x2 — 400x — 600 = 0.
Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x2 — 400x — 600 = 0, просто разделив обе части на 100.
Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.
Покажем, как это работает на примере 12x2— 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x2 — 7x + 8 = 0. Вот так просто.
А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения
умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x2 + 4x — 18 = 0.
Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x2— 3x + 7 = 0 перейти к решению 2x2 + 3x — 7 = 0.
Связь между корнями и коэффициентами
Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:
Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.
Например, можно применить формулы из теоремы Виета:
- x₁ + x₂ = — b/a,
- x₁* x₂ = c/a.
Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x2— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.
Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты: