Точность прогноза считается хорошей при значениях средней относительной ошибки

Наряду с
характеристиками адекватности модели
при оценивании качества модели необходимо
учитывать ее точность.

Как
правило, о точности модели и прогноза
судят по величине погрешности (ошибки).
Ошибка прогноза
это расхождение между
фактическим
и прогнозируемым значением исследуемого
показателя. Использование данного
подхода к оценке точности возможно
только в том случае, когда период
упреждения закончился, и исследователи
имеют фактические значения на период
упреждения или когда разрабатывается
ретропрогноз.

Ретроспективное
прогнозирование разрабатывается для
некоторого момента времени в прошлом,
для которого имеются фактические данные.
В этом случае имеющаяся информация
делится на две части. Первая часть,
включающая более ранние данные,
используется для подбора математической
модели. По построенной математической
модели дается прогноз на последующий
оставшийся период времени. Прогнозные
качества модели оцениваются по более
поздним данным второй части ряда.
Полученные ошибки прогноза в какой-то
мере харак­теризуют точность подобранных
моделей и могут использоваться при
сопоставлении различных моделей
прогнозирования. В то же время при
использовании ошибки ретроспективного
прогноза в качестве меры точности
необходимо учитывать, что она получена
при использовании только части имеющихся
данных. При использовании полного объема
имеющихся данных трансформируется вид
подобранной модели, и изменяются значения
критериев точности и качества.

Отметим,
что если ретроспективное прогнозирование
осуществляется по модели, содержащей
одну или несколько экзогенных пере­менных,
точность прогноза будет определяться
точностью определения значения этих
переменных на пе­риод упреждения. В
этом случае возможны два способа
определения значений экзогенных
переменных: либо воспользоваться
фактическими известными значениями
экзогенных переменных либо ожидаемыми
их значениями. Естественно, что точность
прогноза в первом случае будет выше.

Наличие данных о
реализации прогнозов дает возможность
оценить качество прогнозов величиной:

,

где
р – число
прогнозов, подтвержденных фактическими
данными (фактическая реализация охвачена
интервальным прогнозом);

q
– число прогнозов, не подтвержденных
фактическими данными.

Использование
коэффициентов

для разных моделей имеет смысл в том
случае, если доверительные вероятности
прогнозов приняты одинаковыми.

В том случае, если
прогноз дается в виде точечной оценки,
в качестве показателей точности прогноза
могут использоваться такие статистические
характеристики как средняя абсолютная
и среднеквадратическая ошибка прогноза.

Г.
Тейлом предложен в качестве меры качества
прогноза коэффициент расхождения (или
коэффициент несоответствия):

,

где

— соответственно предсказанное и
фактическое значение переменной.
Коэффициент
,
когда
(случай совершенного
прогнозирования). Коэффициент
,
когда экстраполяция строится исходя
из неизменности приростов. Коэффициент

,
прогноз дает худшие результаты, чем
прогноз методом
простой экстраполяции.

Рассмотренные
выше показатели точности прогноза можно
использовать только
в случае наличия истинных значений
величин, оцениваемых при разработке
прогноза. Согласно этому различают
апостериорную
точность моделей, которая
может быть определена только после
практического использова­ния модели,
и априорную
точность моделей. Априорную или
предполагаемую точность оценива­ют
в условиях отсутствия информации о
результатах эксплуа­тации модели.
Исследуя априорную точность модели, мы
охарактеризуем только точность
аппроксимации.

Чаще
всего в качестве показателей точности
применяются следующие показатели:
абсолютная ошибка
,
средняя абсолютная ошибка
,
средняя квадратическая ошибка
,
относительная ошибка
,
средняя относительная ошибка
,
коэффициент сходимости, коэффициент
детерминации

Абсолютная
ошибка прогноза определяется как
раз­ность между фактическим значением
и его оценкой, полученной расчетным
путем по модели:

,

среднее
абсолютное значение ошибки:

.

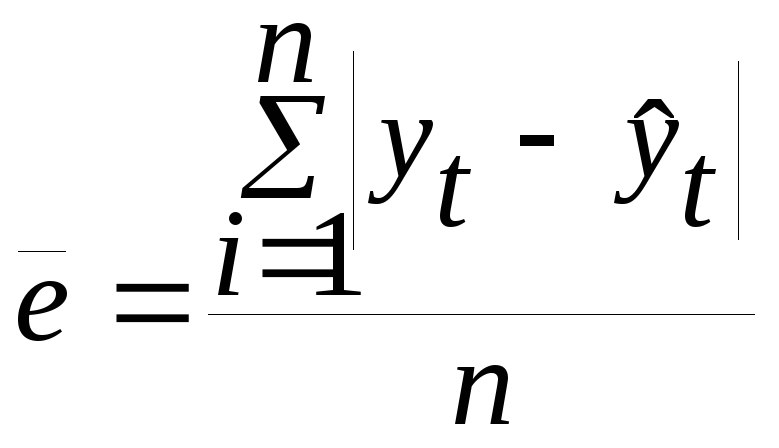
Средняя
квадратическая ошибка прогноза
рассчитывается по формуле:

,

где
п
— период
упреждения,

k
– число оцениваемых параметров модели.

Недостатком
рассмотренных характеристик является
их зависимость от масштаба измерения
значений исследуемого показателя.

В
связи с этим более удобными являются
относительные значения этих величин.
Относительная ошибка рассчитывается
следующим образом:

,

а средняя
относительная ошибка определяется
следующим образом:

.

Последний
показатель чаще других используется
при сравнении точности прогнозов,
осуществляемых по различным методикам.
Обычно лучшим признается тот прогноз,
который имеет меньшее значение этого
показателя. Принято считать, что если
значение средней относительной ошибки
менее 3-5%, то точность хорошая; если
значение средней относительной ошибки
не превышает 10%, то точность хорошая; от
10% до 15% точность удовлетворительная.

Коэффициент
сходимости определяется по следующей
формуле:

,

чем меньше значение
коэффициента сходимости, чем лучше
точность модели.

Коэффициент
детерминации определяется по формуле:

,

и поэтому чем
больше значение коэффициента детерминации,
тем лучше точность модели.

Для
выбора лучшей модели можно использовать
один из рассмотренных показателей либо
воспользоваться обобщенным критерием.

Пример.
Оценить адекватность и точность модели
Хольта, построенной в параграфе 5.3.

Решение. В таблице
5.2 приведены ошибки аппроксимации
,
на основе которых будет оцениваться
адекватность модели. Проверку
случайности колебаний уровней остаточной
компоненты проведем, используя критерий
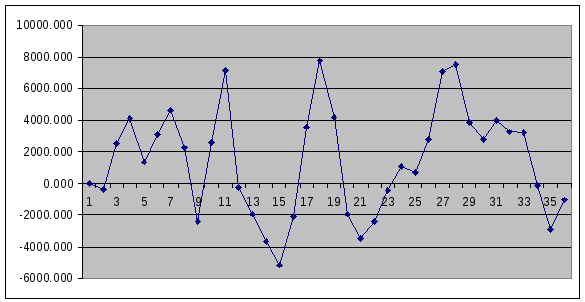
поворотных точек. На рис. 6.2 представлен
ряд остатков, количество поворотных
точек равно 15.

Рис. 6.2. Оценка
адекватности модели. Ряд остатков.

При
n=36:
.
Неравенства 15>17 не выполняется,
следовательно, ряд остатков не является
случайным.

Анализ
соответствия ряда остатков нормальному
закону распределения проведем по RS
– критерию:

.

Расчетное
значение RS
– критерия сравним с табличными
значениями RS
– критерия (таб. 6.1) . Расчетное RS
– критерия попадает в интервал,
ограниченный табличными значениями
(3,6; 5,06), и с уровнем значимости α=0,05
гипотеза о
нормальности распределения остаточной
компоненты принимается.

Так
как остаточная компонента распределена
по нормальному закону, то осуществим
проверку равенства математического
ожидания остаточной компоненты нулю
с помощью t-критерия
Стьюдента:

Расчетное
значениеt-критерия
больше табличного
значения t_α
статистики
Стьюдента
,
следовательно,гипотеза
о равенстве нулю математического
ожидания уровней ряда остатков не
принимается.

Независимость уровней в ряде остатков
проверим по критерию Дарбина–Уотсона
(таб. 6.3).

Таблица 6.3

Расчет d—значенияДарбина–Уотсона

Расчетное
d—значение
равно:

.

Расчетное
значение
d—критерия
сравним с двумя табличными значениями
Дарбина—Уотсона
(1,41; 1,52). Так как расчетное d-значение
меньше нижнего табличного значения
d₁=1,41,
то гипотеза о
независимости ряда остатков отвергается
и модель неадекватна.

Результаты оценки
модели на адекватность приведены в
таблице 6.4.

Таблица 6.4

Результаты
оценки модели на адекватность

Проверяемое свойство	вывод
Случайность	неадекватна
Нормальность	адекватна
Среднее	неадекватна
Независимость	неадекватна
Вывод: модель статистически неадекватна

Средняя
относительная ошибка равна (таб. 5.2):

.

Оцениваемая модель
не является адекватной, и несмотря на
хорошую точность не может использоваться
для прогнозирования.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Существует множество моделей прогноза, но как выбрать среди них ту, которая наиболее точно сделает прогноз?

Из данной статьи вы узнаете:

1. Какие способы оценки прогноза вы можете использовать?
2. Как выбрать оптимальную модель, которая поможет вам сделать максимально точный прогноз?
3. Как рассчитать показатель «Точность прогноза»?

Какие способы оценки прогнозной модели вы можете использовать:

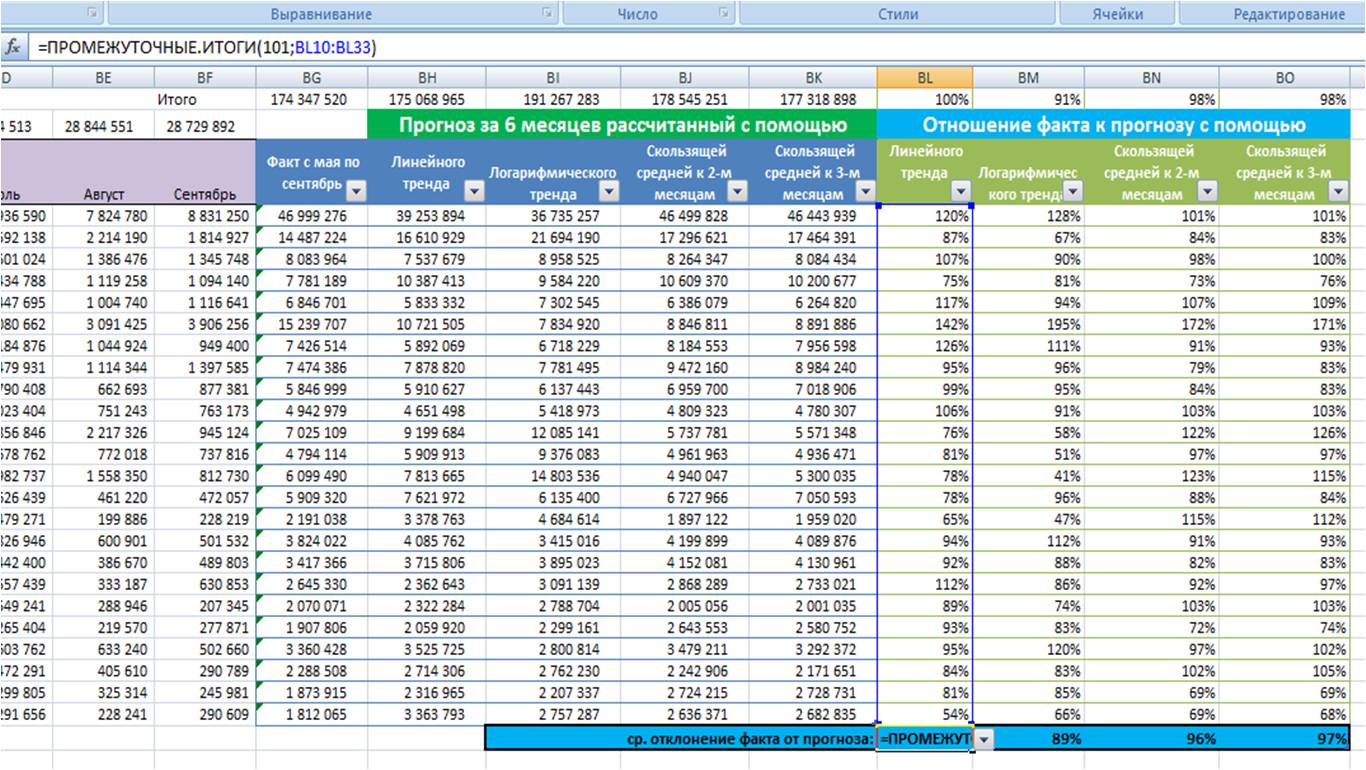
1.  Оценить отношение фактических продаж к прогнозу;

2. Расчет показателя точность прогноза — оценка на сколько точно выбранная модель описывает анализируемые данные;

3. Графический анализ — строим график и визуально оцениваем адекватность модели прогноза относительно фактических продаж за последний период ;
 

1-й способ — Расчет отношения фактических продаж к прогнозу.

Сначала рассчитываем прогноз разными способами и оцениваем отношение фактических продаж к прогнозу. ВАЖНО протестировать модели не по одному товару или направлению продаж, а сразу взять 10 и более товарных позиций или направлений продаж и рассчитать прогноз по ним на минимум на 3 периода вперед (количество периодов и направления прогноза зависят от ваших задач. Если задача — сделать точный прогноз на 6 месяцев, то рассчитываем прогноз на 6 месяцев несколькими вариантами и оцениваем отношение факта к прогнозу по сумме полугода).

Рассчитаем прогноз 4 способами на полгода. Протестируем следующие модели:

1. Линейный тренд + сезонность — лист «Линейный» в приложенном файле (см. статью «Как рассчитать прогноз с учетом роста и сезонности в Excel»)

2. Логарифмический тренд + сезонность — лист «Логарифмический» в приложенном файле (см. статью «5 способов расчета значений логарифмического тренда»)

3. Скользящая средняя с сезонностью к 2-м месяцам — лист «Скользящая к 2-м» (см. статью «Как рассчитать прогноз по методу скользящей средней»);

4. Скользящяя средняя с сезонностью к 3-м месяцам — лист «Скользящая к 3-м»;

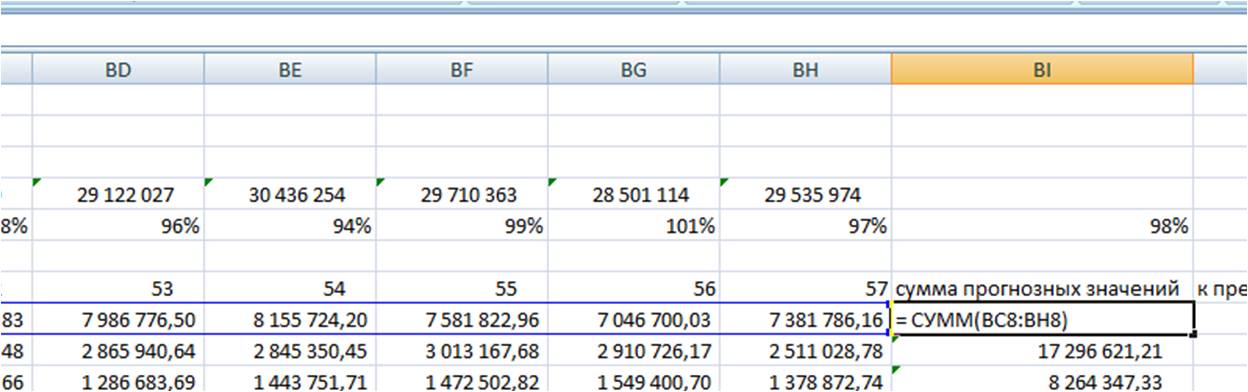
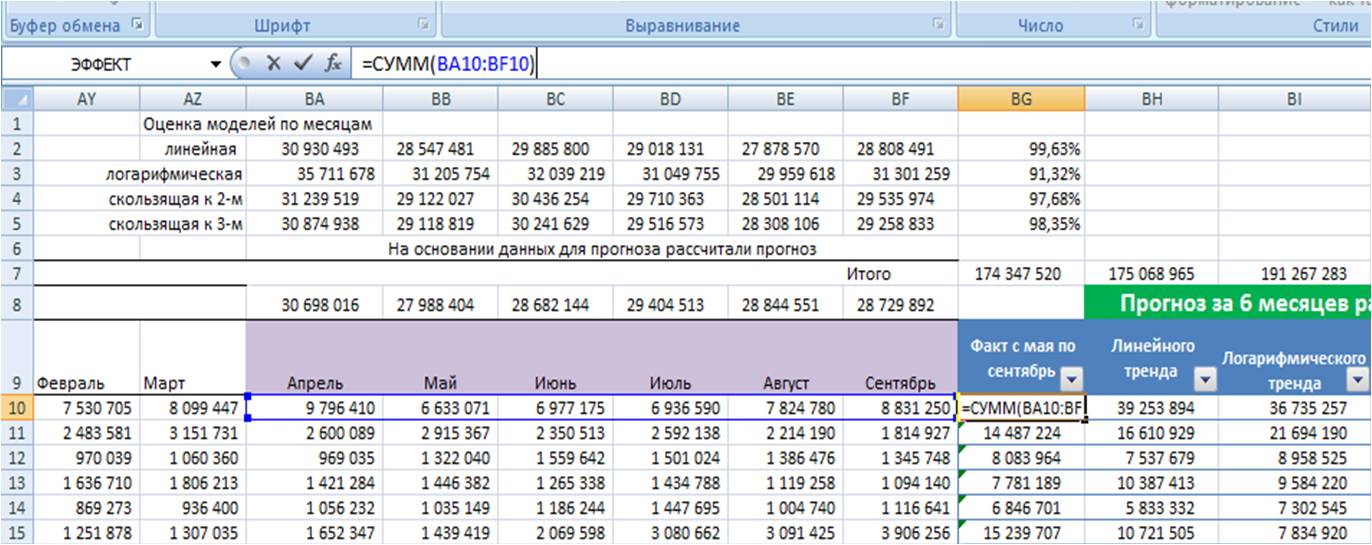
Для каждой из 4-х прогнозных моделей в листе «Оценка моделей»:

• Суммируем прогноз по каждой модели за 6 месяцев;

• Суммируем фактические продажи, которые мы будем сравнивать с прогнозом;

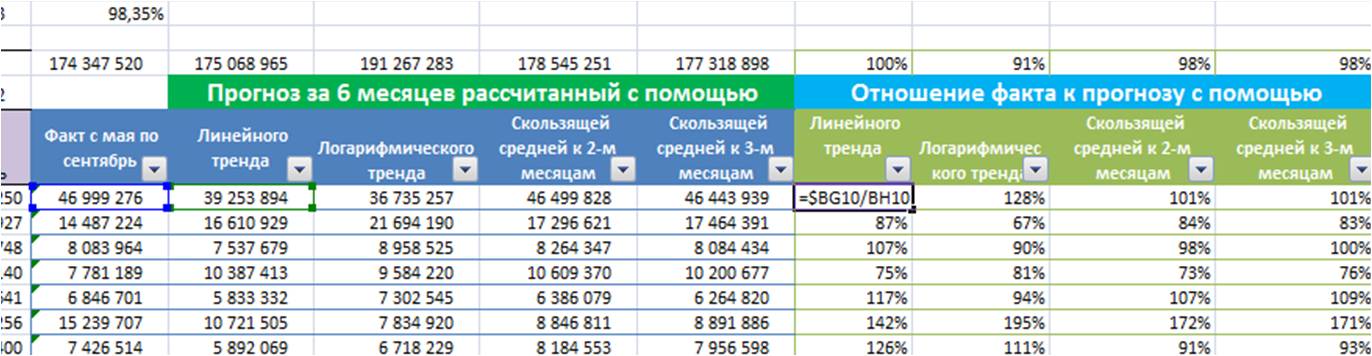
• Рассчитываем отношение факта к прогнозу по каждой позиции для каждой модели;

• Рассчитываем по каждой модели среднее отношение факта к прогнозу;

• Выбираем модель прогноза, которая по показателю «среднее отношение факта к прогнозу» оказалась максимально приближена к 100%;

Для наших данных самой точной моделью оказалась скользящая средняя к 3-м месяцам с сезонностью, среднее отклонение факта от прогноза 97%.

Мы протестировали каждую модель прогноза на реальных данных и выбрали для себя оптимальную, которая в среднем показала минимальное отклонение от факлических продаж.

2-й способ оценки модели прогноза — расчет показателя точность прогноза.

Показатель точность прогноза показывает, на сколько точно выбранная модель прогноза описывает данные. Идея в том, чем точнее выбранная модель описывает фактические данные, тем точнее она сделает прогноз.

Как рассчитать точность прогноза? Рассмотрим на примере расчета для модели прогноза с линейным трендом и сезонностью.

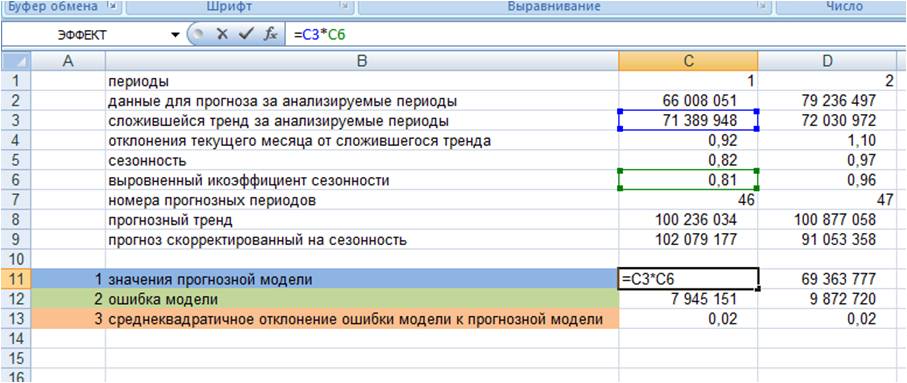
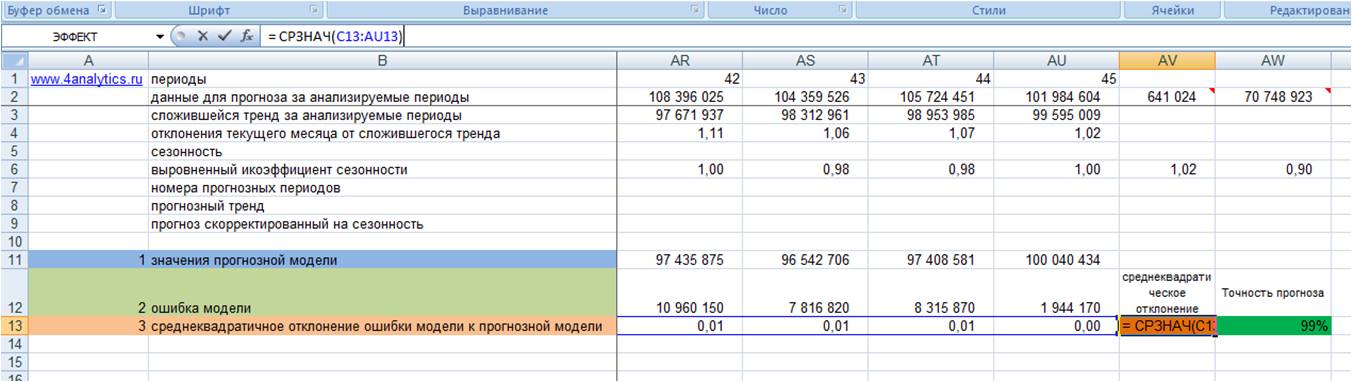
1. Рассчитываем значения прогнозной модели для каждого анализируемого момента времени в прошлом.

Для этого значения тренда для анализируемых периодов умножаем на выровненные коэффициенты сезонности (см. файл с примером)

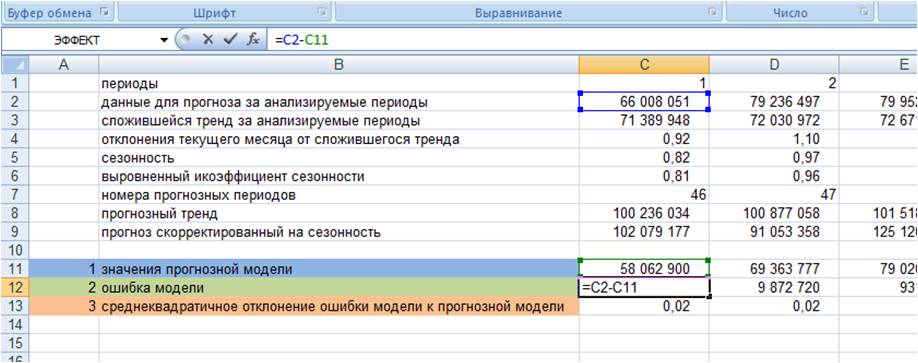
2. Рассчитываем ошибку прогнозной модели. Для этого за каждый период от фактических значений вычитаем значения прогнозной модели.

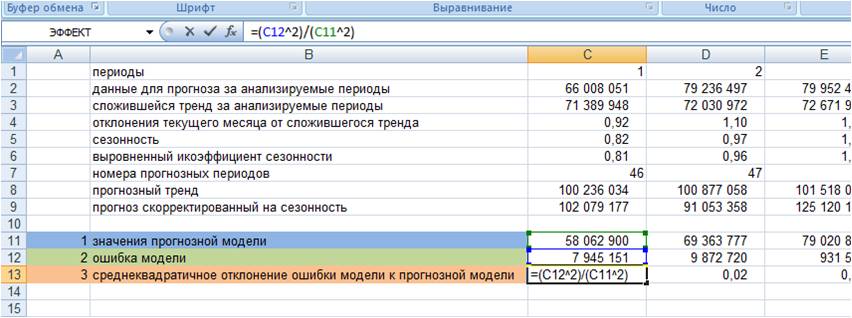
3. Рассчитываем квадратическое отклонение ошибки от значений прогнозной модели (см. файл с примером);

4. Рассчитываем среднее значение квадратического отклонения, т.е. среднеквадратическое отклонение

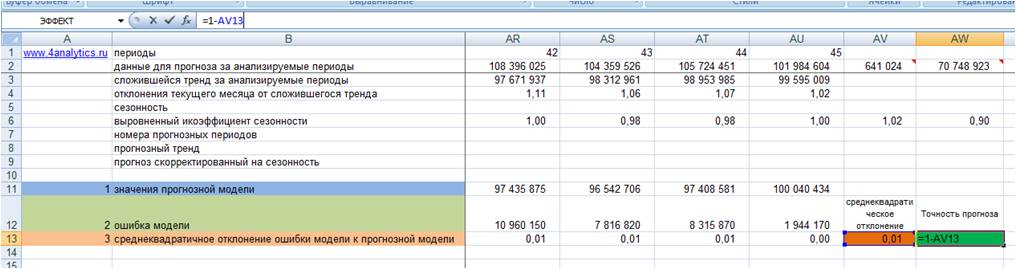
5. Точность прогноза = (1- среднеквадратическое отклонение ошибки прогнозной модели)*100 (см. файл с примером).

Показатель точности прогноза выражается в процентах:

• Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно.

• Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.

 Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда.

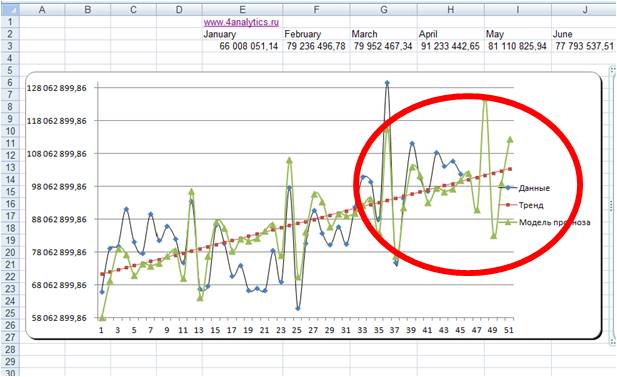
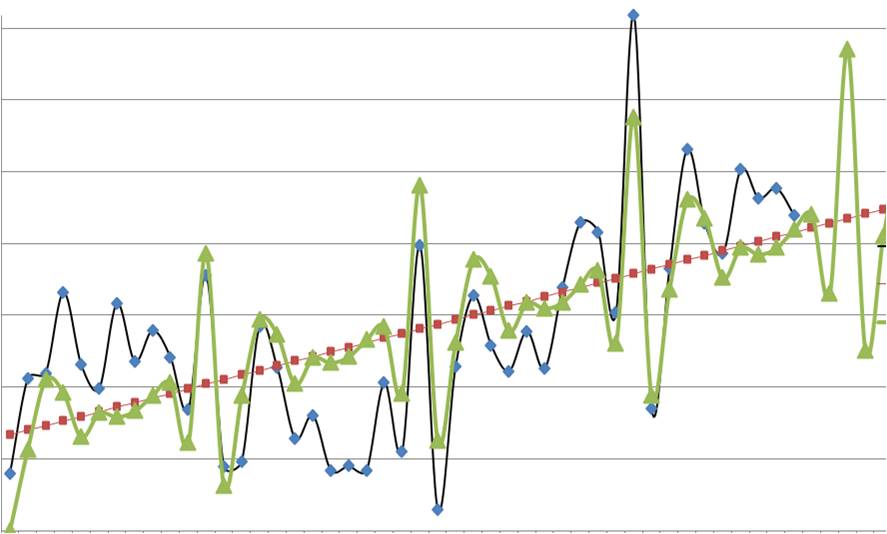
3. Способ оценки прогнозной модели — визуальный.

На график выводим анализируемые данные, тренд, значение модели и прогноз (см. вложенный файл). Обычно визуально видно, какая модель адекватнее строит прогноз . 3-й способ по своей сути схож с 1-м и вторым, только мы верим не цифрам, а тому что мы видим на графике.

Линейная модель:

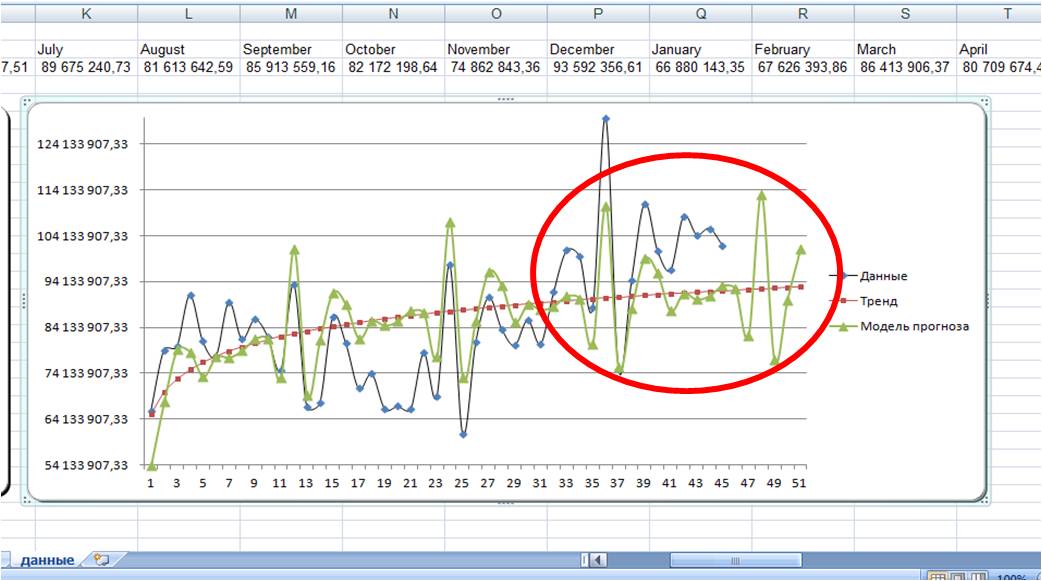
Логарифмическая модель:

По последним периодам видно, что линейная модель более точно описывает данные за последние месяцы, и она, вероятнее всего, сделает более точный прогноз.

Какую модель прогноза выбрать?

1. Которая на основании тестирования на реальных данных для выбранного промежутка времени (месяца, 3-х месяцев, полугода, года) будет делать максимально точный прогноз, т.е. отношение факта к прогнозу будет близко к 1 или 100%.

2. Модель, которая будет максимально точно описывать фактические данные, т.е. показатель точность прогноза будет приближаться к 1, но не всегда модели точно описывающие данные делают адекватные прогнозы (это надо понимать и оценивать графически).

3. Модель, которой визуально вы больше доверяете с точки зрения описания входящих данных и продления прогнозной модели в будущее.

Для повышения точности прогноза я в своей практике стараюсь использовать 3 этих способа параллельно:

• По завершении прогнозного периода и в промежутках всегда оцениваю отношение фактических продаж к прогнозу.

• При построении прогноза анализирую показатель «среднеквадратическое отклонение» и рассчитываю показатель «точность прогноза» для оценки данных и модели.

• А также на график вывожу анализируемые данные и прогнозную модель, для визуального контроля.

Оценивая прогноз по факту или в промежуточные периоды в случае значительных отклонений фактических продаж от прогнозных, разбираю ситуацию и выясняю причины, в случае необходимости вношу корректировки в прогнозную модель.

С помощью программы Forecast4AC PRO вы можете рассчитать показатель точность прогноза автоматически.

Также Forecast4AC умеет автоматически выбирать оптимальную модель прогноза для каждого временного ряда.

+ одним нажатием строить график «Анализируемые данные + модель прогноза», на котором вы можете оценить, как соотносятся между собой:

• анализируемые данные;

• выбранный тренд;

• модель прогноза;

как в анализируемом периоде, так и в будущем. 

Точных прогнозов!

Статья полезная? Поделитесь с друзьями