Наряду с
характеристиками адекватности модели
при оценивании качества модели необходимо
учитывать ее точность.
Как
правило, о точности модели и прогноза
судят по величине погрешности (ошибки).
Ошибка прогноза
это расхождение между
фактическим
и прогнозируемым значением исследуемого
показателя. Использование данного
подхода к оценке точности возможно
только в том случае, когда период
упреждения закончился, и исследователи
имеют фактические значения на период
упреждения или когда разрабатывается
ретропрогноз.
Ретроспективное
прогнозирование разрабатывается для
некоторого момента времени в прошлом,
для которого имеются фактические данные.
В этом случае имеющаяся информация
делится на две части. Первая часть,
включающая более ранние данные,
используется для подбора математической
модели. По построенной математической
модели дается прогноз на последующий
оставшийся период времени. Прогнозные
качества модели оцениваются по более
поздним данным второй части ряда.
Полученные ошибки прогноза в какой-то
мере характеризуют точность подобранных
моделей и могут использоваться при
сопоставлении различных моделей
прогнозирования. В то же время при
использовании ошибки ретроспективного
прогноза в качестве меры точности
необходимо учитывать, что она получена
при использовании только части имеющихся
данных. При использовании полного объема
имеющихся данных трансформируется вид
подобранной модели, и изменяются значения
критериев точности и качества.
Отметим,
что если ретроспективное прогнозирование
осуществляется по модели, содержащей
одну или несколько экзогенных переменных,
точность прогноза будет определяться
точностью определения значения этих
переменных на период упреждения. В
этом случае возможны два способа
определения значений экзогенных
переменных: либо воспользоваться
фактическими известными значениями
экзогенных переменных либо ожидаемыми
их значениями. Естественно, что точность
прогноза в первом случае будет выше.
Наличие данных о
реализации прогнозов дает возможность
оценить качество прогнозов величиной:
,
где
р – число
прогнозов, подтвержденных фактическими
данными (фактическая реализация охвачена
интервальным прогнозом);
q
– число прогнозов, не подтвержденных
фактическими данными.
Использование
коэффициентов
для разных моделей имеет смысл в том
случае, если доверительные вероятности
прогнозов приняты одинаковыми.
В том случае, если
прогноз дается в виде точечной оценки,
в качестве показателей точности прогноза
могут использоваться такие статистические
характеристики как средняя абсолютная
и среднеквадратическая ошибка прогноза.
Г.
Тейлом предложен в качестве меры качества
прогноза коэффициент расхождения (или
коэффициент несоответствия):

где
— соответственно предсказанное и
фактическое значение переменной.
Коэффициент
,
когда
(случай совершенного
прогнозирования). Коэффициент
,
когда экстраполяция строится исходя
из неизменности приростов. Коэффициент
,
прогноз дает худшие результаты, чем
прогноз методом
простой экстраполяции.
Рассмотренные
выше показатели точности прогноза можно
использовать только
в случае наличия истинных значений
величин, оцениваемых при разработке
прогноза. Согласно этому различают
апостериорную
точность моделей, которая
может быть определена только после
практического использования модели,
и априорную
точность моделей. Априорную или
предполагаемую точность оценивают
в условиях отсутствия информации о
результатах эксплуатации модели.
Исследуя априорную точность модели, мы
охарактеризуем только точность
аппроксимации.
Чаще
всего в качестве показателей точности
применяются следующие показатели:
абсолютная ошибка
,
средняя абсолютная ошибка
,
средняя квадратическая ошибка
,
относительная ошибка
,
средняя относительная ошибка
,
коэффициент сходимости, коэффициент
детерминации
Абсолютная
ошибка прогноза определяется как
разность между фактическим значением
и его оценкой, полученной расчетным
путем по модели:
,
среднее
абсолютное значение ошибки:
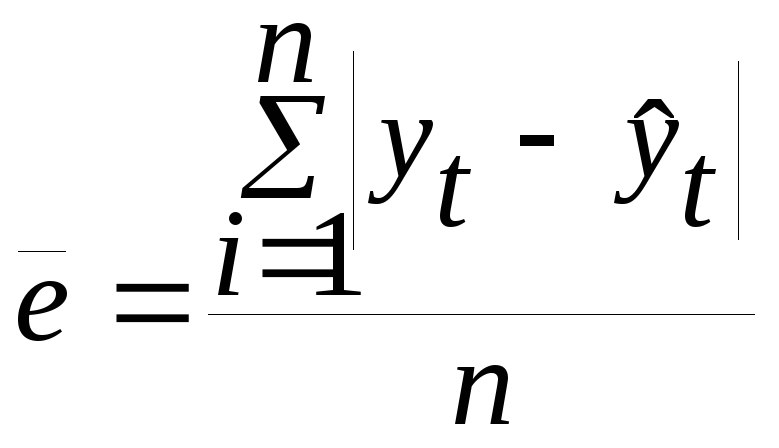
Средняя
квадратическая ошибка прогноза
рассчитывается по формуле:

где
п
— период
упреждения,
k
– число оцениваемых параметров модели.
Недостатком
рассмотренных характеристик является
их зависимость от масштаба измерения
значений исследуемого показателя.
В
связи с этим более удобными являются
относительные значения этих величин.
Относительная ошибка рассчитывается
следующим образом:
,
а средняя
относительная ошибка определяется
следующим образом:
.
Последний
показатель чаще других используется
при сравнении точности прогнозов,
осуществляемых по различным методикам.
Обычно лучшим признается тот прогноз,
который имеет меньшее значение этого
показателя. Принято считать, что если
значение средней относительной ошибки
менее 3-5%, то точность хорошая; если
значение средней относительной ошибки
не превышает 10%, то точность хорошая; от
10% до 15% точность удовлетворительная.
Коэффициент
сходимости определяется по следующей
формуле:

чем меньше значение
коэффициента сходимости, чем лучше
точность модели.
Коэффициент
детерминации определяется по формуле:
,
и поэтому чем
больше значение коэффициента детерминации,
тем лучше точность модели.
Для
выбора лучшей модели можно использовать
один из рассмотренных показателей либо
воспользоваться обобщенным критерием.
Пример.
Оценить адекватность и точность модели
Хольта, построенной в параграфе 5.3.
Решение. В таблице
5.2 приведены ошибки аппроксимации
,
на основе которых будет оцениваться
адекватность модели. Проверку
случайности колебаний уровней остаточной
компоненты проведем, используя критерий
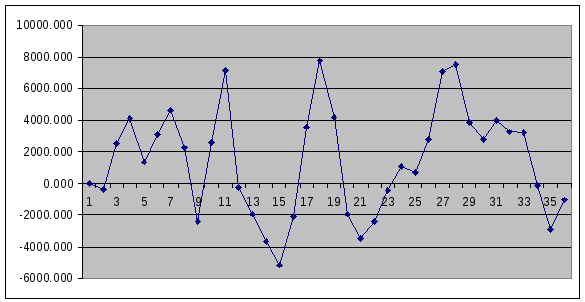
поворотных точек. На рис. 6.2 представлен
ряд остатков, количество поворотных
точек равно 15.
Рис. 6.2. Оценка
адекватности модели. Ряд остатков.
При
n=36:
.
Неравенства 15>17 не выполняется,
следовательно, ряд остатков не является
случайным.
Анализ
соответствия ряда остатков нормальному
закону распределения проведем по RS
– критерию:
.
Расчетное
значение RS
– критерия сравним с табличными
значениями RS
– критерия (таб. 6.1) . Расчетное RS
– критерия попадает в интервал,
ограниченный табличными значениями
(3,6; 5,06), и с уровнем значимости α=0,05
гипотеза о
нормальности распределения остаточной
компоненты принимается.
Так
как остаточная компонента распределена
по нормальному закону, то осуществим
проверку равенства математического
ожидания остаточной компоненты нулю
с помощью t-критерия
Стьюдента:
Расчетное
значениеt-критерия
больше табличного
значения tα
статистики
Стьюдента
,
следовательно,гипотеза
о равенстве нулю математического
ожидания уровней ряда остатков не
принимается.
Независимость уровней в ряде остатков
проверим по критерию Дарбина–Уотсона
(таб. 6.3).
Таблица 6.3
Расчет d—значенияДарбина–Уотсона
|
t |
|
|
|
|
|
1 |
-23.500 |
552.25 |
||
|
2 |
-415.390 |
-391.890 |
153577.772 |
172548.852 |
|
3 |
2553.781 |
2969.171 |
8815978.8 |
6521799.44 |
|
4 |
4108.015 |
1554.234 |
2415642.82 |
16875789.2 |
|
5 |
1357.017 |
-2750.998 |
7567992.09 |
1841494.74 |
|
6 |
3047.488 |
1690.471 |
2857692.36 |
9287182.51 |
|
7 |
4611.776 |
1564.288 |
2446997.23 |
21268477.8 |
|
8 |
2226.788 |
-2384.988 |
5688168.37 |
4958584.19 |
|
9 |
-2442.290 |
-4669.078 |
21800286 |
5964779.36 |
|
10 |
2620.809 |
5063.099 |
25634971.3 |
6868640.89 |
|
11 |
7156.526 |
4535.717 |
20572724.5 |
51215860.7 |
|
12 |
-255.774 |
-7412.299 |
54942183.2 |
65420.1907 |
|
13 |
-1964.630 |
-1708.857 |
2920190.74 |
3859772.09 |
|
14 |
-3692.014 |
-1727.384 |
2983855.54 |
13630969.5 |
|
15 |
-5152.421 |
-1460.407 |
2132789.2 |
26547447.2 |
|
16 |
-2101.028 |
3051.394 |
9311004.57 |
4414317.05 |
|
17 |
3571.246 |
5672.274 |
32174688.1 |
12753798.1 |
|
18 |
7739.490 |
4168.244 |
17374260.7 |
59899710.6 |
|
19 |
4171.509 |
-3567.981 |
12730490.5 |
17401487.7 |
|
20 |
-1955.050 |
-6126.559 |
37534730.7 |
3822222.1 |
|
21 |
-3465.610 |
-1510.560 |
2281790.33 |
12010452.8 |
|
22 |
-2395.256 |
1070.354 |
1145657.1 |
5737252.69 |
|
23 |
-445.847 |
1949.410 |
3800197.94 |
198779.235 |
|
24 |
1050.970 |
1496.817 |
2240461.18 |
1104538.71 |
|
25 |
694.152 |
-356.818 |
127319.3 |
481847.09 |
|
26 |
2752.621 |
2058.469 |
4237296.08 |
7576924.68 |
|
27 |
7090.334 |
4337.713 |
18815752.4 |
50272839.5 |
|
28 |
7485.321 |
394.987 |
156014.473 |
56030029 |
|
29 |
3824.177 |
-3661.144 |
13403973.2 |
14624331.3 |
|
30 |
2773.655 |
-1050.522 |
1103597.19 |
7693161.27 |
|
31 |
3953.251 |
1179.597 |
1391448.08 |
15628196.9 |
|
32 |
3253.170 |
-700.082 |
490114.569 |
10583112.5 |
|
33 |
3170.670 |
-82.500 |
6806.172 |
10053148.7 |
|
34 |
-134.635 |
-3305.305 |
10925041.8 |
18126.5898 |
|
35 |
-2869.411 |
-2734.776 |
7478999.31 |
8233519.15 |
|
36 |
-1039.034 |
1830.377 |
3350281.25 |
1079590.8 |
|
сумма |
341012975 |
468696705 |
Расчетное
d—значение
равно:
.
Расчетное
значение
d—критерия
сравним с двумя табличными значениями
Дарбина—Уотсона
(1,41; 1,52). Так как расчетное d-значение
меньше нижнего табличного значения
d1=1,41,
то гипотеза о
независимости ряда остатков отвергается
и модель неадекватна.
Результаты оценки
модели на адекватность приведены в
таблице 6.4.
Таблица 6.4
Результаты
оценки модели на адекватность
-
Проверяемое
свойствовывод
Случайность
неадекватна
Нормальность
адекватна
Среднее
неадекватна
Независимость
неадекватна
Вывод:
модель статистически неадекватна
Средняя
относительная ошибка равна (таб. 5.2):
.
Оцениваемая модель
не является адекватной, и несмотря на
хорошую точность не может использоваться
для прогнозирования.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Точность прогнозирования
Любому человеку, который занимается прогнозированием продаж, важно и необходимо оценивать корректность своих прогнозов. Для этого существует такой показатель, как «Точность прогнозирования». В данной статье именно о нем я и расскажу.
Хочу обратить внимание на то, что в некоторых компаниях данный показатель называют «Аккуратность прогнозирования». Не могу сказать, что это неправильно, но в данной статье будет фигурировать именно «Точность прогнозирования». Ведь мы оцениваем насколько точно наш прогноз совпадает с фактическими значениями, а не аккуратность, с которой мы его высчитывали.
Точность прогнозирования — это показатель, который характеризует качество прогноза. Он отражает насколько сформированный прогноз совпадает с истинными фактическими значениями.
«Точность прогнозирования»: формула, разновидности «ошибок прогноза».
Итак, чтобы рассчитать точность прогнозирования, необходимо сначала рассчитать ошибку прогнозирования в процентах, а затем, вычесть ее из 100%:
В качестве основной ошибки для расчета точности прогнозирования мы будем использовать Взвешенную Абсолютную Процентную Ошибку (WAPE — Weighted Absolute Percent Error), которая рассчитывается по формуле:
То есть: сумма всех отклонений прогноза от факта по модулю, деленное на сумму всех фактов и умноженное на 100%.
Важно! Если ошибка прогнозирования больше 100%, то точность прогнозирования всегда будет равна 0%.
Вообще, помимо WAPE (которую также называют MAD-Mean Ratio), существует множество ошибок, которые мы можем использовать в качестве основной ошибки для расчета точности прогнозирования. Например:
- Средняя Абсолютная Процентная Ошибка (MAPE — Mean Absolute Percent Error)
- Средняя Процентная Ошибка (MPE — Mean Percent Error)
- Медиана Абсолютной Процентной Ошибки (MdAPE — Median Absolute Percent Error)
- Средняя Абсолютная Масштабированная Ошибка (MASE — Mean Absolute Scaled Error)
И так далее (более подробно смотрите здесь). Однако при расчете точности прогнозирования, WAPE — наиболее оптимальный вариант ошибки, так как он наименее чувствителен к выбросам и искажениям, а также интуитивно-понятен и прост в расчете. В общем, WAPE — наш выбор!
Итоговая формула примет вид:

Примеры расчета точности прогнозирования:
Итак, формула расчета точности у нас есть, теперь мы перейдем непосредственно к примеру расчета:
Все просто. У нас есть исходные данные: SKU, факт продаж и прогноз продаж. Для каждого SKU мы находим отклонения по модулю (|факт-прогноз|), а затем суммируем их, получаем 126. Затем суммируем все фактические показатели, получаем 468. Находим ошибку прогнозирования: делим сумму отклонений на сумму фактических показателей — 126/468 = 0,269, то есть 27%. И вычитаем значение ошибки прогнозирования из 100% и получаем точность 73%. Средний результат.
Также, бывают ситуации, когда необходимо рассчитать не общую точность по всем номенклатурам, а отдельно по каждому клиенту (или номенклатурной группе, или по каналам продаж и т.д.). На таблице ниже изображен изображен именно такой пример:
Суть расчетов не меняется, только теперь находим сумму отклонений и сумму фактов для каждого из клиентов по отдельности. Для первого клиента ошибка прогнозирования равна 126/468 = 27%, соответственно точность равна 73% (то же самое, что и в первом примере), а для второго клиента ошибка прогнозирования равна 206/662 = 31%, и точность равна 69%.
В общем-то и все. Мы нашли точность прогнозирования отдельно для списка SKU и отдельно по каждому клиенту. Важно(!) помнить некоторые правила:
- Если ошибка прогнозирования (WAPE) больше 100% — точность прогнозирования всегда 0%. Математически можно записать это так: Точность = Maximum of (1 — Ошибка, 0)
- Если сумма фактов равна нулю (ошибка подразумевает деление на сумму фактов, а на ноль делить нельзя), то рассматриваем два случая:
- если прогноз тоже = 0, то точность всегда равна 100%
- если прогноз ≠ 0, то точность всегда равна 0%
- Перед нахождением точности необходимо проконсолидировать данные, то есть просуммировать объемы по одинаковым позициям (для более подробной детализации — просуммировать объемы по одинаковым позициям для каждого элемента детализации).
Файл с примерами из статьи можно скачать здесь.
Об авторе
HeinzBr
Автор статей и создатель сайта SHTEM.RU
Из данной статьи вы узнаете:
- Какие способы оценки прогноза вы можете использовать?
- Как выбрать оптимальную модель, которая поможет вам сделать максимально точный прогноз?
- Как рассчитать показатель «Точность прогноза»?
Какие способы оценки прогнозной модели вы можете использовать:
1. Оценить отношение фактических продаж к прогнозу;
2. Расчет показателя точность прогноза — оценка на сколько точно выбранная модель описывает анализируемые данные;
3. Графический анализ — строим график и визуально оцениваем адекватность модели прогноза относительно фактических продаж за последний период ;
1-й способ — Расчет отношения фактических продаж к прогнозу.
Сначала рассчитываем прогноз разными способами и оцениваем отношение фактических продаж к прогнозу. ВАЖНО протестировать модели не по одному товару или направлению продаж, а сразу взять 10 и более товарных позиций или направлений продаж и рассчитать прогноз по ним на минимум на 3 периода вперед (количество периодов и направления прогноза зависят от ваших задач. Если задача — сделать точный прогноз на 6 месяцев, то рассчитываем прогноз на 6 месяцев несколькими вариантами и оцениваем отношение факта к прогнозу по сумме полугода).
Рассчитаем прогноз 4 способами на полгода. Протестируем следующие модели:
-
Линейный тренд + сезонность — лист «Линейный» в приложенном файле (см. статью «Как рассчитать прогноз с учетом роста и сезонности в Excel»)
-
Логарифмический тренд + сезонность — лист «Логарифмический» в приложенном файле (см. статью «5 способов расчета значений логарифмического тренда»)
-
Скользящая средняя с сезонностью к 2-м месяцам — лист «Скользящая к 2-м» (см. статью «Как рассчитать прогноз по методу скользящей средней»);
-
Скользящяя средняя с сезонностью к 3-м месяцам — лист «Скользящая к 3-м»;
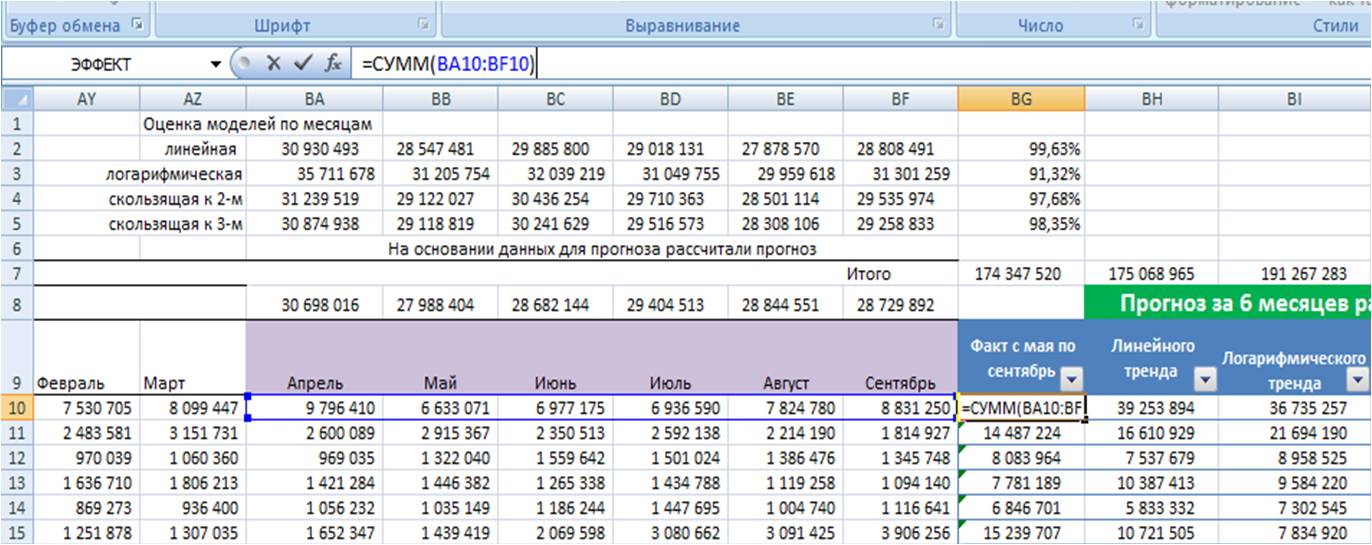
Для каждой из 4-х прогнозных моделей в листе «Оценка моделей»:
-
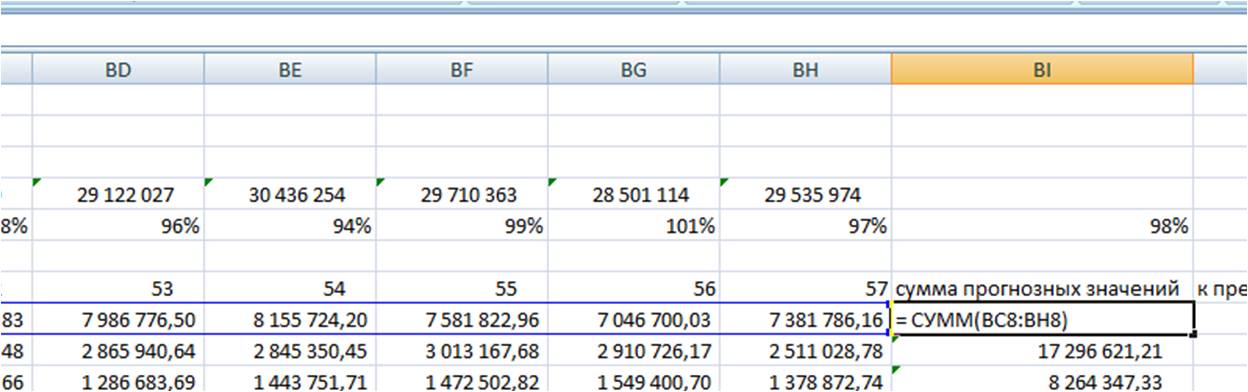
Суммируем прогноз по каждой модели за 6 месяцев;
-
Суммируем фактические продажи, которые мы будем сравнивать с прогнозом;
-
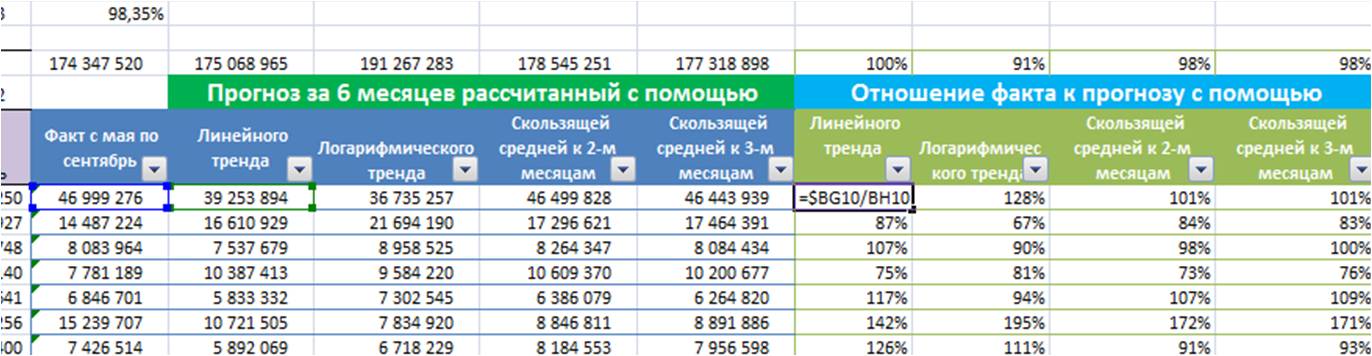
Рассчитываем отношение факта к прогнозу по каждой позиции для каждой модели;
-
Рассчитываем по каждой модели среднее отношение факта к прогнозу;
-
Выбираем модель прогноза, которая по показателю «среднее отношение факта к прогнозу» оказалась максимально приближена к 100%;
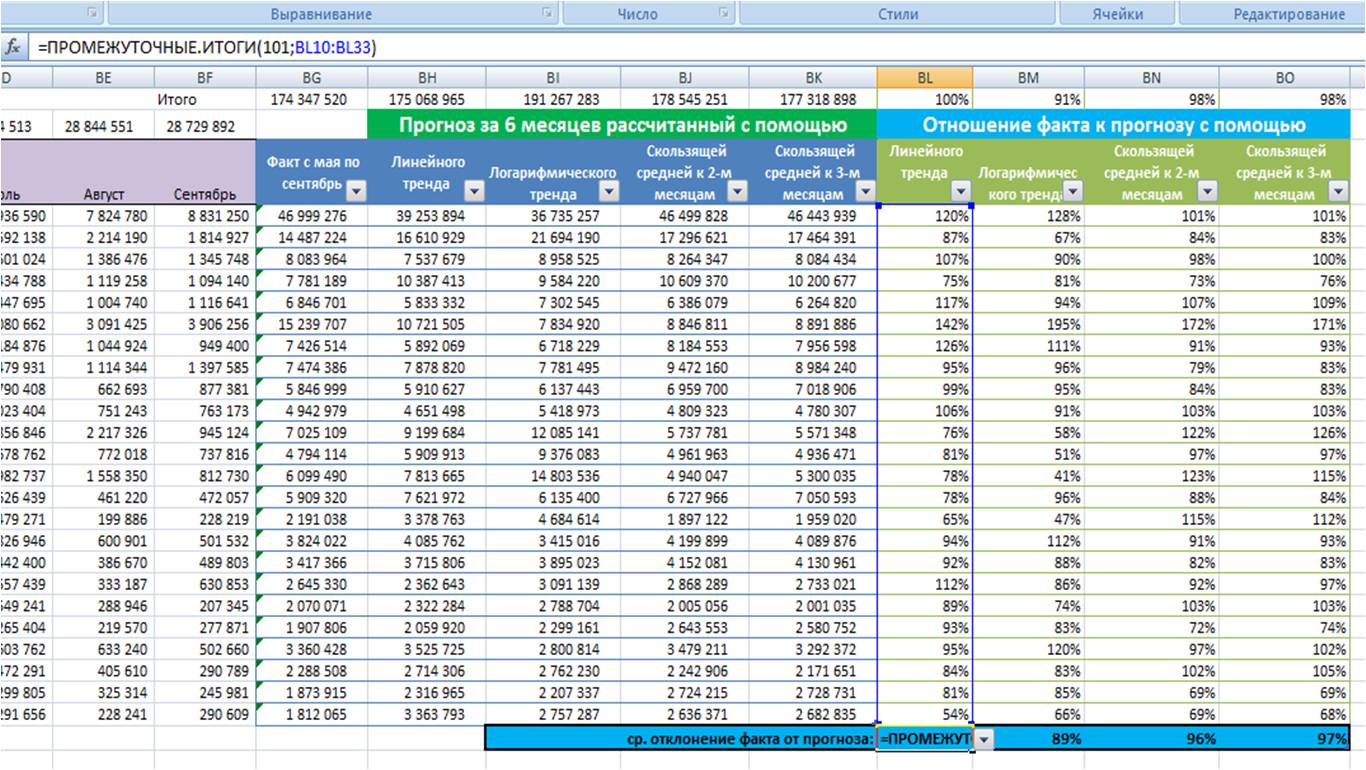
Для наших данных самой точной моделью оказалась скользящая средняя к 3-м месяцам с сезонностью, среднее отклонение факта от прогноза 97%.
Мы протестировали каждую модель прогноза на реальных данных и выбрали для себя оптимальную, которая в среднем показала минимальное отклонение от факлических продаж.
2-й способ оценки модели прогноза — расчет показателя точность прогноза.
Показатель точность прогноза показывает, на сколько точно выбранная модель прогноза описывает данные. Идея в том, чем точнее выбранная модель описывает фактические данные, тем точнее она сделает прогноз.
Как рассчитать точность прогноза? Рассмотрим на примере расчета для модели прогноза с линейным трендом и сезонностью.
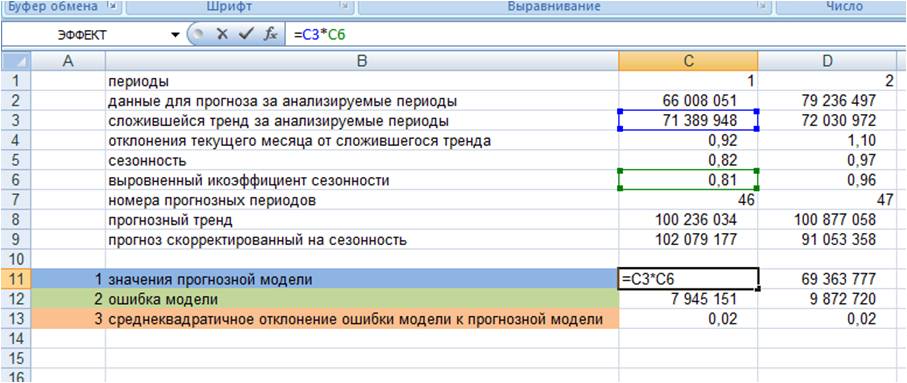
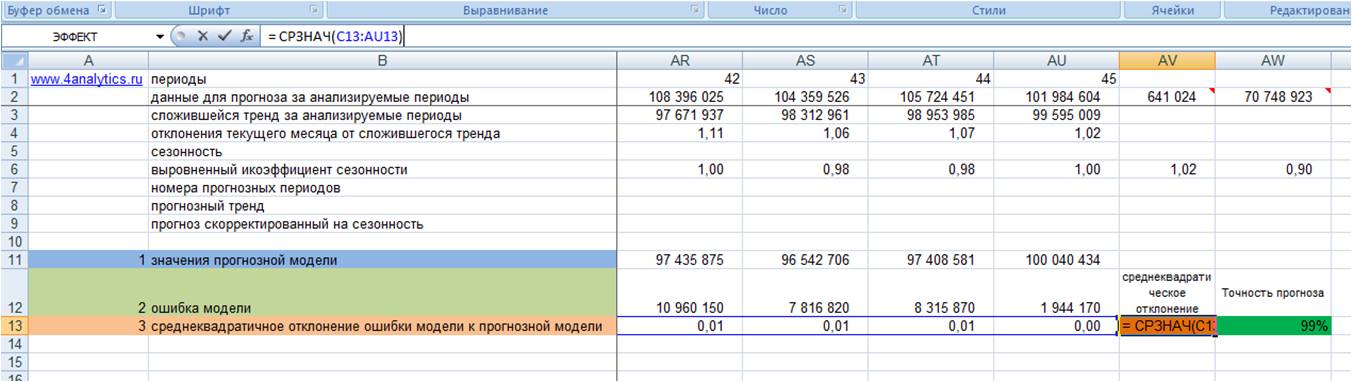
1. Рассчитываем значения прогнозной модели для каждого анализируемого момента времени в прошлом.
Для этого значения тренда для анализируемых периодов умножаем на выровненные коэффициенты сезонности (см. файл с примером)
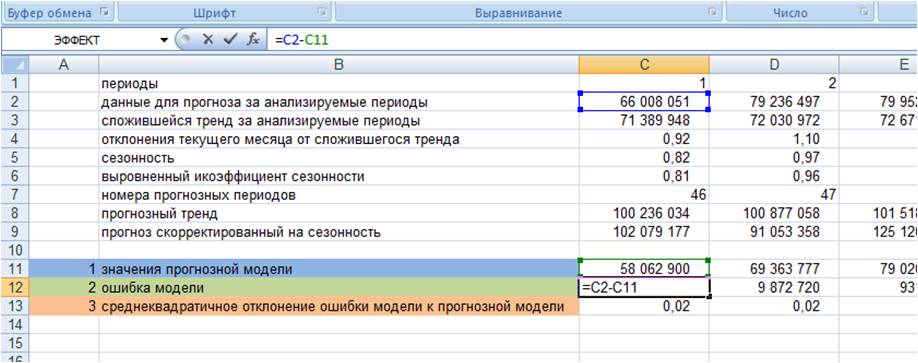
2. Рассчитываем ошибку прогнозной модели. Для этого за каждый период от фактических значений вычитаем значения прогнозной модели.
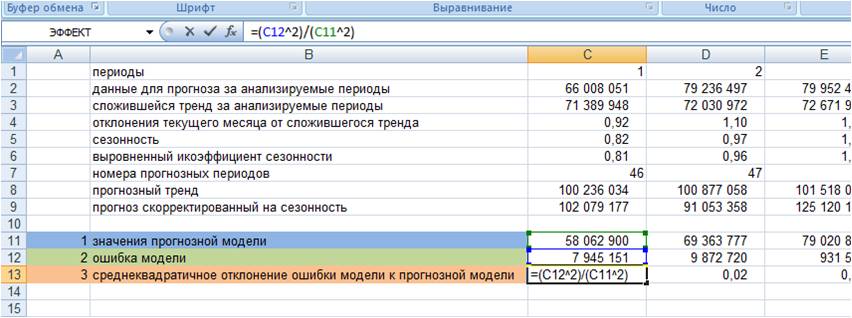
3. Рассчитываем квадратическое отклонение ошибки от значений прогнозной модели (см. файл с примером);
4. Рассчитываем среднее значение квадратического отклонения, т.е. среднеквадратическое отклонение
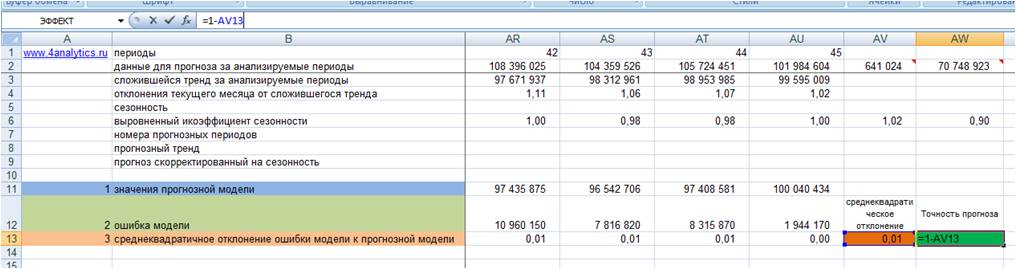
5. Точность прогноза = (1- среднеквадратическое отклонение ошибки прогнозной модели)*100 (см. файл с примером).
Показатель точности прогноза выражается в процентах:
-
Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно.
-
Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.
Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда.
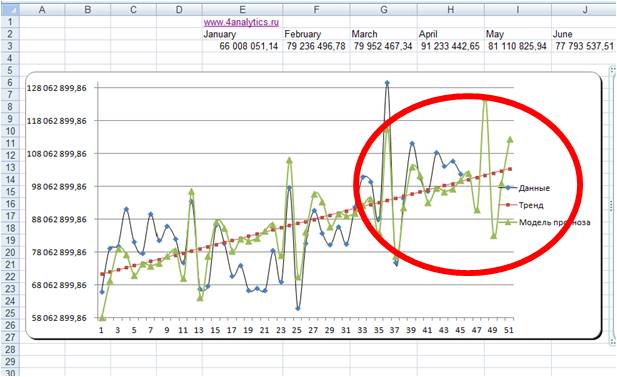
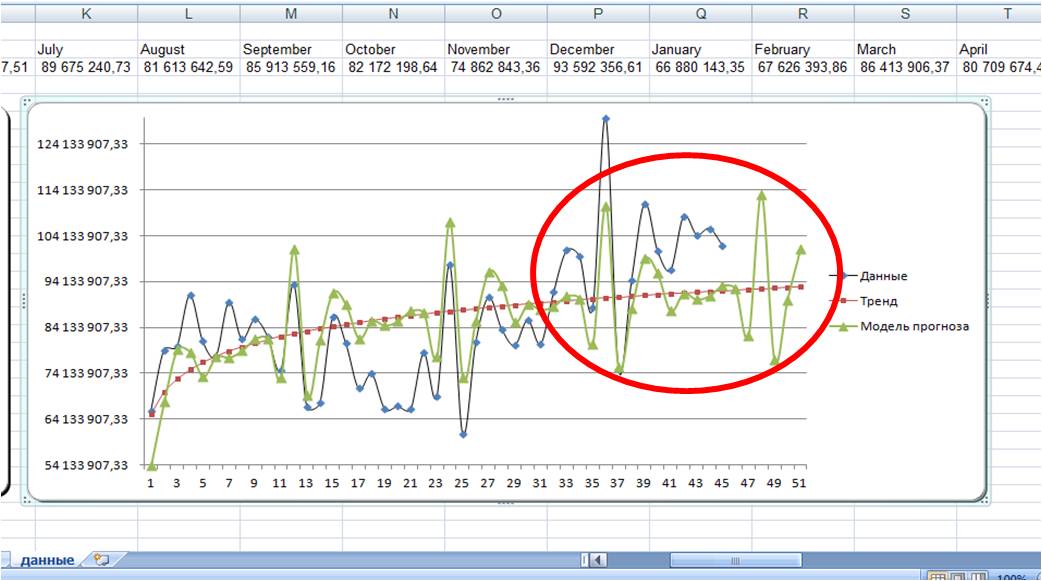
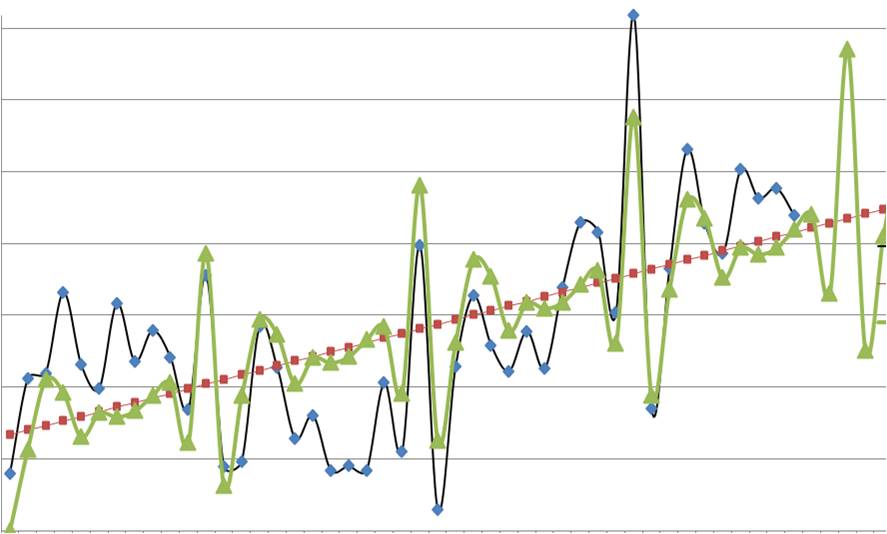
3. Способ оценки прогнозной модели — визуальный.
На график выводим анализируемые данные, тренд, значение модели и прогноз (см. вложенный файл). Обычно визуально видно, какая модель адекватнее строит прогноз . 3-й способ по своей сути схож с 1-м и вторым, только мы верим не цифрам, а тому что мы видим на графике.
Линейная модель:
Логарифмическая модель:
По последним периодам видно, что линейная модель более точно описывает данные за последние месяцы, и она, вероятнее всего, сделает более точный прогноз.
Какую модель прогноза выбрать?
1. Которая на основании тестирования на реальных данных для выбранного промежутка времени (месяца, 3-х месяцев, полугода, года) будет делать максимально точный прогноз, т.е. отношение факта к прогнозу будет близко к 1 или 100%.
2. Модель, которая будет максимально точно описывать фактические данные, т.е. показатель точность прогноза будет приближаться к 1, но не всегда модели точно описывающие данные делают адекватные прогнозы (это надо понимать и оценивать графически).
3. Модель, которой визуально вы больше доверяете с точки зрения описания входящих данных и продления прогнозной модели в будущее.
Для повышения точности прогноза я в своей практике стараюсь использовать 3 этих способа параллельно:
-
По завершении прогнозного периода и в промежутках всегда оцениваю отношение фактических продаж к прогнозу.
-
При построении прогноза анализирую показатель «среднеквадратическое отклонение» и рассчитываю показатель «точность прогноза» для оценки данных и модели.
-
А также на график вывожу анализируемые данные и прогнозную модель, для визуального контроля.
Оценивая прогноз по факту или в промежуточные периоды в случае значительных отклонений фактических продаж от прогнозных, разбираю ситуацию и выясняю причины, в случае необходимости вношу корректировки в прогнозную модель.
С помощью программы Forecast4AC PRO вы можете рассчитать показатель точность прогноза автоматически.
Также Forecast4AC умеет автоматически выбирать оптимальную модель прогноза для каждого временного ряда.
+ одним нажатием строить график «Анализируемые данные + модель прогноза», на котором вы можете оценить, как соотносятся между собой:
-
анализируемые данные;
-
выбранный тренд;
-
модель прогноза;
как в анализируемом периоде, так и в будущем.
Точных прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
Для того чтобы модель линейной регрессии можно было применять на практике необходимо сначала оценить её качество. Для этих целей предложен ряд показателей, каждый из которых предназначен для использования в различных ситуациях и имеет свои особенности применения (линейные и нелинейные, устойчивые к аномалиям, абсолютные и относительные, и т.д.). Корректный выбор меры для оценки качества модели является одним из важных факторов успеха в решении задач анализа данных.
- Среднеквадратичная ошибка (Mean Squared Error)
- Корень из среднеквадратичной ошибки (Root Mean Squared Error)
- Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error)
- Cредняя абсолютная ошибка (Mean Absolute Error)
- Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error)
- Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error)
- Средняя абсолютная масштабированная ошибка (Mean absolute scaled error)
- Средняя относительная ошибка (Mean Relative Error)
- Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error
- R-квадрат
- Скорректированный R-квадрат
- Сравнение метрик
«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.
Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.
Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:
- Среднеквадратичная ошибка (MSE).
- Корень из среднеквадратичной ошибки (RMSE).
- Среднеквадратичная ошибка в процентах (MSPE).
- Средняя абсолютная ошибка (MAE).
- Средняя абсолютная ошибка в процентах (MAPE).
- Cимметричная средняя абсолютная процентная ошибка (SMAPE).
- Средняя абсолютная масштабированная ошибка (MASE)
- Средняя относительная ошибка (MRE).
- Среднеквадратичная логарифмическая ошибка (RMSLE).
- Коэффициент детерминации R-квадрат.
- Скорректированный коэффициент детеминации.
Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.
Рисунок 1. Линейная регрессия
Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.
Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — overline{y}.
В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».
MSE
Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.
Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.
MSE рассчитывается по формуле:
MSE=frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y}_{i})^{2},
где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.
Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.
Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.
RMSE
Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:
RMSE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y_{i}})^{2}}
MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).
Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:
frac{partial RMSE}{partial widehat{y}_{i}}=frac{1}{2sqrt{MSE}}frac{partial MSE}{partial widehat{y}_{i}}
Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.
Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.
MSPE
Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:
MSPE=frac{100}{n}sumlimits_{i=1}^{n}left ( frac{y_{i}-widehat{y}_{i}}{y_{i}} right )^{2}
Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.
MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.
MAE
Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:
MAE=frac{1}{n}sumlimits_{i=1}^{n}left | y_{i}-widehat{y}_{i} right |
Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.
Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.
MAPE
Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:
MAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{left | y_{i} right |}
Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.
SMAPE
Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:
SMAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{(left | y_{i} right |+left | widehat{y}_{i} right |)/2}
Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.
Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и widehat{y}_{i}=90, то SMAPE=5.26.
Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).
MASE
Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:
MASE=frac{MAE_{i}}{MAE_{j}}
MASE симметрична и устойчива к выбросам.
MRE
Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:
MRE=frac{1}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y}_{i}right |}{left | y_{i} right |}
Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.
Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.
Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.
RMSLE
Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:
RMSLE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(log(widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}
Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.
Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.
R-квадрат
Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.
В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.
Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:
R^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}}
Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.
Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.
Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.
Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).
На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.
Скорректированный R-квадрат
Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.
В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).
Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:
R_{adj}^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}/(n-k)}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}/(n-1)}
где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.
Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.
Сравнение метрик
Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:
| Мера | Сильные стороны | Слабые стороны |
|---|---|---|
| MSE | Позволяет подчеркнуть большие отклонения, простота вычисления. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости. |
| RMSE | Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. |
| MSPE | Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер. | Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки. |
| MAPE | Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области. | Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю. |
| SMAPE | Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше. | Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения. |
| MASE | Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели. | Сложность интерпретации. |
| MRE | Позволяет оценить величину ошибки относительно значения целевой переменной. | Неприменима для наблюдений с нулевым значением выходной переменной. |
| RMSLE | Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше | Может быть затруднена интерпретация из-за нелинейности. |
| R-квадрат | Универсальность, простота интерпретации. | Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы. |
| R-квадрат скорр. | Корректно отражает вклад каждой переменной в модель. | Плохо работает, когда входные переменные зависимы. |
В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.
Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.
Другие материалы по теме:
Отбор переменных в моделях линейной регрессии
Репрезентативность выборочных данных
Логистическая регрессия и ROC-анализ — математический аппарат
Оценка ошибки прогнозирования временного ряда
Работая с научными публикациями, сталкиваюсь с различными показателями ошибок прогнозирования временных рядов. Среди всех встречающихся оценок ошибки прогнозирования стоит отметить две, которые в настоящее время, являются самыми популярными: MAE и MAPE.
Пусть ошибка есть разность:
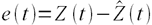
где Z(t) – фактическое значение временного ряда, а 
Тогда формулы для оценок ошибки прогнозирования временных рядов для N отчетов можно записать в следующем виде.
MAPE – средняя абсолютная ошибка в процентах
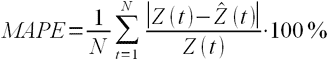
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.
Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.
MAE – средняя абсолютная ошибка

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.
После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.
Кроме указанных иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.
MSE – среднеквадратичная ошибка

RMSE – квадратный корень из среднеквадратичной ошибки

ME – средняя ошибка
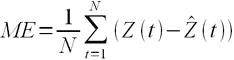
SD – стандартное отклонение
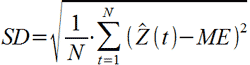
Связь точности и ошибки прогнозирования
Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.
Точность прогноза в % = 100% – MAPE
Величину точности оценивать не принято, говоря о прогнозировании всегда оценивают, то есть определяют значение именно ошибки прогноза, то есть величину MAPE и/или MAE. Однако нужно понимать, что если MAPE = 5%, то точность прогнозирования = 95%. Говоря о высокой точности, мы всегда говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности.
При этом величина MAPE является количественной оценкой именно ошибки, и эта величина нам ясно говорит и о точности прогнозирования, исходя из приведенной выше простой формулы. Таким образом, оценивая ошибку, мы всегда оцениваем точность прогнозирования.