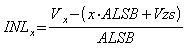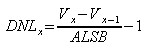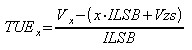Total unadjusted error

3. Parameter calculations D/A converter

The linearity parameter calculations (INLE, DNLE, etc.) of a D/A converter are based on the output voltages of the device.
The output voltages of a D/A converter can be measured by applying the digital codes to the input of the device.

The following parameters will be discussed:

DAC Examples

To explain the linearity parameters of an D/A converter, the plot below can overlay some example DAC devices with an ideal 4 bits DAC.
The plot can show five different kinds of DAC data:

• 1) DAC 1: a DAC with only an offset error
• 2) DAC 2: a DAC with only a gain error
• 3) DAC 3: a DAC with an offset, gain and linearity error, monotonic
• 4) DAC 4: a DAC with an offset, gain and linearity error, non-monotonic
• 5) Random DAC data: random errors. Use the button «New DAC data» for a new DAC

Loading… (javascript must be enabled)

Click on a point

The following DAC data presentations are available:

1. Transfer plot: The transfer plot of the ideal DAC and example DAC (blue line) are overlayed
2. End point overlay: Overlay end point line and DAC error related to the end point line (blue line)
3. Best fit overlay: Overlay best fitting line and DAC error related to the best fitting line (blue line)
4. End point error: The error of the example DAC compared to the end point reference line (error in LSBs)
5. Best fit error: The error of the example DAC compared to the best fitting reference line (in LSBs)
6. Differential error: The error of each step of the example DAC (LSBs)
7. Total unadjusted error: The error of the example DAC compared to the ideal line(in LSBs)

The Differential error (6) shows the error in of each step.

For the first three presentations, the y-axis shows (DAC output) voltages or LSBs and the x-axis (DAC input) codes.
For the other 4 presentations the y-axis shows the error in LSBs.

Parameter calculations

End Point and Best Fitting line

Similar to the ADC error parameter calculations, it is necessary to have a reference line for the parameter calculations.
Also the same reference lines are used:

1. End point line
2. Best fitting line

The end point line is a straight line between the first output voltage and the last output voltage.
So only the first and last measured voltages are used for the calculation of the reference line.
The first and last voltage of the end point error plot will always be zero.

The best fitting line calculation uses all voltages. Also here, the least-squares linear regression algorithm is used.
For the completeness, again the equation of the best fitting line (y = ax + b):

Offset Error

The output voltage when the digital input code (mostly 0 or halve scale) is set to give an ideal output voltage of 0 V (end point calculation).
For the best fitting line calculation the offset error is the offset of the best fitting reference line related to the ideal transfer line.

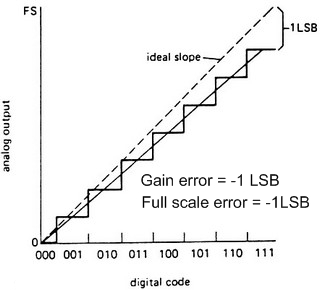
Full scale error

The full scale error is the error of the full scale output voltage (maximum input code) from the ideal full scale output voltage (end point full scale error).
It is equal to the sum of the gain error and offset error.

Gain error

The gain error is equal to the Full scale error with the offset error subtracted.
It is the deviation (of the end point or best fit reference line) from the ideal slope of the transfer characteristic.
The slope can be found in the «a» of the reference line y = ax + b. The gain error can be calculated with the equation (a — 1)(N-1).
Where N is the number of converter steps.

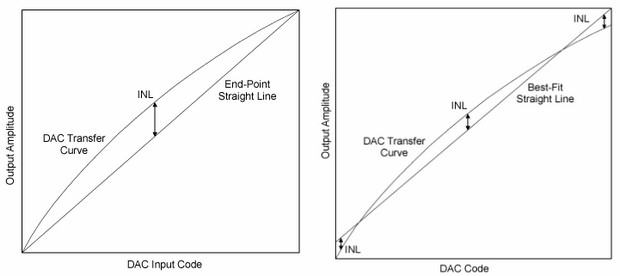
Integral non linearity error (INL/INLE)

Integral non linearity error describes the departure from a reference line.
This reference can be an end point line or best fitting line. It is a measure of the straightness of
the transfer function and can be greater than the differential non-linearity. The size and
distribution of the DNL errors will determine the integral linearity of the converter.
The INL error is calculatated by:

Where V(x) is the output voltage at input code x. Vzs is the zero scale voltage of the reference line. ALSB is the actual (or measured) LSB step.
The actual LSB step is calculated by ILSB/a , where ILSB is the ideal LSB step and «a» is the angle of the reference line (the «a» of y = ax + b).

INL is a static specification and relates to THD (a dynamic specification). However, distortion
performance can not be predicted from the INL specification, except to say that THD tends to
become worse as INL departs from zero.

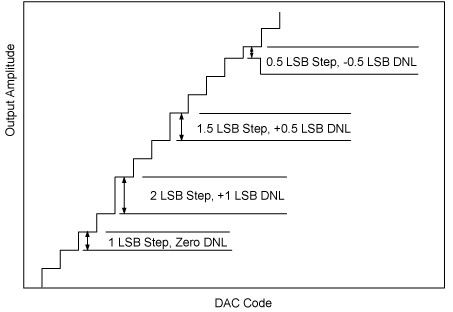
Differential non linearity error (DNL/DNLE)

The maximium deviation of the 1 LSB step.
For an ideal DAC the two adjacent digital codes correspond to an output voltage that are exactly 1 LSB apart.
The 1 LSB step for the DNL calculation is based on the measured (or actual) LSB step.
The actual 1 LSB step is the ideal LSB multiplied by «a» (ILSB x a) where «a» is the angle of the reference line (the «a» of y = ax + b).
In reality the difference between the actual 1 LSB (1 x a) and the ideal 1 LSB step is very small.
The DNL is calculated by:

Where ALSB is the actual 1 LSB step. Vx is the output voltage at input code x and V(x-1) is the output voltage at input code x-1.

A DNLE less than -1 lsb will lead to a non-monotonic transfer function.
DAC 4 is lowering in output voltage at code 7. In the differential error presentation (6), an error of 2.12 LSB can be found.

to plot

Total unadjusted error (TUE)

Total Unadjusted Error is a specification that includes linearity errors, gain error, and offset error.
It is the worst-case deviation from the ideal device performance.
The TUE is calculated by:

Where V(x) is the output voltage at input code x. Vzs is the zero scale voltage of the (ideal) DAC (usually 0V). ILSB is the ideal LSB step.

Select the Total unadjusted error presentation (7) for the TUE. In fact the blue line in the transfer presentation (1) is also a total unadjusted presentation.

to plot

<< Previous (2. Parameters calculations A/D converter)  Next >> (4. Linearity calculations on the ATX7006)

Rev. D | Page 13 of 20

Соседние файлы в папке ADC&DAC

• #
• #
• #
• #
• #
• #
• #

Эти возможности в том или ином виде присутствуют практически в любом современном цифровом осциллографе. Но исключительная полезность цифрового осциллографа определяется не только его способностью визуально отображать форму входного сигнала, но и производить различного рода измерения, что, в общем, и классифицирует осциллограф как «средство измерения».

Большинство ЦЗО способно выполнять измерения достаточно большого типа параметров, например, осциллографы серии WaveRunner производства компании LeCroy измеряют до 40 параметров сигнала, с одновременной индикацией 8 результатов измерений в штатном режиме, а при инсталляции дополнительных опций осциллографы LeCroy старших серий способны приводить измерения до 170 различных параметров. Это широкий набор различных амплитудно-временных измерений, вполне достаточных для удовлетворения потребностей широкого круга пользователей. Список измерений, доступных для осциллографов LeCroy, приведен в приложении 1.

В основе всех видов измерений современного осциллографа лежат два вида измерений — амплитудные и временные. Так же цифровые осциллографы способны осуществлять безразмерные виды измерений, например подсчет числа целых периодов сигнала, числа точек дискретизации, числа пиков гистограммы и пр.

Амплитудные измерения предназначены для измерений параметров амплитуды входного сигнала (или же результатов математической обработки), таких как непосредственно амплитуда, нижнее значение, верхнее значение, пиковое значение, выбросы, среднеквадратическое значение и многие другие.

Временные измерения предназначены для измерений параметров сигнала, нормированных по времени, — это частота, период, длительность, фазовые сдвиги, время нарастания и спада, параметры джиттера и многие другие. Современные ЦЗО имеют некоторые производные виды измерений от амплитуды и времени, в частности, измерение площади сигнала, что применительно к импульсному сигналу определяет его энергию, измерение числа периодов сигнала на заданном участке или измерение числа точек дискретизации, образующих форму сигнала на всем экране или на заданном участке. В ЦЗО также присутствуют специализированные виды измерений, предназначенные для измерения параметров специфических устройств ли режимов, например измерение параметров мощности электрического сигнала, измерение параметров систем последовательной передачи данных, измерение параметров дисковых или оптических приводов, измерения джиттера и многие другие. Но и даже эти специализированные виды измерений базируются на основных результатах измерения амплитудно-временных параметров сигнала.

Измерения амплитудных параметров

Погрешность измерения амплитудных параметров определяется тем, что в большинстве современных ЦЗО используются 8-битные АЦП, что дает теоретическую относительную погрешность измерения (1/2⁸)×100% = 0,39%, с учетом нелинейности входных усилителей, нелинейности АЦП, температурного дрейфа, погрешности коэффициента усиления входных усилителей и т. д., погрешность измерения постоянного напряжения составляет примерно 3%, а погрешность дифференциальных измерений напряжения (читай: как амплитуды) составляет порядка 1,5%. Это достаточно большое значение погрешности измерения, учитывая, что средний вольтметр обеспечивает погрешность измерения постоянного напряжения около 0,025%. Но принимая во внимание, что первично осциллограф — это визуальный прибор, и линейность АЧХ большинства современных осциллографов составляет порядка 0,7 от значения полосы пропускания, а полоса пропускания современного ЦЗО может достигать 18 ГГц (LeCroy SDA 18000), то очевидно, что даже на частотах около 1000 МГц ЦЗО составляет конкуренцию вольтметрам переменного тока или измерителям мощности, имеющим погрешность порядка 3%. А принимая во внимание тот факт, что осциллограф способен производить измерения среднеквадратического значения напряжения сигнала любой формы, а ВЧ-вольтметры переменного тока — только сигнала синусоидальной формы, преимущества осциллографа при измерении амплитудных параметров сигнала становятся очевидными.

Так, на рис. 1 приведена осциллограмма синусоидального сигнала частотой 350 МГц и уровнем 1 В, полученная с экрана осциллографа LeCroy WaveRunner WR-6051A с полосой пропускания 500 МГц. Измерения СКО (окно измерения Р1) индицирует значение 970 мВ. Погрешность измерения амплитуды в данном случае составляет 3%.

Для того чтобы пользователь не воспринимал осциллограф в режиме измерения как вещь саму в себе или же, наоборот, четко представлял, какие параметры и какой алгоритм измерения используется в данный момент, компания LeCroy в своих осциллографах при включении измерений сопровождает осциллограмму, на которой производятся измерения, автоматическими маркерами помощи. На рис. 1 при измерении циклического СКЗ видны маркеры, выделяющие полный цикл (полное число периодов) измеряемого сигнала. Но сигнал, представленный на рис. 1, достаточно простой. На рис. 2 приведена осциллограмма одиночного радиоимпульса в режиме измерения циклического СКЗ, видны области измерения СКЗ и результат измерения — 355 мВ.

Если же для данного сигнала применить алгоритм полного измерения СКЗ, то результат измерения будет абсолютно другой. Так, на рис. 3 изображена осциллограмма измерения полного СКЗ, результат измерения составляет 182 мВ.

Напомним, что среднеквадратическое значение сигнала переменного тока эквивалентно значению постоянного напряжения, способного выделять такое же значение тепла на нагрузке, как и исходный сигнал переменного тока. Очевидно, что для режима измерения циклического СКЗ расчет значения напряжения производится только на полезной части сигнала, обладающей энергией и способной производить работу (в том числе выделять тепло). Для полного СЗК в расчет принимаются и участки сигнала, имеющие нулевое значение амплитуды, и не способные совершать работу, что уменьшает значение СКЗ с 355 мВ до 182 мВ. Это становится наиболее наглядным именно при использовании осциллографов, способных дать инженеру подсказку в виде маркеров, которые кроме всего прочего индицируют в виде горизонтальной зоны значение СЗК, именно в виде эквивалентного постоянного напряжения.

Ранее уже отмечалось, что любой средний вольтметр способен производить измерения амплитуды гораздо более точно, чем цифровой осциллограф. Но это справедливо только для измерения постоянного напряжения или НЧ-напряжения переменного тока синусоидальной формы. При измерении СКЗ сигналов сложной формы погрешность вольтметра увеличивается исходя их коэффициента формы сигнала. Для стандартных сигналов коэффициент формы можно учесть при определении дополнительной погрешности измерения напряжения, и погрешность может возрастать в десятки раз, например, для вольтметра Agilent Technologies 34401 при измерении импульсных сигналов погрешность измерения напряжения может достигать 46%. Для сигналов непредсказуемой формы коэффициент формы учесть невозможно, поэтому и погрешность измерения напряжения становится неопределенной. Цифровой осциллограф производит математическое вычисление среднеквадратического значения формы сигнала из массива данных, полученных в процессе сбора информации, по формуле:

где X₁; X₂; X₃…X_n — отсчеты амплитуды, полученные в результате дискретизации входного сигнала, а n — число отсчетов. Такой алгоритм измерения СКЗ не требует никаких дополнительных поправочных коэффициентов. Для однократных и редких сигналов цифровой осциллограф остается единственным средством измерения СКЗ, да и других амплитудных параметров сигнала тоже. А принимая во внимание тот факт, что осциллограф при измерении СКЗ производит «полное» измерение сигнала, имея в виду одновременное измерение как постоянной составляющей DC, так и переменной составляющей AC, а большинство вольтметров производит измерения отдельно DC и AC, и лишь за редким исключением некоторые типы вольтметров способны производить измерения DC+AC, то становится очевидным, что возможности амплитудных измерений ЦЗО дают пользователю значительные преимущества по отношению к универсальным вольтметрам.

Как ни странно, но даже среди опытных инженеров существует мнение, что цифровой осциллограф производит измерение напряжения по одному периоду периодического сигнала, но как видно из выкладок, представленных выше, это не соответствует действительности. Для определения различных амплитудных параметров сигнала измерения производятся по всему массиву данных, составляющих форму сигнала, но в силу особенности измерения амплитудных параметров, осциллограф действительно может выдать только один результат измерения за один проход развертки, поскольку именно это и является циклом измерения. На рис. 4 приведен пример измерения пикового значения напряжения. Пиковое значение — это разность межу минимальным и максимальным значениями формы сигнала на одной развертке. Очевидно, что для вычисления этого параметра прежде всего необходимо определить как минимальное, так и максимальное значение на всей форме сигнала. Для этого, опять же, необходим анализ всего массива данных точек, образующих форму сигнала.

Очевидно, что для достоверных и быстрых измерений при большом массиве данных осциллограф должен обладать достаточным быстродействием для обеспечения необходимых вычислений. И в этой ситуации не все осциллографы ведут себя одинаково. Так, осциллограф LeCroy, осциллограммы которого приведены выше, при длине памяти 10 Мбайт при отсутствии измерений обеспечивает время сбора осциллограмм 210 мс, при включении одного измерения время сбора осциллограммы увеличивается до 340 мс, а при включении четырех одновременных измерений увеличивается до 430 мс. То есть при включении четырех измерений время сбора осциллограмм увеличивается в 2,04 раза. Если же аналогичные режимы измерений произвести, используя осциллограф Tektronix DPO-4034, то результаты получаются следующие: при отсутствии измерений время сбора осциллограмм составляет 170 мс, при включении одного измерения время сбора осциллограммы увеличивается до 16 с, а при включении одновременно четырех измерений — до 40 с. То есть при включении четырех измерений время сбора осциллограмм у осциллографа Tektronix DPO-4034 увеличивается в 235 раз.

Современные профессиональные осциллографы, например LeCroy, в штатной комплектации (то есть без дополнительных опций) могут обеспечить возможность измерения 11 амплитудных параметров, подробный перечень параметров приведен в таблице (см. на сайте http://www.finestreet.ru/05_65_table.html).

Важной особенностью обеспечения измерений является возможность проведения измерения в выделенной области. В этом случае измерения параметров производятся не по всему массиву данных осциллограммы, а только в пределах указанной области. Большинство же пользователей привыкли, что измерения с использованием ЦЗО нужно производить для простого периодического сигнала по всей осциллограмме, что присутствует на экране ЦЗО и только в таком случае результаты будут достовернымы. На рис. 5 проведен наглядный пример сложного сигнала, представляющего собой прямоугольный сигнал с модулированными базой и верхом. На первый взгляд автоматические измерения амплитудных параметров такого сигнала должны вызвать затруднения у пользователя, но только не у пользователей осциллографов LeCroy.

Для измерения некоторых амплитудных параметров модулирующего сигнала задействуем измерения Р1, Р2 и Р3. Для измерения СКЗ модулирующего сигнала базы (измерения Р1) выделяется только часть модулирующего сигнала базы. Результат составляет 147 мВ. Для измерения СКЗ модулирующего сигнала верха (измерения Р2) выделяется только часть модулирующего сигнала верха. Результат составляет 1,01 В. Для измерения пикового значения модулирующего сигнала верха (измерения Р3) выделяется только часть модулирующего сигнала верха. Результат составляет 482 мВ. Измерения Р4 и Р5 обеспечивают измерения амплитудных параметров основного прямоугольного сигнала — уровня верха и уровня базы, эти измерения производятся без выделения области.

Таким образом, обеспечивая возможность одновременного измерения до 8 параметров сигнала, осциллографы LeCroy так же обеспечивают возможность измерения в 8 различных областях этого сигнала. Справедливости ради отметим, что и другие осциллографы, например Tektronix DPO-7000 или DPO-4000, также позволяют измерять параметры в выделенной области, но для всех измерений (DPO-7000 — это 8 измерений, а для DPO-4000 — это 4 измерения) существует всего одна выделенная область, что существенно ограничивает возможности измерения сложных сигналов.

Измерения временных параметров

Измерения временных параметров — это набор наиболее расширенных и точных видов измерений цифрового осциллографа. Так уже сложилось, что при анализе сигнала по временной оси существует наибольший набор параметров, в штатной комплектации осциллографы LeCroy способны обеспечить до 69 видов измерения, а при инсталляции дополнительных опций общее число всех видов измерений может достигать 180. Основными отличиями цифровых осциллографов по отношению к традиционным аналоговым осциллографам при измерении временных интервалов являются следующие:

1. Цифровой осциллограф обеспечивает автоматическое измерение временных параметров (не стоит забывать и про автоматическое измерение амплитудных параметров), аналоговый осциллограф обеспечивает измерения временных интервалов, используя деления временной шкалы на экране.
2. Цифровой осциллограф обеспечивает погрешность измерения временных до 0,0001%, а лучшие экземпляры аналоговых осциллографов имеют погрешность измерения всего 1,5%.

Погрешность измерения временных параметров (ΔT) цифрового осциллографа определяется погрешностью опорного генератора, частотой дискретизации и собственным джиттером, что может быть выражено формулой:

где T_оп — погрешность установки частоты опорного генератора; F_д — частота дискретизации; T_дж — собственный джиттер осциллографа.

Для осциллографов LeCroy применение специальных алгоритмов интерполяции при проведении автоматических измерений позволяет снизить влияние частоты дискретизации на погрешность измерения более чем в 16 раз, и формула (1) приобретает вид:

Современные технологии электронных элементов дают возможность применения в осциллографах опорных генераторов с погрешностью установки до 10^–6 в год (или 1 ppm), частота дискретизации для наиболее массовых моделей ЦЗО составляет 5 ГГц или 10 ГГц, а в режиме эквивалентной дискретизации до 250 Гвыб/с, собственный джиттер современного осциллографа удается снизить до значений 3 пс (например, SDA-18000). Из этих выкладок следует, что наиболее существенным при определении погрешности измерения временных интервалов как раз и является погрешность установки частоты опорного генератора.

Но на этом и заканчивается идентичность подходов и нормирование погрешностей при измерении временных интервалов различных производителей цифровых осциллографов. Разные производители при измерении временных интервалов накладывают дополнительные требования для достижения декларируемой погрешности измерения. Так, например, компания Tektronix для своих осциллографов серии TDS-5000B для обеспечения погрешности, указанной в формуле (1), при автоматических измерениях дополнительно требует:

1. обеспечить амплитуду сигнала не менее 5 делений;
2. должен быть установлен режим сбора информации «усреднение», с числом усреднений не менее 100;
3. результат измерения определяется как среднее из массива данных при накоплении 1000 результатов измерения частоты. Это требование в общем, тоже понятно, поскольку классический частотомер, при измерении частоты имеет такой параметр, как «время счета», за это время происходит определение среднего значения частоты за весь период измерения, и чем больше время счета, тем более точный результат можно получить. Поскольку осциллограф не имеет времени счета при измерении частоты, то эквивалентом этого параметра является накопление статистики измерения частоты.

Различные производители ЦЗО используют различные алгоритмы автоматического измерения временных интервалов. Большинство производителей, например Tektronix или Agilent Technologies, используют алгоритм измерения частоты по одному периоду сигнала, находящегося сразу после точки запуска развертки. При таком алгоритме измерения первое, что приносится в жертву, — время измерения (оно бесспорно увеличивается). Так, практические измерения показывают, что для упомянутого выше осциллографа Tektronix серии TDS-5000B (при длине памяти 2000 точек для минимизации временных затрат на вычислительный процесс) измерение частоты 10 МГц, полученной от рубидиевого стандарта частоты с погрешностью воспроизведения 10^–10, время измерения, при выполнении всех требований производителя, составляет 1 минуту 23 секунды. Компания LeCroy в своих осциллографах использует алгоритм измерения временного интервала не по одному периоду, а по всем периодам сигнала, присутствующим в массиве данных со статистической обработкой.

Кроме того, для обеспечения погрешности, указанной в формуле (1), компания LeCroy дополнительно требует выполнения двух условий:

1. обеспечить амплитуду сигнала не менее 5 делений;
2. результат измерения определяется как среднее из массива данных при накоплении 1000 результатов измерения частоты.

Очевидно, что такой алгоритм измерения обеспечивает следующие преимущества:

1. значительно повышается скорость измерений;
2. возможность создания и обработки статистических данных, полученных на основе массивов результатов измерений;
3. возможность получения результатов измерения для динамических сигналов.

Практическое измерение показывает, что для накопления статистики и получения достоверного результата при измерении частоты 10 МГц, при частоте дискретизации 5 ГГц, необходимо время 100 мс, что в 930 раз меньше, чем требовалось осциллографу Tektronix.

А осциллограф LeCroy WR-6051А за время измерения 100 мс обеспечил погрешность измерения 1 ppm (при допустимой погрешности измерения 10 ppm) (рис. 6).

Практическая ценность измерения временных интервалов по всему числу периодов, существующих во входном сигнале, обусловлена не только увеличением скорости измерений, но и увеличением достоверности измерения — очевидно, что если сигнал имеет вандер (медленная флуктуация во времени), то при достаточно большом времени измерения и тем более при использовании функции усреднения, достоверность измерения будет уменьшаться.

Кроме того, совмещение особенностей измерения временных интервалов по всей осциллограмме и режима измерения в выделенной области дает новые возможности в измерениях сигналов. На рис. 7 праведен пример частотно-модулированного сигнала (осциллограмма С1) и модулирующего сигнала (осциллограмма С2). Очевидно, что поскольку модулирующий сигнал имеет вид «ступеньки», то и частоты в модулируемом сигнале также изменяются дискретно.

Включив режим измерения частоты осциллограммы С1 для всех восьми измерений Р1…Р8, с той лишь разницей, что для каждого измерения Р1…Р8 измерения частоты производятся в пределах выделенного окна, равного времени одной ступеньки, возможно измерить частоту модулируемого сигнала соответственно каждому уровню модулирующего сигнала.

В заключение обзора «простых» режимов измерения хочется особо отметить, что для получения результатов измерения сложных сигналов иногда не достаточно просто включить тот или иной режим измерения. Комбинирование различных режимов работы цифрового осциллографа, включая математические операции над сигналом, может оказать существенную пользу при измерении его параметров. Так, существует задача измерения временных параметров радиоимпульса — частоты заполнения и периода повторения и длительности импульсов. Если для измерения частоты заполнения можно использовать методы, описанные выше, то автоматическое измерение периода повторения и длительности радиоимпульсов может вызвать затруднение. Для решения этой задачи необходимо выделить огибающую радиоимпульса и измерить период повторения и длительность. Огибающую радиоимпульса можно выделить, используя математическую функцию «прореживание».

На рис. 8 приведен пример радиоимпульса, представляющего собой пакет синусоидальных колебаний частотой 1 МГц и периодом повторения 1,543 мс, каждый пакет содержит 428 колебаний частоты 1 МГц.

Из исходной осциллограммы С1 можно получить следующие результаты:

1. Оно частоты сигнала заполнения. Измерение производится по всему экрану и результат представлен в окне Р1 — 1,0000062 МГц.
2. Измерение числа периодов сигнала в одном пакете — для этого используется измерение в выделенном окне (крайнего левого пакета) и результат представлен в окне Р5 — 428 периодов сигнала.

Из осциллограммы растяжки Z1 можно визуально оценить форму сигнала заполнения и также измерить частоту сигнала заполнения (но более точно), результат представлен в окне Р2 — 1,0000004 МГц.

Из осциллограммы математики F1 можно получить следующие результаты:

1. Измерение периода повторения радиоимпульсов. Измерение производится по всему экрану и результат представлен в окне Р3 — 1,5425064 мс.
2. Измерение длительности одного пакета радиоимпульса, результат представлен в окне Р4 — 428,2652 мкс.

Постобработка результатов измерения

В отличие от цифровых осциллографов других производителей, осциллографы LeCroy способны хранить результаты измерения всего массива данных, а это в зависимости от установленных, опций до 6 млн результатов измерений. Такой массив данных можно представлять в графическом виде, обрабатывать методами математической статистики и выводить результаты статистической обработки, сохранять в виде файлов данных для экспорта в другие программные приложения операционной среды Windows. Все это предоставляет пользователю осциллографов LeCroy широкие дополнительные возможности по анализу сигнала.

График слежения

Например, существует широтно импульсно-модулированный сигнал, в котором по некоторому закону изменяется длительность импульса, и необходимо оценить партеры этого сигнала (ШИМ). Несколько периодов исходного сигнала захвачены осциллографом и отображаются на осциллограмме С1 (рис. 9).

Очевидно, что «широта» импульса в ШИМ-сигнале — это длительность импульса, измерение Р1 как раз и обеспечивает измерение длительности импульса сигнала С1. Для того чтобы наглядно продемонстрировать возможности режима измерения, осциллограмма получена в режиме однократного пуска. Из статистического окна измерения Р1 видно, что на всем сигнале произведено 249 измерений длительностей импульса, а поскольку сигнал является динамическим (его параметр «длительность импульса» изменяется во времени), то окошко измерения Р1 дает только общие представления о длительности импульса (последнее измерение, минимальное значение, максимальное значение и т. д.), но не отражает динамики изменения самого параметра «длительность импульса». Осциллографы LeCroy имеют возможность формировать из массива данных измерения так называемый «график слежения». Этот график представляет собой функцию, в которой горизонтальная ось (ось X) представляет собой временную ось, полностью совпадающую с временной осью развертки, а по оси Y (вертикальной оси) располагаются значения результата измерения заданного параметра. В результате получается временной график измерений выбранного параметра в пределах одной развертки осциллографа. Из рис. 9 четко видно, что ШИМ-сигнал модулируется по закону, близкому к логарифмическому. Используя режим курсорных измерений, можно просто подвести курсор к нужному значению длительности на графике слежения (само значение будет отображаться в дескрипторе графика слежения, в данном случае это F4, а положение курсора по временной оси индицируется во временном поле курсора), и на осциллограмме входного сигнала этим же маркером будет отмечена точка сигнала, соответствующая выбранной длительности. Благодаря растяжке сигнала можно получить изображение сигнала в удобном для визуального наблюдения масштабе — курсор также будет присутствовать на сигнале растяжки.

Для режима измерений можно задать регистрацию только значений, находящихся в пределах указанного допуска. Так, если для сигнала, приведенного на рис. 9, ограничить значения измеренной длительности пределом 440–505 нс, то осциллограф регистрирует только значения длительности, находящиеся в этом пределе, и тренд F4 приобретает вид, отличный от показанного на рис. 10.

Такой вид графика слежения позволяет более наглядно обнаружить на исходном сигнале С1 участки, соответствующие заданным пределам длительности.

Если же вернуться к частотно-модулированному сигналу, приведенному на рис. 8, и применить график слежения к результатам измерения частоты в пределах всей осциллограммы (рис. 11), то полученный график даст более наглядный результат изменения частоты в модулированном сигнале, с учетом динамики изменения сигнала в пределах одной модулирующей ступеньки.

На осциллограмме графика слежения также представляется возможным произвести различные автоматические измерения, характеризующие изменение выбранного параметра. Например, на рис. 12 осциллограмма С1 представляет собой частотно-модулированный сигнал с несущей 1 МГц, девиацией 200 кГц и частотой модулирующего синусоидального сигнала 1,234 кГц.

Осциллограмма F4 представляет собой график слежения изменения частоты в сигнале С1, форма осциллограммы F1 отображает форму модулирующего сигнала. Используя автоматические измерения для данного графика, можно определить минимальное значение частоты (Р4 = 800 кГц), максимальное значение частоты (Р3 = 1,1999 МГц) и частоту модулирующего сигнала (Р2 = 1,233 кГц), что совпадает с заданными параметрами ЧМ-сигнала.

График слежения образуется из массива измерения амплитудных или временных измерений, он позволяет визуально отследить изменения выбранного параметра в пределах одной развертки, а также, используя курсоры, получить результаты измерения выбранного параметра в точке нахождения курсора, но все же он не является реальным массивом результатов измерения. С учетом алгоритма амплитудных измерений (один полученный результат из одного прохода развертки осциллографа) график слежения обеспечивает наглядное отображение только временных измерений, при индикации амплитудных измерений график слежения сводится в одну точку, являющуюся результатом измерений. Реальный массив измерений в графическом виде в осциллографах LeCroy может быть представлен так называемым «трендом».

Тренд

Этот график представляет собой функцию, в которой горизонтальная ось (ось X) представляет ось номера измерения — 1, 2, 3, 4,…n, (эта ось не связана с временной осью развертки осциллографа), а по оси Y (вертикальной оси) располагаются значения результата измерения выбранного параметра. В результате получается график.

Отличиями тренда от графика слежения являются:

1. Тренд строится по любому выбранному виду измерения — амплитудному, временному или вспомогательному. График слежения строится только по временным измерениям.
2. Тренд состоит только из реальных точек значений результатов измерений и представляет собой развернутый массив данных результатов измерений. Число точек тренда задается пользователем и может составлять от 1 до 6 млн (в зависимости от типа осциллографа и установленных опций).
3. В зависимости от выбранного режима тренд может строиться по результатам измерения одного прохода развертки или по всем значениям, полученным в результате измерений.
4. При сохранении тренда в файл сохраняется весь выбранный массив результатов измерений с указанием номера измерения. Далее эти данные можно использовать для обработки внешними средствами.
5. Тренд не имеет возможности регистрации значений, находящихся в пределах указанного допуска, он отображает все значения результата измерения.

Так, при построении тренда и графика слежения для измеренных значений длительности импульса в нерегулярной последовательности в пределах одной развертки тренд и график слежения практически совпадают по форме (рис. 13). Разница состоит в том, что график слежения отображает изменение длительности импульсов во времени и имеет более сглаженный вид, а тренд отображает измеренное значение длительности импульса и имеет более «остроконечный» вид).

Практическая ценность тренда заключается в возможности не только кратковременной, но и длительной регистрации и индикации результатов измерений выбранного параметра. В этом случае тренд будет выглядеть как регистрация данных на бумажном самописце, но без меток реального времени. При необходимости изменение интервала регистрации производится изменением настроек схемы синхронизации, например установкой задержки синхронизации по числу событий. Это позволяет регистрировать, отображать и анализировать медленные измерения тех или иных параметров входного сигнала. На рис. 14 осциллограмма F1 представляет тренд изменения частоты входного сигнала С1, полученный из массива измерения частоты Р1.

На рис. 15 осциллограмма F1 представляет тренд изменения амплитуды входного сигнала С1, полученный из массива измерения среднеквадратического значения Р1.

Способом, аналогичным для графика слежения, на осциллограмме тренда так же можно осуществить различные автоматические измерения, далее строить тренды 2-го уровня для этих измерений, 3-го уровня и так далее.

Осциллографы LeCroy обеспечивают построение тренда в трех режимах:

1. Полный, по всему массиву данных — в этом случае тренд классически строится по всему буферу данных результатов измерения и число точек тренда ограничено 6 млн.
2. С усреднением. В этом режиме одна точка тренда строится как среднее из результатов массива измерения, полученного за один проход развертки. Такой алгоритм позволяет уменьшить шум на тренде, вызванный естественным разбросом параметра сигнала от периода к периоду. Очевидно, что применение данного режима оптимально для временных измерений, где за одни проход развертки осциллограф производит «обмер» все периодов входного сигнала и вычисляет среднее значение. При амплитудных измерениях, когда измерения действительны только для одного периода сигнала, усреднение не дает должного результата.
3. По одной осциллограмме. Линия тренда строится из результатов измерения, полученных при одном проходе развертки. Этот режим, как и усреднение, дает результат только при измерении временных параметров.

На рис. 16 для сигнала С1 частотой 1 МГц, имеющего медленный дрейф порядка 10 МГц, одновременно представлены все три типа трендов: F2 — полный, F1 — с усреднением полный, F3 — по одной осциллограмме.

Сочетание различных функциональных особенностей осциллографов LeCroy предоставляет самые широкие возможности при исследовании различных сигналов, процессов и устройств.

В частности, режим построения тренда можно использовать для измерения амплитудно-частотной характеристики устройств. Для этого достаточно синхронизировать процесс изменения частоты на генераторе тестового сигнала с разверткой осциллографа, произвести измерения амплитуды и частоты на выходе устройства. И по полученным результатам построить тренд изменения амплитуды, что и будет являться АЧХ устройства. Синхронный тренд изменения частоты предназначен для формирования частотных меток АЧХ. На рис. 17 осциллограмма F1 представляет собой АЧХ устройства в диапазоне частот от 100 кГц до 100 МГц. Осциллограмма F2, являющаяся трендом частоты, идентифицирует частотный диапазон АЧХ. Используя курсорные измерения, можно считать с АЧХ устройства информацию об амплитуде и частоте.

Гистограммы

Возможности построения, анализа и измерения гистограмм цифровыми осциллографами LeCroy являются одной из его особенностей по отношению к производителям других ЦЗО, которая превращает просто цифровой осциллограф в мощный аналитический инструмент. Построение гистограмм осциллографом LeCroy — это элемент математической статистики, специально адаптированный для анализа форм и параметров электрических сигналов. Гистограмма в математической статистике — это функция плотности вероятности некоторого распределения, построенная на основе выборки из него. Другими словами, гистограмма — это график, отображающий степень повторяемости данных в больших массивах. Гистограмма позволяет сжать гигантский размер данных в компактный график, удобный для анализа, измерений или просто визуальной оценки. В случае цифрового осциллографа в качестве массива данных выступает массив данных измерения выбранного параметра. Так, на рис. 18 приведена гистограмма измерения сигнала частотой 10 МГц (сам исходный сигнал на картинке не присутствует). Массив данных, из которого строится данная гистограмма, собран при измерении частоты Р1 и представляет собой массив размером более 6 млн значений измерений частоты.

Поскольку сигнал является стабильным и изменения частоты не происходит, то разброс значений частоты вызван естественными причинами хаотического рода. Такая гистограмма является классической и называется нормальной, или Гауссовой. Непрерывная случайная величина X имеет нормальный закон распределения с параметрами α (среднее значение) и σ (сигма, или стандартное отклонение), если ее плотность вероятности ƒ (x) имеет вид:

Основными параметрами гистограммы являются:

1. α (среднее значение);
2. σ (сигма, или стандартное отклонение):
3. диапазон гистограммы:
4. плотность заполнения.

Поскольку гистограмма строится из массива измерения, то основные параметры гистограммы, связанные со статистическими данными результатов измерений, выглядят так:

• α (среднее значение гистограммы) — представляет собой центральную, наиболее вероятную часть гистограммы и измеренное среднее значение гистограммы 10,0002 МГц (рис. 17), маркер «mean» и измерение Р2 равно среднему измеренному значению частоты в измерении Р1 = 10,0002 МГц (значение mean).
• σ (сигма, или стандартное отклонение) — диапазон, в котором сосредоточено 68% всех полученных измеренных значений, равный среднему значению гистограммы ±1 сигма. На рис. 17 обозначен маркерами как mean ±sdev. Значение стандартного отклонения гистограммы Р3 = 14,99 кГц равно стандартному отклонению измерения частоты Р1 (значение sdev = 14,99 кГц). Для сигналов с нулевым средним значением стандартное отклонение равно среднеквадратическому значению (СКЗ) измеренного параметра.
• Диапазон гистограммы — горизонтальный диапазон, в котором сосредоточены все значения гистограммы. Физическая интерпретация диапазона гистограммы — это разность между максимальным и минимальным значениями во всем массиве измерений. На рис. 17 диапазон гистограммы обозначен маркерами range, а его измеренное значение представлено в поле Р4 и его значение 144,3 кГц совпадает с разностью между максимальным и значениями минимальным измерения Р1 (в поле Р1 в явном виде не представлено).
• Плотность заполнения — это общее число измерений, из результатов которых строится гистограмма. Так, измеренное значение плотности гистограммы Р5 совпадает с числом измерений индицируемым в поле измерений Р1 и составляет в обоих случаях 1,749931 млн измерений.

Следующим примером использования гистограмм для наблюдения и анализа формы сигнала может служить гистограмма измерения частоты 1 МГц частотно-модулированного сигнала с девиацией 200 кГц (рис. 19 — осциллограмма F2).

Измерение таких параметров, как верхнее значение и нижнее значение гистограммы, дает значение нижней и верхней частоты в ЧМ-сигнале (измерения Р4 и Р5). А амплитудное значение гистограммы, деленное на 2, дает значение девиации ЧМ-сигнала — измерение Р6 и значение 198 кГц. Для этой гистограммы также можно использовать курсорные измерения для определения других параметров гистограммы—диапазон гистограммы, нижнее и верхнее значения. А применение режимов измерения вспомогательных параметров гистограммы, таких как число пиков гистограммы, дает информацию о количестве стабильных состояний сигнала. Возвращаясь к рис. 9, гистограмма F3 индицирует, что частота сигнала входного сигнала имеет 9 стабильных состояний, а измерение параметров гистограммы предоставит информацию о распределении частоты во входном сигнале.

Итак, как видно, гистограмма способна преобразовать большой объем информации в очень компактный формат, который может быть легко измерен и проанализирован методами математической статистики.