Trial and error example - Исправление ошибок и поиск оптимальных решений проблем

From Wikipedia, the free encyclopedia

Trial and error is a fundamental method of problem-solving^[1] characterized by repeated, varied attempts which are continued until success,^[2] or until the practicer stops trying.

According to W.H. Thorpe, the term was devised by C. Lloyd Morgan (1852–1936) after trying out similar phrases «trial and failure» and «trial and practice».^[3] Under Morgan’s Canon, animal behaviour should be explained in the simplest possible way. Where behavior seems to imply higher mental processes, it might be explained by trial-and-error learning. An example is a skillful way in which his terrier Tony opened the garden gate, easily misunderstood as an insightful act by someone seeing the final behavior. Lloyd Morgan, however, had watched and recorded the series of approximations by which the dog had gradually learned the response, and could demonstrate that no insight was required to explain it.

Edward Lee Thorndike was the initiator of the theory of trial and error learning based on the findings he showed how to manage a trial-and-error experiment in the laboratory. In his famous experiment, a cat was placed in a series of puzzle boxes in order to study the law of effect in learning.^[4] He plotted to learn curves which recorded the timing for each trial. Thorndike’s key observation was that learning was promoted by positive results, which was later refined and extended by B. F. Skinner’s operant conditioning.

Trial and error is also a method of problem solving, repair, tuning, or obtaining knowledge. In the field of computer science, the method is called generate and test (Brute force). In elementary algebra, when solving equations, it is guess and check.

This approach can be seen as one of the two basic approaches to problem-solving, contrasted with an approach using insight and theory. However, there are intermediate methods which for example, use theory to guide the method, an approach known as guided empiricism.

This way of thinking has become a mainstay of Karl Popper’s critical rationalism.

Methodology[edit]

The trial and error approach is used most successfully with simple problems and in games, and it is often the last resort when no apparent rule applies. This does not mean that the approach is inherently careless, for an individual can be methodical in manipulating the variables in an attempt to sort through possibilities that could result in success. Nevertheless, this method is often used by people who have little knowledge in the problem area. The trial-and-error approach has been studied from its natural computational point of view ^[5]

Simplest applications[edit]

Ashby (1960, section 11/5) offers three simple strategies for dealing with the same basic exercise-problem, which have very different efficiencies. Suppose a collection of 1000 on/off switches have to be set to a particular combination by random-based testing, where each test is expected to take one second. [This is also discussed in Traill (1978–2006, section C1.2]. The strategies are:

the perfectionist all-or-nothing method, with no attempt at holding partial successes. This would be expected to take more than 10^301 seconds, [i.e., 2^1000 seconds, or 3·5×(10^291) centuries]
a serial-test of switches, holding on to the partial successes (assuming that these are manifest), which would take 500 seconds on average
parallel-but-individual testing of all switches simultaneously, which would take only one second

Note the tacit assumption here that no intelligence or insight is brought to bear on the problem. However, the existence of different available strategies allows us to consider a separate («superior») domain of processing — a «meta-level» above the mechanics of switch handling — where the various available strategies can be randomly chosen. Once again this is «trial and error», but of a different type.

Hierarchies[edit]

Ashby’s book develops this «meta-level» idea, and extends it into a whole recursive sequence of levels, successively above each other in a systematic hierarchy. On this basis, he argues that human intelligence emerges from such organization: relying heavily on trial-and-error (at least initially at each new stage), but emerging with what we would call «intelligence» at the end of it all. Thus presumably the topmost level of the hierarchy (at any stage) will still depend on simple trial-and-error.

Traill (1978–2006) suggests that this Ashby-hierarchy probably coincides with Piaget’s well-known theory of developmental stages. [This work also discusses Ashby’s 1000-switch example; see §C1.2]. After all, it is part of Piagetian doctrine that children learn first by actively doing in a more-or-less random way, and then hopefully learn from the consequences — which all has a certain resemblance to Ashby’s random «trial-and-error».

Application[edit]

Traill (2008, espec. Table «S» on p.31) follows Jerne and Popper in seeing this strategy as probably underlying all knowledge-gathering systems — at least in their initial phase.

Four such systems are identified:

Natural selection which «educates» the DNA of the species,
The brain of the individual (just discussed);
The «brain» of society-as-such (including the publicly held body of science); and
The adaptive immune system.

Features[edit]

Trial and error has a number of features:

solution-oriented: trial and error makes no attempt to discover why a solution works, merely that it is a solution.
problem-specific: trial and error makes no attempt to generalize a solution to other problems.
non-optimal: trial and error is generally an attempt to find a solution, not all solutions, and not the best solution.
needs little knowledge: trials and error can proceed where there is little or no knowledge of the subject.

It is possible to use trial and error to find all solutions or the best solution, when a testably finite number of possible solutions exist. To find all solutions, one simply makes a note and continues, rather than ending the process, when a solution is found, until all solutions have been tried. To find the best solution, one finds all solutions by the method just described and then comparatively evaluates them based upon some predefined set of criteria, the existence of which is a condition for the possibility of finding a best solution. (Also, when only one solution can exist, as in assembling a jigsaw puzzle, then any solution found is the only solution and so is necessarily the best.)

Examples[edit]

Trial and error has traditionally been the main method of finding new drugs, such as antibiotics. Chemists simply try chemicals at random until they find one with the desired effect. In a more sophisticated version, chemists select a narrow range of chemicals it is thought may have some effect using a technique called structure–activity relationship. (The latter case can be alternatively considered as a changing of the problem rather than of the solution strategy: instead of «What chemical will work well as an antibiotic?» the problem in the sophisticated approach is «Which, if any, of the chemicals in this narrow range will work well as an antibiotic?») The method is used widely in many disciplines, such as polymer technology to find new polymer types or families.

Trial and error is also commonly seen in player responses to video games — when faced with an obstacle or boss, players often form a number of strategies to surpass the obstacle or defeat the boss, with each strategy being carried out before the player either succeeds or quits the game.

Sports teams also make use of trial and error to qualify for and/or progress through the playoffs and win the championship, attempting different strategies, plays, lineups and formations in hopes of defeating each and every opponent along the way to victory. This is especially crucial in playoff series in which multiple wins are required to advance, where a team that loses a game will have the opportunity to try new tactics to find a way to win, if they are not eliminated yet.

The scientific method can be regarded as containing an element of trial and error in its formulation and testing of hypotheses. Also compare genetic algorithms, simulated annealing and reinforcement learning – all varieties for search which apply the basic idea of trial and error.

Biological evolution can be considered as a form of trial and error.^[6] Random mutations and sexual genetic variations can be viewed as trials and poor reproductive fitness, or lack of improved fitness, as the error. Thus after a long time ‘knowledge’ of well-adapted genomes accumulates simply by virtue of them being able to reproduce.

Bogosort, a conceptual sorting algorithm (that is extremely inefficient and impractical), can be viewed as a trial and error approach to sorting a list. However, typical simple examples of bogosort do not track which orders of the list have been tried and may try the same order any number of times, which violates one of the basic principles of trial and error. Trial and error is actually more efficient and practical than bogosort; unlike bogosort, it is guaranteed to halt in finite time on a finite list, and might even be a reasonable way to sort extremely short lists under some conditions.

Jumping spiders of the genus Portia use trial and error to find new tactics against unfamiliar prey or in unusual situations, and remember the new tactics.^[7] Tests show that Portia fimbriata and Portia labiata can use trial and error in an artificial environment, where the spider’s objective is to cross a miniature lagoon that is too wide for a simple jump, and must either jump then swim or only swim.^[8]^[9]

References[edit]

^ Campbell, Donald T. (November 1960). «Blind variation and selective retention in creative thoughts as in other knowledge processes». Psychological Review. 67 (6): 380–400. doi:10.1037/h0040373. PMID 13690223.
^ Concise Oxford Dictionary p1489
^ Thorpe W.H. The origins and rise of ethology. Hutchinson, London & Praeger, New York. p26. ISBN 978-0-03-053251-1
^ Thorndike E.L. 1898. Animal intelligence: an experimental study of the association processes in animals. Psychological Monographs #8.
^ X. Bei, N. Chen, S. Zhang, On the Complexity of Trial and Error, STOC 2013
^ Wright, Serwall (1932). «The roles of mutation, inbreeding, crossbreeding and selection in evolution» (PDF). Proceedings of the Sixth International Congress on Genetics. Volume 1. Number 6: 365. Retrieved 17 March 2014.
^ Harland, D.P. & Jackson, R.R. (2000). ««Eight-legged cats» and how they see — a review of recent research on jumping spiders (Araneae: Salticidae)» (PDF). Cimbebasia. 16: 231–240. Archived from the original (PDF) on 28 September 2006. Retrieved 5 May 2011.
^ Jackson, Robert R.; Fiona R. Cross; Chris M. Carter (2006). «Geographic Variation in a Spider’s Ability to Solve a Confinement Problem by Trial and Error». International Journal of Comparative Psychology. 19 (3): 282–296. doi:10.46867/IJCP.2006.19.03.06. Retrieved 8 June 2011.
^ Jackson, Robert R.; Chris M. Carter; Michael S. Tarsitano (2001). «Trial-and-error solving of a confinement problem by a jumping spider, Portia fimbriata«. Behaviour. Leiden: Koninklijke Brill. 138 (10): 1215–1234. doi:10.1163/15685390152822184. ISSN 0005-7959. JSTOR 4535886.

Process

Bricolage —
In trial and error, one selects a possible answer, applies it to the problem and, if it is not successful, selects (or generates) another possibility that is subsequently tried. The process ends when a possibility yields a solution.

In some versions of trial and error, the option that is a priori viewed as the most likely one should be tried first, followed by the next most likely, and so on until a solution is found, or all the options are exhausted. In other versions, options are simply tried at random.

Methodology

This approach is more successful with simple problems and in games, and is often resorted to when no apparent rule applies. This does not mean that the approach need be careless, for an individual can be methodical in manipulating the variables in an attempt to sort through possibilities that may result in success. Nevertheless, this method is often used by people who have little knowledge in the problem area.

Simplest applications

Ashby (1960, section 11/5) offers three simple strategies for dealing with the same basic exercise-problem; and they have very different efficiencies:
Suppose there are 1000 on/off switches which have to be set to a particular combination by random-based testing, each test to take one second. [This is also discussed in Traill (1978/2006, section C1.2]. The strategies are:

the perfectionist all-or-nothing method, with no attempt at holding partial successes. This would be expected to take more than 10^301 seconds, [i.e. 2^1000 seconds, or 3·5×(10^291) centuries!];
a serial-test of switches, holding on to the partial successes (assuming that these are manifest) would take 500 seconds; while
a parallel-but-individual testing of all switches simultaneously would take only one second.

Trial-and-error Hierarchies

Ashby’s book develops this «meta-level» idea, and extends it into a whole recursive sequence of levels, successively above each other in a systematic hierarchy. On this basis he argues that human intelligence emerges from such organization: relying heavily on trial-and-error (at least initially at each new stage), but emerging with what we would call «intelligence» at the end of it all. Thus presumably the topmost level of the hierarchy (at any stage) will still depend on simple trial-and-error.

Traill (1978/2006) suggests that this Ashby-hierarchy probably coincides with Piaget’s well-known theory of developmental stages. [This work also discusses Ashby’s 1000-switch example; see §C1.2]. After all, it is part of Piagetian doctrine that children learn by first actively doing in a more-or-less random way, and then hopefully learn from the consequences — which all has a certain resemblance to Ashby’s random «trial-and-error».

The basic strategy in many fields?

Traill (2008, espec. Table «S» on p.31) follows Jerne and Popper in seeing this strategy as probably underlying all knowledge-gathering systems — at least in their initial phase.

Four such systems are identified:

Darwinian evolution which «educates» the DNA of the species!
The brain of the individual (just discussed);
The «brain» of society-as-such (including the publicly-held body of science); and
The immune system.

An ambiguity: Can we have «intention» during a «trial»

In the Ashby-and-Cybernetics tradition, the word «trial» usually implies random-or-arbitrary, without any deliberate choice.
However amongst non-cyberneticians, «trial» will often imply a deliberate subjective act by some adult human agent; (e.g. in a court-room, or laboratory). So that has sometimes led to confusion.

Of course the situation becomes even more confusing if one accepts Ashby’s hierarchical explanation of intelligence, and its implied ability to be deliberate and to creatively design — all based ultimately on non-deliberate actions! The lesson here seems to be that one must simply be careful to clarify the meaning of one’s own words, and indeed the words of others. [Incidentally it seems that consciousness is not an essential ingredient for intelligence as discussed above.]

Features

Trial and error has a number of features:

solution-oriented: trial and error makes no attempt to discover why a solution works, merely that it is a solution.
problem-specific: trial and error makes no attempt to generalise a solution to other problems.
non-optimal: trial and error is generally an attempt to find a solution, not all solutions, and not the best solution.
needs little knowledge: trials and error can proceed where there is little or no knowledge of the subject.

Examples

Trial and error has traditionally been the main method of finding new drugs, such as antibiotics. Chemists simply try chemicals at random until they find one with the desired effect. In a more sophisticated version, chemists select a narrow range of chemicals it is thought may have some effect. (The latter case can be alternatively considered as a changing of the problem rather than of the solution strategy: instead of «What chemical will work well as an antibiotic?» the problem in the sophisticated approach is «Which, if any, of the chemicals in this narrow range will work well as an antibiotic?») The method is used widely in many disciplines, such as polymer technology to find new polymer types or families.

The scientific method can be regarded as containing an element of trial and error in its formulation and testing of hypotheses. Also compare genetic algorithms, simulated annealing and reinforcement learning — all varieties for search which apply the basic idea of trial and error.

Biological evolution is also a form of trial and error. Random mutations and sexual genetic variations can be viewed as trials and poor reproductive fitness, or lack of improved fitness, as the error. Thus after a long time ‘knowledge’ of well-adapted genomes accumulates simply by virtue of them being able to reproduce.

Issues with trial and error

Trial and error is usually a last resort for a particular problem, as there are a number of problems with it. For one, trial and error is tedious and monotonous. Also, it is very time-consuming; chemical engineers must sift through millions of various potential chemicals before they find one that works. Fortunately, computers are best suited for trial and error; they do not succumb to the boredom that humans do, and can potentially do thousands of trial-and-error segments in the blink of an eye.

References

Ashby, W. R. (1960: Second Edition). Design for a Brain. Chapman & Hall: London.
Traill, R.R. (1978/2006). Molecular explanation for intelligence…, Brunel University Thesis, HDL.handle.net
Traill, R.R. (2008). Thinking by Molecule, Synapse, or both? — From Piaget’s Schema, to the Selecting/Editing of ncRNA. Ondwelle: Melbourne. Ondwelle.com — or French version Ondwelle.com.

References

↑ Coding Horror: Fail Early, Fail Often

Learning
Types of learning
Avoidance conditioning \| Classical conditioning \| Confidence-based learning \| Discrimination learning \| Emulation \| Experiential learning \| Escape conditioning \| Incidental learning \|Intentional learning \| Latent learning \| Maze learning \| Mastery learning \| Mnemonic learning \| Nonassociative learning \| Nonreversal shift learning \| Nonsense syllable learning \| Nonverbal learning \| Observational learning \| Omission training \| Operant conditioning \| Paired associate learning \| Perceptual motor learning \| Place conditioning \| Probability learning \| Rote learning \| Reversal shift learning \| Second-order conditioning \| Sequential learning \| Serial anticipation learning \| Serial learning \| Skill learning \| Sidman avoidance conditioning \| Social learning \| Spatial learning \| State dependent learning \| Social learning theory \| State-dependent learning \| Trial and error learning \| Verbal learning
Concepts in learning theory
Chaining \| Cognitive hypothesis testing \| Conditioning \| Conditioned responses \| Conditioned stimulus \| Conditioned suppression \| Constant time delay \| Counterconditioning \| Covert conditioning \| Counterconditioning \| Delayed alternation \| Delay reduction hypothesis \| Discriminative response \| Distributed practice \|Extinction \| Fast mapping \| Gagné’s hierarchy \| Generalization (learning) \| Generation effect (learning) \| Habits \| Habituation \| Imitation (learning) \| Implicit repetition \| Interference (learning) \| Interstimulus interval \| Intermittent reinforcement \| Latent inhibition \| Learning schedules \| Learning rate \| Learning strategies \| Massed practice \| Modelling \| Negative transfer \| Overlearning \| Practice \| Premack principle \| Preconditioning \| Primacy effect \| Primary reinforcement \| Principles of learning \| Prompting \| Punishment \| Recall (learning) \| Recency effect \| Recognition (learning) \| Reconstruction (learning) \| Reinforcement \| Relearning \| Rescorla-Wagner model \| Response \| Reinforcement \| Secondary reinforcement \| Sensitization \| Serial position effect \| Serial recall \| Shaping \| Stimulus \| Reinforcement schedule \| Spontaneous recovery \| State dependent learning \| Stimulus control \| Stimulus generalization \| Transfer of learning \| Unconditioned responses \| Unconditioned stimulus
Animal learning
Cat learning \| Dog learning Rat learning
Neuroanatomy of learning

Neurochemistry of learning
Adenylyl cyclase
Learning in clinical settings
Applied Behavior Analysis \| Behaviour therapy \| Behaviour modification \| Delay of gratification \| CBT \| Desensitization \| Exposure Therapy \| Exposure and response prevention \| Flooding \| Graded practice \| Habituation \| Learning disabilities \| Reciprocal inhibition therapy \| Systematic desensitization \| Task analysis \| Time out
Learning in education
Adult learning \| Cooperative learning \| Constructionist learning \| Experiential learning \| Foreign language learning \| Individualised instruction \| Learning ability \| Learning disabilities \| Learning disorders \| Learning Management \| Learning styles \| Learning theory (education) \| Learning through play \| School learning \| Study habits
Machine learning
Temporal difference learning \| Q-learning
Philosophical context of learning theory
Behaviourism \| Connectionism \| Constructivism \| Functionalism \| Logical positivism \| Radical behaviourism
Prominant workers in Learning Theory\|-
Pavlov \| Hull \| Tolman \| Skinner \| Bandura \| Thorndike \| Skinner \| Watson
Miscellaneous\|-
Category:Learning journals \| Melioration theory
edit

Источник

Short description

: Method of problem-solving

Trial and error is a fundamental method of problem-solving.^[1] It is characterized by repeated, varied attempts which are continued until success,^[2] or until the practicer stops trying.

This way of thinking has become a mainstay of Karl Popper’s critical rationalism.

Methodology

Simplest applications

the perfectionist all-or-nothing method, with no attempt at holding partial successes. This would be expected to take more than 10^301 seconds, [i.e., 2^1000 seconds, or 3·5×(10^291) centuries]
a serial-test of switches, holding on to the partial successes (assuming that these are manifest), which would take 500 seconds on average
parallel-but-individual testing of all switches simultaneously, which would take only one second

Hierarchies

Application

Traill (2008, espec. Table «S» on p.31) follows Jerne and Popper in seeing this strategy as probably underlying all knowledge-gathering systems — at least in their initial phase.

Four such systems are identified:

Natural selection which «educates» the DNA of the species,
The brain of the individual (just discussed);
The «brain» of society-as-such (including the publicly held body of science); and
The adaptive immune system.

Features

Trial and error has a number of features:

solution-oriented: trial and error makes no attempt to discover why a solution works, merely that it is a solution.
problem-specific: trial and error makes no attempt to generalize a solution to other problems.
non-optimal: trial and error is generally an attempt to find a solution, not all solutions, and not the best solution.
needs little knowledge: trials and error can proceed where there is little or no knowledge of the subject.

Examples

References

↑ Campbell, Donald T. (November 1960). «Blind variation and selective retention in creative thoughts as in other knowledge processes». Psychological Review 67 (6): 380–400. doi:10.1037/h0040373. PMID 13690223.
↑ Concise Oxford Dictionary p1489
↑ Thorpe W.H. The origins and rise of ethology. Hutchinson, London & Praeger, New York. p26. ISBN:978-0-03-053251-1
↑ Thorndike E.L. 1898. Animal intelligence: an experimental study of the association processes in animals. Psychological Monographs #8.
↑ X. Bei, N. Chen, S. Zhang, On the Complexity of Trial and Error, STOC 2013
↑ Wright, Serwall (1932). «The roles of mutation, inbreeding, crossbreeding and selection in evolution». Proceedings of the Sixth International Congress on Genetics. Volume 1 Number 6: 365. http://www.esp.org/books/6th-congress/facsimile/contents/6th-cong-p356-wright.pdf. Retrieved 17 March 2014.
↑ Harland, D.P.; Jackson, R.R. (2000). «»Eight-legged cats» and how they see — a review of recent research on jumping spiders (Araneae: Salticidae)». Cimbebasia 16: 231–240. http://www.cogs.susx.ac.uk/ccnr/Papers/Downloads/Harland_Cimb2000.pdf. Retrieved 5 May 2011.
↑ Jackson, Robert R.; Fiona R. Cross; Chris M. Carter (2006). «Geographic Variation in a Spider’s Ability to Solve a Confinement Problem by Trial and Error». International Journal of Comparative Psychology 19: 282–296. http://escholarship.org/uc/item/53c3x1w9;jsessionid=34833B994B69E2CA4DA97613EA34F531#page-1. Retrieved 8 June 2011.
↑ Jackson, Robert R.; Chris M. Carter; Michael S. Tarsitano (2001). «Trial-and-error solving of a confinement problem by a jumping spider, Portia fimbriata«. Behaviour (Leiden: Koninklijke Brill) 138 (10): 1215–1234. doi:10.1163/15685390152822184. ISSN 0005-7959.

Example Sentences

Recent Examples on the Web

Having a level of creativity in that spiritual practice — trial and error, development and expansion — is the most important thing in life.

—Evan Nicole Brown, The Hollywood Reporter, 19 Dec. 2022

The reality: Fixing your snoring often requires dedicated trial and error, which can take years of work, says Dr. Winter.

—Paul Kita, Men’s Health, 15 Dec. 2022

Over decades, cities and counties have conquered naturally soggy landscapes with trial and error, upgrades and tweaks of a massive system of gutters to storm pipes to canals to rivers.

—Kevin Spear, Orlando Sentinel, 2 Oct. 2022

Via trial and error, wear testing, and lots of research, our editors have found those not-so-basic basics, elevated versions of staple items, and the go-to brands for each.

—Madeline Fass, Vogue, 29 July 2022

The concept is simple, but it’s the kind of engineering simplicity that nevertheless requires decades of research and trial and error, and error, and error, and error.

—Stephen Ornes, Discover Magazine, 27 Aug. 2019

For many, debt management is learned through trial and error.

—Ashley Stahl, Forbes, 5 Oct. 2022

Start-ups specifically often seek fully dedicated employees, but there’s a real benefit to hiring experienced consultants who help avoid mistakes and trial and error, given their past experiences solving very similar challenges.

—Bradley Jacobs, Fortune, 2 Dec. 2022

Raptor Canyon might appeal to people who want a powerful gaming desktop without putting in the legwork, research, and trial and error that comes with building a computer inside a tiny case.

—Andrew Cunningham, Ars Technica, 30 Nov. 2022

See More

These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘trial and error.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.

Word History

First Known Use

1806, in the meaning defined above

Time Traveler

The first known use of trial and error was
in 1806

Cite this Entry

“Trial and error.” Merriam-Webster.com Dictionary, Merriam-Webster, https://www.merriam-webster.com/dictionary/trial%20and%20error. Accessed 9 Feb. 2023.

Analytical Reasoning: Trial and Error Method

Learn the right approach to handle Analytical Reasoning questions with the help of Hit & Trial method.

Questions in the analytical reasoning section test your ability to analyze the situation, reason the cause/ effect and then find a solution. While questions in most of the competitive exams have options with them, but sometimes, we are not presented with options. A lot of effort is required to identify and reach the right option. What works best in such Analytical Reasoning questions is what we call as a trial and error strategy.

What is Trial and Error Strategy?

Try something (Guess), if it does not work, guess again. Over time, our guesses become more educated — and we tend to require fewer trials to reach our solutions.

Tips to remember:

First of all you need to read the directions of a particular Data Sufficiency question very carefully as examiner can change the directions and even after solving all the questions correctly you mark the wrong answers.
You need to remember the steps involved in solving a particular Data Sufficiency question and follow them in this particular order: Check A (i.e. the first statement), then Check B (i.e. the second statement) and lastly, if required, combine the two statements to get the answer.
Do not make any assumptions while solving Data Sufficiency questions.

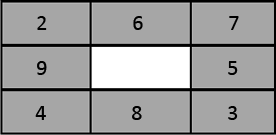
Solved Questions:

Question: 44 people live in eight houses (3 on each side of the Albert Square). Each house has a different number of people living in it. Each line of three houses has 15 people living in it. How many people live in each house?

Solution: Simplifying, we have to get 4 sets of numbers, each of which add up to 15. So start guessing.

The average number of people in a house is 44/8 is roughly 4.5. So what numbers should we take? 2, 3, 4, 5, 6, 7, 8, 9. Now, we should also have an average close to 5 for each set.Let’s start:

Set 1: 3, 5, 7
Set 3: 2, 4, 9
Now, the other two sets will have an overlap. So let’s guess the overlaps:
Set 2: Overlaps are 2 and 7. So the third number will be 6. That’s great! Because we have not used 6 yet.
Set 4: Overlaps are 3 and 9. Then the third number ends up to 3 again. Wrong guess! So we need to try again. Overlaps are 3 and 4. In this case third number works out to be 8, which we have not used. Wonderful!
So here is the answer

Learning

Note that this is not the only solution. There are others possibilities as well.

Analytical Reasoning Practice Question:

Mrs. Choy spent exactly Rs. 10 on 100 eggs for her shop. Large eggs cost her 50 p each. Medium eggs cost her 10 p each. Small eggs cost her 5 p each. For two of the sizes, she bought the same number of eggs. How many of each size did she buy?

Analytical Reasoning — Trial and Error Strategy: Key Learning

imt

Even before guessing the answer, it is important to carefully understand the statement and then narrow down to a set of numbers/ options. These options/ numbers will form a base for using the trial and error strategy.

cat

Источник

Are you still struggling with the topic of factoring trinomials in Algebra? Well, no worries, because you are at the right place.

This article will introduce you to one of the simplest methods of factoring trinomials known as trial and error.

As the name suggests, trial and error factoring entails trying all possible factors until you find the right one.

Trial and error factoring is regarded as one of the best methods of factoring trinomials. It encourages students to develop their mathematical intuition and thus increase their conceptual understanding of the topic.

How to Unfoil trinomials?

Suppose we want to unfoil the general equation of a trinomial ax² + bx + c where a ≠ 1. Here are the steps to follow:

Insert the factors of ax²in the 1^st positions of the two sets of brackets that represent the factors.
Also, insert the possible factors of c into the 2^nd positions of brackets.
Identify both the inner and outer products of the two sets of brackets.
Keep on trying different factors until the sum of the two factors is equal to “bx.”

NOTE:

If c is positive, both factors will have the same sign as “b”.
If c is negative, one factor will have a negative sign.
Never put in the same parentheses’ numbers with a common factor.

Trial and error factoring

Trial and error factoring, which is also referred to as reverse foil or unfoiling, is a method of factoring trinomials built upon different techniques such as foil, factoring by grouping, and some other concepts of factoring trinomials with a leading coefficient of 1.

Example 1

Use trial and error factoring to solve 6x² – 25x + 24

Solution

Paired factors of 6x²are x (6x) or 2x (3x), therefore our parentheses will be;

(x – ?) (6x – ?) or (2x – ?) (3x – ?)

Replace “bx” with possible paired factors of c. Try all paired factors of 24 that will produce -25 The possible choices are (1 & 24, 2 & 12, 3 & 8, 4 & 6). Therefore, the correct factoring is;

6x² – 25x + 24 ⟹ (2x – 3) (3x –

Example 2

Factor x² – 5x + 6

Solution

The factors of the first term x², are x and x. Therefore, insert x in the first position of each parentheses.

x² – 5x + 6 = (x – ?) (x – ?)

Since last term is 6, therefore the possible choices of factors are:

(x + 1) (x + 6)
(x – 1) (x – 6)
(x + 3) (x + 2)
(x – 3) (x – 2)

The correct pair which gives -5x as the middle term is (x – 3) (x – 2). Hence,

(x – 3) (x – 2) is the answer.

Example 3

Factor x² – 7x + 10

Solution

Insert the factors of the first term in the first position of each parentheses.

⟹ (x -?) (x -?)

Try the possible pair of factors of the 10;

⟹ (-5) + (-2) = -7

Now replace the question marks in the parentheses with these two factors

⟹ (x -5) (x -2)

Hence, the correct factoring of x² – 7x + 10 is (x -5) (x -2)

Example 4

Factor 4x² – 5x – 6

Solution

(2x -?) (2x +?) and (4x -?) (x +?)

Try the possible pair of factors;

6 x² − 2x – 151 & 6, 2 & 3, 3 & 2, 6 & 1

Since the correct pair 3 and 2, therefore, (4x – 3) (x + 2) is our answer.

Example 5

Factor the trinomial x² − 2x – 15

Solution

Insert x in the first position of each parentheses.

(x -?) (x +?)

Find two numbers whose product and sum are -15 and -2, respectively. By trial and error, the possible combinations are:

15 and -1;

-1 and 15;

5 and -3;

-5 and 3;

Our correct combination is – 5 and 3. Therefore;

x² − 2x – 15 ⟹ (x -5) (x +3)

How to factor trinomials by grouping?

We can also factor trinomials by using a method of grouping. Let’s walk through the following steps to factor ax² + bx + c where a ≠1:

Find the product of the leading coefficient “a” and the constant “c.”

⟹ a * c = ac

Look for the factors of the “ac” that add to coefficient “b.”
Rewrite bx as a sum or difference of the factors of ac that add to b.
Now factor by grouping.

Example 6

Factor the trinomial 5x² + 16x + 3 by grouping.

Solution

Find the product of the leading coefficient and the last term.

⟹ 5 *3 = 15

Perform trial and error to find pair factors of 15 whose sum is the middle term (16). The correct pair is 1 and 15.

Rewrite the equation by replacing the middle term 16x by x and 15x.

5x² + 16x + 3⟹5x² + 15x + x + 3

Now, factor out by grouping

5x² + 15x + x + 3 ⟹ 5x (x + 3) + 1(x + 3)

⟹ (5x +1) (x + 3)

Example 7

Factor 2x²– 5x – 12 by grouping.

Solution

2x²– 5x – 12

= 2x²+ 3x – 8x – 12

= x (2x + 3) – 4(2x + 3)

= (2x + 3) (x – 4)

Example 8

Factor 6x²+ x – 2

Solution

Multiply the leading coefficient a and the constant c.

⟹ 6 * -2 = -12

Find two numbers whose product and sum are -12 and 1 respectively.

⟹ – 3 * 4

⟹ -3 + 4 = 1

Rewrite the equation by replacing the middle term -5x by -3x and 4x

⟹ 6x²-3x + 4x -2

Finally, factor out by grouping

⟹ 3x (2x – 1) + 2(2x – 1)

⟹ (3x + 2) (2x – 1)

Example 9

Factor 6y² + 11y + 4.

Solution

6y² + 11y + 4 ⟹ 6y² + 3y + y + 4

⟹ (6y² + 3y) + (8y + 4)

⟹ 3y (2y + 1) + 4(2y + 1)

= (2y + 1) (3y + 4)

Источник

Methodology[edit]

Simplest applications[edit]

Hierarchies[edit]

Application[edit]

Features[edit]

Examples[edit]

See also[edit]

References[edit]

Further reading[edit]

Process

Methodology

Simplest applications

Trial-and-error Hierarchies

The basic strategy in many fields?

An ambiguity: Can we have «intention» during a «trial»

Features

Examples

Issues with trial and error

References

See also

References

Methodology

Simplest applications

Hierarchies

Application

Features

Examples

See also

References

Further reading

The Use of Trial and Error To Solve Problems

Author Description

Example Sentences

Word History

Cite this Entry

Share

More from Merriam-Webster on trial and error

Challenging Words You Should Know

Analytical Reasoning: Trial and Error Method

How to Unfoil trinomials?

Trial and error factoring

How to factor trinomials by grouping?