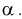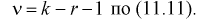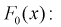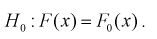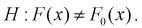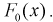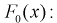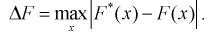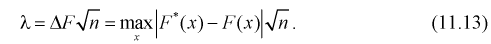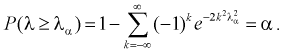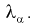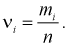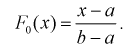Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| |
Верная гипотеза | ||
|---|---|---|---|
| H0 | H1 | ||
| Результат применения критерия |
H0 | H0 верно принята | H0 неверно принята (Ошибка второго рода) |
| H1 | H0 неверно отвергнута (Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Содержание:
Теория статистической проверки гипотез
Пусть имеется выборка
Тогда нулевой гипотезой 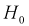
Альтернативной (конкурирующей, противоположной) гипотезой Н называется гипотеза, которая принимается тогда, когда отвергается нулевая.
Целью статистической проверки гипотез является выбор критерия по выборке 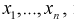
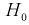
- Отклонение
, когда она на самом деле верна — ошибка первого рода. Вероятность этой ошибки обозначается а и называется уровнем значимости.
- Принятие
когда она на самом деле не верна — ошибка второго рода, вероятность ошибки —
.
Чем серьезнее будут последствия ошибки первого рода, тем меньше надо выбирать уровень значимости 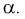
Статистической характеристикой Z гипотезы 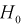
Областью отклонения (критической областью) 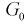
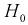
Дополнение области отклонения до всех возможных значений статистической характеристики Z называется областью принятия G.
При попадании статистической характеристики Z в область принятия гипотеза 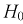
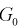
При попадании Z в область принятия гипотеза 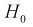
Область отклонения 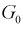
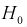
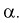
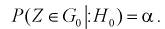
С другой стороны, для того чтобы уменьшить вероятность ошибки второго рода при выбранном 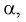
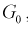
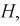
Вероятность 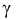
Так как события 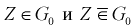
Таким образом, имеем
где 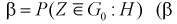
Отметим, что ошибка первого рода существенней, поэтому а мы выбираем, а р — нет (принимаем полученное значение).
Из (11.2) следует, что между 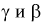
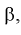
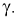
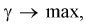
Между 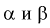
На рис. 11.2 приведены две кривые плотности распределения: одна кривая 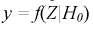
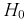
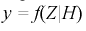
Из рис. 11.2 видно, что при уменьшении 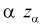
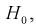
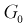
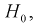
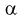
Гипотезы бывают двух видов — параметрические и непараметрические.
Параметрические гипотезы — это гипотезы о проверке параметров законов распределения.
Непараметрические — это гипотезы о виде закона распределения.
Проверка гипотезы равенства математических ожиданий при неизвестной дисперсии (критерий Стьюдента)
Пусть Хи У — независимые нормальные случайные величины.
Введем обозначения:
Пусть дисперсии этих случайных величин равны и неизвестны:
где 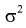
Пусть даны выборки
По выборкам найдем критерий проверки гипотезы 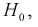
При альтернативной гипотезе
Известно, что случайные величины
имеют распределение 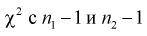
Сумма независимых случайных величин с распределением 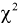
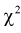
Случайная величина W имеет распределение 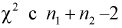
Ранее мы показывали, что несмещенной оценкой математического ожидания является выборочное среднее. Поэтому для проверки гипотезы 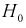
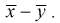
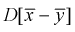
Очевидно, что случайная величина U имеет нормальное распределение, т. к. X и Y нормально распределены. Если проверяемая гипотеза 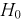
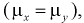
Таким образом, если гипотеза 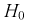
Рассмотрим случайную величину
где 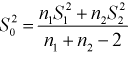
Случайную величину t можно представить в следующем виде через ранее введенные Un W:
Действительно:
т. е. правые части (11.5) и (11.6 или 11.7) совпадают.
Но величина t (11.6) имеет распределение Стьюдента с 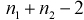
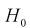
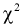
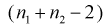
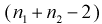
Эту величину t (11.5) примем за статистическую характеристику Z. Проверка гипотезы о равенстве .математических ожиданий состоит в следующем.
По таблицам распределения Стьюдента для заданного уровня значимости 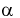
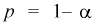
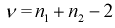
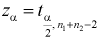
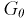
Тогда если фактически найденное по выборкам значение статистической характеристики t (11.5) удовлетворяет условию 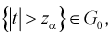
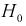
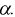
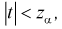
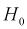
Проверка гипотезы о равенстве дисперсий (критерий Фишера)
Пусть Х и Y — нормальные независимые случайные величины. Обозначим их дисперсии:
По выборкам 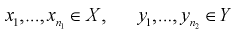
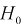
При альтернативной гипотезе 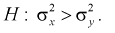
Такая гипотеза выбирается, например, при 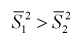
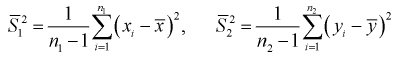
В качестве статистической характеристики возьмем случайную величину
Если гипотеза 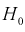
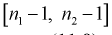
Видим, что величина 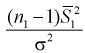
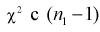
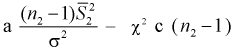
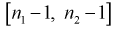
Проверка гипотезы 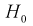
Из таблиц распределения Фишера по выбранному уровню значимости 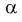
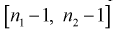
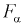
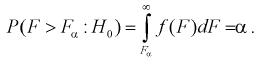
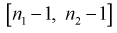
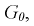
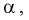
По выборкам, используя (11.8), определяем значение статистической характеристики F. Если фактически вычисленное по формуле (11.8) значение F окажется больше табличного 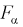
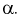
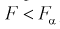
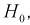
Пример:
Пусть X — чувствительность телевизоров марки «Горизонт», Y — чувствительность телевизоров марки «Витязь». Проведены выборочные измерения чувствительности телевизоров для 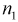
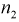
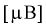
Определить лучшую марку телевизора, если лучшим будет тот, у которого чувствительность в 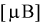
Найдем по результатам измерений средние значения чувствительности, вычисляя
Можно ли сказать, что чувствительность телевизоров марки «Горизонт» лучше? Нет, т. к. выборки, выборочные средние 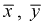
Сначала убедимся в равенстве дисперсий по критерию Фишера — гипотеза
Вычислим несмещенные оценки дисперсий
Используя (11.8), найдем значение статистической характеристики F:
По таблицам распределения Фишера для [6;5] степеней свободы, задавая уровень значимости 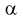
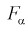
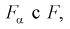
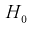
Теперь проверим гипотезу о равенстве математических ожиданий случайных величин X и Y , применяя критерий Стьюдента.
Гипотеза 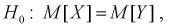
Найдем объединенную выборочную дисперсию:
По формуле (11.5) вычислим статистическую характеристику t :
Задавая уровень значимости 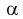
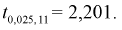
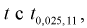
Проверка гипотезы о законе распределения генеральной случайной величины. Критерий Пирсона
Проверка гипотезы о законе распределения генеральной случайной величины. Критерий Пирсона. (Критерий согласия 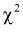
Пусть задана генеральная случайная величинами выборка
Если по выборке построить гистограмму, то по виду гистограммы можно выдвинуть гипотезу о виде закона распределения генеральной случайной величины X. Тогда в качестве нулевой гипотезы 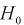
При альтернативной гипотезе
Обычно для построения гистограммы равноинтервальным способом разбивают весь диапазон выборочных значений случайной величины X на 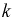
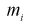
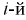
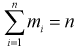
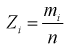
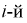
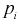
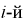
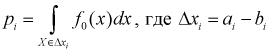
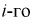
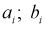
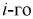
Рассмотрим событие, состоящее в том, что случайная величина X попадет в интервал 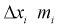
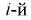
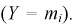
Для введенной ранее случайной величины 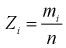
Проведем нормировку случайной величины 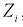
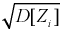
Эта величина распределена по биномиальному закону, т. к. в нее входит случайная величина 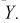
Сумма квадратов нормированных нормальных случайных величин (как было показано ранее) имеет распределение 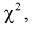
Эта случайная величина имеет закон распределения 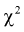
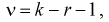
где 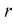
Анализируя правые части формул (11.9) и (11.10), можно отметить, что в критерии согласия 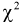
Проверка гипотезы состоит в следующем. Задаем уровень значимости
По таблицам 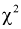
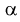
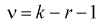
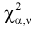
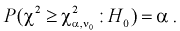
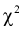
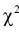
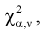
- Если
то нулевая гипотеза
отвергается в пользу альтернативной Н, т. е.
не согласуется с результатами эксперимента.
- Если
, то
, принимается, т. е.
согласуется с экспериментальными данными, закон распределения
подтверждается. При этом вероятность ошибки равна
Критерий Романовского
Рассмотрим неравенство
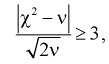
где 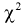
Проверка гипотезы состоит в следующем: если это неравенство выполняется 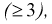
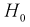
В противном случае гипотеза 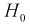
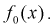
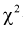
Критерий согласия Колмогорова
В критерии согласия А. Н. Колмогорова проводится сравнение эмпирической и теоретической функций распределения. Укажем этапы проверки гипотез этим критерием.
1. По выборке 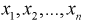
2. По виду графика функции распределения выдвигается гипотеза о виде закона распределения генеральной случайной величины X. Тогда в качестве нулевой гипотезы 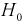
При альтернативной гипотезе
3. По выборке 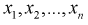
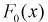
4. На графике эмпирической функции распределения строится график теоретической функции распределения
5. Путем сравнения графиков вычисляется максимальное значение модуля отклонения значений эмпирической функции распределения от теоретической функции распределения
6. Рассчитывают значение 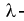
7. Задавая уровень значимости а , определяем квантиль из условия
Отметим, что самостоятельно решать это уравнение не надо, поскольку составлены таблицы квантилей распределения Колмогорова, из которых по заданному уровню значимости 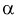
Сравнивая значение 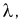
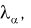
Следует отметить, что критерий Колмогорова применяется тогда, когда полностью известен закон распределения функции распределения F(x) и значения ее параметров. При решении практических задач это не всегда удается выполнить. Для этого прибегают к некоторым дополнительным исследованиям: применяют вероятностные бумаги, строят гистограммы и т. д. Это помогает правильно подобрать теоретический закон распределения для функции распределения F(x). Но в этом случае неизвестны ее параметры. И если их оценивать по этой же выборке, то это может привести к ошибочным выводам в отношении принятой гипотезы. В этом случае следует использовать другие критерии согласия, например 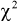
Пример:
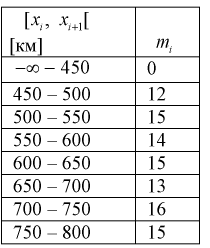
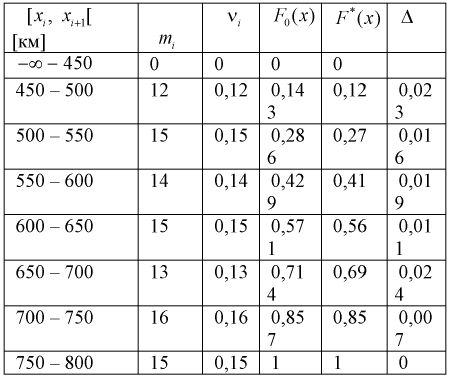
Проведено 100 измерений расстояния радиодальномером до цели. Результаты представлены в виде статистического ряда 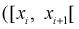
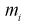
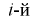
Оценить закон распределения ошибки измерения дальности радиодальномером.
Занесем в таблицу значения относительных частот
Анализ значений относительных частот позволяет выдвинуть гипотезу о равномерном законе распределения. Теоретическая функция распределения для этого закона имеет вид
Принимаем а = 450, b = 800. Полагая 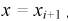
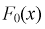
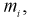
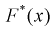
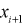
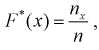
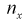
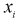
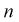
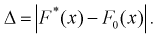
Вычисляем критерий Колмогорова по формуле (11.13), учитывая, что из таблицы 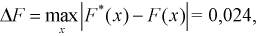
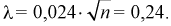
- Линейный регрессионный анализ
- Вариационный ряд
- Законы распределения случайных величин
- Дисперсионный анализ
- Случайные процессы
- Выборочный метод
- Статистическая проверка гипотез
- Статистические оценки
При проверке статистических гипотез ошибка I рода — это ошибочное отклонение действительно истинной нулевой гипотезы (также известной как «ложноположительный» результат или вывод; например: «невиновный человек осужден»), а ошибка II рода — это неспособность отвергнуть нулевую гипотезу, которая на самом деле ложна (также известная как «ложноотрицательный» вывод или вывод; пример: «виновное лицо не осуждено»). [1]Большая часть статистической теории вращается вокруг минимизации одной или обеих этих ошибок, хотя полное устранение любой из них является статистически невозможным, если результат не определяется известным, наблюдаемым причинным процессом. Выбрав низкое пороговое значение (отсечку) и изменив уровень альфа (α), можно повысить качество проверки гипотезы. [2] Знания об ошибках первого рода и ошибках второго рода широко используются в медицине , биометрии и информатике . [ требуется уточнение ]
Интуитивно, ошибки типа I можно рассматривать как ошибки совершения , т. е. исследователь, к несчастью, приходит к выводу, что что-то является фактом. Например, рассмотрим исследование, в котором ученые сравнивают лекарство с плацебо. Если пациенты, получающие препарат, случайно выздоравливают, чем пациенты, получающие плацебо, может показаться, что препарат эффективен, но на самом деле вывод неверен. И наоборот, ошибки II рода — это ошибки упущения .. В приведенном выше примере, если бы пациенты, получавшие лекарство, не выздоравливали быстрее, чем те, кто получал плацебо, но это была случайная случайность, это была бы ошибка II типа. Последствия ошибки типа II зависят от размера и направления пропущенного определения и обстоятельств. Дорогостоящее лекарство для одного из миллиона пациентов может быть несущественным, даже если оно действительно является лекарством.
Определение
Статистическая справка
В статистической теории тестирования понятие статистической ошибки является неотъемлемой частью проверки гипотез . Тест состоит в выборе двух конкурирующих предположений, называемых нулевой гипотезой , обозначаемой H0, и альтернативной гипотезой , обозначаемой H1 .. Это концептуально похоже на приговор в судебном процессе. Нулевая гипотеза соответствует положению подсудимого: точно так же, как предполагается, что он невиновен, пока его вина не доказана, нулевая гипотеза считается истинной, пока данные не дают убедительных доказательств против нее. Альтернативная гипотеза соответствует позиции против подсудимого. В частности, нулевая гипотеза также предполагает отсутствие различий или отсутствие связи. Таким образом, нулевая гипотеза никогда не может состоять в том, что существует различие или ассоциация.
Если результат теста соответствует действительности, значит, принято правильное решение. Однако если результат проверки не соответствует действительности, значит, произошла ошибка. Есть две ситуации, в которых решение неверно. Нулевая гипотеза может быть верной, тогда как мы отвергаем H 0 . С другой стороны, альтернативная гипотеза H 1 может быть верной, тогда как мы не отвергаем H 0 . Различают два типа ошибок: ошибку первого рода и ошибку второго рода. [3]
Ошибка типа I
Первый вид ошибок — это ошибочное отклонение нулевой гипотезы в результате процедуры проверки. Такую ошибку называют ошибкой первого рода (ложноположительной) и иногда называют ошибкой первого рода. С точки зрения примера с залом суда ошибка первого рода соответствует осуждению невиновного подсудимого.
Ошибка типа II
Второй вид ошибок — ошибочное отклонение нулевой гипотезы в результате процедуры проверки. Такая ошибка называется ошибкой второго рода (ложноотрицательная), а также называется ошибкой второго рода. В примере с залом суда ошибка II рода соответствует оправданию преступника. [4]
Частота ошибок кроссовера
Коэффициент перекрестных ошибок (CER) — это точка, в которой ошибки типа I и ошибки типа II равны, и представляет собой лучший способ измерения эффективности биометрии. Система с более низким значением CER обеспечивает большую точность, чем система с более высоким значением CER.
Ложноположительный и ложноотрицательный
Что касается ложноположительных и ложноотрицательных результатов, положительный результат соответствует отклонению нулевой гипотезы, а отрицательный результат соответствует невозможности отвергнуть нулевую гипотезу; «ложный» означает, что сделанный вывод неверен. Таким образом, ошибка I рода эквивалентна ложноположительному результату, а ошибка II рода эквивалентна ложноотрицательному результату.
Таблица типов ошибок
Табличные соотношения между истинностью/ложностью нулевой гипотезы и результатами проверки: [5]
| Таблица типов ошибок |
Нулевая гипотеза ( H 0 ) |
||
|---|---|---|---|
| Истинный |
ЛОЖЬ |
||
| Решение о нулевой гипотезе ( H 0 ) |
Не отвергай |
Правильный вывод (истинно отрицательный) (вероятность = 1 − α ) |
Ошибка типа II (ложноотрицательный) (вероятность = β ) |
| Отклонять |
Ошибка типа I (ложноположительный результат) (вероятность = α ) |
Правильный вывод (истинно положительный) (вероятность = 1 − β ) |
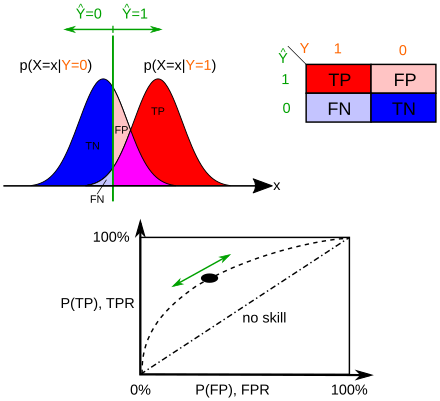
Частота ошибок
Результаты, полученные для отрицательного образца (левая кривая), перекрываются с результатами, полученными для положительных образцов (правая кривая). Перемещая пороговое значение результата (вертикальная полоса), можно уменьшить количество ложноположительных результатов (FP) за счет увеличения количества ложноотрицательных результатов (FN) или наоборот (TP = True Positives, TPR = True Positives). частота, FPR = частота ложных срабатываний, TN = истинные отрицательные значения).
Идеальный тест должен иметь ноль ложноположительных и ноль ложноотрицательных результатов. Однако статистические методы носят вероятностный характер, и нельзя знать наверняка, правильны ли статистические выводы. Всякий раз, когда есть неопределенность, есть вероятность совершить ошибку. Учитывая эту природу статистической науки, все проверки статистических гипотез имеют вероятность совершения ошибок первого и второго рода. [6]
- Частота ошибок первого рода или уровень значимости — это вероятность отклонения нулевой гипотезы при условии, что она верна. Он обозначается греческой буквой α (альфа) и также называется альфа-уровнем. Обычно уровень значимости устанавливается равным 0,05 (5%), подразумевая, что допустимо наличие 5% вероятности ошибочного отклонения истинной нулевой гипотезы. [7]
- Скорость ошибки II рода обозначается греческой буквой β (бета) и связана с мощностью теста , равной 1−β. [8]
Эти два типа частоты ошибок компенсируются друг другом: для любого заданного набора выборок усилия по уменьшению одного типа ошибки обычно приводят к увеличению другого типа ошибки. [9]
Качество проверки гипотез
Та же идея может быть выражена в терминах доли правильных результатов и, следовательно, использована для минимизации частоты ошибок и повышения качества проверки гипотез. Чтобы уменьшить вероятность совершения ошибки первого рода, достаточно просто и эффективно сделать значение альфа (p) более строгим. Чтобы уменьшить вероятность совершения ошибки типа II, которая тесно связана с мощностью анализа, либо увеличение размера выборки теста, либо ослабление альфа-уровня могут увеличить мощность анализа. [10] Тестовая статистика является надежной, если контролируется частота ошибок первого рода.
Также можно использовать различные пороговые значения (отсечки), чтобы сделать тест более специфичным или более чувствительным, что, в свою очередь, повышает качество теста. Например, представьте себе медицинский тест, в котором экспериментатор может измерить концентрацию определенного белка в образце крови. Экспериментатор мог настроить порог (черная вертикальная линия на рисунке), и у людей диагностировали заболевание, если какое-либо число было обнаружено выше этого определенного порога. Согласно изображению, изменение порога приведет к изменению ложноположительных и ложноотрицательных результатов, соответствующих движению по кривой. [11]
Пример
Поскольку в реальном эксперименте невозможно избежать всех ошибок типа I и типа II, важно учитывать степень риска, на который человек готов пойти, чтобы ложно отвергнуть H 0 или принять H 0 . Решением этого вопроса было бы сообщить значение p или уровень значимости α статистики. Например, если p-значение статистического результата теста оценивается как 0,0596, то существует вероятность 5,96%, что мы ошибочно отвергаем H 0 . Или, если мы говорим, что статистика выполняется на уровне α, например 0,05, то мы допускаем ложное отклонение H 0 на уровне 5%. Уровень значимости α, равный 0,05, является относительно распространенным, но не существует общего правила, подходящего для всех сценариев.
Измерение скорости автомобиля
Ограничение скорости на автостраде в США составляет 120 километров в час. Установлено устройство для измерения скорости проезжающих мимо транспортных средств. Предположим, что прибор проведет три измерения скорости проезжающего автомобиля, записывая в виде случайной выборки X 1 , X 2 , X 3 . ГИБДД будет или не будет штрафовать водителей в зависимости от средней скорости. То есть тестовая статистика.
Кроме того, мы предполагаем, что измерения X 1 , X 2 , X 3 моделируются как нормальное распределение N(μ,4). Затем T должно следовать за N (μ, 4/3), а параметр μ представляет собой истинную скорость проезжающего транспортного средства. В этом эксперименте нулевая гипотеза H 0 и альтернативная гипотеза H 1 должны быть
H 0 : µ=120 против H 1 : µ 1 >120.
Если мы выполняем статистический уровень при α = 0,05, то необходимо вычислить
критическое значение c для решения
Согласно правилу замены единиц для нормального распределения. Ссылаясь на Z-таблицу , мы можем получить
Здесь критическая область. То есть, если зафиксированная скорость транспортного средства превышает критическое значение 121,9, водитель будет оштрафован. Тем не менее, еще 5% водителей оштрафованы ложно, так как зафиксированная средняя скорость превышает 121,9, а реальная скорость не превышает 120, что мы называем ошибкой I рода.
Ошибка II рода соответствует случаю, когда истинная скорость транспортного средства превышает 120 километров в час, но водитель не оштрафован. Например, если истинная скорость автомобиля µ=125, вероятность того, что водитель не будет оштрафован, можно рассчитать как
Это означает, что если истинная скорость транспортного средства равна 125, у водителя есть вероятность 0,36% избежать штрафа, когда статистика выполняется на уровне 125, поскольку зарегистрированная средняя скорость ниже 121,9. Если истинная скорость ближе к 121,9, чем к 125, то вероятность избежать штрафа тоже будет выше.
Следует также учитывать компромиссы между ошибкой первого рода и ошибкой второго рода. То есть в этом случае, если ГАИ не хочет ложно штрафовать невиновных водителей, уровень α можно установить на меньшее значение, например 0,01. Однако, если это так, больше водителей, чья реальная скорость превышает 120 километров в час, например 125, с большей вероятностью избегут штрафа.
этимология
В 1928 году Ежи Нейман (1894–1981) и Эгон Пирсон (1895–1980), оба выдающиеся статистики, обсуждали проблемы, связанные с «решением, можно ли считать конкретную выборку вероятной случайным образом взятой из определенной совокупности». «: [12] и, как заметила Флоренс Найтингейл Дэвид , «необходимо помнить, что прилагательное «случайный» [в термине «случайная выборка»] должно относиться к методу отбора пробы, а не к самой пробе». [13]
Они выявили «два источника ошибок», а именно:
- (а) ошибка отклонения гипотезы, которую не следовало отвергать, и
- (b) ошибка, заключающаяся в том, что не удалось отвергнуть гипотезу, которую следовало отвергнуть.
В 1930 году они подробно остановились на этих двух источниках ошибок, отметив, что:
… при проверке гипотез необходимо учитывать два соображения: мы должны иметь возможность уменьшить вероятность отклонения истинной гипотезы до желаемого минимального значения; тест должен быть разработан таким образом, чтобы он отклонял проверяемую гипотезу, когда она, вероятно, окажется ложной.
В 1933 году они заметили, что эти «проблемы редко представляются в такой форме, чтобы мы могли с уверенностью отличить истинную гипотезу от ложной». Они также отметили, что, решая, не отклонить или отвергнуть конкретную гипотезу среди «набора альтернативных гипотез», H 1 , H 2 …, легко сделать ошибку:
…[и] эти ошибки будут двух видов:
- (I) мы отвергаем H 0 [т.е. гипотезу, которую нужно проверить], когда она верна, [14]
- (II) мы не можем отвергнуть H 0 , когда какая-либо альтернативная гипотеза H A или H 1 верна. (Есть различные обозначения для альтернативы).
Во всех статьях, написанных совместно Нейманом и Пирсоном, выражение H 0 всегда означает «гипотезу, подлежащую проверке».
В той же статье они называют эти два источника ошибок ошибками типа I и ошибками типа II соответственно. [15]
Нулевая гипотеза
Стандартной практикой для статистиков является проведение тестов , чтобы определить, может ли быть подтверждена «спекулятивная гипотеза » относительно наблюдаемых явлений мира (или его обитателей). Результаты такого тестирования определяют, разумно ли конкретный набор результатов согласуется (или не согласуется) с предполагаемой гипотезой.
На том основании, что согласно статистической традиции всегда предполагается, что предполагаемая гипотеза неверна, а так называемая «нулевая гипотеза» утверждает, что наблюдаемые явления происходят просто случайно (и что, как следствие, предполагаемый агент не имеет эффект) – тест определит, верна эта гипотеза или нет. Вот почему проверяемую гипотезу часто называют нулевой гипотезой (скорее всего, введенной Фишером (1935, стр. 19)), потому что именно эта гипотеза должна быть либо аннулирована, либо не аннулирована проверкой. Когда нулевая гипотеза аннулируется, можно сделать вывод, что данные подтверждают «альтернативную гипотезу» (которая является исходной гипотезой).
Последовательное применение статистиками соглашения Неймана и Пирсона о представлении «гипотезы, подлежащей проверке» (или «гипотезе, подлежащей аннулированию») выражением H0 , привело к обстоятельствам, при которых многие понимают термин «нулевая гипотеза» как означающий «нулевая гипотеза» — утверждение о том, что рассматриваемые результаты возникли случайно. Это не обязательно так — ключевое ограничение, согласно Фишеру (1966), состоит в том, что «нулевая гипотеза должна быть точной, свободной от неопределенности и двусмысленности, потому что она должна служить основой для «проблемы распределения». из которых критерий значимости является решением». [16]Как следствие этого, в экспериментальной науке нулевая гипотеза обычно представляет собой утверждение о том, что конкретное лечение не имеет эффекта; в наблюдательной науке это то, что нет никакой разницы между значением конкретной измеренной переменной и значением экспериментального предсказания. [ нужна ссылка ]
Статистическая значимость
Если вероятность получения столь же экстремального результата, как и полученный, при условии, что нулевая гипотеза верна, ниже заранее заданной пороговой вероятности (например, 5%), то результат считается статистически значимым . и нулевая гипотеза отвергается.
Британский статистик сэр Рональд Эйлмер Фишер (1890–1962) подчеркивал, что «нулевая гипотеза»:
… никогда не доказывается и не устанавливается, но, возможно, опровергается в ходе экспериментов. Можно сказать, что каждый эксперимент существует только для того, чтобы дать фактам возможность опровергнуть нулевую гипотезу.
- Фишер, 1935, стр. 19.
Домены приложений
Медицина
В медицинской практике различия между применением скрининга и тестирования значительны.
Медицинский осмотр
Скрининг включает в себя относительно дешевые тесты, которые назначаются большим группам населения, ни один из которых не проявляет каких-либо клинических признаков заболевания (например, мазок Папаниколау ).
Тестирование включает гораздо более дорогие, часто инвазивные процедуры, которые назначаются только тем, у кого проявляются некоторые клинические признаки заболевания, и чаще всего применяются для подтверждения предполагаемого диагноза.
Например, в большинстве штатов США требуется скрининг новорожденных на фенилкетонурию и гипотиреоз , а также на другие врожденные заболевания .
Гипотеза: «У новорожденных фенилкетонурия и гипотиреоз».
Нулевая гипотеза (H 0 ): «У новорожденных нет фенилкетонурии и гипотиреоза»,
Ошибка I рода (ложноположительный): Верно то, что у новорожденных нет фенилкетонурии и гипотиреоза, но по имеющимся данным мы считаем, что у них есть нарушения.
Ошибка II типа (ложноотрицательный): Истинный факт заключается в том, что у новорожденных есть фенилкетонурия и гипотиреоз, но мы считаем, что, согласно данным, у них нет нарушений.
Хотя они показывают высокий уровень ложноположительных результатов, скрининговые тесты считаются ценными, поскольку они значительно повышают вероятность обнаружения этих расстройств на гораздо более ранней стадии.
Простые анализы крови, используемые для скрининга возможных доноров крови на ВИЧ и гепатит , имеют значительный уровень ложноположительных результатов; однако врачи используют гораздо более дорогие и гораздо более точные тесты, чтобы определить, действительно ли человек заражен одним из этих вирусов.
Возможно, наиболее широко обсуждаемые ложноположительные результаты в медицинском скрининге связаны с процедурой маммографии для скрининга рака молочной железы.. Уровень ложноположительных маммограмм в США составляет до 15%, что является самым высоким показателем в мире. Одним из последствий высокого уровня ложноположительных результатов в США является то, что за любой 10-летний период половина американских женщин, прошедших скрининг, получают ложноположительные маммограммы. Ложноположительные маммограммы обходятся дорого: в США ежегодно тратится более 100 миллионов долларов на последующее тестирование и лечение. Они также вызывают у женщин ненужное беспокойство. В результате высокого уровня ложноположительных результатов в США до 90–95% женщин, получивших положительный результат маммографии, не имеют этого заболевания. Самый низкий показатель в мире в Нидерландах, 1%. Самые низкие показатели, как правило, в Северной Европе, где маммографические снимки считываются дважды и устанавливается высокий порог для дополнительного тестирования (высокий порог снижает мощность теста).
Идеальный скрининговый тест населения должен быть дешевым, простым в применении и по возможности не давать ложноотрицательных результатов. Такие тесты обычно дают больше ложноположительных результатов, которые впоследствии можно устранить с помощью более сложного (и дорогого) тестирования.
Медицинское обследование
Ложноотрицательные и ложноположительные результаты являются серьезными проблемами в медицинском тестировании .
Гипотеза: «У больных специфическое заболевание».
Нулевая гипотеза (H 0 ): «У пациентов нет специфического заболевания».
Ошибка I типа (ложноположительный результат): «Истинный факт заключается в том, что у пациентов нет определенного заболевания, но врачи судят, что пациент был болен на основании отчетов об испытаниях».
Ложные срабатывания также могут привести к серьезным и нелогичным проблемам, когда искомое состояние встречается редко, как при скрининге. Если тест имеет ложноположительный результат один на десять тысяч, но только один из миллиона образцов (или людей) является истинно положительным, большинство положительных результатов, обнаруженных этим тестом, будут ложными. Вероятность того, что наблюдаемый положительный результат является ложноположительным, можно рассчитать с помощью теоремы Байеса .
Ошибка типа II (ложноотрицательный результат): «Истинный факт заключается в том, что болезнь действительно присутствует, но отчеты об испытаниях дают ложно обнадеживающее сообщение пациентам и врачам об отсутствии болезни».
Ложноотрицательные результаты приводят к серьезным и нелогичным проблемам, особенно когда искомое состояние является распространенным. Если тест с частотой ложноотрицательных результатов всего 10 % используется для проверки популяции с истинной частотой встречаемости 70 %, многие отрицательные результаты, обнаруженные тестом, будут ложными.
Иногда это приводит к неадекватному или неадекватному лечению как больного, так и его заболевания. Типичным примером является использование сердечных нагрузочных тестов для выявления коронарного атеросклероза, хотя известно, что сердечные нагрузочные тесты обнаруживают только ограничения кровотока в коронарных артериях из-за выраженного стеноза .
Биометрия
Биометрическое сопоставление, такое как распознавание отпечатков пальцев , лиц или радужной оболочки глаза , подвержено ошибкам типа I и типа II.
Гипотеза: «Ввод не идентифицирует кого-то в списке искомых людей»
Нулевая гипотеза: «Ввод действительно идентифицирует кого-то в искомом списке людей»
Ошибка I типа (коэффициент ложных отказов): «Истинный факт заключается в том, что человек находится в списке поиска, но система делает вывод, что человек не соответствует данным».
Ошибка II типа (коэффициент ложного совпадения): «Истинный факт заключается в том, что человек не является кем-то из искомого списка, но система делает вывод, что этот человек является тем, кого мы ищем, согласно данным».
Вероятность ошибок типа I называется «коэффициентом ложных отклонений» (FRR) или коэффициентом ложных несоответствий (FNMR), а вероятность ошибок типа II называется «коэффициентом ложного принятия» (FAR) или коэффициентом ложных совпадений ( ФМР).
Если система предназначена для редкого совпадения подозреваемых, то вероятность ошибок типа II можно назвать « коэффициентом ложных тревог ». С другой стороны, если система используется для валидации (а принятие является нормой), то FAR является мерой безопасности системы, а FRR измеряет уровень неудобств для пользователя.
Проверка безопасности
Ложные срабатывания регулярно обнаруживаются каждый день при досмотре в аэропортах , которые, в конечном счете, являются системами визуального контроля . Установленная охранная сигнализация предназначена для предотвращения проноса оружия на самолет; тем не менее, они часто настроены на такую высокую чувствительность, что много раз в день реагируют на мелкие предметы, такие как ключи, пряжки ремней, мелочь, мобильные телефоны и кнопки в обуви.
Здесь нулевая гипотеза состоит в том, что предмет не является оружием, а альтернативная гипотеза состоит в том, что предмет является оружием.
Ошибка первого рода (ложноположительный результат): «Правда в том, что предмет не является оружием, но система все равно подает сигнал тревоги».
Ошибка типа II (ложноотрицательный результат) «Правда в том, что предмет является оружием, но система в это время хранит молчание».
Таким образом, соотношение ложных срабатываний (обнаружение невиновного путешественника как террориста) и истинных срабатываний (обнаружение потенциального террориста) очень велико; и поскольку почти каждый сигнал тревоги является ложноположительным, положительная прогностическая ценность этих скрининговых тестов очень низка.
Относительная стоимость ложных результатов определяет вероятность того, что создатели тестов допустят эти события. Поскольку цена ложноотрицательного результата в этом сценарии чрезвычайно высока (необнаружение бомбы, проносимой в самолет, может привести к сотням смертей), в то время как стоимость ложноположительного результата относительно низка (достаточно простая дальнейшая проверка), наиболее подходящим тест с низкой статистической специфичностью, но высокой статистической чувствительностью (который допускает высокий уровень ложноположительных результатов в обмен на минимальные ложноотрицательные результаты).
Компьютеры
Понятия ложных срабатываний и ложных отрицаний широко распространены в сфере компьютеров и компьютерных приложений, включая компьютерную безопасность , фильтрацию спама , вредоносное ПО , оптическое распознавание символов и многие другие.
Например, в случае фильтрации спама гипотеза состоит в том, что сообщение является спамом.
Таким образом, нулевая гипотеза: «Сообщение не является спамом».
Ошибка типа I (ложное срабатывание): «Методы фильтрации или блокировки спама ошибочно классифицируют законное сообщение электронной почты как спам и, как следствие, мешают его доставке».
Хотя большинство приемов борьбы со спамом могут блокировать или фильтровать большой процент нежелательных сообщений электронной почты, делать это без значительных ложноположительных результатов — гораздо более сложная задача.
Ошибка типа II (ложноотрицательный результат): «Спам-письмо не определяется как спам, но классифицируется как не спам». Низкое количество ложных срабатываний является показателем эффективности фильтрации спама.
Смотрите также
- Бинарная классификация
- Теория обнаружения
- Эгон Пирсон
- Этика в математике
- Ложноположительный парадокс
- Частота ошибок по семейным обстоятельствам
- Показатели эффективности информационного поиска
- Лемма Неймана – Пирсона
- Нулевая гипотеза
- Вероятность гипотезы для байесовского вывода
- Точность и отзыв
- Ошибка прокурора
- Феномен прозоны
- Рабочая характеристика приемника
- Чувствительность и специфичность
- Перекрестные ссылки статистических терминов статистиков и инженеров
- Проверка гипотез, предложенных данными
- Ошибка III типа
Ссылки
- ^ «Ошибка типа I и ошибка типа II» . explorable.com . Проверено 14 декабря 2019 г. .
- ^ Чоу, Ю.В.; Пьетранико, Р .; Мукерджи, А. (27 октября 1975 г.). «Исследования энергии связи кислорода с молекулой гемоглобина». Коммуникации по биохимическим и биофизическим исследованиям . 66 (4): 1424–1431. doi : 10.1016/0006-291x(75)90518-5 . ISSN 0006-291X . ПМИД 6 .
- ^ Современное введение в вероятность и статистику: понимание почему и как . Деккинг, Мишель, 1946-. Лондон: Спрингер. 2005. ISBN 978-1-85233-896-1. OCLC 262680588 .
{{cite book}}: CS1 maint: другие ( ссылка ) - ^ Современное введение в вероятность и статистику: понимание почему и как . Деккинг, Мишель, 1946-. Лондон: Спрингер. 2005. ISBN 978-1-85233-896-1. OCLC 262680588 .
{{cite book}}: CS1 maint: другие ( ссылка ) - ^ Шескин, Дэвид (2004). Справочник по параметрическим и непараметрическим статистическим процедурам . КПР Пресс. п. 54 . ISBN 1584884401.
- ^ Смит, Р.Дж.; Брайант, Р.Г. (27 октября 1975 г.). «Замещения металлов в карбоангидразе: исследование ионно-галоидного зонда». Коммуникации по биохимическим и биофизическим исследованиям . 66 (4): 1281–1286. doi : 10.1016/0006-291x(75)90498-2 . ISSN 0006-291X . ПМИД 3 .
- ^ Линденмайер, Дэвид. (2005). Практическая природоохранная биология . Бургман, Марк А. Коллингвуд, Виктория: CSIRO Pub. ISBN 0-643-09310-9. OCLC 65216357 .
- ^ Чоу, Ю.В.; Пьетранико, Р .; Мукерджи, А. (27 октября 1975 г.). «Исследования энергии связи кислорода с молекулой гемоглобина». Коммуникации по биохимическим и биофизическим исследованиям . 66 (4): 1424–1431. doi : 10.1016/0006-291x(75)90518-5 . ISSN 0006-291X . ПМИД 6 .
- ^ Смит, Р.Дж.; Брайант, Р.Г. (27 октября 1975 г.). «Замещения металлов в карбоангидразе: исследование ионно-галоидного зонда». Коммуникации по биохимическим и биофизическим исследованиям . 66 (4): 1281–1286. doi : 10.1016/0006-291x(75)90498-2 . ISSN 0006-291X . ПМИД 3 .
- ^ Смит, Р.Дж.; Брайант, Р.Г. (27 октября 1975 г.). «Замещения металлов в карбоангидразе: исследование ионно-галоидного зонда». Коммуникации по биохимическим и биофизическим исследованиям . 66 (4): 1281–1286. doi : 10.1016/0006-291x(75)90498-2 . ISSN 0006-291X . ПМИД 3 .
- ^ Морой, К .; Сато, Т. (15 августа 1975 г.). «Сравнение метаболизма прокаина и изокарбоксазида in vitro с помощью микросомальной амидазы-эстеразы печени». Биохимическая фармакология . 24 (16): 1517–1521. doi : 10.1016/0006-2952(75)90029-5 . ISSN 1873-2968 . ПМИД 8 .
- ^ НЕЙМАН, Дж.; ПИРСОН, Э.С. (1928). «Об использовании и интерпретации некоторых критериев тестирования для целей статистического вывода, часть I». Биометрика . 20А (1–2): 175–240. doi : 10.1093/биомет/20а.1-2.175 . ISSN 0006-3444 .
- ↑ CIKF (июль 1951 г.). «Теория вероятностей для статистических методов. Ф. Н. Дэвид. [Стр. ix + 230. Издательство Кембриджского университета. 1949. Цена 155.]». Журнал актуарного общества Staple Inn . 10 (3): 243–244. doi : 10.1017/s0020269x00004564 . ISSN 0020-269X .
- ^ Обратите внимание, что нижний индекс в выражении H 0 является нулем (указывающим на ноль ) , а не «O» (указывающим на оригинал ).
- ^ Нейман, Дж.; Пирсон, ES (30 октября 1933 г.). «Проверка статистических гипотез по отношению к априорным вероятностям». Математические труды Кембриджского философского общества . 29 (4): 492–510. Бибкод : 1933PCPS…29..492N . doi : 10.1017/s030500410001152x . ISSN 0305-0041 .
- ^ Фишер, Р.А. (1966). Дизайн экспериментов . 8-е издание. Хафнер: Эдинбург.
Библиография
- Бетц, М.А. и Габриэль, К.Р. , «Ошибки типа IV и анализ простых эффектов», Журнал статистики образования , Том 3, № 2 (лето 1978 г.), стр. 121–144.
- Дэвид, Ф. Н., «Степенная функция для проверки случайности в последовательности альтернатив», Biometrika , Vol.34, Nos.3/4, (декабрь 1947 г.), стр. 335–339.
- Фишер, Р.А., План экспериментов , Оливер и Бойд (Эдинбург), 1935.
- Гэмбрилл, В., «Ложноположительные результаты тестов на заболевания новорожденных беспокоят родителей», День здоровья (5 июня 2006 г.). [1]
- Кайзер, HF, «Направленные статистические решения», Psychological Review , Vol.67, No.3, (май 1960 г.), стр. 160–167.
- Кимбалл, А.В., «Ошибки третьего рода в статистическом консультировании», Журнал Американской статистической ассоциации , том 52, № 278 (июнь 1957 г.), стр. 133–142.
- Любин, А., «Интерпретация значимого взаимодействия», Образовательные и психологические измерения , Том 21, № 4, (зима 1961 г.), стр. 807–817.
- Мараскуило, Л. А. и Левин, Дж. Р., «Подходящие апостериорные сравнения для взаимодействия и вложенных гипотез в анализе дисперсионных планов: устранение ошибок типа IV», Американский журнал исследований в области образования , Том 7., № 3, (май 1970 г. ), стр. 397–421.
- Митрофф, И. И. и Фезерингем, Т. Р., «О системном решении проблем и ошибках третьего рода», Behavioral Science , том 19, № 6 (ноябрь 1974 г.), стр. 383–393.
- Мостеллер, Ф., « К -выборочный тест проскальзывания для экстремальной совокупности», Анналы математической статистики , том 19, № 1 (март 1948 г.), стр. 58–65.
- Моултон, RT, «Сетевая безопасность», Datamation , Vol.29, No.7 (июль 1983 г.), стр. 121–127.
- Райффа, Х., Анализ решений: вводные лекции о выборе в условиях неопределенности , Аддисон-Уэсли, (чтение), 1968.
Внешние ссылки
- Предвзятость и смешение – презентация Найджела Панета, Высшая школа общественного здравоохранения Питтсбургского университета
Финансовые аналитики часто сталкиваются с конкурирующими идеями о том, как работают финансовые рынки. Некоторые из этих идей развиваются через личные исследования или опыт работы с рынками; другие появляются благодаря взаимодействию с коллегами; и многие другие появляются в результате публикаций в профессиональной литературе по финансам и инвестициям.
Но как может аналитик определить насколько истинны или ложны те или иные идеи?
Когда мы можем свести идею или предположение к определенному утверждению о значении величины, такому как среднее значение совокупности, идея становится статистически проверяемым утверждением или гипотезой.
Аналитик может захотеть исследовать такие вопросы, как:
- Отличается ли средняя доходность данного взаимного фонда от средней эталонной доходности?
- Изменится ли волатильность доходности акции, после того как эта акция будет добавлена в рыночный индекс акций?
- Влияет ли разница между ценами продажи и покупки акции, связанная с числом дилеров, на рынок этой акции?
- Поддерживают ли данные национального рынка облигаций прогноз, полученный на основе экономической теории о временной структуре процентных ставок (связь между доходностью и сроком погашения)?
Для решения этих вопросов, мы используем концепцию и методы проверки статистических гипотез.
Проверка статистических гипотез (англ. ‘hypothesis testing’) является частью статистического вывода, и представляет собой процесс принятия суждений о более крупной группе (совокупности) на основе небольшой фактически наблюдаемой группе (выборке).
Концепции и методы проверки гипотез обеспечивают объективные средства для оценки того, подтверждают ли имеющиеся доказательства гипотезу. После статистической проверки гипотезы мы должны иметь четкое представление о вероятности того, верна ли гипотеза или нет.
Проверка статистических гипотез была мощным инструментом в научном развитии инвестиций. Как написал Роберт Л. Кан (Robert L. Kahn) из Института социальных исследований (Анн-Арбор, штат Мичиган):
«Мельница науки перемалывает только тогда, когда гипотезы и данные находятся в непрерывном и тесном контакте».
Основные акценты этого чтения сосредоточены на основах проверки гипотез и проверке гипотез, касающихся среднего значения и дисперсии, — двух величин, весьма часто использующихся в инвестициях.
Сначала мы приведем обзор процедуры проверки гипотез. Затем обратимся проверке гипотез о среднем, гипотез о разнице между средними и среднем значении разности. В следующем разделе этого чтения, мы рассмотрим проверку гипотез о дисперсии и различиях между дисперсиями, а также проверку гипотез о значении коэффицента корреляции.
В завершение мы рассмотрим непараметрические методы статистического вывода.
Проверка гипотезы, как мы уже упоминали, является частью области статистики, известной как статистический вывод. Традиционно область статистического вывода имеет два направления: статистическая оценка и проверка гипотез.
Статистическая оценка отвечает вопрос:
«Чему равно значение этого параметра (например, среднего значения по совокупности)?»
Ответ на этот вопрос дается в виде доверительного интервала, построенного вокруг точечной оценки. В случае со средним значением, мы строим доверительный интервал для среднего значения совокупности вокруг выборочного среднего, полученного в результате точечной оценки.
Например, предположим, что выборочное среднее равно 50 и 95-процентный доверительный интервал для среднего населения составляет (50 pm 10) (доверительный интервал составляет от 40 до 60). Если доверительный интервал правильно построен, то есть 95-процентная вероятность того, что интервал от 40 до 60 содержит среднее значение совокупности.
Мы обсуждали построение и интерпретацию доверительных интервалов в чтении о выборочном методе и статистической оценке.
Вторая ветвь статистического вывода, проверка гипотез, имеет несколько иную направленность.
Проверка статистических гипотез отвечает на вопрос:
«Равно ли значение параметра (например, среднего значения по совокупности) 45 (или другому конкретному значению)?»
Утверждение «среднее совокупности равно 45» является гипотезой. Статистическая гипотеза (англ. ‘hypothesis’) определяется как утверждение об одной или нескольких совокупностях.
Этот раздел посвящен концепции проверки гипотез. Процесс проверки гипотезы является частью строгого подхода к получению знаний, известного как научный метод (англ. ‘scientific method’).
Научный метод начинается с наблюдений и формулировки теории организации и объяснения наблюдений. Мы судим о правильности теории по ее способности давать точные прогнозы — например, предсказывать результаты новых наблюдений.
Чтобы быть проверяемой, теория должна быть способна делать предсказания, ошибочность которых можно показать.
Если прогнозы верны, мы продолжаем поддерживать теорию, как возможно правильное объяснение наших наблюдений. Когда в результатах наблюдений важна оценка риска, как в области финансов, мы можем попытаться сделать объективное, основанное на вероятности, суждение о том, поддерживают ли новые данные прогноз.
Проверка статистических гипотез играет ключевую роль, когда важна оценка риска.
В своей ежедневной работе финансовый аналитик может сталкиваться с вопросами, на которые он может дать ответы различного качества.
Когда аналитик правильно формулирует проверяемую гипотезу, проверяет ее и составляет отчет о проверке гипотезы, он следует нормам научного метода.
Конечно, логика аналитика, экономическое обоснование, источники информации, и, возможно, другие факторы также оказывают определенное влияние на качество ответа на заданный вопрос.
См. работу Freeley и Steinberg (2008) для обсуждения влияния критического мышления на мотивированное принятие решений.
Мы начнем изучение проверки гипотез со следующего списка из семи шагов.
Этапы проверки статистических гипотез.
Этапы проверки гипотезы заключаются в следующем:
- Формулировка гипотезы.
- Определение соответствующей тестовой статистики (статистики критерия) и ее распределения вероятностей.
- Определение уровня значимости.
- Формулировка правила принятия решения.
- Сбор данных и расчет тестовой статистики.
- Принятие статистического решения.
- Принятие экономического или инвестиционного решения.
Этот список этапов основан на списке из работы Daniel и Terrell (1995).
Мы расскажем о каждом из этих этапов, используя в качестве иллюстрации проверку гипотезы о премии за риск для американских акций. Описанный процесс представляет собой традиционный подход к проверке гипотез.
В завершении мы рассмотрим часто используемую альтернативу этих шагов — подход, основанный на p-значении.
1 этап. Формулировка гипотезы.
Первым шагом в проверке гипотезы является формулировка гипотезы. Мы всегда формулируем две гипотезы: нулевую гипотезу (или нуль), обозначаемую как (H_0), и альтернативную гипотезу, обозначаемую как (H_a).
Определение нулевой гипотезы.
Нулевая гипотеза — это гипотеза, которую нужно проверить. Например, мы могли бы предположить, что среднее по совокупности премии за риск для американских акций меньше или равно нулю.
Нулевая гипотеза (нуль, англ. ‘null hypothesis’) — это утверждение, которое считается истинным, если только используемая для проверки гипотезы выборка не дает убедительные доказательства того, что нулевая гипотеза неверна. Когда такие доказательства присутствуют, мы переходим к альтернативной гипотезе.
Определение альтернативной гипотезы.
Альтернативная гипотеза (альтернатива или конкурирующая гипотеза, англ. ‘alternative hypothesis’) — это гипотеза, которая принимается, когда нулевая гипотеза отвергается. Наша альтернативная гипотеза заключается в том, что среднее по совокупности премии за риск для американских акций больше нуля.
Предположим, что наш вопрос касается значения параметра совокупности (theta), по отношению к одному возможному значению параметра, (theta_0) (они читаются, соответственно, как «тета» и «тета ноль»).
Греческие буквы, такие как (sigma), зарезервированы для параметров совокупности. Римские курсивные буквы, например, (s), используются для выборочных статистик.
Примерами параметра совокупности являются среднее по совокупности (mu) и дисперсия совокупности (sigma^2). Мы можем сформулировать три различные пары нулевых и альтернативных гипотез и обозначить их согласно утверждению альтернативной гипотезы.
Формулировки гипотез.
Мы можем сформулировать нулевые и альтернативные гипотезы тремя различными способами:
- 1-я формулировка: (H_0: theta = theta_0) (нулевая гипотеза) и (H_a: theta neq theta_0) (альтернативная гипотеза «не равно»).
- 2-я формулировка: (H_0: theta leq theta_0) (нулевая гипотеза) и (H_a: theta > theta_0) (альтернативная гипотеза «больше чем»).
- 3-я формулировка: (H_0: theta geq theta_0) (нулевая гипотеза) и (H_a: theta < theta_0) (альтернативная гипотеза «меньше, чем»).
В нашем примере с американскими акциями, (theta = mu_{RP} ), что представляет собой среднее по совокупности премии за риск для американских акций. Кроме того, (theta_0 = 0 ), и мы используем вторую из указанных выше трех пар гипотез.
1-я формулировка представляет собой двустороннюю проверку гипотезы (англ. ‘ two-sided hypothesis test’ или ‘two-tailed hypothesis test’): Мы отвергаем нуль в пользу альтернативы, если данные свидетельствуют о том, что параметр совокупности либо меньше, либо больше, чем (theta_0 ).
В отличие от этого, 2-я и 3-я формулировки являются односторонней проверкой гипотезы (англ. ‘one-sided hypothesis test’ или ‘one-tailed hypothesis test’).
В формулировках 2 и 3 мы отвергаем нуль только тогда, когда данные свидетельствуют о том, что параметр совокупности соответственно, либо больше, либо меньше, чем (theta_0 ). Альтернативная гипотеза имеет только одну сторону.
Обратите внимание, что в каждом из описанных выше случаев, мы формулируем нулевые и альтернативные гипотезы так, что они учитывают все возможные значения параметра. В формулировке 1, например, параметр или равен гипотетическому значению (theta_0 ) (по нулевой гипотезе) или не равен гипотетическому значению (theta_0 ) (по альтернативной гипотезе).
Эти два утверждения логически исчерпывают все возможные значения параметра.
Несмотря на то, что формулировать гипотезы можно различными способами, мы всегда проводим проверку нулевой гипотезы в точке равенства, (theta = theta_0 ). Если нуль это (H_0: theta = theta_0), (H_0: theta leq theta_0) или (H_0: theta geq theta_0), мы на самом деле проверяем (theta = theta_0 ). Логика проста.
Предположим, что гипотетическое значение параметра равно 5.
Рассмотрим нулевую гипотезу (H_0: theta leq 5), с альтернативной гипотезой «больше чем» (H_a: theta > 5) .
Если у нас есть достаточно доказательств, чтобы отклонить (H_a: theta = 5) в пользу (H_a: theta > 5), то у нас, безусловно, также есть достаточные доказательства, чтобы отвергнуть гипотезу о том, что параметр (theta) равен некоторому меньшему значению, например, 4.5 или 4.
Напомним, что расчет для проверки нулевой гипотезы является одинаковым для всех трех формулировок. Различия в трех формулировках мы увидим в ближайшее время, — они заключаются в определении того, следует ли отклонить нулевую гипотезу.
Как мы выбираем нулевые и альтернативные гипотезы?
Вероятно, наиболее распространенными являются альтернативные гипотезы «не равно». Мы отвергаем нуль, поскольку данные свидетельствуют о том, что параметр больше или меньше, чем (theta_0).
Иногда, однако, у нас могут быть условия, имеющие вид «ожидаем», «подозреваем» или «надеемся на то, что», которые означают, что мы хотим найти благоприятные доказательства.
Часть этого обсуждения выбора гипотез взята из работы Bowerman, O’Connell и Murphree (2016).
В этом случае, мы можем сформулировать альтернативную гипотезу, как утверждение о том, что это условие является истинным. При этом нулевой гипотезой будет утверждение о том, что это условие не истинно. Если данные подтверждают отклонение нуля и принятие альтернативы, то мы статистически подтвердили наши ожидания того, что было истиной.
Например, экономическая теория предполагает, что инвесторы требуют положительную премию за риск по акциям (премия за риск определяется как ожидаемая доходность акций за вычетом безрисковой ставки).
Следуя принципу с формулировки альтернативы в виде условия «надеемся на то, что», сформулируем следующие гипотезы:
- (H_0:) Среднее по совокупности премии за риск для американских акций меньше или равно 0.
- (H_a:) Среднее по совокупности премии за риск для американских акций положительно.
Обратите внимание, что альтернативные гипотезы «больше чем» и «меньше чем» отражают убеждения исследователя сильнее, чем альтернативная гипотеза «не равно».
Для того, чтобы подчеркнуть свое нейтральное отношение к гипотезам, исследователь может иногда выбрать альтернативную гипотезу «не равно», когда выбор односторонней альтернативной гипотезы также разумен.
2 этап. Определение тестовой статистики и ее распределения вероятностей.
Второй этап проверки гипотез заключается в определении соответствующей тестовой статистики и ее распределения вероятностей.
Определение тестовой статистики.
Тестовая статистика, тест-статистика или статистика критерия (т.е. статистика, лежащая в основе критерия, англ. ‘test statistic’) является величиной, рассчитанной на основе выборки, значение которой является основанием для принятия решения о том, следует ли отклонить нулевую гипотезу.
Средоточием нашего статистического решения является значение тестовой статистики. Очень часто (во всех случаях, которые мы рассмотрим в этом чтении) тестовая статистика имеет следующий вид:
( Large stBf{Тестовая}{статистика} = { stRm{Выборочная}{статистика} — stRm{Значение параметра}{совокупности при $H_0$} over text{Стандартная ошибка выборочной статистики}} ) (Формула 1)
Для нашей премии за риск, например, интересующий параметр совокупности — это средняя по совокупности премия за риск (mu_{RP}). Мы обозначаем гипотетическое значение среднего по совокупности населения для (H_0) как (mu_0). Переформулировав гипотезу с использованием символов, мы проверяем нуль (H_0: mu_{RP} leq mu_0 ) и альтернативу (H_a: mu_{RP} > mu_0 ).
Однако, поскольку в соответствии с нулем мы проверяем условие ( mu_0 = 0), то мы пишем (H_0: mu_{RP} leq 0 ) и (H_a: mu_{RP} > 0 ).
Выборочное среднее обеспечивает оценку среднего по совокупности. Таким образом, мы можем использовать выборочное среднее премии за риск ( overline X_{RP}), рассчитанное на основе исторических данных, в качестве выборочной статистики в Формуле 1.
Стандартное отклонение выборочной статистики, известное как «стандартная ошибка» статистики, является знаменателем в Формуле 1.
В этом примере выборочной статистикой является выборочное среднее. Для выборочного среднего ( overline X ), рассчитанного по выборке, отобранной из совокупности со стандартным отклонением ( sigma ), стандартная ошибка определяется по одной из двух формул:
(large dst
sigma_{overline X} = {sigma over sqrt n} ) (Формула 2)
если нам известно стандартное отклонение совокупности (sigma), или
(large dst
s_{overline X} = {s over sqrt n} ) (Формула 3)
когда мы не знаем стандартное отклонение совокупности и нам необходимо использовать стандартное отклонение выборки (s) оценки стандартной ошибки.
В этом примере, поскольку мы не знаем стандартное отклонение совокупности, порождающей доходность, мы используем Формулу 3.
Таким образом, тестовая статистика определяется по формуле:
( large dst
{overline X_{RP} — mu_0 over s_{overline X}} = {overline X_{RP} — 0 over s big / sqrt n } )
Заменяя (mu_0) на 0, мы используем тот уже отмеченный факт, что мы тестируем любую нулевую гипотезу в точке равенства, а также тот факт, что здесь (mu_0 = 0).
Итак, мы определили тестовую статистику, чтобы проверить нулевую гипотезу.
Какому распределению вероятностей она соответствует?
В этом чтении мы будет использовать четыре распределения вероятности для тестовых статистик:
- t-распределение Стьюдента (для t-теста);
- Стандартное нормальное или z-распределение (для z-теста);
- Распределение хи-квадрат (( chi^2 )) (для хи-квадрат теста); а также
- F-распределение (для F-теста).
Мы обсудим детали этих вариантов позже, но предположим, что мы можем провести z-тест, основанный на центральной предельной теореме, потому что наша выборка американских акций имеет много наблюдений.
Центральная предельная теорема говорит о том, что выборочное распределение выборочного среднего будет приблизительно нормальным со средним (mu) и дисперсией (sigma^2 / n), когда выборка имеет большой размер.
Выборка, которую мы будем использовать для этого примера, содержит 118 наблюдений.
В итоге, тестовая статистика для проверки гипотезы о средней премии за риск равна ( overline X_{RP} big / s_{overline X}).
Мы можем выполнить z-тест, поскольку мы можем правдоподобно предположить, что тестовая статистика следует стандартному нормальному распределению.
3 этап. Определение уровня значимости.
Третьим этапом проверки гипотез является определение уровня значимости. Когда тестовая статистика рассчитана, возможны два действия:
- Мы отвергаем нулевую гипотезу или
- Мы не отвергаем нулевую гипотезу.
Выбор действия основан на сравнении вычисленной тестовой статистики с заданным возможным значением или значениями. Значения, которые мы выбираем, основаны на выбранном уровне значимости. Уровень значимости отражает то, какие основанные на выборке доказательства нам необходимы, чтобы отвергнуть нуль.
По аналогии с судом, необходимая доказательная база может меняться в зависимости от характера гипотез и серьезности последствий совершения ошибки.
Возможны четыре результата при проверке нулевой гипотезы:
- Мы отвергаем ложную нулевую гипотезу. Это правильное решение.
- Мы отвергаем истинную нулевую гипотезу. Это называется ошибкой I рода (англ. ‘Type I error’).
- Мы не отвергаем ложную нулевую гипотезу. Это называется ошибкой II рода (англ. ‘Type II error’).
- Мы не отвергаем истинную нулевую гипотезу. Это правильное решение.
Проиллюстрируем эти результаты в Таблице 1.
|
Решение |
Ситуация |
|
|---|---|---|
|
(H_0) Истина |
(H_0) Ложь |
|
|
(H_0) не отвергается |
Правильное решение |
Ошибка II рода |
|
(H_0) отвергается (принимается (H_a)) |
Ошибка I рода |
Правильное решение |
Когда мы принимаем решение при проверке гипотезы, мы рискуем допустить ошибку I или II рода. Это взаимоисключающие ошибки:
- Если мы ошибочно отвергаем нуль, мы можем допустить только ошибку I рода.
- Если мы ошибочно не отвергаем нуль, мы можем допустить только ошибку II рода.
Вероятность ошибки I рода при проверке гипотезы обозначается греческой буквой альфа: (alpha). Эта вероятность также известна как уровень значимости проверки (англ. ‘level of significance’).
Например, уровень значимости 0.05 для проверки означает, что есть 5-процентная вероятность отклонения истинной нулевой гипотезы.
Вероятность ошибки II рода обозначается греческой буквой бета: (beta).
Управление вероятностью ошибок двух типов предполагает компромисс. При прочих равных, если мы уменьшаем вероятность ошибки I рода, задав меньший уровень значимости (скажем, 0.01, а не 0.05), мы увеличиваем вероятность совершить ошибку II рода, потому что мы отвергаем нуль реже, в том числе, когда он является ложным.
Единственным способом уменьшить вероятность ошибок обоих типов одновременно является увеличение размера выборки (n).
Количественный компромисс между двумя типами ошибок на практике, как правило, невозможен, потому что вероятность ошибки II рода очень трудно определить количественно.
Рассмотрим пример с парой гипотез: (H_0: theta leq 5) и (H_a: theta > 5).
Поскольку каждое истинное значение (theta) больше 5 делает нулевую гипотезу ложной, каждое значение (theta) больше 5 имеет различную (beta) (вероятность ошибки II рода).
В отличие от этого, нам достаточно только констатировать вероятность ошибки I рода при (theta = 5). Таким образом, как правило, мы указываем только вероятность ошибки I рода, когда выполняем проверку гипотезы.
В то время как уровень значимости проверки является вероятностью ошибочно отвергнуть нулевую гипотезу, то мощностью критерия или мощностью проверки (англ. ‘power of a test’) является вероятность правильного отклонения нулевой гипотезы — то есть вероятность отвергнуть нуль, если он ложный.
Мощность критерия, на самом деле, равна 1 минус вероятность ошибки II рода.
Когда при проведении проверки имеется более одной статистики критерия, мы должны предпочесть самую мощную из них, при прочих равных условиях.
Тем не менее, у нас не всегда есть информация об относительной мощности критерия для конкурирующих статистик критерия.
В итоге, стандартный подход к проверке гипотез включает только определение уровня значимости (вероятности ошибки I рода). Наиболее целесообразно устанавливать этот уровень значимости до расчета тестовой статистики (статистики критерия). Если мы указываем его после вычисления тестовой статистики, на нас может повлиять результат расчета, что умаляет объективность проверки.
Мы можем использовать три наиболее распространенных уровня значимости для проведения проверки гипотезы: 0.10, 0.05 и 0.01.
Если мы можем отклонить нулевую гипотезу на уровне значимости 0.10, то у нас есть доказательства того, что нулевая гипотеза неверна.
Если мы можем отклонить нулевую гипотезу на уровне значимости 0.05, то у нас есть убедительные доказательства того, что нулевая гипотеза неверна.
И если мы можем отклонить нулевую гипотезу на уровне значимости 0.01, то у нас есть очень убедительные доказательства того, что нулевая гипотеза неверна.
Для нашего примера с премией за риск, мы установим уровень значимости 0.05.
4 этап. Формулировка правила принятия решения.
Четвертый этап проверки гипотезы заключается в формулировке правила принятия решения (англ. ‘decision rule’).
Общий принцип формулируется просто.
Когда мы проверяем нулевую гипотезу, если мы находим, что рассчитанное значение статистики критерия (тестовой статистики) является экстремальным или более экстремальным, чем заданное значение или значения, определенные установленным уровнем значимости (alpha), то мы отвергаем нулевую гипотезу. Мы говорим, что результат является статистически значимым (англ. ‘statistically significant’).
В противном случае, мы не отвергаем нулевую гипотезу, и говорим, что результат не является статистически значимым. Значение или значения, с которым мы сравниваем вычисленную статистику критерия, чтобы принять наше решение, являются точками отклонения (критическими значениями) для проверки гипотезы.
Термин «точка отклонения» (англ. ‘rejection point’) является описательным синонимом для более традиционного термина «критическое значение» (англ. ‘critical value’).
Определение критического значения для статистики критерия.
Критическое значение или точка отклонения (англ. ‘critical value’) для тестовой статистики (статистики критерия) представляет собой значение, с которой сравнивается вычисленная тестовая статистика, чтобы решить, следует ли отклонять или не отклонять нулевую гипотезу.
Для односторонней проверки, мы указываем критическое значение, используя символ для тестовой статистики с индексом (alpha), обозначающим заданную вероятность ошибки I рода, например, (z_alpha).
Для двусторонней проверки, мы указываем критическое значение (z_{alpha/2}).
Для того, чтобы проиллюстрировать применение критических значений, предположим, что мы используем z-тест и выбрали уровень значимости 0.05.
Для проверки пары гипотез (H_0: theta = theta_0) и (H_a: theta neq theta_0), существуют два критических значения, — одно отрицательное и одно положительное.
Для двухсторонней проверки при уровне значимости 0.05, суммарная вероятность ошибки I рода должна быть равна 0.05. Таким образом, 0.05 / 2 = 0.025 вероятности должно быть в каждом хвосте распределения тестовой статистики при нулевой гипотезе.
Следовательно, двумя критическими значениями будут (z_{0.025} = 1.96) и (-z_{0.025} = -1.96). Пусть (z) является вычисленным значением тестовой статистики. Мы отвергаем нуль, если находим, что (z < -1.96) или (z > 1.96). И мы не отвергаем нуль, если (-1.96 leq z leq 1.96).
Для проверки пары гипотез (H_0: theta leq theta_0) и (H_a: theta > theta_0) при уровне значимости 0.05, критическим значением будет (z_{0.05} = 1.645). Мы отвергаем нулевую гипотезу, если (z > 1.645). Значение стандартного нормального распределения таково, что 5% результатов лежат правее точки (z_{0.05} = 1.645).
Для проверки пары гипотез (H_0: theta geq theta_0) и (H_a: theta < theta_0), критическим значением будет (-z_{0.05} = -1.645). Мы отвергаем нулевую гипотезу, если (z < -1.645).
График 2 иллюстрирует проверку (H_0: mu = mu_0) и (H_a: mu neq mu_0) при уровне значимости 0.05 с использованием z-теста.
Термин «область принятия гипотезы» (англ. ‘acceptance region’) является традиционным названием для множества значений тестовой статистики, при которых мы не отвергаем нулевую гипотезу.
Традиционное название, однако, неточное. Мы должны избегать использования таких фраз, как «принять нулевую гипотезу», потому что такое утверждение подразумевает неоправданно большую степень убежденности в нуле, когда мы не отвергаем его.
Аналогия с некоторыми судами (например, в Соединенных Штатах) заключается в том, что если присяжные не выносят вердикт о виновности (альтернативная гипотеза), наиболее точным будет сказать, что жюри не удалось отклонить нулевую гипотезу о невиновности обвиняемого (что следует из принципа презумпции невиновности).
По обеим сторонам от области принятия решения находятся области отклонения или критические области (англ. ‘rejection region’ или ‘critical region’).
Если нулевая гипотеза заключается в том, что ( mu = mu_0 ) истинно, тестовая статистика имеет 2.5-процентный шанс попадания в левую критическую область и 2.5-процентный шанс попадания в правую критическую область.
Любое вычисленное значение тестовой статистики, которое попадает в любую из этих двух областей, заставляет нас отвергнуть нулевую гипотезу при уровне значимости 0.05. Критические значения 1.96 и -1.96 рассматриваются как разделительные линии между областями принятия и отклонения гипотезы.
График 2 дает хорошую возможность подчеркнуть взаимосвязь между доверительными интервалами и проверкой гипотез. 95-процентный доверительный интервал для среднего по совокупности (mu), основанного на выборочном среднем (overline X), задается диапазоном от (overline X — 1.96s_{overline X}) до (overline X + 1.96s_{overline X}), где (s_{overline X}) является стандартной ошибкой выборочного среднего (Формула 3).
Так же, как и при проверке гипотезы, мы можем использовать этот доверительный интервал, основанный на стандартном нормальном распределении, когда у нас есть большая выборка.
Альтернативная проверка гипотезы и доверительный интервал используют t-распределение. Мы рассмотрим эти концепции в следующем разделе.
Теперь рассмотрим одно из условий для отклонения нулевой гипотезы:
( dst {overline X — mu_0 over s_{overline X}} > 1.96)
Здесь (mu_0) является гипотетическим значением среднего по совокупности. Условие гласит, что отклонение гипотезы является оправданным, если тестовая статистика превышает 1.96.
Умножив обе стороны неравенства на (s_{overline X}), мы получим ( overline X — mu_0 > 1.96 s_{overline X}), или после преобразования, ( overline X — 1.96 s_{overline X} > mu_0), что можем также записать в виде ( mu_0 < overline X — 1.96 s_{overline X}).
Это выражение означает, что если гипотетическое среднее по совокупности (mu_0), меньше нижнего предела 95-процентного доверительного интервала, основанного на выборочном среднем, мы должны отвергнуть нулевую гипотезу при уровне значимости 5% (тестовая статистика попадает в критическую область справа).
Теперь мы можем взять другое условие для отклонения нулевой гипотезы:
( dst {overline X — mu_0 over s_{overline X}} < -1.96)
и, используя алгебру, как и ранее, мы преобразуем его к виду:
( dst mu_0 > overline X — 1.96 s_{overline X})
Если гипотетическое среднее по совокупности больше, чем верхний предел 95-процентного доверительного интервала, мы отвергаем нулевую гипотезу при уровне значимости 5% (тестовая статистика попадает в критическую область слева).
Таким образом, уровень значимости в двусторонней проверке гипотезы можно интерпретировать точно так же, как доверительный интервал (1 — alpha).
Таким образом, когда гипотетическое значение параметра совокупности для нулевой гипотезы находится вне соответствующего доверительного интервала, то нулевая гипотеза отвергается. Мы могли бы использовать доверительные интервалы для проверки гипотез, но на практике финансовые аналитики, как правило, этого не делают.
Вычисление тестовой статистики (одно число, по сравнению с двумя числами для обычного доверительного интервала) более эффективно. Также, на практике аналитики редко сталкиваются с односторонними доверительными интервалами.
Кроме того, только вычислив тестовую статистику, мы можем получить p-значение, полезный показатель значимости результатов (мы обсудим p-значение далее).
Вернемся к нашей проверке премии за риск.
Мы сформулировали гипотезы (H_0: mu_{RP} leq 0) и (H_a: mu_{RP} > 0). Мы определили тестовую статистику как ( overline X_{RP} / s_{overline X}) и определили, что она следует стандартному нормальному распределению.
Таким образом, мы выполняем односторонний z-тест.
Мы определили уровень значимости 0.05. Для этого одностороннего z-теста, критическая точка при уровне значимости 0.05 составляет 1.645. Мы отвергаем нуль, если вычисленная z-статистика больше, чем 1.645.
График 3 иллюстрирует эту проверку.
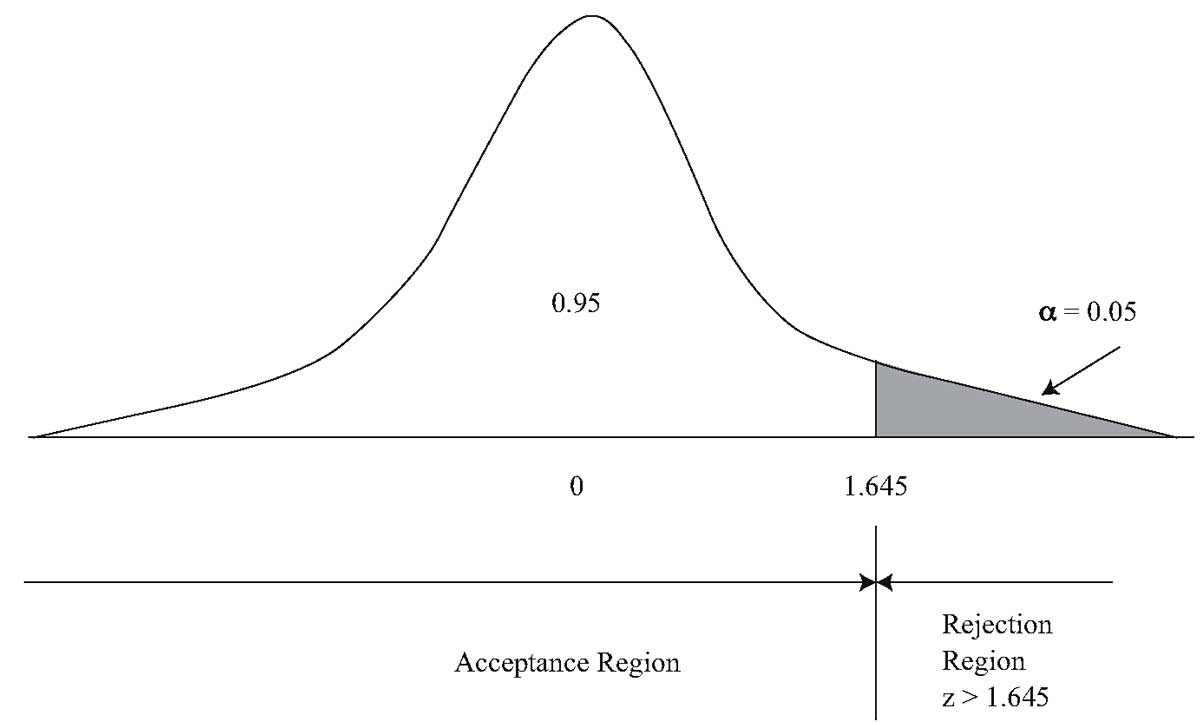
5 этап. Сбор данных и расчет тестовой статистики.
Пятый шаг в проверке гипотез заключается в сборе данные и расчете тестовой статистики. Качество наших выводов зависит не только от уместности статистической модели, но и от качества данных, которые мы используем при проведении проверки.
В первую очередь мы должны проверить данные на наличие ошибок измерений. Нам также необходимо учесть другие проблемы, в том числе систематическую ошибку выборки и систематическую ошибку временного периода.
Систематическая ошибка выборки — это смещение выборки, связанное с систематическим исключением некоторых элементов совокупности в соответствии с определенным признаком.
Одним из типов систематической ошибки выборки является систематическая ошибка выжившего. Например, если мы определим нашу выборку, как облигации взаимных фондов США, которые продолжают деятельность в настоящее время, и мы сделаем выборку доходности только по этим фондам, мы будем систематически исключать фонда, которые не выжили (прекратили деятельность) к настоящему моменту.
Прекратившие деятельность фонды, скорее всего, в среднем хуже оставшихся фондов. В результате, эффективность фондов, рассчитанная на основе этой выборки, может быть смещена вверх.
Систематическая ошибка временного периода связана с вероятностью того, что когда мы используем выборку из временных рядов, наш статистический вывод может быть чувствительным к начальным и конечным датам периода выборки.
В нашей гипотезе о премии за риск мы имеем дело с американскими акциями. Согласно Dimson, Marsh и Staunton (2018) за период с 1900 по 2017 год включительно (118 ежегодных наблюдений), среднеарифметическая премия за риск для американских акций по отношению к доходности облигаций (overline X_{RP}) составила 7.5% в год.
Выборочное стандартное отклонение годовой премии за риск составило 19.5%. Используя Формулу 3, найдем стандартную ошибку выборочного среднего:
( dst s_{overline X} = s big / sqrt n = 19.5% / sqrt {118} ) = 1.795%.
Тестовая статистика равна:
( dst z = overline X_{RP} big / s_{overline X}) = 7.5%/1.795% = 4.18.
6 этап. Принятие статистического решения.
Шестой этап проверки гипотезы означает принятие статистического решения.
В нашем примере, поскольку тестовая статистика (z = 4.18) больше критического значения 1.645, мы отвергаем нулевую гипотезу в пользу альтернативной гипотезы о том, что премия за риск для американских акций является положительной.
Первые шесть шагов являются статистическими шагами. Наше итоговое решение принимается с использованием статистического решения.
7 этап. Принятие экономического или инвестиционного решения.
Седьмой и заключительный шаг в проверке гипотез заключается в принятии экономического или инвестиционного решения. Экономическое или инвестиционное решение принимает во внимание не только статистические решения, но и все соответствующие экономические вопросы.
На шестом этапе, мы нашли убедительные статистические доказательства того, что премия за риск для американских акций является положительной. Величина расчетной премии за риск, 7.5% в год, является также очень значимой экономически.
Исходя из этих соображений, инвестор может принять решение инвестировать часть средств в американские акции. Ряд нестатистических соображений, таких как толерантность инвестора к риску и его финансовое положение, может также повлиять на процесс принятия решений.
Предшествующее обсуждение поднимает проблему, которая часто возникает на этом этапе принятия решений. Мы часто находим, что небольшие различия между переменной величиной и ее гипотетическим значением являются статистически значимыми, но не значимыми экономически.
Например, мы можем проверить инвестиционную стратегию и отклонить нулевую гипотезу о том, что средняя доходность стратегии равна нулю на основе большой выборки.
Формула 1 показывает, что чем меньше стандартная ошибка выборочной статистики (делитель в формуле), тем больше значение тестовой статистики и тем больше шанс на то, что нулевая гипотеза будет отклонена, при прочих равных условиях. Стандартная ошибка уменьшается по мере увеличения размера выборки (n), так что при очень больших выборках, мы можем отклонить нулевую гипотезу.
Мы можем обнаружить, что, хотя стратегия обеспечивает статистически значимую положительную среднюю доходность, результаты не являются экономически значимыми, если учесть транзакционные издержки, налоги и риски.
Даже если мы приходим к выводу, что результаты стратегии являются экономически значимыми, мы должны изучить логику того, почему стратегия могла бы работать в будущем, прежде чем реализовывать ее фактически. Такие соображения нельзя включить в проверку гипотезы.
Перед тем как завершить тему процесса проверки гипотез, мы должны обсудить важный альтернативный подход, называемый подходом проверке гипотез с. Аналитики и исследователи часто включают в отчеты о проверке гипотез p-значение (также называемое предельным уровнем значимости, англ. ‘marginal significance level’).
Определение p-значения.
P-значение (p-уровень значимости или p-критерий, англ. ‘p-value’) является наименьшим уровнем значимости, при котором может быть отвергнута нулевая гипотеза.
Для значения тестовой статистики 4.18 в проверке гипотезы о премии за риск, с помощью функции электронной таблицы для стандартного нормального распределения, мы вычисляем р-значение 0.000015. Мы можем отклонить нулевую гипотезу на этом уровне значимости.
Чем меньше р-значение, тем сильнее доказательства против нулевой гипотезы и в пользу альтернативной гипотезы. P-значение для двухсторонней проверки того, что параметр равен нулю, часто генерируется автоматически с помощью статистических и эконометрических программ.
Мы можем использовать электронные таблицы для расчета p-значения. В Microsoft Excel, например, мы можем использовать функции TTEST, NORMSDIST, CHIDIST и FDIST для расчета р-значений для f-тестов, z-тестов, хи-квадрат тестов, и F-тестов, соответственно.
Мы можем использовать р-значение в рамках процедуры проверки гипотез, представленной выше, в качестве альтернативы критическим значениям.
Если р-значение меньше нашего заданного уровня значимости, мы отвергаем нулевую гипотезу. В противном случае, мы не отвергаем нулевую гипотезу.
Используя p-значение таким образом, мы приходим к такому же выводу, что и при использовании критических значений. Например, поскольку 0.000015 меньше 0.05, мы отвергаем нулевую гипотезу в проверке гипотезы о премии за риск.
P-значение, тем не менее, обеспечивает более точную информацию о силе доказательств, чем подход с использованием критических значений. P-значение 0.000015 указывает на то, что нулевая гипотеза отвергается на гораздо меньшем уровне значимости, чем 0.05.
Если один исследователь рассматривает вопрос, используя уровень значимости 0.05, а другой исследователь использует уровень значимости 0.01, читатель может столкнуться с проблемой, сравнивая полученные результаты.
Эта проблема породила подход к представлению результатов проверки гипотез, при котором указываются p-значения и не указывается спецификация уровня значимости (этап 3). Интерпретация статистических результатов остается на усмотрение пользователя исследования. Этот подход к представлению результатов иногда называют подходом к проверке гипотез с использованием р-значения.
Davidson и MacKinnon (1993) оспорили достоинство этого подхода:
«Подход с использование p-значения по не обязательно заставит нас принять решение о нулевой гипотезе. Если мы получим p-значение равное, скажем, 0.000001, мы почти наверняка захотим отклонить нуль.
Но если мы получим p-значение равное, скажем, 0.04, или даже 0.004, мы не обязаны отклонять его. Мы можем просто отбросить результат прочь, как информацию, которая ставит под сомнение нулевую гипотезу, но сама по себе не убедительна.
Мы считаем, что это несколько агностическое отношение к статистическим проверкам, в которых p-значения рассматриваются просто как части информации, которую мы можем использовать, но можем и не использовать». (Стр. 80)

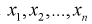
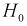 , когда она на самом деле верна — ошибка первого рода. Вероятность этой ошибки обозначается а и называется уровнем значимости.
, когда она на самом деле верна — ошибка первого рода. Вероятность этой ошибки обозначается а и называется уровнем значимости. 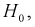 когда она на самом деле не верна — ошибка второго рода, вероятность ошибки —
когда она на самом деле не верна — ошибка второго рода, вероятность ошибки — 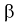 .
.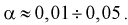
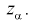
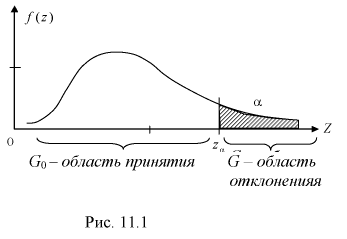
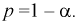
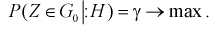
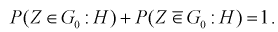

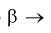
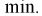
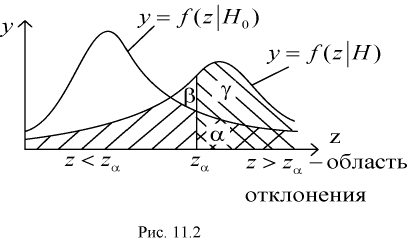

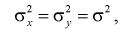
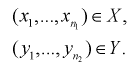
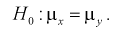
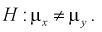
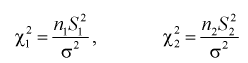
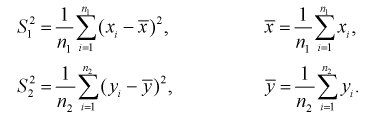
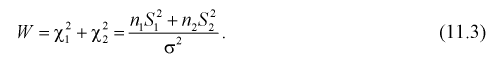
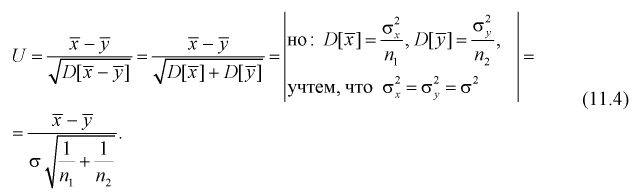
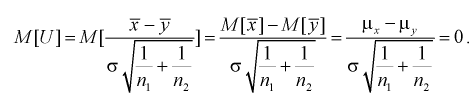
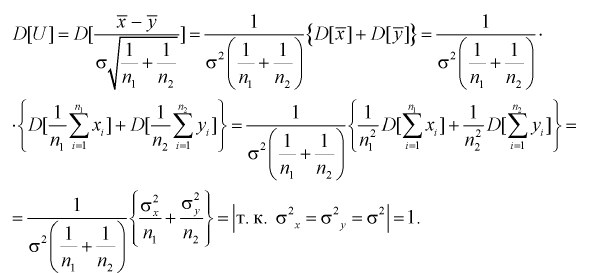
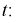


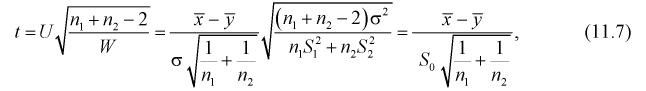
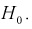
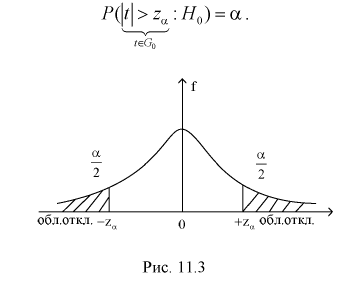
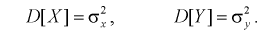
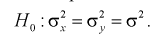

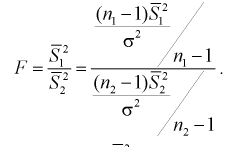
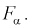
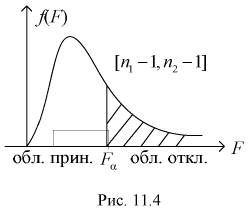
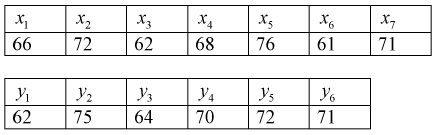
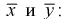
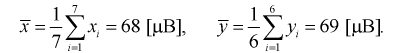
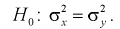
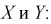
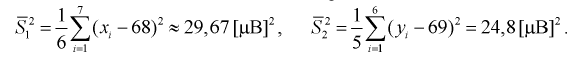
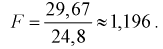
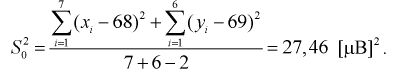
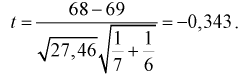
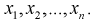
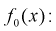
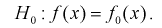
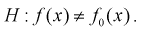
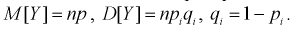
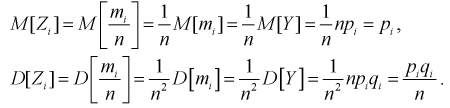
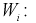
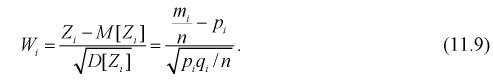
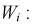

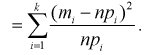

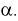
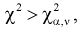 то нулевая гипотеза
то нулевая гипотеза 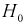 отвергается в пользу альтернативной Н, т. е.
отвергается в пользу альтернативной Н, т. е. 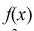 не согласуется с результатами эксперимента.
не согласуется с результатами эксперимента.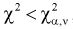 , то
, то 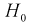 , принимается, т. е.
, принимается, т. е. 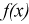 согласуется с экспериментальными данными, закон распределения
согласуется с экспериментальными данными, закон распределения 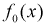 подтверждается. При этом вероятность ошибки равна
подтверждается. При этом вероятность ошибки равна