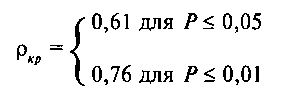Уровень статистической значимости
При
обосновании статистического вывода
следует решить вопрос, где же проходит
линия между принятием и отвержением
нулевой гипотезы? В силу наличия в
эксперименте случайных влияний эта
граница не может быть проведена абсолютно
точно. Она базируется на понятии уровня
значимости. Уровнем значимости называется
вероятность ошибочного отклонения
нулевой гипотезы. Или, иными словами,
уровень значимости
—
это вероятность
ошибки первого рода при принятии решения.
Для обозначения этой вероятности, как
правило, употребляют либо греческую
букву α, либо латинскую букву р.
В дальнейшем мы будем
употреблять букву р.
Исторически
сложилось так, что в прикладных науках,
использующих статистику, и в частности
в психологии, считается, что низшим
уровнем статистической значимости
является уровень р =
0,05; достаточным —
уровень р =
0,01 и высшим уровень р
= 0,001. Поэтому в
статистических таблицах, которые
приводятся в приложении к учебникам по
статистике, обычно даются табличные
значения для уровней р
= 0,05, р
= 0,01 и р
= 0,001. Иногда даются
табличные значения для уровней р
— 0,025 и р
= 0,005.
Величины
0,05, 0,01 и 0,001 — это так называемые
стандартные уровни статистической
значимости. При статистическом анализе
экспериментальных данных психолог в
зависимости от задач и гипотез исследования
должен выбрать необходимый уровень
значимости. Как видим, здесь наибольшая
величина, или нижняя граница уровня
статистической значимости, равняется
0,05 — это означает, что допускается пять
ошибок в выборке из ста элементов
(случаев, испытуемых) или одна ошибка
из двадцати элементов (случаев,
испытуемых). Считается, что ни шесть, ни
семь, ни большее количество раз из ста
мы ошибиться не можем. Цена таких ошибок
будет слишком велика.
Заметим,
что в современных статистических пакетах
на ЭВМ используются не стандартные
уровни значимости, а уровни, подсчитываемые
непосредственно в процессе работы с
соответствующим статистическим
методом. Эти уровни, обозначаемые буквой
р, могут
иметь различное числовое выражение в
интервале от 0 до 1, например, р
= 0,7, р
= 0,23 или р
= 0,012. Понятно, что в
первых двух случаях полученные уровни
значимости слишком велики и говорить
о том, что результат значим нельзя. В то
же время в последнем случае результаты
значимы на уровне 12 тысячных. Это
достоверный уровень.
Правило
принятия статистического вывода таково:
на основании полученных экспериментальных
данных психолог подсчитывает по
выбранному им статистическому методу
так называемую эмпирическую статистику,
или эмпирическое значение. Эту величину
удобно обозначить как Чэмп.
Затем эмпирическая
статистика Чэмп
сравнивается с двумя
критическими величинами, которые
соответствуют уровням значимости в 5%
и в 1% для выбранного статистического
метода и которые обозначаются как Чкр.
Величины Чкр
находятся для данного
статистического метода по соответствующим
таблицам, приведенным в приложении к
любому учебнику по статистике. Эти
величины, как правило, всегда различны
и их в дальнейшем для удобства можно
назвать как Чкр1
и
Чкр2.
Найденные по таблицам
величины критических значений Чкр1
и
Чкр2 удобно
представлять в следующей стандартной
форме записи:
Подчеркнем,
однако, что мы использовали обозначения
Чэмп
и Чкр
как сокращение слова
«число». Во всех статистических методах
приняты свои символические обозначения
всех этих величин: как подсчитанной
по соответствующему статистическому
методу эмпирической величины, так и
найденных по соответствующим таблицам
критических величин. Например, при
подсчете рангового коэффициента
корреляции Спирмена по таблице критических
значений этого коэффициента были найдены
следующие величины критических
значений, которые для этого метода
обозначаются греческой буквой ρ («ро»).
Так для р = 0,05
по таблице найдена величина ρкр1
= 0,61 и для р = 0,01
величина ρкр2
= 0,76.
В
принятой в дальнейшем изложении
стандартной форме записи это выглядит
следующим образом:
Теперь
нам необходимо сравнить наше эмпирическое
значение с двумя найденными по
таблицам критическими значениями.
Лучше всего это сделать, расположив все
три числа на так называемой «оси
значимости». «Ось значимости» представляет
собой прямую, на левом конце которой
располагается 0, хотя он, как правило,
не отмечается на самой этой прямой, и
слева направо идет увеличение числового
ряда. По сути дела это привычная
школьная ось абсцисс ОХ
декартовой системы
координат. Однако особенность этой оси
в том, что на ней выделено три участка,
«зоны». Одна крайняя зона называется
зоной незначимости, вторая крайняя зона
— зоной значимости, а промежуточная —
зоной неопределенности. Границами
всех трех зон являются Чкр1
для р
= 0,05 и Чкр2
для р
= 0,01, как это показано
на рисунке.
В
зависимости от правила принятия решения
(правила вывода), предписанного в данном
статистическом методе возможно два
варианта.
Первый
вариант: альтернативная гипотеза
принимается, если Чэмп≥Чкр.
Или
второй вариант: альтернативная гипотеза
принимается, если Чэмп≤Чкр.
Подсчитанное
Чэмп
по какому либо
статистическому методу должно обязательно
попасть в одну из трех зон.
Если
эмпирическое значение попадает в зону
незначимости, то принимается гипотеза
Н0
об отсутствии различий.
Если
Чэмп
попало в зону значимости,
принимается альтернативная гипотеза
Н1
о
наличии различий,
а гипотеза Н0
отклоняется.
Если
Чэмп
попадает в зону
неопределенности, перед исследователем
стоит дилемма. Так, в зависимости от
важности решаемой задачи он может
считать полученную статистическую
оценку достоверной на уровне 5%, и принять,
тем самым гипотезу Н1,
отклонив гипотезу Н0,
либо — недостоверной
на уровне 1%, приняв тем самым, гипотезу
Н0.
Подчеркнем, однако, что это именно
тот случай, когда психолог может допустить
ошибки первого или второго рода. Как
уже говорилось выше, в этих обстоятельствах
лучше всего увеличить объем выборки.
Подчеркнем
также, что величина Чэмп
может точно совпасть
либо с Чкр1
либо
Чкр2.
В первом случае можно
считать, что оценка достоверна точно
на уровне в 5% и принять гипотезу Н1,
или, напротив, принять гипотезу Н0.
Во втором случае, как правило,
принимается альтернативная гипотеза
Н1
о наличии различий,
а гипотеза Н0
отклоняется.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Проверка статистических гипотез
- Понятие о статистической гипотезе
- Уровень значимости при проверке гипотезы
- Критическая область
- Простая гипотеза и критерии согласия
- Критерий согласия (X^2) Пирсона
- Примеры
п.1. Понятие о статистической гипотезе
Статистическая гипотеза – это предположение о виде распределения и свойствах случайной величины в наблюдаемой выборке данных.
Прежде всего, мы формулируем «рабочую» гипотезу. Желательно это делать не на основе полученных данных, а исходя из природы и свойств исследуемого явления.
Затем формулируется нулевая гипотеза (H_0), отвергающая нашу рабочую гипотезу.
Наша рабочая гипотеза при этом называется альтернативной гипотезой (H_1).
Получаем, что (H_0=overline{H_1}), т.е. нулевая и альтернативная гипотеза вместе составляют полную группу несовместных событий.
Основной принцип проверки гипотезы – доказательство «от противного», т.е. опровергнуть гипотезу (H_0) и тем самым доказать гипотезу (H_1).
В результате проверки гипотезы возможны 4 исхода:
| Верная гипотеза | |||
| (H_0) | (H_1) | ||
| Принятая гипотеза | (H_0) | True Negative (H_0) принята верно |
False Negative (H_0) принята неверно Ошибка 2-го рода |
| (H_1) | False Positive (H_0) отвергнута неверно (H_1) принята неверно Ошибка 1-го рода |
True Positive (H_0) отвергнута верно (H_1) принята верно |
Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».
Например:
К врачу обращается человек с некоторой жалобой.
Гипотеза (H_1) — человек болен, гипотеза (H_0) — человек здоров.
True Negative – здорового человека признают здоровым
True Positive – больного человека признают больным
False Positive – здорового человека признают больным – «ложная тревога»
False Negative – больного человека признают здоровым – «пропуск события»
Уровень значимости при проверке гипотезы
Статистический тест (статистический критерий) – это строгое математическое правило, по которому гипотеза принимается или отвергается.
В статистике разработано множество критериев: критерии согласия, критерии нормальности, критерии сдвига, критерии выбросов и т.д.
Уровень значимости – это пороговая (критическая) вероятность ошибки 1-го рода, т.е. непринятия гипотезы (H_0), когда она верна («ложная тревога»).
Требуемый уровень значимости α задает критическое значение для статистического теста.
Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.
В результате статистического теста на конкретных данных получают эмпирический уровень значимости p. Чем меньше значение p, тем сильнее аргументы против гипотезы (H_0).
Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:
| Уровень значимости (p) |
Решение о гипотезе (H_0) | Вывод для гипотезы (H_1) |
| (pgt 0,1) | (H_0) не может быть отклонена | Статистически достоверные доказательства не обнаружены |
| (0,5lt pleq 0,1) | Истинность (H_0) сомнительна, неопределенность | Доказательства обнаружены на уровне статистической тенденции |
| (0,01lt pleq 0,05) | Отклонение (H_0), значимость | Обнаружены статистически достоверные (значимые) доказательства |
| (pleq 0,01) | Отклонение (H_0), высокая значимость | Доказательства обнаружены на высоком уровне значимости |
Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы (H_1).
Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с (ngeq 100) критический уровень снижают до α=0,01.
п.3. Критическая область
Критическая область – область выборочного пространства, при попадании в которую нулевая гипотеза отклоняется.
Требуемый уровень значимости α, который задается исследователем, определяет границу попадания в критическую область при верной нулевой гипотезе.
Различают 3 вида критических областей
Критическая область на чертежах заштрихована.
(K_{кр}=chi_{f(alpha)}) определяют границы критической области в зависимости от α.
Если эмпирическое значение критерия попадает в критическую область, гипотезу (H_0) отклоняют.
Пусть (K*) — эмпирическое значение критерия. Тогда:
(|K|gt K_{кр}) – гипотеза (H_0) отклоняется
(|K|leq K_{кр}) – гипотеза (H_0) не отклоняется
п.4. Простая гипотеза и критерии согласия
Пусть (x=left{x_1,x_2,…,x_nright}) – случайная выборка n объектов из множества (X), соответствующая неизвестной функции распределения (F(t)).
Простая гипотеза состоит в предположении, что неизвестная функция (F(t)) является совершенно конкретным вероятностным распределением на множестве (X).
Например:
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
(H_0): данные являются выборкой из равномерного распределения на отрезке [-1;1]
Критерий согласия проверяет, согласуется ли заданная выборка с заданным распределением или с другой выборкой.
К критериям согласия относятся:
- Критерий Колмогорова-Смирнова;
- Критерий (X^2) Пирсона;
- Критерий (omega^2) Смирнова-Крамера-фон Мизеса
п.5. Критерий согласия (X^2) Пирсона
Пусть (left{t_1,t_2,…,t_nright}) — независимые случайные величины, подчиняющиеся стандартному нормальному распределению N(0;1) (см. §63 данного справочника)
Тогда сумма квадратов этих величин: $$ x=t_1^2+t_2^2+⋯+t_n^2 $$ является случайной величиной, которая имеет распределение (X^2) с n степенями свободы.
График плотности распределения (X^2) при разных n имеет вид:
С увеличением n распределение (X^2) стремится к нормальному (согласно центральной предельной теореме – см. §64 данного справочника).
Если мы:
1) выдвигаем простую гипотезу (H_0) о том, что полученные данные являются выборкой из некоторого закона распределения (f(x));
2) выбираем в качестве теста проверки гипотезы (H_0) критерий Пирсона, —
тогда определение критической области будет основано на распределении (X^2).
Заметим, что выдвижение основной гипотезы в качестве (H_0) при проведении этого теста исторически сложилось.
В этом случае критическая область правосторонняя.
Мы задаем уровень значимости α и находим критическое значение
(X_{кр}^2=X^2(alpha,k-r-1)), где k — число вариант в исследуемом ряду, r – число параметров предполагаемого распределения.
Для этого есть специальные таблицы.
Или используем функцию ХИ2ОБР(α,k-r-1) в MS Excel (она сразу считает нужный нам правый хвост). Например, при r=0 (для равномерного распределения):
Пусть нам дан вариационный ряд с экспериментальными частотами (f_i, i=overline{1,k}).
Пусть наша гипотеза (H_0) –данные являются выборкой из закона распределения с известной плотностью распределения (p(x)).
Тогда соответствующие «теоретические частоты» (m_i=Ap(x_i)), где (x_i) – значения вариант данного ряда, A – коэффициент, который в общем случае зависит от ряда (дискретный или непрерывный).
Находим значение статистического теста: $$ X_e^2=sum_{j=1}^kfrac{(f_i-m_i)^2}{m_i} $$ Если эмпирическое значение (X_e^2) окажется в критической области, гипотеза (H_0) отвергается.
(X_e^2geq X_{кр}^2) — закон распределения не подходит (гипотеза (H_0) не принимается)
(X_e^2lt X_{кр}^2) — закон распределения подходит (гипотеза (H_0) принимается)
Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 12 | 8 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=60 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 60=10 $$ по 10 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 12 | 8 | 60 |
| (m_i) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| (f_i-m_i) | -2 | 2 | 3 | -3 | 2 | -2 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,4 | 0,4 | 0,9 | 0,9 | 0,4 | 0,4 | 3,4 |
Значение теста: $$ X_e^2=3,4 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
Значит, с вероятностью 95% кубик не фальшивый.
п.6. Примеры
Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 10 | 22 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=72 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 72=12 $$ по 12 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 10 | 22 | 72 |
| (m_i) | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
| (f_i-m_i) | -4 | 0 | 1 | -5 | -2 | 10 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 1,333 | 0,000 | 0,083 | 2,083 | 0,333 | 8,333 | 12,167 |
Значение теста: $$ X_e^2=12,167 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
Значит, с вероятностью 95% кубик фальшивый.
Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
Проверялась гипотеза (H_0) — стрельба случайна.
Если стрельба случайна, то попадание на участок должно иметь распределение, подчиняющееся «закону редких событий» — закону Пуассона с плотностью вероятности: $$ p(k)=frac{lambda^k}{k!}e^{-lambda} $$ где (k) — число попаданий. Чтобы получить значение (lambda), нужно посчитать математическое ожидание данного распределения.
Составим расчетную таблицу:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 28 | 0 | 0 | 7 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Тогда теоретические частоты будут равны: $$ m_i=Ncdot p(k) $$ Получаем:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (p_i) | 0,39365 | 0,36700 | 0,17107 | 0,05316 | 0,01239 | 0,00231 | 0,00036 | 0,00005 | 0,99999 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,1 | 1,3 | 0,2 | 0,0 | 576,0 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | -0,1 | -1,3 | -0,2 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) (результат) | 0,02 | 0,00 | 0,31 | 0,63 | 0,00 | 1,33 | 0,21 | 34,34 | 36,84 |
Значение теста: (X_e^2=36,84)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для (X_{кр}^2=X^2(alpha,k-2)).
Для уровня значимости α=0,05 и k=8, r=1 находим:
(X_{кр}^2approx 12,59)
Получается, что: (X_e^2gt X_{кр}^2)
Гипотеза (H_0) не принимается.
Стрельба не случайна.
Пример 3. В предыдущем примере объединили события x={4;5;6;7} с редким числом попаданий:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4-7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 8 |
Проверялась гипотеза (H_0) — стрельба случайна.
Для последней объединенной варианты находим среднюю взвешенную: $$ x_5=frac{4cdot 7+5cdot 0+6cdot 0+7cdot 1}{7+1}=4,375 $$ Найдем оценку λ.
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 35 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Оценка не изменилась, что указывает на правильное определение средней для (x_5).
Строим расчетную таблицу для подсчета статистики:
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (p_i) | 0,3937 | 0,3670 | 0,1711 | 0,0532 | 0,0121 | 0,9970 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,0 | 574,2 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,02 | 0,00 | 0,31 | 0,63 | 0,16 | 1,12 |
Значение теста: (X_e^2=1,12)
Критическое значение статистики ищем в виде (X_{кр}^2=X^2(alpha,k-2)), где α=0,05 и k=5, r=1
(X_{кр}^2approx 7,81)
Получается, что: (X_e^2lt X_{кр}^2)
Гипотеза (H_0) принимается.
Стрельба случайна.
И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики (X_e^2) в Примере 2, основной вклад внесло слагаемое для (x_i=7). Оно равно 34,34 и поэтому сумма (X_e^2=36,84) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты (x_i=4,375) слагаемое статистики равно 0,16 и сумма (X_e^2=1,12) в итоге мала.
Правильный ответ – в Примере 3.
Стрельба случайна.
Материал из MachineLearning.
Перейти к: навигация, поиск
Содержание
- 1 Стандартная методика проверки статистических гипотез
- 2 Вычисление пи-величины
- 3 Вычисление ROC-кривой
- 4 Литература
- 5 См. также
- 6 Ссылки
Уровень значимости статистического теста — допустимая для данной задачи вероятность ошибки первого рода (ложноположительного решения, false positive), то есть вероятность отклонить нулевую гипотезу, когда на самом деле она верна.
Другая интерпретация:
уровень значимости — это такое (достаточно малое) значение вероятности события, при котором событие уже можно считать неслучайным.
Уровень значимости обычно обозначают греческой буквой (альфа).
Стандартная методика проверки статистических гипотез
В стандартной методике проверки статистических гипотез уровень значимости фиксируется заранее, до того, как становится известной выборка
.
Чрезмерное уменьшение уровня значимости (вероятности ошибки первого рода) может привести к увеличению вероятности ошибки второго рода, то есть вероятности принять нулевую гипотезу, когда на самом деле она не верна (это называется ложноотрицательным решением, false negative).
Вероятность ошибки второго рода связана с мощностью критерия
простым соотношением
.
Выбор уровня значимости требует компромисса между значимостью и мощностью или
(что то же самое, но другими словами)
между вероятностями ошибок первого и второго рода.
Обычно рекомендуется выбирать уровень значимости из априорных соображений.
Однако на практике не вполне ясно, какими именно соображениями надо руководствоваться,
и выбор часто сводится к назначению одного из популярных вариантов
.
В докомпьютерную эпоху эта стандартизация позволяла сократить объём справочных статистических таблиц.
Теперь нет никаких специальных причин для выбора именно этих значений.
Существует две альтернативные методики, не требующие априорного назначения .
Вычисление пи-величины
Достигаемый уровень значимости или пи-величина (p-value) — это наименьшая величина уровня значимости,
при которой нулевая гипотеза отвергается для данного значения статистики критерия .
где
— критическая область критерия.
Другая интерпретация:
достигаемый уровень значимости или пи-величина — это вероятность, с которой (при условии истинности нулевой гипотезы) могла бы реализоваться наблюдаемая выборка, или любая другая выборка с ещё менее вероятным значением статистики
.
Случайная величина имеет равномерное распределение.
Фактически, функция приводит значение статистики критерия
к шкале вероятности.
Маловероятным значениям (хвостам распределения) статистики соотвествуют значения
, близкие к нулю или к единице.
Вычислив значение на заданной выборке
,
статистик имеет возможность решить,
является ли это значение достаточно малым, чтобы отвергнуть нулевую гипотезу.
Данная методика является более гибкой, чем стандартная.
В частности, она допускает «нестандартное решение» — продолжить наблюдения, увеличивая объём выборки, если оценка вероятности ошибки первого рода попадает в зону неуверенности, скажем, в отрезок .
Вычисление ROC-кривой
ROC-кривая (receiver operating characteristic) — это зависимость мощности от уровня значимости
.
Методика предполагает, что статистик укажет подходящую точку на ROC-кривой, которая соответствует компромиссу между вероятностями ошибок I и II рода.
Литература
- Кобзарь А. И. Прикладная математическая статистика. Справочник для инженеров и научных работников. — М.: Физматлит, 2006.
- Цейтлин Н. А. Из опыта аналитического статистика. — М.: Солар, 2006. — 905 с.
- Алимов Ю. И. Альтернатива методу математической статистики. — М.: Знание, 1980.
См. также
- Проверка статистических гипотез — о стандартной методике проверки статистических гипотез.
- Достигаемый уровень значимости, синонимы: пи-величина, p-Value.
Ссылки
- P-value — статья в англоязычной Википедии.
- ROC curve — статья в англоязычной Википедии.
Уровень значимости
- Уровень значимости
-
В статистике величину называют статисти́чески зна́чимой, если мала вероятность чисто случайного возникновения её или ещё более крайних величин. Здесь под крайностью понимается степень отклонения от нуль-гипотезы. Разница называется «статистически значимой», если имеются данные, появление которых было бы маловероятно, если предположить, что эта разница отсутствует; это выражение не означает, что данная разница должна быть велика, важна, или значима в общем смысле этого слова.
Уровень значимости теста — это традиционное понятие проверки гипотез в частотной статистике. Он определяется как вероятность принять решение отклонить нуль-гипотезу, если на самом деле нуль-гипотеза верна (решение известное как ошибка первого рода, или ложноположительное решение.) Процесс решения часто опирается на p-величину (читается «пи-величина»): если p-величина меньше уровня значимости, то нуль-гипотеза отвергается. Чем меньше p-величина, тем более значимой называется тестовая статистика. Чем меньше p-величина, тем сильнее основания отвергнуть нуль-гипотезу.
Уровень значимости обыкновенно обозначают греческой буквой α (альфа). Популярными уровнями значимости являются 5%, 1%, и 0.1%. Если тест выдаёт p-величину меньше α-уровня, то нуль-гипотеза отклоняется. Такие результаты неформально называют «статистически значимыми». Например, если кто-то говорит, что «шансы того, что случившееся является совпадением, равным одному из тысячи», то имеется в виду 0.1 % уровень значимости.
Различные значения α-уровня имеют свои достоинства и недостатки. Меньшие α-уровни дают бо́льшую уверенность в том, что уже установленная альтернативная гипотеза значима, но при этом есть больший риск не отвергнуть ложную нуль-гипотезу (ошибка второго рода, или «ложноотрицательное решение»), и таким образом меньшая статистическая мощность. Выбор α-уровня неизбежно требует компромисса между значимостью и мощностью, и следовательно между вероятностями ошибок первого и второго рода. В отечественных научных работах часто употребляется неправильный термин «достоверность» вместо термина «статистическая значимость».
См. также
- Ложное срабатывание
- Ошибки первого и второго рода
Примечания
George Casella, Roger L. Berger Hypothesis Testing // Statistical Inference. — Second Edition. — Pacific Grove, CA: Duxbury, 2002. — С. 397. — 660 с. — ISBN 0-534-24312-6
О НЕПРАВИЛЬНОМ УПОТРЕБЛЕНИИ ТЕРМИНА «ДОСТОВЕРНОСТЬ» В РОССИЙСКИХ НАУЧНЫХ ПСИХИАТРИЧЕСКИХ И ОБЩЕМЕДИЦИНСКИХ СТАТЬЯХ http://www.biometrica.tomsk.ru/let1.htm
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Уровень значимости» в других словарях:
-
УРОВЕНЬ ЗНАЧИМОСТИ — число столь малое, что можно считать практически несомненным, что событие с вероятностью α не произойдет при единичном опыте. Обычно У. з. фиксируется произвольно, а именно: 0,05, 0,01 и при особой точности 0,005 и т. д. В геол. работах… … Геологическая энциклопедия
-
уровень значимости — статистического критерия (его называют также “альфа уровень” и обозначают греческой буквой ) – это ограничение сверху на вероятность ошибки первого рода (вероятность отвергнуть нулевую гипотезу, когда она на самом деле верна). Типичные значения – … Словарь социологической статистики
-
УРОВЕНЬ ЗНАЧИМОСТИ — англ. level, significance; нем. Signifikanzniveau. Степень риска в том, что исследователь может сделать неправильный вывод об ошибочности статист, гипотезы на основе выборочных данных. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
-
уровень значимости — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN level of significance … Справочник технического переводчика
-
уровень значимости — 3.31 уровень значимости (significance level) α: Заданное значение, представляющее собой верхний предел вероятности отвергнуть статистическую гипотезу, когда эта гипотеза верна. Источник: ГОСТ Р ИСО 12491 2011: Материалы и изделия строительные.… … Словарь-справочник терминов нормативно-технической документации
-
УРОВЕНЬ ЗНАЧИМОСТИ — понятие математической статистики, отражающее степень вероятности ошибочного вывода относительно статистической гипотезы о распределении признака, проверяемой на основе выборочных данных. В психологических исследованиях за достаточный уровень… … Современный образовательный процесс: основные понятия и термины
-
уровень значимости — reikšmingumo lygis statusas T sritis automatika atitikmenys: angl. significance level vok. Signifikanzniveau, n rus. уровень значимости, m pranc. niveau de signifiance, m … Automatikos terminų žodynas
-
уровень значимости — reikšmingumo lygis statusas T sritis fizika atitikmenys: angl. level of significance; significance level vok. Sicherheitsschwelle, f rus. уровень значимости, f pranc. niveau de significance, m … Fizikos terminų žodynas
-
Уровень значимости (критический пороговый уровень статистической значимости) — Уровень значимости (критический, пороговый уровень статистической значимости) * узровень значнасці (крытычны, парогавы ўзровень статыстычнай значнасці) * significance level допускаемая исследователем величина α ошибки, т. е. максимально… … Генетика. Энциклопедический словарь
-
уровень значимости (статистического испытания) — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN significance level (of a statistical test) … Справочник технического переводчика