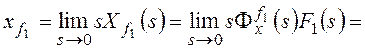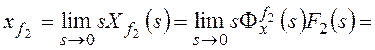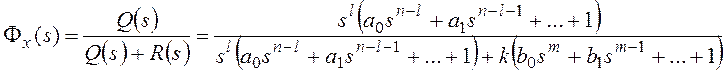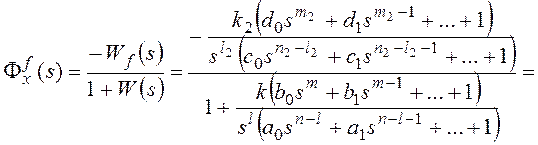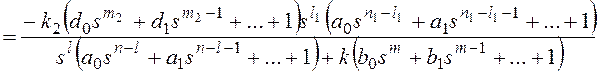Установившаяся ошибка сау

Ошибка
системы по задающему воздействию равна

,

а по
возмущению

т. е.
ошибка системы от возмущения численно
равна изменению регулируемой величины
под влиянием этого возмущения (при
отсутствии задающего воздействия).

 Ввиду
наличия переходных процессов текущее
значение ошибки

резко меняется и не может служить мерой
точности автоматических систем. Поэтому
точность автоматических систем оценивают
величиной установившейся ошибки, которая
имеет место в устойчивой системе после
завершения переходного процесса.

 Необходимо
установить, во-первых, как вычисляются
установившиеся ошибки и, во-вторых,
какие факторы влияют на эти ошибки. Обе
задачи решаются параллельно. Предварительно
отметим, что установившаяся ошибка
вычисляется для значения времени

,
т. е.

.

 Величину
установившейся ошибки можно найти из
дифференциального уравнения системы,
однако ее значительно удобнее вычислять
при помощи передаточной функции ошибки

.
Следовательно,

.

 Данная
формула позволяет найти изображение
ошибки. Для того чтобы найти ошибку как
функцию времени, необходимо сделать
обратное преобразование Лапласа:

,
откуда можно определить установившуюся
ошибку, положив

.

 Рассмотренный
способ вычисления

не рационален. Применим теорему
операционного исчисления о конечном
значении функции. Эта теорема говорит
о том, что если известно изображение

функции

,
то конечное значение оригинала

можно вычислить по формуле

.

 Применяя
эту формулу для решения нашей задачи,
получаем

(1)

 Формула
(1) позволяет вычислить установившуюся
ошибку по задающему воздействию

.
Для определения установившейся ошибки
от возмущения

надо воспользоваться зависимостью

(2)

где

— передаточная функция по возмущению.

 Таким
образом, из формул (1) и (2) следует, что
точность автоматических систем зависит,
во-первых, от внешнего воздействия

или

и, во-вторых, от свойств автоматической
системы, отображаемых передаточной
функцией

или

.

 Задающие
и возмущающие воздействия являются
сложными функциями времени и поэтому
вычисление ошибок значительно усложняется.
Реальные воздействия заменяются
типовыми, в качестве которых применяют
ступенчатую

,
линейную

и квадратичную

функции. Все эти воздействия просто
выражаются при помощи формул; их значения
можно точно вычислить для любого момента
времени, ввиду чего они называются
детерминированными, или регулярными.

30 Вычисление ошибки от задающих воздействий

Учитывая
равенство (1), а также выражение для
передаточной функции ошибки

(3)

получим
формулу для вычисления ошибки от
задающего воздействия.

,

где

— передаточная функция разомкнутой
системы.

При
вычислении ошибок по формуле (3)
учитывается, что изображения по Лапласу
для типовых воздействий

,

,

— соответственно равны:

;

;

.

 Кроме
того, для статистических систем

,
а для астатических систем 1-го и 2-го
порядков примем соответственно

и

,

при
этом

,
где k — коэффициент передачи разомкнутой
системы; W*(р) — передаточная функция
без учета интегрирующих звеньев и
коэффициента передачи.

Ошибки
некоторых автоматических систем
приведены в табл. 3.  Анализ табл. 3
показывает, что статические системы
при ступенчатом воздействии имеют
установившуюся ошибку

, (4)

которая
называется статической, или ошибкой по
положению. Она пропорциональна величине
задающего воздействия и уменьшается с
увеличением коэффициента передачи
разомкнутой системы k.

 Астатические
системы 1-го порядка принципиально точно
отрабатывают ступенчатое воздействие,
но имеют постоянную ошибку при отработке
линейно возрастающего сигнала (табл.
3). Эта ошибка

(5)

пропорциональна
скорости v изменения входного сигнала,
ввиду чего ее называют скоростной
ошибкой, а коэффициент передачи
разомкнутой системы k — добротностью
системы по скорости. Отсутствие
статической ошибки объясняется наличием
в одноцепочечной структурной схеме
системы интегрирующего звена.

 Астатические
системы 2-го порядка принципиально точно
отрабатывают как ступенчатый, так и
линейно возрастающий сигнал. При
отработке квадратичного сигнала имеет
место ошибка

,
(6)

пропорциональная
ускорению а входного сигнала и обратно
пропорциональная коэффициенту усиления
разомкнутой системы k, который называется
добротностью системы по ускорению, а
сама ошибка — ошибкой системы по
ускорению.

 Итак,
с увеличением коэффициента передачи
разомкнутой системы установившиеся
ошибки уменьшаются.

ранее
было показано, что, с увеличением k
ухудшается устойчивость автоматических
систем. Таким образом, требование к
точности противоречит требованию к
устойчивости. Далее будет рассмотрено,
что улучшение устойчивости при заданном
относительно большом значении k
достигается путем включения в систему
корректирующих устройств.

 Чем
больше v, тем точнее система отрабатывает
более сложное воздействие и поэтому
следящие системы и системы управления
выполняют как астатические. Однако с
увеличением порядка астатизма САУ более
склонны к колебаниям в переходных
процессах, и их устойчивость ухудшается.
Поэтому системы с порядком астатизма
более двух на практике почти не
встречаются.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма

Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: , рисунок 116.

Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:

,  ,   и так
далее.

При наличии нескольких воздействий на линейную систему
для определения x_уст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:

, где
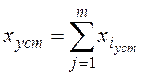
каждое слагаемое, или составляющая сигнала ошибки, определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.

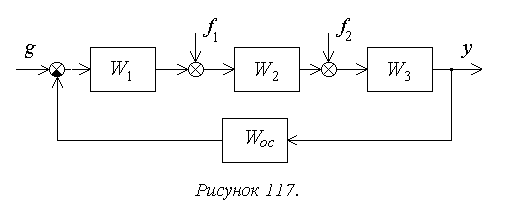
Рассмотрим порядок расчета установившейся ошибки на
следующем достаточно общем примере (рисунок 117).

В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих .

Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке  при известном изображении задающего
воздействия G(s):

, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117

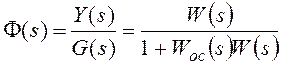
, где  — передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.

Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:

В результате:

.

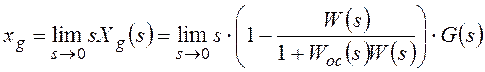
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения  при известном изображении возмущающего
воздействия F(s):

, где
F_f(s) –передаточная функция замкнутой системы по
возмущающему воздействию,

;

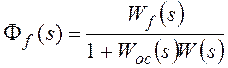
W_f(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).

Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.

Для f₁:                             
,

,

.

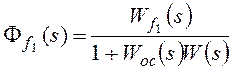
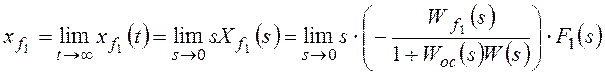
Для f₂:                                
,

,

.

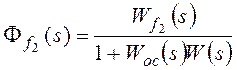
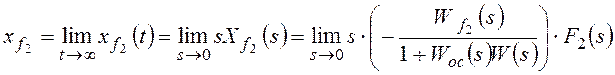
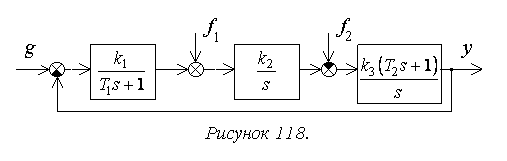
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):

,

, где k=k₁k₂k₃ – коэффициент передачи
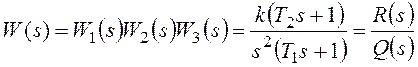
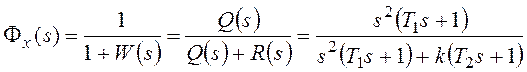
разомкнутой системы.

Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.

При  получим:

.

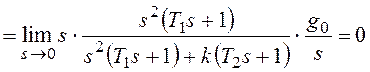
При  получим:

.

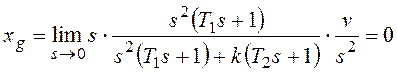
При  получим:

.

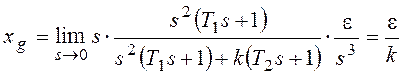
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.

Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.

Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.

Рассмотрим установившуюся
ошибку от возмущения f₁:

,

, где  –
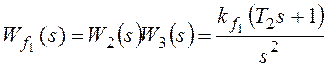
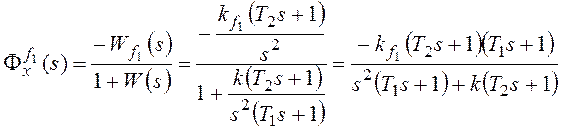
коэффициент передачи разомкнутой системы по возмущению f₁.

При  получим:

.

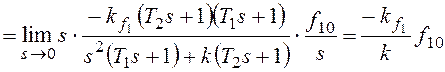
При  получим:

.

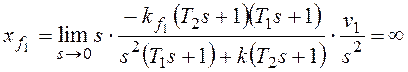
При 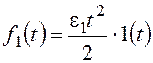 получим
тот же результат.

Отметим, что по возмущению f₁ рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.

Рассмотрим установившуюся
ошибку от возмущения f₂:

,

, где  –
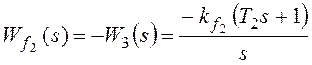
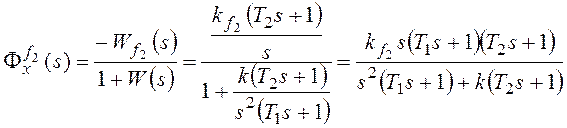
коэффициент передачи разомкнутой системы по возмущению f₂.

При  получим:

.

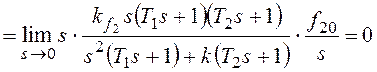
При  получим:

.

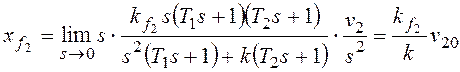
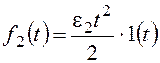
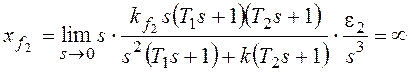
При  получим:

.

По возмущению f₂ рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.

Подведем некоторые итоги:

1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.

2. Постоянные времени
звеньев системы не влияют на ее точность.

3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.

Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.

Рассмотрим структуру,
показанную на рисунке 119.

В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:

, где l³0.

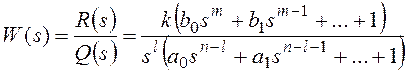
Тогда получим:

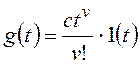
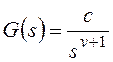
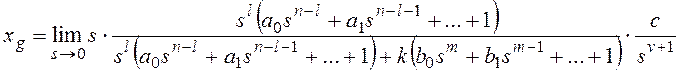
и для общего вида задающего воздействия , которому соответствует изображение ,

.

Результат нахождения этого
предела зависит от соотношения показателей степени:

— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;

— при l=v получаем
константу;

— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.

Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.

Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.

Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.

Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:

,

, где l₁+l₂=l,
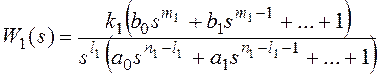
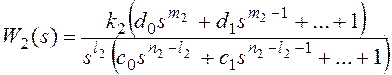
k₁k₂=k, m₁+m₂=m,
n₁+n₂=n,
причем  и .

Тогда получим:

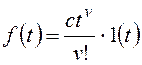
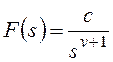
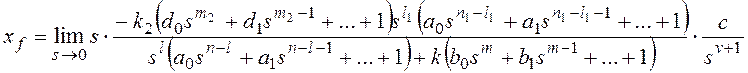
и для общего вида возмущающего воздействия , которому соответствует изображение ,

.

Все вышеприведенные выводы
можно повторить для показателя степени l₁.

Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.

Ошибки САУ в установившихся режимах

Ранее была определена ошибка системы в установившемся режиме при подаче на ее вход задающего воздействия в виде ступенчатой функции, у которой первая и производные более высокого порядка в установившемся режиме равны нулю. Однако на практике задающее воздействие а может быть различной функцией времени, содержащей первую производную, равную скорости изменения задающего воздействия, вторую производную, равную ускорению воздействия, и производные более высокого порядка. Так, задающее воздействие, изменяющееся по закону (рис. 2.10, а), где — начальное значение (скачок) а имеет первую производную которая при изменяется скачком (рис. 2.10, б). Вторая производная от а равна нулю. Такой закон изменения задающего воздействия встречается, например, в режиме захвата цели системой автосопровождения. В этом случае — начальное значение координаты цели (начальное рассогласование), — скорость цели.

В общем случае задающее воздействие может содержать производных и представлено в виде полинома от времени

где — начальное значение задающего воздействия; — начальные значения от первой до

Рис. 2.10. Задающее воздействие, изменяющееся по закону (а) и его первая производная (б).

производных задающего воздействия; значение производной задающего воздействия.

Найдем общее выражение для ошибки системы с астатизмом порядка в установившемся режиме при задающем воздействии, имеющем производных.

Для этого запишем изображение задающего воздействия

и передаточную функцию по ошибке системы с астатизмом порядка

Подставив значение из формулы (2.71) в формулу (2.65), имеем

После подстановки в эту формулу значения а из формулы получаем общее выражение для установившейся ошибки

Из этого выражения получаем следующее.

1. Если то вауст если порядок астатизма системы больше, чем порядок высшей производной задающего воздействия, то ошибка системы в установившемся режиме равна нулю.

2. Если то т. е. если порядок астатизма системы равен порядку высшей производной задающего воздействия, то ошибка системы в установившемся режиме будет иметь определенное значение. Эта ошибка, как видно из выражения (2.73) и последнего выражения, будет вызываться действием только высшей производной задающего воздействия. Составляющие же ошибки от других производных задающего воздействия и начального скачка самого воздействия в этом случае равны нулю.

3. Если то т. е. если порядок астатизма системы ниже, чем порядок высшей производной задающего воздействия, то ошибка системы с течением времени будет увеличиваться до бесконечности.

Следует различать статический установившийся режим, когда задающее воздействие не изменяется во времени, и динамический установившийся режим, когда производная от задающего воздействия есть величина постоянная. Например, в следящей системе режимы равномерного (когда первая производная равноускоренного (вторая производная вращений ведущего вала являются динамическими установившимися режимами. В соответствии с этим различают статические и динамические установившиеся ошибки системы. Ошибки, возникающие при статическом установившемся режиме, называются статическими, а при динамическом установившемся режиме — динамическими.