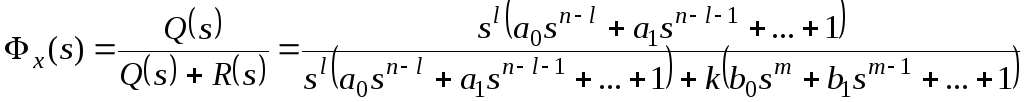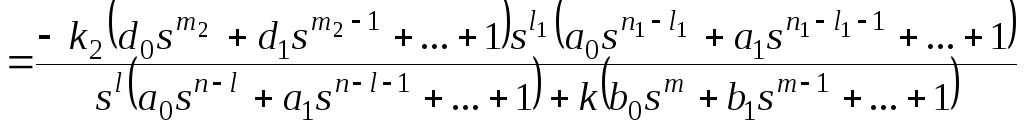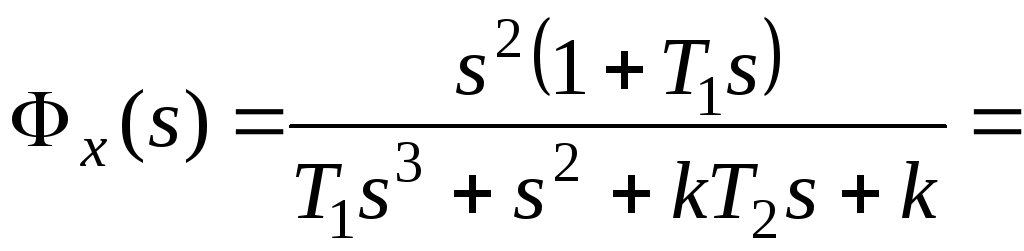Лекция 17.
Расчет
установившейся ошибки в системах
управления. Структурные признаки
астатизма. Коэффициенты ошибок
Установившейся
(статической) ошибкой называют постоянное
значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании
переходного процесса:
,
рисунок 116.
Очевидно,
установившаяся ошибка зависит от законов
изменения и численных характеристик
входных сигналов системы. Поэтому при
ее определении принято рассматривать
так называемые типовые входные сигналы,
законы изменения которых составляют
степенной ряд относительно времени.
Например, для задающего воздействия:
,
,
и так далее.
При наличии
нескольких воздействий на линейную
систему для определения xуст
используется принцип суперпозиции –
реакция линейной системы на совокупность
входных сигналов совпадает с алгебраической
суммой ее реакций на каждый из сигналов
в отдельности:
,
где каждое слагаемое,
или составляющая сигнала ошибки,
определяется
для i-го
входного сигнала при условии, что
остальные тождественно равны нулю.
Такой подход полностью соответствует
определению передаточной функции и
позволяет выполнять расчет установившейся
ошибки на основе структурной схемы
системы.
Рассмотрим порядок
расчета установившейся ошибки на
следующем достаточно общем примере
(рисунок 117).
В соответствии с
принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде
суммы трех составляющих
.
Изображение по
Лапласу ошибки от задающего воздействия
получают через передаточную функцию
замкнутой системы по ошибке
при известном изображении задающего
воздействия G(s):
,
где (s)
– основная передаточная функция
замкнутой системы. Для структурной
схемы на рисунке 117
,
где
— передаточная функция разомкнутой
системы, или прямой цепи системы, для
рассматриваемого примера.
Непосредственно
для расчета установившегося значения
ошибки от задающего воздействия
используют теорему о конечном значении
для преобразования Лапласа:
В результате:
.
Изображение по
Лапласу ошибки от возмущающего воздействия
получают через передаточную функцию
замкнутой системы по ошибке от возмущения
при известном изображении возмущающего
воздействия F(s):
,
где f(s)
–передаточная функция замкнутой системы
по возмущающему воздействию,
;
Wf(s)
– передаточная функция разомкнутой
системы по возмущению (передаточная
функция участка прямой цепи системы от
точки приложения возмущающего воздействия
до выхода системы).
Для структурной
схемы на рисунке 8 необходимо учитывать
два возмущающих воздействия, приложенные
в различные точки системы.
Для f1:
,
,
.
Для f2:
,
,
.
Расчет упрощается
для системы с единичной отрицательной
обратной связью (рисунок 118):
,
,
где k=k1k2k3
– коэффициент передачи разомкнутой
системы.
Найдем установившуюся
ошибку для некоторых типовых вариантов
задающего воздействия.
При
получим:
.
При
получим:
.
При
получим:
.
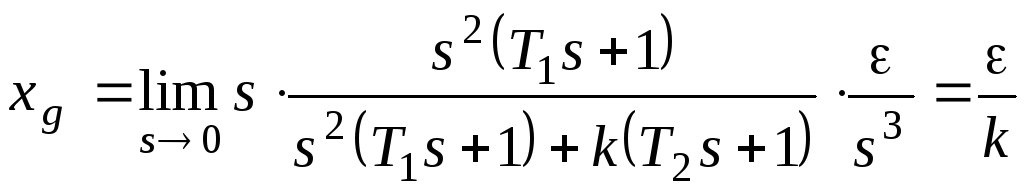
Если установившаяся
ошибка тождественно равна нулю при
каком-либо типовом варианте входного
сигнала, независимо от его численных
характеристик, систему называют
астатической по рассматриваемому
входному сигналу.
Количество типовых
вариантов входного сигнала – членов
степенного ряда, при которых установившаяся
ошибка тождественно равна нулю, определяет
порядок астатизма.
Рассматриваемая
система обладает свойством астатизма
второго порядка по задающему воздействию.
Рассмотрим
установившуюся ошибку от возмущения
f1:
,
,
где
– коэффициент передачи разомкнутой
системы по возмущению f1.
При
получим:
.
При
получим:
.
При
получим тот же результат.
Отметим, что по
возмущению f1
рассматриваемая система не является
астатической. Кроме того, она не в
состоянии отработать два последних
варианта входного сигнала.
Рассмотрим
установившуюся ошибку от возмущения
f2:
,
,
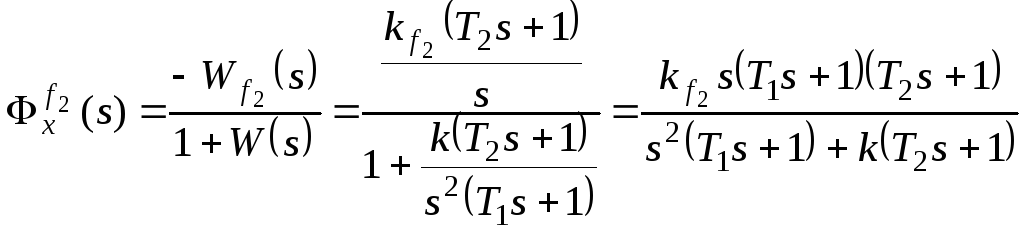
где
– коэффициент передачи разомкнутой
системы по возмущению f2.
При
получим:
.
При
получим:
.
При
получим:
.
По возмущению f2
рассматриваемая система имеет астатизм
первого порядка. Она не в состоянии
отработать возмущающее воздействие,
изменяющееся во времени с постоянным
ускорением.
Подведем некоторые
итоги:
1. Наличие и глубина
свойства астатизма зависят от точки
приложения входного сигнала.
2. Постоянные
времени звеньев системы не влияют на
ее точность.
3. Увеличение
значения коэффициента передачи
разомкнутой системы приводит к снижению
величины установившейся ошибки.
Для систем с
единичной отрицательной обратной связью
существуют достаточно простые структурные
признаки астатизма.
Рассмотрим
структуру, показанную на рисунке 119.
В общем случае
передаточная функция разомкнутой
системы может быть представлена в
следующей форме:
,
где l0.
Тогда получим:
и для общего вида
задающего воздействия
,
которому соответствует изображение
,
.
Результат нахождения
этого предела зависит от соотношения
показателей степени:
— при l>v
установившаяся ошибка равна нулю
независимо от остальных параметров, то
есть имеет место астатизм;
— при l=v
получаем константу;
— при l<v
установившаяся ошибка стремится к
бесконечности, то есть система не в
состоянии отработать входной сигнал.
Учитывая, что
минимальное значение v
нулевое, получаем условие астатизма по
задающему воздействию: l>0.
Таким образом,
структурный признак астатизма по
задающему воздействию в системе с
единичной отрицательной обратной связью
состоит в наличии нулевых корней в
знаменателе передаточной функции
разомкнутой системы, или интегрирующих
звеньев в прямой цепи системы.
Нетрудно также
убедиться, что положительное значение
l
совпадает с порядком астатизма.
Для получения
признака астатизма по возмущающему
воздействию представим передаточные
функции на рисунке 10 в форме:
,
,
где l1+l2=l,
k1k2=k,
m1+m2=m,
n1+n2=n,
причем
и
.
Тогда получим:
и для общего вида
возмущающего воздействия
,
которому соответствует изображение
,
.
Все вышеприведенные
выводы можно повторить для показателя
степени l1.
Таким образом,
структурный признак астатизма по
возмущающему воздействию в системе с
единичной отрицательной обратной связью
состоит в наличии нулевых корней в
знаменателе передаточной функции
участка системы до точки приложения
воздействия, или интегрирующих звеньев
на том же участке.
Более общий подход
к оценке точности линейных систем
управления основан на получении и
использовании коэффициентов ошибок.
Рассмотрим его на примере анализа
реакции системы на задающее воздействие.
Если рассматривать
произвольный закон изменения задающего
воздействия g(t),
то эта функция времени может быть
разложена в степенной ряд относительно
аргумента t.
Члены степенного ряда, как известно,
находятся через производные
,
,
…,
,
…
В общем случае ряд
бесконечен. Поэтому с практической
точки зрения рассматривать такое
представление сигнала целесообразно
только при достаточно плавном его
изменении, когда можно ограничиться
конечным числом членов ряда, имея в
виду, что при n
большем некоторого m
можно принять
,
n>m.
Для задачи оценки
установившейся ошибки при
с формулированное допущение вполне
корректно, так как в противном случае
эта задача не имеет смысла.
Коэффициенты
ошибки получают разложением передаточной
функции замкнутой системы по ошибке в
степенной ряд (ряд Тейлора) относительно
аргумента s:
,
где коэффициенты
разложения в общем случае находят как
значения производных в точке s=0:
.
Передаточные
функции, представляющие собой отношения
полиномов, при достаточно высоком
порядке системы могут оказаться слишком
сложными для дифференцирования. Поэтому
на практике коэффициенты их разложения
в ряд чаще находят путем деления полиномов
– числителя на знаменатель.
С учетом разложения
передаточной функции в ряд можно записать
изображение по Лапласу сигнала ошибки
в следующей форме:
.
Отметим, что с
учетом сформулированного выше допущения
такое представление сигнала ошибки
соответствует
или
.
Перейдя к оригиналу
с учетом теоремы дифференцирования
получим:
.
Вернемся к
рассмотренному выше примеру и предположим,
что задающее воздействие изменяется
по произвольному закону, но при достаточно
больших значениях времени этот закон
аппроксимируется выражением
.
Найдем коэффициенты
разложения передаточной функции по
ошибке
в степенной ряд.
Здесь сразу можно
отметить, что номер первого ненулевого
члена ряда определяется низшей степенью
аргумента s
в числителе дроби, то есть первые два
коэффициента c0
и c1
здесь получаем тождественно равными
нулю.
Далее получим:
В результате
получаем
,
,
,
и так далее.
Найдем производные
задающего воздействия:
,
,
.
Ясно, что для
определения установившейся ошибки
достаточно первых трех коэффициентов:
.
В заключение
отметим, что порядок астатизма системы
по какому-либо входному сигналу совпадает
с количеством нулевых коэффициентов
ошибки, получаемых в разложении в ряд
передаточной функции по ошибке от
данного входного сигнала.
Соседние файлы в папке Конспект ТАУ
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
The deviation of the output of control system from desired response during steady state is known as steady state error. It is represented as $e_{ss}$. We can find steady state error using the final value theorem as follows.
$$e_{ss}=lim_{t to infty}e(t)=lim_{s to 0}sE(s)$$
Where,
E(s) is the Laplace transform of the error signal, $e(t)$
Let us discuss how to find steady state errors for unity feedback and non-unity feedback control systems one by one.
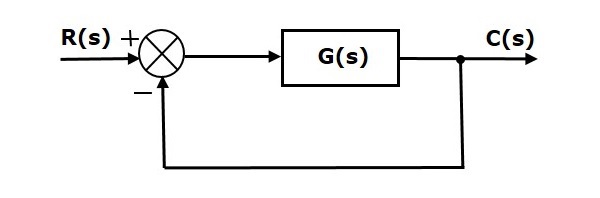
Steady State Errors for Unity Feedback Systems
Consider the following block diagram of closed loop control system, which is having unity negative feedback.
Where,
- R(s) is the Laplace transform of the reference Input signal $r(t)$
- C(s) is the Laplace transform of the output signal $c(t)$
We know the transfer function of the unity negative feedback closed loop control system as
$$frac{C(s)}{R(s)}=frac{G(s)}{1+G(s)}$$
$$Rightarrow C(s)=frac{R(s)G(s)}{1+G(s)}$$
The output of the summing point is —
$$E(s)=R(s)-C(s)$$
Substitute $C(s)$ value in the above equation.
$$E(s)=R(s)-frac{R(s)G(s)}{1+G(s)}$$
$$Rightarrow E(s)=frac{R(s)+R(s)G(s)-R(s)G(s)}{1+G(s)}$$
$$Rightarrow E(s)=frac{R(s)}{1+G(s)}$$
Substitute $E(s)$ value in the steady state error formula
$$e_{ss}=lim_{s to 0} frac{sR(s)}{1+G(s)}$$
The following table shows the steady state errors and the error constants for standard input signals like unit step, unit ramp & unit parabolic signals.
| Input signal | Steady state error $e_{ss}$ | Error constant |
|---|---|---|
|
unit step signal |
$frac{1}{1+k_p}$ |
$K_p=lim_{s to 0}G(s)$ |
|
unit ramp signal |
$frac{1}{K_v}$ |
$K_v=lim_{s to 0}sG(s)$ |
|
unit parabolic signal |
$frac{1}{K_a}$ |
$K_a=lim_{s to 0}s^2G(s)$ |
Where, $K_p$, $K_v$ and $K_a$ are position error constant, velocity error constant and acceleration error constant respectively.
Note − If any of the above input signals has the amplitude other than unity, then multiply corresponding steady state error with that amplitude.
Note − We can’t define the steady state error for the unit impulse signal because, it exists only at origin. So, we can’t compare the impulse response with the unit impulse input as t denotes infinity.
Example
Let us find the steady state error for an input signal $r(t)=left( 5+2t+frac{t^2}{2} right )u(t)$ of unity negative
feedback control system with $G(s)=frac{5(s+4)}{s^2(s+1)(s+20)}$
The given input signal is a combination of three signals step, ramp and parabolic. The following table shows the error constants and steady state error values for these three signals.
| Input signal | Error constant | Steady state error |
|---|---|---|
|
$r_1(t)=5u(t)$ |
$K_p=lim_{s to 0}G(s)=infty$ |
$e_{ss1}=frac{5}{1+k_p}=0$ |
|
$r_2(t)=2tu(t)$ |
$K_v=lim_{s to 0}sG(s)=infty$ |
$e_{ss2}=frac{2}{K_v}=0$ |
|
$r_3(t)=frac{t^2}{2}u(t)$ |
$K_a=lim_{s to 0}s^2G(s)=1$ |
$e_{ss3}=frac{1}{k_a}=1$ |
We will get the overall steady state error, by adding the above three steady state errors.
$$e_{ss}=e_{ss1}+e_{ss2}+e_{ss3}$$
$$Rightarrow e_{ss}=0+0+1=1$$
Therefore, we got the steady state error $e_{ss}$ as 1 for this example.
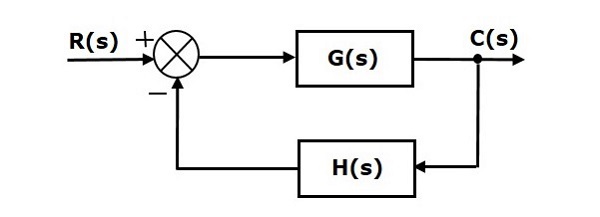
Steady State Errors for Non-Unity Feedback Systems
Consider the following block diagram of closed loop control system, which is having nonunity negative feedback.
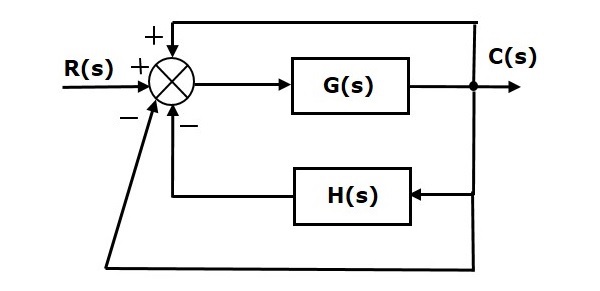
We can find the steady state errors only for the unity feedback systems. So, we have to convert the non-unity feedback system into unity feedback system. For this, include one unity positive feedback path and one unity negative feedback path in the above block diagram. The new block diagram looks like as shown below.
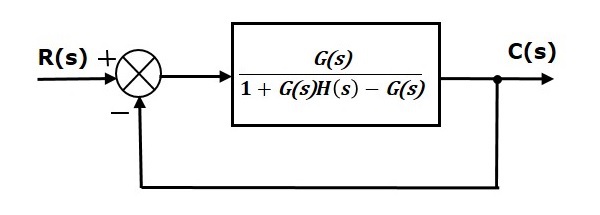
Simplify the above block diagram by keeping the unity negative feedback as it is. The following is the simplified block diagram.
This block diagram resembles the block diagram of the unity negative feedback closed loop control system. Here, the single block is having the transfer function $frac{G(s)}{1+G(s)H(s)-G(s)}$ instead of $G(s)$. You can now calculate the steady state errors by using steady state error formula given for the unity negative feedback systems.
Note − It is meaningless to find the steady state errors for unstable closed loop systems. So, we have to calculate the steady state errors only for closed loop stable systems. This means we need to check whether the control system is stable or not before finding the steady state errors. In the next chapter, we will discuss the concepts-related stability.
The deviation of the output of control system from desired response during steady state is known as steady state error. It is represented as $e_{ss}$. We can find steady state error using the final value theorem as follows.
$$e_{ss}=lim_{t to infty}e(t)=lim_{s to 0}sE(s)$$
Where,
E(s) is the Laplace transform of the error signal, $e(t)$
Let us discuss how to find steady state errors for unity feedback and non-unity feedback control systems one by one.
Steady State Errors for Unity Feedback Systems
Consider the following block diagram of closed loop control system, which is having unity negative feedback.
Where,
- R(s) is the Laplace transform of the reference Input signal $r(t)$
- C(s) is the Laplace transform of the output signal $c(t)$
We know the transfer function of the unity negative feedback closed loop control system as
$$frac{C(s)}{R(s)}=frac{G(s)}{1+G(s)}$$
$$Rightarrow C(s)=frac{R(s)G(s)}{1+G(s)}$$
The output of the summing point is —
$$E(s)=R(s)-C(s)$$
Substitute $C(s)$ value in the above equation.
$$E(s)=R(s)-frac{R(s)G(s)}{1+G(s)}$$
$$Rightarrow E(s)=frac{R(s)+R(s)G(s)-R(s)G(s)}{1+G(s)}$$
$$Rightarrow E(s)=frac{R(s)}{1+G(s)}$$
Substitute $E(s)$ value in the steady state error formula
$$e_{ss}=lim_{s to 0} frac{sR(s)}{1+G(s)}$$
The following table shows the steady state errors and the error constants for standard input signals like unit step, unit ramp & unit parabolic signals.
| Input signal | Steady state error $e_{ss}$ | Error constant |
|---|---|---|
|
unit step signal |
$frac{1}{1+k_p}$ |
$K_p=lim_{s to 0}G(s)$ |
|
unit ramp signal |
$frac{1}{K_v}$ |
$K_v=lim_{s to 0}sG(s)$ |
|
unit parabolic signal |
$frac{1}{K_a}$ |
$K_a=lim_{s to 0}s^2G(s)$ |
Where, $K_p$, $K_v$ and $K_a$ are position error constant, velocity error constant and acceleration error constant respectively.
Note − If any of the above input signals has the amplitude other than unity, then multiply corresponding steady state error with that amplitude.
Note − We can’t define the steady state error for the unit impulse signal because, it exists only at origin. So, we can’t compare the impulse response with the unit impulse input as t denotes infinity.
Example
Let us find the steady state error for an input signal $r(t)=left( 5+2t+frac{t^2}{2} right )u(t)$ of unity negative
feedback control system with $G(s)=frac{5(s+4)}{s^2(s+1)(s+20)}$
The given input signal is a combination of three signals step, ramp and parabolic. The following table shows the error constants and steady state error values for these three signals.
| Input signal | Error constant | Steady state error |
|---|---|---|
|
$r_1(t)=5u(t)$ |
$K_p=lim_{s to 0}G(s)=infty$ |
$e_{ss1}=frac{5}{1+k_p}=0$ |
|
$r_2(t)=2tu(t)$ |
$K_v=lim_{s to 0}sG(s)=infty$ |
$e_{ss2}=frac{2}{K_v}=0$ |
|
$r_3(t)=frac{t^2}{2}u(t)$ |
$K_a=lim_{s to 0}s^2G(s)=1$ |
$e_{ss3}=frac{1}{k_a}=1$ |
We will get the overall steady state error, by adding the above three steady state errors.
$$e_{ss}=e_{ss1}+e_{ss2}+e_{ss3}$$
$$Rightarrow e_{ss}=0+0+1=1$$
Therefore, we got the steady state error $e_{ss}$ as 1 for this example.
Steady State Errors for Non-Unity Feedback Systems
Consider the following block diagram of closed loop control system, which is having nonunity negative feedback.
We can find the steady state errors only for the unity feedback systems. So, we have to convert the non-unity feedback system into unity feedback system. For this, include one unity positive feedback path and one unity negative feedback path in the above block diagram. The new block diagram looks like as shown below.
Simplify the above block diagram by keeping the unity negative feedback as it is. The following is the simplified block diagram.
This block diagram resembles the block diagram of the unity negative feedback closed loop control system. Here, the single block is having the transfer function $frac{G(s)}{1+G(s)H(s)-G(s)}$ instead of $G(s)$. You can now calculate the steady state errors by using steady state error formula given for the unity negative feedback systems.
Note − It is meaningless to find the steady state errors for unstable closed loop systems. So, we have to calculate the steady state errors only for closed loop stable systems. This means we need to check whether the control system is stable or not before finding the steady state errors. In the next chapter, we will discuss the concepts-related stability.
СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Установившаяся ошибка
Система с обратной связью предоставляет инженеру возможность влиять на вид переходной характеристики. Кроме того, как мы уже видели, такая система позволяет значительно уменьшить ее чувствительность к изменению параметров и ослабить влияние возмущений. Однако имеет также смысл исследовать и сравнить установившуюся ошибку в разомкнутой и в замкнутой системах. Установившаяся ошибка — это ошибка, остающаяся после окончания переходного процесса, вызванного внешним воздействием.
+ ~ я»
-R(s) —— *~С>——- *
-Y(s)
G(s)
H(s)
Рис. 4.18. Разомкнутая система управления
Рис. 4.19. Замкнутая система управления В разомкнутой системе, изображенной на рис. 4.18, ошибка равна
ад=ад — ад=[і — стт. (4.48)
В замкнутой системе на рис. 4.19 при H(s) = 1 согласно (4.3)* ошибка равна
Для вычисления установившейся ошибки используется теорема о конечном значении:
lim e(t)= lims£(s). (4.50)
_ 1 —КО А—>0
Приняв для сравнения входной сигнал в виде единичной ступенчатой функции, в разомкнутой системе мы получим:
е0 (о°) = limaf 1 — G(s)] ■ — = lim[l — G(s)] = 1 — G(0).
■v-»0 s -‘->0
В замкнутой системе при H(s) = 1 имеем:
Случай неединичной обратной связи рассматривается в разд. 5.8.
4.5. Установившаяся ошибка
Значение G(s) при 5 = 0 часто называют коэффициентом усиления на нулевой частоте (по постоянному току), и это значение обычно больше единицы. Следовательно, в разомкнутой системе мы получим большую установившуюся ошибку, а в замкнутой системе она будет незначительной.
Анализ выражения (4.51) показывает, что в разомкнутой системе установившаяся ошибка может равняться нулю, если обеспечить выполнение условия 6′(0) = 1. Тогда возникает естественный вопрос: а в чем же заключается преимущество замкнутой системы? Чтобы ответить на этот вопрос, нам придется вернуться к понятию чувствительности. Действительно, в разомкнутой системе можно так подобрать ее параметры, чтобы выполнялось условие С(0) = 1. Однако в процессе эксплуатации системы ее параметры наверняка будут изменяться под влиянием внешних факторов, что приведет к отклонению коэффициента усиления G(0) от единицы. Значит, появится отличная от нуля установившаяся ошибка, устранить которую можно только перенастроив систему. Напротив, в замкнутой системе происходит непрерывное измерение ошибки и вырабатывается сигнал, приводящий к уменьшению ее установившегося значения. Таким образом, мы приходим к выводу, что побудительным мотивом к введению отрицательной обратной связи является снижение чувствительности системы к дрейфу ее параметров, неточности их настройки и внешним возмущающим факторам. Пример оригинальной системы с обратной связью приведен на рис. 4.20.
Рис. 4.20
Грип-11 — это искусственная рука в виде протеза, управляемая с помощью троса. Она может быть использована для переключения скоростей автомобиля, забивания гвоздей, нарезания помидоров и выполнения других несложных задач, требующих двух рук. Ее действие основано на тяговом усилии троса, а сила захвата изменяется в диапазоне от 0 до 110 фунтов. Рука воспроизводит движение большого и указательного пальцев и осуществляет захват, когда на трос воздействуют спинные мышцы человека. Обратная связь осуществляется человеком визуально, но он не испытывает нормального ощущения прикосновения, присущего большинству людей при осторожных действиях с предметом
Способность замкнутой системы уменьшать установившуюся ошибку, вызванную изменениями параметров и неточностью их настройки, мы проиллюстрируем следующим примером. Рассмотрим систему, в которой объект управления имеет передаточную функцию
G(s) = —. (4.53)
TS+ 1
Такая передаточная функция характерна для тепловых объектов, регуляторов напряжения или емкостей с жидкостью при регулировании уровня. При задании входной переменной в
виде единичной ступенчатой функции мы имеем R(s) = 1/5. Тогда в соответствии с (4.51) в разомкнутой системе установившаяся ошибка будет равна
е0(со) = 1 — 6X0) = 1 — К (4.54)
при согласованных единицах измерения R(s) и К. В замкнутой системе (рис. 4.19) мы имеем:
Ec(s) = R(s)-ns)R(s), где T(s) = (7(,v)/[ 1 + GH{s). Установившаяся ошибка равна
ес(оэ)= lim 41 — 7X5)] — = 1 — 7X0).
.v->0 s
Если H(s) = 1/(Т[Л + 1), то Я(0) =1 и G(0) = К. Следовательно,
ес(со) = 1 J! Le_L. (4.55)
1+ К 1+ К
В разомкнутой системе можно было бы, к примеру, задать К= 1, тогда установившаяся ошибка будет равна нулю. В замкнутой системе можно задать большое значение К, например, К = 100. Тогда установившаяся ошибка в ней составит ес(со) = 1/101.
Если теперь в силу каких-то факторов начальное значение К изменится на 10%, т. е. АК/К = 0,1, то в разомкнутой системе появится абсолютное приращение установившейся ошибки Де0(со) = 0,1, а относительное приращение составит
Ае0(со) 0,1
(4.56)
IKOI 1
т. е. также 10%. При таком же приращении АК/К = 0,1 в замкнутой системе установившаяся ошибка составит ес(со) =1/91 (при отрицательном приращении К). Следовательно, абсолютное изменение установившейся ошибки будет равно
Аес (оо ) = ——(4.57) 91 101
а относительное приращение составит
Аес (оо)
= 0,0011, (4.58)
IKOI
или 0,11%. Как говорится, результат в комментариях не нуждается.
Мы постоянно должны задавать себе вопрос: какая связь существует между частотными характеристиками системы и ожидаемым видом её переходной характеристики? Другими словами, если задан набор требований к поведению системы во временной …
Синусоидальный сигнал можно использовать для измерения частотных характеристик разомкнутой системы управления. На практике это связано с получением графиков зависимости амплитуды и фазового сдвига выходного сигнала от частоты. Затем по этим …
Диаграмма Боде для передаточной функции G(s), содержащий несколько нулей и полюсов, строится путём суммирования частотных характеристик, соответствующих каждому отдельно взятому полюсу и нулю. Простоту и удобство данного метода мы проиллюстрируем …
Замкнутая система автоматического регулирования может находиться под воздействием случайного задающего сигнала 
и случайной помехи 
приложенной в произвольной точке системы (рис. 11.26).
Корреляционные функции и спектральные плотности задающего воздействия и помехи будем считать известными. Конечной целью расчета является нахождение корреляционных функций и спектральных плотностей выходной величины 
и ошибки 
Обычно ограничиваются более узкой задачей и определяют только среднеквадратичную ошибку системы регулирования. Это может быть сделано посредством интегрирования по всем
частотам спектральной плотности ошибки или через корреляционную функцию ошибки 
В простейшем случае, когда управляющее воздействие 
представляет собой случайный стационарный процесс со спектральной плотностью 
, а помеха отсутствует; 
расчет можно свести к рассмотренной выше схеме (рис. 11.25). Тогда спектральная плотность ошибки будет
Рис. 11.26.
Частотная передаточная функция по ошибке 
связана с частотными передаточными функциями разомкнутой 
и замкнутой 
системы соотношением
Таким образом, для спектральной плотности ошибки получаем
Интегрирование этого выражения по всем частотам позволяет определить дисперсию и среднеквадратичное значение ошибки:
Вычисление дисперсии и среднеквадратичной ошибки через корреляционные функции может производиться на основании формулы (11.107). В качестве функции веса в рассматриваемом случае должна использоваться функция веса для ошибки 
, связанная с частотной передаточной функцией по ошибке преобразованием Фурье
После нахождения корреляционной функции ошибки 
дисперсия определяется подстановкой 
Однако нахождение среднеквадратичной ошибки посредством использования спектральных плотностей оказывается обычно более простым и поэтому применяется чаще.
В другом простейшем случае, когда задающее воздействие 
а помеха представляет собой случайный стационарный процесс со спектральной плотностью 
, аналогичным образом можно найти спектральную плотность ошибки:
В этом выражении 
представляет собой частотную передаточную функцию;
связывающую изображения Фурье ошибки 
и помехи 
.
В частном случае, когда помеха 
действует на входе системы в месте приложения задающего воздействия, в формуле (11.101) должна использоваться
зоваться частотная передаточная функция замкнутой системы
Рассмотрим теперь общее выражение спектральной плотности ошибки для случая, когда задающее воздействие 
и помеха 
действуют одновременно (рис. 11.26).
Обозначим через 
весовую функцию для ошибки по задающему воздействию и через 
весовую функцию для ошибки по помехе. Тогда ошибку можно представить в виде
Подставим это выражение для ошибки в формулу корреляционной функции (11.51). В результате получим
Отсюда находим
где 
— взаимные корреляционные функции.
Для нахождения спектральной плотности ошибки левую и правую части (11.125) умножим на 
и проинтегрируем по 
от 
до 
. В результате выкладок, аналогичных тем, которые были проделаны при выводе формулы (11.111), получим
В этом выражении 
представляют собой взаимные спектральные плотности полезного сигнала и помехи, а 
— частотные передаточные функции для ошибки по задающему воздействию и помехе. Звездочкой обозначен сопряженный комплекс.
При отсутствии корреляции между полезным сигналом и помехой формула (11.126) упрощается:
В частном случае, когда помеха действует на входе в месте приложения управляющего воздействия и корреляция между ними отсутствует, формула (11.127) может быть представлена в следующем виде;
так как для этого случая частотная передаточная функция 
совпадает с частотной передаточной функцией замкнутой системы 
Все приведенные выше формулы для спектральной плотности ошибки 
могут быть легко переписаны для спектральной плотности выходной величины у (?), если в них заменить частотную передаточную функцию для ошибки 
на частотную передаточную функцию замкнутой системы 