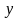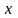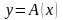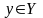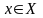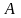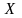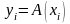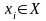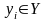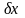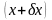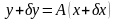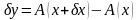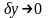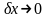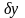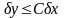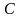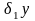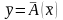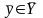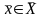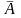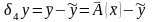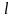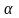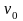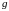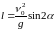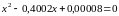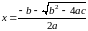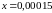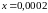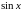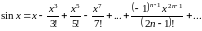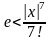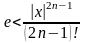|
|
Макеты страниц
Выполнение вычислений на ЭВМ сопровождается появлением вычислительной погрешности, связанной в первую очередь с необходимостью округления результата каждой арифметической операции. Даже если разрядность ЭВМ велика, существует реальная опасность, что выполнение большого числа операций приведет к накоплению погрешности, способной значительно или даже полностью исказить вычисляемый результат. Однако и при небольшом числе действий результат вычислений может оказаться совершенно неправильным, если алгоритм слишком чувствителен к ошибкам округления.
Начинающий вычислитель часто склонен игнорировать ошибки округления. На первых порах при решении простых задач, в особенности если новичок не задумывается о точности найденных решений, его позицию нетрудно понять. Однако решение серьезных задач (когда число арифметических операций превышает миллиарды, в
вычисления вкладываются значительные средства, а результат следует получить с гарантированной точностью и за принятые на основании расчетов решения приходится нести ответственность) предполагает совсем иное отношение к вычислительной погрешности.
1. Порядок выполнения операций.
Решение математической задачи на ЭВМ сводится в конечном итоге к выполнению последовательности простейших арифметических и логических операций. Однако часто одно и то же математическое выражение допускает различные способы вычисления, отличающиеся только порядком выполнения операций. Если вычисления производить точно, то они (при любом способе вычисления) будут приводить к одному результату. Однако результаты вычислений на ЭВМ уже зависят от порядка выполнения операций и различие в вычислительной погрешности может быть весьма значительным.
Рассмотрим простой, но полезный пример вычисления на ЭВМ суммы 

Пусть 





Так как множитель, с которым входит а в формулу для оценки погрешности, убывает с ростом 
Иногда неудачно выбранный порядок операций либо приводит к полной потере точности, либо вообще не дает возможности получить результат из-за переполнения.
Пример 3.29. Пусть на ЭВМ типа IBM PC требуется вычислить произведение 


порядке сразу же приводит к исчезновению порядка, так как 



2. Катастрофическая потеря точности.
Иногда короткая последовательность вычислений приводит от исходных данных, известных с высокой точностью, к результату, содержащему недопустимо мало верных цифр или вообще не имеющему ни одной верной цифры. В этом случае, как было отмечено в § 3.2, принято говорить о катастрофической потере точности. В примере 3.29 мы сталкивались с ситуацией, когда неудачный порядок вычисления произведения привел к неверному нулевому значению результата. Рассмотрим другие примеры.
Пример 3.30. Известно, что функция 

Возможность вычисления значения экспоненты прямым суммированием ряда (3.20) кажется привлекательной. Пусть для вычислений используется 


В сумму вошло 36 слагаемых и значение очередного 

В чем причина катастрофической потери точности? Дело в том, что вычисленные слагаемые ряда неизбежно содержат погрешности, причем для некоторых (для слагаемых с 5-го по 13-е) величина погрешности превосходит значение самого искомого результата. Налицо явный дефект алгоритма, к обсуждению которого мы еще вернемся в конце этого параграфа.
В данном случае переход к вычислениям с удвоенной длиной мантисс 

Однако всего лишь удвоенное значение аргумента 




Заметим тем не менее, что реальные машинные алгоритмы вычисления 
Приведем теперь пример, когда к катастрофической потере точности приводит еще более короткая последовательность вычислений.
Пример 3.31. Пусть при 


Заметим, что при 



Вычисление по эквивалентной формуле 

Интересно отметить, что 
Замечание. Не всегда катастрофическая потеря точности в промежуточных вычислениях действительно является катастрофой.
Все зависит от того, как в дальнейшем используется результат.
3. Обусловленность вычислительного алгоритма.
По аналогии с понятием обусловленности математической задачи можно ввести понятие обусловленности вычислительного алгоритма, отражающее чувствительность результата работы алгоритма к малым, но неизбежным ошибкам округления. Вычислительно устойчивый алгоритм называют хорошо обусловленным, если малые относительные погрешности округления (характеризуемые числом ем) приводят к малой относительной
вычислительной погрешности 
Если 



При очень большом значении числа обусловленности алгоритм можно считать практически неустойчивым.
Применим, например, алгоритм, первоначально предложенный в примере 3.26, для вычисления конечной серии из 



Для решения хорошо обусловленной задачи нет смысла применять плохо обусловленный алгоритм. Именно такими являются алгоритмы, первоначально предложенные в примерах 3.26 и 3.30.
Вернемся к примеру 3.30. Задача вычисления функции 


Рассмотрим задачу суммирования ряда 








Рассмотрим теперь обусловленность алгоритма прямого вычисления по формуле (3.21). Если величина х не слишком мала 

Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И РЕШЕНИЕ ИНЖЕНЕРНЫХ ЗАДАЧ С ПРИМЕНЕНИЕМ ЭВМ
- § 1.2. Основные этапы решения инженерной задачи с применением ЭВМ
- § 1.3. Вычислительный эксперимент
- § 1.4. Дополнительные замечания
- Глава 2. ВВЕДЕНИЕ В ЭЛЕМЕНТАРНУЮ ТЕОРИЮ ПОГРЕШНОСТЕЙ
- § 2.1. Источники и классификация погрешностей результата численного решения задачи
- § 2.2. Приближенные числа. Абсолютная и относительная погрешности
- 2. Правила записи приближенных чисел.
- 3. Округление.
- § 2.3. Погрешности арифметических операций над приближенными числами
- § 2.4. Погрешность функции
- § 2.5. Особенности машинной арифметики
- 2. Представление целых чисел.
- 3. Представление вещественных чисел.
- 4. Арифметические операции над числами с плавающей точкой.
- 5. Удвоенная точность.
- 6. Вычисление машинного эпсилон.
- § 2.6. Дополнительные замечания
- Глава 3. ВЫЧИСЛИТЕЛЬНЫЕ ЗАДАЧИ, МЕТОДЫ И АЛГОРИТМЫ. ОСНОВНЫЕ ПОНЯТИЯ
- § 3.2. Обусловленность вычислительной задачи
- 2. Примеры плохо обусловленных задач.
- 3. Обусловленность задачи вычисления значения функции одной переменной.
- 4. Обусловленность задачи вычисления интеграла …
- 5. Обусловленность задачи вычисления суммы ряда.
- § 3.3. Вычислительные методы
- § 3.4. Корректность вычислительных алгоритмов
- § 3.5. Чувствительность вычислительных алгоритмов к ошибкам округления
- § 3.6. Различные подходы к анализу ошибок
- § 3.7. Требования, предъявляемые к вычислительным алгоритмам
- § 3.8. Дополнительные замечания
- Глава 4. МЕТОДЫ ОТЫСКАНИЯ РЕШЕНИЙ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
- § 4.2. Обусловленность задачи вычисления корня
- § 4.3. Метод бисекции
- § 4.4. Метод простой итерации
- § 4.5. Обусловленность метода простой итерации
- § 4.6. Метод Ньютона
- § 4.7. Модификации метода Ньютона
- § 4.8. Дополнительные замечания
- Глава 5. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- § 5.2. Нормы вектора и матрицы
- § 5.3. Типы используемых матриц
- § 5.4. Обусловленность задачи решения системы линейных алгебраических уравнений
- § 5.5 Метод Гаусса
- § 5.6. Метод Гаусса и решение систем уравнений с несколькими правыми частями, обращение матриц, вычисление определителей
- § 5.7. Метод Гаусса и разложение матрицы на множители. LU-разложение
- § 5.8. Метод Холецкого (метод квадратных корней)
- § 5.9. Метод прогонки
- § 5.10. QR-разложение матрицы. Методы вращений и отражений
- § 5.11. Итерационное уточнение
- § 5.12. Дополнительные замечания
- Глава 6. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- § 6.1. Метод простой итерации
- § 6.2. Метод Зейделя
- § 6.3. Метод релаксации
- § 6.4. Дополнительные замечания
- Глава 7. МЕТОДЫ ОТЫСКАНИЯ РЕШЕНИЙ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
- § 7.2. Метод простой итерации
- § 7.3. Метод Ньютона для решения систем нелинейных уравнений
- 7.4. Модификации метода Ньютона
- § 7.5. О некоторых подходах к решению задач локализации и отыскания решений систем нелинейных уравнений
- § 7.6. Дополнительные замечания
- Глава 8. МЕТОДЫ РЕШЕНИЯ ПРОБЛЕМЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ
- § 8.2. Степенной метод
- § 8.3. Метод обратных итераций
- § 8.4. QR-алгоритм
- § 8.5. Дополнительные замечания
- Глава 9. МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
- § 9.2. Обусловленность задачи минимизации
- § 9.3. Методы прямого поиска. Оптимальный пассивный поиск. Метод деления отрезка пополам. Методы Фибоначчи и золотого сечения
- § 9.4. Метод Ньютона и другие методы минимизация гладких функций
- § 9.5. Дополнительные замечания
- Глава 10. МЕТОДЫ МНОГОМЕРНОЙ МИНИМИЗАЦИИ
- § 10.1. Задача безусловной минимизации функции многих переменных
- § 10.2. Понятие о методах спуска. Покоординатный спуск
- § 10.3. Градиентный метод
- § 10.4. Метод Ньютона
- § 10.5. Метод сопряженных градиентов
- § 10.6. Метода минимизации без вычисления производных
- § 10.7. Дополнительные замечания
- Глава 11. ПРИБЛИЖЕНИЕ ФУНКЦИЙ И СМЕЖНЫЕ ВОПРОСЫ
- § 11.2. Интерполяция обобщенными многочленами
- § 11.3. Полиномиальная интерполяция. Многочлен Лагранжа
- § 11.4. Погрешность интерполяции
- § 11.5. Интерполяция с кратными узлами
- § 11.6. Минимизация оценки погрешности интерполяции. Многочлены Чебышева
- § 11.7. Конечные разности
- § 11.8. Разделенные разности
- § 11.9. Интерполяционный многочлен Ньютона. Схема Эйткена
- § 11.10. Обсуждение глобальной полиномиальной интерполяции. Понятие о кусочно-полиномиальной интерполяции
- § 11.11. Интерполяция сплайнами
- § 11.12. Понятие о дискретном преобразовании Фурье и тригонометрической интерполяции
- § 11.13. Метод наименьших квадратов
- § 11.14. Равномерное приближение функций
- § 11.15. Дробно-рациональные аппроксимации и вычисление элементарных функций
- § 11.16. Дополнительные замечания
- Глава 12. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
- § 12.1. Простейшие формулы численного дифференцирования
- § 12.2. О выводе формул численного дифференцирования
- § 12.3. Обусловленность формул численного дифференцирования
- § 12.4. Дополнительные замечания
- Глава 13. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
- 13.2. Квадратурные формулы интерполяционного типа
- § 13.3. Квадратурные формулы Гаусса
- § 13.4. Апостериорные оценки погрешности. Понятие об адаптивных процедурах численного интегрирования
- § 13.5. Вычисление интегралов в нерегулярных случаях
- § 13.6. Дополнительные замечания
- Глава 14. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 14.1. Задача Коши для дифференциального уравнения первого порядка
- § 14.2. Численные методы решения задачи Коши. Основные понятия и определения
- § 14.3. Использование формулы Тейлора
- § 14.4. Метод Эйлера
- § 14.5. Модификации метода Эйлера второго порядка точности
- § 14.6. Методы Рунге-Кутты
- § 14.7. Линейные многошаговые методы. Методы Адамса
- § 14.8. Устойчивость численных методов решения задачи Коши
- § 14.9. Неявный метод Эйлера
- § 14.10. Решение задачи Коши для систем обыкновенных дифференциальных уравнений и дифференциальных уравнений m-го порядка
- § 14.11. Жесткие задачи
- § 14.12. Дополнительные замечания
- Глава 15. РЕШЕНИЕ ДВУХТОЧЕЧНЫХ КРАЕВЫХ ЗАДАЧ
- § 15.1. Краевые задачи для одномерного стационарного уравнения теплопроводности
- § 15.2. Метод конечных разностей: основные понятия
- § 15.3. Метод конечных разностей: аппроксимации специального вида
- § 15.4. Понятие о проекционных и проекционно-разностных методах. Методы Ритца и Гадеркина. Метод конечных элементов
- § 15.5. Метод пристрелки
- § 15.6. Дополнительные замечания
Обычно задачу
вычисления величины
в зависимости от известного значения
величины
записывают в виде
,
где
и
– элементы соответствующих множеств,
а
– оператор, реализующий вычисление.
Определение 1.1.
Задачу вычисления
будем называть корректно поставленной,
если для любых входных данных
из некоторого множества
решение
задачи существует, единственно и
устойчиво по входным данным (то есть
непрерывно зависит от входных данных
задачи).
В результате,
исходная задача может быть записана в
виде
,
где каждому элементу
соответствует элемент
.
Заметим, что если некоторому
соответствует более одного
,
то для каждого из них целесообразно
рассматривать отдельную задачу
вычисления. В первую очередь в курсе
численных методов интерес представляют
корректно поставленные задачи.
Сделаем несколько
замечаний об устойчивости решения. В
задачах вычисления рассчитывается
значение
,
соответствующее входным данным
.
В реальных условиях имеются возмущенные
входные данные, заданные с погрешностью
,
то есть
и в результате вычислений рассчитывается
возмущенное решение
.
Погрешность
порождает неустранимую погрешность
решения
.
Если решение непрерывно зависит от
входных данных, то
всегда при
и задача устойчива по входным данным.
Отсутствие
устойчивости или слабая устойчивость
решения (сильное влияние вычислительной
погрешности на результат вычисления)
означает, что даже «небольшим» погрешностям
могут соответствовать «большие»
погрешности
,
то есть решение, полученное в результате
выполнения расчетов, будет сильно
отличаться от истинного. Устойчивость
вычислительного процесса – это свойство,
характеризующее скорость накопления
суммарной вычислительной погрешности.
Применять численные методы непосредственно
к неустойчивой задаче бессмысленно,
однако и не любую формально устойчивую
задачу удобно решать практически. Пусть
имеет место следующая оценка погрешности
,
где
– достаточно большое положительное
число. Данная задача формально устойчива,
но неустранимая ошибка решения может
быть сравнительно большой. Представленный
пример соответствует случаю плохой
обусловленности или слабой устойчивости
задачи вычисления.
1.3. Структура погрешности решения задач вычисления
Вычислить погрешность
решения задачи было бы весьма просто,
если бы точное решение было заранее
известно. В этом случае оценка погрешности
была бы получена путем сравнения
вычисленного решения и точного, однако,
точное решение задачи в подавляющем
большинстве случаев заранее неизвестно.
Выходом из такого положения является
изучение причин возникновения погрешностей
и выработка способов их оценки. При
составлении математической модели
объекта (явления, процесса) неизбежно
возникают погрешности в силу идеализации
(упрощения) его действительных свойств,
характеристик и связей, а также
невозможности точного вычисления,
измерения или наблюдения наиболее
важных параметров. Существует
четыре основных источника погрешности
результата вычислений:
-
погрешность
математической модели; -
погрешность
исходных данных задачи; -
погрешность метода
решения задачи; -
погрешность
реализации вычислений, включая
погрешность округления.
Результирующая
погрешность определяется величиной
всех перечисленных выше погрешностей.
Погрешность
математической модели
связана с физическими допущениями при
выборе или построении математической
модели и является результатом
несоответствия математического описания
задачи реальной действительности (может
являться неустранимой). Так как расчет
величины данной погрешности может быть
очень трудоемким, а в некоторых случаях
и вовсе невозможным, далее ее анализ
рассматриваться не будет.
Погрешность,
обусловленная исходными данными задачи
связана с заданием числовых данных,
входящих в математическое описание
задачи. Если исходные данные
заданы с погрешностью
,
то
,
при этом погрешность
может быть неустранимой.
Погрешность
метода решения задачи
связана со способом решения поставленной
математической задачи. Она появляется
в результате замены исходной (например,
нелинейной) математической модели
другой моделью или конечной
последовательностью более простых
(например, линейных) моделей. При
разработке численных методов в их
алгоритмы закладывается возможность
отслеживания таких погрешностей и
доведения их до сколь угодно малого
уровня, поэтому для исследователей
естественным является отношение к
погрешности метода как к устранимой
(условной). Выражение
,
вообще говоря, не может быть «просто»
численно реализовано, задачу вычисления
заменяют «близкой» задачей
.
В результате осуществляется переход
от исходных элементов
и
к элементам других множеств
и
,
которые допускают сравнительно «простую»
численную реализацию. Соответствующим
образом оператор
заменяется на
.
При этом естественно требовать, чтобы
полученная новая задача также была
корректна и чтобы ее решение
было близко к решению
исходной задачи. Величина
представляет собой погрешность метода.
Погрешность
реализации вычислений
(погрешность округлений) обусловлена
необходимостью выполнять арифметические
операции над числами, усеченными до
количества разрядов, зависящего от
технических характеристик применяемой
вычислительной техники (или от возможностей
вычисления значений вручную). При
численной реализации значения
получается элемент
,
при этом само значение
могло обладать погрешностью, связанной
с тем, что промежуточные результаты
вычислений также округлялись. Таким
образом вычислительная погрешность
может быть записана в виде
.
При проведении
вычислений нужно стремиться, чтобы
погрешность метода
была в несколько раз меньше погрешности
исходных данных задачи
.
Вычислительная погрешность
должна быть существенно меньше всех
остальных погрешностей, то есть расчеты
требуется вести с таким количеством
значащих цифр (определяющих точность
вычисления), чтобы погрешность округления
была существенно меньше
,
,
.
Погрешность округления, связанная с
представлением чисел в памяти ЭВМ, будет
рассмотрена более подробно в разд. 1.5.
Рассмотрим примеры,
иллюстрирующие влияние погрешностей
на результаты решения задач вычисления.
Пример 1.1.
Определим дальность
полета снаряда, выпущенного под углом
к горизонту со скоростью
,
при следующих предположениях:
-
земля – инерционная
система отсчета, в которой справедлив
закон инерции, гласящий, что любое тело,
на которое не действуют внешние силы,
находится в состоянии покоя или
равномерного прямолинейного движения. -
ускорение свободного
падения
постоянно;
-
кривизной земли
можно пренебречь и считать ее плоской; -
действием воздуха
на движущийся снаряд можно пренебречь.
Как известно из
курса физики, при таких предположениях
(выбранной схеме идеализации процесса)
задача имеет достаточно простое решение:
,
причем снаряд
движется по параболической траектории.
Однако дальнейшие
исследования данной задачи показывают,
что только пренебрежение сопротивлением
воздуха приводит к существенным ошибкам
(погрешностям) в определении дальности
полета снаряда.
Более строгие и детализированные
математические модели баллистических
траекторий (например, в космонавтике)
учитывают вращение земли вокруг своей
оси, зависимость плотности воздуха и
ускорения свободного падения от высоты,
кривизну земной поверхности и
метеорологические данные, данные о
скорости и направлении ветра, давление
воздуха и т.д.
Пример 1.2.
Попытка расчета
одного из корней уравнения
с промежуточными вычислениями с точностью
до четвертой значащей цифры (см.
определение 1.4 в разд. 1.4), используя
правила округления и обычную формулу
,
приводит к результату
,
вместо точного решения
.
Результат имеет ошибку (погрешность) в
25 %.
Пример 1.3.
Рассмотрим разложение функции
в ряд Тейлора:
.
Полученный ряд
сходится для любого
,
но для вычисления точного значения
необходимо найти сумму бесконечного
ряда чисел, что невозможно реализовать
даже на ЭВМ. На практике вычисляют сумму
некоторого количества первых членов
ряда, а «хвост»,
содержащий бесконечное число членов,
отбрасывают. В результате возникает
ошибка (погрешность) вычисления, которая
для рассматриваемого примера может
быть оценена, например, следующим
образом:
– для четырех членов ряда и
– для произвольного количества
членов ряда.
Соседние файлы в папке 3-й семестр
- #
- #
Conditioning of Problems and Stability of Algorithms
William Ford, in Numerical Linear Algebra with Applications, 2015
Reasons Why the Study of Numerical Linear Algebra Is Necessary
Floating point roundoff and truncation error cause many problems. We have learned how to perform Gaussian elimination in order to row reduce a matrix to upper-triangular form. Unfortunately, if the pivot element is small, this can lead to serious errors in the solution. We will solve this problem in Chapter 11 by using partial pivoting. Sometimes an algorithm is simply far too slow, and Cramer’s Rule is an excellent example. It is useful for theoretical purposes but, as a method of solving a linear system, should not be used for systems greater than 2 × 2. Solving Ax = b by finding A− 1 and then computing x = A− 1b is a poor approach. If the solution to a single system is required, one step of Gaussian elimination, properly performed, requires far fewer flops and results in less roundoff error. Even if the solution is required for many right-hand sides, we will show in Chapter 11 that first factoring A into a product of a lower- and an upper-triangular matrix and then performing forward and back substitution is much more effective. A classical mistake is to compute eigenvalues by finding the roots of the characteristic polynomial. Polynomial root finding can be very sensitive to roundoff error and give extraordinarily poor results. There are excellent algorithms for computing eigenvalues that we will study in Chapters 18 and 19. Singular values should not be found by computing the eigenvalues of ATA. There are excellent algorithms for that purpose that are not subject to as much roundoff error. Lastly, if m ≠ n a theoretical linear algebra course deals with the system using a reduction to what is called reduced row echelon form. This will tell you whether the system has infinitely many solutions or no solution. These types of systems occur in least-squares problems, and we want a single meaningful solution. We will find one by requiring that x be such that ‖b − Ax‖2 is minimum.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123944351000107
Implementation of Discrete Time Systems
Winser Alexander, Cranos Williams, in Digital Signal Processing, 2017
5.11 Matlab Problems for Chapter 5
This section provides homework problems that require the use of Matlab for their solution.
Problem 5.25
(Roundoff Errors)
This problem involves an investigation of the effects of roundoff on the location of the zeros and poles of the system transfer function and on the frequency response. The Matlab function zplane can be used to determine the location of the poles and zeros of the system transfer function and the Matlab function freqz can be used to determine the magnitude and phase of the frequency response.
- 1.
-
The system transfer function for an IIR digital filter is given by
(5.303)H(z)=B(z)A(z)
where
(5.304)B(z)=0.1006−0.4498z−1+1.1211z−2−1.8403z−3+2.1630z−4−1.8403z−5+1.1211z−6−0.4498z−7+0.1006z−8,
(5.305)A(z)=1.0−1.0130z−1+2.8890z−2−1.4483z−3+2.4901z−4−0.3959z−5+0.9169z−6+0.0324z−7+0.1867z−8.
- 2.
-
Use the Matlab zplane function to compute a pole–zero plot for H(z).
- 3.
-
Use the Matlab freqz function to plot the magnitude and phase of the frequency response for H(z).
- 4.
-
The Matlab function iirscale has been provided in the course locker. Use this function to scale the filter coefficients to 10 bit integers.
- 5.
-
Use the Matlab zplane function to compute a pole–zero plot for the scaled version of H(z).
- 6.
-
Use the Matlab freqz function to plot the magnitude and phase of the frequency response for scaled version of H(z).
- 7.
-
Compare the location of the poles and zeros and the frequency response of the resulting scaled filter to those for the original filter. Discuss any observations regarding the location of the poles and zeros as related to the frequency response and the stability of the filter.
Turn in:
- 1.
-
The Matlab script for each part of the problem.
- 2.
-
The plots for each part of the problem.
Problem 5.26
(Difference Equations)
The transfer function for a discrete time system is given by
(5.306)H(z)=B(z)A(z)
where
(5.307)B(z)=0.0281+0.0790z−2+0.0170z−3+0.1000z−4+0.0170z−5+0.0790z−6+0.0281z−8
and
(5.308)A(z)=1.0−3.4739z−1+7.5998z−2−10.8672z−3+11.4306z−4−8.6756z−5+4.7479z−6−1.7004z−7+0.3295z−8.
- 1.
-
Determine the coefficients for the use of second order sections to implement H(z). (Hint) You can use the Matlab routine tf2sos to determine the coefficients.
- 2.
-
Write an appropriate set of difference equations for the implementation of H(z) using the second order section coefficients from part 1.
Problem 5.27
(Second Order Sections)
The system transfer function for an IIR digital filter is given by
(5.309)H(z)=B(z)A(z)
where
(5.310)B(z)=0.0609−0.3157z−1+0.8410z−2−1.4378z−3+1.7082z−4−1.4378z−5+0.8410z−6−0.3157z−7+0.0609z−8,A(z)=1.0−0.8961z−1+2.6272z−2−0.9796z−3+2.1282z−4−0.0781z−5+0.9172z−6+0.0502z−7+0.2602z−8.
- 1.
-
Use the Matlab routine tf2sos to obtain the coefficients for the cascade implementation of H(z) using second order sections.
- 2.
-
Determine the lattice parameters for each of the second order sections separately. Develop block diagrams for the IIR lattice implementation of each of the second order sections.
- 3.
-
Develop appropriate difference equations for the implementation of the overall filter using the second order IIR lattice sections.
Problem 5.28
(IIR Lattice Implementation)
This problem involves the implementation of a sixth order IIR filter using second order lattice sections. The lattice parameters for section 1 are given by
-
K1 =
0.4545
0.5703V1 =
1.2459
0.7137
-1.0000
The lattice parameters for section 2 are
-
K2 =
-0.1963
0.8052V2 =
-0.0475
-1.2347
1.0000
The lattice parameters for section 3 are
-
K3 =
0.8273
0.8835V3 =
-0.1965
0.3783
1.0000
- 1.
-
Write a Matlab function to implement a second order section IIR lattice filter.
- 2.
-
The Matlab routine sampdata has been provided in the course locker under the Matlab Introduction and Examples item. Use the sequence generated by this routine as input for the filter simulations in this problem.
- 3.
-
Write a Matlab routine to simulate the second order section implementation of H(z) using second order IIR lattice sections and your function from part 1. Since the order of the filter is 6, your implementation should have 3 second order sections and you should call your routine 3 times.
- 4.
-
Use the Matlab routine latc2tf to obtain the transfer function equivalent for each of the second order sections. Then write a Matlab routine to call the Matlab routine filter three times to filter the input sequence.
- 5.
-
Compare the output from your routine that uses your second order lattice section filter with the output from your routine that uses the Matlab filter routine and note any differences.
- 6.
-
Turn in your Matlab script, the output plots, and a summary of your observations.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978012804547300005X
The Singular Value Decomposition
William Ford, in Numerical Linear Algebra with Applications, 2015
15.5 Computing the SVD Using MATLAB
Although it is possible to compute the SVD by using the construction in Theorem 15.1, this is far too slow and prone to roundoff error, so it should not be used. The MATLAB function svd computes the SVD:
- a.
-
[U S V] = svd(A)
- b.
-
S = svd(A)
Form 2 returns only the singular values in descending order in the vector S.
Example 15.7
Find the SVD for the matrix of Example 15.5. Notice that σ3 = 4.8021 × 10−16 and yet the rank is 2. In this case, the true value is 0, but roundoff error caused svd to return a very small singular value. MATLAB computes the rank using the SVD, so rank decided that σ3 is actually 0.
>> [U,S,V] = svd(A)
U =
0.158970.8589-0.2112-0.3642-0.244470.17398-0.073783-0.90630.222230.30581-0.953160.17263-0.185520.14793-0.0733870.166480.392560.213390.87898-0.0063535-0.0907460.270060.23251-0.153240.91722
S =
12.691000479050004.8021e-16000000
V =
-0.383870.431250.81650.14430.90139-0.408250.912040.0388950.40825
>> rank(A)
ans =
2
The function svd applies equally well to a matrix of dimension m × n, m < n. Of course, in this case the rank does not exceed m.
Example 15.8
Let A=[79−51010−8931−70−2−88101069]
>> [U S V] = svd(A)
U =
-0.42586-0.89303-0.145390.26225-0.275620.9248-0.865950.355710.35157
S =
22.57700000020.1760000009.5513000
V =
0.27935-0.573830.47040.603320.0082040.085659-0.44176-0.29830.44795-0.37549-0.51939-0.32318-0.277630.383960.541020.109720.60466-0.32426-0.65349-0.1707-0.461910.531380.0076852-0.21915-0.41876-0.336840.068636-0.283520.382970.6924-0.217530.54010.25940.34673-0.466730.5056
>> rank(A)
ans =
3
Since m = 3 and the rank is 3, A has full rank.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123944351000156
Techniques in Discrete-Time Stochastic Control Systems
Bor-Sen Chen, Sen-Chueli Pengt, in Control and Dynamic Systems, 1995
III Stability Analysis of Kalman Filters
The objective of this section will be to obtain a sufficient condition of stability for the state estimator [Eq. (17)] in the nonideal situation, where roundoff errors may occur with every elementary floating-point addition and multiplication. An upper bound on the estimation error degraded for finite-wordlength effects is derived. Before further analysis, some mathematics tools and definitions needed for solving our problem are introduced.
Definition 1
Let the norm of real stochastic vector x∈RN, denoted by ||x||, be defined by [14]
(18)||x||=E[xTx.
Definition 2
(19)||Ax||2=ExTATAx=trExTATAx=trEATAxxT
where tr denotes the trace operator, and
||Ax||2≤||A||2||x||2
where ||A|| denotes the induced norm defined as follows
(20)||A||=λmax(ATAforAisdeterministicλmax(ATAforAisstochastic
Lemma 1
The rounded floating-point sum of two M-vectors can be expressed by
(21)fla+b=I+ΔRa+b
where. A = 2−w, W begin the mantissa length, and
R=diagr1r2⋯rm
where each ri is distributed uniformly between -1 and 1, so that
(22)Eri=0i=1,2,⋯,MErirj=1/3δij
The rounded floating-point product of an M × M matrix A and an M-vector x, also shown in Appendix A, is given as follows:
(23)FLAx=AI+ΔHx
with
H=diagh1h2⋯hm
where hi has zero mean and the variances are approximately given as
(24)Ehi2=i+1/3,fori=1,2,⋯,M−1
(25)EhM2=M/3
(26)Ehihj=i/3,forj>i
Proof: See Appendix A
Using the representations of Eqs. (21) and (23) in Lemma 1, Eq. (17) becomes
(27)x^*k+1=I+ΔR2{AI+ΔH1x^*k+KI+ΔH2×I+ΔR1y*k−CI+ΔH2x^*k}
Upon substitution of Cx(k) + e(k) for y*(k), we have
(28)x^*k+1=A−KCx^*k+Δ(R2A+AH1−KH3C−KR1×C−KCH2−R2KC)x^*k+KCxk+ΔKH3C+KR1C+R2KCxk+Kek+ΔKH3+KR1+R2Kek+termsofhigher‐orderΔ2,Δ3,Δ4
Combining Eqs. (11) and (28), it follows that
(29)xk+1x¯*k+1=AoKCA−KCxkx^*k+0⋮0⋯⋯⋯⋯⋯⋯Δ(KH3C⋮Δ(R2A+AH1−KH3C+KR1C+R2KC⋮−KR1C−KCH2−R2KC×xkx^*k+0K+Δ(KH3+KR1+R2Kek+I0vk
where 0 is the zero matrix, and I is the identity matrix with appropriate dimension. In Eq. (29), because these terms of higher-order Δ2, Δ3, and Δ4 are small, they are ignored. Let
A¯=A0KCA−KCB¯=0⋮0⋯⋯⋯⋯⋯⋯Δ(KH3C⋮Δ(R2A+AH1−KH3C+KR1C+R2KC⋮−KR1C−KCH2−R2KCC¯=0K+Δ(KH3+KR1+R2KD¯=I0
Then Eq. (29) can be rewritten as
(30)xk+1x^*k+1=A¯xkx^*k+B¯xkx^*k+C¯ek+D¯vk
Next, we shall analyze the estimation error due to finite- wordlength implementation of digital Kalman filters. Although the analysis gives precisely the error due to finite-wordlength effects, the calculation is slightly cumbersome. Thus, by ignoring higher quantities in Eq. (28), the actual estimation error of the digital Kalman filter can be expressed by
(31)x*k+1−xk+1≅−A−KCA−KCxkx^*k+[Δ(KH3C+KR1C+R2KC⋮Δ(R2A+AH1−KH3C−KR1C−KCH2−R2KC)]xkx^*k+K+ΔKH3+KR1+R2KEk−vk=A1xkx^*k+B1xkx^*k+C1*ck−D1vk
where
A#=−A−KCA−KCB#=[ΔKH3C+KR1C+R2KC⋮ΔR2A+AH1−KH3C−KR1C−KCH2−R2KC]C#=K+ΔKH3+KR1+R2KD#=I
Because B¯,C¯,B#, and C# are .stochastic, ||B¯||,||C¯||,||B#||, and ||C#|| can he evaluated as follows:
(32)||B¯||=λmaxEB¯TB¯=λmaxF11F12F21F22
where
F11=2−2w{CTEH3KH3C+CTER1KTKR1C+CTKTER2R2KC}F12=2−2WCTKTER2R2−F11F21=2−2WATER2R2KC−F11F22=2−2W{ATER2R2A+EH1HTAH1+E[H2CTKTKCH2}−F11−F12−F22
Referring to Appendix A, the values of E[H3H3], E[R1KTKR1], E[R2R2], etc., can be obtained easily.
(33)||C¯||=λmax(EC¯TC¯=λmaxQ
where
Q=KTK+2−2w{EH3KTKH3+ER1KTKR1+KTER2R2K}
Doing a simple calculation, it is found that the values of ||B#|| and ||C#|| are the same as the values of ||B¯|| and ||C¯||, respectively.
Since D¯, A#, and D# are deterministic, from Eqs. (20), the values of ||D¯||,||A#|| and |[D#|| are obtained and listed below
(34)||D¯||=λmaxDTD=1
(35)||A#||=λmaxATA−CTKTA−ATKC+CTKTKC−ATA−CTKTA−ATKC+CTKTKC−ATA−CTKTA−ATKC+CTKTKCATA−CTKTA−ATKC+CTKTKC
(36)||D#||=λmaxD#TD#=1
It is easy to see that, if Ā is a stable transition matrix for digital filters in infinite precision, then
(37)||A¯||≤mrk,k>0
for some constant m > 0 and 0 ≤ r ≤ 1. Simply choose
r=maxi|λiA¯|
where λi(Ā), for i = 1,2, …, n, denotes the eigenvalues of A. That is, r is the absolute value of the eigenvalue of Ā (or the pole of the digital filter) nearest the unit circle. An estimate of m can be made from
||A¯k||/rk≤m for all k. How to get m is sometimes very difficult. Fortunately, m can be obtained with the aid of a computer.
To derive the stability condition and the actual estimation error bound under the fmite-wordlength effects, the Bellman- Gronwall lemma in discrete form is employed. The lemma is listed as follows :
Lemma 2
[15]
Letuk0∞,fk0∞,and(hk0∞be real–valued sequences on the set of the positive integer Z+. Let
(38)hk≥0,∀k∈Z+
Under these condition, if
(39)uk≤fk+∑i=0k−1hiui,k=0,1,2,⋯
then
(40)uk≤fk+∑i=0k−1Πj=i+1k−11+hjhifik=1,2,⋯
where
Πj=i+1k−11+hj
is set equal to 1 when i = k – 1.
Remark 1
If for some constant h, h(i) ≤ h, ∀i, then Eq.(40)becomes
(41)uk≤fk+h∑i=0k−1(1+h)k−1−ifi
Remark 2
If for some constant f, f(i) ≤ f, ∀i, then Eq.(40)becomes
(42)uk≤fΠi−1k−1i+hi
We make the observation that Eq. (30) has the perturbation term related to
xkx*k
It is feasible for us to apply the Bellman-Gronwall lemma to obtain the stability criterion. Based on Lemma 2 and the preceding definitions, we can relate a sufficient condition of stability on the estimator [Eq. (30)] to roundoff errors in the following theorem.
Theorem 1
Consider the state -estimator system[Eq.(30)] with the induced norms[Eq.(32)], ||e(k)|| = g1 and ||v(k)|| = g2, and suppose the transition matrix Ā fulfills the requirement of Eq.(37). If the stability inequality
(43)r+mB¯<1
is satisfied, then the deteriorated state estimator due to roundoff errors is still stable.
Proof. See Appendix B.
Remark 3
The relationship between the location of the pole nearest to the unit circle and the computational roundoff errors is revealed. From the stability inequality[Eq.(43)], it is seen that the smaller r is, the stronger the stability will be.
Remark 4
From Eqs.(32), (37), and (43), the wordlength W can be determined to guarantee the stabiliti) of the deteriorated system under the finite-wordlength effect.
Remark 5
For a given wordlength W, the stability inequality[Eq.(43)] can be used as a criterion to test the stability of the estimator system deteriorated by the roundoff noise.
Remark 6
From Theorem 1, it is assumed thatm||B¯||is evaluated, and all of the eigenvalues of the Kalman filter must be inside the disk with radiusr<1−m||B¯||to guarantee the stability of the Kalman filter with floating-point computation. However, if the eigenvalues of A – K(k)C in Eq.(13)are not nil within the disk with radius r, a scheme proposed by Anderson[17]is employed to treat the problem. Suppose we artificially multiply the covariances St and S2in the system of Eqs.(7) and ( 
(44)x^k+1=A−KrkCx^k+Krky*k
(45)Krk=APkCTS21/r2k+CPkCT−1
(46)Pk+1=APkAT+S11/r2k−APkCT×S21/r2k+CPkCT−1CPTkAT
Then the estimation error e(k) of the filter in Eq.(14)will converge at least as fast as rk when k increases; i.e., all of the eigenvalues of (A – KT(k.)C) are inside the disk with radius r.
After deriving the sufficient condition under which the deteriorated Kalman filter is stable, we can find one form of bound by the estimate given in Theorem 2.
Theorem 2
Consider the state-estimator system ofTheorem 1if the stability criterion of Eq.(43)is satisfied when k → ∞, then the upper bound of
xkx^*k
can be evaluated as
mg1C¯+g2D¯1−r+mB¯
and the act ual estimation. error||x^*k+1−xk+1||is bounded by
A#+B#mg1C¯+g2D¯1−r+mB¯+g1C#+g2D#
Proof. See Appendix C.
We do not claim that the bound given here is the ultimate tool for solving the problem of the minimal wordlength of implementing digital Kalman filters; however, it can be a reference for a conservative design. This paper does permit an approximate analysis of the performance/cost tradeoff for wordlength design choices.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0090526705800088
Digital Communication System Concepts
Vijay K. Garg, Yih-Chen Wang, in The Electrical Engineering Handbook, 2005
2.7 Sources of Corruption
The sources of corruption include sampling and quantization effects as well as channel effects, as described in the following bulleted list.
- •
-
Quantization noise: The distortion inherent in quantization is a roundoff or truncation error. The process of encoding the PAM waveform into a quantized waveform involves discarding some of the original analog information. This distortion is called quantization noise; the amount of such noise is inversely proportional to the number of levels used in the quantization process.
- •
-
Quantizer saturation: The quantizer allocates L levels to the task of approximating the continuous range of inputs with a finite set of outputs (see Figure 2.11). The range of inputs for which the difference between the input and output is small is called the operating range of the converter. If the input exceeds this range, the difference between the input and output becomes large, and we say that the converter is operating in saturation. Saturation errors are more objectionable than quantizing noise. Generally, saturation is avoided by use of automatic gain control (AGC), which effectively extends the operating range of the converter.
FIGURE 2.11. Uniform Quantization
- •
-
Timing jitter: If there is a slight jitter in the position of the sample, the sampling is no longer uniform. The effect of the jitter is equivalent to frequency modulation (FM) of the baseband signal. If the jitter is random, a low-level wideband spectral contribution is induced whose properties are very close to those of the quantizing noise. Timing jitter can be controlled with very good power supply isolation and stable clock reference.
- •
-
Channel noise: Thermal noise, interference from other users, and interference from circuit switching transients can cause errors in detecting the pulses carrying the digitized samples. Channel-induced errors can degrade the reconstructed signal quality quite quickly. The rapid degradation of the output signal quality with channelinduced errors is called a threshold effect.
- •
-
Intersymbol interference: The channel is always bandlimited. A band-limited channel spreads a pulse waveform passing through it. When the channel bandwidth is much greater than pulse bandwidth, the spreading of the pulse will be slight. When the channel bandwidth is close to the signal bandwidth, the spreading will exceed a symbol duration and cause signal pulses to overlap. This overlapping is called inter-symbol interference ISI), ISI causes system degradation (higher error rates); it is a particularly insidious form of interference because raising the signal power to overcome interference will not improve the error performance:
(2.7)σ2=∫−q/2q/2e2p(e) de=∫−q/2q/2e21q de=q212=average quantization noise power.VP2=(VPP2)2=(Lq2)2=L2q24.
(2.8)(SN)q=(L2q2)/4q2/12=3L2.
In the limit as L → ∞, the signal approaches the PAM format (with no quantization error) and signal-to-quantization noise ratio is infinite. In other words, with an infinite number of quantization levels, there is zero quantization error.
Typically L = 2R, R = Log2L, and q=2VPL=(2VP)/2R.
∴σ2=(2VP2R)2/12=13VP22−2R.
Let P denote the average power of the message signal m(t), and then:
(2.9)(SNR)O=Pσ2=(3PVP2)22R.
The output SNR of the quantizer increases exponentially with increasing number of bits per sample, R. An increase in R requires a proportionate increase in the channel bandwidth.
Example 5
We consider a full-load sinusodial modulating signal of amplitude A that uses all representation levels provided. The average signal power is (assuming a load of 1 Ω):
The equations are written and solved as follows:
P=A22.σ2=13A22−2R.(SNR)o=A22(1/3A22−2R)=32(22R)=1.8+6 R dB.
| L | R [bits] | SNR [decibels] |
|---|---|---|
| 32 | 5 | 31.8 |
| 64 | 6 | 37.8 |
| 128 | 7 | 43.8 |
| 256 | 8 | 49.8 |
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780121709600500700
Introduction
E.K. MILLER, in Time Domain Electromagnetics, 1999
1.6.1 Increasing the Stability of the Time-Stepping Solution
TD solutions have sometimes been found to diverge after a sufficient number of time steps have been computed, evidently because of the accumulation of numerical “noise” in the solution. Thisnoise can have its source in numerical roundoff errors or from analytical and numerical approximations made in developing the computer model. In either case, an interpretation of the divergent result is that such approximations introduce low-amplitude, right-half-plane, nonphysical poles into the model. An example of the latter problem is using segment lengths shorter than the wire diameter, thereby violating the thin-wire approximation [4]. Such poles can come to dominate the overall solution after enough time has passed or when the correct response has decayed enough. In either case, a sharply diverging numerical solution can result.
Various techniques for solving the late-time divergence problem have been reported [55, 98–101]. Tijhuis [101] investigated using an improved time-interpolation scheme to increase the accuracy of time derivatives. Rao et al. [55] used a conjugate gradient technique to control error accumulation over time. Smith [100] describes a procedure that exploits the fact that late-time instabilities, generally being of a high-frequency nature relative to the correct response, can be filtered from the solution by an averaging technique. Note that late-time instabilities occur for objects such as thin PEC plates that do not exhibit internal resonances, and so they represent a distinctly different kind of numerical anomaly. However, these oscillations can be effectively suppressed by following the averaging scheme which is simple, accurate, and involves a negligible amount of extra computation.
Let Im,n be the current coefficient at the mth patch at a time instant t = nΔt. In the current stabilization scheme, Im,n+1 is calculated using explicit methods, and the averaged value, Ĩm,n, is approximated as
(1.6.1)I˜m,n=14(I˜m,n−1+2Im,n+Im,n+1).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780125801904500033
Computer Techniques and Algorithms in Digital Signal Processing
Bhaskar D. Rao, in Control and Dynamic Systems, 1996
1 INTRODUCTION
The implementation of digital filters and the effect of finite wordlength on them has been of interest to many and has received much attention. Finite wordlength introduces errors in several forms: A-D quantization noise, coefficient quantization errors and roundoff errors due to finite precision arithmetic. The types of arithmetic commonly employed are fixed point arithmetic and floating point arithmetic. The problem of using fixed point arithmetic and their effect on digital filters has been extensively studied and is reasonably well understood [1]-[8]. More recently, with the increasing availability of floating point capability in signal processing chips [8], insight into algorithms employing floating point arithmetic is of increasing interest. The analysis of roundoff noise in floating point digital filters has also been studied by many researchers [7]-[23]. This chapter examines the problem of roundoff noise in floating point digital filter implementations, and discusses some of the recent work in this area. A difficulty with roundoff noise analysis of floating point implementations is that the expressions turn out to be cumbersome, and therefore harder to interpret and obtain insights from. Part of the reason for this analytical difficulty lies in the type of errors that result from using finite precision floating point arithmetic. It turns out that an appropriate model for the roundoff errors is an error that is dependent on the input signal thereby complicating the analysis [9, 7]. This is in contrast to the case of fixed point arithmetic, where the roundoff errors can be modeled as independent white noise sequences independent of the input signal. Also, unlike the fixed point case, the order of the computations has an effect on the roundoff error. This element of flexibility in the computational order introduces an additional consideration in the roundoff noise minimization process. This chapter explores tools for enhancing the tractability of the analysis. This involves examining ways of systematically manipulating filters to better track the roundoff errors. Hopefully, better tools to track the errors will result into insights for reducing these errors and implementing robust filters.
The organization of this chapter is as follows. In sec. 2, the nature of the errors that arise from floating point computations are discussed. Using the model and assuming a particular computational order, an expression for the roundoff noise at the output of a digital filter is derived in sec. 3. A procedure to account for the ordering is developed in sec. 4 with the help of a model for floating point inner products. This procedure is then applied for roundoff analysis in sec. 5. A simple procedure for applying the inner product formulation to signal flow graphs is then discussed in sec. 6. The inner product model developed is also used to develop a new approach for evaluating floating point implementation based on a coefficient sensitivity approach in sec. 7. Some examples are discussed in sec. 8 to illustrate the methods developed.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0090526796800399
Multiplication
Miloš D. Ercegovac, Tomás Lang, in Digital Arithmetic, 2004
4.7 Truncating Multiplier
Multiplication of n-bit fractions produces a fraction of 2n bits. Some applications in signal processing keep only the n most-significant bits of the result and dispose of the least-significant bits after performing rounding. If a larger roundoff error is allowed, not all LSB bits of the final result are generated, which leads to a simpler implementation as indicated in Figure 4.26.
FIGURE 4.26. Bit-matrix of a truncated magnitude multiplier.
The error in the result consists of Ered due to simplified reduction, and Ernd due to rounding of the n + k computed bits to the n most-significant bits. To achieve a specific total error smaller than one ulp (unit in the last significant place), the errors Ered and Ernd can be reduced by choosing k, the number of positions not implemented, and by adding a suitable constant to the reduction array. This approach and several others are discussed in detail in the literature mentioned at the end of the chapter.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9781558607989500063
Reciprocal, Division, Reciprocal Square Root, and Square Root by Iterative Approximation
Miloš D. Ercegovac, Tomás Lang, in Digital Arithmetic, 2004
Multiplicative Normalization Method
In this method we need to distinguish between the error in d[j] and the error in R[j].
- 1
-
Error in d[j]:
(7.26)edT[j]=edT[j−1]2+edG[j]
edG[j] includes the error in the two’s complement operation and the roundoff error in the multiplication. As in the NR method, the final error edT[m] is positive as long as the generated error in the last iteration is not negative. Also generated errors are reduced quadratically.
- 2
-
Error in R[j]: If the multiplications R[i]d are performed in full precision, then the error is the same as that of d[j] (including there the errors in roundoff and two’s complement). To that error it is necessary to add the generated errors for all R[i] with i ≤ j. This error corresponds to the roundoff of the multiplication R[i]P[i] That is,
(7.27)eRT[j]=edT[j]+∑i=0jeRG[i]
Note that here e RG [i] is not reduced by the iterations that follow.
Consequently, the error in R[j] is two sided (from below or from above), as illustrated in Figure 7.5.
FIGURE 7.5. Errors in the multiplicative method.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9781558607989500099
Dynamic Systems: Ordinary Differential Equations
STANLEY M. DUNN, … PRABHAS V. MOGHE, in Numerical Methods in Biomedical Engineering, 2006
7.7 Numerical Stability and Error Propagation
Topics of paramount importance in the numerical integration of differential equations are the error propagation, stability, and convergence of these solutions. Two types of stability considerations enter in the solution of ordinary differential equations: inherent stability (or instability) and numerical stability (or instability). Inherent stability is determined by the mathematical formulation of the problem and is dependent on the eigenvalues of the Jacobian matrix of the differential equations, as was shown in Section 7.6. On the other hand, numerical stability is a function of the error propagation in the numerical integration method. The behavior of error propagation depends on the values of the characteristic roots of the difference equations that yield the numerical solution. In this section, we concern ourselves with numerical stability considerations as they apply to the numerical integration of ordinary differential equations.
There are three types of errors present in the application of numerical integration methods. These are the truncation error, the roundoff error, and the propagation error. The truncation error is a function of the number of terms that are retained in the approximation of the solution from the infinite series expansion. The truncation error may be reduced by retaining a larger number of terms in the series or by reducing the step size of integration h. The plethora of available numerical methods of integration of ordinary differential equations provides a choice of increasingly higher accuracy (lower truncation error), at an escalating cost in the number of arithmetic operations to be performed, and with the concomitant accumulation of roundoff errors.
Computers carry numbers using a finite number of significant figures, as was discussed in Chapter 3. A roundoff error is introduced in the calculation when the computer rounds up or down (or just chops) the number to n significant figures. Roundoff errors may be reduced significantly by the use of double precision. However, even a very small roundoff error may affect the accuracy of the solution, especially in numerical integration methods that march forward (or backward) for hundreds or thousands of steps, each step being performed using rounded numbers.
The truncation and roundoff errors in numerical integration accumulate and propagate, creating the propagation error, which, in some cases, may grow in exponential or oscillatory pattern, thus causing the calculated solution to deviate drastically from the correct solution.
Fig. 7.9 illustrates the propagation of error in a numerical integration method. Starting with a known initial condition y0, the method calculates the value y1, which contains the truncation error for this step and a small roundoff error introduced by the computer. The error has been magnified on the figure in order to illustrate it more clearly. The next step starts with y1 as the initial point and calculates y2. But because y1 already contains truncation and roundoff errors, the value obtained for y2 contains these errors propagated, in addition to the new truncation and roundoff errors from the second step. The same process occurs in subsequent steps.
Figure 7.9. Error propagation in numerical integration methods. The error has been magnified in order to illustrate it more clearly.
Error propagation in numerical integration methods is a complex operation that depends on several factors. Roundoff error, which contributes to propagation error, is entirely determined by the accuracy of the computer being used. The truncation error is fixed by the choice of method being applied, by the step size of integration, and by the values of the derivatives of the functions being integrated. For these reasons, it is necessary to examine the error propagation and stability of each method individually and in connection with the differential equations to be integrated. Some techniques work well with one class of differential equations but fail with others.
More detailed discussions of stability of numerical integration methods, and other advanced topics, such as step size control and integration of stiff differential equations, are included in Appendix E of this book.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780121860318500078
Conditioning of Problems and Stability of Algorithms
William Ford, in Numerical Linear Algebra with Applications, 2015
Reasons Why the Study of Numerical Linear Algebra Is Necessary
Floating point roundoff and truncation error cause many problems. We have learned how to perform Gaussian elimination in order to row reduce a matrix to upper-triangular form. Unfortunately, if the pivot element is small, this can lead to serious errors in the solution. We will solve this problem in Chapter 11 by using partial pivoting. Sometimes an algorithm is simply far too slow, and Cramer’s Rule is an excellent example. It is useful for theoretical purposes but, as a method of solving a linear system, should not be used for systems greater than 2 × 2. Solving Ax = b by finding A− 1 and then computing x = A− 1b is a poor approach. If the solution to a single system is required, one step of Gaussian elimination, properly performed, requires far fewer flops and results in less roundoff error. Even if the solution is required for many right-hand sides, we will show in Chapter 11 that first factoring A into a product of a lower- and an upper-triangular matrix and then performing forward and back substitution is much more effective. A classical mistake is to compute eigenvalues by finding the roots of the characteristic polynomial. Polynomial root finding can be very sensitive to roundoff error and give extraordinarily poor results. There are excellent algorithms for computing eigenvalues that we will study in Chapters 18 and 19. Singular values should not be found by computing the eigenvalues of ATA. There are excellent algorithms for that purpose that are not subject to as much roundoff error. Lastly, if m ≠ n a theoretical linear algebra course deals with the system using a reduction to what is called reduced row echelon form. This will tell you whether the system has infinitely many solutions or no solution. These types of systems occur in least-squares problems, and we want a single meaningful solution. We will find one by requiring that x be such that ‖b − Ax‖2 is minimum.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123944351000107
Implementation of Discrete Time Systems
Winser Alexander, Cranos Williams, in Digital Signal Processing, 2017
5.11 Matlab Problems for Chapter 5
This section provides homework problems that require the use of Matlab for their solution.
Problem 5.25
(Roundoff Errors)
This problem involves an investigation of the effects of roundoff on the location of the zeros and poles of the system transfer function and on the frequency response. The Matlab function zplane can be used to determine the location of the poles and zeros of the system transfer function and the Matlab function freqz can be used to determine the magnitude and phase of the frequency response.
- 1.
-
The system transfer function for an IIR digital filter is given by
(5.303)H(z)=B(z)A(z)
where
(5.304)B(z)=0.1006−0.4498z−1+1.1211z−2−1.8403z−3+2.1630z−4−1.8403z−5+1.1211z−6−0.4498z−7+0.1006z−8,
(5.305)A(z)=1.0−1.0130z−1+2.8890z−2−1.4483z−3+2.4901z−4−0.3959z−5+0.9169z−6+0.0324z−7+0.1867z−8.
- 2.
-
Use the Matlab zplane function to compute a pole–zero plot for H(z).
- 3.
-
Use the Matlab freqz function to plot the magnitude and phase of the frequency response for H(z).
- 4.
-
The Matlab function iirscale has been provided in the course locker. Use this function to scale the filter coefficients to 10 bit integers.
- 5.
-
Use the Matlab zplane function to compute a pole–zero plot for the scaled version of H(z).
- 6.
-
Use the Matlab freqz function to plot the magnitude and phase of the frequency response for scaled version of H(z).
- 7.
-
Compare the location of the poles and zeros and the frequency response of the resulting scaled filter to those for the original filter. Discuss any observations regarding the location of the poles and zeros as related to the frequency response and the stability of the filter.
Turn in:
- 1.
-
The Matlab script for each part of the problem.
- 2.
-
The plots for each part of the problem.
Problem 5.26
(Difference Equations)
The transfer function for a discrete time system is given by
(5.306)H(z)=B(z)A(z)
where
(5.307)B(z)=0.0281+0.0790z−2+0.0170z−3+0.1000z−4+0.0170z−5+0.0790z−6+0.0281z−8
and
(5.308)A(z)=1.0−3.4739z−1+7.5998z−2−10.8672z−3+11.4306z−4−8.6756z−5+4.7479z−6−1.7004z−7+0.3295z−8.
- 1.
-
Determine the coefficients for the use of second order sections to implement H(z). (Hint) You can use the Matlab routine tf2sos to determine the coefficients.
- 2.
-
Write an appropriate set of difference equations for the implementation of H(z) using the second order section coefficients from part 1.
Problem 5.27
(Second Order Sections)
The system transfer function for an IIR digital filter is given by
(5.309)H(z)=B(z)A(z)
where
(5.310)B(z)=0.0609−0.3157z−1+0.8410z−2−1.4378z−3+1.7082z−4−1.4378z−5+0.8410z−6−0.3157z−7+0.0609z−8,A(z)=1.0−0.8961z−1+2.6272z−2−0.9796z−3+2.1282z−4−0.0781z−5+0.9172z−6+0.0502z−7+0.2602z−8.
- 1.
-
Use the Matlab routine tf2sos to obtain the coefficients for the cascade implementation of H(z) using second order sections.
- 2.
-
Determine the lattice parameters for each of the second order sections separately. Develop block diagrams for the IIR lattice implementation of each of the second order sections.
- 3.
-
Develop appropriate difference equations for the implementation of the overall filter using the second order IIR lattice sections.
Problem 5.28
(IIR Lattice Implementation)
This problem involves the implementation of a sixth order IIR filter using second order lattice sections. The lattice parameters for section 1 are given by
-
K1 =
0.4545
0.5703V1 =
1.2459
0.7137
-1.0000
The lattice parameters for section 2 are
-
K2 =
-0.1963
0.8052V2 =
-0.0475
-1.2347
1.0000
The lattice parameters for section 3 are
-
K3 =
0.8273
0.8835V3 =
-0.1965
0.3783
1.0000
- 1.
-
Write a Matlab function to implement a second order section IIR lattice filter.
- 2.
-
The Matlab routine sampdata has been provided in the course locker under the Matlab Introduction and Examples item. Use the sequence generated by this routine as input for the filter simulations in this problem.
- 3.
-
Write a Matlab routine to simulate the second order section implementation of H(z) using second order IIR lattice sections and your function from part 1. Since the order of the filter is 6, your implementation should have 3 second order sections and you should call your routine 3 times.
- 4.
-
Use the Matlab routine latc2tf to obtain the transfer function equivalent for each of the second order sections. Then write a Matlab routine to call the Matlab routine filter three times to filter the input sequence.
- 5.
-
Compare the output from your routine that uses your second order lattice section filter with the output from your routine that uses the Matlab filter routine and note any differences.
- 6.
-
Turn in your Matlab script, the output plots, and a summary of your observations.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978012804547300005X
The Singular Value Decomposition
William Ford, in Numerical Linear Algebra with Applications, 2015
15.5 Computing the SVD Using MATLAB
Although it is possible to compute the SVD by using the construction in Theorem 15.1, this is far too slow and prone to roundoff error, so it should not be used. The MATLAB function svd computes the SVD:
- a.
-
[U S V] = svd(A)
- b.
-
S = svd(A)
Form 2 returns only the singular values in descending order in the vector S.
Example 15.7
Find the SVD for the matrix of Example 15.5. Notice that σ3 = 4.8021 × 10−16 and yet the rank is 2. In this case, the true value is 0, but roundoff error caused svd to return a very small singular value. MATLAB computes the rank using the SVD, so rank decided that σ3 is actually 0.
>> [U,S,V] = svd(A)
U =
0.158970.8589-0.2112-0.3642-0.244470.17398-0.073783-0.90630.222230.30581-0.953160.17263-0.185520.14793-0.0733870.166480.392560.213390.87898-0.0063535-0.0907460.270060.23251-0.153240.91722
S =
12.691000479050004.8021e-16000000
V =
-0.383870.431250.81650.14430.90139-0.408250.912040.0388950.40825
>> rank(A)
ans =
2
The function svd applies equally well to a matrix of dimension m × n, m < n. Of course, in this case the rank does not exceed m.
Example 15.8
Let A=[79−51010−8931−70−2−88101069]
>> [U S V] = svd(A)
U =
-0.42586-0.89303-0.145390.26225-0.275620.9248-0.865950.355710.35157
S =
22.57700000020.1760000009.5513000
V =
0.27935-0.573830.47040.603320.0082040.085659-0.44176-0.29830.44795-0.37549-0.51939-0.32318-0.277630.383960.541020.109720.60466-0.32426-0.65349-0.1707-0.461910.531380.0076852-0.21915-0.41876-0.336840.068636-0.283520.382970.6924-0.217530.54010.25940.34673-0.466730.5056
>> rank(A)
ans =
3
Since m = 3 and the rank is 3, A has full rank.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123944351000156
Techniques in Discrete-Time Stochastic Control Systems
Bor-Sen Chen, Sen-Chueli Pengt, in Control and Dynamic Systems, 1995
III Stability Analysis of Kalman Filters
The objective of this section will be to obtain a sufficient condition of stability for the state estimator [Eq. (17)] in the nonideal situation, where roundoff errors may occur with every elementary floating-point addition and multiplication. An upper bound on the estimation error degraded for finite-wordlength effects is derived. Before further analysis, some mathematics tools and definitions needed for solving our problem are introduced.
Definition 1
Let the norm of real stochastic vector x∈RN, denoted by ||x||, be defined by [14]
(18)||x||=E[xTx.
Definition 2
(19)||Ax||2=ExTATAx=trExTATAx=trEATAxxT
where tr denotes the trace operator, and
||Ax||2≤||A||2||x||2
where ||A|| denotes the induced norm defined as follows
(20)||A||=λmax(ATAforAisdeterministicλmax(ATAforAisstochastic
Lemma 1
The rounded floating-point sum of two M-vectors can be expressed by
(21)fla+b=I+ΔRa+b
where. A = 2−w, W begin the mantissa length, and
R=diagr1r2⋯rm
where each ri is distributed uniformly between -1 and 1, so that
(22)Eri=0i=1,2,⋯,MErirj=1/3δij
The rounded floating-point product of an M × M matrix A and an M-vector x, also shown in Appendix A, is given as follows:
(23)FLAx=AI+ΔHx
with
H=diagh1h2⋯hm
where hi has zero mean and the variances are approximately given as
(24)Ehi2=i+1/3,fori=1,2,⋯,M−1
(25)EhM2=M/3
(26)Ehihj=i/3,forj>i
Proof: See Appendix A
Using the representations of Eqs. (21) and (23) in Lemma 1, Eq. (17) becomes
(27)x^*k+1=I+ΔR2{AI+ΔH1x^*k+KI+ΔH2×I+ΔR1y*k−CI+ΔH2x^*k}
Upon substitution of Cx(k) + e(k) for y*(k), we have
(28)x^*k+1=A−KCx^*k+Δ(R2A+AH1−KH3C−KR1×C−KCH2−R2KC)x^*k+KCxk+ΔKH3C+KR1C+R2KCxk+Kek+ΔKH3+KR1+R2Kek+termsofhigher‐orderΔ2,Δ3,Δ4
Combining Eqs. (11) and (28), it follows that
(29)xk+1x¯*k+1=AoKCA−KCxkx^*k+0⋮0⋯⋯⋯⋯⋯⋯Δ(KH3C⋮Δ(R2A+AH1−KH3C+KR1C+R2KC⋮−KR1C−KCH2−R2KC×xkx^*k+0K+Δ(KH3+KR1+R2Kek+I0vk
where 0 is the zero matrix, and I is the identity matrix with appropriate dimension. In Eq. (29), because these terms of higher-order Δ2, Δ3, and Δ4 are small, they are ignored. Let
A¯=A0KCA−KCB¯=0⋮0⋯⋯⋯⋯⋯⋯Δ(KH3C⋮Δ(R2A+AH1−KH3C+KR1C+R2KC⋮−KR1C−KCH2−R2KCC¯=0K+Δ(KH3+KR1+R2KD¯=I0
Then Eq. (29) can be rewritten as
(30)xk+1x^*k+1=A¯xkx^*k+B¯xkx^*k+C¯ek+D¯vk
Next, we shall analyze the estimation error due to finite- wordlength implementation of digital Kalman filters. Although the analysis gives precisely the error due to finite-wordlength effects, the calculation is slightly cumbersome. Thus, by ignoring higher quantities in Eq. (28), the actual estimation error of the digital Kalman filter can be expressed by
(31)x*k+1−xk+1≅−A−KCA−KCxkx^*k+[Δ(KH3C+KR1C+R2KC⋮Δ(R2A+AH1−KH3C−KR1C−KCH2−R2KC)]xkx^*k+K+ΔKH3+KR1+R2KEk−vk=A1xkx^*k+B1xkx^*k+C1*ck−D1vk
where
A#=−A−KCA−KCB#=[ΔKH3C+KR1C+R2KC⋮ΔR2A+AH1−KH3C−KR1C−KCH2−R2KC]C#=K+ΔKH3+KR1+R2KD#=I
Because B¯,C¯,B#, and C# are .stochastic, ||B¯||,||C¯||,||B#||, and ||C#|| can he evaluated as follows:
(32)||B¯||=λmaxEB¯TB¯=λmaxF11F12F21F22
where
F11=2−2w{CTEH3KH3C+CTER1KTKR1C+CTKTER2R2KC}F12=2−2WCTKTER2R2−F11F21=2−2WATER2R2KC−F11F22=2−2W{ATER2R2A+EH1HTAH1+E[H2CTKTKCH2}−F11−F12−F22
Referring to Appendix A, the values of E[H3H3], E[R1KTKR1], E[R2R2], etc., can be obtained easily.
(33)||C¯||=λmax(EC¯TC¯=λmaxQ
where
Q=KTK+2−2w{EH3KTKH3+ER1KTKR1+KTER2R2K}
Doing a simple calculation, it is found that the values of ||B#|| and ||C#|| are the same as the values of ||B¯|| and ||C¯||, respectively.
Since D¯, A#, and D# are deterministic, from Eqs. (20), the values of ||D¯||,||A#|| and |[D#|| are obtained and listed below
(34)||D¯||=λmaxDTD=1
(35)||A#||=λmaxATA−CTKTA−ATKC+CTKTKC−ATA−CTKTA−ATKC+CTKTKC−ATA−CTKTA−ATKC+CTKTKCATA−CTKTA−ATKC+CTKTKC
(36)||D#||=λmaxD#TD#=1
It is easy to see that, if Ā is a stable transition matrix for digital filters in infinite precision, then
(37)||A¯||≤mrk,k>0
for some constant m > 0 and 0 ≤ r ≤ 1. Simply choose
r=maxi|λiA¯|
where λi(Ā), for i = 1,2, …, n, denotes the eigenvalues of A. That is, r is the absolute value of the eigenvalue of Ā (or the pole of the digital filter) nearest the unit circle. An estimate of m can be made from
||A¯k||/rk≤m for all k. How to get m is sometimes very difficult. Fortunately, m can be obtained with the aid of a computer.
To derive the stability condition and the actual estimation error bound under the fmite-wordlength effects, the Bellman- Gronwall lemma in discrete form is employed. The lemma is listed as follows :
Lemma 2
[15]
Letuk0∞,fk0∞,and(hk0∞be real–valued sequences on the set of the positive integer Z+. Let
(38)hk≥0,∀k∈Z+
Under these condition, if
(39)uk≤fk+∑i=0k−1hiui,k=0,1,2,⋯
then
(40)uk≤fk+∑i=0k−1Πj=i+1k−11+hjhifik=1,2,⋯
where
Πj=i+1k−11+hj
is set equal to 1 when i = k – 1.
Remark 1
If for some constant h, h(i) ≤ h, ∀i, then Eq.(40)becomes
(41)uk≤fk+h∑i=0k−1(1+h)k−1−ifi
Remark 2
If for some constant f, f(i) ≤ f, ∀i, then Eq.(40)becomes
(42)uk≤fΠi−1k−1i+hi
We make the observation that Eq. (30) has the perturbation term related to
xkx*k
It is feasible for us to apply the Bellman-Gronwall lemma to obtain the stability criterion. Based on Lemma 2 and the preceding definitions, we can relate a sufficient condition of stability on the estimator [Eq. (30)] to roundoff errors in the following theorem.
Theorem 1
Consider the state -estimator system[Eq.(30)] with the induced norms[Eq.(32)], ||e(k)|| = g1 and ||v(k)|| = g2, and suppose the transition matrix Ā fulfills the requirement of Eq.(37). If the stability inequality
(43)r+mB¯<1
is satisfied, then the deteriorated state estimator due to roundoff errors is still stable.
Proof. See Appendix B.
Remark 3
The relationship between the location of the pole nearest to the unit circle and the computational roundoff errors is revealed. From the stability inequality[Eq.(43)], it is seen that the smaller r is, the stronger the stability will be.
Remark 4
From Eqs.(32), (37), and (43), the wordlength W can be determined to guarantee the stabiliti) of the deteriorated system under the finite-wordlength effect.
Remark 5
For a given wordlength W, the stability inequality[Eq.(43)] can be used as a criterion to test the stability of the estimator system deteriorated by the roundoff noise.
Remark 6
From Theorem 1, it is assumed thatm||B¯||is evaluated, and all of the eigenvalues of the Kalman filter must be inside the disk with radiusr<1−m||B¯||to guarantee the stability of the Kalman filter with floating-point computation. However, if the eigenvalues of A – K(k)C in Eq.(13)are not nil within the disk with radius r, a scheme proposed by Anderson[17]is employed to treat the problem. Suppose we artificially multiply the covariances St and S2in the system of Eqs.(7) and ( 
(44)x^k+1=A−KrkCx^k+Krky*k
(45)Krk=APkCTS21/r2k+CPkCT−1
(46)Pk+1=APkAT+S11/r2k−APkCT×S21/r2k+CPkCT−1CPTkAT
Then the estimation error e(k) of the filter in Eq.(14)will converge at least as fast as rk when k increases; i.e., all of the eigenvalues of (A – KT(k.)C) are inside the disk with radius r.
After deriving the sufficient condition under which the deteriorated Kalman filter is stable, we can find one form of bound by the estimate given in Theorem 2.
Theorem 2
Consider the state-estimator system ofTheorem 1if the stability criterion of Eq.(43)is satisfied when k → ∞, then the upper bound of
xkx^*k
can be evaluated as
mg1C¯+g2D¯1−r+mB¯
and the act ual estimation. error||x^*k+1−xk+1||is bounded by
A#+B#mg1C¯+g2D¯1−r+mB¯+g1C#+g2D#
Proof. See Appendix C.
We do not claim that the bound given here is the ultimate tool for solving the problem of the minimal wordlength of implementing digital Kalman filters; however, it can be a reference for a conservative design. This paper does permit an approximate analysis of the performance/cost tradeoff for wordlength design choices.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0090526705800088
Digital Communication System Concepts
Vijay K. Garg, Yih-Chen Wang, in The Electrical Engineering Handbook, 2005
2.7 Sources of Corruption
The sources of corruption include sampling and quantization effects as well as channel effects, as described in the following bulleted list.
- •
-
Quantization noise: The distortion inherent in quantization is a roundoff or truncation error. The process of encoding the PAM waveform into a quantized waveform involves discarding some of the original analog information. This distortion is called quantization noise; the amount of such noise is inversely proportional to the number of levels used in the quantization process.
- •
-
Quantizer saturation: The quantizer allocates L levels to the task of approximating the continuous range of inputs with a finite set of outputs (see Figure 2.11). The range of inputs for which the difference between the input and output is small is called the operating range of the converter. If the input exceeds this range, the difference between the input and output becomes large, and we say that the converter is operating in saturation. Saturation errors are more objectionable than quantizing noise. Generally, saturation is avoided by use of automatic gain control (AGC), which effectively extends the operating range of the converter.
FIGURE 2.11. Uniform Quantization
- •
-
Timing jitter: If there is a slight jitter in the position of the sample, the sampling is no longer uniform. The effect of the jitter is equivalent to frequency modulation (FM) of the baseband signal. If the jitter is random, a low-level wideband spectral contribution is induced whose properties are very close to those of the quantizing noise. Timing jitter can be controlled with very good power supply isolation and stable clock reference.
- •
-
Channel noise: Thermal noise, interference from other users, and interference from circuit switching transients can cause errors in detecting the pulses carrying the digitized samples. Channel-induced errors can degrade the reconstructed signal quality quite quickly. The rapid degradation of the output signal quality with channelinduced errors is called a threshold effect.
- •
-
Intersymbol interference: The channel is always bandlimited. A band-limited channel spreads a pulse waveform passing through it. When the channel bandwidth is much greater than pulse bandwidth, the spreading of the pulse will be slight. When the channel bandwidth is close to the signal bandwidth, the spreading will exceed a symbol duration and cause signal pulses to overlap. This overlapping is called inter-symbol interference ISI), ISI causes system degradation (higher error rates); it is a particularly insidious form of interference because raising the signal power to overcome interference will not improve the error performance:
(2.7)σ2=∫−q/2q/2e2p(e) de=∫−q/2q/2e21q de=q212=average quantization noise power.VP2=(VPP2)2=(Lq2)2=L2q24.
(2.8)(SN)q=(L2q2)/4q2/12=3L2.
In the limit as L → ∞, the signal approaches the PAM format (with no quantization error) and signal-to-quantization noise ratio is infinite. In other words, with an infinite number of quantization levels, there is zero quantization error.
Typically L = 2R, R = Log2L, and q=2VPL=(2VP)/2R.
∴σ2=(2VP2R)2/12=13VP22−2R.
Let P denote the average power of the message signal m(t), and then:
(2.9)(SNR)O=Pσ2=(3PVP2)22R.
The output SNR of the quantizer increases exponentially with increasing number of bits per sample, R. An increase in R requires a proportionate increase in the channel bandwidth.
Example 5
We consider a full-load sinusodial modulating signal of amplitude A that uses all representation levels provided. The average signal power is (assuming a load of 1 Ω):
The equations are written and solved as follows:
P=A22.σ2=13A22−2R.(SNR)o=A22(1/3A22−2R)=32(22R)=1.8+6 R dB.
| L | R [bits] | SNR [decibels] |
|---|---|---|
| 32 | 5 | 31.8 |
| 64 | 6 | 37.8 |
| 128 | 7 | 43.8 |
| 256 | 8 | 49.8 |
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780121709600500700
Introduction
E.K. MILLER, in Time Domain Electromagnetics, 1999
1.6.1 Increasing the Stability of the Time-Stepping Solution
TD solutions have sometimes been found to diverge after a sufficient number of time steps have been computed, evidently because of the accumulation of numerical “noise” in the solution. Thisnoise can have its source in numerical roundoff errors or from analytical and numerical approximations made in developing the computer model. In either case, an interpretation of the divergent result is that such approximations introduce low-amplitude, right-half-plane, nonphysical poles into the model. An example of the latter problem is using segment lengths shorter than the wire diameter, thereby violating the thin-wire approximation [4]. Such poles can come to dominate the overall solution after enough time has passed or when the correct response has decayed enough. In either case, a sharply diverging numerical solution can result.
Various techniques for solving the late-time divergence problem have been reported [55, 98–101]. Tijhuis [101] investigated using an improved time-interpolation scheme to increase the accuracy of time derivatives. Rao et al. [55] used a conjugate gradient technique to control error accumulation over time. Smith [100] describes a procedure that exploits the fact that late-time instabilities, generally being of a high-frequency nature relative to the correct response, can be filtered from the solution by an averaging technique. Note that late-time instabilities occur for objects such as thin PEC plates that do not exhibit internal resonances, and so they represent a distinctly different kind of numerical anomaly. However, these oscillations can be effectively suppressed by following the averaging scheme which is simple, accurate, and involves a negligible amount of extra computation.
Let Im,n be the current coefficient at the mth patch at a time instant t = nΔt. In the current stabilization scheme, Im,n+1 is calculated using explicit methods, and the averaged value, Ĩm,n, is approximated as
(1.6.1)I˜m,n=14(I˜m,n−1+2Im,n+Im,n+1).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780125801904500033
Computer Techniques and Algorithms in Digital Signal Processing
Bhaskar D. Rao, in Control and Dynamic Systems, 1996
1 INTRODUCTION
The implementation of digital filters and the effect of finite wordlength on them has been of interest to many and has received much attention. Finite wordlength introduces errors in several forms: A-D quantization noise, coefficient quantization errors and roundoff errors due to finite precision arithmetic. The types of arithmetic commonly employed are fixed point arithmetic and floating point arithmetic. The problem of using fixed point arithmetic and their effect on digital filters has been extensively studied and is reasonably well understood [1]-[8]. More recently, with the increasing availability of floating point capability in signal processing chips [8], insight into algorithms employing floating point arithmetic is of increasing interest. The analysis of roundoff noise in floating point digital filters has also been studied by many researchers [7]-[23]. This chapter examines the problem of roundoff noise in floating point digital filter implementations, and discusses some of the recent work in this area. A difficulty with roundoff noise analysis of floating point implementations is that the expressions turn out to be cumbersome, and therefore harder to interpret and obtain insights from. Part of the reason for this analytical difficulty lies in the type of errors that result from using finite precision floating point arithmetic. It turns out that an appropriate model for the roundoff errors is an error that is dependent on the input signal thereby complicating the analysis [9, 7]. This is in contrast to the case of fixed point arithmetic, where the roundoff errors can be modeled as independent white noise sequences independent of the input signal. Also, unlike the fixed point case, the order of the computations has an effect on the roundoff error. This element of flexibility in the computational order introduces an additional consideration in the roundoff noise minimization process. This chapter explores tools for enhancing the tractability of the analysis. This involves examining ways of systematically manipulating filters to better track the roundoff errors. Hopefully, better tools to track the errors will result into insights for reducing these errors and implementing robust filters.
The organization of this chapter is as follows. In sec. 2, the nature of the errors that arise from floating point computations are discussed. Using the model and assuming a particular computational order, an expression for the roundoff noise at the output of a digital filter is derived in sec. 3. A procedure to account for the ordering is developed in sec. 4 with the help of a model for floating point inner products. This procedure is then applied for roundoff analysis in sec. 5. A simple procedure for applying the inner product formulation to signal flow graphs is then discussed in sec. 6. The inner product model developed is also used to develop a new approach for evaluating floating point implementation based on a coefficient sensitivity approach in sec. 7. Some examples are discussed in sec. 8 to illustrate the methods developed.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0090526796800399
Multiplication
Miloš D. Ercegovac, Tomás Lang, in Digital Arithmetic, 2004
4.7 Truncating Multiplier
Multiplication of n-bit fractions produces a fraction of 2n bits. Some applications in signal processing keep only the n most-significant bits of the result and dispose of the least-significant bits after performing rounding. If a larger roundoff error is allowed, not all LSB bits of the final result are generated, which leads to a simpler implementation as indicated in Figure 4.26.
FIGURE 4.26. Bit-matrix of a truncated magnitude multiplier.
The error in the result consists of Ered due to simplified reduction, and Ernd due to rounding of the n + k computed bits to the n most-significant bits. To achieve a specific total error smaller than one ulp (unit in the last significant place), the errors Ered and Ernd can be reduced by choosing k, the number of positions not implemented, and by adding a suitable constant to the reduction array. This approach and several others are discussed in detail in the literature mentioned at the end of the chapter.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9781558607989500063
Reciprocal, Division, Reciprocal Square Root, and Square Root by Iterative Approximation
Miloš D. Ercegovac, Tomás Lang, in Digital Arithmetic, 2004
Multiplicative Normalization Method
In this method we need to distinguish between the error in d[j] and the error in R[j].
- 1
-
Error in d[j]:
(7.26)edT[j]=edT[j−1]2+edG[j]
edG[j] includes the error in the two’s complement operation and the roundoff error in the multiplication. As in the NR method, the final error edT[m] is positive as long as the generated error in the last iteration is not negative. Also generated errors are reduced quadratically.
- 2
-
Error in R[j]: If the multiplications R[i]d are performed in full precision, then the error is the same as that of d[j] (including there the errors in roundoff and two’s complement). To that error it is necessary to add the generated errors for all R[i] with i ≤ j. This error corresponds to the roundoff of the multiplication R[i]P[i] That is,
(7.27)eRT[j]=edT[j]+∑i=0jeRG[i]
Note that here e RG [i] is not reduced by the iterations that follow.
Consequently, the error in R[j] is two sided (from below or from above), as illustrated in Figure 7.5.
FIGURE 7.5. Errors in the multiplicative method.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9781558607989500099
Dynamic Systems: Ordinary Differential Equations
STANLEY M. DUNN, … PRABHAS V. MOGHE, in Numerical Methods in Biomedical Engineering, 2006
7.7 Numerical Stability and Error Propagation
Topics of paramount importance in the numerical integration of differential equations are the error propagation, stability, and convergence of these solutions. Two types of stability considerations enter in the solution of ordinary differential equations: inherent stability (or instability) and numerical stability (or instability). Inherent stability is determined by the mathematical formulation of the problem and is dependent on the eigenvalues of the Jacobian matrix of the differential equations, as was shown in Section 7.6. On the other hand, numerical stability is a function of the error propagation in the numerical integration method. The behavior of error propagation depends on the values of the characteristic roots of the difference equations that yield the numerical solution. In this section, we concern ourselves with numerical stability considerations as they apply to the numerical integration of ordinary differential equations.
There are three types of errors present in the application of numerical integration methods. These are the truncation error, the roundoff error, and the propagation error. The truncation error is a function of the number of terms that are retained in the approximation of the solution from the infinite series expansion. The truncation error may be reduced by retaining a larger number of terms in the series or by reducing the step size of integration h. The plethora of available numerical methods of integration of ordinary differential equations provides a choice of increasingly higher accuracy (lower truncation error), at an escalating cost in the number of arithmetic operations to be performed, and with the concomitant accumulation of roundoff errors.
Computers carry numbers using a finite number of significant figures, as was discussed in Chapter 3. A roundoff error is introduced in the calculation when the computer rounds up or down (or just chops) the number to n significant figures. Roundoff errors may be reduced significantly by the use of double precision. However, even a very small roundoff error may affect the accuracy of the solution, especially in numerical integration methods that march forward (or backward) for hundreds or thousands of steps, each step being performed using rounded numbers.
The truncation and roundoff errors in numerical integration accumulate and propagate, creating the propagation error, which, in some cases, may grow in exponential or oscillatory pattern, thus causing the calculated solution to deviate drastically from the correct solution.
Fig. 7.9 illustrates the propagation of error in a numerical integration method. Starting with a known initial condition y0, the method calculates the value y1, which contains the truncation error for this step and a small roundoff error introduced by the computer. The error has been magnified on the figure in order to illustrate it more clearly. The next step starts with y1 as the initial point and calculates y2. But because y1 already contains truncation and roundoff errors, the value obtained for y2 contains these errors propagated, in addition to the new truncation and roundoff errors from the second step. The same process occurs in subsequent steps.
Figure 7.9. Error propagation in numerical integration methods. The error has been magnified in order to illustrate it more clearly.
Error propagation in numerical integration methods is a complex operation that depends on several factors. Roundoff error, which contributes to propagation error, is entirely determined by the accuracy of the computer being used. The truncation error is fixed by the choice of method being applied, by the step size of integration, and by the values of the derivatives of the functions being integrated. For these reasons, it is necessary to examine the error propagation and stability of each method individually and in connection with the differential equations to be integrated. Some techniques work well with one class of differential equations but fail with others.
More detailed discussions of stability of numerical integration methods, and other advanced topics, such as step size control and integration of stiff differential equations, are included in Appendix E of this book.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780121860318500078