Вектор ошибки evm

Э. Акар, Analog Devices, специалист по измерениям радиочастотных систем

Как измерение модуля вектора ошибки помогает оптимизировать общие характеристики системы

Статья опубликована в журнале Электроника НТБ № 8 2021

Модуль вектора ошибки (Error Vector Magnitude, EVM) — широко применяемый показатель системного уровня, который регламентируется различными стандартами в области связи для испытаний на соответствие в таких приложениях, как беспроводные локальные сети (WLAN 802.11), мобильная связь (4G LTE, 5G) и многие другие. Кроме того, это чрезвычайно важная системная характеристика, позволяющая количественно оценить совокупное влияние всех возможных проблем в системе с помощью одного, простого для понимания параметра. В статье проанализировано, как характеристики более низкого уровня влияют на EVM, рассмотрен ряд практических примеров использования EVM для оптимизации характеристик устройства на уровне системы, показано, как добиться снижения EVM на 15 дБ по сравнению с требованиями большинства стандартов связи.

Большинство инженеров, работающих в области радиочастотных систем, оперируют такими характеристиками, как коэффициент шума, точка пересечения третьего порядка и отношение сигнал — шум. Понимание совокупного влияния этих параметров на общие рабочие характеристики системы может быть сложной задачей. Модуль вектора ошибки позволяет быстро получить представление о работе системы в целом, вместо того, чтобы оценивать несколько разных показателей.

Что такое модуль вектора ошибки?
EVM — это простой показатель для количественной оценки комбинации всех искажений сигнала в системе. Он часто определяется для устройств, использующих цифровую модуляцию, которая может быть представлена в виде графика синфазных (I) и квадратурных (Q) векторов, известного также как «диаграмма созвездия» (constellation diagram) (рис. 1a). Как правило, EVM вычисляется путем нахождения идеального местоположения созвездия для каждого принятого символа, как показано на рис. 1б. Среднеквадратичное значение всех модулей вектора ошибки между местоположениями принятых символов и их ближайшими идеальными местоположениями в созвездии определяет величину EVM устройства [1].

Рис. 1. а — диаграмма созвездия и граница принятия решения; б — вектор ошибки между принятым символом и идеальным местоположением символа

В стандарте IEEE 802.11 приведена формула для вычисления EVM [2]:

где: Lp — количество кадров, Nc — количество несущих, Ri, j — принятый символ, а Si, j — идеальное местоположение символа.
EVM тесно связан с частотой битовых ошибок (BER) данной системы. Когда принятые символы располагаются далеко от целевой точки созвездия, вероятность их попадания в границу принятия решения другой точки созвездия увеличивается. Это приводит к увеличению BER. Важное различие между BER и EVM состоит в том, что BER для переданного сигнала вычисляется на основе переданной битовой комбинации, в то время как EVM вычисляется на основе расстояния от ближайшей точки созвездия символов до местоположения символа. В некоторых случаях символы могут пересекать границу принятия решения, и им присваивается неправильная битовая комбинация. Если символ попадает ближе к другому идеальному местоположению символа, это может улучшить EVM для этого символа. Таким образом, хотя EVM и BER тесно связаны, эта связь может быть нарушена при очень высоких уровнях искажения сигнала.
Современные стандарты в области связи устанавливают минимально допустимый уровень EVM на основе характеристик передаваемого или принятого сигнала, таких как скорость передачи данных и полоса пропускания. Устройства, которые достигают целевого уровня EVM, соответствуют стандарту, в то время как устройства, которые не достигают целевого уровня EVM, не соответствуют его требованиям. Испытательное и измерительное оборудование, предназначенное для проверки на соответствие стандартам, обычно ориентировано на более строгие целевые значения EVM, которые могут быть на порядок ниже требуемых в стандарте. Это позволяет оборудованию определять EVM тестируемого устройства без значительных искажений сигнала.

Что влияет на EVM?
Как показатель ошибки, EVM тесно связан со всеми источниками искажений в системе. Мы можем количественно оценить влияние всех отклонений в системе на EVM, вычислив, как они искажают принимаемые и передаваемые сигналы. Проанализируем влияние нескольких ключевых видов помех, таких как тепловой шум, фазовый шум и нелинейности, на EVM.

Белый шум
Белый шум присутствует во всех радиочастотных системах. Когда шум является единственным искажением в системе, результирующий EVM можно рассчитать по следующей формуле:

где SNR — отношение сигнал — шум системы в дБ, а PAPR — отношение пиковой мощности к средней мощности данного сигнала в дБ.
Обратите внимание, что SNR обычно определяется для однотонального сигнала. Для модулированного сигнала необходимо учитывать PAPR сигнала. Поскольку PAPR однотонального сигнала составляет 3 дБ, это число необходимо вычесть из значения SNR для сигнала с произвольным значением PAPR.
Для высокоскоростных АЦП и ЦАП, уравнение 2 может быть выражено через спектральную плотность шума (NSD):

где NSD — спектральная плотность шума в дБ ПШ / Гц, BW — ширина полосы сигнала в Гц, PAPR — отношение пиковой мощности к средней, а Pbackoff — разница между пиковой мощностью сигнала и полным диапазоном измерений преобразователя.
Эта формула может быть очень удобна для прямого расчета ожидаемого значения EVM устройства с использованием значения NSD, которое обычно указывается для современных высокоскоростных преобразователей. Обратите внимание, что для высокоскоростных преобразователей необходимо учитывать также шум квантования. Величина NSD большинства высокоскоростных преобразователей также включает шум квантования. Следовательно, для этих устройств уравнение 3 отражает не только тепловой шум, но также шум квантования.
Как показывают эти два уравнения, EVM сигнала напрямую зависит от общей полосы пропускания сигнала, отношения пиковой мощности к средней и теплового шума системы.

Как фазовый шум влияет на EVM
Другим видом шума, который влияет на EVM системы, является фазовый шум, который представляет собой случайные флуктуации фазы и частоты сигнала [3]. Все нелинейные элементы схемы вносят фазовый шум. Основные источники фазового шума в данной системе могут быть прослежены вплоть до генераторов. Генератор частоты дискретизации преобразователя данных, используемый для преобразования частоты гетеродин и генератор опорной частоты — все эти устройства могут вносить вклад в общий фазовый шум системы.
Ухудшение характеристик из-за фазового шума зависит от частоты. Для типичного генератора большая часть энергии несущей приходится на его основную частоту генерации, которая называется центральной частотой. Часть энергии сигнала будет распределяться около этой центральной частоты. Отношение амплитуды сигнала в полосе частот 1 Гц при определенном сдвиге частоты к его амплитуде на центральной частоте определяется как фазовый шум при этом конкретном частотном сдвиге, как показано на рис. 2.

Фазовый шум системы напрямую влияет на ее EVM. EVM из-за фазового шума системы можно рассчитать путем интегрирования фазового шума в полосе пропускания. Для большинства современных стандартов связи, в которых используется ортогональная частотная модуляция (OFDM), фазовый шум должен быть интегрирован в диапазоне от примерно 10% разнесения поднесущих до полной ширины полосы сигнала:

где L — плотность фазового шума в одиночной боковой полосе, fsc — разнесение поднесущих, BW — ширина полосы сигнала.
Большинство устройств, генерирующих частоту, имеют низкий фазовый шум на частотах <2 ГГц с типичными уровнями интегрированного джиттера на несколько порядков ниже предельных значений EVM, устанавливаемых в стандартах. Однако для более высокочастотных и более широкополосных сигналов интегрированные уровни фазового шума могут быть значительно выше, что может привести к гораздо более высоким значениям EVM. Обычно это относится к устройствам миллиметрового диапазона, которые работают на частотах выше 20 ГГц. Как мы подробнее обсудим в разделе, посвящен ном описанию примеров проектов, фазовый шум следует рассчитывать для всей системы, чтобы достичь наименьшего общего EVM.

Расчет влияния нелинейностей на EVM
Нелинейности системного уровня приводят к появлению интермодуляционных составляющих, которые могут попадать в полосу пропускания сигнала. Эти помехи могут перекрываться с поднесущими, воздействуя на их амплитуду и фазу. Можно вычислить вектор ошибки, возникающий из-за интермодуляционных помех. Выведем простую формулу для расчета EVM системы из-за интермодуляционных составляющих третьего порядка.

Рис. 3. Интермодуляционные составляющие OFDM-сигнала

Как показано на рис. 3a, двухтональный сигнал создает две интермодуляционные составляющие. Мощность интермодуляционных составляющих можно рассчитать следующим образом:

где Ptone — мощность тестового сигнала, OIP3 — точка пересечения третьего порядка на выходе, Pe — сигнал ошибки, представляющий собой разность мощностей основной частоты и интермодуляционной составляющей.
Для OFDM-сигнала с N тонами, как показано на рис. 3б, уравнение 6 принимает следующий вид:

где Pe, i — ошибка для каждой пары тонов.
Поскольку в каждом местоположении поднесущей имеется N / 2 интермодуляционных составляющих, которые перекрываются, уравнение можно переписать как:

Общая ошибка, включая все местоположения поднесущих, становится равной:

Подставляя уравнение 6 в уравнение 8, EVM можно выразить следующим образом:

где PRMS — среднеквадратичное значение сигнала, C — константа, которая находится в диапазоне от 0 до 3 дБ в зависимости от схемы модуляции.
Как показывает уравнение 11, EVM уменьшается по мере увеличения OIP3 системы. Это ожидаемо, поскольку более высокое значение OIP3 обычно указывает на более линейную систему. Кроме того, когда среднеквадратичная мощность сигнала уменьшается, EVM уменьшается по мере уменьшения мощности нелинейных составляющих.

Оптимизация системных характеристик с помощью EVM
Обычно проектирование на уровне системы начинается с каскадного анализа, при котором низкоуровневые параметры функциональных блоков используются для определения общих характеристик системы, построенной на базе этих блоков. Существуют хорошо зарекомендовавшие себя аналитические формулы и инструменты, которые можно использовать для расчета этих параметров. Однако многие инженеры не знают, как правильно использовать инструменты каскадного анализа для проектирования полностью оптимизированных систем.
В качестве системной характеристики EVM предоставляет инженерам-разработчикам ценную информацию для оптимизации системы. Вместо того, чтобы рассматривать несколько параметров, разработчики получают возможность выбрать оптимальное среднеквадратичное
значение EVM и, тем самым, найти наилучшее проектное решение.

U-образная кривая EVM
Мы можем объединить все параметры системы в один график, учитывая вклад EVM каждого искажения в системе и уровень выходной мощности. На рис. 4 показана типичная U-образная кривая EVM для системы в зависимости от уровня рабочей мощности. При низких уровнях рабочей мощности EVM определяется шумовыми характеристиками системы. На высоких уровнях мощности на EVM влияют нелинейности в системе. Самый низкий уровень EVM для системы обычно определяется комбинацией всех источников ошибок, включая фазовый шум.
Мы можем найти суммарный EVM с помощью уравнения 12:

где EVMWN — вклад EVM, возникающий из-за белого шума, EVMPhN — вклад фазового шума, EVMlinearity — EVM, возникающий из-за нелинейных искажений. Для заданного уровня мощности сумма мощностей всех этих ошибок определяет общий уровень EVM в системе.

Рис. 4. U-образная кривая зависимости EVM от рабочей мощности

Наряду с уравнением 12, U-образная кривая может быть очень полезной для системной оптимизации, когда можно визуализировать комбинацию всех ошибок данной системы.

Пример проекта
Рассмотрим пример проектирования сигнальной цепочки, используя EVM в качестве системного показателя. В этом примере мы спроектируем передатчик миллиметрового диапазона с использованием РЧ ЦАП с дискретизацией, модулятора и генераторов частоты миллиметрового диапазона, а также других устройств формирования сигнала (рис. 5).

Рис. 5. Сигнальная цепь передатчика миллиметрового диапазона

В этой сигнальной цепи используется микросхема AD9082, которая содержит четыре ЦАП и два АЦП с частотой выборки 12 и 6 ГГц соответственно. Эти преобразователи с прямым РЧ-преобразованием обеспечивают гибкость проектного решения для сигнальной цепи миллиметрового диапазона и непревзойденную производительность. На рис. 6 показаны результаты измерения значения EVM для типовой микросхемы AD9082 с помощью 12‑разрядного АЦП AD9213, который обеспечивает скорость выборки 10 Гвыб / с. Кольцевой тест для этой схемы показал уровень EVM всего -62 дБ, что на 27 дБ ниже предельной допустимой величины, определяемой стандартом.

Рис. 6. Результаты измерения EVM для микросхемы AD9082 на промежуточной частоте 400 МГц для сигнала IEEE 802.11ax с полосой пропускания 80 МГц с модуляцией QAM‑1024

В этой схеме также используется интегрированный миллиметровый модулятор ADMV1013, который содержит ряд традиционных блоков сигнальной цепи, таких как умножители частоты, квадратурные смесители и усилители. Чтобы упростить фильтрацию, в этом проекте используется довольно сложная топология цепи промежуточной частоты, в которой на квадратурные смесители модуляторов подаются сигналы с фазой 90°. Это устраняет одну из боковых полос сигнала, преобразованного с повышением частоты, тем самым уменьшается сложность фильтрации по сравнению с преобразованием сигнала с двумя боковыми полосами.
Чтобы оптимизировать эту сигнальную цепь для получения наименьшего значения EVM, сначала проанализируем фазовый шум на уровне системы, затем найдем оптимальное соотношение шума и линейности и, наконец, соберем все функциональные блоки в одну систему.

Улучшение EVM путем оптимизации фазового шума
Как мы обсуждали ранее, фазовый шум всей системы может ограничивать возможность минимизации EVM на частотах миллиметрового диапазона. Проанализируем вклад фазового шума каждого каскада, чтобы убедиться, что выбраны наилучшие компоненты для данной сигнальной цепи. Компоненты, формирующие частоты в этой сигнальной цепи, — это ЦАП, который синхронизируется с помощью синтезатора, и гетеродин. Общий фазовый шум можно выразить следующим образом:

где LTx – общий фазовый шум передатчика, lIF – фазовый шум на выходе ЦАП, lLO – фазовый шум сигнала гетеродина.
Используемый в этом примере ЦАП AD9082 имеет исключительно низкий аддитивный фазовый шум. Общий фазовый шум на выходе, который представляет собой сигнал ПЧ, можно рассчитать по простой формуле:

где LCLK – интегрированный фазовый шум тактового сигнала, fIF – ПЧ-частота на выходе ЦАП, fCLK – частота выборки для ЦАП.
Чтобы выбрать компоненты минимальной сложности и с наименьшим фазовым шумом, проанализируем характеристики двух микросхем, рассматриваемых в качестве кандидатов на роль генератора тактовой частоты и источника сигнала гетеродина.

Рис. 7. Фазовый шум тактового сигнала и сигнала гетеродина для ADF4372 и ADF4401A

На рис. 7 показана характеристика фазового шума сигнала с одной боковой полосой для двух микросхем, наилучшим образом подходящих для использования в качестве синтезаторов частоты для этой сигнальной цепи. Интегрированный фазовый шум для сигнала 5G NR может быть рассчитан путем интегрирования фазового шума источников сигнала в полосе от 6 кГц до 100 МГц (табл. 1).

На типичных для этой сигнальной цепи промежуточных частотах как ADF4372, так и ADF4401A демонстрируют чрезвычайно низкие уровни интегрированного шума. Поскольку для ADF4372 требуется гораздо меньшая площадь печатной платы, это хороший выбор для формирования
частоты выборки для РЧ-преобразователя, который создает ПЧ-сигнал. Микросхема ADF4401A становится выбором для генератора сигнала гетеродина из-за присущего ей низкого начального фазового шума. На частоте 30 ГГц он примерно на 20 дБ ниже интегрированного шума для ADF4372. Такой низкий уровень шума гарантирует, что фазовый шум сигнала гетеродина не станет ограничивать общие показатели EVM для всей системы.
Используя уравнение 13, можно рассчитать общий EVMPhN из-за фазового шума:

Такой уровень модуля вектора ошибка из-за фазового шума более чем достаточен для измерения сигналов с EVM порядка -30 дБ, как определено стандартом для 5G NR.

Оптимизация соотношения шума и линейности
Одна из основных проблем при проектировании РЧ-систем — поиск оптимального соотношения шума и линейности. Улучшение одного из этих двух параметров обычно приводит к неоптимальной величине другого. Анализ EVM на уровне системы может быть очень полезным инструментом для улучшения характеристик системы в целом.

Рис. 8. Оптимизация соотношения шума и линейности системы

Рис. 8 иллюстрирует поиск оптимального соотношения шума и линейности для созданной нами сигнальной цепи. Каждая из кривых получена путем регулировки управляющего напряжения интегрированного усилителя. Для каждой кривой изменялся уровень выходной мощности ЦАП. Заметим, что по мере увеличения уровня мощности EVM уменьшается из-за увеличения общего отношения сигнал – шум системы. После определенного уровня мощности нелинейности всего тракта прохождения сигнала начинают ухудшать показатель EVM. Результирующая U-образная кривая EVM для данной конфигурации усилителя очень узкая.
Регулируя управляющее напряжение усилителя, мы можем перейти к другой кривой, на которой система имеет более низкий EVM. Пунктирная линия на рис. 8 отражает оптимизацию на уровне системы, которая может быть достигнута с помощью интегрированных усилителей микросхемы ADMV1013. Результирующая U-образная кривая после этой оптимизации становится намного шире, что обеспечивает сверхнизкий EVM в широком диапазоне уровней выходной мощности.

Заключение
В статье мы рассмотрели EVM в качестве системного показателя и обсудили, как с помощью EVM можно оптимизировать характеристики системы. Как мы показали, EVM – хороший индикатор многих проблем системного уровня. Все источники ошибок приводят к возникновению поддающегося измерению EVM, который можно использовать для оптимизации общих показателей системы. Мы продемонстрировали также, что с помощью новейших высокоскоростных преобразователей и интегрированных модуляторов миллиметрового диапазона можно достичь характеристик системы приборного уровня и значений EVM на порядки величин более низких по сравнению с требованиями стандартов в области связи.

ЛИТЕРАТУРА
1. Voelker K. M. Apply Error Vector Measurements in Communication Design. – Microwaves & RF, December 1995.
2. IEEE 802.11a‑1999. IEEE Standard for Telecommunications and Information Exchange Between Systems. LAN / MAN Specific Requirements. Part 11: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications: High Speed Physical Layer in the 5 GHz Band. – IEEE Standard
Association, September 1999.
3. Kester W. MT‑008 Tutorial: Converting Oscillator Phase Noise to Time Jitter. – Analog Devices, Inc., 2009.

Источник

From Wikipedia, the free encyclopedia

The error vector magnitude or EVM (sometimes also called relative constellation error or RCE) is a measure used to quantify the performance of a digital radio transmitter or receiver. A signal sent by an ideal transmitter or received by a receiver would have all constellation points precisely at the ideal locations, however various imperfections in the implementation (such as carrier leakage, low image rejection ratio, phase noise etc.) cause the actual constellation points to deviate from the ideal locations. Informally, EVM is a measure of how far the points are from the ideal locations.

Noise, distortion, spurious signals, and phase noise all degrade EVM, and therefore EVM provides a comprehensive measure of the quality of the radio receiver or transmitter for use in digital communications. Transmitter EVM can be measured by specialized equipment, which demodulates the received signal in a similar way to how a real radio demodulator does it. One of the stages in a typical phase-shift keying demodulation process produces a stream of I-Q points which can be used as a reasonably reliable estimate for the ideal transmitted signal in EVM calculation.

Definition[edit]

Constellation diagram and EVM

An error vector is a vector in the I-Q plane between the ideal constellation point and the point received by the receiver. In other words, it is the difference between actual received symbols and ideal symbols. The root mean square (RMS) average amplitude of the error vector, normalized to ideal signal amplitude reference, is the EVM. EVM is generally expressed in percent by multiplying the ratio by 100. ^[1]

The ideal signal amplitude reference can either be the maximum ideal signal amplitude of the constellation, or it can be the root mean square (RMS) average amplitude of all possible ideal signal amplitude values in the constellation. For many common constellations including BPSK, QPSK, and 8PSK, these two methods for finding the reference give the same result, but for higher-order QAM constellations including 16QAM, Star 32QAM, 32APSK, and 64QAM the RMS average and the maximum produce different reference values. ^[2]

The error vector magnitude is sometimes expressed in dB. This is related to the value of EVM in percent as follows:

${displaystyle mathrm {EVM} _{text{dB}}=20log _{10}left({mathrm {EVM} _{%} over 100}right).}$

The definition of EVM depends heavily on the standard that is being used, for example in 3GPP LTE the relevant documents will define exactly how EVM is to be measured. There are discussions ongoing by academics as to some of the problems around EVM measurement.^[3]

Dynamic EVM[edit]

Battery life and power consumption are important considerations for a system-level RF transmitter design. Because the transmit power amplifier (PA) consumes a significant portion of the total system DC power, a number of techniques are employed to reduce PA power usage. Many PAs offer an adjustable DC supply voltage to optimize the maximum RF output power level versus its DC power consumption. Also, most PAs can be powered-down or disabled when not in use to conserve power, such as while receiving or between packets during transmission. In order to maximize power efficiency, the PA must have fast turn-on and turn-off switching times. The highest DC power efficiency occurs when the time delta between PA Enable and the RF signal is minimized, but a short delay can exacerbate transient effects on the RF signal.

Because the power-up/power-down operation of the PA can cause transient and thermal effects that degrade transmitter performance, another metric called Dynamic EVM is often tested. Dynamic EVM is measured with a square wave pulse applied to PA Enable to emulate the actual dynamic operation conditions of the transmitter. The degradation in dynamic EVM is due to the PA transient response affecting the preamble at the start of the packet and causing an imperfect channel estimate. Studies have shown that dynamic EVM with a 50% duty cycle square wave applied to PA Enable to be worse than the static EVM (PA Enable with 100% duty cycle).^[4]

References[edit]

^ «Error Vector Magnitude (Digital Demodulation)».
^ «EVM Normalization Reference (Digital Demod)».
^ Vigilante, McCune, Reynaert. «To EVM or Two EVMs?». doi:10.1109/MSSC.2017.2714398. S2CID 6849707. CS1 maint: multiple names: authors list (link)
^ Power Amplifier Testing For 802.11ac

Источник

From Wikipedia, the free encyclopedia

Definition[edit]

Constellation diagram and EVM

The error vector magnitude is sometimes expressed in dB. This is related to the value of EVM in percent as follows:

${displaystyle mathrm {EVM} _{text{dB}}=20log _{10}left({mathrm {EVM} _{%} over 100}right).}$

Dynamic EVM[edit]

References[edit]

^ «Error Vector Magnitude (Digital Demodulation)».
^ «EVM Normalization Reference (Digital Demod)».
^ Vigilante, McCune, Reynaert. «To EVM or Two EVMs?». doi:10.1109/MSSC.2017.2714398. S2CID 6849707. CS1 maint: multiple names: authors list (link)
^ Power Amplifier Testing For 802.11ac

Источник

Теоретические основы анализа модуля вектора ошибки

На рис. 1 изображена векторная диаграмма, на которой показаны два вектора — опорный вектор, R (k), и реальный измеренный вектор, Z (k), который соответствует траектории принятого символа. Опорный вектор определяет координаты идеальной траектории символа при отсутствии ошибок. Разность между опорным вектором и вектором реально измеренного символа называется вектором ошибки.

Модуль вектора ошибки (EVM, error vector magnitude) представляет собой евклидово расстояние между координатами идеального и реально измеренного символов. В общем случае, EVM усредняется по ансамблю траекторий символов и описывается следующим выражением:

Таким образом, параметр EVM является мерой отношения вектора ошибки к опорному вектору. В совершенной системе, в которой отсутствуют шумы и нелинейности, способные внести искажения в сигнал, измеренный и опорный векторы совпадали бы, и EVM был бы равен нулю. Рассмотрим влияние отношения «сигнал — шум» (ОСШ) для принимаемого символа. При очень большом ОСШ разница между измеренным и опорным векторами, обусловленная шумом и искажениями, очень мала, а EVM стремится к нулю. И, наоборот, большое значение EVM подразумевает, что вектор измеренного символа значительно отличается от идеального опорного вектора, что может быть вызвано только шумом и искажениями (при условии, что при задании опорного вектора не была допущена ошибка). Таким образом, ОСШ и EVM модулированного сигнала связаны друг с другом обратной зависимостью, которая описывается уравнением:

где L — это выигрыш за счет кодирования.

Параметр L учитывает выигрыш, который достигается за счет схемы кодирования сигнала. Информативное сообщение может кодироваться различными способами. Например, в системах с расширением спектра прямой последовательностью информационное сообщение подвергается расширению спектра путем умножения каждого передаваемого бита на прямую (псевдослучайную) последовательность, представляющую собой случайную последовательность нулей и единиц. Последовательность подбирается таким образом, чтобы она была уникальной и слабо коррелированной с последовательностями, которые применяются для кодирования других потоков, передаваемых на той же частоте несущей. Для систем с расширением спектра усиление за счет кодирования равно количеству элементов, или «чипов», в последовательности, используемой для кодирования каждого бита. В децибелах эта величина выражается как 10log₁₀ (частота следования элементов последовательности / скорость данных). Например, для передачи потока данных со скоростью 12,2 кбит/с в трансивере стандарта UMTS используется последовательность со скоростью 3,84 Мчип/с; при этом выигрыш за счет кодирования равен 3,84×10⁶/12,2×10³ = 314,75, или 25 дБ.

Для нахождения зависимости между EVM и BER необходимо определить, как связаны друг с другом ОСШ и вероятность ошибки на символ для конкретной схемы модуляции. Вероятность ошибки на символ для сигналов с квадратурной амплитудной модуляцией (QAM) описывается выражением (3):

где M — порядок модуляции (например, 64 для 64-QAM), γ_b — среднее значение ОСШ на бит, k — число битов на символ (например, 6 битов на комплексный символ для 64-QAM).

Используя выражения (2) и (3), можно построить зависимости частоты ошибки на символ (SER, symbol error rate) и EVM от ОСШ. Зависимость SER от ОСШ показана на рис. 2а. Для форматов QAM с различным порядком она имеет классический вид типа «водопад». Для тех же схем модуляции на рис. 2б изображены зависимости EVM от ОСШ. С помощью этих зависимостей разработчики могут оценить значение частоты ошибок на бит для конкретного приемника. Например, если измеренное значение EVM для некодированного сигнала с модуляцией 256-QAM равно 3%, то ожидаемая частота ошибок на символ составит 600 млн^–1. Другими словами, в последовательности из 10 000 символов в среднем 6 символов будут ошибочными, что соответствует 75 ошибочным битам в последовательности из 1 миллиона битов (BER = 7,5×10^-5).

Используя зависимости, показанные на рис. 2, а также подходящий векторный анализатор сигналов, разработчик может достаточно быстро оптимизировать производительность системы. Это достигается путем контроля значения EVM при изменении таких характеристик сигнального тракта, как тип фильтра, межкаскадное согласование и усиление преобразования. Рис. 3 иллюстрирует некоторые распространенные искажения сигнальных созвездий, которые могут возникать в реальной системе. На основании формы сигнального созвездия можно сделать определенные выводы о природе шумов или искажений, являющихся потенциальной причиной ухудшения EVM.

Пример оптимизации: подсистема трактов ПЧ и модулирующих частот AD8348/AD8362

На рис. 4 показана приемная подсистема для переноса сигнала из области ПЧ в область модулирующих частот с замкнутым контуром автоматической регулировки уровня (automatic level control — ALC), основанная на квадратурном демодуляторе и детекторе среднеквадратической мощности. Микросхема AD8348 обеспечивает точную квадратурную демодуляцию сигналов с частотой от 50 МГц до 1 ГГц. Внутренний делитель частоты гетеродина позволяет работать с частотой гетеродина, равной удвоенной частоте несущей, что облегчает решение проблемы, связанной с паразитным захватом частоты гетеродина (LO-pulling) в полнодуплексных трансиверах. В рассматриваемом примере входной сигнал имеет частоту (ПЧ), равную 190 МГц, а сигнал гетеродина имеет уровень, равный 10 дБм, и частоту, равную 380 МГц. Интегрированный входной усилитель с переменным коэффициентом усиления (variable gain amplifier — VGA), состоящий из резистивного переменного аттенюатора и пост-усилителя с высоким значением IP, обеспечивает переменный коэффициент усиления при сохранении постоянного динамического диапазона, свободного от побочных составляющих. Микросхема AD8362 — это прецизионный измеритель мощности, способный измерять среднеквадратическое значение мощности сигналов в диапазоне от произвольных низких частот до 2,7 ГГц. Данная микросхема не чувствительна к изменению пик-фактора сигнала, что делает ее подходящим решением для измерения истинной среднеквадратической мощности сигналов с цифровой модуляцией.

В схеме на рис. 4 обеспечивается измерение среднеквадратической мощности сигнала в полосе модулирующих частот, поступающего с синфазного канала. Выбор синфазного или квадратурного канала для детектирования произволен, если вектора I и Q имеют псевдослучайный характер, что соответствует истине для большинства схем цифровой модуляции. На основании результата измерения среднеквадратической мощности интегрированный усилитель ошибки формирует управляющий сигнал, подаваемый на вход управления усилением квадратурного демодулятора. Замкнутый контур регулировки адаптивно подстраивает усиление преобразования демодулятора для поддержания постоянного среднеквадратического уровня мощности модулирующего сигнала независимо от его формы. Выходной уровень задается подачей соответствующего напряжения контрольной точки на вывод VSET. Для нахождения оптимальной контрольной точки в схеме ALC и определения подходящего фильтра для цифровой модуляции 256-QAM со скоростью 1 Мсимвол/с использовался метод анализа вектора ошибки.

Несимметричные сигналы с выхода демодулятора подаются на фильтр нижних частот. Для минимизации широкополосного шума и подавления мешающих смежных каналов приема в обоих каналах, I и Q, использовались фильтры Бесселя четвертого порядка. Выбор в пользу фильтра Бесселя обусловлен его малой групповой задержкой, что является необходимым требованием для минимизации межсимвольных помех. На этапе тестирования сначала использовались фильтры Баттерворта и Чебышева, но из-за большей групповой задержки в полосе пропускания значения EVM в системе были хуже. С помощью анализатора сигналов можно очень быстро измерить показатели системы, что позволяет подобрать оптимальную схему фильтра за короткий промежуток времени.

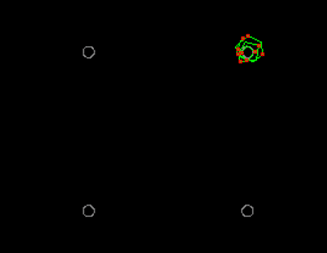
Для измерения EVM в полосе модулирующих частот использовался векторный анализатор сигналов FSQ8 производства Rohde&Schwarz. Оптимальное значение напряжения контрольной точки было найдено путем изменения этого напряжения и наблюдения соответствующего значения EVM. Как показано на рис. 5, при правильном выборе контрольной точки EVM составляет не более 2% в диапазоне входных уровней, превышающем 40 дБ. На рис. 6 показано экспериментально полученное сигнальное созвездие для модуляции 256-QAM. Переменное усиление преобразования демодулятора позволяет создавать схемы, обладающие оптимальными характеристиками BER в более широком динамическом диапазоне, чем при использовании модуляторов с фиксированным коэффициентом усиления.

Рис. 7 иллюстрирует показатели EVM для модуляции QAM меньших порядков при той же ширине полосы сигнала. Для достижения адекватных значений BER при использовании схем модуляции более низкого порядка требуется меньшее ОСШ. Поэтому неудивительно, что для таких схем модуляции показатели EVM еще лучше, а динамический диапазон — немного больше.

Значение EVM можно оценить по напряжению RSSI (Received Signal Strength Indication, индикация уровня принимаемого сигнала) микросхемы AD8362. На рис. 8 показаны результаты измерений напряжения RSSI для нескольких схем модуляции. Зная напряжение RSSI, можно определить уровень мощности сигнала на входе демодулятора с приемлемой погрешностью, который затем может быть использован для предсказания значения EVM при этом уровне входной мощности.

Заключение

Измерение EVM и связанных с ним величин позволяет оценить качество цифрового радиоприемника. Кроме того, при правильном применении методы анализа EVM позволяют идентифицировать вид искажений сигнала и, следовательно, конкретное место возникновения ошибок. Таким образом, анализ EVM представляет собой удобный инструмент для оптимизации сигнального тракта и предсказания динамических характеристик системы.

Источник

Величина вектора ошибки или EVM (иногда также называемая относительной ошибкой созвездия или RCE ) — это мера, используемая для количественной оценки производительности цифрового радиопередатчика или приемника. Сигнал, отправленный идеальным передатчиком или принятый приемником, будет иметь все точки совокупности точно в идеальных местах, однако различные недостатки в реализации (например, утечка несущей, низкий коэффициент отклонения изображения, фазовый шум и т. Д.) Вызывают фактические точки совокупности отклоняться от идеальных мест. Неформально EVM — это мера того, насколько далеко точки находятся от идеальных мест.

Шум, искажения, паразитные сигналы и фазовый шум ухудшают EVM, и, следовательно, EVM обеспечивает комплексную оценку качества радиоприемника или передатчика для использования в цифровой связи. Передатчик EVM может быть измерен с помощью специализированного оборудования, которое демодулирует принимаемый сигнал аналогично тому, как реальное радио демодулятор это делает. На одном из этапов типичного процесса демодуляции с фазовой манипуляцией создается поток точек IQ, который можно использовать в качестве достаточно надежной оценки идеального переданного сигнала при вычислении EVM.

Определение

Диаграмма созвездия и EVM

Вектор ошибки является вектором в плоскости IQ между точкой идеального созвездия и точкой, принимаемой приемником. Другими словами, это разница между реально полученными символами и идеальными символами. Корень средний квадрат (СКО) средняя амплитуда вектора ошибки, нормированы ссылкой амплитуды идеального сигнала, является ЭВМ. EVM обычно выражается в процентах путем умножения отношения на 100%.

Идеальным эталоном амплитуды сигнала может быть либо максимальная идеальная амплитуда сигнала созвездия, либо это может быть среднеквадратическая (RMS) средняя амплитуда всех возможных значений идеальной амплитуды сигнала в созвездии. Для многих распространенных созвездий, включая BPSK, QPSK и 8PSK, эти два метода поиска эталона дают одинаковый результат, но для созвездий QAM более высокого порядка, включая 16QAM, Star 32QAM, 32APSK и 64QAM, среднее значение RMS и максимум дают разные эталоны. ценности.

Величина вектора ошибки иногда выражается в дБ . Это связано со значением EVM в процентах следующим образом:

${ Displaystyle mathrm {EVM (дБ)} = 20 log _ {10} left ({ mathrm {EVM (%)} over mathrm {100 (%)}} right)}$

Определение EVM сильно зависит от используемого стандарта, например, в 3GPP LTE соответствующие документы будут определять, как именно измерять EVM. Ученые обсуждают некоторые проблемы, связанные с измерением EVM.

Динамический EVM

Срок службы батареи и энергопотребление являются важными факторами при проектировании РЧ-передатчика системного уровня. Поскольку усилитель мощности передачи (PA) потребляет значительную часть общей мощности постоянного тока системы, используется ряд методов для уменьшения использования мощности PA. Многие усилители мощности предлагают регулируемое напряжение питания постоянного тока для оптимизации максимального уровня выходной мощности РЧ по сравнению с потребляемой мощностью постоянного тока. Кроме того, большинство PA можно выключить или отключить, когда они не используются, для экономии энергии, например, во время приема или между пакетами во время передачи. Чтобы добиться максимальной энергоэффективности, PA должен иметь быстрое время включения и выключения. Наивысшая эффективность мощности постоянного тока достигается, когда разница во времени между включением PA и РЧ-сигналом минимизирована, но небольшая задержка может усугубить переходные эффекты на РЧ-сигнал.

Поскольку включение / выключение питания PA может вызвать переходные и тепловые эффекты, которые ухудшают характеристики передатчика, часто проверяется другой показатель, называемый Dynamic EVM . Динамический EVM измеряется с помощью прямоугольного импульса, подаваемого на PA Enable для имитации реальных динамических условий работы передатчика. Ухудшение динамического EVM происходит из-за того, что переходная реакция PA влияет на преамбулу в начале пакета и приводит к неточной оценке канала. Исследования показали, что динамический EVM с прямоугольной формой волны 50%, применяемой к PA Enable, хуже, чем статический EVM (PA Enable со 100% рабочим циклом).

Смотрите также

Коэффициент ошибок модуляции
Отношение несущей к шуму
Соотношение сигнал шум

Ссылки

^ http://rfmw.em.keysight.com/wireless/helpfiles/89600b/webhelp/subsystems/digdemod/Content/digdemod_symtblerrdata_evm.htm
^ http://rfmw.em.keysight.com/wireless/helpfiles/89600b/webhelp/subsystems/digdemod/Content/dlg_digdemod_comp_evmnormref.htm
↑ Vigilante, McCune, Reynaert. «К EVM или двум EVM?». DOI : 10.1109 / MSSC.2017.2714398 . S2CID 6849707 . CS1 maint: несколько имен: список авторов ( ссылка )
^ Тестирование усилителя мощности для 802.11ac

Источник

Величина вектора ошибок (EVM) является измерением модулятора или эффективностью демодулятора в присутствии ухудшений. По существу EVM является векторной разностью в установленный срок идеала (переданный) сигнал и измеренного (полученного) сигнала. Если используется правильно, эти измерения могут помочь в идентификации источников ухудшения сигнала, таких как: шум фазы, неустойчивость I-Q, амплитудная нелинейность и искажение фильтра

Эти типы измерений полезны для определения производительности системы в приложениях связи. Например, определение, если система EDGE соответствует 3GPP радио-стандарты передачи, требует точной RMS, EVM, Пикового EVM и 95-й процентили для измерений EVM.

Пользователи могут создать объект EVM двумя способами: использование объекта по умолчанию или путем определения пар значения параметров. Как задано 3GPP стандарт, единица измерения для RMS, Максимума и Процентили измерения EVM является процентилью (%). Для получения дополнительной информации смотрите EVM Measurement или comm.EVM страница справки.

Измерение точности модулятора

Обзор
Структура
Ссылки

Обзор

Communications Toolbox™ обеспечивает два блока, которые можно использовать для измерения точности модулятора: EVM Measurement и MER Measurement.

Этот пример тестирует передатчик EDGE на ухудшения разработки системы с помощью измерений EVM. В этом примере блок EVM Measurements сравнивает идеальный опорный сигнал с измеренным сигналом, и затем вычисляет RMS EVM, максимальный EVM и процентиль значения EVM. Согласно стандарту EDGE [1], величина вектора ошибок полученного сигнала, вычисленного относительно переданной формы волны, не должна превышать следующие значения:

Технические требования измерения стандарта EDGE [2]

Измерение	Мобильная станция	Базовая приемопередающая станция
	Нормальный	Экстремальное значение	Нормальный	Экстремальное значение
RMS	9%	10%	7%	8%
Пиковый EVM	30%	30%	22%	22%
95-я процентиль EVM	15%	15%	11%	11%

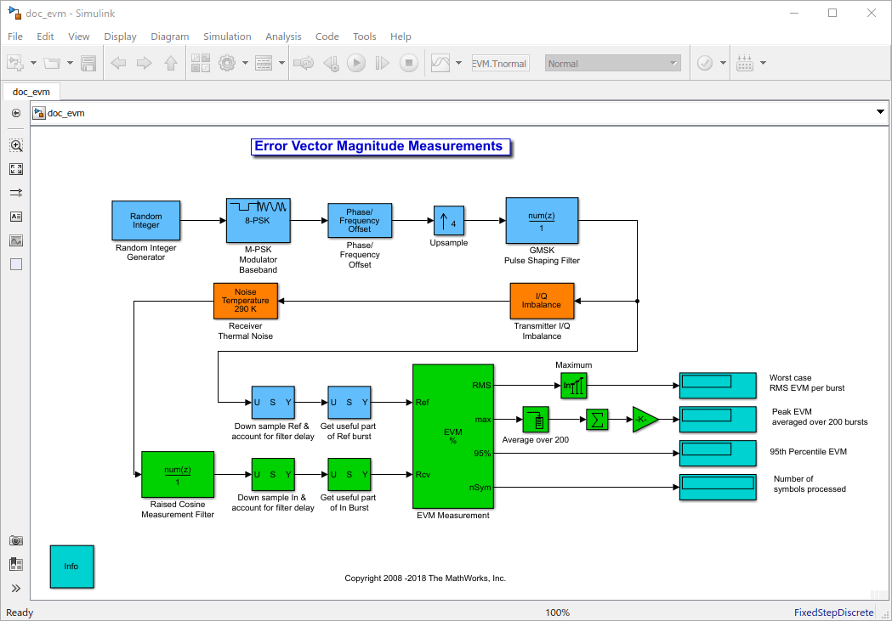
Этот пример использует эту модель.

Можно открыть эту модель путем ввода doc_evm в MATLAB^® командная строка.

Структура

Модель по существу содержит три части:

Передатчик
Ухудшения приемника
Вычисление EVM

Следующие разделы примера содержат описания для каждой части модели.

Передатчик. Следующие блоки включают передатчик:

Random Integer Generator
M-PSK Modulator Baseband
Phase/Frequency Offset
Upsample
Discrete FIR Filter (Simulink)
I/Q Imbalance

Блок Random Integer Generator симулирует случайную генерацию данных. Стандарт EDGE указывает, что передатчик выполняет измерения во время полезной части пакета – исключая биты хвоста – по крайней мере по 200 пакетам. В этом режиме передатчик производит 435 символов на пакет (9 дополнительных счетов символов на задержки фильтра). Блок Phase Offset предоставляет непрерывное вращение фазы 3π/8 сигналу. В целях синхронизации блок Upsample сверхдискретизировал сигнал на коэффициент 4.

Блок Discrete FIR Filter обеспечивает линеаризацию импульса GMSK, основной компонент в разложении Лорана модуляции GMSK [3]. Функция помощника вычисляет коэффициенты фильтра и использует КИХ-цифровой фильтр прямой формы, чтобы создать эффект формирования импульса. Нормализация фильтра обеспечивает усиление единицы в основном касании.

Блок I/Q Imbalance симулирует ухудшения передатчика. Этот блок добавляет вращение в сигнал, симулируя дефект в передатчике под тестом. I/Q amplitude imbalance является 0.5 дБ и I/Q phase imbalance является 1°.

Ухудшения приемника. В этой модели блок Receiver Thermal Noise представляет ухудшения приемника. Эта модель принимает 290 K теплового шума, представляя недостатки оборудования под тестом.

Вычисление EVM. Вычисление EVM полагается на следующие блоки:

Discrete FIR Filter (Simulink)
Selector (Simulink)
EVM Measurement
Display (Simulink)

Блок измерения EVM вычисляет векторную разность идеального опорного сигнала и сигнала, которому повреждают. Выход КИХ-фильтра обеспечивает Reference введите для блока EVM. Выход блока Noise Temperature обеспечивает сигнал, которому повреждают, в Input порт блока EVM.

В то время как блок имеет различные опции нормализации в наличии, стандарт EDGE требует нормализации на Average reference signal power. В целях рисунка в этом примере, блок EVM выходные параметры RMS, максимум и значения измерения процентили.

Экспериментирование с моделью

Запустите модель путем нажатия на кнопку воспроизведения в окне модели Simulink.
Исследуйте выход блока EVM и сравните измерения с пределами в таблице EDGE Standard Measurement Specifications.

В этом примере блок EVM Measurement вычисляет следующее:
- Худшая RMS случая EVM на пакет: 9,77%
- Пиковый EVM: 18,95%
- 95-я процентиль % EVM:14.76
В результате этот симулированный передатчик EDGE проходит тест EVM для Мобильной Станции при экстремальных условиях.
Дважды кликните блок I/Q Imbalance.
Введите 2 в I/Q Imbalance (dB) и нажимают OK.
Кликните по кнопке воспроизведения в окне модели Simulink.
Исследуйте выход блока EVM. Затем сравните измерения с пределами в таблице EDGE Standard Measurement Specifications.

В этом примере блок EVM Measurement вычисляет следующие результаты:
- Худшая RMS случая EVM на пакет: 15,15%
- Пиковый EVM: 29,73%
- 95-я процентиль EVM: 22,55%.
Эти значения EVM явно недопустимы согласно стандарту EDGE. Можно экспериментировать с другими значениями разбаланса I/Q, исследовать удар на вычисления и сравнить их со значениями, введенными в таблице.

Ссылки

[1] 3GPP TS 45.004, “Сети радиодоступа; Модуляция”, Релиз 7, v7.2.0, 2008-02.

[2] 3GPP TS 45.005, “Сеть радиодоступа; Радио-передача и прием”, Релиз 8, v8.1.0, 2008-05.

[3] Лоран, Пьер. “Точная и аппроксимированная конструкция цифровой фазовой модуляции суперпозицией амплитуды модулировала импульсы (AMP)”. Транзакции IEEE на Коммуникациях. Издание COM-34, № 2, февраль 1986, стр 150-160.

Источник

Измерения параметров векторной модуляции

А.В. Пивак к.т.н., АО «ПриСТ»

Измерения параметров модуляции всегда выделялось в отдельный вид измерений. Свидетельством тому является наличие государственных поверочных схем и государственных эталонов амплитудной и частотной модуляций (АМ и ЧМ), большого количества рабочих эталонов по поверке АМ и ЧМ измерителей, рабочих средств измерений параметров аналоговой модуляции. Сейчас аналоговая модуляция уступает место цифровой, при которой аналоговый сигнал несущей частоты модулируется не аналоговым информативным сигналом, а цифровой битовой последовательностью (сам принцип модуляции при этом всё равно остаётся аналоговым). Необходимость перехода от аналоговой к цифровой модуляции обусловлена повсеместным развитием цифровой техники, использующей для передачи информации цифровые потоки данных, а также требованиями по ограничению занимаемой полосы частот (ширины спектра) для электромагнитного модулированного колебания, несущего информацию. Возрастание скоростей и объёма передаваемой информации при ограничении на расширение требуемой для передачи полосы частот приводит к усложнению применяемых схем модуляции и соответственно усложнению необходимой аппаратуры, в том числе и измерительной. Например, следующим уровнем после перехода от аналоговой модуляции к цифровой является мультиплексирование передаваемой информации с разделением во временной области. При этом в той же занимаемой полосе частот и с использованием только одного несущего колебания может разновременно передаваться несколько различных пакетов с цифровой модуляцией (данный принцип используется в сетях сотовой связи стандарта GSM).

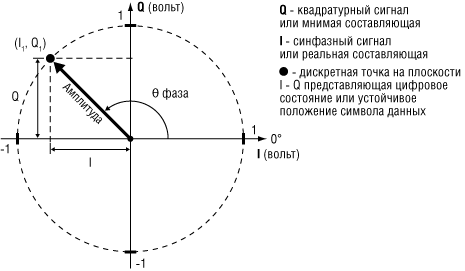
Рисунок 1. Диаграмма состояний векторной модуляции

В процессе модуляции могут изменяться как амплитуда, так и фаза/частота колебаний. Максимальный объём передаваемой информации достигается при одновременном изменении амплитуды и фазы сигнала. Однако сгенерировать или декодировать такой сигнал непосредственно (с помощью амплитудного и фазового модуляторов) тяжело. На практике данное решение осуществляют и описывают с помощью квадратурных модуляторов и полярных координат, образованных парой ортогональных векторов напряжений: синфазного с несущим колебанием I и сдвинутого на 90° Q. Такое представление позволяет рассматривать любую точку в полярных координатах в виде набора координат напряжений (I, Q) либо в виде вектора, определяемого амплитудой и фазой (рис. 1). Соответственно, реализованная и описанная таким образом модуляция называется векторной, а полярные координаты – диаграммой состояний. При этом погрешность векторной модуляции определяется отличием реальной траектории или положения точки, соответствующей заданной модуляции, от идеальной. Для цифровой векторной модуляции наиболее распространённой величиной, описывающей погрешность модуляции, является модуль вектора ошибки EVM, определяемый по формуле:

где (1)

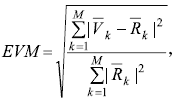
где Rk – это вектор напряжений на диаграмме состояний, соответствующий “идеальному” опорному положению k-го символа из выборки длиной М, а Vk – это вектор, соответствующий измеренному положению k-го символа.

В настоящий момент активно разрабатываются, производятся и применяются лабораторные средства измерения для воспроизведения/измерения векторной модуляции с нормированным значением модуля вектора ошибки. К ним относятся векторные генераторы ВЧ, векторные анализаторы спектра ВЧ, осциллографы (платы аналого-цифрового преобразователя – АЦП) и генераторы сигналов произвольной формы (платы цифро-аналогового преобразователя – ЦАП). Соответственно, встаёт задача метрологического обеспечения измерений векторной модуляции, которая в нашей стране на настоящий момент не решена. Далее будут рассмотрены возможные пути её реализации.

Для начала определим математическую модель процесса измерения, т.е. составим уравнение измерений. Из анализа типовых схем генераторов/измерителей векторной модуляции следует, что они включают в себя следующие основные части: программное обеспечение для цифровой обработки сигналов; ЦАП или АЦП; носители частоты [1]. Схемы генератора и измерителя являются взаимообратимыми, поэтому приведём этапы работы средств измерений векторной модуляции на примере измерителей типа векторных анализаторов спектра:

Сигнал, поступающий на вход анализатора спектра, переносится с помощью встроенного гетеродина на промежуточную частоту (ширина спектра, переносимого на ПЧ обычно составляет 20…160 МГц);
Сигнал промежуточной частоты оцифровывается во временной области с помощью АЦП;
Цифровые отсчёты сигнала поступают в программное обеспечение, где обрабатываются с помощью “цифрового квадратурного модулятора”;
Полученные после программной обработки результаты выводятся в виде раскодированных битов, частотного спектра, временных зависимостей демодулированных напряжений I и Q, полярных координат, модуля векторной ошибки, рассчитываемого по формуле и т.д.

Исходя из определения модуля векторной ошибки, величиной, которая измеряется анализатором, является напряжение Vизм. Тогда, уравнение измерений принимает вид:

где (2)

где Хi – зависимость результата измерений от параметров анализатора спектра, АЦП и алгоритма цифровой обработки сигнала (ЦОС) соответственно, а Vсвч – входной сигнал.

Такими параметрами являются:

для анализатора спектра – собственные тепловые шумы, фазовые шумы гетеродина, нелинейность смесителя, гармонические и негармонические искажения, нелинейность АЧХ и ФЧХ тракта ПЧ, погрешность установки частоты гетеродина;
для АЦП – нелинейность АЦП, погрешность квантования, погрешность частоты дискретизации;
для ЦОС – недостаточная частота дискретизации для обработки требуемой полосы частот, разрывность по фазе между пакетами разновременно собранной информации, неправильное определение используемых фильтров и скорости передачи информации (частоты модулирующего колебания).

Из анализа приведённых факторов сразу же вытекает следующий вывод. Результат измерения векторной ошибки зависит от большого количества факторов, не все из которых зависят собственно от средства измерения. Таким образом, определить жёсткую спецификацию для погрешности измерения EVM “на все случаи жизни” практически невозможно. При этом наиболее проблематичным является определение фильтров, применяемых в процессе векторной модуляции, т.к. отличие предполагаемого в работе фильтра от реально используемого можно оценить только очень примерно. Именно по этой причине производители средств измерений параметров векторной модуляции обычно указывают либо типичные значения погрешностей, либо нормируют погрешности для строго определённых видов модуляции, например АМ/ЧМ, предоставляя право самим пользователям оценивать погрешность измерения для конкретных условий проведения измерений.

Для упрощения дальнейшего анализа сделаем несколько допущений:

влияние фазовых и тепловых шумов гетеродина являются пренебрежимо малыми и в дальнейшем не учитываются;
все погрешности, связанные с настройками теоретических фильтров в программном обеспечении, будем рассматривать как часть погрешности входного сигнала и также не будем учитывать в дальнейшем анализе.

Таким образом, уравнение измерений примет вид:

где (3)

где функция F в случае простейшей модели имеет вид множителя в виде комплексного числа вида k*ejq, а Dас,ацп , Dцос являются погрешностями, вносимыми анализатором спектра со встроенной АЦП и алгоритмом цифровой обработки полученной информации соответственно.

Подставляя уравнение (3) в (1) и заменяя дискретные отсчёты Vk вектора измеренного сигнала Vизм на непрерывный скалярный сигнал Vсвч, а также переводя абсолютные погрешности в относительные, получим после преобразований:

где (4)

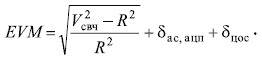
Естественно, применяя более сложные модели с большим количеством переменных, можно получить более точные оценки погрешностей, но при этом усложнить сам процесс анализа. В нашем случае определение составляющих, входящих в уравнение измерений, сводится к получению оценки для погрешности, получаемой при цифровой обработке сигналов с помощью программного обеспечения, и экспериментального определения dас,ацп. Данный эксперимент должен заключаться в подаче на вход анализатора спектра известного сигнала Vсвч, величина напряжения которого прослеживается к эталонам основных единиц системы СИ, и измерения анализатором модуля векторной ошибки. Отличие полученного результата от ожидаемого будет характеризовать dас, ацп.

Для определения погрешности ЦОС воспользуемся версией программного обеспечения (ПО) Modular, предназначенной для генерации цифровой последовательности сигналов с различными видами векторной модуляции и дальнейшего их воспроизведения в виде реальных сигналов с помощью генераторов сигналов произвольной формы с цифро-аналоговыми преобразователями. Используемый генератор имеет характеристики, приведённые в табл. 1. Экспериментальная оценка параметров линейности ЦАП в динамическом (40 дБ) и частотном диапазоне (полоса 1 МГц) на частоте 10 МГц, проведённая с помощью анализатора спектра и вольтметра образцового 1-разряда, составляет не более 0,1% по каждому из параметров. Типичная погрешность линейности фазо-частотной характеристики ЦАП в полосе 1 МГц составляет около 0,5 градуса [2]. Таким образом, можно ожидать, что “нарисованный” с помощью этого генератора сигнал [3], будет отличаться от идеальной математической модели не более, чем на 0,3%.

Таблица 1. Характеристики генератора
Разрядность, бит	Объём памяти, Мб	Максимальная частота дискретизации, МГц
12	16	1200

Затем, с помощью ПО были созданы два реперных модулированных сигнала с несущей частотой 10 МГц и частотой модулирующего колебания 1 кГц:

амплитудно-модулированный сигнал с коэффициентом амплитудной модуляции Кам=100%,
частотно-модулированный сигнал с девиацией частоты 2,4048 кГц, что соответствует первому нулю функции Бесселя.

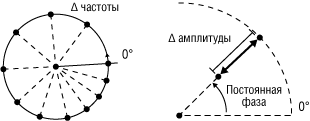
Рисунок 2. Характеристики аналоговой модуляции
на векторной диаграмме

Сигналы создавались исходя из следующих соотношений. Один период сигнала частотой 10 МГц строится по 100 точкам, т.е. используется частота дискретизации 1 ГГц. Общая длительность расчётного сигнала составляет один период модулирующего колебания 1 мс, т.е. проводятся вычисления по 1 Мб точек. Данные сигналы являются сигналами с аналоговой модуляцией, но рассчитываются в ПО по их представлению в векторном формате (рис. 2).

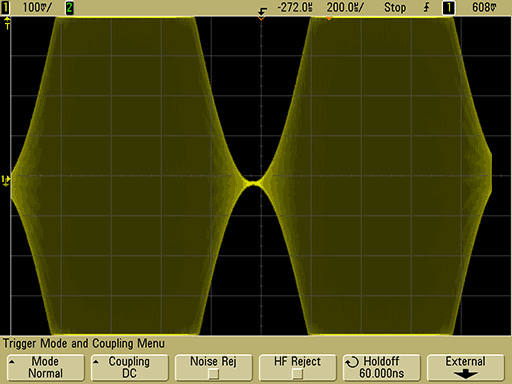
Полученные сигналы были загружены в генератор и были проведены измерения значений Кам и девиации частоты. Точка Кам = 100% устанавливалась как точка соприкосновения положительной и отрицательной частей огибающего колебания по осциллографу (рис.3), а девиация частоты определялась по обращению в ноль центральной спектральной составляющей модулированного сигнала на анализаторе спектра [4]. Погрешность установки измерялась путём изменения параметров модуляции формируемых сигналов в узкой области для установления точных соотношений по образцовым средствам измерений, где погрешность рассчитывалась как разность между номинальным значением параметра модуляции и тем, при котором наблюдалось точное соотношение. Применяемые в качестве образцовых средств измерений анализатор спектра и осциллограф имеют динамический диапазон для проведения требуемых измерений не менее 70 дБ, что обеспечивает относительную разрешающую способность не хуже 0,05%. Полученные в процессе эксперимента погрешности установки параметров модуляции не превысили 0,1%. Учитывая полученный результат, а также экспериментальные оценки параметров ЦАП, суммарная погрешность генератора и алгоритма цифровой обработки, реализованного в ПО, может быть оценена, как не превышающая 0,3%, а вклад собственной погрешности ЦОС – не более 0,1%.

Рисунок 3. Сигнал с Кам=100%
(щелчок по изображению — увеличение)

Для определения dас,ацп рассмотрим уравнение для расчёта модуля векторной ошибки (4). Как следует из уравнения, модуль векторной ошибки фактически является аналогом хорошо известного соотношения “сигнал/шум” [5]. Поэтому экспериментальное определение погрешности измерения модуля векторной ошибки может сводиться к следующей методике:

На векторный анализатор подаётся немодулированный сигнал, принимаемый за опорный R, и включается простейший демодулятор типа QPSK или FSK, результатом измерения будет являться единичная точка на диаграмме состояний.
Измерение зависимости паразитного модуля векторной ошибки от уровня входного сигнала будет давать оценку нижнего шумового предела анализатора по измерению EVM (аддитивную составляющую погрешности).
Затем в полосу несущей немодулированного сигнала добавляется шумовой сигнал известной мощности, который будет отображаться на диаграмме состояний аналогично рис. 4., при этом:

где (5)

где Vшум – напряжение шумового сигнала.

Мощность несущей и мощность шумового сигнала, пропорциональные квадратам напряжений, измеряются отдельно образцовым измерителем мощности. На основании этих результатов рассчитывается набор теоретических значений модуля векторной ошибки как корень квадратный из отношения мощностей шумового сигнала и сигнала несущей. При этом основную роль в погрешности расчёта теоретического значения будут играть погрешности измерения отношения мощностей и погрешности рассогласования, но в настоящее время они могут быть снижены до 0,2%.

Отличие измеренного значения EVM анализатором спектра от теоретического значения является погрешностью измерения EVM (мультипликативной погрешностью), т.к. по [5] погрешность измерения EVM зависит от самой величины EVM.

Рисунок 4. Отображение несущей
с шумовым сигналом на векторной диаграмме

Для практического апробирования методики использовались векторный анализатор спектра совместно с ПО, термоэлектрический измеритель мощности и генератор произвольной формы для формирования шумового сигнала полосой 1 МГц на несущей частоте 10 МГц, в качестве которой использовался собственный выход опорной частоты анализатора спектра. Результаты измерений приведены в табл. 2, при этом считается, что на частоте 10 МГц погрешность рассогласования пренебрежимо мала, а погрешность измерения отношения мощностей менее 20 дБ для термоэлектрического измерителя мощности не превышает 0,1% [6]. Ограничение измерений максимальным EVM 30% и рост погрешности связаны с тем, что используемое программное обеспечение при больших значениях в режиме отображения EVM теряет захват несущей частоты, и, по всей видимости, дальнейший анализ необходимо вести в режиме отображения I(t), Q(t).

Таблица 2. Результаты измерения погрешности EVM
EVM, %	0	10	20	30
Погрешность, %	0,12	0,35	0,43	0,8

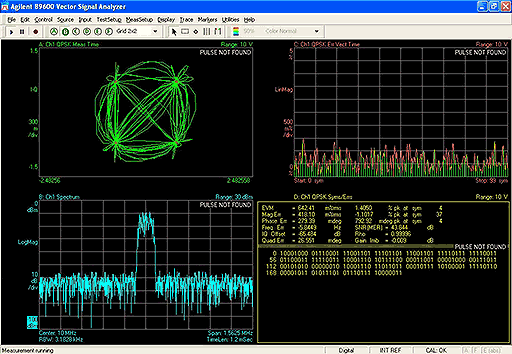
Для проверки полученных результатов с помощью ПО и генератора был сформирован реальный сигнал с векторной модуляцией на несущей 10 МГц, модуляция QPSK, скорость модуляции 100 кГц. Затем сигнал был подан на анализатор спектра и проведена демодуляция. Измеренное значение EVM составило 0,6% (рис. 5). В предположении, что вклад в полученную погрешность равномерно распределён между генератором и анализатором спектра и погрешности некоррелированы, следует, что погрешность анализатора составляет 0,3%. Это значение совпадает с результатами табл. 2 и оценками для погрешности генератора.

Рисунок 5. Результаты измерения сигнала с модуляцией QPSK
(щелчок по изображению — увеличение)

Анализ полученных результатов показывает, что погрешности измерения EVM для векторных анализаторов спектра, выпускаемых в настоящее время, ограничены снизу значением 0,3…0,5%. Причём при возрастании частоты несущей скорости модуляции (полосы модуляции) или усложнения схемы модуляции погрешность измерения будет существенно возрастать.

Полученные в работе результаты для шумового предела погрешности измерения EVM совпадают с теми типичными значениями погрешностей, которые приводят изготовители в технических характеристиках подобных средств измерений [2], а оценки мультипликативной погрешности позволяют заложить основу для их нормирования в широком диапазоне значений EVM.

Таким образом, данная методика может являться своеобразным фундаментом для построения государственной системы метрологического обеспечения измерения векторной модуляции, включая параметры аналоговой модуляции при их выражении в векторной форме. При этом измерение EVM непосредственно привязывается к измерениям мощности сигналов, для которых система метрологического обеспечения уже давно существует.

Автор выражает благодарность господину Бренту Риду за помощь в обсуждении статьи.

Литература

Vector Signal Analysis Basics. Application Note 150–15 // Agilent Technologies.
PSA Series Spectrum Analyzers 40 and 80 MHz Bandwidth Digitizers. Technical Overview // Agilent Technologies.
Пивак А.В. https://prist.ru/info/articles/kni.htm title=В статье рассмотрены методы измерения и воспроизведения напряжений с нормированным значением коэффициента гармоник, основанные на применении цифровой техники. Приведены результаты экспериментальных исследований, которые могут быть использованы при разрабо class=l>Измерение коэффициента гармоник напряжения сигнала, заданного во временной области // Мир измерений. – 2006. – № 6.
Павленко Ю.Ф., Шпаньон П.А. Измерение параметров частотно-модулированных колебаний // Москва: “Радио и связь”. – 1986.
EVM measurement design for 3G test equipment // Willtek Communication, 2003.
Перепелкин А.В. Нелинейность функции преобразования термоэлектрических преобразователей мощности СВЧ // Измерительная техника. – 1988. – №5.

Автор:
Пивак А.В. к.т.н.

Дата публикации:
07.07.2008

Источник

Definition[edit]

Dynamic EVM[edit]

See also[edit]

References[edit]

Definition[edit]

Dynamic EVM[edit]

See also[edit]

References[edit]

Теоретические основы анализа модуля вектора ошибки

Пример оптимизации: подсистема трактов ПЧ и модулирующих частот AD8348/AD8362

Заключение

Определение

Динамический EVM

Смотрите также

Ссылки

Измерение точности модулятора

Обзор

Структура

Ссылки

Измерения параметров векторной модуляции

Литература