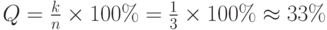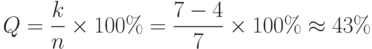Вектор ошибки синдром ошибки

Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ни...

Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.

Давайте же разберёмся, что это такое.

Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.

Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.

Каналы с ошибкой

Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.

Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем $k$ ошибок. Это будет характеристикой канала связи.

Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами ($A$, $B$, $C$, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.

Кодирование и декодирование будем обозначать прямой стрелкой ($rightarrow$), а передачу по каналу связи — волнистой стрелкой ($rightsquigarrow$). Ошибки при передаче будем подчёркивать.

Например, пусть мы хотим передавать только сообщения $A=0$ и $B=1$. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):

$ begin{aligned} A &to 0,\ B &to 1. end{aligned} $

Передача по каналу, в котором возникла ошибка будет записана так:

$ A to 0 rightsquigarrow underline{1} to B. $

Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это $0$ и $1$.

Код с утроением

Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:

$ begin{aligned} A &to 00,\ B &to 11. end{aligned} $

Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:

$ A to 00 rightsquigarrow 0underline{1} to ?. $

Какие выводы мы можем сделать, когда получили $01$? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква $B$. А может, во втором, и была передана $A$.

То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.

$ begin{aligned} A &to 000,\ B &to 111. end{aligned} $

Проверим в деле:

$ A to 000 rightsquigarrow 0underline{1}0 to A?. $

Получили $010$. Тут у нас есть две возможности: либо это $B$ и было две ошибки (в крайних цифрах), либо это $A$ и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква $A$. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.

Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква $A$.

Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.

Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.

Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.

Расстояния между кодами

Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.

И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.

Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.

Пусть мы передавали $000$, а получили $001$. Видно, что эта цепочка больше похожа на исходные $000$, чем на $111$. А так как других кодовых слов у нас нет, то и выбор очевиден.

Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.

Можно ввести некоторую величину $d(alpha, beta)$, равную количеству различающихся цифр в соответствующих разрядах цепочек $alpha$ и $beta$. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.

Например, $d(010, 010) = 0$, так как все цифры в соответствующих позициях равны, а вот $d(010101, 011011) = 3$.

Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:

  1. Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
  2. Расстояние в обе стороны одинаково.
  3. Путь через третью точку не короче, чем прямой путь.

Достаточно разумные требования.

Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):

  1. $d(x, y) geqslant 0,quad d(x, y) = 0 Leftrightarrow x = y;$
  2. $d(x, y) = d(y, x);$
  3. $d(x, z) + d(z, y) geqslant d(x, y)$.

Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.

Окрестности

Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.

Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.

Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.

Так, скажем, окрестность кодового слова $000$ радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:

$ {000, 100, 010, 001}. $

Да, вот так странно выглядят шары в пространстве кодов.

А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим $000$! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.

Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение $x$, мы получим один из кодов, который принадлежит окрестности $x$ радиусом 2.

Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.

Сколько ошибок может исправить код?

Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.

В коде с удвоением между кодовыми словами $00$ и $11$ расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.

Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.

Что интересно, точек касания в нашем странном пространстве у шаров две — это коды $01$ и $10$. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.

В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).

В общем случае получаем следующее.

Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием $d_{min}$ будет успешно работать в канале с $k$ ошибками, если выполняется соотношение

$ d_{min} geqslant 2k+1. $

Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает $k$ ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса $k$ других кодовых слов. Математически это записывается так:

$d_{min}geqslant k + 1.$

Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.

$ begin{aligned} A to 10100,\ B to 01000,\ C to 00111,\ D to 11011.\ end{aligned} $

Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.

A B C D
A — 3 3 4
B 3 — 4 3
C 3 4 — 3
D 4 3 3 —

Минимальное расстояние $d_{min}=3$, а значит $3geqslant2k+1$, откуда получаем, что такой код может исправить до $k=1$ ошибок. Обнаруживает же он две ошибки.

Рассмотрим пример:

$ A to 10100 rightsquigarrow 101underline{1}0. $

Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.

$ begin{aligned} A:, d(10110, 10100) &= 1,\ B:, d(10110, 01000) &= 4,\ C:, d(10110, 00111) &= 2,\ D:, d(10110, 11011) &= 3. end{aligned} $

Минимальное расстояние получилось для символа $A$, значит вероятнее всего передавался именно он:

$ A to 10100 rightsquigarrow 101underline{1}0 to A?. $

Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.

Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.

Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы $2^5 = 32$ варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.

Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.

Интерлюдия: поле GF(2)

Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.

Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):

$ begin{aligned} 0 + 0 &= 0,\ 0 + 1 &= 1,\ 1 + 0 &= 1,\ 1 + 1 &= 0. end{aligned} $

Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.

Множество из двух элементов ${0, 1}$ с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.

У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.

$ x + x = 0. $

Это свойство прямо следует из определения.

$ x + y = x - y. $

А в этом можно убедиться, прибавив $y$ к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.

Проверяем корректность

Вернёмся к коду с утроением.

$ begin{aligned} A &to 000,\ B &to 111. end{aligned} $

Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.

Пусть мы приняли вектор-строку $x$ из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)

$dots rightsquigarrow x = (x_1, x_2, x_3). $

Математически равенство всех трёх цифр можно записать как систему:

$ left{ begin{aligned} x_1 &= x_2,\ x_2 &= x_3. end{aligned} right. $

Или, если воспользоваться свойствами сложения в GF(2), получаем

$ left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right. $

Или

$ left{ begin{aligned} 1cdot x_1 + 1cdot x_2 + 0cdot x_3 &= 0,\ 0cdot x_1 + 1cdot x_2 + 1cdot x_3 &= 0. end{aligned} right. $

В матричном виде эта система будет иметь вид

$ Hx^T = 0, $

где

$ H = begin{pmatrix} 1 & 1 & 0\ 0 & 1 & 1 end{pmatrix}. $

Транспонирование здесь нужно потому, что $x$ — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.

Будем называть матрицу $H$ проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.

Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.

Кодирование

Итак, у нас есть система для проверки

$ left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right. $

Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице $H$) найдём кодовые слова.

Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:

$ H = begin{pmatrix} 1 & 0 & 1 & 0 & 0 \ 0 & 1 & 1 & 0 & 1\ 0 & 0 & 0 & 1 & 1 end{pmatrix}. $

Соответствующая система имеет вид:

$ left{ begin{aligned} x_1 + x_3 &= 0,\ x_2 + x_3 + x_5 &= 0,\ x_4 + x_5 &= 0. end{aligned} right. $

Чтобы найти кодовые слова соответствующего кода нужно её решить.

В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если $a$ и $b$ — решения системы, то для их суммы верно

$H(a+b)^T=Ha^T+Hb^T=0+0=0,$

что означает, что она тоже — решение.

Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.

Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить $x_1, x_2, x_4$.

Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.

Итак, получаем:

$ left{ begin{aligned} x_1 &= x_3,\ x_2 &= x_3 + x_5,\ x_4 &= x_5. end{aligned} right. $

Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.

$ begin{aligned} x_3=1, x_5=0:quad x_1=1, x_2=1, x_4=0 Rightarrow x^{(1)} = (1, 1, 1, 0, 0),\ x_3=0, x_5=1:quad x_1=0, x_2=1, x_4=1 Rightarrow x^{(2)} = (0, 1, 0, 1, 1). end{aligned} $

Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:

$ a_1 x^{(1)}+a_2 x^{(2)}, $

где $a_1, a_2$ равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно $2^2=4$ сочетания.

Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.

$ (a_1, a_2)cdot begin{pmatrix} 1 & 1 & 1 & 0 & 0 \ 0 & 1 & 0 & 1 & 1 end{pmatrix} = aG. $

Строчки здесь — линейно независимые решения, которые мы получили. Матрица $G$ называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:

$ a to aG. $

Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)

$ begin{aligned} 00 &to 00000,\ 01 &to 01011,\ 10 &to 11100,\ 11 &to 10111. end{aligned} $

Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?

$ a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to Hx^T = (110)^T neq 0. $

А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!

Для кода с утроением, кстати, порождающая матрица выглядит очень просто:

$G=begin{pmatrix}1&1&1end{pmatrix}.$

Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.

Ошибка по синдрому

Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!

Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение $x$, а было отправлено кодовое слово $v$. Тогда вектор ошибки по определению

$ e = x - v. $

Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:

$ begin{aligned} v &= x + e,\ x &= v + e. end{aligned} $

В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.

Как мы уже говорили раньше, если мы получили сообщение $x$ с ошибкой, то $Hx^Tneq 0$. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?

Назовём результат умножения на проверочную матрицу синдромом:

$ s(x)=Hx^T.$

И заметим следующее

$ s(x) = Hx^T = H(v+e)^T = He^T = s(e). $

Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.

Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?

А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.

Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.

$s(x)$ $x$
$000$ $underline{00000}, 11100, 01011, 10111$
$001$ $underline{00010}, 11110, 01001, 10101$
$010$ $underline{01000}, 10100, 00011, 11111$
$011$ $01010, 10110, underline{00001}, 11101$
$100$ $underline{10000}, 01100, 11011, 00111$
$101$ $underline{10010}, 01110, 11001, underline{00101}$
$110$ $11000, underline{00100}, 10011, 01111$
$111$ $11010, underline{00110}, underline{10001}, 01101$

В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.

Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.

Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.

$ a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to s(x)=Hx^T = (110)^T to e=(00100). $

Вектор ошибки равен $(00100)$, а значит ошибка в третьем разряде. Как мы и загадали.

Ура, всё работает!

Что же дальше?

Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.

Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.

Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.

Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.

Источник

Вычисление
синдрома для циклических кодов является
довольно простой процедурой.

Пусть
U(x)
и r(х)
‑
полиномы, соответствующие переданному
кодовому слову и принятой последовательности.

Разделив
r(x)
на g(x),
получим

r(x)
= q(x)
g(x)
+ s(x),
(1.73)

где
— q(x)
— частное от деления, s(x)
— остаток от деления.

Если
r(x)
является кодовым полиномом, то он делится
на g(x)
без остатка, то есть s(x)
= 0.

Следовательно,
s(x)

0
является условием наличия ошибки в
принятой последовательности, то есть
синдромом принятой последовательности.

Синдром
s(x)
имеет в общем случае вид

S(x)
= S0
+ S1

x + … + Sn-
k-1
xn-k-1
. (1.74)

Очевидно,
что схема вычисления синдрома является
схемой деления, подобной схемам
кодирования рис. 1.10 или 1.11 .

При
наличии в принятой последовательности
r

хотя бы одной ошибки вектор синдрома S
будет иметь, по крайней мере, один
нулевой элемент, при этом факт наличия
ошибки легко обнаружить, объединив по
ИЛИ
выходы всех ячеек регистра синдрома.

Покажем,
что синдромный многочлен S(x)
однозначно связан с многочленом ошибки
e(x),
а
значит, с его помощью можно не только
обнаруживать, но и локализовать ошибку
в принятой последовательности.

Пусть

e(x)
= e0
+ e1

x
+ e2

x2
+ … + en-1

x
n-1
(1.75)

— полином
вектора ошибки.

Тогда
полином принятой последовательности

r(x)
= U(x)
+ e(x).
(1.76)

Прибавим
в этом выражении слева и справа U(x),
а также учтем, что

r(x)
= q(x)
g(x) + S(x), U(x) = m(x)
g(x), (1.77)

тогда


,
(1.78)

то
есть синдромный
полином S(x)
есть
остаток от
деления полинома ошибки e(x)
на порождающий полином g(x).

Отсюда следует, что по синдрому S(x)
можно однозначно определить вектор
ошибки e(x), а следовательно,
исправить эту ошибку.

На рис. 1.14 приведена схема синдромного
декодера с исправлением однократной
ошибки для циклического (7,4)-кода.
По своей структуре она подобна схеме,
приведенной на рис. 1.6, с той лишь разницей,
что вычисление синдрома принятой
последовательности производится здесь
не умножением на проверочную матрицу,
а делением на порождающий полином. При
этом она сохраняет и недостаток, присущий
всем синдромным декодерам: необходимость
иметь запоминающее устройство, ставящее
в соответствие множеству возможных
синдромов S множество векторов
ошибок e. Цикличность структуры
кода в этом случае не учитывается.

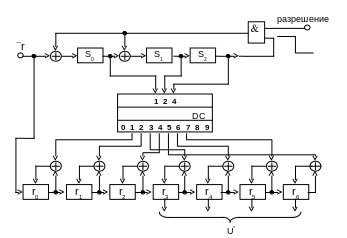
Рис.
1.14

1.3.4. Неалгебраические методы декодирования циклических кодов

Все
методы декодирования линейных блочных
кодов можно разбить на две группы:
алгебраические
и неалгебраические.

В
основе алгебраических методов лежит
решение систем уравнений, задающих
значение и расположение ошибок.
Рассмотренные синдромные декодеры
относятся именно к этой группе методов.

При
неалгебраических методах та же цель
достигается с помощью простых структурных
понятий теории кодирования, позволяющих
находить комбинации ошибок более простым
путем.

Одним
из неалгебраических методов является
декодирование с использованием алгоритма
Меггитта,
пригодного для исправления как одиночных,
так и l-кратных
ошибок (на практике l

3).

При
декодировании в соответствии с алгоритмом
Меггитта также вычисляется синдром
принятой последовательности S(x),
однако используется он иначе, нежели в
рассмотренных ранее синдромных декодерах.

Идея,
лежащая в основе декодера Меггитта,
очень проста и основывается на следующих
свойствах циклических кодов:

—
существует взаимно-однозначное
соответствие между множеством всех
исправляемых ошибок и множеством
синдромов;

—
если S(x)
— синдромный многочлен, соответствующий
многочлену ошибок е(x),

то xS(x)
mod
g(x)
— синдромный многочлен, соответствующий
x
e(x) mod (xn
+ 1).

Равенство
а(x)
= b(x) mod p(x)
читается как “а(x),
сравнимо с b(x)
по модулю р(x)”
и означает, что а(x)
и b(x)
имеют одинаковые остатки от деления на
полином p(x).

Таким
образом, второе
условие
означает, что если
комбинация ошибок циклически сдвинута
на одну позицию вправо, то для получения
нового синдрома нужно сдвинуть содержимое
регистра сдвига с обратными связями,
содержащего S(x),

также на одну позицию вправо.

Следовательно,
основным
элементом декодера Меггитта является
сдвиговый регистр. Структурная схема
декодера Меггитта для циклических кодов
произвольной длины приведена
на рис. 1.15.

Рис.
1.15

Декодер
работает следующим образом. Перед
началом работы содержимое всех разрядов
регистров равно нулю. Принимаемая
последовательность r
в
течение первых n
тактов вводится в буферный регистр и
одновременно с этим в (n—k)-разрядном
сдвиговом регистре с обратными связями
производится ее деление на порождающий
полином g(x).

Через
n
тактов
в буферном регистре оказывается принятое
слово r
,
a в регистре синдрома — остаток от
деления вектора ошибки на порождающий
полином.

Вычисленный
синдром сравнивается со всеми табличными
синдромами, и в случае совпадения с
одним из них старший разряд буферного
регистра исправляется путем прибавления
к его значению единицы.

После
этого синдромный и буферный регистры
один раз циклически сдвигаются. Это
реализует умножение S(x)
на
x
и деление на g(x).
Содержимое ячеек синдромного регистра
теперь равно остатку от деления xS(x)
на g(x)
или синдрому ошибки x
е(x) mod (Хn
+ 1).

Если
новый синдром совпадает с одним их
табличных, то исправляется очередная
ошибка и т.д. Через n
тактов
все позиции будут, таким образом,
исправлены.

Рассмотрим
работу декодера Меггитта для циклического
(7,4)-кода,
исправляющего одиночную ошибку. Схема
декодера изображена на рис. 1.16.

Рис.
1.16

Принцип
работы декодера заключается в том, что
независимо
от того, в какой позиции произошла
ошибка, осуществляется ее сдвиг в
последнюю ячейку буферного регистра с
соответствующим пересчетом синдрома
и ее исправление в этой позиции.

Полином
ошибки в старшем разряде для (7,4)-кода
Хемминга имеет вид е6
(x)
= x6,
соответствующий ему синдромный полином
S6
(x)
= 1 + x3
(
S
= (101)),
детектор ошибки настроен на это значение
синдрома.

Пусть,
например, передана последовательность
U
= (1001011),
ей соответствует кодовый полином U(x)
= 1 + x3
+ x5
+ x6.
Произошла ошибка в третьей позиции е(x)
= x3,
принятый вектор имеет вид r
= (1000011),
его полином r(x)
= 1 + x5
+ x6.

Kогда
принятая последовательность полностью
входит в буферный регистр, в регистре
синдрома оказывается синдром,
соответствующий ошибке е(x)
= x3
S3
= (110).
Поскольку он не совпадает с табличным
для е6,
на выходе детектора ошибок будет 0
и исправления не происходит.

Далее
производятся однократный циклический
сдвиг принятой последовательности в
буферном регистре, однократное деление
синдрома x∙S3
на порождающий полином в регистре с
обратными связями и проверка на совпадение
синдрома с заданным.

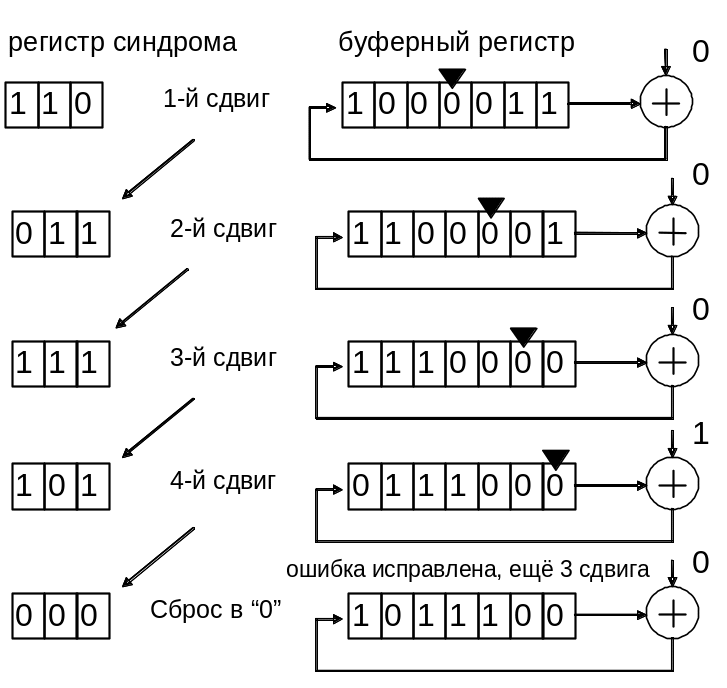
Последовательность
состояний регистров декодера в процессе
декодирования показана на рис. 1.17.

Рис.
1.17

Т
аким
образом, исправление ошибки в декодере
Меггитта осуществляется за 2n
тактов: в течение n
тактов производится ввод принятой
последовательности в буферный регистр,
в течение l
тактов
— исправление ошибки, и еще в течение
n
— l
— восстановление
буферного регистра в исходное состояние
с исправленным словом. Простота декодера
достигается увеличением времени
декодирования.

Следует
отметить, что в связи с успехами в
разработке БИС и устройств памяти в
значительной степени снимается вопрос
о размерах таблиц, связывающих значения
синдрома и вектора ошибки (для синдромных
декодеров) и даже значения кодовых слов
и принятых последовательностей (для
декодера максимального правдоподобия).
Поэтому в перспективе возможно снижение
интереса к кодам, обладающим специальной
структурой, и к методам их декодирования.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #

    10.06.2015684.82 Кб13P4.pdf

  • #
  • #
  • #
  • #
Источник

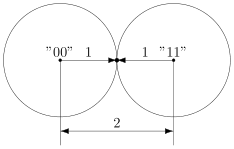
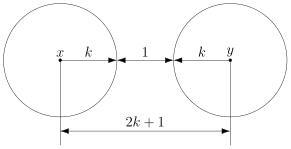
Минимальное расстояние между допустимыми словами кода с контролем по четности равно двум (из
рис.
14.2 видно, что никакие два кодовых слова в рамочках не соединены линиями, то есть не являются соседними). Именно по этой причине одиночная ошибка в кодовом слове превращает это слово в недопустимое.

Платой за помехоустойчивость является необходимость увеличения длины слов по сравнению с обычным кодом. В данном примере только два разряда являются информационными. Это они образуют четыре разных слова. Третий разряд является контрольным и служит только для увеличения расстояния между допустимыми словами. В передаче информации контрольный разряд не участвует, так как является линейно зависимым от информационных. Код с контролем по четности, рассмотренный в качестве примера, позволяет обнаружить одиночные ошибки в блоках данных при передаче данных. Однако он не сможет обнаружить двукратные ошибки потому, что двукратная ошибка переводит кодовое слово через промежуток между допустимыми словами и превращает его в другое допустимое слово.

Таким образом, для того чтобы код приобрел способность к обнаружению и коррекции ошибок, необходимо отказаться от его безызбыточности. Для этого и разделяют всё множество возможных комбинаций двоичных символов на два подмножества: допустимых кодовых слов и недопустимых. Разбиение осуществляется таким образом, чтобы увеличить минимальное кодовое расстояние между допустимыми словами. В этом случае любая однократная ошибка превращает допустимое кодовое слово в недопустимое, что позволяет её обнаружить.

Естественно, что введение дополнительных контрольных разрядов увеличивает затраты на хранение или передачу кодированной информации. При этом фактический объем полезной информации остается неизменным. В этом случае можно говорить об избыточности помехоустойчивого кода, которую формально можно определить как отношение числа контрольных разрядов к общему числу разрядов кодового слова.

Мы уже отмечали, что контрольные разряды не передают информацию и в этом смысле бесполезны. Относительное число контрольных разрядов называется избыточностью Q помехоустойчивого кода

Q=frac {k}{n}times 100%

где n – общее число двоичных разрядов в блоке, а k – число контрольных разрядов.

Например, избыточность рассмотренного трехразрядного кода с контролем по четности составляет:

Q=frac {k}{n}times 100%=frac{1}{3}times 100% approx 33%

Избыточность является важной характеристикой кода, причем чрезмерное увеличение избыточности нежелательно. Важной задачей теории информации является синтез кодов с минимальной избыточностью, обеспечивающих заданную обнаруживающую и корректирующую способность.

В качестве иллюстрирующего примера рассмотрим один из простейших кодов, позволяющих обнаруживать и исправлять однократные ошибки – код Хэмминга. Кодовое слово длиной n содержит k информационных и m контрольных разрядов. Коррекция искаженного i-го разряда заключается в сложении (по модулю 2) принятого кодового слова с вектором вида 0…010…0, содержащем единицу в i-ом разряде.

Для n-разрядного кодового слова существует n таких векторов, соответствующих однократным ошибкам, и один нулевой вектор, соответствующий случаю приема слова без ошибок. Таким образом, m контрольных разрядов должны обеспечивать формирование n + 1 вектора ошибки, то есть должно выполняться неравенство n le 2^m -1. В результате получается (2m-1, 2m-1-m) код, называемый кодом Хэмминга.

Простейший нетривиальный случай, соответствующий m=3, образует (7,4)-код, который можно синтезировать следующим образом. Сопоставим каждому вектору ошибки порядковый номер – синдром (
таблица
14.1). При этом нулевому вектору ошибки соответствует нулевой синдром.

Таблица
14.1.
Векторы ошибок и соответствующие им синдромы

a6 a5 a4 a3 a2 a1 a0 s2 s1 s0
1 0 0 0 0 0 0 0 1 1
0 1 0 0 0 0 0 1 0 1
0 0 1 0 0 0 0 1 1 0
0 0 0 1 0 0 0 1 1 1
0 0 0 0 1 0 0 1 0 0
0 0 0 0 0 1 0 0 1 0
0 0 0 0 0 0 1 0 0 1
0 0 0 0 0 0 0 0 0 0

Рассматривая функции si как свертку по модулю 2 разрядов кодовых слов, получим:

s_0=a_0 bigoplus a_3 bigoplus a_5 bigoplus a_6 \ s_1=a_1 bigoplus a_3 bigoplus a_4 bigoplus a_6 \ s_2=a_2 bigoplus a_3 bigoplus a_4 bigoplus a_5

Функции si должны обращаться в единицу при наличии ошибки в одном из образующих их разрядов, и в ноль – при отсутствии ошибок. Обеспечение этого требования возможно лишь при условии, что часть разрядов формируется специальным образом. В частности, разряды a0, a1, a2 можно рассматривать как свертку по модулю 2 остальных разрядов, участвующих в соответствующих уравнениях:

a_0=a_3 bigoplus a_5 bigoplus a_6 \ a_1= a_3 bigoplus a_4 bigoplus a_6 \ a_2=a_3 bigoplus a_4 bigoplus a_5

Найденные зависимости позволяют генерировать кодовые слова по заданным информационным, а также вычислять синдромы для принятых кодовых слов.

Допустим, исходное информационное слово равно 1101, то есть a6=1, a5=1, a4=1, a3=1. Для преобразования его в допустимое кодовое слово помехоустойчивого (7,4) —кода Хэмминга рассчитаем контрольные разряды по найденным выше зависимостям. В частности,

a_1=1 bigoplus 0 bigoplus 1=1 \ a_1= 1 bigoplus 0 bigoplus 1=0 \ a_2=1 bigoplus 0 bigoplus 1=0

Таким образом, с учетом контрольных разрядов кодовое слово будет равно 1101001.

Если в процессе передачи или хранения слово осталось неискаженным, то его синдром s0…s2 будет соответственно равен: 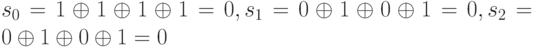s_0 = 1 oplus 1 oplus 1 oplus 1 = 0, s_1 = 0 oplus 1 oplus 0 oplus 1 = 0, s_2 = 0 oplus 1 oplus 0 oplus 1 = 0,. Синдром, состоящий из одних нулей, указывает на отсутствие ошибки и соответствует нулевому вектору ошибки.

Предположим, что в процессе передачи или хранения в результате воздействия внешних факторов оказался искаженным отдельный разряд кодового слова. Например, вместо слова 1101001 было принято слово 1001001. В этом случае синдром окажется отличным от нуля: s0…s2 будет соответственно равен: 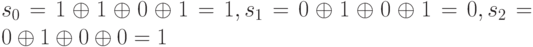s_0 = 1 oplus 1 oplus 0 oplus 1 = 1, s_1 = 0 oplus 1 oplus 0 oplus 1 = 0, s_2 = 0 oplus 1 oplus 0 oplus 0 = 1 Синдром 101 соответствует вектору ошибки 0100000, при этом единица указывает на разряд, в котором эта ошибка произошла. Для ее коррекции достаточно сложить по модулю 2 принятое искаженное кодовое слово с вектором ошибки.

Рассчитаем избыточность (7,4) —кода Хэмминга:

Q=frac {k}{n}times 100%=frac{7-4}{7}times 100% approx 43%

Это очень большое значение. На практике часто применяются существенно более сложные коды, обеспечивающие лучшие характеристики помехоустойчивости при меньшей избыточности.

Источник

Материал из Национальной библиотеки им. Н. Э. Баумана
Последнее изменение этой страницы: 00:05, 25 мая 2017.

Содержание

  • 1 Базовые понятия помехоустойчивого кодирования и декодирования
    • 1.1 Принцип построения помехоустойчивых кодов
    • 1.2 Основные параметры помехоустойчивых кодов
    • 1.3 Оценочные соотношения для параметров помехоустойчивых кодов
  • 2 Линейное блочное кодирование
    • 2.1 Способы задания линейных кодов
    • 2.2 Строение декодера линейного кода
  • 3 Циклические коды
    • 3.1 Устройство кодеров циклического кода
    • 3.2 Коды Хэмминга
    • 3.3 Коды БЧХ
    • 3.4 Мажоритарные коды
  • 4 Итеративные коды
  • 5 Каскадные коды
  • 6 Непрерывные сверточные коды
    • 6.1 Основные параметры сверточных кодов
    • 6.2 Устройство кодера сверточного кода
    • 6.3 Виды и способы задания сверточных кодов
    • 6.4 Методы декодирования сверточных кодов
      • 6.4.1 Декодирование с вычислением проверочной последовательности
      • 6.4.2 Декодирование по принципу максимума правдоподобия
        • 6.4.2.1 Алгоритм Витерби
        • 6.4.2.2 Устройство декодера Витерби
  • 7 Применение кодов в технических системах
    • 7.1 Системы с обратной связью
    • 7.2 Сигнально-кодовые конструкции
    • 7.3 Методы приема сигналов
      • 7.3.1 Прием «в целом»
      • 7.3.2 Прием по наиболее надежным символам
  • 8 См. также

Базовые понятия помехоустойчивого кодирования и декодирования

Кодированием и декодированием (в широком смысле) называют любое преобразование сообщения в сигнал и обратно, сигнала в сообщение, путем установления взаимного соответствия. Преобразование следует считать оптимальным, если в конечном итоге производительность источника и пропускная способность канала окажутся равными, т.е. возможности канала будут полностью использованы. Данное преобразование разбивается на два этапа:

  • модуляция-демодуляция, позволяющая осуществить переход от непрерывного сигнала радиоканала к дискретному;
  • кодирование-декодирование (в узком смысле), во время которого все операции выполняются над последовательностью символов.

В свою очередь, кодирование-декодирование делится на два противоположных по своим действиям действиям этапа:

  • устранение избыточности в принимаемом от источника сигнале (экономное кодирование);
  • внесение избыточности в передаваемый по каналу цифровой сигнал (помехоустойчивое или избыточное кодирование) для повышения достоверности передаваемой информации.

Экономное кодирование направлено на то, чтобы передаваемый дискретный сигнал имел максимальную энтропию, т.е. максимальное среднее количество инфорации на символ. Тогда для его передачи по радиоканалу с выбранным модемом потребуется минимальная полоса частот. Основное свойство дискретного сигнала, в котором полностью устранена избыточность, — равная вероятность и независимость их появления в последовательности. В этом случае среднее количество информации на символ равно .

Примером экономного кодирования является передача речевого сигнала по цифровым каналам. Если ориентироваться только на смысловое (семантическое) содержание, то можно перейти к передаче текста со скоростью 5…10 букв в секунду. С учетом объема алфавита в двоичном канале это потребует скорость передачи 25…50 бит/с. Если устранить избыточность, связанную с неодинаковой вероятностью появления букв и их корреляцией в тексте, то, как показывают расчеты, скорость передачи может быть уменьшена до 10 бит/с. Если передавать речь в цифровой форме, используя аналого-цифровое преобразование, ориентируясь только на ширину спектра и динамический диапазон, то скорость потока двоичных символов составит 32…64 кбит/с. Такая избыточность привела к необходимости разработки специальных кодеков речевых сигналов, называемых вокодерами, которые нашли применение при передаче речи в цифровой форме по радиоканалам. Например, в сотовых системах мобильной связи стандарта GSM скорость передачи составляет 8,5 кбит/с, причем сохраняются не только семантическое содержание, но и индивидуальные особенности говорящего. Подобные кодеки находят применение и при передаче подвижных и неподвижных изображений в цифровых телевизионных каналах.

Принцип построения помехоустойчивых кодов

При помехоустойчивом кодировании в поток передаваемых символов вводятся дополнительные (избыточные) символы для исправления возникающих на приемной стороне ошибок. Это требует увеличения скорости передачи по каналу, что при выбранном типе модема эквивалентно расширению полосы частот сигнала и уменьшению энергии посылки. Поэтому может возникнуть правомерный вопрос о целесообразности использования избыточного кодирования. На этот вопрос дает ответ теорема Шеннона о пропускной способности непрерывного канала связи, из которой следует, что пропускная способность непрерывного канала увеличивается с расширением его полосы, но при оптимальном (в широком смысле) кодировании. Поэтому следует ожидать повышения достоверности передачи при заданной скорости и отношении сигнал/шум в канале при внесении избыточности. Однако не существует оптимального кодека для сообщения, не фиксированного по длительности. Тем не менее, избыточное кодирование стало широко применяться в целях повышения качества передачи, преимущественно в последние десятилетия, когда проблема создания сложных вычислительных устройств в малых габаритах была практически решена.
Рассмотрим принципы кодирования на примере двоичного канала. Допустим, что источник обладает максимальной производительностью. Тогда обязательным условием внесения избыточности является увеличение числа переданных посылок за единицу времени по сравнению с их числом, поступающим от источника. Тип кода определяет принцип, по которому вносятя избыточные символы. В простейшем случае, группе из k символов источника ставится в соответствие n символов, передаваемых по каналу. Такой код называется блочным и записывается условно как (n , k)-код. Возможно также использование непрерывных кодов, характеризующихся тем, что операции кодирования и декодирования производятся над непрерывной последовательностью символов без разбиения на блоки.
Рассмотрим принципы помехоустойчивого кодирования на примере блочного двоичного кода. Если к символам источника добавляются избыточные символы, то код называют систематическим. Если группе информационных символов ставится в соответствие новая группа символов, передаваемая по каналу, в которой информационных символов в явном виде нет, то код называется неразделимым.
Требуется построить такой кодек, чтобы при фиксированной избыточности:

где r — число проверочных символов для разделимого кода, достоверность передачи была бы максимальной.

При передаче безызбыточным примитивным кодом с числом разрядов k в каждом слове все комбинаций являются разрешенными, и ошибка хотя бы в одном символе приводит к тому, что одна разрешенная комбинация переходит в другую, а, следователльно, происходит ошибка в приеме сообщения.
Введение избыточных символов приводит к тому, что полное число комбинаций увеличивается и становится равным , причем часть из них (N-Np) являются запрещенными и могут возникать только тогда, когда в канале происходят ошибки. Этот факт положен в основу обнаружения и исправления ошибок.

Основные параметры помехоустойчивых кодов

Введем понятие кодового расстояния. Предварительно отметим, что для оценки отличия одной кодовой комбинации от другой можно использовать расстояние Хэмминга , определяемое числом разрядов, в которых одна кодовая комбинация отличается от другой. Для двоичного кода:

где и — k-е символы кодовых комбинаций соответственно.

Наименьшее расстояние Хэмминга для данного кода называется кодовым расстоянием. Далее будем его обозначать через d.
При независимых ошибках в канале корректирующую способность кода удается выразить через кодовое расстояние. Пусть имеется код с d = 1. Учитывая, что искажение одного символа изменяет расстояние Хэмминга на одну единицу, при применении кода с d = 1
обнаруживаются не все одиночные ошибки. Для того чтобы код мог обнаруживать любую одиночную ошибку, необходимо обеспечить кодовое расстояние, равное двум. Рассуждая аналогичным образом, получаем, что для обнаружения всех ошибок кратности l требуется код с .
Для исправления всех ошибок некоторой кратности требуется большее кодовое расстояние, чем для их обнаружения. Если кратность исправляемых ошибок равна l, то кодовое расстояние должно удовлетворять условию .
Очевидно, что кодовое расстояние между разрешенными комбинациями можно сделать тем больше, чем больше избыточность. Однако при этом уменьшается длительность посылок и возрастает вероятность ошибок при их приеме. Поэтому вводят понятие эффективности избыточного кодирования как отношение вероятностей ошибочного приема кодовой комбинации из к информационных символов при передаче их примитивным и избыточным кодами:

Если код примитивный, то ошибка возникает, когда хотя бы в одном символе при приеме произошла ошибка. Вероятность такого события равна:

P(k) = 1-(1-Pош.пkPош.п

где Рош.п — вероятность ошибки в приеме одного символа при передаче сообщения примитивным кодом.

Для избыточного кода ошибка в приеме кодовой комбинации будет иметь место тогда, когда число ошибок превысит исправляющую способность кода tи и ее вероятность:

P(n,k) = ош.и(1 — Pош.и

где Рош.п — вероятность ошибки в приеме одного символа при передаче избыточным кодом.

Различие в Рош.п и Рош.и определяется уменьшением длительности посылки при передаче избыточным кодом в n/k раз. Величины Рош.п и Рош.и могут быть найдены, если известен вид модуляции и демодуляции, отношение P0 / N0 и длительность посылок источника.

Оценочные соотношения для параметров помехоустойчивых кодов

Задача построения кода с заданной корректирующей способностью сводится к обеспечению необходимого кодового расстояния при введении избыточности. При этом желательно, чтобы число используемых проверочных символов было минимальным.
Задача определения минимального числа проверочных символов, необходимых для обеспечения заданного кодового расстояния, не решена. Имеется лишь ряд оценок для максимального кодового расстояния при фиксированных n / k, которые часто используются для выяснения того, насколько построенный код близок к оптимальному.
Можно показать, что если существует блочный линейный код (n, k), то для него справедливо неравенство:

Выражение (1) называется верхней границей Хэмминга.
Граница Хэмминга (1) близка к оптимальной для кодов с большими значениями n / k. Для кодов с малыми значениями n / k более точной вляется верхняя граница Плоткина:

Можно также показать, что существует блочный линейный (n , к)-код с кодовым расстоянием d, для которого справедливо неравенство:

называемое нижней границей Варшамова—Гильберта.
Таким образом, границы Хэмминга и Плоткина являются необходимыми условиями существования кода, а граница Варшамова—Гильберта — достаточным. Эти границы позволяют оценить эффективность блочных кодов и целесообразность их применения.

Линейное блочное кодирование

Линейным блочным (n,k) — кодом называется множество N последовательностей длины n над GF(q), называемых кодовыми словами, которое характеризуется тем, что сумма двух кодовых слов является кодовым словом, а произведение любого кодового слова на элемент поля также является кодовым словом. Таким образом, линейный (n, k)-код можно получить из к линейно независимых кодовых комбинаций путем их посимвольного суммирования по модулю 2 в различных сочетаниях. Исходные линейно независимые кодовые комбинации называются базисными.

Способы задания линейных кодов

Представим базисные кодовые комбинации в виде ()-матрицы:

В теории кодирования матрица G называется порождающей. Тогда процесс кодирования заключается в выполнении операции:

где А — вектор размерности k, соответствующий сообщению;

В — вектор размерности n, соответствующий кодовой комбинации.

Порождающая матрица (1) содержит всю необходимую для кодирования информацию. Она должна храниться в памяти кодирующего устройства. Для двоичного кода объем памяти равен двоичных символов. При табличном задании кода кодирующее устройство должно запоминать двоичных символов.
Две порождающие матрицы, отличающиеся друг от друга только порядком расположения столбцов, задают коды, которые имеют одинаковые расстояния Хэмминга между соответстствующими кодовыми комбинациями, а следовательно, одинаковые корректирующие способности. Такие коды называются эквивалентными.
В качестве базисных комбинаций часто выбирают кодовые комбинации, содержащие по одной единице среди информационных символов. При этом порождающую матрицу (1) удается записать в канонической форме:

где I — единичная ( )-подматрица;

Р — ()- подматрица проверочных символов, определяющая свойства кода.

Матрица задает систематический код. Можно показать, что для любого линейного кода существует эквивалентный систематический код.
Линейный (n, k)- код может быть задан так называемой проверочной матрицей Н размерности (). При этом некоторая комбинация В принадлежит коду только в том случае, если вектор В ортогонален всем строкам матрицы H, т. е. если выполняется равенство:

где T — символ транспонирования матрицы.

Поскольку равенство справедливо для любой кодовой комбинации, то:

Если принятая кодовая комбинация совпадает с одной из разрешенных В (это имеет место тогда, когда либо ошибки в принятых символах отсутствуют, либо при действии помех одна разрешенная кодовая комбинация переходит в другую), то:

где S — вектор размерности (), называемый синдромом;

— вектор принятой кодовой комбинации.

В противном случае S не равно 0, причем вид синдрома зависит только от вектора ошибок е. Действительно:

где В — вектор, соответствующий передаваемой кодовой комбинации.

При S = 0 декодер принимает решение об отсутствии ошибок, а при S0 — о наличии ошибок. Число различных синдромов, соответствующих разным сочетаниям ошибок, равно . По конкретному виду синдрома можно (в пределах корректирующей способности кода) указать на ощибочные символы и исправить их.

Строение декодера линейного кода

Декодер линейного кода (рис. 1) состоит из k-разрядного сдвигающего регистра, (n — k) блоков сумматоров по модулю 2, схемы сравнения, анализатора ошибок и корректора. Регистр служит для запоминания информационных символов принятой кодовой последовательности, из которых в блоках сумматоров формируются проверочные символы. Анализатор ошибок по конкретному виду синдрома, получаемого в результате сравнения формируемых на приемной стороне и принятых проверочных символов, определяет места ошибочных символов. Исправление информационных символов проводится в корректоре.

Рис. 1. Структурная схема декодера линейного кода

Заметим, что в общем случае,при декодировании линейного кода с исправлением ошибок, в памяти декодера должна храниться таблица соответствий между синдромами и векторами ошибок, содержащая строк. С приходом каждой кодовой комбинации декодер должен перебрать всю таблицу. При небольших значениях (n — k) эта операция не вызывает затруднений. Однако для высокоэффективных кодов длиной n, равной нескольким десяткам, разность (n — k) принимает такие значения, что перебор таблицы из строк оказывается практически невозможным. Например, для кода, имеющего кодовое расстояние d = 5, таблица состоит из строк.
При заданных значениях n и k существует линейных кодов. Задача заключается в выборе наилучшего (с позиции того или иного критерия) кода. Следует заметить, что до сих пор общие методы синтеза оптимальных линейных кодов не разработаны.

Циклические коды

Циклические коды относятся к классу линейных. Поэтому для их построения достаточно знать порождающую матрицу.
Несмотря на это, можно указать другой, более простой способ построения циклических кодов, основанный на представлении кодовых комбинаций многочленами b(х) вида:

где — символы кодовой комбинации.

Над данными многочленами можно проводить все алгебраические действия с учетом того, что сложение здесь осуществляется по модулю 2.
Каждый циклический (n,k) — код характеризуется так называемым порождающим многочленом. Им может быть любой многочлен р(х) степени (n-k), который делит без остатка двучлен (). Циклические коды характеризуются тем, что многочлены b(х) кодовых комбинаций делятся без остатка на р(х). Поэтому процесс кодирования сводится к нахождению по известным многочленам а(х) и р(х) многочлена b(х), делящегося на р(х), где а(х) — многочлен степени (k—1), соответствующий информационной последовательности символов.
Очевидно, что в качестве многочлена b(х) можно использовать произведение а(х) и р(х). Однако при этом код оказывается несистематическим, что затрудняет процесс декодирования. Поэтому на практике, в основном, применяется следующий метод нахождения многочлена b(х).
Умножим многочлен а(х) на () и полученное произведение разделим на р(х). Пусть:

где m(х) — частное;

с(х) — остаток.

Поскольку операции суммирования и вычитания по модулю 2 совпадают, то выражение (9) перепишем в виде:

Из соотношения (10) следует, что многочлен делится нa р(х) и, следовательно, является искомым.
Многочлен имеет следующую структуру: первые (n — k) членов низшего порядка равны нулю, а коэффициенты остальных совпадают с соответствующими коэффициентами информационного многочлена а(х). Многочлен с(х) имеет степень меньше (n — k). Таким образом, в найденном многочлене b(х) коэффициенты при х в степени (n — k) и выше совпадают с информационными символами, а коэффициенты при остальных членах, определяемые многочленом с(х), совпадают с проверочными символами.
В соответствии с формулой процесс кодирования заключается в умножении многочлена а(х) на и нахождении остатка от деления на р(х) с последующим его сложением по модулю 2 с многочленом .
Операции умножения и деления многочленов легко осуществляются линейными цепями на основе сдвигающих регистров. В качестве иллюстрации на рис. 2, а представлена схема умножения многочлена b(x) степени n = 6 на многочлен по модулю .

Рис. 2. Схемы умножения (а) и деления (б) многочленов (частный случай)

На рис. 2 видно,что после семи тактов в регистре записывается многочлен . При делении многочлена b(х) степени n = 6 на многочлен (рис. 2, б) после семи тактов в регистре оказывается записанным остаток от деления.

Устройство кодеров циклического кода

На основе приведенных схем умножения и деления многочленов строятся кодирующие устройства для циклических кодов. На рис. 3 в качестве примера приведена схема кодера для (7, 4) — кода с порождающим многочленом . В исходном состоянии ключи и находятся в положении 1. Информационные символы поступают одновременно на вход канала и на выход ячейки сдвигающего регистра (это соответствует умножению многочлена а(х) на ). В течение четырех тактов происходит деление многочлена на многочлен . В результате в регистре записывается остаток, представляющий собой проверочные символы. Ключи и перебрасываются в положение 2, и в течение трех последующих тактов содержащиеся в регистре символы поступают в канал.

Рис. 3. Структурная схема кодера циклического кода с порождающим многочленом

Циклический код может быть задан проверочным многочленом h(x). Кодовая комбинация В принадлежит данному циклическому коду, если . Проверочный многочлен связан с порождающим соотношением .

Задание кода проверочным многочленом эквивалентно заданию кода системой проверочных уравнений . Характерной особенностью циклического кода является то, что все проверочные уравнения можно получить из одного путем циклического сдвига индексов символов, входящих в исходное уравнение. Например, для (7, 4) — кода с порождающим многочленом проверочный многочлен имеет вид . Проверочные уравнения получаются из условия (12):

Осуществив умножение и приравняв коэффициенты при нулю, получим следующие уравнения, разрешенные относительно проверочных символов:

В качестве примера на рис. 4 показана схема кодера циклического (7,4) — кода, задаваемого проверочным многочленом , или, что то же самое, проверочными соотношениями . В исходном состоянии ключ находится в положении 1. В течение четырех тактов импульсы поступают в регистр, после чего ключ переводится в положение 2. При этом обратная связь замыкается. Начиная с пятого такта, формируются проверочные символы в соответствии с соотношениями . После седьмого такта все проверочные символы оказываются сформированными, ключ вновь переключается в положение 1. Кодер готов к приему очередного сообщения. Символы кодовой комбинации поступают в канал, начиная с пятого такта.

Рис. 4. Структурная схема кодера циклического кода с проверочным многочленом

Корректирующая способность кода зависит от порождающего многочлена р(х). Поэтому его выбор очень важен при построении циклического кода.Необходимо помнить, что степень порождающего многочлена должна быть равна числу проверочных символов. Кроме того, многочлен р(х) должен делить двучлен .
Обнаружение ошибок при использовании таких кодов заключается в делении многочлена , соответствующего принятой комбинации , на р(х). Если остаток s(x) оказывается равным нулю, то считается, что ошибки нет, в противном случае фиксируется ошибка.
Пусть необходимо построить код, обнаруживающий все одиночные ошибки. В этом случае многочлен ошибок имеет вид , где i = 0, 1, …, n — 1. Решение задачи заключается в нахождении такого многочлена р(х), чтобы многочлен е(х) не делился на р(х). Наиболее простым, удовлетворяющим этому требованию, является многочлен .
Аналогично можно построить код, обнаруживающий ошибки большей кратности.
Многочлен зависит только от многочлена ошибок е(х) и играет ту же роль, что и вектор-синдром. Поэтому ошибки можно исправить на основе таблицы соответствий между е(х) и s(x), хранящейся в памяти декодера, как и при линейных нециклических кодах. Однако свойство цикличности позволяет существенно упростить процедуру декодирования.
Один из алгоритмов исправления ошибок основан на следующих свойствах синдрома циклического кода. Пусть имеется циклический код с кодовым расстоянием d, исправляющий все ошибки до кратности включительно. Тогда можно показать, что:

  • если исправляемый вектор ошибок искажает только проверочные символы, то вес синдрома будет меньше или равен l, а сам синдром будет совпадать с вектором ошибок;
  • если вектор ошибки искажает хотя бы один информационный символ, то вес синдрома будет больше l;
  • если s(x) — остаток от деления многочлена нa р(х), то остатком от деления многочлена на р(х) является многочлен , другими словами, синдром некоторого циклического сдвига многочлена b(х) является соответствующим циклическим сдвигом синдрома исходного многочлена, взятого по модулю р(х).

На рис. 5 представлена схема декодера для (7, 4)-кода с порождающим многочленом . Код имеет кодовое расстояние d=3, что позволяет ему исправлять все однократные ошибки.

Рис. 5. Структурная схема кодера циклического кода с порождающим многочленом

Принятая кодовая комбинация одновременно поступает в буферный регистр сдвига, служащий для запоминания кодовой комбинации и ее циклического сдвига, а также на устройство деления на многочленах для вычисления синдрома. В исходном состоянии ключ находится в положении 1. После семи тактов буферный регистр оказывается загруженным, а в регистре устройства деления будет вычислен синдром. Если вес синдрома больше единицы, то декодер начинает проводить циклические сдвиги комбинации в буферном регистре (при отсутствии новой комбинации на входе) и одновременно вычислять их синдромы в устройстве деления. Если на некотором i-м шаге вес синдрома окажется меньше двух, то ключ переходит в положение 2, обратные связи в регистре деления разрываются. При последующих тактах ошибки исправляются путем подачи содержимого регистра деления на вход сумматора по модулю 2, включенного в буферный регистр. После семи тактов работы декодера в автономном режиме исправленная комбинация в буферном регистре возвращается в исходное положение (информационные символы будут занимать старшие разряды).
Существуют и другие, более универсальные алгоритмы декодирования.

Коды Хэмминга

К циклическим кодам относятся коды Хэмминга, которые являются одним из немногочисленных примеров совершенных кодов. Они имеют кодовое расстояние d= 3 и исправляют все одиночные ошибки. Длина кода выбирается из условия , которое имеет простой смысл: число различных ненулевых синдромов равно числу символов в кодовой последовательности. Так, существуют коды Хэмминга (), в частности, коды: (7, 4), (15, 11), (31, 26), (63, 57) и т. д.
Заметим, что ранее использованный многочлен является порождающим для кода Хэмминга (7, 4).

Коды БЧХ

Среди циклических кодов широкое применение нашли коды Боуза— Чоудхури—Хоквингема (БЧХ). Можно показать, что для любых целых положительных чисел m и l< n/2 существует двоичный код БЧХ длины . с кодовым расстоянием d > 2l + 1, причем число проверочных символов .
Для кодов БЧХ умеренной длины и ФМ при передаче символов можно добиться значительного выигрыша (4 дБ и более). Он достигается при скоростях (1/3 < k/n < 3/4). При очень высоких и очень низких скоростях выигрыш от кодирования существенно уменьшается.

Мажоритарные коды

Иногда целесообразно использовать коды с несколько худшей корректирующей способностью по сравнению с лучшими известными кодами, но простые в реализации. К ним относятся коды, допускающие мажоритарное декодирование. Оно основано на возможности для некоторых циклических кодов выразить каждый информационный символ с помощью Q различных линейных соотношений. Решение о значении символа принимается по мажоритарному принципу. Для исправления всех ошибок до кратности l включительно необходимо иметь (2l + 1) независимых соотношений.
В некоторой области значений параметров мажоритарные коды имеют корректирующую способность, незначительно уступающую корректирующей способности кодов БЧХ. В то же время их реализация сравнительно проста.
Проиллюстрируем принцип мажоритарного декодирования на примере (7, 3) — кода с проверочной матрицей .

Рассматриваемый код является циклическим с порождающим многочленом . Он имеет кодовое расстояние d — 4.
Используя матрицу , можно записать следующие соотношения для символа :

С учетом в декодере имеется возможность четырьмя разными способами вычислить первый информационный символ:

где — принятая кодовая комбинация.

При отсутствии ошибок ,т. е. все проверочные соотношения дают один и тот же результат. При наличии одного ошибочного символа три проверочных соотношения дают правильное значение, а соотношение, в котором участвует ошибочный символ, дает неверный результат. Принимая решение по мажоритарному принципу, декодер выдает правильный символ b.
Пусть ошибочно приняты два символа. Если они входят в различные проверочные соотношения, то два проверочных соотношения дадут значение 1, а два других — значение 0. В этом случае декодер выдает сигнал отказа от декодирования. Если оба искаженных символа входят в одно проверочное соотношение, то все четыре проверки дают один и тот же результат. Декодер выдает правильный символ b.
Аналогично определяются остальные информационные символы. Проверочные соотношения для символов и получаются из циклической перестановкой:


Схема декодера (рис. 6) состоит из сдвигающего регистра, сумматоров по модулю 2 и мажоритарного элемента М. Простота ее обусловлена тем, что в данном случае каждый символ кодовой комбинации участвует в одном проверочном соотношении. Код, для которого выполняется это условие, называется кодом с разделенными проверками.

Рис. 6. Структурная схема декодера циклического мажоритарного (7,3) — кода

Мажоритарное декодирование возможно и тогда, когда один и тот же символ участвует в нескольких проверочных соотношениях. Однако алгоритм декодирования усложняется.

Итеративные коды

Простыми в реализации являются также итеративные и каскадные коды.
Идея построения итеративных кодов заключается в следующем. Информационные символы записываются в виде таблицы из столбцов и строк. К каждой строке таблицы дописываются проверочных символов в соответствии с некоторым кодом . Затем к каждому из столбцов полученной таблицы добавляют проверочных символов в соответствии с некоторым кодом (n_2, k_2). Таким образом строится код длиной с числом информационных символов .
Можно показать, что для полученного двумерного итеративного кода кодовое расстояние d равно , где — кодовые расстояния для кодов соответственно.
Кодовая комбинация двумерного итеративного кода обычно передается последовательно по строкам, начиная с первой. Соответственно, декодирование ведется сначала по строкам, а затем, после приема всего двумерного блока, — по столбцам.
Проиллюстрируем построение кодовой комбинации двумерного итеративного кода. Пусть информационные символы записаны в виде таблицы:

В качестве кодов будем использовать коды с проверкой на четность. Тогда кодовая комбинация будет иметь вид:

Легко показать, что кодовое расстояние этого кода равно 4. Код исправляет все однократные ошибки. Их координаты определяются по номерам строк и столбцов, в которых не выполняется проверка на четность. Одновременно код обнаруживает все двукратные ошибки.
Итеративные коды характеризуются большой длиной, большим кодовым расстоянием и сравнительно простой процедурой декодирования. Недостатком их является малая скорость при заданной исправляющей способности.

Каскадные коды

Каскадные коды получаются комбинированием двух или более кодов и в некоторой степени похожи на итеративные. Кодирование осуществляется следующим образом.

Рис. 7. Cхема каскадного кодирования

Множество () информационных символов (в дальнейшем предполагается, что они двоичные) разбивается на подблоков по символов. Каждый подблок из символов рассматривается, как символ из алфавита объемом . Затем подблоков кодируются кодовыми комбинациями внешнего кода (рис. 7), составленными из подблоков по двоичному символу. Наконец, каждый из подблоков кодируется кодовыми комбинациями внутреннего -кода. Полученное множество кодовых слов внутреннего -кода является кодовым словом каскадного ()-кода. Обычно в качестве внешнего используют код Рида—Соломона с основанием , обеспечивающий максимальное кодовое расстояние при заданных , а в качестве внутреннего — двоичный -код.

Декодирование осуществляется следующим образом. Сначала декодируется внутренний код. При этом получается подблоков, содержащих по символов, которые декодируются внешним кодом. В результате на выходе внешнего декодера появляются подблоков по символов.

Декодирование двумя отдельными декодерами позволяет существенно снизить сложность по сравнению с той, которая потребуется для получения той же вероятности ошибки при одном уровне кодирования.

Каскадные коды, как и итеративные, имеют большую длину и большое кодовое расстояние. Во многих случаях они являются наилучшими среди блочных кодов. В частности, для двоичного симметричного канала при любой скорости передачи, не превосходящей пропускной способности канала, существует каскадный код, при котором вероятность ошибки может быть сколь угодно мала.

Непрерывные сверточные коды

Основные параметры сверточных кодов

Сверточный код — это линейный рекуррентный код. В общем случае он образуется следующим образом. В каждый i-й тактовый момент времени, на вход кодирующего устройства поступает символов сообщения . Выходные символы формируются с помощью рекуррентного соотношения из k символов сообщения, поступивших в данный и предшествующие тактовые моменты времени:

где — коэффициенты, принимающие значения 0 или 1.

Символы сообщения, из которых формируются выходные символы, хранятся в памяти кодирующего устройства. Величина К называется длиной кодового ограничения. Сверточный код имеет избыточность и обозначается .
Типичные параметры сверточного кода: .

Устройство кодера сверточного кода

Кодирующее устройство сверточного кода может быть реализовано с помощью сдвигающего регистра и сумматоров по модулю 2. Для схемы, показанной на рис. 8, на каждый символ сообщения вырабатываются два символа, которые последовательно во времени через коммутатор подаются в канал. Выходные символы являются линейными функциями поступающего информационного символа и комбинации, записанной в первых двух разрядах регистра (логического состояния регистра). Связь между ячейками сдвигающего регистра и сумматорами по модулю 2 удобно описывать порождающими многочленами . Для рассматриваемого случая (описывает связи верхнего сумматора) и (описывает связи нижнего сумматора). Наличие члена в порождающем многочлене означает, что (i + 1)-й разряд регистра сдвига соединен с сумматором. Счет разрядов регистра ведется слева направо.

Рис. 8. Cтруктурная схема кодера сверточного кода ()

Виды и способы задания сверточных кодов

Сверточный код получается систематическим, если в каждый тактовый момент выходные символы совпадают с символами сообщения. На практике обычно используются несистематические сверточные коды.
Различают прозрачные и непрозрачные сверточные коды. Первые характеризуются свойством инвариантности по отношению к операции инвертирования кода, которое заключается в следующем: если значения символов на входе кодера поменять на противоположные, то выходная последовательность символов также инвертируется. Соответственно, декодированная последовательность символов будет иметь такую же неопределенность в знаке, что и принятая последовательность символов, а следовательно, неопределенность знака последовательности можно устранить после декодирования сверточного кода (рис. 9).

Рис. 9. Cхема СПИ при использовании прозрачных сверточных кодов

Указанное свойство прозрачных кодов особенно важно для СПИ, использующих противоположные фазоманипулированные (ФМ) сигналы, которым свойственно явление обратной работы.
Для непрозрачного кода неопределенность знака последовательности символов приходится устранять до сверточного декодирования, что приводит к увеличению вероятности ошибок. Нетрудно показать, что сверточный код будет прозрачным, если каждый его порождающий многочлен содержит нечетное число членов.
Помимо рассмотренного способа задания сверточного кода, возможны и другие. В частности, выходные символы можно рассматривать как свертку импульсной характеристики кодера с информационной последовательностью (отсюда и происходит название кода).
Для пояснения процессов кодирования и декодирования часто используют решетчатую диаграмму, представляющую собой одно из возможных изображений кодового дерева. Такая диаграмма для кодера на рис. 10 состоит из узлов и ветвей (ребер). Число ветвей, исходящих из узла, равно основанию кода. Число узлов равно (). Единичному символу сообщения приписываются штриховые линии, а нулевому — сплошные. Выходные символы записываются над ветвями. Надписи около узлов характеризуют логическое состояние кодирующего устройства. Каждой информационной последовательности символов соответствует определенный путь (определенная траектория) на диаграмме. Кодовая последовательность формируется путем считывания комбинаций над ветвями при прослеживании данного пути. Соответственно, процесс кодирования заключается в выборе одного из путей диаграммы.

Рис. 10. Решетчатая диаграмма для кода 1/2 с K = 3

Корректирующая способность сверточного кода зависит от свободного расстояния , которое, по существу, содержит ту же информацию о коде, что и кодовое расстояние для блочных кодов. Оно определяется как минимальный вес (минимальное число единиц) пути на решетчатой диаграмме, начинающегося и заканчивающегося в нулевом узле. Например, для кода имеем .
В таблице 1 приведены порождающие многочлены оптимальных сверточных кодов с относительной скоростью передачи 1/2 и кодовым ограничением длины 3…8, а также значения свободных расстояний этих кодов.

Таблица 1

Длина кодового ограничения Порождающие многочлены Свободное расстояние
3
5
4
6
5
7
6
8
7
10
8
10

Методы декодирования сверточных кодов

Декодирование с вычислением проверочной последовательности

Декодирование с вычислением проверочной последовательности применяется только для систематических кодов. Оно ничем не отличается от соответствующего метода декодирования блочных кодов. На приемной стороне из принятых информационных символов формируют проверочные символы по тому закону, что и на передающей стороне, которые затем сравнивают с принимаемыми проверочными символами. В результате сравнения образуется проверочная последовательность, которая при отсутствии ошибок состоит из одних нулей. При наличии ошибок на определенных позициях последовательности появляются единичные символы. Закон формирования проверочных символов выбирается таким образом, чтобы по структуре проверочной последовательности можно было определить искаженные символы.

Декодирование по принципу максимума правдоподобия

Декодирование по принципу максимума правдоподобия сводится к задаче отождествления принятой последовательности с одной из возможных, где N — длина информационной последовательности. Решение принимается в пользу той кодовой последовательности, которая в меньшем количестве позиций отличается от принятой. Метод применим для любого сверточного кода. Однако при больших значениях N он практически не реализуем из-за необходимости перебора возможных кодовых последовательностей.

Алгоритм Витерби

Существенное упрощение процедуры декодирования по максимуму правдоподобия предложил А. Витерби. Характерной особенностью его метода является то, что на каждом шаге декодирования запоминается только наиболее правдоподобных путей. Осуществляется это следующим образом. Для определенности будем рассматривать код .
Пусть начальное состояние кодирующего устройства известно. Из анализа решетчатой диаграммы следует, что в любой i- й узел на любом i-м такте из начального состояния ведут несколько путей, которым соответствуют определенные кодовые последовательности. Из всех путей выберем тот, которому соответствует кодовая последовательность , отличающаяся от принятой меньшим числом символов. Этот путь называется «выжившим». Обозначим расстояние Хэмминга между последовательностями и через . Припишем i-му узлу вес, равный . Подобную процедуру проделаем для всех остальных узлов. Возьмем любой k-й узел решетчатой диаграммы в следующий тактовый момент. Он связан с двумя предшествующими узлами, например с i-м и j-м, ветвями ik и jk соответственно (см. рис. 10). Для нахождения правильного пути в узел k вычислим величины и , где — приращения расстояний Хэмминга при продолжении путей в узел k. Эти приращения на¬ходятся по принятому на (I+ 1)-м шаге сегменту последовательности и символам, соответствующим ветвям ik и jk. Если то ветвь ik считается истинной и записывается в память декодирующего устройства. Ветвь jk и все ей предшествующие отбрасываются. Аналогичные операции проделывают и для остальных узлов. В результате на (I+ 1)-м шаге в памяти декодирующего устройства будет храниться путей.
Исследования показывают, что через тактов в кодовом дереве остается лишь один путь с минимальным весом. Поэтому решение о том, какое сообщение передавалось в некоторый (m + 1)-й тактовый момент, можно принимать на -м такте. Для уменьшения объема памяти декодирующего устройства отрезки, по которым приняты решения, стираются. Для этого же из весов всех узлов кодового дерева периодически вычитают минимальный на данном такте вес.
Для пояснения работы декодера, реализующего алгоритм Витерби, рассмотрим следующий пример. Пусть используется ранее рассмотренный код при К = 3, и . Предположим, что передавалась нулевая последовательность, а принятая последовательность имеет вид 10 00 10 00 00 … . Работу декодера иллюстрируют диаграммы (рис. 11, а—д), где числа в узлах характеризуют значения .
На 3-м такте работы декодера (см. рис. 11, б) каждый из путей, «выживших» на предыдущем такте (см. рис. 11, а), раздваивается. Общее число путей становится равным 8. Декодер сравнивает метрики для пар путей, ведущих в каждый узел, и из каждой пары оставляет лишь лучший. Вновь число путей оказывается равным 4. Этот процесс повторяется при каждом приеме новой ветви (см. рис. 11, в, г, д). Заметим, что на 5-м такте (см. рис. 9.33, в) метрика нулевого пути оказывается наилучшей.
«Выживающие» пути могут отличаться друг от друга в течение многих тактов. Однако на 10-м такте (см. рис. 11, д) первые восемь ветвей всех «выживших» путей совпадают. В этот момент, согласно алгоритму Витерби, принимается решение о переданных символах, так как все «выжившие» пути приходят из одного узла.
Глубина (число тактов), на которой происходит слияние путей, является случайной величиной, зависящей от ошибок в принятой последовательности, и заранее не может быть вычислена. Поэтому обычно устанавливают некоторую фиксированную глубину декодирования. При этом каждый раз, обрабатывая новую ветвь, декодер выдает самый старый символ «вы¬жившего» пути с наилучшей метрикой.
В рассмотренном случае принятая последовательность содержала два ошибочных символа, а код имел свободное расстояние, равное 5, что позволило ему исправить эти ошибки. Предположим, что принятая последова¬тельность содержит 3 ошибочных символа и имеет вид 11 01 00 00 …. Такая комбинация ошибок оказывается неисправляемой. Заметим, что на 3-м такте (рис. 11, ё) удаляется правильный путь, что неизбежно приводит к ошибке. Кроме того, все «выжившие» пути имеют одну и ту же первую ветвь. На 5-м такте все выжившие пути имеют одинаковые первые две ветви (рис. 11, ж), а на 11-м такте — первые девять ветвей (рис. 11, з). Хотя при декодировании возникла ошибка, выбранный ошибочный путь отличается от правильного лишь на коротком отрезке, состоящем из трех ветвей. Информационная последовательность, соответствующая выбранному пути, имеет вид 1000, …, т. е. содержит один ошибочный символ. Рассмотренный пример описывает типичное поведение ошибочных последовательностей при использовании алгоритма сверточного декодирования Витерби.

Рис. 11. Диаграмма декодирования исправляемой (а—д) и неисправляемой (ж—з) комбинаций ошибок с помощью алгоритма Витерби

Алгоритм Витерби обладает рядом преимуществ. При небольших значениях длины кодового ограничения декодирующее устройство оказывается достаточно простым, реализуя, в то же время, высокую помехоустойчивость. Так, исследования показывают, что применение сверточных кодов с К= 3, 5 и 7 при фиксированной вероятности ошибки Pош позволяет получить энергетический выигрыш 4…6 дБ по сравнению с системой, использующей ФМ-сигналы без кодирования. Важным преимуществом по сравнению с методом последовательного декодирования является фиксация числа вычислительных операций на один декодированный символ. Декодирование по методу Витерби особенно перспективно в каналах с независимыми ошибками.

Устройство декодера Витерби

Рис. 12. Структурная схема декодера, реализующего алгоритм Витерби

Декодер Витерби (рис. 12) состоит из синхронизатора, устройства управления и тактирования, устройства для вычисления метрик ветвей, устройства для обновления и хранения метрик ветвей, устройства для обновления и хранения гипотетических информационных последовательностей и решающего устройства.
Устройство хранения и обновления метрик путей осуществляет сложение метрик ветвей с хранящимися метриками путей, проделывает необходимые сравнения и запоминает новые метрики путей.
Устройство хранения и обновления гипотетических информационных последовательностей может быть выполнено на сдвигающих регистрах, в каждом из которых хранится полная информационная последовательность символов, соответствующая одному из «выживших» путей. Их число равно числу узлов. После обработки новой ветви регистры обмениваются содержимым в соответствии с тем, какие последовательности «выживают» при сравнении. В последнюю ячейку каждого регистра поступает новый информационный символ, а самый старый символ каждого регистра поступает в выходное решающее устройство.
Выходное решающее устройство принимает решение о переданных информационных символах. Наилучшие результаты получаются, когда в качестве переданного информационного символа берется наиболее старый символ в последовательности с наименьшей метрикой. Иногда используют мажоритарный принцип: за переданный информационный символ берут чаще всего встречающийся символ из самых старых символов всех последовательностей. Устройство управления и тактирования задает необходимый ритм работы декодера.

Применение кодов в технических системах

Системы с обратной связью

Во многих системах, кроме основного (прямого) канала, с помощью которого сообщение передается от источника к потребителю, имеется обратный канал для вспомогательных сообщений, которые позволяют улучшить качество передачи сообщений по прямому каналу.
Наиболее распространены системы с обратной связью, в которых для обнаружения ошибок применяют избыточные коды. Такие системы называются системами с решающей обратной связью, или системами с переспросом. В качестве кодов часто используют коды с проверкой на четность, простейшие итеративные коды, циклические коды и др. Они позволяют хорошо обнаруживать ошибки при сравнительно небольшой избыточности и простой аппаратурной реализации.
Передаваемое сообщение кодируется избыточным кодом. Полученная комбинация передается потребителю и одновременно запоминается в накопителе-повторителе. Принятая последовательность символов декодируется с обнаружением ошибок. Если при этом ошибки не обнаружены, то сообщение поступает потребителю. В противном случае сообщение бракуется и по обратному каналу передается специальный сигнал переспроса. По этому сигналу проводится повторная передача забракованной кодовой комбинации, которая извлекается из накопителя-повторителя.
Можно показать, что если в обратном канале ошибки отсутствуют, то остаточная вероятность ошибочного приема кодовой комбинации имеет вид:

Pост = Pно/(1 — Pо.ош)

где Рно — вероятность необнаруженной ошибки (вероятность того, что переданная кодовая комбинация перешла в другую разрешенную);

Ро.ош — вероятность обнаружения ошибки (вероятность того, что вместо переданной кодовой комбинации принята какая-либо запрещенная кодовая комбинация).

Вероятности Рно и Ро.ош можно найти, если известны свойства канала и задан код. Эквивалентная вероятность ошибки имеет вид:

Pо Pно/k(1 — Pо.ош)

где k — число информационных символов в кодовой комбинации.

Среднее число передач одного сообщения определяется следующим образом:

Qn = 1/(1 — Pо.ош)

Несмотря на то, что обратный канал можно сделать весьма помехоустойчивым (обычно скорость передачи информации в обратном канале значительно меньше, чем в прямом), тем не менее, существует конечная вероятность того, что сигнал переспроса будет принят как сигнал подтверждения, и наоборот. В первом случае сообщение не поступает потребителю, а во втором случае оно поступает дважды. Одним из средств борьбы с ошибками в обратном канале, приводящими к потере сообщения, является использование несимметричного правила декодирования, при котором вероятность ошибочного приема сигнала переспроса существенно меньше вероятности ошибочного приема сигнала подтверждения. Например, сигнал переспроса передается кодовой комбинацией из п единичных символов, а сигнал подтверждения — комбинацией из n нулей. При приеме кодовой комбинации, содержащей хотя бы одну единицу, решение принимается в пользу сигнала переспроса. Очевидно, что в этом случае вероятность ошибочного приема сигнала переспроса можно получит сколь угодно малой.
Для того чтобы к потребителю не поступали лишние сообщения, обусловленные ошибочным приемом сигналов подтверждения, передаваемые кодовые комбинации либо снабжаются номерами, либо дополняются опознавательными символами, по которым можно узнать, передается кодовая комбинация в первый раз или она повторяется. При этом принятая повторная комбинация при отсутствии сигнала переспроса стирается и не поступает потребителю. Возможны и другие способы борьбы с ошибками такого рода.
Системы с решающей обратной связью весьма эффективны в случае каналов с замираниями. При ухудшении состояния канала увеличивается частота переспроса (уменьшается скорость передачи информации), но вероятность ошибочных сообщений, поступающих потребителю, практически не увеличивается. При улучшении состояния канала частота переспроса уменьшается. Таким образом, система как бы автоматически приспосабливается к состоянию канала связи, используя все его возможности в отношении передачи информации.
Следует заметить, что применение решающей обратной связи, конечно, не увеличивает пропускной способности прямого канала, но позволяет более простыми средствами по сравнению с длинными кодами приблизить скорость передачи информации к пропускной способности канала.

Сигнально-кодовые конструкции

Как известно, многопозиционные сигналы, такие как сигналы многократной фазовой модуляции (ФМ) и сигналы амплитудно-фазовой модуляции (АФМ), обеспечивают высокую удельную скорость передачи информации (высокую частотную эффективность) при уменьшении энергетической эффективности, а помехоустойчивые коды позволяют повышать энергетическую эффективность при снижении удельной скорости передачи. Сочетание методов многопозиционной модуляции и помехоустойчивого кодирования дает возможность повысить либо энергетическую эффективность без уменьшения частотной, либо частотную эффективность без снижения энергетической, а в ряде случаев — оба параметра. Задача заключается в формировании таких сигнальных последовательностей, которые можно достаточно плотно разместить в многомерном пространстве (для обеспечения высокой частотной эффективности) и в то же время разнести на достаточно большие расстояния (для обеспечения высокой энергетической эффективности). Такие последовательности, построенные на базе помехоустойчивых кодов и многопозиционных сигналов с плотной упаковкой, называются сигнально-кодовыми конструкциями.
В качестве помехоустойчивого кода обычно используются каскадные, итеративные и сверточные коды, а в качестве многопозиционных сигналов — сигналы многократной ФМ и сигналы АФМ.
Для согласования кодека двоичного помехоустойчивого кода и модема многопозиционных сигналов используется манипуляционный код, при котором большему расстоянию по Хэммингу между кодовыми комбинациями соответствует большее расстояние между соответствующими им сигналами. Этому требованию частично удовлетворяет код Грея. Возможны и другие способы такого преобразования.
На рис. 13 показана структурная схема одной из возможных систем с многоуровневой ФМ и помехоустойчивым кодированием. Сформированные на выходе помехоустойчивого кодера комбинации преобразуются в кодере Грея в последовательность кодовых комбинаций длины m, которые и определяют начальную фазу радиоимпульса фиксированной длительности на выходе фазового модулятора. На приемной стороне принятый сигнал сначала синхронно детектируется фазовым модулятором. Полученная при этом последовательность символов преобразуется декодерами Грея и помехоустойчивого кода в сообщение.
Применение сигнально-кодовых конструкций позволяет существенно приблизиться к границе эффективности, определяемой пропускной способностью канала.

Рис. 13. Структурная схема декодера, реализующего алгоритм Витерби

Методы приема сигналов

Прием «в целом»

До сих пор предполагалось, что кодовые комбинации принимаются посимвольно, т. е. на приемной стороне вначале выносится решение о каждом символе кодовой комбинации, а затем по совокупности n принятых символов принимается решение о том, какая кодовая комбинация была передана.
При избыточных кодах такая двухэтапная процедура принятия решения оказывается неоптимальной. Объясняется это тем, что процесс демодуляции является необратимой операцией и может сопровождаться потерей информации. Действительно, после принятия решения о символе ни соответствующий элемент сигнала, ни фактическое значение результата обработки этого символа (значение апостериорной вероятности или функции правдоподобия) в дальнейшем процессе приема (при декодировании) не принимаются во внимание. В то же время их учет мог бы привести к уменьшению вероятности ошибочного декодирования кодовой комбинации.
Вся информация, содержащаяся в принимаемом сигнале, будет наиболее полно использована, если отказаться от посимвольного приема и демодулировать кодовую комбинацию в целом.
Можно показать, что при использовании кода с избыточностью помехоустойчивость приема «в целом» выше помехоустойчивости поэлементного приема с исправлением ошибок, однако уступает помехоустойчивости поэлементного приема с обнаружением ошибок и переспросом по обратному каналу. При использовании кода без избыточности «прием в целом» не имеет преимуществ по сравнению с поэлементным приемом.
В общем случае вычислить вероятность ошибочного приема кодовой комбинации трудно. Однако иногда, например при использовании ортогональных, биортогональных и симплексных кодов, эту вероятность можно выразить через интегралы, которые можно определить численными методами.
Недостатком «приема в целом» является то, что он требует значительно более сложной аппаратуры по сравнению с поэлементным приемом. В частности, для его реализации требуется корреляторов. Очевидно, что при достаточно эффективном коде (такой код является длинным) прием «в целом» технически нереализуем. Например, если используется (n,k)-код с k = 10, то демодулятор, реализующий прием «в целом», будет состоять из 1024 корреляторов или согласованных фильтров.
В связи с трудностями построения оптимального демодулятора для приема «в целом» большое внимание уделяется алгоритмам приема, которые не используют всю информацию о принятом сигнале, но допускают меньшие потери по сравнению с поэлементным приемом. Такие алгоритмы являются двухэтапными, как и при поэлементном приеме. Однако на первом этапе решение о переданном символе не принимается, а запоминаются значения напряжений на выходах корреляторов или согласованных фильтров, предназначенных для приема различных символов, из которых составляются кодовые комбинации. Такой вид решения называется «мягким». Как известно, эти напряжения пропорциональны логарифму функций правдоподобия и несут информацию о степени соответствия принятого сигнала тому или иному символу. Их использование при дальнейшей обработке (декодировании) и позволяет получить лучшие результаты по сравнению с поэлементным приемом.

Прием по наиболее надежным символам

В реальных системах выходные напряжения обычно квантуются и представляются числами, т. е. вместо оптимального аналогового декодирования по максимуму правдоподобия используют цифровое декодирование. Цифровое декодирование уже при восьми уровнях квантования практически дает такие же результаты, что и аналоговое декодирование. В то же время оно значительно проще в реализации.
Существуют и другие методы приема, занимающие промежуточное положение между поэлементным приемом и «приемом в целом», например прием по наиболее надежным символам. В его основу положен тот факт, что при применении кода с кодовым расстоянием d любую его комбинацию можно декодировать, если «стереть» (d-1) символ. Устройство приема состоит из двух решающих схем. Первая из них вычисляет апостериорные вероятности и принимает предварительно решение о переданном символе. Полученная последовательность символов подается на вторую решающую схему, куда также поступает информация об апостериорных вероятностях. Декодирование выполняется по (n — d + 1) наиболее надежным (имеющим большие значения апостериорной вероятности) символам.
Описанный метод дает лучшие результаты, чем поэлементный прием, так как в нем частично используется информация об апостериорных вероятностях, но уступает приему в целом, так как информация о (d—1) менее надежных символах не используется.

См. также

  • Стеганография
  • Методы защиты видеоинформации
  • Вероятностные характеристики распознавания изображений объектов
  • Структуры сетей связи
  • Общая схема обработки материалов воздушного фотографирования
  • Функциональная схема программного обеспечения АРМ
  • Вероятностные характеристики обнаружения маскированных сообщений
Источник

Вообще говоря, практически все блочные помехоустойчивые коды “достаточно хорошие”, но практически все они требуют построения таблиц размера, экспоненциально зависящего от длины блока. А по теореме о канале с шумом, длина блока должна быть большой. Понятно, что построение и поиск в очень больших таблицах с практической точки зрения нежелательны. Соответственно в основном рассматриваются коды, которые можно построить более просто – под “более просто” в данном случае означает за полиномиальное время от длины блока – желательно, линейное время от длины блока.

На практике, построение практически применимых кодов, настолько хороших, как обещает теорема о канале с шумом, на текущий момент является нерешённой проблемой. Т.е. предел, установленный Шенноном на практике не достигается. Тем не менее, существуют “достаточно хорошие” практически применимые коды.

Очень хорошие коды
Семейство блочных кодов, которые для данного зашумлённого канала дают произвольно малую вероятность ошибки при любой скорости передачи вплоть до пропускной способности канала.
Хорошие коды
Семейство блочных кодов, которые для данного зашумлённого канала дают произвольно малую вероятность ошибки при любой скорости передачи вплоть до некоторого максимума, который может быть меньше пропускной способности канала.
Плохие коды
Семейства блочных кодов, которые не могут обеспечить произвольно малую вероятность ошибки, либо (номинально) могут только при нулевой скорости передачи.
Практические коды
Коды, кодирование-декодирование которых имеет полиномиальную сложность1 при кодировании и декодировании.

Большинство известных кодов являются линейными блочным кодами. Напомним,

((N, K)) блочный код
Множество (2^K) кодовых слов длины (N), кодирующих некий источник с алфавитом мощности (2^K).
((N, K)) блочный линейный код
Блочный код, в котором кодовые слова (brace{vect x^{(s)}}) образуют (K)-мерное линейное векторное пространство, являющееся подпространством (mathcal A_X^N) всех возможных кодовых слов длины (N), т.е. линейная операция над любыми двумя разрешёнными кодовыми словами даёт разрешённое кодовое слово.

Напомним несколько определений из линейной алгебры.

Магма
Множество (M) и бинарная операция (bullet: Mtimes M to M) называются вместе магмой, если (forall a, b in M: abullet b in G), т.е. (M) замкнуто относительно (bullet).
Полугруппа
Магма, ((S, bullet)), такая, что (forall a, b, c in S: (abullet b)bullet c = abullet (bbullet c),) т.е. операция (bullet) ассоциативна.
Моноид
Полугруппа ((S, bullet)), такая, что (exists e in S: forall a in S: abullet e = e bullet a = a), т.е. существует элемент, нейтральный относительно (bullet).
Группа
Моноид ((G, bullet)): (forall a in G, exists b in G: abullet b = bbullet a = e), т.е. для каждого элемента существует обратный ему относительно (bullet).
Абелева группа (Коммутативная группа)
Группа, в которой бинарная операция коммутативна, т.е. (forall a, b in G: abullet b = bbullet a).
Кольцо

Множество (R) и две бинарных операции (+) и (cdot) называются вместе кольцом, если:

  1. ((R, +)) является абелевой группой
  2. ((R, cdot)) является моноидом
  3. Операция (cdot) дистрибутивна по отношению к (+), т.е. (forall a,b,c in R:) (acdot(b+c) = acdot b + acdot c,) ((b+c)cdot a = bcdot a + ccdot a.)
Поле
Кольцо ((R, +, cdot)), в котором операция ((Rsetminusbrace{e}, cdot)) образует абелеву группу, где (e) – нейтральный элемент операции (+).
Поле Галуа (конечное поле)
Поле (GF = (F, +, cdot),) где (F) – конечное множество.

Нетривиальное поле, очевидно, не может содержать менее двух элементов.

Векторное пространство над полем (F)

Поле ((F, +_F, cdot_F)), множество (V) и операции (+: Vtimes Vto V,) (cdot: Ftimes V to V,) такие, что:

  1. ((V, +)) образуют абелеву группу
  2. (forall a,b in F, vin V: acdot(bcdot v) = (acdot_F b) cdot v)
  3. (forall v in V: ucdot v = v), где (uin F) – нейтральный элемент относительно (cdot_F).
  4. (forall ain F, u,v in V: acdot (u+v) = acdot u + acdot v)
  5. (forall a, bin F, v in V: (a+_F b)cdot v = acdot v + bcdot v)

Если любой линейный код образует векторное пространство, то процесс построения кода должен естественным образом описываться в терминах линейной алгебры. Это действительно так.

Операция кодирования может быть представлена в виде матрицы (vect G), такой, что при кодировании сообщения (vect s), кодированный сигнал (vect t = vect G^mathrm T vect s).

Множество всех кодовых слов (brace{vect t}) может быть определено как множество, удовлетворяющее уравнению (vect H vect t = 0,) где (0) – нейтральный элемент операции (+).

Матрица (vect G) называется порождающей матрицей, матрица (vect H) – проверочной матрицей. Они, ясно, должны удовлетворять условию (vect H vect G^mathrm T = vect 0), где (vect 0) – нулевая матрица.

Синдром
Произведение проверочной матрицы и принятого сигнала (vect s = vect H vect r) называется синдромом. Для разрешённых кодовых слов, синдром равен нулю.

Поскольку (vect H vect t = 0), для принятого сигнала (vect r), (vect s = vect H vect r = vect H t + vect H vect e = vect H vect e), где (t) – разрешённое кодовое слово и (e) – ошибка. Таким образом, между синдромом и вектором ошибки можно поставить взаимно однозначное соответствие. Если быть точным, то это возможно, если, по крайней мере, (q^{(n-k)} ge sum_{j=0}^t C_n^j (q-1)^j), где (t) – максимальная кратность ошибки, что совпадает с границей Хэмминга.

Пусть (mathbb F_q^n) – линейное (n)-мерное пространство над полем Галуа мощности (q). Тогда линейный код (C), являющийся подпространством (mathbb F_q^n) можно представить в виде некоторого минимального базиса (k le n) векторов. Векторы этого базиса образуют строки порождающей (ktimes n) матрицы (vect G). Если матрица (vect G) имеет блочную форму (vect G = brack{vect I_k | vect P},) где (I_k) – единичная матрица (ktimes k), (P) – некоторая матрица (k times (n-k)), мы говорим, что (vect G) находится в стандартной форме.

Если (vect G = brack{vect I_k | vect P},) то (vect H = brack{-vect P^{mathrm T} | vect I_{n-k}}) – одно из решений уравнения (vect H vect G^mathrm T = vect 0). Проверочная матрица имеет размер ((n-k)times n).

Следует отметить, что (n) – число символов в коде, (k) – число информационных символов и (n-k) – число проверочных символов.

Линейность гарантирует, что минимальное расстояние Хэмминга между кодовым словом (c_0) и любым другим кодовым словом (cneq c_0) не зависит от (c_0). Действительно, свойство линейности даёт (c-c_0 in C), а из определения расстояния Хэмминга, (d(c_0, c) = d(c-c_0, 0)), тогда [underset{cneq 0}min d(c_0, c) = underset{cneq 0}min d(c-c_0, 0) = underset{cneq 0}min d(c, 0).]

Два кода называются эквивалентными, если их порождающие матрицы отличаются только перестановкой столбцов и элементарными линейными операциями над строками. Такие коды по сути отличаются только положением проверочных символов в кодовых словах.

В менее общих, более практических терминах, коды в основном строятся над двоичными алфавитами. Тогда поле (F) представляет собой двоичное поле Галуа, где операции (+_F) и (cdot_F) соответственно представляют собой сложение (mod 2) и умножение. Элементы векторного пространства, в свою очередь, представляют собой элементы пространства (F^N), сложение является поэлементным сложением (mod 2), умножение – поэлементное умножение.

Коды Хэмминга

Коды Хэмминга – один из наиболее широко известных классов линейных кодов.

Коды Хэмминга конструируются следующим образом: биты, находящиеся в кодовом слове в разрядах с номером, являющимся степенью 2, являются проверочными, остальные – информационные. Значение (i)-го проверочного бита определяется суммой по модулю 2 всех информационных бит с номерами (j), таких, что (i & j neq 0,) где (&) – побитовая конъюнкция двоичных представлений чисел (i) и (j). В каноническом варианте биты нумеруются слева направо.

Число проверочных бит выбирается исходя из возможности исправить 1 ошибку в соответствии с границей Хэмминга: (r = ceil{log_2 (n+1)}). Собственно, обычно поступают наоборот – исходя из числа проверочных бит, определяют максимально возможное число информационных: (2^r — 1 = n). Тогда, кодов Хэмминга с 1 проверочным битом не существует, код Хэмминга с 2 проверочными битами содержит 1 информационный бит и т.д.

Коды Хэмминга обозначаются парой чисел: количеством бит в кодовом слове и количеством информационных бит.

С точки зрения систематического подхода, проверочная матрица кодов Хэмминга (H) состоит из (r) строк и (n) столбцов, причём столбцы различны и не равны нулю. А поскольку (n = 2^r — 1), столбцы этой матрицы неизбежно включают все ненулевые комбинации из (r) бит.

Например, код Хэмминга (7, 4) имеет проверочную матрицу (упорядоченную по возрастанию столбцов) [vect H = begin{pmatrix}
1 & 0 & 1 & 0 & 1 & 0 & 1 \
0 & 1 & 1 & 0 & 0 & 1 & 1 \
0 & 0 & 0 & 1 & 1 & 1 & 1 \
end{pmatrix}]

Или в каноническом варианте (получается перестановкой 1, 2 и 4 столбцов на 5, 6, 7 позиции соответственно):

[vect H = paren{begin{array}{cccc|ccc}
1 & 1 & 0 & 1 & 1 & 0 & 0 \
1 & 0 & 1 & 1 & 0 & 1 & 0 \
0 & 1 & 1 & 1 & 0 & 0 & 1 \
end{array}}]

Каноническая порождающая матрица тогда: [vect G^mathrm T = begin{pmatrix}
1 & 0 & 0 & 0 \
0 & 1 & 0 & 0 \
0 & 0 & 1 & 0 \
0 & 0 & 0 & 1 \
hline
1 & 1 & 0 & 1 \
1 & 0 & 1 & 1 \
0 & 1 & 1 & 1 \
end{pmatrix}]

Порождающая матрица, соответствующая исходной проверочной (получается перестановкой 5,6,7 строк на 1, 2, 4 позиции соответственно): [vect G^mathrm T = begin{pmatrix}
1 & 1 & 0 & 1 \
1 & 0 & 1 & 1 \
1 & 0 & 0 & 0 \
0 & 1 & 1 & 1 \
0 & 1 & 0 & 0 \
0 & 0 & 1 & 0 \
0 & 0 & 0 & 1 \
end{pmatrix}]

Тогда коды для соответствующих сообщений:

Сообщение (vect m) Код (vect G^mathrm T vect m)
0000 0000000
0001 0001111
0010 0010011
0011 0011100
0100 0100101
0101 0101010
0110 0110110
0111 0111001
1000 1000110
1001 1001001
1010 1010101
1011 1011010
1100 1100011
1101 1101100
1110 1110000
1111 1111111

Таблица синдромов:

Синдром Вектор ошибки
110 0000001
101 0000010
011 0000100
111 0001000
100 0010000
010 0100000
001 1000000

Например, получив сообщение r=1101010, вычислим синдром Hr = 110, что соответствует вектору ошибки 1000000. Тогда исходное сообщение c=0101010, m=0101.

Канонический вариант кода Хэмминга получается перестановкой проверочных бит на соответствующие позиции кодового слова:

Сообщение (vect m) Код (vect G^mathrm T vect m)
0000 0000000
0001 1101001
0010 0101010
0011 1000011
0100 1001100
0101 0100101
0110 1100110
0111 0001111
1000 1110000
1001 0011001
1010 1011010
1011 0110011
1100 0111100
1101 1010101
1110 0010110
1111 1111111

Циклические коды

Циклический код – это линейный блоковый код, обладающий свойством цикличности: циклический сдвиг разрешённого кодового слова влево или вправо на 1 бит даёт разрешённое кодовое слово.

При построении циклических кодов, используют формализм операций над многочленами: множество кодовых слов длины (n) представляется как множество многочленов степени (n-1), делящихся без остатка на некоторый многочлен (g(x)) степени (r = n-k), являющийся делителем (x^n-1). Все операции над многочленами производятся по модулю (x^n-1), таким образом, множество таких многочленов образует кольцо, а умножение на (x) соответствует циклическому сдвигу. Проверочный многочлен (h(x) = (x^n-1)/g(x)), для любого разрешённого кодового слова (f(x)), (f(x) h(x) = 0).

Для произвольного сообщения (m(x)) в соответствующем кольце, разрешённое кодовое слово немедленно получается умножением (m(x)) на (g(x)). В таком случае, при (g(x) = sum_{i=0}^{r} g_i x^i), соответствующая порождающая матрица имеет вид [vect G =
begin{pmatrix}
g \
x g \
x^2 g \
vdots \
x^k g \
end{pmatrix} =
begin{pmatrix}
0 & cdots & 0 & 0 & g_r & cdots & g_0 \
0 & cdots & 0 & g_r & cdots & g_0 & 0 \
vdots & & & ddots & & & vdots \
g_r & g_{r-1} & cdots & g_0 & 0 & cdots & 0 \
end{pmatrix}tag{1}] (либо отражённая по горизонтали при обратном порядке бит – мы однако будем исходить из того, что младший бит соответствует нулевой степени)

Однако на практике используется систематический подход, разделяющий информационные и проверочные символы.

Для данного сообщения (m(x)), оно умножается на (x^r) и делится на (g(x)), так, что [m(x) x^r = q(x) g(x) + r(x),] где (q(x)) – частное, (r(x)) – остаток. Тогда кодовое слово [c(x) = q(x)g(x) = m(x)x^r — r(x).]

Тогда кодовые слова представляют из себя конкатенацию исходного сообщения (m(x)) и отрицания остатка от деления (m(x)x^r) на (g(x)), и тогда порождающая матрица имеет вид

[vect G =
begin{bmatrix}
vect I_k | — vect R \
end{bmatrix},] где [vect R = begin{pmatrix}
mathrm{rem}(x^n, g(x))\
mathrm{rem}(x^{n-1}, g(x))\
vdots\
mathrm{rem}(x^r, g(x))\
end{pmatrix}] (либо отражённая по вертикали при обратном порядке бит – мы однако будем исходить из того, что младший бит соответствует нулевой степени)

Синдром (s(x)) определяется как остаток от деления полученного кодового слова на (g(x)). Соответствующий вектор ошибки определяется из (mathrm{rem}(e(x),g(x)) = s(x).) Ясно, что, поскольку кодовые слова имеют делителем (g(x)) по построению, для них синдром равен нулю.

Немаловажным нюансом является то, что выбор порождающего многочлена, вообще говоря, не произволен – это ясно, если внимательно посмотреть на порождающую матрицу.

Действительно, рассмотрим первые две строчки матрицы (vect G) из ((1).) Эти строчки являются разрешёнными кодовыми словами. Нулевой вектор так же является разрешённым кодовым словом. Находя расстояние Хэмминга от нулевого кодового слова до первой строчки (vect G), получаем, что кодовое расстояние циклического кода не может превышать число ненулевых членов в порождающем многочлене. Находя расстояние Хэмминга между первой и второй строчками, получаем, что, если все коэффициенты порождающего многочлена отличны от нуля, то кодовое расстояние не может быть больше 2, а вообще не превышает (2+floor{frac{r-1}{2}}). Соответственно, не более половины “средних” (т.е. кроме старшего и младшего) членов (g(x)) будут ненулевыми, причём младший и старший всегда ненулевые.

Некоторые коды Хэмминга, а именно, коды ((n, k)), в которых (n) и (k-1) являются взаимно простыми (или (k=2)), являются так же циклическими (с точностью до перестановок)

Например, код, эквивалентный коду Хэмминга (7,4) можно представить как циклический код с порождающим многочленом (g(x) = x^3+x+1). Действительно, (n=7), (k=4), (r=3).

m (m(x)) (r(x)) Код
0000 (0) (0) 0000 000
0001 (1) (x+1) 0001 011
0010 (x) (x^2+x) 0010 110
0011 (x+1) (x^2+1) 0011 101
0100 (x^2) (x^2+x+1) 0100 111
0101 (x^2+1) (x^2) 0101 100
0110 (x^2+x) (1) 0110 001
0111 (x^2+x+1) (x) 0111 010
1000 (x^3+0) (x^2+1) 1000 101
1001 (x^3+1) (x^2+x) 1001 110
1010 (x^3+x) (x+1) 1010 011
1011 (x^3+x+1) (0) 1011 000
1100 (x^3+x^2) (x) 1100 010
1101 (x^3+x^2+1) (1) 1101 001
1110 (x^3+x^2+x) (x^2) 1110 100
1111 (x^3+x^2+x+1) (x^2+x+1) 1111 111

Допустим, мы получили код (0011 000), что соответствует многочлену (x^3+x^4). Остаток от деления на (g(x)) (x^2+1), что соответствует ошибке передачи. (x^6/g(x) = x^2+1), тогда синдром соответствует ошибке в 7-м бите. Кодовое слово тогда (1011 000) и исходное сообщение (1011). Таблица синдромов имеет вид:

Синдром Вектор ошибки
1 0000001
x 0000010
x^2 0000100
x+1 0001000
x^2+x 0010000
x^2+x+1 0100000
x^2+1 1000000

О возможности существования очень хороших совершенных кодов

Рассмотрим двоичный симметричный канал с вероятностью перехода (f).

Ёмкость двоичного симметричного канала (C(f) = 1 — H_2(f)) (см. семинар 1, пример 6). По теореме Шеннона о канале с шумом, для достаточно большой длины кода (N), существуют блочные коды, имеющие плотность кодирования (rho), сколь угодно близкую к (C(f)) и исчезающе малую вероятность ошибки. Для больших (N), число битовых ошибок в блоке примерно (fN), следовательно, такие блочные коды можно назвать исправляющими fN ошибок (почти наверняка).

Рассмотрим теперь ДСК, где (f > 1/3). Пусть существует совершенный исправляющий fN ошибок код. Рассмотрим три кодовых слова из этого кода (у такого кода должно быть (2^{Nrho} approx 2^{NC(f)}) кодовых слов, поэтому при больших N найдётся хотя бы три). Без ограничения общности, пусть один из этих кодов будет нулевым (т.е. состоящим из нулей), второй имеет ((u+v)N) первых единиц, прочие нули, третий – (uN) нулей, ((v+w)N) единиц, остальные нули. Все коды (из рассматриваемых трёх) имеют (x = (1-u-v-w)N) нулей в конце. Если это совершенный исправляющий fN ошибок код, то кодовое расстояние должно быть больше (2fN), тогда [u+v > 2 f,] [v+w > 2 f,] [u+w > 2 f,]

Суммируя, получаем: [u+v+w > 3 f.]

Но (f>1/3), и (u+v+w > 1), тогда (x < 0), что невозможно.

То есть, совершенный исправляющий (fN) ошибок код не может иметь даже трёх кодовых слов, не говоря уже о (2^{Nrho}).

О возможности существования очень хороших линейных кодов

Несмотря на невозможность существования очень хороших совершенных кодов, очень хорошие линейные коды существуют. В первую очередь это связано с тем, что на самом деле при длине кодовых слов (Ntoinfty), вероятность того, что в результате изменения (fN) бит в кодовом слове, результат будет неоднозначен, стремится к нулю.

Рассмотрим линейный код с двоичной проверочной матрицей (vect H), имеющей (M) строк и (N) столбцов. Считаем, что (M sim N). Плотность кодирования такого кода по крайней мере [rho ge 1 — frac{M}{N}.] Далее полагаем худший случай, т.е. (rho = 1 — frac{M}{N}.)

Выбирается кодовое слово (vect t), такое, что [vect H vect t = 0 mod 2.]

ДСК добавляет вектор шума (vect x), так, что [vect r = vect t+vect x mod 2.]

Получатель должен восстановить (t) и (x) из (r). Используя подход декодирования по синдрому. Получатель вычисляет синдром [vect z = vect H vect r mod 2 = vect H vect x mod 2.]

Поскольку синдром (vect z) зависит только от вектора шума (vect x), задача декодирования состоит в нахождении наиболее вероятного (vect {hat x}), удовлетворяющего условию [vect H vect {hat x} = vect z mod 2,] который затем можно вычесть из (vect r) чтобы получить наиболее вероятное исходное кодовое слово (vect {hat t}).

Мы хотим показать, что вероятность ошибки стремится к нулю с ростом (N) для случайной матрицы (vect H).

Рассмотрим субоптимальную стратегию. Пусть субоптимальный декодер (назовём его декодером типичных множеств) рассматривает множество типичных векторов шума [T = brace{vect x in X^N : left|log_2frac{1}{P(mathbf x)} — N H(X)right| < beta},] где для ДСК (H(X) = H_2(f)), проверяя, какие из них удовлетворяют найденному синдрому. Если ни один элемент типичного множества не удовлетворяет вычисленному синдрому, или если ему удовлетворяют более одного, то декодер сообщает об ошибке.

Для данной матрицы (vect H), вероятность ошибки можно записать как [P = P_1 + P_2,] где (P_1) – вероятность того, что (vect x) не типичный, а (P_2) – что (vect x) типичный, и по крайней мере ещё один вектор (vect x’) имеет такой же синдром. (P_1) уменьшается с ростом (N), как показано при доказательстве теоремы Шеннона о кодировании источника (см. лекцию 5). (P_2) по сути есть вероятность наличия двух типичных векторов (vect x) и (vect x’), таких, что [vect H(vect x’ — vect x) = 0.]

Введём функцию [f(vect x, vect x’) = left{begin{align}
1, && vect H (vect x’ -vect x) = 0 \
0, && vect H (vect x’ -vect x) neq 0
end{align}right.]

Количество ошибок (N_e) для данного типичного вектора (vect x) тогда [N_e(vect x) le sum_{begin{align}vect x’in T\vect x’neq vect xend{align}} f(vect x, vect x’)]

(N_e(vect x) in brace{0,1}), правая часть может быть больше 1.

Тогда усредняя по (vect x), [P_2 = sum_{xin T} P(vect x) N_e(vect x) le sum_{xin T} P(vect x) sum_{begin{align}vect x’in T\vect x’neq vect xend{align}} f(vect x, vect x’).]

Усредняя по всем матрицам (vect H), [bar P_2 le sum_{vect H} P(vect H) sum_{xin T} P(vect x) sum_{begin{align}vect x’in T\vect x’neq vect xend{align}} f(vect x, vect x’)]

(P(vect x)) не зависит от (vect H), поэтому

[bar P_2 le sum_{xin T} P(vect x) sum_{begin{align}vect x’in T\vect x’neq vect xend{align}} sum_{vect H} P(vect H) f(vect x, vect x’)]

Выражение (sum_{vect H} P(vect H) f(vect x, vect x’)) это по сути вероятность равенства вектора синдрома нулю по всем возможным случайным матрицам (vect H). Она не превышает вероятности равенства нулю случайного вектора, т.е., поскольку вектор синдрома имеет размер (M), [sum_{vect H} P(vect H) f(vect x, vect x’) le 2^{-M}.]

Тогда, [bar P_2 le (sum_{xin T} P(vect x)) paren{abs T -1} 2^{-M} le abs T 2^{-M}.]

При доказательстве теоремы о кодировании источника, было показано, что в типичном множестве примерно (2^{NH(X)}) элементов, тогда [bar P_2 le 2^{NH(X)-M}.]

Если (NH(X)-M < 0), т.е. (H(X) < M/N,) то вероятность средняя вероятность ошибки экспоненциально убывает с ростом (N). Тогда, если в среднем по всем возможным проверочным матрицам вероятность ошибки убывает, то неизбежно существуют такие линейные коды, для которых она так же убывает. Более того, таких кодов большинство.

Отметим, что подставляя условие на энтропию в (rho = 1 — M/N,) получаем [1 — rho = M/N,] [1 — rho > H(X),] [rho < 1 — H(X) = 1-H_2(f),] что совпадает с условием теоремы Шеннона для ДСК.

Отдельно следует отметить, что по сути мы заодно доказали теорему о кодировании источника. Действительно, поскольку мы “угадываем” вектор шума (vect x) длины (N) по вектору синдрома (vect z) длины (M), с исчезающе малой вероятностью ошибки, если (H(X) < M/N), то это означает, что, при достаточно больших (N), существует схема кодирования, позволяющая “почти безошибочно” передать (N) бит сообщения в коде длины (M), так, что (M = N H(X) + varepsilon).

  1. Вообще говоря, имеется ввиду временная или пространственная сложность. Однако в теории сложности алгоритмов доказывается, что (P(n) subseteq PSPACE(n)), т.е. семейство алгоритмов, полиномиальных по времени есть нестрогое подмножество семейства алгоритмов, полиномиальных по памяти, поэтому требование (P) и/или (PSPACE) по сути эквивалентно требованию (P).↩︎

Источник

Like this post? Please share to your friends:
  • Вектор ошибки показывает
  • Вектор ошибки кодирования
  • Вектор ошибки evm
  • Вектор 1950 ошибки
  • Вектор 1350 как удалить ошибки