Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!
Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет
Различают
ошибки регистрации, а
также ошибки
репрезентативности,
которые присущи только выборочному
наблюдению и возникают в результате
того, что выборочная совокупность не
полностью воспроизводит генеральную.
Они могут иметь случайный (непреднамеренный)
и систематический (тенденциозный)
характер.
При собственно-случайной
выборке
отбор из генеральной совокупности
осуществляется посредством жеребьевки
или с помощью таблиц случайных чисел.
Каждым единицам
обеспечивается равная возможность
попадания в выборку, а количество
отобранных в выборочную совокупность
единиц обычно определяется исходя из
принятой доли выборки – это отношение
числа единиц выборочной совокупности
к числу единиц генеральной совокупности
:
.
Применяя выборочный
метод в статистике, обычно используют
два основных вида обобщающих показателей:
среднюю ошибку количественного признака
и относительную величину альтернативного
признака.
Выборочная доля,
или частость, определяется отношением
числа единиц, обладающих изучаемым
признаком
,
к общему числу единиц выборочной
совокупности:
.
Для характеристики
надежности выборочных показателей
различают среднюю
и предельную
ошибки выборки.
Ошибка выборки
или ошибка
репрезентативности
представляют собой разность соответствующих
выборочных и генеральных характеристик:
— для средней
количественного признака
,
где
—
выборочная средняя;
-среднее
значение признака в генеральной
совокупности или генеральная средняя;
— для доли
(альтернативного признака)
,
где
—
выборочная доля;
—
генеральная доля
Средняя ошибка
выборки зависит от следующих моментов:
1) при соблюдении
принципа случайного отбора средняя
ошибка выборки определяется прежде
всего объемом выборки: чем больше
численность при прочих равных условиях,
тем меньше величины средне ошибки
выборки Н: при сокращении средней ошибки
в два раза, объем выборки нужно увеличить
в четыре раза.
2) степени варьирования
признака. Чем меньше вариация признака,
а следовательно, и дисперсия, тем меньше
средняя ошибка выборки, и наоборот.
При случайном
повторном отборе средние ошибки
теоретически рассчитываются по следующим
формулам:
— для средней
количественного признака
,
где
—
дисперсия признака в генеральной
совокупности;
— численность
выборочной совокупности.
— для доли
альтернативного признака
,
где
— дисперсия доли признака в генеральной
совокупности
— численность
выборочной совокупности.
Поскольку практически
дисперсия признака в генеральной
совокупности точно неизвестна, на
практике пользуются значением дисперсии,
рассчитанным для выборочной совокупности
на основании закона больших чисел,
согласно которому выборочная совокупность
при достаточно большом объеме выборки
достаточно точно воспроизводит
характеристики генеральной совокупности.
Т.о., расчетные формулы при случайном
повторном отборе будут выглядеть
следующим образом:
— для средней
количественного признака
,
где
—
дисперсия признака в выборочной
совокупности.
— для доли
альтернативного признака
,
где
— дисперсия доли признака в выборочной
совокупности.
Однако дисперсия
выборочной совокупности не равна
дисперсии генеральной совокупности и
в теории вероятностей доказано, что
генеральная дисперсия выражается через
выборочную следующим соотношением:
,
так как
при достаточно больших
— величина близка к 1, то можно принять,
что,
но в случаях малой выборки, когда объем
выборки не превышает 30 единиц, необходимо
учитывать коэффициент.
Тогда среднюю ошибку малой выборки
можно вычислить по формуле:
.
При случайном
бесповторном отборе поскольку сокращается
численность единиц генеральной
совокупности, то в приведенные формулы
расчета средних ошибок выборки необходимо
подкоренное выражение умножить на
,
представляющий собой долю единиц
генеральной совокупности не попавших
в выборку. Следовательно формулы примут
вид:
— для средней
количественного признака
.
— для доли
альтернативного признака
.
Механическая
выборка
состоит в том, что отбор единиц в
выборочную совокупность из генеральной
разбитой по нейтральному признаку на
равные интервалы (группы) производится
так, что из каждой такой группы в выборку
отбирается лишь одна единица, т.е. он
бесповторный. И для того чтобы избежать
систематической ошибки, отбирается
единица, находящаяся в середине каждой
группы, при этом единицы совокупности
предварительно располагают в определенном
порядке (по алфавиту, или ранжируя
значения какого-либо показателя, не
связанного с изучаемым свойством и
др.).
При достаточно
большой совокупности механический
отбор точности результатов близок к
собственно-случайному. Поэтому для
определения средней ошибки механической
выборки используют формулы собственно
случайной бесповторной выборки.
Типическая
выборка
применяется
для отбора единиц из неоднородной
совокупности. Используется в тех случаях,
когда все единицы генеральной совокупности
можно разбить на несколько качественно
однородных групп по признакам, от которых
зависят изучаемые показатели. Затем из
каждой типической группы собственно-случайной
или механической выборкой производится
индивидуальный отбор единиц в выборочную
совокупность.
Типическая выборка
дает более точные результаты по сравнению
с другими способами отбора единиц в
выборочную совокупность, так как
представительство в ней каждой типической
группы позволяет исключить влияние
межгрупповой дисперсии на среднюю
ошибку выборки и в качестве показателя
вариации выступает средняя из
внутригрупповых дисперсий (остаточная).
Средние ошибки
типической выборки находят по формулам:
— для средней
количественного признака
повторный отбор
,
бесповторный отбор,
где
—
средняя из внутригрупповых дисперсий
по выборочной совокупности.
— для доли
альтернативного признака
повторный отбор
,
бесповторный отбор,
где
-средняя
из внутригрупповых дисперсий доли
альтернативного признака по выборочной
совокупности.
Серийная выборка
предполагает случайный отбор из
генеральной совокупности не отдельных
единиц, а их равновеликих групп (гнезд,
серий), при этом все единицы без исключения
в таких группах подвергаются наблюдению.
Н: при транспортировке товар упакован
и при оценке качества рациональнее
проверить несколько упаковок, чем
вскрывать все упаковки и отбирать
необходимое количество товара.
Поскольку внутри
групп обследуются все без исключения
единицы, средняя ошибка выборки (при
отборе равновеликих серий), зависит
только от межгрупповой дисперсии.
Средние ошибки
серийной выборки находят по формулам:
— для средней
количественного признака
повторный отбор
,
бесповторный отбор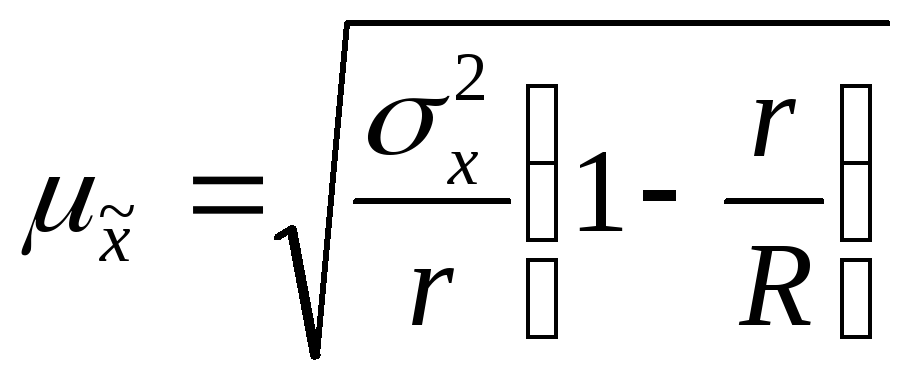
при
где
— число отобранных серий;
—
общее число серий;
—
межгрупповая дисперсия,
—
средняя—
той серии,-общая
средняя по всей выборочной совокупности.
— для доли
альтернативного признака
повторный отбор
,
бесповторный отбор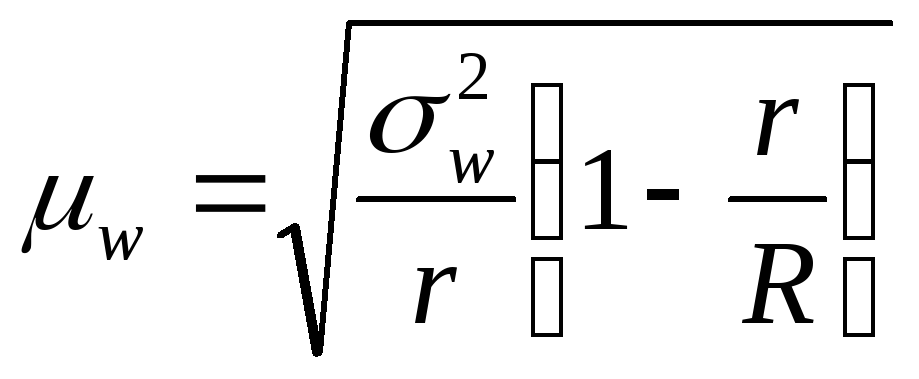
при,
где
—
межгрупповая дисперсия доли,—
доля признака в—
той серии,—
общая доля признака во всей выборочной
совокупности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вопрос № 968
Достаточность аудиторских доказательств представляет собой …
число элементов аудиторской выборки для тестов средств внутреннего контроля
объем проведенных аудиторских процедур
качественную характеристику аудиторских доказательств
количественную меру аудиторских доказательств
Вопрос № 969
Письменная информация, полученная по результатам аудита, должна быть представлена …
любому внешнему пользователю бухгалтерской (финансовой) отчетности
лицам, не относящимся к руководству аудиторской организации
в инспекцию Федеральной налоговой службы, следственные органы и управление по борьбе с экономическими преступлениями
руководству и (или) представителям собственника аудируемого лица
Вопрос № 972
Организация приобрела комплектующие за 36 580 руб., в том числе НДС 18%, оплата произведена с валютного счета. Комплектующие отпущены на нужды основного производства.
Погашение задолженности перед поставщиком за горюче-смазочные материалы отражается бухгалтерской записью …
Д-т 10 «Материалы» К-т 52 «Валютные счета»
Д-т 62 «Расчеты с покупателями и подрядчиками» К-т 52 «Валютные счета»
Д-т 52 «Валютные счета К-т 60 «Расчеты с поставщиками и подрядчиками»
Д-т 60 «Расчеты с поставщиками и подрядчиками» К-т 52 «Валютные счета»
Вопрос № 973
Организация приобрела комплектующие за 36 580 руб., в том числе НДС 18%, оплата произведена с валютного счета. Комплектующие отпущены на нужды основного производства.
Оприходование комплектующих и их отпуск на нужды основного производства отражаются следующими бухгалтерскими записями.
Д-т 01 «Основные средства» К-т 08 «Вложения во внеоборотные активы»
Д-т 20 «Основное производство» К-т 01 «Основные средства»
Д-т 10 «Материалы» К-т 60 «Расчеты с поставщиками и подрядчиками»
Д-т 20 «Основное производство» К-т 10 «Материалы»
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

|
Здесь 
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия, 
|
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
 |
Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
Краткий
курс лекции
Понятие и методы
обоснования аудиторской выборки. Критерии аудиторской выборки.
Международный стандарт аудита 530 «Аудиторская выборка» введен в
действие на территории Российской Федерации приказом Минфина России от
09.01.2019 № 2н
Аудиторская
выборка – это перечень
определенным образом отобранных элементов проверяемой совокупности с целью на
основе их изучения сделать вывод обо всей проверяемой совокупности.
Аудиторская выборка — это применение аудиторских процедур
менее чем ко всем элементам одной статьи отчетности или группы однотипных
операций.
Она дает возможность аудитору получить и оценить аудиторские доказательства в отношении некоторых характеристик
элементов, отобранных для того, чтобы сформировать или помочь сформировать
выводы, касающиеся генеральной совокупности, из которой произведена выборка.
Выборка может быть нестатистической
(произвольной) и статистической.
Нестатистический
выборочный метод – это анализ
по качественным признакам в зонах повышенного аудиторского риска. Как правило,
его применяют при невозможности использовать метод статистической выборки.
Например – проверяемая совокупность неоднородна, разный
уровень эффективности внутреннего контроля в структурных подразделениях
предприятия, небольшое количество хозяйственных операций, имеющих высокий
уровень существенности.
Наиболее распространенными методами нестатистической
(произвольной) выборки являются: блочный отбор (выбор первого элемента
определяет все остальные элементы проверяемого блока), беспорядочный отбор,
оценочные методы.
Статистический
выборочный метод может
применяться для достижения следующих целей:
· обнаружения повторяющихся ошибок, искажений,
проявляющихся с определенной частотой и в определенном количестве;
· оценка масштабов распространения обнаруженных ошибок.
Основными методами статистической выборки при аудите
являются:
— возвратная выборка – не исключаются из процесса отбора
ранее проверенные элементы;
— безвозвратная выборка — исключаются из процесса отбора
ранее проверенные элементы;
— механическая выборка – предполагает предварительное
ранжирование единиц проверяемой совокупности;
— серийная выборка – отбор элементов для проверки
осуществляется не единицами, а сериями и другие методы.
Риск выборки возникает,
когда вывод аудитора, сделанный на основе отобранной совокупности, отличается
от вывода при применении идентичных процедур аудита к генеральной совокупности
в целом.
В аудите различают два типа рисков выборки. Риск
первого типа представляет собой риск того, что аудитор сделает следующие
заключения:
§
риск средств внутреннего контроля ниже, чем в
действительности (при выполнении тестов средств внутреннего контроля);
§
существенной ошибки не существует, вопреки тому,
что в действительности она есть (при выполнении аудиторских процедур проверки
по существу).
Риск данного типа
оказывает влияние на надежность аудита и с большой степенью вероятности может
привести к ненадлежащему аудиторскому мнению.
Риск второго типа
представляет собой риск того, что аудитор придет к следующим выводам:
§
риск средств внутреннего контроля выше, чем в
действительности (при выполнении тестов средств внутреннего контроля);
§
имеет место существенная ошибка, тогда как в
действительности ее не существует (при выполнении аудиторских процедур проверки
по существу).
Риск такого типа
оказывает влияние на эффективность аудита, поскольку он обычно приводит к
дополнительной работе по установлению того, что первоначальные выводы были
неверны.
Риск, не зависящий от
аудиторской выборки, является следствием факторов, которые приводят аудитора к
ошибочному выводу по любым причинам, кроме тех, которые связаны с объемом
выборки (т.е. числом отбираемых для проверки элементов). Риск, связанный с
выборкой, может быть снижен путем увеличения объема отбираемой совокупности, а
не связанный — путем надлежащего планирования задания, текущего контроля за
работой аудиторов и проверки выполнения процедур.
Различают следующие
виды выборки:
§
представительная (репрезентативная) — элементы ее
генеральной совокупности имеют равную вероятность быть отобранными;
§
непредставительная (нерепрезентативная) — элементы ее
генеральной совокупности не имеют равную вероятность быть отобранными. Аудитор
полагается на свое профессиональное суждение при отборе элементов.
Элементами выборки могут
быть натуральные объекты (например, первичные учетные документы) или показатели
в денежном выражении. Аудитор должен стараться сформировать репрезентативную совокупность
путем отбора элементов выборки, которые обладают характеристиками, типичными
для генеральной совокупности, так как целью выборки является получение выводов
по всей генеральной совокупности. При формировании проверяемой совокупности
необходимо исключать предвзятость.
Для построения выборки
аудитор определяет метод отбора элементов, который будет использоваться при
тестировании с целью получения аудиторских доказательств. Различают следующие
методы отбора элементов:
1.
отбор всех элементов (сплошная проверка);
2.
отбор специфических (определенных) элементов;
3.
отбор отдельных элементов (формирование
аудиторской выборки).
Первый метод отбора не
применяют при проведении тестов средств внутреннего контроля, его используют в
отношении аудиторских процедур проверок по существу. Сплошная проверка
целесообразна в следующих случаях:
§
генеральная совокупность состоит из небольшого
числа элементов наибольшей стоимости;
§
неотъемлемый риск и риск средств контроля
являются высокими, а другие средства не позволяют получить достаточные
надлежащие аудиторские доказательства;
§
повторяющийся характер расчетов или иных
процессов, осуществляемых с помощью компьютерной системы бухгалтерского учета,
делает сплошную проверку эффективной с точки зрения соотношения затрат и результатов.
Второй метод
предполагает отбор специфических элементов. Различают специфические элементы
наибольшей стоимости и ключевые элементы. К элементам наибольшей стоимости
относят суммы сальдо счетов, которые превышают планируемую степень точности, т.е.
уровень существенности. При определении ключевых элементов аудитор отбирает
сальдо счетов, существенных качественно, т.е. элементы, по которым возможна
наибольшая вероятность наличия ошибки или искажения, и элементы существенные
количественно, т.е. элементы (например, месяцы), имеющие наибольший оборот по
данному счету в отчетном периоде. При использовании данного метода
осуществляется построение непредставительной выборки, в связи с чем результаты,
полученные по отобранным элементам, не могут быть экстраполированы на всю
совокупность.
Третий метод
представляет собой отбор элементов для построения представительной выборки.
Прежде чем отобрать элементы, необходимо определить объем выборки.
Организация выборочного исследования включает в себя определение:
— величины
выборки (массива, поля проверяемой и генеральной совокупности);
— единицы
наблюдения;
— единицы
отбора;
— методов
отбора;
— объема
выборки;
— проверки
представительности (репрезентативности) выборки;
— порядка
распространения выборочных данных на проверяемую совокупность.
Для достижения
поставленных целей проверки необходимо определение соответствующей проверяемой
совокупности, поскольку именно к ней относится заключение, сделанное на основе
выборки.
В аудите в
качестве элементов могут выступать бухгалтерские записи (проводки), статьи,
записи, из которых делается выборка.
Для составления
проверяемой совокупности вся документация клиента разбивается на однородные
массивы данных по различным признакам (характеру документов, материально ответственным
лицам, временной последовательности и др.).
Например, аудитор
собирает информацию о дебиторской задолженности свыше 600 тыс. руб.,
исследуемой совокупностью будет совокупность всех бухгалтерских документов,
записей, затрагивающих расчеты с дебиторами, но не менее чем на 600 тыс. руб.
Единица отбора
при таком типе выборок совпадает с единицей наблюдения (документом).
Единица
наблюдения при аудиторской проверке объективно обусловлена. Ею может быть
какой-либо раздел или участок бухучета, тип хозяйственных операций. В рамках
одной и той же единицы наблюдения единицы отбора могут быть различными.
Осуществляя
выборку, аудитор может разбить всю изучаемую
совокупность на отдельные группы, элементы, каждый из которых имеет сходные
характеристики. Эта процедура называется стратификацией, она позволяет снизить
разброс (вариацию) данных.
Обычно выборка
должна быть репрезентативной. Это предполагает, что все элементы изучаемой
совокупности имеют равную вероятность быть
отобранными в выборку. Репрезентативность
выборки обеспечивается одним из способов отбора:
— случайный – может проводиться по таблице случайных чисел;
— систематический – предполагает, что элементы отбираются через постоянный
интервал, начиная со случайно выбранного числа.
Интервал строится
либо на определенном числе элементов совокупности (например, изучение каждого
20-го документа из всех документов данной категории), либо на стоимостной их
оценке (например, отбирается тот элемент, на который приходится каждый
следующий миллион рублей в совокупной стоимости элементов);
— комбинированный – представляет собой комбинацию различных методов
случайного и систематического отбора.
Аудитор имеет право
прибегать к нерепрезентативной (непредставительной)
выборке только тогда, когда профессиональное суждение аудитора по итогам
проведения выборки не должно касаться всей совокупности в целом.
Например,
когда аудитор проверяет отдельно взятую группу операций либо класс операций, по
которым установлены возможные ошибки.
Для
любой выборки аудитор обязан:
— анализировать
каждую ошибку, попавшую в выборку;
— экстраполировать
полученные при выборке результаты на всю проверяемую совокупность;
— оценить
риски выборки.
При
анализе ошибок, попавших в выборку, аудитор должен в первую очередь установить
их характер. Формируя выборку, следует описать, для достижения каких целей она
проводится, и применительно к ним оценить найденные в выборке ошибки.
Если поставленные цели проверки не
были достигнуты с помощью выборочного исследования, то аудитор может провести
альтернативные аудиторские процедуры.
Аудитор может оценить качественный
аспект ошибок (их сущность и вызвавшую их причину), а также установить их
влияние на другие участки аудита.
Аудитор должен убедиться, что ошибка
в проверяемой совокупности не превышает допустимую величину. Для этого он
сравнивает ошибку совокупности, полученную посредством распространения, с
допустимой ошибкой.
Если первая ошибка оказалась больше
допустимой, аудитор должен повторно оценить риски выборки, и если сочтет их
неприемлемыми, то ему следует расширить круг аудиторских процедур или применять
аудиторские процедуры, альтернативные уже проведенным.
При определении объема выборки
аудитор должен установить риск выборки, допустимую и ожидаемую ошибки.
Риск выборки заключается в том, что
мнение аудитора по определенному
вопросу, составленное на основе выборочных данных, может отличаться от мнения
по данному вопросу, составленному на основании изучения всей совокупности. Риск
выборки имеется как при тестировании средств системы контроля, так и при
проведении детальной проверки верности отражения в бухучете оборотов и сальдо
по счетам. Различают риски первого и второго рода.
При тестировании средств контроля различают
следующие риски выборки:
— риск первого рода – риск отклонить верную гипотезу,
когда результат выборки свидетельствует
о ненадежности системы контроля, в то время как в действительности система
надежна;
—риск второго рода – риск принять неверную гипотезу,
когда результат выборки свидетельствует о надежности системы, в то время как в действительности
система контроля не обладает необходимой надежностью.
При проведении детальной проверки
верности отражения в учете оборотов и сальдо по счетам выделяют следующие риски
выборки:
— риск первого
рода – риск отклонить верную гипотезу, когда результат выборки свидетельствует,
что проверяемая совокупность содержит существенную ошибку, в то время как
совокупность свободна от такой ошибки;
— риск второго рода – риск принять неверную гипотезу,
когда результат выборки свидетельствует, что проверяемая совокупность не
существенную ошибку.
Риск
отклонения верной гипотезы требует проведения дополнительной работы со стороны
аудиторской организации или экономического субъекта.
Риск
принятия неверной гипотезы ставит под сомнение сами результаты работы аудитора.
Размер
выборки определяется величиной ошибки, которую аудитор считает допустимой.
Допустимая
ошибка устанавливается на стадии планирования аудита. Чем меньше размер
допустимой ошибки, тем больше должен быть объем аудиторской выборки.
Пример 1.
Аудитор располагает информацией по ООО «Контакт»: аудиту подлежат
материально-производственные запасы, общий объем проверяемой совокупности
составляет 500 тыс. руб., уровень существенности – 10 тыс. руб., номера
документов – с 50-го по 1050-й, система внутреннего контроля эффективна, в
бухгалтерском учёте по данным предыдущих проверок нет существенных искажений.
Необходимо построить выборку, указав
первые семь элементов методом случайного отбора (используя таблицу случайных
чисел и соответствующий коэффициент проверки).
Решение задачи:
Для построения выборки необходимо
определить ее элементы:
ЭВ = (ГС ∗ к)/УС,
ЭВ – элементы выборки;
ГС – генеральная совокупность;
к – коэффициент проверки;
УС – уровень существенности.
Из
генеральной совокупности исключаются элементы наибольших значений и ключевые
значения. По условию задачи они отсутствуют. Тогда:
ЭВ
= (500000 ∗ 0,7)/1000 =
35.
Коэффициент
проверки равен 0,7, так как система внутреннего контроля эффективна, в
бухгалтерском учете по данным предыдущих проверок нет существенных искажений.
Далее
определяются элементы выборки методом случайного отбора по формуле:
(ЗК
– ЗН) ∗ СЧ + ЗН,
ЗК – значение конечное;
ЗН – значение начальное;
СЧ – случайное число, взятое из таблицы
случайных чисел случайным образом.
Подставив ЗН, ЗК, имеем:
(1050
– 50) ∗ СЧ + 50.
Используя данный алгоритм, находим семь
первых значений выборки:
1000*0,4877+50=538;
1000*0,0441+50=94;
1000*0,2017+50=252;
1000*0,1797+50=230;
1000*0,7575+50=808;
1000*0,9374+50=987;
1000*0,3228+50=373.
Пример 2.
Аудитор
выборочно изучил 120 документов из 1250. При этом выявленная величина ошибок
(искажений) составила 1850 руб. Определить величину суммарной ошибки во всей
совокупности документов. Какими должны быть выводы и действия аудитора, если
приемлемой считается величина ошибки 17800 руб.?
Решение:
Суммарная
ошибка совокупности рассчитывается по формуле:
Ос=Ов*С/В,
где Ос – ошибка совокупности;
ОВ – ошибка выборки;
С – объем совокупности в целом;
В – объем исследуемой выборки.
Ос=1850*1250/120=19271
руб.
Суммарная
ошибка совокупности (19271 руб.) больше приемлемой величины ошибки (17800
руб.). Поскольку исчисленная суммарная ошибка выше приемлемой величины ошибки,
то финансовая отчетность считается неприемлемой. Аудитор может либо определить,
действительно ли завышенное показание превышает 17800 руб., либо представить заключение
с оговоркой или отрицательное заключение.
Практическое задание
Задание 1
Тест
|
1. Величина допустимой ошибки выборки |
|
|
А) |
Показателя оценки системы внутреннего |
|
Б) |
Уровня |
|
В) |
Риска необнаружения |
|
2. Допустимая ошибка в процессе аудита должна определяться в стадии: |
|
|
А) |
Планирования |
|
Б) |
Ознакомления с |
|
В) |
Проведения проверки |
|
3. Если ошибка в проверяемой совокупности больше допустимой, аудитор |
|
|
А) |
Расширить круг |
|
Б) |
Отказаться от |
|
В) |
Сообщить о данном |
|
4. Методы распространения результатов выборки на всю совокупность: |
|
|
А) |
Четко |
|
Б) |
Определяется |
|
В) |
Устанавливаются |
|
5. Выбор метода построения выборки определяется: |
|
|
А) |
Аудитором в каждой |
|
Б) |
Внутренними |
|
В) |
Стандартами |
|
6. Основная цель стратификации генеральной совокупности: |
|
|
А) |
Распределить |
|
Б) |
Уменьшить риск |
|
В) |
Увеличить допустимую |
|
7. |
|
|
А) |
Ошибки в |
|
Б) |
Арифметические |
|
В) |
Действия, |
|
8. |
|
|
А) |
Количественных |
|
Б) |
Качественных |
|
В) |
Не являются |
|
9.Максимальный |
|
|
А) |
Общая ошибка |
|
Б) |
Аномальная |
|
В) |
Допустимая |
|
10. Если элементы генеральной совокупности не имеют равную |
|
|
А) |
Репрезентативной |
|
Б) |
Нерепрезентативной |
|
В) |
Случайной |
|
11.Аудиторская организация может применять нерепрезентативную выборку |
|
|
А) |
Если не следует |
|
Б) |
Большого объема |
|
В) |
Неоднородности |
|
12.Полный набор элементов, из которых аудитор проводит выборку для |
|
|
А) |
Генеральная |
|
Б) |
Выборочная совокупность |
|
В) |
Стратифицированная |
|
13. |
|
|
А) |
Полный набор |
|
Б) |
Индивидуальные |
|
В) |
Применение |
|
14. |
|
|
А) |
Систематический |
|
Б) |
Бессистемный |
|
В) |
Систематизированный |
|
15. Аудиторская выборка это: а) один из методов аудиторской проверки; |
|
|
А) |
а, б |
|
Б) |
а, б, в |
|
В) |
а, в |
|
16. Отбор элементов из генеральной совокупности через определенный |
|
|
А) |
Статистический |
|
Б) |
Систематический |
|
В) |
Бессистемный |
Задание 2
Задача 2.1
Аудитор должен подтвердить оценку товарных
запасов. По данным бухгалтерского учета стоимость материальных ценностей на
складе составляет 600 000 руб., стоимость выборки — 195 000
руб., обнаруженная ошибка— 3000 руб.
Следует определить планируемую ожидаемую ошибку в
генеральной совокупности.
Задача 2.2.
Размер выборочной
совокупности —250 документов, размер
генеральной совокупности — 2500
Необходимо установить
выборочный интервал и порядок проведения случайной выборки.
Задание 3.
Составить кроссворд
Ключевые слова —
|
А |
У |
Д |
И |
Т |
О |
Р |
С |
К |
А |
Я |
хх |
В |
Ы |
Б |
О |
Р |
К |
А |
Аудитор
Существенность
Репрезентативность
Стратификация
Компиляция
Независимость
Планирование
Конфидициальность
Достаточность (в аудите)
Программа (аудита)
Рекомендованная
литература:
1.
ЭБС
«Юрайт»: Аудит: учебник для СПО/ Н.А.Казакова и др. ; под ред. Н.А.Казаковой — 3-е изд., перераб. и доп. — М.:Изд-во Юрайт,
2018. — 409 с. — (Серия: Профессиональное образование). — ISBN
978-5-534-09320-9/
2. Парушина, Н. В. Аудит: практикум : учеб. пособие /
Н.В. Парушина, С.П. Суворова, Е.В. Галкина. — 3-е изд., перераб. и доп. —
Москва : ИД «ФОРУМ» : ИНФРА-М, 2017. — 286 с. — (Профессиональное образование).
— ISBN 978-5-16-102859-9. — Текст : электронный. — URL:
https://znanium.com/catalog/product/773992
3. Парушина, Н. В.
Аудит: практикум : учеб. пособие / Н.В. Парушина, С.П. Суворова, Е.В. Галкина.
— 3-е изд., перераб. и доп. — Москва : ИД «ФОРУМ» : ИНФРА-М, 2017. — 286 с. —
(Профессиональное образование). — ISBN 978-5-16-102859-9. — Текст :
электронный. — URL: https://znanium.com/catalog/product/773992

















 ) при использовании типического отбора, пропорционального объему типических групп
) при использовании типического отбора, пропорционального объему типических групп














