Будем
рассматривать квантование
с равномерным шагом x=const, т.е. равномерное
квантование.
Как было отмечено в §
3.1.1. в процессе квантования неизбежно
возникает ошибка квантования .
Последовательность ошибок квантования
(kt), возникающая при квантовании
процесса с дискретным временем, называется
шумом квантования. Обычно шум квантования
предполагают стационарным эргодическим
случайным процессом.
Чаще всего
интерес представляют максимальное
значение ошибки квантования, ее среднее
значение , равное математическому
ожиданию шума и среднеквадратическое
отклонение ,
равное квадратному корню из дисперсии
шума
(она характеризует мощность шума
квантования). Все эти величины зависят
от способа округления, применяемого
при квантовании, кроме того
и
зависят от закона распределения w()
мгновенных значений сигнала в пределах
шага квантования.
Считая шаг квантования
x малым по сравнению с диапазоном
изменения сигнала, плотность w(x) в
пределах этого шага можно принять
равномерной, т.е.
.
Различают
квантование с округлением, с усечением
и с усечением модуля.
При квантовании
с округлением истинному значению отсчета
приписывает ближайший разрешенный
уровень квантования независимо от того,
находится он сверху или снизу. Очевидно,
что при этом
|
max=0.5x; |
(3.31а) |
Квантование
с округлением требует определенной
сложности в реализации. Проще выполняется
квантование с усечением, при котором
истинному значению отсчета приписывается
ближайший нижний уровень. При
этом
|
max=x; |
т.е.
максимальное значение погрешности в 2
раза больше, а
,
что приводит к накоплению погрешности
квантования при дальнейшей обработке
квантованной последовательности.
Промежуточное
положение по точности и сложности
реализации занимает квантование с
усечением модуля, которое для положительных
отсчетов является таким же, как и
квантование с усечением. Отрицательным
отсчетам приписывается ближайший
верхний уровень. При этом
то
есть накопление погрешностей не
происходит, но в 2 раза увеличивается
максимальная погрешность, и в 2 раза —
мощность шума квантования
.
Выбирая достаточно большее число уровней
квантования N, шаг квантования.
,
а следовательно и все рассмотренные
погрешности можно сделать необходимо
малыми. При неравномерном законе
распределения мгновенных значений
сигнала квантования с постоянным шагом
не
является оптимальным по критерию
минимума среднеквадратической ошибки
.
Квантуя участки с менее вероятными
значениями сигнала с большим шагом
значение
можно
уменьшить, при этом же количестве уровней
квантования.
3.3. Информация в непрерывных сообщениях
Для
того, чтобы оценить потенциальные
возможности передачи сообщений
по непрерывным каналам, необходимо
вести количественные информационные
характеристики непрерывных сообщений
и каналов.
Обобщим с этой целью понятие энтропии
и взаимной
информации
на ансамбли непрерывных сигналов.
Пусть
Х — случайная величина (сечение или
отсчет случайного процесса), определенная
в некоторой непрерывной области и ее
распределение вероятностей характеризуется
плотностью w(х).
Разобьем область
значений Х на небольшие интервалы
протяженностью x. Вероятность Рк
того, что хк<x<xк+
x, приблизительно равна w(хк)
x т.е.
|
Рк=Р( |
(3.32) |
причем
приближение тем точнее, чем меньше
интервал x. Степень положительности
такого события.
Если
заменить истинные значения Х в пределах
интервала x значениями хк
в начале интервала, то непрерывный
ансамбль заменится дискретным и его
энтропия в соответствии с (1.4)
определится, как
или
с учетом (3.32)
|
|
(3.33) |
Будем
теперь увеличивать точность определения
значения х, уменьшения интервал x. В
пределе при x0 получим
энтропию непрерывной случайной величины.
|
|
(3.34) |
Второй
член в полученном выражении стремится
к
и
совершенно не зависит от распределения
вероятностей Х. Это означает, что
собственная информация любой непрерывной
случайной величины бесконечно велика.
Физический смысл такого результата
становиться понятным, если учесть, что
в конечном диапазоне непрерывная
величина может принимать бесконечное
множество значений, поэтому вероятность
того, что ее реализация будет точно
равна какому-то наперед заданному
конкретному значению является бесконечно
малой величиной 0. В результате энтропия,
определенная в соответствии с (1.4),
характеризующая среднюю степень
неожиданности появления возможных
реализаций для любой непрерывной
случайной величины не зависит от ее
закона распределения и всегда равна
бесконечности. Поэтому для описания
информационных свойств непрерывных
величин необходимо ввести другие
характеристики. Это можно сделать, если
обратить внимание на то, что первое
слагаемое выражении (3.34) является
конечным и однозначно определяется
плотностью распределения вероятности
w(x). Его называют дифференциальной
энтропией и обозначают h(x):
|
|
(3.35) |
Дифференциальная
энтропия обладает следующими свойствами.
1.
Дифференциальная энтропия в отличии
от обычной энтропии дискретного источника
не является мерой собственной информации,
содержащейся в ансамбле значений
случайной величины Х. Она зависит от
масштаба Х и может принимать отрицательные
значения. Информационный смысл имеет
не сама дифференциальная энтропия, а
разность двух дифференциальных энтропий,
чем и объясняется ее название.
2.
Дифференциальная энтропия не меняется
при изменении всех возможных значений
случайной величины Х на постоянную
величину. Действительно, масштаб Х при
этом не меняется и
справедливо равенство
|
|
(3.36) |
Из
этого следует, что h(x) не зависит от
математического ожидания случайной
величины, т.к. изменяя все значения Х на
С мы тем самым изменяем на С и ее среднее,
то есть математическое ожидание.
3.
Дифференциальная энтропия аддитивна,
то есть для объединения ХY независимых
случайный величин Х и Y справедливо:
h(XY)=
h(X)+ h(Y).
Доказательство этого свойства
аналогично доказательству (1.8) аддитивности
обычной энтропии.
4. Из всех
непрерывных величин Х с фиксированной
дисперсией 2
наибольшую дифференциальную энтропию
имеет
величина с гауссовским распределением,
т.е.
|
|
(3.37) |
Доказательство
свойства проведем в два этапа: сначала
вычислим h(x) для гауссовского распределения,
задаваемого плотностью.
где
м — математическое ожидание,
а затем
докажем неравенство (3.37).
Подставив
(3.38) в (3.35) найдем<
Для
доказательства неравенства (3.37) зададимся
произвольным распределением (х) с
дисперсией 2
и математическим ожиданием m и вычислим
интеграл J вида
|
|
Но
в силу неравенства (1.7)
с учетом правила изменения основания
логарифмов (log t = log e ln t)
имеем:
|
|
|
|
так |
Таким
образом
,
откуда
.
Но
как только что было показано,
—
это дифференциальная энтропия гауссовского
распределения. Доказанное неравенство
и означает, что энтропия
гауссовского распределения
максимальна.
Попытаемся теперь
определить с помощью предельного
перехода взаимную
информацию между двумя непрерывными
случайными величинами X и Y. Разбив
области определения Х и Y соответственно
на небольшие интервалы x и y, заменим
эти величины дискретными так же, как
это делалось при выводе формулы
(3.34).
Исходя из выражения
(1.14) можно определить взаимную информацию
между величинами Х и Y .
|
|
(3.39) |
При
этом предельном переходе никаких явных
бесконечностей не появилось, т.е. взаимная
информация оказывается величиной
конечной, имеющей тот же смысл, что и
для дискретных сообщений.
С
учетом того, что
|
(x,y)= (y) |
равенство
(3.39) можно представить в виде
|
|
(3.40) |
Здесь
h(X) — определенная выражением (3.35)
дифференциальная энтропия Х, а
|
|
(3.41) |
h(X/Y)
— условная дифференциальная энтропия.
Можно показать, что во всех случаях
h(X/Y)h(X).
Формула
(3.40) имеет ту же форму, что и (1.13), а
отличается лишь заменой энтропии
дифференциальной энтропией. Легко
убедиться, что основные свойства 1 и 2
(см. пункт 1.3) взаимной информации,
описываемые равенствами (1.15)(1.17),
остаются справедливыми и в этом случае.
3.4 -энтропия
и -производительность
источника непрерывных сообщений
Как
было показано в § 3.3, в одном отсчете
любого непрерывного сообщения содержится
бесконечное количество собственной
информации. И тем не менее, непрерывные
сообщения (телефонные разговоры,
телепередачи) успешно передаются по
каналам связи. Это объясняется тем, что
на практике никогда не требуется
абсолютно точного воспроизведения
переданного сообщения, а для передачи
даже с очень высокой, но ограниченной
точностью, требуется конечное количество
информации, также как и при передаче
дискретных сообщений. Данное обстоятельство
и положено в основу определения
количественной меры собственной
информации, источников непрерывных
сообщений. В качестве такой меры,
принимается минимальное количество
информации, необходимое для воспроизведения
непрерывного сообщения с заданной
точностью. Очевидно, что при таком
подходе собственная информация зависит
не только от свойств источника сообщений,
но и от выбора параметра , характеризующего
точность воспроизведения. Возможны
различные подходы к определению в
зависимости от вида и назначения
передаваемой информации. Наиболее часто
в информационной технике в качестве
используют среднеквадратическое
отклонение между принятым у и переданным
х сигналами, отражающими непрерывные
сообщения, т.е.
|
|
(3.42) |
где
Х и Y – ансамбли сигналов, отражающих
исходное и воспроизведенное сообщения.
Два
варианта сообщения или сигнала,
различающиеся не более, чем на заданное
значение 0,
называются эквивалентными. Взаимная
информация
I(X,Y) между двумя эквивалентными процессами
X(t) и Y(t) может быть определена в соответствии
с (3.40) как
|
I(X,Y)=h(X)-h(X/Y), |
где
h(X) и h(X/Y) – соответственно дифференциальная
и условная дифференциальная энтропии.
Из приведенного выражения видно,
что величина I(X,Y) зависит не только от
собственного распределения (х) ансамбля
Х (см. (3.35)), но и от условного распределения
(x/y) (см. (3.41)), которое определяется
способом преобразования процесса X в
Y. Для характеристики собственной
информации, содержащейся в одном отсчете
процесса Х, нужно устранить ее зависимость
от способа преобразования сообщения Х
в эквивалентное ему сообщение Y. Этого
можно добиться, если под количеством
собственной информации или — энтропией
H(Х)
процесса Х понимать минимизированную
по всем распределениям (X/Y) величину
I(X,Y), при которой сообщения Х
и Y еще эквивалентны, т.е.
|
|
(3.43) |
Таким
образом,
— энтропия
определяет минимальное количество
информации, содержащейся в одном отсчете
непрерывного
сообщения,
необходимое для воспроизведения его с
заданной верностью.
Если ансамбль
сообщений Х представляет собой процесс
с дискретным
временем
с непрерывными отсчетами, то под
— производительностью источника понимают
величину
|
|
(3.44) |
где
с
– количество отсчетов сообщения,
выдаваемых в единицу времени.
В том
случае, когда Х — непрерывный случайный
процесс с ограниченным спектром, вся
информация, содержащаяся в его значениях,
эквивалентна информации, содержащейся
в отсчетах процесса, следующих друг за
другом с интервалом
,
(fm-граничная
частота спектра), т.е. со
скоростью
|
c=2 |
(3.45) |
При
этом
— производительность
источника или процесса по-прежнему
определяется выражением (3.44), где величина
с
рассчитывается из условия (3.45).
В том
случае, если следующие друг за другом
отсчеты процесса коррелированны
(взаимозависимы), величина Н(Х)
в (3.43) должна вычисляться с учетом
вероятностных связей между отсчетами.
Итак,
— производительность источника
непрерывных сообщений представляет
собой минимальное количество информации,
которое нужно создать источнику в
единицу времени, для воспроизведения
его сообщений с заданной верностью.
— производительность называют также
скоростью создания информации при
заданном критерии верности.
Максимально
возможная — производительность
непрерывного
источника Х обеспечивается при гауссовском
распределении Х с дисперсией
(при
этом условии h(X) максимальна (см. (3.37)).
Оценим значение
.
Рассмотрим случай, когда непрерывное
сообщение X(t) представляет собой
стационарный гауссовский процесс с
равномерным энергетическим спектром,
ограниченным частотой Fc,
и с заданной мощностью (дисперсией) Рх,
а критерий эквивалентности задан в
виде (3.42).
Будем считать, что заданная верность
воспроизведения обусловлена действием
аддитивной статистически не связанной
с сигналом помехи (t) с математическим
ожиданием М[]=0 и дисперсией (мощностью)
.
Исходный сигнал Х рассматриваем
как сумму воспроизводящего сигнала Y и
помехи:
|
X=Y+. |
При
этом, поскольку (x/y)= (y+/y)= (/y)=
(), то h(X/Y) полностью определяется
шумом воспроизведения (t). Поэтому max
h(X/Y)=max h(). Так как шум воспроизведения
имеет фиксированную дисперсию
,
то дифференциальная энтропия имеет
максимум (3.37) при гауссовском
распределении шума
|
|
В
свою очередь дифференциальная энтропия
гауссовского источника с дисперсией
.
|
|
Следовательно,
— энтропия на один отсчет
сообщения
|
|
(3.46) |
Величина
характеризует
минимальное отношение сигнал-шум, при
котором сообщения X(t) и Y(t) еще
эквивалентны.
Согласно теореме
Котельникова
шаг
дискретизации
,
а c=2
Fc.
При этом равномерность спектра сообщения
обеспечивает некоррелированность
отстоящих на t друг от друга отсчетов,
а гауссовский характер распределения
X(t) — их независимость. Следовательно,
в соответствии с (3.44)
|
|
или с учетом (3.46)
|
|
(3.47) |
Количество
информации,
выданное таким источником за время Тс
|
|
(3.48) |
Интересно
отметить, что правая часть выражения
(3.48) совпадает с наиболее общей
характеристикой сигнала, называемой
его объемом, если принять динамический
диапазон сигнала D=log
0.
Это означает, что объем сигнала равен
максимальному количеству информации,
которое может содержаться в сигнале
длительностью Тс.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Template:Unreferenced
The difference between the actual analog value and quantized digital value due is called quantization error. This error is due either to rounding or truncation.
Many physical quantities are actually quantized by physical entities. Examples of fields where this limitation applies include electronics (due to electrons), optics (due to photons), biology (due to DNA), and chemistry (due to molecules). This is sometimes known as the «quantum noise limit» of systems in those fields. This is a different manifestation of «quantization error,» in which theoretical models may be analog but physics occurs digitally. Around the quantum limit, the distinction between analog and digital quantities vanishes.
Quantization noise model of quantization error[]
File:Quanterr.png Quantization noise. The difference between the blue and red signals in the upper graph is the quantization error, which is «added» to the original signal and is the source of noise.
Quantization noise is a model of quantization error introduced by quantization in the analog-to-digital conversion (ADC) process in telecommunication systems and signal processing. It is a rounding error between the analogue input voltage to the ADC and the output digitized value. The noise is non-linear and signal-dependent. It can be modelled in several different ways.
In an ideal analog-to-digital converter, where the quantization error is uniformly distributed between −1/2 LSB and +1/2 LSB, and the signal has a uniform distribution covering all quantization levels, the signal-to-noise ratio (SNR) can be calculated from
The most common test signals that fulfil this are full amplitude triangle waves and sawtooth waves.
In this case a 16-bit ADC has a maximum signal-to-noise ratio of 6.0206 · 16=96.33 dB.
When the input signal is a full-amplitude sine wave the distribution of the signal is no longer uniform, and the corresponding equation is instead
Here, the quantization noise is once again assumed to be uniformly distributed. When the input signal has a high amplitude and a wide frequency spectrum this is the case.[1]
In this case a 16-bit ADC has a maximum signal-to-noise ratio of 98.09 dB.
For complex signals in high-resolution ADCs this is an accurate model. For low-resolution ADCs, low-level signals in high-resolution ADCs, and for simple waveforms the quantization noise is not uniformly distributed, making this model inaccurate.[2] In these cases the quantization noise distribution is strongly affected by the exact amplitude of the signal.
Template:Listen
References[]
- ↑ Template:Cite book
- ↑ Template:Cite book
See also[]
- Round-off error
- Dither
- Analog to digital converter
- Quantization
- Quantization noise
- Discretization error
- Signal-to-noise ratio
- Bit resolution
- SQNR
External links[]
- Quantization noise in Digital Computation, Signal Processing, and Control, Bernard Widrow and István Kollár, 2007.
- The Relationship of Dynamic Range to Data Word Size in Digital Audio Processing
- Round-Off Error Variance — derivation of noise power of q²/12 for round-off error
- Dynamic Evaluation of High-Speed, High Resolution D/A Converters Outlines HD, IMD and NPR measurements, also includes a derivation of quantization noise
- Signal to quantization noise in quantized sinusoidal
de:Quantisierungsrauschen
es:Ruido de cuantificación
ja:量子化雑音
ja:量子化誤差
pl:Szum kwantyzacji
ru:Шум квантования
Template:Unreferenced
The difference between the actual analog value and quantized digital value due is called quantization error. This error is due either to rounding or truncation.
Many physical quantities are actually quantized by physical entities. Examples of fields where this limitation applies include electronics (due to electrons), optics (due to photons), biology (due to DNA), and chemistry (due to molecules). This is sometimes known as the «quantum noise limit» of systems in those fields. This is a different manifestation of «quantization error,» in which theoretical models may be analog but physics occurs digitally. Around the quantum limit, the distinction between analog and digital quantities vanishes.
Quantization noise model of quantization error[]
File:Quanterr.png Quantization noise. The difference between the blue and red signals in the upper graph is the quantization error, which is «added» to the original signal and is the source of noise.
Quantization noise is a model of quantization error introduced by quantization in the analog-to-digital conversion (ADC) process in telecommunication systems and signal processing. It is a rounding error between the analogue input voltage to the ADC and the output digitized value. The noise is non-linear and signal-dependent. It can be modelled in several different ways.
In an ideal analog-to-digital converter, where the quantization error is uniformly distributed between −1/2 LSB and +1/2 LSB, and the signal has a uniform distribution covering all quantization levels, the signal-to-noise ratio (SNR) can be calculated from
The most common test signals that fulfil this are full amplitude triangle waves and sawtooth waves.
In this case a 16-bit ADC has a maximum signal-to-noise ratio of 6.0206 · 16=96.33 dB.
When the input signal is a full-amplitude sine wave the distribution of the signal is no longer uniform, and the corresponding equation is instead
Here, the quantization noise is once again assumed to be uniformly distributed. When the input signal has a high amplitude and a wide frequency spectrum this is the case.[1]
In this case a 16-bit ADC has a maximum signal-to-noise ratio of 98.09 dB.
For complex signals in high-resolution ADCs this is an accurate model. For low-resolution ADCs, low-level signals in high-resolution ADCs, and for simple waveforms the quantization noise is not uniformly distributed, making this model inaccurate.[2] In these cases the quantization noise distribution is strongly affected by the exact amplitude of the signal.
Template:Listen
References[]
- ↑ Template:Cite book
- ↑ Template:Cite book
See also[]
- Round-off error
- Dither
- Analog to digital converter
- Quantization
- Quantization noise
- Discretization error
- Signal-to-noise ratio
- Bit resolution
- SQNR
External links[]
- Quantization noise in Digital Computation, Signal Processing, and Control, Bernard Widrow and István Kollár, 2007.
- The Relationship of Dynamic Range to Data Word Size in Digital Audio Processing
- Round-Off Error Variance — derivation of noise power of q²/12 for round-off error
- Dynamic Evaluation of High-Speed, High Resolution D/A Converters Outlines HD, IMD and NPR measurements, also includes a derivation of quantization noise
- Signal to quantization noise in quantized sinusoidal
de:Quantisierungsrauschen
es:Ruido de cuantificación
ja:量子化雑音
ja:量子化誤差
pl:Szum kwantyzacji
ru:Шум квантования
Ошибка квантования
- Ошибка квантования
-
Шум квантования — ошибки, возникающие при оцифровке аналогового сигнала. В зависимости от типа аналого-цифрового преобразования могут возникать из-за округления (до определённого разряда) сигнала или усечения (отбрасывания младших разрядов) сигнала.
Содержание
- 1 Математическое описание
- 1.1 Модель
- 1.2 Детерминированные оценки
- 1.3 Вероятностные оценки
- 2 См. также
- 3 Ссылки
Математическое описание
Модель
Шум квантования можно представить как аддитивный дискретный сигнал
, учитывающий ошибки квантования. Если
— входной сигнал квантователя, а
— его передаточная функция, то имеем следующую линейную модель шума квантования:
Линейная модель используется для аналитического исследования свойств шума квантования.
Детерминированные оценки
Детерминированные оценки позволяют определить абсолютные границы шума квантования:
,
где
— число разрядов квантования (сигнала
),
— шаг квантования
— при округлении
— при усечении.
Вероятностные оценки
Вероятностные оценки основаны на представлении ошибок квантования (сигнала e(nT)) как случайного шумоподобного процесса. Допущения, вводимые относительно шума квантования:
В таком случае математическое ожидание
и дисперсия
шума квантования определяется следующим образом (при квантовании используется дополнительный код):
См. также
- Отношение сигнал-шум
- Дизеринг
Ссылки
- Round-Off Error Variance(англ.)
- «Цифровая обработка сигналов». Л. М. Гольденберг, Б. Д. Матюшкин — М.: Радио и связь, 1985
- 1 Математическое описание
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Ошибка квантования» в других словарях:
-
ошибка квантования — Ошибка, вызванная несоответствием формы выходного (квантованного) и входного (аналогового) сигналов. Зависит от величины шага квантования и частоты дискретизации. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь… … Справочник технического переводчика
-
ошибка квантования — kvantavimo paklaida statusas T sritis automatika atitikmenys: angl. quantization error vok. Quantisierungsfehler, m rus. ошибка квантования, f pranc. erreur de quantification, f … Automatikos terminų žodynas
-
ошибка округления — погрешность, возникающая при квантовании в результате округления амплитуды сигнала до ближайшего уровня квантования. Причина возникновения шума квантования … Русский индекс к Англо-русскому словарь по музыкальной терминологии
-
Аналого-цифровой преобразователь — Четырёхканальный аналого цифровой преобразователь Аналого цифровой преобразователь[1][2] … Википедия
-
АЦП — Четырёхканальный аналого цифровой преобразователь Аналого цифровой преобразователь (АЦП, ADC) устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал). Обратное преобразование осуществляется при помощи ЦАП (DAC)… … Википедия
-
Цифро-аналоговое преобразование — Четырёхканальный аналого цифровой преобразователь Аналого цифровой преобразователь (АЦП, ADC) устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал). Обратное преобразование осуществляется при помощи ЦАП (DAC)… … Википедия
-
шум дробления — Разновидность шума квантования, возникающего при аналого цифровом преобразовании сигнала малого уровня, когда ошибка квантования для разных отсчетов становится не равновероятной. Эффективной мерой снижения шума дробления является использование… … Справочник технического переводчика
-
Quantisierungsfehler — kvantavimo paklaida statusas T sritis automatika atitikmenys: angl. quantization error vok. Quantisierungsfehler, m rus. ошибка квантования, f pranc. erreur de quantification, f … Automatikos terminų žodynas
-
erreur de quantification — kvantavimo paklaida statusas T sritis automatika atitikmenys: angl. quantization error vok. Quantisierungsfehler, m rus. ошибка квантования, f pranc. erreur de quantification, f … Automatikos terminų žodynas
-
kvantavimo paklaida — statusas T sritis automatika atitikmenys: angl. quantization error vok. Quantisierungsfehler, m rus. ошибка квантования, f pranc. erreur de quantification, f … Automatikos terminų žodynas


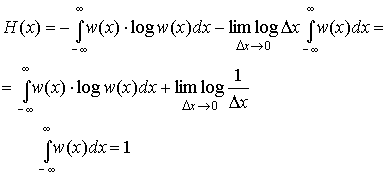

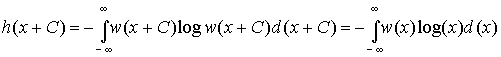


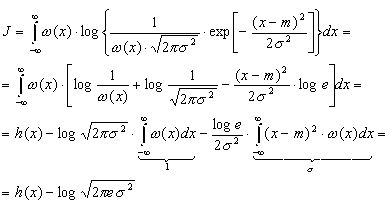



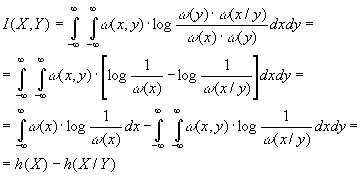
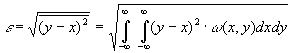



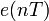 , учитывающий ошибки квантования. Если
, учитывающий ошибки квантования. Если 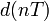 — входной сигнал квантователя, а
— входной сигнал квантователя, а ![F[] !](https://dic.academic.ru/pictures/wiki/files/100/d9a67617bcc2874e5dcee5df989f5f52.png) — его передаточная функция, то имеем следующую линейную модель шума квантования:
— его передаточная функция, то имеем следующую линейную модель шума квантования:![e(nT) = F[d(nT)] - d(nT) !](https://dic.academic.ru/pictures/wiki/files/48/0bf1032d4991203805b67afcb4832b06.png)
![|max[e(nT)]| = frac{1}{m} 2^{-b} = frac{1}{m} Q](https://dic.academic.ru/pictures/wiki/files/97/a2a6cf1f23b3dd15c4169c59cd1338f4.png) ,
,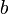 — число разрядов квантования (сигнала
— число разрядов квантования (сигнала 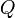 — шаг квантования
— шаг квантования 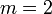 — при округлении
— при округлении 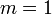 — при усечении.
— при усечении.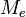 и дисперсия
и дисперсия 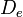 шума квантования определяется следующим образом (при квантовании используется дополнительный код):
шума квантования определяется следующим образом (при квантовании используется дополнительный код):