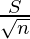What Is the Standard Error?
The standard error (SE) of a statistic is the approximate standard deviation of a statistical sample population.
The standard error is a statistical term that measures the accuracy with which a sample distribution represents a population by using standard deviation. In statistics, a sample mean deviates from the actual mean of a population; this deviation is the standard error of the mean.
Key Takeaways
- The standard error (SE) is the approximate standard deviation of a statistical sample population.
- The standard error describes the variation between the calculated mean of the population and one which is considered known, or accepted as accurate.
- The more data points involved in the calculations of the mean, the smaller the standard error tends to be.
Standard Error
Understanding Standard Error
The term «standard error» is used to refer to the standard deviation of various sample statistics, such as the mean or median. For example, the «standard error of the mean» refers to the standard deviation of the distribution of sample means taken from a population. The smaller the standard error, the more representative the sample will be of the overall population.
The relationship between the standard error and the standard deviation is such that, for a given sample size, the standard error equals the standard deviation divided by the square root of the sample size. The standard error is also inversely proportional to the sample size; the larger the sample size, the smaller the standard error because the statistic will approach the actual value.
The standard error is considered part of inferential statistics. It represents the standard deviation of the mean within a dataset. This serves as a measure of variation for random variables, providing a measurement for the spread. The smaller the spread, the more accurate the dataset.
Standard error and standard deviation are measures of variability, while central tendency measures include mean, median, etc.
Formula and Calculation of Standard Error
The standard error of an estimate can be calculated as the standard deviation divided by the square root of the sample size:
SE = σ / √n
where
- σ = the population standard deviation
- √n = the square root of the sample size
If the population standard deviation is not known, you can substitute the sample standard deviation, s, in the numerator to approximate the standard error.
Requirements for Standard Error
When a population is sampled, the mean, or average, is generally calculated. The standard error can include the variation between the calculated mean of the population and one which is considered known, or accepted as accurate. This helps compensate for any incidental inaccuracies related to the gathering of the sample.
In cases where multiple samples are collected, the mean of each sample may vary slightly from the others, creating a spread among the variables. This spread is most often measured as the standard error, accounting for the differences between the means across the datasets.
The more data points involved in the calculations of the mean, the smaller the standard error tends to be. When the standard error is small, the data is said to be more representative of the true mean. In cases where the standard error is large, the data may have some notable irregularities.
The standard deviation is a representation of the spread of each of the data points. The standard deviation is used to help determine the validity of the data based on the number of data points displayed at each level of standard deviation. Standard errors function more as a way to determine the accuracy of the sample or the accuracy of multiple samples by analyzing deviation within the means.
Standard Error vs. Standard Deviation
The standard error normalizes the standard deviation relative to the sample size used in an analysis. Standard deviation measures the amount of variance or dispersion of the data spread around the mean. The standard error can be thought of as the dispersion of the sample mean estimations around the true population mean. As the sample size becomes larger, the standard error will become smaller, indicating that the estimated sample mean value better approximates the population mean.
Example of Standard Error
Say that an analyst has looked at a random sample of 50 companies in the S&P 500 to understand the association between a stock’s P/E ratio and subsequent 12-month performance in the market. Assume that the resulting estimate is -0.20, indicating that for every 1.0 point in the P/E ratio, stocks return 0.2% poorer relative performance. In the sample of 50, the standard deviation was found to be 1.0.
The standard error is thus:
SE = 1.0/√50 = 1/7.07 = 0.141
Therefore, we would report the estimate as -0.20% ± 0.14, giving us a confidence interval of (-0.34 — -0.06). The true mean value of the association of the P/E on returns of the S&P 500 would therefore fall within that range with a high degree of probability.
Say now that we increase the sample of stocks to 100 and find that the estimate changes slightly from -0.20 to -0.25, and the standard deviation falls to 0.90. The new standard error would thus be:
SE = 0.90/√100 = 0.90/10 = 0.09.
The resulting confidence interval becomes -0.25 ± 0.09 = (-0.34 — -0.16), which is a tighter range of values.
What Is Meant by Standard Error?
Standard error is intuitively the standard deviation of the sampling distribution. In other words, it depicts how much disparity there is likely to be in a point estimate obtained from a sample relative to the true population mean.
What Is a Good Standard Error?
Standard error measures the amount of discrepancy that can be expected in a sample estimate compared to the true value in the population. Therefore, the smaller the standard error the better. In fact, a standard error of zero (or close to it) would indicate that the estimated value is exactly the true value.
How Do You Find the Standard Error?
The standard error takes the standard deviation and divides it by the square root of the sample size. Many statistical software packages automatically compute standard errors.
The Bottom Line
The standard error (SE) measures the dispersion of estimated values obtained from a sample around the true value to be found in the population. Statistical analysis and inference often involves drawing samples and running statistical tests to determine associations and correlations between variables. The standard error thus tells us with what degree of confidence we can expect the estimated value to approximate the population value.
What Is the Standard Error?
The standard error (SE) of a statistic is the approximate standard deviation of a statistical sample population.
The standard error is a statistical term that measures the accuracy with which a sample distribution represents a population by using standard deviation. In statistics, a sample mean deviates from the actual mean of a population; this deviation is the standard error of the mean.
Key Takeaways
- The standard error (SE) is the approximate standard deviation of a statistical sample population.
- The standard error describes the variation between the calculated mean of the population and one which is considered known, or accepted as accurate.
- The more data points involved in the calculations of the mean, the smaller the standard error tends to be.
Standard Error
Understanding Standard Error
The term «standard error» is used to refer to the standard deviation of various sample statistics, such as the mean or median. For example, the «standard error of the mean» refers to the standard deviation of the distribution of sample means taken from a population. The smaller the standard error, the more representative the sample will be of the overall population.
The relationship between the standard error and the standard deviation is such that, for a given sample size, the standard error equals the standard deviation divided by the square root of the sample size. The standard error is also inversely proportional to the sample size; the larger the sample size, the smaller the standard error because the statistic will approach the actual value.
The standard error is considered part of inferential statistics. It represents the standard deviation of the mean within a dataset. This serves as a measure of variation for random variables, providing a measurement for the spread. The smaller the spread, the more accurate the dataset.
Standard error and standard deviation are measures of variability, while central tendency measures include mean, median, etc.
Formula and Calculation of Standard Error
The standard error of an estimate can be calculated as the standard deviation divided by the square root of the sample size:
SE = σ / √n
where
- σ = the population standard deviation
- √n = the square root of the sample size
If the population standard deviation is not known, you can substitute the sample standard deviation, s, in the numerator to approximate the standard error.
Requirements for Standard Error
When a population is sampled, the mean, or average, is generally calculated. The standard error can include the variation between the calculated mean of the population and one which is considered known, or accepted as accurate. This helps compensate for any incidental inaccuracies related to the gathering of the sample.
In cases where multiple samples are collected, the mean of each sample may vary slightly from the others, creating a spread among the variables. This spread is most often measured as the standard error, accounting for the differences between the means across the datasets.
The more data points involved in the calculations of the mean, the smaller the standard error tends to be. When the standard error is small, the data is said to be more representative of the true mean. In cases where the standard error is large, the data may have some notable irregularities.
The standard deviation is a representation of the spread of each of the data points. The standard deviation is used to help determine the validity of the data based on the number of data points displayed at each level of standard deviation. Standard errors function more as a way to determine the accuracy of the sample or the accuracy of multiple samples by analyzing deviation within the means.
Standard Error vs. Standard Deviation
The standard error normalizes the standard deviation relative to the sample size used in an analysis. Standard deviation measures the amount of variance or dispersion of the data spread around the mean. The standard error can be thought of as the dispersion of the sample mean estimations around the true population mean. As the sample size becomes larger, the standard error will become smaller, indicating that the estimated sample mean value better approximates the population mean.
Example of Standard Error
Say that an analyst has looked at a random sample of 50 companies in the S&P 500 to understand the association between a stock’s P/E ratio and subsequent 12-month performance in the market. Assume that the resulting estimate is -0.20, indicating that for every 1.0 point in the P/E ratio, stocks return 0.2% poorer relative performance. In the sample of 50, the standard deviation was found to be 1.0.
The standard error is thus:
SE = 1.0/√50 = 1/7.07 = 0.141
Therefore, we would report the estimate as -0.20% ± 0.14, giving us a confidence interval of (-0.34 — -0.06). The true mean value of the association of the P/E on returns of the S&P 500 would therefore fall within that range with a high degree of probability.
Say now that we increase the sample of stocks to 100 and find that the estimate changes slightly from -0.20 to -0.25, and the standard deviation falls to 0.90. The new standard error would thus be:
SE = 0.90/√100 = 0.90/10 = 0.09.
The resulting confidence interval becomes -0.25 ± 0.09 = (-0.34 — -0.16), which is a tighter range of values.
What Is Meant by Standard Error?
Standard error is intuitively the standard deviation of the sampling distribution. In other words, it depicts how much disparity there is likely to be in a point estimate obtained from a sample relative to the true population mean.
What Is a Good Standard Error?
Standard error measures the amount of discrepancy that can be expected in a sample estimate compared to the true value in the population. Therefore, the smaller the standard error the better. In fact, a standard error of zero (or close to it) would indicate that the estimated value is exactly the true value.
How Do You Find the Standard Error?
The standard error takes the standard deviation and divides it by the square root of the sample size. Many statistical software packages automatically compute standard errors.
The Bottom Line
The standard error (SE) measures the dispersion of estimated values obtained from a sample around the true value to be found in the population. Statistical analysis and inference often involves drawing samples and running statistical tests to determine associations and correlations between variables. The standard error thus tells us with what degree of confidence we can expect the estimated value to approximate the population value.
Генеральная и выборочные совокупности.
Изложенные выше
методы дают возможность достаточно
полно охарактеризовать биологические
совокупности. Каждая совокупность может
быть представлена в виде ряда распределения
значений изучаемого в совокупности
признака. Для ряда распределения можно
определить статистические показатели,
указывающие на наиболее типичный уровень
признака и на степень вариации (разброса)
отдельных единиц совокупности вокруг
этого уровня. Это статистические
показатели, выраженные одним значением
(точечные оценки): математическое
ожидание (среднее арифметическое),
дисперсия, среднее квадратическое
отклонение и интервальные оценки для
заданного уровня вероятности. Так как
все эти показатели – статистические
величины, т.е. основаны на изучении
массовых явлений, возникает очень важный
теоретический и практический вопрос –
насколько они достоверны. Проблема
достоверности занимает важное место в
статистике. В рассмотренных примерах
мы изучали так называемые выборочные
совокупности. Так, для исследования
распределения студентов по возрасту
взята выборка из 100 человек первого
курса. Можно было исследовать выборки,
состоящие из 200, 300 и т.д. человек. Наиболее
общую совокупность, подлежащих изучению
объектов называют генеральной. В
пределе она может рассматриваться как
состоящая из бесконечно большого
количества единиц. Изучить такую
совокупность на практике не представляется
возможным. Для того чтобы по данным
выборки можно было достаточно уверенно
судить об интересующем признаке
генеральной совокупности, выборка
должна правильно представлять пропорции
генеральной совокупности, то есть должна
быть репрезентативной (представительной).
Выборка считается репрезентативной,
если каждый объект выборки отобран
случайно из генеральной совокупности,
то есть все объекты имеют одинаковую
вероятность попасть в выборку. В какой
же мере выборочные совокупности отражают
свойства генеральной совокупности? Как
генеральная, так и выборочные совокупности
характеризуются одинаковыми
закономерностями случайной вариации,
которые можно описать статистическими
показателями: средней арифметической
величиной и средним квадратическим
отклонением. Пусть средняя арифметическая
генеральной совокупности обозначается
, среднее
квадратическое отклонение – ,
соответствующие параметры выборки –
и s. Предположим, для
изучения среднего возраста у студентов
первого курса мы взяли 5 групп. Средние
арифметические этих выборок
образуют свой ряд распределения. При
достаточном количестве вариант в выборке
(n>30), распределение
выборочных средних также подчиняются
нормальному закону. Средней арифметической
величиной этого ряда будет являться
средняя генеральной совокупности .
Вариация же выборочных средних вокруг
может быть
измерена своим средним квадратическим
(стандартным) отклонением. Это отклонение
получило название средней квадратической
ошибки (стандартной ошибки). Стандартная
ошибка может быть вычислена по формуле:
(22)
Так
как
генеральной совокупности неизвестна,
а разница между сигмами генеральной
совокупности и выборки невелика, то в
формуле (22) используют среднее
квадратическое отклонение выборки s:
,
(23)
где
n
– объем выборочной совокупности. Из
формулы (23) следует, что величина
стандартной ошибки обратно пропорциональна
численности выборочной совокупности.
Зная среднюю арифметическую выборочной
совокупности и величину стандартной
ошибки, можно определить интервал, в
котором находится значение средней
генеральной совокупности. Аналогично
уравнению (20) критерий нормированного
отклонения t
для распределения средних арифметических
выборок можно определить как:
t=
,
отсюда
величина доверительного интервала для
генеральной средней:
=
t
.
(24)
Для
выборочной совокупности распределения
студентов по возрасту, доверительный
интервал для генеральной средней с
вероятностью 0,95 будет равен:
=
=21,30,62
(лет).
Таким
образом, стандартная ошибка показывает
степень близости средней арифметической
выборки к генеральной средней.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что такое Стандартная ошибка?
Стандартная ошибка (SE) статистики – это приблизительное стандартное отклонение статистической выборки. Стандартная ошибка – это статистический термин, который измеряет точность, с которой выборочное распределение представляет генеральную совокупность с помощью стандартного отклонения. В статистике выборочное среднее отклоняется от фактического среднего для генеральной совокупности; это отклонение представляет собой стандартную ошибку среднего.
Ключевые моменты
- Стандартная ошибка – это приблизительное стандартное отклонение статистической выборки.
- Стандартная ошибка может включать вариацию между вычисленным средним для генеральной совокупности и тем, которое считается известным или принимаемым как точное.
- Чем больше точек данных участвует в расчетах среднего, тем меньше стандартная ошибка.
Понимание стандартной ошибки
Термин «стандартная ошибка» используется для обозначения стандартного отклонения различных статистических данных выборки, таких как среднее или медианное значение. Например, «стандартная ошибка среднего» относится к стандартному отклонению распределения выборочных средних, взятых из генеральной совокупности. Чем меньше стандартная ошибка, тем более репрезентативной будет выборка для генеральной совокупности.
Связь между стандартной ошибкой и стандартным отклонением такова, что для данного размера выборки стандартная ошибка равна стандартному отклонению, деленному на квадратный корень из размера выборки. Стандартная ошибка также обратно пропорциональна размеру выборки; Чем больше размер выборки, тем меньше стандартная ошибка, поскольку статистика приближается к фактическому значению.
Стандартная ошибка считается частью выводимой статистики. Он представляет собой стандартное отклонение среднего значения в наборе данных. Это служит мерой вариации случайных величин, обеспечивая измерение спреда. Чем меньше разброс, тем точнее набор данных.
Краткая справка
Стандартная ошибка и стандартное отклонение – это меры изменчивости, в то время как меры центральной тенденции включают среднее значение, медианное значение и т. Д.
Требования к стандартной ошибке
Когда производится выборка из генеральной совокупности , обычно рассчитывается среднее или среднее значение. Стандартная ошибка может включать разброс между вычисленным средним для генеральной совокупности и тем, которое считается известным или принимаемым как точное. Это помогает компенсировать любые случайные неточности, связанные со сбором пробы.
В случаях, когда собирается несколько образцов, среднее значение каждой выборки может незначительно отличаться от других, создавая разброс между переменными. Этот разброс чаще всего измеряется как стандартная ошибка, учитывающая различия между средними значениями в наборах данных.
Чем больше точек данных участвует в расчетах среднего, тем меньше стандартная ошибка. Когда стандартная ошибка мала, данные считаются более репрезентативными для истинного среднего значения. В случаях, когда стандартная ошибка велика, данные могут иметь некоторые заметные отклонения.
Стандартное отклонение – это представление разброса каждой точки данных. Стандартное отклонение используется для определения достоверности данных на основе количества точек данных, отображаемых на каждом уровне стандартного отклонения. Стандартные ошибки больше служат способом определения точности образца или точности нескольких образцов путем анализа отклонения в пределах средних.
Загрузить PDF
Загрузить PDF
Стандартной ошибкой называется величина, которая характеризует стандартное (среднеквадратическое) отклонение выборочного среднего. Другими словами, эту величину можно использовать для оценки точности выборочного среднего. Множество областей применения стандартной ошибки по умолчанию предполагают нормальное распределение. Если вам нужно рассчитать стандартную ошибку, перейдите к шагу 1.
-
1
Запомните определение среднеквадратического отклонения. Среднеквадратическое отклонение выборки – это мера рассеянности значения. Среднеквадратическое отклонение выборки обычно обозначается буквой s. Математическая формула среднеквадратического отклонения приведена выше.
-
2
Узнайте, что такое истинное среднее значение. Истинное среднее является средним группы чисел, включающим все числа всей группы – другими словами, это среднее всей группы чисел, а не выборки.
-
3
Научитесь рассчитывать среднеарифметическое значение. Среднеаримфетическое означает попросту среднее: сумму значений собранных данных, разделенную на количество значений этих данных.
-
4
Узнайте, что такое выборочное среднее. Когда среднеарифметическое значение основано на серии наблюдений, полученных в результате выборок из статистической совокупности, оно называется “выборочным средним”. Это среднее выборки чисел, которое описывает среднее значение лишь части чисел из всей группы. Его обозначают как:
-
5
Усвойте понятие нормального распределения. Нормальные распределения, которые используются чаще других распределений, являются симметричными, с единичным максимумом в центре – на среднем значении данных. Форма кривой подобна очертаниям колокола, при этом график равномерно опускается по обе стороны от среднего. Пятьдесят процентов распределения лежит слева от среднего, а другие пятьдесят процентов – справа от него. Рассеянность значений нормального распределения описывается стандартным отклонением.
-
6
Запомните основную формулу. Формула для вычисления стандартной ошибки приведена выше.
Реклама
-
1
Рассчитайте выборочное среднее. Чтобы найти стандартную ошибку, сначала нужно определить среднеквадратическое отклонение (поскольку среднеквадратическое отклонение s входит в формулу для вычисления стандартной ошибки). Начните с нахождения средних значений. Выборочное среднее выражается как среднее арифметическое измерений x1, x2, . . . , xn. Его рассчитывают по формуле, приведенной выше.
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
Вы сможете рассчитать выборочное среднее, подставив значения массы в формулу:
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
-
2
Вычтите выборочное среднее из каждого измерения и возведите полученное значение в квадрат. Как только вы получите выборочное среднее, вы можете расширить вашу таблицу, вычтя его из каждого измерения и возведя результат в квадрат.
- Для нашего примера расширенная таблица будет иметь следующий вид:
-
3
Найдите суммарное отклонение ваших измерений от выборочного среднего. Общее отклонение – это сумма возведенных в квадрат разностей от выборочного среднего. Чтобы определить его, сложите ваши новые значения.
- В нашем примере нужно будет выполнить следующий расчет:
Это уравнение дает сумму квадратов отклонений измерений от выборочного среднего.
- В нашем примере нужно будет выполнить следующий расчет:
-
4
Рассчитайте среднеквадратическое отклонение ваших измерений от выборочного среднего. Как только вы будете знать суммарное отклонение, вы сможете найти среднее отклонение, разделив ответ на n -1. Обратите внимание, что n равно числу измерений.
- В нашем примере было сделано 5 измерений, следовательно n – 1 будет равно 4. Расчет нужно вести следующим образом:
-
5
Найдите среднеквадратичное отклонение. Сейчас у вас есть все необходимые значения для того, чтобы воспользоваться формулой для нахождения среднеквадратичного отклонения s.
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
Следовательно, среднеквадратичное отклонение равно 0,0071624.
Реклама
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
-
1
Чтобы вычислить стандартную ошибку, воспользуйтесь базовой формулой со среднеквадратическим отклонением.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Таким образом в нашем примере стандартная ошибка (среднеквадратическое отклонение выборочного среднего) составляет 0,0032031 грамма.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Советы
- Стандартную ошибку и среднеквадратическое отклонение часто путают. Обратите внимание, что стандартная ошибка описывает среднеквадратическое отклонение выборочного распределения статистических данных, а не распределения отдельных значений
- В научных журналах понятия стандартной ошибки и среднеквадратического отклонения несколько размыты. Для объединения двух величин используется знак ±.
Реклама
Об этой статье
Эту страницу просматривали 48 345 раз.
Была ли эта статья полезной?
Стандартная ошибка относится к стандартному отклонению набора данных, что является важной статистической метрикой. Эту формулу можно использовать для определения точности выборки, отражающей генеральную совокупность. Формула стандартной ошибки представляет собой расхождение между средним значением выборки и средним значением генеральной совокупности.
Стандартная ошибка
Термин «выборка» в статистике относится к определенному набору информации, которая генерируется. Полученные нами данные о росте некоторых людей в населенном пункте, например, могут быть выборочными. Популяция — это совокупность людей, из которых мы делаем выборку. Есть несколько способов определить популяцию, и мы всегда должны четко понимать, что представляет собой популяция. Этот набор требует большого количества вычислений.
Стандартная ошибка показывает, насколько хорошо данная выборка представляет генеральную совокупность. Стандартная ошибка указывает, насколько хорошо среднее значение выборки предсказывает реальное среднее значение генеральной совокупности.
Формула
Формула SE используется для определения надежности выборки, представляющей совокупность. Выборочное среднее, которое отличается от предоставленной генеральной совокупности и выражается как:
SE =
where,
- S denotes standard deviation of the data
- n denotes the number of observations
Примеры проблем
Вопрос 1: Найдите стандартную ошибку для выборки данных: 1, 2, 3, 4, 5.
Решение:
Mean of the given data = (1+2+3+4+5)/5
= 15/5
= 3
Standard Deviation = √((1 – 3)2 + (2 – 3)2 + (3 – 3)2 + (4 – 3)2 + (5 – 3)2)/(5 – 1)
= √((4 + 1 + 0 + 1 + 4)/4)
= √(10/4)
= 1.5
Now, SE = 1.5/√5
= 0.67
Вопрос 2: Найдите стандартную ошибку для выборки данных: 2, 3, 4, 5, 6.
Решение:
Mean of the given data = (2+3+4+5+6)/5
= 20/5
= 4
Standard Deviation = √((2 – 4)2 + (3 – 4)2 + (4 – 4)2 + (5 – 4)2 + (6 – 4)2)/(5 – 1)
= √((4 + 1 + 0 + 1 + 4)/4)
= √(10/4)
= 1.58
Now, SE = 1.58/√5
= 0.706
Вопрос 3: Найдите стандартную ошибку для выборки данных: 10, 20, 30, 40, 45.
Решение:
Mean of the given data = (10+20+30+40+50)/5
= 145/5
= 29
Standard Deviation = √((10 – 29)2 + (20 – 29)2 + (30 – 29)2 + (40 – 29)2 + (45 – 29)2)/(5 – 1)
= √(820/4)
= 14.317
Now, SE = 14.317/√6
= 5.84
Вопрос 4: Найдите стандартную ошибку для выборки данных: 2, 6, 9, 5.
Решение:
Mean of the given data = (2+6+9+5)/4
= 5.5
Standard Deviation = √((2 – 5.5)2 + (6 – 5.5)2 + (9 – 5.5)2 + (5 – 5.5)2)/(4 – 1)
= √(25/3)
= 2.88
Now, SE = 2.8/√5.5
= 1.19
Вопрос 5: Найдите стандартную ошибку для выборки данных: 5, 8, 10, 12.
Решение:
Mean of the given data = (5+8+10+12)/4
= 8.75
Standard Deviation = √((5 – 8.75)2 + (8 – 8.75)2 + (10 – 8.75)2 + (12 – 8.75)2)/(4 – 1)
= √(26.75/3)
= 2.98
Now, SE = 2.98/√8.75
= 1.0074
Стандартное отклонение и стандартная ошибка: в чем разница?
17 авг. 2022 г.
читать 2 мин
В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .
Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.
Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.
Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.
Пример: стандартное отклонение против стандартной ошибки
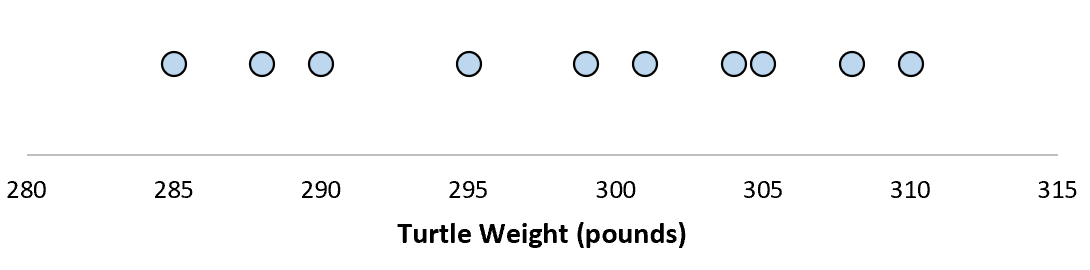
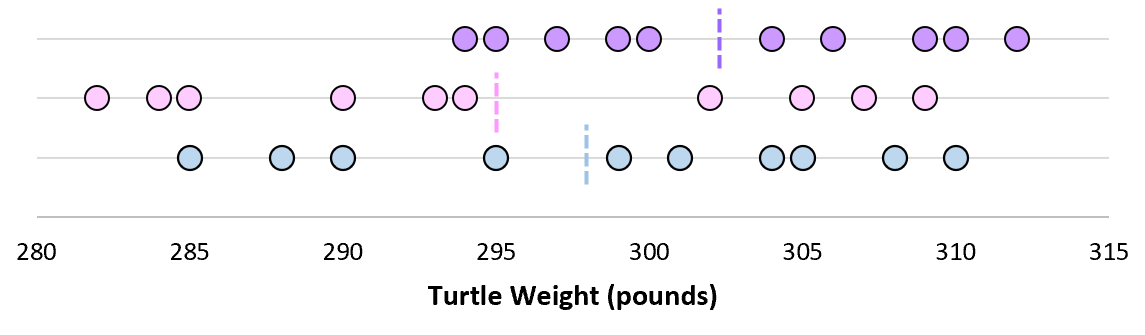
Предположим, мы измеряем вес 10 разных черепах.
Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:
Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.
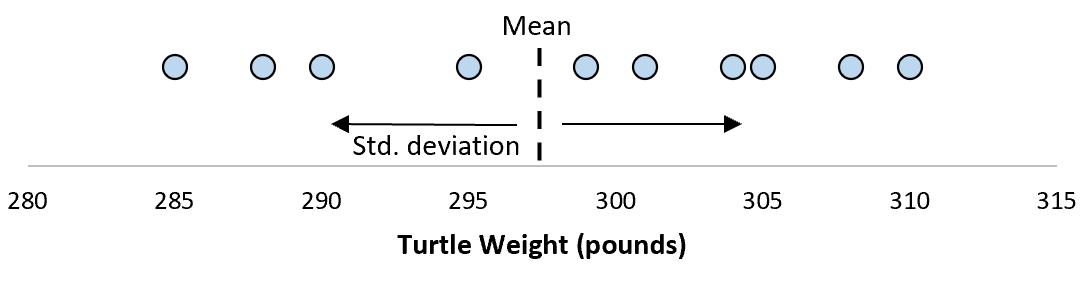
Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:
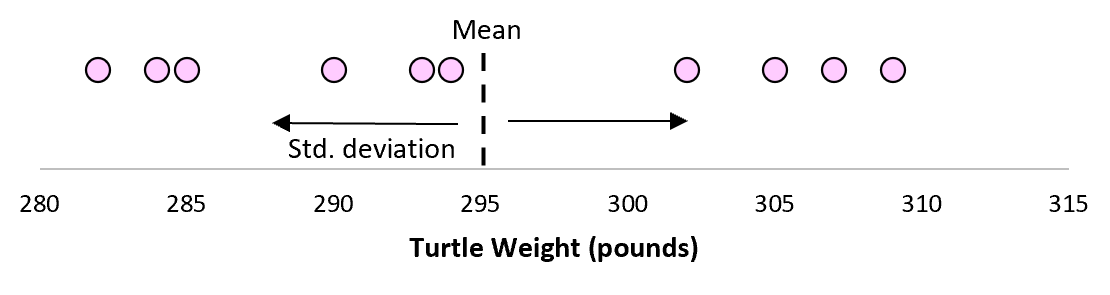
Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:
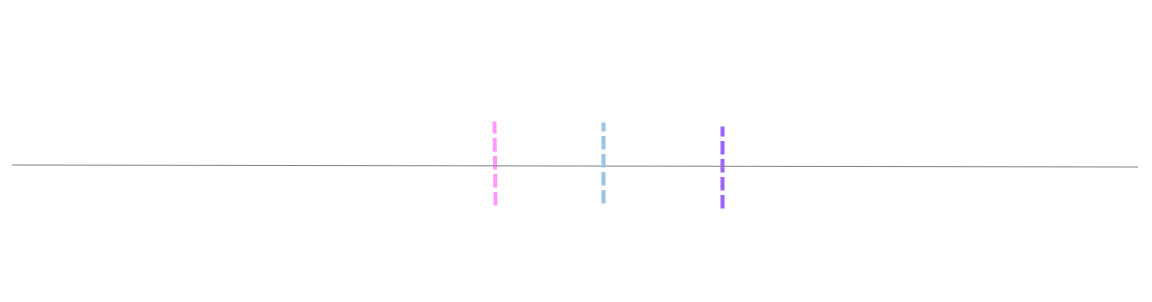
Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:
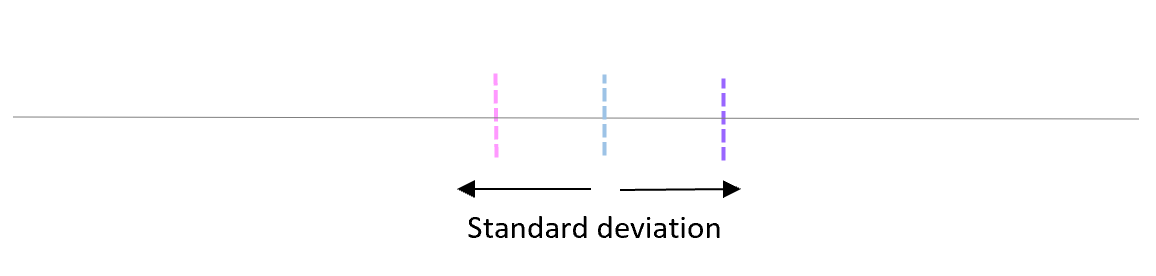
Стандартное отклонение этих средних значений известно как стандартная ошибка.
Формула для фактического расчета стандартной ошибки:
Стандартная ошибка = s/ √n
куда:
- s: стандартное отклонение выборки
- n: размер выборки
Какой смысл использовать стандартную ошибку?
Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.
Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.
Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:
Стандартная ошибка = s/ √n
Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.
Когда использовать стандартное отклонение против стандартной ошибки
Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .
Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .
В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.
Ниже приведены шаги по добавлению полос погрешностей в Excel —
- Шаг 1. Данные выбираются, и на вкладке «Вставка» выбирается линейный график.
- Шаг 2. Щелкнув опцию линейного графика, мы получим следующий линейный график.
- Шаг 3. Опцию полос погрешностей можно найти на вкладке макета в группе анализа. На следующем снимке экрана показано то же самое.
- Шаг 4. Доступны различные варианты планок погрешностей.
- Шаг 5. Планки погрешностей со стандартной ошибкой. Стандартная ошибка, т. Е. SE, в основном представляет собой стандартное отклонение выборочного распределения. Величина SE помогает определить точность оценки параметра. Стандартная ошибка обратно пропорциональна размеру выборки. Это означает, что чем меньше размер выборки, тем больше стандартные ошибки.
На приведенном ниже снимке экрана показаны полосы ошибок со стандартной ошибкой. Все точки данных в серии отображают величину ошибки с одинаковой высотой для полос ошибок Y и одинаковой шириной для полос ошибок X.
На приведенном ниже снимке экрана видно, что прямая линия проводится от минимума максимального значения, то есть красный клен перекрывается с самым удаленным значением вида черный клен. Это означает, что данные для одной группы не отличаются от другой.
Шаг 6. Планки погрешностей с процентами
Он использует процентное значение, указанное в процентном поле, для вычисления суммы ошибки для каждых данных в виде процента от значения этой конкретной точки данных. Планки погрешностей Y и X основаны на процентном соотношении значений точек данных и различаются по размеру в соответствии с процентным значением. По умолчанию это процентное значение 5%.
Значение по умолчанию 5% можно увидеть в параметрах «Дополнительные панели данных», приведенных на снимке экрана ниже.
Шаг 7. Планки погрешностей со стандартным отклонением.
Полосы ошибок со стандартным отклонением — это средняя разница между точками данных и их средним значением. Обычно при создании планок погрешностей учитывается стандартное отклонение в одну точку. Стандартное отклонение используется, когда данные обычно распределены и указатели обычно равноудалены друг от друга.
Линия проводится по максимальной точке данных, т. Е. Красный клен совпадает с максимальной ошибкой точки черного клена. Это означает, что данные для одной группы не отличаются от другой.
Как добавить настраиваемые полосы ошибок в Excel?
Помимо трех планок погрешностей, т. Е. Планок погрешностей со стандартной ошибкой, планок погрешностей со стандартным отклонением и планок погрешностей с процентами, также могут быть созданы пользовательские планки погрешностей.
Индикация минуса — это, по сути, ошибка в нижней части фактического значения. Просто нажмите на вкладку с минусом.
Как и в случае с минусом, также можно взять плюс, который представляет собой ошибку в верхней части фактического значения. Просто нажмите на вкладку с плюсом.
Мы также можем визуализировать планки погрешностей без крышки. На вкладке вертикальных полос погрешностей нам нужно щелкнуть или выбрать направление как в стиле конца, так и без крышки.
Вы можете скачать этот шаблон Excel с индикаторами ошибок здесь — Шаблон с индикаторами ошибок в Excel
То, что нужно запомнить
- Планки погрешностей в Excel — это графическое представление, которое помогает визуализировать изменчивость данных, представленных на двумерной основе.
- Это помогает указать расчетную ошибку или неопределенность, чтобы дать общее представление о том, насколько точным является измерение.
- Точность определяется маркером, нанесенным на исходный график и его точки данных.
- Планки ошибок Excel используются для отображения стандартной ошибки, стандартного отклонения или процентного значения.
- Планки погрешностей обычно заключаются в рисовании линий с кончиками концов, идущих от центра нанесенной точки данных.
- Длина полос погрешностей обычно помогает выявить неопределенность точки данных.
- В зависимости от длины планок погрешностей можно оценить погрешность. Короткая шкала погрешностей показывает, что значения более сконцентрированы, поэтому среднее значение, нанесенное на график, с большей вероятностью будет надежным. С другой стороны, на полосе ошибок указывается, что значения более разбросаны и с меньшей вероятностью будут надежными.
- Планки погрешностей можно настроить с помощью дополнительных планок погрешностей.
- В случае искаженных данных длина с каждой стороны планок ошибок будет несбалансированной.
- Планки погрешностей обычно проходят параллельно оси количественной шкалы. Это означает, что полосы погрешностей можно визуализировать либо по горизонтали, либо по вертикали в зависимости от того, находится ли количественная шкала по оси X или по оси Y.
УЗНАТЬ БОЛЬШЕ >>
Post Views: 398
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
Используя более привычные обозначения, формулу записывают как:
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
Формула стандартной ошибки средней при использовании выборочной дисперсии
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях: