Вероятность недопущения ошибки второго рода при проверке статистических гипотез называется

Тема 3.5.
СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ

План лекции:

1. Понятие гипотезы.

2. Схема статистической
   проверки гипотезы.

Список литературы:

1. Вентцель, Е.С.
   Теория вероятностей [Текст] / Е.С.
   Вентцель. – М.: Высшая школа, 2006. – 575 с.

2. Гмурман, В.Е. Теория
   вероятностей и математическая статистика
   [Текст] / В.Е. Гмурман. — М.: Высшая школа,
   2007. — 480 с.

3. Кремер, Н.Ш. Теория
   вероятностей и математическая статистика
   [Текст] / Н.Ш.
   Кремер — М: ЮНИТИ, 2002. – 543 с.

п.1. Понятие
гипотезы.

Одна
из
часто
встречающихся на практике задач,
связанных с при­менением статистических
методов, состоит в решении вопроса о
том, должно ли на основании данной
выборки быть принято или, напро­тив,
отвергнуто некоторое предположение
(гипотеза) относительно ге­неральной
совокупности (случайной величины).

Например,
новое
лекарство испытано на определенном
числе лю­дей. Можно ли сделать по
данным результатам лечения обоснованный
вывод о том, что новое лекарство более
эффективно, чем применявшие­ся ранее
методы лечения? Аналогичный вопрос
логично задать, говоря о новом правиле
поступления в вуз, о новом методе
обучения, о пользе быстрой ходьбы, о
преимуществах новой модели автомобиля
или тех­нологического процесса и т.
д.

Процедура
сопоставления высказанного предположения
(гипотезы) с выборочными данными
называется проверкой
гипотез.

Задачи
статистической проверки гипотез ставятся
в следующем виде: относительно некоторой
генеральной совокупности высказыва­ется
та или иная гипотеза Н.
Из
этой генеральной совокупности из­влекается
выборка. Требуется указать правило, при
помощи которого можно было бы по выборке
решить вопрос о том, следует ли
отклонить
гипотезу Н
или
принять
ее.

Следует
отметить, что статистическими методами
гипотезу можно
только опровергнуть или не опровергнуть,
но
не доказать. Например,
для
проверки утверждения (гипотеза Н)
автора,
что «в рукописи нет ошибок», рецензент
прочел (изучил)
несколько страниц рукописи.

Если
он обнаружил хотя бы одну ошибку, то
гипотеза Н
отверга­ется,
в противном случае — не отвергается,
говорят, что «результат проверки с
гипотезой согласуется».

Выдвинутая
гипотеза может быть правильной или
неправильной, поэтому возникает
необходимость ее проверки.

Под
статистической
гипотезой (или
просто гипотезой)
понима­ют
всякое высказывание (предположение) о
генеральной совокупности, проверяемое
по
выборке.

Статистические
гипотезы делятся на гипотезы о параметрах
рас­пределения известного вида (это
так называемые параметрические
ги­потезы)
и гипотезы о виде неизвестного
распределения (непараметри­ческие
гипотезы).

Например,
статистическими являются гипотезы:

1. генеральная
   совокупность распределена по закону
   Пуассона;

2. дисперсии
   двух нормальных совокупностей равны
   между собой.

В
первой гипотезе сделано предположение
о виде неизвестного распределения, во
второй – о параметрах двух известных
распределений.

Гипотеза
«на Марсе есть жизнь» не является
статистической, т.к. в ней не идёт речь
ни о виде, ни о параметрах распределения.

Наряду
с выдвинутой гипотезой рассматривают
и противоречащую ей гипотезу. Если
выдвинутая гипотеза будет отвергнута,
то имеет место противоречащая гипотеза.

Таким
образом, одну из гипотез выделяют в
качестве основной
(или
нулевой)
и
обозначают Но,
а другую, являющуюся логическим отрицанием
Н₀,
т. е. противоположную Но
—
в качестве конкурирующей
(или
альтер­нативной)
гипотезы
и обозначают Н₁.

Гипотезу,
однозначно фиксирующую распределение
наблюдений, называют простой
(в
ней идет речь об одном значении параметра),
в противном случае — сложной.

Например,
гипотеза Но,
состоящая
в том что математическое ожи­дание
случайной
величины
X
равно а_о,
т.е. М(Х)=а_о
является
простой. В качестве альтернативной
гипотезы можно рассматривать ги­потезу
Н₁:
М(Х)≠
а_о
(сложная
гипотеза).

Имея
две гипотезы Но
и
Н₁,
надо
на основе выборки Х₁,…
,Х_п
принять
либо основную гипотезу Н₀,
либо
конкурирующую Н₁.

Правило,
по которому принимается решение принять
или откло­нить гипотезу Но
(соответственно,
отклонить или принять Н₁),
назы­вается
статистическим
критерием К (или
просто критерием)
проверки
гипотезы Но.

Проверку
гипотез осуществляют на основании
результатов выбор­ки Х₁,
Х₂,…,
Х_п,
из
которых формируют функцию выборки К_п
=К(Х₁,
Х₂,…,
Х_n),
называемой статистикой
критерия.

Основной
принцип проверки гипотез состоит
в следующем. Мно­жество возможных
значений статистики критерия К_п
разбивается
на два непересекающихся подмножества:
критическую
область S,
т.
е. область отклонения гипотезы Но
и
область

принятия
этой
гипоте­зы. Если фактически наблюдаемое
значение статистики критерия (т. е.
значение критерия, вычисленное по
выборке: К_набл
=К(х₁,х₂,…,
х_п))
попадает
в критическую область S,
то
основная гипотеза Но
отклоняет­ся
и принимается альтернативная гипотеза
Н₁;
если
же К_набл
попадает
в
,
то
принимается Но,
а
Н₁
отклоняется.

При
проверке гипотезы может быть принято
неправильное реше­ние, т.
е. могут быть допущены ошибки двух родов:

Ошибка
первого рода состоит
в том, что отвергается нулевая гипо­теза
Но,
когда
на самом деле она верна.

Ошибка
второго рода состоит
в том, что отвергается альтернатив­ная
гипотеза Н₁,
когда
она на самом деле верна.

Рассматриваемые
случаи наглядно иллюстрирует следующая
таб­лица.

Гипотеза Н0	Отвергается	Принимается
верна	ошибка 1-го рода	правильное решение
неверна	правильное решение	ошибка 2-го рода

Вероятность
ошибки 1-го рода (обозначается через α)
называется
уровнем
значимости критерия.

Очевидно,
α
= P(Н₁Но).
Чем
меньше α,
тем
меньше вероятность отклонить верную
гипотезу. Допустимую ошибку 1-го рода
обычно за­дают заранее.

В
одних случаях считается возможным
пренебречь событиями, ве­роятность
которых меньше 0,05 (α=
0,05
означает, что в среднем в 5 случаях из
100 испытаний верная гипотеза будет
отвергнута), в других случаях, когда
речь идет, например, о разрушении
сооружений, гибе­ли судна и т. п., нельзя
пренебречь обстоятельствами, которые
могут появиться с вероятностью,
равной
0,001.

Обычно
для α
используются
стандартные значения: α
= 0,05;
0,01; 0,005; 0,001.

Вероятность
ошибки 2-го рода обозначается через β,
т.е.
β
= Р(Н₀Н₁).

Величину
1- β,
т.
е. вероятность недопущения ошибки 2-го
рода (отвергнуть неверную гипотезу
принять верную Н₁),
называется
мощностью
критерия.

Чем
больше мощность критерия, тем вероятность
ошибки 2-го рода меньше, что, конечно,
желательно (как и уменьшение α).

Последствия
ошибок 1-го, 2-го рода могут быть совершенно
раз­личными: в одних случаях надо
минимизировать α,
в
другом — β.
Так,
применительно к производству, к торговле
можно сказать, что α
—
риск поставщика (т.е. забраковка по
выборке всей партии изделий, удовлетворяющих
стандарту), β — риск потребителя (т.е.
прием по выборке всей партии изделий,
не удовлетворяющей стандарту);
применительно к судебной системе, ошибка
1-го рода приводит к оправданию виновного,
ошибка 2-го рода — осуждению невиновного.
Или, например, если отвергнуто правильное
решение «продолжить строительство
жилого дома», то эта ошибка первого рода
повлечёт материальный ущерб; если же
принято неправильное решение «продолжать
строительство», несмотря на опасность
обвала стройки, то эта ошибка второго
рода может повлечь гибель людей.

Отметим,
что одновременное
уменьшение ошибок 1-го
и 2-го рода возможно лишь при увеличении
объема выборок. Поэтому
обычно при заданном уровне значимости
α
отыскивается
критерий с наибольшей мощностью.

п.2. Схема
статистической проверки гипотезы.

Методика
проверки гипотез сводится к следующему:

1. Располагая
   выборкой Х₁,
   Х₂,…,Х_п,
   формируют
   нулевую гипотезу Но
   и
   альтернативную Н₁.

2. В
   каждом конкретном случае подбирают
   статистику критерия К_п=К(Х₁,Х₂,…,
   Х_п).

3. По
   статистике критерия К_п
   и
   уровню значимости а
   определяют
   критическую область S
   (и

   ).
   Для
   ее отыскания достаточно найти критическую
   точку k_кр,
   т.е. границу (или квантиль), отделяющую
   область S
   от

   .

Границы
областей определяются, соответственно,
из соотношений: Р(K_п
>
k_кр)
= а,
для
правосторонней критической области S;
Р(K_п
<k_кр)
= а,
для
левосторонней критической обла­сти
S;
Р(K_п
<
)
= Р(K_п
>

)
=,
для двусторонней критической области
S.

Для
каждого критерия имеются соответствующие
таблицы, по ко­торым и находят
критическую точку, удовлетворяющую
приведен­ным выше соотношениям.

1. Для
   полученной реализации выборки
   
   подсчитывают значение критерия, т.е.
   К_набл
   =К(х₁,х2,…,
   х_п)=
   k.

2. Если
   
   (например,
   
   для правосторонней области S),
   то нулевую гипотезу Н₀
   отвергают, если же
   
   (),
   то нет оснований, чтобы отвергнуть
   гипотезу Но.

Во
многих случаях закон распределения
изучаемой случайно вели­чины неизвестен,
но есть основания предположить, что он
имеет вполне определенный вид: нормальный,
биномиальный или какой-либо дру­гой.

Пусть
необходимо проверить гипотезу Но
о
том, что случайная
величина
X
под­чиняется
определенному закону распределения,
заданному функцией распределения F_о(х),
т.
е. Но:
F_х(х)=F_о(х).
Под
альтернативной гипо­тезой Н₁
будем
понимать в данном случае то, что просто
не выполнена основная (т.е. Н₁:
F_х(х)≠
F_о(х)).

Для
проверки гипотезы о распределении
случайной величины X
проведем
выборку, которую оформим в виде
статистического ряда:

xi	x1	x2	…	Xm
ni	n1	n2	…	nm

где


—
объем выборки.

Требуется
сделать заключение: согласуются ли
результаты наблю­дений с высказанным
предположением. Для этого используем
специ­ально подобранную величину —
критерий согласия.

Критерием
согласия называют
статистический критерий проверки
гипотезы о предполагаемом законе
неизвестного распределения. (Он
используется для проверки согласия
предполагаемого вида распреде­ления
с опытными данными на основании выборки.)

Существуют
различные критерии согласия: Пирсона,
Колмогорова, Фишера, Смирнова и др.
Критерий согласия Пирсона — наиболее
часто употребляемый кри­терий для
проверки простой гипотезы о законе
распределения.

Рассмотрим
применение критерия согласия Пирсона
для проверки гипотезы о нормальном
распределении исследуемой случайной
величины X.

По
результатам выборки подсчитывают:

— эмпирическую абсолютную частоту для
каждого варианта;
—
оценку математического ожидания;

— несмещённую оценку среднего
квардатического отклонения; числа

в предположении нормальности случайной
величины X
с параметрами
,
;
числа

— теоретические частоты, где n
– объем выборки.

В
качестве критерия проверки нулевой
гипотезы примем случайную величину
.
Доказано, что при

закон распределения этой случайной
величины, независимо от закона
распределения изучаемой величины X,
стремиться к известному закону

с f
степенями
свободы. Число f
находят из равенства
,
где i
– число частичных интервалов, r
– число параметров предполагаемого
распределения. В случае нормального
закона r=2.

Построим
правостороннюю критическую область,
исходя из требования, что вероятность
попадания критерия в эту область, в
предположении справедливости нулевой
гипотезы, была равна принятому уровню
значимости α:
.
Точка

по данным f
и α находится по таблице критических
точек распределения
.
На основании выборки вычисляем
.
Если
,
то нулевую гипотезу отвергают, в противном
случае её можно принять.

5

Ошибки I и II рода при проверке гипотез, мощность

Общий обзор

Принятие неправильного решения

Мощность и связанные факторы

Проверка множественных гипотез

Общий обзор

Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.

Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (напри­мер, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.

Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака мо­лочной железы одинаковая в двух группах, получаю­щих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.

Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:

1. отвергнуть нулевую гипотезу и принять альтер­нативную гипотезу
   
2. остаться в рамках нулевой гипотезы

Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).

Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.

Принятие неправильного решения

Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.

	Верная гипотеза
H0	H1
Результат  применения  критерия	H0	H0 верно принята	H0 неверно принята  (Ошибка второго рода)
H1	H0 неверно отвергнута  (Ошибка первого рода)	H0 верно отвергнута

Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.

Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.

Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.

Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.

Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.

В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.

К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.

Мощность и связанные факторы

Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).

Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.

Ряд факторов имеют прямое отношение к мощности критерия.

Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.

Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.

Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.

Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.

Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).

Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.

Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.

Проверка множественных гипотез

Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.

Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.

Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.

Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.

Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии

В начало

Содержание портала

Ошибки, встроенные в систему: их роль в статистике

В прошлой статье я указал, как распространена проблема неправильного использования t-критерия в научных публикациях (и это возможно сделать только благодаря их открытости, а какой трэш творится при его использовании во всяких курсовых, отчетах, обучающих задачах и т.д. — неизвестно). Чтобы обсудить это, я рассказал об основах дисперсионного анализа и задаваемом самим исследователем уровне значимости α. Но для полного понимания всей картины статистического анализа необходимо подчеркнуть ряд важных вещей. И самая основная из них — понятие ошибки.

Ошибка и некорректное применение: в чем разница?

В любой физической системе содержится какая-либо ошибка, неточность. В самой разнообразной форме: так называемый допуск — отличие в размерах разных однотипных изделий; нелинейная характеристика — когда прибор или метод измеряют что-то по строго известному закону в определенных пределах, а дальше становятся неприменимыми; дискретность — когда мы чисто технически не можем обеспечить плавность выходной характеристики.

И в то же время существует чисто человеческая ошибка — некорректное использование устройств, приборов, математических законов. Между ошибкой, присущей системе, и ошибкой применения этой системы есть принципиальная разница. Важно различать и не путать между собой эти два понятия, называемые одним и тем же словом «ошибка». Я в данной статье предпочитаю использовать слово «ошибка» для обозначения свойства системы, а «некорректное применение» — для ошибочного ее использования.

То есть, ошибка линейки равна допуску оборудования, наносящего штрихи на ее полотно. А ошибкой в смысле некорректного применения было бы использовать ее при измерении деталей наручных часов. Ошибка безмена написана на нем и составляет что-то около 50 граммов, а неправильным использованием безмена было бы взвешивание на нем мешка в 25 кг, который растягивает пружину из области закона Гука в область пластических деформаций. Ошибка атомно-силового микроскопа происходит из его дискретности — нельзя «пощупать» его зондом предметы мельче, чем диаметром в один атом. Но способов неправильно использовать его или неправильно интерпретировать данные существует множество. И так далее.

Так, а что же за ошибка имеет место в статистических методах? А этой ошибкой как раз и является пресловутый уровень значимости α.

Ошибки первого и второго рода

Ошибкой в математическом аппарате статистики является сама ее Байесовская вероятностная сущность. В прошлой статье я уже упоминал, на чем стоят статистические методы: определение уровня значимости α как наибольшей допустимой вероятности неправомерно отвергнуть нулевую гипотезу, и самостоятельное задание исследователем этой величины перед исследователем.
Вы уже видите эту условность? На самом деле, в критериальных методах нету привычной математической строгости. Математика здесь оперирует вероятностными характеристиками.
И тут наступает еще один момент, где возможна неправильная трактовка одного слова в разном контексте. Необходимо различать само понятие вероятности и фактическую реализацию события, выражающуюся в распределении вероятности. Например, перед началом любого нашего эксперимента мы не знаем, какую именно величину мы получим в результате. Есть два возможных исхода: загадав некоторое значение результата, мы либо действительно его получим, либо не получим. Логично, что вероятность и того, и другого события равна 1/2. Но показанная в предыдущей статье Гауссова кривая показывает распределение вероятности того, что мы правильно угадаем совпадение.

Наглядно можно проиллюстрировать это примером. Пусть мы 600 раз бросаем два игральных кубика — обычный и шулерский. Получим следующие результаты:

До эксперимента для обоих кубиков выпадение любой грани будет равновероятно — 1/6. Однако после эксперимента проявляется сущность шулерского кубика, и мы можем сказать, что плотность вероятности выпадения на нем шестерки — 90%.

Другой пример, который знают химики, физики и все, кто интересуется квантовыми эффектами — атомные орбитали. Теоретически электрон может быть «размазан» в пространстве и находиться практически где угодно. Но на практике есть области, где он будет находиться в 90 и более процентах случаев. Эти области пространства, образованные поверхностью с плотностью вероятности нахождения там электрона 90%, и есть классические атомные орбитали, в виде сфер, гантелей и т.д.

Так вот, самостоятельно задавая уровень значимости, мы заведомо соглашаемся на описанную в его названии ошибку. Из-за этого ни один результат нельзя считать «стопроцентно достоверным» — всегда наши статистические выводы будут содержать некоторую вероятность сбоя.

Ошибка, формулируемая определением уровня значимости α, называется ошибкой первого рода. Ее можно определить, как «ложная тревога», или, более корректно, ложноположительный результат. В самом деле, что означают слова «ошибочно отвергнуть нулевую гипотезу»? Это значит, по ошибке принять наблюдаемые данные за значимые различия двух групп. Поставить ложный диагноз о наличии болезни, поспешить явить миру новое открытие, которого на самом деле нет — вот примеры ошибок первого рода.

Но ведь тогда должны быть и ложноотрицательные результаты? Совершенно верно, и они называются ошибками второго рода. Примеры — не поставленный вовремя диагноз или же разочарование в результате исследования, хотя на самом деле в нем есть важные данные. Ошибки второго рода обозначаются буквой, как ни странно, β. Но само это понятие не так важно для статистики, как число 1-β. Число 1-β называется мощностью критерия, и как нетрудно догадаться, оно характеризует способность критерия не упустить значимое событие.
Однако содержание в статистических методах ошибок первого и второго рода не является только лишь их ограничением. Само понятие этих ошибок может использоваться непосредственным образом в статистическом анализе. Как?

ROC-анализ

ROC-анализ (от receiver operating characteristic, рабочая характеристика приёмника) — это метод количественного определения применимости некоторого признака к бинарной классификации объектов. Говоря проще, мы можем придумать некоторый способ, как отличить больных людей от здоровых, кошек от собак, черное от белого, а затем проверить правомерность такого способа. Давайте снова обратимся к примеру.

Пусть вы — подающий надежды криминалист, и разрабатываете новый способ скрытно и однозначно определять, является ли человек преступником. Вы придумали количественный признак: оценивать преступные наклонности людей по частоте прослушивания ими Михаила Круга. Но будет ли давать адекватные результаты ваш признак? Давайте разбираться.
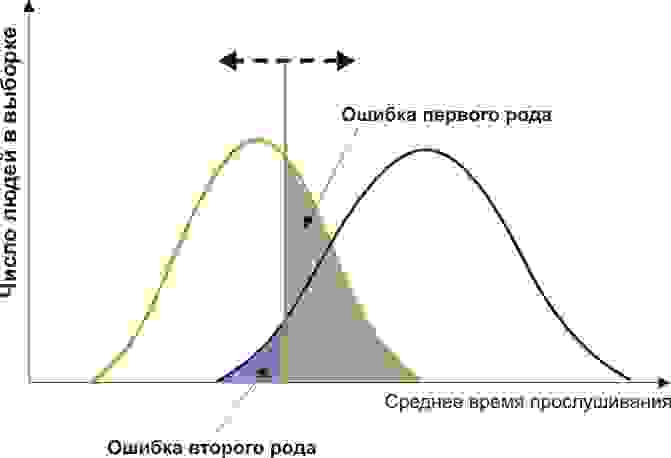
Вам понадобится две группы людей для валидации вашего критерия: обычные граждане и преступники. Положим, действительно, среднегодовое время прослушивания ими Михаила Круга различается (см. рисунок):

Здесь мы видим, что по количественному признаку времени прослушивания наши выборки пересекаются. Кто-то слушает Круга спонтанно по радио, не совершая преступлений, а кто-то нарушает закон, слушая другую музыку или даже будучи глухим. Какие у нас есть граничные условия? ROC-анализ вводит понятия селективности (чувствительности) и специфичности. Чувствительность определяется как способность выявлять все-все интересующие нас точки (в данном примере — преступников), а специфичность — не захватывать ничего ложноположительного (не ставить под подозрение простых обывателей). Мы можем задать некоторую критическую количественную черту, отделяющую одних от других (оранжевая), в пределах от максимальной чувствительности (зеленая) до максимальной специфичности (красная).
Посмотрим на следующую схему:

Смещая значение нашего признака, мы меняем соотношения ложноположительного и ложноотрицательного результатов (площади под кривыми). Точно так же мы можем дать определения Чувствительность = Полож. рез-т/(Полож. рез-т + ложноотриц. рез-т) и Специфичность = Отриц. рез-т/(Отриц. рез-т + ложноположит. рез-т).

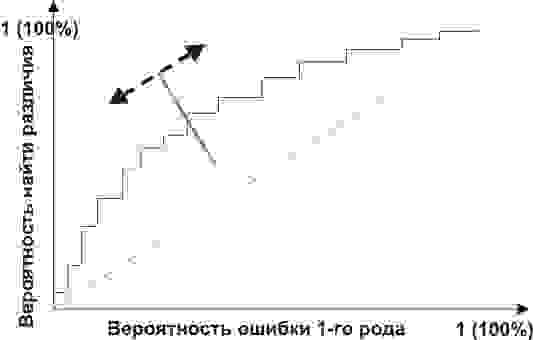
Но главное, мы можем оценить соотношение положительных результатов к ложноположительным на всем отрезке значений нашего количественного признака, что и есть наша искомая ROC-кривая (см. рисунок):

А как нам понять из этого графика, насколько хорош наш признак? Очень просто, посчитать площадь под кривой (AUC, area under curve). Пунктирная линия (0,0; 1,1) означает полное совпадение двух выборок и совершенно бессмысленный критерий (площадь под кривой равна 0,5 от всего квадрата). А вот выпуклость ROC кривой как раз и говорит о совершенстве критерия. Если же нам удастся найти такой критерий, что выборки вообще не будут пересекаться, то площадь под кривой займет весь график. В целом же признак считается хорошим, позволяющим надежно отделить одну выборку от другой, если AUC > 0,75-0,8.

С помощью такого анализа вы можете решать самые разные задачи. Решив, что слишком много домохозяек оказались под подозрением из-за Михаила Круга, а кроме того упущены опасные рецидивисты, слушающие Ноггано, вы можете отвергнуть этот критерий и разработать другой.

Возникнув, как способ обработки радиосигналов и идентификации «свой-чужой» после атаки на Перл-Харбор (отсюда и пошло такое странное название про характеристику приемника), ROC-анализ нашел широкое применение в биомедицинской статистике для анализа, валидации, создания и характеристики панелей биомаркеров и т.д. Он гибок в использовании, если оно основано на грамотной логике. Например, вы можете разработать показания для медицинской диспансеризации пенсионеров-сердечников, применив высокоспецифичный критерий, повысив эффективность выявления болезней сердца и не перегружая врачей лишними пациентами. А во время опасной эпидемии ранее неизвестного вируса вы наоборот, можете придумать высокоселективный критерий, чтобы от вакцинации в прямом смысле не ускользнул ни один чих.

С ошибками обоих родов и их наглядностью в описании валидируемых критериев мы познакомились. Теперь же, двигаясь от этих логических основ, можно разрушить ряд ложных стереотипных описаний результатов. Некоторые неправильные формулировки захватывают наши умы, часто путаясь своими схожими словами и понятиями, а также из-за очень малого внимания, уделяемого неверной интерпретации. Об этом, пожалуй, нужно будет написать отдельно.