Вероятность неисправленных ошибок

Рассмотрим,
чем определяется способность блочного
кода обнаруживать и исправлять ошибки,
возникшие при передаче.

Пусть
U
= (U₀,
U₁,
U₂,
…U_n-1)
— двоичная последовательность длиной
n.

Число
единиц
(ненулевых компонент) в этой
последовательности называется
весом
Хемминга
вектора U
и обозначается w(U).

Например,
вес Хемминга вектора U
=
( 1001011
) равен четырем, для вектора U
=
( 1111111
)
величина w(U)
составит 7 и т.д.

Таким
образом, чем больше единиц в двоичной
последовательности, тем больше ее вес
Хемминга.

Далее, пусть U и V будут
двоичными последовательностями длиной
n.

Число разрядов, в которых эти
последовательности различаются,
называется расстоянием Хемминга между
U и V и обозначается
d( U, V).

Например,
если U
=
( 1001011
), а V
= ( 0100011
), то d(
U, V) = 3.

Задав
линейный код, то есть определив все 2^k
его кодовых слов, можно вычислить
расстояние между всеми возможными
парами кодовых слов. Минимальное из них
называется минимальным
кодовым расстоянием кода
и обозначается d_min.

Можно
проверить и убедиться, что минимальное
кодовое расстояние для рассматриваемого
нами в примерах (7,4)-кода
равно трем: d_min(7,4)
=
3.
Для этого нужно записать все кодовые
слова (7,4)-кода
Хемминга (всего 16 слов), вычислить
расстояния между их всеми парами и взять
наименьшее значение. Однако можно
определить d_min
блочного кода и более простым способом.

Доказано,
что расстояние между нулевым кодовым
словом и одним из кодовых слов, входящих
в порождающую матрицу (строки порождающей
матрицы линейного блочного кода сами
являются кодовыми словами, по определению),
равно d_min.
Но расстояние от любого кодового слова
до нулевого равно весу Хемминга этого
слова. Тогда d_min
равно минимальному
весу Хемминга
для
всех строк порождающей матрицы кода .

Если
при передаче кодового слова по каналу
связи в нем произошла одиночная
ошибка,
то расстояние Хемминга между переданным
словом U
и принятым вектором r

будет равно единице. Если при этом одно
кодовое слово не перешло в другое (а при
d_min
>
1 и при одиночной ошибке это невозможно),
то ошибка будет
обнаружена
при декодировании.

В
общем случае если блочный код имеет
минимальное расстояние d_min,
то он
может обнаруживать любые сочетания
ошибок при их числе, меньшем или равном
d_min
—
1,
поскольку никакое сочетание ошибок при
их числе, меньшем, чем d_min
—
1,
не может перевести одно кодовое слово
в другое.

Но
ошибки могут иметь кратность и большую,
чем d_min—
1,
и тогда они останутся
необнаруженными.

При
этом среднюю вероятность необнаруживаемой
ошибки можно определить следующим
образом.

Пусть
вероятность ошибки в канале связи равна
P_ош.
Тогда вероятность того, что при передаче
последовательности длины n
в ней произойдет одна ошибка, равна

Р₁
= n
P_ош

( 1- Р_ош)^n-1,
(1.36)

соответственно,
вероятность l-кратной
ошибки —

P_l
=C_n^l
P_ош^l

( 1- P_ош)^n-l,
(1.37)

где
C_n^l
— число возможных комбинаций из
n
символов кодовой последо-вательности
по l
ошибок.

По
каналу связи передаются кодовые слова
с различными весами Хемминга. Положим,
что a_i

— число слов с весом i
в данном коде (всего слов в коде длиной
n
—

).

А
теперь определим, что такое необнаруживаемая
ошибка.
Обнаружение ошибки производится путем
вычисления синдрома принятой
последовательности. Если принятая
последовательность не является кодовым
словом ( тогда синдром не равен нулю),
то считается, что ошибка есть. Если же
синдром равен нулю, то полагаем, что
ошибки нет (принятая последовательность
является кодовым словом). Но
тем ли, которое передавалось? Или же в
результате действия ошибок переданное
кодовое слово перешло в другое кодовое
слово данного кода:

r
= U
+ е = V,
(1.38)

то
есть сумма переданного кодового слова
U
и вектора ошибки е
даст новое
кодовое слово V
? В этом случае, естественно, ошибка
обнаружена быть не может.

Но
из определения двоичного линейного
кода следует, что если
сумма кодового слова и некоторого
вектора е
есть кодовое слово, то вектор е
также представляет собой кодовое слово.
Следовательно,
необнаруживаемые ошибки будут возникать
тогда, когда сочетания ошибок будут
образовывать кодовые слова.

Вероятность
того, что вектор е
совпадает с кодовым словом, имеющим вес
i
,
равна

P_i
=
P_ошⁱ

(1- Р_ош)^n-i
. (1.39)

Тогда полная
вероятность возникновения необнаруживаемой
ошибки

.
(1.40)

Пример:
рассматриваемый нами (7,4)-код
содержит по семь кодовых слов с весами
w
= 3 и w
= 4 и одно
кодовое слово с весом w
= 7, тогда

(1.41)

или,
при Р_ош
= 10
^-3,
Р(Е) 
7 
10
^-9.

Другими
словами, если по каналу передается
информация
со скоростью V
=
1кбит/с и в канале в среднем каждую
секунду
будет происходить искажение одного
символа, то в среднем семь принятых слов
на 10⁹
переданных будут проходить через декодер
без обнаружения ошибки (одна необнаруживаемая
ошибка за 270 часов).

Таким
образом, использование даже такого
простого кода позволяет на несколько
порядков снизить вероятность
необнаруживаемых ошибок.

Теперь
предположим, что линейный блочный код
используется для исправления ошибок.
Чем определяются его возможности по
исправлению?

Рассмотрим
пример, приведенный на рис. 1.9. Пусть U
и V
представляют
пару кодовых слов кода с
кодовым расстоянием d
,
равным минимальному — d
_min

для

данного
кода.

Рис.
1.9

Предположим,
передано кодовое слово U,
в
канале произошла одиночная
ошибка
и принят вектор а

(не
принадлежащий коду).

Если
декодирование производится оптимальным
способом, то есть по
методу максимального правдоподобия,
то в
качестве оценки U^*
нужно
выбрать ближайшее к а
кодовое
слово.

Таковым
в данном случае будет U,
следовательно, ошибка будет устранена.

Представим
теперь, что произошло две ошибки и принят
вектор b.

Тогда
при декодировании по максимуму
правдоподобия в
качестве оценки будет выбрано ближайшее
к b
кодовое слово, и им будет
V.
Произойдет ошибка декодирования.

Продолжив
рассуждения для d_min
=
4, d_min
=
5
и т.д., нетрудно сделать вывод, что ошибки
будут устранены, если их кратность l
не превышает величины

l<
INT (( dmin – 1 )/2) ,
(1.41)

где
INT (X)
— целая часть Х.

Так,
используемый нами в качестве примера
(7,4)-код
имеет d_min
= 3 и,
следовательно, позволяет
исправлять лишь одиночные ошибки:

l
= INT
(( d_min
– 1
)/2)=INT((3-1)/2)=1
.
(1.42)

Таким
образом, возможности
линейных блочных кодов по обнаружению
и исправлению ошибок определяются их
минимальным кодовым расстоянием.
Чем
больше d_min,
тем большее число ошибок в принятой
последовательности можно исправить.

А
теперь определим вероятность того, что
возникшая в процессе передачи ошибка
не будет все же исправлена при
декодировании.

Пусть,
как и ранее, вероятность ошибки в канале
будет равна Р_ош.
Ошибки, возникающие в различных позициях
кода, считаем независимыми.

Вероятность
того, что принятый вектор r
будет иметь какие-нибудь (одиночные,
двукратные, трехкратные и т.д.) ошибки,
можно определить как

Р_ош
= P₁
+ P₂
+ P₃
+… + P_n
,
(1.43)

где
Р₁
— вероятность того, что в r
присутствует
одиночная ошибка;

Р₂
—
вероятность того, что ошибка двойная и
т.д.;

Р_n
— вероятность того, что все n
символов
искажены.

Определим вероятность ошибок заданной
кратности:

Р₁
=
Вер{ошибка
в 1-й позиции ИЛИ ошибка во 2-й позиции
..ИЛИ в n-й позиции}
= = Р_ош(1-
Р_ош)^n-1
+ Р_ош(1-
Р_ош)^n-1
+…Р_ош(1-
Р_ош)^n-1
= п 
Р_ош(1-
Р_ош)^n-;
(1.44)

Р₂
=
Вер{ошибка
в 1-й И во 2-й позиции ИЛИ ошибка во 2-й И
в 3-й позиции…}
=

=
P²_ош(1-Р_ош)^n-2
+…Р²_ош(1-
Р_ош)
^n-2 =

Р²_ош(1-
Р_ош)
^n-2.
(1.45)

Аналогичным
образом

Р₃
=

Р³_ош(1-
Р_ош)^n-3
и т.д.
(1.46)

Декодер,
как мы показали, исправляет все ошибки,
кратность которых не превышает

,
(1.47)

то
есть все ошибки кратности J

l будут
исправлены.

Тогда
ошибки декодирования — это ошибки с
кратностью, большей кратности исправляемых
ошибок l,

и их вероятность

.
(1.48)

Для
(7,4)-кода
Хемминга минимальное расстояние d_min
=
3,
т.е. l
=
1.
Следовательно, ошибки кратности 2 и
более исправлены не будут и

.
(1.49)

Если
Р_ош<<
1,
можно считать (1-
Р_ош)

1
и, кроме того, Р³_ош<<
Р²_ош.
Тогда

.
(1.50)

Так, например,
при вероятности ошибки в канале Р_ош
= 10 ^-3 вероятность
неисправления ошибки Р(N) 
2 10
^-5, то есть при такой
вероятности ошибок в канале кодирование
(7.4)-кодом позволяет снизить
вероятность оставшихся неисправленными
ошибок примерно в пятьдесят раз.

Если
же вероятность ошибки в канале будет
в сто раз меньше Р_ош
= 10 ^-5, то вероятность
ее неисправления составит уже Р(N)

210
^-9, или в 5000 раз
меньше!

Таким
образом, выигрыш от помехоустойчивого
кодирования (который можно определить
как отношение числа ошибок в канале к
числу оставшихся неисправленными
ошибок) существенно зависит от свойств
канала связи.

Если
вероятность ошибок в канале велика, то
есть канал не очень хороший, ожидать
большого эффекта от кодирования не
приходится, если же вероятность ошибок
в канале мала, то корректирующее
кодирование уменьшает ее в значительно
большей степени.

Другими
словами, помехоустойчивое кодирование
существенно улучшает свойства хороших
каналов, в плохих же каналах оно большого
эффекта не дает.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #

  10.06.2015684.82 Кб13P4.pdf

• #
• #
• #
• #

При проектировании системы связи с применением
корректирующего кода возникает вопрос о выборе кода. Решая этот вопрос,
необходимо, конечно, учитывать много различных факторов, в частности сложность
кодирования и декодирования, влияющую как на стоимость аппаратуры, так и на ее
надежность. Но если даже отвлечься от чисто технических и экономических
факторов и учитывать только верность и количество передаваемой информации,
задача выбора кода остается не легкой.

Рассмотрим, как можно сравнивать между собой различные коды.
Прежде всего заметим, что, как ясно из результатов предыдущих параграфов,
нельзя сравнивать коды безотносительно к характеристикам канала, для которого
они предназначены. Итак, будем предполагать характеристики канала заданными. В
этом случае выбор кода определяет, с одной стороны, насколько хорошо
используется пропускная способность канала и, с другой стороны, какова верность
принятого декодированного сообщения.

Представляется очень заманчивым определить один параметр,
отражающий обе эти стороны корректирующего кода. На первый взгляд таким
параметром могла бы служить скорость передачи информации, поскольку она связана
как с технической скоростью, так и с вероятностями правильного и ошибочного
приемов. Однако поиски в этом направлении не приводят к цели. Это объясняется
тем, что применение корректирующего кода не может повысить скорость
передачи информации по каналу, а наоборот, как правило, понижает ее.

Для того чтобы пояснить эту
мысль, предположим, что в канале с шумами используется примитивный код. Максимальная
скорость передачи информации будет иметь место при каком-то определенном
распределении вероятностей сообщений источника (например, для постоянного
симметричного канала — при равновероятном распределении, для двоичного
несимметричного канала—при распределении (2.56) и т. п.). Эта максимальная
скорость по определению является пропускной способностью канала.

Согласно обратной теореме
Шеннона передача со сколь угодно высокой верностью возможна лишь со скоростью,
не превышающей пропускной способности. Если бы можно было применить идеальный
код, обеспечивающий заданную высокую верность при скорости передачи, равной
пропускной способности канала, то никакого выигрыша по скорости передачи по
сравнению с примитивным кодированием мы бы не получили. Но даже отсутствие
проигрыша в скорости возможно только в асимптотическом смысле,
когда длина кодируемого блока стремится к бесконечности, как видно, например,
для случайного кодирования из (2.47). Что же касается реально   применимых  
кодов,   то   для   них    всегда  т.е скорость передачи меньше пропускной
способности и, следовательно, меньше скорости, достижимой при
примитивном кодировании, без исправления или обнаружения ошибок. Таким образом,
повышение верности связано с некоторой потерей скорости передачи информации не только по
сравнению с технической скоростью, но и по сравнению с информационной скоростью
при примитивном кодировании. Как правило, эта потеря тем больше, чем выше
требования к верности.

Здесь можно провести несколько
вольную, но поучительную аналогию с добычей ценного металла из руды. Никакой
технологический процесс не позволит получить больше металла, чем его
первоначальное содержание в руде — любой реальный процесс
приводит к некоторым потерям, которые обычно тем значительнее, чем выше
требования к чистоте металла. Точно так же корректирующий код не увеличивает количества
информации, содержащегося в принятом сигнале, а только позволяет
«очистить ее от «примесей» ценой некоторых потерь.

Для того чтобы оценить качество кола с точки зрения
скорости передачи информации, можно воспользоваться его избыточностью.
Действительно, скорость передачи можно определить (пренебрегая неисправленными
при декодировании ошибками) как

,

или согласно (2.23)

Таким образом, при заданном дискретном канале (т. е. при
заданном ) преимущество в скорости передачи информации имеют коды с
меньшей избыточностью. Поэтому выбор корректирующего кода целесообразно производить
следующим образом. Прежде всего отбираются коды, позволяющие в заданном канале
обеспечить требуемую верность передачи, а также удовлетворяющие другим
технико-экономическим требованиям, в частности коды с допустимой сложностью
кодирования и декодирования. Затем из них отбирается код с наименьшей
избыточностью.

При таком подходе необходимо уметь оценивать верность
передачи информации и формулировать требования к ней. К сожалению, в этом
вопросе нет установившейся точки зрения и различные авторы пользуются разными
параметрами для оценки верности.

Довольно часто, особенно в теоретических работах, при
рассмотрении блочных кодов мерой верности считают вероятность правильного
декодирования блока (кодовой комбинации). Мы также пользовались этой мерой в §
2.5 при отыскании асимптотических значений при увеличении длины блока. Однако
для сравнения различных кодов с различной длиной кодовой комбинации и
различной избыточностью такая мера не адекватна, не говоря уж о том, что она не
применима для непрерывных кодов. Так, например, если в одном коде блок содержит
5 информационных символов и правильно декодируется с вероятностью 0,999, а в
другом коде блок содержит 200 информационных символов и правильно декодируется
(в том же канале) с вероятностью 0,99, то было бы опрометчиво считать, что
первый код обеспечивает более высокую верность, нежели второй. Действительно,
если нужно передать сообщение, состоящее, скажем, из 400 информационных
символов, то при использовании первого кода это сообщение займет 80 кодовых
комбинаций и вероятность того, что сообщение будет принято правильно равна. Если же применить
второй код, то все сообщение уложится в 2
кодовые
комбинации и будет принято верно с вероятностью . Таким образом, вероятность правильно
принять сообщение при втором коде больше, чем при первом, хотя вероятность
правильного декодирования кодовой комбинации для первого кода выше, чем для
второго.

Более разумной мерой верности, с которой часто приходится
встречаться (например, [24]), является вероятность правильного приема символа
после исправления ошибок (или после представления декодированного сообщения
примитивным кодом). Обычно удобнее пользоваться не вероятностью правильного
приема после исправления, а её дополнением до единицы — вероятностью
неисправленной ошибки. Такая мера позволяет сравнивать коды с различной длиной
кодовых комбинаций и даже непрерывные коды. Она достаточно объективна и вполне
пригодна для таких систем связи, в которых некоторое количество неисправленных
ошибок в принятом сообщении допустимо, по желательно, чтобы их было меньше.
Чаще всего это происходит, когда само сообщение имеет некоторую избыточность и
отдельные ошибки не искажают его смысла и могут быть исправлены получателем.
Примером служит телеграфная связь при передаче осмысленного текста.

Тем не менее вероятность неисправленной ошибки не является
пригодной мерой верности в тех случаях, когда ошибки в принятом сообщении
вовсе недопустимы, т. с. когда одна ошибка в такой же мере делает сообщение
непригодным, как и тысяча ошибок. Такое положение имеет место в некоторых
системах передачи данных для цифровых вычислительных машин.

Для иллюстрации сказанного вернемся к рассмотренному выше
примеру и вычислим вероятность неисправленной ошибки для двух конкурирующих
кодов. Предположим при этом, что по структуре кодов в случае ошибочного
декодирования кодовой комбинации в среднем половина информационных символов
оказывается искаженной. При первом коде в среднем на 1000 комбинаций (т. е. на
5 000 информационных символов) ошибочно декодируется одна комбинация. Это
значит, что в среднем на 5 000 информационных символов приходится 2,5
неисправленной ошибки, т. е. вероятность неисправленной ошибки равна . Для второго кода
ошибочно декодируется одна комбинация из ста, т. е. на 20000 информационных
символов приходится 100 неисправленных, или вероятность неисправленной ошибки
равна .
Таким образом, вероятность неисправленной ошибки для второго кода в 10 раз
больше, чем для первою, тогда как вероятность ошибочного приема сообщения из
400 информационных символов, как было показано выше, для первого кода почти
втрое больше, чем для второго.

Это
кажущееся противоречие объясняется тем, что при использовании второго кода
неисправленные ошибки группируются более тесно, чем для первого. Поэтому,
хотя во втором коде вероятность неисправленной ошибки больше, чем в первом, вес
же имеется больше шансов избежать образования пачки ошибок при передаче одного
сообщения. Заметим еще, если паше сообщение, содержащее 400 информационных
символов, декодировано неверно, то при использовании первого кода оно будет,
вероятнее всего, содержать 2—3 ошибочно принятых символа, тогда как при втором
коде количество ошибочно принятых символов будет близко к 100. Отсюда можно
заключить, что при телеграфной передаче осмысленного текста лучше применять
первый код, тогда как в тех системах связи, где любые ошибки одинаково
недопустимы, второй код имеет явное преимущество.

Заметим, что именно в тех системах, где любые ошибки
декодирования одинаково недопустимы, чаще всего используются корректирующие
коды. Поэтому именно для них важно иметь меру верности. Но ни вероятность
правильного декодирования кодовой комбинации, ни вероятность неисправленной
ошибки в информационных символах для таких систем, как мы видели, не могут
служить такой мерой.

В предыдущем примере была использована вероятность
правильного декодирования сообщения, содержащего 400 информационных символов.
Но цифра 400 была выбрана совершенно произвольно. Если передавать более
длинное сообщение, то вероятность принять его безошибочно, очевидно,
уменьшится. Легко понять, что при любом блочном коде в канале с шумами с
увеличением длины передаваемого сообщения вероятность его безошибочного
декодирования стремится к нулю. Так, если вероятность правильного декодирования
кодовой комбинации равна , а сообщение содержит  кодовых
комбинаций, то вероятность принять все сообщение без ошибок равна

                         (2.62)

В этом
обозначении   —
 количество информации (в двоичных единицах), содержащееся в кодовой комбинации
(), а  — количество
информации в сообщении. Предполагается, что избыточность источника устранена
при кодировании.

Так как при любом конечном  , то с увеличением   стремится к нулю. Тем
не менее при любых конечных  и  существует положительная вероятность
безошибочного, приема сообщении. Применительно к любой системе связи можно
указать такие значения  и , при которых систему
можно считать практически безупречной. Так, например, если величина  определяется
количеством информации, передаваемой в течение суток, а , то это значит, что в среднем
одни раз за 300 лет наступит такой день, когда сообщение вследствие действия
помех будет принято неправильно. Можно смело утверждать, что почти для любых применений
такая система связи, может считаться безупречной.

Заметим, что принципиальных препятствий для достижения
указанной верности (если пропускная способность канала достаточна) нет, а
технические трудности отнюдь не больше, чем трудность получения аппаратурной
надежности обеспечивающей время наработки на одни отказ порядка 300 лет.

Формула (2.62) справедлива и дли примитивного кодирования,
когда число символов  в кодовой комбинации совпадает с числом
информационных символов . Для двоичного постоянного
симметричного канала при примитивном кодировании  и  и, следовательно,

                        (2.63)

С точки зрения верности декодирования длинного сообщения
две системы связи можно считать эквивалентными, если при достаточном больших  , по крайней
мере в асимптотическом   смысле, т.е.

                          (2.64)

Здесь индексы 1 и 2 относятся к сравниваемым системам.
Отсюда вытекает возможность характеризовать любую систему связи с любым кодом с
помощью вероятности ошибки в эквивалентной ей двоичной системе связи с
примитивным кодом. Назовем эквивалентной вероятностью ошибки  системы связи
величину вероятности ошибки в постоянном симметричном двоичном канале, в
котором система с примитивным кодированием оказывается эквивалентной
рассматриваемой системе [31].

Эквивалентная вероятность ошибки является удобной мерой
для сравнения между собой не только различных кодов, применяемых в одном и том
же канале, но и для сравнения различных систем связи, в которых могут
использоваться различные каналы, различные коды модуляции и организации связи.
При любом фиксированном значении  вероятность ошибочного приема
сигнала, содержащего  двоичных единиц информации,
является монотонной функцией эквивалентной вероятности ошибок.

Для системы с блочным кодом эквивалентную вероятность
ошибок легко вычислить, если известна вероятность  правильного
декодирования кодовой комбинации, содержащей  двоичных единиц информации. Из
(2.62) и (2.63) следует

откуда

       (2.65)

где  — вероятность  ошибочного   декодирования кодовой
комбинации.

Величину  называют эквивалентной вероятностью
правильного приема.

При

                                             (2.66)

Аналогичная величина, названная относительной вероятностью
ошибки декодирования, была введена также в работе В. И. Сифорова [32].

В случае непрерывных кодов, в которых нельзя подразделить
последовательность символов на отдельные комбинации (например, в случае цепного
кода), эквивалентную вероятность ошибок следует определить с помощью
предельного перехода

                               (2.67)

где  — вероятность   ошибочного   приема  
сообщения, содержащего  двоичных единиц информации.

Найдем эквивалентную вероятность ошибки для симметричного
постоянного канала при кодировании без избыточности кодом с основанием  [33, 34].
Если вероятность ошибочного приема символа в рассматриваемом канале равна , то
вероятность безошибочного приема последовательности из  символов равна . Такая
последовательность содержит  двоичных единиц информации.
Таким образом, эквивалентная вероятность правильного приема равна

(приближенное   равенство  справедливо при ), откуда

                                                 (2.68)

Отсюда следует, например, что канал с  и  эквивалентен по достоверности
двоичному каналу с вероятностью ошибок .

В качестве другого примера оценим эквивалентную вероятность
ошибки для описанного выше двоичного систематического кода (7,4). Кодовая
комбинация, содержащая  символов и  двоичных единицы информации,
может быть правильно декодирована, если ошибочно принят не более чем один
символ из семи. Вероятность правильного декодирования равна

Здесь первый член представляет вероятность того, что все
символы приняты верно, а второй член — вероятность того, что искажен один
символ из семи. Эквивалентная вероятность правильного приема равна

При  это выражение можно приближенно записать,
пренебрегая высокими степенями , так:

откуда эквивалентная вероятность ошибок равна

                                      (2.69)

Это выражение можно получить проще, если учесть, что при  вероятность того,
что в симметричном канале будут искажены три или более символов в комбинации,
значительно меньше вероятности ошибочного приема двух символов. Поэтому
вероятность ошибочного декодирования кодовой комбинации  в коде (7, 4) в первом
приближении равна вероятности ошибочного приема каких-либо двух символов из
семи:

откуда с учетом  (2.66)  непосредственно следует  (2.69).

Вообще,  если  двоичный   корректирующий   код является 
плотно  упакованным,  то  рассуждая  аналогичным образом, можно показать, что
при

                               (2.70)

Для не двоичных кодов, исправляющих ошибки
кратности символов
и не исправляющих ошибки большей кратности, при симметричном канале приближенная
зависимость (2.70) также справедлива. Следует только помнить, что под   понимается
количество информации в кодовой комбинации, выраженное в двоичных единицах.
Выражение (2.68) является частным случаем (2.70) при , так как при любом

Если примененный систематический код обеспечивает
возможность исправления ошибки кратности  во всех случаях, а также в некоторых
случаях ошибки более высокой кратности, то вероятность ошибочного декодирования
кодовой комбинации  при
 приблизительно
равна вероятности того, что произойдет ошибочный прием  символа в одном из неисправляемых
сочетаний

где  — число исправляемых сочетаний ошибок
кратности ,
откуда

                       (2.71)

Из полученных выражений видно, что
эффективность корректирующих кодов тем выше, чем меньше вероятность ошибки  в стационарном
симметричном канале. Так, например, при  эквивалентная вероятность ошибки для
кода (7,4) согласно (2.69) приблизительно равна 0,05, т. е. всего лишь в два
раза меньше, чем при примитивном кодировании, тогда как при  эквивалентная вероятность
ошибки оказывается порядка , т. е. в этом случае повышение верности
оказывается весьма существенным.

Подводя
итог, можно отметить, что для объективного сравнения кодов (или систем связи)
можно пользоваться либо вероятностью неисправленной ошибки, либо
эквивалентной вероятностью ошибки. Первая из этих мер пригодна для систем
связи, передающих сообщения, ценность которых не теряется  при небольшом количестве
ошибок, а лишь монотонно уменьшается. Вторая мера удобна в тех случаях, когда
каждое законченное сообщение должно быть принято без ошибок, т. е. когда даже
одиночная ошибка полностью его обесценивает.

 Полосовой фильтр приема ПФпр
выделяет полосу частот телеграфного канала, что позволяет избавиться от помех,
находящихся вне полосы пропускания ПФпр. Далее сигнал усиливается усилителем,
который компенсирует потерю энергии сигнала за счет затухания линии. Обычно
усилитель выполняет дополнительную функцию — функцию ограничения сигнала по
уровню, при этом удается обеспечить постоянство уровня сигнала на входе
демодулятора. Усиленный и ограниченный сигнал подается на фазовый демодулятор
ФД. Здесь осуществляется корреляционный (когерентный) прием, называемый иногда
приемом «методом сравнения полярностей». Опорное напряжение подается на ФД с
устройства выделения опорного напряжения УВОН. Сравнение полярностей
осуществляется в перекодирующем устройстве приема ПКУпр. Если полярности
(i-1)-го и i-го элементов совпадают, то на выходе ПКУпр в качестве i-го
элемента выделяется «1». Если полярности (i-1)-го и i-го элементов разные, то
на выходе ПКУпр выделяется «0».

 Этот способ приема по
сравнению с другими приводит к уменьшению вероятности неправильного приема,
потому что ФД сравнивается по фазе зашумленный сигнал с «чистым» опорным
напряжением.

2.   Оценка влияния помехоустойчивого кодирования на
вероятность

      ошибочного приема символов сообщения и на
скорость передачи               информации.

2.1 
Расчет вероятности неправильного
приема символов и скорости передачи информации при  отсутствии
помехоустойчивого кодирования.

 Вначале рассчитаем
вероятность неправильного приема кодовой комбинации длиной n_kk = 7
единичных элементов в предположении, что помехоустойчивое кодирование не
используется, т.е. кратность исправляемой ошибки tи = 0. Так как 
символы текста передаются кодовыми комбинациями, то вероятность искажения хотя
бы одного единичного элемента кодовой комбинации будет определять вероятность
неправильного дешифрирования (приема) символа.

Для рассматриваемых условий
вероятность неправильного приема символов текста рассчитаем по формуле:

                              ,                                              [10]

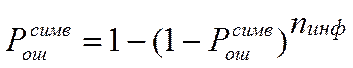
где n _инф.
= n_kk = 7

Величину 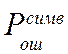 берем
из пункта 1.2,

 = 1- (1-0,242)⁷ = 0,856.

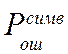
 Рассчитаем скорость передачи
информации для рассматриваемого случая. Поскольку в каждой комбинации есть один
проверочный разряд проверки на четность, то скорость передачи будет равна

,                                                                   
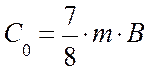
[11]

где m — кратность
модуляции.

 Бит/с.

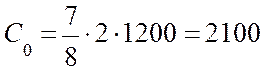
2.2 
Расчет вероятности
неправильного приема символов и скорости передачи информации при использовании
помехоустойчивого кодирования.

  В этом пункте определим, как будет изменяться
вероятность неправильного приема символов текста, если использовать
помехоустойчивые циклические коды, исправляющие одно,  двух и трехкратные
ошибки. Определим, как будет изменяться при этом скорость передачи информации с
увеличением верности передачи символов за счет использования помехоустойчивых
кодов.

 Выберем длину кодовой
комбинации n_kk = 7.

 Определим вероятность
появления на выходе декодера кодовых комбинаций с неисправленными ошибками,
которая будет равна сумме вероятностей ошибок с кратностью t_ош
> t_и.

                                                            
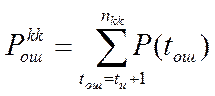
[12]

Рассчитаем вероятность
появления в кодовых комбинациях длиной   ошибок с кратностью t_ош.  Если вероятность ошибочного приема элемента кодовой

комбинации демодулятором
равна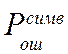,то вероятность возникновения ошибки скратностью t_ош  и определенной
конфигурации будет равна вероятности события, заключающемся в неправильном
приеме t_ош 
элементов кодовой комбинации и правильном приеме остальных n_kk — t_ош
элементов. Вероятность этого события равна 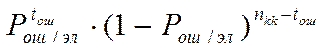. Количество возможных конфигураций ошибок с
кратностью t_ош равно
числу сочетаний из n_kk по t_ош
разрядов.

                                                      [13]

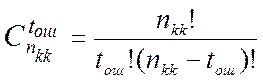
Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.

Я хочу сравнить надежность различных RAID-систем с накопителями (URE/bit = 1e-14) или корпоративными (URE/bit = 1e-15). Формула для определения вероятности успеха восстановления (без учета механических проблем, которые я буду принимать во внимание позже) проста:

error_probability = 1 — (1-per_bit_error_rate)^ bit_read

Важно помнить, что это вероятность получить по крайней мере один URE, а не только один.

Предположим, мы хотим использовать 6 ТБ свободного места. Мы можем получить это с:

• RAID1 с 1+1 дисками по 6 ТБ каждый. Во время восстановления мы читаем 1 диск по 6 ТБ, и риск составляет: 1-(1-1e-14) ^(6e12 * = 38% для потребителя или 4,7% для корпоративных накопителей.

• RAID10 с 2+2 дисками по 3 ТБ каждый. Во время восстановления мы читаем только 1 диск объемом 3 ТБ (тот, который связан с неисправным!) и риск ниже: 1-(1-1e-14) ^(3e12 * = 21% для потребителя или 2,4% для корпоративных накопителей.

• RAID5/RAID Z1 с 2+1 дисками по 3 ТБ каждый. Во время восстановления мы читаем 2 диска по 3 ТБ каждый, и риск составляет: 1-(1-1e-14) ^(2 * 3e12 * = 38% для потребительских или 4,7% или корпоративных дисков.

• RAID5/RAID Z1 с 3+1 дисками по 2 ТБ каждый (часто используется пользователями продуктов SOHO, таких как Synologys). Во время восстановления мы читаем 3 диска по 2 ТБ каждый, и риск составляет: 1-(1-1e-14) ^(3 * 2e12 * = 38% для потребительских или 4,7% или корпоративных дисков.

Вычислить погрешность для допуска на один диск легко, сложнее рассчитать вероятность для систем, допускающих отказы нескольких дисков (RAID6/Z2, RAIDZ3).

Если для восстановления используется только первый диск, а второй считывается снова с начала в случае или URE, то вероятность ошибки равна той, которая рассчитана с квадратным корнем (14,5% для потребителя RAID5 2+1, 4,5% для потребителя RAID1 1+2). Тем не менее, я полагаю (по крайней мере, в ZFS, которая имеет полные контрольные суммы!) что второй диск четности / доступный диск доступен только для чтения там, где это необходимо, а это означает, что требуется всего несколько секторов: сколько URE может произойти на первом диске? не так много, в противном случае вероятность ошибки для систем с допуском одного диска взлетела бы даже больше, чем я рассчитывал

Если я прав, второй диск четности практически снизит риск до крайне низких значений.

Помимо этого, важно иметь в виду, что производители увеличивают вероятность URE для накопителей потребительского класса по маркетинговым причинам (продают больше накопителей корпоративного класса), поэтому ожидается, что даже жесткие диски потребительского класса достигнут 1E-15 URE/ бит считывания ,

Некоторые данные: http://www.high-rely.com/hr_66/blog/why-raid-5-stops-working-in-2009-not/

Поэтому значения, которые я указал в скобках (диски предприятия), реально применимы и к дискам потребителя. А у реальных корпоративных накопителей надежность еще выше (URE/ бит = 1e-16).

Что касается вероятности механических сбоев, они пропорциональны количеству дисков и пропорционально времени, необходимому для восстановления.

страница 1 … страница 2 страница 3 страница 4 страница 5

3. Применение корректирующего кодирования в системах связи

Приведенные ниже несколько типичных примеров применения помогут понять, как эффективнее на практике осуществлять кодирование в системах связи. Один из типичных случаев характерен для систем, в которых требуются очень мощные коды. Обычный метод реализации таких кодов состоит в каскадировании двух или более простых кодов.

Еще одной интересной проблемой является кодирование для каналов, в которых ошибки возникают не независимо, а пакетами. Рассмотренные ранее методы кодирования при этом становятся совершенно неэффективными, поскольку все их характеристики определялись исходя из того, что ошибки в отдельных символах независимы друг от друга.

3.1. Каскадные коды

Каскадные коды были впервые предложены Форни в качестве метода практической реализации кода с большой длиной блока и высокой корректирующей способностью. Эта цель достигается введением нескольких уровней кодирования, обычно – двух.

Основную идею каскадного кодирования с двумя уровнями иллюстрирует рис. 3.1.

Рис. 3.1

В этой схеме комбинацию внутреннего кодера, канала и внутреннего декодера иногда называют суперканалом, аналогично, комбинацию внешнего и внутреннего кодеров — суперкодером, а комбинацию внутреннего и внешнего декодеров – супердекодером.

Длина каскадного кода получается равной N1 = N·n двоичных символов, где N — длина внешнего кода, а n — длина внутреннего кода. При этом информационная длина кода составляет K1 = K · k двоичных символов, а скорость кода R1 = R · r. Несмотря на то, что общая длина кода получается большой и, соответственно, значительно возрастает его исправляющая способность, его декодирование может выполняться с помощью двух декодеров, рассчитанных на длины составляющих его кодов n и N. Это позволяет многократно снизить сложность декодера в сравнении с тем, если бы такая исправляющая способность достигалась одноуровневым кодированием.

Простейшей иллюстрацией к каскадному кодированию является итеративный код, рассмотренный в параграфе 1.2.2. Этот код состоит из простых кодов с проверкой на четность (по строкам и столбцам), но в то же время обладает исправляющей способностью. На практике, конечно, используются гораздо более сложные коды.

Обычно внешнее кодирование выполняется блочными кодами, а внутреннее – более приспособленными для побитовой передачи по радиоканалу сверточными кодами. Каскадное кодирование широко применяется на практике, в частности, при помехоустойчивом кодировании речевой информации в системе сотовой связи формата GSM.

3.2. Кодирование с перемежением

Все рассмотренные ранее методы кодирования и примеры расчета их эффективности относились к каналам без памяти, то есть к каналам, в которых вероятность ошибки постоянна и не зависит от времени. На практике же свойства каналов связи таковы, что ошибки обычно группируются так называемыми пакетами. При постоянной некоторой средней вероятности ошибок на большом интервале времени значение P_ош на отдельных коротких интервалах может значительно превышать  среднее значение — P_{ош ср}. Если для исправления таких ошибок использовать традиционные методы кодирования-декодирования, это потребует применения сложных кодов с большой исправляющей способностью и, соответственно, большой избыточностью.

Одно из возможных решений в таких случаях может состоять в использовании достаточно простого кода, рассчитанного на исправление одиночных ошибок, вместе с парой устройств, выполняющих перемежение закодированных символов перед их передачей в канал и восстановление (деперемежение) после приема. При такой обработке кодовой и принятой последовательностей ошибки на входе декодера распределяются более равномерно.

Устройство перемежения в этой схеме переупорядочивает (переставляет) символы передаваемой последовательности некоторым детерминированным образом. С помощью устройства восстановления производится обратная перестановка, восстанавливающая исходный порядок следования символов. Используются различные способы перемежения-восстановления. Первый способ – периодическое перемежение. Он проще, но при изменении характера помех может оказаться неустойчивым. Более сложное – псевдослучайное перемежение, которое обладает при нестационарных ошибках гораздо большей устойчивостью.

Периодическое перемежение

При периодическом перемежении функция перестановок периодична с некоторым периодом. Перемежение может быть блочным, когда перестановки выполняются над блоком данных фиксированного размера, или сверточным, когда процедура выполняется над непрерывной последовательностью.

Типичное блочное устройство перемежения работает следующим образом. Кодовые символы записываются в матрицу, имеющую N строк и M столбцов построчно, а читаются из нее по столбцам. На приемной стороне операция выполняется в обратном порядке: запись производится по столбцам, а чтение — по строкам. При этом происходит восстановление исходного порядка следования символов. Естественно, что процедуры перемежения и деперемежения должны быть засинхронизированы.

При таком перемежении достигается следующее: любой пакет ошибок длиной m ≤ M переходит на выходе устройства восстановления в одиночные ошибки, каждая пара которых разделена не менее чем N символами. Правда, при этом любая периодическая с периодом M одиночная ошибка превращается в пакет, но вероятность такого преобразования очень мала, хотя и существует. В этом, собственно, и состоит главный недостаток периодического перемежения: если появилась помеха с частотой следования ошибок, совпадающей с периодом перемежения или кратной ему, то до тех пор, пока характеристики помехи не изменятся, из одиночных ошибок будут возникать неисправляемые пакеты ошибок.

Псевдослучайное перемежение

При псевдослучайном перемежении блоки из L символов записываются в память с произвольной выборкой (ЗУПВ), а затем считываются из нее псевдослучайным образом. Порядок перестановок, одинаковый для устройств перемежения и восстановления, можно записать в ПЗУ и использовать его для адресации ЗУПВ.

Как и для периодического перемежения, существует вероятность того, что ошибки будут следовать таким образом (синхронно с перемежением), что одиночные ошибки будут группироваться в пакеты. Но такая вероятность чрезвычайно мала (если, конечно, это не организованная помеха и противник не знает порядка перемежения). Случайное же совпадение порядка следования перестановок при перемежении и импульсов помехи при достаточной длине L практически невероятно.

Что касается характера псевдослучайного перемежения, то для этого могут использоваться любые псевдослучайные последовательности — линейные и нелинейные последовательности максимальной длины, последовательности, основанные на линейном сравнении, а также любые алгоритмы формирования псевдослучайных чисел с необходимым периодом повторения.

На этом краткий экскурс в теорию помехоустойчивого кодирования завершен, более детально в различных аспектах практического применения корректирующего кодирования для повышения помехоустойчивости систем связи можно разобраться с использованием литературных источников [4,5].

Как мы уже отмечали, помехоустойчивое кодирование, вообще-то, не является обязательной операцией при передаче информации. Эта процедура (и соответствующий ей элемент структурной схемы РТС ПИ) может отсутствовать. Однако это может привести к очень существенным потерям в помехоустойчивости системы, значительному уменьшению скорости передачи и снижению качества передачи информации. Поэтому практически все современные системы (за исключением, быть может, самых простых) должны включать и обязательно включают помехоустойчивое кодирование данных.

4. Задачи и практические вопросы к курсу

1. 
   По каналу связи с нормальным белым шумом передается информация со скоростью V_пи = 10 кбит/с. При этом средняя вероятность ошибок в канале составляет P_ош = 10 ^-6.
   

Для улучшения качества передачи информации рассматривается несколько вариантов решения:

— кодирование корректирующим кодом с порождающей матрицей

G = | 111 |;

— кодирование сверточным (6,3)-кодом;

— кодирование (8,4)-кодом Хемминга;

— уменьшение на 20% скорости передачи .

Какое из предложенных решений обеспечит больший эффект, если в первых трех случаях скорость передачи информации должна сохраниться прежней?

2. Порождающая матрица линейного блочного кода имеет вид

G =	1 0 1 0 1 0	.
0 1 0 1 0 1

Определить для данного кода H, d_min. Изобразить схему кодера и декодера.

Определить число ошибок, не исправленных данным кодом за 1 час работы, если V_пи = 10 кбит/с, Р_ош = 10 ^-4.

3. В канале связи с шумами производится кодирование информации с использованием кода с порождающей матрицей вида G = | 11111 |.

На входе приемного устройства на интервале времени, соответствующем длине кодовой последовательности, присутствует колебание вида U(t) (рис. 4.1)

Рис. 4.1

Сигнал U(t) в приемном устройстве подвергается дискретизации (по 3 отсчета на интервал, соответствующий одному символу кодовой последовательности).

Какое решение относительно m примет:

— жесткий мажоритарный декодер;

— мягкий декодер максимального правдоподобия?

4. Для кодера сверточного кода со схемой, показанной на рис. 2.5, определить k₀, n₀, m, n , k , R , b, изобразить кодовое дерево и решетчатую диаграмму, закодировать последовательность m = (1100100000….. , декодировать r с ошибкой во втором кадре с использованием алгоритма Витерби.

5. Предложить вариант схем кодера и декодера сверточного (9.6)-кода Вайнера-Эша (по аналогии с (12,9)-кодом), исправляющего одиночную ошибку на сегменте из трех кодовых кадров. Проиллюстрировать работу кодера и декодера на примере.

6. Схема кодера линейного блочного кода приведена на рис. 4.2. Найти для него H, G, d_min, P_но , Р_ни. Изобразить схему синдромного декодера.

Рис. 4.2

7. Для сверточного кода со схемой рис. 2.5 ((6,3)-код) определить d_min , закодировать последовательность m = (1100000000…… , декодировать принятую последовательность с двойной ошибкой в третьем кадре с использованием алгоритма Витерби и Фано.

8. Изобразить схему кодера и декодера Меггитта для циклического (8,4)-кода. Привести пример кодирования и декодирования с одиночной ошибкой.

9. По каналу связи с шумами передается двоичная информация со скоростью V_пи = 1 Мбит/с. При этом в среднем 1 раз в минуту в канале возникает ошибка.

Для уменьшения частоты ошибок предложено использовать несколько вариантов кодирования:

— (7,4)-кодом Хемминга;

— сверточным (6,3)-кодом;

— кодом с порождающей матрицей вида G = | 111 |.

Какое из предложенных решений обеспечит больший эффект, если скорость передачи информации V_пи должна остаться неизменной?

10. Предложить варианты схем кодера и декодера сверточного (15,12)-кода (по аналогии с (12,9)-кодом Вайнера-Эша, исправляющего одиночную ошибку на сегменте из трех кодовых кадров).

Привести пример кодирования и декодирования.

11. В цифровой двоичной системе связи информация передается со скоростью 2 Мбит/с, при этом в среднем один раз в минуту в канале возникает ошибка.

Как изменится частота появления ошибок, если в канале производить кодирование сверточным (6,3)-кодом и для сохранения скорости передачи информации в 2 раза повысить скорость передачи двоичных символов?

12. Изобразить схему декодера Меггитта для циклического (7,3)-кода. Привести пример кодирования и декодирования с одиночной ошибкой.

13. Порождающая матрица блочного кода имеет вид G = | 111 |. Найти H, d_min, P_но, P_ни данного кода. Изобразить схему кодера и декодера.

14. В канале связи с шумами производится кодирование информации с использованием блочного кода с порождающей матрицей G = | 11111 |. На входе приемного устройства присутствует колебание U(t) вида, показанного на рис. 4.3. Сигнал U(t) подвергается дискретизации, причем на интервал длительностью в один символ приходится два отсчета U(t).

Какое решение относительно m вынесет по принятой реализации:

— мягкий декодер максимального правдоподобия;

— жесткий мажоритарный декодер?

Рис. 4.3

15. Двоичный циклический код, заданный порождающим полиномом

g(x) = 1 + X² + X³ + X⁴,

позволяет исправлять пакеты ошибок длиной 2 (двойные ошибки в соседних символах).

Определить длину кода. Сконструировать декодер Меггитта для данного кода.

1. 
   Порождающая матрица линейного блочного кода G имеет вид
   

	1	1	0	0
G =	1	0	1	0	.
	1	0	0	1

Изобразить схему кодирования и декодирования с использованием данного кода. Определить время до первой не обнаруживаемой кодом ошибки, если скорость передачи составляет V_пи = 1 Мбит/с, а вероятность ошибки в канале равна P_ош = 10 ^-7.

17. Изобразить схему, построить кодовое дерево и решетчатую диаграмму для несистематического сверточного кода с R = 1/3, m = 2 и имеющего порождающие полиномы вида

g₁(x) = 1 + X + X², g₂(x) = 1 + X + X² и g₃(x) = 1 + X².

18. По двоичному каналу связи передается информация со скоростью 9600 бит/с.

20. Итеративный код задан матрицей вида

m₀ m₁ m₂ m₀ + m₁ m₁ + m₂

U = m₃ m₄ m₅ m₃ + m₄ m₄ + m₅

m₆ m₇ m₈ m6 +m₇ m₇ + m₈ .

m₀+m₃ m₁+m₄ m₂+m₅ p₁ p₂

m₅+m₆ m₄+m₇ m₅+m₈ p₃ p₄

Проверочные символы P₁….P₄ формируются путем суммирования всех информационных символов, входящих в соответствующие столбцы и строки матрицы, например p₁ = m₀ + m₁ + m₃ + m₄ + m₆ + m₇ + m₀ + m₃ + +m₁ + m₄ + m₂ + m_5.

Записать порождающую матрицу эквивалентного линейного блочного систематического (n,k)-кода. Определить исправляющую способность кода. Найти вероятность не исправляемой данным кодом ошибки, если вероятность ошибки в канале составляет P_ош = 10 ^-3.

21. Исправляющий двойные ошибки циклический (15,7)-код БЧХ имеет порождающий полином вида

G(x) = X⁸ + X⁷ + X⁶ + X⁴ + 1.

Построить кодер и декодер Меггитта для этого кода.

22. Дискретный источник выдает символы из ансамбля { ai } объемом К = 50.

Какое минимальное число разрядов должен иметь равномерный двоичный код, предназначенный для кодирования символов данного ансамбля? Записать примеры кодовых слов. Какова избыточность примитивного кода, если энтропия источника составляет 3 бит/букву?

23. Ансамбль дискретных символов { a_i } объемом К = 32 имеет энтропию Н(А) = 2 бит/символ.

Найти минимальное количество кодовых символов, которое надо израсходовать на кодирование символа источника равномерным примитивным двоичным кодом. Какое избыточное количество символов по сравнению с оптимальным кодом приходится использовать на один символ источника при примитивном кодировании?

24. Закодировать двоичным кодом Шеннона-Фано ансамбль { a_i } , eсли вероятность символов имеет значения, приведенные ниже.

a₁ a₂ a₃ a₄ a₅ a₆ a₇ a₈

0.25 0.25 0.125 0.125 0.0625 0.0625 0.0625 0.0625

Найти среднее число символов кодовой комбинации. Определить избыточность кода.

25. В цифровой системе телевидения высокой четкости (ТВЧ) передача одного кадра изображения размером 1500*1000 элементов с числом градаций яркости М = 256 производится за Т_к = 40 мс.

Какую полосу частот будет занимать цифровой телевизионный сигнал при использовании примитивной КИМ? Как изменится эта величина, если степень корреляции соседних элементов изображения составляет 0.95 и производится кодирование с полным устранением избыточности?

26. Некоторый дискретный источник выдает независимые символы из ансамбля { a_i } (i = 1,2,…9) с вероятностями, определенными следующим образом:

a₁ a₂ a₃ a₄ a₅ a₆ a₇ a₈ a₉

0.2 0.15 0.15 0.12 0.1 0.1 .08 0.06 0.04

Закодировать символы данного ансамбля кодом Хаффмена. Построить кодовое дерево и определить среднюю длину кодового слова.

27. Циклический (15,4)-код задан порождающим полиномом вида

g(x) = X¹¹+ X⁸ + X⁵ + X³ + X² + X + 1.

Построить кодер и декодер Меггитта для этого кода. Определить минимальное хеммингово расстояние и исправляющую способность кода. Найти вероятность неисправления ошибки, если вероятность ошибки в канале составляет P_ош = 10 ^-5.

28. Показать, что хороший декодер линейного блочного кода должен производить нелинейные операции, для чего доказать:

а) что процедура вычисления синдрома линейна по отношению к вектору ошибок, т.е. если S = F(e), то F(e₁ +e₂ )= F(e₁ )+F(e₂ );

б) что линейный декодер — это такой декодер, у которого функция e = f(S), связывающая синдром и оценку вектора ошибок, удовлетворяет условию f (S₁ +S₂ ) = f(S₁ )+f(S₂ );

в) что если мы хотим, чтобы декодер исправлял все одиночные ошибки, то функция e = f(S), связывающая синдром и оценку вектора ошибок, должна быть нелинейной.

Построить кодер и декодер для (8,7)-кода с проверкой на четность. Определить вероятность необнаруживаемой ошибки, если вероятность ошибки приема символа составляет P_ош = 10^-3 . Изобразить схемы кодера и декодера.

31. Исправляющий три ошибки (23,12)-код является циклическим с порождающим полиномом

G(x) = X¹¹ + X¹⁰ + X⁶ + X⁵ + X⁴ + X² + 1,

или G(x) = X¹¹ + X⁹ + X⁷ + X⁶ + X⁵ + X + 1.

Найти проверочный многочлен h(x) для данного кода. Построить кодер на основе g(x). Построить декодер Меггитта для данного кода.

32. Рассмотреть линейный блочный код, кодовое слово которого формируется по правилу :

U = (x₀, x₁, x₂, x₃, x₄, x₀+x₁+x₂+x₃+x₄, x₀+x₂+x₃+x₄, x₀+x₁+x₂+x₄, x₀+x₁+x₂+x₃ ).

Найти проверочную матрицу кода и параметры n, k .

33. Добавить к коду из предыдущей задачи общую проверку на четность и построить соответствующую проверочную матрицу.

Чему равно минимальное кодовое расстояние полученного кода?

34. Построить для кодов из предыдущих задач порождающие матрицы по проверочным.

35. Двоичный код, предназначенный для кодирования сообщений источника с алфавитом M = 8, содержит следующие кодовые слова:

U₁=00000; U₂=10011; U₃=01010; U₄=11001;

U₅=00101; U₆=10110; U₇=01111; U₈=11100.

Является ли данный код линейным и систематическим?

Определить возможности кода по обнаружению и исправлению ошибок.

Если код является линейным, построить порождающую и проверочную матрицы кода, схемы кодирования и декодирования.

36. Спроектировать блоки кодирования и декодирования данных для системы передачи информации.

Исходные данные:

— источник выдает информацию блоками по 4 бита;

— производительность источника = 0,4 Мбит/с;

— используется (7,3)-код Хемминга;

— затухание сигнала на трассе D = 150 дБ;

— коэффициент усиления передающей и приемной антенн G = 32;

— чувствительность приемника радиолинии N₀ = 10 ^-18 Вт/Гц;

— прием сообщения — посимвольный с использованием ортогональных сигналов.

Определить мощность передатчика системы связи, обеспечивающую вероятность безошибочного приема блока сообщения P = 0,999999.

37. Одним из способов улучшения корректирующих свойств кодов является добавление общей проверки на четность (если число единиц в кодовом слове нечетно, добавляется 1 , если четно — 0), что эквивалентно перекодированию кодовых слов следующим образом:

U₁ = m*G₁ , U₂ = U₁*G_{2 .}

Записать выражение для перекодирующей матрицы G₂, соответствующей исходному (7,3)-коду Хемминга.

Записать выражение для проверочной матрицы нового кода. Изобразить схемы кодирующего и декодирующего устройств.

Как изменится вероятность необнаружения ошибки P(E) в сравнении с исходным (7,3)-кодом, если вероятность ошибки в канале P_ош = 10 ^-5 ?

38. По каналу связи передается информация со скоростью V = 2 кбит/с. Используются двоичные сигналы типа 1 и – 1. Мощность сигнала на входе приемника составляет P = 10 ^-14 Вт. Спектральная плотность мощности помех, привeденная ко входу, N₀ = 10^-18 Вт/Гц. При передаче используется корректирующий (7,3)-код Хемминга.

Определить число необнаруживаемых и неисправленных ошибок, проходящих по каналу связи за один час работы.

39. Для кодирования информации в системе связи используется (7,3)- код Хемминга. Скорость передачи — 1 кбит/с. В канале связи действует нормальная «белая» помеха со спектральной плотностью N₀ = 10 ^-18 Вт/Гц.

При какой мощности сигнала на входе приемника вероятность неисправленной ошибки составит P_ни = 10 ^-8 ?

40. Порождающая матрица кода имеет вид

1 0 0 1 0 0 1

G = 0 1 0 0 1 0 1 .

0 0 1 0 0 1 1

Найти проверочную матрицу кода; изобразить схемы кодирующего и декодирующего устройств; найти минимальное кодовое расстояние кода; определить возможности кода по обнаружению и исправлению ошибок.

Определить вероятность пропуска необнаруживаемой ошибки P(E), если P _ош = 10 ^-6 .

41. Порождающая матрица кода имеет вид

1 0 0 0 0 1 0 1 1 1

0 1 0 0 0 1 1 1 0 1

G = 0 0 1 0 0 1 1 0 1 0 .

0 0 0 1 0 1 1 1 1 0

0 0 0 0 1 1 0 1 0 1

Найти проверочную матрицу кода; изобразить схемы кодирующего и декодирующего устройств; найти d кода; определить возможности кода по обнаружению и исправлению ошибок.

1. 
   Проверочная матрица имеет вид
   

1 1 1 1 1 0 0 0

1 0 1 1 0 1 0 0 .

Н = 1 1 0 1 0 0 1 0

1 1 1 0 0 0 0 1

Найти порождающую матрицу кода; изобразить схемы кодирующего и декодирующего устройств; найти d_min кода; определить возможности кода по обнаружению и исправлению ошибок.

43. С борта космического аппарата (КА) “Марс 2002” передается телевизионное изображение поверхности планеты. Размер кадра изображения — 512*512 элементов, каждый элемент квантуется на 128 уровней и кодируется с использованием сверточного (6,3)-кода. Мощность передатчика КА — 100 Вт, коэффициент усиления антенны — G = 50.

Передача двоичных символов кодовых последовательностей осуществляется с использованием противоположных сигналов. Прием сигнала производится на антенну площадью S = 100 м², чувствительность приемника — N =10 ^-22 Вт/Гц.

За какое время может быть принят один кадр изображения, если прием производится посимвольно и отношение сигнал/шум по мощности на выходе приемника должно составить не менее 500? ( Расстояние до КА R = 50 млн. км.)

Как изменится это время, если вместо помехоустойчивого кодирования использовать передачу элементов изображения ортогональными сигналами и осуществлять прием в целом?

44. В ходе радиолокационного зондирования Венеры, осуществляемого радиолокатором с синтезированной апертурой, производилась передача радиоизображения поверхности кадрами размером 2048*128 элементов, причем каждый элемент квантовался на 64 уровня. Передача осуществлялась с использованием двоичной цифровой радиолинии, использующей противоположные сигналы.

Параметры радиолинии связи:

— мощность передатчика P = 50 Вт;

— коэффициент усиления антенны передатчика G = 40;

— площадь приемной антенны S = 300 м² ;

— чувствительность приемного устройства (спектральная плотность шумов, приведенная ко входу) N₀ = 10^-20 Вт/Гц;

— максимальное расстояние R =10 ⁸ км.

Требуемое отношение сигнал/шум по мощности на выходе приемника радиолинии передачи изображения ( P_с / P_ш ) = 1000 .

Сколько времени понадобится на передачу одного кадра изображения при посимвольном приеме? Как изменится это время, если кодирование элементов изображения производится сверточным (6,3)-кодом, исправляющим двойные ошибки?

45. В цифровой двоичной системе связи информация передается со скоростью 1 Мбит/с, при этом в среднем один раз в минуту в канале происходит ошибка.

Как изменится частота ошибок, если в канале использовать кодирование (7,3)-кодом Хемминга и для сохранения скорости передачи информации длительность передаваемых символов будет уменьшена в (7/3) раза? Определить величину выигрыша (проигрыша) по частоте ошибок за счет кодирования при средней вероятности ошибок в канале без кодирования P_ош = 10 ^-3 … 10 ^-6.

46. Линейный блочный код задан порождающей матрицей G вида

1 0 0 1 1 0

G = 0 1 0 0 1 1 .

0 0 1 1 0 1

Изобразить схему кодера и синдромного декодера для этого кода. Составить таблицу декодирования с исправлением одиночных ошибок для декодера максимального правдоподобия.

47. Составить структурные схемы кодера и синдромного декодера для циклического (7,4)-кода, заданного порождающим полиномом

g( x ) = 1 + x + x³ .

Описать процесс кодирования и декодирования с исправлением одиночных ошибок.

48. Двоичный циклический код, заданный порождающим полиномом

g ( x ) = 1 + x² + x³ + x⁴ ,

позволяет исправлять пакеты ошибок длиной 2 (двойные ошибки в соседних символах).

Чему равна длина этого кода?

Найти минимальное кодовое расстояние данного кода.

Сконструировать систематический кодер для этого кода.

Сколько ошибок в принятой последовательности может обнаружить и исправить данный код?

50. Спроектировать блоки кодирования и декодирования для системы передачи данных со следующими исходными условиями:

— источник выдает непрерывный поток двоичных символов;

— производительность источника V = 0,3 Мбит/с;

— используется сверточный (12,9)-код Вайнера-Эша;

— декодирование сверточного кода — синдромное;

— затухание сигнала на трассе D = 160 дБ;

— коэффициент усиления передающей и приемной антенн G = 32;

— чувствительность приемника N₀ = 10 ^-21 Вт/Гц;

— прием сигнала посимвольный с использованием ортогональных (противоположных) сигналов;

Oпределить мощность передатчика системы связи, обеспечивающего вероятность безошибочного приема символа сообщения P = 10^-10.

51. Напряжение полезного сигнала на входе приемника U = 1 мкВ; входное сопротивление приемника R = 50 Ом ; сигналы противоположные; спектральная плотность помех на входе приемника N₀ = 10 ^-13 Вт/Гц.

При какой длительности интервала наблюдения вероятность ошибочного различения двух противоположных сигналов составит P_oш=10^-5? Как изменится величина Р_ош, если использовать не противоположные, а ортогональные сигналы?

52. Действующее значение напряжения на входе приемника

страница 1 … страница 2 страница 3 страница 4 страница 5

Смотрите также: