Как использование случайности может помочь сделать ваш код быстрее? Лекция Михаила Вялого в Яндексе
Время прочтения
5 мин
Просмотры 28K
И сила и слабость современных компьютеров в том, насколько они точны. Сегодня в нашей серии лекций от Яндекса рассказ о том, как использование случайностей может помочь сделать вычисления более эффективными.
Вероятностные алгоритмы позволяют решать некоторые задачи теоретической информатики, для которых не работают детерминированные алгоритмы. Самый интересный вопрос — это насколько использование случайностей сокращает время работы алгоритма? Частично на этот вопрос уже можно ответить: при некоторых предположениях истинную случайность можно подменить фальшивой и детерминированно смоделировать любой вероятностный алгоритм с незначительной потерей во времени работы. Проверка этих предположений будет, по всей видимости, одной из центральных тем теоретической информатики XXI века.
Лекцию читает старший научный сотрудник Вычислительного центра им. А.А. Дородницына РАН, доцент кафедры математических основ управления МФТИ, кандидат физико-математических наук Михаил Вялый.
Начнём с самого простого. Представим, что у нас есть два калькулятора. Один обычный, а у второго есть дополнительная кнопка, которая при нажатии выдает дополнительный бит. Попробуем ответить на вопрос, полезна ли будет такая функция?
Такая постановка, конечно, слишком общая. Постараемся уточнить ее с точки зрения теоретической информатики. Для этого сначала введем понятие алгоритма. Алгоритм — настолько точно определенная инструкция, что она может быть исполнена механически. Основное свойство детерминированных алгоритмов заключается в том, что каждое следующее состояние однозначно определяется текущим состоянием. Вероятностные алгоритмы отличаются тем, что в любой момент они могут определить значение случайного бита (подбросить монету), который с равной вероятностью будет равен 0 или 1. В процессе исполнения вероятностного алгоритма это может происходить неоднократно, и разные подбрасывания будут независимы.
Как изображено на картинке выше, при детерминированном шаге, вычисления происходят как обычно. Однако при подбрасывании монетки вычисление разветвляется. Вместо линейной последовательности получается дерево вычисления. Каждая ветвь этого дерева называется путем вычисления. Путь характеризуется значениями случайных битов. Каждый раз, подбрасывая монетку, мы выбираем одно из двух направлений движения. Таким образом, мы допускаем некоторую вольность: разрешаем, чтобы алгоритм корректно работал не на всех путях, а только на некоторых. Прежде чем переходить к оценке возможностей ошибки вероятностных алгоритмов, оговорим некоторые технические детали.
Во-первых, у подбрасываемой монетки может быть много сторон (исходов). Во-вторых, вероятности выпадения всех возможных исходов не обязательно должны быть равны. Однако сумма всех возможных исходов всегда равна 1.
Подсчет вероятности ошибки
При подсчете вероятности ошибки вероятностного алгоритма нужно учитывать два правила:
- Вероятности независимых событий перемножаются.
- Вероятности несовместных событий складываются.
Как вообще относиться к алгоритмам, которые могут ошибаться? В конце концов, можно просто задать, какой-нибудь вопрос, требующий ответа «да»/«нет», подбросить двустороннюю монетку, и с вероятностью 1/2 получить верный ответ. Так какая же вероятность ошибки нас устроит? Например, велика ли вероятность ошибки в 9/10? Если ошибку можно обнаружить, и алгоритм допускает повторное исполнение, то не очень.
Если правильный ответ нам неизвестен, задача становится сложнее. Алгоритм дает нам ответ «да» или «нет». Если вероятность ошибки ε < 1/2, то повторения алгоритма позволяют быстро уменьшать вероятность ошибки. Т.е. нужно повторить алгоритм k раз, и выдать тот ответ, который встретился чаще. Пусть вероятность ошибки равна 1/3. Вероятность ошибки при голосовании k независимых исполнений вычисляется следующим образом:
Если вероятность ошибки также равна 1/3, при голосовании 100 независимых исполнений вероятность ошибки можно вычислить так:
С повышением значения k вероятность ошибки будет очень быстро уменьшаться:
Задача об установлении контакта
Допустим, у нас есть два игрока. Они ничего не знают друг о друге, и возможности договориться у них нет. Есть две точки, через которые они могут установить контакт. Время дискретно. В каждый момент участник выбирает место (верхнее или нижнее). Контакт установлен, если в какой-то момент времени оба участника выбрали одно и то же место.
Детерминированного способа, позволяющего установить контакт, не существует. При этом вероятностный алгоритм для установления контакта очень прост: на каждом шаге нужно выбирать место случайно, равновероятно и независимо от предыдущих шагов. Проанализируем этот алгоритм. Вероятность ошибки на каждом шаге составляет 1/2. После t шагов вероятность ошибки будет составлять 2-t, что может быть очень маленькой величиной.
Задача проверки равенства третейским судьей
Рассмотрим задачу с более сложным условием. Алиса знает двоичное слово x длины n. Боб знает слово y той же длины. Они имеют возможность передать Чарли некоторую информацию (слова u и v), по которой Чарли должен решить, равны ли слова x и y. Цель: передать как можно меньше битов при условии, что Чарли правильно отвечает на любых x, y. Алиса с Бобом друг с другом общаться не могут.
Если u и v определяются по x и y детерминированно, т.е. u = f (x), v = g (y), то для решения задачи равенства нужно передать не меньше 2n битов. Путь длина u меньше n. Тогда возможных значений u меньше 2n, т.е. меньше количества возможных значений x.
Для Чарли x1 и x2 неразличимы.
Случайность как «канал связи»
Попробуем решить туже задачу, но теперь представим, что Алиса и Боб имеют доступ к общему источнику случайности. Скажем, к одному и тому же изданию книги «Таблица случайных чисел». Цель: передать как можно меньше битов при условии, что вероятность ошибки Чарли мала на любых x, y.
Попробуем решить эту задачу и определить, можно ли таким образом передавать меньше битов, чем с помощью детерминированного алгоритма.
Алиса и Боб выбирают случайное простое число p (одно и то же, случайность общая для них обоих) в интервале от n до 2n.
Алиса вычисляет U = X mod p, где X – число, двоичная запись которого совпадает со словом Алисы x. Боб поступает аналогично и вычисляет V = Y mod p. Затем они оба посылают двоичные записи чисел U и V Чарли. Чарли говорит, что слова x и y равны, если u = v.
Поскольку 0 ≤ U, V < p ≤ 2n, то длина сообщений ≤ 2 + log n.
В случае x = y Чарли всегда дает правильный ответ. Если x≠y вероятность ошибки Чарли не больше 3/4. Докажем это с помощью теоремы из теории чисел.
Простых чисел довольно много. Для всех достаточно больших n количество π(n) простых чисел от 1 до n удовлетворяет неравенствам:
Если X — Y ≠ 0 делится на простые n ≤ p1 <… < pk ≤ 2n, то
Уменьшение вероятности ошибки
Ошибка предложенного протокола — односторонняя. Это позволяет уменьшать вероятность ошибки путем многократного выполнения протокола. Если Алиса и Боб выбирают s простых модулей (случайно и независимо), вероятность ошибки становится меньше (3/4)s. Взяв достаточно большое s, вероятность ошибки можно сделать сколь угодно малой.
При наличии общей случайности для любого ε > 0 существует такой способ выбора сообщений, который гарантирует решение задачи равенства с вероятностью ошибки меньше ε и передает O(log n) битов. Запись g (n) = O(f(n)) означает, что есть такие числа C и n0, что для всех n > n0 выполняется g(n) < Cf(n).
Протоколы при отсутствии общей случайности
Как доказать, что есть способ выбора сообщений u, v в задаче равенства, при котором Алиса и Боб не знают случайных битов друг друга, передается O(√n log n) битов, а вероятность ошибки меньше 1/3?
Два случайных подмножества размера 2√n в n-элементном множестве пересекаются с вероятностью > 4/5 (примерно 1 − 1/e2). И оказывается, что это почти все, чего мы можем достичь. Рассмотрим частный случай теоремы Бабаи – Киммеля, из которой следует, что при любом способе вероятностного выбора сообщений в задаче равенства, гарантирующем вероятность ошибки меньше 1/3, длина переданных сообщений Ω(√n). Запись g(n) = Ω(f(n)) означает, что есть такие числа C и n0, что для всех n > n0 выполняется g(n) > Cf(n).
Посмотрев лекцию до конца, вы узнаете, как благодаря внедрению случайности можно ускорять работу алгоритма, а также о понятии фальшивой случайности.
Location Information Processing
David Munoz, … Rogerio Enriquez, in Position Location Techniques and Applications, 2009
3.5.2 Circular Error Probability
The circular error probability (CEP) [25] is a simple measure of accuracy defined as the radius of the circle that has its center at the mean and contains half the realizations of a random vector of coordinate estimates. It is a measure of uncertainty in the location estimator q^ relative to its mean E{q^}.. If the location estimator is unbiased, the CEP is a measure of the estimator uncertainty relative to the true NOI position. If the magnitude of the bias vector is bounded by B, then with a probability of one-half, a particular estimate is within a distance of B+ CEP from the true position. This concept is illustrated in Figure 3.15.
FIGURE 3.15. Geometry of the CEP definition.
From its definition, the CEP may be derived by solving the following equation:
(3.49)12=∫∫Rpq^(ζ)dζ1dζ2,
where pqˆ (ζ) is the probability density function of vector estimate qˆ, and the integration region is defined as R={ζ:|ζ−E{q^}|}⩽CEP. Most of the time, a closed-form expression of Equation (3.49) is difficult to find and numerical integration must be performed. However, the following approximation, which is accurate to within 10%, is often used [25]:
(3.50)CEP≈0.75E{(q^−E{q^})H(q^−E{q^})}=0.75λ1+λ2=0.75σ12+σ22.
Here λ1 and λ2 are the eigenvalues of the estimator covariance matrix, which is given by
(3.51)E{(q^−E{q^})H(q^−E{q^})}=[σ12σ12σ12σ12].
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123743534000090
Error Statistics
Deborah G. Mayo, Aris Spanos, in Philosophy of Statistics, 2011
1.3 The Severity Principle
A method’s error probabilities describe its performance characteristics in a hypothetical sequence of repetitions. How are we to use error probabilities in making particular inferences? This leads to the general question:
-
When do data x0 provide good evidence for, or a good test of, hypothesis H?
Our standpoint begins with the situation in which we would intuitively deny x0 is evidence for H. Data x0 fail to provide good evidence for the truth of H if the inferential procedure had very little chance of providing evidence against H, even if H is false.
-
Severity Principle (weak). Data x0 (produced by process G) do not provide good evidence for hypothesis H if x0 results from a test procedure with a very low probability or capacity of having uncovered the falsity of H, even if H is incorrect.
Such a test we would say is insufficiently stringent or severe. The onus is on the person claiming to have evidence for H to show that they are not guilty of at least so egregious a lack of severity. Formal error statistical tools are regarded as providing systematic ways to foster this goal, as well as to determine how well it has been met in any specific case. Although one might stop with this negative conception (as perhaps Fisher and Popper did), we will go on to the further, positive one, which will comprise the full severity principle:
-
Severity Principle (full). Data x0 (produced by process G) provides good evidence for hypothesis H (just) to the extent that test T severely passes H with x0.
Severity rationale vs. low long-run error-rate rationale (evidential vs. behavioral rationale)
Let us begin with a very informal example. Suppose we are testing whether and how much weight George has gained between now and the time he left for Paris, and do so by checking if any difference shows up on a series of well-calibrated and stable weighing methods, both before his leaving and upon his return. If no change on any of these scales is registered, even though, say, they easily detect a difference when he lifts a .1-pound potato, then this may be regarded as grounds for inferring that George’s weight gain is negligible within limits set by the sensitivity of the scales. The hypothesis H here might be:
-
H: George’s weight gain is no greater than δ,
where δ is an amount easily detected by these scales. H, we would say, has passed a severe test: were George to have gained δ pounds or more (i.e., were H false), then this method would almost certainly have detected this.
A behavioristic rationale might go as follows: If one always follows the rule going from failure to detect a weight gain after stringent probing to inferring weight gain no greater than δ, then one would rarely be wrong in the long run of repetitions. While true, this is not the rationale we give in making inferences about George. It is rather that this particular weighing experiment indicates something about George’s weight. The long run properties — at least when they are relevant for particular inferences — utilize error probabilities to characterize the capacity of our inferential tool for finding things out in the particular case. This is the severity rationale.
We wish to distinguish the severity rationale from a more prevalent idea for how procedures with low error probabilities become relevant to a particular application; namely, the procedure is rarely wrong, therefore, the probability it is wrong in this case is low. In this view we are justified in inferring H because it was the output of a method that rarely errs. This justification might be seen as intermediate between full-blown behavioristic justifications, and a genuine inferential justification. We may describe this as the notion that the long run error probability ‘rubs off’ on each application. This still does not get at the reasoning for the particular case at hand. The reliability of the rule used to infer H is at most a necessary and not a sufficient condition to warrant inferring H. What we wish to sustain is this kind of counterfactual statistical claim: that were George to have gained more than δ pounds, at least one of the scales would have registered an increase. This is an example of what philosophers often call an argument from coincidence: it would be a preposterous coincidence if all the scales easily registered even slight weight shifts when weighing objects of known weight, and yet were systematically misleading us when applied to an object of unknown weight. Are we to allow that tools read our minds just when we do not know the weight? To deny the warrant for H, in other words, is to follow a highly unreliable method: it would erroneously reject correct inferences with high or maximal probability (minimal severity), and thus would thwart learning. The stronger, positive side of the severity principle is tantamount to espousing the legitimacy of strong arguments from coincidence. What statistical tests enable us to do is determine when such arguments from coincidence are sustainable (e.g., by setting up null hypotheses). It requires being very specific about which inference is thereby warranted—we may, for example, argue from coincidence for a genuine, non-spurious, effect, but not be able to sustain an argument to the truth of a theory or even the reality of an entity.
Passing a Severe Test.
We can encapsulate this as follows:
-
A hypothesis H passes a severe test T with data x0 if,
-
(S-1) x0 accords with H, (for a suitable notion of accordance) and
-
(S-2) with very high probability, test T would have produced a result that accords less well with H than x0 does, if H were false or incorrect.
Equivalently, (S-2) can be stated:
-
(S-2)*: with very low probability, test T would have produced a result that accords as well as or better with H than x0 does, if H were false or incorrect.
Severity, in our conception, somewhat in contrast to how it is often used, is not a characteristic of a test in and of itself, but rather of the test T, a specific test result x0, and a specific inference H (not necessarily predesignated) being entertained. That is, the severity function has three arguments. We use the notation: SEV (T,x0,H), or even SEV (H), to abbreviate:
-
“The severity with which claim H passes test T with outcome x0”.
As we will see, the analyses may take different forms: one may provide a series of inferences that pass with high and low severity, serving essentially as benchmarks for interpretation, or one may fix the inference of interest and report the severity attained.
The formal statistical testing apparatus does not include severity assessments, but there are ways to use the error statistical properties of tests, together with the outcome x0, to evaluate a test’s severity in relation to an inference of interest. This is the key for the inferential interpretation of error statistical tests. While, at first blush, a test’s severity resembles the notion of a test’s power, the two notions are importantly different; see section 2.
The severity principle, we hold, makes sense of the underlying reasoning of tests, and addresses chronic problems and fallacies associated with frequentist testing. In developing this account, we draw upon other attempts to supply frequentist foundations, in particular by Bartlett, Barnard, Birnbaum, Cox, Efron, Fisher, Lehmann, Neyman, E. Pearson; the severity notion, or something like it, affords a rationale and unification of several threads that we have extracted and woven together. Although mixing aspects from N-P and Fisherian tests is often charged as being guilty of an inconsistent hybrid [Gigerenzer, 1993], the error statistical umbrella, linked by the notion of severity, allows for a coherent blending of elements from both approaches. The different methods can be understood as relevant for one or another type of question along the stages of a full-bodied inquiry. Within the error statistical umbrella, the different methods are part of the panoply of methods that may be used in the service of severely probing hypotheses.
A principle for interpreting statistical inference vs. the goal of science
We should emphasize at the outset that while severity is the principle on which interpretations of statistical inferences are based, we are not claiming it is the goal of science. While scientists seek to have hypotheses and theories pass severe tests, severity must be balanced with informativeness. So for example, trivially true claims would pass with maximal severity, but they would not yield informative inferences 4. Moreover, one learns quite a lot from ascertaining which aspects of theories have not yet passed severely. It is the basis for constructing rival theories which existing tests cannot distinguish, and is the impetus for developing more probative tests to discriminate them (see [Mayo, 2010a]).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780444518620500058
Supervised Learning: The Epilogue
Sergios Theodoridis, Konstantinos Koutroumbas, in Pattern Recognition (Fourth Edition), 2009
10.3 Exploiting the Finite Size of the Data Set
The estimation of the classification error probability presupposes that one has decided upon the data set to which the error counting will be applied. This is not a straightforward task. The set of samples that we have at our disposal is finite, and it has to be utilized for both training and testing. Can we use the same samples for training and testing? If not, what are the alternatives? Depending on the answer to the question, the following methods have been suggested:
- ▪
-
Resubstitution Method: The same data set is used, first for training and then for testing. One need not go into mathematical details in order to see that such a procedure is not very fair. Indeed, this is justified by the mathematical analysis. In [Fole 72] the performance of this method was analyzed using normal distributions. The analysis results show that this method provides an optimistic estimate of the true error probability. The amount of bias of the resubstitution estimate is a function of the ratio N/l, that is, the data set size and the dimension of the feature space. Furthermore, the variance of the estimate is inversely proportional to the data set size N. In words, in order to obtain a reasonably good estimate, N as well as the ratio N/l must be large enough. The results from the analysis and the related simulations show that N/l should be at least three and that an upper bound of the variance is 1/8N. Of course, if this technique is to be used in practice, where the assumptions of the analysis are not valid, experience suggests that the suggested ratio must be even larger [Kana 74]. Once more, the larger the ratio N/l, the more comfortable one feels.
- ▪
-
Holdout Method: The available data set is divided into two subsets, one for training and one for testing. The major drawback of this technique is that it reduces the size for both the training and the testing data. Another problem is to decide how many of the N available data will be allocated to the training set and how many to the test set. This is an important issue. In Section 3.5.3 of Chapter 3, we saw that designing a classifier using a finite data set introduces an excess mean error and a variance around it, as different data sets, of the same size, are used for the design. Both of these quantities depend on the size of the training set. In [Raud 91], it is shown that the classification error probability of a classifier, designed using a finite training data set, N, is always higher than the corresponding asymptotic error probability (N → ∞). This excess error decreases as N increases. On the other hand, in our discussion in the previous section we saw that the variance of the error counting depends on the size of the test set, and for small test data sets the estimates can be unreliable. Efforts made to optimize the respective sizes of the two sets have not yet led to practical results.
- ▪
-
Leave-One-Out Method: This method [Lach 68] alleviates the lack of independence between the training and test sets in the resubstitution method and at the same time frees itself from the dilemma associated with the holdout method. The training is performed using N −1 samples, and the test is carried out using the excluded sample. If this is misclassified, an error is counted. This is repeated N times, each time excluding a different sample. The total number of errors leads to the estimation of the classification error probability. Thus, training is achieved using, basically, all samples, and at the same time independence between training and test sets is maintained. The major disadvantage of the technique is its high computational complexity. For certain types of classifiers (i.e., linear or quadratic) it turns out that a simple relation exists between the leave-one-out and the resubstitution method ([Fuku 90], Problem 10.2). Thus, in such cases the former estimate is obtained using the latter method with some computationally simple modifications.
The estimates resulting from the holdout and leave-one-out methods turn out to be very similar, for comparable sizes of the test and training sets. Furthermore, it can be shown (Problem 10.3, [Fuku 90]) that the holdout error estimate, for a Bayesian classifier, is an upper bound of the true Bayesian error. In contrast, the resubstitution error estimate is a lower bound of the Bayesian error, confirming our previous comment that it is an optimistic estimate. To gain further insight into these estimates and their relation, let us make the following definitions:
- ▪
-
PeN
denotes the classification error probability for a classifier designed using a finite set of N training samples.
- ▪
-
P¯eN
denotes the average
E[PeN]
over all possible training sets of size N.
- ▪
-
Pe is the average asymptotic error as N → ∞.
It turns out that the holdout and leave-one-out methods (for statistically independent samples) provide an unbiased estimate of
P¯eN
. In contrast, the resubstitution method provides a biased (underestimated) estimate of
P¯eN
. Figure 10.1 shows the trend of a typical plot of
FIGURE 10.1. Plots indicating the general trend of the average resubstitution and leave-one-out error probabilities as functions of the number of training points.
P¯eN
and the average (over all possible sets of size N) resubstitution error as functions of N [Fole 72, Raud 91]. It is readily observed that as the data size N increases, both curves tend to approach the asymptotic Pe.
A number of variations and combinations of these basic schemes have also been suggested in the literature. For example, a variation of the leave-one-out method is to leave k > 1, instead of one, samples out. The design and test process is repeated for all distinct choices of k samples. References [Kana 74, Raud 91] are two good examples of works discussing various aspects of the topic.
In [Leis 98] a method called cross-validation with active pattern selection is proposed, with the goal of reducing the high computational burden required by the leave-one-out method. It is suggested not to leave out (one at a time) all N feature vectors, but only k < N. To this end the “good” points of the data set (expected to contribute a 0 to the error) are not tested. Only the k “worst” points are considered. The choice between “good” and “bad” is based on the respective values of the cost function after an initial training. This method exploits the fact that the outputs of the classifier, trained according to the least squares cost function, approximate posterior probabilities, as discussed in Chapter 3. Thus, those feature vectors whose outputs have a large deviation from the desired value (for the true class) are expected to be the ones that contribute to the classification error.
Another set of techniques have been developed around the bootstrap method [Efro 79, Hand 86, Jain 87]. A major incentive for the development of these techniques is the variance of the leave-one-out method estimate for small data sets [Efro 83]. According to the “bootstrap” philosophy, new data sets are artificially generated. This is a way to overcome the limited number of available data and create more data in order to better assess the statistical properties of an estimator. Let X be the set of the available data of size N. A bootstrap design sample set of size N,X*, is formed by random sampling with replacement of the set X. Replacement means that when a sample, say xi, is “copied” to the set X*, it is not removed from X but is reconsidered in the next sampling. A number of variants have been built upon the bootstrap method. A straightforward one is to design the classifier using a bootstrap sample set and count the errors using the samples from X that do not appear in this bootstrap sample set. This is repeated for different bootstrap sample sets. The error rate estimate, e0, is computed by counting all the errors and dividing the sum by the total number of test samples used. However, in [Raud 91] it is pointed out that the bootstrap techniques improve on the leave-one-out method only when the classification error is large.
Another direction is to combine estimates from different estimators. For example, in the so-called 0.632 estimator ([Efro 83]), the error estimate is taken as a convex combination of the resubstitution error, eres, and the bootstrap error e0,
It has been reported that the 0.632 estimator is particularly effective in cases of small size data sets [Brag 04]. An extension of the 0.632 rule is discussed in [Sima 06] where convex combinations of different estimators are considered and the combining weights are computed via an optimization process.
Confusion Matrix, Recall and Precision
In evaluating the performance of a classification system, the probability of error is sometimes not the only quantity that assesses its performance sufficiently. Let us take for example, an M-class classification task. An important issue is to know whether there are classes that exhibit a higher tendency for confusion. The confusion matrix A = [A(i,j)] is defined so that its element A(i,j) is the number of data points whose true class label was i and were classified to class j. From A, one can directly extract the recall and precision values for each class, along with the overall accuracy:
- ▪
-
Recall (Ri). Ri is the percentage of data points with true class label i, which were correctly classified in that class. For example, for a two-class problem, the recall of the first class is calculated as
R1=A(1,1)A(1,1)+A(1,2)
.
- ▪
-
Precision (Pi). Pi is the percentage of data points classified as class i, whose true class label is indeed i. Therefore, for the first class in a two-class problem,
P1=A(1,1)A(1,1)+A(2,1).
- ▪
-
Overall Accuracy (Ac). The overall accuracy, Ac, is the percentage of data that has been correctly classified. Given an M-class problem, Ac is computed from the confusion matrix according to the equation
Ac=1N∑i=1MA(i,i),
where N is the total number of points in the test set.
Take as an example a two-class problem where the test set consists of 130 points from class ω1 and 150 points from class ω2. The designed classifier classifies 110 points from ω1 correctly and 20 points to class ω2. Also, it classifies 120 points from class ω2 correctly and 30 points to class ω1. The confusion matrix for this case is
The recall for the first class is
R1=110130
and the precision
P1=110140
. The respective values for the second class are similarly computed. The accuracy is
Ac=110+120130+150
.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9781597492720500128
Multiple Testing of Hypotheses in Biomedical Research
Hansen Bannerman-Thompson, … Ranajit Chakraborty, in Handbook of Statistics, 2012
6.3 Bonferroni procedure
RejectH01andH02ifX¯≥0.515andY¯≥0.515.RejectH01but notH02ifX¯≥0.515andY¯<0.515.RejectH02but notH01ifX¯<0.515andY¯≥0.515.Do not rejectH01andH02ifX¯<0.515andY¯<0.515.
An explicit calculation gives
FWER=Pr(V≥1∣H01,H02)=0.07<0.08;FWER=Pr(V≥1∣H01)=0.04<0.08;FWER=Pr(V≥1∣H02)=0.04<0.08.
The Bonferroni bound for FWER=Pr(V≥1∣H01,H02) is 0.08 but the actual probability is 0.07. Bonferroni paradigm declares that the above procedure controls FWER at the level 0.08. As a matter of fact, we could say that the procedure controls FWER at the level 0.07.
In this example we could calculate precisely the error probability of each type. If we want to control the error probability FWER=Pr(V≥1∣H01,H02) precisely at the level 0.08, we change the critical value from 0.515–0.5. Look at the following multiple testing procedure.
- 1.
-
Reject both the null hypotheses if X¯≥0.5andY¯≥0.5;
- 2.
-
Reject H01 but not H02 if X¯≥0.5andY¯<0.5;
- 3.
-
Reject H02 but not H01 if X¯<0.5andY¯≥0.5;
- 4.
-
Do not reject H01 and H02 if X¯<0.5andY¯<0.5.
For this test,
FWER=Pr(V≥1∣H01,H02)=0.08;FWER=Pr(V≥1∣H01)=0.0455<0.08;FWER=Pr(V≥1∣H01)=0.0455<0.08.
If the underlying test statistics of the hypotheses are statistically independent, we have a better control of the error probabilities. The following multiple test is designed towards this end.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780444518750000087
Philosophy of Econometrics
Aris Spanos, in Philosophy of Economics, 2012
5.7.4 Revisiting observed Confidence Intervals (CI)
As argued above, the post-data error probabilities associated with a CI are degenerate. In contrast, testing reasoning gives rise to well-defined error probabilities post-data because it compares what actually happened to what it is expected under different scenarios (hypothetical values of μ), since it does not involve TSN.
In view of that, it is evident that one can evaluate the probability of claims of the form given in (26) by relating μ1 to whatever values one is interested in, including x―n±cα2(s/n) for different α, using hypothetical (not factual) reasoning. Indeed, this is exactly how the severity assessment circumvents the problem facing observed CIs, whose own post-data error probabilities are zero or one, and provides an effective way to evaluate inferential claims of the form:
μ≥μ1=μ0+γ,forγ≤0,orμ≤μ1=μ0+γ,forγ≥0
, using well-defined post data error probabilities by relating γ to different values of cα2(s/n); see [Mayo and Spanos, 2006]. The reasoning underlying such severity evaluations is fundamentally different from the factual reasoning underlying a sequence of CIs; section 5.4.
The severity evaluation also elucidates the comparisons between p-values and CIs and can be used to explain why the various attempts to relate p-value and observed confidence interval curves (see [Birnbaum, 1961; Kempthorne and Folks, 1971; Poole, 1987]) were unsuccessful. In addition, it can be used to shed light on the problem of evaluating ‘effect sizes’ (see [Rosenthal et al., 1999]) sought after in some applied fields like psychology and epidemiology; see [Spanos, 2004].
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780444516763500130
Beam Management
Erik Dahlman, … Johan Sköld, in 5G NR (Second Edition), 2021
12.3.1 Beam-Failure Detection
Fundamentally, a beam failure is assumed to have happened when the error probability for the downlink control channel (PDCCH) exceeds a certain value. However, similar to radio-link failure, rather than actually measuring the PDCCH error probability the device declares a beam failure based on measurements of the quality of some reference signal. This is often expressed as measuring a hypothetical error rate. More specifically, the device should declare beam failure based on measured L1-RSRP of a periodic CSI-RS or an SS block that is spatially QCL with the PDCCH.
By default, the device should declare beam failure based on measurement on the reference signal (CSI-RS or SS block) associated with the PDCCH TCI state. However, there is also a possibility to explicitly configure a different CSI-RS on which to measure for beam-failure detection.
Each time instant the measured L1-RSRP is below a configured value is defined as a beam-failure instance. If the number of consecutive beam-failure instances exceeds a configured value, the device declares a beam failure and initiates the beam-failure-recovery procedure.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978012822320800012X
Classifiers Based on Bayes Decision Theory
Sergios Theodoridis, Konstantinos Koutroumbas, in Pattern Recognition (Fourth Edition), 2009
2.3 Discriminant Functions and Decision Surfaces
It is by now clear that minimizing either the risk or the error probability or the Neyman-Pearson criterion is equivalent to partitioning the feature space into M regions, for a task with M classes. If regions Ri, Rj happen to be contiguous, then they are separated by a decision surface in the multidimensional feature space. For the minimum error probability case, this is described by the equation
(2.21)P(ωi|x)−P(ωj|x)=0
From the one side of the surface this difference is positive, and from the other it is negative. Sometimes, instead of working directly with probabilities (or risk functions), it may be more convenient, from a mathematical point of view, to work with an equivalent function of them, for example, gi(x) ≡ f(P(ωi|x)), where f(·) is a monotonically increasing function. gi(x) is known as a discriminant function. The decision test (2.13) is now stated as
(2.22)classify x in ωi if gi(x)>gj(x) ∀j≠i
The decision surfaces, separating contiguous regions, are described by
(2.23)gij(x)≡gi(x)−gj(x)=0, i,j=1,2,…,M, i≠j
So far, we have approached the classification problem via Bayesian probabilistic arguments and the goal was to minimize the classification error probability or the risk. However, as we will soon see, not all problems are well suited to such approaches. For example, in many cases the involved pdfs are complicated and their estimation is not an easy task. In such cases, it may be preferable to compute decision surfaces directly by means of alternative costs, and this will be our focus in Chapters 3 and 4. Such approaches give rise to discriminant functions and decision surfaces, which are entities with no (necessary) relation to Bayesian classification, and they are, in general, suboptimal with respect to Bayesian classifiers.
In the following we will focus on a particular family of decision surfaces associated with the Bayesian classification for the specific case of Gaussian density functions.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9781597492720500049
Mesh Networks: Optimal Routing and Scheduling
Anurag Kumar, … Joy Kuri, in Wireless Networking, 2008
Discussion
- 1.
-
In deriving the scheduling algorithm, we could also consider the error probability on the link. Of course, if the probability of a packet error on a link is nonzero, then the stability region and also the queue evolution equation would need to be changed. However, the MWS algorithm is only slightly different. This is explored in Problem 8.9.
- 2.
-
With a suitable choice of edge weights, the MWS routing and scheduling algorithm is applicable in considerably more general scenarios. For example, we could use the same algorithm when the topology is time varying in a manner that a time average probability for a link to exist can be defined.
- 3.
-
The link activation vectors S could be nonnegative reals. Recall that the transmission bit rate could be a function of the SINR at the receiver. This in turn depends on the transmission power used by the transmitters in the link activation vector. Thus corresponding to a transmission rate vector S, we also need to specify the transmission powers. In such cases, an obvious optimization criterion could be to minimize the energy or power consumption.
- 4.
-
The MWS algorithm is complex to implement. Further, what we have described is a centralized algorithm that requires complete knowledge of the network state. Hence this is not quite a practical algorithm. Many distributed and randomized algorithms have been proposed in the literature.
- 5.
-
The MWS algorithm is a significantly general algorithm and can be applied to a large class of problems. The most notable use is in developing maximum throughput scheduling algorithms in input queued switches.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123742544500090
Different views of spectral efficiency*
Ana I Pérez-Neira, Marc Realp Campalans, in Cross-Layer Resource Allocation in Wireless Communications, 2009
2.3 The bit error rate (BER)
An important reference for the assessment of any modulation scheme is the bit error probability or bit error rate (BER) for the corresponding uncoded system. Unfortunately, for most non-binary modulation techniques (e.g. M-QAM and M-PSK) an exact expression for BER is hard to find.
At high SNR and using Gray mapping [2], it is commonly assumed that an erroneous detected symbol differs from the correct one in only one bit. Consequently, the BER is approximated by the symbol error rate (SER) divided by the number of bits per symbol b.
Closed-form expressions for SER of M-QAM and M-PSK as functions of the SNR can be found in [2]. For M-QAM with square constellations, i.e. b is an even integer, the BER approximation is given by
(2.3)BERMQAM(γ)=2log2M(1-1M)erfc(3γ2(M-1))
where erfc(.) is the complementary error function. For M-PSK modulations the BER approximation is
(2.4)BERMPSK(γ)={erfc(γ)forundefinedlog2M=1,21log2Merfc(γsin(πM))forundefinedlog2M>2
where BPSK and QPSK have the same BER because a QPSK signal can be seen as two independent BPSK signals.
An example is given in Figure 2.2. We observe that for modulations higher than 8-PSK it is preferable to move to QAM modulations. Note that 2-QAM and 4-QAM modulations are equivalent to BPSK and QPSK modulations, respectively. Furthermore, it can be shown that the BER performance of 8-QAM is very close to that of 16-QAM but with one bit per symbol less. Hence, it is quite usual that in commercial systems QAM modulations start at 16-QAM. For instance, 16-QAM and 64-QAM are the two QAM schemes considered by the IEEE802.11g/a standards [3].
Figure 2.2. BER curves for different modulations.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123741417000026
Channel coding
Wenhong Chen, … Li Guo, in 5G NR and Enhancements, 2022
7.3.6.3 Length for CRC
For LDPC codes, the number of CRC bits to achieve a given undetected error probability varies with the block size and code rate. Considering the actual performance requirements, NR finally determines that when the information block size A>3824, the length of CRC added to a TB is L=24 bits, and the generating polynomial is:
(7.13)gCRC24A(D)=D24+D23+D18+D17+D14+D11+D10+D7+D6+D5+D4+D3+D+1
When the information block size A≤3824, a CRC with a length of L=16 bits is added after the TB, and the generating polynomial is:
(7.14)gCRC16(D)=D16+D12+D5+1
If code segmentation (i.e., the number of blocks C>1) is required, a 24-bit CRC is added after each CB, and the generating polynomial is:
(7.15)gCRC24B(D)=D24+D23+D6+D5+D+1
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780323910606000076
Location Information Processing
David Munoz, … Rogerio Enriquez, in Position Location Techniques and Applications, 2009
3.5.2 Circular Error Probability
The circular error probability (CEP) [25] is a simple measure of accuracy defined as the radius of the circle that has its center at the mean and contains half the realizations of a random vector of coordinate estimates. It is a measure of uncertainty in the location estimator q^ relative to its mean E{q^}.. If the location estimator is unbiased, the CEP is a measure of the estimator uncertainty relative to the true NOI position. If the magnitude of the bias vector is bounded by B, then with a probability of one-half, a particular estimate is within a distance of B+ CEP from the true position. This concept is illustrated in Figure 3.15.
FIGURE 3.15. Geometry of the CEP definition.
From its definition, the CEP may be derived by solving the following equation:
(3.49)12=∫∫Rpq^(ζ)dζ1dζ2,
where pqˆ (ζ) is the probability density function of vector estimate qˆ, and the integration region is defined as R={ζ:|ζ−E{q^}|}⩽CEP. Most of the time, a closed-form expression of Equation (3.49) is difficult to find and numerical integration must be performed. However, the following approximation, which is accurate to within 10%, is often used [25]:
(3.50)CEP≈0.75E{(q^−E{q^})H(q^−E{q^})}=0.75λ1+λ2=0.75σ12+σ22.
Here λ1 and λ2 are the eigenvalues of the estimator covariance matrix, which is given by
(3.51)E{(q^−E{q^})H(q^−E{q^})}=[σ12σ12σ12σ12].
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123743534000090
Error Statistics
Deborah G. Mayo, Aris Spanos, in Philosophy of Statistics, 2011
1.3 The Severity Principle
A method’s error probabilities describe its performance characteristics in a hypothetical sequence of repetitions. How are we to use error probabilities in making particular inferences? This leads to the general question:
-
When do data x0 provide good evidence for, or a good test of, hypothesis H?
Our standpoint begins with the situation in which we would intuitively deny x0 is evidence for H. Data x0 fail to provide good evidence for the truth of H if the inferential procedure had very little chance of providing evidence against H, even if H is false.
-
Severity Principle (weak). Data x0 (produced by process G) do not provide good evidence for hypothesis H if x0 results from a test procedure with a very low probability or capacity of having uncovered the falsity of H, even if H is incorrect.
Such a test we would say is insufficiently stringent or severe. The onus is on the person claiming to have evidence for H to show that they are not guilty of at least so egregious a lack of severity. Formal error statistical tools are regarded as providing systematic ways to foster this goal, as well as to determine how well it has been met in any specific case. Although one might stop with this negative conception (as perhaps Fisher and Popper did), we will go on to the further, positive one, which will comprise the full severity principle:
-
Severity Principle (full). Data x0 (produced by process G) provides good evidence for hypothesis H (just) to the extent that test T severely passes H with x0.
Severity rationale vs. low long-run error-rate rationale (evidential vs. behavioral rationale)
Let us begin with a very informal example. Suppose we are testing whether and how much weight George has gained between now and the time he left for Paris, and do so by checking if any difference shows up on a series of well-calibrated and stable weighing methods, both before his leaving and upon his return. If no change on any of these scales is registered, even though, say, they easily detect a difference when he lifts a .1-pound potato, then this may be regarded as grounds for inferring that George’s weight gain is negligible within limits set by the sensitivity of the scales. The hypothesis H here might be:
-
H: George’s weight gain is no greater than δ,
where δ is an amount easily detected by these scales. H, we would say, has passed a severe test: were George to have gained δ pounds or more (i.e., were H false), then this method would almost certainly have detected this.
A behavioristic rationale might go as follows: If one always follows the rule going from failure to detect a weight gain after stringent probing to inferring weight gain no greater than δ, then one would rarely be wrong in the long run of repetitions. While true, this is not the rationale we give in making inferences about George. It is rather that this particular weighing experiment indicates something about George’s weight. The long run properties — at least when they are relevant for particular inferences — utilize error probabilities to characterize the capacity of our inferential tool for finding things out in the particular case. This is the severity rationale.
We wish to distinguish the severity rationale from a more prevalent idea for how procedures with low error probabilities become relevant to a particular application; namely, the procedure is rarely wrong, therefore, the probability it is wrong in this case is low. In this view we are justified in inferring H because it was the output of a method that rarely errs. This justification might be seen as intermediate between full-blown behavioristic justifications, and a genuine inferential justification. We may describe this as the notion that the long run error probability ‘rubs off’ on each application. This still does not get at the reasoning for the particular case at hand. The reliability of the rule used to infer H is at most a necessary and not a sufficient condition to warrant inferring H. What we wish to sustain is this kind of counterfactual statistical claim: that were George to have gained more than δ pounds, at least one of the scales would have registered an increase. This is an example of what philosophers often call an argument from coincidence: it would be a preposterous coincidence if all the scales easily registered even slight weight shifts when weighing objects of known weight, and yet were systematically misleading us when applied to an object of unknown weight. Are we to allow that tools read our minds just when we do not know the weight? To deny the warrant for H, in other words, is to follow a highly unreliable method: it would erroneously reject correct inferences with high or maximal probability (minimal severity), and thus would thwart learning. The stronger, positive side of the severity principle is tantamount to espousing the legitimacy of strong arguments from coincidence. What statistical tests enable us to do is determine when such arguments from coincidence are sustainable (e.g., by setting up null hypotheses). It requires being very specific about which inference is thereby warranted—we may, for example, argue from coincidence for a genuine, non-spurious, effect, but not be able to sustain an argument to the truth of a theory or even the reality of an entity.
Passing a Severe Test.
We can encapsulate this as follows:
-
A hypothesis H passes a severe test T with data x0 if,
-
(S-1) x0 accords with H, (for a suitable notion of accordance) and
-
(S-2) with very high probability, test T would have produced a result that accords less well with H than x0 does, if H were false or incorrect.
Equivalently, (S-2) can be stated:
-
(S-2)*: with very low probability, test T would have produced a result that accords as well as or better with H than x0 does, if H were false or incorrect.
Severity, in our conception, somewhat in contrast to how it is often used, is not a characteristic of a test in and of itself, but rather of the test T, a specific test result x0, and a specific inference H (not necessarily predesignated) being entertained. That is, the severity function has three arguments. We use the notation: SEV (T,x0,H), or even SEV (H), to abbreviate:
-
“The severity with which claim H passes test T with outcome x0”.
As we will see, the analyses may take different forms: one may provide a series of inferences that pass with high and low severity, serving essentially as benchmarks for interpretation, or one may fix the inference of interest and report the severity attained.
The formal statistical testing apparatus does not include severity assessments, but there are ways to use the error statistical properties of tests, together with the outcome x0, to evaluate a test’s severity in relation to an inference of interest. This is the key for the inferential interpretation of error statistical tests. While, at first blush, a test’s severity resembles the notion of a test’s power, the two notions are importantly different; see section 2.
The severity principle, we hold, makes sense of the underlying reasoning of tests, and addresses chronic problems and fallacies associated with frequentist testing. In developing this account, we draw upon other attempts to supply frequentist foundations, in particular by Bartlett, Barnard, Birnbaum, Cox, Efron, Fisher, Lehmann, Neyman, E. Pearson; the severity notion, or something like it, affords a rationale and unification of several threads that we have extracted and woven together. Although mixing aspects from N-P and Fisherian tests is often charged as being guilty of an inconsistent hybrid [Gigerenzer, 1993], the error statistical umbrella, linked by the notion of severity, allows for a coherent blending of elements from both approaches. The different methods can be understood as relevant for one or another type of question along the stages of a full-bodied inquiry. Within the error statistical umbrella, the different methods are part of the panoply of methods that may be used in the service of severely probing hypotheses.
A principle for interpreting statistical inference vs. the goal of science
We should emphasize at the outset that while severity is the principle on which interpretations of statistical inferences are based, we are not claiming it is the goal of science. While scientists seek to have hypotheses and theories pass severe tests, severity must be balanced with informativeness. So for example, trivially true claims would pass with maximal severity, but they would not yield informative inferences 4. Moreover, one learns quite a lot from ascertaining which aspects of theories have not yet passed severely. It is the basis for constructing rival theories which existing tests cannot distinguish, and is the impetus for developing more probative tests to discriminate them (see [Mayo, 2010a]).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780444518620500058
Supervised Learning: The Epilogue
Sergios Theodoridis, Konstantinos Koutroumbas, in Pattern Recognition (Fourth Edition), 2009
10.3 Exploiting the Finite Size of the Data Set
The estimation of the classification error probability presupposes that one has decided upon the data set to which the error counting will be applied. This is not a straightforward task. The set of samples that we have at our disposal is finite, and it has to be utilized for both training and testing. Can we use the same samples for training and testing? If not, what are the alternatives? Depending on the answer to the question, the following methods have been suggested:
- ▪
-
Resubstitution Method: The same data set is used, first for training and then for testing. One need not go into mathematical details in order to see that such a procedure is not very fair. Indeed, this is justified by the mathematical analysis. In [Fole 72] the performance of this method was analyzed using normal distributions. The analysis results show that this method provides an optimistic estimate of the true error probability. The amount of bias of the resubstitution estimate is a function of the ratio N/l, that is, the data set size and the dimension of the feature space. Furthermore, the variance of the estimate is inversely proportional to the data set size N. In words, in order to obtain a reasonably good estimate, N as well as the ratio N/l must be large enough. The results from the analysis and the related simulations show that N/l should be at least three and that an upper bound of the variance is 1/8N. Of course, if this technique is to be used in practice, where the assumptions of the analysis are not valid, experience suggests that the suggested ratio must be even larger [Kana 74]. Once more, the larger the ratio N/l, the more comfortable one feels.
- ▪
-
Holdout Method: The available data set is divided into two subsets, one for training and one for testing. The major drawback of this technique is that it reduces the size for both the training and the testing data. Another problem is to decide how many of the N available data will be allocated to the training set and how many to the test set. This is an important issue. In Section 3.5.3 of Chapter 3, we saw that designing a classifier using a finite data set introduces an excess mean error and a variance around it, as different data sets, of the same size, are used for the design. Both of these quantities depend on the size of the training set. In [Raud 91], it is shown that the classification error probability of a classifier, designed using a finite training data set, N, is always higher than the corresponding asymptotic error probability (N → ∞). This excess error decreases as N increases. On the other hand, in our discussion in the previous section we saw that the variance of the error counting depends on the size of the test set, and for small test data sets the estimates can be unreliable. Efforts made to optimize the respective sizes of the two sets have not yet led to practical results.
- ▪
-
Leave-One-Out Method: This method [Lach 68] alleviates the lack of independence between the training and test sets in the resubstitution method and at the same time frees itself from the dilemma associated with the holdout method. The training is performed using N −1 samples, and the test is carried out using the excluded sample. If this is misclassified, an error is counted. This is repeated N times, each time excluding a different sample. The total number of errors leads to the estimation of the classification error probability. Thus, training is achieved using, basically, all samples, and at the same time independence between training and test sets is maintained. The major disadvantage of the technique is its high computational complexity. For certain types of classifiers (i.e., linear or quadratic) it turns out that a simple relation exists between the leave-one-out and the resubstitution method ([Fuku 90], Problem 10.2). Thus, in such cases the former estimate is obtained using the latter method with some computationally simple modifications.
The estimates resulting from the holdout and leave-one-out methods turn out to be very similar, for comparable sizes of the test and training sets. Furthermore, it can be shown (Problem 10.3, [Fuku 90]) that the holdout error estimate, for a Bayesian classifier, is an upper bound of the true Bayesian error. In contrast, the resubstitution error estimate is a lower bound of the Bayesian error, confirming our previous comment that it is an optimistic estimate. To gain further insight into these estimates and their relation, let us make the following definitions:
- ▪
-
PeN
denotes the classification error probability for a classifier designed using a finite set of N training samples.
- ▪
-
P¯eN
denotes the average
E[PeN]
over all possible training sets of size N.
- ▪
-
Pe is the average asymptotic error as N → ∞.
It turns out that the holdout and leave-one-out methods (for statistically independent samples) provide an unbiased estimate of
P¯eN
. In contrast, the resubstitution method provides a biased (underestimated) estimate of
P¯eN
. Figure 10.1 shows the trend of a typical plot of
FIGURE 10.1. Plots indicating the general trend of the average resubstitution and leave-one-out error probabilities as functions of the number of training points.
P¯eN
and the average (over all possible sets of size N) resubstitution error as functions of N [Fole 72, Raud 91]. It is readily observed that as the data size N increases, both curves tend to approach the asymptotic Pe.
A number of variations and combinations of these basic schemes have also been suggested in the literature. For example, a variation of the leave-one-out method is to leave k > 1, instead of one, samples out. The design and test process is repeated for all distinct choices of k samples. References [Kana 74, Raud 91] are two good examples of works discussing various aspects of the topic.
In [Leis 98] a method called cross-validation with active pattern selection is proposed, with the goal of reducing the high computational burden required by the leave-one-out method. It is suggested not to leave out (one at a time) all N feature vectors, but only k < N. To this end the “good” points of the data set (expected to contribute a 0 to the error) are not tested. Only the k “worst” points are considered. The choice between “good” and “bad” is based on the respective values of the cost function after an initial training. This method exploits the fact that the outputs of the classifier, trained according to the least squares cost function, approximate posterior probabilities, as discussed in Chapter 3. Thus, those feature vectors whose outputs have a large deviation from the desired value (for the true class) are expected to be the ones that contribute to the classification error.
Another set of techniques have been developed around the bootstrap method [Efro 79, Hand 86, Jain 87]. A major incentive for the development of these techniques is the variance of the leave-one-out method estimate for small data sets [Efro 83]. According to the “bootstrap” philosophy, new data sets are artificially generated. This is a way to overcome the limited number of available data and create more data in order to better assess the statistical properties of an estimator. Let X be the set of the available data of size N. A bootstrap design sample set of size N,X*, is formed by random sampling with replacement of the set X. Replacement means that when a sample, say xi, is “copied” to the set X*, it is not removed from X but is reconsidered in the next sampling. A number of variants have been built upon the bootstrap method. A straightforward one is to design the classifier using a bootstrap sample set and count the errors using the samples from X that do not appear in this bootstrap sample set. This is repeated for different bootstrap sample sets. The error rate estimate, e0, is computed by counting all the errors and dividing the sum by the total number of test samples used. However, in [Raud 91] it is pointed out that the bootstrap techniques improve on the leave-one-out method only when the classification error is large.
Another direction is to combine estimates from different estimators. For example, in the so-called 0.632 estimator ([Efro 83]), the error estimate is taken as a convex combination of the resubstitution error, eres, and the bootstrap error e0,
It has been reported that the 0.632 estimator is particularly effective in cases of small size data sets [Brag 04]. An extension of the 0.632 rule is discussed in [Sima 06] where convex combinations of different estimators are considered and the combining weights are computed via an optimization process.
Confusion Matrix, Recall and Precision
In evaluating the performance of a classification system, the probability of error is sometimes not the only quantity that assesses its performance sufficiently. Let us take for example, an M-class classification task. An important issue is to know whether there are classes that exhibit a higher tendency for confusion. The confusion matrix A = [A(i,j)] is defined so that its element A(i,j) is the number of data points whose true class label was i and were classified to class j. From A, one can directly extract the recall and precision values for each class, along with the overall accuracy:
- ▪
-
Recall (Ri). Ri is the percentage of data points with true class label i, which were correctly classified in that class. For example, for a two-class problem, the recall of the first class is calculated as
R1=A(1,1)A(1,1)+A(1,2)
.
- ▪
-
Precision (Pi). Pi is the percentage of data points classified as class i, whose true class label is indeed i. Therefore, for the first class in a two-class problem,
P1=A(1,1)A(1,1)+A(2,1).
- ▪
-
Overall Accuracy (Ac). The overall accuracy, Ac, is the percentage of data that has been correctly classified. Given an M-class problem, Ac is computed from the confusion matrix according to the equation
Ac=1N∑i=1MA(i,i),
where N is the total number of points in the test set.
Take as an example a two-class problem where the test set consists of 130 points from class ω1 and 150 points from class ω2. The designed classifier classifies 110 points from ω1 correctly and 20 points to class ω2. Also, it classifies 120 points from class ω2 correctly and 30 points to class ω1. The confusion matrix for this case is
The recall for the first class is
R1=110130
and the precision
P1=110140
. The respective values for the second class are similarly computed. The accuracy is
Ac=110+120130+150
.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9781597492720500128
Multiple Testing of Hypotheses in Biomedical Research
Hansen Bannerman-Thompson, … Ranajit Chakraborty, in Handbook of Statistics, 2012
6.3 Bonferroni procedure
RejectH01andH02ifX¯≥0.515andY¯≥0.515.RejectH01but notH02ifX¯≥0.515andY¯<0.515.RejectH02but notH01ifX¯<0.515andY¯≥0.515.Do not rejectH01andH02ifX¯<0.515andY¯<0.515.
An explicit calculation gives
FWER=Pr(V≥1∣H01,H02)=0.07<0.08;FWER=Pr(V≥1∣H01)=0.04<0.08;FWER=Pr(V≥1∣H02)=0.04<0.08.
The Bonferroni bound for FWER=Pr(V≥1∣H01,H02) is 0.08 but the actual probability is 0.07. Bonferroni paradigm declares that the above procedure controls FWER at the level 0.08. As a matter of fact, we could say that the procedure controls FWER at the level 0.07.
In this example we could calculate precisely the error probability of each type. If we want to control the error probability FWER=Pr(V≥1∣H01,H02) precisely at the level 0.08, we change the critical value from 0.515–0.5. Look at the following multiple testing procedure.
- 1.
-
Reject both the null hypotheses if X¯≥0.5andY¯≥0.5;
- 2.
-
Reject H01 but not H02 if X¯≥0.5andY¯<0.5;
- 3.
-
Reject H02 but not H01 if X¯<0.5andY¯≥0.5;
- 4.
-
Do not reject H01 and H02 if X¯<0.5andY¯<0.5.
For this test,
FWER=Pr(V≥1∣H01,H02)=0.08;FWER=Pr(V≥1∣H01)=0.0455<0.08;FWER=Pr(V≥1∣H01)=0.0455<0.08.
If the underlying test statistics of the hypotheses are statistically independent, we have a better control of the error probabilities. The following multiple test is designed towards this end.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780444518750000087
Philosophy of Econometrics
Aris Spanos, in Philosophy of Economics, 2012
5.7.4 Revisiting observed Confidence Intervals (CI)
As argued above, the post-data error probabilities associated with a CI are degenerate. In contrast, testing reasoning gives rise to well-defined error probabilities post-data because it compares what actually happened to what it is expected under different scenarios (hypothetical values of μ), since it does not involve TSN.
In view of that, it is evident that one can evaluate the probability of claims of the form given in (26) by relating μ1 to whatever values one is interested in, including x―n±cα2(s/n) for different α, using hypothetical (not factual) reasoning. Indeed, this is exactly how the severity assessment circumvents the problem facing observed CIs, whose own post-data error probabilities are zero or one, and provides an effective way to evaluate inferential claims of the form:
μ≥μ1=μ0+γ,forγ≤0,orμ≤μ1=μ0+γ,forγ≥0
, using well-defined post data error probabilities by relating γ to different values of cα2(s/n); see [Mayo and Spanos, 2006]. The reasoning underlying such severity evaluations is fundamentally different from the factual reasoning underlying a sequence of CIs; section 5.4.
The severity evaluation also elucidates the comparisons between p-values and CIs and can be used to explain why the various attempts to relate p-value and observed confidence interval curves (see [Birnbaum, 1961; Kempthorne and Folks, 1971; Poole, 1987]) were unsuccessful. In addition, it can be used to shed light on the problem of evaluating ‘effect sizes’ (see [Rosenthal et al., 1999]) sought after in some applied fields like psychology and epidemiology; see [Spanos, 2004].
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780444516763500130
Beam Management
Erik Dahlman, … Johan Sköld, in 5G NR (Second Edition), 2021
12.3.1 Beam-Failure Detection
Fundamentally, a beam failure is assumed to have happened when the error probability for the downlink control channel (PDCCH) exceeds a certain value. However, similar to radio-link failure, rather than actually measuring the PDCCH error probability the device declares a beam failure based on measurements of the quality of some reference signal. This is often expressed as measuring a hypothetical error rate. More specifically, the device should declare beam failure based on measured L1-RSRP of a periodic CSI-RS or an SS block that is spatially QCL with the PDCCH.
By default, the device should declare beam failure based on measurement on the reference signal (CSI-RS or SS block) associated with the PDCCH TCI state. However, there is also a possibility to explicitly configure a different CSI-RS on which to measure for beam-failure detection.
Each time instant the measured L1-RSRP is below a configured value is defined as a beam-failure instance. If the number of consecutive beam-failure instances exceeds a configured value, the device declares a beam failure and initiates the beam-failure-recovery procedure.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978012822320800012X
Classifiers Based on Bayes Decision Theory
Sergios Theodoridis, Konstantinos Koutroumbas, in Pattern Recognition (Fourth Edition), 2009
2.3 Discriminant Functions and Decision Surfaces
It is by now clear that minimizing either the risk or the error probability or the Neyman-Pearson criterion is equivalent to partitioning the feature space into M regions, for a task with M classes. If regions Ri, Rj happen to be contiguous, then they are separated by a decision surface in the multidimensional feature space. For the minimum error probability case, this is described by the equation
(2.21)P(ωi|x)−P(ωj|x)=0
From the one side of the surface this difference is positive, and from the other it is negative. Sometimes, instead of working directly with probabilities (or risk functions), it may be more convenient, from a mathematical point of view, to work with an equivalent function of them, for example, gi(x) ≡ f(P(ωi|x)), where f(·) is a monotonically increasing function. gi(x) is known as a discriminant function. The decision test (2.13) is now stated as
(2.22)classify x in ωi if gi(x)>gj(x) ∀j≠i
The decision surfaces, separating contiguous regions, are described by
(2.23)gij(x)≡gi(x)−gj(x)=0, i,j=1,2,…,M, i≠j
So far, we have approached the classification problem via Bayesian probabilistic arguments and the goal was to minimize the classification error probability or the risk. However, as we will soon see, not all problems are well suited to such approaches. For example, in many cases the involved pdfs are complicated and their estimation is not an easy task. In such cases, it may be preferable to compute decision surfaces directly by means of alternative costs, and this will be our focus in Chapters 3 and 4. Such approaches give rise to discriminant functions and decision surfaces, which are entities with no (necessary) relation to Bayesian classification, and they are, in general, suboptimal with respect to Bayesian classifiers.
In the following we will focus on a particular family of decision surfaces associated with the Bayesian classification for the specific case of Gaussian density functions.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9781597492720500049
Mesh Networks: Optimal Routing and Scheduling
Anurag Kumar, … Joy Kuri, in Wireless Networking, 2008
Discussion
- 1.
-
In deriving the scheduling algorithm, we could also consider the error probability on the link. Of course, if the probability of a packet error on a link is nonzero, then the stability region and also the queue evolution equation would need to be changed. However, the MWS algorithm is only slightly different. This is explored in Problem 8.9.
- 2.
-
With a suitable choice of edge weights, the MWS routing and scheduling algorithm is applicable in considerably more general scenarios. For example, we could use the same algorithm when the topology is time varying in a manner that a time average probability for a link to exist can be defined.
- 3.
-
The link activation vectors S could be nonnegative reals. Recall that the transmission bit rate could be a function of the SINR at the receiver. This in turn depends on the transmission power used by the transmitters in the link activation vector. Thus corresponding to a transmission rate vector S, we also need to specify the transmission powers. In such cases, an obvious optimization criterion could be to minimize the energy or power consumption.
- 4.
-
The MWS algorithm is complex to implement. Further, what we have described is a centralized algorithm that requires complete knowledge of the network state. Hence this is not quite a practical algorithm. Many distributed and randomized algorithms have been proposed in the literature.
- 5.
-
The MWS algorithm is a significantly general algorithm and can be applied to a large class of problems. The most notable use is in developing maximum throughput scheduling algorithms in input queued switches.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123742544500090
Different views of spectral efficiency*
Ana I Pérez-Neira, Marc Realp Campalans, in Cross-Layer Resource Allocation in Wireless Communications, 2009
2.3 The bit error rate (BER)
An important reference for the assessment of any modulation scheme is the bit error probability or bit error rate (BER) for the corresponding uncoded system. Unfortunately, for most non-binary modulation techniques (e.g. M-QAM and M-PSK) an exact expression for BER is hard to find.
At high SNR and using Gray mapping [2], it is commonly assumed that an erroneous detected symbol differs from the correct one in only one bit. Consequently, the BER is approximated by the symbol error rate (SER) divided by the number of bits per symbol b.
Closed-form expressions for SER of M-QAM and M-PSK as functions of the SNR can be found in [2]. For M-QAM with square constellations, i.e. b is an even integer, the BER approximation is given by
(2.3)BERMQAM(γ)=2log2M(1-1M)erfc(3γ2(M-1))
where erfc(.) is the complementary error function. For M-PSK modulations the BER approximation is
(2.4)BERMPSK(γ)={erfc(γ)forundefinedlog2M=1,21log2Merfc(γsin(πM))forundefinedlog2M>2
where BPSK and QPSK have the same BER because a QPSK signal can be seen as two independent BPSK signals.
An example is given in Figure 2.2. We observe that for modulations higher than 8-PSK it is preferable to move to QAM modulations. Note that 2-QAM and 4-QAM modulations are equivalent to BPSK and QPSK modulations, respectively. Furthermore, it can be shown that the BER performance of 8-QAM is very close to that of 16-QAM but with one bit per symbol less. Hence, it is quite usual that in commercial systems QAM modulations start at 16-QAM. For instance, 16-QAM and 64-QAM are the two QAM schemes considered by the IEEE802.11g/a standards [3].
Figure 2.2. BER curves for different modulations.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123741417000026
Channel coding
Wenhong Chen, … Li Guo, in 5G NR and Enhancements, 2022
7.3.6.3 Length for CRC
For LDPC codes, the number of CRC bits to achieve a given undetected error probability varies with the block size and code rate. Considering the actual performance requirements, NR finally determines that when the information block size A>3824, the length of CRC added to a TB is L=24 bits, and the generating polynomial is:
(7.13)gCRC24A(D)=D24+D23+D18+D17+D14+D11+D10+D7+D6+D5+D4+D3+D+1
When the information block size A≤3824, a CRC with a length of L=16 bits is added after the TB, and the generating polynomial is:
(7.14)gCRC16(D)=D16+D12+D5+1
If code segmentation (i.e., the number of blocks C>1) is required, a 24-bit CRC is added after each CB, and the generating polynomial is:
(7.15)gCRC24B(D)=D24+D23+D6+D5+D+1
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780323910606000076

|
6.3. ВЕРОЯТНОСТНЫЕ ВЫЧИСЛЕНИЯ |
271 |
С другой стороны, работа над верхними оценками — построение конкретных алгоритмов, как правило, производится в терминах машин с произвольным доступом (RAM).
Упражнение 6.2.6. Покажите, что задача распознавания гамильтоновых графов (т. е. графов, содержащих гамильтонов цикл) принадлежит NP, а задача распознавания негамильтоновых графов принадлежит coNP.
Упражнение 6.2.7. Придумайте полиномиальный алгоритм для проверки, есть ли в заданном графе хотя бы один «треугольник».
Упражнение 6.2.8. Рассмотрим язык DF NT , состоящий из полиномов от нескольких переменных, имеющих целочисленные корни.
Студент утверждает, что DF NT 2 NP , т.к. если оракул-Мерлин предоставит решение v, доказываю-
?
щее принадлежность полинома p 2 DF NT , то верификатор Артур сможет легко проверить: p(v) = 0. Прав ли студент?
6.3Вероятностные вычисления
Вероятностные алгоритмы с односторонней ошибкой. Классы сложно-
сти RP и coRP и отношение к классам NP и coNP. Вероятностная
амплификация для RP и coRP. Вероятностные алгоритмы с двусторонней ошибкой. Класс сложности BPP. Вероятностная амплификация для BPP. Неамплифицируемый класс PP.
Итак, в разделе 6.1.1 мы познакомились с детерминированными машинами Тьюринга, моделями, ко-

|
272 |
Глава 6. ОСНОВЫ ТЕОРИИ СЛОЖНОСТИ ВЫЧИСЛЕНИЙ |
||||||||||||||||||||||
|
6.3. ВЕРОЯТНОСТНЫЕ ВЫЧИСЛЕНИЯ |
273 |
торые можно использовать для описания всех существующих вычислительных устройств, будь то карманный калькулятор или суперкомпьютер. В разделе 6.2.2 мы рассматривали недетерминированные машины Тьюринга — интересную, мощную модель вычислений, полезную для описания классов сложностей задач, но, увы, не соответствующую никаким реальным вычислительным устройствам. Однако оказалось, что можно частично использовать мощь «параллельного перебора», присущую НМТ, привнеся в детерминированный процесс вычисления вероятностную составляющую. Выяснилось, что такие устройства вполне можно построить физически, и что они способны эффективно решать больший класс задач, чем обыкновенные МТ.
Впрочем, по-порядку. Сначала определим ВМТ — вероятностную машину Тьюринга. Существует два подхода к определению ВМТ, приведем их оба.
Определение 6.3.1. Вероятностная машина Тьюринга аналогична недетерминированной машине Тьюринга, только вместо недетерминированного перехода в два состояния машина выбирает один из вариантов с равной вероятностью.
Определение 6.3.2. Вероятностная машина Тьюринга представляет собой детерминированную машину Тьюринга (см. определение 6.1.1 «Машина Тьюринга»), имеющую дополнительно источник случайных битов, любое число которых, например, она может «заказать» и «загрузить» на отдельную ленту и потом использовать в вычислениях обычным для МТ образом.
Оба определения — 6.3.1 «online ВМТ» и 6.3.2 «o ine ВМТ» — очевидно, эквивалентны. Более того, они вполне соответствуют обычному компьютеру, к которому подключен внешний генератор случайных последовательностей на основе случайных физических процессов, таких, как, например, распад долгоживущего радиоактивного изотопа (замер времени между щелчками счетчика Гейгера рядом с образцом изотопа рубидия-85), снятие параметров с нестабильных электрических цепей и т. п.
|
274 |
Глава 6. ОСНОВЫ ТЕОРИИ СЛОЖНОСТИ ВЫЧИСЛЕНИЙ |
Привнесение случайности в детерминированную вычислительную модель (как и привнесение недетерминизма) модифицирует понятие разрешимости. Теперь, говоря о результате работы ВМТ M на входе x, мы можем говорить о математическом ожидании результата E[M(x)] или вероятности вывода того или иного ответа на заданном входе: P[M(x) = 1], P[M(x) = 0], но ограничение на время работы (как правило, полиномиальное) понимается так же, как и для ДМТ.
Вообще, есть вероятностные алгоритмы, не совершающие ошибок при вычислении. Они используют «вероятностную составляющую» для «усреднения» своего поведения на различных входных данных таким образом, чтобы избежать случая, когда часто встречаются «плохие» входные наборы. Такие алгоритмы иногда называют «шервудскими», в честь известного разбойника-перераспределителя ценностей, и мы уже рассматривали один из таких алгоритмов — алгоритм 12 «Quicksort» с вероятностным выбором оси.
ВМТ может быть полезна, как мы увидим дальше, даже если будет иногда ошибаться при вычислении некоторой функции. Разумеется, нас будут интересовать машины, ошибающиеся «нечасто» и, желательно, работающие эффективно, т. е. полиномиальное от длины входа время.
Мы сконцентрируемся на анализе ВМТ, применяющихся для задач разрешения, т. е. задач, в которых нужно получить ответ «0» или «1».
Рассматривая ВМТ, предназначенные для решения таких задач, можно их классифицировать на три основные группы:
1.«zero-error» — ВМТ, не допускающие ошибок. Правда, в этот же класс попадают алгоритмы, которые хоть и не допускают ошибок, могут и не выдать никакого ответа или отвечать «не знаю».
2.«one-sided error» — ВМТ с односторонними ошибками. Например, ВМТ-«автосигнализация» обязательно сработает, если стекло разбито, дверь открыта и происходит автоугон, но могут произойти

|
6.3. ВЕРОЯТНОСТНЫЕ ВЫЧИСЛЕНИЯ |
275 |
и ложные срабатывания (так называемые ошибки второго рода, напомним также, что ошибкой первого рода является «пропуск цели»).
3.«two-sided error» — ВМТ с двусторонними ошибками. Ошибки могут быть и первого, и второго рода,
но вероятность правильного ответа должна быть больше (чем больше, тем лучше) 12 , иначе эта ВМТ ничем не лучше обычной монетки.
Далее мы более подробно рассмотрим перечисленные классы ВМТ и классы языков, эффективно (т. е. полиномиально) распознаваемых ими.
6.3.1Классы RP/coRP. «Односторонние ошибки»
Итак, определим классы языков, эффективно распознаваемых на ВМТ с односторонней ошибкой.
Определение 6.3.3. Класс сложности RP (Random Polynomialme) состоит из всех языков L, для которых существует полиномиальная ВМТ M, такая, что:
|
x 2 L |
) P [M(x) = 1] |
1 |
; |
|
2 |
|||
|
x 2/ L |
) P [M(x) = 0] = 1: |
Cразу же представим аналогичное определение для класса-дополнения coRP fLjL 2 RPg.
Определение 6.3.4. Класс сложности coRP (Complementary Random Polynomialme) состоит из всех языков L, для которых существует полиномиальная ВМТ M, такая, что:

|
276 |
Глава 6. ОСНОВЫ ТЕОРИИ СЛОЖНОСТИ ВЫЧИСЛЕНИЙ |
x 2 L ) P [M(x) = 1] = 1; x 2/ L ) P [M(x) = 0] 12:
Попробуем «популярно представить» языки и ВМТ, упомянутые в этих определениях. Например, для определения 6.3.3 «RP» можно представить автоматическую систему биометрической идентификации на входе в военный бункер, никогда не пускающую солдат противника (x 2/ L), и с вероятностью 12 пускающей своих (x 2 L), правда, возможно, своим потребуется сделать несколько попыток прохода.
Для определения 6.3.4 «coRP» можно представить автоматическую автомобильную сигнализацию, гарантированно подающую сигнал при попытке угона (x 2 L), и с вероятностью 12 не поднимающую ложную тревогу, если происходит что-то другое.
Действительно, первое условие из определения 6.3.4 «coRP» и второе условие из определения 6.3.3 «RP» называют «completeness»-условиями¹¹, а первое условие из определения 6.3.3 «RP» и второе условие из определения 6.3.4 «coRP» — «soundness»-условиями¹². Для тех, кто считает, что сигнализация с вероятностью ложного срабатывания чуть меньше 12 не отличается здравостью и ни на что не годна, просим немного подождать.
Вспомним, что в «o ine»-определении ВМТ (См. определение 6.3.2 «o ine ВМТ») подразумевается отделенность вероятностных данных от обычной ДМТ. Полиномиальная ВМТ делает не более чем полиномиальное (от длины входа) число переходов, и, следовательно, моделирующая ее ДМТ нуждается не более чем в полиномиальной строке случайных битов. Теперь перепишем еще раз определения классов RP и coRP, используя только ДМТ. Выделим элемент случайности в строку y, причем jyj p(jxj), где
¹¹completeness — полнота. ¹²soundness — корректность.

|
6.3. ВЕРОЯТНОСТНЫЕ ВЫЧИСЛЕНИЯ |
277 |
p( ) — некий полином, и заменим условия на вероятность условиями на долю строк y, на которых ДМТ дает тот или иной результат.
Определение 6.3.5. Класс сложности RP состоит из всех языков L, для которых существуют некий полином p( ) и полиномиальная МТ M(x; y), такая, что:
|
x |
2 |
L |
) |
jfy : M(x; y) = 1; jyj p(jxj)gj |
1 |
; |
||
|
2p(jxj) |
2 |
|||||||
|
x 2/ L |
) |
8y M(x; y) = 0: |
Определение 6.3.6. Класс сложности coRP состоит из всех языков L, для которых существуют некий полином p( ) и полиномиальная МТ M(x; y), такая, что:
|
x 2 L ) 8y M(x; y) = 1; |
||||||
|
x / L |
) |
jfy : M(x; y) = 0; jyj p(jxj)gj |
1 |
: |
||
|
2p(jxj) |
2 |
|||||
|
2 |
Теперь вспомним определение класса NP через детерминированную машину Тьюринга (определение 6.2.4 «NP/ДМТ») и сравним его с определением 6.3.5 «RP/ДМТ», опуская одинаковые описания M, y:
|
278 |
Глава 6. ОСНОВЫ ТЕОРИИ СЛОЖНОСТИ ВЫЧИСЛЕНИЙ |
||
|
NP |
RP |
||
|
x 2 L ) 9y; M(x; y) = 1 |
x 2 L ) доля y: M(x; y) = 1 21 |
||
|
x 2/ L ) 8y; M(x; y) = 0 |
x 2/ L ) 8y; M(x; y) = 0 |
Из этого сравнения видно, что класс RP вложен в класс NP. Если для распознавания языка L из NP нам для каждого x 2 L нужен был хотя бы один полиномиальный «свидетель» y, который мы могли предъявить «верификатору», то в случае с классом RP этих свидетелей должно быть достаточно много, согласно определению 6.3.5 «RP/ДМТ» не меньше половины. На самом деле, как мы увидим дальше, этих свидетелей может быть и меньше, а пока очевидны следующие утверждения (см. рис. 6.11):
Теорема 30. RP NP.
Теорема 31. coRP coNP.
Теперь вернемся к пресловутой «одной второй». Рассмотрим некоторый класс ~.
C
|
~ |
|||
|
Определение 6.3.7. Класс сложности C состоит из всех языков L, для которых существует полино- |
|||
|
~ |
|||
|
миальная ВМТ M, такая, что: |
|||
|
x 2 L |
~ |
3 |
|
|
) P [M(x) = 1] |
4; |
||
|
x 2/ L |
~ |
||
|
) P [M(x) = 1] = 0: |
|||
|
~ |
|||
|
Очевидно, т.к. с виду налагаемые условия кажутся более (и уж точно не менее) жесткими, C RP. |
|||
|
~ |
~ |
Можем ли мы утверждать, что RP C и, следовательно, C RP? Оказывается, да.

|
6.3. ВЕРОЯТНОСТНЫЕ ВЫЧИСЛЕНИЯ |
279 |
Стрелки показывают вложенность классов сложности
Рис. 6.11: Классы сложности RP и coRP

|
280 |
Глава 6. ОСНОВЫ ТЕОРИИ СЛОЖНОСТИ ВЫЧИСЛЕНИЙ |
|
|
Лемма 35. |
~ |
~ |
|
RP C |
, и, следовательно, C RP. |
Доказательство. Допустим L 2 RP. Тогда существует ВМТ M(x) со свойствами, описанными в определении 6.3.3 «RP». Для заданного x будем запускать машину M два раза, обозначая результаты запусков через M1(x) и M2(x). Построим машину M,~ дважды вызывающую машину M и выдающую в качестве результата M1(x)_M2(x). Тогда вероятность ошибки первого рода (других ошибок машина M не допускает), случающейся, когда x 2 L, а M(x) = 0 (обозначим эту вероятность pM ), будет меньше 12 . Машина M,~ по построению, тоже будет допускать только ошибки первого рода, но они будут происходить только в случае ошибки машины M на обоих запусках M1(x) и M2(x), и вероятность такой ошибки будет
|
1 |
1 |
1 |
|||||
|
pM~ = |
< |
: |
|||||
|
pM |
pM |
4 |
|||||
|
~ |
удовлетворяет описанию языка |
||||||
|
Соответственно, для заданного языка L построенная нами машина M |
~.
C
Примененный нами метод называется «вероятностным усилением» (или «вероятностной амплификацией» от amplifica on), и, применив его полиномиальное число раз, мы добиваемся экспоненциального уменьшения вероятности ошибки. Таким образом, уже очевидно, что в определениях RP и coRP вместо «одной второй» можно использовать любые константы 12 — с помощью амплификации мы легко можем достичь заданного уровня «здравости».
Можно вполне использовать упоминающуюся шумную сигнализацию, срабатывающую ложно в половине случаев, если заставить ВМТ сигнализации выполнить проверку раз двадцать — тогда вероятность ложной тревоги была бы меньше 100001 . Это, к сожалению, пока является недостижимым уровнем для существующих автосигнализаций.
Более того, «порог», после которой можно «усиливать» вероятность, не обязательно должен быть больше одной второй, он может быть даже очень малым, главное, не быть пренебрежимо малым.
|
6.3. ВЕРОЯТНОСТНЫЕ ВЫЧИСЛЕНИЯ |
281 |
Определение 6.3.8. Класс сложности RPweak состоит из всех языков L, для которых существуют полиномиальная ВМТ M и полином p( ), такие, что:
|
) P [M(x) = 1] |
1 |
||||
|
x 2 L |
; |
||||
|
p( x |
) |
||||
|
x 2/ L |
j j |
||||
|
) P [M(x) = 1] = 0: |
Определение 6.3.9. Класс сложности RPstrong состоит из всех языков L, для которых существуют полиномиальная ВМТ M и полином p( ), такие, что:
x 2 L ) P [M(x) = 1] 1 2 p(jxj);
x 2/ L ) P [M(x) = 1] = 0:
Поначалу кажется, что RPweak — это некоторая релаксация, т. е. определение более широкого класса из-за ослабления ограничений, класса RP, а RPstrong, наоборот, усиление ограничений, и, по крайней мере:
RPstrong RP RPweak:
Однако оказывается, все это определения одного и того же класса.
Лемма 36. RPweak = RPstrong = RP.
Доказательство. Достаточно доказать RPweak RPstrong, для чего мы покажем, как для любого языка L 2 RPweak из машины Mweak (машина M из определения 6.3.8) сделать машину Mstrong, соответствующую определению 6.3.9. Действуем, как и в более простом случае леммы 35 — для данного x машина

|
282 |
Глава 6. ОСНОВЫ ТЕОРИИ СЛОЖНОСТИ ВЫЧИСЛЕНИЙ |
Mstrong запускает t раз машину Mweak и возвращает Логическое ИЛИ от всех результатов запуска. Так же, как и в случае леммы 35, возможна только ошибка первого рода, причем ее вероятность (если x 2 L):
|
P(Mstrong(x) = 0) = (P(Mweak(x) = 0))t(jxj) = (1 |
1 |
)t(jxj) : |
|||||||||||||||||||
|
p( |
x |
) |
|||||||||||||||||||
|
j j |
|||||||||||||||||||||
|
Осталось найти необходимое «для разгона» количество запусков: |
|||||||||||||||||||||
|
(1 |
1 |
)t(jxj) |
2 p(jxj); |
||||||||||||||||||
|
p( x |
) |
||||||||||||||||||||
|
j |
j |
||||||||||||||||||||
|
откуда получаем |
log 2 p(jxj) |
||||||||||||||||||||
|
t( |
x |
) |
2 |
p2 |
( |
x |
): |
||||||||||||||
|
) log |
|||||||||||||||||||||
|
j |
j |
log (1 |
1 |
j |
j |
||||||||||||||||
|
p(jxj) |
т. е. за полиномиальное время мы усиливаем вероятность от «полиномиально малой» до «полиномиально близкой к единице».
6.3.2Класс BPP. «Двусторонние ошибки»
Теперь рассмотрим, что происходит, если допустить возможность двусторонних ошибок, т. е. ошибок первого и второго рода. Определим класс языков, эффективно распознаваемых на ВМТ с двусторонней ошибкой.
|
6.3. ВЕРОЯТНОСТНЫЕ ВЫЧИСЛЕНИЯ |
283 |
Определение 6.3.10. Класс сложности BPP (Bounded-Probability Polynomialme) состоит из всех язы-
ков L, для которых существует полиномиальная ВМТ M, такая, что:
|
x 2 L |
) P [M(x) = 1] |
2 |
; |
|
3 |
|||
|
x 2/ L |
) P [M(x) = 0] |
2 |
: |
|
3 |
Из определения видно, что класс BPP замкнут относительно дополнения.
По опыту раздела 6.3.1 читатель ожидает обобщений определения класса BPP без магической константы «23 », и мы его не разочаруем. Итак, предоставим «свободное» и «жесткое» определения клас-
са BPP.
Определение 6.3.11. Класс сложности BPPweak состоит из всех языков L, для которых существуют:
c, 0 < c < 1 — константа;
p( ) — положительный полином;
M — полиномиальная ВМТ;
такие, что:
|
x 2 L |
) P [M(x) = 1] c + |
1 |
; |
||
|
p( x |
) |
||||
|
j |
j |
||||
|
x 2/ L |
) P [M(x) = 1] < c |
1 |
: |
||
|
p( x |
) |
||||
|
j |
j |
284 Глава 6. ОСНОВЫ ТЕОРИИ СЛОЖНОСТИ ВЫЧИСЛЕНИЙ
Определение 6.3.12. Класс сложности BPPstrong состоит из всех языков L, для которых существуют полиномиальная ВМТ M, и полином p( ), такие, что:
|
x 2 L |
) P [M(x) = 1] 1 |
2 |
p(jxj); |
|
x 2/ L |
) P [M(x) = 0] 1 |
2 |
p(jxj): |
В следующей лемме мы используем следующие результаты из теории вероятностей.
Теорема 32. «Закон Больших Чисел для схемы Бернулли»
Пусть событие A может произойти в любом из t независимых испытаний с одной и той же вероятностью p, и пусть Mt — число осуществлений события A в t испытаниях. Тогда Mtt 7! p, причем
|
для любого » > 0: |
( |
t t |
p |
«) |
(1t»2 |
): |
|||
|
P |
|||||||||
|
M |
p |
p |
|||||||
|
1 |
|||||||||
|
Теорема 33. «Оценка Чернова» (Cherno bounds). |
Пусть M1; : : : ; Mt — независимые события, каждое из которых имеет вероятность p 2 . Тогда вероятность одновременного выполнения более половины событий будет больше, чем 1 exp( 2(p
12 )2t).
Лемма 37. BPPweak = BPP.
|
Доказательство. |
Очевидно, что BPP BPPweak, для этого достаточно положить c 21 и p(jxj) 6. |
||||||||
|
Теперь покажем BPPweak |
BPP. Пусть L 2 BPPweak, обозначим через Mweak ВМТ из определе- |
||||||||
|
ния 6.3.11, построим M из определения 6.3.10 «BPP». |
2 |
(jxj) раз машину Mweak (обозначим |
|||||||
|
На входе x машина M вычислит p(jxj), затем будет запускать t = 6tp |
|||||||||
|
результат i-го запуска через Mi |
) и возвращать «1», если M |
= |
Mi |
> t |
c, или «0» в противном |
||||
|
случае. |
weak |
t |
∑i=1 |
weak |

|
6.3. ВЕРОЯТНОСТНЫЕ ВЫЧИСЛЕНИЯ |
285 |
Рассмотрим Perr = P(M(x) = 0jx 2 L) — вероятность ошибки первого рода:
Perr = P[Mt < t c]:
Заметим, что при x 2 L мат. ожидание «суммарного голосования» машин Miweak будет
|
[ |
] |
(c + |
j j |
) ; |
|||||
|
E Mt(x) = t E Mweaki |
(x) |
t |
1 |
||||||
|
p( |
x |
) |
|||||||
|
откуда, применяя теорему 32 и учитывая, что 0 |
E(Mt) |
1, получаем |
|||||||
|
t |
Вероятность ошибки второго рода Perr = P(M(x) = 1jx 2/ L) оценивается аналогично.
Лемма 38. BPPstrong = BPP.
Доказательство. Очевидно, что BPPstrong BPP, осталось показать обратное вложение. Действуем аналогично лемме 37, строим машину Mstrong, запуская t = 2p(jxj) + 1 раз (пусть будет нечетное число) обычную BPP-машину M и принимая решения на основе «большинства» ее результатов. Если x 2 L, то,

|
286 |
Глава 6. |
ОСНОВЫ ТЕОРИИ СЛОЖНОСТИ ВЫЧИСЛЕНИЙ |
||||||||||||||||
|
согласно теореме 33, вероятность правильного ответа: |
||||||||||||||||||
|
1 |
2 |
|||||||||||||||||
|
P(Mstrong(x) = 1) 1 exp ( |
2 |
(p |
) |
t) = |
||||||||||||||
|
2 |
||||||||||||||||||
|
2 |
1 |
2 |
||||||||||||||||
|
= 1 |
exp ( |
2 |
( |
) |
(2p(jxj) + 1)) = |
|||||||||||||
|
3 |
2 |
|||||||||||||||||
|
= 1 |
exp |
p |
x ) + 1 |
) > 1 e |
j9 j |
> 1 2 p(jxj): |
||||||||||||
|
( 2 (j |
18j |
) |
||||||||||||||||
|
p( x |
Упражнение 6.3.1. Вы разработчик военного программного комплекса, использующего сложновычислимую и секретную функцию F : [0; : : : ; N 1] ! [0; : : : ; m 1], которую подключают к вашему алгоритму в виде отдельного массива длины N, т. е. функция задана таблично на внешней флеш-памяти огромного объема(только вес этой флэшки — 20 кг, которую носят и охраняют два майора-особиста). Функция гомоморфна, т. е.
F ((x + y) mod N) = (F (x) + F (y)) mod m
Однако, утром перед приемными испытаниями, выяснилось, что «флешка побилась», т. е. некоторые значения этой функции стали неверными. Виновные майоры уже расстреляны, а вся команда разработчиков пытается решить проблему.
Инженеры исследовали сбой — и утверждают, что «побилось» не более 16 ячеек, к сожалению, неизвестно каких.
С учетом этого факта вам поставлена задача реализовать простой и быстрый алгоритм, который правильно вычисляет F (x) с вероятностью не меньше 23 .

|
6.3. ВЕРОЯТНОСТНЫЕ ВЫЧИСЛЕНИЯ |
287 |
Стрелки показывают вложенность классов сложности
Рис. 6.12: Классы сложности: BPP и его «соседи»
Упражнение 6.3.2. Все то же, что и в упражнении 6.3.1, но чтобы вероятность ошибки Perr можно было сделать произвольно малой, т. е. 2 p(jxj), и при этом, чтобы выполнение алгоритма было замедлено не больше, чем в O(p(jxj)) раз.
Упражнение 6.3.3. Вводная, что и в упражнении 6.3.1, только теперь достаточно времени (испытания прошли, есть пара недель перед вводом в опытную эксплуатацию), и нужно восстановить значение этой функции за время O(N2).
|
288 |
Глава 6. ОСНОВЫ ТЕОРИИ СЛОЖНОСТИ ВЫЧИСЛЕНИЙ |
6.3.3Класс PP
Теперь познакомимся с максимально широким классом языков, распознаваемых полиномиальной ВМТ.
Определение 6.3.13. Класс сложности PP (Probability Polynomialme) состоит из всех языков L, для которых существует полиномиальная ВМТ M, такая, что:
|
x 2 L |
) P [M(x) = 1] > |
1 |
; |
|
2 |
|||
|
x 2/ L |
) P [M(x) = 0] > |
1 |
: |
|
2 |
По опыту разделов 6.3.1 и 6.3.2 читатель может предположить, что константа «12 » также выбрана произвольно, «для красоты», но здесь это не так. В отличие от определений 6.3.3 «RP», 6.3.10 «BPP», в определении 6.3.13 «PP» мы никак не можем заменить константу «12 » на любую большую константу, т.к. в этом случае нет гарантированной возможности амплификации вероятности за полиномиальное время.
Обратите внимание, что в определении 6.3.13 «PP» важна даже строгость неравенства (что необязательно для определений 6.3.3 «RP», 6.3.10 «BPP»), т. е. нельзя заменить символ «>» на « », т.к. тогда определение полностью «выродится», ведь проверяющую машину можно будет заменить подбрасыванием одной монетки. Единственное ослабление, на которое мы можем пойти, — это пожертвовать строгостью одного из неравенств в определении.
Определение 6.3.14. Класс сложности PPweak состоит из всех языков L, для которых существует полиномиальная ВМТ M, такая, что:
w(jxj)
w(jxj),
(w(jxj)+1).
|
6.3. ВЕРОЯТНОСТНЫЕ ВЫЧИСЛЕНИЯ |
289 |
|
x 2 L |
) P [M(x) = 1] > |
1 |
; |
|
2 |
|||
|
x 2/ L |
) P [M(x) = 0] |
1 |
: |
|
2 |
Упражнение 6.3.4. Что будет, если в определении 6.3.14 в обоих неравенствах поставить « »? Какой класс языков будет определен?
Лемма 39. PPweak = PP.
Доказательство. Очевидно, доказывать нужно только вложение PPweak PP, для чего мы покажем, как для любого языка L 2 PPweak из машины Mweak (машина M из определения 6.3.14) сделать машину M из определения 6.3.13 «PP». Пусть машина Mweak использует не больше w(jxj) случайных бит (см. определение 6.3.2 «o ine ВМТ»), машина M будет использовать p(jxj) = 2 w(jxj) + 1 случайных бит следующим образом:
M(x; r1; :::;rp(jxj) ) (rw(jxj)+1_ :::_rp(jxj))^Mweak(x; r1; :::;rw(jxj) );
причем, «оптимизируя» вычисление этого выражения, мы даже не будем запускать Mweak, если rw(jxj)+1 _ : : : _ rp(jx что, очевидно, может произойти с вероятностью 2
Итак, рассмотрим случай x 2 L. Тогда P(Mweak(x) = 1) > 12 , причем P(Mweak(x) = 1) 12 + 2
т.к. всего вероятностных строк не больше 2w(jxj), и минимальный «квант» вероятности, соответствующий одной вероятностной строке, будет не меньше 2 .

290
|
P(M(x) = 1) = |
(1 |
2 |
||
|
(1 |
2 |
|||
|
= |
1 |
+ 2 |
||
|
2 |
||||
|
Глава 6. |
ОСНОВЫ ТЕОРИИ СЛОЖНОСТИ ВЫЧИСЛЕНИЙ |
|||||||||
|
(w(jxj)+1) |
(M |
(x) = 1) |
||||||||
|
(w( x )+1)) |
P |
1 |
weak |
w( x ) |
||||||
|
j j |
) |
3 |
j j |
1 |
||||||
|
(2 + 2 |
) = |
|||||||||
|
(w(jxj)+1) |
( |
2 |
w(jxj)) |
> |
: |
|||||
|
2 |
2 |
Если x 2/ L, то P(Mweak(x) = 0) 12 , а
P(M(x) = 0) = (1 2 (w(jxj)+1)) P(Mweak(x) = 0)+
+ 2 (w(jxj)+1) (1 2 (w(jxj)+1)) 12 + 2 (w(jxj)+1) > 12:
Исследуем отношение класса PP к известным нам классам сложности.
Теорема 34. PP PSPACE.
Доказательство. Для любого языка L 2 PP из машины MPP (машина M из определения 6.3.13 «PP») можно сделать машину M, которая последовательно запускает MPP на x и всех 2p(jxj) возможных вероятностных строках, и результат определяется по большинству результатов запусков. Машина M будет разрешать язык L и использовать не более полинома ячеек на ленте, т.к. каждый запуск MPP может использовать один и тот же полиномиальный отрезок ленты.
Теорема 35. NP PP.

|
6.3. ВЕРОЯТНОСТНЫЕ ВЫЧИСЛЕНИЯ |
291 |
Доказательство. Покажем, как для любого языка L 2 NP из машины MNP (машина M из определения 6.2.4 «NP/ДМТ») сделать машину M из определения 6.3.14. Пусть размер подсказки y для машины MNP ограничен полиномом p(jxj). Тогда машина M будет использовать p(jxj) + 1 случайных бит следующим образом:
M(x; r1; : : : ; rp(jxj)+1 ) rp(jxj)+1
При x 2 L, P(M(x) = 1) = 12 + 2 p(jxj) > 12 . При x 2/
лемму 39, получаем L 2 PPweak = PP.
Аналогично получаем следующую лемму.
Лемма 40. coNP PP.
_ MNP(x; r1; : : : ; rp(jxj) ):
L, P(M(x) = 0) = 12 . Таким образом, учитывая
6.3.4Класс ZPP. «Алгоритмы без ошибок»
Пока в разделах 6.3.1, 6.3.2 и 6.3.3 мы рассматривали «ошибающиеся» вероятностные алгоритмы распознавания. Еще один интересный класс вероятностных алгоритмов распознавания — алгоритмы, которым в дополнение к стандартным ответам «0» и «1» разрешено выдавать неопределенный ответ «?». Ответ «?» означает «не знаю» и не считается ошибочным в любом случае. Используя эти алгоритмы, мы можем определить еще один класс языков.
Определение 6.3.15. Класс сложности ZPP состоит из всех языков L, для которых существует полиномиальная ВМТ M, возвращающая только ответы «0»,«1»,«?» («не знаю»), причем:
|
x 2 L ) P [M(x) = 1] > |
1 |
^ |
P [M(x) = 1] + P [M(x) = «?»] = 1; |
|
2 |
|||
|
x 2/ L ) P [M(x) = 0] > |
1 |
^ |
P [M(x) = 0] + P [M(x) = «?»] = 1: |
|
2 |
|
292 |
Глава 6. ОСНОВЫ ТЕОРИИ СЛОЖНОСТИ ВЫЧИСЛЕНИЙ |
Оказывается, у этого класса есть и альтернативное определение:
Теорема 36. ZPP = RP coRP.
Доказательство. ZPP RP, т.к. для любого языка L 2 ZPP из машины MZPP (машина M из определения 6.3.15 «ZPP») можно сделать машину M из определения 6.3.3 «RP»:
Answer = MZPP(x)
if Answer = «?» then
Answer = 0 end if
RETURN Answer
Действительно, если x 2 L, то P [MZPP(x) = 1] > 12 , и, следовательно, P [M(x) = 1] 12 . Если x 2/ L, то
P [M(x) = 0] = P [MZPP(x) = 0] + P [MZPP(x) = «?»] = 1:
Аналогично доказывается, что ZPP coRP.
Теперь покажем, что RP coRP ZPP. Изготовим машину M для распознавания ZPP из машин MRP (M из определения 6.3.3 «RP») и McoRP (M из определения 6.3.4 «coRP»), используя «безошибочные» возможности обеих машин:
if MRP(x) = 1 then
RETURN «1» end if
if McoRP(x) = 0 then
RETURN «0» end if
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
12.2. Испытание простоты чисел
Если формулы получения простых чисел, подобно формулам Ферма или Мерсенна, не гарантируют, что полученные числа — простые, то как мы можем генерировать большие простые числа для криптографии? Мы можем только выбрать случайно большое число и провести испытание, чтобы убедиться, что оно — простое.
Нахождение алгоритма, который правильно и эффективно проверяет очень большое целое число и устанавливает: данное число – простое это число или же составной объект, — всегда было проблемой в теории чисел и, следовательно, в криптографии. Однако, недавние исследования (одно из которых мы обсуждаем в этом разделе) выглядят очень перспективными.
Алгоритмы, которые решают эту проблему, могут быть разделены на две обширные категории — детерминированные алгоритмы и вероятностные алгоритмы. Ниже рассматриваются некоторые представители обеих категорий. Детерминированный алгоритм всегда дает правильный ответ. Вероятностный алгоритм дает правильный ответ в большинстве, но не во всех случаях. Хотя детерминированный алгоритм идеален, он обычно менее эффективен, чем соответствующий вероятностный.
Детерминированные алгоритмы
Детерминированный алгоритм, проверяющий простоту чисел, принимает целое число и выдает на выходе признак: это число — простое число или составной объект. До недавнего времени все детерминированные алгоритмы были неэффективны для нахождения больших простых чисел. Как мы коротко покажем, новые взгляды делают эти алгоритмы более перспективными.
Алгоритм теории делимости
Самое элементарное детерминированное испытание на простоту чисел — испытание на делимость. Мы используем в качестве делителей все числа, меньшие, чем 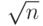
Алгоритм может быть улучшен, если проверять только нечетные номера. Он может быть улучшен далее, если использовать таблицу простых чисел между 2 и 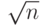
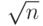

Сложность побитного испытания делимостью показательна.
Пример 12.18
Предположим, что n имеет 200 битов. Какое число разрядных операций должен был выполнить алгоритм делимости?
Решение
Сложность побитовых операций этого алгоритма — 
12.1.
AKS-алгоритм
В 2002 г. индийские ученые Агравал, Каял и Сахсена (Agrawal, Kayal и Saxena) объявили, что они нашли алгоритм для испытания простоты чисел с полиномиальной сложностью времени разрядных операций 0 ((log2nb)). Алгоритм использует тот факт, что 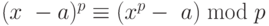
Пример 12.19
Предположим, что n имеет 200 битов. Какое число разрядных операций должен был выполнить алгоритм AKS?
Решение
Сложность разрядной операции этого алгоритма — O((log 2 n b) 12). Это означает, что алгоритму надо только (log2 200) 12 = 39 547 615 483 битовых операций. На компьютере, способном выполнить 1 миллиард битов в секунду, алгоритму требуется только 40 секунд.
Вероятностные алгоритмы
До AKS-алгоритма все эффективные методы для испытания простоты чисел были вероятностные. Эти методы могут использоваться еще некоторое время, пока AKS формально не принят как стандарт.
Вероятностный алгоритм не гарантирует правильность результата. Однако мы можем получить вероятность ошибки настолько маленькую, что это почти гарантирует, что алгоритм вырабатывает правильный ответ. Сложность разрядной операции алгоритма может стать полиномиальной, при этом мы допускаем небольшой шанс для ошибок. Вероятностный алгоритм в этой категории возвращает результат либо простое число, либо составной объект, основываясь на следующих правилах:
a. Если целое число, которое будет проверено, — фактически простое число, алгоритм явно возвратит простое число.
b. Если целое число, которое будет проверено, — фактически составной объект, алгоритм возвращает составной объект с вероятностью 
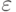
Тест Ферма
Первый вероятностный метод, который мы обсуждаем, — испытание простоты чисел тестом Ферма.
Если n — простое число, то 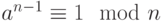
Обратите внимание, что если n — простое число, то сравнение справедливо. Это не означает, что если сравнение справедливо, то n — простое число. Целое число может быть простым числом или составным объектом. Мы можем определить следующие положения как тест Ферма:
Простое число удовлетворяет тесту Ферма. Составной объект может пройти тест Ферма с вероятностью 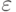
Пример 12.20
Проведите испытание Ферма для числа 561.
Решение
Используем в качестве основания число 2.
2561-1 = 1 mod 561
Число прошло тест Ферма, но это — не простое число, потому что
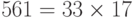
Испытание квадратным корнем
В модульной арифметике, если n — простое число, то квадратный корень равен только 1 (либо +1, либо –1). Если n — составной объект, то квадратный корень — +1 или (-1), но могут быть и другие корни. Это называют испытанием простоты чисел квадратным корнем. Обратите внимание, что в модульной арифметике –1 означает n–1.
Пример 12.21
Каковы квадратные корни 1 mod n, если n равно 7 (простое число)?
Решение
Единственные квадратные корни 1 mod n – это числа 1 и –1. Мы можем видеть, что
12 = 1 mod 7 (–1)2 = 1 mod 7 22 = 4 mod 7 (–2)2 = 4 mod 7 32 = 2 mod 7 (–3)2 = 2 mod 7
Заметим, что тест не дает результатов для 4, 5 и 6, потому что 4 = –3 mod 7,
5 = –2 mod 7 и 6 = –1 mod 7.
Пример 12.22
Каков квадратный корень из 1 mod n, если n равно 8 (составное)?
Решение
Имеется три решения: 1, 3, 5 и 7 (которые дают –1). Мы можем также видеть, что
12 = 1 mod 8 (–1)2 = 1 mod 8 32 = 1 mod 8 (–5)2 = 1 mod 8
Пример 12.23
Каков квадратный корень из 1 mod n, если n равно 17 (простое)?
Решение
Имеются только два решения, соответствующие поставленной задаче: это 1 и (–1).
12 = 1 mod 17 (-1)2 = 1 mod 17 22 = 4 mod 17 (-2)2 = 4 mod 17 32 = 9 mod 17 (-3)2 = 9 mod 17 42 = 16 mod 17 (-4)2 = 16 mod 17 52 = 8 mod 17 (-5)2 = 8 mod 17 62 = 2 mod 17 (-6)2 = 2 mod 17 72 = 15 mod 17 (-7)2 = 15 mod 17 82 = 13 mod 17 (-8)2 = 13 mod 17
Заметим, что не надо проверять целые числа, большие 8, потому что 9 = –8 mod 17
Пример 12.24
Каков квадратный корень из 1 mod n, если n равно 22 (составное)?
Решение
Сюрприз в том, что имеется только два решения: +1 и –1, хотя 22 — составное число.
12 = 1 mod 22 (-1)2 = 1 mod 22
Хотя во многих случаях имеется испытание, которое показывает нам однозначно, что число составное, но это испытание провести трудно. Когда дано число n, то все числа, меньшие, чем n (кроме чисел 1 и n–1), должны быть возведены в квадрат, чтобы гарантировать, что ни одно из них не равно 1. Это испытание может использоваться для чисел (не +1 или –1), которые в квадрате по модулю n дают значение 1. Этот факт помогает в испытании Миллера–Рабина, которое рассматривается в следующем разделе.
Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Содержание
- 1 Определения
- 2 О смысле ошибок первого и второго рода
- 3 Вероятности ошибок (уровень значимости и мощность)
- 4 Примеры использования
- 4.1 Радиолокация
- 4.2 Компьютеры
- 4.2.1 Компьютерная безопасность
- 4.2.2 Фильтрация спама
- 4.2.3 Вредоносное программное обеспечение
- 4.2.4 Поиск в компьютерных базах данных
- 4.2.5 Оптическое распознавание текстов (OCR)
- 4.2.6 Досмотр пассажиров и багажа
- 4.2.7 Биометрия
- 4.3 Массовая медицинская диагностика (скрининг)
- 4.4 Медицинское тестирование
- 4.5 Исследования сверхъестественных явлений
- 5 См. также
- 6 Примечания
Определения
Пусть дана выборка 

где 

,
сопоставляющий каждой реализации выборки 
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно. [1][2]
| Верная гипотеза | |||
|---|---|---|---|
 |
 |
||
| Результат применения критерия |
 |
 верно принята верно принята |
 неверно принята неверно принята (Ошибка второго рода) |
 |
 неверно отвергнута неверно отвергнута (Ошибка первого рода) |
 верно отвергнута верно отвергнута |
О смысле ошибок первого и второго рода
Как видно из вышеприведённого определения, ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы 



С учётом этого ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня. Слово «положительный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (т.е. показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.
В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т.п. В информационных технологиях часто используют английский термин false positive без перевода.
Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.
Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).
Слово «отрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают отрицательный результат (т.е. показывают отсутствие заболевания у пациента), когда на самом деле пациент страдает этим заболеванием. Такой результат называется ложноотрицательным.
В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т.п. В информационных технологиях часто используют английский термин false negative без перевода.
Степень чувствительности системы защиты должна представлять собой компромисс между вероятностью ошибок первого и второго рода. Где именно находится точка баланса, зависит от оценки рисков обоих видов ошибок.
Вероятности ошибок (уровень значимости и мощность)
Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают греческой буквой 

Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой 


Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объема, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Примеры использования
Радиолокация
В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «ложная тревога» и «пропуск цели» являются одним из основных элементов как теории, так и практики построения радиолокационных станций. Вероятно, это первый пример последовательного применения статистических методов в целой технической области.
Компьютеры
Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность). Moulton (1983, с.125) отмечает, что в данном контексте возможны следующие нежелательные ситуации:
- когда нарушители классифицируются как авторизованные пользователи (ошибки первого рода)
- когда авторизованные пользователи классифицируются как нарушители (ошибки второго рода)
Фильтрация спама
Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама ошибочно классифицирует легитимное email-сообщение как спам и препятствует его нормальной доставке. В то время как большинство «антиспам»-алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).
Ошибка второго рода происходит, когда антиспам-система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности антиспам-алгоритма.
Пока не удалось создать антиспамовую систему без корреляции между вероятностью ошибок первого и второго рода. Вероятность пропустить спам у современных систем колеблется в пределах от 1% до 30%. Вероятность ошибочно отвергнуть валидное сообщение — от 0,001 % до 3 %. Выбор системы и её настроек зависит от условий конкретного получателя: для одних получателей риск потерять 1% хорошей почты оценивается как незначительный, для других же потеря даже 0,1% является недопустимой.
Вредоносное программное обеспечение
Понятие ошибки первого рода также используется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус. Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с антитроянскими и антишпионскими программами.
Поиск в компьютерных базах данных
При поиске в базе данных к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска, когда поисковый алгоритм анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков, многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря. Однако это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек, которые используемый алгоритм расценил как «a».
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т.п. (см. обнаружение взрывчатых веществ, металлодетекторы).
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия
Ошибки первого и второго рода являются большой проблемой в системах биометрического сканирования, использующих распознавание радужной оболочки или сетчатки глаза, черт лица и т.д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т.п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении.[3]
Массовая медицинская диагностика (скрининг)
В медицинской практике есть существенное различие между скринингом и тестированием:
- Скрининг включает в себя относительно дешёвые тесты, которые проводятся для большой группы людей при отсутствии каких-либо клинических признаков болезни (например, мазок Папаниколау).
- Тестирование подразумевает гораздо более дорогие, зачастую инвазивные, процедуры, которые проводятся только для тех, у кого проявляются клинические признаки заболевания, и которые, в основном, применяются для подтверждения предполагаемого диагноза.
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию и гипотиреоз, помимо других врождённых аномалий. Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии.[4]
Простые анализы крови, используемые для скрининга потенциальных доноров на ВИЧ и гепатит, имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.
Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография). В США уровень ошибок первого рода в маммограммах достигает 15%, это самый высокий показатель в мире.[5] Самый низкий уровень наблюдается в Нидерландах, 1%.[6]
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам кардиотестирования при выявлении коронарного атеросклероза, хотя известно, что кардиотестирование выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70%, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными.[7]
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т.д.), которое имеет обычное объяснение.[8]
См. также
- Статистическая значимость
- Ложноположительный
- Атака второго рода
- Случаи ложного срабатывания систем предупреждения о ракетном нападении
- Receiver_operating_characteristic
Примечания
- ↑ ГОСТ Р 50779.10-2000. «Статистические методы. Вероятность и основы статистики. Термины и определения.». Стр. 26
- ↑ Valerie J. Easton, John H. McColl. Statistics Glossary: Hypothesis Testing.
- ↑ Данный пример как раз характеризует случай, когда классификация ошибок будет зависеть от назначения системы: если биометрическое сканирование используется для допуска сотрудников (нулевая гипотеза: «проходящий сканирование человек действительно является сотрудником»), то ошибочное отождествление будет ошибкой второго рода, а «неузнавание» — ошибкой первого рода; если же сканирование используется для опознания преступников (нулевая гипотеза: «проходящий сканирование человек не является преступником»), то ошибочное отождествление будет ошибкой первого рода, а «неузнавание» — ошибкой второго рода.
- ↑ Относительно скрининга новорожденных, последние исследования показали, что количество ошибок первого рода в 12 раз больше, чем количество верных обнаружений (Gambrill, 2006. [1])
- ↑ Одним из последствий такого высокого уровня ошибок первого рода в США является то, что за произвольный 10-летний период половина обследуемых американских женщин получают как минимум одну ложноположительную маммограмму. Такие ошибочные маммограммы обходятся дорого, приводя к ежегодным расходам в 100 миллионов долларов на последующее (ненужное) лечение. Кроме того, они вызывают излишнюю тревогу у женщин. В результате высокого уровня подобных ошибок первого рода в США, примерно у 90-95% женщин, получивших хотя бы раз в жизни положительную маммограмму, на самом деле заболевание отсутствует.
- ↑ Наиболее низкие уровни этих ошибок наблюдаются в северной Европе, где маммографические плёнки считываются дважды, и для дополнительного тестирования устанавливается повышенное пороговое значение (высокий порог снижает статистическую эффективность теста).
- ↑ Вероятность того, что выдаваемый тестом результат окажется ошибкой первого рода, может быть вычислена при помощи Теоремы Байеса.
- ↑ На некоторых сайтах приведены примеры ошибок первого рода, например: Атлантическое Сообщество Паранормальных явлений (The Atlantic Paranormal Society, TAPS) и Морстаунская организация по Исследованию Привидений (Moorestown Ghost Research).
Вероятность ошибки является основным показателем качества распознавания образов, и поэтому её оценивание представляет собой очень важную задачу. Вероятность ошибки есть сложная функция, представляющая собой n-кратный интеграл от плотности вероятности при наличии сложной границы. Поэтому при её вычислении часто приходится обращаться к экспериментальным методам.
При оценке вероятности ошибки рассматривают две задачи. Первая из них состоит в оценивании вероятности ошибки по имеющейся выборке в предположении, что задан классификатор [3].
Вторая задача заключается в оценке вероятности ошибки при заданных распределениях. Для этой ошибки вероятность ошибки зависит как от используемого классификатора, так и от вида распределения. Поскольку в распоряжении имеется конечное число объектов, нельзя построить оптимальный классификатор. Поэтому параметры такого классификатора представляют собой случайные величины [3].
Оценка вероятности ошибки для заданного классификатора.
1) Неизвестны априорные вероятности — случайная выборка.
Предположим, что заданы распределения обоих классов и классификатор. Задача заключается в оценивании вероятности ошибки по N объектам, полученным в соответствии с этими распределениями.
Когда неизвестны априорные вероятности P(Ci), i=1, 2, то можно случайно извлечь N объектов и проверить, даёт ли данный классификатор правильные решения для этих объектов. Такие объекты называют случайной выборкой.
Пусть ф — число объектов, неправильно классифицированных в результате этого эксперимента. Величина ф есть дискретная случайная величина. Обозначим истинную вероятность ошибки через е. Распределение значений величины ф является биномиальным:
. (1.64)
Оценка максимального правдоподобия из уравнения (1.56) равна
, (1.65)
т.е. оценка максимального правдоподобия равна отношению числа неправильно классифицированных объектов к общему числу объектов.
Математическое ожидание и дисперсия биномиального распределения соответственно равны
, (1.66)
. (1.67)
Таким образом, оценка является несмещённой.
2) Известны априорные вероятности — селективная выборка.
Если известны априорные вероятности классов P(Ci), i=1, 2, то можно извлечь N1=P(C1)N и N2=P(C2)N объектов соответственно и проверить их с помощью заданного классификатора. Такой процесс известен как селективная выборка. Пусть ф1 и ф2 — число неправильно классифицированных объектов соответственно из классов C1 и C2. Поскольку ф1 и ф2 взаимно независимы, то совместная плотность вероятности ф1 и ф2 будет равна

где еi — истинная вероятность ошибки для класса Ci. В этом случае оценка максимального правдоподобия равна
. (1.69)
Математическое ожидание и дисперсия оценки соответственно
, (1.70)
. (1.71)
Таким образом, оценка (1.69) также несмещённая.
Нетрудно показать, что дисперсия (1.71) меньше, чем дисперсия (1.67). Это естественный результат, поскольку в случае селективной выборки используется априорная информация.
Изложенное выше легко обобщить на случай M классов. Для этого надо лишь изменить верхние пределы у сумм и произведений в формулах (1.68) — (1.71) с 2 на M.
Оценка вероятности ошибки, когда классификатор заранее не задан.
Когда даны N объектов в случае отсутствия классификатора, то можно использовать эти объекты как для проектирования классификатора, так и для проверки его качества. Очевидно, оцениваемая вероятность ошибки зависит от данных распределений и используемого классификатора.
Предположим, что всегда используется байесовский классификатор, минимизирующий вероятность ошибки. Тогда минимальную вероятность ошибки байесовского классификатора, которую необходимо оценить, можно рассматривать как фиксированный параметр при заданных распределениях. Кроме того, эта вероятность является минимальной для данных распределений.
Как правило, вероятность ошибки есть функция двух аргументов:
е (И1, И2), (1.72)
где И1 — множество параметров распределений, используемых для синтеза байесовского классификатора, а И2 — множество параметров распределений, используемых для проверки его качества.
Оптимальная классификация объектов, характеризуемых распределением с параметром И2, осуществляется байесовским классификатором, который построен для распределения с параметром И2. Поэтому
е (И2, И2) ? е (И1, И2). (1.73)
Пусть для данной задачи И — вектор истинных параметров, а — его оценка. Таким образом, оценка является случайным вектором и е0=е (И, И). Для любого конкретного значения оценки на основании (1.73) справедливы неравенства
, (1.74)
. (1.75)
Выполнив над обеими частями неравенств (1.74) и (1.75) операцию математического ожидания, получим
, (1.76)
. (1.77)
Если
, (1.78)
то для вероятности ошибки байесовского классификатора имеет место двустороннее ограничение
. (1.79)
Левое неравенство (1.79) основано на предположении (1.78) и не доказано для произвольных истинных плотностей вероятности. Однако это неравенство можно проверить многими экспериментальными способами. Из выражения (1.5) видно, что равенство (1.78) выполняется тогда, когда оценка проверяемой плотности вероятности, основанная на N наблюдениях, является несмещённой и классификатор заранее фиксирован. Следует отметить, что нижняя граница менее важна, чем верхняя.
Обе границы вероятности ошибки можно интерпретировать следующим образом:
1) : одни и те же N объектов используются и для синтеза байесовского классификатора, и для последующей классификации. Этот случай назовём C-методом. Из (1.79) следует, что C-метод даёт, вообще говоря, заниженную оценку вероятности ошибки.
2) : для синтеза байесовского классификатора используются N объектов, а классифицируются объекты из истинных распределений. Эту процедуру называют U-методом. U-метод также даёт смещённую оценку вероятности ошибки е0. Это смещение таково, что его математическое ожидание является верхней границей вероятности ошибки. Объекты из истинного распределения могут быть заменены объектами, которые не были использованы для синтеза классификатора и независимы от объектов, по которым классификатор был синтезирован. Когда число классифицируемых объектов увеличивается, их распределение стремится к истинному распределению.
Для реализации U-метода имеется много возможностей. Рассмотрим две типовые процедуры.
1. Метод разбиения выборки. Вначале имеющиеся объекты разбивают на две группы и используют одну из них для синтеза классификатора, а другую — для проверки его качества. Основной вопрос, характерный для этого метода, заключается в том, как разделить объекты.
2. Метод скользящего распознавания. Во втором методе попытаемся использовать имеющиеся объекты более эффективно, чем в методе разбиения выборки. Для оценки необходимо, вообще говоря, извлечь много выборок объектов и синтезировать большое количество классификаторов, проверить качество каждого классификатора с помощью неиспользованных объектов и определить среднее значение показателя качества. Подобная процедура может быть выполнена путём использования только имеющихся N объектов следующим образом. Исключая один объект, синтезируется классификатор по имеющимся N-1 объектам, и классифицируется неиспользованный объект. Затем эту процедуру повторяют N раз и подсчитывают число неправильно классифицированных объектов. Этот метод позволяет более эффективно использовать имеющиеся объекты и оценивать . Один из недостатков этого метода заключается в том, что приходится синтезировать N классификаторов.
Метод разбиения выборки.
Для того, чтобы разбить имеющиеся объекты на обучающую и экзаменационную выборки, изучим, как это разбиение влияет на дисперсию оценки вероятности ошибки.
Вначале предположим, что имеется бесконечное число объектов для синтеза классификатора и N объектов для проверки его качества. При бесконечном числе объектов синтезируемый классификатор является классификатором для истинных распределений, и его вклад в дисперсию равен нулю. Для фиксированного классификатора организуем селективную выборку. В этом случае распределение оценки подчиняется биномиальному закону с дисперсией
, (1.80)
где еi — истинная вероятность ошибки для i-го класса.
С другой стороны, если имеется N объектов для синтеза классификатора и бесконечное число экзаменационных объектов, то оценка вероятности ошибки выражается следующим образом:
, (1.81)
где Гi — область пространства признаков, соответствующая i-му классу. В этом случае подынтегральные выражения постоянны, но граница этих областей изменяется в зависимости от выборки из N объектов.
Дисперсию оценки вычислить сложно. Однако в случае нормальных распределений с равными корреляционными матрицами интегралы в (1.81) можно привести к одномерным интегралам
,(1.81)
где зi и у2i определяются условными математическими ожиданиями:
,(1.82)
,(1.83)
. (1.84)
Это преобразование основано на том, что для нормальных распределений с равными корреляционными матрицами байесовский классификатор — линейный, а распределение отношения правдоподобия также является нормальным распределением.
Следует заметить, что даже если две истинные корреляционные матрицы равны, то оценки их различны. Однако для простоты предположим, что обе эти оценки равны и имеют вид
, (1.85)
где Ni — число объектов x(i)j класса i, используемых для синтеза классификатора.
Выражение для математического ожидания оценки достаточно громоздкое, здесь приводится простейший случай, когда P(C1)=P(C2) и N1=N2:
, (1.86)
, (1.87)
где d — расстояние между двумя векторами математических ожиданий, определяемое по формуле
. (1.88)
Величина е0 является минимальной вероятностью ошибки байесовского классификатора. Так как е0 — минимальное значение оценки , то распределение для является причинным Причинным распределением называется распределение p(x)=д(x-о), где д(x-о) — дельта-функция.. Поэтому можно определить оценку дисперсии величины, основанную на её математическом ожидании. Предположим, что плотность вероятности является плотностью вероятности гамма-распределения, которое включает в себя широкий класс причинных распределений. Тогда
(1.89)
при Де>0 (b?0 и c>0).
Математическое ожидание и дисперсия плотности вероятности (1.89) соответственно равны
, (1.90)
. (1.91)
Исключив c, получим верхнюю границу дисперсии , т.е.
(1.91)
при b ? 0.
Таким образом, степень влияния числа обучающих объектов на оценку вероятности ошибки е0 в случае нормальных распределений с равными корреляционными матрицами и равными априорными вероятностями равна
. (1.92)
Величину sэксп следует сравнивать с величиной sтеор, которая характеризует влияние числа объектов в экзаменационной выборке на оценку вероятности ошибки. Значение sтеор получается подстановкой в формулу (1.80) значений P(C1) = P(C2) =0.5 и е1 = е2 = е0:
. (1.93)
Исключение задания класса для объектов экзаменационной выборки.
Для того, чтобы оценить вероятность ошибки как при обучении, так и на экзамене, требуются выборки объектов, в которых известно, какой объект к какому конкретному классу принадлежит. Однако в некоторых случаях получение такой информации связано с большими затратами.
Рассмотрим метод оценки вероятности ошибки, не требующий информации о принадлежности объектов экзаменационной выборки к конкретному классу. Применение этого метода наиболее эффективно в случае, когда при оптимальном разбиении выборки на обучающую и экзаменационную число объектов в экзаменационной выборке больше, чем в обучающей.
Введём критическую область для задач классификации M классов:
,(1.94)
где P(x) — плотность вероятности смеси, t — критический уровень, 0 ? t ? 1. Условие (1.94) устанавливает, что если для данного объекта x значения P(C1)p(x/C1), вычисленные для каждого класса Mi, не превышают величины (1-t)p(x), то объект х не классифицируют вообще; в противном случае объект x классифицируют и относят его к i-му классу. Таким образом, вся область значений x делится на критическую область Гr(t) и допустимую область Гa(t), причём размеры обеих областей являются функциями критического уровня t.
При таком решающем правиле вероятность ошибки е(t), коэффициент отклонения r(t) и коэффициент правильного распознавания c(t) будут равны
, (1.95)
, (1.96)
е(t) = 1 — c(t) — r(t). (1.97)
Предположим, что область отклонения увеличивается на Гr(t) за счёт замены значения t на t-Дt. Тогда те x, которые раньше классифицировались правильно, теперь отклоняются:
(1.98)
при xДГr(t). Интегрируя (1.98) в пределах области ДГr(t), получим
(1 — t)Дr(t) ? -Дc(t) < (1 — t+Дt)Дr(t), (1.99)
где Дr(t) и Дc(t) — приращения r(t) и c(t), вызванные изменениями t. Из формулы (1.97) следует, что неравенство (1.99) можно переписать следующим образом:
— tДr(t) ? Де(t) < -У(t — Дt)Дr(t). (1.100)
Полагая Дt>0, получаем интеграл Стилтьеса
. (1.101)
Уравнение (1.101) показывает, что вероятность ошибки е(t) может быть вычислена после того, как установлена зависимость между значениями t и r(t). Из решающего правила (1.94) следует, что при t = 1-1/M область отклонения отсутствует, так что байесовская ошибка е0= е(1-1/M). Кроме того, из формулы (1.101) можно установить взаимосвязь между вероятностью ошибки и коэффициентом отклонения, так как изменение вероятности ошибки можно вычислить как функцию от изменения коэффициента отклонения.
Воспользуемся выражением (1.94) для исключения задания класса объектов экзаменационной выборки. Для этого поступим следующим образом.
1. Для определения ДГr(kt0) при t = kt0, k = 0, 1, …, m = (1-1/M)t0, где t0 — дискретный шаг переменной t, будем использовать относительно дорогостоящие классифицируемые объекты.
2. Подсчитаем число неклассифицированных объектов экзаменационной выборки, которые попали в область ДГr(kt0), разделим это число на общее число объектов и обозначим полученное соотношение через Дr(kt0).
3. Тогда из выражения (1.94) следует, что оценка вероятности ошибки
. (1.102)
В описанной процедуре использовалось то, что коэффициент отклонения является функцией от плотности вероятности смеси, а не от плотностей вероятности отдельных классов. Поэтому после того, как по классифицированным объектам найдены расширенные области отклонения, в дальнейшем для оценивания Дr(t) и вероятности ошибки е(t) нет необходимости использовать классифицированные объекты.



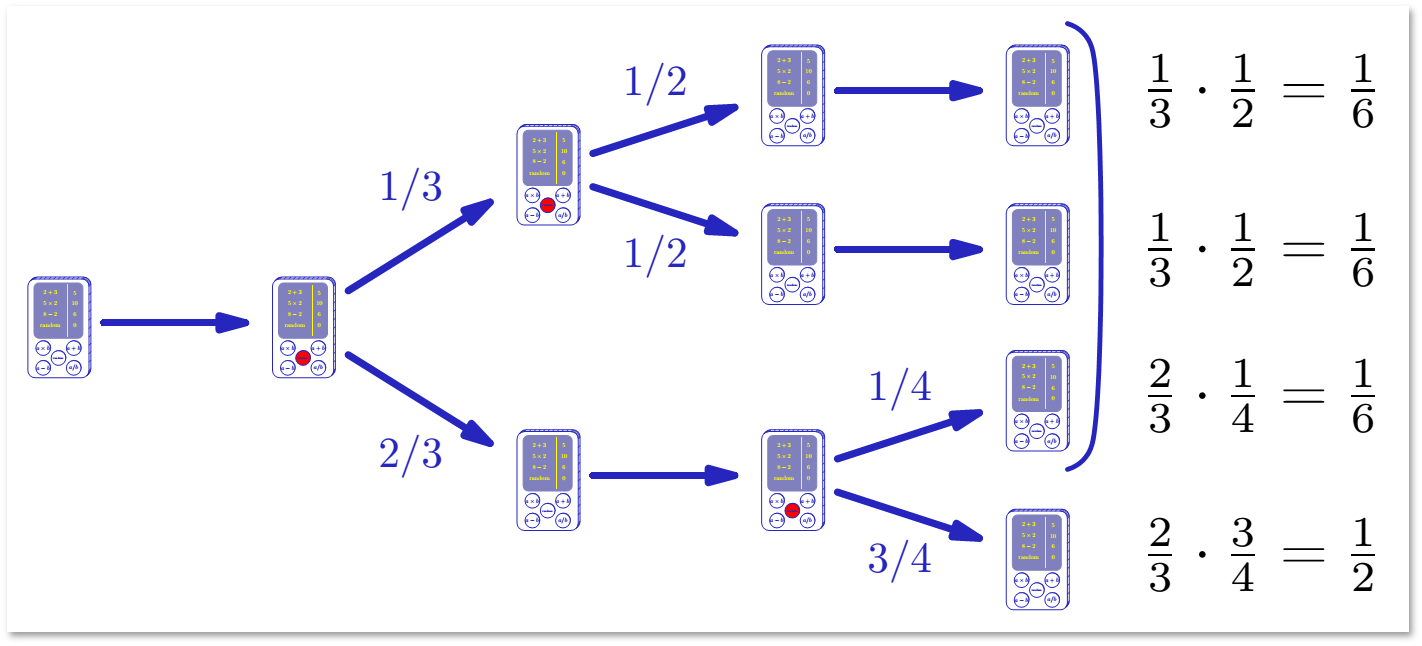

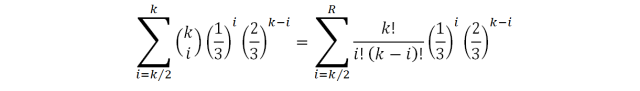

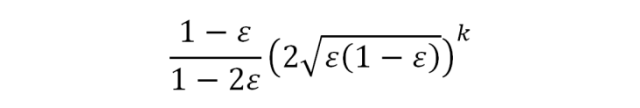
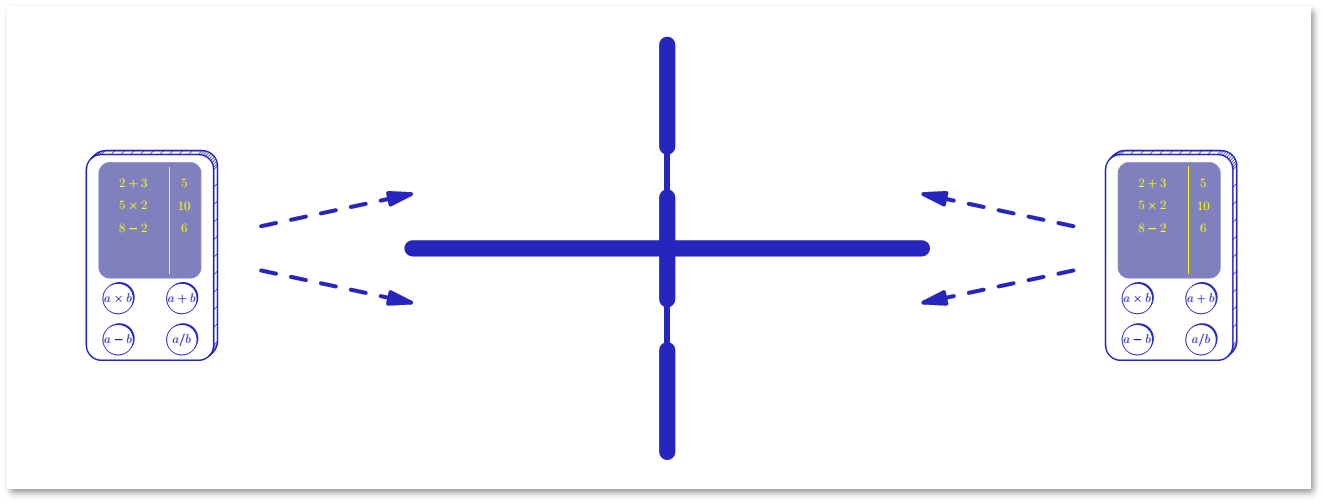

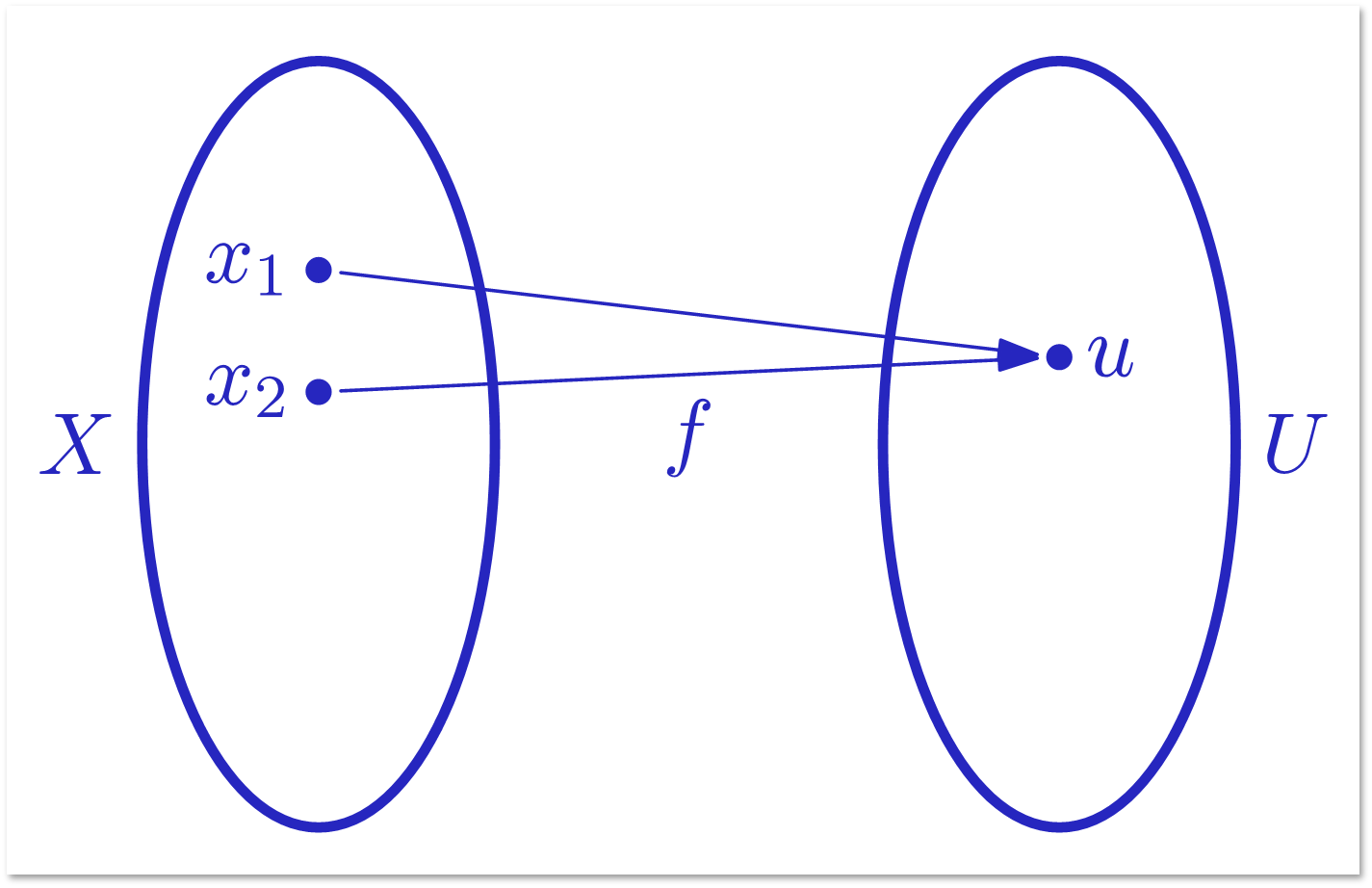









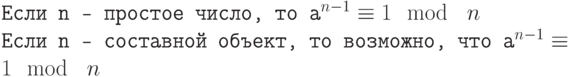
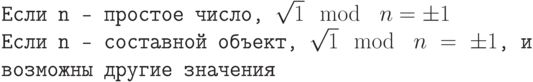

 ,
, соответствует гипотезе
соответствует гипотезе  .
. .
.






































