Вначале хочу заметить, если вы задаетесь таким вопросом, то скорее всего вы используйте функцию чек-суммы не по прямому назначению. А значит, вы делаете что-то неправильно.
Насколько я понял, вам интересно, одинаков ли шанс получить коллизию, если на входе строка из букв, или строка из цифр. Хочу заметить, что если у вас откуда-то приходят случайные строки длиной 5 символов (для примера), то шанс что у вас появятся одинаковые строки из цифр на много-много порядков выше, чем когда приходят строки из букв.
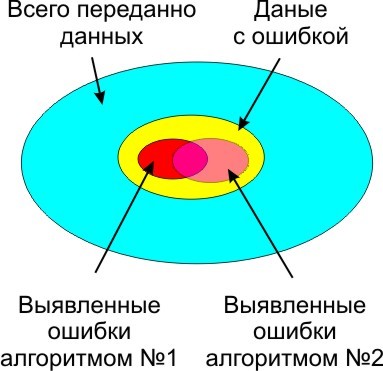
Что бы показать, что шансы получить коллизию одинаковы, я сгенерировал 100 млн чек-сумм для строк длиной 20 (я взял 20, что бы не создавались одинаковые строки из чисел), и посчитал коллизии внутри строк из чисел, внутри строк из букв, и взаимные коллизии между строками из чисел и букв. Вот мой код на C#:
private static uint crc32(byte[] data)
{
uint crc = 0xffffffff;
uint poly = 0xedb88320;
for (int i = 0; i < data.Length; i++)
{
uint c = (crc ^ data[i]) & 0xff;
for (int k = 0; k < 8; k++)
c = (c & 1) != 0 ? poly ^ (c >> 1) : c >> 1;
crc = c ^ (crc >> 8);
}
return crc ^ 0xffffffff;
}
static void Main(string[] args)
{
byte[][] digits = new byte[0x10000][];
for (int i = 0; i < 0x10000; i++)
digits[i] = new byte[0x10000];
byte[][] chars = new byte[0x10000][];
for (int i = 0; i < 0x10000; i++)
chars[i] = new byte[0x10000];
var rnd = new Random(123);
int iterations = 100000000;
byte[] buffer = Encoding.ASCII.GetBytes("12345678901234567890");
for (int i = 0; i < iterations; i++)
{
int index = rnd.Next(20);
buffer[index]++;
if (buffer[index] > '9')
buffer[index] = (byte)'0';
uint crc = crc32(buffer);
digits[crc >> 16][crc & 0xFFFF]++;
}
buffer = Encoding.ASCII.GetBytes("abcdefwxyzabcdefwxyz");
for (int i = 0; i < iterations; i++)
{
int index = rnd.Next(20);
buffer[index]++;
if (buffer[index] > 'z')
buffer[index] = (byte)'a';
uint crc = crc32(buffer);
chars[crc >> 16][crc & 0xFFFF]++;
}
int digitsCollisions = 0;
for (int i = 0; i < 0x10000; i++)
for (int j = 0; j < 0x10000; j++)
if (digits[i][j] > 1)
digitsCollisions += digits[i][j];
int charsCollisions = 0;
for (int i = 0; i < 0x10000; i++)
for (int j = 0; j < 0x10000; j++)
if (chars[i][j] > 1)
charsCollisions += chars[i][j];
int digitsCharsCollisions = 0;
for (int i = 0; i < 0x10000; i++)
for (int j = 0; j < 0x10000; j++)
if (chars[i][j] > 0 && digits[i][j] > 0)
digitsCharsCollisions += chars[i][j] * digits[i][j];
Console.WriteLine(digitsCollisions);
Console.WriteLine(charsCollisions);
Console.WriteLine(digitsCharsCollisions);
}
Результат:
2298490
2304243
2330855
Как видно, вероятность получить коллизию одинаковая.
В другом тесте я брал длину входных данных 10 байт, и вместо случайных чисел просто брал строковое представление числа i. Результат получился другой:
4431872
2301156
2324554
Как видно, коллизий на числах в 2 раза больше, хотя чек-сумма считалась на уникальных входных данных. Это происходит потому, что в случайной строке из букв длиной 10 байт больше энтропии, чем в строке чисел. CRC-32 не является полноценной криптографической хеш-фукнцией, и в ней нет лавинного эффекта. С хорошей хеш-функцией мы бы получили одинаковый результат.
Вначале хочу заметить, если вы задаетесь таким вопросом, то скорее всего вы используйте функцию чек-суммы не по прямому назначению. А значит, вы делаете что-то неправильно.
Насколько я понял, вам интересно, одинаков ли шанс получить коллизию, если на входе строка из букв, или строка из цифр. Хочу заметить, что если у вас откуда-то приходят случайные строки длиной 5 символов (для примера), то шанс что у вас появятся одинаковые строки из цифр на много-много порядков выше, чем когда приходят строки из букв.
Что бы показать, что шансы получить коллизию одинаковы, я сгенерировал 100 млн чек-сумм для строк длиной 20 (я взял 20, что бы не создавались одинаковые строки из чисел), и посчитал коллизии внутри строк из чисел, внутри строк из букв, и взаимные коллизии между строками из чисел и букв. Вот мой код на C#:
private static uint crc32(byte[] data)
{
uint crc = 0xffffffff;
uint poly = 0xedb88320;
for (int i = 0; i < data.Length; i++)
{
uint c = (crc ^ data[i]) & 0xff;
for (int k = 0; k < 8; k++)
c = (c & 1) != 0 ? poly ^ (c >> 1) : c >> 1;
crc = c ^ (crc >> 8);
}
return crc ^ 0xffffffff;
}
static void Main(string[] args)
{
byte[][] digits = new byte[0x10000][];
for (int i = 0; i < 0x10000; i++)
digits[i] = new byte[0x10000];
byte[][] chars = new byte[0x10000][];
for (int i = 0; i < 0x10000; i++)
chars[i] = new byte[0x10000];
var rnd = new Random(123);
int iterations = 100000000;
byte[] buffer = Encoding.ASCII.GetBytes("12345678901234567890");
for (int i = 0; i < iterations; i++)
{
int index = rnd.Next(20);
buffer[index]++;
if (buffer[index] > '9')
buffer[index] = (byte)'0';
uint crc = crc32(buffer);
digits[crc >> 16][crc & 0xFFFF]++;
}
buffer = Encoding.ASCII.GetBytes("abcdefwxyzabcdefwxyz");
for (int i = 0; i < iterations; i++)
{
int index = rnd.Next(20);
buffer[index]++;
if (buffer[index] > 'z')
buffer[index] = (byte)'a';
uint crc = crc32(buffer);
chars[crc >> 16][crc & 0xFFFF]++;
}
int digitsCollisions = 0;
for (int i = 0; i < 0x10000; i++)
for (int j = 0; j < 0x10000; j++)
if (digits[i][j] > 1)
digitsCollisions += digits[i][j];
int charsCollisions = 0;
for (int i = 0; i < 0x10000; i++)
for (int j = 0; j < 0x10000; j++)
if (chars[i][j] > 1)
charsCollisions += chars[i][j];
int digitsCharsCollisions = 0;
for (int i = 0; i < 0x10000; i++)
for (int j = 0; j < 0x10000; j++)
if (chars[i][j] > 0 && digits[i][j] > 0)
digitsCharsCollisions += chars[i][j] * digits[i][j];
Console.WriteLine(digitsCollisions);
Console.WriteLine(charsCollisions);
Console.WriteLine(digitsCharsCollisions);
}
Результат:
2298490
2304243
2330855
Как видно, вероятность получить коллизию одинаковая.
В другом тесте я брал длину входных данных 10 байт, и вместо случайных чисел просто брал строковое представление числа i. Результат получился другой:
4431872
2301156
2324554
Как видно, коллизий на числах в 2 раза больше, хотя чек-сумма считалась на уникальных входных данных. Это происходит потому, что в случайной строке из букв длиной 10 байт больше энтропии, чем в строке чисел. CRC-32 не является полноценной криптографической хеш-фукнцией, и в ней нет лавинного эффекта. С хорошей хеш-функцией мы бы получили одинаковый результат.
A cyclic redundancy check (CRC) is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to digital data. Blocks of data entering these systems get a short check value attached, based on the remainder of a polynomial division of their contents. On retrieval, the calculation is repeated and, in the event the check values do not match, corrective action can be taken against data corruption. CRCs can be used for error correction (see bitfilters).[1]
CRCs are so called because the check (data verification) value is a redundancy (it expands the message without adding information) and the algorithm is based on cyclic codes. CRCs are popular because they are simple to implement in binary hardware, easy to analyze mathematically, and particularly good at detecting common errors caused by noise in transmission channels. Because the check value has a fixed length, the function that generates it is occasionally used as a hash function.
Introduction[edit]
CRCs are based on the theory of cyclic error-correcting codes. The use of systematic cyclic codes, which encode messages by adding a fixed-length check value, for the purpose of error detection in communication networks, was first proposed by W. Wesley Peterson in 1961.[2]
Cyclic codes are not only simple to implement but have the benefit of being particularly well suited for the detection of burst errors: contiguous sequences of erroneous data symbols in messages. This is important because burst errors are common transmission errors in many communication channels, including magnetic and optical storage devices. Typically an n-bit CRC applied to a data block of arbitrary length will detect any single error burst not longer than n bits, and the fraction of all longer error bursts that it will detect is (1 − 2−n).
Specification of a CRC code requires definition of a so-called generator polynomial. This polynomial becomes the divisor in a polynomial long division, which takes the message as the dividend and in which the quotient is discarded and the remainder becomes the result. The important caveat is that the polynomial coefficients are calculated according to the arithmetic of a finite field, so the addition operation can always be performed bitwise-parallel (there is no carry between digits).
In practice, all commonly used CRCs employ the Galois field, or more simply a finite field, of two elements, GF(2). The two elements are usually called 0 and 1, comfortably matching computer architecture.
A CRC is called an n-bit CRC when its check value is n bits long. For a given n, multiple CRCs are possible, each with a different polynomial. Such a polynomial has highest degree n, which means it has n + 1 terms. In other words, the polynomial has a length of n + 1; its encoding requires n + 1 bits. Note that most polynomial specifications either drop the MSB or LSB, since they are always 1. The CRC and associated polynomial typically have a name of the form CRC-n-XXX as in the table below.
The simplest error-detection system, the parity bit, is in fact a 1-bit CRC: it uses the generator polynomial x + 1 (two terms),[3] and has the name CRC-1.
Application[edit]
A CRC-enabled device calculates a short, fixed-length binary sequence, known as the check value or CRC, for each block of data to be sent or stored and appends it to the data, forming a codeword.
When a codeword is received or read, the device either compares its check value with one freshly calculated from the data block, or equivalently, performs a CRC on the whole codeword and compares the resulting check value with an expected residue constant.
If the CRC values do not match, then the block contains a data error.
The device may take corrective action, such as rereading the block or requesting that it be sent again. Otherwise, the data is assumed to be error-free (though, with some small probability, it may contain undetected errors; this is inherent in the nature of error-checking).[4]
Data integrity[edit]
CRCs are specifically designed to protect against common types of errors on communication channels, where they can provide quick and reasonable assurance of the integrity of messages delivered. However, they are not suitable for protecting against intentional alteration of data.
Firstly, as there is no authentication, an attacker can edit a message and recompute the CRC without the substitution being detected. When stored alongside the data, CRCs and cryptographic hash functions by themselves do not protect against intentional modification of data. Any application that requires protection against such attacks must use cryptographic authentication mechanisms, such as message authentication codes or digital signatures (which are commonly based on cryptographic hash functions).
Secondly, unlike cryptographic hash functions, CRC is an easily reversible function, which makes it unsuitable for use in digital signatures.[5]
Thirdly, CRC satisfies a relation similar to that of a linear function (or more accurately, an affine function):[6]
where 





as a result, even if the CRC is encrypted with a stream cipher that uses XOR as its combining operation (or mode of block cipher which effectively turns it into a stream cipher, such as OFB or CFB), both the message and the associated CRC can be manipulated without knowledge of the encryption key; this was one of the well-known design flaws of the Wired Equivalent Privacy (WEP) protocol.[7]
Computation[edit]
To compute an n-bit binary CRC, line the bits representing the input in a row, and position the (n + 1)-bit pattern representing the CRC’s divisor (called a «polynomial») underneath the left end of the row.
In this example, we shall encode 14 bits of message with a 3-bit CRC, with a polynomial x3 + x + 1. The polynomial is written in binary as the coefficients; a 3rd-degree polynomial has 4 coefficients (1x3 + 0x2 + 1x + 1). In this case, the coefficients are 1, 0, 1 and 1. The result of the calculation is 3 bits long, which is why it is called a 3-bit CRC. However, you need 4 bits to explicitly state the polynomial.
Start with the message to be encoded:
11010011101100
This is first padded with zeros corresponding to the bit length n of the CRC. This is done so that the resulting code word is in systematic form. Here is the first calculation for computing a 3-bit CRC:
11010011101100 000 <--- input right padded by 3 bits 1011 <--- divisor (4 bits) = x³ + x + 1 ------------------ 01100011101100 000 <--- result
The algorithm acts on the bits directly above the divisor in each step. The result for that iteration is the bitwise XOR of the polynomial divisor with the bits above it. The bits not above the divisor are simply copied directly below for that step. The divisor is then shifted right to align with the highest remaining 1 bit in the input, and the process is repeated until the divisor reaches the right-hand end of the input row. Here is the entire calculation:
11010011101100 000 <--- input right padded by 3 bits
1011 <--- divisor
01100011101100 000 <--- result (note the first four bits are the XOR with the divisor beneath, the rest of the bits are unchanged)
1011 <--- divisor ...
00111011101100 000
1011
00010111101100 000
1011
00000001101100 000 <--- note that the divisor moves over to align with the next 1 in the dividend (since quotient for that step was zero)
1011 (in other words, it doesn't necessarily move one bit per iteration)
00000000110100 000
1011
00000000011000 000
1011
00000000001110 000
1011
00000000000101 000
101 1
-----------------
00000000000000 100 <--- remainder (3 bits). Division algorithm stops here as dividend is equal to zero.
Since the leftmost divisor bit zeroed every input bit it touched, when this process ends the only bits in the input row that can be nonzero are the n bits at the right-hand end of the row. These n bits are the remainder of the division step, and will also be the value of the CRC function (unless the chosen CRC specification calls for some postprocessing).
The validity of a received message can easily be verified by performing the above calculation again, this time with the check value added instead of zeroes. The remainder should equal zero if there are no detectable errors.
11010011101100 100 <--- input with check value
1011 <--- divisor
01100011101100 100 <--- result
1011 <--- divisor ...
00111011101100 100
......
00000000001110 100
1011
00000000000101 100
101 1
------------------
00000000000000 000 <--- remainder
The following Python code outlines a function which will return the initial CRC remainder for a chosen input and polynomial, with either 1 or 0 as the initial padding. Note that this code works with string inputs rather than raw numbers:
def crc_remainder(input_bitstring, polynomial_bitstring, initial_filler): """Calculate the CRC remainder of a string of bits using a chosen polynomial. initial_filler should be '1' or '0'. """ polynomial_bitstring = polynomial_bitstring.lstrip('0') len_input = len(input_bitstring) initial_padding = (len(polynomial_bitstring) - 1) * initial_filler input_padded_array = list(input_bitstring + initial_padding) while '1' in input_padded_array[:len_input]: cur_shift = input_padded_array.index('1') for i in range(len(polynomial_bitstring)): input_padded_array[cur_shift + i] = str(int(polynomial_bitstring[i] != input_padded_array[cur_shift + i])) return ''.join(input_padded_array)[len_input:] def crc_check(input_bitstring, polynomial_bitstring, check_value): """Calculate the CRC check of a string of bits using a chosen polynomial.""" polynomial_bitstring = polynomial_bitstring.lstrip('0') len_input = len(input_bitstring) initial_padding = check_value input_padded_array = list(input_bitstring + initial_padding) while '1' in input_padded_array[:len_input]: cur_shift = input_padded_array.index('1') for i in range(len(polynomial_bitstring)): input_padded_array[cur_shift + i] = str(int(polynomial_bitstring[i] != input_padded_array[cur_shift + i])) return ('1' not in ''.join(input_padded_array)[len_input:])
>>> crc_remainder('11010011101100', '1011', '0') '100' >>> crc_check('11010011101100', '1011', '100') True
CRC-32 algorithm[edit]
This is a practical algorithm for the CRC-32 variant of CRC.[8] The CRCTable is a memoization of a calculation that would have to be repeated for each byte of the message (Computation of cyclic redundancy checks § Multi-bit computation).
Function CRC32 Input: data: Bytes // Array of bytes Output: crc32: UInt32 // 32-bit unsigned CRC-32 value
// Initialize CRC-32 to starting value crc32 ← 0xFFFFFFFF
for each byte in data do nLookupIndex ← (crc32 xor byte) and 0xFF crc32 ← (crc32 shr 8) xor CRCTable[nLookupIndex] // CRCTable is an array of 256 32-bit constants
// Finalize the CRC-32 value by inverting all the bits crc32 ← crc32 xor 0xFFFFFFFF return crc32
In C, the algorithm looks as such:
#include <inttypes.h> // uint32_t, uint8_t uint32_t CRC32(const uint8_t data[], size_t data_length) { uint32_t crc32 = 0xFFFFFFFFu; for (size_t i = 0; i < data_length; i++) { const uint32_t lookupIndex = (crc32 ^ data[i]) & 0xff; crc32 = (crc32 >> 8) ^ CRCTable[lookupIndex]; // CRCTable is an array of 256 32-bit constants } // Finalize the CRC-32 value by inverting all the bits crc32 ^= 0xFFFFFFFFu; return crc32; }
Mathematics[edit]
Mathematical analysis of this division-like process reveals how to select a divisor that guarantees good error-detection properties. In this analysis, the digits of the bit strings are taken as the coefficients of a polynomial in some variable x—coefficients that are elements of the finite field GF(2) (the integers modulo 2, i.e. either a zero or a one), instead of more familiar numbers. The set of binary polynomials is a mathematical ring.
Designing polynomials[edit]
The selection of the generator polynomial is the most important part of implementing the CRC algorithm. The polynomial must be chosen to maximize the error-detecting capabilities while minimizing overall collision probabilities.
The most important attribute of the polynomial is its length (largest degree(exponent) +1 of any one term in the polynomial), because of its direct influence on the length of the computed check value.
The most commonly used polynomial lengths are 9 bits (CRC-8), 17 bits (CRC-16), 33 bits (CRC-32), and 65 bits (CRC-64).[3]
A CRC is called an n-bit CRC when its check value is n-bits. For a given n, multiple CRCs are possible, each with a different polynomial. Such a polynomial has highest degree n, and hence n + 1 terms (the polynomial has a length of n + 1). The remainder has length n. The CRC has a name of the form CRC-n-XXX.
The design of the CRC polynomial depends on the maximum total length of the block to be protected (data + CRC bits), the desired error protection features, and the type of resources for implementing the CRC, as well as the desired performance. A common misconception is that the «best» CRC polynomials are derived from either irreducible polynomials or irreducible polynomials times the factor 1 + x, which adds to the code the ability to detect all errors affecting an odd number of bits.[9] In reality, all the factors described above should enter into the selection of the polynomial and may lead to a reducible polynomial. However, choosing a reducible polynomial will result in a certain proportion of missed errors, due to the quotient ring having zero divisors.
The advantage of choosing a primitive polynomial as the generator for a CRC code is that the resulting code has maximal total block length in the sense that all 1-bit errors within that block length have different remainders (also called syndromes) and therefore, since the remainder is a linear function of the block, the code can detect all 2-bit errors within that block length. If 





A polynomial 
Specification[edit]
The concept of the CRC as an error-detecting code gets complicated when an implementer or standards committee uses it to design a practical system. Here are some of the complications:
- Sometimes an implementation prefixes a fixed bit pattern to the bitstream to be checked. This is useful when clocking errors might insert 0-bits in front of a message, an alteration that would otherwise leave the check value unchanged.
- Usually, but not always, an implementation appends n 0-bits (n being the size of the CRC) to the bitstream to be checked before the polynomial division occurs. Such appending is explicitly demonstrated in the Computation of CRC article. This has the convenience that the remainder of the original bitstream with the check value appended is exactly zero, so the CRC can be checked simply by performing the polynomial division on the received bitstream and comparing the remainder with zero. Due to the associative and commutative properties of the exclusive-or operation, practical table driven implementations can obtain a result numerically equivalent to zero-appending without explicitly appending any zeroes, by using an equivalent,[9] faster algorithm that combines the message bitstream with the stream being shifted out of the CRC register.
- Sometimes an implementation exclusive-ORs a fixed bit pattern into the remainder of the polynomial division.
- Bit order: Some schemes view the low-order bit of each byte as «first», which then during polynomial division means «leftmost», which is contrary to our customary understanding of «low-order». This convention makes sense when serial-port transmissions are CRC-checked in hardware, because some widespread serial-port transmission conventions transmit bytes least-significant bit first.
- Byte order: With multi-byte CRCs, there can be confusion over whether the byte transmitted first (or stored in the lowest-addressed byte of memory) is the least-significant byte (LSB) or the most-significant byte (MSB). For example, some 16-bit CRC schemes swap the bytes of the check value.
- Omission of the high-order bit of the divisor polynomial: Since the high-order bit is always 1, and since an n-bit CRC must be defined by an (n + 1)-bit divisor which overflows an n-bit register, some writers assume that it is unnecessary to mention the divisor’s high-order bit.
- Omission of the low-order bit of the divisor polynomial: Since the low-order bit is always 1, authors such as Philip Koopman represent polynomials with their high-order bit intact, but without the low-order bit (the
or 1 term). This convention encodes the polynomial complete with its degree in one integer.
These complications mean that there are three common ways to express a polynomial as an integer: the first two, which are mirror images in binary, are the constants found in code; the third is the number found in Koopman’s papers. In each case, one term is omitted. So the polynomial 
In the table below they are shown as:
| Name | Normal | Reversed | Reversed reciprocal |
|---|---|---|---|
| CRC-4 | 0x3 | 0xC | 0x9 |
Obfuscation[edit]
CRCs in proprietary protocols might be obfuscated by using a non-trivial initial value and a final XOR, but these techniques do not add cryptographic strength to the algorithm and can be reverse engineered using straightforward methods.[11]
Standards and common use[edit]
Numerous varieties of cyclic redundancy checks have been incorporated into technical standards. By no means does one algorithm, or one of each degree, suit every purpose; Koopman and Chakravarty recommend selecting a polynomial according to the application requirements and the expected distribution of message lengths.[12] The number of distinct CRCs in use has confused developers, a situation which authors have sought to address.[9] There are three polynomials reported for CRC-12,[12] twenty-two conflicting definitions of CRC-16, and seven of CRC-32.[13]
The polynomials commonly applied are not the most efficient ones possible. Since 1993, Koopman, Castagnoli and others have surveyed the space of polynomials between 3 and 64 bits in size,[12][14][15][16] finding examples that have much better performance (in terms of Hamming distance for a given message size) than the polynomials of earlier protocols, and publishing the best of these with the aim of improving the error detection capacity of future standards.[15] In particular, iSCSI and SCTP have adopted one of the findings of this research, the CRC-32C (Castagnoli) polynomial.
The design of the 32-bit polynomial most commonly used by standards bodies, CRC-32-IEEE, was the result of a joint effort for the Rome Laboratory and the Air Force Electronic Systems Division by Joseph Hammond, James Brown and Shyan-Shiang Liu of the Georgia Institute of Technology and Kenneth Brayer of the Mitre Corporation. The earliest known appearances of the 32-bit polynomial were in their 1975 publications: Technical Report 2956 by Brayer for Mitre, published in January and released for public dissemination through DTIC in August,[17] and Hammond, Brown and Liu’s report for the Rome Laboratory, published in May.[18] Both reports contained contributions from the other team. During December 1975, Brayer and Hammond presented their work in a paper at the IEEE National Telecommunications Conference: the IEEE CRC-32 polynomial is the generating polynomial of a Hamming code and was selected for its error detection performance.[19] Even so, the Castagnoli CRC-32C polynomial used in iSCSI or SCTP matches its performance on messages from 58 bits to 131 kbits, and outperforms it in several size ranges including the two most common sizes of Internet packet.[15] The ITU-T G.hn standard also uses CRC-32C to detect errors in the payload (although it uses CRC-16-CCITT for PHY headers).
CRC-32C computation is implemented in hardware as an operation (CRC32) of SSE4.2 instruction set, first introduced in Intel processors’ Nehalem microarchitecture. ARM AArch64 architecture also provides hardware acceleration for both CRC-32 and CRC-32C operations.
Polynomial representations of cyclic redundancy checks[edit]
The table below lists only the polynomials of the various algorithms in use. Variations of a particular protocol can impose pre-inversion, post-inversion and reversed bit ordering as described above. For example, the CRC32 used in Gzip and Bzip2 use the same polynomial, but Gzip employs reversed bit ordering, while Bzip2 does not.[13]
Note that even parity polynomials in GF(2) with degree greater than 1 are never primitive. Even parity polynomial marked as primitive in this table represent a primitive polynomial multiplied by 
| Name | Uses | Polynomial representations | Parity[20] | Primitive[21] | Maximum bits of payload by Hamming distance[22][15][21] | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Normal | Reversed | Reciprocal | Reversed reciprocal | ≥ 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2[23] | ||||
| CRC-1 | most hardware; also known as parity bit | 0x1 | 0x1 | 0x1 | 0x1 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-3-GSM | mobile networks[24] | 0x3 | 0x6 | 0x5 | 0x5 | odd | yes [25] | – | – | – | – | – | – | – | – | – | – | – | – | – | 4 | ∞ |

|
||||||||||||||||||||||
| CRC-4-ITU | ITU-T G.704, p. 12 | 0x3 | 0xC | 0x9 | 0x9 | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-5-EPC | Gen 2 RFID[26] | 0x09 | 0x12 | 0x05 | 0x14 | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-5-ITU | ITU-T G.704, p. 9 | 0x15 | 0x15 | 0x0B | 0x1A | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-5-USB | USB token packets | 0x05 | 0x14 | 0x09 | 0x12 | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-6-CDMA2000-A | mobile networks[27] | 0x27 | 0x39 | 0x33 | 0x33 | odd | ||||||||||||||||
| CRC-6-CDMA2000-B | mobile networks[27] | 0x07 | 0x38 | 0x31 | 0x23 | even | ||||||||||||||||
| CRC-6-DARC | Data Radio Channel[28] | 0x19 | 0x26 | 0x0D | 0x2C | even | ||||||||||||||||
| CRC-6-GSM | mobile networks[24] | 0x2F | 0x3D | 0x3B | 0x37 | even | yes [29] | – | – | – | – | – | – | – | – | – | – | 1 | 1 | 25 | 25 | ∞ |

|
||||||||||||||||||||||
| CRC-6-ITU | ITU-T G.704, p. 3 | 0x03 | 0x30 | 0x21 | 0x21 | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-7 | telecom systems, ITU-T G.707, ITU-T G.832, MMC, SD | 0x09 | 0x48 | 0x11 | 0x44 | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-7-MVB | Train Communication Network, IEC 60870-5[30] | 0x65 | 0x53 | 0x27 | 0x72 | odd | ||||||||||||||||
| CRC-8 | DVB-S2[31] | 0xD5 | 0xAB | 0x57 | 0xEA[12] | even | no [32] | – | – | – | – | – | – | – | – | – | – | 2 | 2 | 85 | 85 | ∞ |

|
||||||||||||||||||||||
| CRC-8-AUTOSAR | automotive integration,[33] OpenSafety[34] | 0x2F | 0xF4 | 0xE9 | 0x97[12] | even | yes [32] | – | – | – | – | – | – | – | – | – | – | 3 | 3 | 119 | 119 | ∞ |

|
||||||||||||||||||||||
| CRC-8-Bluetooth | wireless connectivity[35] | 0xA7 | 0xE5 | 0xCB | 0xD3 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-8-CCITT | ITU-T I.432.1 (02/99); ATM HEC, ISDN HEC and cell delineation, SMBus PEC | 0x07 | 0xE0 | 0xC1 | 0x83 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-8-Dallas/Maxim | 1-Wire bus[36] | 0x31 | 0x8C | 0x19 | 0x98 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-8-DARC | Data Radio Channel[28] | 0x39 | 0x9C | 0x39 | 0x9C | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-8-GSM-B | mobile networks[24] | 0x49 | 0x92 | 0x25 | 0xA4 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-8-SAE J1850 | AES3; OBD | 0x1D | 0xB8 | 0x71 | 0x8E | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-8-WCDMA | mobile networks[27][37] | 0x9B | 0xD9 | 0xB3 | 0xCD[12] | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-10 | ATM; ITU-T I.610 | 0x233 | 0x331 | 0x263 | 0x319 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-10-CDMA2000 | mobile networks[27] | 0x3D9 | 0x26F | 0x0DF | 0x3EC | even | ||||||||||||||||
| CRC-10-GSM | mobile networks[24] | 0x175 | 0x2BA | 0x175 | 0x2BA | odd | ||||||||||||||||
| CRC-11 | FlexRay[38] | 0x385 | 0x50E | 0x21D | 0x5C2 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-12 | telecom systems[39][40] | 0x80F | 0xF01 | 0xE03 | 0xC07[12] | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-12-CDMA2000 | mobile networks[27] | 0xF13 | 0xC8F | 0x91F | 0xF89 | even | ||||||||||||||||
| CRC-12-GSM | mobile networks[24] | 0xD31 | 0x8CB | 0x197 | 0xE98 | odd | ||||||||||||||||
| CRC-13-BBC | Time signal, Radio teleswitch[41][42] | 0x1CF5 | 0x15E7 | 0x0BCF | 0x1E7A | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-14-DARC | Data Radio Channel[28] | 0x0805 | 0x2804 | 0x1009 | 0x2402 | even | ||||||||||||||||
| CRC-14-GSM | mobile networks[24] | 0x202D | 0x2D01 | 0x1A03 | 0x3016 | even | ||||||||||||||||
| CRC-15-CAN | 0xC599[43][44] | 0x4CD1 | 0x19A3 | 0x62CC | even | |||||||||||||||||

|
||||||||||||||||||||||
| CRC-15-MPT1327 | [45] | 0x6815 | 0x540B | 0x2817 | 0x740A | odd | ||||||||||||||||
| CRC-16-Chakravarty | Optimal for payloads ≤64 bits[30] | 0x2F15 | 0xA8F4 | 0x51E9 | 0x978A | odd | ||||||||||||||||
| CRC-16-ARINC | ACARS applications[46] | 0xA02B | 0xD405 | 0xA80B | 0xD015 | odd | ||||||||||||||||
| CRC-16-CCITT | X.25, V.41, HDLC FCS, XMODEM, Bluetooth, PACTOR, SD, DigRF, many others; known as CRC-CCITT | 0x1021 | 0x8408 | 0x811 | 0x8810[12] | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-16-CDMA2000 | mobile networks[27] | 0xC867 | 0xE613 | 0xCC27 | 0xE433 | odd | ||||||||||||||||
| CRC-16-DECT | cordless telephones[47] | 0x0589 | 0x91A0 | 0x2341 | 0x82C4 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-16-T10-DIF | SCSI DIF | 0x8BB7[48] | 0xEDD1 | 0xDBA3 | 0xC5DB | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-16-DNP | DNP, IEC 870, M-Bus | 0x3D65 | 0xA6BC | 0x4D79 | 0x9EB2 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-16-IBM | Bisync, Modbus, USB, ANSI X3.28, SIA DC-07, many others; also known as CRC-16 and CRC-16-ANSI | 0x8005 | 0xA001 | 0x4003 | 0xC002 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-16-OpenSafety-A | safety fieldbus[34] | 0x5935 | 0xAC9A | 0x5935 | 0xAC9A[12] | odd | ||||||||||||||||
| CRC-16-OpenSafety-B | safety fieldbus[34] | 0x755B | 0xDAAE | 0xB55D | 0xBAAD[12] | odd | ||||||||||||||||
| CRC-16-Profibus | fieldbus networks[49] | 0x1DCF | 0xF3B8 | 0xE771 | 0x8EE7 | odd | ||||||||||||||||
| Fletcher-16 | Used in Adler-32 A & B Checksums | Often confused to be a CRC, but actually a checksum; see Fletcher’s checksum | ||||||||||||||||||||
| CRC-17-CAN | CAN FD[50] | 0x1685B | 0x1B42D | 0x1685B | 0x1B42D | even | ||||||||||||||||
| CRC-21-CAN | CAN FD[50] | 0x102899 | 0x132281 | 0x064503 | 0x18144C | even | ||||||||||||||||
| CRC-24 | FlexRay[38] | 0x5D6DCB | 0xD3B6BA | 0xA76D75 | 0xAEB6E5 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-24-Radix-64 | OpenPGP, RTCM104v3 | 0x864CFB | 0xDF3261 | 0xBE64C3 | 0xC3267D | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-24-WCDMA | Used in OS-9 RTOS. Residue = 0x800FE3.[51] | 0x800063 | 0xC60001 | 0x8C0003 | 0xC00031 | even | yes[52] | – | – | – | – | – | – | – | – | – | – | 4 | 4 | 8388583 | 8388583 | ∞ |

|
||||||||||||||||||||||
| CRC-30 | CDMA | 0x2030B9C7 | 0x38E74301 | 0x31CE8603 | 0x30185CE3 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-32 | ISO 3309 (HDLC), ANSI X3.66 (ADCCP), FIPS PUB 71, FED-STD-1003, ITU-T V.42, ISO/IEC/IEEE 802-3 (Ethernet), SATA, MPEG-2, PKZIP, Gzip, Bzip2, POSIX cksum,[53] PNG,[54] ZMODEM, many others | 0x04C11DB7 | 0xEDB88320 | 0xDB710641 | 0x82608EDB[15] | odd | yes | – | 10 | – | – | 12 | 21 | 34 | 57 | 91 | 171 | 268 | 2974 | 91607 | 4294967263 | ∞ |

|
||||||||||||||||||||||
| CRC-32C (Castagnoli) | iSCSI, SCTP, G.hn payload, SSE4.2, Btrfs, ext4, Ceph | 0x1EDC6F41 | 0x82F63B78 | 0x05EC76F1 | 0x8F6E37A0[15] | even | yes | 6 | – | 8 | – | 20 | – | 47 | – | 177 | – | 5243 | – | 2147483615 | – | ∞ |

|
||||||||||||||||||||||
| CRC-32K (Koopman {1,3,28}) | Excellent at Ethernet frame length, poor performance with long files | 0x741B8CD7 | 0xEB31D82E | 0xD663B05D | 0xBA0DC66B[15] | even | no | 2 | – | 4 | – | 16 | – | 18 | – | 152 | – | 16360 | – | 114663 | – | ∞ |

|
||||||||||||||||||||||
| CRC-32K2 (Koopman {1,1,30}) | Excellent at Ethernet frame length, poor performance with long files | 0x32583499 | 0x992C1A4C | 0x32583499 | 0x992C1A4C[15] | even | no | – | – | 3 | – | 16 | – | 26 | – | 134 | – | 32738 | – | 65506 | – | ∞ |
| CRC-32Q | aviation; AIXM[55] | 0x814141AB | 0xD5828281 | 0xAB050503 | 0xC0A0A0D5 | even | ||||||||||||||||

|
||||||||||||||||||||||
| Adler-32 | Often confused to be a CRC, but actually a checksum; see Adler-32 | |||||||||||||||||||||
| CRC-40-GSM | GSM control channel[56][57][58] | 0x0004820009 | 0x9000412000 | 0x2000824001 | 0x8002410004 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-64-ECMA | ECMA-182 p. 51, XZ Utils | 0x42F0E1EBA9EA3693 | 0xC96C5795D7870F42 | 0x92D8AF2BAF0E1E85 | 0xA17870F5D4F51B49 | even | ||||||||||||||||
 
|
||||||||||||||||||||||
| CRC-64-ISO | ISO 3309 (HDLC), Swiss-Prot/TrEMBL; considered weak for hashing[59] | 0x000000000000001B | 0xD800000000000000 | 0xB000000000000001 | 0x800000000000000D | odd | ||||||||||||||||

|
Implementations[edit]
- Implementation of CRC32 in GNU Radio up to 3.6.1 (ca. 2012)
- C class code for CRC checksum calculation with many different CRCs to choose from
CRC catalogues[edit]
- Catalogue of parametrised CRC algorithms
- CRC Polynomial Zoo
See also[edit]
- Mathematics of cyclic redundancy checks
- Computation of cyclic redundancy checks
- List of hash functions
- List of checksum algorithms
- Information security
- Simple file verification
- LRC
References[edit]
- ^ «An Algorithm for Error Correcting Cyclic Redundance Checks». drdobbs.com. Archived from the original on 20 July 2017. Retrieved 28 June 2017.
- ^ Peterson, W. W.; Brown, D. T. (January 1961). «Cyclic Codes for Error Detection». Proceedings of the IRE. 49 (1): 228–235. doi:10.1109/JRPROC.1961.287814. S2CID 51666741.
- ^ a b Ergen, Mustafa (21 January 2008). «2.3.3 Error Detection Coding». Mobile Broadband. Springer. pp. 29–30. doi:10.1007/978-0-387-68192-4_2. ISBN 978-0-387-68192-4.
- ^ Ritter, Terry (February 1986). «The Great CRC Mystery». Dr. Dobb’s Journal. 11 (2): 26–34, 76–83. Archived from the original on 16 April 2009. Retrieved 21 May 2009.
- ^ Stigge, Martin; Plötz, Henryk; Müller, Wolf; Redlich, Jens-Peter (May 2006). «Reversing CRC – Theory and Practice» (PDF). Humboldt University Berlin. p. 17. SAR-PR-2006-05. Archived from the original (PDF) on 19 July 2011. Retrieved 4 February 2011.
The presented methods offer a very easy and efficient way to modify your data so that it will compute to a CRC you want or at least know in advance.
- ^ «algorithm design — Why is CRC said to be linear?». Cryptography Stack Exchange. Retrieved 5 May 2019.
- ^ Cam-Winget, Nancy; Housley, Russ; Wagner, David; Walker, Jesse (May 2003). «Security Flaws in 802.11 Data Link Protocols» (PDF). Communications of the ACM. 46 (5): 35–39. CiteSeerX 10.1.1.14.8775. doi:10.1145/769800.769823. S2CID 3132937. Archived (PDF) from the original on 26 May 2013. Retrieved 1 November 2017.
- ^ «[MS-ABS]: 32-Bit CRC Algorithm». msdn.microsoft.com. Archived from the original on 7 November 2017. Retrieved 4 November 2017.
- ^ a b c Williams, Ross N. (24 September 1996). «A Painless Guide to CRC Error Detection Algorithms V3.0». Archived from the original on 2 April 2018. Retrieved 23 May 2019.
- ^ Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). «Section 22.4 Cyclic Redundancy and Other Checksums». Numerical Recipes: The Art of Scientific Computing (3rd ed.). Cambridge University Press. ISBN 978-0-521-88068-8. Archived from the original on 11 August 2011. Retrieved 18 August 2011.
- ^ Ewing, Gregory C. (March 2010). «Reverse-Engineering a CRC Algorithm». Christchurch: University of Canterbury. Archived from the original on 7 August 2011. Retrieved 26 July 2011.
- ^ a b c d e f g h i j Koopman, Philip; Chakravarty, Tridib (June 2004). Cyclic Redundancy Code (CRC) Polynomial Selection For Embedded Networks (PDF). The International Conference on Dependable Systems and Networks. pp. 145–154. CiteSeerX 10.1.1.648.9080. doi:10.1109/DSN.2004.1311885. ISBN 978-0-7695-2052-0. S2CID 793862. Archived (PDF) from the original on 11 September 2011. Retrieved 14 January 2011.
- ^ a b Cook, Greg (15 August 2020). «Catalogue of parametrised CRC algorithms». Archived from the original on 1 August 2020. Retrieved 18 September 2020.
- ^ Castagnoli, G.; Bräuer, S.; Herrmann, M. (June 1993). «Optimization of Cyclic Redundancy-Check Codes with 24 and 32 Parity Bits». IEEE Transactions on Communications. 41 (6): 883–892. doi:10.1109/26.231911.
- ^ a b c d e f g h Koopman, Philip (July 2002). «32-Bit Cyclic Redundancy Codes for Internet Applications». Proceedings International Conference on Dependable Systems and Networks (PDF). The International Conference on Dependable Systems and Networks. pp. 459–468. CiteSeerX 10.1.1.11.8323. doi:10.1109/DSN.2002.1028931. ISBN 978-0-7695-1597-7. S2CID 14775606. Archived (PDF) from the original on 16 September 2012. Retrieved 14 January 2011.
- ^ Koopman, Philip (21 January 2016). «Best CRC Polynomials». Carnegie Mellon University. Archived from the original on 20 January 2016. Retrieved 26 January 2016.
- ^ Brayer, Kenneth (August 1975). Evaluation of 32 Degree Polynomials in Error Detection on the SATIN IV Autovon Error Patterns (Report). National Technical Information Service. ADA014825. Archived from the original on 31 December 2021. Retrieved 31 December 2021.
- ^ Hammond, Joseph L. Jr.; Brown, James E.; Liu, Shyan-Shiang (1975). «Development of a Transmission Error Model and an Error Control Model». NASA Sti/Recon Technical Report N (published May 1975). 76: 15344. Bibcode:1975STIN…7615344H. ADA013939. Archived from the original on 31 December 2021. Retrieved 31 December 2021.
- ^ Brayer, Kenneth; Hammond, Joseph L. Jr. (December 1975). Evaluation of error detection polynomial performance on the AUTOVON channel. NTC 75 : National Telecommunications Conference, December 1-3, 1975, New Orleans, Louisiana. Vol. 1. Institute of Electrical and Electronics Engineers. pp. 8-21–5. Bibcode:1975ntc…..1….8B. OCLC 32688603. 75 CH 1015-7 CSCB.
- ^ CRCs with even parity detect any odd number of bit errors, at the expense of lower hamming distance for long payloads. Note that parity is computed over the entire generator polynomial, including implied 1 at the beginning or the end. For example, the full representation of CRC-1 is 0x3, which has two 1 bits. Thus, its parity is even.
- ^ a b «32 Bit CRC Zoo». users.ece.cmu.edu. Archived from the original on 19 March 2018. Retrieved 5 November 2017.
- ^ Payload means length exclusive of CRC field. A Hamming distance of d means that d − 1 bit errors can be detected and ⌊(d − 1)/2⌋ bit errors can be corrected
- ^ is always achieved for arbitrarily long messages
- ^ a b c d e f ETSI TS 100 909 (PDF). V8.9.0. Sophia Antipolis, France: European Telecommunications Standards Institute. January 2005. Archived (PDF) from the original on 17 April 2018. Retrieved 21 October 2016.
- ^ «3 Bit CRC Zoo». users.ece.cmu.edu. Archived from the original on 7 April 2018. Retrieved 19 January 2018.
- ^ Class-1 Generation-2 UHF RFID Protocol (PDF). 1.2.0. EPCglobal. 23 October 2008. p. 35. Archived (PDF) from the original on 19 March 2012. Retrieved 4 July 2012. (Table 6.12)
- ^ a b c d e f Physical layer standard for cdma2000 spread spectrum systems (PDF). Revision D version 2.0. 3rd Generation Partnership Project 2. October 2005. pp. 2–89–2–92. Archived from the original (PDF) on 16 November 2013. Retrieved 14 October 2013.
- ^ a b c «11. Error correction strategy». ETSI EN 300 751 (PDF). V1.2.1. Sophia Antipolis, France: European Telecommunications Standards Institute. January 2003. pp. 67–8. Archived (PDF) from the original on 28 December 2015. Retrieved 26 January 2016.
- ^ «6 Bit CRC Zoo». users.ece.cmu.edu. Archived from the original on 7 April 2018. Retrieved 19 January 2018.
- ^ a b Chakravarty, Tridib (December 2001). Performance of Cyclic Redundancy Codes for Embedded Networks (PDF) (Thesis). Philip Koopman, advisor. Carnegie Mellon University. pp. 5, 18. Archived (PDF) from the original on 1 January 2014. Retrieved 8 July 2013.
- ^ «5.1.4 CRC-8 encoder (for packetized streams only)». EN 302 307 (PDF). V1.3.1. Sophia Antipolis, France: European Telecommunications Standards Institute. March 2013. p. 17. Archived (PDF) from the original on 30 August 2017. Retrieved 29 July 2016.
- ^ a b «8 Bit CRC Zoo». users.ece.cmu.edu. Archived from the original on 7 April 2018. Retrieved 19 January 2018.
- ^ «7.2.1.2 8-bit 0x2F polynomial CRC Calculation». Specification of CRC Routines (PDF). 4.2.2. Munich: AUTOSAR. 22 July 2015. p. 24. Archived from the original (PDF) on 24 July 2016. Retrieved 24 July 2016.
- ^ a b c «5.1.1.8 Cyclic Redundancy Check field (CRC-8 / CRC-16)». openSAFETY Safety Profile Specification: EPSG Working Draft Proposal 304. 1.4.0. Berlin: Ethernet POWERLINK Standardisation Group. 13 March 2013. p. 42. Archived from the original on 12 August 2017. Retrieved 22 July 2016.
- ^ «B.7.1.1 HEC generation». Specification of the Bluetooth System. Vol. 2. Bluetooth SIG. 2 December 2014. pp. 144–5. Archived from the original on 26 March 2015. Retrieved 20 October 2014.
- ^ Whitfield, Harry (24 April 2001). «XFCNs for Cyclic Redundancy Check Calculations». Archived from the original on 25 May 2005.
- ^ Richardson, Andrew (17 March 2005). WCDMA Handbook. Cambridge University Press. p. 223. ISBN 978-0-521-82815-4.
- ^ a b FlexRay Protocol Specification. 3.0.1. Flexray Consortium. October 2010. p. 114. (4.2.8 Header CRC (11 bits))
- ^ Perez, A. (1983). «Byte-Wise CRC Calculations». IEEE Micro. 3 (3): 40–50. doi:10.1109/MM.1983.291120. S2CID 206471618.
- ^ Ramabadran, T.V.; Gaitonde, S.S. (1988). «A tutorial on CRC computations». IEEE Micro. 8 (4): 62–75. doi:10.1109/40.7773. S2CID 10216862.
- ^ «Longwave Radio Data Decoding using and HC11 and an MC3371» (PDF). Freescale Semiconductor. 2004. AN1597/D. Archived from the original (PDF) on 24 September 2015.
- ^ Ely, S.R.; Wright, D.T. (March 1982). L.F. Radio-Data: specification of BBC experimental transmissions 1982 (PDF). Research Department, Engineering Division, The British Broadcasting Corporation. p. 9. Archived (PDF) from the original on 12 October 2013. Retrieved 11 October 2013.
- ^ Cyclic Redundancy Check (CRC): PSoC Creator™ Component Datasheet. Cypress Semiconductor. 20 February 2013. p. 4. Archived from the original on 2 February 2016. Retrieved 26 January 2016.
- ^ «Cyclic redundancy check (CRC) in CAN frames». CAN in Automation. Archived from the original on 1 February 2016. Retrieved 26 January 2016.
- ^ «3.2.3 Encoding and error checking». A signalling standard for trunked private land mobile radio systems (MPT 1327) (PDF) (3rd ed.). Ofcom. June 1997. p. 3. Archived (PDF) from the original on 14 July 2012. Retrieved 16 July 2012.
- ^ Rehmann, Albert; Mestre, José D. (February 1995). «Air Ground Data Link VHF Airline Communications and Reporting System (ACARS) Preliminary Test Report» (PDF). Federal Aviation Authority Technical Center. p. 5. Archived from the original (PDF) on 2 August 2012. Retrieved 7 July 2012.
- ^ «6.2.5 Error control». ETSI EN 300 175-3 (PDF). V2.5.1. Sophia Antipolis, France: European Telecommunications Standards Institute. August 2013. pp. 99, 101. Archived (PDF) from the original on 1 July 2015. Retrieved 26 January 2016.
- ^ Thaler, Pat (28 August 2003). «16-bit CRC polynomial selection» (PDF). INCITS T10. Archived (PDF) from the original on 28 July 2011. Retrieved 11 August 2009.
- ^ «8.8.4 Check Octet (FCS)». PROFIBUS Specification Normative Parts (PDF). 1.0. Vol. 9. Profibus International. March 1998. p. 906. Archived from the original (PDF) on 16 November 2008. Retrieved 9 July 2016.
- ^ a b CAN with Flexible Data-Rate Specification (PDF). 1.0. Robert Bosch GmbH. 17 April 2012. p. 13. Archived from the original (PDF) on 22 August 2013. (3.2.1 DATA FRAME)
- ^ «OS-9 Operating System System Programmer’s Manual». www.roug.org. Archived from the original on 17 July 2018. Retrieved 17 July 2018.
- ^ Koopman, Philip P. (20 May 2018). «24 Bit CRC Zoo». users.ece.cmu.edu. Archived from the original on 7 April 2018. Retrieved 19 January 2018.
- ^ «cksum». pubs.opengroup.org. Archived from the original on 18 July 2018. Retrieved 27 June 2017.
- ^ Boutell, Thomas; Randers-Pehrson, Glenn; et al. (14 July 1998). «PNG (Portable Network Graphics) Specification, Version 1.2». Libpng.org. Archived from the original on 3 September 2011. Retrieved 3 February 2011.
- ^ AIXM Primer (PDF). 4.5. European Organisation for the Safety of Air Navigation. 20 March 2006. Archived (PDF) from the original on 20 November 2018. Retrieved 3 February 2019.
- ^ ETSI TS 100 909 Archived 17 April 2018 at the Wayback Machine version 8.9.0 (January 2005), Section 4.1.2 a
- ^ Gammel, Berndt M. (31 October 2005). Matpack documentation: Crypto – Codes. Matpack.de. Archived from the original on 25 August 2013. Retrieved 21 April 2013. (Note: MpCRC.html is included with the Matpack compressed software source code, under /html/LibDoc/Crypto)
- ^ Geremia, Patrick (April 1999). «Cyclic redundancy check computation: an implementation using the TMS320C54x» (PDF). Texas Instruments. p. 5. Archived (PDF) from the original on 14 June 2012. Retrieved 4 July 2012.
- ^ Jones, David T. «An Improved 64-bit Cyclic Redundancy Check for Protein Sequences» (PDF). University College London. Archived (PDF) from the original on 7 June 2011. Retrieved 15 December 2009.
Further reading[edit]
- Warren Jr., Henry S. (2013). Hacker’s Delight (2 ed.). Addison Wesley. ISBN 978-0-321-84268-8.
External links[edit]
- Mitra, Jubin; Nayak, Tapan (January 2017). «Reconfigurable very high throughput low latency VLSI (FPGA) design architecture of CRC 32». Integration, the VLSI Journal. 56: 1–14. doi:10.1016/j.vlsi.2016.09.005.
- Cyclic Redundancy Checks, MathPages, overview of error-detection of different polynomials
- Williams, Ross (1993). «A Painless Guide to CRC Error Detection Algorithms». Archived from the original on 3 September 2011. Retrieved 15 August 2011.
- Black, Richard (1994). «Fast CRC32 in Software». The Blue Book. Systems Research Group, Computer Laboratory, University of Cambridge. Algorithm 4 was used in Linux and Bzip2.
- Kounavis, M.; Berry, F. (2005). «A Systematic Approach to Building High Performance, Software-based, CRC generators» (PDF). Intel. Archived (PDF) from the original on 16 December 2006. Retrieved 4 February 2007., Slicing-by-4 and slicing-by-8 algorithms
- Kowalk, W. (August 2006). «CRC Cyclic Redundancy Check Analysing and Correcting Errors» (PDF). Universität Oldenburg. Archived (PDF) from the original on 11 June 2007. Retrieved 1 September 2006. — Bitfilters
- Warren, Henry S. Jr. «Cyclic Redundancy Check» (PDF). Hacker’s Delight. Archived from the original (PDF) on 3 May 2015. — theory, practice, hardware, and software with emphasis on CRC-32.
- Reverse-Engineering a CRC Algorithm Archived 7 August 2011 at the Wayback Machine
- Cook, Greg. «Catalogue of parameterised CRC algorithms». CRC RevEng. Archived from the original on 1 August 2020. Retrieved 18 September 2020.
- Koopman, Phil. «Blog: Checksum and CRC Central». Archived from the original on 16 April 2013. Retrieved 3 June 2013. — includes links to PDFs giving 16 and 32-bit CRC Hamming distances
- Koopman, Philip; Driscoll, Kevin; Hall, Brendan (March 2015). «Cyclic Redundancy Code and Checksum Algorithms to Ensure Critical Data Integrity» (PDF). Federal Aviation Administration. DOT/FAA/TC-14/49. Archived (PDF) from the original on 18 May 2015. Retrieved 9 May 2015.
- Koopman, Philip (January 2023). Mechanics of Cyclic Redundancy Check Calculations – via YouTube.
- ISO/IEC 13239:2002: Information technology — Telecommunications and information exchange between systems — High-level data link control (HDLC) procedures
- CRC32-Castagnoli Linux Library
A cyclic redundancy check (CRC) is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to digital data. Blocks of data entering these systems get a short check value attached, based on the remainder of a polynomial division of their contents. On retrieval, the calculation is repeated and, in the event the check values do not match, corrective action can be taken against data corruption. CRCs can be used for error correction (see bitfilters).[1]
CRCs are so called because the check (data verification) value is a redundancy (it expands the message without adding information) and the algorithm is based on cyclic codes. CRCs are popular because they are simple to implement in binary hardware, easy to analyze mathematically, and particularly good at detecting common errors caused by noise in transmission channels. Because the check value has a fixed length, the function that generates it is occasionally used as a hash function.
Introduction[edit]
CRCs are based on the theory of cyclic error-correcting codes. The use of systematic cyclic codes, which encode messages by adding a fixed-length check value, for the purpose of error detection in communication networks, was first proposed by W. Wesley Peterson in 1961.[2]
Cyclic codes are not only simple to implement but have the benefit of being particularly well suited for the detection of burst errors: contiguous sequences of erroneous data symbols in messages. This is important because burst errors are common transmission errors in many communication channels, including magnetic and optical storage devices. Typically an n-bit CRC applied to a data block of arbitrary length will detect any single error burst not longer than n bits, and the fraction of all longer error bursts that it will detect is (1 − 2−n).
Specification of a CRC code requires definition of a so-called generator polynomial. This polynomial becomes the divisor in a polynomial long division, which takes the message as the dividend and in which the quotient is discarded and the remainder becomes the result. The important caveat is that the polynomial coefficients are calculated according to the arithmetic of a finite field, so the addition operation can always be performed bitwise-parallel (there is no carry between digits).
In practice, all commonly used CRCs employ the Galois field, or more simply a finite field, of two elements, GF(2). The two elements are usually called 0 and 1, comfortably matching computer architecture.
A CRC is called an n-bit CRC when its check value is n bits long. For a given n, multiple CRCs are possible, each with a different polynomial. Such a polynomial has highest degree n, which means it has n + 1 terms. In other words, the polynomial has a length of n + 1; its encoding requires n + 1 bits. Note that most polynomial specifications either drop the MSB or LSB, since they are always 1. The CRC and associated polynomial typically have a name of the form CRC-n-XXX as in the table below.
The simplest error-detection system, the parity bit, is in fact a 1-bit CRC: it uses the generator polynomial x + 1 (two terms),[3] and has the name CRC-1.
Application[edit]
A CRC-enabled device calculates a short, fixed-length binary sequence, known as the check value or CRC, for each block of data to be sent or stored and appends it to the data, forming a codeword.
When a codeword is received or read, the device either compares its check value with one freshly calculated from the data block, or equivalently, performs a CRC on the whole codeword and compares the resulting check value with an expected residue constant.
If the CRC values do not match, then the block contains a data error.
The device may take corrective action, such as rereading the block or requesting that it be sent again. Otherwise, the data is assumed to be error-free (though, with some small probability, it may contain undetected errors; this is inherent in the nature of error-checking).[4]
Data integrity[edit]
CRCs are specifically designed to protect against common types of errors on communication channels, where they can provide quick and reasonable assurance of the integrity of messages delivered. However, they are not suitable for protecting against intentional alteration of data.
Firstly, as there is no authentication, an attacker can edit a message and recompute the CRC without the substitution being detected. When stored alongside the data, CRCs and cryptographic hash functions by themselves do not protect against intentional modification of data. Any application that requires protection against such attacks must use cryptographic authentication mechanisms, such as message authentication codes or digital signatures (which are commonly based on cryptographic hash functions).
Secondly, unlike cryptographic hash functions, CRC is an easily reversible function, which makes it unsuitable for use in digital signatures.[5]
Thirdly, CRC satisfies a relation similar to that of a linear function (or more accurately, an affine function):[6]
where 





as a result, even if the CRC is encrypted with a stream cipher that uses XOR as its combining operation (or mode of block cipher which effectively turns it into a stream cipher, such as OFB or CFB), both the message and the associated CRC can be manipulated without knowledge of the encryption key; this was one of the well-known design flaws of the Wired Equivalent Privacy (WEP) protocol.[7]
Computation[edit]
To compute an n-bit binary CRC, line the bits representing the input in a row, and position the (n + 1)-bit pattern representing the CRC’s divisor (called a «polynomial») underneath the left end of the row.
In this example, we shall encode 14 bits of message with a 3-bit CRC, with a polynomial x3 + x + 1. The polynomial is written in binary as the coefficients; a 3rd-degree polynomial has 4 coefficients (1x3 + 0x2 + 1x + 1). In this case, the coefficients are 1, 0, 1 and 1. The result of the calculation is 3 bits long, which is why it is called a 3-bit CRC. However, you need 4 bits to explicitly state the polynomial.
Start with the message to be encoded:
11010011101100
This is first padded with zeros corresponding to the bit length n of the CRC. This is done so that the resulting code word is in systematic form. Here is the first calculation for computing a 3-bit CRC:
11010011101100 000 <--- input right padded by 3 bits 1011 <--- divisor (4 bits) = x³ + x + 1 ------------------ 01100011101100 000 <--- result
The algorithm acts on the bits directly above the divisor in each step. The result for that iteration is the bitwise XOR of the polynomial divisor with the bits above it. The bits not above the divisor are simply copied directly below for that step. The divisor is then shifted right to align with the highest remaining 1 bit in the input, and the process is repeated until the divisor reaches the right-hand end of the input row. Here is the entire calculation:
11010011101100 000 <--- input right padded by 3 bits
1011 <--- divisor
01100011101100 000 <--- result (note the first four bits are the XOR with the divisor beneath, the rest of the bits are unchanged)
1011 <--- divisor ...
00111011101100 000
1011
00010111101100 000
1011
00000001101100 000 <--- note that the divisor moves over to align with the next 1 in the dividend (since quotient for that step was zero)
1011 (in other words, it doesn't necessarily move one bit per iteration)
00000000110100 000
1011
00000000011000 000
1011
00000000001110 000
1011
00000000000101 000
101 1
-----------------
00000000000000 100 <--- remainder (3 bits). Division algorithm stops here as dividend is equal to zero.
Since the leftmost divisor bit zeroed every input bit it touched, when this process ends the only bits in the input row that can be nonzero are the n bits at the right-hand end of the row. These n bits are the remainder of the division step, and will also be the value of the CRC function (unless the chosen CRC specification calls for some postprocessing).
The validity of a received message can easily be verified by performing the above calculation again, this time with the check value added instead of zeroes. The remainder should equal zero if there are no detectable errors.
11010011101100 100 <--- input with check value
1011 <--- divisor
01100011101100 100 <--- result
1011 <--- divisor ...
00111011101100 100
......
00000000001110 100
1011
00000000000101 100
101 1
------------------
00000000000000 000 <--- remainder
The following Python code outlines a function which will return the initial CRC remainder for a chosen input and polynomial, with either 1 or 0 as the initial padding. Note that this code works with string inputs rather than raw numbers:
def crc_remainder(input_bitstring, polynomial_bitstring, initial_filler): """Calculate the CRC remainder of a string of bits using a chosen polynomial. initial_filler should be '1' or '0'. """ polynomial_bitstring = polynomial_bitstring.lstrip('0') len_input = len(input_bitstring) initial_padding = (len(polynomial_bitstring) - 1) * initial_filler input_padded_array = list(input_bitstring + initial_padding) while '1' in input_padded_array[:len_input]: cur_shift = input_padded_array.index('1') for i in range(len(polynomial_bitstring)): input_padded_array[cur_shift + i] = str(int(polynomial_bitstring[i] != input_padded_array[cur_shift + i])) return ''.join(input_padded_array)[len_input:] def crc_check(input_bitstring, polynomial_bitstring, check_value): """Calculate the CRC check of a string of bits using a chosen polynomial.""" polynomial_bitstring = polynomial_bitstring.lstrip('0') len_input = len(input_bitstring) initial_padding = check_value input_padded_array = list(input_bitstring + initial_padding) while '1' in input_padded_array[:len_input]: cur_shift = input_padded_array.index('1') for i in range(len(polynomial_bitstring)): input_padded_array[cur_shift + i] = str(int(polynomial_bitstring[i] != input_padded_array[cur_shift + i])) return ('1' not in ''.join(input_padded_array)[len_input:])
>>> crc_remainder('11010011101100', '1011', '0') '100' >>> crc_check('11010011101100', '1011', '100') True
CRC-32 algorithm[edit]
This is a practical algorithm for the CRC-32 variant of CRC.[8] The CRCTable is a memoization of a calculation that would have to be repeated for each byte of the message (Computation of cyclic redundancy checks § Multi-bit computation).
Function CRC32 Input: data: Bytes // Array of bytes Output: crc32: UInt32 // 32-bit unsigned CRC-32 value
// Initialize CRC-32 to starting value crc32 ← 0xFFFFFFFF
for each byte in data do nLookupIndex ← (crc32 xor byte) and 0xFF crc32 ← (crc32 shr 8) xor CRCTable[nLookupIndex] // CRCTable is an array of 256 32-bit constants
// Finalize the CRC-32 value by inverting all the bits crc32 ← crc32 xor 0xFFFFFFFF return crc32
In C, the algorithm looks as such:
#include <inttypes.h> // uint32_t, uint8_t uint32_t CRC32(const uint8_t data[], size_t data_length) { uint32_t crc32 = 0xFFFFFFFFu; for (size_t i = 0; i < data_length; i++) { const uint32_t lookupIndex = (crc32 ^ data[i]) & 0xff; crc32 = (crc32 >> 8) ^ CRCTable[lookupIndex]; // CRCTable is an array of 256 32-bit constants } // Finalize the CRC-32 value by inverting all the bits crc32 ^= 0xFFFFFFFFu; return crc32; }
Mathematics[edit]
Mathematical analysis of this division-like process reveals how to select a divisor that guarantees good error-detection properties. In this analysis, the digits of the bit strings are taken as the coefficients of a polynomial in some variable x—coefficients that are elements of the finite field GF(2) (the integers modulo 2, i.e. either a zero or a one), instead of more familiar numbers. The set of binary polynomials is a mathematical ring.
Designing polynomials[edit]
The selection of the generator polynomial is the most important part of implementing the CRC algorithm. The polynomial must be chosen to maximize the error-detecting capabilities while minimizing overall collision probabilities.
The most important attribute of the polynomial is its length (largest degree(exponent) +1 of any one term in the polynomial), because of its direct influence on the length of the computed check value.
The most commonly used polynomial lengths are 9 bits (CRC-8), 17 bits (CRC-16), 33 bits (CRC-32), and 65 bits (CRC-64).[3]
A CRC is called an n-bit CRC when its check value is n-bits. For a given n, multiple CRCs are possible, each with a different polynomial. Such a polynomial has highest degree n, and hence n + 1 terms (the polynomial has a length of n + 1). The remainder has length n. The CRC has a name of the form CRC-n-XXX.
The design of the CRC polynomial depends on the maximum total length of the block to be protected (data + CRC bits), the desired error protection features, and the type of resources for implementing the CRC, as well as the desired performance. A common misconception is that the «best» CRC polynomials are derived from either irreducible polynomials or irreducible polynomials times the factor 1 + x, which adds to the code the ability to detect all errors affecting an odd number of bits.[9] In reality, all the factors described above should enter into the selection of the polynomial and may lead to a reducible polynomial. However, choosing a reducible polynomial will result in a certain proportion of missed errors, due to the quotient ring having zero divisors.
The advantage of choosing a primitive polynomial as the generator for a CRC code is that the resulting code has maximal total block length in the sense that all 1-bit errors within that block length have different remainders (also called syndromes) and therefore, since the remainder is a linear function of the block, the code can detect all 2-bit errors within that block length. If 





A polynomial 
Specification[edit]
The concept of the CRC as an error-detecting code gets complicated when an implementer or standards committee uses it to design a practical system. Here are some of the complications:
- Sometimes an implementation prefixes a fixed bit pattern to the bitstream to be checked. This is useful when clocking errors might insert 0-bits in front of a message, an alteration that would otherwise leave the check value unchanged.
- Usually, but not always, an implementation appends n 0-bits (n being the size of the CRC) to the bitstream to be checked before the polynomial division occurs. Such appending is explicitly demonstrated in the Computation of CRC article. This has the convenience that the remainder of the original bitstream with the check value appended is exactly zero, so the CRC can be checked simply by performing the polynomial division on the received bitstream and comparing the remainder with zero. Due to the associative and commutative properties of the exclusive-or operation, practical table driven implementations can obtain a result numerically equivalent to zero-appending without explicitly appending any zeroes, by using an equivalent,[9] faster algorithm that combines the message bitstream with the stream being shifted out of the CRC register.
- Sometimes an implementation exclusive-ORs a fixed bit pattern into the remainder of the polynomial division.
- Bit order: Some schemes view the low-order bit of each byte as «first», which then during polynomial division means «leftmost», which is contrary to our customary understanding of «low-order». This convention makes sense when serial-port transmissions are CRC-checked in hardware, because some widespread serial-port transmission conventions transmit bytes least-significant bit first.
- Byte order: With multi-byte CRCs, there can be confusion over whether the byte transmitted first (or stored in the lowest-addressed byte of memory) is the least-significant byte (LSB) or the most-significant byte (MSB). For example, some 16-bit CRC schemes swap the bytes of the check value.
- Omission of the high-order bit of the divisor polynomial: Since the high-order bit is always 1, and since an n-bit CRC must be defined by an (n + 1)-bit divisor which overflows an n-bit register, some writers assume that it is unnecessary to mention the divisor’s high-order bit.
- Omission of the low-order bit of the divisor polynomial: Since the low-order bit is always 1, authors such as Philip Koopman represent polynomials with their high-order bit intact, but without the low-order bit (the
or 1 term). This convention encodes the polynomial complete with its degree in one integer.
These complications mean that there are three common ways to express a polynomial as an integer: the first two, which are mirror images in binary, are the constants found in code; the third is the number found in Koopman’s papers. In each case, one term is omitted. So the polynomial 
In the table below they are shown as:
| Name | Normal | Reversed | Reversed reciprocal |
|---|---|---|---|
| CRC-4 | 0x3 | 0xC | 0x9 |
Obfuscation[edit]
CRCs in proprietary protocols might be obfuscated by using a non-trivial initial value and a final XOR, but these techniques do not add cryptographic strength to the algorithm and can be reverse engineered using straightforward methods.[11]
Standards and common use[edit]
Numerous varieties of cyclic redundancy checks have been incorporated into technical standards. By no means does one algorithm, or one of each degree, suit every purpose; Koopman and Chakravarty recommend selecting a polynomial according to the application requirements and the expected distribution of message lengths.[12] The number of distinct CRCs in use has confused developers, a situation which authors have sought to address.[9] There are three polynomials reported for CRC-12,[12] twenty-two conflicting definitions of CRC-16, and seven of CRC-32.[13]
The polynomials commonly applied are not the most efficient ones possible. Since 1993, Koopman, Castagnoli and others have surveyed the space of polynomials between 3 and 64 bits in size,[12][14][15][16] finding examples that have much better performance (in terms of Hamming distance for a given message size) than the polynomials of earlier protocols, and publishing the best of these with the aim of improving the error detection capacity of future standards.[15] In particular, iSCSI and SCTP have adopted one of the findings of this research, the CRC-32C (Castagnoli) polynomial.
The design of the 32-bit polynomial most commonly used by standards bodies, CRC-32-IEEE, was the result of a joint effort for the Rome Laboratory and the Air Force Electronic Systems Division by Joseph Hammond, James Brown and Shyan-Shiang Liu of the Georgia Institute of Technology and Kenneth Brayer of the Mitre Corporation. The earliest known appearances of the 32-bit polynomial were in their 1975 publications: Technical Report 2956 by Brayer for Mitre, published in January and released for public dissemination through DTIC in August,[17] and Hammond, Brown and Liu’s report for the Rome Laboratory, published in May.[18] Both reports contained contributions from the other team. During December 1975, Brayer and Hammond presented their work in a paper at the IEEE National Telecommunications Conference: the IEEE CRC-32 polynomial is the generating polynomial of a Hamming code and was selected for its error detection performance.[19] Even so, the Castagnoli CRC-32C polynomial used in iSCSI or SCTP matches its performance on messages from 58 bits to 131 kbits, and outperforms it in several size ranges including the two most common sizes of Internet packet.[15] The ITU-T G.hn standard also uses CRC-32C to detect errors in the payload (although it uses CRC-16-CCITT for PHY headers).
CRC-32C computation is implemented in hardware as an operation (CRC32) of SSE4.2 instruction set, first introduced in Intel processors’ Nehalem microarchitecture. ARM AArch64 architecture also provides hardware acceleration for both CRC-32 and CRC-32C operations.
Polynomial representations of cyclic redundancy checks[edit]
The table below lists only the polynomials of the various algorithms in use. Variations of a particular protocol can impose pre-inversion, post-inversion and reversed bit ordering as described above. For example, the CRC32 used in Gzip and Bzip2 use the same polynomial, but Gzip employs reversed bit ordering, while Bzip2 does not.[13]
Note that even parity polynomials in GF(2) with degree greater than 1 are never primitive. Even parity polynomial marked as primitive in this table represent a primitive polynomial multiplied by 
| Name | Uses | Polynomial representations | Parity[20] | Primitive[21] | Maximum bits of payload by Hamming distance[22][15][21] | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Normal | Reversed | Reciprocal | Reversed reciprocal | ≥ 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2[23] | ||||
| CRC-1 | most hardware; also known as parity bit | 0x1 | 0x1 | 0x1 | 0x1 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-3-GSM | mobile networks[24] | 0x3 | 0x6 | 0x5 | 0x5 | odd | yes [25] | – | – | – | – | – | – | – | – | – | – | – | – | – | 4 | ∞ |

|
||||||||||||||||||||||
| CRC-4-ITU | ITU-T G.704, p. 12 | 0x3 | 0xC | 0x9 | 0x9 | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-5-EPC | Gen 2 RFID[26] | 0x09 | 0x12 | 0x05 | 0x14 | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-5-ITU | ITU-T G.704, p. 9 | 0x15 | 0x15 | 0x0B | 0x1A | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-5-USB | USB token packets | 0x05 | 0x14 | 0x09 | 0x12 | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-6-CDMA2000-A | mobile networks[27] | 0x27 | 0x39 | 0x33 | 0x33 | odd | ||||||||||||||||
| CRC-6-CDMA2000-B | mobile networks[27] | 0x07 | 0x38 | 0x31 | 0x23 | even | ||||||||||||||||
| CRC-6-DARC | Data Radio Channel[28] | 0x19 | 0x26 | 0x0D | 0x2C | even | ||||||||||||||||
| CRC-6-GSM | mobile networks[24] | 0x2F | 0x3D | 0x3B | 0x37 | even | yes [29] | – | – | – | – | – | – | – | – | – | – | 1 | 1 | 25 | 25 | ∞ |

|
||||||||||||||||||||||
| CRC-6-ITU | ITU-T G.704, p. 3 | 0x03 | 0x30 | 0x21 | 0x21 | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-7 | telecom systems, ITU-T G.707, ITU-T G.832, MMC, SD | 0x09 | 0x48 | 0x11 | 0x44 | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-7-MVB | Train Communication Network, IEC 60870-5[30] | 0x65 | 0x53 | 0x27 | 0x72 | odd | ||||||||||||||||
| CRC-8 | DVB-S2[31] | 0xD5 | 0xAB | 0x57 | 0xEA[12] | even | no [32] | – | – | – | – | – | – | – | – | – | – | 2 | 2 | 85 | 85 | ∞ |

|
||||||||||||||||||||||
| CRC-8-AUTOSAR | automotive integration,[33] OpenSafety[34] | 0x2F | 0xF4 | 0xE9 | 0x97[12] | even | yes [32] | – | – | – | – | – | – | – | – | – | – | 3 | 3 | 119 | 119 | ∞ |

|
||||||||||||||||||||||
| CRC-8-Bluetooth | wireless connectivity[35] | 0xA7 | 0xE5 | 0xCB | 0xD3 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-8-CCITT | ITU-T I.432.1 (02/99); ATM HEC, ISDN HEC and cell delineation, SMBus PEC | 0x07 | 0xE0 | 0xC1 | 0x83 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-8-Dallas/Maxim | 1-Wire bus[36] | 0x31 | 0x8C | 0x19 | 0x98 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-8-DARC | Data Radio Channel[28] | 0x39 | 0x9C | 0x39 | 0x9C | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-8-GSM-B | mobile networks[24] | 0x49 | 0x92 | 0x25 | 0xA4 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-8-SAE J1850 | AES3; OBD | 0x1D | 0xB8 | 0x71 | 0x8E | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-8-WCDMA | mobile networks[27][37] | 0x9B | 0xD9 | 0xB3 | 0xCD[12] | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-10 | ATM; ITU-T I.610 | 0x233 | 0x331 | 0x263 | 0x319 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-10-CDMA2000 | mobile networks[27] | 0x3D9 | 0x26F | 0x0DF | 0x3EC | even | ||||||||||||||||
| CRC-10-GSM | mobile networks[24] | 0x175 | 0x2BA | 0x175 | 0x2BA | odd | ||||||||||||||||
| CRC-11 | FlexRay[38] | 0x385 | 0x50E | 0x21D | 0x5C2 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-12 | telecom systems[39][40] | 0x80F | 0xF01 | 0xE03 | 0xC07[12] | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-12-CDMA2000 | mobile networks[27] | 0xF13 | 0xC8F | 0x91F | 0xF89 | even | ||||||||||||||||
| CRC-12-GSM | mobile networks[24] | 0xD31 | 0x8CB | 0x197 | 0xE98 | odd | ||||||||||||||||
| CRC-13-BBC | Time signal, Radio teleswitch[41][42] | 0x1CF5 | 0x15E7 | 0x0BCF | 0x1E7A | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-14-DARC | Data Radio Channel[28] | 0x0805 | 0x2804 | 0x1009 | 0x2402 | even | ||||||||||||||||
| CRC-14-GSM | mobile networks[24] | 0x202D | 0x2D01 | 0x1A03 | 0x3016 | even | ||||||||||||||||
| CRC-15-CAN | 0xC599[43][44] | 0x4CD1 | 0x19A3 | 0x62CC | even | |||||||||||||||||

|
||||||||||||||||||||||
| CRC-15-MPT1327 | [45] | 0x6815 | 0x540B | 0x2817 | 0x740A | odd | ||||||||||||||||
| CRC-16-Chakravarty | Optimal for payloads ≤64 bits[30] | 0x2F15 | 0xA8F4 | 0x51E9 | 0x978A | odd | ||||||||||||||||
| CRC-16-ARINC | ACARS applications[46] | 0xA02B | 0xD405 | 0xA80B | 0xD015 | odd | ||||||||||||||||
| CRC-16-CCITT | X.25, V.41, HDLC FCS, XMODEM, Bluetooth, PACTOR, SD, DigRF, many others; known as CRC-CCITT | 0x1021 | 0x8408 | 0x811 | 0x8810[12] | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-16-CDMA2000 | mobile networks[27] | 0xC867 | 0xE613 | 0xCC27 | 0xE433 | odd | ||||||||||||||||
| CRC-16-DECT | cordless telephones[47] | 0x0589 | 0x91A0 | 0x2341 | 0x82C4 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-16-T10-DIF | SCSI DIF | 0x8BB7[48] | 0xEDD1 | 0xDBA3 | 0xC5DB | odd | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-16-DNP | DNP, IEC 870, M-Bus | 0x3D65 | 0xA6BC | 0x4D79 | 0x9EB2 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-16-IBM | Bisync, Modbus, USB, ANSI X3.28, SIA DC-07, many others; also known as CRC-16 and CRC-16-ANSI | 0x8005 | 0xA001 | 0x4003 | 0xC002 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-16-OpenSafety-A | safety fieldbus[34] | 0x5935 | 0xAC9A | 0x5935 | 0xAC9A[12] | odd | ||||||||||||||||
| CRC-16-OpenSafety-B | safety fieldbus[34] | 0x755B | 0xDAAE | 0xB55D | 0xBAAD[12] | odd | ||||||||||||||||
| CRC-16-Profibus | fieldbus networks[49] | 0x1DCF | 0xF3B8 | 0xE771 | 0x8EE7 | odd | ||||||||||||||||
| Fletcher-16 | Used in Adler-32 A & B Checksums | Often confused to be a CRC, but actually a checksum; see Fletcher’s checksum | ||||||||||||||||||||
| CRC-17-CAN | CAN FD[50] | 0x1685B | 0x1B42D | 0x1685B | 0x1B42D | even | ||||||||||||||||
| CRC-21-CAN | CAN FD[50] | 0x102899 | 0x132281 | 0x064503 | 0x18144C | even | ||||||||||||||||
| CRC-24 | FlexRay[38] | 0x5D6DCB | 0xD3B6BA | 0xA76D75 | 0xAEB6E5 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-24-Radix-64 | OpenPGP, RTCM104v3 | 0x864CFB | 0xDF3261 | 0xBE64C3 | 0xC3267D | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-24-WCDMA | Used in OS-9 RTOS. Residue = 0x800FE3.[51] | 0x800063 | 0xC60001 | 0x8C0003 | 0xC00031 | even | yes[52] | – | – | – | – | – | – | – | – | – | – | 4 | 4 | 8388583 | 8388583 | ∞ |

|
||||||||||||||||||||||
| CRC-30 | CDMA | 0x2030B9C7 | 0x38E74301 | 0x31CE8603 | 0x30185CE3 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-32 | ISO 3309 (HDLC), ANSI X3.66 (ADCCP), FIPS PUB 71, FED-STD-1003, ITU-T V.42, ISO/IEC/IEEE 802-3 (Ethernet), SATA, MPEG-2, PKZIP, Gzip, Bzip2, POSIX cksum,[53] PNG,[54] ZMODEM, many others | 0x04C11DB7 | 0xEDB88320 | 0xDB710641 | 0x82608EDB[15] | odd | yes | – | 10 | – | – | 12 | 21 | 34 | 57 | 91 | 171 | 268 | 2974 | 91607 | 4294967263 | ∞ |

|
||||||||||||||||||||||
| CRC-32C (Castagnoli) | iSCSI, SCTP, G.hn payload, SSE4.2, Btrfs, ext4, Ceph | 0x1EDC6F41 | 0x82F63B78 | 0x05EC76F1 | 0x8F6E37A0[15] | even | yes | 6 | – | 8 | – | 20 | – | 47 | – | 177 | – | 5243 | – | 2147483615 | – | ∞ |

|
||||||||||||||||||||||
| CRC-32K (Koopman {1,3,28}) | Excellent at Ethernet frame length, poor performance with long files | 0x741B8CD7 | 0xEB31D82E | 0xD663B05D | 0xBA0DC66B[15] | even | no | 2 | – | 4 | – | 16 | – | 18 | – | 152 | – | 16360 | – | 114663 | – | ∞ |

|
||||||||||||||||||||||
| CRC-32K2 (Koopman {1,1,30}) | Excellent at Ethernet frame length, poor performance with long files | 0x32583499 | 0x992C1A4C | 0x32583499 | 0x992C1A4C[15] | even | no | – | – | 3 | – | 16 | – | 26 | – | 134 | – | 32738 | – | 65506 | – | ∞ |
| CRC-32Q | aviation; AIXM[55] | 0x814141AB | 0xD5828281 | 0xAB050503 | 0xC0A0A0D5 | even | ||||||||||||||||

|
||||||||||||||||||||||
| Adler-32 | Often confused to be a CRC, but actually a checksum; see Adler-32 | |||||||||||||||||||||
| CRC-40-GSM | GSM control channel[56][57][58] | 0x0004820009 | 0x9000412000 | 0x2000824001 | 0x8002410004 | even | ||||||||||||||||

|
||||||||||||||||||||||
| CRC-64-ECMA | ECMA-182 p. 51, XZ Utils | 0x42F0E1EBA9EA3693 | 0xC96C5795D7870F42 | 0x92D8AF2BAF0E1E85 | 0xA17870F5D4F51B49 | even | ||||||||||||||||
 
|
||||||||||||||||||||||
| CRC-64-ISO | ISO 3309 (HDLC), Swiss-Prot/TrEMBL; considered weak for hashing[59] | 0x000000000000001B | 0xD800000000000000 | 0xB000000000000001 | 0x800000000000000D | odd | ||||||||||||||||

|
Implementations[edit]
- Implementation of CRC32 in GNU Radio up to 3.6.1 (ca. 2012)
- C class code for CRC checksum calculation with many different CRCs to choose from
CRC catalogues[edit]
- Catalogue of parametrised CRC algorithms
- CRC Polynomial Zoo
See also[edit]
- Mathematics of cyclic redundancy checks
- Computation of cyclic redundancy checks
- List of hash functions
- List of checksum algorithms
- Information security
- Simple file verification
- LRC
References[edit]
- ^ «An Algorithm for Error Correcting Cyclic Redundance Checks». drdobbs.com. Archived from the original on 20 July 2017. Retrieved 28 June 2017.
- ^ Peterson, W. W.; Brown, D. T. (January 1961). «Cyclic Codes for Error Detection». Proceedings of the IRE. 49 (1): 228–235. doi:10.1109/JRPROC.1961.287814. S2CID 51666741.
- ^ a b Ergen, Mustafa (21 January 2008). «2.3.3 Error Detection Coding». Mobile Broadband. Springer. pp. 29–30. doi:10.1007/978-0-387-68192-4_2. ISBN 978-0-387-68192-4.
- ^ Ritter, Terry (February 1986). «The Great CRC Mystery». Dr. Dobb’s Journal. 11 (2): 26–34, 76–83. Archived from the original on 16 April 2009. Retrieved 21 May 2009.
- ^ Stigge, Martin; Plötz, Henryk; Müller, Wolf; Redlich, Jens-Peter (May 2006). «Reversing CRC – Theory and Practice» (PDF). Humboldt University Berlin. p. 17. SAR-PR-2006-05. Archived from the original (PDF) on 19 July 2011. Retrieved 4 February 2011.
The presented methods offer a very easy and efficient way to modify your data so that it will compute to a CRC you want or at least know in advance.
- ^ «algorithm design — Why is CRC said to be linear?». Cryptography Stack Exchange. Retrieved 5 May 2019.
- ^ Cam-Winget, Nancy; Housley, Russ; Wagner, David; Walker, Jesse (May 2003). «Security Flaws in 802.11 Data Link Protocols» (PDF). Communications of the ACM. 46 (5): 35–39. CiteSeerX 10.1.1.14.8775. doi:10.1145/769800.769823. S2CID 3132937. Archived (PDF) from the original on 26 May 2013. Retrieved 1 November 2017.
- ^ «[MS-ABS]: 32-Bit CRC Algorithm». msdn.microsoft.com. Archived from the original on 7 November 2017. Retrieved 4 November 2017.
- ^ a b c Williams, Ross N. (24 September 1996). «A Painless Guide to CRC Error Detection Algorithms V3.0». Archived from the original on 2 April 2018. Retrieved 23 May 2019.
- ^ Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). «Section 22.4 Cyclic Redundancy and Other Checksums». Numerical Recipes: The Art of Scientific Computing (3rd ed.). Cambridge University Press. ISBN 978-0-521-88068-8. Archived from the original on 11 August 2011. Retrieved 18 August 2011.
- ^ Ewing, Gregory C. (March 2010). «Reverse-Engineering a CRC Algorithm». Christchurch: University of Canterbury. Archived from the original on 7 August 2011. Retrieved 26 July 2011.
- ^ a b c d e f g h i j Koopman, Philip; Chakravarty, Tridib (June 2004). Cyclic Redundancy Code (CRC) Polynomial Selection For Embedded Networks (PDF). The International Conference on Dependable Systems and Networks. pp. 145–154. CiteSeerX 10.1.1.648.9080. doi:10.1109/DSN.2004.1311885. ISBN 978-0-7695-2052-0. S2CID 793862. Archived (PDF) from the original on 11 September 2011. Retrieved 14 January 2011.
- ^ a b Cook, Greg (15 August 2020). «Catalogue of parametrised CRC algorithms». Archived from the original on 1 August 2020. Retrieved 18 September 2020.
- ^ Castagnoli, G.; Bräuer, S.; Herrmann, M. (June 1993). «Optimization of Cyclic Redundancy-Check Codes with 24 and 32 Parity Bits». IEEE Transactions on Communications. 41 (6): 883–892. doi:10.1109/26.231911.
- ^ a b c d e f g h Koopman, Philip (July 2002). «32-Bit Cyclic Redundancy Codes for Internet Applications». Proceedings International Conference on Dependable Systems and Networks (PDF). The International Conference on Dependable Systems and Networks. pp. 459–468. CiteSeerX 10.1.1.11.8323. doi:10.1109/DSN.2002.1028931. ISBN 978-0-7695-1597-7. S2CID 14775606. Archived (PDF) from the original on 16 September 2012. Retrieved 14 January 2011.
- ^ Koopman, Philip (21 January 2016). «Best CRC Polynomials». Carnegie Mellon University. Archived from the original on 20 January 2016. Retrieved 26 January 2016.
- ^ Brayer, Kenneth (August 1975). Evaluation of 32 Degree Polynomials in Error Detection on the SATIN IV Autovon Error Patterns (Report). National Technical Information Service. ADA014825. Archived from the original on 31 December 2021. Retrieved 31 December 2021.
- ^ Hammond, Joseph L. Jr.; Brown, James E.; Liu, Shyan-Shiang (1975). «Development of a Transmission Error Model and an Error Control Model». NASA Sti/Recon Technical Report N (published May 1975). 76: 15344. Bibcode:1975STIN…7615344H. ADA013939. Archived from the original on 31 December 2021. Retrieved 31 December 2021.
- ^ Brayer, Kenneth; Hammond, Joseph L. Jr. (December 1975). Evaluation of error detection polynomial performance on the AUTOVON channel. NTC 75 : National Telecommunications Conference, December 1-3, 1975, New Orleans, Louisiana. Vol. 1. Institute of Electrical and Electronics Engineers. pp. 8-21–5. Bibcode:1975ntc…..1….8B. OCLC 32688603. 75 CH 1015-7 CSCB.
- ^ CRCs with even parity detect any odd number of bit errors, at the expense of lower hamming distance for long payloads. Note that parity is computed over the entire generator polynomial, including implied 1 at the beginning or the end. For example, the full representation of CRC-1 is 0x3, which has two 1 bits. Thus, its parity is even.
- ^ a b «32 Bit CRC Zoo». users.ece.cmu.edu. Archived from the original on 19 March 2018. Retrieved 5 November 2017.
- ^ Payload means length exclusive of CRC field. A Hamming distance of d means that d − 1 bit errors can be detected and ⌊(d − 1)/2⌋ bit errors can be corrected
- ^ is always achieved for arbitrarily long messages
- ^ a b c d e f ETSI TS 100 909 (PDF). V8.9.0. Sophia Antipolis, France: European Telecommunications Standards Institute. January 2005. Archived (PDF) from the original on 17 April 2018. Retrieved 21 October 2016.
- ^ «3 Bit CRC Zoo». users.ece.cmu.edu. Archived from the original on 7 April 2018. Retrieved 19 January 2018.
- ^ Class-1 Generation-2 UHF RFID Protocol (PDF). 1.2.0. EPCglobal. 23 October 2008. p. 35. Archived (PDF) from the original on 19 March 2012. Retrieved 4 July 2012. (Table 6.12)
- ^ a b c d e f Physical layer standard for cdma2000 spread spectrum systems (PDF). Revision D version 2.0. 3rd Generation Partnership Project 2. October 2005. pp. 2–89–2–92. Archived from the original (PDF) on 16 November 2013. Retrieved 14 October 2013.
- ^ a b c «11. Error correction strategy». ETSI EN 300 751 (PDF). V1.2.1. Sophia Antipolis, France: European Telecommunications Standards Institute. January 2003. pp. 67–8. Archived (PDF) from the original on 28 December 2015. Retrieved 26 January 2016.
- ^ «6 Bit CRC Zoo». users.ece.cmu.edu. Archived from the original on 7 April 2018. Retrieved 19 January 2018.
- ^ a b Chakravarty, Tridib (December 2001). Performance of Cyclic Redundancy Codes for Embedded Networks (PDF) (Thesis). Philip Koopman, advisor. Carnegie Mellon University. pp. 5, 18. Archived (PDF) from the original on 1 January 2014. Retrieved 8 July 2013.
- ^ «5.1.4 CRC-8 encoder (for packetized streams only)». EN 302 307 (PDF). V1.3.1. Sophia Antipolis, France: European Telecommunications Standards Institute. March 2013. p. 17. Archived (PDF) from the original on 30 August 2017. Retrieved 29 July 2016.
- ^ a b «8 Bit CRC Zoo». users.ece.cmu.edu. Archived from the original on 7 April 2018. Retrieved 19 January 2018.
- ^ «7.2.1.2 8-bit 0x2F polynomial CRC Calculation». Specification of CRC Routines (PDF). 4.2.2. Munich: AUTOSAR. 22 July 2015. p. 24. Archived from the original (PDF) on 24 July 2016. Retrieved 24 July 2016.
- ^ a b c «5.1.1.8 Cyclic Redundancy Check field (CRC-8 / CRC-16)». openSAFETY Safety Profile Specification: EPSG Working Draft Proposal 304. 1.4.0. Berlin: Ethernet POWERLINK Standardisation Group. 13 March 2013. p. 42. Archived from the original on 12 August 2017. Retrieved 22 July 2016.
- ^ «B.7.1.1 HEC generation». Specification of the Bluetooth System. Vol. 2. Bluetooth SIG. 2 December 2014. pp. 144–5. Archived from the original on 26 March 2015. Retrieved 20 October 2014.
- ^ Whitfield, Harry (24 April 2001). «XFCNs for Cyclic Redundancy Check Calculations». Archived from the original on 25 May 2005.
- ^ Richardson, Andrew (17 March 2005). WCDMA Handbook. Cambridge University Press. p. 223. ISBN 978-0-521-82815-4.
- ^ a b FlexRay Protocol Specification. 3.0.1. Flexray Consortium. October 2010. p. 114. (4.2.8 Header CRC (11 bits))
- ^ Perez, A. (1983). «Byte-Wise CRC Calculations». IEEE Micro. 3 (3): 40–50. doi:10.1109/MM.1983.291120. S2CID 206471618.
- ^ Ramabadran, T.V.; Gaitonde, S.S. (1988). «A tutorial on CRC computations». IEEE Micro. 8 (4): 62–75. doi:10.1109/40.7773. S2CID 10216862.
- ^ «Longwave Radio Data Decoding using and HC11 and an MC3371» (PDF). Freescale Semiconductor. 2004. AN1597/D. Archived from the original (PDF) on 24 September 2015.
- ^ Ely, S.R.; Wright, D.T. (March 1982). L.F. Radio-Data: specification of BBC experimental transmissions 1982 (PDF). Research Department, Engineering Division, The British Broadcasting Corporation. p. 9. Archived (PDF) from the original on 12 October 2013. Retrieved 11 October 2013.
- ^ Cyclic Redundancy Check (CRC): PSoC Creator™ Component Datasheet. Cypress Semiconductor. 20 February 2013. p. 4. Archived from the original on 2 February 2016. Retrieved 26 January 2016.
- ^ «Cyclic redundancy check (CRC) in CAN frames». CAN in Automation. Archived from the original on 1 February 2016. Retrieved 26 January 2016.
- ^ «3.2.3 Encoding and error checking». A signalling standard for trunked private land mobile radio systems (MPT 1327) (PDF) (3rd ed.). Ofcom. June 1997. p. 3. Archived (PDF) from the original on 14 July 2012. Retrieved 16 July 2012.
- ^ Rehmann, Albert; Mestre, José D. (February 1995). «Air Ground Data Link VHF Airline Communications and Reporting System (ACARS) Preliminary Test Report» (PDF). Federal Aviation Authority Technical Center. p. 5. Archived from the original (PDF) on 2 August 2012. Retrieved 7 July 2012.
- ^ «6.2.5 Error control». ETSI EN 300 175-3 (PDF). V2.5.1. Sophia Antipolis, France: European Telecommunications Standards Institute. August 2013. pp. 99, 101. Archived (PDF) from the original on 1 July 2015. Retrieved 26 January 2016.
- ^ Thaler, Pat (28 August 2003). «16-bit CRC polynomial selection» (PDF). INCITS T10. Archived (PDF) from the original on 28 July 2011. Retrieved 11 August 2009.
- ^ «8.8.4 Check Octet (FCS)». PROFIBUS Specification Normative Parts (PDF). 1.0. Vol. 9. Profibus International. March 1998. p. 906. Archived from the original (PDF) on 16 November 2008. Retrieved 9 July 2016.
- ^ a b CAN with Flexible Data-Rate Specification (PDF). 1.0. Robert Bosch GmbH. 17 April 2012. p. 13. Archived from the original (PDF) on 22 August 2013. (3.2.1 DATA FRAME)
- ^ «OS-9 Operating System System Programmer’s Manual». www.roug.org. Archived from the original on 17 July 2018. Retrieved 17 July 2018.
- ^ Koopman, Philip P. (20 May 2018). «24 Bit CRC Zoo». users.ece.cmu.edu. Archived from the original on 7 April 2018. Retrieved 19 January 2018.
- ^ «cksum». pubs.opengroup.org. Archived from the original on 18 July 2018. Retrieved 27 June 2017.
- ^ Boutell, Thomas; Randers-Pehrson, Glenn; et al. (14 July 1998). «PNG (Portable Network Graphics) Specification, Version 1.2». Libpng.org. Archived from the original on 3 September 2011. Retrieved 3 February 2011.
- ^ AIXM Primer (PDF). 4.5. European Organisation for the Safety of Air Navigation. 20 March 2006. Archived (PDF) from the original on 20 November 2018. Retrieved 3 February 2019.
- ^ ETSI TS 100 909 Archived 17 April 2018 at the Wayback Machine version 8.9.0 (January 2005), Section 4.1.2 a
- ^ Gammel, Berndt M. (31 October 2005). Matpack documentation: Crypto – Codes. Matpack.de. Archived from the original on 25 August 2013. Retrieved 21 April 2013. (Note: MpCRC.html is included with the Matpack compressed software source code, under /html/LibDoc/Crypto)
- ^ Geremia, Patrick (April 1999). «Cyclic redundancy check computation: an implementation using the TMS320C54x» (PDF). Texas Instruments. p. 5. Archived (PDF) from the original on 14 June 2012. Retrieved 4 July 2012.
- ^ Jones, David T. «An Improved 64-bit Cyclic Redundancy Check for Protein Sequences» (PDF). University College London. Archived (PDF) from the original on 7 June 2011. Retrieved 15 December 2009.
Further reading[edit]
- Warren Jr., Henry S. (2013). Hacker’s Delight (2 ed.). Addison Wesley. ISBN 978-0-321-84268-8.
External links[edit]
- Mitra, Jubin; Nayak, Tapan (January 2017). «Reconfigurable very high throughput low latency VLSI (FPGA) design architecture of CRC 32». Integration, the VLSI Journal. 56: 1–14. doi:10.1016/j.vlsi.2016.09.005.
- Cyclic Redundancy Checks, MathPages, overview of error-detection of different polynomials
- Williams, Ross (1993). «A Painless Guide to CRC Error Detection Algorithms». Archived from the original on 3 September 2011. Retrieved 15 August 2011.
- Black, Richard (1994). «Fast CRC32 in Software». The Blue Book. Systems Research Group, Computer Laboratory, University of Cambridge. Algorithm 4 was used in Linux and Bzip2.
- Kounavis, M.; Berry, F. (2005). «A Systematic Approach to Building High Performance, Software-based, CRC generators» (PDF). Intel. Archived (PDF) from the original on 16 December 2006. Retrieved 4 February 2007., Slicing-by-4 and slicing-by-8 algorithms
- Kowalk, W. (August 2006). «CRC Cyclic Redundancy Check Analysing and Correcting Errors» (PDF). Universität Oldenburg. Archived (PDF) from the original on 11 June 2007. Retrieved 1 September 2006. — Bitfilters
- Warren, Henry S. Jr. «Cyclic Redundancy Check» (PDF). Hacker’s Delight. Archived from the original (PDF) on 3 May 2015. — theory, practice, hardware, and software with emphasis on CRC-32.
- Reverse-Engineering a CRC Algorithm Archived 7 August 2011 at the Wayback Machine
- Cook, Greg. «Catalogue of parameterised CRC algorithms». CRC RevEng. Archived from the original on 1 August 2020. Retrieved 18 September 2020.
- Koopman, Phil. «Blog: Checksum and CRC Central». Archived from the original on 16 April 2013. Retrieved 3 June 2013. — includes links to PDFs giving 16 and 32-bit CRC Hamming distances
- Koopman, Philip; Driscoll, Kevin; Hall, Brendan (March 2015). «Cyclic Redundancy Code and Checksum Algorithms to Ensure Critical Data Integrity» (PDF). Federal Aviation Administration. DOT/FAA/TC-14/49. Archived (PDF) from the original on 18 May 2015. Retrieved 9 May 2015.
- Koopman, Philip (January 2023). Mechanics of Cyclic Redundancy Check Calculations – via YouTube.
- ISO/IEC 13239:2002: Information technology — Telecommunications and information exchange between systems — High-level data link control (HDLC) procedures
- CRC32-Castagnoli Linux Library
Простой расчет контрольной суммы
Время прочтения
12 мин
Просмотры 191K
При передачи данных по линиям связи, используется контрольная сумма, рассчитанная по некоторому алгоритму. Алгоритм часто сложный, конечно, он обоснован математически, но очень уж неудобен при дефиците ресурсов, например при программировании микроконтроллеров.
Чтобы упростить алгоритм, без потери качества, нужно немного «битовой магии», что интересная тема сама по себе.
Без контрольной суммы, передавать данные опасно, так как помехи присутствуют везде и всегда, весь вопрос только в их вероятности возникновения и вызываемых ими побочных эффектах. В зависимости от условий и выбирается алгоритм выявления ошибок и количество данных в контрольной сумме. Сложнее алгоритм, и больше контрольная сумма, меньше не распознанных ошибок.
Причина помех на физическом уровне, при передаче данных.
Вот пример самого типичного алгоритма для микроконтроллера, ставшего, фактически, промышленным стандартом с 1979 года.
Расчет контрольной суммы для протокола Modbus
void crc_calculating(unsigned char puchMsg, unsigned short usDataLen) /*##Расчёт контрольной суммы##*/
{
{
unsigned char uchCRCHi = 0xFF ; /* Инициализация последнего байта CRC */
unsigned char uchCRCLo = 0xFF ; /* Инициализация первого байта CRC */
unsigned uIndex ; /* will index into CRC lookup table */
while (usDataLen--) /* pass through message buffer */
{
uIndex = uchCRCHi ^ *puchMsg++ ; /* Расчёт CRC */
uchCRCLo = uchCRCLo ^ auchCRCHi[uIndex] ;
uchCRCHi = auchCRCLo[uIndex] ;
}
return (uchCRCHi << 8 | uchCRCLo) ;
/* Table of CRC values for high–order byte */
static unsigned char auchCRCHi[] = {
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01,
0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81,
0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0,
0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01,
0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01,
0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01,
0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40
};
/* Table of CRC values for low–order byte */
static char auchCRCLo[] = {
0x00, 0xC0, 0xC1, 0x01, 0xC3, 0x03, 0x02, 0xC2, 0xC6, 0x06, 0x07, 0xC7, 0x05, 0xC5, 0xC4,
0x04, 0xCC, 0x0C, 0x0D, 0xCD, 0x0F, 0xCF, 0xCE, 0x0E, 0x0A, 0xCA, 0xCB, 0x0B, 0xC9, 0x09,
0x08, 0xC8, 0xD8, 0x18, 0x19, 0xD9, 0x1B, 0xDB, 0xDA, 0x1A, 0x1E, 0xDE, 0xDF, 0x1F, 0xDD,
0x1D, 0x1C, 0xDC, 0x14, 0xD4, 0xD5, 0x15, 0xD7, 0x17, 0x16, 0xD6, 0xD2, 0x12, 0x13, 0xD3,
0x11, 0xD1, 0xD0, 0x10, 0xF0, 0x30, 0x31, 0xF1, 0x33, 0xF3, 0xF2, 0x32, 0x36, 0xF6, 0xF7,
0x37, 0xF5, 0x35, 0x34, 0xF4, 0x3C, 0xFC, 0xFD, 0x3D, 0xFF, 0x3F, 0x3E, 0xFE, 0xFA, 0x3A,
0x3B, 0xFB, 0x39, 0xF9, 0xF8, 0x38, 0x28, 0xE8, 0xE9, 0x29, 0xEB, 0x2B, 0x2A, 0xEA, 0xEE,
0x2E, 0x2F, 0xEF, 0x2D, 0xED, 0xEC, 0x2C, 0xE4, 0x24, 0x25, 0xE5, 0x27, 0xE7, 0xE6, 0x26,
0x22, 0xE2, 0xE3, 0x23, 0xE1, 0x21, 0x20, 0xE0, 0xA0, 0x60, 0x61, 0xA1, 0x63, 0xA3, 0xA2,
0x62, 0x66, 0xA6, 0xA7, 0x67, 0xA5, 0x65, 0x64, 0xA4, 0x6C, 0xAC, 0xAD, 0x6D, 0xAF, 0x6F,
0x6E, 0xAE, 0xAA, 0x6A, 0x6B, 0xAB, 0x69, 0xA9, 0xA8, 0x68, 0x78, 0xB8, 0xB9, 0x79, 0xBB,
0x7B, 0x7A, 0xBA, 0xBE, 0x7E, 0x7F, 0xBF, 0x7D, 0xBD, 0xBC, 0x7C, 0xB4, 0x74, 0x75, 0xB5,
0x77, 0xB7, 0xB6, 0x76, 0x72, 0xB2, 0xB3, 0x73, 0xB1, 0x71, 0x70, 0xB0, 0x50, 0x90, 0x91,
0x51, 0x93, 0x53, 0x52, 0x92, 0x96, 0x56, 0x57, 0x97, 0x55, 0x95, 0x94, 0x54, 0x9C, 0x5C,
0x5D, 0x9D, 0x5F, 0x9F, 0x9E, 0x5E, 0x5A, 0x9A, 0x9B, 0x5B, 0x99, 0x59, 0x58, 0x98, 0x88,
0x48, 0x49, 0x89, 0x4B, 0x8B, 0x8A, 0x4A, 0x4E, 0x8E, 0x8F, 0x4F, 0x8D, 0x4D, 0x4C, 0x8C,
0x44, 0x84, 0x85, 0x45, 0x87, 0x47, 0x46, 0x86, 0x82, 0x42, 0x43, 0x83, 0x41, 0x81, 0x80,
0x40
};
}
}
Не слабый такой код, есть вариант без таблицы, но более медленный (необходима побитовая обработка данных), в любом случае способный вынести мозг как программисту, так и микроконтроллеру. Не во всякий микроконтроллер алгоритм с таблицей влезет вообще.
Давайте разберем алгоритмы, которые вообще могут подтвердить целостность данных невысокой ценой.
Бит четности (1-битная контрольная сумма)
На первом месте простой бит четности. При необходимости формируется аппаратно, принцип простейший, и подробно расписан в википедии. Недостаток только один, пропускает двойные ошибки (и вообще четное число ошибок), когда четность всех бит не меняется. Можно использовать для сбора статистики о наличии ошибок в потоке передаваемых данных, но целостность данных не гарантирует, хотя и снижает вероятность пропущенной ошибки на 50% (зависит, конечно, от типа помех на линии, в данном случае подразумевается что число четных и нечетных сбоев равновероятно).
Для включения бита четности, часто и код никакой не нужен, просто указываем что UART должен задействовать бит четности. Типично, просто указываем:
включение бита четности на микроконтроллере
void setup(){
Serial.begin(9600,SERIAL_8N1); // по умолчанию, бит четности выключен;
Serial1.begin(38400,SERIAL_8E1); // бит четности включен
Serial.println("Hello Computer");
Serial1.println("Hello Serial 1");
}
Часто разработчики забывают даже, что UART имеет на борту возможность проверки бита четности. Кроме целостности передаваемых данных, это позволяет избежать устойчивого срыва синхронизации (например при передаче данных по радиоканалу), когда полезные данные могу случайно имитировать старт и стоп биты, а вместо данных на выходе буфера старт и стоп биты в случайном порядке.
8-битная контрольная сумма
Если контроля четности мало (а этого обычно мало), добавляется дополнительная контрольная сумма. Рассчитать контрольную сумму, можно как сумму ранее переданных байт, просто и логично
Естественно биты переполнения не учитываем, результат укладываем в выделенные под контрольную сумму 8 бит. Можно пропустить ошибку, если при случайном сбое один байт увеличится на некоторое значение, а другой байт уменьшится на то же значение. Контрольная сумма не изменится. Проведем эксперимент по передаче данных. Исходные данные такие:
- Блок данных 8 байт.
- Заполненность псевдослучайными данными Random($FF+1)
- Случайным образом меняем 1 бит в блоке данных операцией XOR со специально подготовленным байтом, у которого один единичный бит на случайной позиции.
- Повторяем предыдущий пункт 10 раз, при этом может получится от 0 до 10 сбойных бит (2 ошибки могут накладываться друг на друга восстанавливая данные), вариант с 0 сбойных бит игнорируем в дальнейшем как бесполезный для нас.
Передаем виртуальную телеграмму N раз. Идеальная контрольная сумма выявит ошибку по количеству доступной ей информации о сообщении, больше информации, выше вероятность выявления сбойной телеграммы. Вероятность пропустить ошибку, для 1 бита контрольной суммы:
.
Для 8 бит:
,
на 256 отправленных телеграмм с ошибкой, одна пройдет проверку контрольной суммы. Смотрим статистику от виртуальной передачи данных, с помощью простой тестовой программы:
Статистика
1: 144 (тут и далее — вероятность прохождения ошибки)
1: 143
1: 144
1: 145
1: 144
1: 142
1: 143
1: 143
1: 142
1: 140
Общее число ошибок 69892 из 10 млн. итераций, или 1: 143.078
Или условный КПД=55%, от возможностей «идеальной» контрольной суммы. Такова плата за простоту алгоритма и скорость обработки данных. В целом, для многих применений, алгоритм работоспособен. Используется одна операция сложения и одна переменная 8-битовая. Нет возможности не корректной реализации. Поэтому алгоритм и применяется в контроллерах ADAMS, ICP, в составе протокола DCON (там дополнительно может быть включен бит четности, символы только ASCI, что так же способствует повышению надежности передачи данных и итоговая надежность несколько выше, так как часть ошибок выявляется по другим, дополнительным признакам, не связанных с контрольной суммой).
Не смотря на вероятность прохождения ошибки 1:143, вероятность обнаружения ошибки лучше, чем 1:256 невозможна теоретически. Потери в качестве работы есть, но не всегда это существенно. Если нужна надежность выше, нужно использовать контрольную сумму с большим числом бит. Или, иначе говоря, простая контрольная сумма, недостаточно эффективно использует примерно 0.75 бита из 8 имеющихся бит информации в контрольной сумме.
Для сравнения применим, вместо суммы, побитовое сложение XOR. Стало существенно хуже, вероятность обнаружения ошибки 1:67 или 26% от теоретического предела. Упрощенно, это можно объяснить тем, что XOR меняет при возникновении ошибке еще меньше бит в контрольной сумме, ниже отклик на единичный битовый сбой, и повторной ошибке более вероятно вернуть контрольную сумму в исходное состояние.
Так же можно утверждать, что контрольная сумма по XOR представляет из себя 8 независимых контрольных сумм из 1 бита. Вероятность того, что ошибка придется на один из 8 бит равна 1:8, вероятность двойного сбоя 1:64, что мы и наблюдаем, теоретическая величина совпала с экспериментальными данными.
Нам же нужен такой алгоритм, чтобы заменял при единичной ошибке максимальное количество бит в контрольной сумме. Но мы, в общей сложности, ограниченны сложностью алгоритма, и ресурсами в нашем распоряжении. Не во всех микроконтроллерах есть аппаратный блок расчета CRC. Но, практически везде, есть блок умножения. Рассчитаем контрольную сумму как произведение последовательности байт, на некоторую «магическую» константу:
CRC=CRC + byte*211
Константа должна быть простой, и быть достаточно большой, для изменения большего числа бит после каждой операции, 211 вполне подходит, проверяем:
Статистика
1: 185
1: 186
1: 185
1: 185
1: 193
1: 188
1: 187
1: 194
1: 190
1: 200
Всего 72% от теоретического предела, небольшое улучшение перед простой суммой. Алгоритм в таком виде не имеет смысла. В данном случае теряется важная информация из отбрасываемых старших 8..16 бит, а их необходимо учитывать. Проще всего, смешать функцией XOR с младшими битами 1..8. Приходим к еще более интенсивной модификации контрольной суммы, желательно с минимальным затратами ресурсов. Добавляем фокус из криптографических алгоритмов
CRC=CRC + byte*211
CRC= CRC XOR (CRC SHR 8); // "миксер" битовый, далее его применяем везде
CRC=CRC AND $FF; //или просто возвращаем результат как 8, а не 16 бит
- Промежуточная CRC для первого действия 16-битная (после вычислений обрезается до 8 бит) и в дальнейшем работаем как с 8-битной, если у нас 8-битный микроконтроллер это ускорит обработку данных.
- Возвращаем старшие биты и перемешиваем с младшими.
Проверяем:
Статистика
1: 237
1: 234
1: 241
1: 234
1: 227
1: 238
1: 235
1: 233
1: 231
1: 236
Результат 91% от теоретического предела. Вполне годится для применения.
Если в микроконтроллере нет блока умножения, можно имитировать умножение операций сложения, смещения и XOR. Суть процесса такая же, модифицированный ошибкой бит, равномерно «распределяется» по остальным битам контрольной суммы.
CRC := (CRC shl 3) + byte;
CRC := (CRC shl 3) + byte;
CRC:=(CRC XOR (CRC SHR 8)) ; // как и в предыдущем алгоритме
Результат:
Статистика
1: 255
1: 257
1: 255
1: 255
1: 254
1: 255
1: 250
1: 254
1: 256
1: 254
На удивление хороший результат. Среднее значение 254,5 или 99% от теоретического предела, операций немного больше, но все они простые и не используется умножение.
Если для внутреннего хранения промежуточных значений контрольной суммы отдать 16 бит переменную (но передавать по линии связи будем только младшие 8 бит), что не проблема даже для самого слабого микроконтроллера, получим некоторое улучшение работы алгоритма. В целом экономить 8 бит нет особого смысла, и 8-битовая промежуточная переменная использовалась ранее просто для упрощения понимания работы алгоритма.
Статистика
1: 260
1: 250
1: 252
1: 258
1: 261
1: 255
1: 254
1: 261
1: 264
1: 262
Что соответствует 100.6% от теоретического предела, вполне хороший результат для такого простого алгоритма из одной строчки:
CRC:=CRC + byte*44111; // все переменные 16-битные
Используется полноценное 16-битное умножение. Опять же не обошлось без магического числа 44111 (выбрано из общих соображений без перебора всего подмножества чисел). Более точно, константу имеет смысл подбирать, только определившись с предполагаемым типом ошибок в линии передачи данных.
Столь высокий результат объясняется тем, что 2 цикла умножения подряд, полностью перемешивают биты, что нам и требовалось. Исключением, похоже, является последний байт телеграммы, особенно его старшие биты, они не полностью замешиваются в контрольную сумму, но и вероятность того, что ошибка придется на них невелика, примерно 4%. Эта особенность практически ни как не проявляется статистически, по крайней мере на моем наборе тестовых данных и ошибке ограниченной 10 сбойными битами. Для исключения этой особенности можно делать N+1 итераций, добавив виртуальный байт в дополнение к имеющимся в тестовом блоке данных (но это усложнение алгоритма).
Вариант без умножения с аналогичным результатом. Переменная CRC 16-битная, данные 8-битные, результат работы алгоритма — младшие 8 бит найденной контрольной суммы:
CRC := (CRC shl 2) + CRC + byte;
CRC := (CRC shl 2) + CRC + byte;
CRC:=(CRC XOR (CRC SHR 8));
Результат 100.6% от теоретического предела.
Вариант без умножения более простой, оставлен самый минимум функций, всего 3 математических операции:
CRC:=byte + CRC;
CRC:=CRC xor (CRC shr 2);
Результат 86% от теоретического предела.
В этом случае потери старших бит нет, они возвращаются в младшую часть переменной через функцию XOR (битовый миксер).
Небольшое улучшение в некоторых случаях дает так же:
- Двойной проход по обрабатываемым данным. Но ценой усложнения алгоритма (внешний цикл нужно указать), ценой удвоения времени обработки данных.
- Обработка дополнительного, виртуального байта в конце обрабатываемых данных, усложнения алгоритма и времени работы алгоритма практически нет.
- Использование переменной для хранения контрольной суммы большей по разрядности, чем итоговая контрольная сумма и перемешивание младших бит со старшими.
Результат работы рассмотренных алгоритмов, от простых и слабых, к сложным и качественным:
16-битная контрольная сумма
Далее, предположим что нам мало 8 бит для формирования контрольной суммы.
Следующий вариант 16 бит, и теоретическая вероятность ошибки переданных данных 1:65536, что намного лучше. Надежность растет по экспоненте. Но, как побочный эффект, растет количество вспомогательных данных, на примере нашей телеграммы, к 8 байтам полезной информации добавляется 2 байта контрольной суммы.
Простые алгоритмы суммы и XOR, применительно к 16-битной и последующим CRC не рассматриваем вообще, они практически не улучают качество работы, по сравнению с 8-битным вариантов.
Модифицируем алгоритм для обработки контрольной суммы разрядностью 16 бит, надо отметить, что тут так же есть магическое число 8 и 44111, значительное и необоснованное их изменение ухудшает работу алгоритма в разы.
CRC:=CRC + byte16*44111; //все данные 16-битные
CRC:=CRC XOR (CRC SHR 8);
Результат:
Статистика
1: 43478
1: 76923
1: 83333
1: 50000
1: 83333
1: 100000
1: 90909
1: 47619
1: 50000
1: 90909
Что соответствует 109% от теоретического предела. Присутствует ошибка измерений, но это простительно для 10 млн. итераций. Так же сказывается алгоритм создания, и вообще тип ошибок. Для более точного анализа, в любом случае нужно подстраивать условия под ошибки в конкретной линии передачи данных.
Дополнительно отмечу, что можно использовать 32-битные промежуточные переменные для накопления результата, а итоговую контрольную сумму использовать как младшие 16 бит. Во многих случаях, при любой разрядности контрольной суммы, так несколько улучшается качество работы алгоритма.
32-битная контрольная сумма
Перейдем к варианту 32-битной контрольной суммы. Появляется проблема со временем отводимым для анализа статистических данных, так как число переданных телеграмм уже сравнимо с 2^32. Алгоритм такой же, магические числа меняются в сторону увеличения
CRC:=CRC+byte32*$990C9AB5;
CRC:=CRC XOR (CRC SHR 16);
За 10 млн. итераций ошибка не обнаружена. Чтобы ускорить сбор статистики обрезал CRC до 24 бит:
CRC = CRC AND $FFFFFF;
Результат, из 10 млн. итераций ошибка обнаружена 3 раза
Статистика
1: 1000000
1: no
1: no
1: no
1: 1000000
1: no
1: 1000000
1: no
1: no
1: no
Вполне хороший результат и в целом близок к теоретическому пределу для 24 бит контрольной суммы (1:16777216). Тут надо отметить что функция контроля целостности данных равномерно распределена по всем битам CRC, и вполне возможно их отбрасывание с любой стороны, если есть ограничение на размер передаваемой CRC.
Для полноценных 32 бит, достаточно долго ждать результата, ошибок просто нет, за приемлемое время ожидания.
Вариант без умножения:
CRC := (CRC shl 5) + CRC + byte;
CRC := (CRC shl 5) + CRC;
CRC:=CRC xor (CRC shr 16);
Сбоя для полноценной контрольной суммы дождаться не получилось. Контрольная сумма урезанная до 24 бит показывает примерно такие же результаты, 8 ошибок на 100 млн. итераций. Промежуточная переменная CRC 64-битная.
64-битная контрольная сумма
Ну и напоследок 64-битная контрольная сумма, максимальная контрольная сумма, которая имеет смысл при передачи данных на нижнем уровне:
CRC:=CRC+byte64*$5FB7D03C81AE5243;
CRC:=CRC XOR (CRC SHR 8); // магическое число 1..20
Дождаться ошибки передачи данных, до конца существования вселенной, наверное не получится 
Метод аналогичный тому, какой применили для CRC32 показал аналогичные результаты. Больше бит оставляем, выше надежность в полном соответствии с теоретическим пределом. Проверял на младших 20 и 24 битах, этого кажется вполне достаточным, для оценки качества работы алгоритма.
Так же можно применить для 128-битных чисел (и еще больших), главное подобрать корректно 128-битные магические константы. Но это уже явно не для микроконтроллеров, такие числа и компилятор не поддерживает.
Комментарии
В целом метод умножения похож на генерацию псевдослучайной последовательности, только с учетом полезных данных участвующих в процессе.
Рекомендую к использованию в микроконтроллерах, или для проверки целостности любых переданных данных. Вполне рабочий метод, уже как есть, не смотря на простоту алгоритма.
Мой проект по исследованию CRC на гитхаб.
Далее интересно было бы оптимизировать алгоритм на более реальных данных (не псевдослучайные числа по стандартному алгоритму), подобрать более подходящие магические числа под ряд задач и начальных условий, думаю можно еще выиграть доли процента по качеству работы алгоритма. Оптимизировать алгоритм по скорости, читаемости кода (простоте алгоритма), качеству работы. В идеале получить и протестировать образцы кода для всех типов микроконтроллеров, для этого как-раз и нужны примеры с использованием умножения 8, 16, 32 битных данных, и без умножения вообще.
-
Задачка.
1. полное отсутствие ошибок при передаче инфы в пакете(ах) низкоскоростного канала связи (30-200 кб/c);
2. алгоритмы и полиномы восстановления битовых искажений не интересуют;
3. математики и криптоаналитики, судя по гугл-анализу говорят — CRC32 фигня.
Для 100%контроля полной целостности пакетов не годятся, есть реальная вероятность такого искажения бит-потока, пакета, когда CRC32 даст НОРМУ! А это НЕДОПУСТИМО!4. решение — пакет передается всегда равными блоками, никакой CRC не использовать, он просто шифруется, допустим AES-256 на передаче, ключ известен на приемной и передающей стороне. Сбой=отсутствие дешифрации пакета, для этого внутри пакета, помимо данных закладываем опознавательную сигнатуру, ну и некий сетевой номер, пусть это некий аналог IP.
Совсем неясно, не занаю, как доказать (математически ну очень желательно) невозможность прохождения ложного (сбойного искаженного) пакета на приемной стороне?
Вот про то, как невозможно, проблемно, сложно подобрать ключ, вероятность этого дела к разным криптоалгоритмам читал, находил, а как Вам задачка, так сказать с другой стороны?
Аналогов не видел. Может ссылку дадите или разрулите сходу, что данное решение верно? -
737061
New Member
- Публикаций:
-
0
- Регистрация:
- 3 авг 2007
- Сообщения:
- 74
VaStaNi
Я не совсем вкурил в задачу, но чебы не использовать какой-нибудь «сильный» хэш для каждого пакета, и соответственно вероятность «ошибки» будет настолько низка по определению этого алгоритма, что можно считать ее равно 0. -
а чем AES-256 не сильный хеш???
допустим у меня 32 байта блок, в нем 24 байта DATA, а отстальное, добавочки, что говорил.
Пропускаем через AES-256, далее «выплюнул» в канал.
КАК ДОКАЗАТь, что приемник НИКОГДА не подхватит ЛОЖЬ?
НУ пусть для злобы дня и темы ,перед глазами Япония и ее АЭС управление представится
Не моделировать годами в подхвате сбоя!? А как вероятность показать?
ЗЫ
тут про AES так пишутhttp://diskcryptor.net/wiki/CryptoUsageRisks-
Поэтому стойким считается тот шифр, для которого пока что не придумали практичного метода взлома. Однако если такого метода ещё не придумали, то это не значит что его не придумают никогда, хотя применительно к хорошо изученным шифрам (AES, Twofish, Serpent) вероятность взлома в ближайшие 10 лет пренебрежительно мала.
-
-
737061
New Member
- Публикаций:
-
0
- Регистрация:
- 3 авг 2007
- Сообщения:
- 74
VaStaNi
ну смотри. надо просто посмотреть какова вероятность что при сбое биты изменятся так что хэш получится правильный. Я тебе сразу говорю что вероятность -> 0. Как доказывать мат корректно я не помню, но думаю надо рассмотреть условные вероятности для битов те P(h(1)=x1,…,h(n)=xn | d(z)=L) h хэш d данные, те мы смотрим вероятность что хэш получится правильный для измененных данных (x1,x2,..,xn) при условии что на z позиции произошел сбой, но я еще раз повторяю она стремится к 0, просто следует из «сильности» хэша. Возможно пишу бред, криптографией не когда не занимался делаю прикидки на основе тер вера. -
737061
New Member
- Публикаций:
-
0
- Регистрация:
- 3 авг 2007
- Сообщения:
- 74
А вот насчет никогда ответ простой НИКАК. Просто вероятность будет стремится к 0, на самом деле этого достаточно.
-
Да и я никогда не занимался и тем более настолько математически не покажу…
Ну а показать выкладки хотелось бы, дабы сторонний суперматематический ум там некий, проверочные организации там всякие приняли однозначный вывод да стремится к нулю и на 100000…. лучше чем … … … и CRC32, который вот тут вот …., а ЭТО ДАННОЕ РЕШЕНИЕ — достойная модернизация ….
Ну и самому спать спокойно, тоже нужно, зачем лишнее на себя брать -
artkar
New Member
- Публикаций:
-
0
- Регистрация:
- 17 авг 2005
- Сообщения:
- 400
- Адрес:
- Russia
А што это такое?
Во! Сила 737061
-
OLS
New Member
- Публикаций:
-
0
- Регистрация:
- 8 янв 2005
- Сообщения:
- 322
- Адрес:
- Russia
О чем же всё таки вопрос ?
Сколько бит необходимо для гарантии незначимости вероятности ошибки ?
Возьмите суммарную пропускную способность Ваших каналов (например, 16 х 200 кбит/с = 3.2 Мбит/с).
Выберите период, на который Вы сделаете прогноз (например, 5 лет) — на бесконечность Вам никогда не дадут, т.к. есть экспоненциальное
увеличение мощностей и пропускных способностей — даже документы по стойкости шифров рассчитываются на определенный весьма небольшой период.
Рассчитайте, сколько пакетов по 32 байта будет передано, если использовать этот канал этот период времени со 100% загрузкой — (3.200.000/8/32*3600*24*365*5)=2^41 штук.
Задайтесь, приемлемой вероятностью события — например 0,001 — т.е. «это вероятность того, что за 5 лет в используемых каналах связи будет хотя бы однажды не обнаружено повреждение переданных данных».
И получите : 41 бит + 10 бит = 51 бит контрольной суммы необходимы Вам в каждом 32-байтном пакете для решения Вашей задачи.или
Может ли внутри контейнера, защищенного блочным шифром, использоваться обычная CRC для контроля целостности (без угроз подделки CRC извне) ?
Я считаю, что может, если у Вас есть ограничения по вычислительным мощностям и Вы не можете позволить по-настоящему криптостойкую сумму. Но если ключ шифрования фиксированный, то серьезно подумайте о методе создания цепочек (chaining modes), т.к. на мой взгляд OFB или CFB здесь будут не очень удачным решением. CBC — наверное, да, а лучше всего сразу искать цепочки со встроенным подтверждением целостности — таких уже разработано за последние годы много.
А если содержимое пакетов однотипно, то защищайтесь еще и от replay attack, иначе Ваши пакеты не дешифруя могут «подкинуть» в канал через определенное нужное злоумышленнику время повторно.
-
ближе второе. Сейчас попытаюсь изложить и сформулировать еще раз
ну вот тут вижу как бы что это лишнее(в смысле CRC внутри, это же доп.затраты? А эффект?), хотя если это совет, как грамотного криптоаналитика, то прислушаюсь…
можно сказать и ограничения есть, т.к. вторая сторона пусть управляющие контроллеры АСУТП, пусть на AVR контроллерах, хотя и на других можно. Есть уже (нашел) сорцы ассемблерные AES на них в реализации! Режимы там всякие CFB, OFB пока смутно понимаю, вкуривать пытаюсь…
Надеюсь помогут вот тут. Ну хоть ткнуть, конктерно поняв мою задачу(ниже).
Типа тебе вот типа CFB надо, ключ не менее… будет толк и точка.где то толковое почитать есть? Сориенироваться не могу, что мне лучше в них, какой вот?
в AES это достижимо? Опять же сорцы есть, хочется не заморачиваться. Кто такие, где читать если нет в нем этого?
ну про «подкинуть», как бы не ставится задачка защищаться
Хотя если учитывать всякое там перемешивание бит в крипто, то можно в пакетик данных счетчик времени, даты текущий ставить или некое время жизни пакета, как в TCP… тогда это устраняется, да? Я в нужном русле решаю проблемс этот?
ИТАК.
1. Пусть необходимо максимально достоверно передать блок данных конкретному устройству в некой низкоскоростной сети. Таких устройств пусть их 30 шт. Полудуплекс. Блок данных унифицирован, т.е. известен его формат внутри, длина постоянна, пусть это 32 или 64 или 128 байт, пока решаю, как дробить на фрагменты, так сказать элементарных достоверных передач! Есть там и сетевой номер и сигнатура (будет ли верно это?) по которой собственно + номер этот сетевой — устройство понимает решение(!), что пакет дешифрирован ВЕРНО и ДАННЫЕ — это его данные! Тогда принимаем данные за абсолютную истину и ВЫПОЛНЯЕМ свою функцию по ним!
Ни чужое(другого устройства), ни искаженное типа молниями, облучениями, ни магнитными бурями ни чем другим, не должно быть принято к исполнению!2. Пусть выбрано, также, что блоки эти шифруются/дешифруются AES-256 с известным ключём по всем сетевым точкам (устройствам, включая хост или комп.)
Понятно, что идеального в нашем несовершенном мире ничего нет, но!
Вопрос тут в максимально достижимости устойчивости данных (ну и системы вцелом, естественно) ПОСРЕДСТВОМ КРИПТОалгоритмики, как более совершенного средства защиты целостности информации и распознания фальши(сбоев)!
Понимаю так, что чем круче крипто, тем более «чувствуется» искажение любого бита в любом месте пакета в данном случае, а значит ЛОЖЬ(сбой) не пройдет, или максимально НЕ пройдет. Понятно и то, что чем лучше базовые принципы — тем лучше итог, но как, насколько не могу оценить, показать, доказать… Чувствовать мало.
Может и так быть, думаю, что длина пакета влияет на результат и длина ключа(это понятно в принципе) и неоднородность данных на выявление ложного случая(сбоя)…
С удовольствием выслушаю взвешенные под задачу советы, замечания, мои заблуждения быть может. -
artkar
New Member
- Публикаций:
-
0
- Регистрация:
- 17 авг 2005
- Сообщения:
- 400
- Адрес:
- Russia
Если у тебя блок из 24 байтов, то тагда количество комбинаций равно 2^(8*24), для ЦРЦ 32 количество элементов в списке коллизий, при условии канешн што твой пакет (24 байта) не меняет размер, равно 160 — это значит в этом блоке возможно столько комбинаций которые дадут одинаковый ЦРЦ, следовательно вероятность пропущения ошибки равна 160/2^(8*24) это колосальное число у меня даже не влазит в калькулятор 2.5489470578119236432462086364286e-56, Но если тебя и эта вероятность не устраивает тагда можно взять для ЦРЦ другой порождающий полином G(x), равный допустим 24 байтам, тогда теоритически вероятность равна нулю, но! нужно учесть что и полином может так измениться что совпадет битый ЦРЦ с битыми данными, но вероятность просто фантастически маленькая, но всё же не ноль!
-
вот этот математически доказуемый факт очень не нравится. Потенциально. При том, что на тех же аппаратно-программных средствах, можно сделать и лучше, и устойчивее, и жестче. Т.к. доверять будем лишь одному — факту успешной дешифрации принятого пакета.
Вот еще интересный для себя под задачку алгорим присмотрел — ANUBIS. Вики говоритТут опять пишут ТОЛЬКО про уязвимость со стороны ключа. Непонятно вот почему про сами данные ни словца. Либо с данными (мутации всякие, перестановки, комбинаторика) все еще более серьезно обстоит и это даже НЕ обсуждается и НЕ доказывается в плане безопасности(и это типа только мне не понятно, а остальным все и так ясно, как Божий день), либо так сложно, что нет смысла этим заниматься… годы нужны для этого?
Ну вот типа инволюции обратимы, написано. Это для аппаратуры типа просто для реализации, я так понял. А как это на устойчивости сказывается неясно. Лучше это скажем AESа или нет? Или это «на пальцах» не покажешь, суровая математика нужна…
Может тут все банально получается. И если для ключа(со стороны ключа) нужно 2^127 комбинаций, допустим, то «автоматически» это означает, что для данных это значение НЕ МЕНЬШЕ? Или не факт????? -
asmlamo
Well-Known Member
- Публикаций:
-
0
- Регистрация:
- 18 май 2004
- Сообщения:
- 1.720
>1. полное отсутствие ошибок при передаче инфы в пакете(ах) низкоскоростного канала связи
Любая нормальная хеш функция.
Если задача именно о ошибках а не о злонамеренном вмешательстве.
-
VaStaNi
В сообщении #9 OLS вроде бы достаточно ясно изложил суть, но вот анекдот по данной теме:
Какова вероятность встретить на улице динозавра?
1/2 — либо встречу, либо нет.
В общем тебе нужно рассуждать точно так же, если от блока данных вычислить хорошую хеш функцию длиной n бит, то все её значения сделует считать равновероятными, а вероятность что у искажённого сообщения окажется такой же хеш — 1/2^n. Если количество переданных сообщений N существенно меньше 2^n, то вероятность незамеченной ошибки можно считать равной N/2^n. -
Black_mirror, спасибо за рассуждения
ну вот пытаюсь определиться с понятием «хорошая» следующим образом.
Получается у меня, обобщив посты следующее:
1. чем меньше блок и чем больше ключ тем лучше
2. длина пакета передачи не может быть меньше блока шифрования и очень хорошо если кратна им.
Дополнение данных дописыванием байт до кратности блоку лишь улучшает достижение цели, особенно если дописывание имеет динамику и информационный, справочный смысл функционирования (текущее время передачи пакета, например)
3. по рекомендациям OLS, лучше использовать CBC mode, но при длине пакета = 1-2 блока шифрования его преимущества теряются, глядя сюда
4. при равенстве степеней полиномов в AES и Anubis, Anubis видится более выгодным под задачу, т.к. можно заюзать по п.1 ключ в 320 бит при блоке в 128 бит, возможно при этом будет плюсом, что выбор в пользу tweak для чипов малой мощности даст плюс, как упрощение в реализации программного кода…
Если есть существенные заблуждения, неправильная оценка и ошибки, просьба указать.
PS.
Всмотревшись в блок-схемы по CBC «вижу» сетевой номер и пр. ID устройства типа серийный номер изделия… в таком чудесном блочке как: «вектор инициализации». Если это будет работать, тогда только CBC! Крутой битовый замес, а-ля «белый шум»…
Вижу это, как МегаФичу при решении задачи… несладко придется хосту однако, но все для победы! -
OLS
New Member
- Публикаций:
-
0
- Регистрация:
- 8 янв 2005
- Сообщения:
- 322
- Адрес:
- Russia
Если у Вас есть проблемы с вычислительной сложностью, возьмите
в качестве блочного шифра — ГОСТ 28147-89
в качестве контрольной суммы любые 8 байт от MD2.В качестве IV в схеме CBC лучше подавать не сырые данные (время, номер пакета, сетевой номер, ID и т.п.), а уже прошедшие один цикл шифрования, чтобы убрать любые корреляции. Учтите, что IV приемная сторона должна иметь возможность узнать/вычислить, т.е. все ее части должны быть несекретными и каким-то образом передаваться на приемную сторону.
-
Винокуров пишет в сравнительной статье, что и ГОСТ и AES почти равны по всем статьям включая 8 битки для выполнения алгоритма… Конечный выбор видимо будет судя по сложности воплощения в жизнь в железе.
это типа MAC? Или это с «другой песни»? ) Мне уже от аббревиатур этих в глазах рябит и череп сносит, начитался этой пурги…)))
Или тут должен быть иной алгоритм (совсем не «родной») для первичного, так сказать преобразования открытых известных значений типа ID для получение этого вектора инициализации?
В виках: -
OLS
New Member
- Публикаций:
-
0
- Регистрация:
- 8 янв 2005
- Сообщения:
- 322
- Адрес:
- Russia
Я предлагал просто пройтись один раз тем же самым криптоалгоритмом тем же самым ключом по открытым данным, которые Вы планируете использовать в качестве IV, для того, чтобы убрать возможную явную корреляцию между битами IV (ведь с схеме CBC он (IV) накладывается на первый блок обычным XOR-ом).
-
Вернулся к расчету вероятности. Хотябы ориентировочный, оценочный расчет, опираясь на пост #14 вижу так.
— пусть, например, битовый объем данных = ключу = хешу = 128 бит
— вероятность НЕОБНАРУЖЕННОЙ ошибки НЕ белее чем 128 / 2^128 = 3,76 E-37, что практически ноль.
Учитывая, что в процессе очень ответственных управленческих задач АСУ ТП хост, как правило, не ограничивается одним управляющим пакетом(приказ выполнить управление, регулирование), а требует замыкающего ответного квитирования от подчиненного(как ответ «ЕСТЬ мой генерал!»), то в итоге можно считать цель достигнутой. Т.е. 100% гарантия построения надежной системы идеологически достигнута, сабж можно считать исчерпаным.

|