Вероятность ошибки второго рода формула - Исправление ошибок и поиск оптимальных решений проблем

Понятие статистической гипотезы. Общая постановка задачи проверки гипотез.

Проверка
статистических гипотез тесно связана
с теорией оценивания параметров. В
естествознании, технике экономике для
вычисления того или иного случайного
факта часто прибегают к высказыванию
гипотез, которые можно проверить
статистически (то есть, опираясь на
результаты наблюдений в случайной
выборке). Под статистическими
подразумевают такие гипотезы,
которые относятся или к виду, или к
отдельным параметрам распределения
случайной величины. Например, статистической
является гипотеза о том, что распределение
производительности труда рабочих,
выполняющих одинаковую работу в
одинаковых условиях, имеет нормальный
закон распределения. Статистической
будет также гипотеза о том, что средние
размеры деталей, производимых на
однотипных, параллельно работающих
станках, не различаются.

Статистическая
гипотеза называется простой,
если она однозначно определяет
распределение случайной величины
,
в противном случае гипотеза называется
сложной.
Например, простой гипотезой является
предположение о том, что случайная
величина

распределена по нормальному закону с
математическим ожиданием, равным нулю,
и дисперсией равной единице. Если
высказывается предположение, что
случайная величина

имеет нормальное распределение с
дисперсией, равной единице, а математическое
ожидание – число из отрезка
,
то это сложная гипотеза. Другим примером
сложной гипотезы является предположение
о том, что непрерывная случайная величина

с вероятностью

принимает значение из интервала
,
в этом случае распределение случайной
величины

может быть любым из класса непрерывных
распределений.

Часто распределение
величины

известно, и по выборке наблюдений
необходимо проверить предположения о
значении параметров этого распределения.
Такие гипотезы называются параметрическими.

Проверяемая
гипотеза называется нулевой
и обозначается
.
Наряду с гипотезой

рассматривают одну из альтернативных
(конкурирующих) гипотез
.
Например, если проверяется гипотеза о
равенстве параметра

некоторому заданному значению
,
то есть
,
то в качестве альтернативной гипотезы
можно рассматривать одну из следующих
гипотез:
,
где

– заданное значение, причём
.
Выбор альтернативной
гипотезы определяется конкретной
формулировкой задачи.

Правило, по которому
принимается решение принять или отклонить
гипотезу
,
называется критерием
и обозначается
.
Так как решение принимается на основе
выборки наблюдений случайной величины
,
необходимо выбрать подходящую статистику,
называемую в этом случае статистикой

критерия
.
При проверке простой параметрической
гипотезы

в качестве статистики критерия выбирают
ту же статистику, что и для оценки
параметра
.

Проверка
статистической гипотезы основывается
на принципе, в соответствии с которым
маловероятные события считаются
невозможными, а события, имеющие большую
вероятность,– достоверными. Этот принцип
можно реализовать следующим образом.
Перед анализом выборки фиксируется
некоторая малая вероятность
,
называемая уровнем
значимости.
Пусть
–
множество значений статистики
,
а

– такое подмножество, что при условии
истинности гипотезы

вероятность попадания статистики

критерия в

равна
,
то есть
.

Обозначим

выборочное значение статистики
,
вычисленное по выборке наблюдений.
Критерий формулируется так: отклонить
гипотезу
,
если
;
принять гипотезу
,
если
.
Критерий, основанный на использовании
заранее заданного уровня значимости,
называется критерием
значимости.
Множество

всех значений статистики

критерия, при которых принимается
решение отклонить гипотезу
,
называется критической
областью;
область

называется областью
принятия гипотезы
.

Уровень значимости

определяет размер критической области
.
Положение критической области на
множестве значений статистики

зависит от формулировки альтернативной
гипотезы
.
Например, если проверяется гипотеза
,
причём альтернативная гипотеза
формулируется как:
,
то критическая область размещается на
правом (левом) «хвосте» распределения
статистики
,
то есть имеет вид неравенства
,
где
–
значения статистики
,
которые принимаются с вероятностями

и

при условии, что верна гипотеза
.
В этом случае критерий называется
односторонним
(соответственно – правосторонним
и левосторонним).
Если альтернативная гипотеза формулируется
как
,
то критическая область размещается на
обеих «хвостах» распределения статистики
,
то есть определяется совокупностью
неравенств

В этом случае
критерий называется двусторонним.

Расположение
критической области

для различных альтернативных гипотез
показано рисунках, приведённых выше,
где
–
плотность распределения статистики

критерия при условии, что верна гипотеза
,

–
область принятия гипотезы,
.

Проверку
параметрической статистической гипотезы
с помощью критерия значимости можно
разбить на этапы:

сформулировать
проверяемую ()
и альтернативную ()
гипотезы;
назначить уровень
значимости
;
выбрать статистику

критерия для проверки гипотезы
;
определить
выборочное распределение статистики

при условии, что верна гипотеза
;
в зависимости от
формулировки альтернативной гипотезы
определить критическую область

одним из неравенств

или совокупностью неравенств
;
получить выборку
наблюдений и вычислить выборочные
значения

статистики критерия;
принять статистическое
решение: если
,
то отклонить гипотезу

как не согласующуюся с результатами
наблюдений; если
,
то принять гипотезу
,
то есть считать, что гипотеза

не противоречит результатам наблюдений.^¹

ПРИМЕР 3.
По паспортным данным автомобильного
двигателя расход топлива на 100км пробега
составляет 10л. В результате изменения
конструкции двигателя ожидается, что
расход топлива уменьшится. Для проверки
проводятся испытания 25-и случайно
отобранных автомобилей с модернизированным
двигателем. Выборочное среднее расходов
топлива на 100км пробега по результатам
испытаний составило 9,3л. Предположим,
что выборка расходов топлива получена
из нормально распределённой генеральной
совокупности со средним^²

и дисперсией
.
Используя критерий значимости, проверить
гипотезу, утверждающую, что изменение
конструкции двигателя не повлияло на
расход топлива.

Решение.
Проверим гипотезу о среднем

нормально распределённой генеральной
совокупности. Проверку проведём по
этапам:

проверяемая
гипотеза
;
альтернативная гипотеза
;
уровень значимости
;
в качестве
статистики

критерия используем статистику
математического ожидания – выборочное
среднее
;
так как выборка
получена из нормально распределённой
генеральной совокупности, выборочное
среднее также имеет нормальное
распределение с дисперсией
.
При условии, что верна гипотеза
,
математическое ожидание этого
распределения равно 10. Нормированная
статистика

имеет нормальное распределение;
альтернативная
гипотеза

предполагает уменьшение расхода
топлива, следовательно, нужно использовать
односторонний критерий. Критическая
область определяется неравенством
.
По таблице (см. приложение) находим
;
выборочное значение
нормированной статистики критерия

;

статистическое
решение: так как выборочное значение
статистики критерия принадлежит
критической области, гипотеза

отклоняется. Следует считать, что
изменение конструкции двигателя привело
к уменьшению расхода топлива. Границу

критической области для исходной
статистики

критерия можно получить из соотношения
,
откуда
.
Таким образом, критическая область для
статистики

определяется неравенством
.

Решение,
принимаемое на основе критерия значимости,
может быть ошибочным.
Пусть выборочное значение статистики
критерия попадает в критическую область,
и гипотеза

отклоняется в соответствии с критерием.
Если, тем не менее, гипотеза

верна, то принимаемое решение неверно.
Ошибка, совершаемая при отклонении
правильной гипотезы
,
называется ошибкой
первого рода.
Вероятность ошибки первого рода равна
вероятности попадания статистики
критерия в критическую область при
условии, что верна гипотеза
,
то есть равна уровню значимости
:
.

Ошибка второго
рода происходит
тогда, когда гипотеза

принимается, но в действительности
верна гипотеза
.
Вероятность

ошибки второго рода вычисляется по
формуле:

ПРИМЕР 4.
В условиях примера 3 предположим, что
наряду с гипотезой

рассматривается альтернативная гипотеза
.
В качестве статистики критерия снова
возьмём выборочное среднее
.
Предположим, что критическая область
задана неравенством
.
Найти вероятность ошибок первого и
второго рода для критерия с такой
критической областью.

Решение.
Найдём вероятность ошибки первого рода.
Статистика

критерия при условии, что верна гипотеза
,
имеет нормальное распределение с
математическим ожиданием, равным 10, и
дисперсией, равной
.
используя таблицу (см. приложение), по
формуле

находим:

Это означает, что
принятый критерий классифицирует
примерно 8% автомобилей, имеющих расход
10л на 100км пробега, как автомобили,
имеющие меньший расход топлива.

При условии, что
верна гипотеза
,
статистика

имеет нормальное распределение с
математическим ожиданием, равным 9Б и
дисперсией, равной
.
Нетрудно в этом случае найти вероятность
ошибки второго рода, воспользовавшись
формулой
:

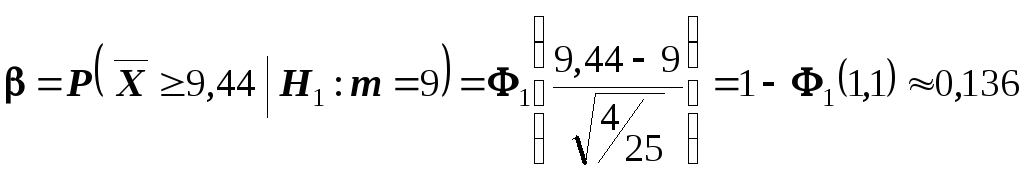
Следовательно, в
соответствии с принятым критерием 13,6%
автомобилей, имеющих расход топлива
9л на 100км пробега, классифицируются
как автомобили, имеющие расход топлива
10л.

Соседние файлы в папке Теор.вер. (лекции)

Источник

Статистические гипотезы

Определение статистической гипотезы. Нулевая и альтернативная, простая и сложная гипотезы. Ошибки первого и второго рода. Статистический критерий, наблюдаемое значение критерия. Критическая область. Область принятия нулевой гипотезы; критическая точка. Общая методика построения право-, лево- и двухсторонней критических областей

Понятие и определение статистической гипотезы

Проверка статистических гипотез тесно связана с теорией оценивания параметров. В естествознании, технике, экономике для выяснения того или иного случайного факта часто прибегают к высказыванию гипотез, которые можно проверить статистически, т. е. опираясь на результаты наблюдений в случайной выборке. Под статистическими подразумеваются такие гипотезы, которые относятся или к виду, или к отдельным параметрам распределения случайной величины. Например, статистической является гипотеза о том, что распределение производительности труда рабочих, выполняющих одинаковую работу в одинаковых условиях, имеет нормальный закон распределения. Статистической будет также гипотеза о том, что средние размеры деталей, производимые на однотипных, параллельно работающих станках, не различаются.

Статистическая гипотеза называется простой, если она однозначно определяет распределение случайной величины , в противном случае гипотеза называется сложной. Например, простой гипотезой является предположение о том, что случайная величина распределена по нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице. Если высказывается предположение, что случайная величина имеет нормальное распределение с дисперсией, равной единице, а математическое ожидание — число из отрезка [a;b] , то это сложная гипотеза. Другим примером сложной гипотезы является предположение о том, что непрерывная случайная величина с вероятностью 1slash 3 принимает значение из интервала (1;5) , в этом случае распределение случайной величины может быть любым из класса непрерывных распределений.

Часто распределение величины известно, и по выборке наблюдений необходимо проверить предположения о значении параметров этого распределения. Такие гипотезы называются параметрическими.

Проверяемая гипотеза называется нулевой и обозначается H_0 . Наряду с гипотезой H_0 рассматривают одну из альтернативных (конкурирующих) гипотез H_1 . Например, если проверяется гипотеза о равенстве параметра Theta некоторому заданному значению Theta_0 , то есть H_0colonTheta=Theta_0 , то в качестве альтернативной гипотезы можно рассмотреть одну из следующих гипотез: $H_1^{(1)}colonTheta>Theta_0;$ $H_1^{2}colonTheta<Theta_0;$ $H_1^{3}colonThetaneTheta_0;$ $H_1^{4}colonTheta=Theta_1,$ где Theta_1 — заданное значение, Theta_1neTheta_0 . Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.

Правило, по которому принимается решение принять или отклонить гипотезу H_0 , называется критерием . Так как решение принимается на основе выборки наблюдений случайной величины , необходимо выбрать подходящую статистику, называемую в этом случае статистикой критерия . При проверке простой параметрической гипотезы H_0colonTheta=Theta_0 в качестве статистики критерия выбирают ту же статистику, что и для оценки параметра Theta .

Проверка статистической гипотезы основывается на принципе, в соответствии с которым маловероятные события считаются невозможными, а события, имеющие большую вероятность, — достоверными; Этот принцип можно реализовать следующим образом. Перед анализом выборки фиксируется некоторая малая вероятность alpha , называемая уровнем значимости. Пусть — множество значений статистики , а $V_ksubseteq{V}$ — такое подмножество, что при условии истинности гипотезы H_0 вероятность попадания статистики критерия в V_k равна alpha , то есть $P{Zin{V_k/H_0}}=alpha$ .

Обозначим $z_text{v}$ выборочное значение статистики , вычисленное по выборке наблюдений. Критерий формулируется так: отклонить гипотезу H_0 , если $z_text{v}in{V_k}$ ; принять гипотезу H_0 , если $z_text{v}in{Vsetminus{V_k}}$ . Критерий, основанный на использовании заранее заданного уровня значимости, называют критерием значимости. Множество V_k всех значений статистики критерия , при которых принимается решение отклонить гипотезу H_0 , называется критической областью; область $Vsetminus{V_k}$ называется областью принятия гипотезы H_0 .

Уровень значимости alpha определяет размер критической области V_k . Положение критической области на множестве значений статистики зависит от формулировки альтернативной гипотезы H_1 . Например, если проверяется гипотеза H_0colonTheta=Theta_0 , а альтернативная гипотеза формулируется как H_1colonTheta>Theta_0~(Theta<Theta_0) , то критическая область размещается на правом (левом) «хвосте» распределения статистики , т. е. имеет вид неравенства $Z>z_{1-alpha}(Z<z_alpha)$ , где $z_{1-alpha},z_alpha$ — значения статистики , которые принимаются с вероятностями соответственно 1-alpha и alpha при условии, что верна гипотеза H_0 . В этом случае критерий называется односторонним (соответственно правосторонним и левосторонним). Если альтернативная гипотеза формулируется как H_1colonThetaneTheta_0 , то критическая область размещается на обоих «хвостах» распределения , то есть определяется совокупностью неравенств $Z<z_{alpha/2}$ и $Z>z_{1-alpha/2}$ в этом случае критерий называется двухсторонним.

Расположение критической области V_k для различных альтернативных гипотез показано на рис. 30, где f(z|H_0) — плотность распределения статистики критерия при условии, что верна гипотеза H_0 , $Vsetminus{V_k}$ — область принятия гипотезы, $P{Zin{Vsetminus{V_k}}}=1-alpha$ .

Критическая область и статистические гипотезы

Проверку параметрической статистической гипотезы с помощью критерия значимости можно разбить на этапы:

1) сформулировать проверяемую (H_0) и альтернативную (H_1) гипотезы;

2) назначить уровень значимости alpha ;

3) выбрать статистику критерия для проверки гипотезы H_0 ;

4) определить выборочное распределение статистики при условии, что верна гипотеза H_0 ;

5) в зависимости от формулировки альтернативной гипотезы определить критическую область V_k одним из неравенств $z>z_{1-alpha},$ Z<z_alpha или совокупностью неравенств $Z<z_{alpha/2}$ и $Z>z_{1-alpha/2}$ ;

6) получить выборку наблюдений и вычислить выборочные значения $z_text{v}$ статистики критерия;

7) принять статистическое решение: если $z_text{v}in{V_k}$ , то отклонить гипотезу H_0 как не согласующуюся с результатами наблюдений; если $z_text{v}in{Vsetminus{V_k}}$ , то принять гипотезу H_0 , т. е. считать, что гипотеза H_0 не противоречит результатам наблюдений.

Обычно при выполнении пп. 4-7 используют статистику с нормальным распределением, статистику Стьюдента, Фишера.

Пример 3. По паспортным данным автомобильного двигателя расход топлива на 100 км пробега составляет 10 л. В результате изменения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки проводятся испытания 25 случайно отобранных автомобилей с модернизированным двигателем, причем выборочное среднее расходов топлива на 100 км пробега по результатам испытаний составило 9,3 л. Предположим, что выборка расходов топлива получена из нормально распределенной генеральной совокупности со средним и дисперсией D=4 л². Используя критерий значимости, проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.

Решение. Проверим гипотезу о среднем нормально распределенной генеральной совокупности. Проверку проведем по этапам:

1) проверяемая гипотеза $H_0colon{m=10}$ ; альтернативная гипотеза $H_1colon{m<10}$ ;

2) уровень значимости alpha=0,!05 ;

3) в качестве статистики критерия используем статистику математического ожидания — выборочное среднее;

4) так как выборка получена из нормально распределенной генеральной совокупности, выборочное среднее также имеет нормальное распределение с дисперсией $frac{D}{n}=frac{4}{25}$ . При условии, что верна гипотеза H_0 , математическое ожидание этого распределения равно 10. Нормированная статистика $Z=frac{overline{X}-10}{sqrt{4/25}}$ имеет нормальное распределение;

5) альтернативная гипотеза $H_1colon{m<10}$ предполагает уменьшение расхода топлива, следовательно, нужно использовать односторонний критерий. Критическая область определяется неравенством $Z<z_{alpha}$ . По прил. 5 находим $z_{0,!05}=-z_{0,!95}=-1,!645$ ;

б) выборочное значение нормированной статистики критерия

$z_text{v}=frac{9,!3-10}{sqrt{4/25}}=-frac{0,!7}{0,!4}=-1,!75;$

7) статистическое решение: так как выборочное значение статистики критерия принадлежит критической области, гипотеза H_0 отклоняется: следует считать, что изменение конструкции двигателя привело к уменьшению расхода топлива. Границу $overline{x}_k$ критической области для исходной статистики критерия можно получить из соотношения $frac{overline{x}_k-10}{sqrt{4/25}}=-1,!645$ , откуда $overline{x}_k=9,!342$ , т. е. критическая область для статистики определяется неравенством X<9,!342 .

Ошибки первого и второго рода

Решение, принимаемое на основе критерия значимости, может быть ошибочным. Пусть выборочное значение статистики критерия попадает в критическую область, и гипотеза H_0 , отклоняется в соответствии с критерием. Если, тем не менее, гипотеза H_0 верна, то принимаемое решение неверно. Ошибка, совершаемая при отклонении правильной гипотезы if о, называется ошибкой первого рода. Вероятность ошибки первого рода равна вероятности попадания статистики критерия в критическую область при условии, что верна гипотеза H_0 , т. е. равна уровню значимости alpha:

$alpha=P{Zin{V_k/H_0}}.~~~~~~~~~~(11.1)$

Ошибка второго рода происходит тогда, когда гипотеза H_0 принимается, но в действительности верна гипотеза H_1 . Вероятность beta ошибки второго рода вычисляется по формуле

$beta=P{Zin{Vsetminus{V_k}/H_1}}.~~~~~~~~~~(11.2)$

Пример 4. В условиях примера 3 предположим, что наряду с гипотезой $H_0colon{m=10}$ л рассматривается альтернативная гипотеза $H_1colon{m=9}$ л. В качестве статистики критерия снова возьмем выборочное среднее overline{X} . Предположим, что критическая область задана неравенством overline{X}<9,!44 л. Найти вероятности ошибок первого и второго рода для критерия с такой критической областью.

Решение. Найдем вероятность ошибки первого рода. Статистика overline{X} критерия при условии, что верна гипотеза $H_0colon{m=10}$ л, имеет нормальное распределение с математическим ожиданием, равным 10, и дисперсией, равной sqrt{4/25} . Используя прил. 5, по формуле (11.1) находим

${alpha=P{overline{X}<9,!44/H_0colon{m=10}}=Phi_1!left(frac{9,!44-10}{sqrt{4/25}}right)=Phi_1(-1,!4)=1-Phi_1(1,!4)approx0,!08.}$

Это означает, что принятый критерий классифицирует примерно 8% автомобилей, имеющих расход 10 л на 100 км пробега, как автомобили, имеющие меньший расход топлива. При условии, что верна гипотеза $H_1colon{m=9}$ л, статистика overline{X} имеет нормальное распределение с математическим ожиданием, равным 9, и дисперсией, равной sqrt{4/25} . Вероятность ошибки второго рода найдем по формуле (11.2):

${beta=P{overline{X}geqslant9,!44/H_1colon{m=9}}=Phi_1!left(frac{9,!44-9}{sqrt{4/25}}right)1-Phi_1(1,!1)approx0,!136.}$

Следовательно, в соответствии с принятым критерием 13,6% автомобилей, имеющих расход топлива 9 л на 100 км пробега, классифицируются как автомобили, имеющие расход топлива 10 л.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Ошибки I и II рода при проверке гипотез, мощность

Общий обзор

Принятие неправильного решения

Мощность и связанные факторы

Проверка множественных гипотез

Общий обзор

Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.

Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.

Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.

Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:

отвергнуть нулевую гипотезу и принять альтернативную гипотезу
остаться в рамках нулевой гипотезы

Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).

Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.

Принятие неправильного решения

Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.

	Верная гипотеза
H₀	H₁
Результат применения критерия	H₀	H₀ верно принята	H₀ неверно принята (Ошибка второго рода)
H₁	H₀ неверно отвергнута (Ошибка первого рода)	H₀ верно отвергнута

Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.

Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.

Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.

Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.

Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.

В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.

К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.

Мощность и связанные факторы

Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).

Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.

Ряд факторов имеют прямое отношение к мощности критерия.

Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.

Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.

Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.

Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.

Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).

Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.

Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.

Проверка множественных гипотез

Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.

Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.

Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.

Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.

Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии

В начало

Содержание портала

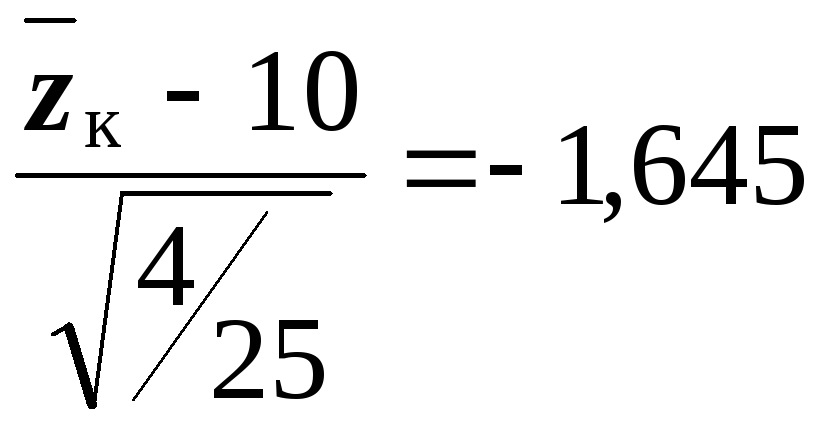Источник

Понятие статистической гипотезы. Общая постановка задачи проверки гипотез.

Статистические гипотезы

Понятие и определение статистической гипотезы

Ошибки первого и второго рода

Ошибки I и II рода при проверке гипотез, мощность

Общий обзор

Принятие неправильного решения

Мощность и связанные факторы

Проверка множественных гипотез