Помехоустойчивость
кода можно оценить вероятностью искажения
(ошибки) символов дискретных сообщений,
которые передаются кодовыми комбинациями.
Выше отмечалось, что по мере увеличения
избыточности кода его помехоустойчивость
улучшается. Однако реальная
помехоустойчивость кодов с избыточностью
зависит и от конкретного способа приема
(регистрации) кодовых комбинаций
(символов). Применяется поэлементный
прием и прием в целом кодовых комбинаций.
При поэлементном
приеме осуществляется регистрация
каждого из символов, составляющих
кодовую комбинацию. Последовательность
поочередно принятых сигналов образует
кодовую комбинацию, которая регистрируется
декодером и подается на устройство
преобразования кодовых комбинаций в
символы сообщения.
При приеме в целом
производится регистрация кодовых
сигналов. Под кодовым
сигналом
при этом
принимается вся последовательность
элементарных сигналов, составляющих
кодовую комбинацию.
Предположим, что
вероятность искажения отдельного
сигнала в кодовой комбинации равна
.
Будем полагать, что искажения различных
сигналов в кодовой комбинации статистически
независимые (что является справедливым
для каналов с постоянными параметрами
и флуктуационной помехой). Вероятность
того, что при поэлементном приеме
комбинация изn
элементов содержит равно
ошибок по
биномиальному закону, равна
,
(8.37)
где
— вероятность
искажения одного элемента кодовой
комбинации.
Вероятность
правильной регистрации кодовой комбинации
из n
элементов равна вероятности того, что
в ней содержится не более
ошибок

(8.38)
Число ошибок
и менее
исправляется кодом c
.
Тогда вероятность
ошибочного декодирования кодовой
комбинации

(8.39)
При оценке
эффективности помехоустойчивых кодов
используют так называемую эквивалентную
вероятность ошибки
,
определяемую по формуле
,
(8.40)
где
— количество информационных разрядов.
Эквивалентная
вероятность ошибки определяет вероятность
ошибки элементарного символа в двоичном
симметричном канале без памяти, в котором
система с примитивным кодированием
обеспечивает при передаче того же
количества информации ту же вероятность
ошибочного декодирования кодовой
комбинации, что и система с избыточным
кодом.
8.5. Блочные линейные коды
8.5.1. Математическое описание процессов кодирования и декодирования
Линейным блочным
— кодом называется множество
последовательностей длины
над
,
называемых кодовыми словами, которое
характеризуется тем, что сумма двух
кодовых слов является кодовым словом,
а произведение любого кодового слова
на элемент поля также является кодовым
словом.
Поле
,
состоящее из конечного числа элементовназываетсяконечным
полем
или полем
Галуа. Для
любого числа
,
являющегося степенью простого числа,
существует поле, насчитывающееэлементов. Поле не может содержать менее
двух элементов. Поле, включающее только
0 и 1, обозначим GF(2). Правила сложения и
умножения в поле с двумя элементами
представлены в табл. 8.11.
Таблица 8.11. Правила
сложения и умножения в поле с двумя
элементами
|
|
0 |
1 |
х |
0 |
1 |
|
|
0 |
0 |
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
1 |
0 |
1 |
Двоичные кодовые
комбинации, являющиеся упорядоченными
последовательностями из
элементов поля
,
рассматриваются в теории кодирования
как частный случай последовательностей
изn
элементов поля
.
Обычно
,
где— некоторое целое число. Если
,
линейные коды называются групповыми,
так как кодовые слова образуют
математическую структуру, называемую
группой. При формировании этого кода
линейной операцией является суммирование
по mod2.
При задании кода
обычно указывают, какие информационные
элементы принимают участие в формировании
каждого из k
проверочных разрядов. Например, для
кода с n=5,
m=3
и k=2
каждый проверочный разряд
определяется суммированием по модулю
2 по правилу
;
,
где
— информационные разряды. Комбинация
такого кода записывается в видеили в обратном
.
При задании кода можно указать все
разрешенные для этого кода комбинации.
Для линейных кодов способ задания можно
значительно упростить. Дляm
информационных разрядов число всех
разрешенных кодовых комбинаций будет
равняться
.
Пусть
(табл.8.12). Так как в каждой кодовой
комбинации такого кода три информационных
элемента, то число возможных комбинаций
кода будет равно.
Проверочные
элементы формируются как сумма по модулю
два информационных элементов, а именно:

(8.41)
Так для кодовой
комбинации №4
в соответствии с
правилами суммирования по модулю 2.
Для задания кода
нет необходимости записывать в таблицу
все используемые комбинации данного
кода. Код может быть задан матрицей,
которая содержит один из возможных
наборов линейно независимых строк. Под
линейно независимыми кодовыми комбинациями
понимают такие, сумма по модулю 2 которых
(в любом сочетании) не равняется нулю.
Выберем из всех кодовых комбинаций
только линейно независимые. Так для
приведенного выше кода линейно
независимыми будут группы комбинаций:
|
1. 1 0 0 1 0 2. 0 1 0 1 1 3. |
1. 1 0 0 1 0 4. 1 1 0 0 1 5. |
1. 1 0 0 1 0 4. 1 1 0 0 1 7. |
|
|
(1) |
(2) |
(3) |
Можно выбрать и
другие группы линейно независимых
комбинаций этого кода. Путем поэлементного
сложения по модулю 2 любого сочетания
из приведенных выше в группах комбинаций
не удается получить нулевой комбинации.
Для первой группы:
|
1. 1
2. ——————— 1 |
1. 1
3. —————— 1 |
2. 0
3. ——————— 0 |
1. 1
2. 3. ————- 1 |
|
4. |
5. |
6. |
7. |
Обычно линейно
независимые кодовые комбинации записывают
в виде матрицы размером
,
которая называетсяпорождающей
и обозначается
.
Чаще всего порождающие матрицы записывают
в так называемойканоничной
форме. При
этом первые или последние
столбцов этой матрицы образуютединичную
матрицу.
Таким образом,
любая из трех приведенных выше комбинаций
может быть порождающей для систематического
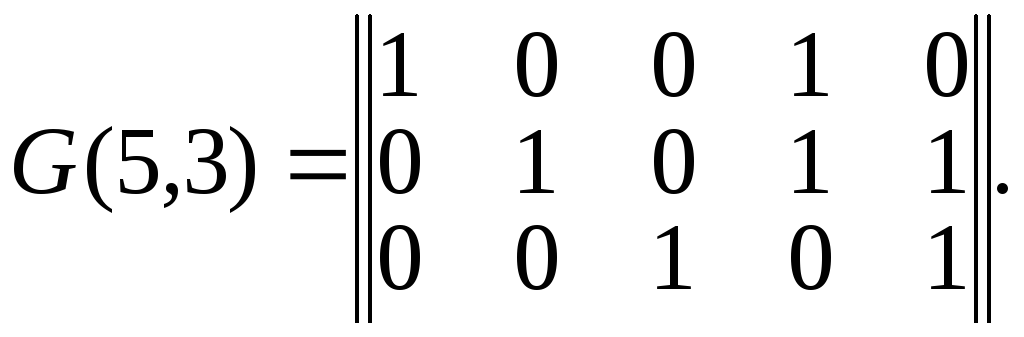
(5,3) кода с
.
В общем виде производящую матрицу из
строк и
столбцов записывают так:

(8.42)
Здесь первые
столбцов являются информационными, а
последниестолбцов – проверочными. Производящую
матрицуобычно записывают в канонической форме
или
. (8.43)
где
– число
проверочных элементов,
— матрица информационных элементов,
представляет собой единичную матрицу
размерности,
т.е. квадратная матрица, у которой единицы
находятся только на главной диагонали,— матрица проверочных элементов,
размерность которой.
Для рассматриваемого
примера – (5,3) кода каноническая форма
порождающей матрицы имеет вид
Из данного примера
видно, что первые три столбца составляют
единичную матрицу; четвертый столбец
указывает, что при формировании первого
проверочного разряда принимают участие
первый и второй информационные разряды.
Пятый столбец указывает, что при
формировании второго проверочного
разряда принимают участие второй и
третий информационные разряды.
Для

(8.44)
Затем выделяется
подматрица
являющаяся транспонированной матрицей
:
если

.
(8.45)
Затем полученной
матрице
справа приписывается единичная матрица
и получается проверочная матрицаН.
.
(8.46)
Проверочная матрица
очень удобна для определения места
ошибки в кодовой комбинации, а следовательно
и исправления ошибки.
Проверочная матрица
однозначно связана с порождающей
соотношением
,
(8.47)
Где умножение и
суммирование соответствующих элементов
матриц производится по модулю 2.
Пример.
Для порождающей
матрицы, G(5,3)
проверочная матрица имеет вид
Тогда
Допустим, что
переданная кодовая комбинация записана
в виде вектора

Процесс декодирования
математически описывают произведением
проверочной матрицы
и вектора – столбца, отображающего
принятую кодовую комбинацию,
где— вектор ошибки
,
(8.49)
где
– результат декодирования (синдром);
— знак транспортирования.
В теории кодирования
синдром, который также называют
опознавателем ошибки, обозначает
совокупность признаков, характерных
для определённой ошибки. Для исправления
ошибки на стороне приёма необходимо
знать не только факт её существования,
но и её местонахождение, которое
определяется по установленному виду
вектора ошибки.
Поскольку связь
между порождающей и проверочной
матрицами, определяется равенством
,
то получим
.
(8.50)
Если обозначить
-й
столбец проверочной матрицы, то
.
Вектор ошибки
содержит «1» на тех позициях, символы
на которых искажены. Пусть эти позиции
имеют номера,
тогда будет справедливо равенство
.
(8.51)
Следовательно,
если необходимо обнаружить
ошибок, то должно быть выполнено условие
,
при любом сочетании
искаженных символов.
Если же необходимо
исправить
ошибок, то сумма по модулю 2 для любого
конкретных столбцов проверочной матрицы
должна быть вполне определенной, которая
не совпадает с аналогичной суммой для
другихстолбцов. Так, например, при исправлении
одиночной ошибки все столбцы проверочной
матрицы должны быть разными, то естьпри любых
и
;
.
Если же необходимо исправить одиночную
ошибку и обнаружить пакет, состоящий
из трех или двух ошибок, то необходимо
выполнить следующие условия:
при
(для исправления одиночной ошибки);
при любых
и
(для обнаружения пакета из двух ошибок);
при любых
и
(для обнаружения пакета из трех ошибок).
Матрицы
и
можно поменять ролями. Тогда матрица
будет порождающей, а
— проверочной.
Коды, взаимосвязанные
между собой таким образом, называют
дуэльными (двойственными).
Соседние файлы в папке Пособие ТЕЗ_рус12
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
|
Макеты страниц
Неполный декодер для корректирующего 



Рассмотрим случай использования линейных кодов в каналах, вносящих в символы ошибки независимо и симметрично. Выражения для указанных вероятностей зависят от распределения весов кода и поэтому полезны лишь в случае, когда оно известно. В предыдущем параграфе получено распределение весов для кодов Рида-Соломона, так что для этих кодов мы можем вычислить вероятности ошибочного декодирования и неудачного декодирования.
Рассматриваемые каналы представляют собой 






Мы рассмотрим лишь неполный декодер, который не принимает решения о декодировании вне радиуса упаковки кода. Каждое принятое слово, лежащее от ближайшего кодового слова на расстоянии, не превышающем 


Исследуем условные вероятности ошибочного и неудачного декодирования в случае линейного кода при условии, что передано слово, целиком состоящее из нулей. Каждое другое переданное слово приводит к тем же самым условным вероятностям, так что они являются также безусловными вероятностями. На рис. 14.2 изображены три области, в которые может попасть принятое слово.

Рис. 14.2. Области декодирования.
Вероятность правильного декодирования — это вероятность того, что принятое слово попадает в область, покрытую редкой штриховкой. Вероятность неправильного декодирования — это вероятность того, что принятое слово попадет в область, покрытую частой штриховкой. Вероятность неудачного декодирования — это вероятность того, что принятое слово попадет в незаштрихованную область. Сумма этих трех вероятностей равна I, поэтому достаточно найти формулы лишь для двух из них. Начнем с самого простого.
Теорема 14.2.1. Вероятность правильного декодирования декодера, исправляющего ошибки в пределах радиуса упаковки кода, равна

Доказательство. Число способов, которыми можно разместить конфигурации из 


Хотя теорема справедлива для любых объемов алфавита, в формулу входит лишь вероятность появления ошибочного символа. Не имеет значения, как она распадается на вероятности конкретных опжбочпых значений. В следующей теореме, касающейся неудачного декодировании, необходимо подсчитать число способов, которыми могут быть сделаны ошибки. Некоторые
конфигурации ошибок, вероятности которых нужно просуммировать, приведены на рис. 14.3.
Пусть 










Теорема 14.2.2. Число конфигураций ошибок веса 


Доказательство. Равенству, которое требуется доказать, эквивалентно равенство

что может быть проверено подстановкой 





Рис. 14.3. Некоторые слова, вызывающие ошибку декодирования.
Оглавление
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВВЕДЕНИЕ
- 1.1. ДИСКРЕТНЫЙ КАНАЛ, СВЯЗИ
- 1.2. ИСТОРИЯ КОДИРОВАНИЯ, КОНТРОЛИРУЮЩЕГО ОШИБКИ
- 1.3. ПРИЛОЖЕНИЯ
- 1.4. ОСНОВНЫЕ ПОНЯТИЯ
- 1.5. ПРОСТЕЙШИЕ КОДЫ
- ГЛАВА 2. ВВЕДЕНИЕ В АЛГЕБРУ
- 2.1. 2-ПОЛЕ И 6-10-ПОЛЕ
- 2.2. ГРУППЫ
- 2.3. КОЛЬЦА
- 2.4. ПОЛЯ
- 2.5. ВЕКТОРНЫЕ ПРОСТРАНСТВА
- 2.6. ЛИНЕЙНАЯ АЛГЕБРА
- ГЛАВА 3. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 3.1. СТРУКТУРА ЛИНЕЙНЫХ БЛОКОВЫХ КОДОВ
- 3.2. МАТРИЧНОЕ ОПИСАНИЕ ЛИНЕЙНЫХ БЛОКОВЫХ КОДОВ
- 3.3. СТАНДАРТНОЕ РАСПОЛОЖЕНИЕ
- 3.4. КОДЫ ХЭММИНГА
- 3.5. СОВЕРШЕННЫЕ И КВАЗИСОВЕРШЕННЫЕ КОДЫ
- 3.6. ПРОСТЫЕ ПРЕОБРАЗОВАНИЯ ЛИНЕЙНОГО КОДА
- 3.7. КОДЫ РИДА—МАЛЛЕРА
- ГЛАВА 4. АРИФМЕТИКА ПОЛЕЙ ГАЛУА
- 4.2. КОНЕЧНЫЕ ПОЛЯ, ОСНОВАННЫЕ НА КОЛЬЦЕ ЦЕЛЫХ ЧИСЕЛ
- 4.3. КОЛЬЦА МНОГОЧЛЕНОВ
- 4.4. КОНЕЧНЫЕ ПОЛЯ, ОСНОВАННЫЕ НА КОЛЬЦАХ МНОГОЧЛЕНОВ
- 4.5. ПРИМИТИВНЫЕ ЭЛЕМЕНТЫ
- 4.6. СТРУКТУРА КОНЕЧНОГО ПОЛЯ
- ГЛАВА 5. ЦИКЛИЧЕСКИЕ КОДЫ
- 5.2. ПОЛИНОМИАЛЬНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- 5.3. МИНИМАЛЬНЫЕ МНОГОЧЛЕНЫ И СОПРЯЖЕНИЯ
- 5.4. МАТРИЧНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- 5.5. КОДЫ ХЭММИНГА КАК ЦИКЛИЧЕСКИЕ КОДЫ
- 5.6. ЦИКЛИЧЕСКИЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ
- 5.7. ЦИКЛИЧЕСКИЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ПАКЕТЫ ОШИБОК
- 5.8. ДВОИЧНЫЙ КОД ГОЛЕЯ
- 5.9. КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ
- ГЛАВА 6. СХЕМНАЯ РЕАЛИЗАЦИЯ ЦИКЛИЧЕСКОГО КОДИРОВАНИЯ
- 6.1. ЛОГИЧЕСКИЕ ЦЕПИ ДЛЯ АРИФМЕТИКИ КОНЕЧНОГО ПОЛЯ
- 6.2. ЦИФРОВЫЕ ФИЛЬТРЫ
- 6.3. КОДЕРЫ И ДЕКОДЕРЫ НА РЕГИСТРАХ СДВИГА
- 6.4. ДЕКОДЕР МЕГГИТТА
- 6.5. ВЫЛАВЛИВАНИЕ ОШИБОК
- 6.6. УКОРОЧЕННЫЕ ЦИКЛИЧЕСКИЕ КОДЫ
- 6.7. ДЕКОДЕР МЕГГИТТА ДЛЯ. КОДА ГОЛЕЯ
- ГЛАВА 7. КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА
- 7.2. ДЕКОДЕР ПИТЕРСОНА ГОРЕНСТЕЙНА—ЦИРЛЕРА
- 7.3. КОДЫ РИДА СОЛОМОНА
- 7.4. СИНТЕЗ АВТОРЕГРЕССИОННЫХ ФИЛЬТРОВ
- 7.5. БЫСТРОЕ ДЕКОДИРОВАНИЕ КОДОВ БЧХ
- 7.6. ДЕКОДИРОВАНИЕ ДВОИЧНЫХ КОДОВ БЧХ
- 7.7. ДЕКОДИРОВАНИЕ С ПОМОЩЬЮ АЛГОРИТМА ЕВКЛИДА
- 7.8. КАСКАДНЫЕ (ГНЕЗДОВЫЕ) КОДЫ
- 7.9. КОДЫ ЮСТЕСЕНА
- ГЛАВА 8. КОДЫ, ОСНОВАННЫЕ НА СПЕКТРАЛЬНЫХ МЕТОДАХ
- 8.2. ОГРАНИЧЕНИЯ СОПРЯЖЕННОСТИ И ИДЕМПОТЕНТЫ
- 8.3. СПЕКТРАЛЬНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- 8.4. РАСШИРЕННЫЕ КОДЫ РИДА-СОЛОМОНА
- 8.5. РАСШИРЕННЫЕ КОДЫ БЧХ
- 8.6. АЛЬТЕРНАНТНЫЕ КОДЫ
- 8.7. ХАРАКТЕРИСТИКИ АЛЬТЕРНАНТНЫХ КОДОВ
- 8.8. КОДЫ ГОППЫ
- 8.9. КОДЫ ПРЕПАРАТЫ
- ГЛАВА 9. АЛГОРИТМЫ, ОСНОВАННЫЕ НА СПЕКТРАЛЬНЫХ МЕТОДАХ
- 9.2. ИСПРАВЛЕНИЕ СТИРАНИЙ И ОШИБОК
- 9.3. ДЕКОДИРОВАНИЕ РАСШИРЕННЫХ КОДОВ РИДА—СОЛОМОНА
- 9.4. ДЕКОДИРОВАНИЕ РАСШИРЕННЫХ КОДОВ БЧХ
- 9.5. ДЕКОДИРОВАНИЕ ВО ВРЕМЕННОЙ ОБЛАСТИ
- 9.6. ДЕКОДИРОВАНИЕ ЗА ГРАНИЦЕЙ БЧХ
- 9.7. ДЕКОДИРОВАНИЕ АЛЬТЕРНАНТНЫХ КОДОВ
- 9.8. ВЫЧИСЛЕНИЕ ПРЕОБРАЗОВАНИЙ В КОНЕЧНЫХ ПОЛЯХ
- ГЛАВА 10. МНОГОМЕРНЫЕ СПЕКТРАЛЬНЫЕ МЕТОДЫ
- 10.1. КОДЫ-ПРОИЗВЕДЕНИЯ
- 10.2. КИТАЙСКИЕ ТЕОРЕМЫ ОБ ОСТАТКАХ
- 10.3. ДЕКОДИРОВАНИЕ КОДА-ПРОИЗВЕДЕНИЯ
- 10.4. МНОГОМЕРНЫЕ СПЕКТРЫ
- 10.5. БЫСТРЫЕ КОДЫ БЧХ
- 10.6. ДЕКОДИРОВАНИЕ МНОГОМЕРНЫХ КОДОВ
- 10.7. ДЛИННЫЕ КОДЫ НАД МАЛЫМИ ПОЛЯМИ
- ГЛАВА 11. БЫСТРЫЕ АЛГОРИТМЫ
- 11.1. ЛИНЕЙНАЯ СВЕРТКА И ЦИКЛИЧЕСКАЯ СВЕРТКА
- 11.2. БЫСТРЫЕ АЛГОРИТМЫ СВЕРТКИ
- 11.3. БЫСТРЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.4. АЛГОРИТМЫ АГАРВАЛА—КУЛИ ВЫЧИСЛЕНИЯ СВЕРТОК
- 11.5. АЛГОРИТМ ВИНОГРАДА БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.6. УСКОРЕННЫЙ АЛГОРИТМ БЕРЛЕКЭМПА—МЕССИ
- 11.7. РЕКУРРЕНТНЫЙ АЛГОРИТМ БЕРЛЕКЭМПА—МЕССИ
- 11.8. УСКОРЕННОЕ ДЕКОДИРОВАНИЕ КОДОВ БЧХ
- 11.9. СВЕРТКА В СУРРОГАТНЫХ ПОЛЯХ
- ГЛАВА 12. СВЕРТОЧНЫЕ КОДЫ
- 12.2. ОПИСАНИЕ СВЕРТОЧНЫХ КОДОВ С ПОМОЩЬЮ МНОГОЧЛЕНОВ
- 12.3. ИСПРАВЛЕНИЕ ОШИБОК И ПОНЯТИЯ РАССТОЯНИЯ
- 12.4. МАТРИЧНОЕ ОПИСАНИЕ СВЕРТОЧНЫХ КОДОВ
- 12.5. НЕКОТОРЫЕ ПРОСТЫЕ СВЕРТОЧНЫЕ КОДЫ
- 12.6. АЛГОРИТМЫ СИНДРОМНОГО ДЕКОДИРОВАНИЯ
- 12.7. ОБЕРТОЧНЫЕ КОДЫ ДЛЯ ИСПРАВЛЕНИЯ ПАКЕТОВ ОШИБОК
- 12.8. АЛГОРИТМ ДЕКОДИРОВАНИЯ ВИТЕРБИ
- 12.9. АЛГОРИТМЫ ПОИСКА ПО РЕШЕТКЕ
- ГЛАВА 13. КОДЫ И АЛГОРИТМЫ ДЛЯ ДЕКОДИРОВАНИЯ МАЖОРИТАРНЫМ МЕТОДОМ
- 13.1. ДЕКОДИРОВАНИЕ МАЖОРИТАРНЫМ МЕТОДОМ
- 13.2. СХЕМЫ МАЖОРИТАРНОГО ДЕКОДИРОВАНИЯ
- 13.3. АФФИННЫЕ ПЕРЕСТАНОВКИ ДЛЯ ЦИКЛИЧЕСКИХ КОДОВ
- 13.4. ЦИКЛИЧЕСКИЕ КОДЫ, ОСНОВАННЫЕ НА ПЕРЕСТАНОВКАХ
- 13.5. СВЕРТОЧНЫЕ КОДЫ С МАЖОРИТАРНЫМ ДЕКОДИРОВАНИЕМ
- 13.6. ОБОБЩЕННЫЕ КОДЫ РИДА—МАЛЛЕРА
- 13.7. ЕВКЛИДОВО-ГЕОМЕТРИЧЕСКИЕ КОДЫ
- 13.8. ПРОЕКТИВНО-ГЕОМЕТРИЧЕСКИЕ КОДЫ
- ГЛАВА 14. КОМПОЗИЦИЯ И ХАРАКТЕРИСТИКИ КОНТРОЛИРУЮЩИХ ОШИБКИ КОДОВ
- 14.2. ВЕРОЯТНОСТИ ОШИБОЧНОГО ДЕКОДИРОВАНИЯ И НЕУДАЧНОГО ДЕКОДИРОВАНИЯ
- 14.3. РАСПРЕДЕЛЕНИЕ ВЕСОВ СВЕРТОЧНЫХ КОДОВ
- 14.4. ГРАНИЦЫ МИНИМАЛЬНОГО РАССТОЯНИЯ ДЛЯ БЛОКОВЫХ КОДОВ
- 14.5. ГРАНИЦЫ МИНИМАЛЬНОГО РАССТОЯНИЯ ДЛЯ СВЕРТОЧНЫХ КОДОВ
- ГЛАВА 15. ЭФФЕКТИВНАЯ ПЕРЕДАЧА СИГНАЛОВ ПО ЗАШУМЛЕННЫМ КАНАЛАМ
- 15.1. ОГРАНИЧЕННЫЙ ПО ПОЛОСЕ ГАУССОВСКИЙ КАНАЛ
- 15.2. ЭНЕРГИЯ НА БИТ И ЧАСТОТА ОШИБОК НА БИТ
- 15.3. МЯГКОЕ ДЕКОДИРОВАНИЕ БЛОКОВЫХ КОДОВ
- 15.4. МЯГКОЕ ДЕКОДИРОВАНИЕ СВЕРТОЧНЫХ КОДОВ
- 15.5. ПОСЛЕДОВАТЕЛЬНОЕ ДЕКОДИРОВАНИЕ
- ЛИТЕРАТУРА
— одна из возможных мер характеризации точности воспроизведения сообщений, передаваемых по каналу связи (см. также Сообщений точность воспроизведения). Пусть для передачи сообщения x, вырабатываемого источником сообщений и принимающего Мразличных возможных значений 1,. . ., М с распределением вероятностей р m=Р{x=m}, m=l, , . . , M, используется нек-рый канал связи. Тогда для фиксированных методов кодирования и декодирования (см. также Информации передача).О. д. в. Р е, т, m=1, . . ., М, определяется равенством

где 

Особый интерес представляет изучение оптимальной О. д. в. 

где нижняя грань берется по всевозможным методам кодирования и декодирования. Ввиду трудностей получения точного выражения для 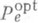






где a(N) и b(N).стремятся к нулю с ростом N,aфункции Er(R).и Esp(R).определяются следующим образом:
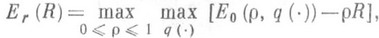

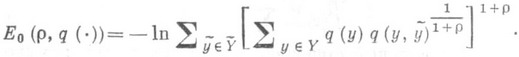
Здесь 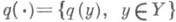


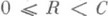

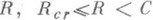


Для значении 
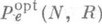
Лит.:[1] Галлагер Р., Теория информации и надежная связь, пер. с англ., М., 1974; 12] Файнстейн А., Основы теории информации, пер. о англ., М., I960.
Р. Л. Добрушин, В. В. Прелов.
НАДЕ АППРОКСИМАЦИЯ — наилучшая рациональная аппроксимация степенного ряда. Пусть
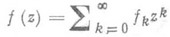
— произвольный степенной ряд (формальный или сходящийся), 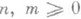
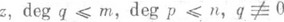


где s(j) — индекс первого из отличных от нуля коэффициентов ряда

Функцию p п, т можно определить также как отношение p п, т=p/qлюбых многочленов 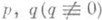

При фиксированных п, т существует единственная П. а. p п, т ряда (1). Таблица 
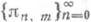
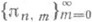
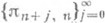
Вычисление функции p п, т сводится к решению системы линейных уравнений, коэффициенты к-рых выражаются через коэффициенты fk, k=0, l,. . ., n+m, заданного ряда. Если отличен от нуля определитель Ганкеля

то знаменатель q п, т функции p п, т определяется по формуле

(нормировка q п, т(0)=1; явная формула может быть написана и для числителя функции p п, т). При этом
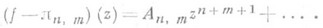
Последнее соотношение иногда принимают за определение П. а.; в этом случае П. а. могут не существовать для нек-рых (n, т). Для обозначения П. а. типа ( п, т).заданного ряда f часто употребляется символ [n/m] = [n/m]f.
Для эффективного вычисления П. а. удобнее пользоваться не явными формулами, а рекурентными соотношениями, существующими в таблице Паде. Разработано большое количество алгоритмов для машинного вычисления П. а.; эти вопросы имеют особенно важное значение в связи с приложениями (см. [17], [18]).
Впервые общую задачу об интерполяции заданных значений функции в n+m+1 различных точках посредством рациональной функции класса R п, т рассмотрел О. Коши [1]; К. Якоби [2] распространил результаты О. Коши на случай кратных узлов интерполяции. Случай одного (n+m+1 )-кратного узла интерполяции соответствует П. а. Понятие П. а. сформировалось в кон. 19 в. в рамках классич. теории непрерывных дробей (Г. Фробениус [3], А. Паде [4]). Фундаментальные результаты о диагональных П. а. были получены П. Л. Чебышевым, А. А. Марковым, Т. Стильтьесом (Т. Stieltjes) в терминах непрерывных дробей; ими были обнаружены и исследованы связи диагональных П. а. с ортогональными многочленами, квадратурными формулами, проблемой моментов и другими вопросами классич. анализа (см. [7] — [9]). Начало изучению строк таблицы Паде было положено работами о радиусах мероморфности функции, заданной степенным рядом, и о сходимости строк таблицы Паде в кругах мероморфности (см. [5], [6]).
С нач. 20 в. П. а. становятся самостоятельным объектом анализа и составляют важную главу теории рациональных приближений аналитич. ций. Используя для своего построения локальные данные (коэффициенты степенного ряда), они позволяют изучать глобальные свойства соответствующей аналитич. ции (аналитич. продолжение, характер и расположение особенностей и т. п.) и вычислять значение функции за пределами круга сходимости степенного ряда.
Наряду с классическими П. а. рассматриваются различные их обобщения: общие процессы интерполяции посредством рациональных функций со свободными полюсами (многоточечные аппроксимации Паде); рациональные аппроксимации рядов по заданной системе многочленов (напр., по ортогональным многочленам); совместные П. а. (аппроксимации Паде — Эрмита); рациональные аппроксимации (типа П. а.) степенных рядов от нескольких переменных и др.
Лит.:[1] Саuсhу A.-L., Cours d’analyse de I’Ecole royale polyteclmique, pt. 1- Analyse algebrique, P., 1821; [2] Jacobi C. G. J., «J. reine und angew. Math.», 1846, Bd SO, S. 127-56; [3] Frоbenius G., там же, 1881, Bd 90, S. 1 — 17; [4] Pade H., «Ann. scient. Ecole norm, super.», 1892, t. 9, p. 1-93; [5] Hadamard J., «J. math, pures et appl.», 1892, t. 8, p. 101-86; [6] Mоntessus deBalloreB.de, «Bull. Soc. math. France», 1902, t. 3(1, p. 28-36; [7] Чебышев П. Л., Полн. собр. соч., т. 3, М.- Л., 1948; [8] Марков А. А., Избр. труды по теории непрерывных дробей и теории функций, наименее уклоняющихся от нуля, М.- Л., 1948; [9] Стилтьес Т., Исследования о непрерывных дробях, пер. с франц., Хар.- К.. 1936; [10] Wall H. S., Analytic theory of continued fractions, Toronto — N. Y,- L., 1948; [11] Perron O., Die Lehre von den Kettenbruchen, 3 Aufl., Bd 2, Stuttg., 1957; [12] The Fade approximant in theoretical physics, N. Y.- L., 1970; [13] Pade approximants and their applications, L.-N. Y., 1973; [14]
Pade approximants method and its applications to mechanics, В.- Hdlb.- N. Y., 1976; [15] В a k e r G. A., Essentials of Fade approximants, N. Y.- San Franc.- L., 1975; [16] Fade and rational approximation, N. Y.- [a. o.], 1977; [17] Gilewicz J., Approximants dc Pade, В.- Hdlb.- N. Y., 1978; [18] Pade approximation and its applications, В.- Hdlb.- N. Y., 1979.
В. А. Рахманов.
Математическая энциклопедия. — М.: Советская энциклопедия.
.
1977—1985.
Презентация на тему: » Помехоустойчивое кодирование Вероятность ошибочного декодирования.» — Транскрипт:
1
Помехоустойчивое кодирование Вероятность ошибочного декодирования
2
Модель двоичного симметричного канала p p
3
Чтобы гарантировать обнаружение до s ошибок, минимальное расстояние Хэмминга в блоковом коде должно быть d min = s + 1. Замечание
4
Геометрическая интерпретация нахождения d min при обнаружении ошибок
5
Чтобы гарантировать исправление до t ошибок, минимальное расстояние Хэмминга в блоковом коде должно быть d min = 2t + 1. Замечание
6
Геометрическая интерпретация нахождения d min при исправлении ошибок
7
Вероятность ошибки Вероятность ошибочного слова веса i равна Вероятность ошибки веса i равна
8
Вероятность ошибочного декодирования Ошибочное слово совпадает с некоторым кодовым словом (то есть вектор ошибки — кодовое слово)
9
где – число кодовых слов веса i.
10
Пример Данные кодируются (7,4)-кодом Хэмминга Канал с АБГШ, отношение сигнал/шум – 6дБ – это эквивалентно вероятности ошибки двоичного символа, равной 0,023. Скорость передачи – 16 кбит/сек
11
Пример Решение. Кодовое слово будет передаваться без ошибок, если все 7 двоичных символов переданы верно.
12
Вероятность ошибочного слова Пример. Рассмотрим код с повторением C = {000, 111}. Вероятность правильного декодирования для слова 000 есть (1 — p) 3 + 3p(1 — p) 2, для слова 111 есть (1 — p) 3 + 3p(1 — p) 2. Тогда P err (C) = 1 — ((1 — p) 3 + 3p(1 — p) 2 ) есть вероятность ошибочного слова. Пример. Пусть p = 0.01, тогда P err (C) = и лишь одно слово из 3555 дойдет до получателя с ошибкой.
13
Вероятность ошибочного слова где — количество ошибочных слов веса i.