1.1 Задачи теории ошибок
В
теории ошибок на основе теории вероятностей
с использованием методов математической
статистики решают следующие задачи:
-
Изучение
причин возникновения ошибок измерений,
их свойств и законов распределения их
вероятностей; -
Определение
наиболее надёжного значения искомой
величины из результатов её многократных
измерений; -
Оценка
точности непосредственно выполненных
результатов измерений и предвычисление
ожидаемой точности функций измеренных
величин; -
Установление
допусков, т.е. критериев, ограничивающих
использование результатов измерений
в заданных пределах точности.
1.2 Классификация ошибок измерений
Ошибки
измерений подразделяют на грубые,
систематические и случайные.
К
грубым
ошибкам относят ошибки, вызванные
промахами и просчётами наблюдателя,
неисправностями приборов, резким
ухудшением внешних условий и др. С целью
их обнаружения измерения выполняются
многократно (не менее двух раз). Результаты
измерений, содержащие грубые ошибки,
необходимо выявлять и исключать из
обработки.
К
систематическим
относят
ошибки, которые входят в результаты
измерений по тому или иному закону, как
функции источников возникновения
ошибок. В практике геодезических
измерений применяют следующие способы
уменьшения влияния систематических
ошибок:
-
Устанавливают
закон появления систематических ошибок,
после чего ошибки уменьшают введением
поправок в результаты измерений; -
Применяют
соответствующую методику измерений
для того, чтобы систематические ошибки
действовали не односторонне, а изменяли
знаки; -
Используют
определённую методику обработки
результатов измерений.
Случайные
ошибки являются наиболее ярким примером
случайной величины. Их закономерности
обнаруживаются только в массовом
проявлении. Случайные ошибки неизбежны
при измерениях и не могут быть исключены
из единичного измерения. Влияние их
можно лишь ослабить, повышая качество
и количество измерений, а также надлежащей
математической обработкой результатов
измерений. Причин возникновения случайных
ошибок измерений много: влияние внешних
условий, неточности изготовления и
юстировки приборов, неточности выполнения
операций наблюдателем и т.д. Очевидно,
что случайные ошибки являются результатом
суммирования большого числа независимых
элементарных ошибок. На основании
центральной предельной теоремы Ляпунова
можно считать, что случайные ошибки
измерений подчиняются нормальному
закону распределения.
В
дальнейшем условно примем, что в любых
измерениях грубые ошибки отсутствуют,
основная часть систематических ошибок
исключена из результатов, а остаточные
систематические ошибки ничтожно малы,
т.е. будем рассматривать только случайные
ошибки (,
гдехi —
результат измерений, Х —
истинное значение измеряемой величины.)
Очевидно, что
,
а.
1.3 Свойства случайных ошибок измерений
-
Случайные
ошибки по абсолютной величине с заданной
вероятностью
не должны
превышать определённого предела,
равного
(t —
коэффициент, для которого
,m —
средняя
квадратическая ошибка)); -
Положительные
и отрицательные случайные ошибки,
равные по абсолютной величине, одинаково
часто встречаются в ряде измерений; -
Среднее
арифметическое из значений случайных
ошибок при неограниченном увеличении
числа измерений имеет пределом нуль,
т.е.
|
|
Это
свойство называют свойством компенсации.
Отклонение
от нуля свидетельствует о наличии в
результатах измерений систематических
ошибок.
-
Малые
по абсолютной величине случайные ошибки
встречаются в ряде измерений чаще, чем
большие.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
На чтение 9 мин Просмотров 1к. Опубликовано 03.10.2021
Теория ошибок измерений изучает свойства ошибок и законы их распределения, методы обработки измерений с учетом их ошибок, а также способы вычисления числовых характеристик точности измерений. При многократных измерениях одной и той же величины результаты измерений получаются неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются разными по величине и по знаку ошибками. Задача теории ошибок – нахождение наиболее надежного значения измеренной величины, оценка точности результатов измерений и их функций и установление допусков, ограничивающих использование результатов обработки измерений.
По своей природе ошибки бывают грубые, систематические и случайные.
Грубые ошибки являются результатом промахов и просчетов. Их можно избежать при внимательном и аккуратном отношении к работе и организации надежного полевого контроля измерений. В теории ошибок грубые ошибки не изучаются.
Систематические ошибки имеют определенный источник, направление и величину. Если источник систематической ошибки обнаружен и изучен, то можно получить формулу влияния этой ошибки на результат измерения и затем ввести в него поправку; это исключит влияние систематической ошибки. Пока источник какой-либо систематической ошибки не найден, приходится считать ее случайной ошибкой, ухудшающей качество измерений.
Случайные ошибки измерений обусловлены точностью способа измерений (строгостью теории), точностью измерительного прибора, квалификацией исполнителя и влиянием внешних условий. Закономерности случайных ошибок проявляются в массе, то-есть, при большом количестве измерений; такие закономерности называют статистическими. Освободить результат единичного измерения от случайных ошибок невозможно; невозможно также предсказать случайную ошибку единичного измерения. Теория ошибок занимается в основном изучением случайных ошибок.
Случайная истинная ошибка измерения Δ – это разность между измеренным значением величины l и ее истинным значением X:
(1.25)
Свойства случайных ошибок. Случайные ошибки подчиняются некоторым закономерностям:
1. при данных условиях измерений абсолютные значения случайных ошибок не превосходят некоторого предела; если какая-либо ошибка выходит за этот предел, она считается грубой,
2. положительные и отрицательные случайные ошибки равновозможны,
3. среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений. Третье свойство случайных ошибок записывается так:
(1.26)
4. малые по абсолютной величине случайные ошибки встречаются чаще, чем большие.
Кроме того, во всей массе случайных ошибок не должно быть явных закономерностей ни по знаку, ни по величине. Если закономерность обнаруживается, значит здесь сказывается влияние какой-то систематической ошибки.
Средняя квадратическая ошибка одного измерения. Для оценки точности измерений можно применять разные критерии; в геодезии таким критерием является средняя квадратическая ошибка. Это понятие было введено Гауссом; он же разработал основные положения теории ошибок. Средняя квадратическая ошибка одного измерения обозначается буквой m и вычисляется по формуле Гаусса:
(1.27)
где: ;
n – количество измерений одной величины.
Средняя квадратическая ошибка очень чувствительна к большим по абсолютной величине ошибкам, так как каждая ошибка возводится в квадрат. В то же время она является устойчивым критерием для оценки точности даже при небольшом количество измерений; начиная с некоторого n дальнейшее увеличение числа измерений почти не изменяет значения m; доказано, что уже при n = 8 значение m получается достаточно надежным.
Предельная ошибка ряда измерений обозначается Δпред; она обычно принимается равной 3*m при теоретических исследованиях и 2*m или 2.5*m при практических измерениях. Считается, что из тысячи измерений только три ошибки могут достигать или немного превосходить значение Δпред = 3*m.
Отношение mx/X называется средней квадратической относительной ошибкой; для некоторых видов измерений относительная ошибка более наглядна, чем m. Относительная ошибка выражается дробью с числителем, равным 1, например, mx/X = 1/10 000.
Средняя квадратическая ошибка функции измеренных величин. Выведем формулу средней квадратической ошибки функции нескольких аргументов произвольного вида:
F = f( X, Y, Z … ), (1.28)
здесь: X, Y, Z … – истинные значения аргументов,
F – истинное значение функции.
В результате измерений получены измеренные значения аргументов lX, lY, lZ, при этом:

где ΔX, ΔY, ΔZ – случайные истинные ошибки измерения аргументов.
Функцию F можно выразить через измеренные значения аргуметов и их истинные ошибки:
Разложим функцию F в ряд Тейлора, ограничившись первой степенью малых приращений ΔX, ΔY, ΔZ:
(1.30)
Разность является случайной истинной ошибкой функции с противоположным знаком, поэтому:
(1.31)
Если выполнить n измерений аргументов X, Y, Z, то можно записать n уравнений вида (1.31). Возведем все эти уравнения в квадрат и сложим их; суммарное уравнение разделим на n и получим
В силу третьего свойства случайных ошибок члены, содержащие произведения случайных ошибок, будут незначительными по величине, и их можно не учитывать; таким образом,
(1.32)
Как частные случаи формулы (1.32) можно написать выражения для средней квадратической ошибки некоторых функций:
Если функция имеет вид произведения нескольких аргументов,
F = x * y * z,
то для нее можно записать выражение относительной ошибки функции:
(1.33)
которое в некоторых случаях оказывается более удобным, чем формула (1.32).
Принцип равных влияний. В геодезии часто приходится определять средние квадратические ошибки аргументов по заданной средней квадратической ошибке функции. Если аргумент всего один, то решение задачи не представляет трудности. Если число аргументов t больше одного, то возникает задача нахождения t неизвестных из одного уравнения, которую можно решить, применяя принцип равных влияний. Согласно этому принципу все слагаемые правой части формулы (1.32) или (1.33) считаются равными между собой.
Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,

Сложим эти равенства, суммарное уравнение разделим на n и получим:
(1.35)
Величина (1.36)
называется средним арифметическим или простой арифметической серединой. Запишем (1.35) в виде
по третьему свойству ошибок (1.26) можно написать:
что означает, что при неограниченном возрастании количества измерений простая арифметическая середина стремится к истинному значению измеряемой величины. При ограниченном количестве измерений арифметическая середина является наиболее надежным и достоверным значением измеряемой величины.
Запишем формулу (1.36) в виде
и подсчитаем среднюю квадратическую ошибку арифметической середины, которая обозначается буквой M. Согласно формуле (1.32) напишем:
или
Но ml1 = ml2 = … = mln= m по условию задачи, так как величина X измеряется при одних и тех же условиях. Тогда в квадратных скобках будет n * m2, одно n сократится и в итоге получим:
M2 = m2/n
или
(1.37)
то-есть, средняя квадратическая ошибка арифметической середины в корень из n раз меньше ошибки одного измерения.
Вычисление средней квадратической ошибки по уклонениям от арифметической середины. Формулу Гаусса (1.27) применяют лишь в теоретических выкладках и при исследованиях приборов и методов измерений, когда известно истинное значение измеряемой величины. На практике оно, как правило, неизвестно, и оценку точности выполняют по уклонениям от арифметической середины.
Пусть имеется ряд равноточных измерений величины X:
l1, l2 , …, ln .
Вычислим арифметическую середину X0 = [1]/n и образуем разности:

Сложим все разности и получим [l] – n * X0 = [V]. По определению арифметической середины n * X0 = [l], поэтому:
[V] = 0. (1.39)
Величины V называют вероятнейшими ошибками измерений; именно по их значениям и вычисляют на практике среднюю квадратическую ошибку одного измерения, используя для этого формулу Бесселя:
(1.40)
Приведем вывод этой формулы. Образуем разности случайных истинных ошибок измерений Δ и вероятнейших ошибок V:

Разность (X0 – X) равна истинной ошибке арифметической середины; обозначим ее Δ0 и перепишем уравнения (1.41):

Возведем все уравнения (1.42) в квадрат, сложим их и получим:
.
Второе слагаемое в правой части этого выражения равно нулю по свойству (1.39), следовательно,
.
Разделим это уравнение на n и учтя, что [Δ2]/n =m2, получим:
(1.43)
Заменим истинную ошибку арифметической середины Δ0 ее средней квадратической ошибкой ; такая замена практически не изменит правой части формулы (1.43). Итак,
,
откуда ;
после перенесения (n-1) в правую часть и извлечения квадратного корня получается формула Бесселя (1.40).
Для вычисления средней квадратической ошибки арифметической середины на основании (1.37) получается формула:
(1.44)
Веса измерений. Измерения бывают равноточные и неравноточные. Например, один и тот же угол можно измерить точным или техническим теодолитом, и результаты таких измерений будут неравноточными. Или один и тот же угол можно измерить разным количеством приемов; результаты тоже будут неравноточными. Понятно, что средние квадратические ошибки неравноточных измерений будут неодинаковы. Из опыта известно, что измерение, выполненное с большей точностью (с меньшей ошибкой), заслуживает большего доверия.
Вес измерения – это условное число, характеризующее надежность измерения, степень его доверия; вес обозначается буквой p. Значение веса измерения получают по формуле:
p = C/m2 (1.45)
где C – в общем случае произвольное положительное число.
При неравноточных измерениях одной величины наиболее надежное ее значение получают по формуле средневесовой арифметической середины:
(1.46)
или X0 = [l*p] / [p] .
Ошибку измерения, вес которого равен 1, называют средней квадратической ошибкой единицы веса; она обозначается буквой m. Из формулы (1.45) получаем
откуда (1.47)
то-есть, за число C принимают квадрат ошибки единицы веса.
Подсчитаем вес P средневесовой арифметической середины. По определению веса имеем:
(1.48)
Согласно (1.46) и (1.32) напишем:
Подставим сюда вместо mli2 их выражения через вес m2 = C/p , тогда:
Подставим это выражение в формулу (1.48) и получим,
P = [p], (1.49)
то-есть, вес средневесовой арифметической середины равен сумме весов отдельных измерений.
В случае равноточных измерений, когда веса всех измерений одинаковы и равны единице, формула (1.49) принимает вид:
P = n. (1.50)
При обработке больших групп измерений (при уравнивании геодезических построений по МНК) вычисляются значение ошибки единицы веса, веса измерений и других элементов после уравнивания, а ошибка любого уравненного элемента подсчитывается по формуле:
(1.51)
где pi – вес i-того элемента.
Слайд 1ТЕМА ЛЕКЦИИ:
«ОБЩИЕ ПОНЯТИЯ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ»

Слайд 2
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Маслов А.В. Геодезия: учеб. и уч.
пособие для вузов/ А.В. Маслов, А.В. Гордеев, Ю.Г. Батраков: –
М.: Колос, 2006. – 598 с.
Маслов А.В. Геодезические работы при землеустройстве: учеб. пособие для вузов / А.В. Маслов, А.Г. Юнусов, Г.И. Горохов − 2-е изд., перераб. и доп. — М.: Недра, 1990. – 215 с. .
Неумывакин Ю.К. Геодезическое обеспечение землеустроительных и кадастровых работ: справ. пособие/ Ю.К.Неумывакин, М.И. Перский: – М.: «Картгеоцентр» — «Геодезиздат», 1996. – 344 с.
Геодезия: учеб.-метод. комплекс / БГСХА; сост. С.И. Помелов, Д.А. Чиж. – Горки, 2006. – 256 с.
Практикум по геодезии / Под ред.Бакановой В.В. – М.: Недра, 1989 .

Слайд 3 Задачи теории ошибок измерений.
Сущность и виды измерений.
Ошибки измерений,
их классификация и свойства.
Понятие о законах распределения ошибок.
Числовые характеристики
точности измерений.

Слайд 41. Задачи теории ошибок измерений.
Геодезические
работы связаны с различными методами измерений длин линий, углов, превышений,
площадей и пр. Любые измерения, как бы тщательно они не выполнялись, сопровождаются неизбежными ошибками (погрешностями) поэтому измеренные значения величин будут отклоняться от истинных.
На практике измерения выполняют так, чтобы получить результаты с некоторой заданной точностью. Для обоснования необходимой и достаточной точности измерений надо знать причины возникновения ошибок измерений и их свойства. Эти вопросы рассматриваются в теории ошибок измерений, которая в свою очередь основывается на теории вероятностей и математической статистики.

Слайд 5Теория ошибок измерений решает
четыре основные задачи:
1. Изучение законов
возникновения и распределения ошибок измерений и вычислений.
2. Оценка точности результатов
измерений и их функций.
З. Отыскание наиболее надёжного значения определяемой величины и характеристики точности.
4. Установление допусков, ограничивающих использование результатов измерений в заданных пределах точности, т. е. критериев указывающих на наличие грубых ошибок.

Слайд 62. Сущность и виды измерений.
Измерения
различают на непосредственные (прямые), посредственные (косвенные), равноточные, неравноточные, необходимые, дополнительные
(избыточные), зависимые и независимые.
Под измерением данной физической величины понимается процесс сравнения ее с другой физической величиной того же рода, принятой за единицу измерения.
Полученное именованное число называется результатом измерения.

Слайд 7 Непосредственными или прямыми называ-ются измерения,
при которых измеряемая величина непосредственно сравнивается с единицей меры.
Например,
измерения линий лентой, углов транспортиром и т.д.
Посредственными или косвенными называются измерения, когда искомая величина находится путем измерения других величин.
Например, определение неприступных расстояний.

Слайд 8 Под равноточными понимают измерения, полученные
одним и тем же прибором (или различными приборами одного класса
точности), одним и тем же или равноценны-ми методами, одинаковым числом приемов и в одинаковых условиях.
Пример: измерения углов теодолитами одинаковой точности.
Если указанные условия не соблюдаются, то результаты измерений будут неравноточ-ными. Например, измерение углов теодо-литами разной точности или одним теодо-литом, но разным числом приемов.

Слайд 9 Необходимыми считаются измерения, которые
позволяют получить искомую величину только один раз.
Если одна величина измерена n-раз, то одно измерение будет необходимым, а остальные n–1 — избыточными.
Например, для определения всех сторон и углов в треугольнике необходимо знать не менее трех его элементов, в т.ч. хотя бы одну сторону. Если измерены все углы и стороны, то три величины будут избыточными.
Избыточные измерения нужны для контроля и повышения точности определения искомых величин, а также оценки точности искомых величин.

Слайд 10 Зависимыми называют измерения, имеющие некоторые
общие источники ошибок.
Например, высоты точек А и
В, полученные нивелированием от репера R, будут зависимы, т.к. ошибки превышений в звене RA будут для них общими (рис.1).
Если проложить самостоятельные ходы до точек А и В, то их высоты будут независимыми (рис.2).
Рис.1
Рис.2

Слайд 113. Ошибки измерений, их классификация и свойства.
Ошибкой результата измерения называется разность между результатом измерения и
точным (истинным) значением измеряемой величины, т.е.
∆= l–x, (1)
где ∆ – ошибка измерения (иcтинная ошибка);
l – результат измерения;
x – точное значение величины.

Слайд 12 Причинами возникновения
ошибок являются неточности в изготовлении и юстировке приборов, влияние внешних
условий, неточности выполнения операций наблюдателем, изменения самого объекта измерения и несовершенство метода измерений.
В соответствии с источниками возникновения различают ошибки:
1) приборов;
2) внешние;
3) личные;
4) объекта;
5) метода измерений.
Приведенная классификация ошибок по источникам возникновения имеет большое значение при изучении приборов и методов измерений.

Слайд 13 В теории ошибок более
важное значение имеет классификация ошибок по закономерностям их появления. По
характеру действия на конечный результат ошибки делятся на грубые, систематические и случайные.
Грубые ошибки (промахи) вызываются невнима-тельностью наблюдателя или неисправностью прибора. Они превосходят по абсолютной величине некоторый предел, установленный для данных условий измерений.
Измерения, содержащие грубые ошибки, бракуются и заменяются новыми. Для выявления грубых ошибок производятся избыточные измерения (линии измеряют дважды, в треугольнике измеряют все три угла и т. п.).

Слайд 14Систематические ошибки подразделяются на постоянные, переменные и односторонне действующие.
Постоянные
систематические ошибки при измерении одной и той же величины несколько
раз, всякий раз появляются с одним знаком и одинаковые по величине. Например, ошибки за счет неточного центрирования теодолита при измерении углов несколькими приемами будут одинаковыми в каждом приеме.
Переменные систематические ошибки меняются от приема к приему, следуя определённому закону. Например, ошибки в направлениях, обусловленные эксцентриситетом алидады, или ошибками нанесения штрихов лимба теодолита.
Односторонне действующие систематические ошибки изменяются случайным образом, но сохраняют знак. Например, ошибка в длине линии из-за отклонения мерной ленты от створа.

Слайд 15 Случайными называются ошибки, которые не связаны
функциональной зависимостью с какими-либо факторами. Ни величину, ни знак случайной
ошибки заранее предсказать нельзя. В последовательности появления ошибок тоже нет никакой закономерности. Однако, если рассматривать их в большом количестве, то выявляются определенные статистические закономерности.

Слайд 16Случайные ошибки основного типа обладают следующими вероятными свойствами:
1. По
абсолютной величине ошибки не превосходят некоторого предела.
2. Положительные и
отрицательные ошибки, равные по абсолютной величине, имеют равные вероятности, т.е. встречаются одинаково часто.
З. Чем больше ошибка по абсолютной величине, тем меньше ее вероятность появления.
4. Среднее арифметическое из значений случайных ошибок при неограниченном возрастании числа измерений одной и той же величины имеет пределом нуль, т. е. математическое ожидание ошибки равно нулю
.

Слайд 174. Понятие о законах распределения ошибок.
Свойства случайных ошибок
являются проявлением закона их распределения.
В общем случае закон распределения
ошибок отражает связь между размером ошибки и вероятностью ее появления.
PΔ= f(Δ)dΔ, (2)
где Р∆ – вероятность появления ошибки в интервале (∆, ∆+d∆);
∆ – случайная ошибка;
f(∆) – плотность распределения ошибок.

Слайд 18Распределение случайных ошибок измерений наиболее точно описывается законом нормального
распределения.
Плотность нормального распределения выражается формулой
(3)
где σ – среднее квадратическое отклонение случайной ошибки.

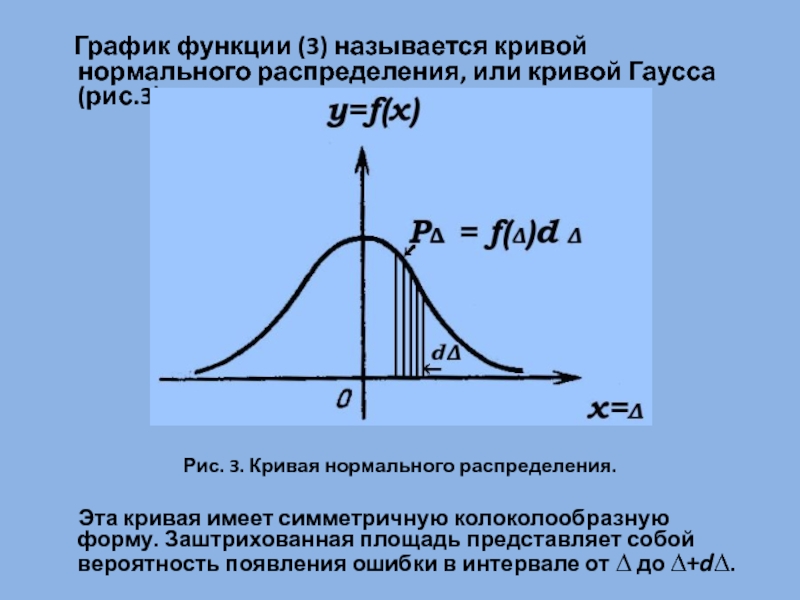
Слайд 19 График функции (3) называется кривой нормального
распределения, или кривой Гаусса (рис.3).
Рис. 3. Кривая нормального распределения.
Эта кривая имеет симметричную колоколообразную форму. Заштрихованная площадь представляет собой вероятность появления ошибки в интервале от ∆ до ∆+d∆.
Слайд 20Есть ошибки, которые подчиняются закону равномерного или равновероятного распределения,
к примеру, ошибки округления. Плотность распределения их выражается формулой:
(4)
где α – наибольшее значение ошибки.

Слайд 21Основными характеристиками распределения случайной величины являются математическое ожидание и
дисперсия.
Математическим
ожиданием дискретной случайной величины х называют сумму произведений всех возможных значений случайной величины на соответствующие им вероятности р
. (5)

Слайд 22 Для непрерывной случайной величины с
плотностью распределения f(x) матема-тическое ожидание определяется по формуле:
. (6)

Слайд 23Дисперсией случайной величины Х называ-ется число, определяемое по формуле:

Слайд 24Положительное значение квадратного корня из дисперсии называют стандартом или
средним квадратическим отклонением
. (8)

Слайд 25 Для случайных ошибок измерений, как
уже отмечалось, математическое ожидание равно нулю
=0. Поэтому
, (9)
или
(10)
при n стремящемуся к бесконечности.

Слайд 265.Числовые характеристики точности измерений.
В
качестве теоретической характеристики точности измерений обычно пользуются средним квадратическим отклонением
σ.
Поскольку величина σ не известна, практически пользуются ее приближенным значением – средней квадратической ошибкой (СКО), определяемой по формуле:
, (11)
где ∆1, ∆2, …, ∆n – истинные ошибки измерений.

Слайд 27При большом значении n
m ≈ σ. (12)
При ограниченном числе измерений величина m будет характеризовать величину σ с некоторой ошибкой. Для оценки точности определения самой средней квадратической ошибки существует формула:
(13)

Слайд 28Оценку точности измерений характеризуют также предельной ошибкой, вычисляемой по
формуле:
∆пр= τm, (14)
где τ – коэффициент, значение которого прини-мают таким, чтобы была мала вероятность появления ошибки больше вероятной.

Слайд 29 Обычно для τ принимают значения
3, 2.5, или 2.
В дальнейшем
при решении задач по оценке точности измерений будем пользоваться формулой
∆пр= 3m.
Для оценки точности иногда пользуются средней ошибкой v и вероятной ошибкой r. Средняя ошибка вычисляется по формуле
(15)

Слайд 30При нормальном распределении средняя ошибка v связана со средней
квадратичеcкой ошибкой m примерным соотношением
(16)
Если все ошибки расположить в ряд по возрастанию абсолютных значений, то ошибка оказавшаяся в середине ряда будет вероятной. Со средней квадратической ошибкой она связана соотношением
(17)
Ошибка, выраженная в единицах измерения, называется абсолютной. Отношение ее к измеренной величине называется относительной ошибкой.


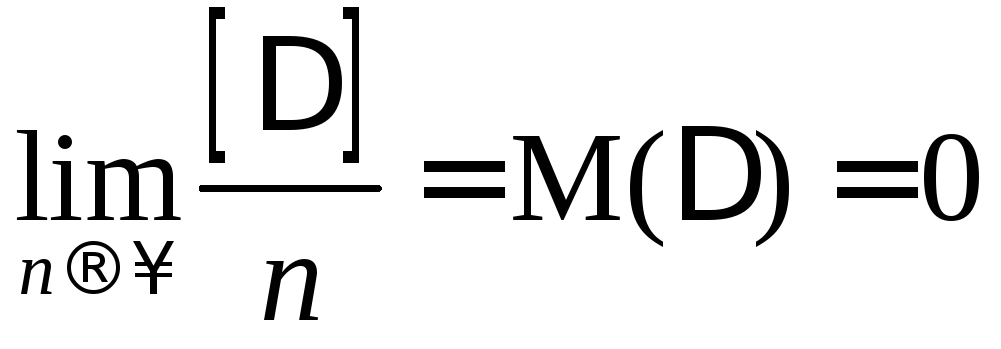 .
.


