Содержание
- Документация
- Обнаружение пересечения нулем
- Демонстрация эффектов чрезмерного обнаружения пересечения нулем
- Предотвращение чрезмерных нулевых пересечений
- Как средство моделирования может пропустить События пересечения нулем
- Обнаружение пересечения нулем в блоках
- Блоки тот нуль регистра пересечения
- Пример реализации: блок насыщения
- Похожие темы
- Открытый пример
Документация
Обнаружение пересечения нулем
Решатель переменного шага динамически настраивает размер временного шага, заставляя его увеличиться, когда переменная изменяется медленно и уменьшиться, когда переменная изменяется быстро. Это поведение заставляет решатель делать много небольших шагов около разрыва, потому что переменная быстро изменяется в этой области. Это улучшает точность, но может привести к чрезмерным временам симуляции.
Simulink ® использует метод, который, как известно как обнаружение пересечения нулем , точно определял местоположение разрыва, не обращаясь к чрезмерно маленьким временным шагам. Обычно этот метод улучшает время выполнения симуляции, но это может заставить некоторые симуляции останавливаться перед намеченным временем завершения.
Simulink использует два алгоритма с этой целью: неадаптивный и адаптивный. Для получения информации об этих методах см. Алгоритмы Пересечения нулем.
Демонстрация эффектов чрезмерного обнаружения пересечения нулем
Этот пример предоставляет три модели, которые иллюстрируют поведение пересечения нулем: example_bounce_two_integrators , example_doublebounce , и example_bounce .
example_bounce_two_integrators модель демонстрирует, как чрезмерные нулевые пересечения могут заставить симуляцию останавливаться перед намеченным временем завершения, если вы не используете адаптивный алгоритм.
example_bounce модель использует лучший проект модели, реализовывая динамику мяча с помощью двойного интегратора, чем example_bounce_two_integrators .
example_doublebounce модель демонстрирует, как адаптивный алгоритм успешно решает сложную систему с двумя отличными требованиями пересечения нулем.
Рассмотрите example_bounce_two_integrators модель. Это использует два один интегратора, чтобы вычислить вертикальную скорость и положение мяча за время симуляции.
Откройте модель путем выполнения open_system(‘example_bounce_two_integrators’) в командной строке.
Если блок-схема появляется, установите детали Решателя> опции Пересечения нулем> Параметр алгоритма в панели Решателя параметров конфигурации Модели к Nonadaptive . Установите время остановки модели к 20 с. Можно изменить эти настройки в панели инструментов Simulink или панели Решателя параметров конфигурации модели.
Можно теперь просмотреть и анализировать результаты симуляции.
После более близкого исследования последнего фрагмента симуляции вы будете видеть, что скорость наводит чуть выше нуля.
Измените Время остановки симуляции в 25 с и симулируйте модель. Симуляция останавливается с ошибкой из-за чрезмерных последовательных событий пересечения нулем при Сравнивании С блоками Нуля и Положения.
Несмотря на то, что можно увеличить этот предел путем корректировки Параметров конфигурации Модели> Решатель>, Количество последовательного нулевого параметра пересечений, внося то изменение все еще не позволяет симуляции продолжаться в течение 25 с.
Измените детали Решателя> опции Пересечения нулем> Параметр алгоритма в панели Решателя параметров конфигурации Модели к Adaptive и симулируйте модель снова в течение 25 с.
Увеличивая масштаб прошлых 5 секунд симуляции, вы видите, что результаты — больше завершенное и ближе к ожидаемому аналитическому решению динамики прыгающего мяча. Сумма болтовни, которую вы видите, является последствием состояний системы, приближающихся к нулю, и ожидается в числовых симуляциях.
example_bounce модель использует блок Second-Order Integrator, чтобы смоделировать динамику прыгающего мяча. Это — предпочтительный метод смоделировать двойное интегрирование динамики мяча для эффективности решателя. Сравнить эффективность решателя для example_bounce_two_integrators и example_bounce , попытайтесь запустить Solver Profiler на обеих моделях. Для подробного сравнения обеих моделей смотрите Симуляцию Прыгающего мяча.
Для сравнения друг с другом адаптивных и неадаптивных алгоритмов обнаружения пересечения нулем смотрите Двойной Прыгающий мяч: Использование Адаптивного Местоположения Пересечения нулем.
Предотвращение чрезмерных нулевых пересечений
Используйте следующую таблицу, чтобы предотвратить чрезмерные ошибки пересечения нулем в вашей модели.
Увеличьте число позволенных нулевых пересечений
Увеличьте значение Number of consecutive zero crossings. опция на Solver разделяет на области в диалоговом окне Configuration Parameters.
Это может дать ваше время достаточно модели, чтобы разрешить нулевое пересечение.
Ослабьте Signal threshold
Выберите Adaptive из выпадающего Algorithm и увеличьте значение опции Signal threshold на панели Solver в диалоговом окне Configuration Parameters.
Решатель требует, чтобы меньше времени точно определило местоположение нулевого пересечения. Это может уменьшать время симуляции и устранить чрезмерное количество последовательных ошибок пересечения нулем. Однако ослабление Signal threshold может уменьшать точность.
Используйте алгоритм Adaptive
Выберите Adaptive из Algorithm, выпадающего на панели Solver в диалоговом окне Configuration Parameters.
Этот алгоритм динамически настраивает порог пересечения нулем, который улучшает точность и сокращает количество последовательных нулевых обнаруженных пересечений. С этим алгоритмом у вас есть опция определения и Time tolerance и Signal threshold.
Отключите обнаружение пересечения нулем для определенного блока
Снимите флажок Enable zero-crossing detection на диалоговом окне параметра блока.
Выберите Use local settings от Zero-crossing control, выпадающего на панели Solver диалогового окна Configuration Parameters.
Локально отключающее обнаружение пересечения нулем препятствует тому, чтобы определенный блок остановил симуляцию из-за чрезмерных последовательных нулевых пересечений. Все другие блоки продолжают извлекать выгоду из увеличенной точности, которую обеспечивает обнаружение пересечения нулем.
Отключите обнаружение пересечения нулем для целой модели
Выберите Disable all от Zero-crossing control, выпадающего на панели Solver диалогового окна Configuration Parameters.
Это препятствует тому, чтобы нулевые пересечения были обнаружены где угодно в вашей модели. Последствие — то, что ваш номер модели более длинные преимущества от увеличенной точности, которую обеспечивает обнаружение пересечения нулем.
При использовании ode15s решатель, рассмотрите корректировку порядка числовых формул дифференцирования
Выберите значение из Maximum order выпадающий на панели Solver диалогового окна Configuration Parameters.
Для получения дополнительной информации смотрите Максимальный порядок.
Уменьшайте максимальный размер шага
Введите значение для Max step size опция на панели Solver диалогового окна Configuration Parameters.
Решатель предпринимает шаги достаточно маленький, чтобы разрешить нулевое пересечение. Однако сокращение размера шага может увеличить время симуляции и редко необходимо при использовании адаптивного алгоритма.
Как средство моделирования может пропустить События пересечения нулем
Возврат и модели двойного возврата, в Симуляции Прыгающего мяча и Двойного Прыгающего мяча: Использование Адаптивного Местоположения Пересечения нулем показывает, что высокочастотные колебания о разрыве (болтовня) могут заставить симуляцию преждевременно останавливаться.
Для решателя также возможно полностью пропустить нулевые пересечения, если ошибочные допуски решателя являются слишком большими. Это возможно, потому что проверки метода обнаружения пересечения нулем, чтобы видеть, изменило ли значение сигнала знак после главного временного шага. Изменение знака указывает, что произошло нулевое пересечение, и алгоритм пересечения нулем ищет точное время пересечения. Однако, если нулевое пересечение происходит во временном шаге, но значения вначале и конец шага не указывают на изменение знака, решатель переступает через пересечение, не обнаруживая его.
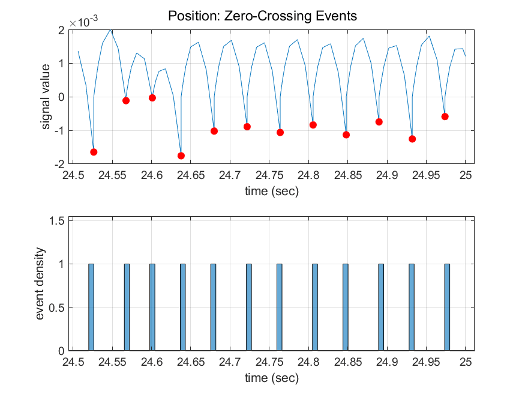
Следующий рисунок показывает сигнал, что кресты обнуляют. Прежде всего интегратор переступает через событие, потому что знак не изменился между временными шагами. Во втором решатель обнаруживает изменение знака и поэтому обнаруживает событие пересечения нулем.
Рассмотрите реализацию 2D интегратора модели возврата.
Профилирование прошлых 0,5 с симуляции с помощью Solver Profiler показывает, что симуляция обнаруживает 44 события пересечения нулем в блоке Compare To Zero и 22 события при выходе блока Position .
Увеличьте значение параметра Relative tolerance к 1e-2 вместо 1e-3 по умолчанию . Можно изменить этот параметр в разделе Solver Details панели Solver в диалоговом окне Configuration Parameters или использовании set_param задавать RelTol как ‘1e-2’ .
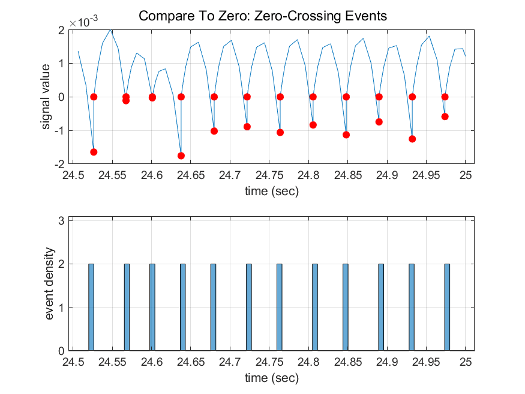
Профилирование прошлых 0,5 с симуляции с новой относительной погрешностью решателя показывает, что обнаруживает только 24 события пересечения нулем в блоке Compare To Zero и 12 событий при выходе блока Position .
Обнаружение пересечения нулем в блоках
Блок может указать набор переменных пересечения нулем, каждая из которых является функцией переменной состояния, которая может иметь разрыв. Функция пересечения нулем проходит через нуль от положительной или отрицательной величины, когда соответствующий разрыв происходит. Зарегистрированные переменные пересечения нулем обновляются в конце каждого шага симуляции, и любая переменная, которая изменила знак, идентифицирована как имевший событие пересечения нулем.
Если какие-либо нулевые пересечения обнаруживаются, программное обеспечение Simulink интерполирует между предыдущими и текущими значениями каждой переменной, которая изменила знак, чтобы оценить времена нулевых пересечений, то есть, разрывов.
Примечание
Алгоритм обнаружения Пересечения нулем может заключить в скобки события пересечения нулем только для сигналов типа данных double .
Блоки тот нуль регистра пересечения
В следующей таблице перечислены блоки, которые указывают нулевые пересечения, и объясняет, как блоки используют нулевые пересечения.
| Измените тип | Измените процедуру | Преимущества |
|---|---|---|
Один, чтобы обнаружить, когда входной сигнал пересекает нуль или в повышении или в падающем направлении.
Два, один, чтобы обнаружить, когда верхний порог занят, и один, чтобы обнаружить, когда более низкий порог занят.
Один, чтобы обнаружить, когда сигнал равняется константе.
Один, чтобы обнаружить, когда сигнал равняется нулю.
Два, один, чтобы обнаружить, когда мертвая зона вводится (входной сигнал минус нижний предел), и один, чтобы обнаружить, когда из мертвой зоны выходят (входной сигнал минус верхний предел).
Один, Если порт Enable в блоке Subsystem, он предусматривает возможность обнаружить нулевые пересечения. Для получения дополнительной информации, Используя Enabled Подсистемы.
Один, чтобы обнаружить, когда входной сигнал имеет разрыв или в повышении или в падающем направлении
Один, чтобы обнаружить, когда входной сигнал имеет разрыв или в повышении или в падающем направлении
Один или два. Если нет никакого выходного порта, существует только один нуль, пересекающийся, чтобы обнаружить, когда входной сигнал поразил пороговое значение. Если существует выходной порт, второе нулевое пересечение используется, чтобы возвратить выход 0 от 1, чтобы создать подобный импульсу выход.
Один, чтобы обнаружить, когда, Если условие соблюдают.
Если порт сброса присутствует, чтобы обнаружить, когда сброс происходит.
Если выход ограничивается, существует три нулевых пересечения: один, чтобы обнаружить, когда верхний предел насыщения достигнут, один, чтобы обнаружить, когда более низкий предел насыщения достигнут, и один, чтобы обнаружить, когда насыщение оставляют.
Один, для каждого элемента выходного вектора, чтобы обнаружить, когда входной сигнал является новым минимумом или максимумом.
Один, чтобы обнаружить, когда заданное отношение верно.
Один, если реле выключено, чтобы обнаружить переключатель — на точке. Если реле работает, чтобы обнаружить выключать точку.
Два, один, чтобы обнаружить, когда верхний предел достигнут или оставлен, и один, чтобы обнаружить, когда нижний предел достигнут или оставлен.
Пять, два, чтобы обнаружить, когда state x верхнее или нижний предел достигнуты, два, чтобы обнаружить, когда dx состояния/ dt верхний или нижний предел достигнут, и один, чтобы обнаружить, когда состояние оставляет насыщение.
Один, чтобы обнаружить, когда вход пересекается через нуль.
Один, чтобы обнаружить, когда входной сигнал имеет разрыв или в повышении или в падающем направлении
Один, чтобы обнаружить время шага.
Один, чтобы обнаружить, когда условие переключателя происходит.
Один, чтобы обнаружить, когда условие случая соблюдают.
Один, Если порт Triggered в блоке Subsystem, он предусматривает возможность обнаружить нулевые пересечения. Для получения дополнительной информации смотрите Используя Триггируемые подсистемы.
Два, один для разрешать порта и один для триггерного порта. Для получения дополнительной информации см.: Используя Enabled и Triggered подсистемы
Примечание
Обнаружение пересечения нулем также доступно для Stateflow ® стройте диаграмму, который использует режим непрерывного времени. Смотрите Конфигурируют диаграмму Stateflow для Симуляции Непрерывного времени (Stateflow) для получения дополнительной информации.
Пример реализации: блок насыщения
Примером блока Simulink, который указывает нулевые пересечения, является блок Saturation. Обнаружение пересечения нулем идентифицирует эти события состояния в блоке Saturation:
Входной сигнал достигает верхнего предела.
Входной сигнал оставляет верхний предел.
Входной сигнал достигает нижнего предела.
Входной сигнал оставляет нижний предел.
Блоки Simulink, которые задают их собственные события состояния, как рассматривается, имеют внутренние нулевые пересечения . Используйте блок Hit Crossing, чтобы получить явное уведомление о событии пересечения нулем. Смотрите Блоки, Что Нулевые Пересечения Регистра для списка блоков, которые включают нулевые пересечения.
Обнаружение события состояния зависит от конструкции внутреннего сигнала пересечения нулем. Этот сигнал не доступен блок-схемой. Для блока Saturation сигналом, который используется, чтобы обнаружить нулевые пересечения для верхнего предела, является zcSignal = UpperLimit U , где u входной сигнал.
Сигналы пересечения нулем имеют атрибут направления, который может иметь эти значения:
при повышении — происходит нулевое пересечение, когда сигнал повышается до или через нуль, или когда сигнал оставляет нуль и становится положительным.
при падении — происходит нулевое пересечение, когда сигнал падает на или через нуль, или когда сигнал оставляет нуль и становится отрицательным.
также — Нулевое пересечение происходит, если или повышение или падающее условие происходят.
Для верхнего предела блока Saturation направление нулевого пересечения также . Это позволяет вводу и отъезду событий насыщения быть обнаруженным с помощью того же сигнала пересечения нулем.
Похожие темы
Открытый пример
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
Источник
Adblock
detector
| Блок | Количество нулевых обнаружений пересечения |
|---|---|
Модератор: vetal
Andreyak777 » Пн авг 04, 2014 12:10 pm
То, что другие люди говорят обо мне, никак не характеризует меня. Зато отлично характеризует их.
-
Andreyak777
- Избран тонером
-
Князь » Пн авг 04, 2014 12:15 pm

Добавлено спустя 4 минуты 28 секунд:
Andreyak777 писал(а):U163
Это ты про что?
Добавлено спустя 14 минут 44 секунды:
Я понял про что ты! Но это принтер!
-
Князь
- Учит других ломать принтеры
-
- Сайт
- ICQ
- Персональный альбом
Andreyak777 » Пн авг 04, 2014 12:42 pm
То, что другие люди говорят обо мне, никак не характеризует меня. Зато отлично характеризует их.
-
Andreyak777
- Избран тонером
-
Andreyak777 » Пн авг 04, 2014 12:43 pm
То, что другие люди говорят обо мне, никак не характеризует меня. Зато отлично характеризует их.
-
Andreyak777
- Избран тонером
-
Князь » Пн авг 04, 2014 12:49 pm
Andreyak777 писал(а):компом определяется?
Блин я его уже разобрал=) Сегодня не успею! Завтра проверю! Но по факту при замене форматера проблема уходит!
-
Князь
- Учит других ломать принтеры
-
- Сайт
- ICQ
- Персональный альбом
Князь » Вт авг 05, 2014 8:31 am
СТРОНЦИЙ писал(а):Князь, дорогой, а ты пробовал обновить прошивку ? Если уж и прошивка не поможет то бери форматер, тот что испытал на себе силу грозы, лопату, и выкапывай ему могилку, другого варианта нет. Если форматер «сдох» то значит «сдох».
Да и мануалка советует при подобной ошибке менять форматер.
Прошивку обновлять не пробовал, но попробую!
dviz писал(а):Насколько я помню, это проблема БП, но она куда-то в память записывается и надо сбрасывать. В 1120D может есть какой-нибудь полный сброс памяти?
Проблема была в БП, потом я его заменил на аналогичный! Про сброс памяти не в курсе на плате только флэшка M29W320EB и 24С64
-
Князь
- Учит других ломать принтеры
-
- Сайт
- ICQ
- Персональный альбом
Князь » Пн авг 11, 2014 5:24 am

З.Ы. Собственно дамп
DUMP_24C64_Kuocera_FS-1120D
Последний раз редактировалось Князь Пн авг 11, 2014 7:45 am, всего редактировалось 2 раз(а).
- За это сообщение автора Князь поблагодарили: 2
- andrei_busko, apopovv
-
Князь
- Учит других ломать принтеры
-
- Сайт
- ICQ
- Персональный альбом
-
-
Kyocera 1035 «бледная» печать
srMax в форуме Принтеры, МФУ, факсы, копиры формата A4
- 2
- 13593
srMax
Пт янв 23, 2015 2:49 pm
-
Kyocera 1035 «бледная» печать
-
-
Taskalfa 180 ошибка «Е» и «Встряхните картр. с тонером»
manik.76 в форуме Принтеры, МФУ, копиры формата A3
- 3
- 9235
dviz
Пн фев 20, 2017 1:35 pm
-
Taskalfa 180 ошибка «Е» и «Встряхните картр. с тонером»
-
-
Kyocera Ecosys M2635dn «поворот» изображения
Искатель в форуме Принтеры, МФУ, факсы, копиры формата A4
- 10
- 5779
MatrixAgent
Ср апр 08, 2020 5:18 am
-
Kyocera Ecosys M2635dn «поворот» изображения
-
-
Стирание вала ведущей шестерни в «печке» Kyocera M2035dn
Грецкий орех в форуме Принтеры, МФУ, факсы, копиры формата A4
- 12
- 2973
СТРОНЦИЙ
Пн дек 13, 2021 3:35 pm
-
Стирание вала ведущей шестерни в «печке» Kyocera M2035dn
-
-
Kyocera taskalfa 3501 «открыта крышка основного блока»
Юрий Яраскин в форуме Принтеры, МФУ, копиры формата A3
- 3
- 2676
Goldwater
Пт сен 10, 2021 1:31 pm
-
Kyocera taskalfa 3501 «открыта крышка основного блока»
Вернуться в Принтеры, МФУ, факсы, копиры формата A4
Кто сейчас на форуме
Сейчас этот форум просматривают: Владислав Петунин и гости: 56
Обнаружение пересечения нулем
Решатель переменного шага динамически настраивает размер временного шага, заставляя его увеличиться, когда переменная изменяется медленно и уменьшиться, когда переменная изменяется быстро. Это поведение заставляет решатель делать много небольших шагов около разрыва, потому что переменная быстро изменяется в этой области. Это улучшает точность, но может привести к чрезмерным временам симуляции.
Simulink® использует метод, который, как известно как обнаружение пересечения нулем, точно определял местоположение разрыва, не обращаясь к чрезмерно маленьким временным шагам. Обычно этот метод улучшает время выполнения симуляции, но это может заставить некоторые симуляции останавливаться перед намеченным временем завершения.
Simulink использует два алгоритма с этой целью: неадаптивный и адаптивный. Для получения информации об этих методах см. Алгоритмы Пересечения нулем.
Демонстрация эффектов чрезмерного обнаружения пересечения нулем
Этот пример предоставляет три модели, которые иллюстрируют поведение пересечения нулем: example_bounce_two_integrators, example_doublebounce, и example_bounce.
example_bounce_two_integrators модель демонстрирует, как чрезмерные нулевые пересечения могут заставить симуляцию останавливаться перед намеченным временем завершения, если вы не используете адаптивный алгоритм.
example_bounce модель использует лучший проект модели, реализовывая динамику мяча с помощью двойного интегратора, чем example_bounce_two_integrators.
example_doublebounce модель демонстрирует, как адаптивный алгоритм успешно решает сложную систему с двумя отличными требованиями пересечения нулем.
Рассмотрите example_bounce_two_integrators модель. Это использует два один интегратора, чтобы вычислить вертикальную скорость и положение мяча за время симуляции.
-
Откройте модель путем выполнения
open_system('example_bounce_two_integrators')в командной строке. -
Если блок-схема появляется, установите детали Решателя> опции Пересечения нулем> Параметр алгоритма в панели Решателя параметров конфигурации Модели к
Nonadaptive. Установите время остановки модели к 20 с. Можно изменить эти настройки в панели инструментов Simulink или панели Решателя параметров конфигурации модели. -
Симулируйте модель.
Можно теперь просмотреть и анализировать результаты симуляции.
После более близкого исследования последнего фрагмента симуляции вы будете видеть, что скорость наводит чуть выше нуля.
Измените Время остановки симуляции в 25 с и симулируйте модель. Симуляция останавливается с ошибкой из-за чрезмерных последовательных событий пересечения нулем при Сравнивании С блоками Нуля и Положения.
Simulink will stop the simulation of model 'example_bounce_two_integrators' because the 2 zero crossing signal(s) identified below caused 1000 consecutive zero crossing events in time interval between 20.357636989536076 and 20.357636990631594.
--------------------------------------------------------------------------------
Number of consecutive zero-crossings : 1000
Zero-crossing signal name : RelopInput
Block type : RelationalOperator
Block path : 'example_bounce_two_integrators/Compare To Zero/Compare'
--------------------------------------------------------------------------------
--------------------------------------------------------------------------------
Number of consecutive zero-crossings : 500
Zero-crossing signal name : IntgLoLimit
Block type : Integrator
Block path : 'example_bounce_two_integrators/Position'
--------------------------------------------------------------------------------
Несмотря на то, что можно увеличить этот предел путем корректировки Параметров конфигурации Модели> Решатель>, Количество последовательного нулевого параметра пересечений, внося то изменение все еще не позволяет симуляции продолжаться в течение 25 с.
Измените детали Решателя> опции Пересечения нулем> Параметр алгоритма в панели Решателя параметров конфигурации Модели к Adaptive и симулируйте модель снова в течение 25 с.
Увеличивая масштаб прошлых 5 секунд симуляции, вы видите, что результаты — больше завершенное и ближе к ожидаемому аналитическому решению динамики прыгающего мяча. Сумма болтовни, которую вы видите, является последствием состояний системы, приближающихся к нулю, и ожидается в числовых симуляциях.
example_bounce модель использует блок Second-Order Integrator, чтобы смоделировать динамику прыгающего мяча. Это — предпочтительный метод смоделировать двойное интегрирование динамики мяча для эффективности решателя. Сравнить эффективность решателя для example_bounce_two_integrators и example_bounce, попытайтесь запустить Solver Profiler на обеих моделях. Для подробного сравнения обеих моделей смотрите Симуляцию Прыгающего мяча.
Для сравнения друг с другом адаптивных и неадаптивных алгоритмов обнаружения пересечения нулем смотрите Двойной Прыгающий мяч: Использование Адаптивного Местоположения Пересечения нулем.
Предотвращение чрезмерных нулевых пересечений
Используйте следующую таблицу, чтобы предотвратить чрезмерные ошибки пересечения нулем в вашей модели.
| Измените тип | Измените процедуру | Преимущества |
|---|---|---|
|
Увеличьте число позволенных нулевых пересечений |
Увеличьте значение Number of consecutive zero crossings. опция на Solver разделяет на области в диалоговом окне Configuration Parameters. |
Это может дать ваше время достаточно модели, чтобы разрешить нулевое пересечение. |
|
Ослабьте Signal threshold |
Выберите Adaptive из выпадающего Algorithm и увеличьте значение опции Signal threshold на панели Solver в диалоговом окне Configuration Parameters. |
Решатель требует, чтобы меньше времени точно определило местоположение нулевого пересечения. Это может уменьшать время симуляции и устранить чрезмерное количество последовательных ошибок пересечения нулем. Однако ослабление Signal threshold может уменьшать точность. |
|
Используйте алгоритм Adaptive |
Выберите Adaptive из Algorithm, выпадающего на панели Solver в диалоговом окне Configuration Parameters. |
Этот алгоритм динамически настраивает порог пересечения нулем, который улучшает точность и сокращает количество последовательных нулевых обнаруженных пересечений. С этим алгоритмом у вас есть опция определения и Time tolerance и Signal threshold. |
|
Отключите обнаружение пересечения нулем для определенного блока |
|
Локально отключающее обнаружение пересечения нулем препятствует тому, чтобы определенный блок остановил симуляцию из-за чрезмерных последовательных нулевых пересечений. Все другие блоки продолжают извлекать выгоду из увеличенной точности, которую обеспечивает обнаружение пересечения нулем. |
|
Отключите обнаружение пересечения нулем для целой модели |
Выберите |
Это препятствует тому, чтобы нулевые пересечения были обнаружены где угодно в вашей модели. Последствие — то, что ваш номер модели более длинные преимущества от увеличенной точности, которую обеспечивает обнаружение пересечения нулем. |
|
При использовании |
Выберите значение из |
Для получения дополнительной информации смотрите Максимальный порядок. |
|
Уменьшайте максимальный размер шага |
Введите значение для |
Решатель предпринимает шаги достаточно маленький, чтобы разрешить нулевое пересечение. Однако сокращение размера шага может увеличить время симуляции и редко необходимо при использовании адаптивного алгоритма. |
Как средство моделирования может пропустить События пересечения нулем
Возврат и модели двойного возврата, в Симуляции Прыгающего мяча и Двойного Прыгающего мяча: Использование Адаптивного Местоположения Пересечения нулем показывает, что высокочастотные колебания о разрыве (болтовня) могут заставить симуляцию преждевременно останавливаться.
Для решателя также возможно полностью пропустить нулевые пересечения, если ошибочные допуски решателя являются слишком большими. Это возможно, потому что проверки метода обнаружения пересечения нулем, чтобы видеть, изменило ли значение сигнала знак после главного временного шага. Изменение знака указывает, что произошло нулевое пересечение, и алгоритм пересечения нулем ищет точное время пересечения. Однако, если нулевое пересечение происходит во временном шаге, но значения вначале и конец шага не указывают на изменение знака, решатель переступает через пересечение, не обнаруживая его.
Следующий рисунок показывает сигнал, что кресты обнуляют. Прежде всего интегратор переступает через событие, потому что знак не изменился между временными шагами. Во втором решатель обнаруживает изменение знака и поэтому обнаруживает событие пересечения нулем.
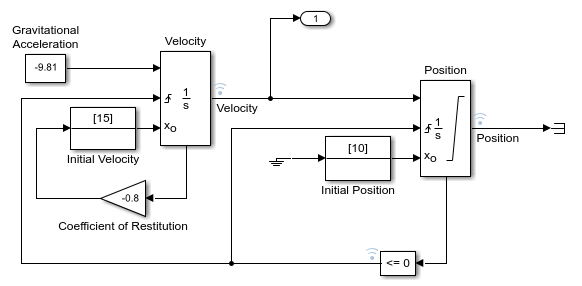
Рассмотрите реализацию 2D интегратора модели возврата.
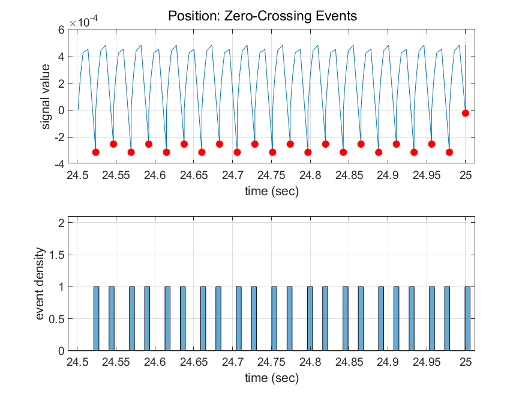
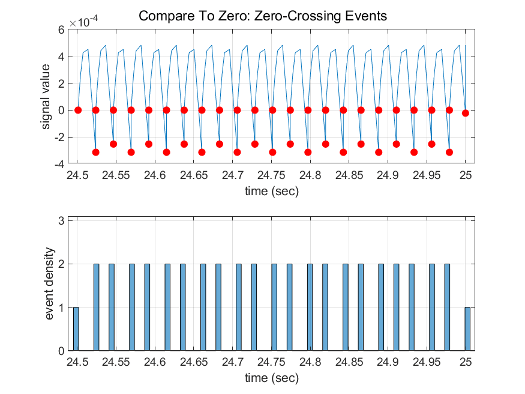
Профилирование прошлых 0,5 с симуляции с помощью Solver Profiler показывает, что симуляция обнаруживает 44 события пересечения нулем в блоке Compare To Zero и 22 события при выходе блока Position.
Увеличьте значение параметра Relative tolerance к 1e-2 вместо 1e-3 по умолчанию. Можно изменить этот параметр в разделе Solver Details панели Solver в диалоговом окне Configuration Parameters или использовании set_param задавать RelTol как '1e-2'.
Профилирование прошлых 0,5 с симуляции с новой относительной погрешностью решателя показывает, что обнаруживает только 24 события пересечения нулем в блоке Compare To Zero и 12 событий при выходе блока Position.
Обнаружение пересечения нулем в блоках
Блок может указать набор переменных пересечения нулем, каждая из которых является функцией переменной состояния, которая может иметь разрыв. Функция пересечения нулем проходит через нуль от положительной или отрицательной величины, когда соответствующий разрыв происходит. Зарегистрированные переменные пересечения нулем обновляются в конце каждого шага симуляции, и любая переменная, которая изменила знак, идентифицирована как имевший событие пересечения нулем.
Если какие-либо нулевые пересечения обнаруживаются, программное обеспечение Simulink интерполирует между предыдущими и текущими значениями каждой переменной, которая изменила знак, чтобы оценить времена нулевых пересечений, то есть, разрывов.
Примечание
Алгоритм обнаружения Пересечения нулем может заключить в скобки события пересечения нулем только для сигналов типа данных double.
Блоки тот нуль регистра пересечения
В следующей таблице перечислены блоки, которые указывают нулевые пересечения, и объясняет, как блоки используют нулевые пересечения.
| Блок | Количество нулевых обнаружений пересечения |
|---|---|
|
Abs |
Один, чтобы обнаружить, когда входной сигнал пересекает нуль или в повышении или в падающем направлении. |
|
Backlash |
Два, один, чтобы обнаружить, когда верхний порог занят, и один, чтобы обнаружить, когда более низкий порог занят. |
|
Сравните с постоянным |
Один, чтобы обнаружить, когда сигнал равняется константе. |
|
Сравните с нулем |
Один, чтобы обнаружить, когда сигнал равняется нулю. |
|
Dead Zone |
Два, один, чтобы обнаружить, когда мертвая зона вводится (входной сигнал минус нижний предел), и один, чтобы обнаружить, когда из мертвой зоны выходят (входной сигнал минус верхний предел). |
|
Enable |
Один, Если порт Enable в блоке Subsystem, он предусматривает возможность обнаружить нулевые пересечения. Для получения дополнительной информации, Используя Enabled Подсистемы. |
|
From File |
Один, чтобы обнаружить, когда входной сигнал имеет разрыв или в повышении или в падающем направлении |
|
From Workspace |
Один, чтобы обнаружить, когда входной сигнал имеет разрыв или в повышении или в падающем направлении |
|
Hit Crossing |
Один или два. Если нет никакого выходного порта, существует только один нуль, пересекающийся, чтобы обнаружить, когда входной сигнал поразил пороговое значение. Если существует выходной порт, второе нулевое пересечение используется, чтобы возвратить выход 0 от 1, чтобы создать подобный импульсу выход. |
|
If |
Один, чтобы обнаружить, когда, Если условие соблюдают. |
|
Integrator |
Если порт сброса присутствует, чтобы обнаружить, когда сброс происходит. Если выход ограничивается, существует три нулевых пересечения: один, чтобы обнаружить, когда верхний предел насыщения достигнут, один, чтобы обнаружить, когда более низкий предел насыщения достигнут, и один, чтобы обнаружить, когда насыщение оставляют. |
|
MinMax |
Один, для каждого элемента выходного вектора, чтобы обнаружить, когда входной сигнал является новым минимумом или максимумом. |
|
Relational Operator |
Один, чтобы обнаружить, когда заданное отношение верно. |
|
Relay |
Один, если реле выключено, чтобы обнаружить переключатель — на точке. Если реле работает, чтобы обнаружить выключать точку. |
|
Saturation |
Два, один, чтобы обнаружить, когда верхний предел достигнут или оставлен, и один, чтобы обнаружить, когда нижний предел достигнут или оставлен. |
|
Second-Order Integrator |
Пять, два, чтобы обнаружить, когда state x верхнее или нижний предел достигнуты, два, чтобы обнаружить, когда dx состояния/dt верхний или нижний предел достигнут, и один, чтобы обнаружить, когда состояние оставляет насыщение. |
|
Sign |
Один, чтобы обнаружить, когда вход пересекается через нуль. |
|
Signal Editor |
Один, чтобы обнаружить, когда входной сигнал имеет разрыв или в повышении или в падающем направлении |
|
Step |
Один, чтобы обнаружить время шага. |
|
Switch |
Один, чтобы обнаружить, когда условие переключателя происходит. |
|
Switch Case |
Один, чтобы обнаружить, когда условие случая соблюдают. |
|
Trigger |
Один, Если порт Triggered в блоке Subsystem, он предусматривает возможность обнаружить нулевые пересечения. Для получения дополнительной информации смотрите Используя Триггируемые подсистемы. |
|
Enabled and Triggered Subsystem |
Два, один для разрешать порта и один для триггерного порта. Для получения дополнительной информации см.: Используя Enabled и Triggered подсистемы |
Пример реализации: блок насыщения
Примером блока Simulink, который указывает нулевые пересечения, является блок Saturation. Обнаружение пересечения нулем идентифицирует эти события состояния в блоке Saturation:
-
Входной сигнал достигает верхнего предела.
-
Входной сигнал оставляет верхний предел.
-
Входной сигнал достигает нижнего предела.
-
Входной сигнал оставляет нижний предел.
Блоки Simulink, которые задают их собственные события состояния, как рассматривается, имеют внутренние нулевые пересечения. Используйте блок Hit Crossing, чтобы получить явное уведомление о событии пересечения нулем. Смотрите Блоки, Что Нулевые Пересечения Регистра для списка блоков, которые включают нулевые пересечения.
Обнаружение события состояния зависит от конструкции внутреннего сигнала пересечения нулем. Этот сигнал не доступен блок-схемой. Для блока Saturation сигналом, который используется, чтобы обнаружить нулевые пересечения для верхнего предела, является zcSignal = UpperLimit U, где u входной сигнал.
Сигналы пересечения нулем имеют атрибут направления, который может иметь эти значения:
-
при повышении — происходит нулевое пересечение, когда сигнал повышается до или через нуль, или когда сигнал оставляет нуль и становится положительным.
-
при падении — происходит нулевое пересечение, когда сигнал падает на или через нуль, или когда сигнал оставляет нуль и становится отрицательным.
-
также — Нулевое пересечение происходит, если или повышение или падающее условие происходят.
Для верхнего предела блока Saturation направление нулевого пересечения также. Это позволяет вводу и отъезду событий насыщения быть обнаруженным с помощью того же сигнала пересечения нулем.
Похожие темы
- Концепции Алгебраических циклов
- Сравните решатели
A variable-step solver dynamically adjusts the time step size, causing it to increase when
a variable is changing slowly and to decrease when the variable changes rapidly. This
behavior causes the solver to take many small steps in the vicinity of a discontinuity
because the variable is rapidly changing in this region. This improves accuracy but can lead
to excessive simulation times.
Simulink® uses a technique known as zero-crossing detection to
accurately locate a discontinuity without resorting to excessively small time steps. Usually
this technique improves simulation run time, but it can cause some simulations to halt
before the intended completion time.
Simulink uses two algorithms for this purpose: nonadaptive and adaptive. For
information about these techniques, see Zero-Crossing Algorithms.
Demonstrating Effects of Excessive Zero-Crossing Detection
This example provides three models that illustrate zero-crossing behavior: example_bounce_two_integrators, example_doublebounce, and example_bounce.
The example_bounce_two_integrators model demonstrates how excessive zero crossings can cause a simulation to halt before the intended completion time unless you use the adaptive algorithm.
The example_bounce model uses a better model design, implementing the dynamics of the ball using a double integrator, than example_bounce_two_integrators.
The example_doublebounce model demonstrates how the adaptive algorithm successfully solves a complex system with two distinct zero-crossing requirements.
Consider the example_bounce_two_integrators model. It uses two single integrators to compute the vertical velocity and position of the ball over the time of the simulation.
-
Open the model by running
open_system('example_bounce_two_integrators')at the command line. -
Once the block diagram appears, set the Solver details > Zero-crossing options > Algorithm parameter in the Solver pane of the Model configuration parameters to
Nonadaptive. Set the stop time of the model to 20 s. You can change this setting in the Simulink toolstrip or the Solver pane of the model configuration parameters. -
Simulate the model.
You can now view and analyze the simulation results.
Upon closer examination of the last portion of the simulation, you will see that velocity hovers just above zero.
Change the simulation Stop time to 25 s and simulate the model. The simulation stops with an error due to excessive consecutive zero-crossing events at the Compare To Zero and Position blocks.
Simulink will stop the simulation of model 'example_bounce_two_integrators' because the 2 zero crossing signal(s) identified below caused 1000 consecutive zero crossing events in time interval between 20.357636989536076 and 20.357636990631594.
--------------------------------------------------------------------------------
Number of consecutive zero-crossings : 1000
Zero-crossing signal name : RelopInput
Block type : RelationalOperator
Block path : 'example_bounce_two_integrators/Compare To Zero/Compare'
--------------------------------------------------------------------------------
--------------------------------------------------------------------------------
Number of consecutive zero-crossings : 500
Zero-crossing signal name : IntgLoLimit
Block type : Integrator
Block path : 'example_bounce_two_integrators/Position'
--------------------------------------------------------------------------------
Although you can increase this limit by adjusting the Model Configuration Parameters > Solver > Number of consecutive zero crossings parameter, making that change still does not allow the simulation to go on for 25 s.
Change the Solver details > Zero-crossing options > Algorithm parameter in the Solver pane of the Model configuration parameters to Adaptive and simulate the model again for 25 s.
Zooming in on the last 5 seconds of the simulation, you can see that the results are more complete and closer to the expected analytical solution of the dynamics of a bouncing ball. The amount of chatter you see is a consequence of the system’s states approaching zero and is expected in numerical simulations.
The example_bounce model uses a Second-Order Integrator block to model the dynamics of the bouncing ball. This is the preferred method to model the double integration of the ball’s dynamics for solver performance. To compare the solver performance for example_bounce_two_integrators and example_bounce, try running the Solver Profiler on both models. For a detailed comparison of both models, see Simulation of Bouncing Ball.
For a side-by-side comparison of adaptive and nonadaptive zero-crossing detection algorithms, see Double Bouncing Ball: Use of Adaptive Zero-Crossing Location.
Preventing Excessive Zero Crossings
Use the following table to prevent excessive zero-crossing errors in your
model.
| Change Type | Change Procedure | Benefits |
|---|---|---|
|
Increase the number of allowed zero |
Increase the value of the Number of consecutive |
This may give your model enough time to resolve the zero |
|
Relax the Signal |
Select Adaptive from the |
The solver requires less time to precisely locate the zero |
|
Use the Adaptive |
Select Adaptive from the |
This algorithm dynamically adjusts the zero-crossing |
|
Disable zero-crossing detection for a specific |
|
Locally disabling zero-crossing detection prevents a |
|
Disable zero-crossing detection for the entire |
Select |
This prevents zero crossings from being detected anywhere |
|
If using the |
Select a value from the |
For more information, see Maximum order. |
|
Reduce the maximum step size |
Enter a value for the |
The solver takes steps small enough to resolve the zero |
How the Simulator Can Miss Zero-Crossing Events
The bounce and double-bounce models, in Simulation of Bouncing Ball and Double Bouncing Ball: Use of Adaptive Zero-Crossing Location show that high-frequency fluctuations
about a discontinuity (chattering) can cause a simulation to prematurely halt.
It is also possible for the solver to entirely miss zero crossings if the solver error
tolerances are too large. This is possible because the zero-crossing detection technique
checks to see if the value of a signal has changed sign after a major time step. A sign
change indicates that a zero crossing has occurred, and the zero-crossing algorithm
searches for the precise crossing time. However, if a zero crossing occurs within a time
step, but the values at the beginning and end of the step do not indicate a sign change,
the solver steps over the crossing without detecting it.
The following figure shows a signal that crosses zero. In the first instance, the
integrator steps over the event because the sign has not changed between time steps. In
the second, the solver detects sign change and therefore detects the zero-crossing
event.
Consider the two-integrator implementation of the bounce model.
Profiling of the last 0.5 s of the simulation using the Solver Profiler shows that the
simulation detects 44 zero-crossing events at the Compare To Zero block
and 22 events at the output of the Position block.
Increase the value of the Relative tolerance parameter to
1e-2 instead of the default 1e-3. You can
change this parameter in the Solver Details section of the
Solver pane in the Configuration
Parameters dialog or using set_param to specify
RelTol as '1e-2'.
Profiling the last 0.5 s of the simulation with the new relative tolerance of the
solver shows that it detects only 24 zero-crossing events at the Compare To
Zero block and 12 events at the output of the Position
block.
Zero-Crossing Detection in Blocks
A block can register a set of zero-crossing variables, each of which is a function of
a state variable that can have a discontinuity. The zero-crossing function passes
through zero from a positive or negative value when the corresponding discontinuity
occurs. The registered zero-crossing variables are updated at the end of each simulation
step, and any variable that has changed sign is identified as having had a zero-crossing
event.
If any zero crossings are detected, the Simulink software interpolates between the previous and current values of each
variable that changed sign to estimate the times of the zero crossings, that is, the discontinuities.
Note
The Zero-Crossing detection algorithm can bracket zero-crossing events only
for signals of data type double.
Blocks That Register Zero Crossings
The following table lists blocks that register zero crossings and explains how the
blocks use the zero crossings.
| Block | Number of Zero Crossing Detections |
|---|---|
|
Abs |
One, to detect when the input signal crosses zero in either |
|
Backlash |
Two, one to detect when the upper threshold is engaged, and |
|
Compare To Constant |
One, to detect when the signal equals a |
|
Compare To Zero |
One, to detect when the signal equals zero. |
|
Dead |
Two, one to detect when the dead zone is entered (the input |
|
Enable |
One, If an Enable port is inside of a Subsystem block, it |
|
From |
One, to detect when the input signal has a discontinuity in |
|
From |
One, to detect when the input signal has a discontinuity in |
|
Hit |
One or two. If there is no output port, there is only one |
|
If |
One, to detect when the If condition is met. |
|
Integrator |
If the reset port is present, to detect when a reset If the output is limited, there are three |
|
MinMax |
One, for each element of the output vector, to detect when |
|
Relational |
One, to detect when the specified relation is |
|
Relay |
One, if the relay is off, to detect the switch-on point. If |
|
Saturation |
Two, one to detect when the upper limit is reached or left, |
|
Second-Order |
Five, two to detect when the state x |
|
Sign |
One, to detect when the input crosses through |
|
Signal Editor |
One, to detect when the input signal has a discontinuity in |
|
Step |
One, to detect the step time. |
|
Switch |
One, to detect when the switch condition |
|
Switch |
One, to detect when the case condition is |
|
Trigger |
One, If a Triggered port is inside of a Subsystem block, it |
|
Enabled and Triggered |
Two, one for the enable port and one for the trigger port. |
|
From |
One, to detect when the input signal has a discontinuity in |
Implementation Example: Saturation Block
An example of a Simulink block that registers zero crossings is the Saturation block. Zero-crossing detection identifies these state events
in the Saturation block:
-
The input signal reaches the upper limit.
-
The input signal leaves the upper limit.
-
The input signal reaches the lower limit.
-
The input signal leaves the lower limit.
Simulink blocks that define their own state events are considered to have
intrinsic zero crossings. Use the Hit Crossing block to receive explicit notification of a
zero-crossing event. See Blocks That Register Zero Crossings for a list of
blocks that incorporate zero crossings.
The detection of a state event depends on the construction of an internal
zero-crossing signal. This signal is not accessible by the block diagram. For the
Saturation block, the signal that is used to detect zero crossings for the upper
limit is zcSignal = UpperLimit — u, where
u is the input signal.
Zero-crossing signals have a direction attribute, which can have these
values:
-
rising — A zero crossing occurs when a signal rises
to or through zero, or when a signal leaves zero and becomes
positive. -
falling — A zero crossing occurs when a signal falls
to or through zero, or when a signal leaves zero and becomes
negative. -
either — A zero crossing occurs if either a rising or
falling condition occurs.
For the Saturation block upper limit, the direction of the zero
crossing is either. This enables the entering and leaving
saturation events to be detected using the same zero-crossing signal.
Related Topics
- Algebraic Loop Concepts
- Compare Solvers
Timing synchronization plays the role of the heart of a digital communication system. We have already seen how a timing locked loop, commonly known as symbol timing PLL, works where I explained the intuition behind the maximum likelihood Timing Error Detector (TED). A simplified version of maximum likelihood TED, known as Early-Late Timing Error Detector, was also covered before. Today we discuss a different timing synchronization philosophy that is based on zero-crossing principle. It is commonly known as Gardner timing recovery.
Background
Before we start this topic, I recommend that you read about Pulse Amplitude Modulation (PAM) for an introduction to digital systems, the framework in which timing synchronization algorithms are described here. The notations for the main parameters are the following.
- Sample time (inverse of sample rate): $T_S$
- Symbol time (inverse of symbol rate): $T_M$
- Data symbols: $a[m]$
- Timing error: $epsilon _Delta$
- Timing error estimate: $hat epsilon _Delta$
The samples at the matched filter output in a Pulse Amplitude Modulated (PAM) system are denoted by
begin{equation*}
cdots, z((n-2)T_S), z((n-1)T_S), z(nT_S)), z((n+1)T_S), z((n+2)T_S), cdots
end{equation*}
where $T_S$ is the sampling time and the oversampling factor is 2. The question is: How do we know which sample corresponds to the symbol peak? At the startup time of the Rx, all we have is a series of samples spaced by half-symbol period $T_M/2$ where $T_M$ is the symbol time. Depending on the actual $epsilon_Delta$, we could have
begin{align*}
z((n-2)T_S) ~&rightarrow~ z((m-1)T_M+hat epsilon_Delta) quad text{Symbol Peak}\
z((n-1)T_S) ~&rightarrow~ z(mT_M-frac{T_M}{2}+hat epsilon_Delta) \
z(nT_S) ~&rightarrow~ z(mT_M+hat epsilon_Delta) quad text{Symbol Peak} \
z((n+1)T_S) ~&rightarrow~ z(mT_M+frac{T_M}{2}+hat epsilon_Delta) \
z((n+2)T_S) ~&rightarrow~ z((m+1)T_M+hat epsilon_Delta) quad text{Symbol Peak}
end{align*}
or we could have either $z((n-1)T_S)$ or $z((n+1)T_S)$ correspond to the symbol peak with other samples identified around accordingly. This is because frame synchronization can take us to the correct symbol level only, not the sample.
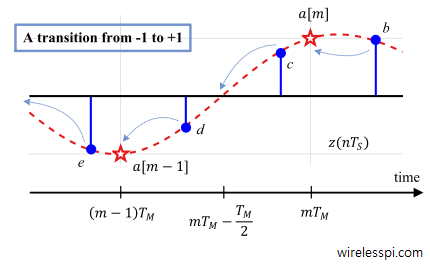
To answer this question, consider the figure below with samples denoted as $b$, $c$, $d$ and $e$.
Applying the early-late equation for three TED samples $b$, $c$ and $d$,
begin{equation*}
e_D[m] = ccdot (b-d) > 0
end{equation*}
However, if we had identified the three TED samples as $c$, $d$ and $e$, then
begin{equation}label{eqTimingSyncELTEDexample}
e_D[m] = dcdot (c-e)
end{equation}
Since $c-e$ $>$ $0$ and $d$ is negative,
begin{equation*}
d cdot(c-e) < 0
end{equation*}
Instead of $hat epsilon_Delta<epsilon_Delta$, the early-late TED then would treat this as a case of late sampling $hat epsilon_Delta>epsilon_Delta$ (and hence the negative output in the above expression). The TLL would have brought the sampling instant earlier until the middle sample $d$ reached the instant $(m-1)T_M$ and hence identified as $z((m-1)T_M)$. The left and right samples, namely $e$ and $c$, approach zero in the meanwhile, as illustrated by the figure above.
Towards Zero Crossings
An alternative strategy is a zero crossing timing error detector where the algorithm targets the zero crossings of the waveform. This is done by negating the slope. So let us find out what happens with negating the slope in an early-late expression, for which we again consider the same samples $c$, $d$ and $e$ considered above in Eq (ref{eqTimingSyncELTEDexample}) with respect to the last figure above.
begin{align*}
e_D[m] = dcdotbig{-(c-e)big} = dcdot (e-c)
end{align*}
Since $d$ is negative while $e-c$ is also negative,
begin{equation*}
d cdot(e-c) > 0
end{equation*}
Thus, the sampling instant will be pushed forward until the middle sample $d$ reaches $mT_M-T_M/2$. Then, the left neighbouring sample $e$ will coincide with symbol $a[m-1]$ while the right neighbouring sample $c$ will coincide with $a[m]$. In this game of $3$ samples, the middle sample approaches the zero crossing. This is the philosophy of the zero crossing TEDs.
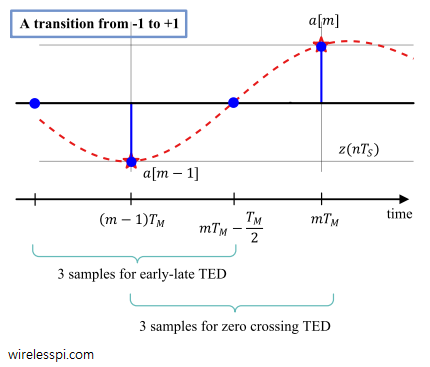
The converging locations of zero crossing TED as well as early-late TED for the above example are shown in the figure below. Notice that if we had chosen samples $b$, $c$ and $d$ in a zero crossing TED, the middle sample again would have converged towards zero.
From the above analysis, we can form a timing error detector as
begin{equation}label{eqTimingSyncGardnerTED}
e_D[m] = zleft(mT_M-frac{T_M}{2}+hat epsilon_Deltaright)bigg{zleft((m-1)T_M+hat epsilon_Deltaright) – z(mT_M+hat epsilon_Delta)bigg}
end{equation}
This non-data-aided version is called the Gardner Timing Error Detector (TED) due to its inventor F. M. Gardner. Its data-aided and decision-directed versions are commonly known as Zero Crossing Timing Error Detector (TED). By using the data symbols $a[m-1]$ and $a[m]$ in place of $z((m-1)T_M+hat epsilon_Delta)$ and $z(mT_M+hat epsilon_Delta)$, respectively, we get the data-aided variant.
begin{equation}label{eqTimingSyncZCTEDDA}
e_D[m] = zleft(mT_M-frac{T_M}{2}+hat epsilon_Deltaright)bigg{a[m-1] – a[m]bigg}
end{equation}
On the same note, a decision-directed form can be created as
begin{equation}label{eqTimingSyncZCTEDDD}
e_D[m] = zleft(mT_M-frac{T_M}{2}+hat epsilon_Deltaright)bigg{hat a[m-1] – hat a[m]bigg}
end{equation}
where the symbol decision $hat a[m]$ for a binary PAM case is
begin{equation*}
hat a[m] = A times text{sign} Big{ z(mT_M+hat epsilon_Delta)Big}
end{equation*}
Like derivative and early-late TEDs, a zero crossing approach also depends on balancing the magnitudes of two samples taken midway from either side of the symbol. Consequently, its performance also suffers when the excess bandwidth $alpha$ is small. See this article for an intuitive explanation of how excess bandwidth impacts the performance of timing synchronization.
Gardner TED is based on the ideas from a wave difference method and a digital Data Transition Tracking Loop (DTTL) (used as a symbol synchronizer in the telemetry Rx of the Mariner Mars 1969 mission.
Receiver Structure
The Rx structure for a zero crossing or Gardner TED is quite similar to that for early-late TED and is drawn in the figure below for a decision-directed setting (click on the image to enlarge it).
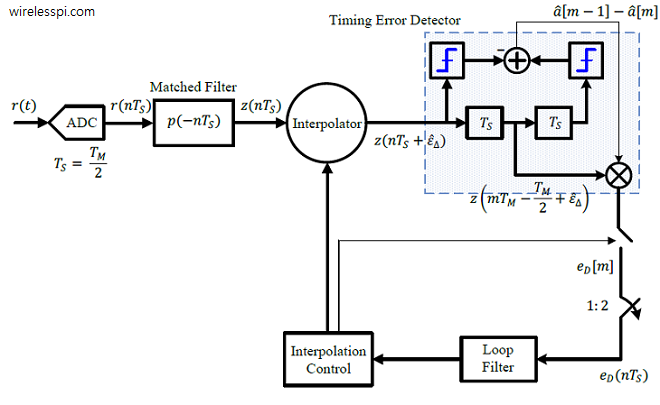
The Rx signal $r(t)$ is sampled at a rate of $F_S=2/T_M$, or $T_S=T_M/2$, to generate $r(nT_S)$ at $L=2$ samples/symbol. Next, the sampled signal $r(nT_S)$ is matched filtered at the same rate with its output being $z(nT_S)$. Under the command of an interpolation control block, an interpolator resamples these matched filter outputs at instants $hat epsilon_Delta$ to produce $z(nT_S+hat epsilon_Delta)$. Since this system runs at a rate of 2 samples/symbol, the delay block $T_S$ (that represents a delay of 1 sample) supplies the samples at half a symbol duration, i.e., $z(mT_M-T_M/2+hat epsilon_Delta)$.
The interpolation control block also identifies the time instants $(m-1)T_M$ and $mT_M$ at which the outputs $hat a[m-1]$ and $hat a[m]$ are taken out of the decision block and the error signal $e_D[m]$ is formed once per symbol. In the case of Gardner TED, the matched filter outputs $z((m-1)T_M+hat epsilon_Delta)$ and $z(mT_M+hat epsilon_Delta)$ are directly used instead of $hat a[m-1]$ and $hat a[m]$ in forming the TED output. This signal $e_D[m]$ is then upsampled by $2$ to create $e_D(nT_S)$ that then matches the sample rate $F_S$ of the loop filter and the interpolation control.
Example
Now we simulate a Gardner TED for the same set of parameters as for a derivative TED here except $L$ which is $2$ in this case, i.e.,
begin{align*}
text{Modulation} quad rightarrow&quad 2-text{PAM}, \ L quad =& quad 2 ~text{samples/symbol}, \ alpha quad =& quad 0.4, \
B_n T_Mquad =& quad 1/200, \ zeta quad =& quad 1/sqrt{2}, \ epsilon_Delta quad =& quad 0.25 T_M
end{align*}
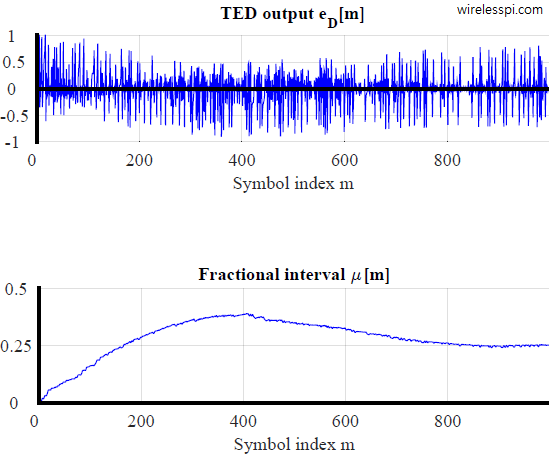
Again, the PI loop filter coefficients are computed from Eq (4) of the PLL article where $K_0$ is unity while a simple routine is used to compute the derivative of the mean curve at $epsilon_Delta=0$ for $K_D$. The output error signal $e_D[m]$ for a Gardner TED is shown in the figure below where the estimate of the timing offset $epsilon_Delta=0.25T_M$ is seen converging to its true value. We call this estimate as a fractional interval $mu[m]$. The TLL is seen to converge in approximately $800$ symbols.
Finally, the zero crossing TED for a QAM scheme is given by the sum of inphase and quadrature parts. For example, from Eq (ref{eqTimingSyncZCTEDDA}), the data-aided version can be written as
begin{equation*}
begin{aligned}
e_D[m] &= z_Ileft(mT_M-frac{T_M}{2}+hat epsilon_Deltaright)bigg{a_I[m-1] – a_I[m]bigg} + \
&hspace{.3in}z_Qleft(mT_M-frac{T_M}{2}+hat epsilon_Deltaright)bigg{a_Q[m-1] – a_Q[m]bigg}
end{aligned}
end{equation*}
Carrier Independent Operation
One of the reasons for popularity of Gardner TED was the belief that its operation is independent of the carrier phase as well as a small frequency offset. Many sources still cite the Gardner TED as having an extra feature of rotationally invariant (carrier independent operation) and hence very suitable for timing acquisition when a significant carrier phase offset and possibly a small carrier frequency offset is present in the Rx signal.
As it turns out, this carrier independent operation is not exclusive to the Gardner TED. In fact, this is a feature of the non-data-aided fashion in which the TED processes the Rx samples. For passband modulation schemes, the Gardner TED is given from complex samples by the inphase part of a conjugate product instead of a simple product.
begin{equation*}
e_D[m] = bigg[zleft(mT_M-frac{T_M}{2}+hat epsilon_Deltaright)bigg{z^*left((m-1)T_M+hat epsilon_Deltaright) – z^*left(mT_M+hat epsilon_Deltaright)bigg}bigg]_I
end{equation*}
From the definition of a complex conjugate $V^*$, we know that
begin{align*}
begin{aligned}
|V^*| &= |V| \
measuredangle V^* &= – measuredangle V
end{aligned}
end{align*}
Consequently, the phase of the middle sample is canceled by the common phase of the two samples in the brackets above. However, the non-data-aided version of early-late TED exhibits exactly the same property for complex samples.
begin{equation*}
e_D[m] = bigg[z(mT_M+hat epsilon_Delta) left{z^*left(mT_M+frac{T_M}{2}+hat epsilon_Deltaright) – z^*left(mT_M-frac{T_M}{2}+hat epsilon_Deltaright)right}bigg]_I
end{equation*}
In terms of complex signals, $expleft(jthetaright)$ is the phase rotation of the middle sample while $expleft(-jthetaright)$ can be taken as common from the terms in the brackets.
In conclusion, as long as there is a conjugate product being taken between the complex samples having the same phase rotation, the TED is essentially carrier independent and Gardner TED is not unique in this regard. Having said that, the presence of a rotating phase in the constellation can perturb the timing error detectors to some extent in terms of the jitter and acquisition time.
Final Remarks
There are some final comments in regards to this discussion as follows.
- There has been a long standing confusion in synchronization community regarding the non-data-aided early-late and Gardner timing error detectors that has been clarified here.
- For an example of a timing recovery system that can be implemented after carrier recovery at 1 sample/symbol, see the Mueller and Muller algorithm.
- Feedforward techniques that do not require a PLL are also possible such as digital filter and square timing synchronization.
E808-0001-05
Detection Description
Remedy
E808-0002-05
Detection Description
Remedy
E811-0000-05
Detection Description
Remedy
E880-0001-00
Detection Description
Remedy
Zero cross signal detection error
After the start of the zero cross signal detection, the frequency between 43 Hz and 67 Hz could
not be detected for 0.5 consecutive sec.
[Related parts]
— Harness between the DC Controller PCB (J115) and the AC Driver PCB (J322)
— Power Supply Unit
— DC Controller PCB
[Remedy] Check/replace the related harness/cable, connector and parts.
[Reference]
Before replacing the DC Controller PCB, back up the service mode data and restore the backup
data after the replacement so the data may be able to be protected.
— Backup: COPIER (LEVEL2)> FUNCTION> SYSTEM> DSRAMBUP
— Restoration: COPIER (LEVEL2)> FUNCTION> SYSTEM> DSRAMRES
Zero cross signal detection error
Error due to disconnection of the fixing loopback signal
After the frequency of zero cross signal fell into the specified frequency band, the frequency
between 43 Hz and 67 Hz could not be detected for 0.5 consecutive sec.
[Related parts]
— Harness between the DC Controller PCB (J121) and the Fixing Drawer (J1001)
— DC Controller PCB
— Fixing Unit
[Remedy] Check/replace the related harness/cable, connector and parts.
[Reference]
Before replacing the DC Controller PCB, back up the service mode data and restore the backup
data after the replacement so the data may be able to be protected.
— Backup: COPIER (LEVEL2)> FUNCTION> SYSTEM> DSRAMBUP
— Restoration: COPIER (LEVEL2)> FUNCTION> SYSTEM> DSRAMRES
Fuse in the Fixing Fuse PCB blowout error
The fuse in the Fixing Fuse PCB was not blown out at power-on.
[Related parts]
— Fixing Fuse PCB (UN31)
— Fixing Unit
— DC Controller PCB (UN049)
[Remedy] Check/replace the related harness/cable, connector and parts.
[Reference]
Before replacing the DC Controller PCB, back up the service mode data and restore the backup
data after the replacement so the data may be able to be protected.
— Backup: COPIER (LEVEL2)> FUNCTION> SYSTEM> DSRAMBUP
— Restoration: COPIER (LEVEL2)> FUNCTION> SYSTEM> DSRAMRES
Controller Fan error
It was detected that the Controller Fan was locked.
[Related parts]
— Main Controller Cooling Fan
— Main Controller PCB (UN05)
[Remedy] Check/replace the related harness/cable, connector and parts.
[Reference] Before replacing the Main Controller PCB, back up the service mode data (approx. 2
min) and restore the backup data after the replacement so the data may be able to be protected.
— Backup: COPIER (LEVEL2)> FUNCTION> SYSTEM> RSRAMBUP
— Restoration: COPIER (LEVEL2)> FUNCTION> SYSTEM> RSRAMRES
461
7. Error/Jam/Alarm
RE: Problem in zero cross detection?
2006/05/15 10:38:13
(permalink)
You seem to have problems in many different layers, that may interact and overshadow each other.
As a first guess, I would say your main problem is EMI. That is almost always a safe bet in AC-connected and thyristor switching equipment. How is your gate firing circuitry? Is the thyristor close to the PIC? Do you have a parallel VDD/VSS power distribution, or even a ground plane for the PIC?
The second most frequent plague is bad or insufficient power supply decoupling for the PIC. If you are driving large capacitice loads with the PIC (power mosfet gates, for example), the load switching can drain the PIC decoupling cap and expose the PIC core to unexpected current starvation during clock switching, if the power supply is not very low impedance. It is much easier than it seems to have a high impedance power supply, and impedances of 25ohms to 75ohms are not uncommon. You must use low esr X7R multilayer ceramic caps of no less than 100nF for each pic VDD/VSS pair of pins, and place the cap very close to the pin. If high capacitive loads are being sourced, place a 1µF to 10µF ceramic capacitor near the PIC.
Another possible source of error is board layout. You said that your AC line is transformer-isolated. If the transformer is operating lightly loaded, it can be succeptible to inductive coupling from high/fast EMI noise. The transformer may also show phase delay respecting to the actual zero-cross point, and the AC switching transients may be shifted and distorted by the coupling transformer. In that case, the PIC may be switching the thyristor too far on the cycle, without enough load hold current to guarantee the thyristor latching.
Another possible problem is if you have a inductive load being driven by your thyristor. In that case, the voltage zero-cross will not be in phase with the load current cross, and this may give the PIC with too little phase marging. In this case, you may need to trigger a long pulse train for the whole remaining cycle, instead of a single pulse to guarantee the gate to latch even with severe inductive loads.
There is an alternative way of guaranteeing that the PIC will detect a perfect zero cross:
If you have a on-chip analog comparator, you can set the comparator internal reference to 0V (just select internal comparator VREF and turn off the VREF module). Then you can use a AC wave connected to the comparator input. Use a series limiting resistor and 2 low-leakage current schottky diodes in antiparallel to limit the AC voltage to {-250mV..+250mV}. You will have a clean simetrical zero cross interrupt with less than a few microseconds of phase delay.